A highly-accelerated volumetric brain examination using optimized Wave-CAIPI encoding

Abstract

BACKGROUND

Rapid volumetric imaging protocols could better utilize limited scanner resources.

PURPOSE

To develop and validate an optimized 6-minute high-resolution volumetric brain MRI examination using Wave-CAIPI encoding.

STUDY TYPE

Prospective

POPULATION/SUBJECTS

10 healthy subjects and 20 patients with a variety of intracranial pathologies

FIELD STRENGTH/ SEQUENCE

At 3T, MPRAGE, T2w SPACE, SPACE FLAIR and SWI were acquired at 9-fold acceleration using Wave-CAIPI and for comparison at 2–4-fold acceleration using conventional GRAPPA.

ASSESSMENT

Extensive simulations were performed to optimize the Wave-CAIPI protocol and minimize both g-factor noise amplification and potential T1/T2 blurring artifacts. Moreover, refinements in the auto-calibrated reconstruction of Wave-CAIPI were developed to ensure high-quality reconstructions in the presence of gradient imperfections. In a randomized and blinded fashion three neuroradiologists assessed the diagnostic quality of the optimized 6-minute Wave-CAIPI exam and compared it to the roughly 3× slower GRAPPA accelerated protocol using both an individual and head-to-head analysis.

STATISTICAL TEST

A non-inferiority test was used to test whether the diagnostic quality of Wave-CAIPI was non-inferior to the GRAPPA acquisition, with a 15% non-inferiority margin.

RESULTS

Among all sequences, Wave-CAIPI achieved negligible g-factor noise amplification (g_avg≤1.04) and burring artifacts from T1/T2 relaxation. Improvements of our auto-calibration approach for gradient imperfections enabled increased robustness to gradient mixing imperfections in tilted-FOV prescriptions as well as variations in gradient and ADC sampling rates. In the clinical evaluation, Wave-CAIPI achieved similar mean scores when compared to GRAPPA (MPRAGE: Ø_W=4.03, Ø_G=3.97; T2wSPACE: Ø_W=4.00, Ø_G=4.00; SPACE FLAIR: Ø_W=3.97, Ø_G=3.97; SWI: Ø_W=3.93, Ø_G=3.83) and was statistically non-inferior (N=30, p<0.05 for all sequences).

DATA CONCLUSION

The proposed volumetric brain exam retained comparable image quality when compared to the much longer conventional protocol.

INTRODUCTION

In an era of increasing medical imaging utilization and declining reimbursements for MRI exams (1,2), fast MR imaging techniques allow limited scanner resources to serve an increasing demand in several ways. Shortening the overall duration of the MRI exam facilitates increased patient throughput and reduces the chance of involuntary motion artifacts (3). In vulnerable populations such as pediatric or claustrophobic patients, fast MR imaging exams may also improve patient compliance and potentially obviate the need for sedation and its concomitant risks (4).

To limit the duration of each individual scan and reduce motion sensitivity, conventional imaging protocols often rely on thick-slice imaging (4–5 mm) as well as slice gaps (20–30%) that result in loss of information and partial-volume artifacts. Such approaches also lead to the need for redundant acquisitions at multiple imaging orientations to allow for multi-planar viewing. Furthermore, scan time is often further cut by reducing the spatial resolution along the phase- or partition-encoding directions and applying partial-Fourier techniques, often at the cost of smoothing and ringing artifacts.

Over the last decade, parallel imaging techniques such as GRAPPA (5) and SENSE (6) have been widely used in clinical practice to accelerate MRI acquisitions by taking advantage of the inherent image encoding information of modern multi-channel receiver arrays. Nonetheless, most clinical protocols apply only moderate parallel imaging acceleration (R = 2 or 3) to avoid image artifacts and large g-factor noise penalties. Nonetheless, these approaches have given rise to fast brain protocols comprised of 2D sequences (7,8). The CAIPIRINHA (Controlled Aliasing in Parallel Imaging Results in Higher Acceleration) approach has been developed to enable higher accelerations in parallel imaging. It modifies the k-space under-sampling pattern to increase the distance between aliased voxels and allows for a better use of the available coil sensitivity variations. CAIPIRINHA has been employed to reduce the scan time of 2D sequences using Simultaneous Multi-Slice (SMS) (9) as well as to speed up time-consuming 3D scans (10).

Advanced acquisition techniques such as echo-planar (EPI) or spiral imaging have been introduced to further reduce the scan time by acquiring a large portion of k-space per readout. This enables high temporal and spatial resolution, which makes it particularly useful for dynamic applications such as cardiac, functional or diffusion imaging. However, these techniques are very susceptible to magnetic field strength variations (caused by inappropriate shimming or chemical shifts) which may lead to spatial shifts, geometric distortions and signal dropout in EPI or blurring artifacts and signal voids in spiral imaging. Several strategies have been proposed to address these issues. Dividing the data acquisition into multiple shots (11,12) and/or employing parallel imaging (13–15) to shorten the readout duration was shown to improve the image quality. This enabled very rapid clinical brain exams with multi-contrast information to be available in just a few minutes of scan time (16,17).

The work in this contribution focuses on the Wave-CAIPI (18) acquisition technique which synergistically combines and extends two controlled aliasing approaches, 2D-CAIPI and Bunch Phase Encoding (BPE) (19) to achieve controlled aliasing in all three spatial directions (x, y, z). This allows Wave-CAIPI to take advantage of the full 3D coil sensitivity information of multi-channel arrays which was shown to enable an order of magnitude acceleration for both SMS and 3D imaging sequences (18,20,21) with negligible g-factor noise amplification using commercial 32-channel receiver coils at 3T. As Wave-CAIPI traverses k-space in a line-by-line manner with constant velocity along the readout (k_x) it also does not exhibit undesirable image distortion/blurring artifacts from magnetic field strengths variations (20). The key features of the Wave-CAIPI technique include i) the development of an efficient parallel imaging reconstruction strategy (18) and ii) an automated gradient calibration method that can estimate Wave gradient trajectory errors caused by system imperfections on the fly without need for calibration scans (22).

The goal of this work is to validate the feasibility of the Wave-CAIPI encoding to achieve a 6-minute volumetric brain exam employing the principal clinical contrasts (T1, T2, inversion recovery T2, and T2*/SWI) with high, mostly isotropic spatial resolution. We assess the clinical feasibility of the protocol to maintain adequate image quality while substantially reducing scan time.

MATERIALS AND METHODS

Overview Of The Wave-CAIPI Acquisition And Reconstruction

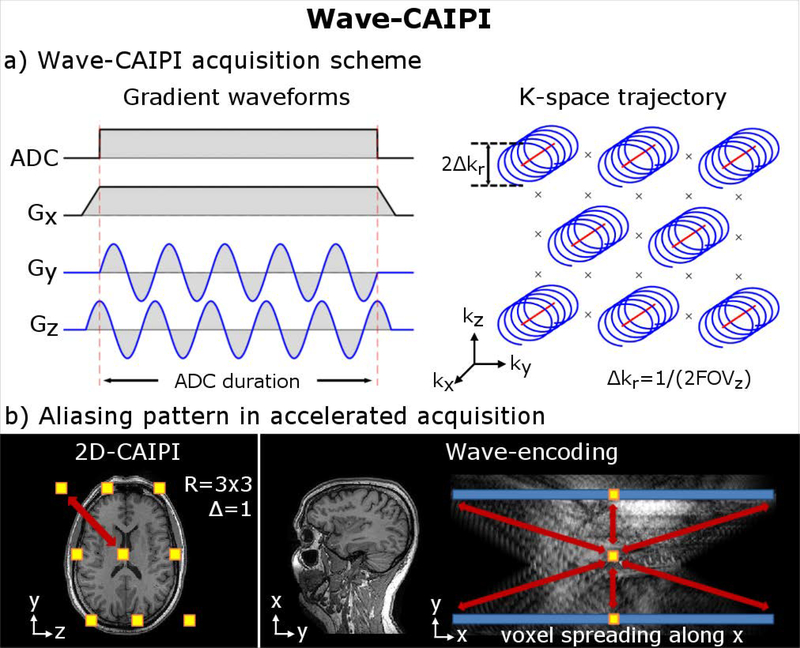
Wave-CAIPI utilizes a staggered k_y-k_z under-sampling of 2D CAIPIRINHA to create controlled aliasing along the y-z plane. It also extends the use of the sinusoidal g_y gradient of BPE into both g_y and g_z directions with a quarter cycle shift between them to create a corkscrew trajectory in k-space (Fig. 1a). This causes a voxel-spreading effect along the readout (x) direction in image space, where the amount of spreading varies linearly as a function of the y and z positions. In an accelerated acquisition, this spreading adds a controlled aliasing effect along x to supplement the controlled aliasing along y and z from 2D-CAIPIRINHA (Fig. 1b). Therefore, controlled aliasing in all three spatial directions is achieved. This both increases the distance between the aliasing voxels and allows the full use of the 3D coil sensitivity information of modern multi-channel receiver arrays in the un-aliasing process. The result is high accelerations with good reconstruction and minimal g-factor-related signal-to-noise (SNR) penalty (18,21).

Figure 1.

(a): Wave-CAIPI encoding employs sinusoidal gradients during the readout to achieve a corkscrew trajectory in k-space (corkscrew radius Δk_r). At R=3×3, the center position of each corkscrew is arranged in a staggered pattern as per 2D-CAIPIRINHA sampling at Δk_y and Δk_Z distances of 3/FOV apart. The Wave gradients then add an additional corkscrew modulation around this of size, e.g. Δk_r=1/2FOV. This leads to a voxel-spreading effect along the readout (x) direction in image-space, where the amount of spreading varies linearly as a function of the y and z coordinates. (b) The combined effect of 2D-CAIPIRINHA (shifted aliasing pattern, see yellow boxes) and Wave-encoding (voxel spreading along blue bar) increases the distance between collapsing voxels along all three spatial dimensions (see red arrows). This allows full use of the 3D sensitivity profile of multi-channel receivers in the un-aliasing reconstruction which improves the image quality and mitigates noise amplification.

For the image reconstruction, an efficient generalized SENSE model with a point spread function (PSF) framework (18) can be used which does not require k-space re-gridding:

$$M\sum _{\widehat{x}}PSF\left[\widehat{x},y,z\right]C_{i}m[x-\widehat{x},y,z]=\mathrm{w}\mathrm{a}\mathrm{v}{\mathrm{e}}_{\mathrm{i}}\left[x,y,z\right]$$ [1]

Here, m denotes the final image, C_i the coil sensitivity of the i-th channel, PSF the Wave point-spread-function, M a matrix that sums over collapsing voxels in an accelerated acquisition, and wave_i the measured scanner data in image space. (Note: the convolution from Eq. 1 can be solved more efficiently using a multiplication in hybrid space [k_x,y,z])

Although the PSF (from Eq. 1) is known theoretically, non-ideal gradient encoding can cause deviations from the desired sinusoidal k-space trajectory, which may result in substantial blurring or ghosting artifacts. To limit eddy currents, the Wave-encoding utilizes smooth sinusoidal gradients rather than e.g. triangle gradient waveforms which could have made better use of the available gradient slew rate but contain sharp turns. Moreover, for the estimation of gradient imperfections, we use an auto-calibrated gradient estimation approach (22), which is entirely data-driven and does not require additional calibration scans. This method relies on a compact representation of the Wave-encoding’s sinusoidal phase modulation and its imperfections, which can be described accurately using only two Fourier coefficients. We treat these as unknowns in a modified SENSE-based reconstruction and jointly solve for them and the un-aliased image pixels using an iterative joint optimization which minimizes the mean square error of the data consistency term. To speed up this non-linear optimization, the calculation is performed on nine representative test locations of aliased voxel groups (and not the whole 3D image). Once the gradient trajectory is estimated, the SENSE-based Wave-CAIPI image reconstruction (Eq. 1) is performed on the entire dataset to obtain the desired image.

In Appendix A2., we examined cases where hardware constraints prevented sparsity of the Wave-encoding’s sinusoidal phase modulation in Fourier domain which impaired the quality of the auto-calibrated gradient estimation approach. A small modification to the Wave-encoding gradients was developed to mitigate associated artifacts.

Optimization Of The Wave Corkscrew To Reduce Noise Amplification And Blurring Artifacts

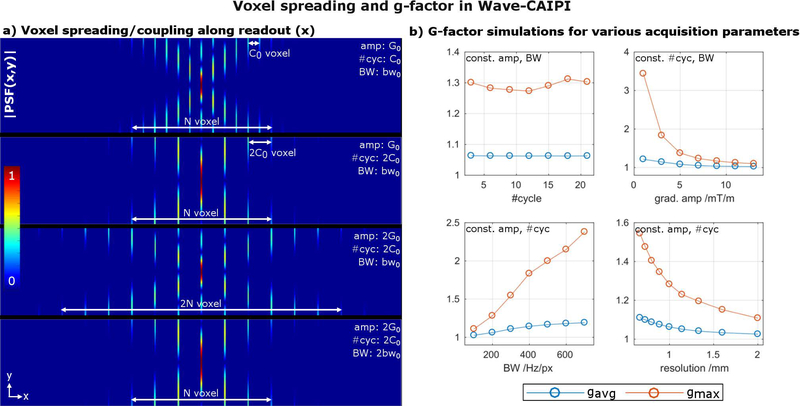
We tested several strategies to minimize both noise amplification (g-factor) and Wave-specific blurring artifacts that arise when there is a large signal modulation along the echo train due to T1 and T2 relaxations. First, we characterized the Wave corkscrew design parameters (Wave gradient amplitude, number of sinusoidal cycles and acquisition bandwidth) and their effect on the voxel spreading/coupling along the readout. For this, several point-spread-functions (PSF) were computed and the extent and shape of the impulse-response-function compared (Fig. 2a). To investigate the relation between spreading/coupling and noise amplification, g-factor maps were computed for a R=3×3 accelerated scan as a function of the acquisition parameters: number of sinusoidal cycles, Wave gradient amplitude, acquisition bandwidth and resolution (Fig. 2b). To reduce the large number of calculations needed to span this multi-dimensional space, each of these parameters was changed one at a time, while the others were held constant.

Figure 2:

(a) The sinusoidal gradients in Wave-CAIPI introduce a discrete voxel spreading/coupling effect along the readout direction illustrated by |PSF(x,y)|. To a good approximation, the spacing between coupled voxels is given by the #cycles, whereas the extent of voxel spreading for a given y or z coordinate is affected by the Wave gradient amplitude and acquisition bandwidth. (b) The g-factor reflects the results from a) and is mainly governed by the extent of voxel spreading (gradient amplitude, bandwidth, resolution) and nearly independent of the voxel coupling (#cycles).

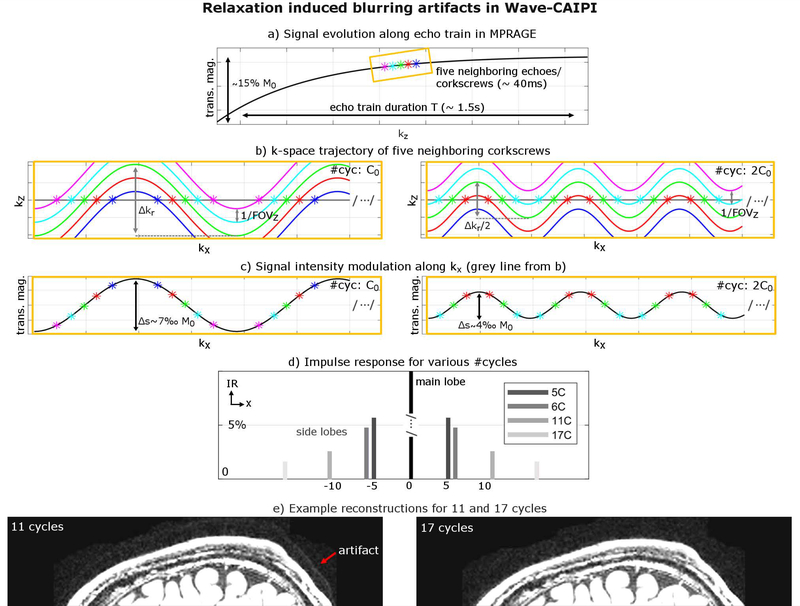
Besides g-factor, we also studied strategies to reduce Wave ringing/blurring artifacts caused by relaxation. 3D sequences usually acquire several lines of k-space within one repetition which leads to a signal modulation from T1 and/or T2 relaxation. This, in turn, causes blurring along the phase/partition (PE/PAR) encoding direction in conventional Cartesian imaging sequences. In Wave-CAIPI, this blurring along PE/PAR may also lead to artifacts along the readout, as the voxel spreading effect from Wave-CAIPI depends on the spatial y and z positions. In order to characterize and mitigate associated artifacts, we investigated the amount of data mixing of five neighboring echoes (corkscrews) acquired along the T1 signal recovery of an MPRAGE sequence, where standard linear partition encoding increments (kz) were applied during the inversion recovery. We computed the impulse response for different corkscrew radii through varying the number of sinusoidal cycles (5, 6, 11 and 17) while keeping the gradient amplitude fixed and compared the amplitude of the corresponding side lobes (Fig. 3). Additionally, we validated our findings in-vivo using a Wave-MPRAGE acquisition for 11 and 17 cycles.

Figure 3:

Signal modulation from T1/T2 relaxation can lead to blurring artifacts due to the mixing of various Wave corkscrews with different signal intensities. (a) Signal intensity of five neighboring corkscrews along the echo train in MPRAGE. (b) Doubling the #cycles while keeping all other acquisition parameters fixed halves the k-space radius Δk_r. (c) This reduces the amount of data-mixing along k_x and hence the amplitude of the signal intensity modulation Δs, which in turn minimizes side lobes in the corresponding impulse response as shown in (d). (e) in-vivo reconstructions reflect the simulation results and show reduced artifacts for 17 cycles (without sacrificing g-factor performance).

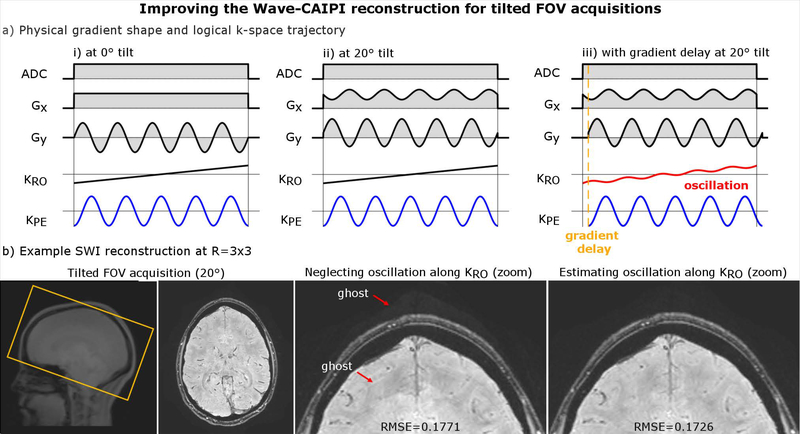
Reconstruction Model For Tilted-FOV Acquisitions

In clinical routine, the imaging Field-of-View (FOV) is often tilted to fit the desired region of interest, which can be achieved by linearly mixing the (x, y, z) gradients. In a Wave-CAIPI acquisition, a tilted FOV results in oscillating Wave gradient waveforms on all physical gradient axes, rather than just along y and z (Fig. 4a). Nevertheless, the k-space traversal along the logical readout, phase- and partition-encoding directions remains unchanged which suggests that the Wave-CAIPI reconstruction should not be affected. However, in practice, gradient hardware imperfections can be different for the x, y and z gradients causing the readout (x) k-space traversal to be not strictly linear but superimposed with a small portion of the sinusoidal k-space traversal from the phase/partition encoding direction. As this modulation cannot be captured by Eq. 1., we developed a modified Wave-CAIPI reconstruction with additional degrees of freedom to capture variations along all logical axes

$$M\sum _{\widehat{x}}PSF\left[\widehat{x},x,y,z\right]C_{i}m[x-\widehat{x},y,z]=\mathrm{w}\mathrm{a}\mathrm{v}{\mathrm{e}}_{\mathrm{i}}[x,y,z]$$ [2]

where with Eq. 2, the point spread function is now a function of x, y and z rather than just y and z as per Eq. 1. In the Appendix A.3, we further demonstrate that the frequency of the sinusoidal k-space sampling along k_x (compare Fig. 4a) is identical to k_y and/or k_z, but occurs at a much smaller amplitude. This allowed us to extend the auto-calibrated gradient estimation using two additional degrees of freedom and obtain a more accurate PSF capturing all relevant gradient imperfections. The performance of this technique was validated in-vivo using a 20°-tilted SWI scan and compared to the standard method using Eq. 1.

Figure 4:

(a) In tilted FOV acquisitions, gradient delays may introduce a small oscillation on top of the linear readout k-space traversal. (b) Neglecting this non-linearity will cause small artifacts in a Wave-CAIPI reconstruction (using Eq. 1), which can be mitigated by estimating associated imperfections on all three gradient axes (Eq. 2). This is also reflected in a RMSE reduction, as the improved model better fits to the acquired data.

Optimization Of The Wave-CAIPI Sequence Protocol And Evaluation

Wave-CAIPI was implemented into the following 3D prototype sequences: MPRAGE, T2w SPACE (variable flip angle 3D TSE), SPACE FLAIR and Susceptibility Weighted Imaging (SWI). Here, the order of the sampling of the individual partition/phase encoding corkscrews is kept in the same identical fashion as in standard acquisitions, with linear phase (PE) and partition (PAR) encoding increments throughout the acquisition. To achieve robust, high-quality imaging at R=9-fold acceleration, we optimized the acquisition parameter of each sequence based on findings from the proposed analyses above. The image reconstruction was performed online using our prototype acquisition/reconstruction framework (Siemens ICE environment) and took roughly 2 min after each acquisition using standard scanner CPU hardware. The required coil sensitivity maps for the SENSE-based reconstruction were computed online using ESPIRiT (23) and a low-resolution gradient echo (GRE) reference scan (24×24 lines of k-space, ~2 sec scan time). As motion may have occurred in between scans, this short calibration acquisition was acquired prior to each Wave-CAIPI sequence.

For benchmark of comparison, all sequences in the proposed brain protocol were also acquired using GRAPPA acceleration which is widely used in clinical routine. For healthy controls, a fixed protocol prescription was used (R=3×1 for MPRAGE and SWI, R=2×2 for SPACE T2w/FLAIR), which can be achieved by GRAPPA without significant SNR loss and artifacts. This resulted in roughly 15 minutes of total scan time for the comparison protocol. For patients, scans at a lower acceleration (R=2×1) were used for the image quality comparison, as such acceleration is typically employed in standard clinical scans at our institution.

With Institutional Review Board approval and informed consent/ assent, in-vivo experiments were performed on 10 healthy individuals (6 male, 4 female, 24–36 years of age) and 20 patients with a variety of intracranial pathologies (12 male, 8 female, 25–85 years of age). Among the patients, 8 had brain tumors (all glioblastoma multiforme, GBM), 6 had white matter hyperintensities of presumed vascular origin (24), 3 had stroke and 1 had multiple sclerosis (MS). For brain tumor patients, MPRAGE was also acquired following gadolinium contrast administration. However, due to the small number of patients with post-contrast imaging (8), these scans were only used to show general feasibility but excluded from the statistical assessment of image quality. All scans were performed on 3T MRI scanners (MAGNETOM Skyra or MAGNETOM Prisma, Siemens Healthcare, Erlangen, Germany) using a Siemens 32-channel head coil.

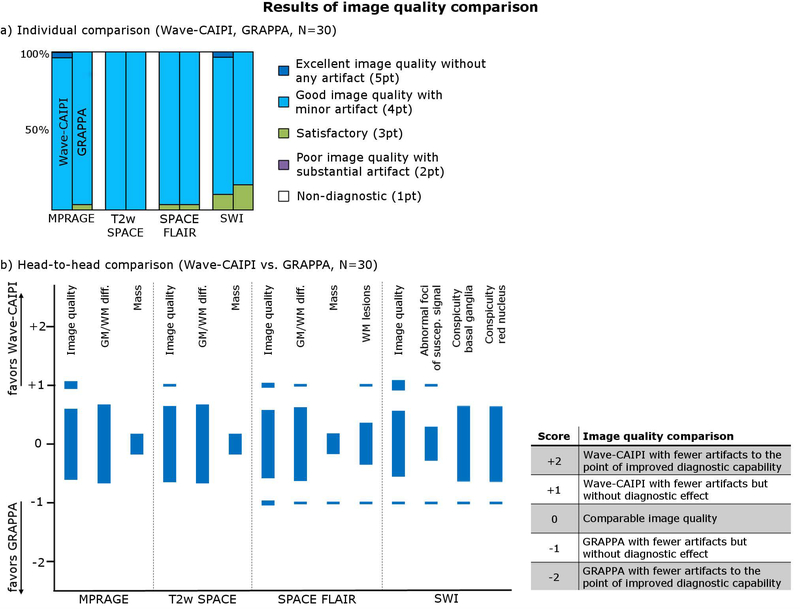
Three neuroradiologists (S.Y.H., 7 years of experience; M.G.L., 5 years of experience; J.C., 7 years of experience) assessed the diagnostic quality of the fast Wave-CAIPI exam and compared it to the GRAPPA protocol. All images were evaluated in a randomized and blinded fashion. The image quality of each scan was first evaluated individually using a point scale from 1 (Non-diagnostic) to 5 (Excellent image quality without any artifact) (see Fig. 7a). Wave-CAIPI- and GRAPPA-accelerated scans were compared head-to-head for: image quality, gray white matter differentiation, evaluation of mass lesions (if present), evaluation of white matter lesions (if present), evaluation of abnormal foci of susceptibility signal (if present), and conspicuity of basal ganglia, red nuclei, substantia nigra, and dentate nuclei (SWI only) using the scale described in Fig. 7b. Disagreements were resolved by consensus. For non-inferiority testing (25), a non-inferiority margin of 15% was chosen, with the null hypothesis that the proportion of cases where GRAPPA was preferred over Wave-CAIPI was > 15%. We used the Z statistic to calculate the probability of the GRAPPA sequence being preferred over the Wave-CAIPI sequence in more the 15% of cases, with a type 1 error rate (α) of 0.05. The null hypothesis was rejected if the one-sided p-value was less than 0.05. We performed this calculation only on those variables which were evaluated on more than 20 cases.

Figure 7:

(a) Results of individual image quality comparison for Wave-CAIPI and GRAPPA. (b) Results of head-to-head comparison (Wave-CAIPI vs. GRAPPA).

RESULTS

Subfigure 2a shows the voxel spreading/coupling effect along the readout for different Wave corkscrew parameters. The results in this subfigure demonstrate that the extent of the voxel spreading (i.e. controlled aliasing along x) is mainly determined by the Wave’s gradient amplitude and acquisition bandwidth and not by the number of Wave cycles. For example, increasing the gradient amplitude by two roughly doubles the extent of the PSF and the amount of spreading along the readout. In contrast, the number of Wave cycles determines the distance between coupled voxels along the readout without changing the extent of the voxel spreading. However, the spacing between coupled voxels along the readout does not appear to affect the impact of controlled aliasing as much as the extent of voxel spreading, as evidenced by the approximately constant g-factor as a function of the number of cycles but a strong dependency on the gradient amplitude, bandwidth and resolution (subfigure 2b) (see Discussion section for further explanations on resolution).

Figure 3a shows five neighboring echoes (corkscrews) along the T1 signal recovery curve of an MPRAGE acquisition that were acquired sequentially in a given TR. Doubling the number of sinusoidal cycles, halves the corkscrew radius Δk_r in k-space (see Fig. 3b), which reduces the number of echoes that mix along a line of k_x and thus decreases the signal intensity modulation as shown in subfigure 3c. This is also reflected in the calculated impulse response (Fig. 3d) showing roughly 3× smaller side lobes for 17 cycles in comparison to 5 cycles and reduced artifacts in the in-vivo MPRAGE scan for high number of cycles (Fig. 3e). Note that Wave blurring artifacts can also be reduced by increasing the bandwidth and/or decreasing the gradient amplitude; however, this will come at the cost of a higher g-factor noise penalty. A detailed quantitative analysis of Wave blurring artifacts in MPRAGE and T2w SPACE for various brain tissues is provided in Appendix A.1.

Figure 4 demonstrates artifacts that may arise in tilted-FOV acquisitions due to different gradient imperfections along G_x, G_y, and G_z. Subfigure 4a shows the physical gradient shape (G_x, G_y) and logical k-space trajectory (K_RO, K_PE) for Wave-encoding along the phase-encoding (PE) direction, with and without a FOV tilt prescription. Note, the analysis of playing out Wave-encoding along the partition-encoding (PAR) direction is analogous and omitted here. In the tilted case (ii), due to the rotation, the constant G_x and oscillating G_y gradient from (i) are now linearly superimposed and mixed across the two physical axes, but the k-space traversal along the logical readout (RO) and phase-encoding (PE) directions remains unchanged. In practice, physical gradients have slightly different hardware imperfections. A slightly non-linear response of the readout amplifier introduces a small oscillation in the k-space traversal, as depicted in (iii). The PSF framework from Eq. 1 neglects this effect, causing a small replica along the readout, as shown in Fig. 4b. However, this artifact can be removed using the modified reconstruction model based on Eq. 2, which estimates and accounts for gradient imperfections along all logical axes. This improvement is also reflected in a lower RMSE value, since the new model better fits to the acquired data.

Each of the Wave-CAIPI sequences was optimized individually and the resulting acquisition protocol is described in Table 1. In sequences acquired at a small readout bandwidth (e.g. 200 Hz/px in MPRAGE, 100 Hz/px in SWI) moderate gradient amplitudes (e.g. ~8 mT/m) provided sufficient voxel spreading to maintain low g-factor noise amplification (g_avg~1) at R=3×3 acceleration (compare Fig. 2b). While maximizing the number of cycles (without exceeding the gradient’s slew rate constraints) did not change the extent of voxel spreading or g-factor performance (see Fig. 2a,b), it helped to minimize blurring artifacts as demonstrated in Fig. 3d and Appendix A.1 (impulse response of Wave blurring <3% for various tissue types in MPRAGE). Moreover, in the flow-compensated Wave SWI sequence, a high number of cycles was used to reduce the additional velocity encoding from the Wave gradients during the readout and minimize potential flow-encoding artifacts (flow compensation can only ensure zero velocity encoding at k_x=0). Sequences acquired at a higher readout bandwidth (e.g. 592 Hz/px in SPACE T2w, FLAIR) required a larger gradient amplitude (~ 3×) when compared to the MPRAGE sequence to retain a similar voxel spreading effect. However, high bandwidth (short ADC duration) and gradient slew rate constraints prevented high number of cycles which may introduce blurring artifacts. A good trade-off was achieved by individually tuning the PE- and PAR-encoding axis. In sequences with linear k-space reordering (e.g. in SPACE T2w, FLAIR), signal modulation from T1/T2 relaxation occurs mostly along one physical gradient axis, therefore higher number of cycles were applied along this direction (impulse response of Wave blurring <2% for various tissue types in T2w SPACE; see Appendix A.1). Along the remaining axis (PAR), small number of cycles but large gradient amplitude was utilized to prevent large g-factor SNR loss.

Table 1:

Acquisition parameters for Wave-CAIPI and GRAPPA-accelerated sequences. Note that in Wave SWI two echoes were acquired in order to improve the SNR. For all GRAPPA-accelerated scans, integrated reference lines were used, whereas Wave-CAIPI utilized a short (~2 sec) external reference scan for the computation of the sensitivity maps. “Turbo factor” indicates the number of echoes (corkscrews) acquired per TR.

	MPRAGE		T2w SPACE		SPACE FLAIR		SWI
	GRAPPA	Wave	GRAPPA	Wave	GRAPPA	Wave	GRAPPA	Wave
Acceleration	3×1	3×3	2×2	3×3	2×2	3×3	3×1	3×3
Acquisition time [min]	4:14	1:14	2:38	1:19	4:07	2:00	3:35	1:29
FOV [mm3]	256×256×192		256×256×192		256×256×192		240×210×144
Resolution [mm]	1×1×1		1×1×1		1×1×1		0.8×0.8×1.5
Freq, PE, PAR dir.	S/I, A/P, R/L		S/I, A/P, R/L		S/I, A/P, R/L		A/P, R/L, S/I
TE1/TE2/TI/TR [ms]	3.5/−/1100/2500		104/−/−/3200		104/−/−/5000		21/−/−/30	19/36/−/46
Turbo factor	192		270	252	267	252	-
Bandwidth [Hz/px]	200		592		592		100
ADC duration [ms]	5.07		1.69		1.69		10.02
Wave: amp [mTm−1] (PE, PAR)	-	8, 8	-	8, 24	-	8, 24	-	8,8
Wave: #cycles (PE, PAR)	-	17, 17	-	6, 2	-	6, 2	-	31, 31
Reference lines	24×24		24×24		24×24		24×24

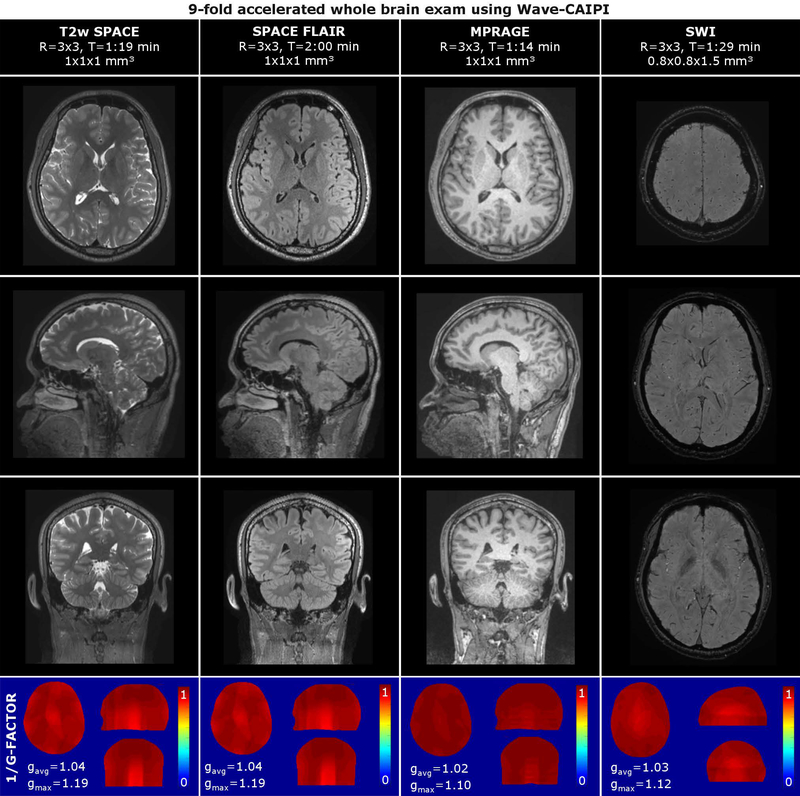
Figure 5 shows the results of the 6-minute Wave-CAIPI exam. Due to the isotropic resolution (1×1×1 mm³) and 3D encoding of the MPRAGE and SPACE sequences (T2w, FLAIR), these datasets can be reformatted and viewed in arbitrary orientations without loss of resolution. All scans achieved good SNR and contrast, despite 9-fold acceleration (R=3×3). The average g-factor was found to be close to 1 for all sequences (g_avg≤1.04). The peak g-factors occurred in the posterior aspect of the brain at the posterior end of the coil array where the coil sensitivities both drop off and become similar providing limited encoding ability for parallel imaging. The peak g-factors are highest for the SPACE sequences where a larger readout bandwidth was used.

Figure 5:

Volumetric 6-min Wave-CAIPI exam comprising MPRAGE, T2w SPACE, SPACE FLAIR and SWI at R=9-fold acceleration. Inverse g-factor maps are reported in the bottom of the figure.

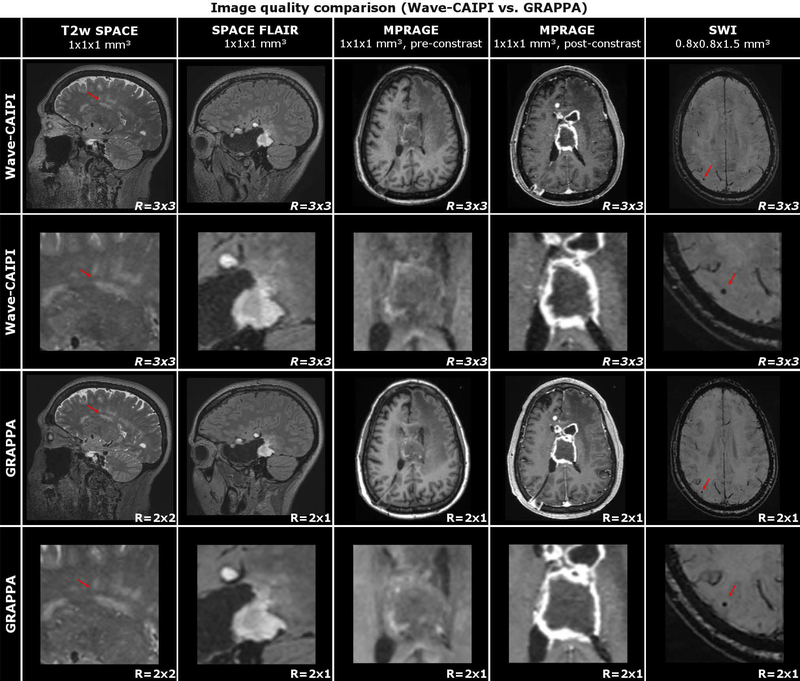
Figure 6 shows an image quality comparison between the Wave-CAIPI and the comparative exam in exemplary slices from four different patients with various intracranial pathologies. White matter hyperintensities are demonstrated in T2w SPACE, brain tumor in SPACE FLAIR and MPRAGE (pre- and post-contrast), and microbleeds in SWI. Despite the much higher acceleration, the Wave-CAIPI images show image quality and contrast which is comparable to the conventional acquisition. This is also reflected by the radiologist’s ranking summarized in Fig. 7 and Table 2 (raw scores are available in Table 3). In the individual comparison, Wave-CAIPI achieved similar mean scores when compared to GRAPPA (MPRAGE: Ø_W=4.03, Ø_G=3.97; T2wSPACE: Ø_W=4.00, Ø_G=4.00; SPACE FLAIR: Ø_W=3.97, Ø_G=3.97; SWI: Ø_W=3.93, Ø_G=3.83) and was statistically non-inferior (N=30, p<0.05 for all sequences). In the head-to-head comparison, the majority of scans also provided comparable quality and Wave satisfied the non-inferiority test for all of the variables that were statistically evaluated, including image quality and gray/white matter differentiation.

Figure 6:

Image quality comparison (Wave-CAIPI vs. GRAPPA) of four different patients with varying intracranial pathologies. In T2w SPACE, 61-year-old female with chronic small vessel disease. In SPACE FLAIR, 41-year-old female with history of right temporal craniotomy for resection of a glioblastoma. In pre- and post-contrast MPRAGE, 59-year-old female with a glioblastoma and intraventricular extension of tumor. In SWI, 74-year-old male with ischemic stroke and chronic white matter disease.

Table 2:

Adjudicated results from image quality assessment and non-inferiority test for the Wave-CAIPI exam

Individual comparison								Head-to-head comparison
	Score								Score
Sequence	1pt	2pt	3pt	4pt	5pt	Mean	P	Sequence	−2	−1	0	+1	+2	P
MPRAGE								MPRAGE
Wave-CAIPI	0	0	0	29	1	4.03	<0.01	Image quality	0	0	27	3	0	<0.01
GRAPPA	0	0	1	29	0	4.00		GM-WM diff.	0	0	30	0	0	<0.01
								Mass	0	0	8	0	0	-
T2w SPACE								T2w SPACE
Wave-CAIPI	0	0	0	30	0	4.00	<0.01	Image quality	0	0	29	1	0	<0.01
GRAPPA	0	0	0	30	0	4.00		GM-WM diff.	0	0	30	0	0	<0.01
								Mass	0	0	8	0	0	-
SPACE FLAIR								SPACE FLAIR
Wave-CAIPI	0	0	1	29	0	3.97	<0.01	Image quality	0	2	26	2	0	<0.01
GRAPPA	0	0	1	29	0	3.97		GM-WM diff.	0	1	28	1	0	<0.01
								Mass	0	1	7	0	0	-
SWI								WM lesion	0	1	16	1	0	-
Wave-CAIPI	0	0	3	26	1	3.93	<0.01	SWI
GRAPPA	0	0	5	25	0	3.83		Image quality	0	1	25	4	0	<0.01
5pt: Excellent image quality without any artifact 4pt: Good image quality with minor artifact 3pt: Satisfactory 2pt: Poor image quality with substantial artifact 1pt: Non-diagnostic								Abnormal foci of susc. signal	0	1	13	1	0	-
								Conspicuity basal ganglia	0	1	29	0	0	<0.01
								Conspicuity red nuclei, substantia nigra, dentate nuclei	0	1	29	0	0	<0.01
								+2: Wave-CAIPI with fewer artifacts to the point of improved diagnostic capability +1: Wave-CAIPI with fewer artifacts but without diagnostic effect 0: Comparable image quality −1: GRAPPA with fewer artifacts but without diagnostic effect −2: GRAPPA with fewer artifacts to the point of improved diagnostic capability

Table 3:

Raw scores from image quality assessment

Individual comparison						Head-to-head comparison
	Raw scores from readers 1/2/3						Raw scores from readers 1/2/3
Sequence	1pt	2pt	3pt	4pt	5pt	Sequence	−2	−1	0	+1	+2
MPRAGE						MPRAGE
Wave-CAIPI	0/0/0	0/0/0	0/0/0	28/13/30	2/17/0	Image quality	0/0/0	0/10/0	26/16/28	4/4/2	0/0/0
GRAPPA	0/0/0	1/0/0	1/0/2	28/6/28	0/24/0	GM-WM diff.	0/0/0	1/7/0	29/22/30	0/1/0	0/0/0
						Mass	0/0/0	0/2/0	8/11/8	0/0/0	0/0/0
T2w SPACE						T2w SPACE
Wave-CAIPI	0/0/0	0/0/0	0/0/0	30/5/30	0/25/0	Image quality	0/0/0	0/0/0	29/25/29	1/5/1	0/0/0
GRAPPA	0/0/0	1/0/0	0/0/1	29/8/29	0/22/0	GM-WM diff.	0/0/0	1/0/0	29/26/30	0/4/0	0/0/0
						Mass	0/0/0/	0/0/0	8/13/9	0/2/0	0/0/0
SPACE FLAIR						SPACE FLAIR
Wave-CAIPI	0/0/0	0/0/0	1/0/1	29/18/29	0/12/0	Image quality	0/0/0	2/11/1	26/11/29	2/8/0	0/0/0
GRAPPA	0/0/0	1/0/0	2/1/0	27/10/30	0/19/0	GM-WM diff.	0/0/0	1/5/0	28/22/30	1/3/0	0/0/0
						Mass	0/0/0	1/2/1	7/2/7	0/1/0	0/0/0
SWI						WM lesion	0/0/0	1/1/1	15/14/18	1/4/0	0/0/0
Wave-CAIPI	0/0/0	0/0/0	4/0/5	25/11/25	1/19/0	SWI
GRAPPA	0/0/0	1/0/0	6/1/5	23/10/25	0/19/0	Image quality	0/0/0	4/5/2	22/15/25	3/10/3	1/0/0
5pt: Excellent image quality without any artifact 4pt: Good image quality with minor artifact 3pt: Satisfactory 2pt: Poor image quality with substantial artifact 1pt: Non-diagnostic						Abnormal foci of susc. signal	0/0/0	1/1/1	14/13/14	1/3/0	0/0/0
						Conspicuity basal ganglia	0/0/0	1/12/0	29/17/30	0/1/0	0/0/0
						Conspicuity red nuclei, substantia nigra, dentate nuclei	0/0/0	1/8/0	29/21/30	0/1/0	0/0/0
						+2: Wave-CAIPI with fewer artifacts to the point of improved diagnostic capability +1: Wave-CAIPI with fewer artifacts but without diagnostic effect 0: Comparable image quality −1: GRAPPA with fewer artifacts but without diagnostic effect −2: GRAPPA with fewer artifacts to the point of improved diagnostic capability

DISCUSSION

We demonstrated a 6-minute high-resolution whole-brain exam using Wave-CAIPI encoding which overall retained the diagnostic image quality of a much longer (~3×) conventional protocol. The addition of the Wave readout created a more complex optimization approach which we addressed with extensive simulations. In a small blinded clinical comparison study, three radiologists evaluated the diagnostic quality between the two acquisition techniques. Based on the statistical analysis, Wave-CAIPI yielded non-inferior diagnostic quality when compared to GRAPPA, in particular when assessing image quality and gray/white matter differentiation. Abnormalities were also evaluated as part of the head-to-head comparison but excluded from statistical testing because of the small number of cases available in this study. The radiologists’ scores for the small number of cases with clinical pathology were similar, which is promising and suggestive of similar performance but requires further evaluation in larger more comprehensive clinical studies.

Previous studies have demonstrated the benefits of accelerated brain MRI protocols using echo-planar imaging for the evaluation of ischemic stroke (17) as well as parallel imaging for general neurological indications in the inpatient setting (7)(26). We anticipate that the Wave-CAIPI exam will provide several advantages over conventional techniques beyond faster acquisition. In comparison to conventional 2D slice-by-slice imaging, the 3D exam offers the potential for increased diagnostic information from avoiding a low-resolution direction or slice gaps. The isotropic resolution provides multi-planar viewing in arbitrary orientations eliminating the need for redundant acquisitions in other planes. In motion-prone populations, we expect increased patient compliance and comfort with the Wave-CAIPI exam, as each scan only takes about 1–2 minutes of scan time.

Several design strategies were investigated and implemented in order to achieve high-quality imaging with good SNR and minimal artifacts. We investigated the effect of the Wave parameters on the amount of voxel spreading and g-factor performance, and found that noise amplification is mainly determined by the Wave’s gradient amplitude and is relatively independent of the number of sinusoidal cycles. This can be explained intuitively by recognizing that the gradient amplitude controls the slope of the sinusoidal phase modulation imparted along k_x. To the first order, this modulation can be approximated by triangle Waves, made up of interspersed positive and negative linear phase ramps. The slope of this linear modulation then determines the extent of voxel spreading in image domain along the positive and negative x direction. Increasing the gradient amplitude increases the amount of phase accumulation between subsequent samples along k_x which in turn increases the overall amount of voxel spreading in the image domain. In contrast, a higher number of cycles (assuming fixed gradient amplitude) only reduces the radius of the k-space corkscrew without affecting the slope of phase modulation. This hardly changes the g-factor but determines the coupling of voxels along the readout. Analogously, higher readout bandwidth (all other parameters being fixed) results in a shorter ADC dwell time (for a given FOV) and hence reduced slope. Similarly, higher spatial resolution increases the overall extent of k-space that is traversed which also reduces the relative slope, causing higher g-factor penalty. While the explanations given in this section provide an intuitive understanding of the relationship between the Wave corkscrew parameters, voxel spreading/coupling and g-factor noise amplification, it does not ultimately exclude g-factor sub-optimality as each parameter was optimized one at a time. A more exhaustive g-factor search may lead to better performance.

Besides noise amplification, we also optimized the Wave-CAIPI sequences to mitigate artifacts arising from relaxation during the encoding. In the qualitative and quantitative analyses, we demonstrated that the interaction of different Wave corkscrews with varying signal amplitudes during PE and PAR encodings causes blurring artifacts due to T1/T2 relaxation. However, increasing the number of Wave cycles while holding the gradient amplitude constant (smaller corkscrew radius in k-space) was found to reduce the amount of mixing and mitigated associated artifacts to a negligible level without compromising on g-factor performance, as shown in the in-vivo example. For high bandwidth acquisitions (such as in the SPACE sequences, T2w and FLAIR), slew rate constraints of the gradient hardware may impede the use of a high number of cycles with sufficient gradient amplitude. In these cases, individually optimizing the Wave parameters for each gradient axis (corkscrew with elliptical k-space transversal) was found to improve results, both in simulations and in-vivo experiments.

We solved several technical challenges in the Wave-CAIPI acquisition and reconstruction framework to ensure high-quality imaging. Improvements of the auto-calibrated trajectory estimation ensured high accuracy and robustness for arbitrary protocols. Furthermore, we developed and validated an improved Wave-CAIPI reconstruction model that enables tilted-FOV acquisitions in the presence of hardware imperfections. This is particularly important for the SWI sequence, where the FOV is often tilted to capture the region of interest. Although the improved model increased the computational complexity, the online reconstruction on standard scanner hardware using a standard 32-channel head coil required less than 2 minutes for whole-brain coverage. Even faster reconstruction times are anticipated from a GPU implementation.

The GRAPPA protocols used in this work were based on the ones used in clinical practice at our institution. This was chosen to ensure that the radiologists evaluating the image quality have comparison scans available which they are familiar with and comfortable to read. However, further optimization of these GRAPPA protocols is possible, particularly given that the SNR of the GRAPPA exam was higher than that of Wave-CAIPI. This should help achieve higher accelerations and reduce scan time. Possible optimizations include the use of 2D acceleration (in SWI and MPRAGE), CAIPIRINHA sampling, as well as the use of short external calibration scans as was used in Wave-CAIPI. Nonetheless, at the acceleration factor of R=9 as achieved by Wave-CAIPI, the GRAPPA based protocol would contain very high noise amplification and artifacts as previously demonstrated in (21).

A limitation to this initial clinical evaluation was the small number of patients as well as the fact that multiple diseases were evaluated simultaneously. As such the outcome of this study cannot claim non-inferiority for the diagnostic evaluation of a specific clinical pathology (e.g. GBM or MS). For this, a more rigorous diagnostic comparison targeting specific clinical indications will be required in future studies.

In conclusion, we utilized Wave-CAIPI to enable an encoding-intensive high-resolution protocol using mostly isotropic resolution. The data acquisition and image reconstruction of each imaging sequence was optimized to prevent large g-factor noise amplification and image artifacts. In a small series of patients and healthy volunteers, the diagnostic quality of the fast Wave-CAIPI exam was non-inferior to the comparison protocol with roughly 3× longer duration.

Supplementary Material

Supp FigS1

Figure S1: Blurring artifacts in MPRAGE and SPACE (T2w) were simulated quantitatively for gray matter (GM), white matter (WM) and cerebrospinal fluid (CSF). Based on the specific signal evolutions, impulse- response functions were computed for various numbers of sinusoidal cycles.

Supp figS2

Figure S2: Alignment between the ADC and Wave k-space trajectory (kz) is necessary to prevent side lobes (red) of the phase modulation in Fourier domain. In the auto-calibrated trajectory estimation these additional peaks cannot be determined accurately which causes ringing artifacts in the reconstructed images.

APPENDIX

A.1. Quantitative Analysis Of Wave Blurring Artifacts In MPRAGE And SPACE

Fig. 2b provides an intuitive picture and a qualitative understanding of blurring artifacts in Wave-CAIPI. In this section, we provide several simulations to quantitatively determine these artifacts in the MPRAGE and T2w SPACE sequences. For this purpose, signal evolutions were computed for gray matter (GM), white matter (WM) and cerebrospinal fluid (CSF) using Extended-Phase-Graph (27) and the sequence parameters from Table 1. The following approximate T1/T2 relaxation times were assumed GM=1400ms/90ms, WM=800ms/70ms, CSF=4000ms/300ms, which are in good agreement with (28). To quantitatively determine the effect on Wave blurring, impulse response functions for various numbers of sinusoidal cycles and gradient amplitudes were computed. The results of these simulations are depicted in Fig. S1. Note that in T2w SPACE the maximum achievable Wave’s gradient amplitude under consideration of the system slew rate constraint was used for all of the simulations to keep the g-factor as low as possible.

A.2. Optimization Of The Wave Gradient Sampling For Auto-calibrated Reconstructions

In this section, we examine cases where hardware constraints may impair the quality of our auto-calibrated gradient estimation. In MRI systems, the gradient raster time is typically fixed, while the ADC’s dwell time varies depending on the acquisition parameters. Figure S2 shows a scenario where the gradient raster time (ΔT_grad =duration of one gradient sample) is a non-integer multiple of the ADC’s dwell time (ΔT_ADC =duration of one ADC sample), causing the total gradient and ADC duration to differ slightly. In this case, the cosine Wave along G_z is not completed at the end of the ADC duration and the period of the resulting sinusoidal phase modulation is no longer an exact multiple of the readout duration. As a result, the Fourier transform of the phase modulation is not sparse but contains additional side-lobes (≤ 5‰ of the center frequency coefficient) as demonstrated in red in subfigure S2b. Modifying the frequency of the sinusoidal Wave gradient trajectory preserved the sparsity in Fourier domain and removed associated ringing artifacts in an auto-calibrated MPRAGE reconstruction as shown in subfigure Fig. S2c. However, changing only the gradient amplitude, would linearly scale the output of the Fast Fourier Transformation (FFT) without affecting the existence of side-lobes.

A.3. Wave-CAIPI K-space Traversal In Tilted-FOV Acquisitions

Many clinical sequences use a tilted FOV prescription to fit the desired imaging region of interest. However, as demonstrated in Fig. 4, different hardware imperfections of the physical gradient axes may lead to a non-linear k-space traversal along the readout direction which would lead to artifacts in a Wave-CAIPI reconstruction if not estimated accurately. In this section, we investigate how different delay times of the physical gradient axes as well as small deviations of the maximum gradient amplitude affect the resulting PSF. In practice, modelling these two imperfections seemed to capture a large portion of these reconstruction artifacts; however, including more parameters may further refine the image quality. Note that for simplicity Wave-encoding is restricted to the y direction only, but the calculation can also be generalized to both y and z.

A FOV tilt (angle of rotation ϕ) is achieved by multiplying the physical x and y gradient shape with a rotation matrix. In the presence of a constant readout gradient G_x and an oscillating Wave gradient G_y(t), the overall gradient trajectory played on the scanner is given by

$$\overrightarrow{G}(t)=\left[G_{x}cos\varphi -G_y\sin \left(\omega t\right)sin\varphi \right]{\overrightarrow{e}}_x+\left[G_{x}sin\varphi +\left(1+ϵ\right)G_y\sin \left(\omega \left(t-\Delta t\right)\right)cos\varphi \right]{\overrightarrow{e}}_y$$

Here, G_x and G_y denote the maximum amplitudes of the readout and Wave gradients, $\omega =\frac{2\pi C}{T}$ the frequency of the waveform, C the number of sinusoidal cycles per readout, T the ADC duration, t the current time point, and ${\overrightarrow{e}}_x,{\overrightarrow{e}}_y$ unit vectors in the direction of the physical gradients. Moreover, a small constant Δt was added to the time-dependent component of the y gradient, to account for different delay times between the physical x and y gradients. Analogously, ϵ was introduced to account for a small gradient amplitude deviation. Using a trigonometric identity, we obtain

$$\overrightarrow{G}(t)=\left[G_{x}cos\varphi -G_y\sin \left(\omega t\right)sin\varphi \right]{\overrightarrow{e}}_x+\left[G_{x}sin\varphi +\left(1+ϵ\right)G_y\left\{\sin \left(\omega t\right)cos\left(\omega \mathrm{\Delta }t\right)-sin\left(\omega \mathrm{\Delta }t\right)cos\left(\omega t\right)\right\}\cos \left(\varphi \right)\right]{\overrightarrow{e}}_y$$

As gradient delays (Δt ≈ 1–5 μs) are typically several orders of magnitude smaller than the ADC duration T, we apply a first order approximation for t > Δt

$$\begin{gathered} \overrightarrow{G}\left(t\right)=\left[G_{x}cos\varphi -G_y\sin \left(\omega t\right)sin\varphi \right]{\overrightarrow{e}}_x \\ +\left[G_{x}sin\varphi +(1+ϵ)G_y\left\{\sin \left(\omega t\right)-\omega \mathrm{\Delta }t\cos \left(\omega t\right)\right\}cos\varphi \right]{\overrightarrow{e}}_y \end{gathered}$$

Neglecting terms proportional to ϵΔt and transforming to the tilted acquisition coordinate system (${\overrightarrow{e}}_{RO},{\overrightarrow{e}}_{PE}$) yields

$$\overrightarrow{G}\mathrm{\prime }(t)=\left\{G_x-G_y\sqrt{{\left(\omega \mathrm{\Delta }t\right)}^2+{ϵ}^2}\cos \left(\omega t+{\mathrm{\phi }}_{\mathrm{R}\mathrm{O}}\right)cos\varphi sin\varphi \right\}{\overrightarrow{e}}_{RO}+G_y^{\mathrm{\prime }}\sin \left(\omega t+{\mathrm{\phi }}_{\mathrm{P}\mathrm{E}}\right){\overrightarrow{e}}_{PE}$$

The above result reveals that differences in delay times between the physical gradient axes as well as small gradient amplitude deviations introduce an oscillation along the readout direction. The frequency ω of this term matches the waveform along the phase encoding, but appears at a much smaller amplitude. While the resulting change in phase φ_PE and amplitude $G_y^{\prime }$ along the PE direction can be captured by Eq. 1, the additional oscillation along the readout requires a more complex model, such as described in Eq. 2.