Radiation Force as a Physical Mechanism for Ultrasonic Neurostimulation of the Ex Vivo Retina

Abstract

Focused ultrasound has been shown to be effective at stimulating neurons in many animal models, both in vivo and ex vivo. Ultrasonic neuromodulation is the only noninvasive method of stimulation that could reach deep in the brain with high spatial-temporal resolution, and thus has potential for use in clinical applications and basic studies of the nervous system. Understanding the physical mechanism by which energy in a high acoustic frequency wave is delivered to stimulate neurons will be important to optimize this technology. We imaged the isolated salamander retina of either sex during ultrasonic stimuli that drive ganglion cell activity and observed micron scale displacements, consistent with radiation force, the nonlinear delivery of momentum by a propagating wave. We recorded ganglion cell spiking activity and changed the acoustic carrier frequency across a broad range (0.5–43 MHz), finding that increased stimulation occurs at higher acoustic frequencies, ruling out cavitation as an alternative possible mechanism. A quantitative radiation force model can explain retinal responses and could potentially explain previous in vivo results in the mouse, suggesting a new hypothesis to be tested in vivo. Finally, we found that neural activity was strongly modulated by the distance between the transducer and the electrode array showing the influence of standing waves on the response. We conclude that radiation force is the dominant physical mechanism underlying ultrasonic neurostimulation in the ex vivo retina and propose that the control of standing waves is a new potential method to modulate these effects.

SIGNIFICANCE STATEMENT Ultrasonic neurostimulation is a promising noninvasive technology that has potential for both basic research and clinical applications. The mechanisms of ultrasonic neurostimulation are unknown, making it difficult to optimize in any given application. We studied the physical mechanism by which ultrasound is converted into an effective energy form to cause neurostimulation in the retina and find that ultrasound acts via radiation force leading to a mechanical displacement of tissue. We further show that standing waves have a strong modulatory effect on activity. Our quantitative model by which ultrasound generates radiation force and leads to neural activity will be important in optimizing ultrasonic neurostimulation across a wide range of applications.

Introduction

Ultrasonic neuromodulation has been demonstrated in the brains of human (Legon et al., 2014; Lee et al., 2015, 2016a; Monti et al., 2016), monkey (Deffieux et al., 2013; Wattiez et al., 2017), sheep (Lee et al., 2016b), rat (Younan et al., 2013), mouse (Tyler et al., 2008; Tufail et al., 2010; King et al., 2012, 2014; Li et al., 2016; Ye et al., 2016), and retina of salamander (Menz et al., 2013) and rat (Jiang et al., 2018). The capability of ultrasound to reach any brain structure noninvasively through the skull and the highly developed technology to deliver ultrasound make this approach promising both for basic studies of neural function and clinical applications. Yet results in different preparations have varied, including both excitatory and inhibitory effects. The development of this approach would benefit greatly from a quantitative understanding of the mechanisms of ultrasonic neuromodulation, allowing the process to be optimized in terms of efficacy of stimuli, efficiency, and spatiotemporal distribution of effects.

In the process of transduction of a stimulus into a biological response, one can distinguish the physical mechanism, such as acoustic pressure or thermal energy from the biophysical mechanism that senses that energy, including changes in membrane capacitance or particular ionic channels. Here we focus on the physical mechanism by which an acoustic wave is converted into an effective stimulus for a neuron, a process that is currently not understood. The leading candidates for physical mechanism are radiation pressure, the process by which an absorbed or reflected wave delivers momentum, and cavitation, which includes the stable or unstable formation of bubbles, creating a mechanical disturbance, and thermal energy.

Radiation force is a nonlinear effect proportional to the acoustic wave amplitude, thus creating a continuous, nonoscillating force for a stimulus of constant amplitude (Rudenko et al., 1996). By this mechanism, a carrier wave with a frequency too high to have a direct biological effect can be converted into a low-frequency mechanical force with dynamics of the envelope of the wave. When radiation force is exerted on a liquid, this results in bulk flow of fluid known as acoustic streaming. Tissue attenuation increases with carrier frequency; therefore, radiation force and also heating will increase with frequency.

Cavitation can occur if the acoustic pressure wave becomes sufficiently negative, causing gas bubbles to form that oscillate at the carrier frequency (Nightingale et al., 2015). Inertial cavitation occurs when those oscillations change in size and eventually burst the bubble, creating a destructive violent event. In stable cavitation, the bubble does not burst and is hypothesized to produce safe neuromodulation. Cavitation is less likely at higher carrier frequencies because it becomes more difficult to sustain oscillations in the bubble.

In this study, we use optical imaging to measure displacements in the retina and vary the acoustic frequency to test which of these mechanisms is most likely. We find that ultrasonic stimulation in the retina is consistent with a model whereby radiation force produced micron-scale mechanical displacements. The acoustic frequency dependence is consistent with radiation force but inconsistent with cavitation. In addition, we see that standing waves influence the effects of ultrasound. We conclude that radiation force is the primary physical mechanism for ultrasound to stimulate the retina.

Materials and Methods

Experimental design and statistical analysis.

We conducted several different types of experiments for the purpose of establishing whether radiation force is the dominant physical mechanism responsible for ultrasonic neurostimulation; the details of these experiments are described below in the appropriate subsections. In terms of experimental design, our goal is to use at least two retinas from 2 different salamanders and record from at least 30 ganglion cells for electrophysiology experiments. For the imaging experiments, we used three retinas from 3 salamanders; for the 43 MHz electrophysiology, we used three retinas from 3 salamanders; for 15 MHz recordings, we used two retinas from 2 salamanders; and for lower frequency recordings (2.9 MHz, 1.9 MHz, and 500 kHz), we used two retinas from 2 salamanders. For electrophysiological recordings, the number of cells for each experiment is indicated either in the figures or in the figure legends. Data are available upon request.

All statistics used have well-known definitions and require no additional information (e.g., mean, SEM, squared Pearson correlation coefficient r²).

Electrophysiology.

Multielectrode array (MEA) recordings were performed as described previously (Manu and Baccus, 2011) The isolated retina of the tiger salamander of either sex was adhered by surface tension to a dialysis membrane (Spectrapor 7 50000, Thermo Fisher Scientific) attached to a custom Delrin holder. The holder was placed on a motorized micromanipulator (MP-385–2, Sutter Instruments) and lowered onto a multielectrode electrode array (ThinMEA, Multichannel Systems) ganglion cell side down. For 43 MHz experiments where the focal spot < 100 μm, a high-density array was used (5×6, 10 μm diameter electrode, 30 μm spacing). For all other lower-frequency experiments, a lower density array was used (8 × 8, 10 μm diameter, 100 μm spacing), which better matches the focal spot size. Full-field flashes from a red LED were sometimes used to verify that ganglion cells were responding normally to visual stimuli, especially if conditions of ultrasound stimulation did not show a response. Error bars are SEM unless otherwise noted.

Ultrasound transducers and stimuli.

We used four different transducers, 43 MHz (custom), 15 MHz (Panametrics, A319S, 0.5 diameter, 2 inch focal length), 2.25 MHz (Olympus, V305) and 0.5 MHz (Olympus, V301), to span a large frequency range. The 2.25 MHz transducer had a relatively wide bandwidth and was operated at multiple frequencies (1.9 and 2.9 MHz). Transducers (15, 2.25, and 0.5 MHz) were fitted with a water-filled cone that was sealed with either Parafilm (2.25 and 0.5 MHz) or plastic wrap (15 MHz) and mounted on a motorized micromanipulator (MP-385–2, Sutter Instruments). A camera from below was used to position the transducers so that the center of the focal spot was in the center of the array. Transducers were lowered into the bath above the retina, and height was adjusted so that the focal point was on the retina. Ultrasound propagated from the transducer, through the water-filled cone, perfusion fluid, dialysis membrane, retina, and then reflected off the glass/metal surface of the MEA (see Fig. 1). A function generator (model 8116A, Hewlett-Packard) provided the carrier frequency that was gated by the analog output of a National Instruments DAQ board. This signal was amplified by a 50 dB RF power amplifier (model 320L, Electronic Navigation Industries) and fed into the transducer. A hydrophone was used to measure power output from the water-filled cones into a tank of water as a function of three spatial dimensions (see Fig. 2), except for 43 MHz, which is too high for a conventional hydrophone, and for which power was extrapolated from hydrophone measurements at 20 MHz. All power measurements are the spatial peak, I_SP, because with a 100% duty cycle (continuous wave [CW]) I_SPPA = I_SPTA (i.e., pulse average = temporal average) in free space (water tank). These free space hydrophone measurements are not corrected for the reflection off of the MEA under experimental conditions and the resulting standing wave. The free space measurements we have provided are useful for reproducing our results and making relative comparisons across carrier frequencies. However, these measurements do not accurately describe the actual power distributed in space under experimental conditions where we have standing waves between the transducer and the MEA. Ultrasound transducer characteristics, such as numerical aperture, efficiency, and acoustic impedance matching, will all play a role in determining the standing waves that result from reflection off the MEA. CW is used for all experiments, so the only relevant parameters are carrier frequency, power, pulse duration, and repetition rate, which are given for each experiment.

Figure 1.

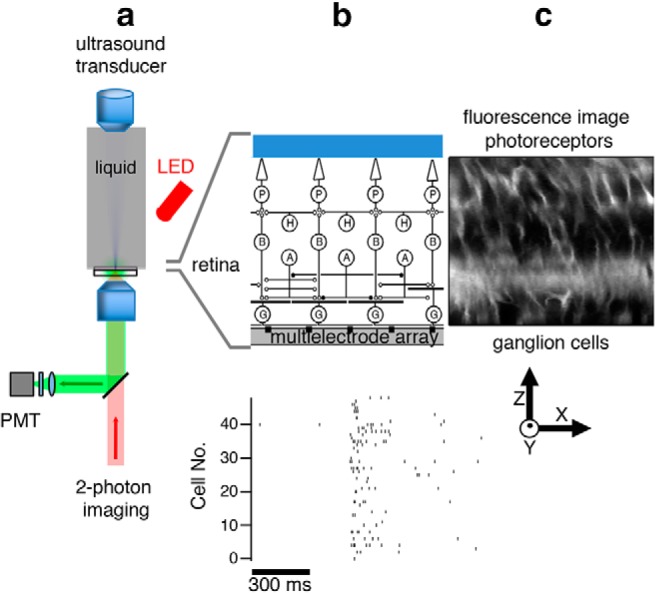
Experimental configuration for ultrasonic stimulation and optical measurement in the retina. a, Schematic diagram of ultrasound transducer mounted vertically and immersed in perfusion fluid with the focal point on the retina. Two-photon imaging is performed from below while a red LED from above can be used for visual stimulation. b, Top, Expanded view showing that the retina placed ganglion side down on an MEA. P, Photoreceptors; H, horizontal cells; B, bipolar cells; A, amacrine cells; G, ganglion cells. The ultrasound field spans the width of the entire retina. The ultrasound field in free space is shown in Figure 2. Bottom, A population of ganglion cell spiking activity recorded with an MEA in response to ultrasound. c, Retinal image using the dye FM4–64 (showing cell membranes and processes) is a slice in the X-Z plane.

Figure 2.

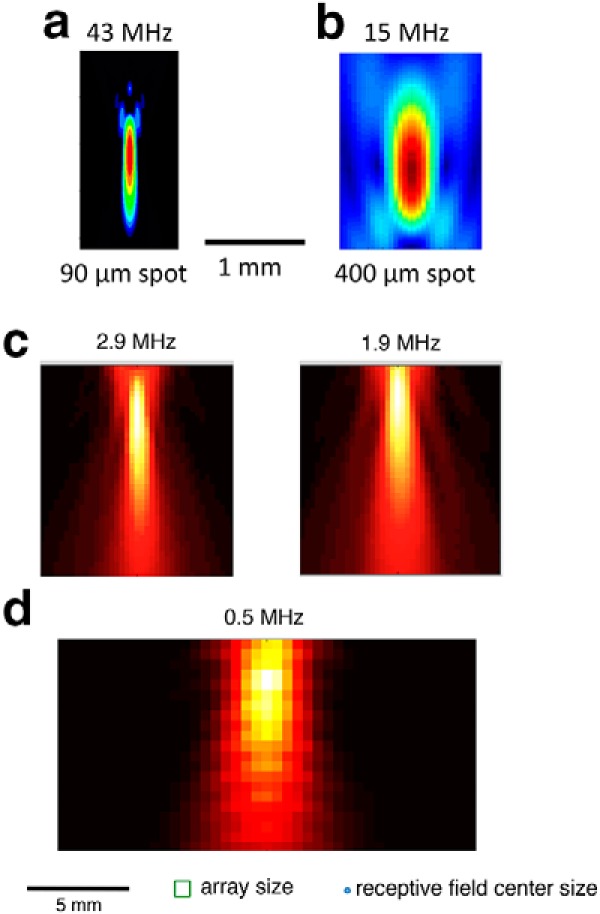
Spatial distribution of intensity for different transducers and carrier frequencies. a, X-Z plot of intensity for 43 MHz transducer, having a 90 μm lateral and 1330 μm longitudinal focal volume (−3 dB). b, 15 MHz transducer. Scale bar: a, b, 1 mm. c, A 2.25 MHz transducer was operated at two different frequencies. Left, 2.9 MHz. Right, 1.9 MHz. d, 0.5 MHz transducer. Scale bar: c, d, 5 mm. Bottom, Array size and typical ganglion cell receptive field center size.

Imaging.

The styryl dye FM4–64 was bath-applied by immersing the isolated retina in a concentration of 82 μm (100 μg in 2 ml) FM4–64 in oxygenated Ringer's for 1 h before placement on the MEA. This dye inserts itself in the outer leaflet of the cell membrane where it becomes fluorescent, allowing us to image changes in position and shape of the cell membrane with ultrasonic stimulation.

A custom two-photon laser scanning microscope in the inverted configuration was used to image the retina during ultrasonic stimulation. A simplified diagram is shown in Figure 1a. Excitation at 970 nm from a Ti:sapphire laser (Tsunami, Spectra-Physics) was focused on the retina by a × 40 1.2 NA (Carl Zeiss) objective and the epifluorescence passed through an emission filter (FF01–725/150–25) and laser-light blocking filter (Semrock, FF01–680/SP-25), which was then collected by a PMT (H7422-P, Hamamatsu). The imaged area was selected to cover the ultrasound focal spot. We recorded a frame of 512 × 128 pixels at a rate of 18.6 frames per second for 1000 frames at one level in the retina. We started at the MEA and collected images in 1 μm steps for a total of 120 μm, covering the entire retina in depth, imaging 1000 frames at every step. The average laser power was set to 10 mW. ScanImage (now supported by Vidrio Technologies) software was used to record images.

The mirror position of the scanning galvanometers was recorded on the same computer that generates and records the ultrasound stimuli (1 s on, 1 s off, 40W/cm²), allowing us to compute the timing of the image at any pixel relative to the ultrasound stimulus. The laser scanning and ultrasound stimulus were desynchronized, such that any given pixel will be recorded at random times during the 2 s period of ultrasound stimulation. In theory, we can get temporal resolution approaching the dwell time of a single pixel with a sufficiently large dataset; in practice, we binned the data in 10 ms bins for a sufficient signal-to-noise ratio. To compute vector fields reflecting the effect of ultrasound, we used unwarpJ, which is an imageJ plug-in that performs spline-based elastic registration of two images. We compared steady-state images in the ultrasound on and off conditions.

Because of the large area of scanning at a high frame rate (20 Hz), we corrected for most distortion at the edge of the frame by computing the average actual mirror position based on control experiments recording mirror positions with slow mirror velocities and no distortion and then recording actual mirror positions at high velocities. This distortion does not affect our analysis, which is based on changes in the images as a function of time in the cycle of ultrasonic stimulation.

Modeling radiation force to explain retinal displacement.

To model the observed displacement as an effect of radiation force, we assumed the ultrasound field at 43 MHz was transmitted through a multilayered medium composed of water, retina, glass, and air, and calculated assuming 40 W/cm² incident power. The retina layer was 150 μm thick, and the glass layer was 180 μm thick. Water and air media were assumed to be half-spaces. The model includes the following: acoustic streaming (the bulk flow of fluid from radiation force acting on the liquid medium between the transducer and the retina), radiation pressure on the retina-water and retina-glass interfaces (Lee and Wang, 1993), radiation pressure from absorption in the retina, and the interference pattern that is a consequence of wave reflection off the MEA. The speed of sound and density parameters are standard values from the literature (Thijssen et al., 1985), the attenuation at 43 MHz was set at 4.01 dB/cm for water and 22.02 dB/cm for retina (de Korte et al., 1994). Estimated radiation pressures were then used in COMSOL Multiphysics finite element software to calculate the deformation of the retina in response to ultrasound. The retina was considered to be an incompressible material (i.e., Poisson ratio of 0.5). We determined the value of the elastic modulus (0.5 kPa) that gives 4 μm of maximum displacement in the direction of the propagating wave as seen in the data. Since soft tissues, such as retina, exhibit large deformation with nonlinear strains, a large deformation model was used to estimate the displacement field in the retina.

Model of standing wave amplitude as a function of transducer-MEA distance.

A COMSOL model to simulate standing waves was similar to the model described above, except that, after the incident wave reflected off the MEA, we allowed for that wave to perfectly reflect off the face of the transducer. In this case, retinal deformation was not calculated. The frequency is set to 1.9 MHz, and the nominal intensity is 56 W/cm² (intensity at the focus in free space). The standing wave amplitude shown in Figure 8a is calculated by averaging intensity values on-axis in the retina. Zero distance refers to the reference position where the focal point is coincident with the retina-MEA interface.

Figure 8.

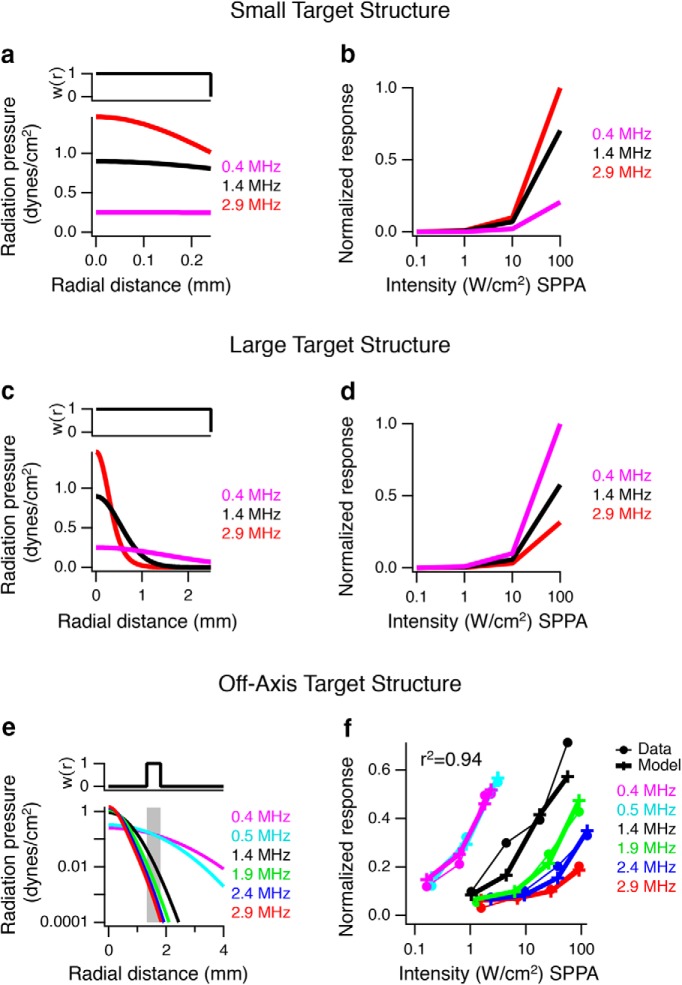
Target size and location influence acoustic frequency dependence in a model of in vivo stimulation. The same model was used as in Figure 7, except that it was applied to different sized target structures, and no output nonlinearity was used. a, Top, Spatial weighting, w(r), for a cylindrical target (radius = 0.25 mm and depth = 2.5 mm) as a function of distance from the center of the ultrasound focus. Bottom, Radiation pressure profile as a function of distance from the focus for three lower frequencies representative of in vivo stimulation at I = 1 W/cm². b, Model responses computed as the cumulative spatially weighted radiation force in the volume of the target structure, showing that higher frequencies are more effective with a target structure smaller than the focus of the highest frequency. Responses were normalized to the maximum effective response. c, Same as in a for a target structure with a radius of 2.5 mm. d, Same as in b for the larger 2.5 mm target, showing that lower frequencies are more effective when the target is much larger than the focus of the higher frequencies. e, f, Radiation force model applied to in vivo mouse ultrasonically stimulated brain behavioral data. The spatial weighting function and sigmoidal parameters were optimized to fit the data of Ye et al. (2016). e, Optimized spatial weighting function w(x,r), indicating that an off-target focus (depth x of 2.5 mm and r = 1.33–1.81 mm, shaded region), would be necessary to account for the data. f, Normalized behavior response (% success) from Ye et al. (2016) for 2.9, 2.4, 1.9, 1.4, 0.5, and 0.4 MHz with solid circles and thin lines as a function of intensity compared with the radiation force model output, crosses with thick lines.

Modeling radiation force to explain both retinal neural activity and mouse behavior.

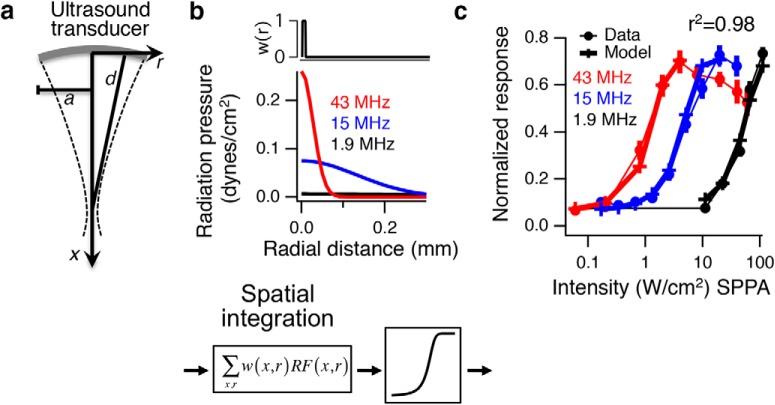
A quantitative radiation force model was used to fit neural population activity in the retina and behavior from stimulating mouse brain. The model is based on analytic equations valid for linear low-amplitude ultrasound in free space (Rudenko et al., 1996, their Eqs. 13, 14, and 16) and cylindrical coordinate system (Ye et al., 2016, their Eq. 9). For the retina, this model does not account for the reflection off of the MEA and the resulting standing waves, the presence of coupling cones, and the dialysis membrane. For 1.9 MHz, where standing wave effects are large, we use the data from the transducer position with the lowest threshold. The analytic expression takes as input the absorption coefficient (retina is similar to brain, so we used the same parameters as Ye et al., 2016), the carrier frequency (f), intensity (I), radius of the transducer (a), and focal length (d), to estimate radiation force in 3D space expressed in a cylindrical coordinate system where x is axial distance from the transducer and r is the radial distance away from the central axis. Radiation force weighted unit volume (Σw(x, r)RF(x, r), 10 μm grid in cylindrical coordinates, approximately the size of cell somas) is summed over a volume defined by three parameters: between two radii r₁ and r₂ and depth, and then passed through a sigmoid (Eq. 1). The only differences between the salamander retina model and mouse brain model is the volume of summation and the parameters of the sigmoids. The focus is assumed to be at the surface of the brain for mouse, and retina for salamander. The optimal values for salamander retina were determined to be the smallest possible volume around the focus r₁ = 0, r₂ = 5 μm, depth = 10 μm, equivalent to the maximum radiation force (see Fig. 7).

Figure 7.

A radiation force model predicts responses in the retina. a, An analytic expression was used to calculate radiation force in a cylindrical coordinate system based on transducer characteristics. a, Radius of transducer; d, focal distance; f, frequency; I, intensity; x, axial distance; r, radial distance, from Rudenko et al. (1996). b, Radiation force model of retinal response. Cumulative radiation pressure at I = 1 W/cm² is shown versus radial distance for the three frequencies. The radiation force is multiplied by a spatial weighting function, which in the retina is very small (∼10 μm) and equivalent to the peak radiation force, and then passed through an optimized sigmoidal nonlinearity to generate the model responses. c, Normalized population response for 43, 15, and 1.9 MHz as a function of intensity is compared with the radiation force model output (n > 20 cells in each case).

For mouse brain, we used the same general structure of the model used for retina but with different parameters for the volume of summation and sigmoid. The mouse brain model did not include a coupling cone or the effects of going through skull, nor any standing wave effects. We first explored the effect different sized brain target structures (volume of summation) would have on the simulation with no output nonlinearity (see Fig. 8a–d). The first version of the model assumed the active brain region was a small cylindrical structure with radius of 0.25 mm and depth of 2.5 mm coincident with the focal spot (see Fig. 8a,b). In the second version, the activated brain region was allowed to be much larger (radius of 2.5 mm, depth 2.5 mm; see Fig. 8c,d) to demonstrate how low frequencies might be more effective than high frequencies from integrating over a large volume. The third version of the model (see Fig. 8e,f) incorporates an output sigmoidal nonlinearity, and the activated brain target is allowed to be off-axis.: The size and location of the brain target structure are allowed to be free parameters to best fit the data (r₁ = 1.33 mm, r₂ = 1.81 mm, depth = 2.5 mm; see Fig. 8e,f). When r₁ = 0 the volume is a cylinder, but when r₁ > 0, it defines a tube in a 3D cylindrical coordinate system. Radial symmetry dictates that any angular sector of this tube will generate the same solution, so we arbitrarily choose a 30° section of the tube to approximate the anatomically relevant part of the brain.

The spatially integrated radiation force was passed through a sigmoid to yield a normalized response, R, as follows:

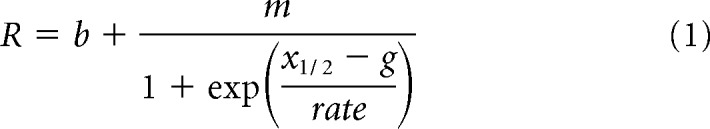The sigmoid represents neural nonlinearities with the following free parameters that best fit the data: g is the output of weighted linear summation of radiation force, m is the saturation level (0.73 in retina, 1.0 in mouse), x_½ is the radiation force value at half-maximal (2.16e-7 in retina, 4.4e-5 in mouse), “rate” is the gain (1.09e-7 in retina, 6.3e-4 in mouse), b determines the output at zero intensity (0.064 for retina; 0.06 for mouse frequencies 2.9, 2.4, 1.9, 1.4 MHz; 0.11 for frequencies 0.4, 0.5 MHz). Units of radiation force at any point in space are in dynes/cm³. Free parameters (location and volume of summation and sigmoidal parameters) were found by minimizing the total root mean square error between the data and the model. Figures 7b and 8a, c, e show an intermediate stage of the model for I = 1W/cm². Radiation force is integrated along the optimal depth dimension (for retina 10 μm and for brain 2.5 mm), yielding cumulative radiation pressure as a function of radius r for different frequencies.

Results

Radiation force causes physical displacement within the retina

Ultrasonic stimulation was applied to a preparation used for measuring neural activity consisting of the retina placed on a planar MEA patterned on a glass slide (180 μm thickness). We imaged the retina through the glass MEA with a two-photon laser-scanning microscope after applying the membrane dye FM 4–64 to the bathing medium (Fig. 1). A stack of images was recorded from the MEA up to the photoreceptor level while repeatedly stimulating the retina with ultrasound (43 MHz carrier, 1 s on, 1 s off) (Menz et al., 2013), at a power level known to cause strong neurostimulation (I_SP = 40 W/cm²). The ultrasonic stimulation and scanning laser were uncorrelated, allowing all points in the volume to be imaged relative to the onset of the ultrasound stimulus, although on different trials. Using the time that the laser scanned each pixel, we reconstructed a movie of the average intensity at each pixel for the entire volume at a 10 ms resolution with respect to the ultrasound stimulus (Movie 1). At the onset of ultrasound, a sudden displacement toward the MEA was observed that lasted the duration of the stimulus. The XZ spatial distribution of intensity for all transducers used in this study is shown in Figure 2a (43 MHz).

Movie 1.

A video showing ultrasonic displacement in the retina at 43 MHz (I_SP = 40 W/cm²). A slice through the retina with the ultrasound transducer above the top, focus left of center, ganglion cells at bottom, photoreceptors at top. White pixels indicate where dye is embedded in cell membrane. Movie contains a single 2 s period and is best viewed in loop mode continuously. White bar at right represents when ultrasound is on (one second). Black bar represents when ultrasound is turned off (1 s).

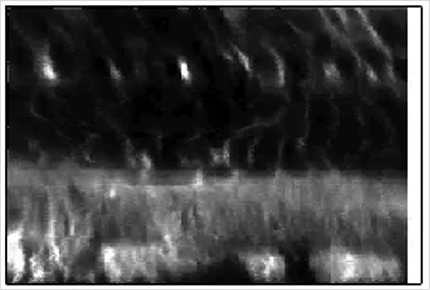
We converted these displacements between steady-state On and Off ultrasound into a vector field using image processing software (see Materials and Methods) (Fig. 3a). The vector field, which was consistent with qualitative observations from the movie, showed that displacement was centered at the ultrasound focus, was greatest in the outer retina, and decreased to zero near the ganglion cell layer. Lateral to the focal point, displacement direction became progressively more lateral. Other fluctuations in displacements were observed that could be a consequence of inhomogeneity in the retina, such as differing mechanical properties of inner plexiform layer and cell body layers.

Figure 3.

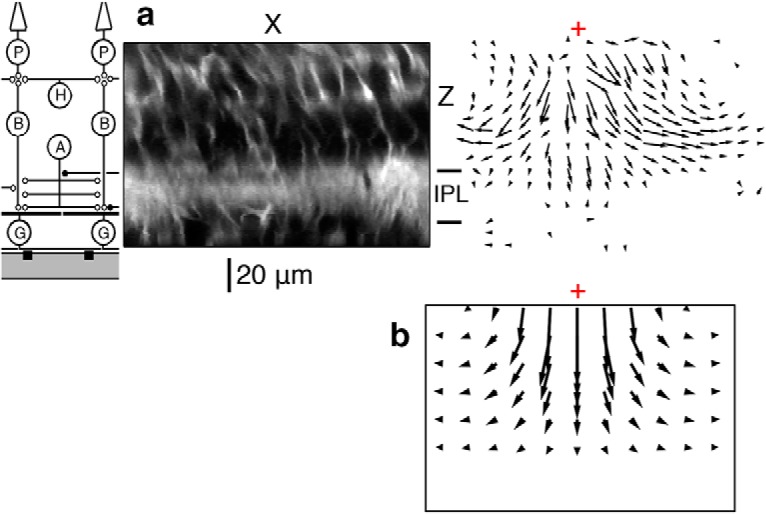
Ultrasonic radiation force causes displacement in the retina at 43 MHz (I_SP = 40 W/cm²). a, Left, Schematic of the retinal circuit aligned vertically with images to the right. Middle, X-Z retinal slice taken near the ultrasound focus. Right, An X-Z slice through a vector field showing displacement (relative magnitude and direction), resulting from ultrasonic stimulation. Red cross represents the center of focus. The vector field was computed from the image at steady ultrasound ON relative to ultrasound OFF. b, Vector field of displacement using a simulation of radiation force acting on the retina, E (Young's modulus of elasticity) = 0.5 kPa. Middle top, Maximum displacement (4 μm). Scale of vectors is different from the scale of the image. The red cross is the center of focus.

To interpret the potential mechanism of this displacement, we modeled the expected mechanical response of the retina from radiation force using finite element analysis (COMSOL). In the simulation, we considered the following factors: acoustic streaming (the bulk flow of fluid due to radiation force acting on a fluid), reflection from the water-retina and retina-MEA interfaces, absorption in the retina, and the interference pattern that results from the wave reflecting off the MEA. It was determined that 88% of displacement can be accounted for by the combination of reflection from the water-retina interface combined with the interference pattern (i.e., standing wave) that comes from wave reflection off the MEA, 9% comes from absorption, and 3% from acoustic streaming. A key parameter for this calculation is the Young's modulus of elasticity for the retina. However, the literature has values that vary by three orders of magnitude, depending on the method of measurement (McKee et al., 2011). We thus allowed the Young's modulus to be a free parameter and fit the model to account for the maximum observed displacement, which was 4 μm. The resulting value of Young's modulus was 0.5 kPa, which is close to the range found in the retina (0.1–2.0 kPa) with the scanning force microscopy method (Lu et al., 2006). The general features of the simulated vector field qualitatively matched the experimental vector field of displacement: large downward motion in the outer retina right under the focus, which decreases to zero at the level of the MEA (Fig. 3b). In the simulation, the retina was modeled as a homogeneous medium, so features, such as the large change in displacement at the boundary of the inner plexiform layer, were not captured.

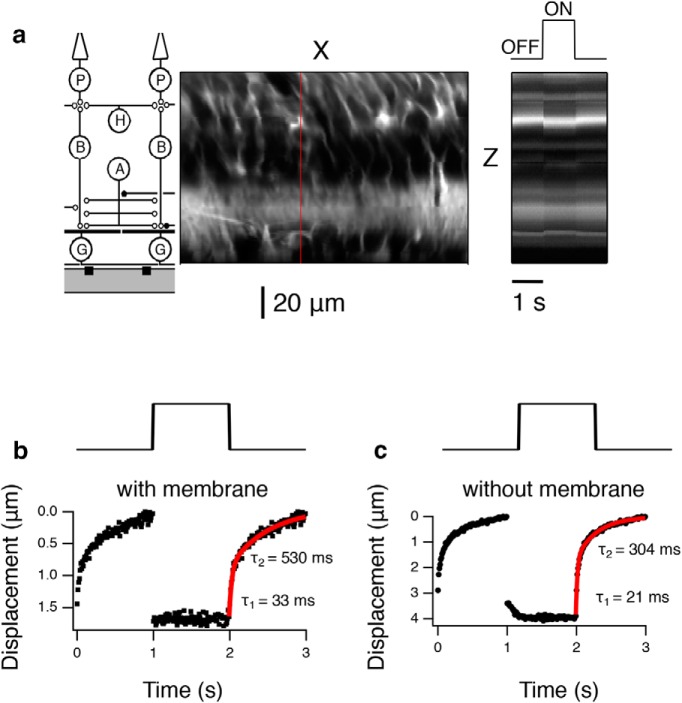
To quantify the displacement, we found a region with high image contrast with the largest displacement and examined the change of displacement in 10 ms time bins (Fig. 4a). In a normal experiment, an optically clear dialysis membrane is used to hold the retina down against the MEA to facilitate ganglion cell recordings. Under this condition, we observed a maximum of ∼2 μm of displacement in the downward direction of the incident ultrasonic wave (Fig. 4b). Since we do not know the acoustic properties of the dialysis membrane, we were concerned that the displacement was caused by radiation force acting on the membrane. We performed an experiment with a hole cut into the dialysis membrane so that there was only Ringer's solution between the transducer and the retina. Under this condition, the displacement was significantly larger, 4 μm (Fig. 4c).

Figure 4.

Dynamics of ultrasonic displacement in the retina at 43 MHz (I_SP = 40 W/cm²). a, Left, Schematic of the retinal circuit aligned vertically with images to the right. Middle, X-Z image slice. Red line indicates the spatial cross section, which is then shown as a function of time at right. Right, Temporal changes during 1 s ultrasound OFF, 1 s ON, and 1 s OFF. b, Maximum downward displacement with the dialysis membrane in place. A Gaussian was fit to the bright spot in each 10 ms time bin, and the mean position plotted as a function of time. Top, Stimulus trace showing the timing of ultrasound onset and offset. Bottom, Vertical displacement as a function of time. The relaxation after stimulus offset is shown fit with a double exponential (red curve). c, Maximum downward displacement without the dialysis membrane in the pathway.

The vertical displacement occurred very rapidly (<10 ms), consistent with the expected temporal dynamics of radiation force (Prieto et al., 2013). The fast onset of displacement is consistent with the fast response of neurons to ultrasonic stimulation (Menz et al., 2013). The recovery to baseline, which reflected the elastic properties of the retina was slower and was fit by double exponential with time constants of 33 and 530 ms (Fig. 4b) and 21 and 304 ms (Fig. 4c).

Relationship between displacement and ultrasonic neurostimulation

To examine the relationship between displacement and neural activity, we then compared measurements of these two quantities as a function of stimulus intensity. We imaged a level in the retina above the inferior parietal lobule midway through the retina that showed considerable lateral displacement. We varied the ultrasound intensity from below the threshold of neural activation to above the level of a saturating response (Fig. 5). We computed the displacement at this level as a function of ultrasound intensity and compare this relationship with that of the normalized firing as a function of ultrasound intensity taken from a different preparation (Fig. 5b). Neural activity was observed at a threshold of ∼1 W/cm², a level at the threshold of detectability of tissue displacement. The shapes of the two curves were different, with displacement increasing approximately linearly with stimulus intensity, and neural activity having a saturating dependence on intensity that was sigmoidal on a logarithmic scale. For each intensity value, we plotted the normalized firing rate versus displacement (Fig. 5c). There was a rapid increase in firing over submicron values of displacement, after which neural activity saturated. This indicates that submicron scale displacement was correlated with neural activity and gives a scale for the biophysical mechanisms that could transduce these displacements to produce activity.

Figure 5.

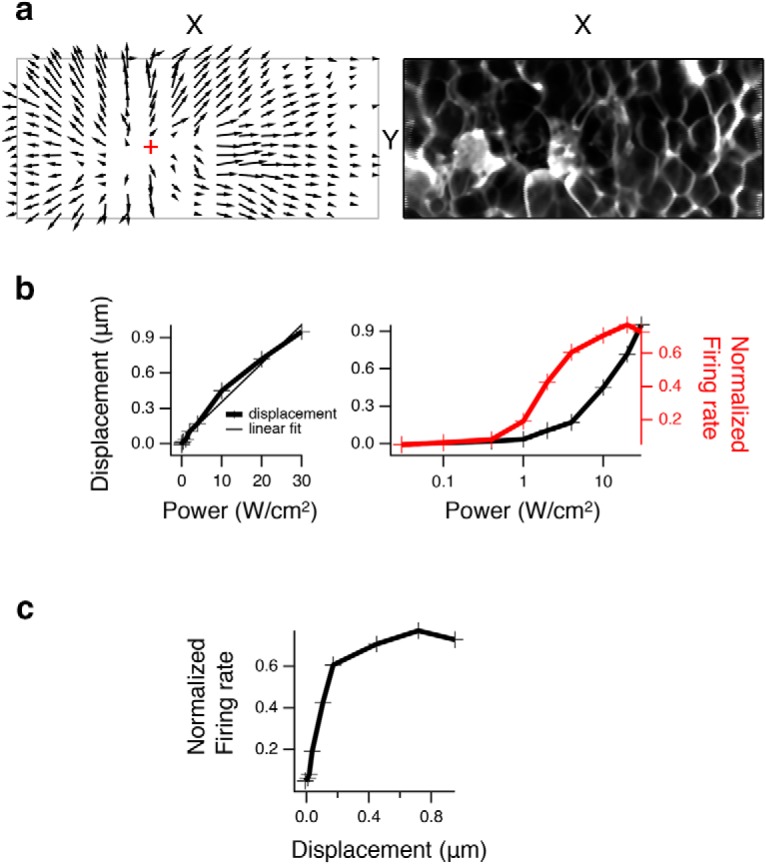
Relationship between displacement and neural activity at 43 MHz. a, Left, An X-Y slice through the focus (red cross represents point of minimal displacement) at a depth of maximal lateral displacement about midway through the retina that shows lateral displacement vector field in all directions moving away from the focal point. Right, X-Y slice with ultrasound OFF used in a. b, Left, Maximum lateral displacement (in X-Y for a given depth) is plotted versus intensity. +, Data points. Thin line is a linear regression fit (r² = 0.98). Right, Normalized population firing rate (n = 61) is plotted versus intensity and superimposed over displacement versus intensity, where the x axis is now on a log scale. c, Normalized population firing rate is plotted versus displacement from b for each intensity value.

Dependence of neural response on acoustic frequency

Absorption increases with higher acoustic frequency, and thus both radiation force and heating are expected to increase with higher carrier frequency. In contrast, the probability of cavitation decreases with higher carrier frequency because of the shorter time interval available to cause a bubble to form out of solution and to keep it oscillating. Many protocols of ultrasonic neurostimulation use lower frequencies (<1 MHz) to allow sufficient energy to penetrate the skull, which is known as transcranial neurostimulation. It is conceivable that at lower frequencies a different mechanism such as cavitation is involved (Plaksin et al., 2016). We therefore changed carrier frequency in several steps between 43 and 0.5 MHz to measure activation of retinal ganglion cells by ultrasound at different frequencies on the retina.

To more completely characterize the response at a given frequency, we varied both pulse intensity and duration across a wide range for the 43 MHz transducer (Fig. 6a, left). As the pulse duration was decreased <100 ms, greater intensity is required to achieve stimulation (Fig. 6b). This relationship is consistent with the threshold being proportional to the integral of the pulse to obtain total energy, as is also found in electrical stimulation (Boinagrov et al., 2014).

Figure 6.

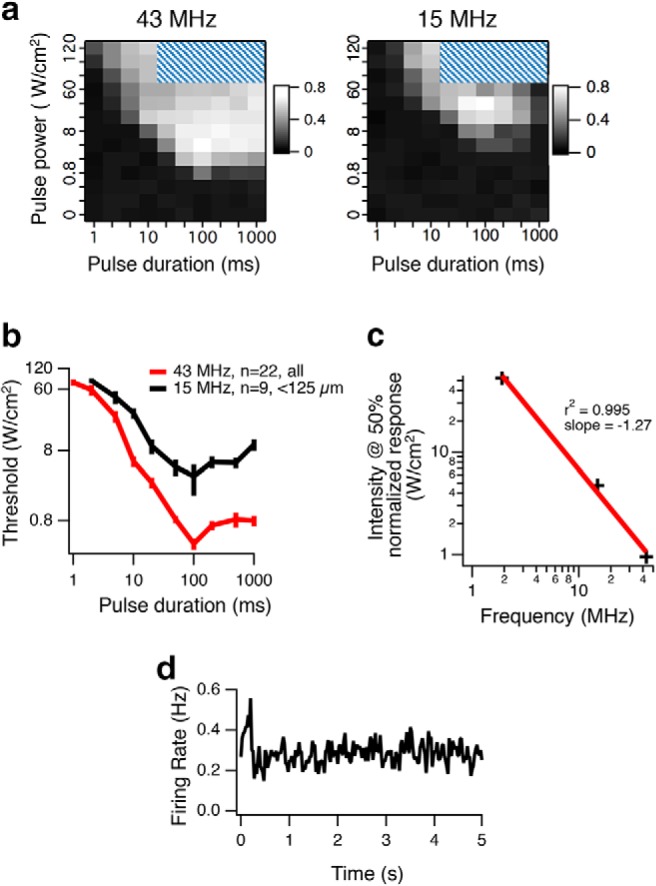
Ultrasonic stimulation at higher acoustic frequency has a lower threshold. a, Left, Normalized population (n = 22) firing rate is plotted as a function of intensity I_SP and pulse duration for 43 MHz. Cross-hatching indicates parameters not tested. Right, Same plot for 15 MHz for cells <125 μm from the focus (n = 9). b, Threshold of stimulation as a function of pulse duration. Average thresholds across cells (error bars indicate SEM) at each pulse duration for 43 and 15 MHz. c, In separate experiments, normalized population responses were measured for three carrier frequencies (43, 15, and 1.9 MHz; see Fig. 7c). The half-maximal intensity is plotted against carrier frequency (black +). Red linear regression line has a slope of −1.27, indicating that the exponent on frequency dependence is 1.27; this compares with a value of 1.18 (Goss et al., 1979) that was used in the radiation force models of Figure 7. d, The population peristimulus time histogram (n = 75) generates a very weak response to ultrasound (100 ms ON starting at time 0, repeated every 5 s) for a 500 kHz transducer at I_SP = 1.6 W/cm².

Using the same stimuli, at 15 MHz, a greater intensity was required to stimulate neurons compared with 43 MHz (Fig. 6a). A 100 ms pulse duration was still optimal, and this value was used as the default pulse duration in other experiments (Fig. 6a,b). The increase in neural activity with increasing acoustic frequency was qualitatively consistent with radiation force, and inconsistent with cavitation as a mechanism. It is also inconsistent with in vivo mouse results, which show that relatively higher frequencies (in the range 0.3–2.9 MHz) require more intensity to stimulate neurons (Ye et al., 2016). We considered the possibility that, for frequencies above some threshold (e.g., 15–43 MHz), radiation force is dominant; but for frequencies below some threshold (e.g., 0.3–2.9 MHz), cavitation is the dominant mechanism. To test these different mechanisms at different frequency range hypothesis and to resolve this paradox, we used the exact same transducer-amplifier combinations with carrier frequencies of 1.9 MHz and 500 kHz from the mouse in vivo experiments on our MEA ex vivo retina setup.

We found that at 43, 15, and 1.9 MHz, the intensity at half-maximal varied as a function of frequency raised to a power of 1.27 (Fig. 6c), close to the previously measured value of 1.18 in cat brain (Goss et al., 1979). Finally, at 500 kHz, at the maximum achievable spatial peak power with our transducer (I_SP = 1.6 W/cm²), responses of single cells to this stimulus could not be detected with significance and were only detectable when averaging across a population of neurons (Fig. 6d). The results at all frequencies tested are consistent with radiation force as the single physical mechanism across the entire range of frequencies used (0.5–43 MHz), indicating other physical mechanisms do not play a major role.

A radiation force model explains retinal ultrasonic neurostimulation

We then tested whether retinal neural activity could be fit with a single quantitative model of radiation force across the range of intensities and frequencies tested. The model is structured to be the simplest possible that minimizes root mean square error between the model and data. The neural response was assumed to be proportional to the sum of radiation force over some unknown volume followed by a sigmoidal nonlinearity. We used an analytical model of radiation force valid for linear low-amplitude ultrasound in free space (Rudenko et al., 1996, their Eqs. 13, 14, and 16), which has absorption coefficient, the carrier frequency, intensity, radius of the transducer, and focal length as parameters, to estimate radiation force in 3D space expressed in a cylindrical coordinate system. From this model, we computed the radiation force for each intensity, transducer, and spatial location, and then passed this value through a stage of spatial integration representing the neural properties that sense ultrasound and then a sigmoidal function to predict neural activity. The free parameters of the model defined the volume of spatial integration and shape of the sigmoid, which was fixed across all intensities and acoustic frequencies. In the retina, the spatial integration was centered on the transducer focus, and the optimized scale of integration was small (10 μm diameter, 10 μm depth), which was equivalent to computing the maximum radiation force. This model showed that the analytically computed maximum radiation force could be used to predict the neural response from 1.9 to 43 MHz with a single sigmoidal neural activation function in the retina (Fig. 7).

Size and location of the target neural structure changes acoustic frequency dependence

Although this model could predict retinal activity, previous studies in the in vivo mouse using much lower frequencies (300 kHz to 2.9 MHz) and recording muscle twitches (Ye et al., 2016) have shown that higher frequencies have greater thresholds, the opposite result seen in the retina. From these results, cavitation was proposed as a possible mechanism. Although different mechanisms may be involved in different systems, one must also consider that, to date, lower acoustic frequencies have been applied with a focal spot of a larger volume due to effects of diffraction. As frequency is lowered, although radiation force would decrease with approximately the square of the acoustic frequency, the focal volume would increase with approximately the third power. Assuming a neural or behavioral response is driven by stimulation of a specific volume of the brain, a higher frequency with a smaller focal spot might be less effective at activating that volume than a lower frequency, even though the higher frequency generates more radiation force per unit volume at the focus. We considered the effect of target size using the same basic radiation force model as used for the retina, except that we omitted the final threshold and assumed linear spatial summation within this structure. We first considered a small cylindrical target structure at the ultrasound focus with a radius of 0.25 mm and a depth of 2.5 mm. In this case, similar to our retina data, we found that higher frequencies would be more effective (Fig. 8a,b). However, with a larger target structure (radius of 2.5 mm and depth of 2.5 mm), the acoustic frequency dependence reversed, such that lower acoustic frequencies were more effective by virtue of the larger stimulus volume for lower frequencies (Fig. 8c,d).

A second effect that could influence the frequency dependence is whether the target neural structure is located off-axis, not at the focus. In this case, a smaller focal spot at a higher acoustic frequency may miss the target structure, potentially increasing further the effectiveness of lower acoustic frequencies. Experimental evidence supporting this second effect was demonstrated by Li et al. (2016) who showed that 5 MHz was equally effective as 1 MHz at eliciting mouse EMG when positioned at the most sensitive location, but 5 MHz quickly became less effective than 1 MHz when the position was moved by just a few hundred microns. It is not clear, however, whether their results are confounded by stimulation through an auditory pathway (Guo et al., 2018; Sato et al., 2018). We therefore tested whether the same model of radiation force used to predict retinal responses could be used to predict responses in the mouse in vivo (Ye et al., 2016) with different parameters for spatial integration and the sigmoid. We found that, if we assume that the brain region responsible for the behavior is actually an off-axis volume where high-frequency radiation force drops off rapidly (w(x, r) = 1.33 −1.81 mm from the focus, depth = 2.5 mm; Fig. 8e), then this version of the model closely predicts mouse in vivo responses (Fig. 8f; r² = 0.94). Both the retinal and mouse models share the same analytical formula for radiation force and form of sigmoidal neural activation and differ only in spatial integration and parameters for sigmoidal neural activation. An intermediate model result is shown in Figure 7b, and 8a, c, e where radiation force at I = 1 W/cm² is integrated along depth (10 μm for retina, 2.5 mm for brain) to show cumulative radiation pressure versus radial distance for different frequencies. The cumulative radiation pressure threshold required to generate neural activity was found to be similar for both salamander retina and mouse brain (∼0.1 dynes/cm²). Because of the uncertainty of the size and location of the target structure relative to the stimulus in the in vivo studies, we can conclude from this simulation only that some conditions exist whereby a radiation force model could potentially account for both the current retinal results and previous in vivo results, including the greater efficacy of low acoustic frequency. This would require that in vivo stimuli were presented off target for a certain size neural structure. These results point out the critical need to control for the acoustic focal volume and the location of stimulation relative to the target structure to determine whether a single model can account for in vitro and in vivo results.

Thermal effects likely do not contribute to ultrasonic stimulation of the retina

We measured temperature rise under our experimental conditions using small (76 μm) thermocouples (J and K type, OMEGA) placed on the array with a retina held in place on top of the thermocouple. With the perfusion running as during ultrasonic stimulation, the temperature change is not measurable at 60 W/cm² and 15 MHz, and without perfusion, we measure only 0.1°C-0.2°C increase. Small thermocouples suffer from sources of artifact, such as ultrasound reflection off the thermocouple and conduction of heat away from the source and heating due to friction from radiation force moving the transducer relative to tissue. This latter artifact is much greater with pulsed ultrasound, where the thermocouple will oscillate at the pulse repetition frequency (PRF), whereas we are using CW. We expect that these artifacts are minor as the thermocouple was attached to the bottom of the dish, thereby reducing friction since the thermocouple cannot move. The ultrasound will reflect off the glass surface of the MEA in any event, so reflection off the thermocouple is not significantly different from the normal experimental condition. We found that perfusion removed heat much more effectively than the thermocouple wire, such that under normal conditions of ultrasound stimulation with perfusion running, we cannot measure any temperature rise from ultrasound. Although these studies do not categorically rule out thermal effects at a fine spatial scale, we find no evidence of significant thermal effects. Higher-resolution spatial-temporal measurements of temperature changes in the future will be useful to examine whether any thermal effects do exist.

Standing waves

In the retinal preparation, below the tissue is a glass MEA of thickness 180 μm, followed by an air space. The top and bottom surfaces of the MEA create a large mismatch in acoustic impedance, which is expected to reflect ultrasound. Thus, the space between the transducer and MEA may form a cavity that could generate a standing wave, where locations spaced at one-half the acoustic wavelength (λ) would experience destructive interference (nodes), and intervening locations experiencing constructive interference (antinodes). The acoustic pressure in the standing wave is converted into radiation pressure through absorption generating alternating high- and low-pressure volumes that do not temporally modulate at the carrier frequency. The relationship between acoustic pressure standing waves and radiation pressure is well known in micro-fluidics (Bruus, 2012; Lenshof et al., 2012), where it is used to physically move small particles, including individual biological cells, to a desired location. Radiation pressure is greatest at antinodes and smallest at nodes, causing tissue at nodes to be compressed by adjacent high-pressure antinodes and tissue at antinodes to be stretched by adjacent low-pressure nodes. Such mechanical pressure on tissue could have an additional influence on neural activity. We tested the neural effects of standing waves by simply changing the distance between the transducer and the MEA. This will not change the locations of the nodes and antinodes as they are fixed by the carrier frequency, but the change in cavity length will affect the amplitude of standing waves, with a maximal standing wave amplitude when the cavity length is a multiple of λ/2. To illustrate this effect, we computed a COMSOL simulation of the transducer-electrode array cavity with a perfect reflection off the transducer face, which produced a large modulation in acoustic intensity in the retina with a characteristic period of λ/2 in transducer distance (Fig. 9a). At the spatial sampling of this stimulation, calculated radiation force was nearly perfectly correlated with acoustic intensity (r = 0.9997; data not shown). Our transducers are not perfectly reflecting, and it is not clear whether reflections are off the transducer face or from the face of a plastic coupling cone covered with Parafilm. A more realistic simulation with less than perfect reflection would generate a smaller depth of modulation, but the period would still be λ/2.

Figure 9.

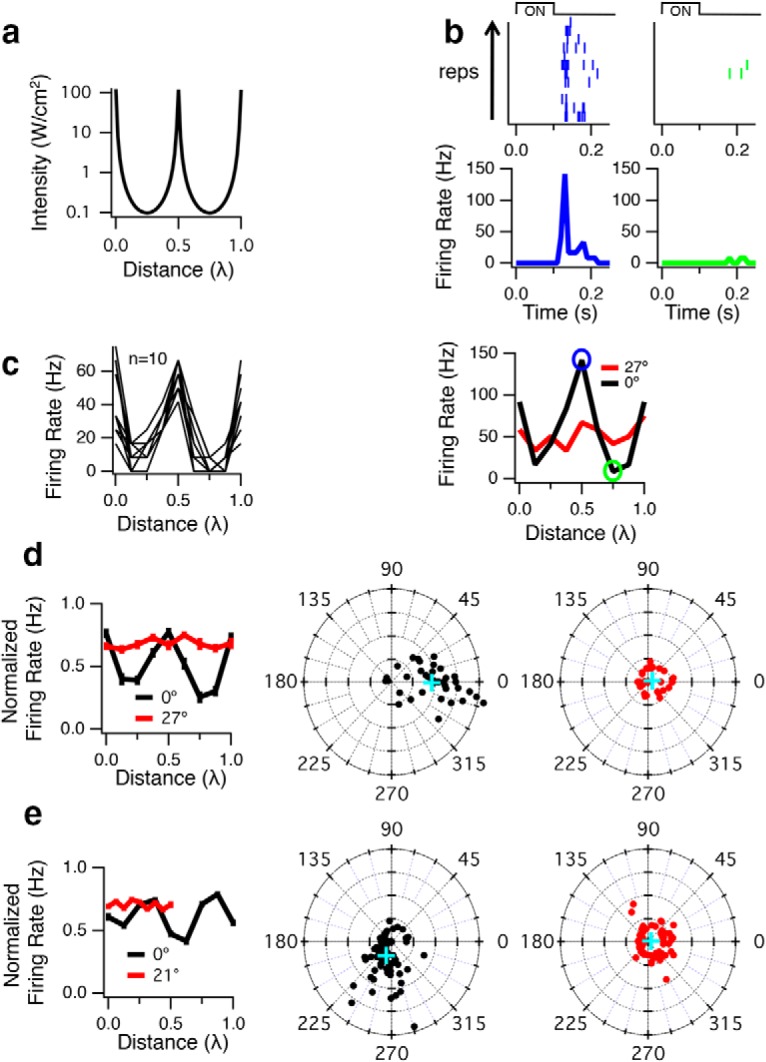
Standing waves modulate ultrasonic neurostimulation. a, COMSOL simulation at 1.9 MHz and a nominal intensity of 56 W/cm² (focal intensity in free space) of a transducer with an ideal reflective surface, demonstrating a periodic modulation in acoustic intensity as a function of changing transducer distance to the MEA expressed in wavelengths. The intensity plotted is the on axis; average values in the retina. Zero distance indicates that the focal point of the transducer is coincident with the retina-MEA interface. Positive values of distance expressed in terms of wavelength indicate the transducer moving further away from the MEA. An ideal reflective transducer is shown to illustrate the periodicity of modulation with distance, and a transducer with lower reflectivity as we used would produce a smaller modulation at the same period. b, A 2.25 MHz transducer was operated with a carrier frequency of 2.9 MHz (λ = 517 μm). I_SP = 155 W/cm², and a 100 ms pulse was repeated every 15 s for 12 trials. Top, Raster plots and peristimulus time histograms of the response of one cell when the vertically oriented transducer was moved a distance of 0.5λ (blue) and 0.75λ (green). Bottom, Peak firing rate response from this cell when the transducer was vertical (0°, black), showing strong modulation with a period of λ/2 as the transducer was moved away from the MEA. Distance is measured in terms of wavelength relative to a starting position, which was chosen to maximize the population response. Also shown is the response when the transducer was tilted at an angle of 27° relative to vertical (red). c, Peak firing rate responses from 10 other cells when the transducer was vertical, demonstrating that many cells exhibit the same pattern of response with respect to transducer distance. d, Left, Normalized population response for vertical (0°, n = 37) and tilted (27°, n = 30) transducers. Middle, FFT of firing rate versus distance. The amplitude and phase are shown at a frequency of 2 cycles/λ for each cell that responds to ultrasound when the transducer is vertical (0°). In this plot, distance from the center represents the depth of modulation (normalized by the mean, linear scale) of the response by the transducer position at a period of λ/2. The angle is the phase of the 2 cycles/λ Fourier component, indicating the transducer distance at which the response was maximal. Blue cross represents the mean population response. Right, FFT of firing rate versus distance when transducer was tilted at 27°. e, Left, Same as in d, except the 2.25 MHz transducer was operated at a carrier frequency of 1.9 MHz (λ = 789 μm), and angle of the transducer when tilted was 21°; I_SP = 95 W/cm² (n = 90 for 0°, and n = 78 for 21°). Middle, The average phase differs from d because the transducer was not repositioned to set the peak response at the starting position. Right, For the tilted condition (21°), the distance traveled was only one full cycle (λ/2) with smaller step sizes.

We tested the effects of standing waves at relatively low frequencies, 2.9 MHz (λ = 517 μm, λ/4 = 129 μm) and 1.9 MHz (λ = 789 μm, λ/4 = 197 μm), close to where most ultrasonic neurostimulation studies are conducted, yet high enough that we can still get robust responses, and where the λ/4 distance is large and comparable with the thickness of the retina (∼120–150 μm). The ultrasound stimulus was a CW 100 ms pulse, which we had previously found to be optimal at higher frequencies (Fig. 6b) and was very close to the 80 ms CW pulse used for in vivo mouse stimulation (Ye et al., 2016). The stimulus was repeated every 5 s to minimize potential adaptation effects. A single 2.25 MHz transducer with relatively wide bandwidth was used for both frequencies, and intensities were measured by hydrophone separately at each frequency in free space.

We found that the firing rate of some cells was very strongly modulated by the distance between the transducer and the MEA with a period of λ/2, consistent with standing waves (Fig. 9b,c). Across the population, we quantified the standing wave effect by computing the Fourier transform of the firing rate as a function of transducer distance and examining the amplitude at a frequency of 2 cycles/λ as well as the phase angle of the response (Fig. 9d; at 2.9 MHz) relative to the starting position (0°, vertically mounted transducer) with the focus at the MEA and moving away from the MEA. The population showed that the response was modulated at a period of λ/2, consistent with a strong standing wave effect.

We then tested whether standing waves were necessary for neurostimulation by tilting the transducer at an angle of 27° to vertical. Although a spatial interference pattern still occurs between the incident and reflected waves, the depth of modulation will not be as great as when the transducer is positioned vertically, and such a pattern would move with distance between the transducer and glass. We found that the tilted transducer condition still generated a response (Fig. 9d), but the response modulation with distance was greatly reduced. At an angle of 27°, the average across the population showed a depth of modulation of 26 times less than when the transducer was vertical. We further tested that standing waves were also observed at 1.9 MHz, λ/4 = 197 μm, using the same transducer, and similarly found that the population response was modulated at a period of λ/2 and that this average effect on the population diminished when the transducer was tilted an angle of 21° (Fig. 9e). From these results, we conclude that standing waves influence the response but are not necessary for stimulation.

Discussion

Our results show that ultrasonic neurostimulation in the retina produces radiation force and micron-scale displacement. A quantitative model of radiation force across multiple acoustic frequencies and power levels indicates that radiation force is the likely physical mechanism of action. We further show that standing waves can modulate neural activity, suggesting a potential new method to further control activity.

Thermal effects of ultrasound

Estimates of temperature rise based on I_SPTA, pulse duration, density, and specific heat capacity and absorption coefficient (O'Brien, 2007) are very small (0.007°C–0.04°C for in vivo studies in humans and sheep) (Lee et al., 2015, 2016a,b). Furthermore, these methods assume all energy goes to an increase in temperature, and do not account for heat loss by conduction or convection, so the actual temperature rise should be lower. Previously, at 43 MHz and 30 W/cm², well above stimulation threshold, we could not measure a temperature rise with the perfusion running, although we could measure a 0.5°C increase from prolonged stimulation without perfusion. In a study using Caenorhabditis elegans (Kubanek et al., 2018), mutants lacking thermosensitive receptors behaved like WT animals, whereas mutants that lack touch sensory neurons have an impaired response to ultrasound. Together, there is no evidence for heating as a physical mechanism for brief ultrasonic neurostimulation.

Cavitation

We found using the same transducers, amplifier, frequencies, and power settings that successfully stimulated in vivo mouse that in the retina, higher acoustic frequencies were more effective than lower frequencies, thus ruling out cavitation as a possible physical mechanism (Figs. 6, 7). Cavitation can be measured with subharmonic cavitation detectors (Vykhodtseva et al., 1995; Gateau et al., 2011). To date, there is no study demonstrating the existence of cavitation in the brain using parameters for neurostimulation in the CNS. Cavitation requires gas bubbles; however, outside of the lungs and the digestive tract, biological tissue is generally bubble free (Church et al., 2008). An in vivo sheep brain study with a 660 kHz carrier found that at least 12.7 MPa was required to measure a nucleation event with both passive and active cavitation detection (Gateau et al., 2011), whereas threshold pressures for low-power ultrasonic modulation in vivo brain studies are much less than 1 MPa (Naor et al., 2016). In another study using in vivo rabbit brain, cavitation only occurred at the very high power of 2000 W/cm² at ∼1 MHz (Vykhodtseva et al., 1995), showing obvious tissue damage (Vykhodtseva et al., 1995).

A hypothesis of ultrasonic neurostimulation is neuronal intramembrane cavitation excitation, which is a theoretical model that has been fit to empirical results (Krasovitski et al., 2011; Plaksin et al., 2014, 2016). The intramembrane cavitation hypothesis asserts that stable cavitation exists inside the cell membrane causing a change in cell capacitance that ultimately leads to action potential firing. Although this model has been fit to various in vivo experimental data, it does not describe our data because of the strong correlation between greater neural activity and higher ultrasonic frequency.

Pressure phosphenes

It has been known since ancient Greece that mechanical deformation of the eyeball generates pressure phosphenes (the appearance of light when there is none). Although it is still not known which retinal cells are responsible, it is clear that mechanical force can result in ganglion cell activity. Studies with deformation of the cat eyeball showed that different ganglion cells respond through network stimulation, likely in the outer retina (Grüsser et al., 1989a,b). Most importantly they conclude that mechanical strain is the cause, not retinal ischemia from high intraocular pressure. The authors speculated that inhibitory horizontal cells or amacrine cells might be sensitive to strain because of their lateral connections. A phenomenon that has been known for thousands of years supports the concept of mechanical strain on neurons as the cause for this neural stimulation.

Potential biophysical mechanisms

Leading candidates for biophysical mechanisms are mechanosensitive ion channels, capacitive effects from mechanical deformation of the cell membrane, and direct effects on endocytosis/exocytosis. A simple biophysical mechanism that could transduce mechanical strain is a change in membrane capacitance, which can result from radiation force (Prieto et al., 2013). Alternatively, stretching, compressing, or bending of the cell membrane may cause the opening or closing of mechanosensitive ion channels, which are found in all parts of the nervous system. These serve different functions, such as controlling osmotic pressure to guiding developing neurons (Orr et al., 2006; Haswell et al., 2011). Sensitive channels that are good candidates to convert mechanical stress from ultrasound into neural activity include Piezo, TRAAK, TREK-1, and TREK-2 (Brohawn, 2015; Syeda et al., 2016). In a study expressing mechanosensitive ion channels (two-pore-domain potassium family [K2P]: TREK-1, TREK-2, TRAAK, and sodium channel NA_v1.5) in Xenopus oocyte, ultrasound was found to significantly influence membrane current of the potassium channels and had a small effect on the sodium channel (Kubanek et al., 2016). In C. elegans, ultrasonic neurostimulation requires mechanosensitive channels (Kubanek et al., 2018).

It is known that high static pressure will suppress synaptic activity. This is the physiological basis for High Pressure Neurological Syndrome, a danger for deep-sea divers exposed to pressures >1 MPa (Heinemann et al., 1987; Jain, 1994; Aviner et al., 2016), but one from which divers fully recover without permanent damage. Potential mechanisms are differential activation of calcium channels (Aviner et al., 2016), or a direct effect on exocytosis (Heinemann et al., 1987). In general, multiple mechanisms of ultrasonic neurostimulation could operate under different conditions, including stimulus parameters or type of tissue.

Implications for sonogenetics

A recent approach to modulating neural activity is the genetic targeting of molecules sensitive to ultrasonic stimulation. Termed either “sonogenetics” (Ibsen et al., 2015) or “acoustic mechanogenetics” (Pan et al., 2018), such methods promise to create an alternative to optogenetic approaches that benefit from the depth of penetration possible with ultrasound compared with light. Key to the design of such approaches is the knowledge of the physical mechanisms by which ultrasound can act. Ultrasound effects acting through radiation force as we have identified here could potentially be used to activate sonogenetic probes. In doing so, in any given tissue, mechanical sensitivity of sonogenetic probes should exceed the endogenous sensitivity to ultrasound.

Effects on ganglion cells

The large displacements in the outer retina shown in this study are consistent with ultrasonic activation of neurons in the retinal network, which provide inputs to the ganglion cells. Previously, we observed that blocking synaptic transmission with CdCl₂ (Menz et al., 2013) abolished ultrasonic neurostimulation, indicating that we were not directly stimulating ganglion cells. One might assume, therefore, that the biophysical mechanisms of transduction are not present in the ganglion cell soma or dendrites. However, our present results show that little displacement was observed in the ganglion cell layer (Fig. 3). Thus, it may be that the ganglion cell soma can be directly activated by ultrasound if appropriate mechanical strain is applied. Further studies varying the geometry of the recording setup to produce mechanical strain at the ganglion cell level will be needed to assess whether ganglion cells can be activated directly.

Comparison with another ex vivo retina study

Another ex vivo retina study at 2.25 MHz in rats (Jiang et al., 2018) showed that neurons frequently exhibit multiple response peaks with a temporal pattern that varies with intensity. We have seen similar effects using 1.9 MHz. Our intensity levels at 1.9 MHz are approximately one order of magnitude greater those used by Jiang et al. (2018), which could be due to species differences in either mechanical properties or biophysical mechanisms. The rat retina contains blood vessels making it mechanically stiffer, and salamander retina somas are relatively large (15 μm diameter). Or there may be a different distribution of mechanosensitive ion channels.

Relationships to in vivo studies

The models shown in Figure 8 demonstrate that, when the focal volume is not controlled for, the larger focal volume at low frequency may have a profound effect on the acoustic frequency dependence. Although it may be possible to explain both retinal and in vivo results with a single unifying model, the extent to which focal volume has played a role in previous in vivo studies is unknown. As is typical in many studies, the relationship between the ultrasound focal volume and the target structure is not unknown. Our model suggests that the spatial overlap of the ultrasound field and the target structure are important in measuring the effect of acoustic frequency, and that optimized and customized targeting of brain tissue in each experiment is important in creating interpretable results. Some kind of measurement technology is needed to verify where the ultrasound focus is actually located in the brain and what area of the brain is activated to make in vivo behavioral results interpretable. How likely is it that the activated brain region is off-target for in vivo rodent work? When determining the spatial location of the transducer that produces the highest probability of a behavioral response, large variability in this spatial map was found across mice when tested at relatively higher frequencies (1.4–2.9 MHz) (Ye et al., 2016, their Fig. S15). This spatial variability most likely arises from the ultrasound focus targeting different areas of the brain in different mice, even when the external location of the transducer is intended to be the same.

In addition, the interpretation of some in vivo results is potentially confounded by the possibility of inadvertent stimulation of the auditory pathway when ultrasound is modulated in the range of audible frequencies (Guo et al., 2018; Sato et al., 2018). This modulation in the audible frequency range was not done in the studies of Ye et al. (2016), and CW stimuli were used. The challenge for future studies is to find that region of ultrasound stimulus parameter space that generates direct neurostimulation without the auditory confound. Our studies of the ex vivo retina are, of course, free from auditory effects, thus making it a useful system to study the parameter space of direct neurostimulation. Our exploration of the stimulus parameter space has shown that a CW pulse of relatively long duration (e.g., 100 ms; Fig. 6b) has the lowest threshold. Notably, for the in vivo mouse model, a CW pulse of 80 ms was determined to be optimal (Ye et al., 2016). In the domain of CW pulses, there are fewer stimulus parameters (duration, intensity, and spatial location of the transducer for in vivo experiments), making it relatively easier to cover the entire relevant stimulus parameter space as we did in Figure 6a. The introduction of a PRF increases the dimensionality of the stimulus parameter space by adding modulation frequency and duty cycle, making it impractical to explore the entire stimulus parameter space in addition to the confound of stimulating hair cells in the cochlea. Guo et al. (2018) used CW pulses of ≤10 ms; and although Sato et al. (2018) used 80 ms pulses, they were not CW (a PRF of 1.5 kHz is in the audible range). Neither study used longer duration CW pulses, as we have done here. The difficulty in exploring such a large parameter space is a strong motivating factor to develop a theory of ultrasonic neurostimulation that can guide us to the optimal stimulus. One can view stimulation of auditory or vestibular organs as being an off-focus activated brain region where low frequencies will be more effective due to their larger focal volumes as demonstrated in Figure 8. Recent research has demonstrated how to avoid auditory stimulation by smoothing the sharp edges on an 80 ms CW pulse of ultrasound, thereby eliminating the auditory brainstem response without affecting motor responses in normal hearing mice (Mohammadjavadi et al., 2019).

A number of studies have looked at standing waves in rodent skulls, by both measurement and simulation (O'Reilly et al., 2010; Younan et al., 2013; Constans et al., 2017). The small skull size combined with sub-MHz frequencies that are not well focused in the axial direction will generate standing waves as a consequence of reflections off the opposite side of the head. These uncontrolled standing waves have the potential to stimulate parts of the brain that were not targeted.

Pattern Interference Radiation Force (PIRF) neural stimulator

The conventional approach to ultrasonic neurostimulation is to use a single transducer with a focus at the target (Fig. 10a). This produces radiation force, maximal at the focus, that will tend to generate tissue displacement in the axial direction, as well as strain. Deriving from our observations that the ultrasound transducer and MEA create a cavity that generates standing waves that influence the response, we propose the use of two opposing ultrasonic transducers for ultrasonic neurostimulation. This geometry will compress neural tissue (at nodes) and stretch other tissue (at antinodes), thus maximizing strain at very low power. From the acousto-fluidics literature, it is well known that there are two basic methods for generating standing waves in a resonant cavity (Lenshof et al., 2012). A single transducer generates a wave that reflects off an opposing surface (equivalent to our ex vivo setup with the array being the reflective surface). Alternatively, one can use two opposing transducers, which is much more practical for stimulating the in vivo brain. Two opposing transducers are also more versatile, giving independent control over carrier frequency, phase, and temporal envelope. By generating a focused standing wave between two opposing transducers (Fig. 10b), the resulting high-frequency oscillation (period λ/2) in radiation force will stretch tissue located at high-pressure areas and compress tissue located in low-pressure areas. With two opposing transducers, the focal region will be defined by the physical location of the transducers, but if each transducer is replaced by a phased array of transducers, then the focal regions (potentially multiple foci stimulated at independent times) can be determined electronically. PIRF multifocal stimulation with variable time delays could be useful to exploit synaptic plasticity to strengthen or weaken synaptic connections between different brain regions with all of the parameters under electronic control.

Figure 10.

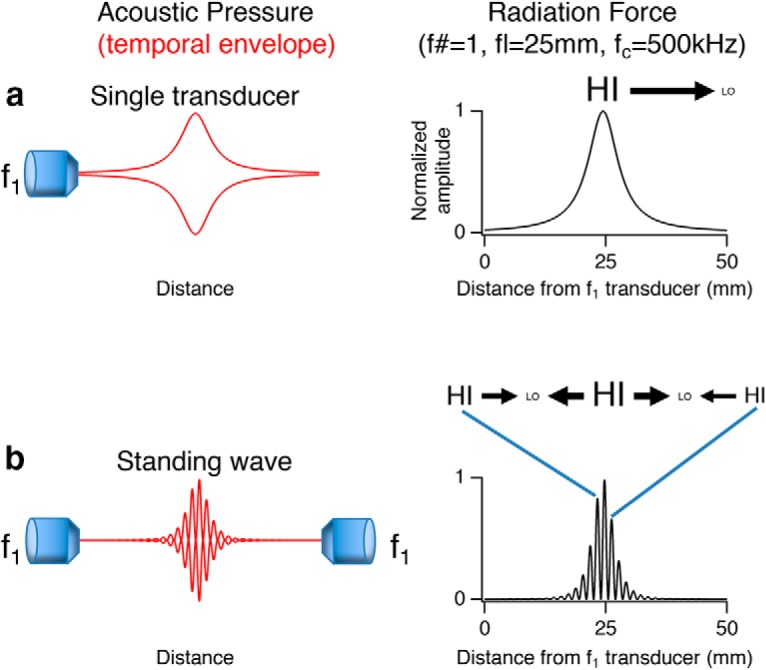
Design of PIRF neural stimulator. Left, Diagrams of acoustic pressure for various transducer configurations. Red traces represent the envelope of the acoustic pressure in time. Right, Radiation force in axial direction computed for a transducer of focal length 25 mm (f# = 1 and carrier frequency = 500 kHz) for the different transducer configurations. Black arrows indicate the direction and relative magnitude of radiation force from HI (high pressure region) to LO (low pressure region). a, The simplest case of a single transducer. b, Radiation force for two transducers operating at the same frequency with overlapping focal volumes to generate a standing wave.

One ultrasonic neuromodulation study used two confocal transducers operated at 1.75 and 2.25 MHz to generate a beat pattern at 500 kHz (Mehic et al., 2014). However, a 500 kHz difference frequency is likely too large to be optimally effective. In comparison, vibro-acoustography generally uses difference frequencies in the range of 20–100 kHz to mechanically vibrate tissue via dynamic radiation force to measure elasticity (Doherty et al., 2013).

Pulsed radiation force can produce confounds

Many published studies (for review, see Naor et al., 2016) have claimed that “pulsatile” ultrasound (i.e., modulating the carrier with a square wave) is more effective stimulus than CW, often with a PRF in the 1–2 kHz range, but no theoretical reason has been given to explain why. Studies showing that ultrasound can act through an auditory pathway also show that 1 kHz PRF was most effective (Guo et al., 2018). There is at least one report of normal human subjects with earplugs inserted hearing high-frequency tones that are correlated with the intensity and PRF of transcranial Doppler ultrasonic imaging (Magee and Davies, 1993). Although it is still unclear how activation of the auditory system might influence the many behavioral or neural recordings, our results suggest that radiation force would translate the envelope of stimulation (i.e., the PRF into a mechanical stimulus). The direct conversion of the envelope of the stimulus to a mechanical stimulus through radiation force could explain why pulse repetition frequencies in the audible range are chosen as being more effective. In vivo researchers should address this potential confound, such as by using deafened animals, using continuous stimuli (King et al., 2014;Ye et al., 2016), or smoothing the edges of ultrasound pulses to reduce audible frequency components (Wattiez et al., 2017; Mohammadjavadi et al., 2019). Other potential confounds to direct brain stimulation in addition to the auditory system are activation of the vestibular and somatosensory systems. Direct measurements of brain activity will be important as opposed to relying exclusively on behavioral outcomes.

In conclusion, there exists a strong theoretical and empirical understanding of using radiation force to exert mechanical strain in the fields of acousto-fluidics (Bruus, 2012; Lenshof et al., 2012) and elasticity imaging (Doherty et al., 2013). Here we show a new application of these principles to ultrasonic neurostimulation. Our findings suggest that future approaches to ultrasonic neurostimulation should explore the parameter space defined by these alternative methods of generating radiation force. An understanding of the physical mechanism of action will allow studies in this area to pursue how radiation force might be manipulated to optimize stimulation in different applications and simultaneously provide insights into biophysical mechanisms.