Investigating mechanisms of tendon damage by measuring multi-scale recovery following tensile loading

Abstract

Tendon pathology is associated with damage. While tendon damage is likely initiated by mechanical loading, little is known about the specific etiology. Damage is defined as an irreversible change in the microstructure that alters the macroscopic mechanical parameters. In tendon, the link between mechanical loading and microstructural damage, resulting in macroscopic changes, is not fully elucidated. In addition, tendon damage at the macroscale has been proposed to initiate when tendon is loaded beyond a strain threshold, yet the metrics to define the damage threshold are not determined. We conducted multi-scale mechanical testing to investigate the mechanism of tendon damage by simultaneously quantifying macroscale mechanical and microstructural changes. At the microscale, we observe full recovery of the fibril strain and only partial recovery of the interfibrillar sliding, indicating that the damage initiates at the interfibrillar structures. We show that non-recoverable sliding is a mechanism for tendon damage and is responsible for the macroscale decreased linear modulus and elongated toe-region observed at the fascicle-level, and these macroscale properties are appropriate metrics that reflect tendon damage. We concluded that the inflection point of the stress-strain curve represents the damage threshold and, therefore, may be a useful parameter for future studies. Establishing the mechanism of damage at multiple length scales can improve prevention and rehabilitation strategies for tendon pathology.

1. Introduction

Tendon pathology, including pain and dysfunction, is common in both sports and occupational settings, and there is a need to understand the source of pathology to improve prevention and rehabilitation strategies [1,2]. Many studies associate tendon pathology with microstructural changes and damage initiated by mechanical loading [3–9], yet the specific etiology of tendon damage remains unknown. Although many studies have addressed damage in tendon, quantification of tendon damage remains challenging, in part because a precise definition with appropriate engineering context, has generally not been used for tendon.

In this study, we define damage, consistent with the definition established in engineering and applied to other materials, as an irreversible change in the microstructure that alters the macroscopic mechanical parameters [10]. Examples of microstructural changes include microcracks in metals [10–13], interlamellar debonding in polymers [14,15], matrix microcracking in composites [16,17], and voids in ceramics [18]; all of these irreversible rearrangements in microstructure produce impaired macroscopic mechanical properties, such as lowered modulus, are initiated by microscale deformation. In tendon, histological [19] and microscopic [20,21] studies have shown microstructural changes that appear to represent damage, however, these were not directly linked to mechanics. Similarly, changes to macroscale mechanical behavior such as reduced modulus and decreased failure stress and strain are well-known when tendon is loaded to high stresses and/or for multiple cycles [1,6,22–24]. While these are likely in response to microstructural damage, the link to microstructural change is not fully elucidated. Thus, evaluation of tendon at multiple length scales to identify the microstructural source is a critical aspect in the study of tendon damage.

Another key feature in the definition of damage, in addition to microstructural changes described above, is that it must be irreversible. Tendon, due to its viscoelastic properties, can partially recover its macroscale mechanical properties after loading [21,25]. However, many studies attempted to quantify the macroscale mechanical response immediately after loading, without decoupling the effects of time-dependent recovery from permanent change [26,27]. Quantification of damage must distinguish between the irreversible (non-recoverable, permanent) and recoverable changes in mechanical parameters (strictly related to mechanical effects, separate from cell contributions to healing).

The microstructural location for tendon damage is unclear. Some studies have identified structural changes of fibrils in the form of collagen kinking and discontinuities [20,22] or increase in D-period [28], while other studies suggest damage is localized to the interfibrillar structure, which connects adjacent collagen fibrils together [26,29]. It is possible that both occur or that damage in one location may precede the other. Mathematical shear lag modeling of tendon has suggested that plastic deformation of the interfibrillar structure replicates the macroscale mechanical behavior of tendon fascicles (matching the equilibrium stresses and predicting fibril strain); however, elastic deformation of fibrils cannot replicate this macroscale mechanical behavior [29,30]. Thus, shear lag modeling suggests that microstructural damage is localized to the interfibrillar structure and produces the observed changes in mechanical response at the fascicle-level. In this study we aim to experimentally identify the microstructural source of damage by investigating tendon structure and deformation at the fibril-level. Throughout this study, as in previous work [28–35], we define the microscale structures observed using confocal microscopy as “fibril-level” because they are at the hierarchical level below the tendon fascicle and there is no evidence of fibers in the tissue [32,36].

Damage in tendon at the fascicle-level has been proposed to initiate when tendon is loaded beyond a strain threshold [37–40], but metrics to define the damage threshold are not well established. While some studies use a non-recoverable length change (i.e., laxity) to identify the threshold [41–43], others use the beginning of strain-softening behavior [22,44]. A recent study hypothesized that the inflection point in the stress-strain curve, which marks the point where the response shifts from strain-stiffening to strain-softening, may mark the damage threshold in soft tissue [45]. Thus, we will investigate if the inflection point in the stress-strain curve represents the initiation of damage.

In summary, the objective of this study was to elucidate the tendon damage mechanisms. The key definition of damage, an irreversible change in the microstructure that alters the macroscopic mechanical parameters, was applied. Microstructural changes were quantified at the fibril-level and macroscale mechanical changes were simultaneously quantified at the fascicle-level. Experiments were designed to ensure damage was measured only as a non-recoverable change in mechanical behavior by allowing the tissue to recover after applying potentially damaging loading, and the threshold for damage initiation was determined. Understanding the mechanism of damage can improve prevention and rehabilitation strategies for tendon pathology.

2. Methods

2.1. Sample preparation

Rat tail tendon fascicles were harvested from eleven 6–8 month old Sprague-Dawley male rats that were sacrificed for a separate lACUC-approved study. These tails were previously frozen at −20 C, where the maximum number of freeze thaw cycle was limited to three [46,47]. Our pilot study showed that there was no effect of freezing on tissue for any of the mechanical testing parameters [47]. On the day of the experiment, each fascicle was dissected from a tail. We stained each sample with 10 μg/ml 5-DTAF (5-(4,6-Dichlorotriazinyl) aminofluorescein, Life Technologies) to minimize the effect of DTAF on mechanics [31]. We tested on a custom-made uniaxial testing device with PBS bath mounted on an inverted confocal microscope (LSM 5 LIVE, objective Plan-Apochromat 10x/0.45) as previously described [29]. Each sample was soaked in PBS to stabilize pH at room temperature for at least 3 h before testing to allow the sample to reach equilibrium, which was determined by monitoring cross-sectional area in our pilot study. ln addition, all the samples were kept at room temperature from the beginning of DTAF staining to the end of mechanical testing.

2.2. Mechanical testing protocol

Mechanical testing on a total of 8 groups with n = 7 fascicles per group was performed. Each fascicle was randomly assigned to a strain level 2, 4, 6, or 8%, while also randomizing the number of freeze-thaw cycles for each strain group (on average 2 freeze-thaw cycles were used per group). In addition, within each strain level, each fascicle was randomly assigned to either “No Rest” or “Rest” group. We preloaded each fascicle to 0.5 g (~5 mN) to define the reference length and preconditioned with 5 cycles of 4% grip strain (i.e., grip-to-grip displacement). After ramping to its target strain level, we held the strain level constant for 15 min to reach equilibrium, followed by unloading to the reference length. The “No Rest” or “Rest” group was used to compare the effect of 60-min unloaded rest on fascicle-level parameters and separate the recoverable from non-recoverable deformation (Fig. 1). The No Rest group was immediately loaded to failure after unloading, whereas the Rest group was held at its reference length for 60 min before loading to failure.

Fig. 1.

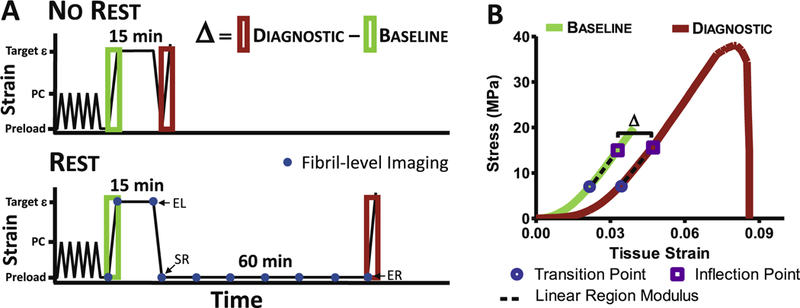
Mechanical loading profile schematic. (A) Definition of Δ = Diagnostic − Baseline was used to quantify damage when loaded to target ε (i.e., strain levels 2,4,6 or 8%) after preconditioning (PC). For No Rest group, fascicle was loaded to failure immediately after unloading, whereas Rest group was allowed to rest for 60 min at the reference length before loading to failure. The blue dots represent when confocal images were taken for quantifying fibril-level deformation. EL (end of loading), SR (start of rest), and ER (end of rest) marked on the figure are used for calculating fibril-level recovery. (B) Representative stress-strain curve with fascicle-level parameters. All the loading and unloading rates were 1%/s. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The fascicle-level parameters calculated from the initial ramp were defined as “Baseline” and the parameters calculated from the ramp-to-failure were defined as “Diagnostic” (Fig. 1). Note that the parameters quantified at the Baseline for all four strain levels and both No Rest and Rest groups are identical. The strain rate for all loading and unloading was 1%/s, and only the fascicles that failed in the mid-substance were included in the following analysis. We excluded samples that failed at the grip (n = 2) or slipped during preconditioning (n = 3) from this study and additional fascicles were added to achieve desired sample size. Thus, all the samples failed at mid-substance.

2.3. Data acquisition

To measure the tissue strain, we applied two ink markers directly on the tendon using a permanent marker, and imaged with CCD camera to track displacement of markers using digital image correlation (Vic 2D, Correlated Solutions). In addition, we quantified the transverse strain and fibril-level parameters (i.e., fibril strain and interfibrillar sliding) using a confocal microscope. The confocal image stacks (15 fps; 0.94 × 0.94 × 4.351 μm pixel⁻¹) were taken after preconditioning to reconstruct the cross-sectional profile of each sample. This profile was fitted with an ellipse to determine the sample cross sectional area by measuring both the major and minor axes. We acquired images at 10 time points, represented by blue dots (Fig. 1A): after preconditioning (i.e., reference image), at the beginning and end of the relaxation period, and every 10 min during the 60-min rest period. Note that data for No Rest group can only be quantified after preconditioning, at the beginning and end of the relaxation period. Thus, we only report data acquired using confocal microscope for Rest groups, but we have carried out identical staining and imaging procedure for both No Rest and Rest groups.

2.4. Data analysis

2.4.1. Fascicle-level parameters

The fascicle-level stress-strain (σ-ε) data up to inflection point, defined as a point where the stress-strain curve shifts from strain-stiffening to strain-softening [45], was used to determine the transition point and modulus. This was to ensure that we were quantifying the modulus of the linear region before strain-softening (Fig. 1B). The inflection point was calculated by fitting a cubic smoothing spline using the csaps function in MATLAB and finding the first zero crossing point of the second derivative.

The σ-ε data from zero to the inflection point was then fit with a nonlinear constitutive model (Eq. (1)) to simultaneously calculate linear region modulus (E), transition strain (p), and transition stress (q), where the transition point was defined as the end of the non-linear toe-region (Fig. 1B) [48]:

$$\sigma =\left\{\begin{array}{ll}A(\exp (B\epsilon )-1),\hfill & \forall \epsilon \le p\hfill \\ E(\epsilon -p)+q,\hfill & \forall \epsilon >p\hfill \end{array}\right\}$$ (1)

This equation was fully defined by three parameters: p and the constants A and B. Using the MATLAB function fmincon, the parameter values (A, B, and p) were simultaneously optimized to minimize the mean square error. To describe tendon nonlinear behavior, we chose a widely used exponential model. By using the constitutive model and optimization, the continuity between the toe and linear region is enforced and the quantification of parameters is objective and reproducible.

The fascicle-level parameters including the linear region modulus, transition strain, transition stress, inflection point strain, and inflection point stress were calculated for both Baseline and Diagnostic. To quantify the effect of damage, we calculated the change in each parameter (Δ), defined as Δ = Diagnostic − Baseline (Fig. 1). In case of no damage, the values of the parameters for the Diagnostic and Baseline are the same and the Δ is zero. In contrast, the Δ is a non-zero value if there is an observable effect of damage. The linear region and inflection point occur above the 2% grip strain, so we excluded the Baseline 2% strain group data for the linear region modulus, inflection point strain, and inflection point stress (Appendix A).

The ultimate stress and strain were also quantified for the fascicles that failed within the load cell limit of 10 N. The fascicles that did not fail were excluded in the ultimate stress and strain analyses but included in all the other analyses. In total for the 2, 4, 6, and 8% strain levels, respectively, the number of fascicles excluded in the ultimate stress and strain analyses were n = 3, n = 1, n = 1, and n = 2 for No Rest groups and n = 2, n = 1, n = 2, and n = 0 for Rest groups.

The transverse strain (ε_T) was calculated by measuring the change in fascicle width (w), where w was the major axis of the cross-sectional profile acquired from confocal images, as ε_T = (w_o − w_i)/w_o), where w_o is the reference width and w_i is width at the strain increment of interest. The confocal images were used instead of CCD camera images to quantify transverse strain since the resolution of ccD camera is not high enough to measure small changes in sample width. In addition, we fitted an exponential decay function, f (t) = A * exp(−t/τ) + C, where A and C are constants, to quantify the transverse strain recovery response by quantifying the time constant (τ).

2.4.2. Fibril-level parameters

Using a confocal microscope, four lines were photobleached perpendicular to the fibril direction and separated by 200 μm to measure the fibril-level deformations. The lines were tracked to calculate the fibril strain and interfibrillar sliding, a measurement for deformation of interfibrillar structure, as previously described [29]. The fibril strain was defined as the change in distance between pairs of photobleached lines, and the interfibrillar sliding was defined as the average tortuosity (i.e., waviness) of all four lines (Supplementary Material 1).

The interfibrillar sliding was decomposed into recoverable (i.e., elastic and viscoelastic) and non-recoverable portions from the values for interfibrillar sliding at the end of loading (EL), start of rest (SR), and end of rest (ER), Fig. 1A. The elastic sliding recovery, defined as the instantaneous recovery upon unloading, was calculated as:

$$\frac{EL-SR}{EL}\times 100\%$$ (2)

The viscoelastic sliding recovery, defined as the time-dependent recovery at ER after subtracting out the elastic sliding recovery, was calculated as:

$$\frac{SR-ER}{EL}\times 100\%$$ (3)

Finally, the non-recoverable sliding was defined as the percentage of permanent sliding that remained at ER. It was calculated as the sliding value at EL minus the elastic and viscoelastic recovery. We also fit an exponential decay equation, f (t) =A * exp(−t/τ) + C, to the interfibrillar sliding recovery response to quantify the time constant (τ) and to confirm that 60-min rest period was sufficient time to reach equilibrium.

Two fascicles from the 8% strain level, one each for No Rest and Rest groups, were removed for both fascicle-and fibril-level analyses because the Δ linear region moduli for these samples were more than two standard deviations from the population average. For the fibril-level analysis, one additional sample from Rest group at the 8% strain level had diffused photobleached lines and was removed only for the fibril-level analysis. For the fascicle-level analysis, the final reported sample size was n = 7, n = 7, n = 7, and n = 6 for both No Rest and Rest groups at the 2, 4, 6, and 8% strain levels, respectively. For the fibril-level analysis, the final reported sample size was n = 7, n = 7, n = 7, n = 5 for Rest group at the 2, 4, 6, and 8% strain levels, respectively.

2.5. Statistical methods

All the statistical analyses were conducted using Graphpad Prism. To determine which fascicle-level parameters exhibit strain dependency, each of the parameters including Δ transition strain, Δ transition stress, Δ linear region modulus, Δ inflection point strain, and Δ inflection point stress was correlated with tissue strain by fitting a linear regression line. We chose not to conduct ANOVA for our statistics because the quantified tissue strain varied within the same grip strain group. In addition, correlations can provide continuous strain dependent mechanical behavior of tendon. Thus, separating groups in terms of strain levels to perform ANOVA is not ideal. The extra-sum-of-squares F-test was performed to determine the effect of the 60-min rest period on fascicle-level parameters by comparing the slopes of linear regression between the No Rest and Rest groups. In addition, each of the three decomposed interfibrillar sliding components (i.e., elastic recovery, viscoelastic recovery and non-recovery) was correlated with tissue strain by fitting a linear regression line to determine the level of strain dependency of damage at the fibril-level. similarly, the non-recoverable sliding was correlated with Diagnostic linear region modulus, Diagnostic transition strain, and Diagnostic inflection point strain to relate the damage at the fibril-level to the changes of mechanical response at the fascicle-level. The significance was set at p = 0.05 and Pearson’s correlation (r) is reported.

3. Results

3.1. Fascicle-level parameters

At the fascicle-level, tendon experienced a permanent change in mechanical parameters (i.e., macroscale observation of damage) that was strain-dependent (Fig. 2, Table 1). For Rest groups, the Δ transition strain increased (Fig. 2A, p < 0.0001) with applied tissue strain and the Δ linear region modulus decreased with applied tissue strain (Fig. 2C, p< 0.0005). The Δ inflection point strain (Fig. 2D, p< 0.0005) and A inflection point stress (Fig. 2E, p < 0.005), and the ultimate strain (supplementary Material 2A, p < 0.01) were also dependent on the applied tissue strain. These results show that damage is strain dependent. some parameters including the Δ transition stress (Fig. 2B) and ultimate stress (Supplementary Material 2B) did not exhibit strain dependency. In addition, the modulus values are similar to previous rat tail tendon results (Appendix A) [29,49,35] and fascicles were loaded to the same magnitude of physiological stress [50]. The fascicle-level parameters that are strain-dependent, including the Δ transition strain, linear region modulus, inflection point strain, and inflection point stress, may be used as macro-scale metrics to quantify damage.

Fig. 2.

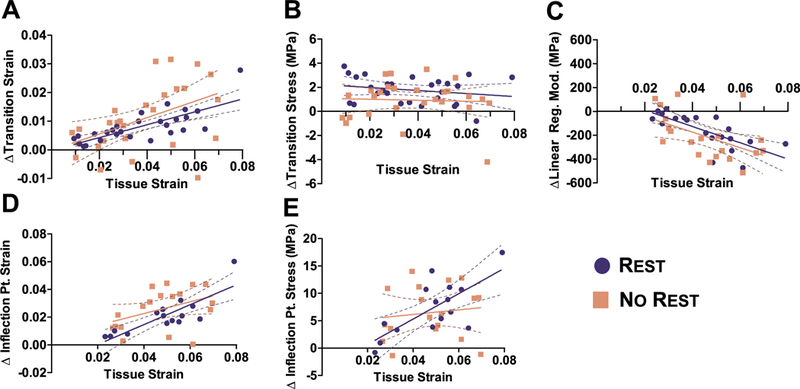
Fascicle-level tensile behavior. At the fascicle-level, tendon experienced a permanent change in mechanical parameters that was strain-dependent for (A) Δ transition strain, (C) Δ linear region modulus, (D) Δ inflection point strain, and (E) stress, but not for (B) Δ transition stress for Rest group. For any of the parameters, there was no difference between the slopes of No Rest and Rest groups, suggesting the 60-min rest period does not alter the fascicle-level parameters and verifies that parameters measured are non-recoverable.

Table 1.

Summary of Pearson’s correlation and p-value for No Rest and Rest. All parameter that have p-value < 0.05 are bolded and Pearson’s correlation that have values greater than ±0.70 are italicized.

	No Rest		Rest		No Rest vs. Rest
	p-value	r	p-value	r	p-value
Δ Transition Strain	<0.05	0.47	<0.0001	0.73	0.59
Δ Transition Stress (MPa)	0.82	0.42	0.28	−0.21	0.68
Δ Linear Region Modulus (MPa)	<0.0005	−0.66	<0.0001	−0.76	0.88
Δ Inflection Pt. Strain	0.083	0.42	<0.0005	0.83	0.30
Δ Inflection Pt. Stress (MPa)	0.61	0.12	<0.005	0.72	0.08
Ultimate Strain	<0.05	0.44	<0.01	0.53	0.81
Ultimate Stress (MPa)	<0.05	−0.50	0.12	−0.34	0.19

Although only Rest group is needed to separate recoverable viscoelastic effects from damage, we also included No Rest group to study the effect of viscoelastic recovery on mechanical parameters. Ultimately, there was no difference between the slopes of No Rest and Rest for any parameters (Fig. 2, Table 1). For both No Rest and Rest groups, the Δ transition strain (Fig. 2A, p<0.05), Δ linear region modulus (Fig. 2c, p < 0.0005), and ultimate strain (supplementary Material 2A, p < 0.05) were significantly correlated with applied strain. However, a few parameters in No Rest had different set of significant correlations than seen in the Rest group. For example, the correlation of ultimate stress (supplementary Material 2B, p < 0.05) was significant only for No Rest group, Δ inflection point strain and stress did not show strain dependency for No Rest group. The different set of significant correlations between two groups might be attributed to a minor role of viscoelasticity or experimental variation, since there was no statistical difference between the slopes of two groups. The summary of statistical analyses with Pearson’s correlations and p values are included in Table 1. No difference between the two groups suggest the 60-min rest period does not alter the fascicle-level parameters and verifies that parameters measured are non-recoverable.

Not only do the strain-dependent correlations suggested tendon damage, the x-intercept of these correlations suggest the damage threshold, shown here for Rest group. The x-intercept of the Δ linear region modulus was 0.021 (Fig. 2c), and the x-intercept of the Δ inflection point strain and stress (Fig. 2D and E) was 0.017. Interestingly, these x-intercepts correspond to the averaged Baseline inflection point of the 4, 6 and 8% strain-level tests (Rest: 0.024 ± 0.005, Appendix A), suggesting that the inflection point coincides with the damage threshold at the fascicle-level. In contrast, x-intercept for the Δ transition strain was zero, such that this parameter increased instantaneously when loaded (Fig. 2A), which implies that the transition strain behaves differently than the inflection point strain. We have also included inflection stress and strain measured in grip strain (supplementary Material 3).

Transverse strain fully recovered at all strain levels (Fig. 3A) and the time-dependency of the transverse strain recovery was quantified using an exponential decay function shown above. The time constant ranged from τ = 0.13 min at 2% strain up to τ = 19.3 min at 8% strain and was strain-dependent (Fig. 3B, n = 22). Some samples recovered their transverse strain immediately upon unloading and were not included in the curvefit (n = 5).

Fig. 3.

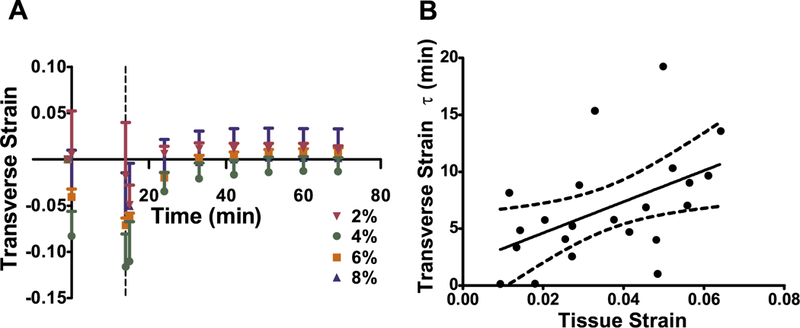
Transverse strain recovery. (A) Transverse strain fully recovered over time for all strain groups. The dashed line represents when samples were unloaded and error bars represent SEM. (B) The transverse τ was dependent on applied tissue strain. The dashed lines represent the 95% confidence intervals.

3.2. Fibril-level parameters

At the fibril-level, the fibril strain fully recovered while the interfibrillar sliding only partially recovered (Fig. 4). The deformation of the load bearing collagen fibrils fully recovered elastically (i.e., instantaneously) in all strain groups (Fig. 4A), indicating that the fibrils are undamaged. On the other hand, the interfibrillar sliding recovery was time-dependent and only partially recovered – up to 50% of the sliding was non-recoverable (Fig. 4B). Fibril strain and sliding during the relaxation period are shown in Supplementary Material 4 and are not further discussed as a similar study was previously conducted [29]. In addition, the time constant (τ) for inter-fibrillar sliding recovery did not show any strain dependency, where the average τ was 7.43 min across all strain levels (Fig. 4C, r = 0.01, p > 0.95). This is further evidence that the 60-min rest period was sufficient for the viscoelastic response to reach an equilibrium, leaving the remaining non-recoverable effects as damage.

Fig. 4.

Fibril-level deformation of tendon fascicles. (A) Fibril strain fully recovered for all strain groups, suggesting that the collagen fibrils are undamaged. On the other hand, (B) interfibrillar sliding only partially recovered, exhibiting damage at the fibril-level. Dashed line represents when samples were unloaded and error bars represent SEM. (C), The interfibrillar sliding τ was strain independent and averaged 7.43 min, suggesting that 60-min rest was long enough for interfibrillar sliding recovery. The dashed lines represent the 95% confidence intervals.

The interfibrillar sliding recovery was decomposed and each component was plotted against tissue strain to quantify damage at the fibril-level (Fig. 5). Elastic sliding recovery (Fig. 5A, r = −0.55, p < 0.005) and non-recoverable sliding (Fig. 5C, r = 0.66, p < 0.0005) both correlated with tissue strain. However, viscoelastic sliding recovery was not correlated with strain (p = 0.44) and averaged 27.5 ± 8.9% across all applied strain levels (Fig. 5B).

Fig. 5.

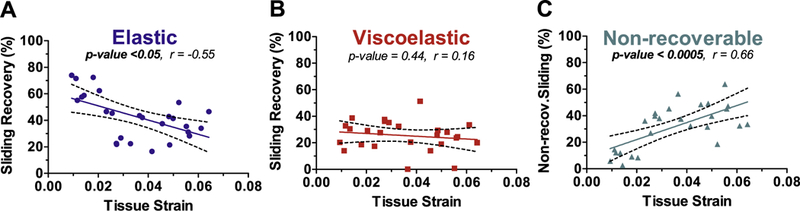
Decomposed interfibrillar sliding recovery. Interfibrillar sliding recovery was decomposed to elastic, viscoelastic, and non-recoverable portions. (A) Elastic recovery decreased with tissue strain while (B) viscoelastic recovery showed no strain dependency. (C) Non-recoverable sliding increased with tissue strain due to the decrease in elastic recovery. The dashed lines represent the 95% confidence intervals.

3.3. Relationship between fascicle and fibril parameters

The non-recoverable sliding observed at the fibril-level was evaluated for correlation with the Diagnostic fascicle-level parameters for Rest group (Fig. 6). The linear region modulus decreased with increasing non-recoverable sliding (Fig. 6A, r = −0.54, p <0.005), and the transition strain increased with increasing non-recoverable sliding (Fig. 6B, r = 0.63, p < 0.001). The inflection point strain also increased with non-recoverable sliding (Fig. 6C, r = 0.64, p <0.0005), while the inflection point stress did not (r = 0.10, p >0.62, data not shown). These correlations support the notion that the non-recoverable sliding at the fibril-level contributes to the mechanical behavior at the fascicle-level, consistent with the definition of tendon damage as an irreversible change in the microstructure that alters the macroscopic mechanical parameters.

Fig. 6.

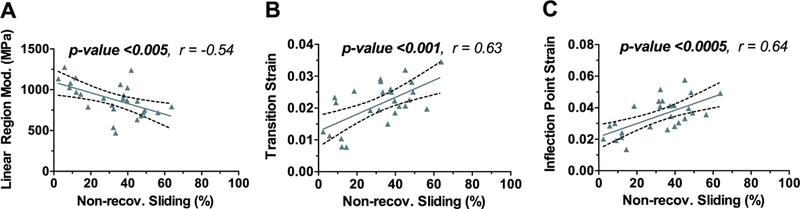
Relationship between fascicle mechanics and non-recoverable sliding. (A) Diagnostic linear region modulus, (B) Diagnostic transition strain, and (C) Diagnostic inflection point strain was dependent on non-recoverable sliding. These correlations support the notion that the non-recoverable sliding at the fibril-level contributes to the mechanical behavior at the fascicle-level. The dashed lines represent the 95% confidence intervals.

4. Discussion

This study quantified tendon damage, an irreversible change in the microstructure that alters the macroscopic mechanical parameters [10], by identifying the microstructural fibril-level changes that correlated with altered macroscopic mechanical parameters at the fascicle-level. Analysis of the fibril-level microscale deformations demonstrated that the fibril strain fully recovered following loading and unloading (Fig. 4A). However, interfibrillar sliding was only partially recoverable, suggesting tendon damage is localized to the interfibrillar structures (Figs. 4B, 5). At the fascicle-level, irreversible mechanical parameter alterations included a strain-dependent increased transition strain (an elongated toe region, Fig. 2A), decreased linear modulus (Fig. 2C), and increased inflection point strain (Fig. 2D). In addition, we demonstrated that the inflection point of the stress-strain curve represents the damage threshold and therefore, may be a useful parameter for future studies.

4.1. Microstructural fibril-level damage and mechanisms

The microstructural observations in this study for full elastic recovery of fibril strain and non-recoverable interfibrillar sliding are consistent with findings for equine common digital extensor tendon, another positional tendon. In that study, the equine tendon fibril elongation showed 90% recovery after tensile loading, while the interfibrillar sliding showed only 50% recovery [26]. The partial non-recoverable interfibrillar sliding (Fig. 4), suggests that tendon damage was localized to the interfibrillar structures. This result directly supports the assumptions made in a previous mathematical shear lag model, where plastic deformation of the interfibrillar structure was the only condition able to replicate experimental observations [30].

This study provides strong evidence that tendon damage first occurs by interfibrillar sliding and is not related to damage in fibrils. We did not see any evidence of ‘fibers’ and the DTAF lines were continuous down to the resolution of optical microscope. Together, this suggests that interfibrillar damage was occurring at a hierarchical level one below the fascicle-level, which is the fibril-level [32,36]. However, this finding for damage in the interfibrillar structure differs from other observations where the damage in the form of collagen fibril kinking and discontinuities were observed after fatigue loading [20,22]. The tendons in these studies, however, were subjected to higher applied strains [22,28,51] or substantial amount of cycle loading [20]. Thus, damage of the load bearing collagen fibrils may occur after interfibrillar sliding damage, when the interfibrillar structures can no longer transmit shear loads. This is partially supported by a recent study where damage in the load bearing collagen fibrils of rat tail tendon was detected by the exposure of the collagen epitope at 7.5% grip strain [52]. The threshold is much larger than the initiation of damage in this study at ~4% grip strain. The relatively low damage threshold in our study implies that damage initiates at the interfibrillar structures and damage on interfibrillar structure may precede the damage on load bearing collagen fibrils.

While this study identified interfibrillar sliding as a mechanism of tendon damage, the compositional structures responsible for interfibrillar sliding elastic recovery (Fig. 5A) and for loss of sliding recovery (Fig. 5C) remain unknown. Although it is hard to draw any conclusion about the component of interfibrillar structure with our optical observations (Supplementary Material 1), it is possible that small diameter collagen fibrils may be the microstructure providing for interfibrillar sliding recovery. The bifurication and fusion of the smaller fibril diameter collagen fibrils between larger fibril have been observed in many studies [53–55]. We recently used serial block-face scanning electron microscopy to demonstrate that a network of small diameter fibrils wrap around and fuse with larger collagen fibrils, suggesting that these smaller diameter fibrils may be the shear load transferring structures [33]. Moreover, digestion of all non-collagenous matrix with trypsin did not affect the interfibrillar sliding in rat tail tendon [33], consistent with GAG digestion studies of macroscale mechanics [56]. Although we and others have previously used the terminology “interfibrillar matrix” to describe the material that provides interfibrillar shear load transfer, we now suggest small diameter collagen fibrils and not “matrix” may be responsible for shear load transfer. Thus, we describe this material as the interfibrillar “structure” to avoid confusion. Further investigation is needed to identify structural contributors to tendon damage, particularly at length scales below the fibril-level [22,28,51,52].

4.2. Macroscale fascicle-level changes reflecting tendon damage

Damage was observed in several fascicle-level mechanical parameters including the transition strain, linear region modulus, and inflection point strain. Therefore, these three parameters can be used as metrics to quantify effect of tendon damage. Although the inflection point stress was strongly dependent on applied strain, it did not correlate with the non-recoverable sliding like other parameters, suggesting inflection point stress may not be a good metric for damage. These fascicle-level metrics are similar to those other studies have utilized, such as tissue lengthening or laxity (which was measured indirectly by Δ transition strain in this study) and linear region modulus for tendon [21,42] and ligament [37,41,43].

4.3. Damage threshold

The study suggests that the damage threshold occurs at the inflection point of the stress-strain curve where strain softening begins (Fig. 1B). Evidence to support this as the damage threshold is that the strain value for the inflection point during Baseline loading was similar to the independent calculations of x-intercepts for the strain dependent fascicle-level parameters (Fig. 2C, D, E). Furthermore, the inflection point strain strongly correlates with the non-recoverable sliding (Fig. 6), suggesting that the inflection point also marks the damage threshold at the fibril-level.

The limitation of the study is that damage was induced with a single type of loading protocol with one strain rate: a ramp at 1%/s to a prescribed strain level that was held static for a 15 min stress relaxation. it is possible that different mechanisms of damage with other types of loading can occur, particularly with cyclic loading. in addition, it is unknown whether damage occurred during loading (i.e., as soon as tendon was stretched beyond a damage threshold) or damage occurred during the holding (stressrelaxation) period. Future studies will need to address the role of loading rate [57] and viscoelasticity [52]. Indeed, we performed cyclic preconditioning at 4% grip strain, which is presumably above the threshold of the static stress relaxation protocol we performed. However, our pilot data showed there was no difference in any of the fascicle-level parameters between 2% and 4% preconditioning level (Supplementary Material 5). Thus, not only the strain magnitude but also the loading type (i.e., static vs. cyclic) and duration (i.e., 10 s vs. 15 min) of loading may have different contributions to damage. In addition, the rat tail tendon fascicle is a model system that can elucidate fundamental mechanics of tendon, yet the damage mechanism in other tendons, especially the ones that bear higher loads may be different [26,58]. Future studies need to address factors that can contribute to damage mechanism.

4.4. Irreversible damage versus viscoelastic recoverable effects

The experimental design, where the damage-inducing loading and stress relaxation was followed by 60-min rest, was important to separate irreversible damage from viscoelastic effects. Two viscoelastic effects were measured: the transverse strain recovery (Fig. 3) and the viscoelastic portion of the interfibrillar sliding recovery (Fig. 5B). It is likely that both of these viscoelastic responses were governed by fluid flow [59,60]. As predicted by biphasic theory, tensile stress-induced contraction in transverse direction is governed by fluid exudation during loading [60,61] and the recovery of transverse strain should be caused by fluid influx back into the tissue. The transverse strain fully recovered for all strain groups without any non-recoverable portion (Fig. 3) and the time constant, while strain dependent, was between 5 and 15 min. In addition, the viscoelastic portion of interfibrillar sliding recovery was not strain dependent (Fig. 5B) and had a time constant of 7.4 min, similar in magnitude to the transverse strain recovery. Thus, this study design successfully separated irreversible damage from viscoelastic, likely fluid-flow based, effects.

5. Conclusion

This study used multi-scale mechanics to experimentally elucidate tendon damage mechanisms, where damage was defined as an irreversible change in the microstructure that alters the macroscopic mechanical parameters. Key advances of this study were that damage was measured as non-recoverable change in mechanical behavior (by allowing the tissue to recover after applying potentially damaging loading) and the threshold for damage initiation was determined. In contrast to the observed full recovery of the load bearing collagen fibrils, the interfibrillar sliding only partially recovered, indicating that the damage was localized to the interfibrillar structures. We concluded that non-recoverable sliding is a mechanism for tendon damage and is responsible for the decreased linear modulus and elongated toe-region observed at the fascicle-level. These fascicle level changes in transition strain (end of the toe region) and linear region modulus are therefore appropriate metrics of tendon damage. We also demonstrated that the inflection point of the stress-strain curve can successfully mark the threshold of damage in tendon. Understanding the mechanism of damage at the fibril-level and consequent changes in tendon mechanical response at the fascicle-level can improve prevention and rehabilitation strategies for tendon pathology.

Statement of Significance.

Tendon pathology is associated with mechanically induced damage. Damage, as defined in engineering, is an irreversible change in microstructure that alters the macroscopic mechanical properties. Although microstructural damage and changes to macroscale mechanics are likely, this link to microstructural change was not yet established. We conducted multiscale mechanical testing to investigate the mechanism of tendon damage by simultaneously quantifying macroscale mechanical and microstructural changes. We showed that non-recoverable sliding between collagen fibrils is a mechanism for tendon damage. Establishing the mechanism of damage at multiple length scales can improve prevention and rehabilitation strategies for tendon pathology.

Appendix A.

Baseline and Diagnostic values for fascicle-level parameters. Table includes Baseline and Diagnostic values for fascicle-level parameters for both No Rest and Rest groups (average ± SD).

		2%		4%		6%		8%
		No Rest	Rest	No Rest	Rest	No Rest	Rest	No Rest	Rest
Transition	Baseline	0.013 ± 0.006	0.010 ± 0.006	0.014 ± 0.006	0.015 ± 0.006	0.017 ± 0.009	0.017 ± 0.005	0.020 ± 0.009	0.016 ± 0.009
Strain	Diagnostic	0.015 ± 0.006	0.014 ± 0.006	0.021 ± 0.003	0.021 ± 0.005	0.064 ± 0.089	0.026 ± 0.004	0.042 ± 0.009	0.030 ± 0.016
Transition	Baseline	4.39 ± 1.22	2.26 ± 0.50	4.40 ± 1.2	5.02 ± 1.15	5.48 ± 1.99	5.30 ± 1.28	6.32 ± 2.63	4.89 ± 1.61
Stress (MPa)	Diagnostic	4.57 ± 4.52	4.70 ± 1.60	5.86 ± 1.39	6.49 ± 1.25	6.99 ± 1.84	6.83 ± 1.69	6.71 ± 1.80	6.68 ± 2.25
Linear Reg.	Baseline			973 ± 176	976 ± 233	1010 ± 172	872 ± 170	895 ± 120	984 ± 220
Mod (MPa)	Diagnostic	1315 ± 356	1082 ± 115	923 ± 185	936 ± 217	771 ± 263	736 ± 126	526 ± 155	653 ± 156
Inflection	Baseline			0.021 ± 0.004	0.022 ± 0.002	0.025 ± 0.008	0.024 ± 0.005	0.028 ± 0.007	0.022 ± 0.009
Pt. Strain	Diagnostic	0.024 ± 0.006	0.024 ± 0.007	0.033 ± 0.004	0.032 ± 0.005	0.050 ± 0.010	0.047 ± 0.006	0.063 ± 0.007	0.051 ± 0.020
Inflection	Baseline			13.4 ± 2.24	16.0 ± 2.73	14.0 ± 3.82	12.3 ± 2.75	13.9 ± 3.51	14.3 ± 6.02
Pt. Stress (MPa)	Diagnostic	16.7 ± 11.1	16.0 ± 7.98	16.5 ± 2.85	16.3 ± 3.11	22.7 ± 3.53	22.6 ± 2.46	20.7 ± 6.28	24.8 ± 10.7
Ultimate Strain		0.081 ± 0.038	0.078 ± 0.020	0.088 ± 0.019	0.082 ± 0.017	0.100 ± 0.019	0.092 ± 0.010	0.107 ± 0.009	0.097 ± 0.019
Ultimate Stress (MPa)		61.6 ± 9.11	50.0 ± 7.04	47.7 ± 11.1	45.7 ± 9.80	49.7 ± 11.1	49.3 ± 2.76	32.0 ± 9.34	52.4 ± 20.9