Bayesian Estimation of Causal Direction in Acyclic Structural Equation Models with Individual-specific Confounder Variables and Non-Gaussian Distributions

Abstract

Several existing methods have been shown to consistently estimate causal direction assuming linear or some form of nonlinear relationship and no latent confounders. However, the estimation results could be distorted if either assumption is violated. We develop an approach to determining the possible causal direction between two observed variables when latent confounding variables are present. We first propose a new linear non-Gaussian acyclic structural equation model with individual-specific effects that are sometimes the source of confounding. Thus, modeling individual-specific effects as latent variables allows latent confounding to be considered. We then propose an empirical Bayesian approach for estimating possible causal direction using the new model. We demonstrate the effectiveness of our method using artificial and real-world data.

1. Introduction

Aids to uncover the causal structure of variables from observational data are welcomed additions to the field of machine learning (Pearl, 2000; Spirtes et al., 1993). One conventional approach makes use of Bayesian networks (Pearl, 2000; Spirtes et al., 1993). However, these suffer from the identifiability problem. That is, many different causal structures give the same conditional independence between variables, and in many cases one cannot uniquely estimate the underlying causal structure without prior knowledge (Pearl, 2000; Spirtes et al., 1993).

To address these issues, Shimizu et al. (2006) proposed LiNGAM (Linear Non-Gaussian Acyclic Model), a variant of Bayesian networks (Pearl, 2000; Spirtes et al., 1993) and structural equation models (Bollen, 1989). Unlike conventional Bayesian networks, LiNGAM is a fully identifiable model (Shimizu et al., 2006), and has recently attracted much attention in machine learning (Spirtes et al., 2010; Moneta et al., 2011). If causal relations exist among variables, LiNGAM uses their non-Gaussian distributions to identify the causal structure among the variables. LiNGAM is closely related to independent component analysis (ICA) (Hyvärinen et al., 2001b); the identifiability proof and estimation algorithm are partly based on the ICA theory. The idea of LiNGAM has been extended in many directions, including to nonlinear cases (Hoyer et al., 2009; Lacerda et al., 2008; Hyvärinen et al., 2010; Zhang and Hyvärinen, 2009; Peters et al., 2011a).

Many causal discovery methods including LiNGAM make the strong assumption of no latent confounders (Spirtes and Glymour, 1991; Dodge and Rousson, 2001; Shimizu et al., 2006; Hyvärinen and Smith, 2013; Hoyer et al., 2009; Zhang and Hyvärinen, 2009). These methods have been used in various application fields (Ramsey et al., 2014; Rosenström et al., 2012; Smith et al., 2011; Statnikov et al., 2012; Moneta et al., 2013). However, in many areas of empirical science, it is often difficult to accept the estimation results because latent confounders are ignored. In theory, we could take a non-Gaussian approach (Hoyer et al., 2008b) that uses an extension of ICA with more latent variables than observed variables (overcomplete ICA) to formally consider latent confounders in the framework of LiNGAM. Unfortunately, current versions of the overcomplete ICA algorithms are not very computationally reliable since they often suffer from local optima (Entner and Hoyer, 2011).

Thus, in this paper, we propose an alternative Bayesian approach to develop a method that is computationally simple in the sense that no iterative search in the parameter space is required and it is capable of finding the possible causal direction of two observed vari-ables in the presence of latent confounders. We first propose a variant of LiNGAM with individual- specific effects. Individual differences are sometimes the source of confounding (von Eye and Bergman, 2003). Thus, modeling certain individual-specific effects as latent variables allows a type of latent confounding to be considered. A latent confounding vari-able is an unobserved variable that exerts a causal influence on more than one observed variables (Hoyer et al., 2008b). The new model is still linear but allows any number of latent confounders. We then present a Bayesian approach for estimating the model by integrating out some of the large number of parameters, which is of the same order as the sample size. Such a Bayesian approach is often used in the field of mixed models (Demidenko, 2004) and multilevel models (Kreft and De Leeuw, 1998), although estimation of causal direction is not a topic studied within it.

Granger causality (Granger, 1969) is another popular method to aid detection of causal direction. His method depends on the temporal ordering of variables whereas our method does not. Therefore, our method can be applied to cases where temporal information is not available, i.e., cross-sectional data, as well as those where it is available, i.e., time-series data.

The remainder of this paper is organized as follows. We first review LiNGAM (Shimizu et al., 2006) and its extension to latent confounder cases (Hoyer et al., 2008b) in Section 2. In Section 3, we propose a new mixed-LiNGAM model, which is a variant of LiNGAM with individual-specific effects. We also propose an empirical Bayesian approach for learning the model. We empirically evaluate the performance of our method using artificial and real-world sociology data in Sections 4 and 5, respectively, and present our conclusions in Section 6.

2. Background

In this section, we first review the linear non-Gaussian structural equation model known as LiNGAM (Shimizu et al., 2006). We then discuss an extension of LiNGAM to cases where latent confounding variables exist (Hoyer et al., 2008b).

In LiNGAM (Shimizu et al., 2006), causal relations between observed variables x_l (l = 1, ..., d) are modeled as

$$x_l={\mu }_l+\sum _{k(m)<k(l)}{b}_{lm}{x}_m+e_l,$$ (1)

where k(l) is a causal ordering of the variables x_l. The causal orders k(l) (l = 1, ..., d) are unknown and to be estimated. In this ordering, the variables x_l form a directed acyclic graph (DAG) so that no later variable determines, i.e., has a directed path to, any earlier variable in the DAG. The variables e_l are latent continuous variables called error variables, μ_l are intercepts or regression constants, and b_lm are connection strengths or regression coefficients.

In matrix form, the LiNGAM model in Eq. (1) is written as

$$\mathit{x}=\mathit{\mu }+\mathbf{B}\mathit{x}+\mathit{e},$$ (2)

where the vector μ collects constants μ_l, the connection strength matrix B collects regression coefficients (or connection strengths) b_lm, and the vectors x and e collect observed variables x_l and error variables e_l, respectively. The zero/non-zero pattern of b_lm corresponds to the absence/existence pattern of directed edges (direct effects). It can be shown that it is always possible to perform simultaneous, equal row and column permutations on the connection strength matrix B to cause it to become strictly lower triangular, based on the acyclicity assumption (Bollen, 1989). Here, strict lower triangularity is defined as a lower triangular structure with the diagonal consisting entirely of zeros. Errors e_l follow non-Gaussian distributions with zero mean and non-zero variance, and are jointly independent. This model without assuming non-Gaussianity distribution is called a fully recursive model in conventional structural equation models (Bollen, 1989). The non-Gaussianity assumption on e_l enables the identification of a causal ordering k(l) and the coefficients b_lm based only on x (Shimizu et al., 2006), unlike conventional Bayesian networks based on the Gaussianity assumption on e_l (Spirtes et al., 1993).

To illustrate the LiNGAM model, the following example is considered, whose corresponding directed acyclic graph is provided in Fig. 1:

$$\left[\begin{array}{l}{x}_1\hfill \\ x_2\hfill \\ x_3\hfill \end{array}\right]=\left[\begin{array}{ccc}0& 0& 3\\ -5& 0& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{l}{x}_1\hfill \\ x_2\hfill \\ x_3\hfill \end{array}\right]+\left[\begin{array}{c}{e}_1\\ e_2\\ e_3\end{array}\right].$$ (3)

Figure 1:

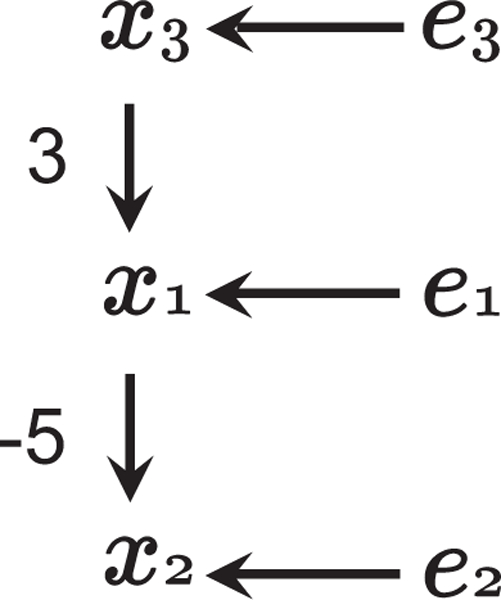
An example graph of LiNGAMs

In this example, x₃ is equal to error e₃ and is exogenous since it is not affected by either of the other two variables x₁ and x₂. Thus, x₃ is in the first position of such a causal ordering such that B is strictly lower triangular, x₁ is in the second, and x₂ is the third, i.e., k(3) = 1, k(1) = 2, and k(2) = 3. If we permute the variables x₁ to x₃ according to the causal ordering, we have

$$\left[\begin{array}{l}{x}_3\hfill \\ x_1\hfill \\ x_2\hfill \end{array}\right]=\left[\begin{array}{ccc}0& 0& 0\\ 3& 0& 0\\ 0& -5& 0\end{array}\right]\left[\begin{array}{l}{x}_3\hfill \\ x_1\hfill \\ x_2\hfill \end{array}\right]+\left[\begin{array}{c}{e}_3\\ e_1\\ e_2\end{array}\right].$$ (4)

It can be seen that the resulting connection strength (or regression coefficient) matrix is strictly lower triangular.

Several computationally efficient algorithms for estimating the model have been proposed (Shimizu et al., 2006, 2011; Hyvärinen and Smith, 2013). As with ICA, LiNGAM is identiable under the assumptions of non-Gaussianity and independence among error variables (Shimizu et al., 2006; Comon, 1994; Eriksson and Koivunen, 2003).¹ However, for the estimation methods to be consistent, additional assumptions, e.g., the existence of their moments or some other statistic, must be made to ensure that the statistics computed in the estimation algorithms exist. The idea of LiNGAM can be generalized to nonlinear cases (Hoyer et al., 2009; Tillman et al., 2010; Zhang and Hyvärinen, 2009; Peters et al., 2011b).

The assumption of independence among e_l means that there is no latent confounding variable (Shimizu et al., 2006). A latent confounding variable is an unobserved variable that contributes to the values of more than one observed variable (Hoyer et al., 2008b). However, in many applications, there often exist latent confounding variables. If such latent confounders are completely ignored, the estimation results can be seriously biased (Pearl, 2000; Spirtes et al., 1993; Bollen, 1989). Therefore, in Hoyer et al. (2008b), LiNGAM with latent confounders, called latent variable LiNGAM, was proposed, and the model can be formulated as follows:

$$x_l={\mu }_l+\sum _{k(m)<k(l)}{b}_{lm}{x}_m+\sum _{q=1}^Q{\lambda }_{lq}{f}_q+e_l,$$ (5)

where f_q are non-Gaussian individual-specific effects f_q with zero mean and unit variance and λ_lq denote the regression coefficients (connection strengths) from f_q to x_l. This model is written in matrix form as follows:

$$\mathit{x}=\mathit{\mu }+\mathbf{B}\mathit{x}+\mathbf{\Lambda }\mathit{f}+\mathit{e},$$ (6)

where the difference from LiNGAM in Eq. (2) is the existence of a latent confounding variable vector f. The vector f collects f_q. The matrix Λ collects λ_lq and is assumed to be of full column rank.

Another way to represent latent confounder cases would be to use dependent error variables. Denoting Λf + e in Eq. (6) by, $\tilde{\mathit{e}}$, we have

$$\mathit{x}=\mathit{\mu }+\mathbf{B}\mathit{x}+\mathbf{\Lambda }\mathit{f}+\mathit{e}$$ (7)

$$=\mathit{\mu }+\mathbf{B}\mathit{x}+\tilde{\mathit{e}},$$ (8)

Where $\tilde{e}$ are dependent due to the latent confounders f_q. Observed variables that are equal to dependent errors, $\tilde{e}$ are connected by bi-directed arcs in their graphs. An example graph is given in Fig. 4. This representation can be more general since it is easier to extend it to represent nonlinearly dependent errors. In this paper, however, we use the aforementioned representation using independent errors and latent confounders since linear relations of the observed variables, latent confounders, and errors are necessary for our approach.

Figure 4:

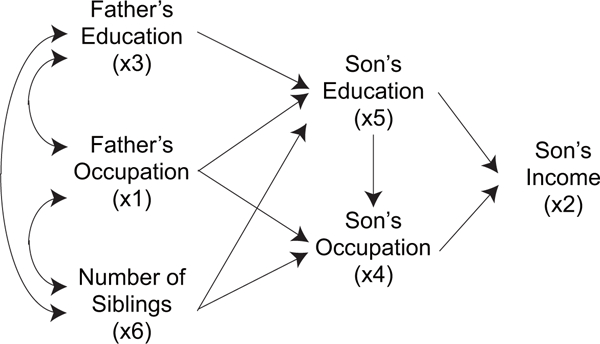
Status attainment model based on domain knowledge. Usually, the relations of x₁, x₃, and x₆, represented by bi-directed arcs, are not modeled.

Without loss of generality, the latent confounders f_q are assumed to be jointly independent since any dependent latent confounders can be remodeled by linear combinations of independent latent variables if the underlying model is linear acyclic and the error variables are independent (Hoyer et al., 2008b). To illustrate this, the following example model is considered:

$${\overline{f}}_1=e_{{\overline{f}}_1}$$ (9)

$${\overline{f}}_2={\omega }_{21}{\overline{f}}_1+e_{{\overline{f}}_2}$$ (10)

$$x_1={\lambda }_{11}{\overline{f}}_1+e_1$$ (11)

$$x_2={\lambda }_{21}{\overline{f}}_1+e_2$$ (12)

$$x_3={\lambda }_{32}{\overline{f}}_2+e_3$$ (13)

$$x_4=b_{43}{x}_3+{\lambda }_{42}{\overline{f}}_2+e_4,$$ (14)

where errors, $e_{{\overline{f}}_1}\left(={\overline{f}}_1\right)$, $e_{{\overline{f}}_2}$, and e₁−e₄ are non-Gaussian and independent. The associated graph is shown in Fig. 2. The relations of ${\overline{f}}_1$, ${\overline{f}}_2$, and x₁−x₄, are represented by a directed acyclic graph and latent confounders, ${\overline{f}}_1$ and ${\overline{f}}_2$ are dependent. In matrix form, this example model can be written as

$$\left[\begin{array}{l}{x}_1\hfill \\ x_2\hfill \\ x_3\hfill \\ x_4\hfill \end{array}\right]=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ b_{43}& 0& 0& 0\end{array}\right]\left[\begin{array}{l}{x}_1\hfill \\ x_2\hfill \\ x_3\hfill \\ x_4\hfill \end{array}\right]+\left[\begin{array}{cc}{\lambda }_{11}& 0\\ {\lambda }_{21}& 0\\ 0& {\lambda }_{32}\\ 0& {\lambda }_{42}\end{array}\right]\left[\begin{array}{c}{\overline{f}}_1\\ {\overline{f}}_2\end{array}\right]+\left[\begin{array}{c}{e}_1\\ e_2\\ e_3\\ e_4\end{array}\right].$$ (15)

Figure 2:

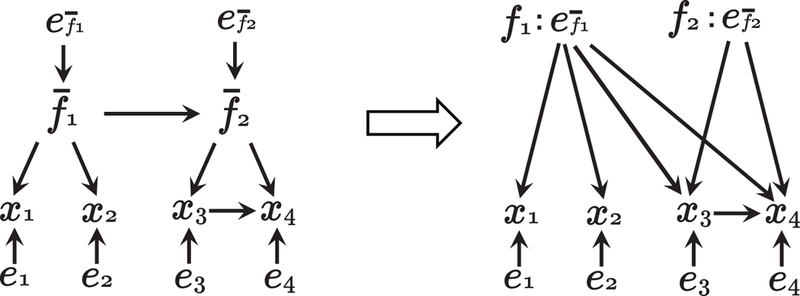
An example graph to illustrate the idea of independent latent confounders.

The relations of ${\overline{f}}_1$ and ${\overline{f}}_2$ to $e_{{\overline{f}}_1}$ and $e_{{\overline{f}}_2}$ in Eqs. (9)–(10):

$$\left[\begin{array}{l}{\overline{f}}_1\hfill \\ {\overline{f}}_2\hfill \end{array}\right]=\left[\begin{array}{cc}1& 0\\ {\omega }_{21}& 1\end{array}\right]\left[\begin{array}{l}{e}_{{\overline{f}}_1}\hfill \\ e_{{\overline{f}}_2}\hfill \end{array}\right],$$ (16)

we obtain

$$\underset{\mathit{x}}{\underbrace{\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right]}}=\underset{\mathbf{B}}{\underbrace{\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ b_{43}& 0& 0& 0\end{array}\right]}}\underset{\mathit{x}}{\underbrace{\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_4\end{array}\right]}}+\underset{\mathbf{\Lambda }}{\underbrace{\left[\begin{array}{cc}{\lambda }_{11}& 0\\ {\lambda }_{21}& 0\\ {\lambda }_{32}{\omega }_{21}& {\lambda }_{32}\\ {\lambda }_{42}{\omega }_{21}& {\lambda }_{42}\end{array}\right]}}\underset{\mathit{f}}{\underbrace{\left[\begin{array}{c}{e}_{{\overline{f}}_1}\\ e_{{\overline{f}}_2}\end{array}\right]}}+\underset{\mathit{e}}{\underbrace{\left[\begin{array}{c}{e}_1\\ e_2\\ e_3\\ e_4\end{array}\right]}}.$$ (17)

This is a latent variable LiNGAM in Eq. (6) taking, $f_1=e_{{\overline{f}}_1}$ and $f_2=e_{{\overline{f}}_2}$ since $e_{{\overline{f}}_1}$ and $e_{{\overline{f}}_2}$, are non-Gaussian and independent.

Moreover, the faithfulness of x_l and f_q to the generating graph is assumed. The faithfulness assumption (Spirtes et al., 1993) here means that when multiple causal paths exist from one variable to another, their combined effect does not equal exactly zero (Hoyer et al., 2008b). The faithfulness assumption can be considered to be not very restrictive from the Bayesian viewpoint (Spirtes et al., 1993) since the probability of having exactly the parameter values that do not satisfy faithfulness is zero (Meek, 1995).

In the framework of latent variable LiNGAM, it has been shown (Hoyer et al., 2008b) that the following three models are distinguishable based on observed data², i.e., the three different causal structures induce different data distributions:

$$\text{Model}3:\{\begin{array}{ll}{x}_1=\hfill & {\sum }_{q=1}^Q{\lambda }_{1q}{f}_q+e_1\hfill \\ x_2=\hfill & {\sum }_{q=1}^Q{\lambda }_{2q}{f}_q+e_2\hfill \end{array},$$ (18)

$$\text{Model}4:\{\begin{array}{l}{x}_1={\sum }_{q=1}^Q{\lambda }_{1q}{f}_q+e_1\hfill \\ x_2=b_{21}{x}_1+{\sum }_{q=1}^Q{\lambda }_{2q}{f}_q+e_2\hfill \end{array},$$ (19)

$$\text{Model}5:\{\begin{array}{l}{x}_1=b_{12}{x}_2+{\sum }_{q=1}^Q{\lambda }_{1q}{f}_q+e_1\hfill \\ x_2={\sum }_{q=1}^Q{\lambda }_{2q}{f}_q+e_2,\hfill \end{array},$$ (20)

where λ_1qλ_2q ≠ 0 due to the definition of latent confounders, that is, that they contribute to determining the values of more than two variables.

An estimation method based on overcomplete ICA (Lewicki and Sejnowski, 2000) explicitly modeling all the latent confounders f_q was proposed (Hoyer et al., 2008b). However, in current practice, overcomplete ICA estimation algorithms often get stuck in local optima and are not sufficiently reliable (Entner and Hoyer, 2011). A Bayesian approach for estimating the latent variable LiNGAM in Eq. (6) has been proposed in Henao and Winther (2011). These previous approaches that explicitly model latent confounders (Hoyer et al., 2008b; Henao and Winther, 2011) need to select the number of latent confounders, and which can be quite large. This could lead to further computational difficulty and statistically unreliable estimates.

In Chen and Chan (2013), a simple approach based on fourth-order cumulants for estimating latent variable LiNGAM was proposed. Their approach does not need to explicitly model the latent confounders, however it requires the latent confounders f_q to be Gaussian. The development of nonlinear methods that incorporate latent confounders is ongoing (Zhang et al., 2010).

None of these latent confounder methods incorporate the individual-specific effects that we model in the next section to consider latent confounders f_q in the latent variable LiNGAM of Eq. (6).

3. Linear non-Gaussian acyclic structural equation model with individual-specific effects

In this section, we propose a new Bayesian method for learning the possible causal direction of two observed variables in the presence of latent confounding variables, assuming that the causal relations are acyclic, i.e., there is not a feedback relation.

3.1. Model

The LiNGAM (Shimizu et al., 2006) for observation i can be described as follows:

$$x_l^{(i)}={\mu }_l+\sum _{k(m)<k(l)}{b}_{lm}{x}_m^{(i)}+e_l^{(i)}.$$ (21)

The random variables, $e_l^{(i)}$ are non-Gaussian and independent. The distributions of, $e_l^{(i)}(i=1,\cdots ,n)$ are commonly assumed to be identical³ for every l. A linear non-Gaussian acyclic structural equation model with individual-specific effects for observation i is formulated as follows:

$$x_l^{(i)}={\mu }_l+{\tilde{\mu }}_l^{(i)}+\sum _{k(m)<k(l)}{b}_{lm}{x}_m^{(i)}+e_l^{(i)},$$ (22)

where the difference from LiNGAM is the existence of individual-specific effects, ${\tilde{u}}_l^{(i)}$. The parameters, ${\tilde{u}}_l^{(i)}$ are independent of, $e_l^{(i)}$ and are correlated with $x_l^{(i)}$ through the structural equations in our Bayesian approach, introduced below. This means that the observations are generated from the identifiable LiNGAM, possibly with different parameter values of the means ${\mu }_l+{\tilde{\mu }}_l^{(i)}$. We call this a mixed-LiNGAM, named after mixed models (Demidenko, 2004), as it has effects ${\mu }_l$ and $b_{lm}$ that are common to all the observations and individual-specific effects ${\tilde{u}}_l^{(i)}$. We note that causal orderings of variables k(l) (l = 1, ..., d) are identical for all the observations in the sample.

To use a Bayesian approach for estimating the mixed-LiNGAM, we need to model the distributions of error variables e_l and prior distributions of the parameters including individual-specific effects ${\tilde{u}}_l^{(i)}$, unlike previous LiNGAM methods (Shimizu et al., 2006; Hoyer et al., 2008b). These individual-specific effects, whose number is of the same order as the sample size, are integrated out in the Bayesian method developed in Section 3.2, assuming an informative prior for them similar to the estimation of conventional mixed models (Demidenko, 2004). More details on the distributions of error variables and prior distributions of parameters are given in Section 3.2. These distributional assumptions were implied to be robust to some extent to their violations, at least in the artificial data experiments of Section 4.

We now relate the mixed-LiNGAM model above with the latent variable LiNGAM (Hoyer et al., 2008b). The latent variable LiNGAM in Eq. (6) for observation i is written as follows:

$$x_l^{(i)}={\mu }_l+\sum _{k(m)<k(l)}{b}_{lm}{x}_m^{(i)}+\underset{{\tilde{\mu }}_i^{(i)}}{\underbrace{\sum _{q=1}^Q{\lambda }_{lq}{f}_q^{(i)}+e_l^{(i)}}}.$$ (23)

This is a mixed-LiNGAM taking ${\tilde{\mu }}_l^{(i)}={\sum }_{q=1}^Q{\lambda }_{lq}{f}_q^{(i)}$. In contrast to the previous approaches for latent variable LiNGAM (Hoyer et al., 2008b; Henao and Winther, 2011), we do not explicitly model the latent confounders f_q and rather simply include their sums ${\tilde{\mu }}_l^{(i)}={\sum }_{q=1}^Q{\lambda }_{lq}{f}_q^{(i)}$ in our model as its parameters since our main interest lies in estimation of the causal relation of observed variables x_l and not in the estimation of their relations with latent confounders f_q. Our method does not estimate λ_lq or the number of latent confounders Q.

3.2. Estimation of possible causal direction

We apply a Bayesian approach to estimate the possible causal direction of two observed variables using the mixed-LiNGAM proposed above. We compare the following two mixed- LiNGAM models with opposite possible directions of causation. Model 1 is

$$x_1^{(i)}={\mu }_1+{\tilde{\mu }}_1^{(i)}+e_1^{(i)}$$ (24)

$$x_2^{(i)}={\mu }_2+{\tilde{\mu }}_2^{(i)}+b_{21}{x}_1^{(i)}+e_2^{(i)},$$ (25)

where b₂₁ is non-zero. In Model 1, x₂ does not cause x₁. The second model, Model 2, is

$$x_1^{(i)}={\mu }_1+{\tilde{\mu }}_1^{(i)}+b_{12}{x}_2^{(i)}+e_1^{(i)}$$ (26)

$$x_2^{(i)}={\mu }_2+{\tilde{\mu }}_2^{(i)}+e_2^{(i)},$$ (27)

where b₁₂ is non-zero. In Model 2, x₁ does not cause x₂. The two models have the same number of parameters, but opposite possible directions of causation.

Once the possible causal direction is estimated, one can see if the common causal coefficient (connection strength) b₂₁ or b₁₂ is likely to be zero by examining its posterior distribution.⁴ We focus here on estimating the possible direction of causation as in many previous works (Dodge and Rousson, 2001; Hoyer et al., 2009; Zhang and Hyvärinen, 2009; Chen and Chan, 2013; Hyvärinen and Smith, 2013), and do not go to the computation of the posterior distribution⁵ since estimation of the possible causal direction of two observed variables in the presence of latent confounders has been a very challenging problem in causal inference and is the main topic of this paper.

We apply standard Bayesian model selection techniques to help assess the causal direction of x₁ and x₂. We use the log-marginal likelihood for comparing the two models. The model with the larger log-marginal likelihood is regarded as the closest to the true model (Kass and Raftery, 1995).

Let $\mathcal{D}$ be the observed dataset ${\left[{\mathit{x}}^{{(1)}^T},\cdots ,{\mathit{x}}^{{(n)}^T}\right]}^T$, where ${\mathit{x}}^{(i)}={\left[x_1^{(i)},x_2^{(i)}\right]}^T$. Denote Models 1 and 2 by M₁ and M₂. The log-marginal likelihoods of M₁ and M₂ are

$$\log \left\{p\left(M_r|\mathcal{D}\right)\right\}=\log \left\{p\left(\mathcal{D}|M_r\right)p\left(M_r\right)/p(\mathcal{D})\right\}$$ (28)

$$=\log \left\{p\left(\mathcal{D}|M_r\right)\right\}+\log \left\{p\left(M_r\right)\right\}-\log p(\mathcal{D})$$ (29)

$$\begin{gathered} =\log \left\{\int p\left(\mathcal{D}|{\mathit{\theta }}_r,M_r\right)p\left({\mathit{\theta }}_r|M_r,{\mathit{\eta }}_r\right)d{\mathit{\theta }}_r\right\} \\ +\log p\left(M_r\right)-\log p\left(\mathcal{D}\right)(r=1,2), \end{gathered}$$ (30)

where η₁, η₂ are the hyper-parameter vectors regarding the distributions of the parameters θ₁and θ₂, respectively. Since the last term log p($\mathcal{D}$) is constant with respect to M_r, we can drop it. To select suitable values for these hyper-parameters, we take an ordinary empirical Bayesian approach. First, we compute the log-marginal likelihood for every combination of the two models M_r and a number of candidate hyper-parameter values of η_r. Next, we take the model and hyper-parameter values that give the largest log-marginal likelihood, and finally estimate that the model with the largest log-marginal likelihood is better than the other model.

In basic LiNGAM (Shimizu et al., 2006), we have (Hyvärinen et al., 2010; Hoyer and Hyttinen, 2009)

$$p(x)=\prod _l{p}_{e_l}\left(x_l-{\mu }_l-\sum _{k(m)<k(l)}{b}_{lm}{x}_m\right).$$ (31)

Thus, in the same manner, the likelihoods under mixed-LiNGAM $p\left(\mathcal{D}|{\mathit{\theta }}_r,M_r\right)(r=1,2)$ are given by

$$p\left(\mathcal{D}|{\mathit{\theta }}_r,M_r\right)={\Pi }_{i=1}^{n}p\left({\mathit{x}}^{(i)}|{\mathit{\theta }}_r,M_r\right)$$ (32)

$$=\{\begin{array}{l}\prod _{i=1}^n{p}_{e_1^{(i)}}\left(x_1^{(i)}-{\mu }_1-{\tilde{\mu }}_1^{(i)}|{\mathit{\theta }}_1,M_1\right)\\ \times p_{e_2^{(i)}}\left(x_2^{(i)}-{\mu }_2-{\tilde{\mu }}_2^{(i)}-b_{21}{x}_1^{(i)}|{\mathit{\theta }}_1,M_1\right)\text{for}{M}_1\\ \prod _{i=1}^n{p}_{e_1^{(i)}}\left(x_1^{(i)}-{\mu }_1-{\tilde{\mu }}_1^{(i)}-b_{12}{x}_2^{(i)}|{\mathit{\theta }}_2,M_2\right)\\ \times p_{e_2^{(i)}}\left(x_2^{(i)}-{\mu }_2-{\tilde{\mu }}_2^{(i)}|{\mathit{\theta }}_2,M_2\right)\text{for}{M}_2\end{array}.$$ (33)

We model the parameters and their prior distributions as follows.⁶ The prior probabilities of M₁ and M₂ are uniform:

$$p\left(M_1\right)=p\left(M_2\right).$$ (34)

The distributions of the error variables $e_1^{(i)}$ and $e_2^{(i)}$ are modeled by Laplace distributions with zero mean and variances of var $\left(e_1^{(i)}\right)=h_1^2$ and var $\left(e_2^{(i)}\right)=h_2^2$ as follows:

$$p_{e_1^{(i)}}=Laplace\left(0,|h_1|/\sqrt{2}\right)$$ (35)

$$p_{e_2^{(i)}}=Laplace\left(0,|h_2|/\sqrt{2}\right).$$ (36)

Here, we simply use a symmetric super-Gaussian distribution, i.e., the Laplace distribution, to model $p_{e_1^{(i)}}$ and $p_{e_2^{(i)}}$, as suggested in Hyvärinen and Smith (2013). Such super-Gaussian distributions have been reported to often work well in non-Gaussian estimation methods including independent component analysis and LiNGAM (Hyvärinen et al., 2001b; Hyvärinen and Smith, 2013). In some cases, a wider class of non-Gaussian distributions might provide a better model for $p_{e_1^{(i)}}$ and $p_{e_2^{(i)}}$, e.g., the generalized Gaussian family (Hyvärinen et al., l 2 2001b), a finite mixture of Gaussians, or an exponential family distribution combining the Gaussian and Laplace distributions (Hoyer and Hyttinen, 2009).

The parameter vectors θ₁ and θ₂ are written as follows:

$${\mathit{\theta }}_1={\left[{\mu }_l,b_{21},h_l,{\tilde{\mu }}_l^{(i)}\right]}^T(l=1,2;i=1,\cdots ,n)$$ (37)

$${\mathit{\theta }}_2={\left[{\mu }_l,b_{12},h_l,{\tilde{\mu }}_l^{(i)}\right]}^T(l=1,2;i=1,\cdots ,n).$$ (38)

The prior distributions of common effects are Gaussian as follows:

$${\mu }_1~N\left(0,{\tau }_{{\mu }_1}^{cmmn}\right)$$ (39)

$${\mu }_2~N\left(0,{\tau }_{{\mu }_2}^{cmmn}\right)$$ (40)

$$b_{12}~N\left(0,{\tau }_{b_{12}}^{cmmn}\right)$$ (41)

$$b_{21}~N\left(0,{\tau }_{b_{21}}^{cmmn}\right)$$ (42)

$$h_1~N\left(0,{\tau }_{h_1}^{cmmn}\right)$$ (43)

$$h_2~N\left(0,{\tau }_{h_2}^{cmmn}\right),$$ (44)

where ${\tau }_{{\mu }_1}^{cmmn}$, ${\tau }_{{\mu }_2}^{cmmn}$, ${\tau }_{b_{12}}^{cmmn}$, ${\tau }_{b_{21}}^{cmmn}$, ${\tau }_{h_1}^{cmmn}$ and ${\tau }_{h_2}^{cmmn}$ are constants.

Generally speaking, we could use various informative prior distributions for the individual-specific effects and then compare candidate priors using the standard model selection approach based on the marginal likelihoods. Below we provide two examples.

If the data is generated from a latent variable LiNGAM, a special case of mixed-LiNGAM, as shown in Section 3.1, the individual-specific effects are the sums of many non-Gaussian independent latent confounders f_q and are dependent. The central limit theorem states that the sum of independent variables becomes increasingly close to the Gaussian (Billingsley, 1986). Therefore, in many cases, it could be practical to approximate the non-Gaussian distribution of a variable that is the sum of many non-Gaussian and independent variables by a bell-shaped curve distribution (Sogawa et al., 2011; Chen and Chan, 2013). This motivates us to model the prior distribution of individual-specific effects by the multivariate t-distribution as follows:

$$\left[\begin{array}{c}{\tilde{\mu }}_1^{(i)}\\ {\tilde{\mu }}_2^{(i)}\end{array}\right]=\text{diag}\left({\left[\sqrt{{\tau }_1^{indvdl}},\sqrt{{\tau }_2^{indvdl}}\right]}^T\right){\mathbf{\text{C}}}^{-1/2}\mathit{u},$$ (45)

where ${\tau }_1^{indvdl}$ and ${\tau }_2^{indvdl}$ are constants, $\mathit{u}~t_{\nu }(\mathbf{0},\mathbf{\Sigma })$ and $\mathbf{\Sigma }=\left[{\sigma }_{ab}\right]$ is a symmetric scale matrix whose diagonal elements are 1s. A random variable vector u that follows the multivariate t-distribution t_v(0, Σ) can be created by $\frac{\mathit{y}}{\sqrt{v/\nu }}$ where y follows the Gaussian distribution N(0, Σ), v follows the chi-squared distribution with v degrees of freedom, and y and v are statistically independent (Kotz and Nadarajah, 2004). Note that u_i have energy correlations (Hyvärinen et al., 2001a), i.e., correlations of squares cov $\left(u_i^2,u_j^2\right)>0$ due to the common variable v. C is a diagonal matrix whose diagonal elements give the variance of elements of u, i.e., $\mathbf{C}=\frac{\nu }{\nu -2}$ diag(Σ) for v > 2. The degree of freedom v is here taken to be six. The kurtosis of the univariate Student’s t-distribution with six degrees of freedom is three, the same as that of the Laplace distribution.

The hyper-parameter vectors η₁ and η₂ are

$${\eta }_l={\left[{\tau }_{{\mu }_1}^{cmmn},{\tau }_{{\mu }_2}^{cmmn},{\tau }_{b_{12}}^{cmmn},{\tau }_{b_{21}}^{cmmn},{\tau }_{h_1}^{cmmn},{\tau }_{h_2}^{cmmn},{\tau }_1^{indvdl},{\tau }_2^{indvdl},{\sigma }_{21}\right]}^T(l=1,2)$$ (46)

We want to take the constants ${\tau }_{{\mu }_1}^{cmmn}$, ${\tau }_{{\mu }_2}^{cmmn}$, ${\tau }_{b_{12}}^{cmmn}$, ${\tau }_{b_{21}}^{cmmn}$, ${\tau }_{h_1}^{cmmn}$ and ${\tau }_{h_2}^{cmmn}$ to be sufficiently large so that the priors for the common effects are not very informative. Whether these constants are sufficiently large depends on the scales of the variables. In the experiments in Sections 4–5, we set ${\tau }_{{\mu }_1}^{cmmn}={\tau }_{b_{12}}^{cmmn}={\tau }_{h_1}^{cmmn}={10}^2\times \widehat{\text{var}}\left(x_1\right)$ and ${\tau }_{{\mu }_2}^{cmmn}={\tau }_{b_{21}}^{cmmn}={\tau }_{h_2}^{cmmn}={10}^2\times \widehat{\text{var}}\left(x_2\right)$ so that they reflect the scales of the corresponding variables.

Moreover, we take an empirical Bayesian approach for the individual-specific effects. We test ${\tau }_l^{indvdl}=0,{0.2}^2\times \widehat{\text{var}}\left(x_l\right),\dots ,{0.8}^2\times \widehat{\text{var}}\left(x_l\right),{1.0}^2\times \widehat{\text{var}}\left(x_l\right)(l=1,2)$. That is, we uniformly vary the hyper-parameter value from that with no individual-specific effects, i.e., 0, to a larger value, i.e., ${1.0}^2\times \widehat{\text{var}}\left(x_l\right)$, which implies very large individual differences. Further, we test σ₁₂ = 0, ±0.3, ±0.5, ±0.7, ±0.9, i.e., the value with zero correlation and larger values with stronger correlations. This means that we test uncorrelated individual-specific effects as well as correlated ones. We take the ordinary Monte Carlo sampling approach to compute the log-marginal likelihoods with 1000 samples for the parameter vectors θ_r (r = 1,2).

The assumptions for our model are summarized in Table 1. Generally speaking, if the actual probability density function of individual-specific effects is unimodal and most often provides zero or very small absolute values and with few large values, i.e., many of the individual-specific effects are close to zero and many individuals have similar intercepts, the estimation is likely to work. If the individuals have very different intercepts, the estimation will not work very well.

Table 1:

Summary of the assumptions for our mixed-LiNGAM model

$\text{Model:}{x}_l^{(i)}={\mu }_l+{\tilde{\mu }}_l^{(i)}+{\sum }_{k(m)<k(l)}{b}_{lm}{x}_m^{(i)}+e_l^{(i)}(l,m=1,2;l\ne m),$ where blm are non-zero.

$e_l^{(i)}$ (l = 1, 2; i = 1, ..., n) are i.i.d..

$e_l$ (l = 1, 2) are mutually independent.

$e_l$ (l = 1, 2) follow Laplace distributions with zero mean and standard deviations $|h_l|$

Prior distributions:

μl, blm and hl (l = 1, 2; m = 1, 2; l ≠ m) follow Gaussian distributions with zero mean and variance ${\tau }_{\mu l}^{cmmn},{\tau }_{b_{lm}}^{\mathrm{cmmn}},\text{and}{\tau }_{h_l}^{cmmn}$

${\tilde{\mu }}_l^{(i)}(l=1,2;i=1,\cdots ,n)$ are the sum of latent confounders $f_q^{(i)}:\sum _{q=1}^Q{\lambda }_{lq}{f}_q^{(i)}$ and are independent of $e_l^{(i)}$.

${\tilde{\mu }}_l^{(i)}$ (l = 1, 2; i = 1, ..., n) are i.i.d..

μl (l = 1, 2) follow multivariate t-distributions with v degrees of freedom, zero mean, variances ${\tau }_l^{indvdl}$ and correlation σ12 (here, v = 6).

Hyper-parameters:

${\tau }_{{\mu }_l}^{\mathrm{cmmn}},{\tau }_{b_{lm}}^{cmmn}\text{and}{\tau }_{h_l}^{cmmn}$ (l = 1, 2; m = 1, 2; l ≠ m) are set to be large values so that the priors are not very informative.

${\tau }_l^{indvdl}$ (l = 1, 2) are uniformly varied from zero to large values.

σ12 are uniformly varied in the interval between −0.9 and 0.9.

An alternative way of modeling the prior distribution of individual-specific effects would be to use the multivariate Gaussian distribution as follows:

$$\left[\begin{array}{c}{\tilde{\mu }}_1^{(i)}\\ {\tilde{\mu }}_2^{(i)}\end{array}\right]=\text{diag}\left({\left[\sqrt{{\tau }_1^{indvdl}},\sqrt{{\tau }_2^{indvdl}}\right]}^T\right)\mathit{z},$$ (47)

where ${\tau }_1^{indvdl}$ and ${\tau }_2^{indvdl}$ are constants, $\mathit{z}~N(\mathbf{0},\mathbf{\Sigma })$ and $\mathbf{\Sigma }=\left[{\sigma }_{ab}\right]$ is a symmetric scale matrix whose diagonal elements are ones. Gaussian individual-specific effects or latent con- founders would not lead to losing the identifiability (Chen and Chan, 2013) since each observation still is generated by the identifiable non-Gaussian LiNGAM. However, if errors are Gaussian, there is no guarantee that our method can find correct possible causal direction. We could detect their Gaussanity by compariging our mixed-LiNGAM models with Gaussain error models based on their log-marginal likelihoods. If the errors are actually Gaussian or close to be Gaussian, Gaussian error models would provide larger log-marginal likelihoods. This would detect situations where our approach cannot find causal direction.

4. Experiments on artificial data

We compared our method with seven methods for estimating the possible causal direction between two variables: i) LvLiNGAM⁷ (Hoyer et al., 2008b); ii) SLIM⁸(Henao and Winther, 2011) iii) LiNGAM-GC-UK (Chen and Chan, 2013); iv) ICA-LiNGAM⁹ (Shimizu et al., 2006); v) DirectLiNGAM¹⁰ (Shimizu et al., 2011); vi) Pairwise LiNGAM¹¹ (Hyvärinen and Smith, 2013); vii) Post-nonlinear causal model (PNL) ¹² (Zhang and Hyvärinen, 2009). Their assumptions are summarized in Table 2. The first seven methods assume linearity, and the eighth allows a very wide variety of nonlinear relations. The last four methods assume that there are no latent confounders. We tested the prior t- and Gaussian distributions for individual-specific effects in our approach. LvLiNGAM and SLIM require to specify the number of latent confounders. We tested 1 and 4 latent confounder(s) for LvLiNGAM since its current implementation cannot handle more than four latent confounders, whereas we tested 1, 4 and 10 latent confounders(s) for SLIM. LiNGAM-GC-UK (Chen and Chan, 2013) assumes that errors are simultaneously super-Gaussian or sub-Gaussian and that latent confounders are Gaussian.

Table 2:

Summary of the assumptions of eight methods

	Functional form?	Latent confounders allowed?	Number of latent confounders necessary to be specified?	Iterative search in the parameter space required?	Distributional assumptions necessary?
Our approach	Linear	Yes	No	No	Yes
LvLiNGAM	Linear	Yes	Yes	Yes	No13
SLIM	Linear	Yes	Yes	No	Yes
LiNGAM-GC-UK	Linear	Yes	No	No	Yes
ICA-LiNGAM	Linear	No	N/A	Yes	No
DirectLiNGAM	Linear	No	N/A	No	No
Pairwise LiNGAM	Linear	No	N/A	No	No
PNL	Nonlinear	No	N/A	Yes	No

We generated data using the following latent variable LiNGAM with Q latent confounding variables, which is a mixed-LiNGAM:

$$x_1^{(i)}={\mu }_1+\sum _{q=1}^Q{\lambda }_{1q}{f}_q^{(i)}+e_1^{(i)}$$ (48)

$$x_2^{(i)}={\mu }_2+b_{21}{x}_1^{(i)}+\sum _{q=1}^Q{\lambda }_{2q}{f}_q^{(i)}+e_2^{(i)},$$ (49)

where μ₁ and μ₂ were randomly generated from N(0,1), and b₂₁, λ_1q, λ_2q were randomly generated from the interval (−1.5, −0.5) ∪ (0.5, 1.5). We tested various numbers of latent confounders Q = 0, 1, 6, 12. The zero values indicate that there are no latent confounders. An example graph used to generate artificial data is given in Fig. 3.

Figure 3:

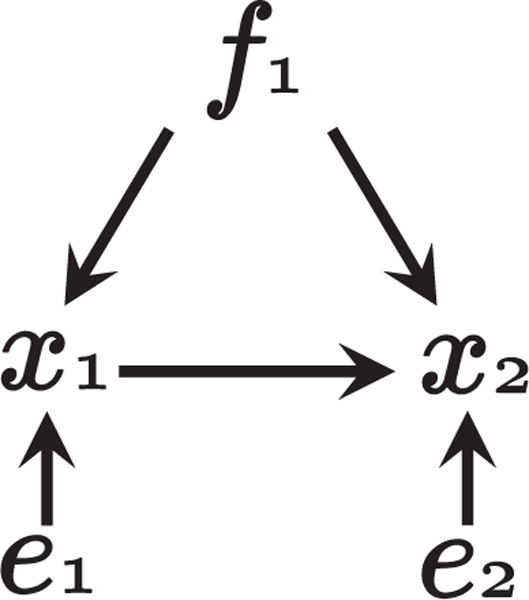
The associated graph of the model used to generate artificial data when the number of latent confounders Q = 1.

The distributions of the error variables e₁, e₂, and latent confounders f_q were identical for all observations. The distributions of the error variables e₁, e₂, and latent confounders f_q were randomly selected from the 18 non-Gaussian distributions used in Bach and Jordan (2002) to see if the Laplace distribution assumption on error variables and t- or Gaussian distribution assumption on individual-specific effects in our method were robust to different non-Gaussian distributions. These include symmetric/non-symmetric distributions, super-Gaussian/sub-Gaussian distributions, and strongly/weakly non-Gaussian distributions. The variances of e₁ and e₂ were randomly selected from the interval (0.52, 1.5²). The variances of f_q were 1s.

We permuted the variables according to a random ordering and inputted them to the eight estimation methods. We conducted 100 trials, with sample sizes of 50, 100, and 200. For the data with the number of latent confounders Q = 0, all the methods should find the correct causal direction for large enough sample sizes, as there were no latent confounders, which here means no individual-specific effects. The last four comparative methods should find the data with the number of latent confounders Q = 1,6,12 very difficult to analyze, because, unlike the other approaches, they assume no latent confounders.

To evaluate the performance of the algorithms, we counted the number of successful discoveries of possible causal direction and estimated their standard errors. We can calculate the 95% confidence intervals around the sample estimate of the number of successes based on the Gaussian approximation to the binomial distribution. If two approaches have overlapping confidence intervals, then they do not have a statistically significant difference at 5% level.

Table 3 shows the results. In the case with no latent confounders (Q = 0), the numbers of successes of linear methods that allow no latent confounders, ICA-LiNGAM, Di-rectLiNGAM, and Pairwise LiNGAM, were significantly larger or not significantly different from those of the methods that allow latent confounders. This would be because those latent confounder methods included many redundant parameters. In the cases that incorporated latent confounders (Q = 1, 6, 12), our two methods gave the largest numbers of successes for all the nine cases except the case of our method with Gaussian individual- specific effects with Q = 1 and sample size 200. In three of the nine cases, our two methods were significantly better than the others, although, in the other cases, they were not significantly different from LvLiNGAM or/and ICA-LiNGAM.

Table 3:

Number of successful discoveries (100 trials)

	Sample size
	50	100	200
Number of latent confounders Q = 0:
Our approach (t-distributed individual-specific effects)	88 (3.25)	91 (2.86)	86 (3.47)
Our approach (Gaussian individual-specific effects)	91 (2.86)	87 (3.36)	91 (2.86)
LvLiNGAM (1 latent confounder)	73 (4.44)	83 (3.76)	83 (3.76)
LvLiNGAM (4 latent confounders)	52 (5.00)	68 (4.66)	66 (4.74)
SLIM (1 latent confounder)	29 (4.54)	30 (4.58)	25 (4.33)
SLIM (4 latent confounders)	34 (4.74)	31 (4.62)	36 (4.80)
SLIM (10 latent confounders)	30 (4.58)	29 (4.54)	30 (4.58)
LiNGAM-GC-UK	33 (4.70)	28 (4.49)	35 (4.77)
ICA-LiNGAM	93 (2.55)	93 (2.55)	96 (i.96)
DirectLiNGAM	87 (3.36)	95 (2.18)	97 (1.71)
Pairwise LiNGAM	89 (3.13)	95 (2.18)	95 (2.18)
Post-nonlinear causal model	74 (4.39)	71 (4.54)	75 (4.33)
Number of latent confounders Q = 1:
Our approach t-distributed individual-specific effects)	83 (3.76)	80 (4.00)	80 (4.00)
Our approach Gaussian individual-specific effects)	79 (4.07)	87 (3.36)	69 (4.62)
LvLiNGAM (1 latent confounder)	66 (4.74)	71 (4.54)	73 (4.44)
LvLiNGAM 4 latent confounders)	63 (4.83)	58 (4.94)	67 (4.70)
SLIM (1 latent confounder)	40 (4.90)	47 (4.99)	25 (4.33)
SLIM 4 latent confounders)	40 (4.90)	34 (4.74)	44 (4.96)
SLIM (10 latent confounders)	47 (4.99)	39 (4.88)	41 (4.92)
LiNGAM-GC-UK	24 (4.27)	32 (4.66)	32 (4.66)
ICA-LiNGAM	74 (4.39)	71 (4.54)	67 (4.70)
DirectLiNGAM	48 (5.00)	52 (5.00)	54 (4.98)
Pairwise LiNGAM	54 (4.98)	58 (4.94)	61 (4.88)
Post-nonlinear causal model	55 (4.97)	58 (4.94)	57 (4.95)
Number of latent confounders Q = 6:
Our approach t-distributed individual-specific effects)	88 (3.25)	81 (3.92)	87 (3.36)
Our approach Gaussian individual-specific effects)	84 (3.67)	85 (3.57)	87 (3.36)
LvLiNGAM (1 latent confounder)	58 (4.94)	70 (4.58)	70 (4.58)
LvLiNGAM 4 latent confounders)	64 (4.80)	61 (4.88)	63 (4.83)
SLIM (1 latent confounder)	50 (5.00)	63 (4.83)	47 (4.99)
SLIM 4 latent confounders)	45 (4.97)	47 (4.99)	43 (4.95)
SLIM (10 latent confounders)	58 (4.94)	48 (5.00)	58 (4.94)
LiNGAM-GC-UK	29 (4.54)	28 (4.49)	21 (4.07)
ICA-LiNGAM	74 (4.39)	72 (4.49)	47 (4.99)
DirectLiNGAM	37 (4.83)	48 (5.00)	39 (4.88)
Pairwise LiNGAM	48 (5.00)	51 (5.00)	37 (4.83)
Post-nonlinear causal model	55 (4.97)	42 (4.94)	46 (4.98)
Number of latent confounders Q = 12:
Our approach t-distributed individual-specific effects)	88 (3.25)	86 (3.47)	89 (3.13)
Our approach Gaussian individual-specific effects)	91 (2.86)	89 (3.13)	91 (2.86)
LvLiNGAM (1 latent confounder)	52 (5.00)	55 (4.97)	65 (4.77)
LvLiNGAM 4 latent confounders)	65 (4.77)	58 (4.94)	64 (4.80)
SLIM (1 latent confounder)	51 (5.00)	55 (4.97)	60 (4.90)
SLIM 4 latent confounders)	45 (4.97)	51 (5.00)	63 (4.83)
SLIM 10 latent confounders)	61 (4.88)	54 (4.98)	54 (4.98)
LiNGAM-GC-UK	21 (4.07)	25 (4.33)	29 (4.54)
ICA-LiNGAM	68 (4.66)	72 (4.49)	72 (4.49)
DirectLiNGAM	37 (4.83)	39 (4.88)	38 (4.85)
Pairwise LiNGAM	56 (4.96)	42 (4.94)	43 (4.95)
Post-nonlinear causal model	51 (5.00)	43 (4.95)	46 (4.98)

Largest numbers of successful discoveries were underlined.

Standard errors are shown in parentheses, which are computed assuming that the number of successes follow a binomial distribution.

Table 4 shows the average computational times. The computational complexity of the current implementation of our methods is clearly larger than that of the other linear methods ICA-LiNGAM, DirectLiNGAM, Pairwise LiNGAM, LvLiNGAM with 1 latent confounder, SLIM and LiNGAM-GC-UK and comparable to LvLiNGAM with 4 latent confounders and the nonlinear method PNL.

Table 4:

Average CPU time (s)

	Sample size
	50	100	200
Number of latent confounders Q = 0
Our approach (t-distributed individual-specific effects)	27.20	56.93	141.84
Our approach (Gaussian individual-specific effects)	35.48	69.59	117.10
LvLiNGAM (1 latent confounder)	2.41	2.55	9.91
LvLiNGAM (4 latent confounders)	22.25	30.12	87.96
SLIM (1 latent confounder)	5.89	6.25	6.81
SLIM (4 latent confounders)	7.60	8.14	9.13
SLIM (10 latent confounders)	10.88	12.02	13.96
LiNGAM-GC-UK	0.00	0.00	0.00
ICA-LiNGAM	0.04	0.03	0.02
DirectLiNGAM	0.00	0.01	0.01
Pairwise LiNGAM	0.00	0.00	0.00
Post-nonlinear causal model	19.59	27.68	57.37
Number of latent confounders Q = 1:
Our approach (t-distributed individual-specific effects)	35.87	65.55	131.25
Our approach (Gaussian individual-specific effects)	37.12	75.11	114.37
LvLiNGAM (1 latent confounder)	2.40	2.53	13.93
LvLiNGAM (4 latent confounders)	21.50	29.50	92.19
SLIM (1 latent confounder)	5.88	6.01	6.69
SLIM (4 latent confounders)	7.59	8.19	8.96
SLIM (10 latent confounders)	10.96	11.79	13.68
LiNGAM-GC-UK	0.00	0.00	0.00
ICA-LiNGAM	0.05	0.03	0.03
DirectLiNGAM	0.01	0.01	0.01
Pairwise LiNGAM	0.00	0.00	0.00
Post-nonlinear causal model	18.17	28.83	51.63
Number of latent confounders Q = 6:
Our approach (t-distributed individual-specific effects)	42.66	76.29	132.43
Our approach (Gaussian individual-specific effects)	33.13	69.07	104.83
LvLiNGAM (1 latent confounder)	2.40	2.56	9.38
LvLiNGAM (4 latent confounders)	22.17	30.12	83.01
SLIM (1 latent confounder)	5.89	6.22	6.77
SLIM (4 latent confounders)	7.58	8.18	9.11
SLIM (10 latent confounders)	11.03	12.02	13.91
LiNGAM-GC-UK	0.00	0.00	0.00
ICA-LiNGAM	0.06	0.05	0.05
DirectLiNGAM	0.01	0.01	0.01
Pairwise LiNGAM	0.00	0.00	0.00
Post-nonlinear causal model	18.71	29.62	52.21
Number of latent confounders Q = 12:
Our approach (t-distributed individual-specific effects)	29.16	59.30	134.89
Our approach (Gaussian individual-specific effects)	32.18	68.14	104.76
LvLiNGAM (1 latent confounder)	2.35	2.50	13.58
LvLiNGAM (4 latent confounders)	21.51	30.10	94.08
SLIM (1 latent confounder)	5.90	6.03	6.62
SLIM (4 latent confounders)	7.58	7.99	8.97
SLIM (10 latent confounders)	10.92	11.68	13.74
LiNGAM-GC-UK	0.00	0.00	0.00
ICA-LiNGAM	0.07	0.08	0.07
DirectLiNGAM	0.01	0.02	0.02
Pairwise LiNGAM	0.00	0.00	0.00
Post-nonlinear causal model	18.21	29.21	51.89

The MATLAB code for performing these experiments is available on our website.¹⁴

5. An experiment on real-world data

We analyzed the General Social Survey data set, taken from a sociological data repository (http://www.norc.org/GSS+Website/). The data consisted of six observed variables: x₁: prestige of father’s occupation, x₂: son’s income, x₃: father’s education, x₄: prestige of son’s occupation, x₅: son’s education, and x₆: number of siblings.¹⁵ The sample selection was conducted based on the following criteria: i) non-farm background; ii) ages 35–44; iii) white; iv) male; v) in the labor force at the time of the survey; vi) not missing data for any of the covariates; and vii) data taken from 1972–2006. The sample size was 1380.

The possible directions were determined based on the domain knowledge in Duncan et al. (1972), shown in Fig. 4. The causal relations of x₁, x₃, and x₆ usually are not modeled in the literature since there are many other determinants of these three exogenous observed variables that are not part of the model. However, the possible causal directions among the three variables would be x₁ ← x₃, x₆ ← x₁, and x₆ ← x₃ based on their temporal orders.

Table 5 shows the results. Our mixed-LiNGAM approach with the t-distributed individual-specific effects gave the largest number of successful discoveries and achieved the highest precision. The second best method was our mixed-LiNGAM approach with the Gaussian individual-specific effects, which found one less correct possible directions than the t-distribution version. The third best method was LvLiNGAM with 1 latent confounder, which found two less correct possible directions than the t-distribution version. This would be mainly because our two methods allow individual-specific effects and the other methods do not, although these results are not significantly different for the number of trials 15.

Table 5:

Comparison of eight methods

Possible directions	Our approach		LvLiNGAM			SLIM
	t-dist.	Gaussian	Num.	lat. conf.		Num.	lat. conf.
			1	4	1	4	10
x1(FO) ← x3(FE)	✓	✓		✓			✓
x2(SI) ← x1(FO)	✓	✓				✓	✓
x2(SI) ← x3(FE)	✓	✓			✓	✓	✓
x2(SI) ← x4(SO)	✓	✓			✓	✓
x2(SI) ← x5(SE)	✓	✓	✓	✓	✓		✓
x2(SI) ← x6(NS)	✓	✓	✓	✓
x4(SO) ← x1 (FO)	✓	✓	✓	✓	✓	✓	✓
x4(SO) ← x3(FE)	✓	✓	✓		✓	✓	✓
x4(SO) ← x5(SE)	✓	✓	✓	✓
x4(SO) ← x6(NS)	✓	✓	✓	✓	✓
x5(SE) ← x1(FO)					✓
x5(SE) ← x3(FE)	✓		✓	✓	✓	✓
x5(SE) ← x6(NS)	✓	✓	✓	✓	✓
x6(NS) ← x1(FO)			✓				✓
x6(NS) ← x3(FE)			✓	✓		✓	✓
Num. of successes	12	11	10	9	9	7	8
Standard errors	1.55	1.71	1.83	1.90	1.90	1.93	1.93
Precisions	0.80	0.73	0.67	0.60	0.60	0.47	0.53
Possible directions	LiNGAM-GC-UK	ICA	Direct	Pairwise	PNL
x1(FO) ← x3(FE)		✓	✓
x2(SI) ← x1(FO)		✓	✓		✓
x2(SI) ← x3(FE)		✓			✓
x2(SI) ← x4(SO)		✓	✓		✓
x2(SI) ← x5(SE)		✓			✓
x2(SI) ← x6(NS)		✓			✓
x4(SO) ← x1(FO)			✓	✓
x4(SO) ← x3(FE)			✓		✓
x4(SO) ← x5(SE)		✓			✓
x4(SO) ← x6(NS)		✓
x5(SE) ← x1(FO)	✓		✓	✓
x5(SE) ← x3(FE)			✓		✓
x5(SE) ← x6(NS)
x6(NS) ← x1(FO)	✓		✓
x6(NS) ← x3(FE)	✓		✓		✓
Num. of successes	3	8	9	2	9
Standard errors	1.55	1.93	1.90	1.32	1.90
Precisions	0.20	0.53	0.60	0.13	0.60

FO: Father’s Occupation

FE: Father’s Education

SI: Son’s Income

SO: Son’s Occupation

SE: Son’s Education

NS: Number of Siblings

ICA: ICA-LiNGAM (Shimizu et al., 2006)

Direct: DirectLiNGAM (Shimizu et al., 2011)

Pairwise: Pairwise LiNGAM (Hyvärinen and Smith, 2013)

PNL: Post-nonlinear causal model (Zhang and Hyvärinen, 2009)

Table 6 shows the estimated hyper-parameter values of our mixed-LiNGAM approach with the t-distributed individual-specific effects that performed best in the sociology data experiment. Either the estimated hyper-parameter ${\widehat{\tau }}_1^{indvdl}$ and ${\widehat{\tau }}_2^{indvdl}$ that represents the magnitudes of individual differences was non-zero in all pairs except (x₄, x₅). The non- ignorable influence of latent confounders was implied between the pairs (x₂, x₄), (x₂, x₆) and (x₃, x₆) since both ${\widehat{\tau }}_1^{indvdl}$ or ${\widehat{\tau }}_2^{indvdl}$ were non-zero for the pairs. In addition, for the pair (x₂, x₆), there might exist some nonlinear influence of latent confounders, since ${\widehat{\sigma }}_{12}$ is zero, i.e., the individual-specific effects were linearly uncorrelated but dependent.¹⁶ If ${\widehat{\sigma }}_{12}$ were larger, it would have implied a larger linear influence of the latent confounders on the pair (x₂, x₆). The estimates of the hyper-parameter ${\tau }_1^{indvdl}$ were very large for the pairs (x₂, x₆) and (x₄, x₁), which implied very large individual differences regarding x₂ and x₄ respectively. This might imply that the estimated directions could be less reliable, although they were correct in this example.

Table 6:

Estimated hyper-parameter values of our method with t-distributed individual- specific effects

Pairs analyzed	Possible directions	Estimated directions	${\widehat{\tau }}_1^{indvdl}$	${\widehat{\tau }}_2^{indvdl}$	${\widehat{\sigma }}_{12}$
(x1(FO), x3(FE))	←	←	0.42$\widehat{\text{var}}$ (x1)	0	−0.7
(x2(SI), x1(FO))	←	←	0.82$\widehat{\text{var}}$ (x2)	0	0.3
(x2(SI), x3(FE))	←	←	0.82$\widehat{\text{var}}$ (x2)	0	−0.5
(x2(SI), x4(SO))	←	←	0.22$\widehat{\text{var}}$ (x2)	0.42$\widehat{\text{var}}$ (x4)	−0.5
(x2(SI), x5(SE))	←	←	0	0.42$\widehat{\text{var}}$ (x5)	0
(x2(SI), x6(NS))	←	←	1.02$\widehat{\text{var}}$ (x2)	0.62$\widehat{\text{var}}$ (x6)	0
(x4(SO), x1(FO))	←	←	1.02$\widehat{\text{var}}$ (x4)	0	0.9
(x4(SO), x3(FE))	←	←	0	0.22$\widehat{\text{var}}$ (x3)	−0.3
(x4(SO), x5(SE))	←	←	0	0	−0.3
(x4(SO), x6(NS))	←	←	0.62$\widehat{\text{var}}$ (x4)	0	−0.7
(x5(SE), x1(FO))	←	→	0	0.82$\widehat{\text{var}}$ (x1)	0.3
(x5(SE), x3(FE))	←	←	0.62$\widehat{\text{var}}$ (x5)	0	−0.5
(x5(SE), x6(NS))	←	←	0.22$\widehat{\text{var}}$ (x5)	0	−0.3
(x6(NS), x1(FO))	←	→	0.22$\widehat{\text{var}}$ (x6)	0	−0.9
(x6(NS), x3(FE))	←	→	0.22$\widehat{\text{var}}$ (x6)	0.62$\widehat{\text{var}}$ (x3)	0.5

FO: Father’s Occupation

FE: Father’s Education

SI: Son’s Income

SO: Son’s Occupation

SE: Son’s Education

NS: Number of Siblings

${\tau }_1^{indvdl}\text{and}{\tau }_2^{indvdl}$ represent the variances of the individual-specific effects for the variable pairs in the left-most column.

σ₁₂ represents the correlation parameter value of the individual-specific effects for the variable pairs in the left-most column.

Another point to note is that both our methods with t-distributed and Gaussian individual-specific effects failed to find the possible direction x₅ ← x₁, although the causal relation is expected to occur from the domain knowledge (Duncan et al., 1972). This failure would be attributed to the model misspecification since the sample size was very large. Since the estimate of the hyper-parameter ${\tau }_1^{indvdl}$ regarding x₅ was zero, the influence of latent confounders might be small for this pair, although the estimate of ${\tau }_2^{indvdl}$ was not small and the individual difference regarding x₅ seemed substantial. Modeling both latent confounders and nonlinear relations and/or allowing a wider class of non-Gaussian distributions might lead to better performance. This is an important line of future research.

6. Conclusions

We proposed a new variant of LiNGAM that incorporated individual-specific effects in order to allow latent confounders. We further proposed an empirical Bayesian approach to estimate the possible causal direction of two observed variables based on the new model. In experiments on artificial data and real-world sociology data, the performance of our method was better than or at least comparable to that of existing methods.

For more than two variables, one approach would be to apply our method on every pair of the variables. Then, we can estimate a causal ordering of all the variables by integrating the estimation results. This approach is computationally much simper than trying all the possible causal orderings. Once a causal ordering of the variables is estimated, the remaining problem is to estimate regression coefficients or their posterior distributions. Then, one can see if there are direct causal connections between these variables. Although this could still be computationally challenging for large numbers of variables, the problem reduces to a significantly simpler one by identifying their causal orders. Thus, it is sensible to develop methods that can estimate causal direction of two variables allowing latent confounders.

Future work will focus on extending the model to allow cyclic and nonlinear relations and a wider class of non-Gaussian distributions as well as evaluating our method on various real-world data. Another important direction is to investigate the degree to which the model selection is sensitive to the choice of prior distributions.