Fitting Skeletal Object Models Using Spherical Harmonics Based Template Warping

Abstract

We present a scheme that propagates a reference skeletal model (s-rep) into a particular case of an object, thereby propagating the initial shape-related layout of the skeleton-to-boundary vectors, called spokes. The scheme represents the surfaces of the template as well as the target objects by spherical harmonics and computes a warp between these via a thin plate spline. To form the propagated s-rep, it applies the warp to the spokes of the template s-rep and then statistically refines. This automatic approach promises to make s-rep fitting robust for complicated objects, which allows s-rep based statistics to be available to all. The improvement in fitting and statistics is significant compared with the previous methods and in statistics compared with a state-of-the-art boundary based method.

I. Introduction

The ability to accurately and robustly represent sets of similar objects is an important and well-studied problem in computer vision [1], [2] and medical image analysis applications [3], [4]. Skeletal models for representing objects have shown particular strengths. As a result of their property of providing a shape-based coordinate system for the object interior and near exterior, they provide special capabilities for mechanical modeling [5]–[8] and for the image match term used in segmentation [9], [10]. Because they capture not only global boundary locations but also local object width properties and boundary directional properties, they have provided stronger statistical summaries of object populations, and these have led to improved prior terms needed for segmentation, which together with the advantages for the image match term have yielded superior segmentations [9].

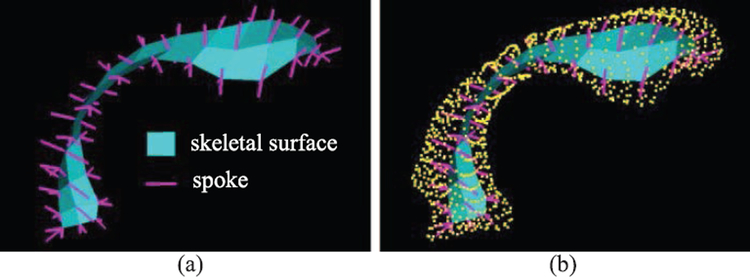
A particular form of quasi-medial skeletal model called the s-rep[11] has been shown in numerous recent papers to be more powerful for various statistical pattern recognition objectives, e.g., in classification (diagnosis) [12], hypothesis testing [13] and in the general probability distribution properties of specificity, generalization, and compactness [14] as compared to boundary point distribution models (PDMs) [15]. This s-rep consists of a grid of spoke vectors proceeding from the skeletal surface to the object boundary (Fig. 1).

Fig. 1.

(a) The template lateral ventricle s-rep; (b) that s-rep with its SPHARM boundary shown as yellow points. The magenta lines proceeding from the skeletal surface (cyan) to the object’s boundary are spokes.

To gain this expanded capability, s-reps must be fit tightly to the training objects in a way producing correspondence. Methods previously available [11], [13], [16] to obtain such fits can be summarized as 1) define a template s-rep (denoted as ${\mathcal{T}}_{srep}$); 2) solve an optimization problem that fits the interpolated form of ${\mathcal{T}}_{srep}$ to each target object; 3) compute the mean of the generated s-reps; 4) repeat this fitting process by replacing ${\mathcal{T}}_{srep}$ with the mean. This standard fitting process has been tedious to use and has required much manual intervention, leading to weaknesses in correspondence as well as limited use of this representation by others than those in or closely collaborating with our laboratory. Moreover, it performs poorly for more complex objects with variable bending and twisting.

Means of propagating a reference model into a particular object have been applied to PDMs. Cootes et al. presented such a method based on PDM statistics, active shape models [17]. Davies et al. [18] proposed a method for improving such statistical shape models by putting them into inter-object correspondence based on minimum description length. Styner et al. [19] demonstrated a thin plate spline (TPS) warping that maps objects to a common medial branching topology while matching their PDM boundaries perfectly.

In this letter we improve s-rep fitting by initializing the optimization in steps 2–4 above with a TPS-based propagation of ${\mathcal{T}}_{srep}$ into the target object. For complicated objects this leads to much more automatic fits with good correspondence. This promises to make the advantages of s-reps described above available to all users of shape statistics.

The propagation uses the spherical harmonics point distribution model (SPHARM-PDM) [3] representing both ${\mathcal{T}}_{srep}$ and the target object as the basis for computing the TPS warp and then applies that warp to the skeleton-to-boundary spoke vectors of ${\mathcal{T}}_{srep}$.

Our main contribution is two-fold: 1) a novel scheme for fitting significantly improved s-reps via TPS warping; 2) an effective way to propagate the correspondence provided by the initial shape model.

The remainder of this letter is organized as follows. Section II describes the input and related formulations. Section III presents our proposed method. Experimental results are given in Section IV, followed by a discussion in Section V.

II. Initial Shape Model and SPHARM Surface

The input to the proposed method is a predefined template s-rep ${\mathcal{T}}_{srep}$ (see Fig. 1(a)), which is iteratively fitted to the object using the standard pipeline discussed in Section I under supervision; and a population of target PDMs sampled from each object. These PDMs can be those extended from any 3D surface detection method (e.g., [20], [21]). As aforementioned, here we use the SPHARM-PDM which is an up-to-date, open source, public available framework that has been extensively used in shape statistics [14], [18], [22]–[25] and medical image applications [26]–[29] to describe binary segmented magnetic resonance (MR) images. Spherical harmonics (SPHARM) describes a surface x(θ, φ) using

$$\underset{\_}{x}(\theta ,\phi )=\sum _{l=0}^{\infty }\sum _{m=-l}^l{\underset{\_}{c}}_l^m{Y}_l^m(\theta ,\phi ),$$ (1)

where the basis functions $Y_l^m(\theta ,\phi )$, −l ≤ m ≤ l and order m are defined on θ ∈ [0, π] × φ ∈ [0, 2π] and where the 3D coefficients ${\underset{\_}{c}}_l^m$ are obtained by solving the least-squares problems in each spatial coordinate directions.

Every point p_i on the surface is one-to-one mapped to a parameter vector (θ_i, φ_i) on the unit sphere. The bijective mapping of the surface to the sphere is done by modifying the parameter vectors in a constrained optimization procedure considering minimal quadrilateral distortion and area preservation that is used to force every object region to map to a region of proportional area in parameter space. Each object’s optimization is preceded by a setting of its axis and prime meridian using second moments of its {p_i}.

A homogeneous sampling of the spherical parameter space uses a linear, uniform icosahedron subdivision along each edge of the original icosahedron. Suppose we get a set of parameter vectors (θ_i, φ_i) through the homogeneous sampling on the spherical parameter space. The PDM of the object surface can be obtained directly by putting the coefficients into Eq. (1), thus a sampled point ${\overrightarrow{p}}_i$ at location (θ_i, φ_i) takes on the form:

$${\overrightarrow{p}}_i=\sum _{l=0}^K\sum _{m=-l}^l{\underset{\_}{c}}_l^m{Y}_l^m\left({\theta }_i,{\phi }_i\right),$$ (2)

where K is a linear subdivision level of the icosahedron, which was selected depending on the complexity of the objects.

In this letter each lateral ventricle was sampled by a linear subdivision level K = 10, which composes a PDM consisting of 1002 points. All PDMs were normalized to the unit space.

III. Method

The main issue addressed in this letter is the automatic and robust TPS-based propagation of a reference s-rep into unseen target objects. The following sections present the main components of our novel scheme: 1) get TPS deformations from ${\mathcal{T}}_{srep}$ to each of the target PDMs; 2) warp ${\mathcal{T}}_{srep}$ by each TPS deformation; 3) refine the warped target s-reps.

A. Thin Plate Spline Deformation

Given landmarks {p_k = (x_k, y_k, z_k), k = 1, …, m} that must map into target landmarks {p_k′ = (x_k′, y_k′, z_k′), k = 1, …, m}, the TPS [30] provides the deformation that minimizes the bending energy

$$\underset{{ℝ}^3}{\iint }\left(f_{xx}^2+f_{yy}^2+f_{zz}^2+2f_{xy}^2+2f_{yz}^2+2f_{zx}^2\right)dxdydz$$ (3)

where $f_{ij}^2,i,j\in \left\{x,y,z\right\}$ denotes the squares of the second-order partial derivatives. That deformation maps any point p = (x, y, z) into the target point p′ = (x′, y′, z′) by the equation

$$p^{\prime }=\underset{\_}{\Delta x}+Ap+\sum _{k=1}^m{\omega }_{k}U\left(\left|p-p_k\right|\right)$$ (4)

where U(s) = s²ln(s) and the three values in the translation $\underset{\_}{\Delta x}$, the nine values in the 3 × 3 matrix A, and the 3m values of the weights ω_k of the warp basis functions U(|p − p_k|) are computed by solving linear equations involving vectors connecting corresponding landmarks in {p_k} and {p_k′}.

B. Deriving the Warps for Target PDMs

The process starts from getting the SPHARM boundary for ${\mathcal{T}}_{srep}$ (Fig. 1(a)), which is achieved by applying the same formula as for the target PDMs presented in Section II. The resulting PDM acts as the template PDM (see Fig. 1(b)).

The calculation of the warp T_j for each target PDM j can be done by solving the linear equations discussed in Section III-A, where the landmarks {p_k} are the boundary points in the SPHARM-PDM derived from ${\mathcal{T}}_{srep}$ and the landmarks {p_k′} are analogous points in each of the target PDMs. Applying T_j to spoke’s two endpoints p yields the corresponding spoke endpoints p′.

For a population of N target objects, we get a set of mapping functions {T_j,j = 1,…,N} each defining a warp T_j that can be applied to deform the spoke endpoint pairs in ${\mathcal{T}}_{srep}$ to get its warped target s-rep.

C. Creating Initializing Warped S-Reps

The process of creating a warped target s-rep (denoted as ${\mathcal{W}}_{srep}$) is summarized in Table I. The set of transforms {T_j} are applied to the “landmark pairs” (the tail and tip of each spoke) of the template s-rep. The resulting “landmark pairs” are used to produce the jth target s-rep. Each spoke has a position (the coordinate of the spoke tail), a direction (a unit vector pointing from tail to tip) and a radius (the length of the spoke vector).

TABLE I.

Process for the Creation of Target S-Reps

Input: Tsrep and {Tj, j = 1, … , N.}
Output: {${\mathcal{W}}_{srep}$}
for the jth TPS transformation Tj
for each spoke of Tsrep
tpsSpokeTail = applyTPS(Tj, spokeTail);
tpsSpokeTip = applyTPS(Tj, spokeTip);
spokeRadius = calculateSpokeRadius(tpsSpokeTail, tpsSpokeTip);
spokeDirection = calculateUnitDir(tpsSpokeTail, tpsSpokeTip);
saveNewSpoke(tpsSpokeTail, spokeRadiu, spokeDirection);
end
saveNewSrep();
end

These warped s-reps can be refined by slightly modifying each spoke’s length and direction to optimize the fit to the binary image. The refinement process is beyond the scope of this letter. The evaluations described in the next section are all based on the warped s-reps without refinement.

IV. Experimental Results

The proposed method was evaluated on a set of real world lateral ventricle objects semi-automatically segmented from MR images in neonate datasets [31]. We selected 94 lateral ventricles for our tests presented here. The program was implemented in C++, all experiments were done on a 64-bit 3.20 GHz Intel Quad Core PC with 8 GB RAM. It takes about 11 minutes to get the SPHARM-PDM surface, 5 minutes to get the TPS propagated s-rep, and 29 minutes to get the standardly fitted s-rep for one object.

We first investigated the smoothness of the surfaces implied by the propagated s-reps resulting from the proposed approach. Then we compared these s-reps with those from the standard method. Following this we evaluated the statistics of these s-reps via three commonly used measurements: generalization G(M), specificity S(M) and compactness C(M), which were first introduced by Davies [32] and have been widely used in previous literature [18], [26], [33]. Briefly, a lower value is desirable for all three metrics. Finally, we studied the shape variability captured by the proposed method and the baseline.

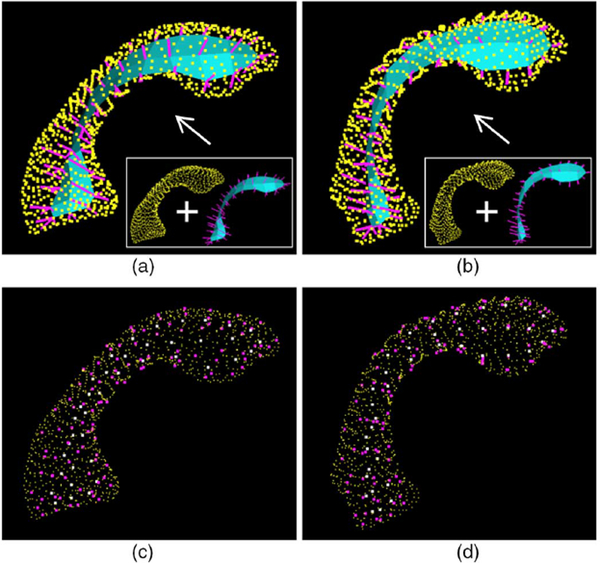
As described in Section II, our input objects were described by the SPHARM-PDMs, which also provide the ground truth to evaluate if our warped s-reps imply the correct object boundaries (similar to the input surfaces). Fig. 2 shows two example objects described by SPHARM-PDMs with the corresponding warped target s-reps shown inside.

Fig. 2.

Visualization of two example objects (each column is an object) with the propagated s-reps shown inside of their own baseline (SPHARM-PDM). (a) and (b) are the s-reps fitted into the baseline (yellow points); (c) and (d) are the spokes ends (spoke tail (white), spoke tip (magenta)) fitted into the baseline.

In Figs. 2(a),(b) we can see that all the spokes (magenta lines) located in the object interior (bounded by the yellow points). All the spoke tips (magenta points in Figs. 2(c), (d) lie approximately on the baseline surface (yellow points, the SPHARMPDM). These tell us that our warped target s-reps achieve a rather smooth surface.

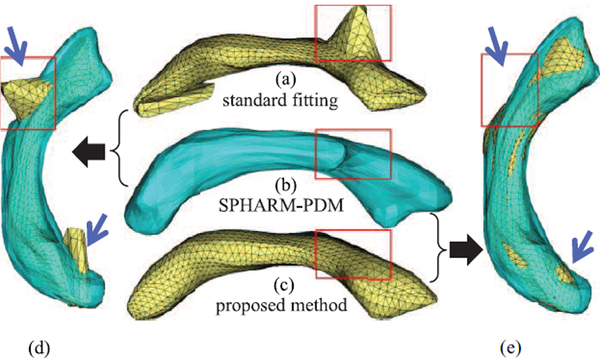
To further evaluate the propagated fitting, we compared the implied boundary of the s-reps resulting from the proposed method with those from the aforementioned standard fitting process that was extensively used for fitting relatively simple objects (e.g., [12], [13], [15], [34]). Results show that the proposed method achieves reasonable smooth surfaces with improved overlap with the target object, while there are error regions from their methods (e.g., Fig. 3).

Fig. 3.

(a) The surface for the standardly fitted s-rep; (b) the surface for the SPHARM-PDM (which is the baseline); (c) the surface for our propagated s-rep; (d) and (e) are the overlap of the baseline onto (a) and (c), respectively. The red frames indicate the approximate corresponding positions. The blue arrows indicate the significant differences of the two methods in comparison. (a) standard fitting (b) SPHARM-PDM (c) proposed method.

The erroneous bumps in Figs. 3(a), (d) show the surface implied by a standardly fitted s-rep. These bumps need to be adjusted manually followed by redoing of the fitting; even this doesn’t guarantee better fit for complicated objects. But our method (Figs. 3(c), (e)) automatically yields significantly improved s-reps with smooth surfaces. This is because the TPS warps are globally smooth and robust to narrow/thin regions, unlike the previous method for matching the s-rep model to the objects. Also, problems of poor convergence of the previous optimization method when initialized poorly are avoided.

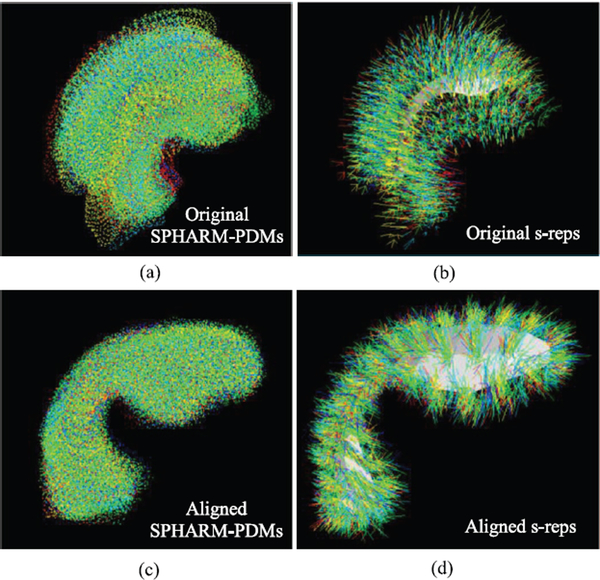
To evaluate the statistics of the resulting propagated s-reps, a Procrustes alignment was performed to remove the translation, scaling and rotation variances introduced by each model. Figs. 4(a), (b) display all the 94 samples in the population together; each was represented by the SPHARM-PDMs and the s-reps. The alignment brings the shapes closer (Figs. 4(c), (d)).

Fig. 4.

All the 94 training shapes overlaid on top of each other. Each shape is described by the SPHARM-PDM (a) and the s-rep (b). After applying the Procrustes alignment, the shapes described by both shape models get close and tight as (c) and (d). Colors indicate different shapes in the population.

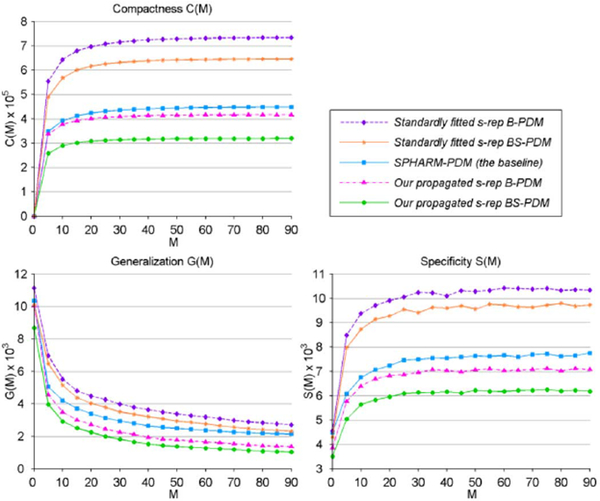
The correspondence quality among our propagated s-reps, the standardly fitted s-reps and the baseline are compared in Fig. 5. We collected two types of PDMs implied by s-rep spokes: B-PDM, which has 106 points (only spoke tip points) and BS-PDM, which has 212 points (spoke tail-and-tip points). Fig. 5 tells us that the proposed method achieves lower values than other methods in all three measurements, which means that our warped s-reps are superior.

Fig. 5.

Comparisons of correspondence quality among different PDMs. M is the shape parameters used for constructing new instances.

Table II lists the contribution of the first six eigenmodes for B-PDM and BS-PDM from our warped s-reps and the baseline; we can see that the total shape variances captured by these eigenmodes are 83.5%, 83.9% and 80.4% respectively. This suggests that the proposed model captures more shape variance even if we only consider the object boundaries implied by s-reps (B-PDM) and describes the object with lower dimension. On inspection, all three types of PDMs appear to be of good quality; each main eigenmode describes a plausible pattern of variation observed in the population (see Fig. 6 for a visualization of the first eigenmode).

TABLE II.

Shape Variances of Different Methods (%)

Point set	λ1	λ2	λ3	λ4	λ5	λ6	Sum
B-PDM	42.7	15.3	11.3	6.2	5.0	3.0	83.5
BS-PDM	37.8	18.6	11.8	7.1	5.5	3.1	83.9
SPHARM-PDM	40.4	15.7	10.5	6.0	5.1	2.9	80.4

Fig. 6.

From left to right column: B-PDM, BS-PDM and SPHARM-PDM. The middle row is the mean shape resulting from different point sets; the top and bottom rows are $\pm \sqrt{{\lambda }_1}$ respectively.

V. Conclusion

We presented a novel scheme that propagates a reference skeletal model (${\mathcal{T}}_{srep}$) to a set of biomedical objects to obtain their fitted s-reps. This is done by representing the surfaces of ${\mathcal{T}}_{srep}$ as well as the target objects by spherical harmonics and computing a thin plate spline warp between these, and applying this warp to ${\mathcal{T}}_{srep}$. Experimental results proved that 1) this automatic scheme creates stable s-reps that are robust for complicated objects; 2) the propagated s-reps have significantly improved fitting and model properties as compared with the standardly fitted s-reps; 3) the propagated s-reps in the presence of considerable shape variability gain over the baseline. The resulting s-reps can be further statistically improved in spoke correspondence (e.g., [14]). In the future, we expect to obtain better fits by using shape change statistics in the refinement step. The resulting s-reps can be applied to achieve better results on classification, hypothesis testing and probability distribution estimation, as well as a variety of medical image applications dependent on these statistical analyses.