Ultrafast nonlocal collective dynamics of Kane plasmon-polaritons in a narrow-gap semiconductor

Surface light-matter waves in a semiconductor driven by an ultrafast laser reach relativistic regime.

Abstract

The observation of ultrarelativistic fermions in condensed-matter systems has uncovered a cornucopia of novel phenomenology as well as a potential for effective ultrafast light engineering of new states of matter. While the nonequilibrium properties of two- and three-dimensional (2D and 3D) hexagonal crystals have been studied extensively, our understanding of the photoinduced dynamics in 3D single-valley ultrarelativistic materials is, unexpectedly, lacking. Here, we use ultrafast scanning near-field optical spectroscopy to access and control nonequilibrium large-momentum plasmon-polaritons in thin films of a prototypical narrow-bandgap semiconductor Hg_0.81Cd_0.19Te. We demonstrate that these collective excitations exhibit distinctly nonclassical scaling with electron density characteristic of the ultrarelativistic Kane regime and experience ultrafast initial relaxation followed by a long-lived highly coherent state. Our observation and ultrafast control of Kane plasmon-polaritons in a semiconducting material using light sources in the standard telecommunications fiber-optics window open a new avenue toward high-bandwidth coherent information processing in next-generation plasmonic circuits.

INTRODUCTION

The alloys of Hg_1−xCd_xTe are important infrared (IR) semiconducting materials owing to their high optical sensitivity and tunability of the bandgap E_g(x) as a function of Cd concentration x. The gap is large at x = 1 (about 1.65 eV) and inverts to −0.3 eV at x = 0, with a zero crossing around x_c = 0.15 (1). Compounds with a small positive gap are commonly used photoconductors in IR detectors (1), while quantum wells of HgTe and CdTe with an inverted, negative gap have been theoretically predicted and found to host a topological quantum spin Hall state featuring spin-polarized ultrarelativistic band dispersion (2, 3). Since this latter seminal prediction, a wide array of topologically nontrivial states has been proposed to occur in Hg_1−xCd_xTe-based materials (4).

The Hg_1−xCd_xTe compound with x ≈ x_c, at which the bandgap vanishes, features a highly nontrivial band structure with a single Dirac cone located at the center of the Brillouin zone and intercepted at the Dirac point by another, nearly massless band. This band structure was first theoretically investigated by Kane (5) and represents one of the first solid-state realizations of fermions with ultrarelativistic dispersion (6). This materials family has recently expanded markedly with the discovery of numerous compounds hosting Dirac and Weyl fermions (7–9), which give rise to a rich array of unique physical phenomena (10, 11). The presence of three degenerate bands at the Dirac point in the Kane band structure gives rise to a curiosity that only exists as a nonfundamental quasiparticle in matter: a pseudospin-1 fermion (fundamental particles with spin-1 are restricted to boson statistics) (12). These fermions have several purely quantum attributes, such as an unusual, non–π-quantized topological phase (12), split-peak magneto-optical spectrum, and linear dependence of the plasmonic oscillation frequency on the Fermi energy (6, 12, 13). Key aspects of the nontrivial electrodynamics of Kane fermions are also retained in the presence of a gap in the electronic structure, with no complete degeneracy at the center of the Brillouin zone, as long as the bandgap is not too large (6).

Recently, it has further been proposed that even the topologically trivial phase of the HgTe/CdTe quantum well can become a topological insulator when driven out of equilibrium by laser excitation (Floquet topological insulator) (14). Photoexcitation of narrow-gap semiconductors with a controllable magnitude of the bandgap, such as Hg_1−xCd_xTe, has been further predicted to potentially result in plasmon amplification by stimulated particle-hole recombination when population inversion has been achieved and the plasma energy is tuned on resonance with the bandgap (15) [similar ideas have recently been explored in the context of graphene (16–19) and Josephson plasmons (20)]. The latter nonequilibrium process holds the promise for reducing or completely eliminating plasmonic dissipation and, thus, markedly enhancing coherence, a highly desirable property in plasmonic circuitry (21). However, the achievement of plasmonic amplification by stimulated emission requires population inversion, which depends sensitively on the relaxation dynamics of photoexcited charge carriers.

As a consequence, topological and plasmonic engineering of ultrarelativistic collective excitations in Hg_1−xCd_xTe using light fields requires effective access to and control of the nonequilibrium charge-carrier dynamics in this material, preferably using easily scalable industrial laser technology. Despite the technological importance of Hg_1−xCd_xTe, its ultrafast quasiparticle response has remained underexplored in contrast to other common semiconducting and semimetallic compounds (22–24). Previous monochromatic investigations of wide-bandgap compositions of Hg_1−xCd_xTe in the near-IR spectral range succeeded in extracting average collective relaxation times on the order of 0.5 to 2 ps (25). A spectrally integrated pump-probe study of a narrow-bandgap composition (x = 0.2) in the terahertz spectral range arrived at a similar conclusion (26).

Here, we report the all-optical ultrafast generation and broadband detection of coherent plasmon-polaritonic response in narrow-bandgap Hg_0.81Cd_0.19Te in a mid-IR spectral range from 80 to 140 meV. We use field enhancement in a scattering-type scanning near-field optical spectroscope (Fig. 1A) to produce large electric field gradients in the nanovolume between the tip and the sample, enabling the generation of large-momentum collective modes (compared with the nearly vanishing momentum of IR photons) (28). Our experimental apparatus is capable of the direct observation of these modes both spectroscopically and in real space (29, 30) with subpicosecond temporal resolution (23, 31–33). Furthermore, both the amplitude and phase of the near-field signal are simultaneously acquired using an interferometric detection scheme, as described in (23, 33–37). Access to the complex IR response in a broad spectral range facilitates reliable artifact-free (38) extraction of the photoinduced charge-carrier characteristics as well as their temporal dynamics as the material returns to equilibrium. High near-field gradients used by this technique further lead to a substantially reduced penetration depth of electromagnetic radiation into the material under investigation, improving the sensitivity to the optical response of thin and ultrathin films (see the Supplementary Materials for more details).

Fig. 1. Plasmonic pumping experiment and photoinduced near-field optical response in Hg_0.81Cd_0.19Te.

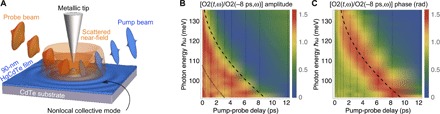
(A) Nano-optical spectroscopy was carried out by means of apertureless scattering-type near-field optical microscope based on a metallic tip of an atomic-force microscope illuminated with broadband IR light and photoexcited with a femtosecond fiber laser operating in the conventional telecommunications window of the Er-doped optical fiber (1530 to 1565 nm) (23); high-fluence data in Fig. 3C were obtained using a free-space amplified laser system (see Materials and Methods). Strong field enhancement and gradient in the sample-tip nanocavity enable large light-matter momentum transfer (on the order of inverse tip radius) and, thus, the excitation and nanospectroscopy of large-momentum collective modes (27), overcoming the long-wavelength restriction of conventional IR optics. (B and C) Photon-energy dependence of the amplitude (B) and phase (C) of the normalized transient near-field signal demodulated at the second harmonic of the tip tapping frequency (O2: O, optical; 2, second harmonic). The spectra are plotted for various pump-probe delays from 0 to 12.2 ps and a pump pulse energy of 1 nJ. The dashed and dotted lines indicate the location of the primary and secondary plasmon-polaritonic feature, respectively. Solid black vertical lines indicate the time delays at which data were obtained.

RESULTS

Our main experimental observations are shown in Fig. 1 (B and C). We directly detect the formation of a transient plasma edge in the near-field amplitude and the corresponding peak in the near-field phase [dashed lines in Fig. 1 (B and C)] during the first 200 fs after the excitation of the sample with 1-nJ pulse energy of 0.8-eV photons. A conspicuous additional feature of the experimental data in Fig. 1B is the existence of a pronounced dip below the main plasma edge [dotted line in Fig. 1B and arrows in Fig. 2 (D and E)]. We attribute these primary and secondary features to the in-phase (high-energy feature; dashed line) and antiphase (low-energy feature; dotted line) coupled collective oscillations of charge on the top and bottom surfaces of the Hg_0.81Cd_0.19Te thin film (39).

Fig. 2. Ultrafast dynamics of coupled surface plasmon-polaritons.

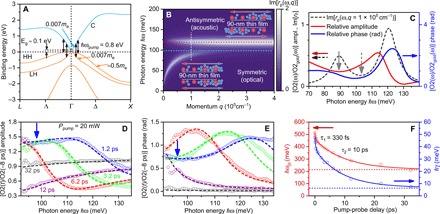
(A) Schematic of the electronic band structure of Hg_0.81Cd_0.19Te along several high-symmetry directions in the Brillouin zone without taking into account small intrinsic doping present in our samples. On the basis of the data in (40), C, HH, and LH denote the electron conduction band, heavy-hole, and light-hole valence band, respectively. Quasi-linear ultrarelativistic segments of band structure near Γ result from a large spin-orbit coupling. Vertical arrows show the optical transitions accessible to the optical pump with a photon energy of 0.8 eV. Note that the LH-C transitions have a much lower joint density of states than HH-C. The bandgap in this compound is ≈0.05 to 0.1 eV at 300 K and substantially temperature dependent (1). Effective masses of low-energy charge-carriers are indicated. (B) Imaginary part of the reflection coefficient r_p(ω, q) as a function of frequency ω and in-plane momentum transfer q calculated for a 90-nm thin film of Hg_0.81Cd_0.19Te on top of CdTe substrate, as described in the text. The two surface modes expected in a thin metallic film (one per interface; red and cyan dashed lines) experience mutual repulsion at long wavelengths due to the coupling between the symmetric and antisymmetric charge oscillations in these modes. (C) Near-field amplitude (red) and phase (blue) calculated using the reflection coefficient in (B) in the lightning rod model of near-field sample-tip interaction referenced to those of gold. The black dashed line is a cut of Im[r_p(ω, q)] at q₀ = 1/100 nm = 10⁵ cm⁻¹ [white dashed line in (B)]. The gray vertical arrows indicate the depression in the near-field amplitude (solid) and Im[r_p(ω, q₀)] (dashed) between the two branches of the surface plasmon-polariton. (D and E) Photon energy dependence of the amplitude (D) and phase (E) of the normalized transient near-field signal demodulated at the second harmonic of the tip tapping frequency, presented for select pump-probe delays (open symbols). Arrows indicate the location of the secondary plasmon-polaritonic feature. Dashed lines are the result of a fit using the model dielectric function in Eq. 1 incorporated into the multilayer response of the Hg_0.81Cd_0.19Te thin film on a CdTe substrate. (F) Unscreened plasma frequency ω_pl and scattering rate γ of plasmon-polariton quasiparticles as a function of the pump-probe delay (open symbols), extracted from the fit in (D) and (E). Red and blue solid lines in (F) are the result of a biexponential fit of the dependence of the plasma frequency and scattering rate, respectively, on the pump-probe delay. Horizontal red and blue dashed lines indicate the residual plasma frequency and scattering rate due to long-lived quasiparticle response (>30-ps lifetime).

To support this interpretation and extract the microscopic characteristics of the quasiparticle dynamics in Hg_0.81Cd_0.19Te quantitatively, we build a model of the material’s dielectric response and use it to describe the experimentally obtained near-field signal in the lightning rod formalism of near-field sample-tip interaction (28). The key electronic contributions to the photoexcited optical response can be established using the band diagram shown in Fig. 2A and the photon energy in the pump pulses (0.8 eV). This analysis demonstrates that only the conduction and valence states near the Γ point of the Brillouin zone are affected by the pump photons, while the L valley remains unpopulated.

The electronic band structure near the Γ point is formed by a light electron conduction (C) band and a light-hole (LH) and heavy-hole (HH) valence bands, all of which are affected by photoexcitation. Because of the largest density of states of the HH band and, consequently, its joint density of states with the C band, optical absorption in the HH-C dipole transitions dominates that in the LH-C transitions, and most of the photoexcited charge carriers are created in the C and HH bands. The itinerant charge-carrier response, which determines the reflectivity of the sample and the near-field signal, is characterized by the plasma frequency ω_pl ~ (n/m_band)^1/2 (in the case of a parabolic band; n is the carrier density and m_band is the band mass). Given the substantially smaller mass of the C-band electrons (0.007m_e) than that of HH-band holes (0.55m_e) (1), the photoinduced optical response is dominated by the charge carriers in the light C band. As a result, the transient free charge-carrier dielectric response of the sample can be described simply by a single Drude term accounting for the quasi-equilibrium electron gas in the C band

$$\mathrm{\epsilon }(t)={\mathrm{\epsilon }}_{\infty }-\frac{{\mathrm{\omega }}_{\text{pl}}^2(t)}{{\mathrm{\omega }}^2+\mathit{i}\gamma (t)\mathrm{\omega }}$$ (1)

where ω_pl(t) and γ(t) are the transient unscreened quasiparticle plasma frequency and scattering rate, respectively; ε_∞ is the total contribution of all higher-energy interband transitions to the dielectric permittivity and is ≈11 for the investigated composition (1). At t = 0, the pump and probe beams fully overlap; at times well before zero the dielectric response is that of equilibrium Hg_0.81Cd_0.19Te (with small ω_pl and γ due to intrinsic doping).

To get a qualitative understanding of the large-momentum optical response of the Hg_0.81Cd_0.19Te film, we first evaluate the momentum-dependent electromagnetic reflection coefficient r_p(ω, q). This property, taken in a relatively broad range of momenta of order q ~ 1/a, where a is the tip radius (10 to 100 nm), can then be used as input for a model of near-field interaction (28) to describe our experimental data quantitatively. We use Eq. 1 in a multilayer model (see the Supplementary Materials) to compute the r_p(ω, q) of a 90-nm thin-film Hg_0.81Cd_0.19Te on a CdTe substrate. To illustrate a realistic case, we use a representative unscreened plasma frequency ω_pl = 440 meV and charge-carrier scattering rate γ = 12 meV along with the trivial optical response of the CdTe substrate in our spectral range (ε ≈ ε_∞ ≈ 7.8). The imaginary part of the resulting r_p(ω, q) in the energy-momentum range accessed by our experimental apparatus is shown in Fig. 2B (the same quantity is plotted at low momenta, near the light cone, as well as for different film thicknesses in the Supplementary Materials). Two dispersive collective modes are evident and originate in plasmonic charge oscillations at the two interfaces of the metallic thin film: film-substrate and film-air. In the high-q limit, these two modes tend asymptotically to independent surface plasmon modes (red and cyan horizontal dashed lines). At lower in-plane momenta, charge oscillations at the two interfaces couple and screen each other differently in the symmetric and antisymmetric eigenmodes of mutual dynamics, resulting in a mode repulsion.

Using the r_p(ω, q) in Fig. 2B and experimental parameters such as a tip radius of 100 nm and a tip tapping amplitude in the lightning rod model of near-field interaction (28), we can now quantitatively compute the photon energy dependence of the amplitude and phase of the near-field signal. The results of such a calculation are plotted in Fig. 2C (red and blue line for the near-field amplitude and phase, respectively). Both the primary and secondary feature identified in the experimental data in Fig. 1 (B and C) are reproduced, justifying the constructed model. The cut of Im[r_p(ω, q)] at the momentum corresponding to the inverse tip radius q = 1/100 nm (white dashed line in Fig. 2B and black dashed line in Fig. 2C) demonstrates explicitly that the two features identified in our experiment can be assigned to the two interfacial plasmon-polaritonic modes (the characteristic depression in the signal between the primary and secondary feature is indicated by gray arrows).

We can now use the above model to extract the characteristics of the photoinduced optical response from our experimental data. Figure 2 (D and E) shows the amplitude and phase of the ratio of the near-field signal at a pump-probe delay t [O₂(t, ω)] to that at t = −8 ps [O₂(t = −8 ps, ω)] in the fully relaxed, equilibrium state (open symbols). Both signals were obtained by demodulating the light scattered from the tip-sample interaction volume at the second harmonic of the tip tapping frequency. The corresponding transient near-field response of Hg_0.81Cd_0.19Te before and at different times after the arrival of the pump pulse, referenced to gold, is shown in the Supplementary Materials along with representative raw spectra. We plot our fit results in Fig. 2 (D and E) as dashed lines of the color matching that of experimental data. The excellent quality of the fit demonstrates that our model captures all of the essential microscopic ingredients contributing to the observed transient signal. It thus allows us to reliably extract the dynamical properties of quasiparticle excitations [ω_pl(t) and γ(t)] as a function of pump-probe delay t. We plot the temporal dependence of these quantities in Fig. 2F. Both quantities show a biexponential relaxation behavior with a distinct fast (330 fs) and slow (10 ps) time scale. In the case of the scattering rate, the fast relaxation is consistent with the energy transfer from the quasi-equilibrium photoinjected itinerant-carrier population to optical phonons, with both subsystems rapidly reaching a steady state (phonon bottleneck) (41). The subsequent 10-ps relaxation is the consequence of further energy dissipation via the decay of optical phonons into acoustic phonons due to lattice anharmonicity (41). Calculations of the dispersion of the optical phonon modes and electron-phonon coupling strength in HgCdTe with a similar composition are consistent with this interpretation (42). The aforementioned effects lead to a gradual cooling of the photoexcited charge carriers and optical phonons, resulting in a decrease of the scattering rate. The red shift of the plasmon-polaritonic features observed in our experiments (Figs. 1, B and C, and 2, D and E) occurs because of the decrease of the quasiparticle concentration as particle-hole recombination takes place, mainly via Auger-1 processes (involving two electrons and one hole), which are known to dominate in Hg_0.81Cd_0.19Te at high temperatures and charge-carrier densities (43).

The initial relaxation does not lead to the full recovery of the equilibrium state: We identify a long-lived residual quasiparticle response (dashed horizontal lines in Fig. 2F) persisting longer than 30 ps and exhibiting a sizable unscreened plasma frequency of 213 meV with a very high degree of coherence (scattering rate below 6 meV). A possible origin of this long-lived state with low quasiparticle scattering may lie in the shallow surface defect states, which trap photoexcited carriers as they cool down and inhibit fast particle-hole recombination. Lower electronic temperature and more limited scattering phase space available to these quasiparticles result in a strongly reduced scattering rate.

Using the extracted quasiparticle scattering rate shown in Fig. 2F and the computed dispersion of the two plasmon-polaritonic branches in Fig. 2B, we can estimate the corresponding quasiparticle propagation lengths in Hg_0.81Cd_0.19Te. The lowest value of the quasiparticle scattering rate for the case when the plasmonic features are still visible in the raw data of Fig. 1 (B and C) is ℏγ ≈ 20 meV at a pump-probe delay of 8.2 ps. This scattering rate corresponds to a lifetime of about 200 fs, comparable with the quasiparticle lifetime in doped semiconductors such as n-InSb and an order of magnitude lower than in graphene under ambient conditions (44). The group velocities ℏv = ∂ℏω(q)/∂q of the two modes in Fig. 2B near the maximum of the tip coupling function (q ≈ 1 × 10⁵ cm⁻¹; vertical dashed line in Fig. 2B) are 15 meV/(10⁵ cm⁻¹) and 2 meV/(10⁵ cm⁻¹) for the lower and upper branch, respectively. The propagation length is obtained as v/γ and found to be 75 and 10 nm for the quasiparticles in the lower and upper branch, respectively. These values are smaller than one plasmon-polaritonic wavelength in the experimentally accessible momentum-energy range and one to two orders of magnitude lower than those in high-mobility graphene at ambient temperature (29, 30, 44). Therefore, the determination of plasmon-polaritonic characteristics via real-space interferometry is impossible and can only be performed using ultrafast spectroscopy with large momentum transfer used in our work. Should plasmon coherence enhancement by stimulated emission be realized in Hg_1−xCd_xTe, the quasiparticle lifetime could be increased by many orders of magnitude and bring direct visualization of propagating plasmon-polaritons into the experimentally accessible regime.

Having demonstrated the effective ultrafast generation of plasmon-polaritons with energies in excess of the bandgap in Hg_0.81Cd_0.19Te, we proceed to determine the dispersive characteristics of the electronic band structure underpinning the collective quasiparticle optical response. As an example of this approach, the investigation of the electron density dependence of the plasma frequency in a conventional wide-bandgap semiconductor (as illustrated in Fig. 3A) provides access to the electronic effective mass and its deviation from parabolicity upon increasing chemical potential (45). Parabolic band dispersion of a typical semiconductor results in an entirely classical square-root dependence of plasma frequency on electron density in all dimensions (13): ${\mathrm{\omega }}_D^{\text{pl}}\sim \sqrt{n_D{e}^2/\mathrm{\epsilon }m}$, where n_D is the carrier density per unit D-dimensional volume, e and m are the electron charge and effective mass, respectively, and ε is the dielectric constant of the medium. Quantum mechanical corrections only appear in the nonlocal (high-q) limit. On the contrary, in the case of relativistic (linear) electronic dispersion, plasma frequency becomes completely nonclassical (ℏ appears in the leading term) and features a distinct density dependence of the plasma frequency in every dimension (13): ${\mathrm{\omega }}_D^{\text{pl}}\sim n_D^{(D-1)/2D}$. In a narrow-bandgap semiconductor, such as Hg_0.81Cd_0.19Te, the dispersion of light electrons and holes is expected to be parabolic at energies comparable with the bandgap and linear at larger energies, as shown in Fig. 3B, due to the dominant spin-orbit coupling.

Fig. 3. Quasi-relativistic quantum quasiparticle response in Hg_0.81Cd_0.19Te.

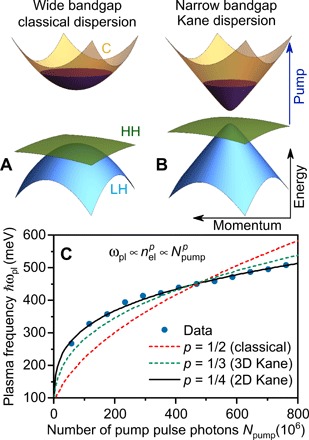
(A and B) Classical parabolic (A) and quasi-relativistic Kane (B) low-energy electronic band structure in a semiconductor. Quasi-linear ultrarelativistic segments of the Kane band structure result from a large spin-orbit coupling. The strong itinerant response is dominated by charge-carriers photoexcited predominantly from the HH band to the C band, as indicated by a blue arrow. (C) Dependence of the unscreened plasma frequency (blue symbols) on the number of photons per pump pulse (photon energy is 1.38 eV in this case). The latter is proportional to the number of photoexcited charge-carriers well below the saturated-absorption regime. Solid black as well as dashed green and red lines indicate the best fit to the experimental data obtained using the power-law dependence with exponent p of the plasma frequency on itinerant electron density in the case of classical parabolic (dashed red; p = 1/2) as well as 3D (dashed green; p = 1/3) and 2D (solid black; p = 1/4) quasi-linear Kane dispersion of the C band (see text). The latter two dependencies are purely quantum and have no classical analog (13).

Pump-probe optical spectroscopy can thus be used not only to distinguish between the classical and quantum plasmon dispersion but also to specify the dimensionality of the quasiparticle response in the relativistic case. Using the above model of near-field sample-tip interaction, we extracted the maximum photoinduced frequency of plasmon-polaritons in Hg_0.81Cd_0.19Te as a function of the photon number per pulse at maximum pump-probe overlap (zero delay between the pump and the probe pulse). We have chosen this regime for the study of the fluence dependence of the nonequilibrium plasma frequency due to the fluence-dependent relaxation rate of photoexcited charge carriers, which makes the instantaneous carrier density at a given nonzero time delay a function of not only absorbed fluence but also pump-probe delay itself. To fully quantify the latter effect, a detailed study of the relaxation dynamics, as shown in Fig. 2, has to be carried out at every fluence. This investigation will be a subject of future work.

The results of our fluence-dependent study are shown in Fig. 3C (symbols). The photoexcited density of conduction electrons is proportional to the photon number per pulse, provided that the absorption coefficient is linear in the range of applied pump fluences. This condition is typically satisfied up to pump fluences close to the damage threshold of the material. In the case of Hg_1−xCd_xTe, it has been demonstrated (25) that nonlinearities in the absorption coefficient at x = 0.4 are below 1% up to the largest photoinduced electron densities of 10¹⁸ cm⁻³ used in our work. The fit of the experimental data using a power-law dependence of the plasma frequency on the electron density reveals that the classical expression (p = 1/2) fails to reproduce the data, while the exponents expected in the two-dimensional (2D) and 3D relativistic case of Kane electronic dispersion of a narrow-bandgap semiconductor match the experimental data quite well. The 2D expression provides an even better fit to the experimental data than the 3D expression, suggesting that the electrodynamics of this material is still substantially affected by the residual quantization in the conduction band and that the 90-nm film can be considered as a wide quantum well.

The extracted plasma frequency of photoexcited charge carriers allows us to infer their density n as well as the quasi-equilibrium Fermi energy E_F. A linear band dispersion in both 3D and 2D results in purely quantum mechanical expressions for the plasma frequency in the leading term (14): ${\mathrm{\omega }}_{\text{pl}}^{(\text{lin},3\mathrm{D})}\propto n^{1/3}{v}_{\mathrm{F}}/\sqrt{\mathrm{\hslash }}\propto E_{\mathrm{F}}/\sqrt{\mathrm{\hslash }}$ (momentum independent) and ${\mathrm{\omega }}_{\text{pl}}^{(\text{lin},2\mathrm{D})}\propto n^{1/4}{q}^{1/2}{v}_{\mathrm{F}}/\sqrt{\mathrm{\hslash }}\propto \sqrt{{\mathit{qE}}_{\mathrm{F}}}$. The dependence on E_F results from the fact that $k_{\mathrm{F}}^{3\mathrm{D}}={(3{\mathrm{\pi }}^{2}n)}^{1/3}$, $k_{\mathrm{F}}^{2\mathrm{D}}={(2\mathrm{\pi }n)}^{1/2}$, and E_F = ℏv_Fk_F. Here, k_F and v_F are the Fermi wave vector and velocity, respectively, and q is the quasiparticle momentum. Thus, the plasma frequency of itinerant charge carriers scales linearly with the Fermi energy in 3D and sublinearly in 2D. In the 3D case, the proportionality constant between ω^{(lin, 3D)} and E_F is found to be ≈1 for v_F ≈ 10⁶ m/s in Hg_0.81Cd_0.19Te (6). The maximum quasi-equilibrium Fermi energy of Hg_0.81Cd_0.19Te attained in our experiment is, therefore, 500 meV in 3D and can be estimated to be of similar magnitude near q = 110⁵ cm⁻¹ (vertical dashed line in Fig. 2B) in the hypothetical purely 2D case of a Hg_0.81Cd_0.19Te monolayer. In both cases, this quantity is much greater than the bandgap (50 to 100 meV), indicating that photoinduced quasiparticles reach well into the ultrarelativistic Kane regime.

CONCLUSIONS

Our results provide the first spectrally resolved demonstration of ultrafast plasmonic control and establish the properties of the quasi-equilibrium charge carriers in a member of a technologically important family of semiconductors (Hg,Cd)Te hosting topologically nontrivial compounds. We provide direct spectroscopic evidence for a distinctly nonclassical scaling of the plasma frequency with electron density as a consequence of quasi-relativistic electronic band dispersion. The large light-matter momentum transfer afforded by the near-field interaction allows us to spectroscopically access both the symmetric and antisymmetric mode of the coupled charge oscillations at the top and bottom surface of the thin film. The dynamics of the itinerant response reveals both a fast initial relaxation and a persistent long-lived highly coherent residual electronic population. The large-momentum plasmon-polaritonic response can be effectively manipulated via photoexcitation using laser light within the standard erbium transparency window in fiber-optical telecommunication links. Already at moderate pump fluences these collective excitations reach the regime of Kane ultrarelativistic dispersion. The effective tuning of the plasmon-polaritonic response throughout a broad IR spectral range demonstrated in our work along with the readily tunable bandgap in (Hg,Cd)Te paves the way toward ultrafast active low-loss plasmonics using plasmon amplification by stimulated emission when plasmon energy is on resonance with the bandgap. The near-field optical microscopy/spectroscopy technique used here will be instrumental in directly visualizing this enhancement of quasiparticle coherence in ultrathin (Hg,Cd)Te films by means of real-space interferometry.

MATERIALS AND METHODS

Thin-film growth and characterization

Thin films of Hg_0.81Cd_0.19Te were grown in the [001] crystallographic direction using molecular beam epitaxy on a CdTe substrate, likewise with the [001] orientation. Prepared film was characterized by means of x-ray diffraction measurements, from which the Hg concentration (81%) and the thin-film thickness (90 nm) were determined (see the Supplementary Materials). Because of the lattice mismatch between the substrate and the epitaxially grown thin film, the latter is strained to 0.2 to 0.3% compared with the bulk material of the same composition. The stoichiometry and lattice strain of the film indicate that the bandgap is 50 to 100 meV, consistent with our experimental observations. The bandgap is further known to exhibit a very strong temperature dependence (1), which can be used as an effective control parameter in addition to chemical composition.

Time-resolved near-field measurements

The broadband near-field experiments were performed using a scattering-type scanning near-field optical microscope (s-SNOM; www.neaspec.com). The microscope can be operated in the Fourier transform IR spectroscopy mode of the asymmetric Michelson interferometer configuration. In this measurement regime, the spectral content of a broadband light source is recovered from the interferogram recorded as a function of the reference arm mirror position, adjustable in a range of several centimeters.

Our s-SNOM was equipped with two distinct ultrafast light sources with different repetition rates. The high–repetition rate source provides the highest signal-to-noise ratio, while the low–repetition rate laser allows for a two orders of magnitude higher pump fluence to be used without damaging the metallic tip of the atomic-force microscope through heating.

The high–repetition rate mid-IR source (LASNIX) is based on an ultrafast system, which produces ultrashort (40 fs) near-IR pulses (λ = 1.56 μm) in a 40-MHz Er-doped fiber laser (TOPTICA Photonics), with an integrated pulse picker. Ultrashort pulses of broadband mid-IR probe light were generated by difference-frequency mixing of narrow-band and supercontinuum near-IR pulses in a 2-mm-thick, z-cut GaSe crystal. Ultrafast temporal resolution (~200 fs) is set by the spectral band width of the probe, as described in (23, 24). The pump laser beam is split off the narrow-band output of the source laser and is delayed with respect to the probe beam using a motorized variable delay stage.

The low–repetition rate system is based on the ultrafast PHAROS Yb:KGW solid-state laser (LIGHT CONVERSION, http://lightcon.com), which operates at single pulse to 1-MHz repetition rate with up to 20-W output power. The Pharos module was used to pump a twin optical parametric amplifier, which, in turn, feeds a custom difference-frequency generation unit. The latter outputs a highly stable and widely tunable mid-IR beam with powers up to 10 mW at 10-μm center wavelength and 750-kHz repetition rate.

All pump-probe near-field measurements were carried out using the pump beam polarized perpendicular to the tip shaft to minimize the near-field enhancement of electromagnetic fields in this beam in proximity to the tip apex. While this near-field enhancement of the pump can be used to amplify the pump fluence by more than an order of magnitude, it also introduces several substantial complications into the data analysis, such as ultrafast diffusion of photoinduced charge carriers from the tip-sample nanovolume. In the absence of near-field enhancement of the pump, the effect of the pump beam on the sample is equivalent to that in standard far-field pump-probe experiments.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/8/eaau9956/DC1

Section S1. Sample characterization

Section S2. Photoinduced near-field optical response

Section S3. Reflection coefficient r_p(ω, q)

Section S4. Simulated far-field optical response

Fig. S1. Sample characterization.

Fig. S2. Photoinduced near-field optical response.

Fig. S3. Reference measurements and unnormalized spectra.

Fig. S4. Large-momentum plasmonic modes in Hg_0.81Cd_0.19Te/CdTe.

Fig. S5. Skin depth in bulk Hg_0.81Cd_0.19Te.

Fig. S6. Calculated far-field IR response.