Accurate and transferable multitask prediction of chemical properties with an atoms-in-molecules neural network

We introduce a modular, chemically inspired deep neural network model for prediction of several atomic and molecular properties.

Abstract

Atomic and molecular properties could be evaluated from the fundamental Schrodinger’s equation and therefore represent different modalities of the same quantum phenomena. Here, we present AIMNet, a modular and chemically inspired deep neural network potential. We used AIMNet with multitarget training to learn multiple modalities of the state of the atom in a molecular system. The resulting model shows on several benchmark datasets state-of-the-art accuracy, comparable to the results of orders of magnitude more expensive DFT methods. It can simultaneously predict several atomic and molecular properties without an increase in the computational cost. With AIMNet, we show a new dimension of transferability: the ability to learn new targets using multimodal information from previous training. The model can learn implicit solvation energy (SMD method) using only a fraction of the original training data and an archive median absolute deviation error of 1.1 kcal/mol compared to experimental solvation free energies in the MNSol database.

INTRODUCTION

The high computation cost of quantum chemical (QM) methods has become a critical bottleneck, which limits a researcher’s abilities to study larger realistic atomistic systems, as well as long-time scales relevant to an experiment. Hence, robust approximate but accurate methods are required for continued scientific progress. Machine learning (ML) has been successfully applied to approximate potential energy surfaces of molecules (1–4), obtain atomic forces (5), and even predict reaction synthesis (6). ML techniques have become popular for the use in predicting QM molecular properties. ML models seek to learn a “black box” function that maps a molecular structure to the property of interest. Until recently, many ML-based potentials relied on a philosophy of parametrization to one chemical system at a time (7). These methods can achieve high accuracy with relatively small amounts of QM data but are not transferable to new chemical systems. Using this approach for any new system requires a new set of QM calculations and extra parametrization time for each new study. Recent breakthroughs in the development of ML models in chemistry have produced general purpose models that accurately predict potential energies and other molecular properties for a broad class of chemical systems (2, 3, 8–10). General purpose models promise to make ML a viable alternative to empirical potentials and classical force fields. Force fields are known to have many weaknesses, for example, poor description of the underlying physics and lack of transferability, and are hard to improve in accuracy systematically.

Various techniques for improving the accuracy and transferability of ML potentials have been used. Active learning methods (11, 12), which provide a consistent and automated improvement in accuracy and transferability, have contributed greatly to the success of general purpose models. An active learning algorithm achieves this by deciding what new QM calculations should be performed and then adding the new data to the training dataset. The act of letting the ML algorithm drive sampling is shown to greatly improve the transferability of an ML potential. Further, transfer learning methods allow the training of accurate ML potentials by combining multiple QM approximations (13). Several recent reviews summarized the rapid progress in this field (14, 15).

The success of modern ML may be largely attributed to a highly flexible functional form for fitting to high-dimensional data. ML is known to extract complex patterns and correlations from these data. These data can contain counterintuitive statistical correlations that are difficult for humans to comprehend. With a few notable exceptions (16, 17), these models do not capture the underlying physics of electrons and atoms. These statistical fits are often fragile, and the behavior of an ML potential far from the training data could be nonphysical. The essential challenge for ML is to capture the correct physical behavior. Therefore, the immediate frontiers in ML lie in physics-aware artificial intelligence (PAI) and explainable artificial intelligence (XAI) (18). Future PAI methods will learn a model with relevant physics-inspired constraints included. The inclusion of physics-inspired constraints promises to deliver better performance by forcing the model to obey physical laws and cope better with sparse and/or noisy data. XAI will step even further, complementing models with logical reasoning and explanations of their actions, to ensure that researchers are getting the right answer for the right reasons (18).

Natural phenomena often inspire the structure of ML models and techniques (19). For example, the human brain is constantly interacting with various types of information related to the physical world; each piece of information is called a modality. In many systems, multiple data modalities can be used to describe the same process. One such physical system is the human brain, which provides more reliable information processing based on multimodal information (20). Many ML-related fields of research have successfully applied multimodal ML model training (21). In chemistry, molecules, which are often represented by structural descriptors, can also be described with accompanying properties (dipole moments and partial atomic charges) and even electron densities. The multimodal learning that treats multimodal information as inputs has been an actively developing field in recent years (22). Multimodal and multitask learning aims at improving the generalization performance of a learning task by jointly learning multiple related tasks together and could increase the predictivity of a model (23). This boost is caused by the use of additional information that captures the implicit mapping between the learnable endpoints.

Here, we present the AIMNet (atoms-in-molecules), a chemically inspired, modular deep neural network (DNN) molecular potential. We use multimodal and multitask learning to obtain an information-rich representation of an atom in a molecule. We show the state-of-the-art accuracy of the model to simultaneously predict energies, atomic charges, and volumes. We also show how the multimodal information about the atom state could be used to efficiently learn new properties, such as solvation free energies, with much less training data.

RESULTS

The AIMNet architecture

The name and concept of the AIMNet model is inspired by Bader’s theory of atoms in molecules (AIM) (24). The quantum theory of AIM is a model in which a molecule could be partitioned into interacting atoms via an observable electron density distribution function. When atoms combine into a molecule, their electron density changes due to interaction with other atoms. In density functional theory (DFT), the final solution for the electron density and energy for the molecule is usually obtained with an iterative self-consistent field (SCF) procedure. Within the AIM model, each step of the SCF-like procedure could be viewed as the change of electron density distribution within atomic basins to reflect changes in the basins of neighboring atoms. In the AIMNet model, instead of electron density, atoms are characterized by learnable feature vectors and complex interatomic interactions are approximated with the DNN.

The high-level architecture of the AIMNet model is shown in Fig. 1. The model uses atomic coordinates (R) and numbers (Z) as inputs and transforms them into atom-centered environment vectors (AEVs) that are used as features for embedding, interaction, update, and AIM neural network blocks. The model predicts a set of molecular and/or atomic properties (p). The overall algorithm can be summarized as follows

Fig. 1. Architecture of the AIMNet model.

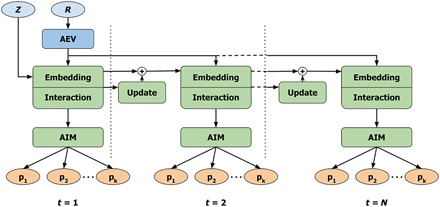
The model uses atomic numbers Z and coordinates R as input features. The coordinates are transformed with ANI-type symmetry functions into AEVs. Atom types are represented with learnable atomic feature vectors (AFV), which are used as embedding vectors for AEVs. The interaction of an atom with its environment produces the AIM representation of the atom used to predict a set of target atom properties {p_k}. The environment-dependent update to AFV within N iterations is used to make the embedding vectors for each atom consistent with its environment. Input data are colored in blue, predicted endpoints are in orange, and neural network blocks are in green.

1) Encode relative positions R of all neighboring atoms as AEVs.

2) Select initial atomic feature vectors (AFVs) corresponding to atomic numbers.

3) For each atom, embed its AEV into the space of AFVs of neighboring atoms, combining geometrical and atomic feature information.

4) Calculate interaction of the atom with the environment to get AIM representation of the atom.

5) Calculate atom properties from the AIM representation.

6) Calculate environment-dependent update to the AFVs and repeat steps 3 to 5 until converged.

At step 6, the AFV for every atom in the molecule is updated, which changes the embedding at the next iteration. This is effectively describing the interactions between atoms by passing messages (25, 26) through the neural network. Convergence is a learned feature of the model, when the state of each atom (AFV) is consistent with the state of its neighbors and subsequent updates are approaching zero. Therefore, we call this procedure “SCF-like.” The implementation details of individual AIMNet blocks are given below.

Embedding block

Geometrical arrangement for ith atom of a molecule are encoded as a set of ANI-type (3, 7) radial ${\mathbf{g}}_{\text{ij}}^{(\mathbf{r})}$ and angular ${\mathbf{g}}_{\text{ijk}}^{(\mathbf{a})}$ AEVs with indexes j corresponding to every neighboring atom and jk to every unique pair of neighbors

$${\mathbf{g}}_{\text{ij}}^{(\mathbf{r})}=\text{exp}(-{\eta }^{(r)}(r_{\mathit{ij}}-{\mathbf{r}}_{\mathbf{s}}^{(\mathbf{r})}\left)\right)f_C(r_{\mathit{ij}})$$ (1)

$${\mathbf{g}}_{\text{ijk}}^{(\mathbf{a})}=2^{1-\mathrm{\zeta }}(1+(\text{cos}{\mathrm{\theta }}_{\mathit{ijk}}-{\mathrm{\theta }}_{\mathrm{s}}^{(\mathbf{a})⊺}\left)\right)\text{exp}(-{\mathrm{\eta }}^{(a)}{(\frac{r_{\mathit{ij}}+r_{\mathit{ik}}}{2}-{\mathbf{r}}_{\mathbf{s}}^{(\mathbf{a})})}^2)f_C(r_{\mathit{ij}})f_C(r_{\mathit{ik}})$$ (2)

$$f_C(r_{\mathit{ij}})=0.5\text{cos}(\mathrm{\pi } \text{min}(\frac{r_{\mathit{ij}}}{R_C},1\left)\right)+0.5$$ (3)

Here, r and θ are the distances and angles between atoms and f_c is the cosine cutoff function, which smoothly zeroes AEVs for neighbors located outside of cutoff radius R_C, chosen at 4.6 Å for radial AEVs and at 3.1 Å for angular AEVs. All hyperparameters for AEVs, such as radial and angular probe vectors r_s and θ_s, respectively and probe widths η and ζ match the ANI-1x model (12) (see also the Supplementary Materials for details).

The ${\mathbf{g}}_{\text{ij}}^{(\mathbf{r})}$and ${\mathbf{g}}_{\text{ijk}}^{(\mathbf{a})}$ AEVs contain only geometrical information but not atom types. To differentiate neighbors by atom type, we embed these vectors into the space of learnable AFVs defined for every chemical element Z as ℝ, a_z ∈ ℝ^d, with dimensionality d being another hyperparameter of the model (here used d = 16). We selected the outer product of ${\mathbf{g}}_{\text{ij}}^{(\mathbf{r})}$ and a_j as an embedding operation for radial AEVs. The result is a matrix ${\mathbf{G}}_{\text{ij}}^{(\mathbf{r})}$ ∈ ℝ^{m × d}, where m is the dimensionality of ${\mathbf{g}}_{\text{ij}}^{(\mathbf{r})}$ (the size of probe vectors r_s in Eq. 1) and d is the size of AFVs. By their design, symmetry functions (Eqs. 1 to 3) are many body functions, i.e., they could be summed for all the neighbors of an atom, providing an integral description of the atomic environment (3). The same applies to outer products ${\mathbf{G}}_{\text{ij}}^{(\mathbf{r})}$, given a sufficiently large embedding vector a_j. We obtain radial features of atomic environment of the ith atom as a fixed-length vector after flattening the corresponding matrix

$${\mathbf{G}}_{\mathbf{i}}^{(\mathbf{r})}={\displaystyle \sum _j}{\mathbf{g}}_{\text{ij}}^{(\mathbf{r})}\cdot {\mathbf{a}}_{\mathbf{j}}^{⊺}$$ (4)

Embedding of the angular symmetry functions ${\mathbf{g}}_{\text{ijk}}^{(\mathbf{a})}$ requires atom-pair feature vectors ${\mathbf{a}}_{\text{jk}}^{*}$defined for every combination of chemical elements. If introduced as learnable parameters of the model, then the size of this embedding layer would grow as O(N²)with the number of chemical elements. Instead, in the AIMNet model, we learn an interaction between AFVs, which give appropriate atom-pair atomic features ${\mathbf{a}}_{\text{jk}}^{*}$. We construct concatenation of elementary symmetric polynomials, e.g., element-wise multiplication and addition of two AFVs and use it as an input layer for multilayer neural network or perceptron function (MLP) ℱ_MLP1

$${\mathbf{a}}_{\text{jk}}^{*}={\mathcal{F}}_{{\text{MLP}}_1}([{\mathbf{a}}_{\mathbf{j}}\circ {\mathbf{a}}_{\mathbf{k}},{\mathbf{a}}_{\mathbf{j}}+{\mathbf{a}}_{\mathbf{k}}])$$ (5)

Analogous to the radial part, the combined angular AEV is defined as

$${\mathbf{G}}_{\mathbf{i}}^{(\mathbf{a})}={\displaystyle \sum _{\mathit{jk}}}{\mathbf{g}}_{\text{ijk}}^{(\mathbf{a})}\cdot {\mathbf{a}}_{\text{jk}}^{*⊺}$$ (6)

The embedding stage is finalized by application of another neural network to the concatenation of embedded radial and angular symmetry functions

$${\mathbf{f}}_{\mathbf{i}}={\mathcal{F}}_{{\text{MLP}}_2}\left(\right[{\mathbf{G}}_{\mathbf{i}}^{(\mathbf{r})},{\mathbf{G}}_{\mathbf{i}}^{(\mathbf{a})}\left]\right)$$ (7)

The ℱ_MLP2 function extracts information about the environment of the atom; therefore, vector f is referred to as the atomic environment field.

In this work, the AIMNet model was trained to learn six diverse atomic or molecular properties. In addition to molecular energies, we used modules for atomic electric moments of the atoms up to l = 3, i.e., atomic charge, dipole, quadrupole, and octupole, as well as atomic volumes. Figure 2 provides correlation plots for four predicted quantities. Atomic dipoles and quadrupoles are probably not very useful per se and could be considered as “auxiliary.” Hence, the accuracy of their fits is summarized in the Supplementary Materials.

Fig. 2. Performance of the AIMNet model on the DrugBank subset of the COMP6-SFCl benchmark.

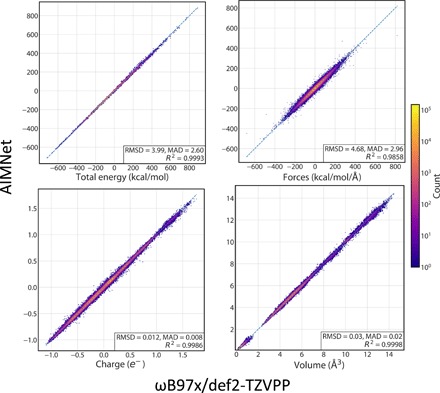
Plots show correlation between ground-truth DFT (x axes) and predicted with AIMNet (y axes) values for total molecular energies, components of force vectors on atoms (∂E/∂R), atomic charges, and volumes. For each plot, units for both axes and for RMSD and mean absolute deviation values are the same. Logarithm of point density is shown with color.

The accuracy of fit is assessed on the DrugBank subset of the COMP6-SFCl benchmark. This benchmark contains properties of 23,203 nonequilibrium conformations of 1253 drug-like molecules. The median molecule size is 43 atoms, more than three times larger than molecules in the training dataset. Thus, this benchmark shows transferability and extensibility of the AIMNet model. The root mean square error (RMSE) of the energy predictions is 4.0 kcal/mol within the range of about 1500 kcal/mol. For comparison, an ensemble of ANI models trained and evaluated on the same datasets has an RMS energy error of 5.8 kcal/mol and a force error of 7.1 kcal mol^–1Å^–1. Predicted components of atomic forces have RMS deviation (RMSD) = 4.7 kcal mol^–1Å^–1, highlighting the AIMNet model utility to reproduce the curvature of molecular potential energy surfaces accurately and thus its applicability for geometry optimization and molecular dynamics. Atomic charges could be learned up to a “chemical accuracy” of 0.01e. Overall, this level of accuracy for both AIMNet and ANI-1x is on par with the best single-molecule potentials constructed with the original Behler-Parrinello (BP) descriptor (27).

Iterative SCF-like update

The AIMNet model was trained with outputs from every SCF-like pass contributing equally to the cost function (see the Supplementary Materials for details). This way, the model learns to give the best possible answer for each pass, given the input AFVs. The AFVs are improved with every iteration, leading to lower errors. The model with t = 1 is conceptually similar to the ANI-1x network since no updates are made to the atomic features in both models [in BP-type networks, the representation of atomic features is hidden within the neural network (NN) layers], and the receptive field of the AIMNet model is roughly equal to the size of the AEV descriptor in ANI-1x. Figure 3 shows the aggregated performance of prediction for energies (E), relative conformer energies (ΔE), and forces (F) improves with increasing number of passes t. As expected, the accuracy of AIMNet with t = 1 is very similar or better compared to the ANI-1x network. The second iteration (t = 2) provides the biggest boost in performance for all quantities. After t = 3, results do not change much; therefore, we used t = 3 to train all models in the paper. Overall, the biggest gains in accuracy were up to 0.75 kcal/mol for relative energies and 1.5 kcal mol^–1Å^–1 for forces. This corresponds to about 15 to 20% error reduction.

Fig. 3. AIMNet predictions with different number of iterative passes t evaluated on the DrugBank subset of the COMP6-SFCl benchmark.

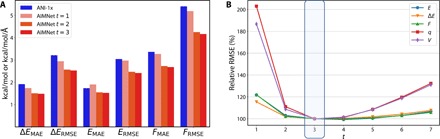
(A) Comparison of AIMNet performance at different t values with ANI-1x model trained on exactly the same dataset for relative conformer energies (ΔE), total energies (E), and atomic forces (F). (B) AIMNet accuracy in prediction of total energies (E), relative conformer energies (ΔE), atomic forces (F), charges (q), and volumes (V) at different t values. Relative RMSE is calculated as ratio of RMSE at given t divided by RMSE at t = 3 (the values used to train model).

Notably, there is a major difference between an SCF-like update and a real SCF procedure used along with DFT methods. Convergence of the SCF procedure is determined by the variational principle, e.g., the solution is electron density distribution that minimizes the total energy. The AIMNet model is not variational; lower energy does not imply more correct prediction. Therefore, there is no guarantee for convergence of SCF-like updates. Although, on average, AIMNet converges very fast, within two or three iterations, this behavior is controlled by the L2 regularization we used during training for every learned parameter. The model learns to make better prediction using the smallest possible update to the AEVs. After training with t = 3, the output of the model not only does not improve with larger number of iterations but also does not explode because of the accumulation of errors. We tested the model with up to six updates and found that, at t = 7, the AIMNet still performs better than with t = 1 (Fig. 3B).

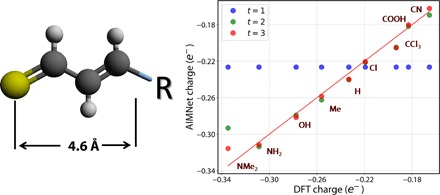
Figure 3B shows that atomic charges and volumes are much more sensitive toward the iterations than energies and forces. To illustrate the importance of long-range interactions on charge redistribution, let us consider a simple but realistic series of substituted thioaldehydes (Fig. 4). Here, a substituent R is located as far as 5 Å away from the sulfur atom. This distance is longer than the cutoff radius of 4.6 Å we used in AEV construction. However, because of a conjugated chain and the high polarizability of sulfur, the partial atomic charge on sulfur could change by as much as 0.15e by varying R with different electron-donating or electron-withdrawing groups. The AIMNet model with t = 1 (as well as all neural network potentials (NNPs) with local geometric descriptors) will incorrectly predict that the sulfur partial charge in all molecules is equal. The correct trend could be recovered with either an increase of the radius for local environment (usually at a substantial computational cost and potentially an impact on model extensibility) or with iterative updates to the AFVs. AIMNet with t = 2 reproduces DFT charges on the sulfur atom notably better than with t = 1, except for the most polar ones. At t = 3, the charge redistribution in the AIMNet model completes and quantitatively reproduces DFT charges for all molecules considered.

Fig. 4. DFT ωB97x/def2-TZVPP atomic charges on the sulfur atom of substituted thioaldehyde and AIMNet prediction with a different number of iterative passes t.

The nature of the AFV representation

To gain insights into the learned latent information inside the AFVs, we performed a parametric t-distributed stochastic neighbor embedding (pt-SNE) (28) of this 16-dimensional (16D) space into a 2D space. The pt-SNE is an unsupervised dimensionality reduction technique. pt-SNE learns a parametric mapping between the high-dimensional data space and the low-dimensional latent space using a DNN in such a way that the local structure of the data in the high-dimensional space is preserved as much as possible in the low-dimensional space. Figure 5 shows the 2D pt-SNE for 3742 DrugBank molecules or about 327 k atoms in total.

Fig. 5. pt-SNE of AFVs (t = 3) for a set of drug-like molecules.

(B) Feature vectors for different chemical elements. Values of feature vectors at t = 1 (before SCF-like update) marked with cross symbol. (A and C) Feature vectors for several of the most common types of the carbon and hydrogen atom environments.

In the AIMNet model, the AFVs are used to discriminate atoms by their chemical types. The trivial discrimination could be achieved with orthogonal vectors (which would effectively be a one-hot encoding). The pt-SNE of AFVs in Fig. 6A shows that the location of clusters corresponding to different chemical elements resembles their positions in the periodic table. The pt-SNE component on the horizontal axis roughly corresponds to a period and vertical component to a group in the periodic table. Embeddings for hydrogen atoms are closer to halogens than to any other element. It is interesting to note the wide spread of the points corresponding to sulfur and hydrogen atoms. In the case of sulfur, this is the only element in the set that may have distinctly different valence states (6 and 2) in common organic molecules.

Fig. 6. Performance of the AIMNet model on several benchmark sets compared to MM, semiempirical, DFT, and ab initio QM methods.

(A and B) Torsion benchmark of Sellers et al. (29) for gas phase and solvent models. The dots correspond to mean absolute error (MAE) for each of the 62 torsion profiles for each method. (C) The dots correspond to absolute error for relative conformer energy for each of the 196 conformers in the dataset. (A to C) The boxes represent the upper and lower quartiles, while the whiskers represent 1.5 times the interquartile range or the minimum/maximum values. The methods are ordered in descending median errors from top to bottom. Boxes colored by the class of the computational method (ML, MM, SQM, DFT, and ab initio). The basis sets used to obtain reference energies are 6-311+G**, for (A) and (B), and def2-TZVPD, for (C), where applicable but not specified. (D) Correlation plot of experimental solvation energies for 238 neutral molecules from the MNSol database (31) and AIMNet predictions, calculated as the difference between the prediction of DFT and DFT(SMD) energies.

The most structure and diversity in the pt-SNE plot is observed for carbon atoms. In Fig. 5A, we show a zoomed in region of the carbon atoms, with coloring by the hybridization and structure of local chemical environments. Two main distinct clusters corresponding to sp² (or aromatic) and sp³ C atoms appear. Inside every cluster, atoms are grouped by the local bonding environment. There is also a clear trend in the increase of substituent polarity from the top to the bottom of the plot. Similarly, the spread for the H atoms is determined mainly by the parent sp² and sp³ carbon atoms or heteroatom environments (Fig. 5C).

Conformations and dihedral profiles benchmark

One of the most promising applications of the NNPs for computational drug discovery is conformer generation and ranking. Therefore, we evaluated the performance of the AIMNet model against two distinct external datasets. Both are tailored to benchmark the performance of molecular potentials to describe conformer energies, which have high-quality CCSD(T)/CBS reference data.

The small-molecule torsion benchmark of Sellers et al. (29) measures the applicability of an atomistic potential in drug discovery. This benchmark includes 62 torsion profiles from molecules containing the elements C, H, N, O, S, and F computed with various force fields, semiempirical QM, DFT, and ab initio QM methods. These methods are compared to CCSD(T)/CBS reference calculations. Figure 6A provides the performance of the methods presented in Sellers et al. (29) together with AIMNet single-point calculations on MP2/6-311+G** optimized geometries. According to this benchmark, the AIMNet potential is much more accurate compared to semiempirical methods and OPLS-type force fields, which is specifically tailored to describe conformation energies of drug-like molecules. The performance of the AIMNet model could be directly compared to MP2/6-311+G** and DFT methods.

Another benchmark set, MPCONF196 (30), measures the performance of various potentials to rank both the low- and high-energy conformers of acyclic and cyclic peptides and several macrocycles, including 13 compounds in total. The reference data were obtained as single-point calculations at the CCSD(T)/CBS level (Tight-DLPNO approximation for the largest molecules in the dataset) on MP2/cc-pVTZ geometries. Figure 6C shows a comparison of AIMNet to a subset of methods benchmarked in the original paper of Řezáč et al. (30). The DFT methods fall into two categories, depending on whether dispersion corrections were included or not, with highly empirical M06-2x being somewhere in between. The AIMNet model has been trained to reproduce the ωB97x functional without explicit dispersion correction. Therefore, its performance is clearly worse compared to the dispersion-corrected counterpart. However, much of the error could be reduced by adding an empirical D3 dispersion correction to AIMNet energies. The benchmark data show that the AIMNet model is on par with traditional DFT functionals without dispersion correction, and it clearly outperforms semiempirical methods, even methods that have built-in dispersion correction.

Learning new properties

The multimodal knowledge residing inside the AIM layer could be exploited to efficiently learn new atomic properties without retraining the whole model. This could be done by using a precomputed AIM layer as atom descriptors and learning a neural network model with a relatively small number of parameters that fits the AIM layer to the new property.

We show the ability to learn atomic energies with an implicit solvent approximation. For this exercise, a subset of 480 k structures was taken from the training data and molecular energies were calculated at the SMD(Water)-ωB97x/def2-TZVPP level of theory. The AIM layer was computed using a pretrained AIMNet model and was then used as a descriptor for training a simple DNN model to learn the Solvation Moldel D (SMD) energy. The shape and activation function of the DNN was selected to be the same as in the base AIMNet model. The total number of trained parameters was about 32 k. If this newly trained DNN model is placed as an additional task p in the AIMNet model (see Fig. 1), then it would predict energies with implicit solvent correction in addition to six other properties.

The performance of the AIMNet model trained this way was assessed against experimental solvation free energies of neutral molecules in the MNSol database (31). The geometries of 414 molecules were optimized using the gas phase and SMD version of AIMNet. The Hessian matrix was calculated by means of analytical second derivatives of the energies with respect to coordinates using the PyTorch autograd module. Thermal correction to the Gibbs free energy was computed in Harmonic and rigid rotor approximations for the ideal gas at 298 K. The results are shown in Fig. 6D. The AIMNet model clearly outperforms SMD applied with semiempirical and tight binding DFT (DFTB) methods that have RMSD and mean absolute error on solvation energies of 2.8 to 2.9 kcal/mol on this benchmark set, even after reoptimization of the atomic radii (32).

Last, we also compared the performance of the AIMNet model with other solvent-corrected QM and molecular mechanics (MM) methods for predicting torsional profiles of small drug-like molecules on the aforementioned benchmark data of Sellers et al. (29). This benchmark is important for predicting molecular conformations of solvated molecules (Fig. 6B). It shows the performance of the solvent-corrected AIMNet model on torsion profiles compared to QM and MM methods. The results show that OPLS(GBSA), PCM-B3LYP, and AIMNet have very similar accuracy when predicting the conformations of solvated molecules. Note that the solvent-corrected energy evaluation with AIMNet has no additional computational cost. It takes 90 s to compute both the gas phase and SMD single-point energies of 36 angles for each of the 62 torsions (40 ms per energy evaluation) using an ensemble of 5 AIMNet models on a single Nvidia M5000 graphics processing unit (GPU).

DISCUSSION

The AIMNet framework presented here is transforming ML methods from simple potential energy predictors to fully functional simulation methods. Most ML property predictors introduced to date require an individual ML model or some set of QM calculations for every quantity and system of interest. In most practical applications, multiple physical quantities are required for a complete analysis of the problem at hand. For example, molecular dynamics requires conservative energy predictions to provide the correct forces for nuclear propagation, while the distribution of other properties over the simulation might be of interest for computing results comparable to experiment (e.g., dipole moments for infrared spectra). In contrast to straightforward training of separate models for each individual property, AIMNet trains to these quantities simultaneously with multimodal and multitask training techniques. The AIMNet potential achieves these predictions with a negligible increase in computational cost over a single energy evaluation.

The AIMNet model makes it possible to discover a joint latent representation, via the AIM layer, which captures relationships across various modalities. Different modalities typically carry different kinds of information. Since there is much structure in this complex data, it is difficult to discover the highly nonlinear relationships that exist between features across different modalities. This might explain why the traditional ML research in the chemical and materials sciences has focused on the design of optimal descriptors or representation learning, rather than maximizing learning by taking advantage of the information inherent in different modalities of information-rich datasets.

Inside the AIMNet model, the AIM layer is trained to automatically produce an information-rich representation for every atom but is also constrained by different modalities to implicitly encode more physical information. The primary benefit of such an information-rich representation is the ability to learn secondary (additional) tasks without retraining the overall model. This is very useful for properties that are hard to compute or with scarce experimental data. For example, we have shown that, after training the AIMNet model to the energy, partial atomic charges, and atomic volumes, the new additional task to predict SMD solvation energy only based on the AIM layer vector could achieve predictions of the Gibbs free energy of solvation with the accuracy of 1.8 kcal/mol using just 6% of ANI-1x data. This accuracy is comparable to the differences of DFT methods with different solvation models.

Three key ingredients allow AIMNet to achieve the high level of accuracy that it accomplishes. First, it overcomes the sparsity of training data with multitask and multimodal learning. To make this learning transferrable, the second ingredient is to find a joint information-rich representation of an atom in a molecule that allows learning to multiple modalities. Last, for the best performance and accounting of long-range interactions, AIMNet uses an iterative SCF-like procedure. The number of iterative passes t could serve as a single, easy-to-use parameter that determines the length scale of interactions inside the chemical system since more iterations increase the effective information transfer distance.

As with any supervised ML method, the critical property of the trained model is an ability to generalize to new samples not seen within the training dataset. In the case of NNPs, this is usually discussed in terms of transferability and extensibility—the ability to generalize to vast chemical compound space while retaining applicability to larger molecules than those in the training set. The AIMNet model introduces multimodality as a new dimension for generalization of NNPs—applicability to a wide range of molecular and atomic properties and ease of learning new properties.

MATERIALS AND METHODS

Dataset preparation

The training dataset was constructed on the basis of ANI-1x data (12). The data were recalculated at the ωB97x/def2-TZVPP level and include molecular energies and atomic forces, as well as minimal basis iterative stockholder [MBIS (33), a variant of Hirshfeld partitioning] atomic electric moments (atomic charges and norms of atomic dipoles, quadrupoles, and octupoles) and atomic volumes. The active learning method described in detail by Smith et al. (12) was used to extend the dataset with molecules containing F, S, and Cl elements, in addition to H, C, N, and O in the original dataset. The active learning procedure to select the data was conducted using ANI-1x NNP. The extension contains 3.3 M conformers of molecules containing one of F, S, or Cl atoms. Table S1 provides the main characteristics of the original dataset, extension, and resulting extended dataset.

To test the performance of AIMNet, we used the recently developed COMP6 benchmark (12). COMP6 is a comprehensive benchmark suite composed of five benchmarks that cover broad regions of organic and biochemical space (for molecules containing C, N, O, and H atoms) and a sixth built from the existing S66x8 (34) noncovalent interaction benchmark. We have extended the COMP6 benchmark to include molecules with S, F, and Cl elements and refer to it as COMP6-SFCl. For this, we have selected new molecules for DrugBank and GDB subsets, following the same rules and procedures, reported for original COMP6. Table S2 summarizes the most important characteristics of the extension and resulting COMP6-SFCl dataset.

All DFT calculations were performed using ORCA 4.0 (35) software package using RIJCOSX (36) approximate handling of exchange integrals. After collecting all calculated energies and forces, we noticed that about 0.01% of the data points have unusually large forces, which could mean some sort of numerical errors or wrong solution of SCF equations. The data points with any component of atomic force vectors more than 4 E_h/bohr were discarded. MBIS atomic properties were calculated using the HORTON (37) library. A linear model was used to calculate average per-atom energies in the training dataset, which is essentially an average self-energy term for each element. This linear fitting over the entire dataset was performed with respect to the number of each atomic element in a given molecule as the input. The AIMNet model is trained to the QM calculated energy minus the self-energies of the atoms in molecule. The energy obtained from this process is roughly analogous to the process of computing an atomization energy but without any per-atom bias, e.g., normalized atomization energy. The linear fitting parameters are listed in the table S3. Before training, all target properties were scaled to have unit variance.

For training, the dataset was randomly split into five folds of equal size. Four folds were merged together to form a training dataset. The fifth fold was used as the validation dataset. This way, five unique cross-validation (CV) splits were formed. An ensemble of five AIMNet models were trained, one for each CV split. All the predictions reported for both AIMNet and ANI models are the averaged prediction of the ensemble of models.

Implementation of the AIMNet model

The AIMNet model was implemented with PyTorch (38). All components of the AIMNet model, including AEV construction, use exclusively tensor operations, which makes the model end-to-end differentiable. Two variants of the model were implemented. The first uses a list of neighboring atoms and includes only those pairs in construction of AEVs. This implementation scales as O(N) with molecule size. The second variant of the model evaluates every possible pair of atoms to construct ${\mathbf{g}}_{\text{ij}}^{(\mathbf{r})}$ and ${\mathbf{g}}_{\text{ijk}}^{(\mathbf{a})}$ scales as O(N³). The contribution from atom pairs more distant than cutoff radius is zero and does not change, resulting in ${\mathbf{G}}_{\text{ij}}^{(\mathbf{r})}$ and ${\mathbf{G}}_{\mathbf{i}}^{(\mathbf{a})}$. Learned parameters of the AIMNet model could be used with both implementations. The AIMNet model used original ANI atom-centered symmetry functions, as described and implemented in (36).

Training the AIMNet model

Network sizes (depth and number of parameters) were determined through hyperparameter searches conducted as multiple separate experiments and listed in table S4. Nonlinear exponential linear units (39) an activation function with α = 1.0 was used in all AIMNet model layers. Model training was done on four GPUs in parallel. Each batch of the training data contained an average of 380 molecules. The gradients from four batches were averaged, making an effective batch size of 1520 molecules, with molecules of different sizes. Amstrad (40) optimization method was used to update the weights during training. An initial learning rate of 10⁻³ was dynamically annealed with the “reduce on plateau” schedule: The learning rate was multiplied by 0.9 once the model failed to improve its validation set predictions within six epochs.

The cost function for multitarget multipacks training was defined as weighted mean squared error loss

$$L^{\text{tot}}=\frac{1}{N}{\displaystyle \sum _t^T}{\displaystyle \sum _p}{\displaystyle \sum _i^N}{w}_t{w}_p{(y_{\mathit{tpi}}-{\widehat{y}}_{\mathit{tpi}})}^2$$ (1.1)

where indices t, p, and i correspond to pass number, target property, and sample, respectively; w_t and w_e are the weights for the iterative pass and target property, respectively; y and ŷ are target and predicted properties, respectively; and N is the number of samples. In the case of per-molecule target properties (energies), the y values in the cost function were divided by the number of atoms in molecule, so errors are per atom for all target properties. We used equal weights for every pass, e.g., w_t = 1/T, where T is the total number of passes. Values for w_p were selected in such a way that all target properties give approximately equal contribution to the combined cost function. In relative terms, the weights for molecular energies, charges, and volumes correspond to 1 kcal/mol, 0.0063e, and 0.65 ų, respectively. We also found that training results are not very sensitive to the choice of the weights w_p.

To accelerate training, the models were initially trained with t = 1. Then, the weights of the last layer of update network were initialized with zeros to produce zero atomic feature update and the model was trained with t = 3 passes. We also used cold restarts (resetting the learning rate and moving averages information for the optimizer) to archive better training results. For t = 1, the networks were trained for 500 epochs on average, followed by 500 epochs with t = 3 for a total of about 270 hours on a workstation with dual Nvidia GTX 1080 GPUs. Typical learning curves are shown in fig. S1.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/8/eaav6490/DC1

Fig. S1. Typical learning curves for training the AIMNet model.

Table S1. Descriptive statistics for ANI-1x dataset, the extension with molecules containing S, F, or Cl atoms, and resulted combined extended dataset ANI-1x-SFCl.

Table S2. Descriptive statistics for COMP6 dataset, extension containing molecules with S, F, or Cl atoms, and resulted combined extended dataset COMP6-SFCl.

Table S3. Self-energies for atoms used to compute normalized atomization energies.

Table S4. Neural network architectures for each AIMNet block.

Table S5. Performance of ANI-1x and AIMNet on COMP6-SFCl dataset.