Evidence for a strain-tuned topological phase transition in ZrTe₅

In situ strain is used to induce a topological phase transition in single-crystal ZrTe₅.

Abstract

A phase transition between topologically distinct insulating phases involves closing and reopening the bandgap. Near the topological phase transition, the bulk energy spectrum is characterized by a massive Dirac dispersion, where the bandgap plays the role of mass. We report measurements of strain dependence of electrical transport properties of ZrTe₅, which is known to host massive Dirac fermions in the bulk due to its proximity to a topological phase transition. We observe that the resistivity exhibits a pronounced minimum at a critical strain. We further find that the positive longitudinal magnetoconductance becomes maximal at the critical strain. This nonmonotonic strain dependence is consistent with the switching of sign of the Dirac mass and, hence, a strain-tuned topological phase transition in ZrTe₅.

INTRODUCTION

Appreciation of the topological aspects of band structure has fundamentally changed the way we understand the electronic properties of solids. Band insulators with time reversal symmetry can be classified into normal insulators (NIs), weak topological insulators (WTIs), and strong topological insulators (STIs) based on their Z₂ topological indices (1–3). Changing Z₂ indices requires closing and reopening the bandgap, and topologically distinct insulating phases are separated by a gapless Dirac or Weyl semimetal phase. The relationship between these phases is summarized in the general phase diagram proposed by Murakami and Kuga (2, 3), as shown in Fig. 1A. These topological phases have been intensively studied in the past decade (4–10). In contrast, the transition between these phases is less explored because it requires changing the band parameters of the solid. It has been demonstrated that topological phase transitions can be induced either by chemical doping or by thermal lattice expansion (11–14). Nevertheless, the precise in situ control of topological phase transition in a three-dimensional (3D) system is still an outstanding challenge.

Fig. 1. Topological phase diagram and band structures of ZrTe₅.

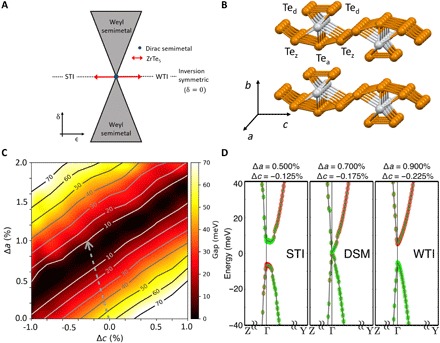
(A) Universal phase diagram of topological insulators proposed by Murakami for a 3D system (2, 3, 10). The control parameter 𝛿 describes the breaking of inversion symmetry. The control parameter ϵ does not break inversion symmetry. (B) Crystal structure of ZrTe₅. Chains of ZrTe₃ prisms (consisting of Te_a and Te_d atoms) extend along the a axis. These chains are connected by Te_z atoms along the c axis to form layers. These layers are vdW bonded in the b axis direction. (C) Size of bandgap E_g at the Γ point as functions of strains in the a and c lattice directions. The dashed gray arrow indicates the anisotropic strain induced by a uniaxial stress along the a axis direction, as governed by the calculated Poisson’s ratio ϵ_aa = −4.0ϵ_cc. (D) Band structures for different strain states taken at points along the Poisson’s ratio path. These points (from left to right) correspond to STI, Dirac semimetal, and WTI, respectively. Fermi level is defined as the zero energy, and the k-point labeling is based on the primitive unit cell. A band inversion involving Te_d and Te_z p orbitals (shown as red and green colors, respectively) is seen in the STI phase.

The transition-metal pentatellurides ZrTe₅ is an ideal material to realize in situ control of topological phase transitions. ZrTe₅ is a van der Waals (vdW) layered material crystallized in the Cmcm orthorhombic space group. Each layer consists of ZrTe₃ chains extending along the a lattice direction, and the layers are stacked along the b lattice direction (Fig. 1B). The material has received substantial interest because its monolayer form is predicted to be a large bandgap quantum spin Hall insulator (15). It was also suggested that the 3D bulk band structure is very close to the phase boundary between WTI and STI (15–17), indicated by the red line in the universal phase diagram shown in Fig. 1A (2, 10). Early studies of optical conductivity (18), quantum oscillations (19, 20), photoemission, and negative longitudinal magnetoresistance (NLMR) (21) have supported the predicted Dirac semimetal-like band structure in the bulk, with a single Dirac point at the center of the Brillouin zone, Γ. Unlike topological Dirac semimetals such as Na₃Bi or Cd₃As₂, there is no additional crystalline symmetry to protect the Dirac point in ZrTe₅, and more recent spectroscopy measurements revealed that its band structure is better described by a massive Dirac dispersion, where mass plays the role of bandgap. The bandgap size measured by different experiments varies, ranging from 10 to 80 meV, and there are conflicting reports on whether the material is a WTI or STI (22–25), or changes with temperature (26). These experimental findings suggest that the electronic structure of ZrTe₅ may be very sensitive to external perturbation, such as lattice distortion.

In this work, we present evidence for a strain-tuned topological phase transition corresponding to a sign change of the Dirac bandgap in ZrTe₅. This conclusion is a result of extensive measurements of bulk electrical transport of ZrTe₅ as a function of in situ tunable anisotropic strain. Although the measurement of surface states is often regarded as the smoking gun evidence of topological insulators, close to a topological phase transition the small bandgap and the Dirac-like dispersion in the bulk impose severe challenges for identifying surface states (25). Here, we focus on the bulk transport properties, which are highly sensitive to the mass of bulk Dirac fermions near a topological phase transition. We observe that the resistivity exhibits a nonmonotonic strain dependence and reaches a minimum at a critical strain. The nonmonotonic strain dependence is distinct from the expected behavior of a conventional semiconductor, yet it is consistent with the sign switching of the Dirac mass of a gapped Dirac semimetal. We further found that the NLMR also shows a nonmonotonic strain dependence and becomes maximal at the critical strain. The extracted helicity relaxation time increases by 10-fold as the strain approaches the critical value. Our study presents ZrTe₅ as a promising platform for on-demand control of nontrivial topological properties of materials.

RESULTS

Figure 1C shows a contour map of the size of the bandgap E_g at Γ as a function of ϵ_aa and ϵ_cc, i.e., strain (%) along the a and c lattice directions, calculated by density functional theory (DFT). It shows a V-shaped valley, with the minimum of the valley (corresponding to E_g = 0) extending along the diagonal direction. Z₂ topological indices were also computed, and the E_g = 0 line is the phase boundary between STI and WTI (see fig. S7). Figure 1C reveals a highly anisotropic strain dependence of E_g: The steepest gradient of E_g is along the direction in which ϵ_aa and ϵ_cc have opposite signs, as the case when a uniaxial stress is applied along the a lattice direction. In contrast, the strain induced by applying hydrostatic pressure corresponds to a trajectory that is almost parallel to the contour lines. The Poisson’s ratio of the anisotropic strain, ϵ_cc/ϵ_aa = −0.25, induced by a-axis uniaxial stress, was obtained using a fully relaxed vdW-DFT calculation, and it is indicated as the gray arrow in Fig. 1C. It requires less than a percent of ϵ_aa to reach the WTI-STI phase boundary. We note that there is uncertainty in the DFT bandgap size for a given set of lattice constants. For example, several spectroscopy measurements reported E_g as low as 10 meV, which is significantly lower than the calculated 60-meV bandgap at zero strain (23, 24). Hence, the actual strain required to pass through E_g = 0 could be smaller (see Fig. 1D).

We use the bulk electrical transport to study the putative strain-tuned topological phase transition in ZrTe₅. As the bulk energy bandgap closes and reopens, the electrical transport properties, such as resistivity, will fall and rise again. The resistivity is determined by the properties of quasiparticles near the chemical potential; hence, the strain effect on resistivity will be larger if the doping is lower so that the chemical potential is closer to the band edge. Therefore, we used the flux method to grow single crystals of ZrTe₅, which is known to yield crystals closer to perfect chemical stoichiometry with ultralow carrier density (p-type, 10¹⁵ cm⁻³) (27). The resistivity of ZrTe₅ depends on both strain and temperature (see Figure 2). Figure 2C shows the resistivity as a function of temperature for several freestanding ZrTe₅ single crystals before they were mounted on the strain apparatus. The insulating temperature dependence is consistent with other flux-grown crystals in the literature, indicating that, at base temperature, the chemical potential of our samples lies just slightly below the valence band maximum (25, 28).

Fig. 2. Temperature and strain dependence of resistivity of ZrTe₅.

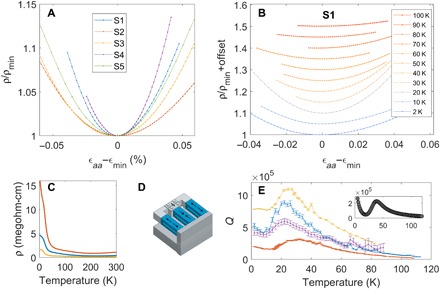
(A) Strain dependence of resistivity of ZrTe₅ at T = 2 K for five samples S1 to S5. A clear minimum in resistivity can be seen for each sample. The resistivity is normalized by its minimum value ρ_min, which varies between 1 and 16 milli-Ohm⋅cm. The x axis is the strain along the a lattice direction, which is estimated on the basis of the method described in Materials and Methods. (B) Resistivity versus strain for temperatures between 2 and 100 K. A clear minimum can be seen for the entire temperature range. (C) Resistivity versus temperature for three ZrTe₅ crystals S1 to S3, as measured before gluing onto the three-piezo strain apparatus. (D) Three-piezostack apparatus used to deliver strain. (E) Quadratic coefficient Q obtained from fitting $\frac{\mathrm{\rho }}{{\mathrm{\rho }}_{\text{min}}}=1+Q{({\mathrm{ϵ}}_{\mathit{aa}}-{\mathrm{ϵ}}_{\text{min}})}^2$. The sensitivity of the response to strain shows a nonmonotonic temperature dependence, as discussed in the main text. Inset: Coefficient Q computed using Boltzmann transport equations (Materials and Methods). The main calculated features agree with the experimental data: A local minimum then maximum is seen with increasing temperature. The relative strength and temperature of these features depend on the carrier density input into the model (see Materials and Methods for more information).

Uniaxial stress was applied along the a axis of the ZrTe₅ crystals using a piezoelectric apparatus introduced by Hicks et al. (29, 30), as shown in Fig. 2D. Resistivity (ρ_aa) and strain (ϵ_aa) were measured along the a axis (Materials and Methods). The strain dependence of the resistivity, i.e., the elastoresistivity, is nonmonotonic at T = 2 K, as shown in Fig. 2A. For all samples measured, the resistivity shows a minimum at a critical strain ϵ_min and increases as the sample is strained away from ϵ_min. There is an uncertainty in determining the zero-strain state, i.e., the absolute value of ϵ_min, due to the mismatch of thermal contraction between the sample and apparatus. Nevertheless, on the basis of a detailed analysis, we estimated that ϵ_min < 0.12% (Materials and Methods). For all the data shown here, ϵ_aa is measured from ϵ_min. We note that, although the size of the strain response varies from sample to sample, the appearance of a resistivity minimum is a robust phenomenon seen in every case. It is well known that the resistivity of semiconductors can have a large linear response to strain due to its sensitivity to the position of band edges as a function of strain. Such a nonmonotonic strain dependence is very unusual but is precisely what is expected for the STI-WTI topological phase transition as described above.

The nonmonotonic elastoresistivity is quadratic in the vicinity of ϵ_min. This is consistent with expectations based on the massive Dirac Hamiltonian, which has been shown to successfully describe the magneto-optical spectrum of ZrTe₅ (23, 24, 31). In general, the k ∙ p Hamiltonian of a small bandgap semiconductor gives a dispersion $E(\mathbf{k})=\pm \sqrt{m^2+{\mathrm{\hslash }}^2{v}_{\mathrm{\alpha }}^2{k}_{\mathrm{\alpha }}^2}$, where m, which is half of the bandgap E_g = 2∣m∣, is analogous to the rest mass of a relativistic free particle, and v_α and k_α are the Fermi velocities and crystal momentum. Because the strain (ϵ_aa, ϵ_bb, and ϵ_cc) induced by the uniaxial stress does not break the D_2h point group symmetry of ZrTe₅, the parameters of the Hamiltonian, including m, should vary linearly with strain. The band inversion process corresponds to the change in the sign of m as it is tuned through zero by strain. However, the physical observables that determine the resistivity, including bandgap, density of states (DOS), and velocity, do not depend on the sign of m and thus must vary as m² to lowest order. As a result, the resistivity will also be parabolic in strain.

The linear elastoresistivity coefficient in nondegenerate semiconductors is proportional to the ratio of deformation potential (∂E_g/∂ϵ) to temperature (k_BT) (32). We derive a similar relation for the quadratic elastoresistivity coefficient measured in ZrTe₅. At low temperature in the quantum degenerate regime when k_BT ≪ E_F, the Fermi energy E_F plays the same role as k_BT. On the basis of dimensional analysis, the quadratic coefficient ∆ρ/ρ is determined by m normalized by E_F

$$\frac{\mathrm{∆}\mathrm{\rho }(\mathrm{ϵ})}{\mathrm{\rho }}\approx {\left(\frac{m}{E_{\mathrm{F}}}\right)}^2={\left(\frac{\frac{\mathrm{\partial }\mathit{m}}{\mathrm{\partial }\mathrm{ϵ}}}{E_{\mathrm{F}}}\right)}^2{\mathrm{ϵ}}^2$$

We also performed a Boltzmann transport calculation and obtain the same expression. The calculation assumes the simplest situation where a fixed number of relativistic electrons are scattered from charged impurities (Materials and Methods). This expression agrees with the expectation that the sensitivity of resistivity to strain decreases as the chemical potential moves away from the band edge. Using the deformation potential, ∂m/∂ϵ, calculated by DFT in the above formula, a fit of the quadratic coefficient yields a Fermi energy of 4 to 8 meV and a carrier density of 0.3 × 10¹⁵ to 2.4 × 10¹⁵cm⁻³. These values are comparable with angle-resolved photoemission spectroscopy and transport measurements of similar samples (23, 33).

We note that, in Fig. 2A, a slight deviation from perfectly quadratic behavior can be seen. Away from the critical strain, we do expect this deviation from quadratic (symmetric) behavior due to the higher-order strain dependence or the strain dependence of other band parameters such as v_α, which we assumed to be a constant in the Boltzmann transport model. In addition, the Poisson ratio may also be different for large compressive and tensile strain states.

We also measured the elastoresistivity at higher temperatures, which shows quadratic behavior up to 100 K. The quadratic coefficient exhibits a nonmonotonic temperature dependence, as shown in Fig. 2E. This is a consequence of a crossover from the quantum degenerate to nondegenerate regime as temperature increases. By including the Fermi-Dirac distribution in the Boltzmann transport calculation, we are able to reproduce the nonmonotonic temperature dependence of the quadratic coefficient, as shown in the inset of Fig. 2E. The overall qualitative agreement suggests that the transport properties of ZrTe₅ are well captured by the dynamics of massive Dirac fermions with a strain tunable mass across a wide temperature range.

If the bandgap is truly zero at ϵ_min, then the band structure at that point is equivalent to a massless Dirac semimetal, which is known to host the chiral anomaly when electric and magnetic fields are parallel. A manifestation of the chiral anomaly is NLMR, which has been observed in ZrTe₅ previously (21). This effect was initially considered in gapless Weyl or Dirac semimetals (34, 35), yet for a gapped Dirac semimetal, essentially the same mechanism could still apply in the semiclassical regime provided that E_g/E_F << 1 (36). In a gapped Dirac semimetal, electron helicity plays the same role as chirality in gapless semimetals. The helicity relaxation rate is proportional to (E_g/E_F)². As a result, we expect a suppression of NLMR (i.e., positive longitudinal magnetoconductivity) when the bandgap opens.

To investigate this, we measured the strain dependence of longitudinal magneto-transport (I ∥ B ∥ a; see Materials and Methods for field alignment). Figure 3 (A and B) shows the resistivity versus field for different strain states. An NLMR is clearly observable, and it disappears if the field is misaligned by more than 1° (fig. S6), consistent with the literature (21, 28). At ϵ_aa = ϵ_min (gray curves), the NLMR reaches its maximum, and it is progressively suppressed when the sample is strained away from this point. Two other samples were measured and show the same strain dependence (fig. S5). The magnetoresistance shows an upturn once the field surpasses the quantum limit (estimated to be 2 T for 10¹⁵ cm⁻³ carrier density) (19, 27). We notice that the upturn is shifted to higher fields on the STI side, which may be related to the unusual behavior of lowest Landau levels of topological insulators (37). Nevertheless, we leave the study of high-field magnetoresistance for future works and focus on the weak field semiclassical regime (B < 0.5 T), in which the magnetoconductance Δσ = σ(B) − σ₀ is positive except showing a small dip near zero field (Fig. 3C). The magnetoconductance was fitted with a quadratic field dependence, σ = σ₀ + αB² (see Materials and Methods for details of fitting). The quadratic coefficient α is proportional to the helicity relaxation time (36), and it shows a 10-fold increase as ϵ_aa approaches ϵ_min (Fig. 3D). This diverging behavior is consistent with the suppression of helicity relaxation due to the vanishing of the bandgap at ϵ_aa = ϵ_min.

Fig. 3. Strain dependence of longitudinal magnetoresistance and magnetoconductance of ZrTe₅ at T = 2 K.

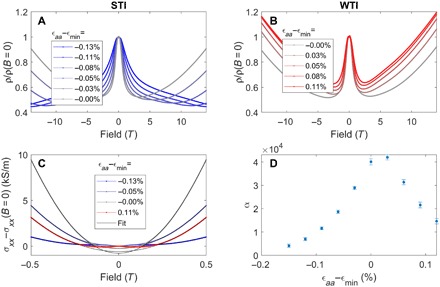
NLMR for negative strains (A) and positive strains (B) measured relative to ϵ_min, corresponding to the STI and WTI phases, respectively. The negative magnetoresistance is strongest at ϵ_min, at which ZrTe₅ is a gapless Dirac semimetal. Straining the crystal away from ϵ_min suppresses the negative magnetoresistance. (C) Weak field positive magnetoconductance for several strain set points close to ϵ_min. The conductance is fitted to the equation σ(B) = σ₀ + αB² (black solid curves), where α is a positive coefficient proportional to the helicity relaxation time. (D) Quadratic coefficient α as a function of strain measured relative to ϵ_min.

DISCUSSION

Our extensive transport measurements and detailed data analysis have revealed an exceptionally delicate topological ground state of ZrTe₅. The highly nonlinear elastoresistivity from a nonsymmetry breaking strain is consistent with the sign switching of the Dirac mass. This is further corroborated by the diverging strain dependence of positive longitudinal magnetoconductance near the transition point, which is a more profound consequence of the vanishing of the Dirac mass. In this sense, our study not only represents a new approach to characterize topological phase transitions but also demonstrates a method to precisely control phenomena associated with the chiral anomaly. We note that the applied strain does not break inversion symmetry. It is possible to apply an external electric field to exfoliated thin flakes to break inversion symmetry and induce the Weyl semimetal phase shown in Fig. 1A.

One defining signature that distinguishes STI from WTI is the existence of surface states on all crystal facets, which is not addressed in the current study. On the other hand, all of our transport data on ZrTe₅ present strong evidence of an in situ strain-tuned topological phase transition in this material. We note that our experimental setup for applying strain is compatible with photoemission and scanning tunneling spectroscopy measurements. Future studies incorporating spectroscopic techniques capable of measuring surface states and band topology should be able to provide a comprehensive understanding of topological phase transitions.

MATERIALS AND METHODS

Material growth and sample preparation

Single-crystal ZrTe₅ was grown with the flux method (21). Zr slugs (99.9% pure, Alfa Aesar) and Te shot (99.9999% pure, Alfa Aesar) were loaded into a quartz ampule in a Zr:Te ratio of 1:100. The ampule was warmed to 900°C in 9 hours, kept at 900°C for 72 hours, and then cooled to 505°C in 48 hours. To promote large crystal growth, the ampule was repetitively cooled to 440°C and warmed to 505°C. Last, the ampule was cooled to 460°C and decanted in a centrifuge at this temperature.

For electrical transport measurements, single crystals of typical dimensions 1.5 mm × 0.1 mm × 0.02 mm were sputtered with gold, and then 25-μm-diameter gold wires were placed on the crystals and adhered with silver paint. The resistance was measured with an SRS830 lock-in amplifier and an SRS CS580 current source. Given the needle-like nature of the single crystals, the resistance was measured along the a axis of the crystal.

Strain apparatus

Uniaxial stress was applied to single crystals using a homebuilt three-piezostack device (shown in fig. S1). Three piezoelectric actuators are aligned in parallel with each other. A U-shaped titanium block was glued to the outer two piezoelectric actuators, and a small titanium block was glued to the middle actuator, forming a small gap between these blocks. Applying a voltage to the outer piezostacks while applying an equal and opposite voltage to the middle piezostack will strain the piezostacks and change the gap size.

A crystal is glued across this apparatus gap. Tuning this gap with the piezostack voltage will apply uniaxial stress to the crystal. For a similar apparatus, Hicks et al. (29) showed that gluing only the bottom surface of the crystal to these plates can lead to strain gradients between the top and bottom surfaces of the crystal. These gradients can be suppressed by submerging the crystal in glue, as we did. Hicks et al. showed that the strain gradients are small when the ratio of t/L_G (sample thickness to gap size) is small. For our measurements, this ratio is small, ranging from 0.02 to 0.08. We simulated the strain distribution with finite element analysis. Our finite element analysis does show that there are still some small strain gradients along the vertical axis of the crystal, mostly confined to the bottom quarter of the crystal. The strain along the a axis ϵ_aa is equal to α∆L/L, where the change of the gap size ∆L/L is estimated by a strain gauge glued on the piezostacks. The constant α takes into account a strain relaxation effect, which is estimated by finite element analysis and is typically about 0.8. The strain along the b axis and c axis are determined by the Poisson’s ratio. The resistance-strain dependence identified in this work is a smoothly varying function. Because of this, these small strain gradients have minimal impact on our interpretation of the spatially average resistance.

Care was taken during the construction of the three-piezo apparatus to ensure fine alignment of the piezostacks, minimizing any stress in the secondary axes. First, a “scaffolding” piece was machined with indents the exact dimensions of the piezoelectric actuators and the titanium blocks. The actuators and blocks were placed in these indents and then glued together while secured in precise alignment. The scaffolding block was then removed after the glue dried. Second, the middle titanium block and the outer titanium block were machined with a thin flexor plate connecting them. This flexor plate restricts motion between the blocks in any axis except the primary strain axis.

Strain was measured by a foil strain gauge glued to one of the piezostacks, measuring ϵ^piezo. The displacement strain of the device was estimated as this strain multiplied by the mechanical advantage of the apparatus, ${\mathrm{ϵ}}_{\mathit{xx}}^{\text{disp}}=2L_{\mathrm{p}}/L_{\mathrm{G}}{\mathrm{ϵ}}^{\text{piezo}}$, where L_p is the length of the piezostack, L_G is the length of the gap the sample is glued across, and ${\mathrm{ϵ}}_{\mathit{xx}}^{\text{disp}}$ is the displacement of the apparatus. Because of a low signal-to-noise ratio associated with the strain gauge measurement, we presented data plotted against piezostack voltage rather than plotted directly against the measured strain. We then calibrated this with a strain per volt calibration fitted from the strain measurement. We carefully minimized the amplitude of the voltage sweeps applied to the piezostacks, staying centered around ϵ_min to minimize any hysteresis effect in the piezostacks.

Finite element analysis

We used the ANSYS Academic Research Mechanical 19.1 finite element analysis software to calculate the strain transmission in the primary axis and deformation in the secondary axis for all of our ZrTe₅ samples. The model is shown in fig. S2. The stiffness tensor for ZrTe₅ was taken from a previously calculated value by the Materials Project (38). The sample is modeled as mounted to the strain apparatus in a puddle of epoxy. The Young’s modulus and Poisson’s ratio of the epoxy were given the same values as the work done by Hicks et al. (29). For each crystal measured, the model took the exact crystal dimensions and gap size of the apparatus as inputs and computed an average relaxation constant α, defined as ${\mathrm{ϵ}}_{\mathit{aa}}=\mathrm{\alpha }{\mathrm{ϵ}}_{\mathit{xx}}^{\text{disp}}$ for ${\mathrm{ϵ}}_{\mathit{xx}}^{\text{disp}}=\pm 0.1\%$, where ϵ_aa is the strain delivered to the crystal. Our results are shown in table S1.

Experimental procedure

After cooling to 2 K, the sample was warmed by incremental temperature set points. In situ stress was applied to the crystal at each temperature set point by applying a triangle voltage waveform across the outer two piezo actuators and an equal and opposite sign waveform across the middle actuator. For each temperature set point, the voltage waveform was allowed to loop several times to inspect any hysteresis effects. The magnitude and offset of this waveform were adjusted during warming to stay centered around the resistance minimum. At temperatures 80 K and higher, it took an increasing amount of compressive strain to stay centered on the resistance minimum. At these temperatures, the samples often buckled as negative strain was applied. This buckling led to a large hysteresis developing in the resistance-strain relation, and the experiment was terminated.

Calibration to zero-strain state

One of the advantages of the three-piezo apparatus compared to direct gluing to a single piezostack is that the thermal strain is minimized. This is because the large thermal expansion of the outer two piezostacks was compensated by the expansion of the middle piezostack. However, there was still a non-negligible thermal strain resulting from the mismatch of thermal expansions between the crystal and the titanium pieces of the apparatus. Because titanium is known to have a smaller thermal expansion compared to most materials, it is expected that cooling the apparatus will impart a tensile strain to a mounted crystal. By tuning the controllable strain of the apparatus, this thermal strain can be compensated if a reference calibration is available.

A zero-strain calibration was constructed by measuring the resistance of crystals before gluing to the strain apparatus. After measuring the zero-strain resistance, crystals were glued to the apparatus and the resistance was measured while cooling from 300 to 2 K. The apparatus strain could then be adjusted to tune the strained resistance to the calibration resistance, keeping the crystal in the zero-strain state. For most crystals, we were able to track the zero-strain state of the crystal down to about 60 K. Between 60 and 300 K, crystals always had a positive gauge factor (GF) (tensile strain increased resistance). This indicates that, in this temperature range, the zero-strain state resides at higher strains compared to ϵ_min. Below 60 K, two things occurred that made tracking zero-strain state difficult. The first was that the resistance sensitivity to strain became weak—the GF approached zero. This indicates that the crystal either approaches or passes through ϵ_min below 60 K. The second difficulty is that the resistance of the mounted crystal measured a slightly higher value than the calibration resistance for temperatures below 60 K. This occurred even when the strained crystal was tuned to ϵ_min.

The higher resistance measured on the strain apparatus compared to the unstrained crystal can be attributed to a slight aging effect in the crystals. Figure S3 (A and B) shows two ZrTe5 crystals, with the resistance versus temperature measured twice. The second measurement was performed after the crystals were left sitting in atmosphere for 18 days. Between measurements, the 2 K resistance increased 2.4 and 3.4% for each crystal. The difference in resistance between crystals is negligible above 60 K, the same approximate temperature below which we are unable to tune the strained resistance to the unstrained resistance. Because of this slight aging effect, we were unable to locate the zero-strain state of crystals glued to the apparatus at low temperatures. Figure S3C shows the resistance of a strained crystal to its unstrained resistance, measured 1 day apart. Even with only 1 day between measuring the unstrained crystal and the strained crystal, there is still a slight aging effect that prohibits tracking the zero-strain state.

To estimate the location of the zero-strain state, i.e., the absolute value of ϵ_min, we performed the following experiment. Crystals were glued directly on the side wall of a single piezostack, as shown in fig. S4 (B and C). The piezostack has unusual highly anisotropic thermal expansion properties; it expands by about 0.1% along the polling direction and contracts along the transverse direction as it is cooled to liquid helium temperatures. Gluing crystals oriented parallel and perpendicular to the piezostack polling axis imparts a very different strain during cooling, mimicking scenarios where samples were glued on substrates with different thermal expansion coefficients. Tuning the piezostack voltage at 2 K adds a much smaller tunable strain (~ 0.01 to 0.02%) on top of this thermal strain. Using this tunable strain, we were able to measure a linear elastoresistance. The slope of this linear response, defined as $\text{GF}=(\frac{\mathrm{∆}\mathrm{\rho }}{\mathrm{\rho }})/(\frac{\mathrm{∆}L}{L})$, measures the local derivative of the nonlinear resistivity versus strain curves. A positive or negative GF indicates which side of ϵ_min the thermally strained crystal resides on. As seen in fig. S4, the parallel (perpendicular) orientations measure a positive (negative) GF at 2 K. This indicates the sensitivity of the thermal strain to sample preparation and allows us to make an estimate of ϵ_min. On the basis of published data for the thermal expansion of similar piezostacks and ZrTe₅, cooling to 2 K strains the perpendicular glued sample by about +0.08% (39, 40). The parallel glued sample is strained even more than this. We measured GF (2 K) = −73 for the perpendicular glued sample. This indicates that the parallel glued thermal strain is between −0.04 and −0.01% with respect to ϵ_min, as calibrated by the quadratic response we measured for samples in this work. Combining this with our estimate for the thermal strain, we estimated that ϵ_min is at most +0.12% at 2 K. With the DFT estimate of dE_G/dε~6000 meV, this estimates an upper bound of the E_G in the zero-strain state of 72 meV, which is consistent with most reported values of the E_G.

Measurement of the longitudinal magnetoresistance

Longitudinal magnetoresistance was measured at strain set points for field parallel the current along the a axis. In addition to the results reported in Fig. 3 (A and B), two other crystals were measured (shown in fig. S5). For all crystals, we measured a positive magnetoconductance after a small dip in the magnetoconductance for very low fields. The small dip in longitudinal magnetoconductance near zero field is commonly observed in other materials that exhibit chiral anomaly. Its origin is not completely understood. Two possibilities are weak antilocalization effect and the classical Lorentz longitudinal magnetoresistance in anisotropic metals that saturates when ω_cτ ~ 1. The positive magnetoconductance was suppressed for strains as low as 0.02% away from ϵ_min for both compressive and tensile strains.

NLMR is only observed for magnetic fields finely aligned to the current, I ∥ B ∥ a. We aligned our apparatus such that the magnetic field is parallel to the a axis of the sample. The apparatus itself was machined to within 20-μm precision so that the plane of the edge of apparatus can be very precisely aligned to the magnetic field (<1°). The primary opportunity for misalignment is the crystal being misaligned within the plane of the apparatus. To minimize misalignment along this axis, we used an optical microscope to inspect and adjust the alignment of the crystal after it was placed in glue on the apparatus. The glue adhering the crystal dried slowly enough to allow time for alignment adjustment under the optical microscope. We found that we can frequently align crystals within 1° of alignment using this simple technique.

To verify that the crystal and apparatus were fully aligned with magnetic fields, we constructed a strain apparatus on a Quantum Design DynaCool single-axis rotation puck (as shown in fig. S6A). We tuned ϵ_aa to ϵ_min, which we know from Fig. 3 will have the strongest NLMR response. We then measured longitudinal magnetoresistance for several angles between field and a axis, from −1.0° to +0.5° in increments of 0.25° (shown in fig. S6B). We found that the NLMR was only observed for alignments better than 1.0°, which is consistent with other results (28). Because NLMR is not observed for misalignments 1° or greater even for ϵ_aa = ϵ_min, the observation of NLMR is evidence that our crystals are aligned to within 1° of accuracy or less.

Further details about the fitting of longitudinal magnetoconductance

Positive magnetoconductance was fitted to the equation σ(B) = σ₀ + αB², where α is a positive coefficient that is proportional to helicity relaxation time. To eliminate errors to the fit associated with the dip of magnetoconductance near zero field, the data were fitted only for the magnetic field bounded between a lower bound and 0.5T, B_LB <∣B∣ < 0.5T. Figure S7A shows representative data and fitted curves for B_LB = 0.2T. The coefficient α as a function of strain is plotted in fig. S7B. The coefficient α peaks at ϵ_min, as discussed in the main text. α is plotted for several choices of B_LB, and the choice of B_LB is found to not significantly influence the strain dependence of α. For the data shown in Fig. 3C, B_LB = 0.2T, and the error bars are determined by varying the fitting range.

Boltzmann transport theory of massive Dirac semimetal

In the quantum degenerate regime, the conductivity of a 3D electron gas can be expressed as

$$\mathrm{\sigma }=\frac{e^2}{3{\mathrm{\pi }}^2\mathrm{\hslash }}{k}_{\mathrm{F}}^{2}l$$

where k_F is the Fermi wave vector determined by the carrier density and l is the mean free path. In ZrTe₅, the carriers are most likely originated from the ionization of impurities, and the carrier density is determined by the number of impurities n_i. Close to zero gap, the ionization is practically insensitive to the modulation of bandgap due to strain. Therefore, we assumed that carrier density and k_F are independent of the strain, and the strain dependence of conductivity is dominated by the change of mean free path. At low temperature, the mean free path is limited by scattering from the ionized impurity centers and can be expressed in terms of the impurity concentration n_i and the i transport cross-section σ_tran

$$\frac{1}{l}=n_i{\mathrm{\sigma }}_{\text{tran}}$$

Near the Γ point, the band structure of ZrTe₅ obeys a relativistic Dirac dispersion E² = m² + ℏ²k²v². The scattering cross-section for this relativistic dispersion by a Coulomb potential obeys the relativistic Mott formula

$${\mathrm{\sigma }}_{\text{tran}}=\int \mathit{do}\frac{d\mathrm{\sigma }}{\mathit{do}}[1-\text{cosθ}]$$

$${\mathrm{\sigma }}_{\text{tran}}=\frac{\mathrm{\pi }{\mathrm{\alpha }}^2}{k^2}{\displaystyle {\int }_{-1}^1}d\text{cosθ}\frac{{\mathrm{\beta }}^{-2}-{\text{sin}}^2\mathrm{\theta }/2}{{\text{sin}}^2\mathrm{\theta }/2}$$

$${\mathrm{\sigma }}_{\text{tran}}~\frac{8\mathrm{\pi }{\mathrm{\alpha }}^2}{k^2{\mathrm{\beta }}^2}\mathit{\text{ln}}\frac{1}{{\mathrm{\theta }}_0}$$

where θ₀ is the small angle cutoff due to the screening of the Coulomb interaction, and $\mathrm{\alpha }=\frac{e^2}{\mathrm{\hslash }\mathit{v}\mathrm{ϵ}}$ is the dimensionless coupling constant, where ϵ is the static dielectric constant. β = v²ℏ²k²/(m² + v²ℏ²k²) follows from $\mathrm{\beta }=\frac{1}{\mathrm{\hslash }\mathit{v}}\frac{\mathrm{\partial }E}{\mathrm{\partial }k}$ applied to the dispersion E² = m² + ℏ²k²v².

Because $\mathrm{\rho }\propto \frac{1}{l}=n_i{\mathrm{\sigma }}_{\text{tran}}(m)$, it follows that

$$\frac{\mathrm{\rho }(m)-\mathrm{\rho }(m=0)}{\mathrm{\rho }(m=0)}\approx \frac{\mathrm{\beta }(m=0)-\mathrm{\beta }(m)}{\mathrm{\beta }(m)}=1+{\left(\frac{m}{E_F}\right)}^2$$

which is the result in the main text. The carrier density for each sample measured based on this computation is estimated in table S1.

Temperature dependence of resistivity/gap relation

A semiclassical Boltzmann transport model was used to compute the temperature dependence of the resistivity sensitivity to strain. The Dirac band at the Γ point is assumed to dominate conduction, and the conductivity can be expressed as

$${\mathrm{\sigma }}_{\mathit{xx}}=-e^2\int g(E)\mathrm{\tau }(E){\mathrm{\nu }}_x{(E)}^2\frac{\mathrm{\delta }f}{\mathrm{\delta }E}\mathit{dE}$$

where $v_x=\frac{1}{\mathrm{\hslash }}\frac{\mathrm{\partial }E}{\mathrm{\partial }{k}_x}.$The scattering time τ can be expressed as $\frac{l(E)}{v_x}$, where l(E) is the energy-dependent scattering length mentioned above, inversely proportional to σ_tran. We assume that scattering off of charged impurities is the dominant scattering mechanism in this simplistic model. Given the Dirac dispersion of E² = m² + ℏ²k²v², the DOS can be written as

$$g(E)=\frac{E\sqrt{E^2-m^2}}{{\mathrm{\pi }}^2{\mathrm{\hslash }}^3{v}^3}$$

Combining these, the conductivity may be written as

$$\frac{{\mathrm{\sigma }}_{\mathit{xx}}(m)}{{\mathrm{\sigma }}_{\mathit{xx}}(m=0)}=(\int \frac{{(E^2-m^2)}^3}{E^2}\frac{1}{2\text{cosh}\left(\frac{E-\mathrm{\mu }}{k_{B}T}\right)+2}\mathit{dE})÷(\int \frac{E^4}{2\text{cosh}\left(\frac{E-\mathrm{\mu }}{k_{B}T}\right)+2}\mathit{dE})$$

Given the chemical potential μ as a function of temperature, $\frac{{\mathrm{\sigma }}_{\mathit{xx}}(T,m)}{{\mathrm{\sigma }}_{\mathit{xx}}(T,m=0)}$ can be computed for a range of temperatures, and a quadratic relation between 1/σ_xx and m can be fitted.

All that is left in the model is to compute μ(T). This can easily be done by charge conservation. The impurity doping n_i is defined as n – p, where n and p are the electron and hole densities. n(T) and p(T) can be computed as

$$n={\displaystyle {\int }_0^{\infty }}g(E)\frac{1}{e^{E-\mathrm{\mu }}+1}\mathit{dE}$$

$$p={\displaystyle {\int }_{\infty }^0}g(E)(1-\frac{1}{e^{E-\mathrm{\mu }}+1})\mathit{dE}$$

Given n_i as the input parameter, μ(T) can be solved numerically by enforcing n_i = n(T) − p(T) for electron doping or n_i = p(T) − n(T) for hole doping. The only other input parameter for our computational model is the velocity v that appears in the Dirac dispersion. We used v_a, v_b, v_c = 1.7,5.2,2.2 × 10⁵m/s, as measured by SdH oscillations (19).

DFT calculations

The electronic structure and energy gap of ZrTe₅ under strain were calculated by the Quantum Espresso package (41) based on DFT. The Perdew-Burke-Ernzerhof exchange-correlation functional (PBE-GGA) (42) with spin-orbit coupling and projector augmented wave (43) method were used. The unstrained lattice parameters (a = 3.97976 Å, c = 13.6762 Å) were determined by experimental data at 10 K (40), and an 11 × 11 grid in the parameter ranges of 1.0a to 1.02a and 0.99c to 1.01c was considered for studying the gap behavior with lattice variation. The raw data of the zone-center gap are shown in fig. S8A, and the interpolated data with 2D cubic splines are shown in Fig. 1C. An 8 × 8 × 4 momentum grid was used in the self-consistent calculation, and the kinetic energy cutoff and convergence criterion were set to 30 and 10⁻⁷ rydberg, respectively. The DFT band structures for ZrTe₅ in different strained states are shown in fig. S9. The labeling of the high-symmetry k-points was based on the Brillouin zone of the primitive unit cell.

The topological Z₂ indices of different strained structures were also computed to identify their topological nature. With input from the electronic structure calculations of Quantum Espresso, the maximally localized Wannier functions were first computed using the Wannier90 package (44), which, in turn, allowed the determination of Z₂ indices by tracking hybrid Wannier charge centers using the WannierTools package (45). As shown in fig. S8B, the bottom right of the phase diagram is an STI with Z₂ indices (1;110), and the upper left is a WTI [with Z₂ indices (0;110)]. Phase transition between the STI and WTI states was directly controlled by closing the energy gap at the Brillouin zone center.

Additional structure relaxation calculations were performed with the vdW-DFT (46, 47), corrected using the exchange-hole dipole moment model (48). The vdW-DFT fully relaxed lattice parameters of layer-structured ZrTe₅ are within 1% error compared to the unstrained experimental data. To determine the Poisson ratio, conventional cells of different fixed lattice parameters along the a axis were considered, while the b and c lattice parameters were allowed to evolve freely in the structure relaxation calculations. The results are shown in fig. S8C.

We have computed the DOS around the Γ point for different strained structures shown in Fig. 1D. Specifically, we made a k-grid of 21 × 21 × 11 points around the Γ point (±0.01 b₁, ±0.01 b₂, ±0.01 b₃) and counted the states within E_fermi ± 𝝙, where 𝝙 ranges from 6 to 10 meV (corresponding to 70 to 120 K) to plot the DOS for different strained states. As shown in fig. S8D, the resulting DOS around the Γ point has a fairly parabolic strain dependence. We also performed a third-order polynomial fit y(x) = a₃x³ + a₂x² + a₁x + a₀ for the curves [where y stands for the DOS and x stands for 𝝙a] and found that, within the range of interests, the anharmonic term a₃x³ is roughly 1000 times smaller than a₂x². Therefore, to leading order, a parabolic strain dependence of DOS near the Γ point remains a valid assumption.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/8/eaav9771/DC1

Fig. S1. Schematic and picture of piezo device.

Fig. S2. Finite element analysis of strain transmission.

Fig. S3. Sample aging and zero-strain tuning.

Fig. S4. Comparison between three-piezo and single-piezo elastoresistivity measurement.

Fig. S5. Additional longitudinal magneto-transport measurement as a function of strain.

Fig. S6. Angle dependence of longitudinal magnetoresistance.

Fig. S7. Fitting of positive longitudinal magnetoconductance.

Fig. S8. DFT calculations of Z₂ topological indices, Poisson ratio, and DOS.

Fig. S9. DFT band structures for ZrTe₅ in different strained states.

Table S1. Dimensions, 2 K resistivity, and QC of each sample crystal.