Abstract
With the advent of convolutional neural networks (CNN), supervised learning methods are increasingly being used for whole brain segmentation. However, a large, manually annotated training dataset of labeled brain images required to train such supervised methods is frequently difficult to obtain or create. In addition, existing training datasets are generally acquired with a homogeneous magnetic resonance imaging (MRI) acquisition protocol. CNNs trained on such datasets are unable to generalize on test data with different acquisition protocols. Modern neuroimaging studies and clinical trials are necessarily multi-center initiatives with a wide variety of acquisition protocols. Despite stringent protocol harmonization practices, it is very difficult to standardize the gamut of MRI imaging parameters across scanners, field strengths, receive coils etc., that affect image contrast. In this paper we propose a CNN-based segmentation algorithm that, in addition to being highly accurate and fast, is also resilient to variation in the input acquisition. Our approach relies on building approximate forward models of pulse sequences that produce a typical test image. For a given pulse sequence, we use its forward model to generate plausible, synthetic training examples that appear as if they were acquired in a scanner with that pulse sequence. Sampling over a wide variety of pulse sequences results in a wide variety of augmented training examples that help build an image contrast invariant model. Our method trains a single CNN that can segment input MRI images with acquisition parameters as disparate as T1-weighted and T2-weighted contrasts with only T1-weighted training data. The segmentations generated are highly accurate with state-of-the-art results (overall Dice overlap= 0.94), with a fast run time (≈ 45 seconds), and consistent across a wide range of acquisition protocols.
Keywords: MRI, brain, segmentation, convolutional neural networks, robust, harmonization
1. Introduction
Whole brain segmentation is one of the most important tasks in a neuroimage processing pipeline, and is a well-studied problem (Fischl et al., 2002; Shiee and et al., 2010; Wang et al., 2013; Asman and Landman, 2012; Wachinger et al., 2017). The segmentation task involves taking as input an MRI image, usually a T1-weighted (T1-w) image, of the head, and generating a labeled image with each voxel getting a label of the structure it lies in. Most segmentation algorithms output labels for right/left white matter, gray matter cortex, and subcortical structures such as the thalamus, hippocampus, amygdala, and others. Structure volumes and shapes estimated from a volumetric segmentation are routinely used as biomarkers to quantify differences between healthy and diseased populations (Fischl et al., 2002), track disease progression (Frisoni et al., 2009; Jack et al., 2011; Davatzikos et al., 2005), and study aging (Resnick et al., 2000). Segmentation of a T1-w image is also used to localize and analyze the functional and diffusion signals from labeled anatomy after modalities such as functional MRI (fMRI), PET (positron emission tomography), and diffusion MRI are co-registered to the T1-w image. This enables the study of effects of external intervention or treatment on various properties of the segmented neuroanatomy (Desbordes et al., 2012; Mattsson et al., 2014). In this work we are primarily concerned about whole brain segmentation of adult humans (age range 18 to 90 years).
An ideal segmentation algorithm needs to be highly accurate. Accuracy is frequently measured with metrics such as Dice coefficient and Jaccard index, that quantify overlap of predicted labels with a manually labeled ground truth. An accurate segmentation algorithm is more sensitive to and can detect the subtle changes in volume and shape of brain structures in patients with neurodegenerative diseases (Jack et al., 2011). Fast processing time is also a desirable property for segmentation algorithms. Segmentation is one of the time-consuming bottlenecks in neuroimaging pipelines (Fischl et al., 2002). A fast, memory-light segmentation algorithm can process a larger dataset quickly and can potentially be adopted in real-time image analysis pipelines.
For MRI, however, it is also critical that the segmentation algorithm be robust to variations in the contrast properties of the input images. MRI is an extremely versatile modality, and a variety of image contrasts can be achieved by changing the multitude of imaging parameters. Large, modern MRI studies acquire imaging data simultaneously at multiple centers across the globe to gain access to a larger, more diverse pool of subjects (Thompson et al., 2014; Mueller et al., 2005). It is very difficult to perfectly harmonize scanner manufacturers, field strengths, receive coils, pulse sequences, resolutions, scanner software versions, and many other imaging parameters across different sites. Variation in imaging parameters leads to variation in intensities and image contrast across sites, which in turn leads to variation in segmentation results. Most segmentation algorithms are not designed to be robust to these variations (Han et al., 2006; Jovicich and et al., 2013; Nyúl and Udupa, 1999; Focke et al., 2011). Segmentation algorithms can introduce a site-specific bias in any analysis of multi-site data that is dependent on structure volumes or shapes obtained from that algorithm. In most analyses, the inter-site and inter-scanner variations are regressed out as confounding variables (Kostro et al., 2014) or the MRI images are pre-processed in order to provide consistent input to the segmentation algorithm (Nyúl and Udupa, 1999; Madabhushi and Udupa, 2006; Roy et al., 2013; Jog et al., 2015). However, a segmentation algorithm that is robust to scanner variation precludes the need to pre-process the inputs.
1.1. Prior Work
Existing whole brain segmentation algorithms can be broadly classified into three types: (a) model-based, (b) multi-atlas registration-based, and (c) supervised learning-based. Model-based algorithms (Fischl et al., 2002; Pohl et al., 2006; Pizer et al., 2003; Patenaude et al., 2011; Puonti et al., 2016) fit an underlying statistical atlas-based model to the observed intensities of the input image and perform maximum a posteriori (MAP) labeling. They assume a functional form (e.g. Gaussian) of intensity distributions and results can degrade if the input distribution differs from this assumption. Recent work by Puonti et al. (2016) builds a parametric generative model for brain segmentation that leverages manually labeled training data and also adapts to changes in input image contrast. In a similar vein, work by Bazin and Pham (2008) also uses a statistical atlas to minimize an energy functional based on fuzzy c-means clustering of intensities. Model-based methods are usually computationally intensive, taking 0.5–4 hours to run. With the exception of the work by Puonti et al. (2016) and Bazin and Pham (2008), most model-based methods are not explicitly designed to be robust to variations in input T1-w contrast and fail to work on input images acquired with a completely different contrast such a proton density weighted (PD-w) or T2-weighted (T2-w).
Multi-atlas registration and label fusion (MALF) methods (Rohlfing et al., 2004; Heckemann et al., 2006; Sabuncu et al., 2010; Zikic et al., 2014; Asman and Landman, 2012; Wang et al., 2013; Wu et al., 2014) use an atlas set of images that comprises pairs of intensity images and their corresponding manually labeled images. The atlas intensity images are deformably registered to the input intensity image, and the corresponding atlas label images are warped using the estimated transforms into the input image space. For each voxel in the input image space, a label is estimated using a label fusion approach. MALF algorithms achieve state-of-the-art segmentation accuracy for whole brain segmentation (Asman and Landman, 2012; Wang et al., 2013) and have previously won multi-label segmentation challenges (Landman and Warfield, 2012). However, they require multiple computationally expensive registrations, followed by label fusion. Efforts have been made to reduce the computational cost of deformable registrations with linear registrations (Coupé et al., 2011), or reducing the task to a single deformable registration (Zikic et al., 2014). However, if the input image contrast is significantly different from the atlas intensity images, registration quality becomes inconsistent, especially across different multi-scanner datasets. If the input image contrast is completely different (PD-w or T2-w) from the atlas images (usually T1-w), the registration algorithm needs to use a modality independent optimization metric such as cross-correlation or mutual information, which also affects registration consistency across datasets.
Accurate whole brain segmentation using supervised machine learning approaches has been made possible in the last few years by the success of deep learning methods in medical imaging. Supervised segmentation approaches built on CNNs have produced accurate segmentations with a runtime of a few seconds or minutes (Li et al., 2017; Wachinger et al., 2017; Roy et al., 2018). These methods have used 2D slices (Roy et al., 2018) or 3D patches (Li et al., 2017; Wachinger et al., 2017) as inputs to custom-built fully convolutional network architectures, the U-Net (Ronneberger et al., 2015) or residual architectures (He et al., 2016) to produce voxel-wise semantic segmentation outputs. The training of these deep networks can take hours to days, but the prediction time on an input image is in the range of seconds to minutes, thus making them an attractive proposition for whole brain segmentation. CNN architectures for whole brain segmentation tend to have millions of trainable parameters but the training data is generally limited. A manually labeled training dataset can consist of only 20–40 labeled images (Buckner et al., 2004; Landman and Warfield, 2012) due to the labor-intensive nature of manual annotation. Furthermore, the training dataset is usually acquired with a fixed acquisition protocol, on the same scanner, within a short period of time, and generally without any substantial artifacts, resulting in a pristine set of training images. Unfortunately, a CNN trained on such limited data is unable to generalize to an input test image acquired with a different acquisition protocol and can easily overfit to the training acquisitions. Despite the powerful local and global context that CNNs generally provide, they are more vulnerable to subtle contrast differences between training and test MRI images than model-based and MALF-based methods. A recent work by Karani et al. (2018) describes a brain segmentation CNN trained to consistently segment multi-scanner and multi-protocol data. This framework adds a new set of batch normalization parameters in the network as it encounters training data from a new acquisition protocol. To learn these parameters, the framework requires that a small number of images from the new protocol be manually labeled, which may not always be possible.
1.2. Our Contribution
We describe Pulse Sequence Adaptive Convolutional Neural Network (PSACNN); a CNN-based whole brain MRI segmentation approach with an augmentation scheme that models the forward models of pulse sequences to generate a wide range of synthetic training examples during the training process. Data augmentation is regularly used in training of CNNs when training data is scarce. Typical augmentation in computer vision applications involves rotating, deforming, and adding noise to an existing training example, pairing it with a suitably transformed training label, and adding it to the training batch data. Once trained this way, the CNN is expected to be robust to these variations, which were not originally present in the given training dataset.
In PSACNN, we aim to augment CNN training by using existing training images and creating versions of them with a different contrast, for a wide range of contrasts. The CNN thus trained will be robust to contrast variations. We create synthetic versions of training images such that they appear to have been scanned with different pulse sequences for a range of pulse sequence parameters. These synthetic images are created by applying pulse sequence imaging equations to the training tissue parameter maps. We formulate simple approximations of the highly nonlinear pulse sequence imaging equations for a set of commonly used pulse sequences. Our approximate imaging equations typically have a much smaller number (3 to be precise) of imaging parameters. Estimating these parameters would typically need multi-contrast images that are not usually available, so we have developed a procedure to estimate these approximate imaging parameters using intensity information present in that image alone.
When applying an approximate imaging equation to tissue parameter maps, changing the imaging parameters of the approximate imaging equation changes the contrast of the generated synthetic image. In PSACNN, we uniformly sample over the approximate pulse sequence parameter space to produce candidate pulse sequence imaging equations and apply them to the training tissue parameters to synthesize images of training brains with a wide range of image contrasts. Training using these synthetic images results in a segmentation CNN that is robust to the variations in image contrast.
A previous version of PSACNN was published as a conference paper (Jog and Fischl, 2018). In this paper, we have extended it by removing the dependence on the FreeSurfer atlas registration for features. We have also added pulse sequence augmentation for T2-weighted sequences, thus enabling the same trained CNN to segment T1-w and T2-w images without an explicitly T2-w training dataset. We have also included additional segmentation consistency experiments conducted on more diverse multi-scanner datasets.
Our paper is structured as follows: In Section 2, we provide a background on MRI image formation, followed by a description of our pulse sequence forward models and the PSACNN training workflow. In Section 3, we show an evaluation of PSACNN performance on a wide variety of multi-scanner datasets and compare it with state-of-the-art segmentation methods. Finally, in Section 4 we briefly summarize our observations and outline directions for future work.
2. Method
2.1. Background: MRI Image Formation
In MRI the changing electromagnetic field stimulates tissue inside a voxel to produce the voxel intensity signal. Let S be the acquired MRI magnitude image. S(x), the intensity at voxel x in the brain is a function of (a) intrinsic tissue parameters and (b) extrinsic imaging parameters. We will refer to the tissue parameters as nuclear magnetic resonance or NMR parameters in order to distinguish them from the imaging parameters. The principal NMR parameters include proton density (ρ(x)), longitudinal (T1(x)) and transverse (T2(x)), and relaxation times. In this work we only focus on ρ, T1, T2 and denote them together as β(x) = [ρ(x),T1(x),T2(x)]. Let the image S be acquired using a pulse sequence ΓS. Commonly used pulse sequences include Magnetization Prepared Gradient Echo (MPRAGE) (Mugler and Brookeman, 1990), Multi-Echo MPRAGE (van der Kouwe et al., 2008) Fast Low Angle Shot (FLASH), Spoiled Gradient Echo (SPGR), T2-Sampling Perfection with Application optimized Contrasts using different flip angle Evolution (T2-SPACE) (Mugler, 2014) and others. Depending on the type of the pulse sequence ΓS, its extrinsic imaging parameters can include repetition time (TR), echo time (TE), flip angle (α), gain (G), and many others. The set of imaging parameters is denoted by ΘS = {TR,TE,α,G,…}. The relationship between voxel intensity S(x) and the NMR parameters (β(x)) and imaging parameters (ΘS) is encapsulated by the imaging equation as shown in Eqn. 1
| (1) |
For example, for the FLASH sequence, the imaging parameters are ΘFLASH = {TR,TE,α,G}, and the imaging equation is shown in Eqn. 2 (Glover, 2004):
| (2) |
Most pulse sequences do not have a closed form imaging equation and a Bloch simulation is needed to estimate the voxel intensity (Glover, 2004). There has been some work in deriving the imaging equation for MPRAGE (Deichmann et al., 2000; Wang et al., 2014). Unfortunately, these closed form equations do not always match the scanner implementation of the pulse sequence. Different scanner manufacturers and scanner software versions have different implementations of the same pulse sequence. Sometimes additional pulses like fat suppression are added to improve image quality, further deviating from the closed form theoretical equation. Therefore, if such a closed form theoretical imaging equation with known imaging parameters (from the image header) is applied to NMR maps ([ρ,T1,T2]) of a subject, the resulting synthetic image will systematically differ from the observed, scanner-acquired image. To mitigate this difference, we deem it essential to estimate the imaging parameters purely from the observed image intensities themselves. This way, when the imaging equation with the estimated parameters is applied to the NMR maps, we are likely to get a synthetic image that is close to the observed, scanner-acquired image. However, to enable estimation of imaging parameters purely from the image intensities requires us to approximate the closed form theoretical imaging equation to a much simpler form and with fewer parameters. Therefore, we do not expect the estimated parameters of an approximate imaging equation to match with the scanner parameters (such as TR or TE). The approximation of the imaging equation and its estimated parameters are deemed satisfactory if they produce intensities similar to an observed, scanner-acquired image, when applied to NMR maps. Our approximations of the theoretical closed form imaging equations for a number of commonly used pulse sequences are described next in Section 2.2.
2.2. Pulse Sequence Approximation and Parameter Estimation
In this work we primarily work with FLASH, MPRAGE, SPGR, and T2-SPACE images. Our goal is to be able to estimate the pulse sequence parameters ΘS from the intensity information of S. Intensity histograms of most pulse sequence images for the adult brain present peaks for the three main tissue classes in the brain: cerebro-spinal fluid (CSF), gray matter (GM), and white matter (WM). The mean class intensities can be robustly estimated by fitting a three-class Gaussian mixture model to the intensity histogram. Let Sc, Sg, Sw be the mean intensities of CSF, GM, and WM, respectively. Let βc, βg, βw be the mean NMR [ρ,T1,T2] values for CSF, GM, and WM classes, respectively. In this work, we extracted these values from a previously acquired dataset with relaxometry acquisitions (Fischl et al., 2004), but they could also have been obtained from previous studies (Wansapura et al., 1999). We assume that applying the pulse sequence equation ΓS to the mean class NMR values results in mean class intensities in S. This assumption leads to a three equation system as shown in Eqns. (3)–(5), where the unknown is ΘS:
| (3) |
| (4) |
| (5) |
To solve a three equation system, it is necessary that ΘS have three or fewer unknown parameters. From the FLASH imaging equation in Eqn. 2, it is clear that there are more than three unknowns (four, to be precise) in the closed form imaging equation, which is also true for most pulse sequences. Therefore, to enable us to solve the system in Eqns. (3)–(5), we formulate a three-parameter approximation for pulse sequences like FLASH, SPGR, MPRAGE, and T2-SPACE. Our approximation for the FLASH sequence is shown in Eqns. (6)–(8):
| (6) |
| (7) |
| (8) |
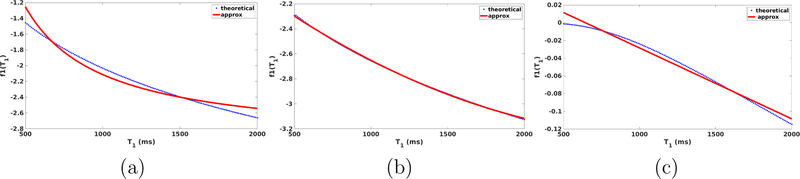
where ΘFLASH = {θ0,θ1,θ2} forms our parameter set. We assume that B1 inhomogeneities have been corrected from all images and therefore do not include them in the forward models. We replace by T2 as they are highly correlated quantities due to the relation . f1(T1) and f2(T2) in Eqn. 7 model the contribution of T1 and T2 components respectively to the voxel intensity. Figure 1(a) shows the theoretical f1(T1) and our approximation θ1/T1 for FLASH. For the range of values of T1 in the human brain (500,3000) ms at 1.5 T, our approximation fits f1(T1) well. The error increases for long T1 regions, which are generally CSF voxels in the brain, and relatively easy to segment. The SPGR pulse sequence is very similar to FLASH and so we use the same approximation for it (Glover, 2004).
Figure 1:
(a) Fit of T1 component in the FLASH equation (blue) and our approximation (red), (b) fit of T1 component (blue) with our approximation (red) for MPRAGE, (c) fit of T1 component (blue) with our approximation (red) for T2-SPACE
For the MPRAGE sequence, we chose to approximate a theoretical derivation provided by Wang et al. (2014). Assuming the echo time TE is small, which it typically is to avoid - induced loss, the effects in our approximation are not significant. Therefore, we use two parameters θ1 and θ2 to model a quadratic dependence on T1, which is an approximation of the derivation by Wang et al. (2014), resulting in Eqn. (9) as our three-parameter approximation for MPRAGE. Comparison with the theoretical dependence on T1 is shown in Fig. 1(b), and our approximation shows a very good fit.
| (9) |
T2-SPACE is a turbo spin echo sequence. The intensity produced at the nth echo of a turbo spin echo sequence is given by Eqn. 10:
| (10) |
where F ≈ 1 for a first order approximation (Glover, 2004), TD is the time interval between last echo and TR, and TEn is the nth echo time. Our three-parameter approximation for Eqn. 10 is given in Eqn. 11:
| (11) |
The comparison with the theoretical equation as shown in Fig. 1(c) shows good fit for T1 dependence for T1 values in the GM-WM range. The error increases for very short T1 (bone) and very long T1 (CSF) voxels. This has minimal impact on the segmentation accuracy as they have sufficient contrast to segment regardless of small deviations from the model.
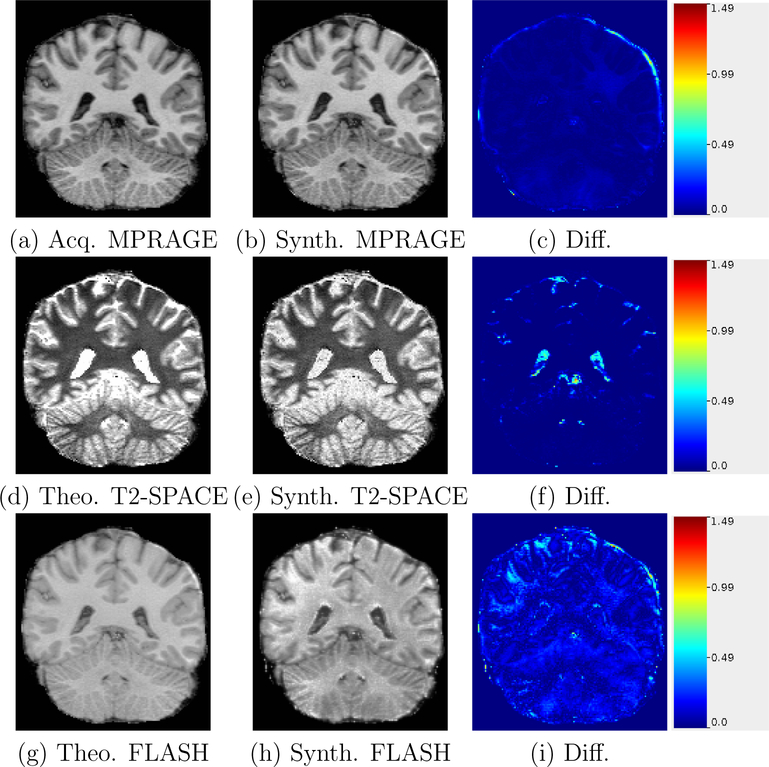
In Fig. 2(a) we show an acquired MPRAGE, Fig. 2(b) our approximately synthesized MPRAGE, and in Fig. 2(c), their absolute intensity difference image. Our MPRAGE approximate equation (Eqn. 9) is a close fit to the theoretical steady state Bloch equation and the synthesized MPRAGE has a very small image difference with the acquired MPRAGE.
Figure 2:
Acquired/theoretical equation generated images compared with approximate synthesis images used in PSACNN training. The difference images are shown in the right column. The color scale shows the absolute intensity difference ranges from 0 to 1.5, where the maximum intensity in the image is 1.5.
In Fig. 2(d) we show a T2-SPACE image synthesized by applying the theoretical steady state Bloch equation (Eqn. 11), Fig. 2(e) our approximately synthesized T2-SPACE, and in Fig. 2(f), their absolute intensity difference image. Our T2-SPACE approximate equation (Eqn. 11) is a close fit to the theoretical steady state Bloch equation for the gray-white matter T1 values. The difference image (Fig. 2(f)) also shows very small values in those regions. The fit errors increase (almost 30%) for CSF voxels, which is also visible in the difference image in the ventricle regions. However the image gradient between white matter and ventricles is still quite high in the Fig. 2(e) and the boundaries are therefore sharp, ensuring that the segmentation will not be much different than for the theoretical image in Fig. 2(f).
In Figs. 2(g)–(i), we show theoretical FLASH, approximate FLASH, and the difference image, respectively. The intensity differences are small for gray-white matter (except for a few outlier regions) but increase for CSF.
Our three-parameter approximations are such that the equation system in Eqns. (3)–(5) becomes linear in terms of ΘS and can be easily and robustly solved for each of the pulse sequences. The exact theoretical equations have more than three parameters, and even if they had fewer parameters, the exponential interaction of parameters with T1 and T2 renders solving the highly nonlinear system very unstable. Using our formulated approximate versions of pulse sequence equations, given any image S and the pulse sequence used to acquire it, we can estimate the three parameter set , denoted by hat to distinguish it from the unknown parameter set ΘS.
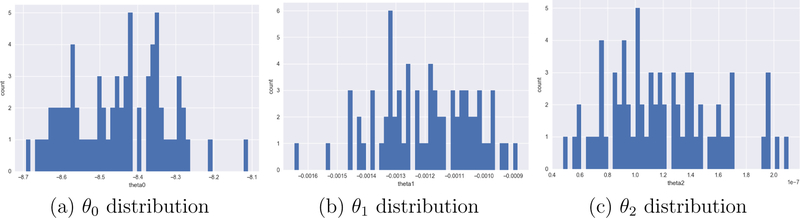
More importantly, the three-parameter [θ0,θ1,θ2] approximations establish a compact, 3-dimensional parameter space for a pulse sequence. Given any test image, its approximate pulse sequence parameter set is a point in this 3-dimesional parameter space, found by calculating the mean class intensities and solving the equation system in Eqns. (3)–(5). We estimated the parameter sets for a variety of test MPRAGE images acquired on 1.5 T and 3 T scanners from Siemens Trio/Vision/SONATA/Avanto/Prisma and GE Signa scanners using our method. The estimated parameter distributions are shown in Figs. 3(a)–3(c). These give us an idea of the range of parameter values and their distribution for the MPRAGE sequence. We use this information to grid the parameter space in 50 bins between [0.8min(θm), 1.2max(θm)] for m ∈ {0,1,2} such that any extant test dataset parameters are included in this interval and are close to a grid point. We create such a 3D grid for FLASH/SPGR and T2-SPACE as well. In Section 2.3 we describe PSACNN training that depends on sampling this grid to come up with candidate pulse sequence parameter sets. We will use these candidate parameter sets to create augmented, synthetic training images.
Figure 3:
Estimated MPRAGE parameters θ0, θ1, and θ2 distributions for a variety of 1.5 T and 3 T datasets from Siemens Trio/SONATA/Prisma/Avanto, GE Signa scanners.
2.3. PSACNN Training
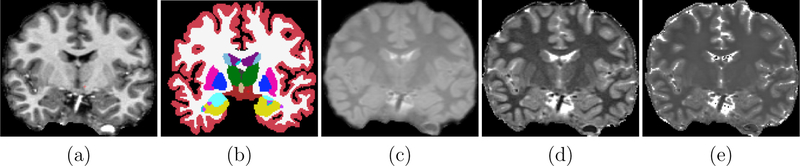
Let be a collection of M T1-w images with a corresponding expert manually labeled image set . The paired collection is referred to as the training image set. Let be acquired with a pulse sequence ΓA, where ΓA is typically MPRAGE that presents a good gray-white matter contrast. For PSACNN, we require that in addition to , we have the corresponding NMR parameter maps for each of the M training subjects. For each i ∈ {1,…,M} we have B(i) = [ρ(i),T1(i),T2(i)], where ρ(i) is a map of proton densities, and T1(i) and T2(i) store the longitudinal (T1), and transverse (T2) relaxation time maps respectively. Most training sets do not acquire or generate the NMR maps. In case they are not available, we outline an image synthesis procedure in Section 2.5 to generate these from available T1-w MPRAGE images A(i). Example images from are shown in Fig. 4.
Figure 4:
PSACNN training images for a training subject i: (a) Training MPRAGE (A(i)), (b) Training Label Image (Y(i)), (c) ρ(i) (PD) map, (d) T1(i), (e) T2(i).
We extract patches p(i)(x) of size 96 × 96 × 96 from voxels × of A(i). p(i)(x) is paired with a corresponding patch y(i)(x) extracted from the label image Y(i). Training pairs of [p(i)(x);y(i)(x)] constitute the unaugmented data used in training. A CNN trained on only available unaugmented patches will learn to segment images with the exact same contrast as the training MPRAGE images and will not generalize to test images of a different contrast. We use the approximate forward models of pulse sequences as described in Section 2.2 to generate synthetic images that appear to have been imaged by that pulse sequence.
Consider a pulse sequence ΓS, which could be MPRAGE, FLASH, SPGR, or T2-SPACE, for each of which we have established a three-parameter space. We uniformly sample the [θ0,θ1,θ2] grid that is created for ΓS as described in Section 2.2 to get a candidate set . Next, we extract 96 × 96 × 96-sized NMR parameter patches from where the NMR patch at voxel x is denoted by [ρ(i)(x),T1(i)(x),T2(i)(x)]. We create an augmented patch by applying the test pulse sequence equation ΓS, with the sampled pulse sequence parameter set , to training NMR patches as shown in Eqn. 12:
| (12) |
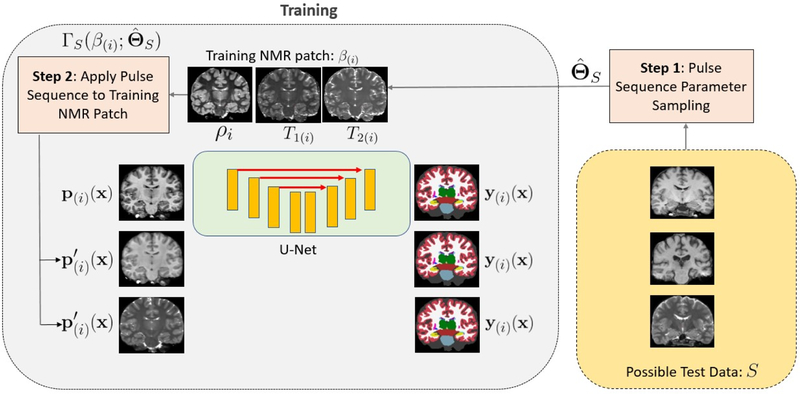
The synthetic patch therefore has the anatomy from the ith training subject, but the image contrast of a potential test pulse sequence ΓS with as its parameters, as shown in Fig. 5. The synthetic patch is paired with the corresponding label patch y(i)(x) extracted from Yi to create the augmented pair that is introduced in the training. The CNN, therefore, learns weights such that it maps both and p(i)(x) to the same label patch y(i)(x), in effect learning to be invariant to differences in image contrast. CNN weights are typically optimized by stochastic optimization algorithms that use mini-batches composed of training samples to update the gradients of the weights in a single iteration. In our training, we construct a mini-batch comprising four training samples: one sample of the original, unaugmented MPRAGE patch, and one each of synthetic FLASH/SPGR, synthetic T2-SPACE, and a synthetic MPRAGE patch. Each synthetic patch is generated with a parameter set chosen from the 3D parameter space grid of its pulse sequence (ΓS). Over a single epoch, we cover all parameter sets from the 3D parameter space grid of ΓS to train the CNN with synthetic patches that are mapped to the same label patch forcing it to learn invariance across different . Invariance across pulse sequences is achieved by including patches from all four pulse sequences in each mini-batch. The training workflow is presented in Fig. 5. On the right side of Fig. 5 are possible test images that were acquired by different pulse sequences. On the left side of Fig. 5 are the synthetic training images generated by applying the approximate pulse sequence equations to training NMR maps shown on the top center. All synthetic images are matched with the same label map at the output of the network. The patches are shown as 2D slices for the purpose of illustration.
Figure 5:
Workflow of PSACNN training.
2.4. PSACNN Network Architecture
We use the U-Net (Ronneberger et al., 2015) as our preferred voxel-wise segmentation CNN architecture, but any sufficiently powerful fully convolutional architecture can be used. Graphical processing unit (GPU) memory constraints prevent us from using entire 256 × 256 × 256-sized images as input to the U-Net and so we use 96 × 96 × 96-sized patches as inputs. Our U-Net instance (shown in Fig. 6) has five pooling layers and corresponding five upsampling layers. These parameters were constrained by the largest model size we could fit in the GPU memory. Prior to each pooling layer are two convolutional layers with filter size of 3 × 3 × 3, ReLu activation, and batch normalization after each of them. The number of filters in the first convolutional layers is 32, and it doubles after each pooling layer. The last layer has a softmax activation with L = 41 outputs. The U-Net is trained to minimize a soft Dice-based loss averaged over the whole batch. The loss is shown in Eqn. 13, where x denotes the voxels present in each label patch ytrue(b) and ypred(b) of the bth training sample in a batch of NB samples. During training ypred(b) is a 96 × 96 × 96 × L-sized tensor with each voxel recording the softmax probability of it belonging to a particular label. ytrue(b) is a similar-sized one-hot encoding of the label present at each of the voxels. The 4D tensors are flattened prior to taking element-wise dot products and norms.
| (13) |
The Dice loss in Eqn. 13 is an un-weighted Dice loss. Several methods have been developed to address the label imbalance in loss calculation for smaller subcortical region labels versus large white or gray matter labels. Relative frequency of labels (Roy et al., 2018) has been used as weights to scale the Dice-based loss while calculating it over a batch. Generalized dice loss (Sudre et al., 2017), exponential logarithmic loss (Wong et al., 2018), and others have also been used. However, in our experiments we did not observe a significant difference in predictions from networks trained using an un-weighted Dice loss versus a frequency-weighted Dice loss (Roy et al., 2018) after more than 10 epochs. For example, some of the smaller structures such as the left-right accumbens, fourth ventricle, etc. were not found at all by networks trained for fewer than 10 epochs with an un-weighted Dice loss, but were segmented correctly once it was trained for more than 10 epochs. These structures were detected in earlier epochs when using the frequency-weighted Dice loss but there were other gross segmentation errors that made further training necessary. We speculate that label imbalance plays a big role when learning rates are not set appropriately for a segmentation task and small labels are missed. For our setup, with an initial learning rate of 0.001, we did not observe a difference between weighted and un-weighted Dice loss and chose to use the un-weighted version to avoid any bias for the smaller labels.
Figure 6:
U-Net architecture used in PSACNN
We use the Adam optimization algorithm to minimize the loss. Each epoch uses 600K augmented and unaugmented training pairs extracted from a training set of 16 subjects out of a dataset with 39 subjects that were acquired with 1.5 T Siemens Vision MPRAGE acquisitions (TR=9.7 ms, TE=4 ms TI=20 ms, voxel-size=1 × 1 × 1.5 mm3) with expert manual labels done as per the protocol described by Buckner et al. (2004). We refer to this dataset as the Buckner dataset in the rest of the manuscript. After each training epoch, the trained model is a applied to a validation dataset that is generated from 3 of the remaining 23 (= 39 – 16) subjects. Training is stopped when the validation loss does not decrease any more, which is usually around 10 epochs. For prediction, we sample overlapping 96 × 96 × 96-sized patches from the test image with a stride of 32. We apply the trained network to these patches. The resultant soft predictions (probabilities) are averaged in the overlapping regions and the class with the maximum probability is chosen as the hard label at each voxel.
2.5. Synthesis of Training NMR Maps
As described in Section 2.3, PSACNN requires the training dataset to be the collection . But most training datasets only contain and do not acquire or estimate the NMR parameter maps . In this section, we will describe a procedure to synthesize maps from the available image set .
We use a separately acquired dataset of eight subjects, denoted as dataset , with multi echo FLASH (MEF) images with four flip angles 3°, 5°, 10°, and 20°. Proton density (ρ) and T1 maps were calculated by fitting the known imaging equation for FLASH to the acquired four images (Fischl et al., 2004). The ρ values are estimated up to a constant scale. Note that this dataset is completely distinct from the PSACNN training dataset with no overlapping subjects. For each subject j ∈ {1,…8} in , we first estimate the three mean tissue class intensities Sc, Sg, and Sw. We then estimate the MEF parameters using our approximation of the FLASH equation in Eqn. 8 and solving the equation system in Eqns. 3–5. Next, the voxel intensity SMEF (j)(x) for each voxel x, using the approximate FLASH imaging equation in Eqn. 8 and the estimated gives us Eqn. 14:
| (14) |
The only unknown in Eqn. 14 is T2(j)(x), which we can solve for. This forms for each subject in .
Next, we consider each of the PSACNN training images A(i) in . We use the approximate forward model of the ΓA sequence (typically MPRAGE) and the pulse sequence parameter estimation procedure in Section 2.2 to estimate ΓA imaging parameters for all PSACNN training images A(i). We use the estimated as parameters in the ΓA equation and apply it to the NMR maps BF of dataset as shown in Eqn. 15, to generate synthetic ΓA images of subjects in dataset .
| (15) |
For each PSACNN training image A(i), we have eight synthetic SsynA(j,i), j ∈ {1,…,8} of subjects in dataset with the same imaging parameter set and therefore, the same image contrast as A(i). We pair up the synthetic images and proton density maps to create a training dataset to estimate proton density map for subject i in the PSACNN training set. We extract 96 × 96 × 96-sized patches from the synthetic images and map them to patches from the proton density maps. A U-Net with specifications similar to that described in Section 2.3 is used to predict proton density patches from synthetic image patches, the only difference being the final layer that outputs 96 × 96 × 96 × 1-sized continuous valued output while minimizing the mean squared error loss. The trained U-Net is applied to patches extracted from A(i) to synthesize ρ(i). The image contrast of the synthetic ΓA images from dataset is the same as A(i).by design, which makes the training and test intensity properties similar and the trained U-Net can be applied correctly to patches from A(i). Two other similar image synthesis U-Nets are trained for synthesizing T1(i) and T2(i) from A(i). Thus, to estimate [ρ(i),T1(i),T2(i)] for subject i of the PSACNN training dataset, we need to train three separate U-Nets. In total, for M PSACNN training subjects, we need to train 3M U-Nets, which is computationally expensive, but a one-time operation to permanently generate the NMR maps that are necessary for PSACNN, from available images. It is possible to train only 3 U-Nets for all M images from as they have the exact same acquisition, however their estimated parameters are not exactly equal and have a small variance. Therefore, we chose to train 3 U-Nets per image to ensure subject-specific training. Our expectation is that generated NMR maps will be more accurate than those generated using a single U-Net per NMR parameter map for all subjects.
The training dataset (Buckner) cannot be shared due to Institutional Review Board requirements. The trained PSACNN network and the prediction script are freely available on the FreeSurfer development version repository on Github (https://github.com/freesurfer/freesurfer).
2.6. Application of PSACNN for 3 T MRI
Our training dataset of was obtained on a 1.5 T Siemens Vision scanner. The tissue NMR parameters, ρ, T1, T2 are different at 3 T field strength than 1.5 T. This might lead to the conclusion that it is not possible to create synthetic 3 T images during PSACNN augmentation as, in principle, we cannot apply 3 T pulse sequence imaging equations to 1.5 T NMR maps. Ideally, we would prefer to have a training dataset with maps at both 1.5 T and 3 T, which unfortunately is not available to us. However, our imaging equation approximations allow us to frame a 3 T imaging equation as a 1.5 T imaging equation with certain assumptions about the relationship between 1.5 T and 3 T NMR parameters. For instance, consider the FLASH approximate imaging equation in Eqn. 8. When estimating the imaging parameters of this equation, we construct an equation system (for 1.5 T in Eqn. 16, reframed as Eqn. 18), as described in Section 2.2. We assume that the 3 T FLASH sequence will have the same equation as the 1.5 T FLASH. This is a reasonable assumption because the sequence itself need not change with the field strength.
| (16) |
| (17) |
| (18) |
We can express the equation system for a 3 T pulse sequence in Eqn. 19, where B3 is 3×3-sized matrix similar to B1.5 in Eqn. 18, but with mean tissue NMR values at 3 T, which can be obtained from previous studies (Wansapura et al., 1999). It is possible to estimate a 3 × 3-sized matrix K, where B3 = B1.5K. K is given by, . Now, given a 3 T image, we first calculate the mean tissue intensities s. The ρ values are mean tissue proton density values and do not depend on field strength. Therefore, we can write Eqn. 19, that is similar to Eqn. 18. Substituting B3 in Eqn. 19, we get Eqn. 20 and reframe it as Eqn. 21.
| (19) |
| (20) |
| (21) |
Therefore, we can treat the parameters for 3 T (θ3) as linearly transformed (by K−1) parameters θ1.5. In essence, we can thus treat 3 T images as if they have been acquired with a 1.5 T scanner (with 1.5 T NMR tissue values) but with a parameter set θ3 = K−1θ1.5.
However, while applying a 3 T equation to 1.5 T NMR maps to generate a synthetic 3 T image, the above relationship of B3 = B1.5K implies a stronger assumption that [1,1/T1υ3,1/T2υ3]T = KT [1,1/T1υ1.5,1/T2υ1.5]T, where the [1,1/T1υ3,1/T2υ3] is a row vector with NMR values at any voxel υ at 3 T and [1,1/T1υ1.5,1/T2υ1.5] is a row vector of NMR values at 1.5 T for the same anatomy. K will have to be estimated using a least squares approach using all the 1.5 T and 3 T values at all voxels, which are not available to us. This linear relationship between 1.5 T and 3 T NMR parameters is likely not theoretically valid, but nevertheless works well in practice on healthy adult brain images as can be seen from empirical results presented in Section 3 and Figs. 3(a)–(c), where we can see the estimated parameters from a variety of 1.5 T and 3 T MPRAGE scans. These are restricted in a small enough range because the contrast changes for MPRAGE between 1.5 T and 3 T are not drastically different and a linear relationship between the two NMR vectors is likely a good enough approximation.
3. Experiments and Results
We evaluate the performance of PSACNN and compare it with unaugmented CNN (CNN), FreeSurfer segmentation (ASEG) (Fischl et al., 2002), SAMSEG (Puonti et al., 2016), and MALF (Wang et al., 2013). We divide the experiments into two halves. In the first half, described in Section 3.2, we evaluate segmentation accuracy as measured by Dice overlap on datasets with manual labels. In the second half, described in Section 3.3, we evaluate the segmentation consistency of all five algorithms. Segmentation consistency is evaluated by calculating the coefficient of variation of structure volumes for the same set of subjects that have been scanned at multiple sites/scanners or sequences.
3.1. Training Set and Pre-processing
As described in Section 2.4, we randomly chose a subset comprising 16 out of 39 subjects representing the whole age range from the Buckner dataset These subjects have 1.5 T Siemens Vision MPRAGE acquisitions and corresponding expert manual label images and were used as our training dataset for CNN, PSACNN, and as the atlas set for MALF. ASEG segmentation in FreeSurfer and SAMSEG are model-based methods that use a pre-built probabilistic atlas prior. The atlas priors for ASEG and SAMSEG are built from 39 and 20 subjects respectively, from the Buckner dataset.
For MALF, we use cross-correlation as the registration metric and the parameter choices specific to brain MRI segmentation and joint label fusion as suggested by the authors in (Wang et al., 2013).
For PSACNN, we use the same single trained network that is trained from real and augmented MPRAGE, FLASH, SPGR, and T2-SPACE patches of the 16-subject training data for all the experiments. We do not re-train it for a new test dataset or a new experiment.
All input images from the training and test datasets are brought into the FreeSurfer conformed space (resampled to isotropic 1×1×1 mm3) skullstripped and intensity inhomogeneity corrected (Sled et al., 1998) by the pre-processing stream of FreeSurfer (Fischl et al., 2004). The intensities are scaled such that they lie in the [0,1] interval.
For the unaugmented CNN specifically, we further standardize the input image intensities such that their white matter mean (as identified by fitting a Gaussian mixture model to the intensity histogram) is fixed to 0.8. The CNN results were significantly worse on multi scanner data without this additional scaling. We also tested using piece-wise linear intensity standardization (Nyúl and Udupa, 1999) on input images to the unaugmented CNN but the results were better for white matter mean standardization. There is no such scaling required for the other methods including PSACNN.
3.2. Evaluation of Segmentation Accuracy
We evaluate all algorithms in three settings, where the test datasets have varying degrees of acquisition differences with the training Buckner dataset. Specifically, where the test dataset is acquired by:
Same scanner (Siemens Vision), same sequence (MPRAGE) as the training dataset
Different scanner (Siemens SONATA), same sequence (MPRAGE with different parameters) as the training set.
Different scanner (GE Signa), different sequence (SPGR) as the training dataset.
3.2.1. Same Scanner, Same Sequence Input
In this experiment we compare the performance of segmentation algorithms on test data with the exact same acquisition parameters as the training data. The test data consists of 20 subject MPRAGEs from the Buckner data that are independent of the 16 subjects used for training and 3 for validation of the CNN methods.
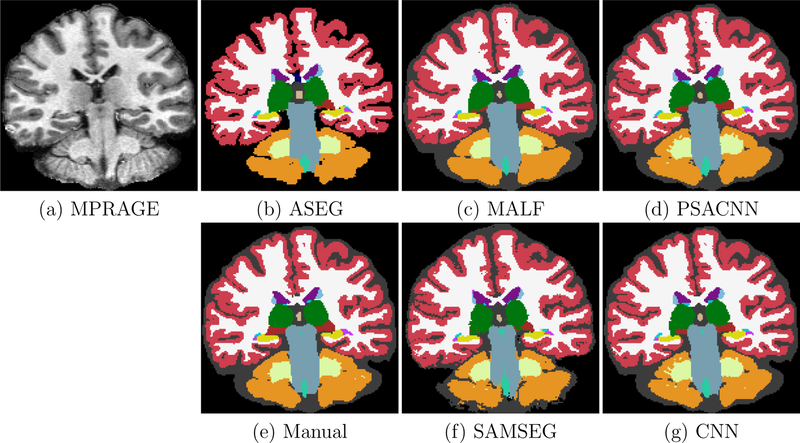
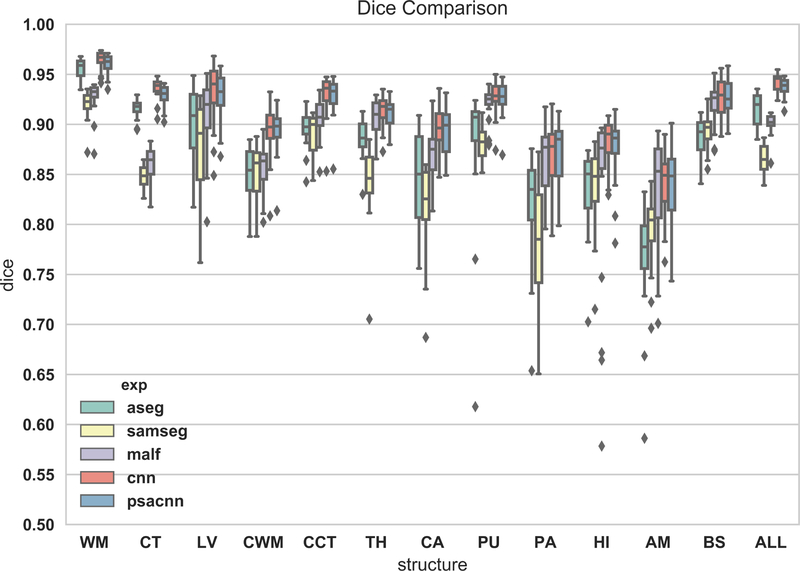
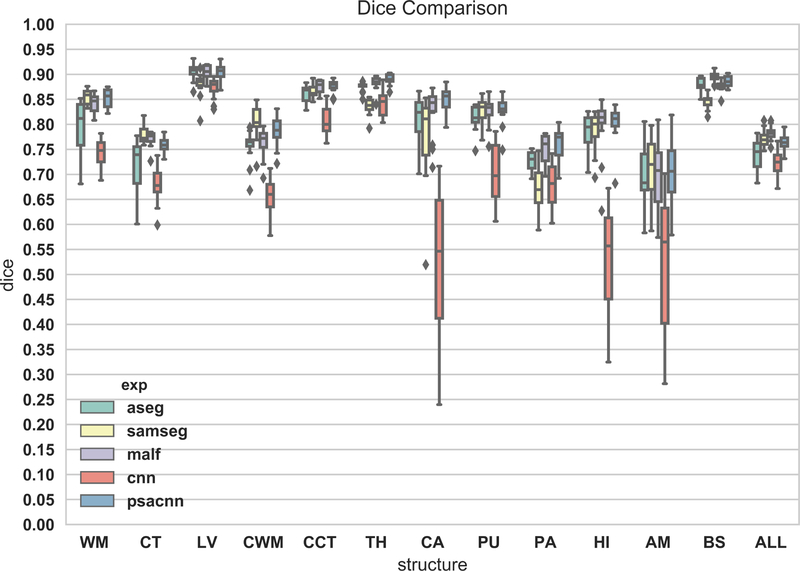
Figure 7 shows an example input test subject image, its manual segmentation, and segmentations of the various algorithms. All algorithms perform reasonably well on this dataset. We calculated the Dice coefficients of the labeled structures for all the algorithms (see Fig. 8). From the Dice coefficient boxplots (generated from 20 subjects) shown in Fig. 8 we observe that CNN (red) and PSACNN (blue) Dice overlap (ALL Dice = 0.9396) is comparable to each other and is significantly better (paired t-test p < 0.05) than ASEG (green), SAMSEG (yellow), and MALF (purple) for many of the subcortical structures, and especially for whole white matter (WM) and gray matter cortex (CT) labels. This suggests that large patch-based CNN methods do provide a more accurate segmentation than state-of-the-art approaches like MALF and SAMSEG for a majority of the labeled structures. But, since the training and test acquisition parameters are exactly same, there is no significant difference between CNN and PSACNN.
Figure 7:
Input Buckner MPRAGE with segmentation results from ASEG, SAMSEG, MALF, CNN, and PSACNN, along with manual segmentations.
Figure 8:
Dice coefficient boxplots of selected structures for all five methods on 20 subjects of the Buckner dataset. Acronyms: white matter (WM), cortex (CT), lateral ventricle (LV), cerebellar white matter (CWM), cerebellar cortex (CCT), thalamus (TH), caudate (CA), putamen (PU), pallidum (PA), hippocampus (HI), amygdala (AM), brain-stem (BS), overlap for all structures (ALL).
3.2.2. Different Scanner, Same Sequence Input
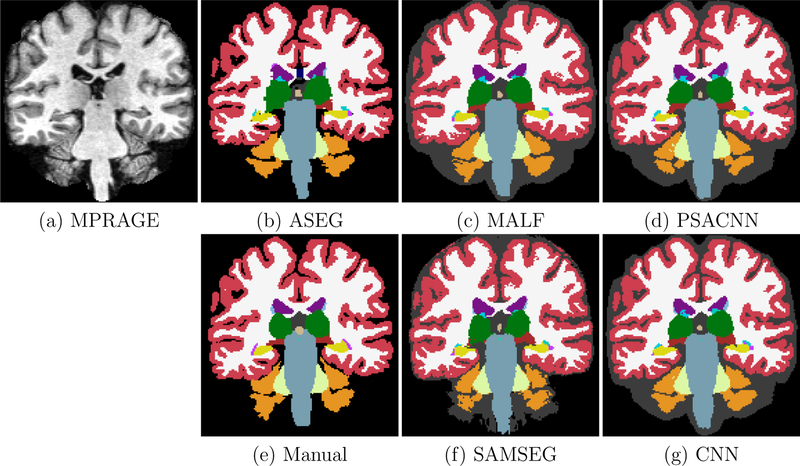
In this experiment we compare the accuracy of PSACNN against other methods on the Siemens13 dataset that comprises 13 subject MPRAGE scans acquired on a 1.5 T Siemens SONATA scanner with a similar pulse sequence as the training data. The Siemens13 dataset has expert manual segmentations generated with the same protocol as the training data (Buckner et al., 2004). Figure 9 shows the segmentation results for all the algorithms. The image contrast (see Fig. 9(a)) for the Siemens13 dataset is only slightly different from the training Buckner dataset. Therefore, all algorithms perform fairly well on this dataset. Figure 10 shows the Dice overlap boxplots calculated over 13 subjects. Similar to the previous experiment, the unaugmented CNN and PSACNN have a superior Dice overlap compared to other methods (statistically significantly better for five of the nine labels shown), but are comparable to each other as the test acquisition is not very different from the training acquisition.
Figure 9:
Input Siemens13 MPRAGE with segmentation results from ASEG, SAMSEG, MALF, CNN, and PSACNN, along with manual segmentations. Acronyms: white matter (WM), cortex (CT), lateral ventricle (LV), cerebellar white matter (CWM), cerebellar cortex (CCT), thalamus (TH), caudate (CA), putamen (PU), pallidum (PA), hippocampus (HI), amygdala (AM), brain-stem (BS), overlap for all structures (ALL).
Figure 10:
Dice evaluations on Siemens13 dataset. Acronyms: white matter (WM), cortex (CT), lateral ventricle (LV), cerebellar white matter (CWM), cerebellar cortex (CCT), thalamus (TH), caudate (CA), putamen (PU), pallidum (PA), hippocampus (HI), amygdala (AM), brain-stem (BS), overlap for all structures (ALL).
3.2.3. Different Scanner, Different Sequence Input
In this experiment we compare the accuracy of PSACNN against other methods on the GE14 dataset comprising 14 subjects scanned on a 1.5 T GE Signa scanner with the SPGR (spoiled gradient recalled) sequence (TR = 35 ms, TE = 5 ms, α = 45°, voxel size=0.9375 × 0.9375 × 1.5 mm3). All the subjects have expert manual segmentations generated with the same protocol as the training data, but the manual labels are visibly different than training data, with a much thicker cortex (Fig. 11(e)). This is likely because the GE14 SPGR scans (Fig. 11(a)) present a noticeably different GM-WM image contrast than the MPRAGE training data. Consequently, as seen in Fig. 12, all methods show a reduced overlap, but the unaugmented CNN (red boxplot) has the worst performance of all as it is unable to generalize to an SPGR sequence (despite white matter peak intensity standardization). Some obvious CNN errors are for small subcortical structures such as hippocampus (yellow in Fig. 11(g)) labeled as thalamus (green label). PSACNN (ALL Dice=0.7636) on the other hand, is robust to the contrast change due to pulse sequencebased augmentation, and produces segmentations that are comparable to the state-of-the-art algorithms such as SAMSEG (ALL Dice=0.7708) and MALF (ALL Dice=0.7804) in accuracy, with 1–2 orders of magnitude lower processing time.
Figure 11:
Input GE14 SPGR with segmentation results from ASEG, SAMSEG, MALF, CNN, and PSACNN, along with manual segmentations.
Figure 12:
Dice evaluations on GE14 dataset. Acronyms: white matter (WM), cortex (CT), lateral ventricle (LV), cerebellar white matter (CWM), cerebellar cortex (CCT), thalamus (TH), caudate (CA), putamen (PU), pallidum (PA), hippocampus (HI), amygdala (AM), brain-stem (BS), overlap for all structures (ALL).
3.3. Evaluation of Segmentation Consistency
The experiments described in Section 3.2 demonstrate that PSACNN is a highly accurate segmentation algorithm and better or comparable to the state-of-the-art segmentation algorithms. In this section, we evaluate the segmentation consistency of all algorithms on three distinct multi-scanner/multi-sequence datasets.
3.3.1. Four Scanner Data
In this experiment we tested the consistency of the segmentation produced by the various methods on four datasets acquired from 13 subjects;
MEF: 3D Multi-echo FLASH, scanned on Siemens Trio 3 T scanner, voxel-size 1×1×1.33 mm3, sagittal acquisition, TR=20 ms, TE=1.8+1.82n ms, flip angle 30°.
TRIO: 3D MPRAGE, scanned on Siemens Trio 3 T scanner, voxel-size 1 × 1 × 1.33 mm3, sagittal acquisition, TR=2730 ms, TE=3.44 ms, TI=1000 ms, flip angle 7°.
GE: 3D MPRAGE, scanned on GE Signa 1.5 T scanner, voxel-size 1 × 1 × 1.33 mm3, sagittal acquisition, TR=2730 ms, TE=3.44 ms, TI=1000 ms, flip angle 7°.
Siemens: 3D MPRAGE, scanned on Siemens Sonata 1.5 T scanner, voxel-size 1×1×1.33 mm3, sagittal acquisition, TR=2730 ms, TE=3.44 ms, TI=1000 ms, flip angle 7°.
For each structure l in each subject, we calculated the standard deviation (σl) of the segmented label volume over all datasets. We divided this by the mean of the structure volume (μl) for that subject, over all the datasets. This gives us , the coefficient of variation for structure l for each subject. In Table 1, we calculated the mean coefficient of variation (in %) over the 13 subjects in the Four Scanner Dataset. The lower the coefficient of variation, the more consistent is the segmentation algorithm in predicting the structure volume across multi-scanner datasets. From Table 1, we can observe that PSACNN has the lowest coefficient of variation in five of the nine structures and is the second lowest in three others. In the structures where PSACNN has the lowest coefficient of variation, it is statistically significantly lower (p < 0.05, Wilcoxon signed rank test) than the third placed method, but not the second-placed method. SAMSEG has the lowest coefficient of variation for CA (caudate) and LV (lateral ventricle), whereas MALF is the lowest for HI (hippocampus) and AM (amygdala).
Table 1:
Mean (and std. dev.) of the coefficient of variation (in %) of structure volumes over all four datasets with all algorithms.
| ASEG | SAMSEG | MALF | CNN | PSACNN | |
|---|---|---|---|---|---|
| Mean (Std) | Mean (Std.) | Mean (Std) | Mean (Std.) | Mean (Std.) | |
| WM | 11.02 (7.19) | 2.46 (2.14) | 3.21 (1.23) | 17.27 (3.83) | 1.99 (1.19) |
| CT | 5.10 (3.75) | 3.16 (1.30) | 2.13 (0.73) | 7.21 (2.95) | 1.81 (1.30) |
| TH | 3.72 (1.49) | 2.13 (0.62) | 1.12 (0.55) | 6.08 (7.13) | 1.05 (0.62) |
| CA | 3.76 (2.10) | 1.04 (1.47) | 2.42 (1.50) | 18.62 (11.05) | 2.15 (1.04) |
| PU | 7.42 (2.03) | 2.99 (0.86) | 2.03 (0.95) | 10.70 (4.16) | 1.05 (0.86) |
| PA | 5.22 (3.32) | 8.52 (4.45) | 3.83 (2.44) | 5.04 (3.37) | 3.11 (4.45) |
| HI | 3.18 (1.23) | 2.45 (0.95) | 1.46 (0.88) | 16.28 (10.21) | 1.47 (0.54) |
| AM | 5.27 (2.20) | 2.09 (1.09) | 1.99 (1.19) | 14.37 (6.75) | 2.16 (0.98) |
| LV | 5.61 (6.53) | 3.12 (5.90) | 4.72 (6.26) | 10.40 (6.98) | 4.58 (6.72) |
Bold results show the minimum coefficient of variation.
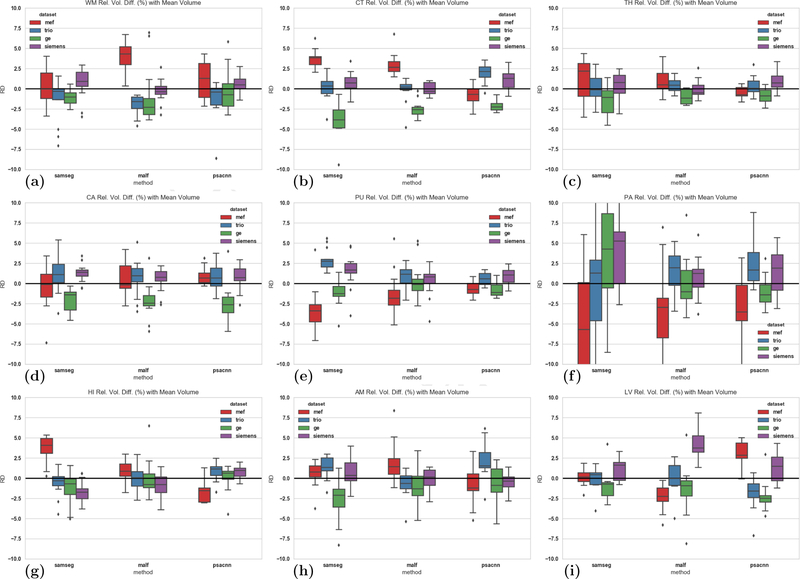
Next, we calculated the signed relative difference of structure volume estimated for a particular dataset with respect to the mean structure volume across all four datasets and show them as boxplots in Fig. 13 (MEF in red, TRIO in blue, GE in green, Siemens in purple.). Ideally, a segmentation algorithm would have zero bias and would produce the exact same segmentation for different acquisitions of the same subject. But the lower the bias, the more consistent is the algorithm across different acquisitions. Figures 13(a)–(i) show the relative difference for each of the nine structures for SAMSEG, MALF, PSACNN. There is a small, statistically significant bias (difference from zero, thick black line) for most structures and algorithms, which suggests that there is a scope for further improvement for all algorithms. The relative differences also give us an insight into which datasets show the most difference from the mean, a fact that is lost when the coefficient of variation is calculated.
Figure 13:
Signed relative difference of volumes of (a) WM, (b) CT, (c) TH, (d) CA, (e) PU, (f) PA, (g) HI, (h) AM, (i) LV from mean structure volume over all four datasets. Left group of boxplots shows SAMSEG, middle shows MALF, right-most shows PSACNN. The colors denote different datasets, MEF (red), TRIO (blue), GE (green), Siemens (purple)
PSACNN results for a majority of the structures (Fig. 13(a), Fig. 13(c), for example) show lower median bias (< 2.5%), lower standard deviation, and fewer outliers. MALF has lower bias when segmenting HI (Fig. 13(g)), AM (Fig. 13(h)), whereas SAMSEG has better consistency when segmenting the LV structure (Fig. 13(i)). MEF uses a different pulse sequence than all the other datasets that have MPRAGE sequences. For most structures and algorithms shown in Fig. 13, we observe that MEF shows the maximum relative volume difference from the mean (red boxplot in Figs. 13(a), (b) for example). The Siemens acquisitions(TRIO in blue and Siemens in purple) show similar consistency to each other despite the differences in field strength (3 T vs 1.5 T).
3.3.1. Four Scanner Data
In this experiment we tested the consistency of the segmentation produced by the various methods on four datasets acquired from 13 subjects;
MEF: 3D Multi-echo FLASH, scanned on Siemens Trio 3 T scanner, voxel-size 1×1×1.33 mm3, sagittal acquisition, TR=20 ms, TE=1.8+1.82n ms, flip angle 30°.
TRIO: 3D MPRAGE, scanned on Siemens Trio 3 T scanner, voxel-size 1 × 1 × 1.33 mm3, sagittal acquisition, TR=2730 ms, TE=3.44 ms, TI=1000 ms, flip angle 7°.
GE: 3D MPRAGE, scanned on GE Signa 1.5 T scanner, voxel-size 1 × 1 × 1.33 mm3, sagittal acquisition, TR=2730 ms, TE=3.44 ms, TI=1000 ms, flip angle 7°.
Siemens: 3D MPRAGE, scanned on Siemens Sonata 1.5 T scanner, voxel-size 1×1×1.33 mm3, sagittal acquisition, TR=2730 ms, TE=3.44 ms, TI=1000 ms, flip angle 7°.
For each structure l in each subject, we calculated the standard deviation (σl) of the segmented label volume over all datasets. We divided this by the mean of the structure volume (μl) for that subject, over all the datasets. This gives us , the coefficient of variation for structure l for each subject. In Table 1, we calculated the mean coefficient of variation (in %) over the 13 subjects in the Four Scanner Dataset. The lower the coefficient of variation, the more consistent is the segmentation algorithm in predicting the structure volume across multi-scanner datasets. From Table 1, we can observe that PSACNN has the lowest coefficient of variation in five of the nine structures and is the second lowest in three others. In the structures where PSACNN has the lowest coefficient of variation, it is statistically significantly lower (p < 0.05, Wilcoxon signed rank test) than the third placed method, but not the second-placed method. SAMSEG has the lowest coefficient of variation for CA (caudate) and LV (lateral ventricle), whereas MALF is the lowest for HI (hippocampus) and AM (amygdala).
Next, we calculated the signed relative difference of structure volume estimated for a particular dataset with respect to the mean structure volume across all four datasets and show them as boxplots in Fig. 13 (MEF in red, TRIO in blue, GE in green, Siemens in purple.). Ideally, a segmentation algorithm would have zero bias and would produce the exact same segmentation for different acquisitions of the same subject. But the lower the bias, the more consistent is the algorithm across different acquisitions. Figures 13(a)–(i) show the relative difference for each of the nine structures for SAMSEG, MALF, PSACNN. There is a small, statistically significant bias (difference from zero, thick black line) for most structures and algorithms, which suggests that there is a scope for further improvement for all algorithms. The relative differences also give us an insight into which datasets show the most difference from the mean, a fact that is lost when the coefficient of variation is calculated.
PSACNN results for a majority of the structures (Fig. 13(a), Fig. 13(c), for example) show lower median bias (< 2.5%), lower standard deviation, and fewer outliers. MALF has lower bias when segmenting HI (Fig. 13(g)), AM (Fig. 13(h)), whereas SAMSEG has better consistency when segmenting the LV structure (Fig. 13(i)). MEF uses a different pulse sequence than all the other datasets that have MPRAGE sequences. For most structures and algorithms shown in Fig. 13, we observe that MEF shows the maximum relative volume difference from the mean (red boxplot in Figs. 13(a), (b) for example). The Siemens acquisitions(TRIO in blue and Siemens in purple) show similar consistency to each other despite the differences in field strength (3 T vs 1.5 T).
3.3.2. Multi-TI Three Scanner Data
In this experiment we tested the segmentation consistency of PSACNN on a more extensive dataset collected at the University of Oslo. The dataset consists of 24 subjects, each scanned on three Siemens scanners, Avanto, Skyra, and Prisma, with the MPRAGE sequence and two inversion times (TI)–850 ms and 1000 ms. The dataset descriptions in detail are as follows:
A850: 3D MPRAGE, scanned on Siemens Avanto 1.5 T scanner, voxel-size 1.25 × 1.25×1.2 mm3, sagittal acquisition, TR=2400 ms, TE=3.61 ms, TI=850 ms, flip angle 8°.
A1000: 3D MPRAGE, scanned on Siemens Avanto 1.5 T scanner, voxel-size 1.25 × 1.25 × 1.2 mm3, sagittal acquisition, TR=2400 ms, TE=3.61 ms, TI=1000 ms, flip angle 8°.
S850: 3D MPRAGE, scanned on Siemens Skyra 3 T scanner, voxel-size 1 × 1 × 1 mm3, sagittal acquisition, TR=2300 ms, TE=2.98 ms, TI=850 ms, flip angle 8°.
S1000: 3D MPRAGE, scanned on Siemens Skyra 3 T scanner, voxel-size 1 × 1 × 1 mm3, sagittal acquisition, TR=2400 ms, TE=2.98 ms, TI=1000 ms, flip angle 8°.
P850: 3D MPRAGE, scanned on Siemens Prisma 3 T scanner, voxel-size 1×1×1 mm3, sagittal acquisition, TR=2400 ms, TE=2.22 ms, TI=850 ms, flip angle 8°
P1000: 3D MPRAGE, scanned on Siemens Prisma 3 T scanner, voxel-size 0.8×0.8×0.8 mm3, sagittal acquisition, TR=2400 ms, TE=2.22 ms, TI=1000 ms, flip angle 8°
We calculate the coefficient of variation of structure volumes across these six datasets similar to our experiment in Section 3.3.1, and are shown in Table 2. From Table 2 we can observe that PSACNN structure volumes have the lowest coefficient of variation for six of the nine structures. For WM, TH, PA, and HI structures PSACNN coefficient of variation is significantly lower than the next best method (p < 0.05 using the paired Wilcoxon signed rank test). SAMSEG is significantly lower than MALF for the CT structure. As compared to Table 1 the coefficients of variation are lower as the input MPRAGE sequences are the preferred input for all of these methods (except SAMSEG).
Table 2:
Mean (and std. dev.) of the coefficient of variation (in %) of structure volumes over all six datasets with all algorithms.
| ASEG | SAMSEG | MALF | CNN | PSACNN | |
|---|---|---|---|---|---|
| Mean (Std) | Mean (Std.) | Mean (Std) | Mean (Std.) | Mean (Std.) | |
| WM | 2.82 (0.71) | 3.06 (0.92) | 2.30 (0.80) | 6.01 (0.98) | 1.91 (0.70)* |
| CT | 2.68 (0.67) | 1.42 (0.77)* | 1.80 (0.82) | 4.57 (1.37) | 1.85 (0.70) |
| TH | 3.70 (1.32) | 1.93 (0.72) | 1.37 (0.59) | 3.38 (1.35) | 0.85 (0.60)* |
| CA | 2.02 (0.60) | 2.38 (1.31) | 1.80 (1.05) | 1.68 (1.33) | 1.68 (0.85) |
| PU | 2.62 (1.22) | 2.88 (1.78) | 1.24 (0.74) | 3.08 (1.13) | 1.27 (0.86) |
| PA | 4.67 (2.50) | 2.10 (2.29) | 2.65 (1.41) | 5.69 (1.41) | 1.17 (0.56)* |
| HI | 2.48 (0.78) | 2.23 (3.54) | 1.99 (1.60) | 6.31 (2.08) | 1.00 (0.41)* |
| AM | 6.50 (1.79) | 2.44 (2.42) | 1.93 (1.28) | 3.87 (1.28) | 1.54 (0.56) |
| LV | 2.00 (0.82) | 2.33 (1.36) | 2.66 (2.38) | 5.94 (1.87) | 2.21 (0.86) |
Bold results show the minimum coefficient of variation.
indicates significantly lower (p < 0.05, using the paired Wilcoxon signed rank test) coefficient of variation than the next best method.
In Figs. 14(a)–(i) we show the mean (over 24 subjects) signed relative volume difference (in %) with the mean structure volume averaged over all six acquisition for nine structures. We focus on SAMSEG, MALF, and PSACNN for this analysis. The boxplot colors denote different datasets, A850 (red), P850 (blue), S850 (green), A1000 (purple), P1000 (orange), S1000 (yellow). There is a small, statistically significant bias (difference from 0, thick black line) for most structures and algorithms. The bias is much smaller than that observed in Fig. 13 for the Four Scanner Dataset. PSACNN results for a majority of the structures (for example, Figs. 14(a), (c), (d), (f)) show lower median (< 2.5%), lower standard deviation, and fewer outliers. MALF has lower bias when segmenting, CT (14(b)), whereas SAMSEG has better consistency when segmenting the LV structure (14(i)).
Figure 14:
Signed relative difference of volumes of (a) WM, (b) CT, (c) TH, (d) CA, (e) PU, (f) PA, (g) HI, (h) AM, (i) LV from mean structure volume over all four datasets. In each figure, left group of boxplots shows SAMSEG, middle shows MALF, right-most shows PSACNN. The colors denote different datasets, A850 (red), P850 (blue), S850 (green), A1000 (purple), P1000 (orange), S1000 (yellow).
From Fig. 14(a), which shows the relative volume difference for WM–which can act as an indicator of the gray-white contrast present in the image–we can see that for all methods, images from same scanner, regardless of TI, show similar relative volume differences. The WM relative volume difference for A850 is most similar to A1000, and similarly for the Prisma and Skyra datasets. For PSACNN, this pattern exists for other structures such as CA, PA, PU, HI, AM, LV as well. This suggests that change in the image contrast due to change in the inversion time TI from 850 ms to 1000 ms, has a smaller effect on PSACNN segmentation consistency than a change of scanners (and field strengths).
3.3.3. MPRAGE and T2-SPACE Segmentation
In this experiment we use the same trained PSACNN network to segment co-registered MPRAGE and T2-SPACE acquisitions for 10 subjects that were acquired in the same imaging session. The acquisition details for both the sequences are as follows:
MPRAGE: 3D MPRAGE, scanned on Siemens Prisma 3 T scanner, voxel-size 1×1×1 mm3, sagittal acquisition, TR=2530 ms, TE=1.69 ms, TI=1250 ms, flip angle 7°.
T2-SPACE: 3D T2-SPACE, scanned on Siemens Prisma 3 T scanner, voxel-size 1×1×1 mm3, sagittal acquisition, TR=3200 ms, TE=564 ms, flip angle 120°.
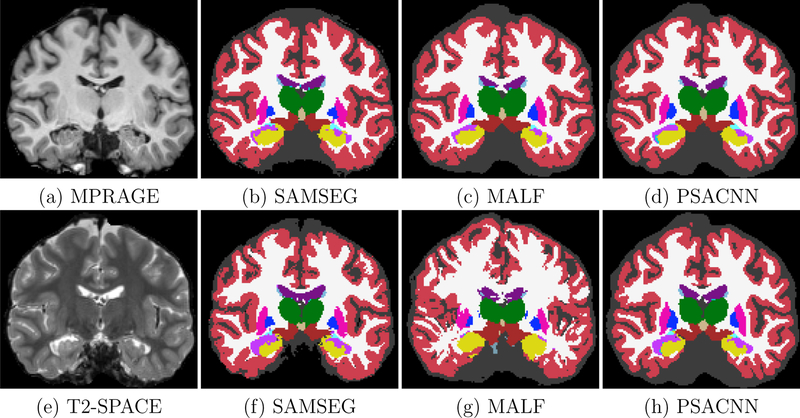
Figures 15(a)–(i) show the input MPRAGE and T2-SPACE images with their corresponding segmentations by SAMSEG, MALF, and PSACNN. ASEG and CNN are not built or trained for non-T1-w images so we did not use them for comparison. We calculated the unsigned relative volume difference of structures segmented for the T2-SPACE dataset with the same on the MPRAGE dataset. Table 3 shows the unsigned relative volume difference for a subset of the structures. PSACNN shows the minimum unsigned relative volume difference for six of the nine structures, with significantly better performance for subcortical structures including TH, CA, PU, and HI. SAMSEG has significantly lower volume difference for PA and LV. All algorithms shows a large volume difference for lateral ventricles (LV). The LV has a complex geometry with a long boundary and a segmentation one-two voxels inside or outside the LV of the MPRAGE image can cause a large relative volume difference. Synthetic T2-SPACE images generated in the PSACNN augmentation can match the overall image contrast with the real T2-SPACE images, however we believe the intensity gradient from white matter (dark) to CSF (very bright) is not accurately matched to the intensity gradient in the real, test T2-SPACE images, possibly due to resolution differences in the training and test data. This points to avenues of potential improvement in PSACNN augmentation. MALF (Fig. 15(c) and Fig. 15(g)) shows a diminished performance despite using a cross-modal registration metric like cross-correlation in the ANTS registration between the T1-w atlas images and the T2-w target images.
Figure 15:
Input (a) MPRAGE and (e) T2-SPACE images with segmentations by SAMSEG (b) and (f), MALF (c) and (g), and PSACNN (d) and (h)
Table 3:
Mean (and std. dev.) of the unsigned relative volume difference (in %) of structure volumes for T2-SPACE dataset with respect to MPRAGE dataset.
| SAMSEG | MALF | PSACNN | |
|---|---|---|---|
| Mean (Std) | Mean (Std.) | Mean (Std) | |
| WM | 5.20 (2.38) | 5.01 (2.74) | 3.74 (1.30) |
| CT | 8.22 (1.04) | 2.98 (2.16) | 2.95 (1.42) |
| TH | 7.71 (2.72) | 13.60 (6.13) | 4.22 (2.17)* |
| CA | 9.15 (2.66) | 34.51 (13.23) | 3.98 (2.72)* |
| PU | 5.31 (1.99) | 10.60 (7.92) | 2.48 (1.57)* |
| PA | 2.85 (1.70)* | 42.36 (15.01) | 13.35 (10.12) |
| HI | 14.17 (5.82) | 30.12 (12.14) | 3.18 (2.05)* |
| AM | 12.46 (4.50) | 10.49 (4.48) | 10.69 (4.42) |
| LV | 16.44 (5.93)* | 41.92 (47.89) | 25.83 (7.13) |
Bold results show the minimum unsigned relative difference.
indicates significantly lower (p < 0.05, using the paired Wilcoxon signed rank test) unsigned relative volume difference than the next best method.
Since these two acquisitions were co-registered, we can calculate the Dice overlap between MPRAGE and T2-SPACE labeled structures, as shown in Table 4. As we can observe, PSACNN shows a significantly higher overlap than the next best method on six of the nine structures, and tying with SAMSEG for thalamus (TH). SAMSEG shows a significantly higher overlap for PA and LV.
Table 4:
Mean (and std. dev.) of the Dice coefficient for structures of T2-SPACE dataset with respect to MPRAGE dataset.
| SAMSEG | MALF | PSACNN | |
|---|---|---|---|
| Mean (Std) | Mean (Std.) | Mean (Std) | |
| WM | 0.91 (0.01) | 0.57 (0.01) | 0.94 (0.00)* |
| CT | 0.85 (0.01) | 0.59 (0.00) | 0.89 (0.01)* |
| TH | 0.92 (0.01) | 0.80 (0.03) | 0.92 (0.01) |
| CA | 0.88 (0.01) | 0.65 (0.04) | 0.90 (0.00)* |
| PU | 0.88 (0.02) | 0.71 (0.05) | 0.91 (0.02)* |
| PA | 0.89 (0.02)* | 0.71 (0.03) | 0.81 (0.05) |
| HI | 0.84 (0.04) | 0.60 (0.03) | 0.88 (0.02)* |
| AM | 0.83 (0.03) | 0.65 (0.06) | 0.88 (0.01)* |
| LV | 0.90 (0.03)* | 0.63 (0.10) | 0.87 (0.03) |
Bold results show the maximum Dice coefficient.
indicates significantly higher (p < 0.05, using the paired Wilcoxon signed rank test) Dice than the next best method.
The PSACNN network is trained jointly on T1-w + T2-w synthetic examples, as described in Section 2.3. We also observe that performance of a jointly trained PSACNN network on T2-SPACE images is not significantly different than a network trained on purely T2-w synthetic examples, as long as they are exposed to the same number of synthetic T2-w training examples. The average Dice (over all the labels) for a pure T2-w-trained network on T2-SPACE data from 10 subjects with respect to T1-w + T2-w trained network was 0.982 (std. dev. 0.02). This suggests that addition of synthetic T1-w examples in training does not affect the T2-SPACE segmentation accuracy.
4. Conclusion and Discussion
We have described PSACNN, which uses a new strategy for training CNNs for the purpose of consistent whole brain segmentation across multi-scanner and multi-sequence MRI data. PSACNN shows significant improvement over state-of-the-art segmentation algorithms in terms accuracy based on our experiments on multiple manually labeled datasets acquired with different acquisition settings as shown in Section 3.2.
For modern large, multi-scanner datasets, it is imperative for segmentation algorithms to provide consistent outputs on a variety of differing acquisitions. This is especially important when imaging is used to quantify the efficacy of a drug in Phase III of its clinical trials. Phase III trials are required to be carried out in hundreds of centers with access to a large subject population across tens of countries (Murphy and Koh, 2010), where accurate and consistent segmentation across sites is critical. The pulse sequence parameter estimation based augmentation strategy in training PSACNN allows us to train the CNN for a wide range of input pulse sequence parameters, leading to a CNN that is robust to input variations. In Section 3.3, we compared the variation in structure volumes obtained via five segmentation algorithms for a variety of T1-weighted (and T2-weighted) inputs and PSACNN showed the highest consistency among all for many of the structures, with many structures showing less than 1% coefficient of variation. Such consistency enables detection of subtle changes in structure volumes in cross-sectional (healthy vs. diseased) and longitudinal studies, where variation can occur due to scanner and protocol upgrades.
PSACNN training includes augmented, synthetic MRI images generated by approximate forward models of the pulse sequences. Thus, as long as we can model the pulse sequence imaging equation, we can include multiple pulse sequence versions of the same anatomy in the augmentation and rely on the representative capacity of the underlying CNN architecture (U-Net in our case) to learn to map all of them to the same label map in the training data. We formulated approximate forward models of pulse sequences to train a network that can simultaneously segment MPRAGE, FLASH, SPGR, and T2-SPACE images consistently. Moreover, the NMR maps used in PSACNN need not perfectly match maps acquired using relaxometry sequences. They merely act as parameters that when used in our approximate imaging equation accurately generate the observed image intensities.
Recently image augmentation using domain adaptation methods has been used in training CNNs. These domain adaptation methods have been primarily driven by variants of generative adversarial networks (GAN) Goodfellow et al. (2014). These include domain transfer network Taigman et al. (2016), pix2pix Isola et al. (2016), CycleGAN Zhu et al. (2017), StarGAN Choi et al. (2018), and many others that take images from a source domain and synthesize them in a target domain and include them in the training. In contrast, PSACNN synthesis essentially creates images from a wide range of domains and introduces them to the deep network in order for the network to be robust to differences in these domains. The deep domain adaptation methods need to model and learn the distributions that generate the source and target images and hence they require a large number of images in both the domains for training. In contrast, PSACNN needs only a single image from a target domain in order to estimate its pulse sequence equation and apply it to the training NMR parameters and synthesize training images that appear to be from the target domain.
Being a CNN-based method, PSACNN is 2–3 orders of magnitude faster than current state-of-the-art methods such as MALF and SAMSEG. On a system with an NVidia GPU (we tested Tesla K40, Quadro P6000, P100, V100) PSACNN completes a segmentation for a single volume within 45 seconds. On a single thread CPU, it takes about 5 minutes. SAMSEG and MALF take 15–30 minutes if they are heavily multi-threaded. On a single thread SAMSEG takes about 60 minutes, whereas MALF can take up to 20 hours. Pre-processing for PSACNN (inhomogeneity correction, skullstripping) can take up to 10—15 minutes, whereas SAMSEG does not need any pre-processing. With availability of training NMR maps of whole head images, PSACNN will be able to drop the time consuming skullstripping step. A fast, consistent segmentation method like PSACNN considerably speeds up neuroimaging pipelines that traditionally take hours to completely process a single subject.
PSACNN in its present form has a number of limitations we intend to work on in the future. The current augmentation does not include matching resolutions of the training and test data. This is the likely reason for overestimation of lateral ventricles in the T2-SPACE segmentation, as the training data and the synthetic T2-SPACE images generated from them have a slightly lower resolution than the test T2-SPACE data. Acquiring higher resolution training dataset with relaxometry sequences for ground truth PD, T1, and T2 values will also help. Our pulse sequence models are approximate and can be robustly estimated. However, we do not account for any errors in the pulse sequence parameter estimation and the average NMR parameters. A probabilistic model that models these uncertainties to further make the estimation robust is a future goal. The pulse sequence parameter estimation also assumes the same set of parameters across the whole brain. It does not account for local differences, for example variation in the flip angle with B1 inhomogeneities.
PSACNN currently uses 96×96×96-sized patches to learn and predict the segmentations. This is a forced choice due to limitations in the GPU memory. However, using entire images would require significantly more training data than 20–40 labeled subjects. It is unknown how such a network would handle unseen anatomy. Further, it will be interesting to extend PSACNN to handle pathological cases involving tumors and lesions.
In conclusion, we have described PSACNN, a fast, pulse sequence resilient whole brain segmentation approach. The code has been made available as a part of the FreeSurfer development version repository (https://github.com/freesurfer/freesurfer). Further validation and testing will need to be carried out before its release.
Acknowledgments
Support for this research was provided in part by the BRAIN Initiative Cell Census Network grant U01MH117023, the National Institute for Biomedical Imaging and Bioengineering (P41EB015896, 1R01EB023281, R01EB006758, R21EB018907, R01EB019956), the National Institute on Aging (5R01AG008122, R01AG016495), the National Institute of Mental Health the National Institute of Diabetes and Digestive and Kidney Diseases (1-R21-DK-108277–01), the National Institute for Neurological Disorders and Stroke (R01NS0525851, R21NS072652, R01NS070963, R01NS083534, 5U01NS086625,5U24NS10059103, R01NS105820), and was made possible by the resources provided by Shared Instrumentation Grants 1S10RR023401, 1S10RR019307, and 1S10RR023043. Additional support was provided by the NIH Blueprint for Neuroscience Research (5U01-MH093765), part of the multi-institutional Human Connectome Project. In addition, BF has a financial interest in CorticoMetrics, a company whose medical pursuits focus on brain imaging and measurement technologies. BF’s interests were reviewed and are managed by Massachusetts General Hospital and Partners HealthCare in accordance with their conflict of interest policies. This project has also received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skodowska-Curie grant agreement No 765148, Danish Council for Independent Research under grant number DFF-6111–00291, and NIH: R21AG050122 National Institute on Aging.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Asman AJ, Landman BA, 2012. Formulating spatially varying performance in the statistical fusion framework. IEEE TMI 31, 1326–1336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bazin PL, Pham DL, 2008. Homeomorphic brain image segmentation with topological and statistical atlases. Medical Image Analysis 12, 616–625. Special issue on the 10th international conference on medical imaging and computer assisted intervention - MICCAI 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckner R, Head D, et al. , 2004. A unified approach for morphometric and functional data analysis in young, old, and demented adults using automated atlas-based head size normalization: reliability and validation against manual measurement of total intracranial volume. NeuroImage 23, 724–738. [DOI] [PubMed] [Google Scholar]
- Choi Y, Choi M, Kim M, Ha JW, Kim S, Choo J, 2018. Stargan: Unified generative adversarial networks for multi-domain image-to-image translation, in: The IEEE Conference on Computer Vision and Pattern Recognition (CVPR) [Google Scholar]
- Coupé P, Manjn JV, Fonov V, Pruessner J, Robles M, Collins DL, 2011. Patch-based segmentation using expert priors: Application to hippocampus and ventricle segmentation. NeuroImage 54, 940–954. [DOI] [PubMed] [Google Scholar]
- Davatzikos C, Shen D, Gur R, et al. , 2005. Whole-brain morphometric study of schizophrenia revealing a spatially complex set of focal abnormalities. Archives of General Psychiatry 62, 1218–1227. [DOI] [PubMed] [Google Scholar]
- Deichmann R, Good CD, Josephs O, Ashburner J, Turner R, 2000. Optimization of 3-D MP-RAGE sequences for structural brain imaging. NeuroImage 12, 112–127. [DOI] [PubMed] [Google Scholar]
- Desbordes G, Neg L, Pace T, Wallace B, Raison C, Schwartz E, 2012. Effects of mindful-attention and compassion meditation training on amygdala response to emotional stimuli in an ordinary, non-meditative state. Frontiers in Human Neuroscience 6, 292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischl B, Salat DH, et al. , 2002. Whole brain segmentation: Automated labeling of neuroanatomical structures in the human brain. Neuron 33, 341–355. [DOI] [PubMed] [Google Scholar]
- Fischl B, Salat DH, van der Kouwe AJ, et al. , 2004. Sequence-independent segmentation of magnetic resonance images. NeuroImage 23, S69–S84. [DOI] [PubMed] [Google Scholar]
- Focke N, Helms G, Kaspar S, Diederich C, Tth V, Dechent P, Mohr A, Paulus W, 2011. Multi-site voxel-based morphometry not quite there yet. NeuroImage 56, 1164–1170. [DOI] [PubMed] [Google Scholar]
- Frisoni GB, Prestia A, Zanetti O, Galluzzi S, Romano M, Cotelli M, Gennarelli M, Binetti G, Bocchio L, Paghera B, Amicucci G, Bonetti M, Benussi L, Ghidoni R, Geroldi C, 2009. Markers of alzheimer’s disease in a population attending a memory clinic. Alzheimer’s and Dementia 5, 307–317. [DOI] [PubMed] [Google Scholar]
- Glover GH, 2004. Handbook of MRI pulse sequences volume 18 Elsevier Academic Press. [Google Scholar]
- Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, Bengio Y, 2014. Generative adversarial nets, in: Advances in neural information processing systems, pp. 2672–2680. [Google Scholar]
- Han X, Jovicich J, Salat D, et al. , 2006. Reliability of MRI-derived measurements of human cerebral cortical thickness: The effects of field strength, scanner upgrade and manufacturer. NeuroImage 32, 180–194. [DOI] [PubMed] [Google Scholar]
- He K, Zhang X, Ren S, Sun J, 2016. Deep residual learning for image recognition, in: The IEEE Conference on Computer Vision and Pattern Recognition (CVPR) [Google Scholar]
- Heckemann RA, Hajnal JV, Aljabar P, Rueckert D, Hammers A, 2006. Automatic anatomical brain mri segmentation combining label propagation and decision fusion. NeuroImage 33, 115–126. [DOI] [PubMed] [Google Scholar]
- Isola P, Zhu JY, Zhou T, Efros AA, 2016. Image-to-image translation with conditional adversarial networks. arxiv [Google Scholar]
- Jack CR, Barkhof F, Bernstein MA, Cantillon M, Cole PE, DeCarli C, Dubois B, Duchesne S, Fox NC, Frisoni GB, Hampel H, Hill DL, Johnson K, Mangin JF, Scheltens P, Schwarz AJ, Sperling R, Suhy J, Thompson PM, Weiner M, Foster NL, 2011. Steps to standardization and validation of hippocampal volumetry as a biomarker in clinical trials and diagnostic criterion for alzheimers disease. Alzheimer’s and Dementia 7, 474–485.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jog A., Carass A., Ro S., Pha DL., Prince JL., 2015. MR image synthesis by contrast learning on neighborhood ensembles. MedIA 24, 63–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jog A, Fischl B, 2018. Pulse sequence resilient fast brain segmentation, in: Medical Image Computing and Computer-Assisted Intervention - MICCAI 2018 – 21st International Conference, Proceedings, Springer Verlag. [Google Scholar]
- Jovicich J, et al. , 2013. Brain morphometry reproducibility in multi-center 3T MRI studies: A comparison of cross-sectional and longitudinal segmentations. NeuroImage 83, 472–484. [DOI] [PubMed] [Google Scholar]
- Karani N, Chaitanya K, Baumgartner C, Konukoglu E, 2018. A lifelong learning approach to brain MR segmentation across scanners and protocols. arXiv preprint arXiv:1805.10170 [Google Scholar]
- Kostro D, Abdulkadir A, Durr A, Roos R, Leavitt BR, Johnson H, Cash D, Tabrizi SJ, Scahill RI, Ronneberger O, Klppel S, 2014. Correction of inter-scanner and within-subject variance in structural mri based automated diagnosing. NeuroImage 98, 405–415. [DOI] [PubMed] [Google Scholar]
- van der Kouwe AJ, Benner T, Salat DH, Fischl B, 2008. Brain morphometry with multiecho mprage. NeuroImage 40, 559–569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landman BA, Warfield SK, 2012. MICCAI 2012 workshop on multi-atlas labeling, in: Medical Image Computing and Computer Assisted Intervention Conference 2012: MICCAI 2012 Grand Challenge and Workshop on Multi-Atlas Labeling Challenge Results [Google Scholar]
- Li W, Wang G, Fidon L, Ourselin S, Cardoso MJ, Vercauteren T, 2017. On the compactness, efficiency, and representation of 3D convolutional networks: Brain parcellation as a pretext task, in: IPMI [Google Scholar]
- Madabhushi A, Udupa JK, 2006. New methods of MR image intensity standardization via generalized scale. Med. Phys 33, 3426–3434. [DOI] [PubMed] [Google Scholar]
- Mattsson N, on behalf of the Alzheimers Disease Neuroimaging Initiative, Tosun D, on behalf of the Alzheimers Disease Neuroimaging Initiative, Insel PS, on behalf of the Alzheimers Disease Neuroimaging Initiative, Simonson A, on behalf of the Alzheimers Disease Neuroimaging Initiative, Jack CR Jr, on behalf of the Alzheimers Disease Neuroimaging Initiative, Beckett LA, on behalf of the Alzheimers Disease Neuroimaging Initiative, Donohue M, on behalf of the Alzheimers Disease Neuroimaging Initiative, Jagust W, on behalf of the Alzheimers Disease Neuroimaging Initiative, Schuff N, on behalf of the Alzheimers Disease Neuroimaging Initiative, Weiner MW, on behalf of the Alzheimers Disease Neuroimaging Initiative, 2014. Association of brain amyloid- with cerebral perfusion and structure in alzheimers disease and mild cognitive impairment. Brain 137, 1550–1561.24625697 [Google Scholar]
- Mueller SG., Weiner MW., Thal LJ., Petersen RC., Jack C., Jagust W., Trojanowski JQ., Toga AW., Beckett L., 2005. The Alzheimer’s disease neuroimaging initiative. Neuroimaging Clin. N. Am 15, 869–877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mugler JP, 2014. Optimized three-dimensional fast-spin-echo MRI. Journal of Magnetic Resonance Imaging 39, 745–767. [DOI] [PubMed] [Google Scholar]
- Mugler JP, Brookeman JR, 1990. Three-dimensional magnetization-prepared rapid gradient-echo imaging (3D MPRAGE). Mag. Reson. Med 15, 152–157. [DOI] [PubMed] [Google Scholar]
- Murphy P, Koh DM, 2010. Imaging in clinical trials. Cancer Imaging 10, S74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nyúl LG, Udupa JK, 1999. On standardizing the MR image intensity scale. Mag. Reson. Med 42, 1072–1081. [DOI] [PubMed] [Google Scholar]
- Patenaude B, Smith SM, Kennedy DN, Jenkinson M, 2011. A Bayesian model of shape and appearance for subcortical brain segmentation. NeuroImage 56, 907–922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pizer SM, Fletcher PT, Joshi S, Thall A, Chen JZ, Fridman Y, Fritsch DS, Gash AG, Glotzer JM, Jiroutek MR, Lu C, Muller KE, Tracton G, Yushkevich P, Chaney EL, 2003. Deformable m-reps for 3d medical image segmentation. Int. J. Comput. Vision 55, 85–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pohl KM, Fisher J, Grimson WEL, Kikinis R, Wells WM, 2006. A Bayesian model for joint segmentation and registration. NeuroImage 31, 228–239. [DOI] [PubMed] [Google Scholar]
- Puonti O, Iglesias JE, Leemput KV, 2016. Fast and sequence-adaptive whole-brain segmentation using parametric Bayesian modeling. NeuroImage 143, 235–249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Resnick SM, Goldszal AF, Davatzikos C, Golski S, Kraut MA, Metter EJ, Bryan R, Zonderman A, 2000. One-year Age Changes in MRI Brain Volumes in Older Adults. Cerebral Cortex 10, 464–472. [DOI] [PubMed] [Google Scholar]
- Rohlfing T, Brandt R, Menzel R, Maurer CR, 2004. Evaluation of atlas selection strategies for atlas-based image segmentation with application to confocal microscopy images of bee brains. NeuroImage 21, 1428–1442. [DOI] [PubMed] [Google Scholar]
- Ronneberger O, Fischer P, Brox T, 2015. U-net: Convolutional networks for biomedical image segmentation, in: MICCAI 2015, pp. 234–241. [Google Scholar]
- Roy AG, Conjeti S, Navab N, Wachinger C, 2018. Quicknat: Segmenting MRI neuroanatomy in 20 seconds. CoRR abs/1801.04161 1801.04161. [Google Scholar]
- Roy S, Carass A, Prince JL, 2013. Magnetic resonance image example-based contrast synthesis. Medical Imaging, IEEE Transactions on 32, 2348–2363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sabuncu MR, Yeo BTT, Leemput KV, Fischl B, Golland P, 2010. A generative model for image segmentation based on label fusion. IEEE Transactions on Medical Imaging 29, 1714–1729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shiee N, et al. , 2010. A topology-preserving approach to the segmentation of brain images with Multiple Sclerosis lesions. NeuroImage 49, 1524–1535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sled JG, Zijdenbos AP, Evans AC, 1998. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Trans. Med. Imag 17, 87–97. [DOI] [PubMed] [Google Scholar]
- Sudre CH, Li W, Vercauteren T, Ourselin S, Jorge Cardoso M, 2017. Generalised dice overlap as a deep learning loss function for highly unbalanced segmentations, in: Cardoso MJ, Arbel T, Carneiro G, Syeda-Mahmood T, Tavares JMR, Moradi M, Bradley A, Greenspan H, Papa JP, Madabhushi A, Nascimento JC, Cardoso JS, Belagiannis V, Lu Z (Eds.), Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support, Springer International Publishing, Cham: pp. 240–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taigman Y, Polyak A, Wolf L, 2016. Unsupervised cross-domain image generation. CoRR abs/1611.02200 1611.02200. [Google Scholar]
- Thompson PM, Stein JL, et al. , the Alzheimer’s Disease Neuroimaging Initiative, EPIGEN Consortium, IMAGEN Consortium, Saguenay Youth Study (SYS) Group, 2014. The ENIGMA consortium: large-scale collaborative analyses of neuroimaging and genetic data. Brain Imaging and Behavior 8, 153–182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wachinger C, Reuter M, Klein T, 2017. DeepNAT: Deep convolutional neural network for segmenting neuroanatomy. NeuroImage [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H, Suh JW, Das SR, Pluta JB, Craige C, Yushkevich PA, 2013. Multi-atlas segmentation with joint label fusion. IEEE Transactions on Pattern Analysis and Machine Intelligence 35, 611–623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, He L, Zheng H, Lu ZL, 2014. Optimizing the magnetization-prepared rapid gradient-echo (MP-RAGE) sequence. PloS one 9, e96899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wansapura JP, Holland SK, Dunn RS, Ball WS, 1999. NMR relaxation times in the human brain at 3.0 Tesla. Jrnl of Mag. Reson. Imaging 9, 531–538. [DOI] [PubMed] [Google Scholar]
- Wong KCL, Moradi M, Tang H, Syeda-Mahmood T, 2018. 3d segmentation with exponential logarithmic loss for highly unbalanced object sizes, in: Frangi AF, Schnabel JA, Davatzikos C, Alberola-López C, Fichtinger G (Eds.), Medical Image Computing and Computer Assisted Intervention – MICCAI 2018, Springer International Publishing, Cham: pp. 612–619. [Google Scholar]
- Wu G, Wang Q, Zhang D, Nie F, Huang H, Shen D, 2014. A generative probability model of joint label fusion for multi-atlas based brain segmentation. Medical Image Analysis 18, 881–890. Sparse Methods for Signal Reconstruction and Medical Image Analysis. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu JY., Park T., Isola P., Efros AA., 2017. Unpaired image-to-image translation using cycle-consistent adversarial networks, in: Computer Vision (ICCV), 2017 IEEE International Conference on [Google Scholar]
- Zikic D, Glocker B, Criminisi A, 2014. Encoding atlases by randomized classification forests for efficient multi-atlas label propagation. Medical Image Analysis 18, 1262–1273. Special Issue on the 2013 Conference on Medical Image Computing and Computer Assisted Intervention. [DOI] [PubMed] [Google Scholar]