TRActs Constrained by UnderLying INfant Anatomy (TRACULInA): An Automated Probabilistic Tractography Tool with Anatomical Priors for Use in the Newborn Brain

Abstract

The ongoing myelination of white-matter fiber bundles plays a significant role in brain development. However, reliable and consistent identification of these bundles from infant brain MRIs is often challenging due to inherently low diffusion anisotropy, as well as motion and other artifacts. In this paper we introduce a new tool for automated probabilistic tractography specifically designed for newborn infants. Our tool incorporates prior information about the anatomical neighborhood of white-matter pathways from a training data set. In our experiments, we evaluate this tool on data from both full-term and prematurely born infants and demonstrate that it can reconstruct known white-matter tracts in both groups robustly, even in the presence of differences between the training set and study subjects. Additionally, we evaluate it on a publicly available large data set of healthy term infants (UNC Early Brain Development Program). This paves the way for performing a host of sophisticated analyses in newborns that we have previously implemented for the adult brain, such as pointwise analysis along tracts and longitudinal analysis, in both health and disease.

1. Introduction

Robust and reproducible tools for studying normal brain development and early brain injury from neuroimaging data are of great interest. During the later stages of pregnancy and the early neonatal period the brain is developing very rapidly and is also very vulnerable to injury [1, 2]. Myelination is a critical component of brain development. Myelin serves to insulate the axonal membranes and accelerate impulse conduction, which is vital to motor and cognitive processes [3]. During the second trimester of pregnancy and in the early months of postnatal life, myelination progresses rapidly in a specific sequence, advancing from central to peripheral, inferior to superior, and posterior to anterior [4]. Diffusivity and anisotropy measures extracted from diffusion MRI (dMRI) scans are sensitive indicators of changes in tissue microstructure and have been proposed as biomarkers for characterizing various processes of normal or atypical brain development, including myelination, pre-myelination, and white matter (WM) injury [5–8].

While diffusivity maps extracted from dMRI data are often used in clinical practice, their interpretation is typically qualitative. This allows WM abnormalities to be identified, but not to be localized reliably within specific WM pathways. Robust and automated methods for reconstructing WM pathways in infants are crucial for enhancing the clinical analysis of diffusion measures, both in characterizing normal development and in understanding injury to the neonatal brain. For this reason, there is great interest in tractography algorithms that can reconstruct WM pathways from dMRI data. Manually labeled deterministic tractography has been used to characterize abnormal development of the corticospinal tract associated with preterm birth [2], congenital heart disease [9], and other perinatal neurologic conditions such as congenital hemiparesis [10]. Other potential applications range from acute brain injury in the setting of perinatal hypoxic ischemic injury [11] and inborn errors of metabolism [12], to developmental abnormalities such as dyslexia [13]. Although it is possible to average diffusion measures within manually drawn regions of interest (ROIs) inside each pathway [4], reconstructing the pathways with the aid of an automated tractography algorithm reduces operator bias and increases reproducibility [2, 14].

In studies of the adult brain, most of the methods that have been proposed for delineating WM pathways involve seeding a local (a.k.a. streamline) tractography algorithm in every voxel of the brain and then isolating the streamlines that correspond to a specific WM pathway. In the multi-ROI approach, a number of different ROIs are drawn manually and the tractography streamlines that pass through all ROIs are identified [15, 16]. Most methods that eliminate manual labeling either attempt to automate the multi-ROI method by warping the ROIs from a template space into each subject’s individual space [17–19], or use an automated algorithm to cluster whole-brain tractography streamlines based on their similarity and identify the clusters that correspond to specific tracts by comparing them to an atlas [20–25]. We have developed a method for automated reconstruction of WM pathways that differs from both the multi-ROI and the clustering approach, as it uses global tractography and incorporates prior information about the anatomical neighborhood of the WM pathways in the tractography step itself, rather than in a post hoc labeling step [26].

The methods described above rely on information and atlases specific to adult brain scans. Our own automated tractography method has been applied to children as young as 4.5 years of age [27, 28] and the anatomical segmentation on which it relies has been shown to be accurate in the same age range [29]. However, due to large changes in brain morphology during infancy, as well as the ongoing myelination that leads to a gradual reversal of MRI contrast, it is extremely challenging to establish accurate point-to-point correspondence between adult atlases and an infant brain. The concurrent pruning of connections, which affects the coherence of axon bundles, as well as the greater partial volume effects due to the small brain size, further complicate the analysis of infant data. Thus infant-specific methods and atlases are unquestionably necessary to extend any automated segmentation and tractography tools to the early postnatal brain.

Even if an infant-specific atlas were introduced, methods designed for the processing of adult brains would not be guaranteed to perform well in infant brains. For example, the low anisotropy of infant WM can confound local tractography methods -- which grow a WM pathway step-by-step, using the diffusion orientation one voxel at a time -- and can thus force them to stop prematurely or take wrong turns. Therefore, even if ROIs were warped to the individual from an infant atlas, there may not be any streamlines recovered that satisfy all the rules defined by inclusion and exclusion ROIs. Due to the different rates of myelination of different pathways, a multi-ROI approach may work for some pathways but not others. As a result, even as tools for automated trac- tography have been developed for adult brains, their applications to infant data have been rare. To date, most tractography studies in infants have relied on manual labeling (e.g., the studies reviewed in [30], as well as more recent studies [31–38]). The majority of studies have focused on the corticospinal tract [32, 38–48] and the corpus callosum [33, 34, 38, 43, 45–54], some have studied the thalamic [33, 40–42, 51, 55] or optic radiations [36, 43, 48, 56–59], while other pathways have been studied much less frequently [30].

One approach to semi-automated labeling of WM bundles that has been used to study infant cohorts in health and disease [60–68] does so on an average brain. This approach, implemented in the UNC-Utah NA-MIC framework [69], relies on a set of manually selected pathways of interest in a study-specific template reference coordinate frame. These are used to initialize the definition of WM tracts, which are then refined interactively. Among the few studies that have attempted to automate the segmentation of WM in infants in individual space, one study performed a volumetric segmentation instead of tractography, assigning one or more labels to each WM voxel given the tensor at that voxel and an atlas [45]; one study transformed seed voxels from a template brain to each individual to reconstruct a small number of tracts [47]; and one study performed manual labeling of tracts in a set of subjects and then computed an average volumetric label for each tract to map to other subjects [48].

In this work, we propose a fully automated method for global probabilistic tractography with anatomical priors by adapting the framework of our previously proposed algorithm [26] to the infant brain. Unlike local tractography, which uses the local diffusion orientation in a single voxel to determine in which direction to grow a WM pathway, global tractography fits the shape of the pathway using the diffusion orientations over its entire trajectory. For this reason, global tractography is not sensitive to a localized region of high uncertainty or low anisotropy (e.g., a crossing or lesion) somewhere along the pathway and it does not stop prematurely, as it models the entire trajectory of the pathway as a curve between two end regions. Furthermore, our anatomical priors encode only the relative positions (anterior, posterior, etc.) of each WM pathway with respect to its surrounding anatomical structures. We do not rely on exact spatial alignment between the study and training subjects; we only assume that the main WM pathways, such as the corpus callosum, uncinate fasciculus, etc., go through the same broad anatomical areas of anatomy in all subjects. This is in contrast with multi-ROI techniques, where the ROIs define absolute coordinates that the pathways must go through in a template space, and therefore require highly accurate registration of individuals to that space.

The main goals of this work are to show the feasibility of reconstructing 14 major WM pathways automatically in full-term and pre-term newborns with our approach, and to investigate the robustness of the approach to differences between the training and test data. Our contributions are as follows: (1) We develop a training data set that consists of WM pathways labeled manually in dMRI data of full-term and pre-term newborns. (2) We introduce an infant-specific, automated processing stream for skull-stripping and segmentation of T₁-weighted images. (3) We integrate the elements above into a fully automated dMRI processing pipeline that includes pre-processing and global probabilistic tractography with infant-specific anatomical priors. (4) We demonstrate that our automated tractography method is robust to differences between test and training subjects, and specifically that it can be applied to data from different acquisition sites and different subject populations than the data included in the training set. (5) Finally, we investigate the robustness of our approach to errors in the anatomical segmentation or in the registration of individuals to template space.

2. Methods

2.1. Infant data sets

We use two sets of infant MRI data, both to build our training data set of manually labeled tracts, and to test our automated tractography. For a concise summary of the demographic and imaging information, see Table 1.

Table 1:

Demographic data of neonates. (F = female; M = male; GA = gestational age; cGA = corrected GA; w = weeks; d = days; full =full-term, pre = pre-term; ICV = intracranial volume; BCH = Boston Children’s Hospital; MC = Marseille Conception; MN = Marseille Nord.)

Subject	Sex	GA at birth	Postnatal age at MRI (cGA) (days)	Group	ICV (mm3)	Scanner	Center
Subj001	F	38 w 3 d	15 d (40 w 4 d)	full	340165	Siemens 3T	BCH1
Subj002	M	41 w	44 d (47 w 3 d)	full	461331	Siemens 3T	BCH1
Subj003	M	37 w	28 d (41 w 0 d)	full	343537	Siemens 3T	BCH1
Subj004	F	39 w 6 d	1 d (40 w 0 d)	full	336347	Siemens 3T	BCH2
Subj005	F	37 w 5d	2 d (38 w 0 d)	full	297390	Siemens 3T	BCH2
Subj006	M	39 w	22 d (42 w 1 d)	full	426657	Siemens 3T	BCH1
Subj007	F	39 w 4 d	18 d (42 w 1 d)	full	369386	Siemens 3T	BCH1
Subj008	F	40 w 5 d	3 d (41 w 1 d)	full	335964	Siemens 3T	BCH2
Subj009	M	39 w	4 d (39 w 4 d)	full	332852	Siemens 3T	BCH2
Subj010	F	40 w 5 d	4 d (41 w 2 d)	full	389807	Siemens 3T	BCH2
Subj011	M	28 w	86 d (40 w 2 d)	pre	430307	Siemens 1.5T	MC
Subj012	F	28 w	91 d (41 w 0 d)	pre	352977	Philips 3T	Reims
Subj013	F	31 w	60 d (39 w 4d)	pre	374415	Philips 3T	Reims
Subj014	M	28 w 6 d	91 d (41 w 6 d)	pre	305587	Siemens 1.5T	MN
Subj015	M	27 w 5 d	97 d (41 w 4 d)	pre	396077	Siemens 1.5T	MN
Subj016	F	26 w	96 d (39 w 5 d)	pre	354192	Siemens 1.5T	MC
Subj017	M	28 w 1 d	86 d (40 w 3 d)	pre	360933	Siemens 1.5T	MN
Subj018	F	31 w	69 d (40 w 6 d)	pre	353388	Philips 3T	Reims
Subj019	F	29 w 2 d	82 d (41 w 0 d)	pre	378923	Philips 3T	Reims
Subj020	F	26 w 3 d	104 d (41 w 2 d)	pre	345970	Siemens 1.5T	MC
Subj021	F	30 w 6 d	68 d (40 w 4d)	pre	338848	Philips 3T	Reims
Subj022	F	24 w 4 d	132 d (43 w 3 d)	pre	308913	Siemens 1.5T	MC
Subj023	F	27 w 2 d	72 d (37 w 4 d)	pre	339572	Siemens 1.5T	MC

2.1.1. Demographics

Full-term infants: (a) BCH1: We retrospectively selected brain images of 5 full-term newborns (4F, 1M) scanned on a 3 Tesla magnet at Boston Children’s Hospital (BCH) between 2009 and 2012. All the MRI studies were clinically indicated. To be included in the study, the subject’s brain had to be considered structurally normal by both the attending pediatric neuroradiologist responsible for the exam as well as the pediatric neuroradiologist in our research team (PG). As a common event in the post delivery period, extracranial hematomas were not considered significant abnormalities to exclude the subject. The study was approved by the Committee on Clinical Investigation at BCH. (b) BCH2: Five healthy, full-term infants (2F, 3M) were selected from a cohort recruited at the Brigham and Women’s Hospital (BWH) and Beth Israel Deaconess Medical Center (BIDMC) as part of a prospective data collection study between 2014–2017. The protocol was reviewed and approved by the institutional review boards at BCH, BWH and BIDMC. Written consent was obtained from parents. Only full-term neonates whose mothers had no known medical conditions or complications during pregnancy were included in the study. Pre-term infants: Thirteen subjects (9F, 4M) were selected from a prospective cohort study on a subsample of children born prematurely and otherwise included in the French national cohort EPIPAGE2 (http://epipage2.inserm.fr/index.php/en/), including a total number of 581 children. Participation in the study was voluntary and the study complied with the rights of children and families. The competent Patient Protection Committee approved this study on June 28, 2011 and the recruitment period ran from July 19, 2011, to October 31, 2012. Children for this study were recruited during their hospitalization in the neonatology unit and all survivors were enrolled for longitudinal full cognitive assessment follow-up, if parents consented. Pre-term infants born between 26 and 31 completed weeks of gestation in one of the 16 neonatology departments in 12 regions participating in this study were included. At term-corrected age, i.e., gestational age (GA) of 39–41 weeks, conventional MRI was performed to study the cerebral morphology. Our subjects were selected from 3 centers: Reims, Marseille Conception, and Marseille Nord. Children with severe chromosomal anomaly as well as with central nervous system malformation diagnosed prenatally or on examinations in the neonatal period (transfontanellar ultrasound and/or MRI) were excluded from the study.

2.1.2. Imaging data

All infants were imaged without sedation, during natural sleep. Full-term infants: Ten full-term infants, born at 37–41 weeks, were scanned within the first week of life at BCH using a Siemens 3T Skyra with a 32-channel head coil. Tl-weighted structural MRI (sMRI) data were acquired with a motion-compensated multi-echo magnetization-prepared rapid gradient-echo (MPRAGE) sequence (1 mm isotropic resolution, TR=2520 ms, TE=1.74 ms, flip angle 7°, T_acq = 2:41 min) and dMRI data were acquired with an echo-planar imaging (EPI) sequence (5 b=0 volumes, 30 volumes with b=1000 s/mm², 2 mm isotropic resolution, TE = 104 ms, TR = 3400 ms, T_acq = 2:45 min, GRAPPA factor 2, simultaneous multi-slice factor 2). Pre-term infants: Thirteen premature subjects, born at 26–31 weeks, were imaged at 38–43 weeks, either on a 3T Philips or on a 1.5T Siemens scanner, both using an 8-channel coil. On the Philips scanner, sMRI data were acquired with a fast field echo sequence (1.2 mm coronal slices and in-plane resolution of 0.27 mm, TR = 18.9 ms, TE = 4.6 ms, flip angle 8°, T_acq = 2:34 min) and dMRI data were acquired with an EPI sequence (1 b=0 volume, 32 b=1000 s/mm² volumes, 3 mm axial slices and in-plane resolution of 1.56 mm, TE = 68 ms, TR = 2981 ms, T_acq = 2:35 min). On the Siemens scanner, sMRI data were acquired with a fast low-angle shot (FLASH) sequence (4.0 mm sagittal slices and in-plane resolution of 0.43 mm, TR = .38 ms, TE = 5.52 ms, flip angle 90°, T_acq = 2:40 min) and dMRI data were acquired with an EPI sequence (2 b=0 volumes, 24 b=1000 s/mm² volumes, 2.2 mm axial slices and in-plane resolution of 1.97 mm, TE = 98 ms, TR = 7600 ms, T_acq = 2:43 min).

2.2. Structural MRI data analysis

Our automated tractography relies on a subject-specific segmentation of cortical and subcortical structures. We obtained this automatically from each subject’s sMRI data using an infant-specific data processing framework [70]. First, we used our novel double-consensus skull-stripping approach [71] to identify the brain region using a modified version of the tool developed by Doshi et al. [72]. Even though it is a challenging task in the newborn population, our tool achieved over 90% overlap with expert-delineated brain masks, as measured by the Dice overlap coefficient. Then, for the segmentation, we applied a Bayesian multi-label atlas fusion algorithm whose implementation was based on [73]. This step used two sets of information: (1) ground-truth anatomical information from an extended version (a total of 26) of our manually annotated training data set [74] and (2) the consistency of voxel intensities within target regions and their relation to the propagated labels [75]. The latter is critical for segmenting scans with potentially varying degrees of myelination and is in contrast with tools that rely on intensity distribution information from the training images. We used DRAMMS [76] to co-register the images between the training subjects and the test subject for the automated segmentation task.

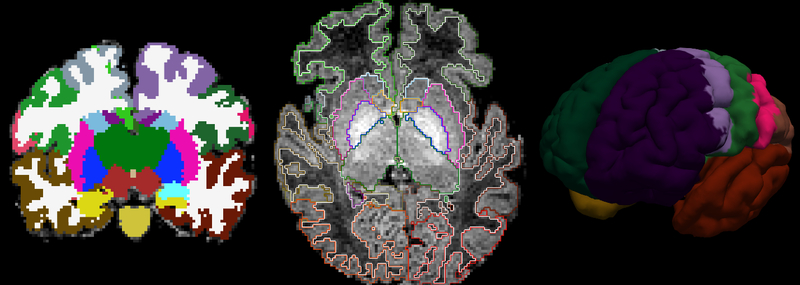
In total, our segmentation algorithm identified 23 subcortical regions [74] and 7 cortical areas per hemisphere, including the prefrontal, premotor, primary motor, primary somatosensory, posterior parietal, occipital, and temporal regions. A highly representative segmentation outcome from our pipeline is presented in Figure 1. The set of cortical labels used in this study follows those from the adult connectivity and infant resting-state literature [77]. In order to define and identify their location in our training data set, we used the relevant literature on adult studies, anatomy references, and the FreeSurfer adult brain segmentation descriptions [78–83]. To maintain accuracy and consistency, the resulting segmentations of all subjects were reviewed by the same neuroradiologist (CJ) in the three orthogonal planes for tridimensional accuracy check. For a summary of the sMRI processing steps see Figure 2 and for the full list of segmentation labels see Supplementary Table 1.

Figure 1. Anatomical segmentation.

Cortical and subcortical segmentation labels of an infant are shown, from left to right, in coronal view, axial view displayed over the structural MRI, and surface view.

Figure 2: Image processing pipeline.

An outline of processing steps is shown for images in the training data set (top) and the test subjects (bottom).

2.3. Diffusion MRI data pre-processing

The dMRI data were first inspected visually to ensure that they exhibited minimal distortion and that none of the volumes had intensity drop-out artifacts induced by head motion. We included subjects in our data only if all dMRI volumes passed visual inspection. We used tools from the FSL libraries for preprocessing the images [84]. In detail, the following steps were performed: (1) Extraction of diffusion gradients and the corresponding b-values from the input DICOM images, (2) Eddy-current distortion correction by affine registration to the first b=0 volume with FSL/eddy_correct, (3) Skull-stripping of the b=0 volume using FSL/BET [85], (4) Fitting of the ball-and-stick model of diffusion with FSL/bedpostX [86], using two anisotropic compartments and all other default parameters, and (5) Rigid registration with 6 degrees of freedom (DOF) between each subject’s skull-stripped sMRI and b=0 dMRI volumes using FSL/flirt [87, 88] with mutual information as a cost function. All of the resulting transformations were visually inspected for accuracy. For a summary of the dMRI processing steps see Figure 2.

As measure of the quality of our datasets, we computed, using outputs from step (4) of our diffusion preprocessing pipeline, the 95% uncertainty on the orientation angle (i.e., the 95% confidence angle from the mean direction)[89, 90]. Low uncertainty reflects high contrast-to-noise ratio. We included the mean and standard deviation of the average of such measurements in Supplementary Table 3 for future comparison with other data sets.

Motion artifacts can potentially confound any analysis of dMRI data. To quantify head motion in each scan, we derived volume-by-volume translation and rotation parameters from step (2), as well as the percentage of bad slices and slice-by-slice signal drop-out measures that are specific to dMRI data [91]. The registration-based measures are better at capturing slower, between-volume motion, whereas the intensity-based measures are better at capturing more rapid, within-volume motion. We used an unpaired two-tail Student T-test to compare these four parameters between our prematurely born and full-term infants. None of these tests indicated statistically significant difference between the two groups. A summary of all these motion parameters is listed in Supplementary Table 2.

2.4. Manual annotation of WM pathways

Our algorithm requires training data in the form of manually labeled WM pathways. For this purpose, we performed deterministic tractography seeded on the whole brain for all of our subjects using the Diffusion Toolkit [92] and annotated a set of major WM pathways with TrackVis [92]. The pathways of our choice are all crucial in development and relatively well-characterized by neuroanatomists: the forceps major and minor of the corpus callosum (FMIN, FMAJ), corticospinal tract (CST), inferior longitudinal (ILF), inferior fronto-occipital (IFOF), superior longitudinal (SLF), uncinate (UF) fasciculi and the fornix (FORNIX). Intra-hemispheric pathways, i.e., all except FMIN and FMAJ, were labeled on both hemispheres, leading to a total of 14 pathways. Figure 3 shows the manually annotated pathways for a representative subject. The pathway annotation process involved drawing ROIs to isolate streamlines belonging to each pathway. We closely followed the pathway descriptions from [93] as well as a set of highly reproducible rules from [94, 95]. For the sake of consistency, our neuroradiologist (CJ) -- who has had 5 years of experience in image analysis -- checked, corrected and finalized all the manual annotations completed by our trained experts.

Figure 3. Manually labeled pathways.

Manual annotation of WM tracts in a premature sample subject is shown with the subject’s Tl-weighted image in the background: CST (purple), FMIN and FMAJ (red), IFOF (cyan), ILF (orange), UF (blue), FORNIX (fuchsia) and SLF (gray). Left: Axial view with inclusion ROIs. Right: 3D view, no ROIs.

We computed the inter- and intra-rater variability of this manual labeling protocol, for the purpose of assessing its reproducibility in our newborn cohort, as well as benchmarking the results of our automated reconstruction For the inter-rater comparison, 12 pathways (left and right UF, IFOF, ILF, CST, SLF, and FORNIX) from 5 subjects were segmented by two independent expert labelers. For the intra-rater comparison, 8 pathways (left and right UF, IFOF, ILF and FMIN, FMAJ) from 13 subjects were labeled by the same expert labeler (CJ) on two separate occasions, more than a year apart. The mean and standard deviation of the modified Hausdorff distance (MHD) for the inter-rater experiments were (1.5355, 1.4450) and for the intra-rater ones were (1.4360, 1.8023) (see Figure 4). We defined the MHD between two labels as the minimum distance of each point on one label from the other label, averaged over all points on the two labels.

Figure 4. Inter- and intra-rater variability of our manual tract labeling procedure on newborns.

For the former, 12 pathways (left and right UF, IFOF, ILF, CST, SLF, and FORNIX) from 5 subjects were segmented by two independent expert labelers and for the latter, 8 pathways (left and right UF, IFOF, ILF and FMIN, FMAJ) from 13 subjects were labeled by the same expert labeler (CJ) on two separate occasions, more than a year apart.

The training data required to compute anatomical priors for our automated tractography consist of the manually outlined tracts and the automated anatomical segmentation of each individual training subject. We refer to this collection of individual data as an “atlas” (Figure 1 and 3 together). This is not to be confused with atlases that consist of voxel-wise population averages of imaging data in a template space.

Common spatial coordinate space

We established an unbiased common spatial coordinate space from the sMRI volumes of our training subjects with a robust template construction tool that uses 12-DOF affine registration [96] (Figure 2). This served as a reference space for computing anatomical priors from the training data, as will be discussed in the next section. For reasons that will become clearer in the following, we did not compute any population average of the training data in this space. We only computed a spatial transformation relating the test subject and each of the training subjects to this common coordinate space.

2.5. Automated global probabilistic tractography

We incorporated the automated infant anatomical segmentations and manually labeled tracts into a Bayesian framework for global tractography with anatomical priors, following the approach of TRActs Constrained by UnderLying Anatomy (TRACULA) [26]. A WM pathway of interest $\mathcal{F}$ is modeled as a cubic spline, and its control points are perturbed to draw samples from the posterior probability distribution $P(\mathcal{F}|Y)$ of the pathway $\mathcal{F}$ given a subject’s diffusion-weighted images Y. The posterior probability distribution is written as

$$P(\mathcal{F}|Y)\propto P(Y|\mathcal{F})p(\mathcal{F}),$$ (1)

where the likelihood term $P(Y|\mathcal{F})$ models the variability in the measured dMRI data given the shape of the pathway in the specific subject and the prior distribution $P(\mathcal{F})$ models the variability in the anatomy of the pathway among subjects. We computed the likelihood term as in [97], using a Gaussian distribution with a mean that was computed from the “ball-and-stick” forward model of diffusion. However, instead of assuming equal prior probability for all possible paths as in [97], we used a prior of the form

$$p(\mathcal{F}|A,{\left\{{\mathcal{F}}_k\right\}}_{k=1}^n,{\left\{A_k\right\}}_{k=1}^n)={\prod }_{j\in \mathcal{F}}[n_{jA(j)}+1]/[n_{jA(j)}+{\overline{n}}_{jA(j)}+2],$$ (2)

where A is the anatomical segmentation map of the test subject, ${\mathcal{F}}_k$, k = 1, ...,n is the manually labeled WM pathway of interest in the k-th training subject, A_k, k = 1,..., n is the anatomical segmentation map of the k-th training subject, and n_jA(j), ${\overline{n}}_{jA(j)}$ are the total numbers of streamlines in the training subjects that do or do not neighbor, respectively, the anatomical segmentation label A(j) at position j along the pathway of interest. Such a prior probability was computed separately for the labels that the pathway passed through, and for the labels that the pathway neighbored in each of a set of directions (left, right, anterior, posterior, etc.) The prior distribution $P(\mathcal{F})$ in (1) is the product of a set of priors of the form (2), each computed for neighboring labels in a different direction.

In the notation established above, what we refer to as our “atlas” is the collection of manually labeled streamlines $\left\{{\mathcal{F}}_k\right\}$ and anatomical segmentations {A_k}. The information that we extract from this atlas is the relative positions (left, right, anterior, posterior, etc.) of the points in $\left\{{\mathcal{F}}_k\right\}$ with respect to the labels in {A_k}, for each of the k training subjects. Thus the subjects need to be aligned to a template space only to ensure that the definitions of left, right, anterior, posterior, etc. are common across all subjects. Exact voxel-by-voxel alignment of subjects is not required because the absolute coordinates of the streamlines in $\left\{{\mathcal{F}}_k\right\}$ or the labels in {A_k} in template space are never used.

As described in more detail elsewhere [26, 98], we relied on a random sampling algorithm to draw sample paths from the distribution $P(\mathcal{F}|Y)$. At each iteration, we obtained a new candidate sample of the path $\mathcal{F}$ by perturbing the control points of the spline that defined $\mathcal{F}$ in the test subject’s individual dMRI space. We computed the posterior probability (1) of the new sample path to determine if the sample would be accepted or rejected. This involved computing the likelihood $P(Y|\mathcal{F})$, which is a measure of how well the path fits the orientations of the ball-and-stick model in the voxels that the path goes through in dMRI space, and the prior $P(\mathcal{F})$, which is a measure of how well the neighboring segmentation labels of the path matched the ones of the manually labeled streamlines in the training set. As the definitions of left, right, anterior, posterior, etc. have to be the same between the test and training subjects to be able to compare neighboring labels across subjects, the segmentation labels and the coordinates of the sample paths have to be transformed from the test subject’s dMRI space to the template for this computation. However, this is only done to determine which label is the left, right, anterior, posterior, etc. neighbor of each point along the path. Once the posterior probability (1) is computed, the random sampling algorithm determines if the candidate sample path will be accepted or rejected. All accepted paths are summed to obtain an estimate of the posterior distribution $P(\mathcal{F}|Y)$. As the paths are defined and perturbed in the native dMRI space of the test subject, the estimated distribution is also in that space.

For each pathway, we initialized $\mathcal{F}$ by finding the median of the manually labeled streamlines in the training set, mapping it into the native dMRI space, and fitting a spline to it. This was the only step that required relatively good alignment between the test and training subjects. However, a burn-in period (a set of 200 initial iterations where path samples were drawn and discarded) ensured that this initial guess was refined before we began drawing the path samples that we would use to estimate $P(\mathcal{F}|Y)$. After the burn-in period, a total of 7500 sample paths were drawn, and every fifth sample was retained to estimate the posterior distribution. Note that our algorithm performs some initial parsing of the streamlines included in the training data, so that any of those streamlines that are outliers in terms of length are not used at all, and any of them that are outliers in terms of ending location are not used to initialize the random sampling in the test subject. For the infant data that we analyzed in the present work, our algorithm took 1 −2 min per tract on a Linux computer with 2 Quad Core Xeon processors, 3.0 GHz CPU and 32GB of RAM.

Figure 5 provides a visual illustration of how our tractography method works and how it differs from methods that follow the multi-ROI approach. Multi-ROI methods use local tractography, seeded in ROIs that have been transformed from a template space to the individual. Deterministic rules, based on additional inclusion and exclusion ROIs that are also transformed from the template space, are applied post hoc to eliminate incorrect tractography streamlines. In contrast to the multi-ROI approach, our method uses global tractography, where the WM pathway is modeled as a spline and its posterior probability distribution is estimated based on (1). Figure 6 illustrates the practical implications of these conceptual differences between the two approaches. With multi-ROI methods, it is possible that very few or even no streamlines will be found that satisfy the rules defined by the inclusion and exclusion ROIs. Figure 6 shows an example where a failure of the multi-ROI approach to find a satisfactory number of streamlines with local deterministic tractography is solved by using local probabilistic tractography, and one where it is not. Of course, it may be possible to address each specific failure of the multi-ROI approach with other fixes, including alternative local tractography methods, alternative seeding strategies, etc. Rather than seek custom solutions for each specific tract, we propose a different solution – one that relies on global probabilistic tractography and that uses prior probabilities on the anatomical neighborhood of the tracts instead of deterministic, ROI-based rules.

Figure 5. Approaches to automating WM pathway reconstruction.

Left: In the multi-ROI approach, a set of seed ROIs (white rectangles), and possibly some additional inclusion/exclusion ROIs, are transformed from a template space to the individual. Local tractography from the seed ROIs is performed (yellow arrows). A set of deterministic rules on which ROIs the tractography streamlines can or cannot go through is applied post hoc. Right: In contrast to the multi-ROI approach, TRACULInA uses global tractography. The WM pathway is modeled as a spline (yellow curve) and its control points (orange dots) are perturbed iteratively. The posterior probability of the curve given the data is computed via a likelihood term (fitting the shape of the curve to the diffusion data) and a prior term (fitting the shape of the curve to its anatomical neighborhood, as obtained from an automated segmentation).

Figure 6. Challenges of the multi-ROI approach.

Two examples of tracts that were challenging to label with the multi-ROI approach. Left column: In both examples, local deterministic tractography with the tensor model finds only few streamlines. Middle column: In example a (top row, inferior longitudinal fasciculus), using local probabilistic tractography with a multi-compartment model, and seeding either in a frontal ROI (heat color map) or an occipital ROI (jet color map) succeeds in identifying the tract. In example b (bottom row, uncinate fasciculus), seeding in an orbitofrontal ROI (jet color map) yields mostly corpus callosum streamlines, whereas seeding in a temporal ROI (heat color map) yields mostly inferior longitudinal streamlines. Therefore the uncinate fasciculus is not identified. (Note that all tractography outputs are displayed as maximum intensity projections on a single slice.) Right column: In both cases, TRACULInA, which relies on global probabilistic tractography with a multi-compartment model and anatomical neighborhood priors, succeeds in identifying the tracts.

2.6. Experiments

2.6.1. Robustness to differences between test and training data

For each of the full-term and premature infants in our data set, we reconstructed the posterior distributions of each of the 14 WM pathways, using combinations of the remaining subjects as the training set. We quantified the difference between the automatically reconstructed probabilistic pathway solutions and their manually labeled deterministic counterparts by their modified Hausdorff distance. Although the manually labeled bundles are also obtained from diffusion tractography, and therefore cannot be considered ground truth, the manual mul- ti-ROI labeling method represents the best-case performance of an automated multi-ROI method. Before computing the MHD, the posterior probability distribution estimated by our automated tractography method was thresholded by masking out all values below 20% of the maximum. In this way the comparison was based on the center of the distribution and not its tails.

An important question for any method that relies on prior information from a training set is whether it is applicable to test data acquired with acquisition methods and from populations different than the data included in the training set. In the case of infants, in particular, where data is scarce and data quality is variable, it would be crucial to be able to pool data from different acquisition sites and studies in the training data. We investigated the robustness of our algorithm to differences between the training and test data by performing automated tractography on each test subject with three different training sets: full-term subjects only, pre-term subjects only, and all subjects. Whenever the test subject belonged to a population included in the training set, we removed the test subject from the training set. We investigated whether the MHD between automatically reconstructed and manually labeled pathways, as well as the fractional anisotropy (FA) and mean diffusivity (MD) of the automatically reconstructed tracts, depended on which set of subjects were included in our training set.

2.6.2. Robustness to errors in the anatomical segmentation

We investigated how errors in the boundaries of the anatomical segmentation labels affect the performance of our automated tractography by perturbing the borders of the test subject’s segmentation labels. This was done by randomly assigning to each voxel the anatomical segmentation label of one of its neighboring voxels. An example of the severity of segmentation errors generated by this approach is shown in Figure 7. We then performed the automated tractography using this perturbed segmentation and computed the accuracy of the reconstruction, as quantified by MHD between automatically reconstructed and manually labeled pathways.

Figure 7. Simulated segmentation and registration errors.

Automated structural segmentation of an individual subject in its original form (a) and after we perturbed the borders of the segmentation labels (b) or perturbed the registration from individual structural space to template space (c). All versions of the segmentation are shown in template space for the purposes of visual comparison. Our method is robust to such errors because the prior information that we use is only on the relative positions (left, right, etc.) of tracts with respect to different structures, and also because errors that may appear dramatic in the resolution of the structural space have less of an effect in the lower resolution of diffusion space.

2.6.3. Robustness to errors in the registration to the common coordinate space

We investigated how the accuracy of the registration between the individual and template spaces affects the performance of our automated tractography by introducing both scaling and shearing errors to the affine registration matrix obtained from the robust registration between the individual sMRI and the template. For each subject, random scaling and shearing factors in x, y, and z were drawn from a uniform distribution in the 0 – 10% range. This generated scaling and shearing matrices that were then multiplied with the subject’s original registration matrix to compute a perturbed registration matrix. An example of the severity of registration errors generated by this approach is shown in Figure 7. We repeated the automated pathway reconstruction using this perturbed registration and computed the accuracy of the reconstruction, as quantified by the MHD between the automatically reconstructed and manually labeled pathways.

2.6.4. Reconstruction without an individual anatomical segmentation

As a special case of segmentation and registration errors, we modeled the scenario where a subject did not have a Tl-weighted scan and hence we could not obtain an individual anatomical segmentation. For each of our subjects, we selected randomly another subject, and used that other subject’s anatomical segmentation. We mapped segmentations from one subject to the dMRI space of another subject by composing the Tl-to-dMRI registration of the subject whose segmentation we were using with an affine registration between the two subjects’ FA maps. We repeated the automated pathway reconstruction for each subject using the segmentation of a different, randomly selected subject and computed the accuracy of the reconstruction, as quantified by the MHD between the automatically reconstructed and manually labeled pathways.

2.6.5. Application to a large infant data set

Finally, we evaluate our method on a larger set of healthy, full-term infants with a greater range of ages (0–5 months). This data set is available publicly through the NIMH Data Archive (https://ndar.nih.gov), project number 1974, “Early Development in Twins”. For this study, pregnant women with twin fetuses were recruited from outpatient OB-GYN clinics as part of the UNC Early Brain Development Studies (http://www.earlybrainresearch.org) between 2004 and 2014. Most MRI scans were acquired on a 3T Siemens Allegra and the remaining on a 3T Siemens Tim Trio. For one set of the Allegra cohort, dMRI data were acquired using an EPI sequence with 1 b=0 volume, 6 b=1000 s/mm² volumes with non-colinear diffusion encoding directions, 2 mm isotropic resolution, TE=73ms, TR=5200ms. The acquisition was repeated 5 times for a total 35 volumes per scan session. For the rest of the Allegra cohort, dMRI data were acquired with 7 b=0 volumes, 42 b=1000 s/mm² volumes with non-collinear diffusion-encoding directions, 2 mm isotropic resolution, TE=82ms, TR=7680ms. The Trio scans had acquisition parameters similar to the second Allegra protocol: 7 b=0 volumes, 42 b=1000 s/mm² volumes with non-collinear diffusion-encoding directions, 2 mm isotropic resolution, TE=83ms, TR=7200ms. Axial T1-weighted scans with 1 mm isotropic resolution were also collected. For more information about these data, see [64, 99].

The full downloaded data set consists of images from N=248 subjects (129 female). We retain those that have both T1- and diffusion-weighted MRI data, leaving us with a set of N=223 subjects (118 female). Numbers of subjects by sex and age at scan are shown in Table 2. We do not exclude any subjects based on data quality, as our goal is to test our method on a data set with the full variability that would be typical of a large study. We reconstruct tracts in each of these subjects, using the manually labeled tracts from our own 23 neonatal subjects (both full-term and pre-term) as the training set. As we do not have manually labeled tracts in the UNC subjects, we evaluate the ability of our method to detect previously reported effects of increasing FA and decreasing MD in the first 5 months of life. Note that we do not have access to the zygocity of the UNC subjects or the scanner type for each scan. Age at scan is available to us as an integer number of months, hence we are not able to fit continuous curves to the diffusion measures as a function of age. Instead we perform an analysis of variance on the FA and MD with factors of tract, age, and sex.

Table 2:

Demographie data of UNC infants (from https://ndar.nih.gov).

Age at scan (months)	0	1	2	3	4	5	Total
Number of subjects	10	128	61	21	0	3	223
Number of female subjects	8	64	36	7	0	3	118

3. Results

Our tool reconstructed the set of 14 WM pathways successfully in both full-term and pre-term subjects. We considered our automated pathway reconstruction for a test subject to be successful when the required set of WM pathways were all recovered at their expected spatial locations, verified by our neuroanatomist (CJ). Figure 8 displays the full set of 14 automatically reconstructed pathways in a premature subject (same subject whose manually labeled WM pathways are shown in Figure 3), using all the remaining 22 subjects as the training set.

Figure 8. Automatically reconstructed pathways.

The outputs of automated global probabilistic tractography in a premature sample subject (same as Figure 2) are shown with the subject’s T1-weighted image in the background. The estimated posterior distribution of eacho pathway is displayed as an isosurface in axial and 3D sagittal views: CST (purple), FMIN and FMAJ (red), IFOF (cyan), ILF (orange), UF (blue), FORNIX (fuschia) and SLF (gray).

Figure 9 shows box plots of the MHD between our automatically reconstructed and manually labeled tracts for each combination of test and training data. Each experiment is denoted as t|T, where t indicates the test set and T the training set (t, T ϵ {F,P,A}). We use “F”, “P”, and “A” to denote, respectively, the set of full-term only, pre-term only, or all subjects. We organized our results into five experiments: F|F, A|A, P|P, F|P and P|F. The horizontal line inside each box marks the median, whereas the edges of the box mark the 25^th and 75^th percentiles. The median MHD over all the analyses performed here was 2.3mm, and the interquartile range was 2.3mm. This indicates that, in most cases, the distance between the automatically reconstructed and manually labeled tracts was less than 2 diffusion voxels. Note that some differences between the manual and automated approaches may indeed be desirable. This would be the case, for example, when the manual multi-ROI approach cannot find a specific tract but our automated approach, aided by its global model and anatomical priors, can (see Figure 6).

Figure 9. Accuracy of automated WM pathway reconstruction.

Modified Hausdorff distances (in mm) between automatically reconstructed and manually labeled pathways are plotted for the 14 pathways. For each pathway, we show results with 5 combinations of test and training data, each denoted as (test set) | (training set), F: full-term, P: pre-term, A: all subjects

A three-way analysis of variance (ANOVA) on the MHD, where the three factors were tract (14 levels), test set (2 levels: full-term or pre-term), and training set (3 levels: full-term, pre-term, or all) shows a significant effect of tract and test set (p < 10⁻¹⁶), but not of training set (p = 0.266). That is, the accuracy of the reconstruction depends on the test data but not on the training data. This implies that, for a given test subject, the accuracy is similar whether the training set consists of full-term subjects only, pre-term subjects only, or subjects from both groups.

There was no statistically significant difference in intracranial volume (ICV) between the subjects scanned at the Boston and French sites (p=0.714 based on a two-sided T-test). Adding ICV as a continuous factor to the analysis of variance on MHD showed no statistically significant effect of ICV on accuracy of the algorithm (p=0.755).

Figures 10 and 11 show box plots of the average FA and MD, respectively, of the automatically reconstructed pathways for each combination of test and training sets. Three-way ANOVAs with factors of tract, test set, and training set show a significant effect of tract on both FA and MD (p < 10⁻¹⁶), a significant effect of test set on FA (p < 10⁻⁶) and a trend effect of test set on MD (p = 0.068), but no effect of training set on FA (p = 0.996) or on MD (p = 0.662). The lack of an effect of training set on either measure suggests that the estimates of FA and MD that we extract from our automated tractography are stable, regardless of the set of subjects that we include in our training set.

Figure 10. Effect of training set on FA.

Average fractional anisotropy (FA) of the automatically reconstructed pathways for each combination of test and training sets. For all 14 pathways, we show results with 5 combinations of test and training data, each denoted as (test set) | (training set), F: full-term, P: pre-term, A: all subjects.

Figure 11. Effect of training set on MD.

Average mean diffusivity (MD) of the automatically reconstructed pathways for each combination of test and training sets. For all 14 pathways, we show results with 5 combinations of test and training data, each denoted as (test set) | (training set), F: full-term, P: pre-term, A: all subjects.

The goal of this study was not to test hypotheses on FA or MD differences between full-term and pre-term subjects, as the two sets of subjects were scanned at different centers with different acquisition protocols. Therefore, we cannot determine from this data whether the effect of the test set is due to acquisition differences or actual population differences between full-term and pre-term infants. However, the lack of an effect of the training set allows us to conclude the following: it is possible to use a training set that combines data from different studies, or to use a training set built from data different than the test data to be analyzed, without affecting the diffusion measures in the test data extracted from the automatically reconstructed WM pathways.

Figure 12 shows scatter plots of FA or MD values of each tract, as obtained from the manually annotated vs. automatically reconstructed pathway. Note that, as the automated reconstruction uses probabilistic tractog- raphy and the manual labeling uses deterministic tractography, we did not anticipate the FA and MD values from the two to be equal. However, linear regression analyses showed the values extracted with the manual and automated approaches to be associated with each other with high statistical significance (FA: R²=0.58, p<10⁻¹²; MD: R²=0.75, p<10⁻¹²). Results by tract are shown in Supplementary Table 4.

Figure 12. Correlation of measures obtained with the manual and automated approach.

The scatter plots show FA and MD values extracted from manual labeling with local deterministic tractography vs. automated reconstruction with global probabilistic tractography using the full set of training data. Results are shown by pathway, where we have grouped together corresponding left- and right-hemisphere pathways, as well as the two corpus callosum (CC) pathways.

When we introduced errors in the boundaries of the anatomical segmentation labels, the median MHD was 2.42mm and the interquartile range was 1.99mm. We repeated the analysis of variance on MHD above, with the addition of the segmentation (original or perturbed) as a factor. This analysis showed no statistically significant effect of segmentation (p=0.380). When we introduced errors in the registration matrix between the individual and template space, the median MHD was 2.44mm and the interquartile range was 2.26mm. Once again we repeated the analysis of variance on MHD, now with the addition of the registration (original or perturbed) as a factor. This analysis showed no statistically significant effect of registration (p=0.287). When we reconstructed pathways for each subject using an anatomical segmentation from a different subject, the median MHD was 2.36mm and the interquartile range was 2.08mm. This time we performed the analysis of variance on MHD with the source of the segmentation (the same subject or a different subject) as a factor. This analysis showed no statistically significant effect of the source of the segmentation (p=0.686). Thus the effect of using a segmentation from a different subject mapped to the test subject with affine registration appears to be even subtler than the effects of the perturbed segmentations and registrations that we tested above.

Figures 13 and 14 show, respectively, plots of FA and MD by age for the UNC infant data set. These plots show clear trends of increasing FA and decreasing MD with age, with low variance as indicated by the standard error bars. Analyses of variance showed highly statistically significant effects of tract and age for both FA and MD (p<10⁻¹⁶). There was a trend towards a statistically significant effect of sex for FA (p=0.08) but not for MD (p=0.67). These findings persisted when we repeated the analysis using only subjects aged 0–3 months; hence they were not driven by the 3 subjects who were 5 months old.

Figure 13. FA vs. age in UNC infant dataset.

Average FA of automatically reconstructed pathways in infants aged 0–5 months, with standard error bars.

Figure 14. MD vs. age in UNC infant dataset.

Average MD of automatically reconstructed pathways in infants aged 0–5 months, with standard error bars.

4. Discussion

We have proposed a framework for automated reconstruction of WM pathways from infant dMRI and sMRI data, which relies on global probabilistic tractography with prior knowledge on the anatomy of the pathways of interest. All computational components have been adapted or newly developed specifically for this population, including: the training data set of 14 manually annotated WM pathways, the robust infant skull-stripping and anatomical segmentation pipeline, and the fully automated dMRI processing pipeline, including global probabilistic tractography with priors on the anatomical neighbors of the WM pathways.

The main features of our approach are:

1. Infant-specific training set. Due to the large geometric differences, as well as the reversed MR contrast between newborns and myelinated children or adults, it is extremely challenging to align newborn data to an atlas built from older child or adult data. Hence, generic image analysis tools do not apply to infants. We addressed this by developing a population-specific training data set that includes manually labeled WM tracts and cortical and subcortical segmentation labels automatically computed from newborn MRI data. Our pipeline currently relies on 1mm-resolution, T1-weighted images to obtain these segmentation labels. Such images can be acquired in a reasonable amount of time with 3D MPRAGE sequences thanks to acceleration in two planes. Thus 3D T1-weighted scans are in widespread use in clinical pediatric neuroimaging [100–102]. We have shown, however, that our method is flexible enough to use even in the absence of a high-resolution, T1 -weighted scan that would be required to obtain this individualized anatomical segmentation.

2. Global tractography. The global approach to tractography models a pathway as a curve between two end regions and fits the shape of this curve to the diffusion orientations in all voxels at once. This approach is well-suited to reconstructing known WM pathways, such as the 14 pathways in our training set, because it is guaranteed to reach both ends of the pathway, as opposed to local tractography, which may stop before reconstructing the entire trajectory of the pathway. In infant data, in particular, where diffusion anisotropy is low, multi-ROI approaches that rely on local tractography [15–19] are not guaranteed to find streamlines that intersect all target ROIs. (This is illustrated in Fig. 5.) Furthermore, as opposed to approaches that produce volumetric labels [45, 48], our method produces tractography solutions. These solutions are curves that can be parameterized by arc length, allowing point-wise analyses of diffusion measures along a pathway. An additional feature of the Bayesian framework that our global tractography method employs is that one can compute a measure of confidence in the existence of a pathway, via the ratio of the evidence for a model that imposes a connection over one that does not [97]. By contrast, with local tractography, the absence of a tract would be inferred typically by the lack of streamlines that can reach one ending of the tract when seeded in the other ending. However, such a lack could be, for example, due to streamlines that are interrupted by a local abnormality (such as a lesion) somewhere along the tract, rather than the absence of the tract itself.

3. Anatomical priors. Our approach does not impose deterministic rules, such as ROIs that streamlines must or must not go through. Instead, it computes the prior probability that a pathway goes through or next to each of a set of anatomical segmentation labels, as a function of position along the pathway, given a set of manually labeled pathways from training subjects. The contribution of this prior to the posterior probability distribution is greater for areas that have less anatomical variability across subjects, and vice versa. Therefore our approach encodes individual variability in a way that a label drawn on an average brain and warped to the test subject does not. Finally, our priors rely only on the relative positions between a WM pathway and its surrounding structures, instead of the exact spatial coordinates of the pathway in a template space, and therefore do not require perfect alignment between test and training subjects in template space. As a result, we have been able to demonstrate here that our approach is robust to errors in the registration from individual structural space to template space, as well as errors in the borders of the anatomical segmentation labels.

The goal of our experiments on our own small dataset of full-term and pre-term neonates was not to test hypotheses on differences in diffusion measures between full-term and pre-term subjects, as the data from the two populations were acquired with different MRI sequences and scanners. Therefore, it would be misleading to report group differences here, as we are unable to distinguish between differences due to gestational age at birth and differences due to acquisition methods. However, we did find a significant effect of test set in our analyses of variance. Post hoc analyses showed that these effects were for the most part due to pathways reconstructed from full-term data having higher FA and lower MD than those reconstructed from pre-term data. Such FA and/or MD differences have been reported previously [30, 47, 48, 103]. However, the literature contains contradictory findings. The small number of studies, combined with the variability in methodological approaches, makes it difficult to reach a consensus. We hope that the tools that we have developed will facilitate automated and robust data analysis for larger group studies in the future.

We used our dataset of full-term and pre-term neonates to evaluate the accuracy of our automated tractography by comparing automatically reconstructed and manually labeled pathways. Despite the challenges posed by short acquisition times and low contrast due to incomplete WM maturation in newborn data, our tool reconstructed all 14 WM pathways in all test subjects with good accuracy. We reconstructed the pathway solutions in each test subject using different training sets that contained full-term only, pre-term only, or both full-term and pre-term subjects. We found no significant effect of training set on the distances between automatically reconstructed and manually labeled pathways, or on the FA and MD of the automatically reconstructed pathways. This suggests that our approach is robust to differences between the test and training subjects. Therefore, it is possible to pool data in the training set from different studies, which may involve various populations and acquisition protocols, and to use our algorithm on data from studies other than those of the training set. These results are not only very promising but also novel. Previously, we had demonstrated in adult subjects that the performance of our approach in a disease population did not depend on whether the training set included healthy or diseased subjects [104]. However, all subjects in that study had been scanned with the same acquisition methods on the same scanner. The present work is the first illustration that our method is robust to differences in acquisition methods between the test and training data. It is also the first illustration that the method is robust to errors in the individual anatomical segmentation or the inter-individual registration. This robustness stems from the fact that our anatomical priors encode only the relative positions between a WM pathway and its surrounding structures. That is, we do not assume that the pathway has the same size, shape, or integrity in the test subjects as in the training set subjects, only that its relative position with respect to its surrounding anatomy is preserved. In addition, registration or segmentation errors that may appear dramatic in the resolution of the sMRI space have less of an effect in the lower resolution of the dMRI space. Finally, we were able to apply our method to a large dataset of full-term subjects from the UNC Early Brain Development Program. This cohort featured a greater age range (0–5 months) than our own neonate subjects, who were used to train our algorithm. Despite this difference between the populations of the test and training data, our results from the UNC dataset show the age-related increase in FA and decrease in MD that we expected from prior studies [105–107].

In both our data and the UNC data, we observed a significant effect of tract on FA and MD, which can be explained by the asynchronous myelination of different WM pathways. Starting in the late second trimester and continuing through early infancy, myelin progressively accumulates in specialized processes from the oligodendrocytes, which surrounds the axons and form the myelin sheaths [3]. The age-related increase in myelin content results in a decrease in MD and an increase in FA, which occurs first in WM pathways that support functions that are required early in life [8, 108]. From an anatomic perspective, myelination progresses in a well- known sequence, advancing from central to peripheral, inferior to superior, and posterior to anterior, so that at birth (or term equivalent age), the most mature pathways based on histology analysis and anatomical images are the cerebellar peduncles, dorsal brain stem, and CST [4, 109]. The heterochronous and asynchronic maturation of different WM pathways explains the tract-specific differences in MD and FA observed in our experiments. Our observations of higher FA and lower MD in the CST and fomices relative to other white-matter pathways, both in our and in the UNC data, correlate well with those reported by Dubois et. al [110], based on manually segmented deterministic tractography [111].

The present work will make available, for the first time, a robust, fully automated dMRI tractography tool that is applicable not only to healthy infants, but also infants born prematurely. As part of this development, we also established, to the best of our knowledge, the largest manually annotated tractography data set for newborn infants including 23 subjects. We plan to release our automated tractography tool in source and binary format, along with the training set, i.e., the collection of individual manually labeled pathways and anatomical segmentations, for research use under the modified “MIT-style” license of the FreeSurfer package [112]. The tool takes advantage of our existing code base, including features such as point-wise analysis of diffusion measures along a pathway, and joint analysis of data from multiple time points for longitudinal tractography studies [98].

Limitations

The main limitation of our study is that the acquisition protocols do not take advantage of the latest advances in dMRI acquisition, such as scanners with higher gradient strengths that allow data with greater b-values to be collected at high resolution. In the future, the emergence and public sharing of data sets from initiatives such as the Developing Human Connectome Project (http://www.developingconnectome.org/) will enable us to incorporate higher-quality training data into our robust tools. Another limitation of our study, and of any other study that defines WM pathways based on dMRI data, is the absence of definitive ground-truth data on the connectional anatomy of the human brain. We are in the process of collecting such data using optical coherence tomography in post mortem human brains, and we will update our definitions of WM pathways based on these data in the future. Finally, at present, we are unable to comment on the amount of measurement error expected from our versus other methods, due to the absence of a publicly available infant scan/rescan diffusion MRI dataset that would facilitate such a reliability study.

Future directions

It is plausible that using a non-linear registration method between the individual sMRI and template space might improve the accuracy of our method. However, our analysis showed that introducing rather substantial errors in our inter-subject registration matrix had a negligible effect on the accuracy of our automated tractography. Hence, we do not anticipate that subtler, local changes in the registration will have a substantial effect on it, either. Nonetheless, we plan to investigate this point further in the future by incorporating non-linear inter-subject registration for the creation of our common unbiased atlas space. For this purpose we will use the combined volumetric and surface (CVS) method [113], which has been demonstrated to outperform other methods in the alignment of tractography solutions [114].

We note that our newly proposed tractography pipeline could accommodate different newborn-specific anatomical segmentation approaches. Here, we have relied on 3D T1 -weighted scans for obtaining individual segmentations. In clinical pediatric neuroimaging, 3D T1-weighted scans are widespread [100–102], while T2-weighted data in clinical practice are often acquired using 2D sequences with high in-plane resolution but with slice thickness 2.5–4mm. However, some recent research studies use 3D T2-weighted sequences [115–117], and there are pediatric structural processing tools that require either multimodal T2- and T1-weighted or only T2-weighted data. It would be very informative to evaluate the performance of our tools with anatomical segmentations that come from different image sequences (such as [118–120]), a combination of image sequences (such as [112, 121–124]) and / or alternate training data sets (such as [125]). Updating our sMRI segmentation pipeline to also accommodate T2-weighted MRI images, would also allow for a more direct comparison of the performance of our tool to existing pediatric image analysis tools that rely on that contrast. To this end, methods that “synthesize” one type of MRI contrast from the other [126, 127] can provide additional flexibility.

Finally, differences in head motion between groups can lead to spurious findings of group differences in dMRI measures. In the future, we plan to establish a prospective imaging study to quantify these effects in infants and to investigate how they affect our atlas building and group comparisons. However, note that, as indicated by the results of our previous study on the effects of head motion in children [128, 129], motion affects the estimated values of the various dMRI microstructural measures, such as FA. Therefore the problem is not specific to tractography and would also be present in a voxel-based or ROI-based study of these measures.