Summary
In a meta-analysis, we assemble a sample of independent, non-identically distributed p-values. The Fisher’s combination procedure provides a chi-squared test of whether the p-values were sampled from the null uniform distribution. After rejecting the null uniform hypothesis, we are faced with the problem of how to combine the assembled p-values. We first derive a distribution for the p-values. The distribution is parameterized by the standardized mean difference (SMD) and the sample size. It includes the uniform as a special case. The maximum likelihood estimate of the SMD can then be obtained from the independent, non-identically distributed p-values. The MLE can be interpreted as a weighted average of the study-specific estimate of the effect size with a shrinkage. The method is broadly applicable to p-values obtained in the maximum likelihood framework. Simulation studies show our method can effectively estimate the effect size with as few as 6 p-values in the meta-analyses. We also present a Bayes estimator for SMD and a method to account for publication bias. We demonstrate our methods on several meta-analyses that assess the potential benefits of citicoline for patients with memory disorders or patients recovering from ischemic stroke.
Keywords: Distribution of p-values, Standardized mean difference, Bayesian estimator, Citicoline
1 |. INTRODUCTION
In a meta-analysis, we usually can not access the individual patient data and have to work with aggregated data such as the reported p-values. A common approach is to estimate the overall effect size. In this report we will concentrate on combining the different p-values to provide such an estimate.
Let represent a sample of independent p-values obtained from n studies assembled in a meta-analysis. We assume the studies are randomized placebo-controlled 2-arm studies. The p-values were obtained from the between-group comparisons. The goal of the meta-analysis is to combine these p-values to provide an overall summary of the data. Not only it is convenient, but the combination approach can be nearly as powerful as the combined analysis of pooled individual data1.
The Fisher’s combination procedure (Fisher, 19322; Section 14.8.3 of Sutton, Abrams et al. 2000, page 2203)
provides a statistic with a chi-squared distribution with 2n degrees of freedom if the pi are independently sampled from the uniform distribution, i.e. the distribution of the p-values under the null hypothesis of no between-group difference.
As is often the case in a meta-analysis, after we reject the null hypothesis, we are still faced with the problem of how to combine the assembled p-values. There are other methods to combine p-values. Cousins’ review paper4 is a summary with some historical account. Won (2009)5, Chen and Nadarajah (2014)6, and Chen, Yang et al. (2014)7 provide some recent developments on the topic. Briefly, the combination procedure takes the form of
| (1) |
where wi ≥ 0 is the weight given to study i and H(p) is a cumulative distribution function (CDF)-based transformation of p. When H(p) is the inverse CDF of the standard normal, then procedure (1) gives various z-test, either weighted or unweighted. When wi = 1 and H(p) is the inverse CDF of the chi-squared distribution, then (1) is the Lancaster (1961)8 generalization of the Fisher’s test. Chen, Yang et al. (2014)7 further generalize the test (1) by adopting the gamma CDF for H(p). These methods essentially transform the p-values to various quantiles, then the test statistic is constructed as a weighted average of the quantiles. The thinking follows the reverse process of how the p-values were obtained albeit the p-values may be obtained through different test statistics in different studies but one CDF-based transformation function H(p) is uniformly applied.
What transformation function H(p) we should apply remains a natural question. Our attempt to answer this question has led us to another fundamental question concerning the distribution of the assembled p-values under the alternative hypotheses. In this work, we first address this question by developing a distribution for the p-values for the common two-tailed normal test. The distribution provides us a theoretical approach to combining the p-values. Another issue with the existing methods is that the p-values were usually obtained from studies with different sample sizes. The sample sizes and the underlying true difference impacts the distribution of p-values. We show this relationship between the distribution and the sample size in Section 2 when we present our derived distribution (2). With this set-up the assembled p-values form an independent, non-identically distributed sample. This led us to a maximum likelihood estimate (MLE) of the common overall effect size. This is motivated by the objective of a meta-analysis to integrate evidence to come to an overall summary of the efficacy. We will focus on the standardized mean difference which is a common effect size measure used in the meta-analysis literature (see Section 2.4.2, page 31 of Sutton, Abrams et al. 20003). Three real data meta-analysis examples in Section 5 further demonstrate its utility. In Section 6, we comment on a connection between our method and some existing methods of the form (1). Finally, another common issue concerning meta analyses is that the p-values may be obtained using different test statistics in different studies. We discuss this issue and comment on an advantage of our methods in Section 6. It is demonstrated in real meta-analyses in Section 5.2.
In Section 2, we derive a distribution for p-values specifically for the normal test. Using this distribution we first develop the MLE of the standardized mean difference in Section 3.1, followed by a Bayesian estimator in Section 3.2. Then we propose a method to account for publication bias in Section 3.3. We demonstrate the three methods on three meta-analysis examples in Section 5. We conclude the manuscript with a discussion in Section 6.
2 |. DISTRIBUTIONS FOR P-VALUES
In a two-sided hypothesis testing, consider a continuous-valued test statistic X with cumulative distribution function F(·) and density function f(·) under the null hypothesis. Define xp to be the p–th percentile of the statistic X so F(xp) = p. Under a specific alternative hypothesis, suppose the test statistic X follows the cumulative distribution G(·) with density function g(·). Then ψ(p) = ψ(p | G) denoting the density function for the generated p-value p is g(x1−p)/f(x1−p), or the likelihood ratio evaluated at the upper p–th quantile of F. This result can be traced to Pearson (1938)9 for goodness of fit tests and later it was used to understand the interpretation of p-values by Hung, O’Neill et al. (1997)11 and Donahue (1999)10. Yu and Zelterman (2017)12 used it to develop a parametric model to estimate the proportion from the null in p-value mixtures. Koziol and Tuckwell (1999)13 used this result to develop a Bayesian method to combine statistical tests.
The current work concentrate on the two-tailed normal test. We derive the density function for the p-value first. Then we develop several approaches to combining p-values to provide an estimate of the standardized mean difference.
The quantile function for the two-tailed normal test is x1−p = Φ−1(1 − p/2). The density function for the test statistic under an alternative is for where Φ and ϕ denote the distribution and density functions of the standard normal distribution, respectively. The density of p for this folded normal test is
| (2) |
using the ratio A similar result to (2) for the one sample normal test was obtained by Genovese and Wasserman (2004)14. Yu and Zelterman (2017)12 also derived the distribution for p-values generated using the chi-squared test. These distributions may provide alternatives to model p-values. However, their parameterization does not provide as clear an intepretation as distribution (2). We will use distribution (2) to estimate the standardized mean difference in the examples in Section 5. We restrict δ ≥ 0 in (2) for identifiability.
Its cumulative distribution is
| (3) |
from (2).
In a two-sample normal test with means μ1, μ2 and common variance σ2, we have
| (4) |
where denotes the effect size and denotes a sample size-based coefficient. The parameter d is also noted as the standardized mean difference (SMD). The SMD is a common measure used in the meta-analysis literature (see Section 2.4.2, page 31 of Sutton, Abrams et al. 20003). The density function (2) is plotted in Figure 1 for several combinations of SMD and sample sizes (n1, n2).
FIGURE 1.
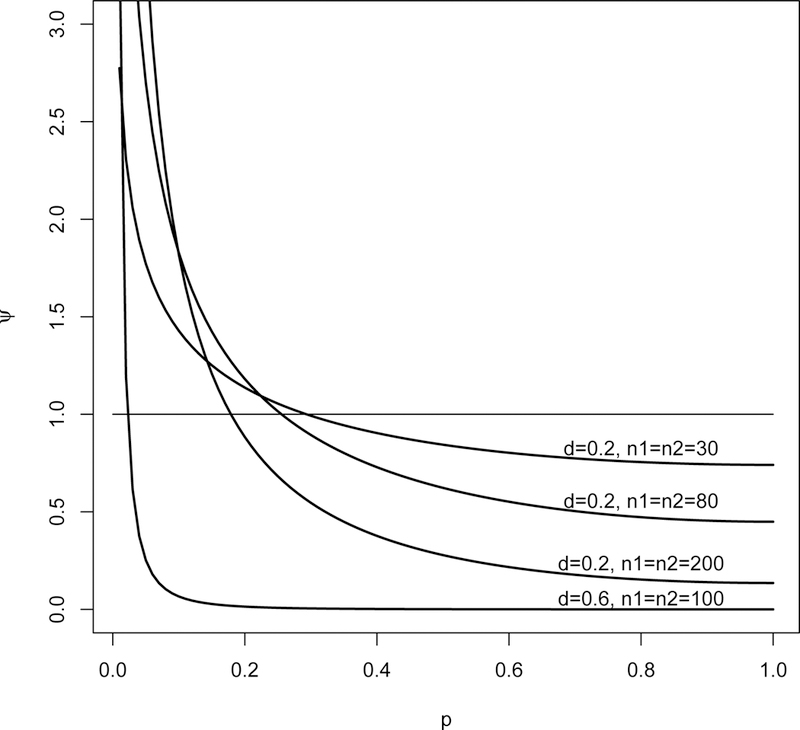
Density function (2) for 4 combinations of effect size and sample sizes: d = 0.2 and n1 = n2 = 30, d = 0.2 and n1 = n2 = 80, d = 0.2 and n1 = n2 = 200, d = 0.6 and n1 = n2 = 100.
If the standard deviation σ is not known, the two-sample t-test is often conducted. For a two-tailed t-test with df, the numerator of is and the denominator is Here the probability density function for the non-central t distribution with non-centrality parameter δt can be found in Johnson, Kotz, and Balakrishnan (1995, p 516). The two-tailed quantile function is where H denotes the distribution function of the (central) t distribution. The density of p for the two-tailed t test is then
| (5) |
The t-statistic can be written as
| (6) |
where are sample mean and is the pooled estimate of the standard deviation. Then we can see the non-centrality parameter which is the same function of the sample size and the SMD as for the normal test. When the degree of freedom is large, the t-test statistic (6) behaves like the normal test. The rest of the work will focus on developing estimators of SMD for the normal test.
Three estimates of SMD, including the maximum likelihood estimate (MLE), a Bayesian estimate, and an estimate that accounts for publication bias, are developed next.
3 |. ESTIMATES OF THE COMMON EFFECT SIZE SMD
3.1 |. Maximum likelihood estimate of d
Let represent a sample of independent p-values obtained from n studies such as those assembled in a meta-analysis. In the ith study, n1i and n2i denote the study-specific sample sizes.
We recognize different studies may have different μ2i − μ1i and σi for reasons such as the studies may be conducted on different populations and/or may have used different measurement instruments. This issue of study heterogeneity is discussed elsewhere15,16. In this report we focus on a meta-analysis in which the investigator would like to combine the p-values to infer what an overall effect is. We use the SMD d to represent this common overall effect although the individual may vary. At the end of this section, we will generate the convexity plot developed by Lambert and Roeder (1995)17 for our model and the plot provides an indication of heterogeneity. We also conduct simulations to assess the impact of heterogeneity on our estimate in Section 4.
With this set-up, are independent non-identically distributed from the density function (2) with a common overall effect size d. The likelihood function for d is
| (7) |
where
Its score function with respect to d is
| (8) |
The observed information is
There are a couple of remarks regarding (8).
Zero is one root of the score function (8). However, could be positive, zero, or negative. This is consistent with the maximum likelihood theory when a local maximum occurs on the boundary of the parameter space. So the root d = 0 could correspond to a local extremum of the likelihood (7) and not necessarily the MLE, or the root d = 0 is the MLE when the null hypothesis is true.
If we assume there is only one p-value observation, then the score function (8) is
| (9) |
This score function shows that if the sample size is not small and the effect size d is away from zero, then the fraction
in (9) is approximately one. Then the estimate is with a slight negligible shrinkage represented by the above fraction. If the sample size is small and the effect size d is close to zero, then the shrinkage fraction in (9) may be much smaller than one, providing a significant shrinkage of the effect size estimate towards zero.
Figure 2 shows the log likelihood function for 4 sets of p-values that we analyze in Section 5.1. These figures show the log likelihood function is maximized when the score function is zero. We also studied the log likelihood for a fixed effect size d but with different sample sizes (n1, n2) in the individual studies to understand their impact on the likelihood function and the consequence on the estimate of d. At the maximum, the negative second derivative with respect to d is larger when the assembled studies have larger sample sizes, suggesting larger observed information and consequently smaller variance of the MLE.
FIGURE 2.
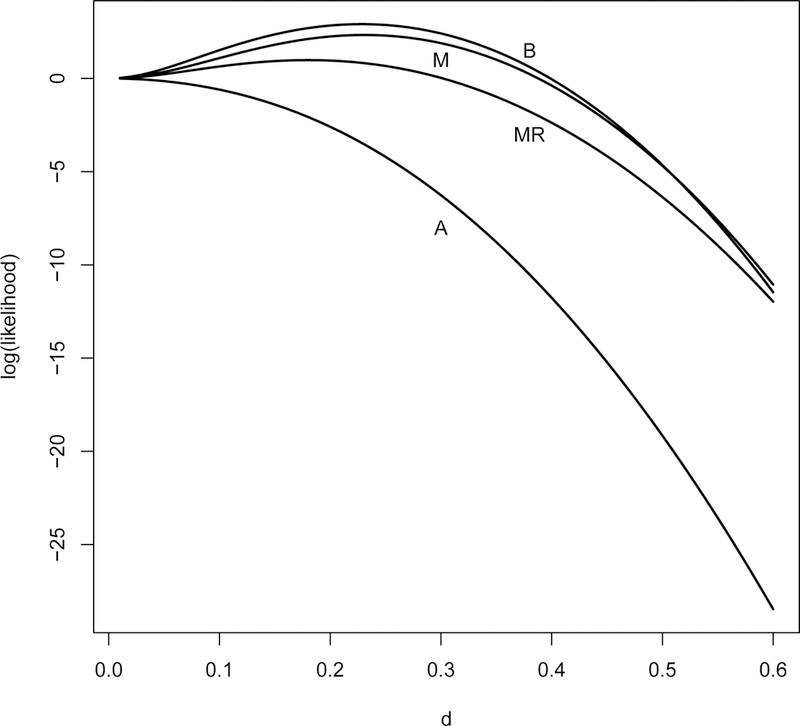
Log-likelihood function for endpoints attention (A), memory (M), behavioural (B), and memory recall (MR) of the CDP data example analyzed in Section 5.1.
Figure 2 shows the MLE exists for the 4 sets of observed p-values, however, we can not solve the score function (8) for a closed-form solution. The MLE can be obtained by iterating
| (10) |
until convergence, i.e. is sufficiently small. This algorithm is not the Newton iterations. It is to solve for the intersections of a linear and a non-linear function of d.
Some algebra shows that
where and are the mean responses for groups 1 and 2 in study i. This leads to an unbiased estimator of the effect size from study i. Therefore the overall estimate (10) could be interpreted as a weighted average with weight of the study specific estimates of the effect size each with a shrinkage factor.
To directly maximize the likelihood (7), we have developed R programs to evaluate the log likelihood numerically to obtain the MLE and its standard error. The negative log likelihood of (7) is minimized using the optimization routine nlm in R. This routine uses a Newton-type algorithm and it also provides an estimate of the Hessian matrix that was used to construct the confidence interval reported in Table 2 for an example that we use to demonstrate our methods.
TABLE 2.
Estimated overall effect size for various endpoints for the data analyzed by Fioravanti and Yanagi (2005)15 on the effect of citicoline. The sample sizes (n1, n2) for the citicoline and placebo groups are also noted under the p-values if they are different for the endpoints.
| Endpoint |
|||||
|---|---|---|---|---|---|
| Study† | Sample Size (n1, n2) |
Attention | Memory | Behavioural | Memory Recall |
| Alvarez 1999 | (12, 16) | 0.7313 | 0.4932 | ||
| Barbagallo 1988 | (60, 65) | 0.3471 | 0.9718 | 0.2894 | |
| ( 56 59) | (44 47) | (60 65) | |||
| Bonavita 1983 | (20, 20) | 1.5e-08 | |||
| Capurso 1996 | (17, 14) | 0.1122 | 0.2347 | 0.1122 | |
| Cohen 2003 | (15, 15) | 0.5770 | 0.3523 | 0.9400 | 0.3523 |
| Falchi Delitala 1984 | (15, 15) | 1.03e-08 | |||
| Madariaga 1978 | (16, 16) | 0.0017 | |||
| Motta 1985 | (25, 25) | 0.0482 | 0.2402 | 0.2404 | |
| Piccoli 1994 | (43, 43) | 0.8660 | 0.5579 | 0.6370 | 0.5579 |
| (34, 33) | (35, 34) | (43, 43) | (35 34) | ||
| Senin 2003 | (220, 232) | 0.9530 | 0.1107 | 0.3956 | 0.1107 |
| (216, 226) | (216, 221) | (220, 232) | (216, 221) | ||
| Sinforiani 1986 | (26, 32) | 0.6253 | 0.0596 | 0.0417 | 0.0596 |
| Spiers 1996 | (46, 44) | 0.5272 | |||
| Estimates | |||||
| MLE | 0.000 | 0.2283 | 0.2307 | 0.1801 | |
| 95% CI | N/A | (.0856, .3709) | (.0828, .3787) | (.0018, .3583) | |
| ‡ | 0.000 | 0.2252 | 0.2253 | 0.1039 | |
| 95% CI | N/A | (.0821, .3683) | (.0757, .3748) | (.0000, .3253) | |
| Bayes | 0.07 | 0.22 | 0.22 | 0.17 | |
| 95% CI | (.00, .19) | (.06, .37) | (.04, .37) | (.01, .34) | |
We next present an indication of heterogeneity among the studies. The indication is the convexity plot developed by Lambert and Roeder (1995)17. These plots are C(z) against z with
Where is the MLE of d and is its estimated standard error. The convexity plot indicates heterogeneity when we see a convex plot. Figure 6 shows the plots for a real data example in Section 5.1.
FIGURE 6.
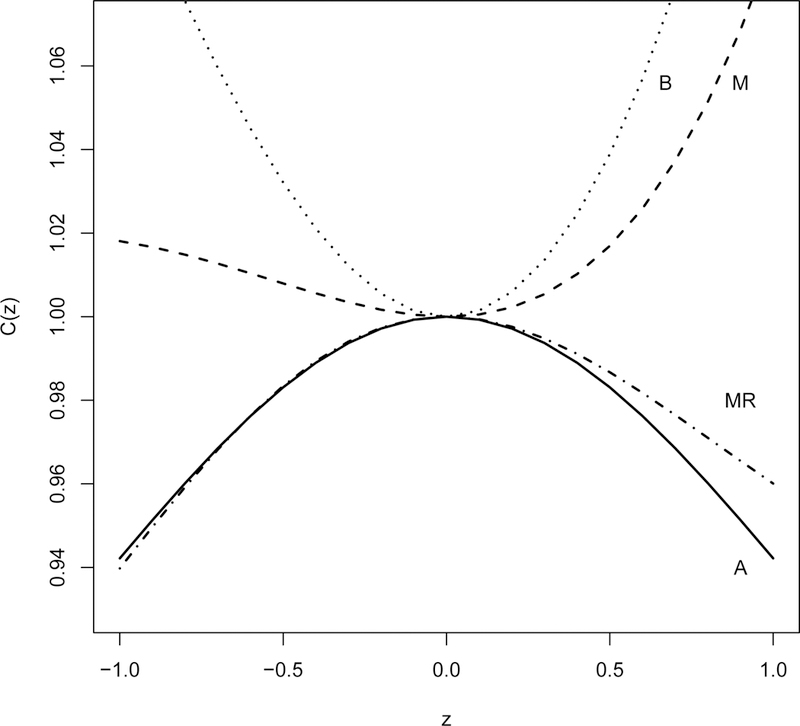
This convexity plot indicates a large amount of heterogeneity in behavior (B); a small amount in memory (M); but none in attention (A) or memory recall (MR).
3.2 |. Bayes estimate of SMD
With distribution (2) derived in Section 2, it is natural to develop a Bayesian estimate of the SMD d. The likelihood is given in (7). Let d have a prior distribution Here we consider a couple of prior distributions for In our set-up, the range for d is d ≥ 0. The gamma distribution would be a natural choice since it has a non-negative support. However, in meta-analysis, the value for d is rarely larger than 0.5. A quick power calculation tells us we only need 26 subjects per group to have 80% power to detect an effect size d = 0.8 with type I error rate of 0.05 using the 2-sample t-test. Meta-analyses are usually applied to a situation where several small or medium sample-sized studies were conducted. The studies showed a trend for a relatively small effect size and many of the studies did not demonstrate statistical significance. A combined meta-analysis would help us assemble the evidence for better inference. Such examples are presented in Section 5. With this consideration, we used the uniform (0, 1) distribution to quantify our knowledge on d that we believe d is equally likely between 0 and 1. In a second example where we infer the log odds-ratio (OR), we used uniform [−2, 2] prior. In neither example, we could obtain a closed-form expression for the posterior distribution of d or the log OR. We obtained the posterior distribution through MCMC simulations using the rstan package18. We ran 20,000 iterations with 3 chains. The mean of the posterior and the 95% credible intervals are reported in Tables 2 and 3.
TABLE 3.
Meta analysis estimate for various sets of patients: (A) all patients, (B) patients not treated with rt-PA, and (C) patients who started the highest dose of citicoline from studies reported by Secades et al. (2016)20, and (D) a meta analysis by Davalos et al. (2012)21. The sample sizes (n1, n2) for the citicoline and placebo groups are noted under the p-values if the study contributes a subset of subjects to the analysis.
| Meta Analyses by Secades et al. (2016) |
|||||
|---|---|---|---|---|---|
| Study† | Sample Size (n1, n2) |
(A) All patients |
(B) Not on rt-PA |
(C) On highest dose |
(D) Dávalos 2012 study |
| Boudouresques 1980 | (23, 22) | .0092 | .0092 | ||
| Goas 1980 | (31,33) | .0264 | .0264 | ||
| Corso 1982 | (17, 16) | .9943 | .9943 | ||
| Tazaki 1988 | (136, 136) | .00005 | .00005 | .00005 | |
| USA 1 1997 | (193, 64) | .3169 | .3169 | .2353 | .3169 |
| (65, 64) | |||||
| USA 2 1999 | (267, 127) | .4440 | .4440 | .4440 | |
| USA 3 2000 | (52, 48) | .9085 | .9085 | .9085 | |
| USA 4 2001 | (452, 446) | .0240 | .0240 | .0044 | .0240 |
| (396, 368) | |||||
| Alviarez 2007 | (29, 30) | .3668 | .3668 | .3668 | |
| ICTUS 2012 | (1148, 1150) | .5384 | .7153 | .7153 | .5384 |
| (613, 615) | (613, 615) | ||||
| Estimates | |||||
| MLE | 1.10 | 1.13 | 1.09 | 1.09 | |
| 95% CI | (1.03, 1.17) | (1.04, 1.21) | (.99, 1.19) | (1.02, 1.16) | |
| ‡ | 1.10 | 1.13 | 1.07 | 1.08 | |
| 95% CI | (1.02, 1.17) | (1.04, 1.21) | (0.97, 1.18) | (1.01, 1.16) | |
| Bayes | 1.09 | 1.12 | 1.09 | 1.08 | |
| 95% CI | (1.02, 1.17) | (1.03, 1.21) | (1.01, 1.19) | (1.01, 1.16) | |
3.3 |. A model to account for publication bias
We next propose a method to account for the publication bias that has been of concern in meta-analysis. It is well-recognized that studies with larger p-values are more difficult to be accepted for publication by journals and this bias results to truncated p-values when they are assembled from the literature. To minimize this bias, investigators are urged to conduct a thorough search on the subject to include as complete a sample of studies as possible, even to use their connections to obtain data from known but not published studies. Statistically this phenomenon can be described as the observed p-values are truncated at a threshold. Since p-values larger than the threshold τ were not accepted for publication, the observed (published) p-values follow a truncated distribution
| (11) |
where the denominator is evaluated using the CDF (3). Then the PDF (11) can be used in the likelihood function (7) to obtain a publication bias-corrected MLE of d.
A practical issue here is how to choose the threshold τ in the model. A reasonable approximation would be to use the maximum p-value of the observed sample as the threshold. We assume p-values larger than this threshold are truncated. The estimates based on the truncated distribution (11) can be similarly obtained using the numerical methods as used in Section 3.1. These estimates for several real data examples are reported in Tables 2 and 3 in Section 5.
Another publication bias concerns unequal probabilities for studies with different p-values to get accepted by journals. That means the studies we assembled have different probabilities getting into the meta-analysis sample. One way to account for this bias is to use inverse probability weighting19. However, to apply inverse probability weighting, we need to know a prior or to be able to estimate the sampling probability for each p-value, and this is beyond the focus of the current work. The inverse probability weighting can be readily applied to our method if the probabilities are known.
4 |. SIMULATION STUDIES
We simulate a spectrum of possible meta-analyses. The scenarios are determined by the number of studies (n = 6 or 12), sample size in the studies (1/3 each with sample size of (30, 50, 80) or 1/3 each with sample size of (100, 150, 200) in both arms), and the effect size d = 0.2 to 0.6. Table 1 shows the power for the studies at the two ends of the spectrum. At one extreme, investigators conduct 6 studies with sample size of (30, 50, 80, 30, 50, 80) in both arms. The powers range from 11% to 24% for an overall effect size of 0.2. This represents a situation in which investigators try to combine p-values from a group of under-powered studies. The other extreme is that investigators try to combine a group of well-powered studies, and there are many situations between the two scenarios. As our method is based on the maximum likelihood, we focused the simulation on its small sample performance (n = 6 or 12). This sample size is also consistent with many meta-analyses in practice. For each simulation scenario, the number of simulation replicates was set to 500.
TABLE 1.
Effect size, sample size and study power.
| Effect Size d | n1 = n2 | Power (%) | Effect Size d | n1 = n2 | Power (%) |
|---|---|---|---|---|---|
| 0.2 | 30 | 11 | 0.6 | 30 | 62 |
| 0.2 | 50 | 16 | 0.6 | 50 | 84 |
| 0.2 | 80 | 24 | 0.6 | 80 | 96 |
| 0.2 | 100 | 29 | 0.6 | 100 | 98 |
| 0.2 | 150 | 40 | 0.6 | 150 | > 99 |
| 0.2 | 200 | 51 | 0.6 | 200 | > 99 |
Figure 3 shows the estimates (averaged over 500 simulation replicates) along with the point-wise 95% confidence interval (dotted lines) against the true effect size. The top two panels show that our methods can estimate the effect size well for a broad range of the effect size. The right panel shows that the increased sample sizes n1i and n2i in the studies help with the estimate in terms of smaller standard errors. This suggests the practical value of combining a set of p-values from small under-powered studies. The bottom two panels show the estimates for the same simulation set-up except for a sample of 12 p-values in stead of 6 as in the two top panels. The estimates show similar excellent performance in terms of bias. The improvement with more (n = 12) studies in the meta-analysis mainly comes as smaller standard errors of the estimates. This is reflected as better power for the test against H0 : d = 0 that we discuss next. It may not be the case in practice, but we can report the study-specific SMD estimate in these simulated meta-analyses. As a comparison, we report the weighted sample mean of these study-specific SMD estimates. The inverse of the squared standard error of the estimates was used as the weight. These weighted means were almost identical to our estimates. The absolute difference between the two was in the range of 0.0002 to 0.002 for the simulated scenarios in Figure 3.
FIGURE 3.
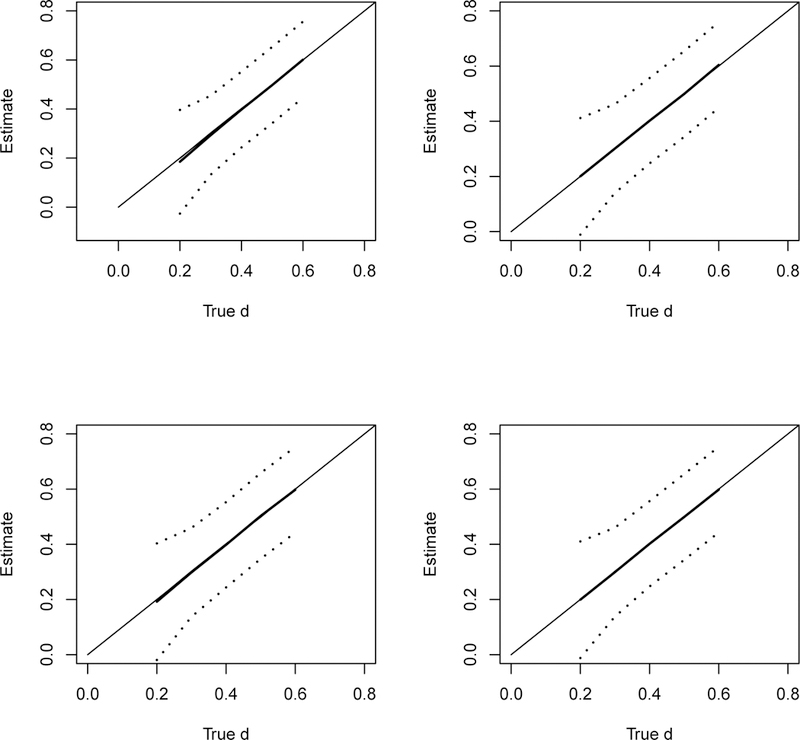
Top: Estimate of d versus true d from a sample of 6 p-values, left: 1/3 each with sample size of (30, 50, 80) and right: 1/3 each with sample size of (100, 150, 200) in both arms of the study; Bottom: same as top 2 panels except that the estimates were based on a sample of 12 p-values. The solid line is the MLE and the dotted lines are point-wise 95% confidence bound. We also report the weighted sample mean of the study-specific SMD estimates. The inverse of the squared standard error of the estimates was used as the weight. These weighted means were almost identical to our estimates and the two plots are not distinguishable.
From these simulations, we can also report the power of the Wald test against H0 : d = 0. As expected, the power of this test depends on d, the sample size n1i and n2i in the ith study, and the number of studies n in the meta-analysis. For the simulations shown in the upper left panel of Figure 3, i.e 6 studies with sample size of (30, 50, 80, 30, 50, 80) in both arms, the power was 62.6% and 91.6% for d = 0.2 and 0.3, respectively; and 100% power for d ≥ 0.4. When the sample size becomes (100, 150, 200, 100, 150, 200) per arm in the 6 studies (upper right panel), the power improves to 97.4% for d = 0.2; and 100% power for d ≥ 0.3. On the other hand, when the number of studies increases to n = 12 in the meta-analysis with 4 each with sample size (30, 50, 80) in both arms (lower left panel), the power improves to 79.6% for d = 0.2; and 100% power for d ≥ 0.3. For the scenario with n = 12 studies with larger sample size (lower right panel), the power improves to 100% for d ≥ 0.2.
In the above simulations, all the studies included in the meta-analysis have exactly the same effect size. In practice, these studies may have heterogeneous d’s. We simulated the scenario with n = 6 studies with sample size of (30, 50, 80, 30, 50, 80) in both arms, but the effect size d spreads as a sequence of 0.125, 0.135, 0.145, 0.155, 0.165, 0.175 with mean 0.15. Scenarios of similar sequentially-spreaded effect sizes with means of 0.20, 0.25, 0.30, and 0.35 are also simulated. Figure 4 shows the estimates (averaged over 500 simulation replicates) along with the point-wise 95% confidence interval (dotted lines) against the average of the heterogeneous effect size among the 6 studies. Here we use the arithmetic average of the heterogeneous effect size to represent the simulation scenario for plotting purpose. The average itself is not meaningful. This is the case where a true overall common effect size does not exist, however we used our methods to estimate such an overall effect. The estimates are 0.145, 0.195, 0.259, 0.310, 0.362, which happen to be close to the average effect size. The top line in Figure 4 is the power of the Wald test against H0 : d = 0. In this case with heterogeneous effect size, the power is slightly smaller than but fairly close to the power in the above correct configurations of scenarios each with one exact common effect size.
FIGURE 4.
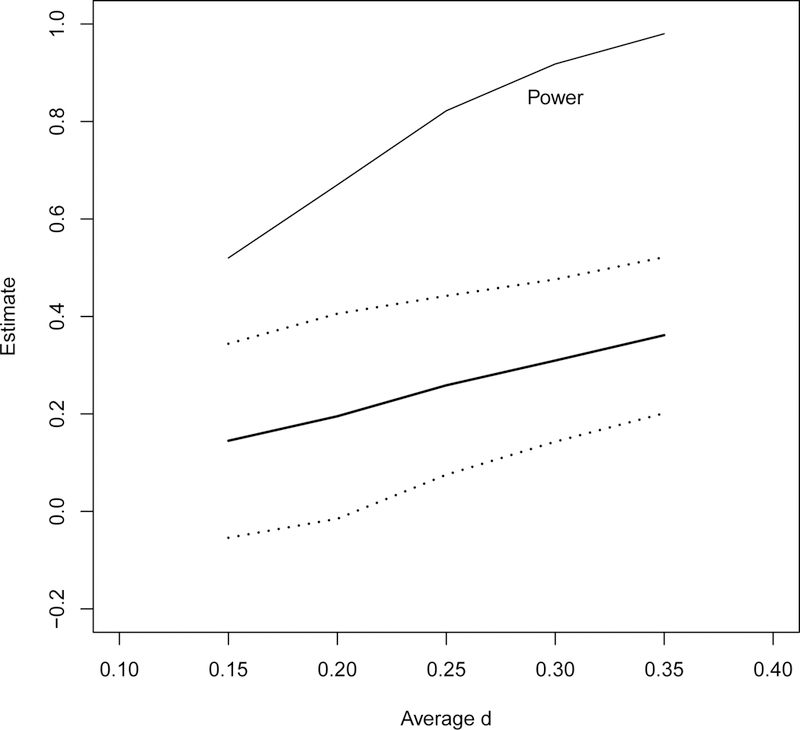
Estimate of d versus average d from a sample of 6 p-values with heterogeneous sequentially-spreaded effect size, 1/3 each with sample size of (30, 50, 80). The effect sizes for the 6 studies are 0.125, 0.135, 0.145, 0.155, 0.165, and 0.175 with mean 0.15, and 0.175 to 0.225 with mean 0.20, 0.225 to 0.275 with mean 0.25, 0.275 to 0.325 with mean 0.30, and 0.325 to 0.375 with mean 0.35. The solid line is the MLE and the dotted lines are point-wise 95% confidence bound. The top line is the empirical power of the Wald test against H0 : d = 0.
From these simulations, we have observed our methods provide a good estimate of the overall common effect size when all the studies have the same SMD. When the effect size is heterogeneous, our methods still provide a reasonable summary of the overall effect. The Wald test against the null hypothesis H0 : d = 0 has excellent power when the true d or the estimate of d in the case with heterogeneous effect size is not too small in a meta-analysis with as few as 6 studies.
5 |. META ANALYSES OF THE EFFECTS OF CITICOLINE
Citicoline, also named Cytidinediphosphocholine or CDP-choline, is a widely available supplement in the US. It is a drug approved for the treatment of acute ischemic stroke in Europe20. It has been studied in many clinical trials to evaluate its potential benefits for patients with memory disorders15 and ischemic stroke20,21,22. Many meta-analyses have been conducted to assemble the evidence15,20. Here we reanalyze three recent meta-analyses to demonstrate our methods.
5.1 |. Effect of citicoline on memory function and behavior
Fioravanti and Yanagi (2005)15 reported a carefully-conducted meta-analysis to assess the efficacy of citicoline in the treatment of cognitive, emotional, and behavioral deficits associated with chronic cerebral disorders in the elderly. The outcomes they examined include attention, memory, behavioral, the Alzheimer’s disease assessment scale (ADAS-cog), clinical evaluation of improvement, the clinicians global impression of change (CIBIC) score, and tolerability measures. Among the endpoints, clinical evaluation of improvement and tolerability measures are assessed using odds ratios. Outcomes ADAS-cog and CIBIC score were only assessed in 1 study and 2 studies, respectively. Therefore, in this report only continuous outcomes attention, memory, behavioral, and memory recall are analyzed using our methods.
Table 2 summarizes the studies included in this meta-analysis and their contributions to the 4 continuous endpoints. The p-values are calculated from the means and standard deviations reported in the analysis tables in Fioravanti and Yanagi (2005)15 using the two-sample t-test. Almost identical p-values were obtained when we also applied the two-sample normal test. The bottom of Table 2 are estimated effect size with their 95% confidence intervals (CI) based on these p-values using our methods.
For endpoint attention, its log-likelihood plotted in Figure 2 shows a maximum at zero, suggesting a close to zero SMD.
For endpoint memory measures, the MLE of the SMD is 0.23 with 95% CI (0.09, 0.37). The study of Bonavita (1983)23 contributed a very small p-value. The meta-analysis by Fioravanti and Yanagi (2005)15 deemed this study an outlier since it “used an idiosyncratic non-standardized procedure for memory evaluation”, and they repeated their analysis with this study removed. We would like to note in our set-up this is not a reason to remove a study from the meta analysis. Table Analysis 1.2 in Fioravanti and Yanagi (2005)15 clearly shows that there was heterogeneity among the studies that collected memory measures. The density curves for p-values given in Figure 1 show that small “outlier” p-values are possible. Instead, we borrow the concept of Dfbeta from the regressions to evaluate each p-value’s impact on the estimate. We obtained when each p-value is deleted from the sample in a jackknife. The dashed lines in Figure 5 are the jackknife for the endpoints. As expected, these jackknife estimates deviate in both directions from the estimate using the full sample. Some of the deviations are sizable, however, we would like to note the sample size (the number of p-values) is small in this meta-analysis and any one p-value could potentially have a significant impact on the overall estimate. We need to exercise caution when removing any one study from the meta-analysis.
FIGURE 5.
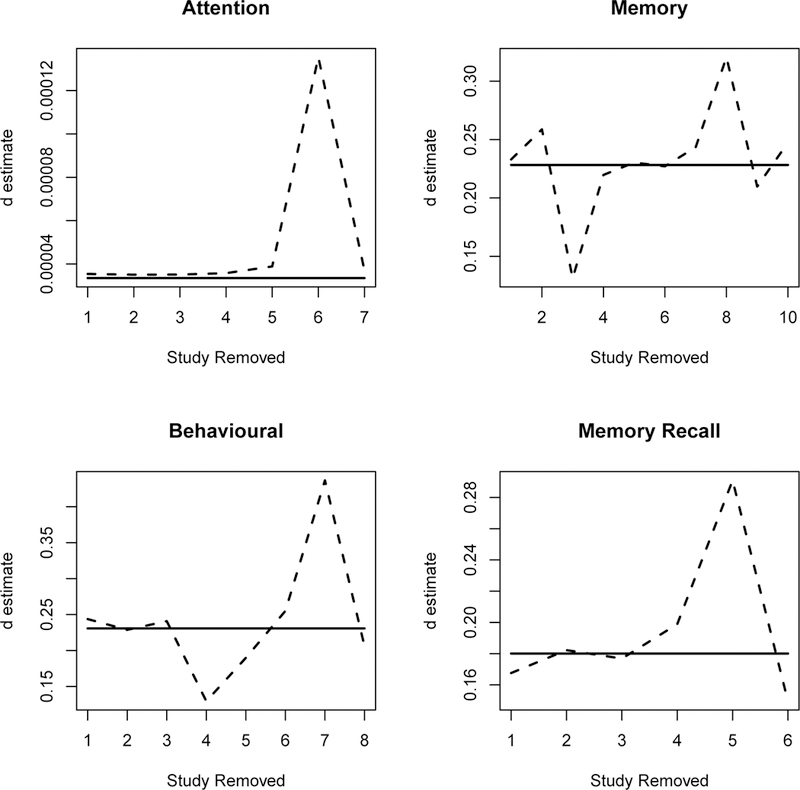
Jackknife influence of each p-value on solid line for using the full sample, dashed line for jackknife with the p-value from one study removed.
Figure 6 shows the convexity plots discussed at the end of Section 3.1 for this data example. These plots suggest a large amount of heterogeneity in behavior (B); a small amount in memory (M); but none in attention (A) or memory recall (MR).
The MLE based on the truncated distribution (11) are similar to the regular MLE except for the endpoint memory recall. It is because the maximum p-values were 0.9530, 0.9718, and 0.9400 for the other 3 endpoints, which result to very little truncation. On the other hand, the maximum p-value was 0.5579 for the endpoint memory recall. This results to a notable difference on the estimates.
The Bayesian estimates using non-informative uniform (0, 1) prior are also reported in Table 2. These Bayesian estimates are consistent with the MLE’s.
In summary, our analyses are consistent with the results reported in Fioravanti and Yanagi (2005)15 for these endpoints, supporting a small but statistically significant treatment effect of citicoline on memory, behavioral, and memory recall.
5.2 |. Effect of citicoline on recovery from stroke
The effect of citicoline on recovery from stroke has not been consistent. While the largest trial to date, the International Citicoline Trial on acUte Stroke (ICTUS)21, found no benefit of administering citicoline on survival or recovery from stroke, many early smaller-sized trials and two meta-analyses20,21 support some beneficial effect in the treatment of acute ischemic stroke.
Secades at al. (2016)20 conducted a systematic review to identify published randomized, double-blinded, placebo-controlled clinical trials of citicoline in patients with acute ischemic stroke. They assembled 10 studies to conduct a meta analysis to assess if treatment with citicoline (started within 14 days of stroke onset) improves independence when compared with placebo. The binary outcome independence is defined as a modified Rankin Scale score of 0–2 or equivalent. The contributions of these studies to the 3 meta-analyses are summarized in Table 3.
When reporting the results of the ICTUS trial, Dávalos et al.21 also conducted a meta analysis to put their results in the context. They included five studies and their ICTUS in the meta analysis. These 5 studies are a subset of the studies in the meta analysis by Secades at al. (2016)20. The reasons why Dávalos et al. (2012) included these studies can be found on page 35521. The results are in the last column of Table 3.
These meta-analyses reported odds-ratio (OR) as the efficacy measure since the outcome independence is binary. We worked with the log OR since the common model-based MLE of log OR is asymptotically normally distributed. This is generally true for many model-based parameter estimates based on the maximum likelihood theory. Our methods can be broadly applied to combine p-values from these studies due to the normality of the estimates.
For all 4 meta-analyses, our methods provided OR estimates that are smaller than the originally reported estimates20,21, suggesting a small but still statistically significant citicoline effect. The MLE based on the truncated distribution (11) are very close to the regular MLE since there is very little truncation in the p-values. The Bayesian estimates using non-informative uniform [−2, 2] prior are also reported in Table 3. These Bayesian estimates are almost identical with the MLE’s. We also run the analysis using normal (0,1000) prior, and the estimates are almost unchanged.
In summary, our analyses are consistent with the results reported in earlier meta-analyses20,21, suggesting a smaller but still statistically significant treatment effect of citicoline on post-stroke independence.
6 |. DISCUSSION
This work started with a set of p-values to be combined and we ended up developing an estimator of SMD. We would like to comment on a connection between our maximum likelihood-based method and some of the existing methods in the literature.
The popular z-tests can be generally formulated as:
| (12) |
where wi is the weight for study i. When all wi = 1, test (12) is the unweighted Stouffer test by Stouffer et al. (1949)24. A limitation of this approach is that studies with different sample sizes give us estimates with different precision and this needs to be accounted for when we combine the studies. When wi = ni, where ni is the sample size for study i, test (12) is called the Mosteller-Bush test25. Our method is similar to this procedure, but with a shrinkage factor that discounts studies with small sample sizes. Other researchers suggested that we use the square root of the sample size or the inverse of the estimated standard error as weights1. Our MLE provides a theoretical justification on choosing the weight and it has a built-in shrinkage against chance finding in small-sized studies.
Another issue in meta-analysis is that the assembled p-values may be obtained using different test statistics. For tests that are not associated with an effect size indicator, e.g. nonparametric tests, dequivalent or requivalent developed and discussed in Rosenthal and Rubin (2003)26, Kraemer (2005)27, and Hsu (2005)28 may be obtained for the individual studies. Then traditional weighting schema may be used to combine them. We derived the distribution of the p-values for the 2-tailed normal test and the t-test. The MLE of the SMD is developed for the normal test. This may appear to be a limitation of our method since our method would be ideally applied to a set of p-values obtained using the normal test. However, it is straight forward for readers to extend the MLE for their specific tests or even for a mixture of tests as long as the parameter has the same interpretation since the likelihood can be constructed accordingly for p-values from different tests. In the case of regression analysis of randomized clinical trials with two arms, when covariates that are orthogonal to the treatment assignment are included in the model, the estimate of the between-arm difference remains the same, but the residual error variance σ2 decreases. The net effect is improved power. However, when the number of covariates is far less than the sample size, the distribution of the p-values follows (5) from a t-test and is approximately in the form of (2). Furthermore, given the relationship between the normal test and the t-test and the chi-squared test, our methods can be applied to combine p-values obtained using these test statistics. We present such an example of inference on the log OR in Section 5.2. In other scenarios, such as when p-values are obtained using the Wald test, the score test, or the likelihood ratio test, we would not suggest our method would fit for all of them. The distribution of the p-values needs to be individually derived for these scenarios.
We developed our method for a 2-tailed test in which the direction of the efficacy is lost as is the case for many other methods discussed above. This appears to be a limitation. From the technical aspect, our method can be modified to combine one-sided p-values. However, one-sided test is not common and needs to be justified prospectively for use in practice (Section 5.5, page 25, International Conference on Harmonisation of Technical Requirements for Registration of Pharmaceuticals for Human Use, 199829). Furthermore, one should always carefully examine the studies included in the meta-analysis and be particularly cautious when combining a set of p-values where some of the studies point to opposite directions of efficacy if ever one decides to pursue such a meta-analysis.
There is nonparametric work14,30,31,32 that describes distributions for p-values. These non-parametric distributions may fit the p-value mixtures well, however, they did not explicitly parameterize the effect size and the sample size in the distribution. Therefore, it is difficult to utilize them in meta-analyses. Our method using derived distributions for p-values allows us to establish a spectrum of estimates for the SMD, including an estimator to account for publication bias and Bayesian estimators.
ACKNOWLEDGMENT
This work was supported in part by Vanderbilt CTSA grant 1ULTR002243 from NIH/NCATS, R01 CA149633 from NIH/NCI, R21 HL129020, P01 HL108800 from NIH/NHLBI, R01 FD004778 from FDA (CY) and grants P50-CA196530, P30-CA16359, R01-CA177719, R01-ES005775, R41-A120546, U48-DP005023, and R01-CA168733 awarded by NIH (DZ).
Footnotes
Financial disclosure
None reported.
Conflict of interest
The authors declare no potential conflict of interests.
References
- 1.Zaykin DV (2011). Optimally weighted Z-test is a powerful method for combining probabilities in meta-analysis, Journal of Evolutionary Biology 24(8):1836–1841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Fisher RA (1932). Statistical Methods for Research Workers. Oliver and Boyd, Edinburgh. [Google Scholar]
- 3.Sutton A, Abrams K, Jones D, Sheldon T, Song F (2000). Methods for meta-analysis in medical research. Chichester: John Wiley. [Google Scholar]
- 4.Cousins RD (2008). Annotated bibliography of some papers on combining significances or p-values, arXiv:0705.2209v2. [Google Scholar]
- 5.Won S, Morris N, Lu Q, Elston RC (2009). Choosing an optimal method to combine P-values. Statistics in Medicine 28(11):1537–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chen Z, Nadarajah S (2014). On the optimally weighted z-test for combining probabilities from independent studies. Computational Statistics & Data Analysis 70:387–394. [Google Scholar]
- 7.Chen Z, Yang W, Liu Q, Yang J, Li J, Yang MQ (2014). A new statistical approach to combining p-values using gamma distribution and its application to genome-wide association study. BMC Bioinformatics 15 (Suppl 17):S3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lancaster H (1961). The combination of probabilities: an application of orthonormal functions. Australian Journal of Statistics 3:20–33. [Google Scholar]
- 9.Pearson ES (1938). The Probability transformation for testing goodness of fit and combining independent tests of significance. Biometrika 30:134–148. [Google Scholar]
- 10.Donahue RMJ (1999). A note on information seldom reported via the p value. The American Statistician 53: 303–306. [Google Scholar]
- 11.Hung HMJ, O’Neill RT, Bauer P, and Kohne K (1997). The behavior of the p-value when the alternative hypothesis is true. Biometrics 53: 11–22. [PubMed] [Google Scholar]
- 12.Yu C, Zelterman D. (2017). A parametric model to estimate the proportion from the null in microarray studies using a distribution for p-values, Computational Statistics & Data Analysis 114:105–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Koziol JA, Tuckwell HC (1999). A Bayesian method for combining statistical tests. Journal of Statistical Planning and Inference 78:317–323. [Google Scholar]
- 14.Genovese C, Wasserman L (2004). A stochastic process approach to false discovery control. The Annals of Statistics 32:1035–1061. [Google Scholar]
- 15.Fioravanti M, Yanagi M (2005). Cytidinediphosphocholine (CDP-choline) for cognitive and behavioural disturbances associated with chronic cerebral disorders in the elderly (Cochrane Review) Cochrane Database of Systematic Reviews. Update Software: Oxford, 2000, Issue 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Higgins JP, Thompson SG (2002). Quantifying heterogeneity in a meta-analysis. Statistics in Medicine 21(11):1539–58. [DOI] [PubMed] [Google Scholar]
- 17.Lambert D, Roeder K (1995). Overdispersion diagnostics for generalized linear models. Journal of the American Statistical Association, 90: 1225–36. [Google Scholar]
- 18.Stan Development Team (2018). RStan: the R interface to Stan. https://cran.r-project.org/web/packages/rstan/vignettes/rstan.html.
- 19.Horvitz DG, Thompson DJ (1952). A generalization of sampling without replacement from a finite universe. Journal of the American Statistical Association 47: 663–685. [Google Scholar]
- 20.Secades JJ, Alvarez-Sabín J, Castillo J, Díez-Tejedor E, Martínez-Vila E, Rios J, Oudovenko. (2016). Citicoline for Acute Ischemic Stroke: a systematic review and formal meta-analysis of randomized, double-blind, and placebo-controlled trials. Journal of Stroke and Cerebrovascular Diseases 25: 1984–1996. [DOI] [PubMed] [Google Scholar]
- 21.Dávalos A, Alvarez-Sabín J, Castillo J, Díez-Tejedor E, Ferro J, Martínez-Vila E, Serena J, Segura T, Cruz VT, Masjuan J, Cobo E, Secades JJ for the International Citicoline Trial on acUte Stroke (ICTUS) trial investigators. (July 2012). Citicoline in the treatment of acute ischaemic stroke: an international, randomised, multicentre, placebo-controlled study (ICTUS trial). Lancet 380 (9839): 349–57. [DOI] [PubMed] [Google Scholar]
- 22.Overgaard K (2014). The Effects of Citicoline on Acute Ischemic Stroke: A Review. Journal of Stroke and Cerebrovascular Diseases 23: 1764–1769. [DOI] [PubMed] [Google Scholar]
- 23.Bonavita E, Chioma V, Dall’Oca P, Fini C, Michelini M, Ruggi MR, Merli R, Ferro O (1983). Double-blind study on CDP-choline activity in primitive mild cognitive deterioration cases. Minerva Psichiatrica 24:53–62. [PubMed] [Google Scholar]
- 24.Stouffer SA, Suchman EA, DeVinney LC, Star SA, and Williams RM Jr. (1949). The American Soldier, Vol. 1: Adjustment During Army Life. Princeton University Press, Princeton. [Google Scholar]
- 25.Mosteller F, and Bush RR (1954). Selected quantitative techniques In: Handbook of Social Psychology, Vol. 1 Lindzey G, editor, pp. 289–334. Addison-Wesley, Cambridge, Mass. [Google Scholar]
- 26.Rosenthal R, and Rubin DB (2003). r(equivalent): A simple effect size indicator. Psychological Methods 8:492–496. [DOI] [PubMed] [Google Scholar]
- 27.Kraemer HC (2005). A simple effect size indicator for two-group comparisons? A comment on r(equivalent). Psychological Methods 10:413–419. [DOI] [PubMed] [Google Scholar]
- 28.Hsu LM (2005). Some properties of r(equivalent): A simple effect size indicator. Psychological Methods 10:420–427. [DOI] [PubMed] [Google Scholar]
- 29.International Conference on Harmonisation of Technical Requirements for Registration of Pharmaceuticals for Human Use (1998), Statistical Principles for Clinical Trials, E9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Broberg P (2005). A comparative review of estimates of the proportion unchanged genes and the false discovery rate. BMC Bioinformatics 6: 199–218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Langaas M, Lindqvist BH, and Ferkingstad E (2005). Estimating the proportion of true null hypotheses, with application to DNA microarray data. Journal of the Royal Statistical Society B 67: 555–72. [Google Scholar]
- 32.Tang Y, Ghosai S, Roy A. (2007). Nonparametric Bayesian estimation of positive false discovery rates. Biometrics 63: 1126–34. [DOI] [PubMed] [Google Scholar]


