System-level matching of structural and functional connectomes in the human brain

Abstract

The brain can be considered as an information processing network, where complex behavior manifests as a result of communication between large-scale functional systems such as visual and default mode networks. As the communication between brain regions occurs through underlying anatomical pathways, it is important to define a “traffic pattern” that properly describes how the regions exchange information. Empirically, the choice of the traffic pattern can be made based on how well the functional connectivity between regions matches the structural pathways equipped with that traffic pattern. In this paper, we present a multimodal connectomics paradigm utilizing graph matching to measure similarity between structural and functional connectomes (derived from dMRI and fMRI data) at node, system, and connectome level. Through an investigation of the brain’s structure-function relationship over a large cohort of 641 healthy developmental participants aged 8 to 22 years, we demonstrate that communicability as the traffic pattern describes the functional connectivity of the brain best, with large-scale systems having significant agreement between their structural and functional connectivity patterns. Notably, matching between structural and functional connectivity for the functionally specialized modular systems such as visual and motor networks are higher as compared to other more integrated systems. Additionally, we show that the negative functional connectivity between the default mode network (DMN) and motor, frontoparietal, attention, and visual networks is significantly associated with its underlying structural connectivity, highlighting the counterbalance between functional activation patterns of DMN and other systems. Finally, we investigated sex difference and developmental changes in brain and observed that similarity between structure and function changes with development.

1. Introduction

Human cognition that enables basic actions and their coordination is presumably driven by the complex and dynamic functional interactions among brain regions (Bressler and Menon 2010). These functional interactions are facilitated through and constrained by anatomical connections between regions (Honey et al. 2009). The question of how the rich functional dynamics emanate from static anatomical connections has been a major focus of research (Menon 2011). Addressing this question has a crucial role in understanding neurodevelopment (Gu et al. 2015) and investigating disorders in which connectivity is affected, such as traumatic brain injury (TBI), autism, and a variety of other neuropsychiatric conditions (Cocchi et al. 2014; Ecker et al. 2015; Xiao et al. 2015).

Recent years have seen the evolution of connectomics, the study of brain connectivity, in which structural and functional connectivity of the brain are modeled as graphs of interconnected regions with weighted edges representing the strength of connectivity (Hagmann et al. 2008, Bullmore and Sporns 2009; Rubinov and Sporns 2010). Within such a representation, the relationship between the structure and function was initially studied at the level of individual edges between nodes, seeking correlations between functional and structural connectivity of brain regions (Honey et al. 2009, Hermundstad et al. 2013). Although strong functional connections were shown to exist in the presence of direct structural connections, relatively weaker functional connections were also evident in the absence of direct structural connections (Honey et al. 2010). Presence of such indirect connections among regions (Mišić et al. 2016) requires a system level analysis to have a better understanding of how indirect functional connections are facilitated through anatomical pathways.

1.1. Traffic patterns in the brain

Several studies in the emerging field of network neuroscience (Bassett and Sporns 2017) have presented the brain as an information processing network with special characteristics such as small worldness (Watts and Strogatz 1998), existence of hub regions (van den Heuvel and Sporns 2013), and community structure (Newman 2018). By modeling the brain as an information processing network, the structural pathways of the brain can be regarded as a geographical map where the functional interactions among brain regions would be considered as the traffic flow over the pathways. This perspective accounts for indirect functional interactions between regions by assuming information exchange through intermediate regions, which then requires defining the nature of the traffic pattern. Shortest path has been the most commonly adopted model for describing the interactions among regions, as it complies with the established theory of efficiency of brain networks (Bullmore and Sporns 2012). The main assumption of this model is that communication between regions is established through the unique optimal (shortest) path between them (van den Heuvel et al. 2012). Despite its widespread use, shortest path suffers from restricting communication to a single pathway and requires global knowledge of the network for finding the unique paths between pairs, limiting its adaptability to brain networks. To overcome these limitations, “diffusive” traffic patterns such as path transitivity (Goñi et al. 2014) and communicability (Estrada and Hatano 2008) were introduced, which assume information exchange between regions through multiple parallel pathways that are not necessarily the shortest, providing a better explanation for the communication in the brain, especially in the case of disruption of shortest connectivity due to pathology (Grayson et al. 2016). Recently, a deep neural network-based approach was shown to predict function from structure efficiently, albeit providing little insight into the pattern of communication due to complex structure of deep learning methods (Rosenthal et al. 2018). Despite several studies in the field, the exact communication scheme that the brain adopts is difficult to ascertain and an extensive comparative analysis of traffic patterns is desirable.

1.2. Structure-function relationships at the level of large-scale functional systems

Analyzing the network structure of the brain further revealed that the human brain is functionally organized into large-scale systems, such as the default mode network (DMN), vision, and attention that interact at multiple temporal and spatial scales, giving rise to complex behavior (Bressler and Menon 2010). These findings triggered a shift of focus in the investigation of structure-function relationships from the level of individual connections towards network level interactions (Mišić and Sporns 2016). An early study demonstrated that functional systems in the brain are connected through structural white matter tracts that facilitate the communication between systems (van den Heuvel et al. 2009). Recently, the relationships between structural and functional networks have been studied by investigating correlations between sets of structural and functional connections in humans (Mišić et al. 2016), and by investigating multiplex network models in rats (Crofts et al. 2016). Another recent study showed the distributed effects of removing a single region from the rhesus monkey brain, highlighting the global functional effects of local structural changes in the brain (Grayson et al. 2016). Although the structure-function relationship of certain systems such as DMN or vision are investigated individually in literature, a comprehensive analysis over major functional systems allowing comparison between their structure-function relationship is still lacking. Despite their promising results, such studies have a common limitation as they only consider the structural underpinnings of positive functional connectivity, while ignoring negative functional connectivity. Thus, it is desirable to jointly investigate the structural underpinnings of positive and negative functional connectivity of major functional systems.

1.3. Change in structure-function relationship with sex and age

Several studies have demonstrated behavioral differences between sexes, such as enhanced motor skills in males (Moreno-Briseño et al. 2010) and better social cognition skills in females (Williams et al. 2009). Structural and functional connectivity differences across sexes have been shown to characterize these behavioral differences (Satterthwaite et al. 2014; Ingalhalikar et al. 2014; Tunç et al. 2016), providing insights into the differential developmental trajectories of sexes. Although the structural and functional connectivity differences across sexes are widely studied independently, sex difference in the structure-function relationship remains unexplored.

Developmental changes in structure and function of the human brain have been widely studied, with several studies reporting an increase in brain volume as well as structural and functional connectivity in early childhood and “pruning” in structural and functional connectivity with age in adolescence (Satterthwaite et al. 2013; Gu et al. 2015). Despite several studies investigating developmental changes in structural and functional connectivity independently, maturation of structure-function relationship with age have seldom been considered (Supekar et al. 2010; Betzel et al. 2014).

1.4. Graph matching as a tool for investigating the structure-function relationship in the human brain

Although various methods are devised for the analysis of the structure-function relationship of the brain, the topological information stored in the connectome is generally neglected that could otherwise be beneficial for identifying relationships between nodes as well as subnetworks. Considering the fact that the connectomes are graphs, the problem of finding (dis)similarities between structural and functional connectomes can be considered as an instance of the graph matching problem (Conte et al. 2004). The main idea in graph matching is to find a mapping between similar nodes and edges of two graphs along with an overall similarity measure, which subsequently facilitates statistical analyses, such as classification, clustering, or regression, based on the observed similarities. Graph matching is a robust method for defining similarity between network-like structures as it considers the network topology in similarity calculations in addition to local network features, and allows defining similarity measures from individual nodes to node clusters at various levels. Although widely applied in pattern recognition and computer vision over several decades (Conte et al. 2004, Osmanlıoğlu et al. 2016), graph matching techniques have only recently started to emerge as similarity metrics in neuroscience research (Ktena et al. 2017, Osmanlıoğlu et al. 2018). The studies in this setting commonly utilize connectomes obtained from a single modality (such as fMRI, EEG, or DTI) and investigate group differences across samples using various techniques, such as graph edit distance (Ktena et al. 2016), graph embedding (Richiardi et al. 2012), graph kernels (Mokhtari and Hossein-Zadeh, 2013), or Reeb graph matching (Shi et al. 2014). Such methods have been used for determining brain states over fMRI, labeling brain regions (Yang and Kruggel, 2009), and finding similar brains in a dataset (Shi et al. 2014). As these studies investigate connectomic similarity over a single connectivity type, it is desirable to extend the use of graph matching into finding similarity across different connectivity types, such as structural and functional connectivity of human brain.

1.5. Contributions

Using a large cohort of 641 participants aged 8 to 22 years, we sought to elaborate how functional interactions between large-scale systems derived from resting state functional connectivity are shaped by underlying structural pathways reconstructed using diffusion tensor imaging. Considering the brain as an information processing network, we used graph matching to investigate the relationship between the structure and function of the human brain. Specifically:

• We proposed matching accuracy obtained through graph matching as a similarity measure to quantify similarity between the structural and functional connectivity in the human brain at node, systems, and connectome level.

• Using graph matching, we investigated the traffic pattern that best describes the structure-function relationship in the brain. We made a comprehensive comparison of seven traffic patterns (i.e., direct connections, weighted and unweighted shortest path, search information, path transitivity, and weighted and unweighted communicability) and showed that weighted communicability provides the best explanation for the functional connectivity of the brain.

• We investigated how structure-function relationships determine the interactions among large-scale functional systems (e.g. DMN, vision, motor, frontoparietal) and how network characteristics of these systems affect their inter-relationship. We showed that systems display significant agreement between their structural and functional connectivity patterns, indicating that functional connectivity profiles of large-scale functional systems are shaped by their structural connectivity. We further showed that functionally modular systems such as visual and motor have stronger agreement between their structure and function, which supports the hypothesis that these systems act as sensory modules having sparse structural and functional connectivity with other systems (Bassett and Sporns 2017).

• We demonstrated that negative functional connectivity of DMN with the motor, frontoparietal, attention, and visual systems are significantly associated with their underlying structural connectivity with respect to the rest of the brain. This result points to the possible structural basis of the dynamic counterbalance between activation patterns of the task-negative (DMN) and the task-positive (other) systems (Fox et al. 2005).

• We investigated sex differences in structure-function relationship and how the structure-function relationship changes with age. Although differences across genders have been reported for structural (Ingalhalikar et al. 2014; Tunç et al. 2016) and functional (Satterthwaite et al. 2014) connectomes independently, we did not observe a consistent significant group difference between the sexes in how functional interactions arise from structural connectivity. On the other hand, we showed that similarity between structural and functional connectivity decreases during development, possibly indicating that the communication pattern in the brain becomes more complex with age.

2. Materials and methods

Fig. 1 gives an overview of the proposed matching approach for evaluating the structure-function relationship in the human brain. In this section, we first present the details of the dataset used and the process through which structural and functional connectomes are derived from MRI image data. We then explain the graph matching approach and propose matching accuracy as a measure of similarity between structural and functional connectomes. Finally, we provide details of statistical tools that are used in our analysis for evaluating the significance of matching results, identifying the group difference between sexes, and investigating the relationship between age and structure-function similarity.

Figure 1.

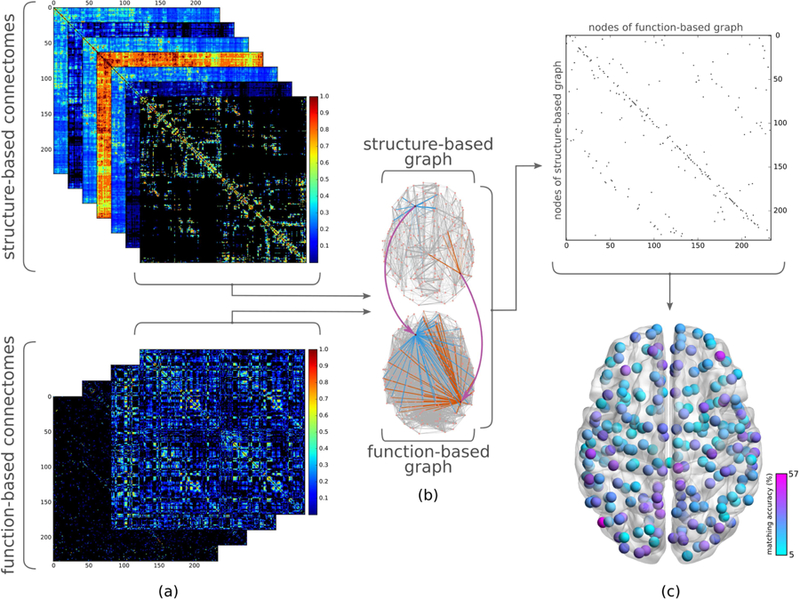
Overview of study of structure-function relationship using graph matching. (a) (top) Separate connectomes corresponding to various traffic patterns are derived from the weighted structural connectome (i.e., direct connections, unweighted and weighted shortest path, search information, path transitivity, unweighted and weighted communicability). (bottom) Positive and negative functional connectivities for full and partial correlation-based functional connectomes are considered separately in order to investigate structural underpinnings of positive and negative functional connectivity independently. (b) Taking one structure and one function derived connectome, the similarity between their graph representations is calculated using graph matching, yielding a binary matching matrix (c) (top) which contains ones to indicate nodes of a structure-based graph (rows) mapped to those of a function-based graph (columns) with the most similar connectivity patterns, and zeros elsewhere. (Note the difference between a matching matrix and a connectome: a cell of the matching matrix corresponds to a node of structure-based graph matching to a node of function-based graph, whereas a cell in the connectome indicates two regions of the brain being structurally or functionally connected.) (c) (bottom) Averaging the resulting binary matching matrices for all subjects, we obtain the likelihood of accurately matching each structural region with its functional counterpart.

2.1. Participants

The cross-sectional dataset used in this study was acquired as part of the Philadelphia Neurodevelopmental Cohort (PNC) containing scans of 1601 subjects. Institutional Review Board approval was obtained from the University of Pennsylvania and the Children’s Hospital of Philadelphia. Participants were excluded from this analysis due to poor structural and functional imaging data quality or a history that suggested potential abnormalities of brain development such as a history of medical problems that might affect brain function, a history of inpatient psychiatric hospitalization, or current use of psychotropic medication. The final study sample included 641 participants between 8 and 22 years of age (see Table 1).

Table 1.

Demographics of the age-matched samples of the males and females

	Count	Age years (SD)
Total	641	15.61 (3.37)
Females	380	15.60 (3.31)
Males	261	15.62 (3.45)

2.2. Data acquisition, preprocessing, and connectomes

2.2.1. Image acquisition

Resting-state functional MRI (fMRI) and diffusion weighted MRI (dMRI) scans were acquired for each individual, on the same 3T Siemens Tim Trio 3 Tesla whole-body scanner and 32-channel head coil at the Hospital of the University of Pennsylvania. Resting-state BOLD fMRI was acquired using a whole-brain, single-shot, multislice, gradient-echo echo planar sequence (TR/TE = 3000/2ms, flip angle = 90, FOV = 192×192mm, matrix = 64×64, gap = 0, resolution = 3×3×3mm, volumes = 124). DTI scans were acquired using a twice-refocused spin-echo single-shot echo-planar imaging sequence (TR/TE = 8100/82ms, flip angle = 90/180/180, FOV = 240×240mm, resolution = 1.9×1.9×2mm, gap = 0, volumes = 71, 64 diffusion directions with b=1000s/mm² and 7 b = 0 images).

2.2.2. Parcellations

In order to capture the robustness of structure-function relationship across various resolutions of the same atlas, as well as across different atlases of comparable resolution, we parcellated the structural and functional data into 129, 234, and 463 regions using three scales of the Lausanne atlas (Hagmann et al. 2008) as well as 400 regions of the Schaefer atlas (Schaefer et al. 2017). In our analysis, we considered the Lausanne 234 parcellation as the basis and used the rest of the parcellations for validation of our results.

2.2.3. Generating functional connectomes

The preprocessing of fMRI data involved motion correction, signal stabilization, band-pass filtering, alignment, skull stripping, and segmentation (see Satterthwaite et al. 2014 for details). In our analysis, we mainly investigated the relationship between the structural connectomes and full correlation-based functional connectomes which we estimated using Pearson’s correlation between time points (referred as “full connectomes”). Additionally, we investigated relationship between structural and partial correlation based functional connectivity, where we obtained partial functional connectomes using L1 regularization (referred as “partial connectomes”) (see section SI.1. for details). We then calculated the Fisher z-transform of the resulting correlation matrices to obtain the finalized functional connectomes. We considered positive and negative connections separately and derived two weighted connectomes for each (referred as “function-based connectomes”), where nodes correspond to the brain regions and the edges correspond to the absolute value of functional activities (Fig. 1.a. bottom).

2.2.4. Generating structural connectomes

We preprocessed data with a pipeline involving skull stripping, registration, Eddy current, motion, and distortion correction. We performed deterministic tractography (see Baum et al. 2017 for details). After preprocessing of dMRI data, we obtain a structural connectivity matrix with the same regions as functional connectomes, where the number of streamlines between regions are used as an indicator of the strength of their connectivity. Representing the regions as nodes and fiber counts between regions as edge weights, we constructed a weighted structural connectome. Using this connectome as the base, we derived the following seven weighted connectomes (referred as “structure-based connectomes”) for considering various traffic patterns that are devised in the literature, simulating the functional interactions between brain regions (Fig. 1.a top) (see section SI.2 for a detailed explanation of communication patterns).

• Direct connections (DC): This pattern represents the standard weighted structural connectome which models direct communication between regions.

• Unweighted shortest path (USP): Commonly considered as the communication pattern of the brain (Honey et al. 2009), this traffic pattern assumes that the communication between regions occurs through minimum number of intermediary regions.

• Weighted shortest path (WSP): Being the weighted version of the USP, this scenario assumes that the communication occurs through the path with maximal number of connecting fibers.

• Search information (SI): An extension to WSP, search information (Goñi et al. 2014) quantifies the accessibility of the shortest path between two nodes within the network by measuring the amount of knowledge needed to access the path.

• Path transitivity (PT): Being another extension to WSP, this traffic pattern (Goñi et al. 2014) quantifies the density of local detours available on the shortest path between two nodes, assuming that having alternate reroutes at nodes over the shortest path will facilitate communication.

• Unweighted communicability (UC): This traffic pattern considers communication as a diffusion process as it assumes that the communication between regions occurs through multiple pathways simultaneously (Estrada and Hatano 2008). This unweighted version considers the strength of connection between two nodes to be proportional to the number of possible walks between them.

• Weighted communicability (WC): In this weighted version of UC, strength of edges are taken into account in the calculation of diffuse connectivity between regions.

2.2.5. Data and code availability

The PNC dataset is publicly available in the raw format at [https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000607.v3.p2]. Processed connectomic data that support the findings of this study and the code that is developed for calculating matching accuracy are available from the corresponding author, upon reasonable request.

2.3. Matching accuracy: A connectomic similarity measure based on graph matching

Having obtained seven structure- and four function-based connectomes, our goal was to find similarities in the connectivity patterns across different modalities. Since graph theory provides a rich repertoire of tools that can be utilized to characterize the properties of brain networks and solve various network related problems (Fornito et al. 2013), we considered structure- and function-based connectomes as weighted undirected graphs. We then evaluated the problem of finding similar connectivity patterns across connectomes as an inexact graph matching problem (Conte et al. 2004) (Fig. 1.b) with the goal of finding a mapping between similar nodes of two given graphs. One way to tackle inexact graph matching is by formulating it as an instance of the combinatorial optimization problem known as linear assignment (Koopmans and Beckmann 1957). Given two sets of nodes A and B, and a cost function c: A X B → ℝ determining the cost of assigning each node in A to a corresponding node in B, the linear assignment problem aims to find a one-to-one mapping function f: A → B between the nodes of the two sets minimizing the following objective function:

$${\sum }_{a\in A}c(a,f(a)).$$

In order to define assignment cost c(∙,∙) between nodes of graphs, we annotated each node with a k-dimensional feature vector for a parcellation with k ROIs representing their connectivity with the rest of the nodes in the graph and considered Euclidean distance between feature vectors as the cost function for the matching problem. We then used the Hungarian algorithm (Kuhn 1955) for matching nodes of structural graphs with that of functional graphs.

By applying this graph matching, we obtain a k x k matching matrix (Fig. 1.c. top), representing a one-to-one mapping between the nodes of the two graphs, identifying the functional node that exhibits the most similar connectivity pattern for each structural node. Since structural and functional graphs were of the same size, we regarded a structural node matching its corresponding functional counterpart as an accurate match. Our choice of using matching accuracy as a measure of structure-function relationship stemmed from the observation that two regions with strong anatomical connectivity tended to display strong functional connectivity as well. Generalizing this observation of pairwise relationships between nodes to network level connectivity, we expected the structural connectivity signature of nodes (connectivity of a node to the rest of the brain) to be similar to their functional connectivity signature.

The matching algorithm can arbitrarily match nodes having weak connectivity information. In order to filter out such arbitrary matchings, we calculated the statistical significance of matching a structural node to a functional node accurately by using a permutation test with 1000 permutations. Each time, we randomly shuffled the edges of the original structural graphs while preserving the node degree distribution. Note that shuffling only changes the order of edges in the connectivity signature of nodes. It does not alter the relative ordering of nodes in the connectome. We then matched the shuffled structure-based graphs with the function-based graphs. This produced a null distribution of matching probabilities for each node pair, corresponding to the null hypothesis that the probabilities obtained from matching random graphs would be greater than or equal to the actual matching probability. Comparing the actual matching probability to the null distribution, we estimated the likelihood (i.e. p-value) of observing the actual or a higher probability value when the null hypothesis is true. We denoted a match as statistically significant if this likelihood was 0.05 or smaller.

Using accurate matches as the basis, we then defined similarity measures between connectomes quantifying similarity at three levels.

- Connectome level:

Calculated as the percentage of nodes with statistically significant accurate matches, structure-function matching accuracy at connectome level quantifies how well the associated traffic pattern explains the functional connectivity for the given subject. We note that a structure-function matching accuracy of 100% implies that the structure-based connectome fully explains the observed functional connectivity, whereas a 0% accuracy indicates a lack of resemblance between the two graphs.

- Node level:

By performing graph matching between structural and functional graphs for each subject and taking the average of the resulting matching matrices across all subjects, we obtained a k x k average matching matrix where each cell indicates the likelihood of mapping a structural node to a functional node. Hence, the diagonal entries of the average matching matrix denote the matching accuracy at node level (Fig 1.c. bottom and Fig. 2.a).

Figure 2.

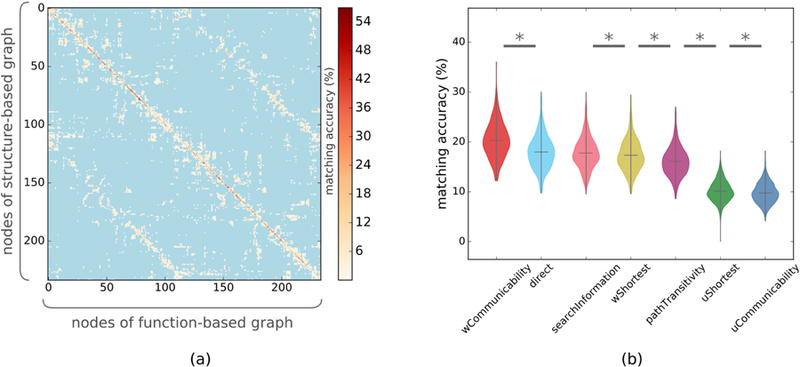
Determining the traffic pattern of human brain. (a) Average of the structure-positive function matching matrix across subjects in the Lausanne 234 atlas, where diagonal entries are deemed accurate matches. As neighboring regions within the same hemisphere are ordered consecutively in the matching matrix, we observe that most of the mismatches occur between either neighboring or contralateral regions. (b) Matching various structure-based connectomes with full positive functional connectomes, we observe that weighted communicability achieves the highest matching accuracy. (* indicates a significant group difference, obtained by a paired t-test with p≤0.05 after FDR correction)

- System level:

Grouping regions of the connectomes into seven functional systems as described in Thomas Yeo et al. 2011, that is, visual, motor, dorsal, ventral, limbic, frontoparietal, and default mode network, along with an additional module grouping subcortical regions, (Fig. 4) we evaluated the structure-function matching accuracy at system level. While calculating the structure-function matching accuracy of a subject at the system level, we regarded an accurate match to be the statistically significant mapping of a structural node to a functional node belonging to the same system. We calculated matching accuracy of systems as the average matching scores at system level across subjects.

Figure 4.

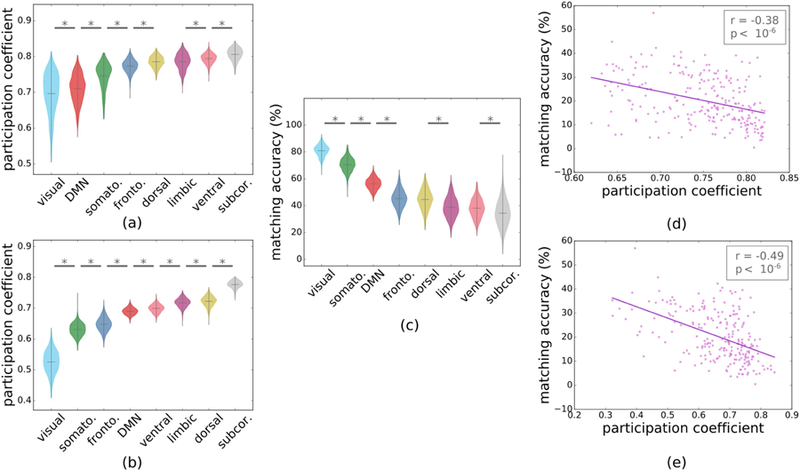
Relationship between system modularity and structure-function matching. Average participation coefficient of large-scale systems in (a) positive full functional and (b) structural connectomes. (c) Structure-positive function matching accuracies at large-scale system level (* indicates p≤0.05 after FDR correction). Correlation between structure-function matching accuracy and participation coefficient for individual regions in (d) positive functional and (e) structural connectomes.

2.4. Effect of network topology of systems over structure-function matching

We also explored whether there exists an association between the network structures of the functional systems and the systematic difference that is observed among their structure-function matching accuracies. To this end, we used the participation coefficient (PC) as a summary measure of network topology quantifying how much a given node is connected to other nodes within and between functional modules (Rubinov and Sporns 2010). Weighted PC for a node i is defined as follows:

$$P{C}_i=1-\sum _{m\in M}{\left(\frac{k_i(m)}{k_i}\right)}^2$$

where M is the set of functional modules, k_i is the strength of node i, and k_i(m) is the strength of connections that node i makes with the nodes in functional module m. In order to quantify the segregation of specific systems, we averaged PC_i across brain regions included in each system. Low PC in a system implies a specialized network while high PC suggests high interaction with other networks.

2.5. Sex difference in structure-function matching

Previous works on this dataset and others have demonstrated sex differences in structural and functional connectivity, when investigated separately (Gur et al. 1999; Ingalhalikar et al. 2014; Tunç et al. 2016). We investigated whether the structure-function relationship varies across sexes. We compared the connectome and system level matching accuracies of males and females using the two sample t-test.

2.6. Developmental changes in structure-function matching

Investigating whether the relationship between the structure and function also changes with age, we first calculated Pearson’s correlation between connectome level matching accuracy and age, which revealed a significant negative correlation. We further investigated whether the inverse relationship between age and matching varies between sexes. In our evaluation, we used multivariate linear regression to model matching accuracy as a linear combination of age and sex.

3. Results

3.1. Comparison of traffic patterns

The model adopted by the brain to shape the message passing traffic along the underlying anatomical pathways is crucial for describing the communication between directly and indirectly connected brain regions. Among several models that are offered in the literature (Estrada and Hatano 2008; van den Heuvel et al. 2012; Goñi et al. 2014), we compared the efficacy of structure-function matching based on the unweighted and weighted shortest path, search information, path transitivity, unweighted and weighted communicability as well as only direct connections.

We first calculated the matching between the structure-based connectomes and full positive functional connectome. We observed that structural connectomes that were generated using weighted communicability (WC) as the traffic pattern achieved the highest connectome level matching accuracy score of 20.3%, which was followed by direct connections (DC) with 18.0% accuracy with a significant group difference as assessed by a paired t-test (p<10⁻³⁰, Cohen’s d=0.676) (Fig 2.b). With a marginal difference in accuracy, DC was followed by search information (SI), weighted shortest path (WSP), and path transitivity (PT) with 17.8%, 17.3%, and 16.1% matching accuracies, respectively, where the group difference between DC and SI was not statistically significant (p=0.25, Cohen’s d=0.065) while it was significant but weak for SI and WSP (p=0.01, Cohen’s d=0.139) and WSP and PT (p<10⁻¹², Cohen’s d=0.411) after FDR correction. Unweighted versions of the shortest path (USP) and communicability (UC) achieved lowest scores with 10.1% and 9.7%, respectively. Analyzing the structure-function relationship at node level (Fig 2.a), we observed that structure of lateral occipital, superio-frontal, superio-parietal, isthmus cingulate, rostral anterior cingulate, cuneus, and precuneus accurately matched their function in both left and right hemispheres more than other regions (see Table SI.1 for a detailed list).

Calculating the matching between structural and positive partial functional connectomes, we observed that weighted communicability, again, outperformed all other traffic patterns with 18.6% matching accuracy. As in the previous experiment, WC was followed by direct communication with 17.3% accuracy and the derivatives of shortest path with their relative ordering being mostly preserved (see section SI.1. for detailed results).

3.2. Validating structure-function matching with correlation of connectomes

In order to validate our graph matching approach as a viable method to define similarity between structural and functional connectivity in brain, we investigated whether the commonly used correlation-based approach would produce similar results (Honey et al. 2009; Hermundstad et al. 2013). We observed a highly similar ordering of traffic patterns when we used Pearson’s correlation as a similarity measure to calculate edgewise relationship between structural and functional connectomes, supporting our matching accuracy-based findings (see section SI.5 for details).

3.3. Structure-function matching at system level

We next investigated structure-function matching at the level of eight functional systems (visual, somatomotor, dorsal attention, ventral attention, limbic, frontoparietal, default mode network, and subcortical) obtained by grouping regions according to the mapping presented in (Thomas Yeo et al. 2011) (Fig. 3.a). We observed that the majority of significant matchings (63.5%) occurred within the same system (Fig. 3.b). Reducing the overall matching matrix into eight systems, we observed that the overall matching score increased to 51.1% when comparing the structural graph with the positive functional graph, with a statistically significant structure-function matching within each system (p<10⁻⁴ after FDR correction). Matching was highest for visual, somatomotor, and DMN systems (Fig. 3.c) with matching accuracies being 81.0%, 70.5%, and 56.3%, respectively, indicating a strong structure-function matching.

Figure 3.

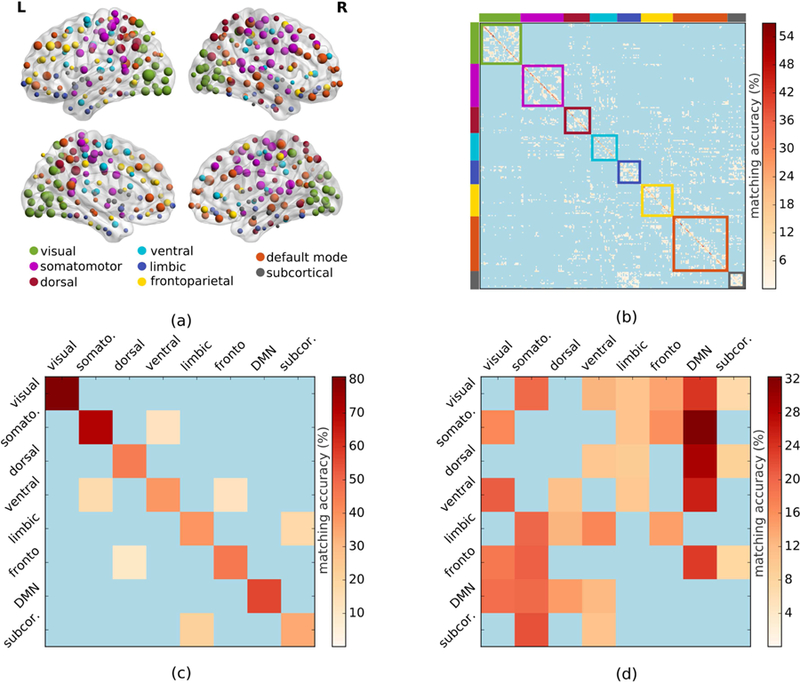
Structure-function matching at system level. (a) By investigating node level matching accuracies over the brain, we found that regions of some of the systems achieved higher accuracies than that of others. (b) Regions belonging to the same functional systems in the average matching matrix were grouped together, demonstrating that most of the structure-function matchings occurred within systems. (c) Matching of structure and positive-function-based graphs at system level using weighted communicability as the traffic pattern. (d) Matching results obtained by repeating the same experiment with negative-function-based graph.

The strong relationship between the structure-based graphs and positive function-based graphs led us to investigate how the underlying structural connectivity was related to negative functional connectivity. Applying graph matching between the WC-based structural connectome and negative full functional connectome, we observed that structural connectivity of the visual, somatomotor, dorsal, ventral, and frontoparietal systems matched the negative functional connectivity of the default mode network significantly (p<10⁻⁴ for all), with relatively high matching accuracies (Fig. 3.d). Among the five systems, the matching accuracies of the somatomotor and dorsal systems were especially high.

3.4. System modularity and structure-function matching

Due to higher structure-function matching in the visual, motor and DMN systems, we investigated whether this result was driven by their modular characteristics, namely, how much these systems participate in the rest of the brain network. We evaluated modularity using the participation coefficients (PC) of systems (average of PC of their nodes) on functional and structural connectomes. We observed that visual, motor, frontoparietal, and DMN had low PC in both cases, indicating modularity of these systems (Fig 4.a and 4.b). Comparing the PC of systems with their structure-function matching accuracies (Fig. 4.c), we observed that the systems with low PC (visual and motor) had high matching scores. We further noted moderate negative correlations between structure-function matching and the PC of individual nodes of the structural and functional connectomes, which showed that regions connecting to few sub-networks (low PC) presented a high correspondence between structural and functional connectivity (Pearson’s r=−0.486, p<10⁻⁶ and Pearson’s r=−0.376, p<10⁻⁶) (Fig. 4.d and 4.e).

3.5. Stability of structure-function matching across various parcellations and atlases

Connectomic analysis of brain relies heavily on the parcellation of the brain into regions of interest (ROI), where results of analysis can widely vary according to the density of ROIs and the choice of parcellation scheme (Moreno-Dominguez et al. 2014, Craddock et al. 2012). In order to ensure the reproducibility of the structure-function matching results that we obtained through a base parcellation over the Lausanne atlas with 234 ROIs, we first evaluated the effect of the number of regions in the connectome on the matching accuracy. We parcellated the brain into 129 and 463 ROIs over the Lausanne atlas (Hagmann et al. 2008), where the regions correspond to super- and sub-regions of the 234 ROI base parcellation, respectively. We also investigated whether our results were specific to the parcellation scheme of Lausanne atlas, which was obtained from analyzing a population of 5 male participants within the age range of 24 to 32 years. In order to test this, we evaluated structure-function matching using connectomes parcellated using the Schaefer atlas with 400 ROIs, where parcellation was defined based on a population of 1489 subjects (57.6% female) within the age range of 18 to 35 years (Schaefer et al. 2017).

We observed that weighted communicability consistently achieves the highest structure-function matching accuracy across all schemes, with 19.7% and 15.5% over the 129 and 463 ROI parcellations of Lausanne atlas and 16.4% over the 400 ROI parcellation of the Schaefer atlas (Fig. SI.4). We noted that the relative order of the communication patterns was also highly consistent across parcellations. Evaluating the structure-function matching at system level, we observed that the structure of systems consistently matched their function across parcellations, with visual, somatomotor, and DMN achieving higher accuracy, validating our initial results (Fig. 5). In matching structure with negative function, we observed that structure of some of the systems matched with the function of DMN as in the Lausanne 234 parcellation, with the matching of the somatomotor and the ventral systems being the most consistent (see section SI.6 for a detailed discussion).

Figure 5.

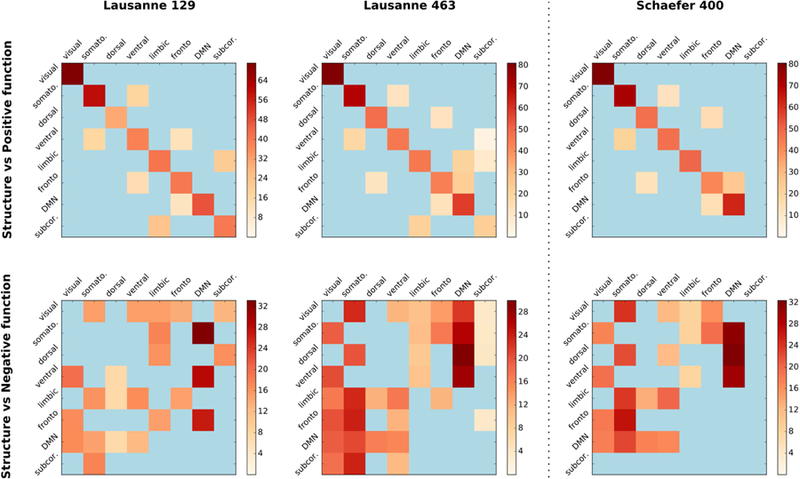
Effect of parcellation on structure-function matching at system level. We evaluated (left and middle columns) the structure-function matching at a low (129 ROIs) and a high (463 ROIs) resolution over the Lausanne atlas in order to study the effect of parcellation resolution on the matching, and (right column) the effect of parcellation scheme by carrying out the matching experiments using the Schaefer atlas consisting of 400 regions of the brain cortex only. Top and bottom rows show matching of structural connectivity with positive and negative functional connectivity, respectively.

3.6. Sex difference in structure-function matching

An investigation of sex differences in structure-function matching demonstrated that weighted communicability achieves the highest matching accuracy for both sexes at connectome level over all parcellation schemes. Furthermore, WC as the traffic pattern elucidated a significant yet weak group difference (p=0.007, Cohen’s d=0.225) between males and females over the Lausanne 234 parcellation (Fig. 6.a). We note that this group difference between structure-function matching of sexes does not remain statistically significant for other parcellations (Lausanne 129: p=0.97, Cohen’s d=0.003, Lausanne 463: p=0.13, Cohen’s d=0.12, Schaefer 400: p=0.12, Cohen’s d=0.13). At the system level, the only statistically significant group difference was observed for the frontoparietal system (p=0.001, Cohen’s d=0.3, FDR corrected) over the base parcellation, while no significant group difference was observed over other parcellations.

Figure 6.

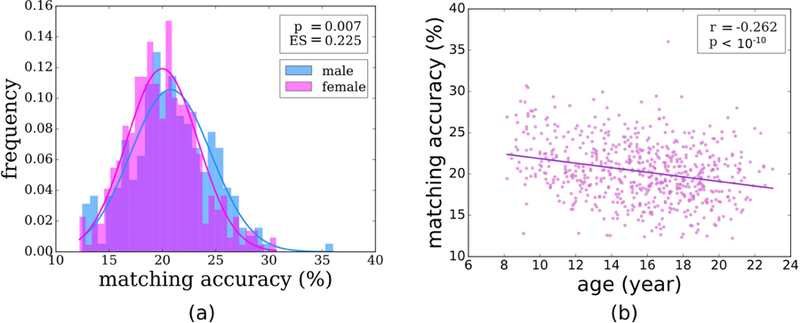
Relationship between structure-function matching and (a) sex and (b) age.

3.7. Developmental changes in structure-function matching

Investigating the relationship between the connectome level structure-function matching accuracy and age revealed a significant negative correlation (Pearson’s r=−0.262, p<10⁻¹⁰) over the base parcellation (Fig. 6.b), indicating that matching reduced with age. We further observed that this inverse correlation is consistent across parcellations of Lausanne 129 (r=−0.176, p<10⁻⁵), Lausanne 463 (r=−0.333, p<10⁻¹⁷), and Schaefer 400 (r=−0.317, p<10-¹⁵), where the correlation gets stronger with higher parcellation resolution. Expanding our investigation to the system level, we observed significant correlations in the limbic and dorsal systems highly consistently across parcellations, after FDR correction (Table 2). We also observed significant but weak correlations in the frontoparietal and DMN systems at higher resolution parcellations.

Table 2.

Pearson’s correlation coefficient calculated between structure-function matching and age across various parcellations.

	Overall	Systems
		Limbic	Dorsal	Fronto.	DMN	Ventral	Visual	Subcor.
Lausanne 129	−0.176 (p<10−5)	−0.134 (p<0.01)	−0.126 (p<0.01)	−0.045 (p=0.35)	−0.030 (p=0.51)	−0.062 (p=0.27)	0.024 (p=0.55)	−0.044 (p=0.35)
Lausanne 234	−0.262 (p<10−10)	−0.123 (p=0.01)	−0.092 (p=0.08)	−0.082 (p=0.10)	0.021 (p=0.68)	−0.037 (p=0.48)	−0.006 (p=0.88)	−0.036 (p=0.48)
Lausanne 463	−0.333 (p<10−17)	−0.234 (p<10−6)	−0.171 (p<10−4)	−0.100 (p=0.03)	−0.064 (p=0.17)	−0.077 (p=0.10)	−0.043 (p=0.33)	−0.038 (p=0.34)
Schaefer 400	−0.317 (p<10−15)	−0.289 (p<10−6)	−0.220 (p<10−6)	−0.097 (p=0.03)	−0.142 (p<10−3)	−0.025 (p=0.52)	−0.056 (p=0.18)	---

We further investigated whether the relationship between age and matching accuracy differed between sexes. We obtained a significant fit to our linear model with adjusted R²=0.078 (p<10⁻¹¹) where both age (p<10⁻¹⁰) and sex (p=0.004) were significant predictors over the base parcellations. Evaluating the consistency of this result over other parcellations, we observed that sex became an insignificant predictor with p>0.05 despite the model fit retaining its significance in Lausanne 129 (adj. R²=0.031, p<10⁻⁴), Lausanne 463 (adj. R²=0.112, p<10⁻¹⁶), and Schaefer 400 (adj. R²=0.102, p<10⁻¹⁵) parcellations.

4. Discussion

The relationship between structural and functional connectivity of brain regions has gained increased attention due to its significance in normative and clinical applications (Honey et al. 2010; Sporns 2013; Baum et al. 2017). Understanding the mechanisms of how functional deficits result from underlying structural changes, for instance, have advanced understanding of brain plasticity and injury (Draganski et al 2004; Sharp et al. 2011). Several empirical and computational (Honey et al. 2009; Mišić et al. 2016) studies have demonstrated a robust relationship between the two modalities, suggesting that many properties of functional connectivity are affected by the topological and geometric features of the underlying structural connectivity (Bullmore and Sporns 2009; Goñi et al. 2014).

We investigated the relationship between the structural and functional connectivity of the brain at the level of large-scale systems. Using a large cohort of 641 subjects aged 8 to 22 years, we first compared several traffic patterns proposed in the literature modeling functional activity and demonstrated that a diffusive pattern provides a better explanation for brain functional connectivity compared to other models. We then showed that the functional interaction between systems strongly match their underlying structural connectivity. Additionally, we investigated whether there exists any disparity between sexes in the structure-function relationship, and noted a lack of consistent significant group difference. We finally showed that the way structure explains functional connectivity in brain reduces with age, where the reduction at system level is especially significant in limbic and dorsal systems.

4.1. A diffusive traffic pattern better explains functional connectivity

Defining a traffic pattern is essential for characterizing how the brain’s functional connectivity arises through interactions among brain regions, given the underlying structural pathways among them. As we demonstrated in Fig.2, Fig.SI.1, and Fig.SI.6, communicability (Estrada and Hatano 2008), a diffusive traffic pattern that considers all possible walks for establishing communication between regions, best explains the observed direct and indirect functional connectivity, as compared to other traffic patterns that focus on the shortest path and its surroundings (Honey et al. 2009; Goñi et al. 2014). Due to its diffusive structure, communicability suggests that dynamic interactions among neuronal clusters are not simply shaped by the shortest path between them, or even in the broader context that the shortest path is embedded in the brain network, but rather are influenced by the whole set of structural connections in the brain. Such a holistic model of communication combines local properties of neuronal clusters with meso-scale and global features of the entire network, further highlighting the utility of a complex systems approach in future cognitive neuroscience studies. As shortest path and its extensions (i.e., WSP, SI, PT) achieve no better matching accuracy than direct connections over most parcellations, this work indicates that the shortest path assumption might not reflect the actual communication pattern in the brain any better than the direct connections. Unweighted versions of the shortest path (USP) and communicability (UC) consistently achieve the lowest scores across parcellations, indicating that the strength of connection between regions plays a significant role in the communication between brain regions.

These findings provide an insight into how information propagates in the brain, facilitating a framework for better predicting functional outcomes of structural changes, especially in clinical conditions. This knowledge could be crucial for studies in TBI where it is important to understand how the functional recovery is impacted by the structural changes; to address questions like whether the functional recovery is due to neuroplasticity or due to the rerouting of function to alternate structural pathways. The same would apply to studying changes in brain tumor patients after surgery and radiation. This traffic pattern could explain the functional recovery or cognitive deficits that appear as a result of structural changes.

4.2. Functional connectivity profiles of large-scale functional systems are shaped by their structural connectivity

Studies on the functional connectivity of the brain have revealed stable large-scale functional systems (Bressler and Menon 2010; Thomas Yeo et al. 2011) that consist of sets of brain regions with coupled activation patterns. These functional systems are believed to form a basis for the cognitive capacities of the human brain (Mattar et al. 2015). Therefore, the interactions among these systems are of prime interest to cognitive neuroscience studies in development (Gu et al. 2015), learning (Bassett et al. 2011), and specific cognitive capacities such as executive functioning (Baum et al. 2017) or memory (Rugg and Vilberg 2013). Similarly, atypicalities in the dynamic interactions among functional systems have been associated with many disorders and diseases (Menon 2011).

An intriguing question is how functional connectivity profiles of large-scale systems of the brain network are shaped by their structural connectivity. As suggested by several studies, including this work, functional interactions among brain regions are not influenced only by direct structural connectivity, but also by indirect connections between regions (Honey et al. 2009; van den Heuvel 2012; Mišić et al. 2014), as well as by the global properties of the brain network (Goñi et al. 2014). Our analysis of structure-function relationship at the node level revealed that the individual regions that achieved highest accurate matching probabilities belong to visual, DMN, and somatomotor systems, with lateral occipital, superio-frontal, superio-parietal, isthmus cingulate, rostral anterior cingulate, cuneus, and precuneus being accurately matched in both left and right hemispheres more than other regions (Table SI.1). We also observed that a majority of the regions (nodes) get matched either to their neighboring regions on the same hemisphere or to the mirroring regions and their neighbors in contralateral hemisphere, indicating a similarity of connectivity patterns among mirroring and neighboring regions (Fig 2.a). This motivated us to investigate the relationship between structural and functional connectivity of large-scale functional systems by considering their connectivity to the rest of the brain. Our results, presented in Fig. 3 and Fig. 5, suggest that the positive functional connectivity of a functional system is strongly influenced by its structural connectivity. The functional connectivity of each system best matched with its own structural connectivity with communicability as the traffic pattern. This finding further supports communicability to be a reliable model of information processing in brain, explaining the relationship between functional and structural connectivity.

As we have demonstrated in Fig.4, the agreement between structural and positive functional connectivity of systems that are relatively more segregated (that is, having less connectivity with other systems), such as the motor and visual systems, are stronger compared to the other systems. The average participation coefficient of motor and visual systems (both for structural and functional connectivity) were among the lowest three systems, suggesting that brain regions comprising these systems predominantly connect within the system and hence are segregated. The stronger agreement between structural and functional connectivity in such segregated systems may suggest that these systems act as sensory modules (Fodor 1983) with sparse structural and functional connectivity with other systems. These findings are notable considering commonly suggested lower cognitive roles of motor and visual systems (Gur et al. 2012), further supporting their being sensory modules. These findings might also indicate that using weighted communicability to describe the traffic pattern in the brain is able to explain the functional behavior of modular systems better given their underlying structural connectivity. Of note, although it does not display modular characteristics as the motor and vision systems do, DMN followed these two modular systems with the third highest matching accuracy. Other systems that are involved in higher level cognitive tasks (Sporns et al. 2004; Bressler and Menon 2010; Telesford et al. 2016) and have more diffuse connectivity showed a significantly weaker relationship between their structural and functional connectivity. Accordingly, the functional connectivity of such higher level systems is less influenced by their structural connectivity. Our results suggest that the relationship between structural and functional connectivity of large-scale functional systems may characterize their cognitive role as well -- a promising direction for future studies.

4.3. Dynamic interactions between task-positive and task-negative systems are supported by structural connectivity

The default mode network (DMN) is a set of brain regions that displays greater activity at wakeful rest compared to performance of differing goal-directed tasks (Raichle et al. 2001; Buckner et al. 2008). It is commonly referred to as the task-negative network due to exhibiting decreased activity during task performances, while the networks that are activated during goal-directed task performances are regarded as task-positive (Fox et al. 2005). DMN and task-positive networks interact and jointly control decision making, working memory, and other high-level cognitive operations (Dosenbach et al. 2007; Anticevic et al. 20012; Chen et al. 2013).

Notably, when matching negative functional connectivity of large-scale systems with their structural connectivity, the highest matching accuracies were observed between DMN and several task-positive systems, including dorsal and ventral attention, frontoparietal, motor, and visual systems. Several studies suggested that the DMN may have an important role in integrating different cognitive processes (Greicius et al. 2003; Gu et al. 2015). It was further demonstrated that DMN shows strong structural and functional connectivity with other systems (Esposito et al. 2006; Bonnelle et al. 2012), as well as making strong connections with several of its hub regions (Hagmann et al. 2008). Our results support these findings, and further suggest that the task-induced deactivation patterns observed between DMN and other systems (Greicius et al. 2003; Buckner et al. 2008) may be shaped by the structural connections that these systems make with the rest of the brain. That is, how DMN and other systems are structurally embedded inside the brain network determines their system level functional roles and how they interact with each other.

4.4. Relationship between structural and functional connectivity might not be affected by sex

Functional and structural brain connectivity differences between the sexes have recently drawn great attention (Gur et al. 1999; Ingalhalikar et al. 2014; Tunç et al. 2016) due to their potential in offering important considerations for differential developmental trajectories and personalized medicine, as well as for social policy making. Sex differences in brain connectivity is an intriguing scientific pursuit also due to many observed behavioral differences between sexes, including enhanced motor skills in males (Moreno-Briseño et al. 2010) and better social cognition skills in females (Williams et al. 2009). Several studies have demonstrated that such behavioral differences are indeed accompanied by underlying structural and functional connectivity differences (Satterthwaite et al. 2014; Tunç et al. 2016). Our results (Fig.6.a) add another dimension to the discussion of sex differences by showing that neither the kind of relationship between structural and functional connectivity (that is, communicability) nor the strength of this relationship (that is, structure-function matching accuracy) demonstrate any significant difference between sexes. Despite many reported differences both in structural and functional connectivity between sexes, when studied separately, our result seems to suggest that the underlying mechanism of information processing in the brain is consistent between sexes. Indeed, the relationship between structural and functional connectivity and the mechanism that underlies this relationship is an integral aspect of the human brain network. That this mechanism is not modulated by sex might suggest that communicability can be adopted as the traffic pattern of choice for studying information processing in both sexes.

4.5. Relationship between structural and functional connectivity changes with development

Studies on connectomic maturation in the brain have reported significant age-related structural and functional changes in early development as well as across the human lifespan (Satterthwaite et al. 2013, Gu et al. 2015). In several of those studies, structural and functional connectivity were shown independently to reduce with age after childhood, while the rates of change in structure and function were reported to be uneven in the relatively limited number of studies that have analyzed the development of the structure-function relationship (Supekar et al. 2010, Betzel et al. 2014).

Our results demonstrate a reduction in connectome level structure-function similarity by age (Fig.6.b), which points to an uneven rate of change in the structural and functional connectivity during development. Our result supports previous findings that report change in structure-function relationship during development, such as functional connectivity in the DMN of children aged 7 to 9 reaching adult-like levels despite having weak structural connectivity (Supekar et al. 2010) and another study reporting a temporal lag between development of structural and functional connectivity in normal aging (Tsang et al. 2017). Negative correlation of structure-function matching with age may also imply that communicability as the traffic pattern becomes insufficient in explaining how the functional connectivity arises from structural pathways in later stages of development. Supporting previous findings (Betzel et al. 2014), this might suggest that the traffic pattern assumed in brain is dynamic and develops with age, possibly becoming more complex during adolescence. Investigating performance of various traffic patterns across ages is a promising direction for future research.

Our results further demonstrate that the agreement between structural and functional connectivity considerably reduces with age in limbic and dorsal systems (Table 2). This may indicate that the structural and functional connectivity develops at varying rates in these systems within the age range of 8 to 22 years. In conjunction with the negative correlation observed in DMN and lack of significant correlation in other systems, these results may imply that these systems develop at varying degrees before and during adolescence (Hoff et al. 2013). This would also make for an exciting and independent future study.

4.6. Future work

In this study, we demonstrated structure-function matching at system level, along with the adoption of graph matching as a similarity measure describing the relationship between structural and functional connectivity. Our matching scheme utilizes Euclidean distance between the connectivity signatures of regions to obtain the best matching between the structural and functional regions, where contribution of regions to the distance is uniform, making the algorithm sensitive to noise. Modulating the contribution of regions and investigating various distance functions can be considered in future studies. Additionally, a combination of traffic patterns may also be explored in the future instead of using each model exclusively. Although the large sample size used in this study provides significant statistical power, the cross-sectional design of the samples is a limiting factor especially for evaluating the relationship between age and structure-function similarity. Investigating the reproducibility of results over a longitudinal dataset is a promising future research direction. We also note that, reproducibility of connectivity maps in brain, especially over rs-fMRI data, is known to be affected by several parameters such as the preprocessing pipeline or the state of mind of the subject at the time of scan (Zuo and Xing 2014). Consequently, results reported in this study should be considered taking the limitations of the medium into account. Studying the variation of the structure-function relationship during development requires additional investigation of adolescence, amongst other factors, that will be undertaken in the future. The discussion of sex differences and developmental changes are anecdotal to the main contribution of the paper, which was to investigate the communication pattern that best explains the structure-functional relationship in the brain.

5. Conclusion

In summary, we demonstrated that functional interactions in the brain occur through multiple structural pathways at the same time rather than a unique shortest path, and a strong structure-function matching at the level of functional systems is attainable with the use of such a diffusive traffic pattern. Our findings also provide an insight into the structural underpinnings of functional deactivation patterns between DMN and task positive systems. These results widen our understanding in structure-function interactions at the level of large-scale functional systems, paving the way for future studies in how pathology induced structure-function alterations affect information processing in the brain.