In vitro superharmonic contrast imaging using a hybrid dual frequency probe.

Abstract

Superharmonic imaging is an ultrasound contrast imaging technique which differentiates microbubble echoes from tissue through detection of higher order bubble harmonics in a broad frequency range well above the excitation frequency. Application of superharmonic imaging in 3-D allows specific visualization of the tissue microvasculature with high resolution and contrast, a technique referred to as acoustic angiography. Due to the need to transmit and receive across a bandwidth which spans up to the fifth harmonic of the fundamental and higher, this imaging approach requires imaging probes comprising dedicated transducers for transmit and receive. In this work, we report on a new dual frequency probe including two 1.7-MHz rectangular transducers positioned one on each side of a 20-MHz 256-element array. Finite-element-modeling-based design, fabrication processes and assembly of the transducer are described, as well as integration with a high frequency ultrasound imaging platform. Dualfrequency single plane-wave imaging was performed with a microbubble contrast agent in flow phantoms and compared to conventional high-frequency B-mode imaging, and resolution and contrast-to-tissue ratio were quantified. This work represents an intermediate but informative step toward the development of dual-frequency imaging probes solely based on array technology, specifically designed for clinical applications of acoustic angiography.

Introduction:

Superharmonic contrast imaging (SpHI) is a technique exploiting the signal generated by microbubble (MB) contrast agents in a frequency range higher than twice the transmit frequency. The term was coined by Bouakaz et al. (2002) in a study where they demonstrated the potential of this technique to improve the contrast-to-tissue ratio (CTR) relative to standard second harmonic contrast imaging. According to their simulation work based on the KZK model for nonlinear propagation and a modified Rayleigh-Plesset for MB nonlinear oscillations, CTR should increase with harmonic number. Experimentally, with a transmit at 0.8 MHz (2 cycles, mechanical index: MI=1) and a receive in the 2.7-4.7 MHz frequency range, Bouakaz et al. (2002) reported an increase of 35-40dB in contrast-to-tissue ratio in vitro, which was in good agreement with their simulation work. Kruse and Ferrara (2005) later reported that, above a pressure threshold between 100 and 200 kPa, a single lipid-shell microbubble excited by a 10-cycle 1-MHz pulse could generate transient signals, with broadband spectra extending beyond 40 MHz. These transient signals occurred just after peak compression, in agreement with simulation work, and are attributed to high wall velocity in this phase of MB oscillations. In vitro, in a configuration with two separate single element focused transducers, one to transmit a mono-cycle pulse at 2.25 MHz (λ=685 μm) and the other to receive in a broad frequency range centered at 15 MHz, they were able to detect this transient signal and resolve two parallel 200-μm cellulose tubes filled with MBs and positioned 400 μm apart.

Whether the signal received from microbubbles is broadband or harmonic in nature, requirements for a good CTR in SpHI are identical: a good sensitivity on the receive side in a large bandwidth located beyond the 2^nd (and possibly the 3^rd) harmonic of the transmit frequency. It has been generally agreed that these requirements are not easily fulfilled using a single standard transducer (single element or array) for both transmit (Tx) and receive (Rx). To tackle this challenge, and with microvasculature contrast imaging as the target application, we designed and built a hybrid dual-frequency (DF) transducer comprising a broadband 2-MHz focused annular element confocally aligned with a broadband 30-MHz focused transducer (Lukacs et al 2009) positioned in its center. There are two main advantages in decoupling the transmit and receive paths for SpHI: a higher signal-to-noise ratio (SNR), and the ability to separate efficiently the Rx bandwidth from the Tx frequency and its lower harmonics, while keeping the Rx bandwidth large enough to guarantee a good axial resolution. Also, in this configuration, the high frequency transducer can be used for standard high-frequency, high resolution B-mode imaging. This DF transducer was integrated into a wobbling scanhead operated by a single channel micro-ultrasound scanner (Vevo770, VisualSonics Inc., Toronto, Canada). Axial and lateral resolutions were around 100 and 300 μm, respectively, and a maximum increase in CTR of 17.2dB was found relative to high-frequency B-mode imaging (Gessner et al. 2010). Gessner et al. (2013) evaluated the capability of this DF transducer in detecting the microvasculature for evaluation of its architecture. They determined that high-resolution superharmonic images of the microvasculature were comparable to those obtained with photoacoustics and μCT, and this imaging approach has subsequently been referred to as acoustic angiography (AA). Further AA investigations have been performed using this confocal DF device, and variants in terms of Tx and Rx frequencies. Shelton et al. (2015) estimated microvascular tortuosity metrics and vascular density, during tumor evolution in a basal breast cancer mouse model. All these parameters were found to be higher in tumors than in surrounding tissues, to increase with tumor size, and were attributed to angiogenesis-related vascular remodeling. Rao et al. (2016) showed that micro vascular tortuosity is increased beyond tumor margins. The potential of AA in molecular imaging was also demonstrated in a study by Shelton et al. (2016), where α_vβ₃-targeted microbubbles could be detected in a fibrosarcoma model in rat, their position relative to the microvasculature evaluated, as well as the size of the closest vessels. Later, Shelton et al. (2017) reported on the first-in-human application of AA to breast and peripheral vasculature, and recently Kasoji et al. (2018) demonstrated the sensitivity of AA-estimated vascular volume density in tumor following radiation therapy.

Although the confocal dual-frequency probes used in these studies have shown great potential for visualization and characterization of the microvasculature in preclinical applications due to their good axial and lateral resolutions, they present several limitations which ultimately will hinder clinical translation of this technology. Critical limitations are the limited focal distance and limited depth-of-field associated with a single fixed focus, mechanical scanning (and consequent low frame rate), and multiple exposures of MB during acquisition of an image. A dual-frequency probe based on array technology could overcome some of these limitations. Several dual-frequency array geometries have already been reported, which include interleaved low and high frequency elements (Bouakaz et al. 2002; van Neer et al. 2010), parallel arrays (Stephens et al. 2006, 2008; Ferin et al. 2007), and stacked active layers (Ferin et al. 2007; Li et al. 2016; Li 2017; Wang et al. 2017; Wang et al. 2018). If the high frequency (HF) elements are to be used also in standard imaging mode, the interleaved geometry is not a viable solution, mostly because the increase in the pitch between HF elements to make space for the low frequency (LF) elements would result in grating lobe artefacts. Stacking active layers has shown promise, although at the expense of reduced resolution due to a lower bandwidth relative to single active layer arrays (Ferin et al. 2007; Li et al. 2016; Li 2017). Apart from the overall foot print, the parallel array geometry presents interesting advantages relative to the others: the performance of each array is, in principal, not altered by the presence of their neighbor(s), and several degrees of freedom in the geometry of the assembly allow for adjustments to achieve desired beam specifications. Hu et al. (2010) reported the use of a dual frequency probe comprising two outer 1.5-MHz array and a colinear 5.4-MHz center array. The center element was used to exert a radiation force onto functionalized microbubbles, pushing them toward the vessel walls. The outer and center arrays were used on transmit and receive, respectively for bound microbubbles imaging in vitro. The same probe was used in a follow up in vivo validation of this molecular imaging approach (Hu et al. 2013). Although no details regarding the low frequency and high frequency beams of this probe, and resulting imaging resolutions, were released, the absolute bandwidth of the receiving probe (~4 MHz, according to our calculation) theoretically constitutes a limitation for resolving vessels smaller than 200-μm in diameter). Also, theoretically, the lateral resolution and slice thickness are expected to be lower and higher, respectively, than those of a typical clinical probe of the same center frequency and bandwidth. Furthermore, the proximity of the transmit frequency and receive frequency range might limit CTR, since any low order harmonics from tissue would be detected on receive.

In the present study, we report on the design and fabrication of a prototype hybrid dualfrequency (1.7 MHz/20 MHz) probe in a parallel geometry, which should theoretically provide better resolutions, and potentially better CTR than the probe used by Hu et al. (2010, 2013). Acoustic characterization and integration of the device with a commercial high-frequency scanner are described. Finally, preliminary results of superharmonic contrast imaging experiments performed in vitro using plane waves on transmit are presented.

Material and Methods:

Design and assembly

The purpose of this study was to develop a DF probe for acoustic angiography, capable of generating a low frequency transmit beam that is narrow in the elevation direction, elongated in the propagation (axial) direction, and coaligned with the beam of a high-frequency array used on receive. The LF depth-of-field should overlap, the focal region of the HF array where the beamwidth in the elevation direction is the narrowest. Furthermore, the LF elevation beamwidth should be as small as possible in that region to minimize the thickness of imaging slice in which microbubbles are insonated. This was to be done without altering the capabilities of the HF array to operate in other imaging modes. The parallel geometry described by Stephens et al. (2006) and Ferin et al. (2007) can fulfill this last requirement and was therefore adopted. On receive, a commercial 256-element 21-MHz array transducer (MS250; FUJIFILM-VisualSonics Inc., Toronto, Canada) and a Vevo2100 scanner (FUJIFILM-VisualSonics Inc.) were to be used. Since the characteristics of the LF beam in the azimuthal direction was not a primary concern for this initial investigation, flat rectangular 1.7-MHz single element transducers were positioned one on each side of and parallel to the HF array, to generate a uniform beam (i.e. plane wave) in the azimuth. To create coaxially aligned HF and LF beam, the two LF transducers propagation axes were tilted relative to the axis of the HF array to produce a region of constructive interference of the two individual LF beams along the HF imaging axis (Fig.1-a). In all the descriptions and results hereafter, the X, Y and Z axes correspond to the azimuth, elevation and propagation axes of the HF array, respectively, with the origin located at the center of the HF array front face. The characteristics of the LF beam interference pattern in the elevation and propagation direction depend on the transmitted frequency and bandwidth, the LF transducer width W, the positions (y_c, z_c) of the LF transducers relative to the center of the HF array, and tilt angle α. The influence of all these parameters was systematically investigated by simulation using PZFlex (OnScale Inc., Cupertino, CA).

Figure 1:

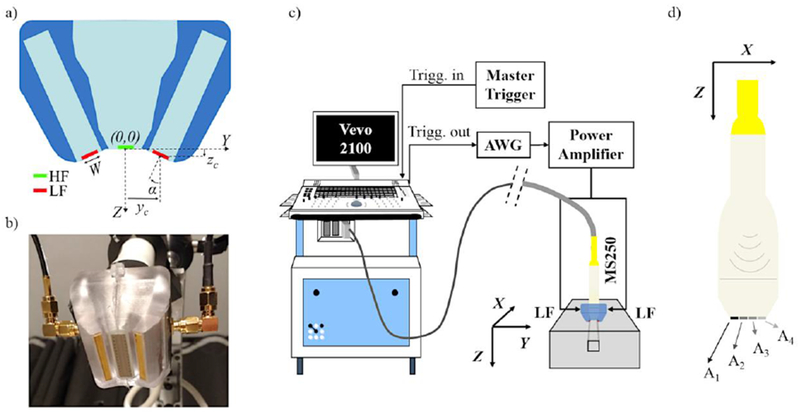
(a) Schematic of the elevation cross-section of the dual-frequency assembly with LF transducers in red and high frequency (HF) array in green; (b) picture of the dual frequency probe used in experiments showing the LF transducers running parallel to the 21 MHz array front face; (c) Experimental setup for superharmonic imaging (SpHI) experiments in a single wall less channel phantom; (d) In SpHI-mode, four 64-element apertures are successively used on receive to collect 256 element data, therefore necessitating 4 transmit events for the beamforming of a single frame.

Once the design parameters were optimized as to fulfill our requirements for LF beam shape and LF and HF beam overlap, the LF transducers were manufactured. A 1-3 piezocomposite (PZT5H, CTS, Albuquerque, NM; Epo-Tek 301, Epoxy Technology, Billerica, MA) was selected as the active layer to provide a broad bandwidth, allowing the transmission of short duration pulses. The piezocomposite was fabricated using a traditional dice-and-fill method; the composite pitch and kerf were 270 μm and 70 μm, respectively. The composite was lapped to the desired thickness, gold electrodes were sputtered onto the front and back surfaces, and a tungsten-loaded epoxy (Epo-Tek 301) backing was applied on the back side. Neither matching layer nor lens were used. The stacks were then cut to size (2.9 × 30 mm) using a dicing saw, electrodes were wire-connected, and the electrical impedance measured. To hold the LF transducer pair and the MS250 probe together, a casing was designed using MS250 CAD drawings provided by VisualSonics, and 3D-printed. The full assembly of the dual-frequency probe is shown on Fig. 1-b.

Beam characterization

LF and HF pressure beam distributions were measured to verify their superposition in the elevation direction, and the conformity of the LF beam to predictions from simulation. Briefly, the probe was kept at a fixed position in a water tank with its axes aligned with the axes of 3D micro-positioning system (U511-, Aerotech Inc., Pittsburgh, PA). This system was used to position and move a 40-μm needle hydrophone (NH0040, Precision Acoustics Ltd, Dorchester, UK; calibrated by the National Physical Laboratory, Teddington, Middlesex, UK) relative to the probe. For LF pressure beam measurements, an arbitrary waveform generator (AWG2021, Tektronix Inc., Beaverton, OR) was used to generate the excitation pulse which was amplified by a RF power amplifier (240L, ENI, Rochester, NY), and transmitted in parallel to the two LF transducers. For HF pressure beam measurements, the Vevo2100 was switched to Pulsed-Wave Doppler mode and the transmit parameters (21 MHz, 1 cycle) were set in engineering mode. On receive, signals collected by the hydrophone were pre-amplified (AU1579, L3 Narda-Miteq, Hauppauge, NY), low pass filtered (BLP-70+, Mini-Circuits, Brooklyn, NY), and digitized at 500-MHz sampling frequency (DP210, Acqiris SA, Switzerland). Averaging was used to increase the signal to noise ratio. For the HF and LF data acquisitions, the digitizer was triggered by the scanner (“Tx Trigger”) and the AWG, respectively. Acquired RF signals were corrected for the hydrophone sensitivity and transfer functions of preamplifier, using Matlab (The MathWorks Inc., Natick, MA).

Plane wave contrast agent imaging

The contrast imaging experiments were designed to test the capability of the dual-frequency probe for superharmonic contrast imaging and the implementation of a SpHI-mode on the Vevo2100, and to evaluate the potential increase in CTR achieved by SpHI relative to high-frequency B-mode using Micromarker™ microbubbles (FUJIFILM-VisualSonics, Toronto, Canada). The SpHI-mode was developed from the photoacoustic (PA) mode already implemented on the scanner for the following reasons: 1/the LF transducer pair generates plane waves (in azimuth) exposing the whole field-of-view (FOV) on each LF transmit event, just as it is on each laser pulse in PA imaging. The beamformer comprises 64 channels on receive and the HF array has 256 elements, enabling a complete FOV to be imaged using 4 transmit events, whereas 256 transmit events would be required if SpHI was implemented based on a standard line-by-line B-mode acquisition scheme. 2/Un-beamformed IQ data can be acquired, so that the orientation of the transmit stacks can be accounted for in the receive beamforming. 3/The data acquisition delay relative to transmit trigger can be adjusted in PA-mode. 4/Regular high-frequency B-mode frame acquisitions can be interleaved with SpHI-mode frame acquisition, allowing for a direct comparison of CTR between the SpHI-mode and B-mode.

Data acquisition

Contrast imaging experiments were performed in vitro in a wall-less phantom consisting of a 1.5×1.5 mm² channel casted in a 1% (w/w) agar matrix (BD™ Difco Agar, Technical, # 281210, Fisher Scientific Canada) containing 4% (w/w) silicon dioxide particles (# S5631, Sigma Aldrich). The channel was orientated along the azimuth of the MS250 probe, parallel to its front face, and positioned near its natural elevation focus. The contrast agent was diluted in PBS down to a concentration of 2×10⁶ microbubbles/ml. The solution was loaded in the channel by gravity feed and stabilized (i.e. no flow) before each data acquisition. This no-flow condition represents the worst-case scenario for contrast agent stability, since microbubbles being imaged should remain in the LF beam focal plane for the longest time. For the estimation of SNR and CTR, data were also collected in water and in the agar/SiO₂ matrix (6 mm away from the channel laterally), respectively, using the same acquisition settings.

The setup for SpHI data acquisition is shown in Fig.1-c. On the transmit side, a trigger signal (20-Hz pulse repetition frequency) generated by a pulse generator (PM5715, Philips, USA) was substituted for the “flash-lamp” trigger generated by the Vevo-LAZR laser subsystem (FUJIFILM-Visualsonics Inc.) and fed to the scanner (Vevo2100). The subsequent delayed “Q-switch” trigger generated by the scanner, which in normal PA operation releases the laser pulse, was used to trigger the transmission of a LF electric pulse by the waveform generator (AWG2021) and served as the time reference for data acquisition. The pulse was then amplified by the power amplifier (240L) to drive the two LF transducers connected in parallel. 1.7-MHz symmetrical Gaussian-enveloped pulses were used, with a fractional bandwidth (BW) of 50% or 100%, and various amplitudes. On receive, both the acquisition delay relative to the transmit trigger and the number of acquired samples (for SpHI-mode) were adjusted in engineering mode, to include the propagation time of the LF acoustic pulse to the field of view. Four transmit events were necessary to acquire a single frame, each of them being used to collect data from one of the four 64-element sub-apertures (Fig.1-d). For each LF transmit pulse setting, 100 frames of SpHI un-beamformed IQ data interleaved with 100 frames of HF B-mode IQ beamformed data were acquired. In HF B-mode the transmit focus was set to 18 mm and the transmit amplitude kept constant across all data acquisitions. Whereas signals acquired in HF B-mode were already beamformed by the scanner, channel signals acquired in SpHI-mode were beamformed offline as described below. Signal processing and analysis were performed using Matlab.

Additionally, 3-D contrast imaging experiments were performed with solutions ranging from 2×10⁶ to 1.2×10⁷ microbubbles/ml. These solutions were inserted (successively) in several 200-μm diameter cellulose tubes tortuously embedded in a 1% (w/w) agar matrix, to be imaged. The phantom was mechanically scanned in the HF array elevation direction and over a 27.7 mm distance, with 1 frame acquired every 254 μm, for a total of 109 frames. The envelopes of beamformed signals were calculated and log compressed. Following reconstruction of the 3D image data sets, maximum intensity projection (MIP) images were generated along the scan (elevation), azimuthal and propagation axes, for both HF B-mode and SpHI-mode, for comparison.

SpHI mode beamforming

In a traditional configuration where transmit and receive are performed by the same array transducer, beamforming algorithms based on delays and sum are relatively straightforward when assuming uniform speed of sound C in the propagation medium, because there is a linear relationship between the distance z of the target to the array and the total transmit-receive time-of-flight (TOF):

$$TOF(z)=\frac{2z}{C}$$ (1)

Once the time of flight corresponding to distance z is known, signals received by the different elements of the aperture are delayed according to their positions x_e relative to the azimuthal position of the target:

$$\Delta t(x_e,z)=\frac{1}{C}\left[{(x_e^2+z^2)}^{\frac{1}{2}}-z\right]$$ (2)

In our dual-frequency transducer arrangement for SpHI (Fig. 2), where there is an offset of the transmit aperture relative to the receive aperture in the elevation direction and an angulation of the propagation axes, the relationship between the transmit time-of-flight TOF^tr from the LF transducers to a point z on the axis of the receiving HF array and the distance z is less trivial. If we assume that the TOF^tr on transmit is the shortest distance from the LF transducers (centered at ±y_c, z_c) to point z on the HF array axis normalized to the speed of sound, there are three different zones to consider, which are bounded by:

$$\begin{gathered} z_1=z_c+y_c/tan\alpha -W/(2\times sin\alpha ) \\ {z}_2=z_c+y_c/tan\alpha +W/(2\times sin\alpha ) \end{gathered}$$ (3)

Figure 2:

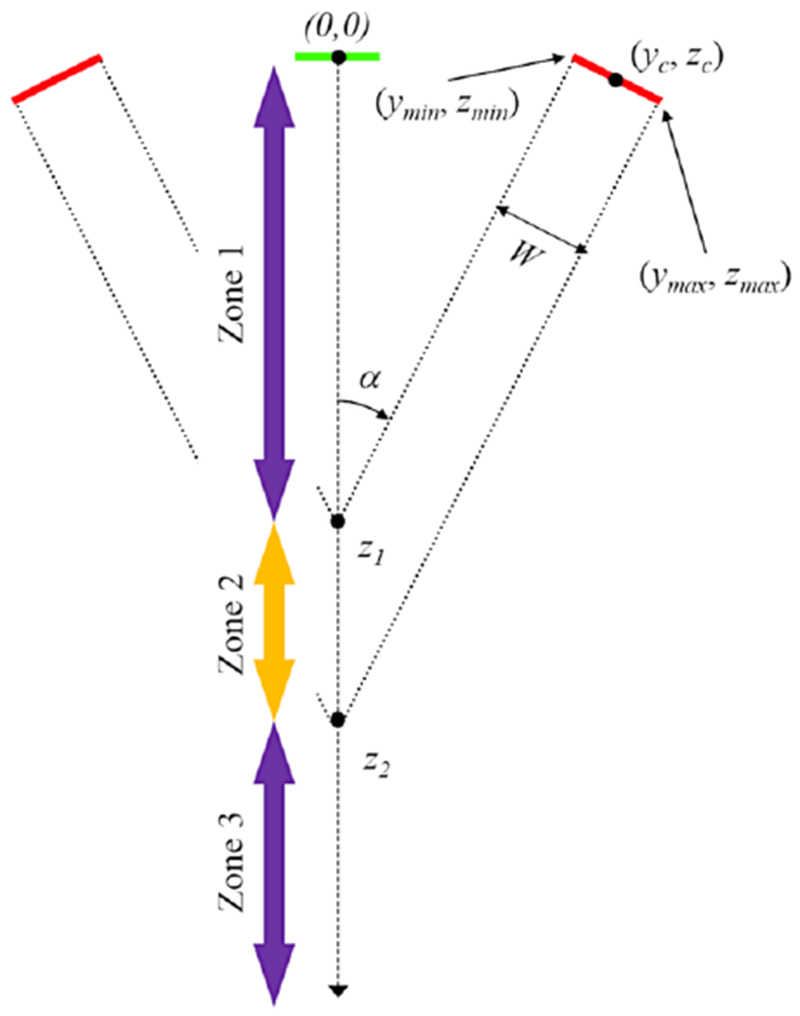
Schematic of the transmit path showing the relevant parameters used in the calculation of the time-of-flight to and from positions on the probe center axis for beamforming purposes.

In Zone 1, the shortest distance is between (0, z) and the inner edge of the stack (y_min, Z_min), whereas in Zone 3 it is between the outer edge (y_max, z_max) and (0, z). In Zone 2, the shortest distance is between the point at the surface from the stack from which is issued the line perpendicular to the stack surface and the intersection point with the HF array axis at distance z. The relationship between TOF^tr and z is linear in Zone 2, but quadratic in Zones 1 and 3:

$$\begin{gathered} TO{F}^{tr}(z)=\frac{1}{C}{\left[{(z-z_c+\frac{W}{2}\sin \alpha )}^2+{(y_c-\frac{W}{2}\cos \alpha )}^2\right]}^{\frac{1}{2}}0\le z\le z_1 \\ \frac{1}{C}((z-z_c)\cos \alpha +y_c\sin \alpha )z_1\le z\le z_2 \\ \frac{1}{C}{\left[{(z-z_c-\frac{W}{2}\sin \alpha )}^2+{(y_c+\frac{W}{2}\cos \alpha )}^2\right]}^{\frac{1}{2}}z\ge z_2 \end{gathered}$$ (4)

On receive the time-of-flight is simply given by:

$$TO{F}^{rec}(z)=\frac{z}{C}$$ (5)

The total time-of-flight is thus given by:

$$TOF(z)=TO{F}^{tr}(z)+TO{F}^{rec}(z)$$ (6)

In our beamforming scheme, equation (7) was solved in z first, for the range of times corresponding to the acquired samples:

$$TOF\left(z_n\right)=T_0+nTn\ge 0$$ (7)

with T₀ and T corresponding to the delay between transmission of the HF pulse and acquisition of the first sample, and the inverse of the sampling frequency of the reconstituted RF signals, respectively. Note that given the long period of the transmitted pulse, T₀ also comprised a delay corresponding to the time at which the strongest transient signals were expected to be generated relative to the beginning of the transmitted pressure waveform, i.e. close to the steepest transition between negative and positive pressure (see Kruse et al. 2005). Once z_n were known, beamforming delays Δt(x_e, z_n) were calculated using equation (2) for a depth-independent receive aperture of 64 elements. Neither apodization nor time-gain compensation were used. Beamforming was applied to RF data, which were reconstituted by re-modulating the up-sampled envelopes calculated from un-beamformed IQ channel data.

Signal-to-noise and contrast-to-tissue ratios

For both imaging modes (B-mode and SpHI-mode), the spatial mean $\overline{E}$ of the beamformed signal envelopes were calculated for each acquired frame, in a region of interest corresponding to the channel containing microbubbles ($\overline{E_{mode}^c}$), the agar/SiO₂ matrix (at the same depth, but 6 mm away from the channel laterally; $\overline{E_{mode}^m}$) and the water bath (no phantom in the beam; $\overline{E_{mode}^w}$). SNR and CTR were then estimated as follows:

$$SN{R}_{mode}^{c,m}=20{\log }_{10}(\overline{E_{mode}^{c,m}}∕\overline{E_{mode}^w})$$ (8)

$$CT{R}_{mode}=SN{R}_{mode}^c-SN{R}_{mode}^m$$ (9)

In these equations and throughout the manuscript, mode=HFB for HF B-mode and mode=SpHI for SpHI-mode. Since $\overline{E_{mode}^w}$ and $\overline{E_{mode}^m}$ are not expected to vary with frame number, the variations of $SN{R}_{mode}^c$ and $CT{R}_{mode}$ should also reflect the potential variations in signal from microbubbles with the number of LF exposures.

Results

Influence of geometrical parameters on LF beam

Examples of simulated LF beams in the elevation plane with various angles α and stack inner edge position y_min (see Fig.2) are shown on Fig.3-a–c, for a constant stack width W of 3 mm, and a 1.7-MHz 1-cycle 1-V electrical excitation applied to the modeled elements. For all these beams, the maximum pressure amplitude is observed near the surface of the LF transducers. However, the interference of the two LF beams generates a local and narrow elongated main lobe of elevated pressure amplitude around the intersection of their center axes and along the center axis of the assembly, and two side-lobes of lower amplitude. The location of the axial peak pressure amplitude z_peak, and the depth-of-field along the assembly axis the decreases with increasing α at constant y_min (Fig.3-d), and with decreasing y_min at constant α (Fig.3-e). The peak pressure on the assembly axis also increases with increasing α or decreasing y_min (data not shown). The width of the main lobe and the width and elevation position of the side lobes, measured at distances z_peak, decrease with increasing α at constant y_min, whereas the amplitude of sidelobes relative to that of the main lobe is rather independent of this parameter (Fig.3-f). On the other hand, an increase of y_min at constant α only affects the amplitude of the sidelobes relative to that of the main lobe (Fig.3-g).

Figure 3:

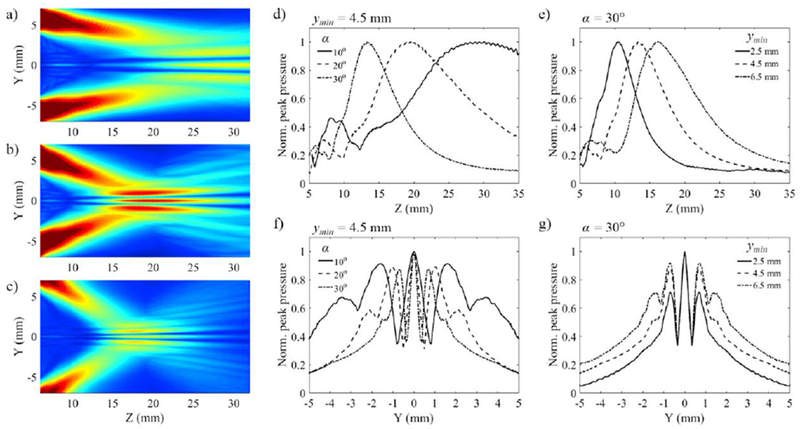
Simulated beams for a 1-cycle 1.7 MHz transmit pulse. The interference of the two individual LF beams generates a narrow center lobe and sidelobes, whose characteristics (position, dimensions) depend on the combination (α, y_min): (a) α= 10°, y_min= 4.5 mm; (b) α= 20°, y_min= 4.5 mm; (c) α= 30°, y_min= 7.5 mm. Elevation (y) and propagation (z) beam profiles showing the influence of α (d, f) and y_min (e, g) taken individually on the location and width of the main lobe, location and width of the sidelobes, and the depth of field on axis.

Comparison of simulation with hydrophone measurements

Extrapolating from LF beam simulations, the dimensions, positioning and orientation of the LF transducer pair were chosen such that the LF focal distance in the elevation plane z_peak was close to that of the previously characterized HF beam (elevation focus: 15 mm, −6dB elevation beam width: 500 μm at focal distance). The width W was set to 2.9 mm, the angle α to 27° and (y_min, z_min) to (7.16 mm, 0.07 mm). This leads to (y_c, z_c) being equal to (8.45 mm, 0.73 mm). In the azimuthal direction, the length of the LF transducers was set to 30 mm to produce a uniform LF beam along the entire length of the HF array, which is 23 mm.

Hydrophone measurements and electrical impedance measurements were performed and compared to simulation results in Fig.4. Simulated (Fig.4-a) and measured (Fig.4-b) beams with a 100%-BW transmit are overall in good agreement in the elevation plane. The peak pressure on axis was found at around 18.5 mm from the face of the HF array as predicted (Fig.4-c), however the measured depth-of-field was slightly lower than predicted by simulation (13.5 mm vs 15 mm in simulation, at −6dB). The beam profiles in the elevation direction measured at z_peak (~18 mm) are in good agreement, even though a slight dissymmetry and a slightly larger distance between secondary lobes were observed in the measured profile (Fig.4-d). Nonetheless, the main lobe width agrees with prediction.

Figure 4:

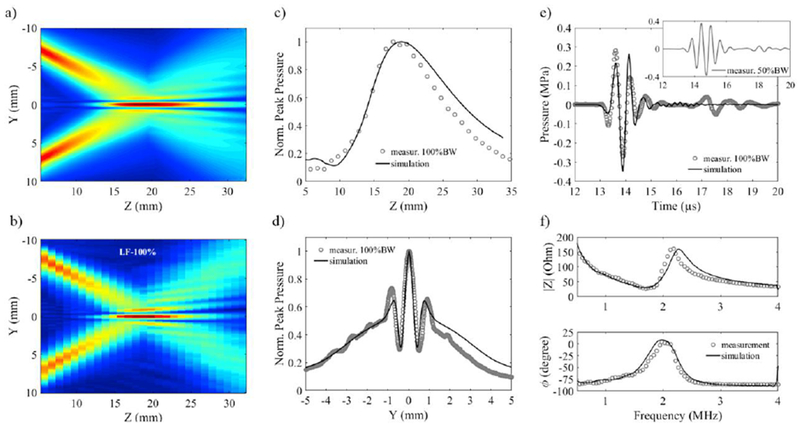
Comparisons of measurements (100%-bandwidth excitation) with simulation. Cross section in the elevation plane for: (a) simulation and (b) measurement (W= 2.9 mm, α= 27° and y_min= 7.16 mm); (c) beam profile on center axis; (d) beam profile in the elevation direction at focal distance (z_peak = 18.5 mm); (e) comparison of the pressure waveforms at z_peak (the insert corresponds to the pressure waveforms obtained with a 50%-bandwidth excitation); (f) Comparison of simulated and measured electrical impedance of the LF transducers.

Simulated and measured pressure waveforms are also in relatively good agreement (Fig.4-e). The second, lower amplitude, pulse observed in the hydrophone measurement is due to the finite dimension of the stacks in the azimuthal direction, which is not considered in the 2-D simulation. Measured and simulated impedances are comparable (Fig.4-f). The −6dB bandwidth of the stacks extrapolated from measurement and simulation is 78% and 76%, respectively.

Alignment with high frequency array beam

The alignment of the low and high frequency beam axes in the elevation plane is shown on Fig.5. In this figure, all beams were measured on transmit, with either a 1.7-MHz 100%-BW Gaussian-enveloped excitation (Fig.5-a) or a 1.7-MHz 50%-BW Gaussian-enveloped excitation (Fig.5-b) for the LF transducers, and a 21-MHz 1-cycle excitation for the HF array with azimuthal focusing set to 18 mm (Fig.5-c). In the azimuthal plane, the LF amplitude is uniform across the 23-mm HF array length (Fig.5-d). Increasing the fractional bandwidth of the LF transmit excitation, i.e., decreasing pulse duration, results in a lower relative amplitude of the secondary lobes, without affecting the width of the main lobe (Fig.5-a, b, e). For a theoretical 1-cycle pulse with no ring down, no secondary lobe should be detected past the trough corresponding to the destructive interference of the two LF stack beams. Instead, a local maximum, about 6dB lower than the main lobe should be observed, from which the pressure amplitude should decrease monotonically with increasing distance along the elevation direction. However, due to the limited bandwidth of the LF transducers, the transmitted acoustic pulse is longer than 1-cycle even with the 100%-BW electrical excitation, yielding secondary lobes in the region of interference.

Figure 5:

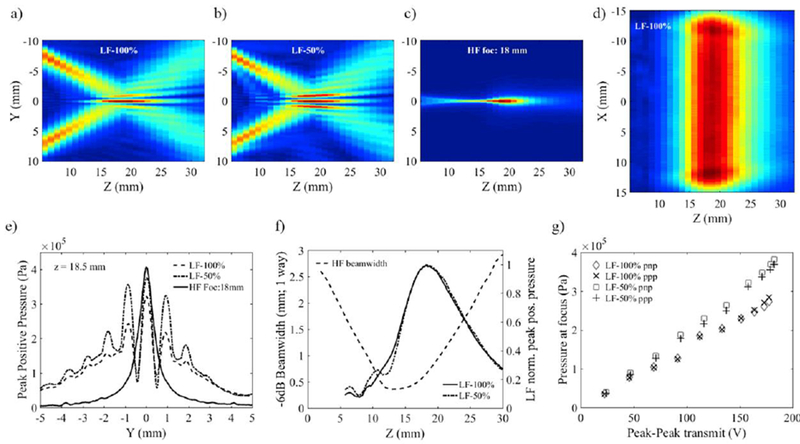
Cross-sections in the elevation plane of the transmit LF beam with: (a) 100%-BW excitation, (b) 50%-BW excitation and (c) transmit HF beam focusing at 18 mm showing the alignment of the center axes of the LF and HF component of the dual-frequency probe; (d) cross-section of the LF beam in the azimuthal plane showing the uniformity of the plane wave amplitude along the HF array length (23 mm); (e) HF and LF elevation beam profiles measured on transmit at LF focal distance; (f) LF transmit beam profiles on center axis superimposed on the variations of the HF beamwidth as a function of depth; (g) LF peak pressure as a function of transmit voltage amplitude.

Assuming transmit-receive reciprocity for the HF beam, and assuming the same aperture is used for dynamic focusing on receive as that used on transmit, the HF receive beam should mostly cover the main lobe of the LF transmit beam. Therefore, the HF receive beam would mostly cover the main lobe of the LF transmit beam and have poor sensitivity to the signals scattered from the LF secondary lobes (Fig.5-e). Given that the LF focal distance was chosen to be 3 mm deeper than the focus of the HF array in the elevation direction, the −6dB beamwidth on receive is expected to vary from 0.5 to 2 mm over the −6dB focal depth of the LF transmit beam (Fig.5-f), and is less than the distance between the two secondary lobe peaks at any given distance z.

Peak pressure range

Peak pressures at the focus of the LF transmit beam were measured in a water bath as a function of electrical excitation amplitude (Fig.5-g). They ranged from 36 to 272 kPa and 40 to 382 kPa for the 100%-BW and 50%-BW pulse, respectively. Pressure peak amplitudes increased linearly with transmit voltage. At the highest transmit voltage, the level of second harmonic detected at the focus was 29 dB below the fundamental, and higher harmonics were below the noise floor (−60 dB), demonstrating that non-linear propagation was insignificant in the voltage range and subsequent pressure range used in this study. Due to the limited bandwidth of the LF transducers and higher harmonic distortion (odd harmonics only) generated by the power amplifier with the 100%-BW excitation than with the 50%-BW excitation, the peak pressure measured with the 100%-BW excitation was lower than that obtained with the 50%-BW excitation (at equivalent peak-peak voltage amplitude) and increased less rapidly with increasing excitation amplitude. In HF B-mode the pressure amplitude measured at 18.5 mm, i.e. in the channel containing microbubbles, was always 425 kPa.

Contrast Agent imaging

Single wall-less channel phantom

Typical images of the phantom obtained using HF focused B-mode and plane wave SpHI-mode are shown on Fig.6-a. From visual evaluation of these two first interleaved frames (out of 200: 100 HF B-modes interleaved with 100 SpHI-modes), CTR_HPB is about OdB, if we compare the image intensity in the channel to that of the matrix above and under the channel, whereas CTR_SpHI is at least 30dB (estimated from the dynamic range of the image). Briefly, this difference in CTR is due to a combination of factors, which include the generation of a broadband signal by the microbubbles in SpHI-mode, with frequency content extending over the bandwidth of the HF array on receive (Fig.6-b).

Figure 6:

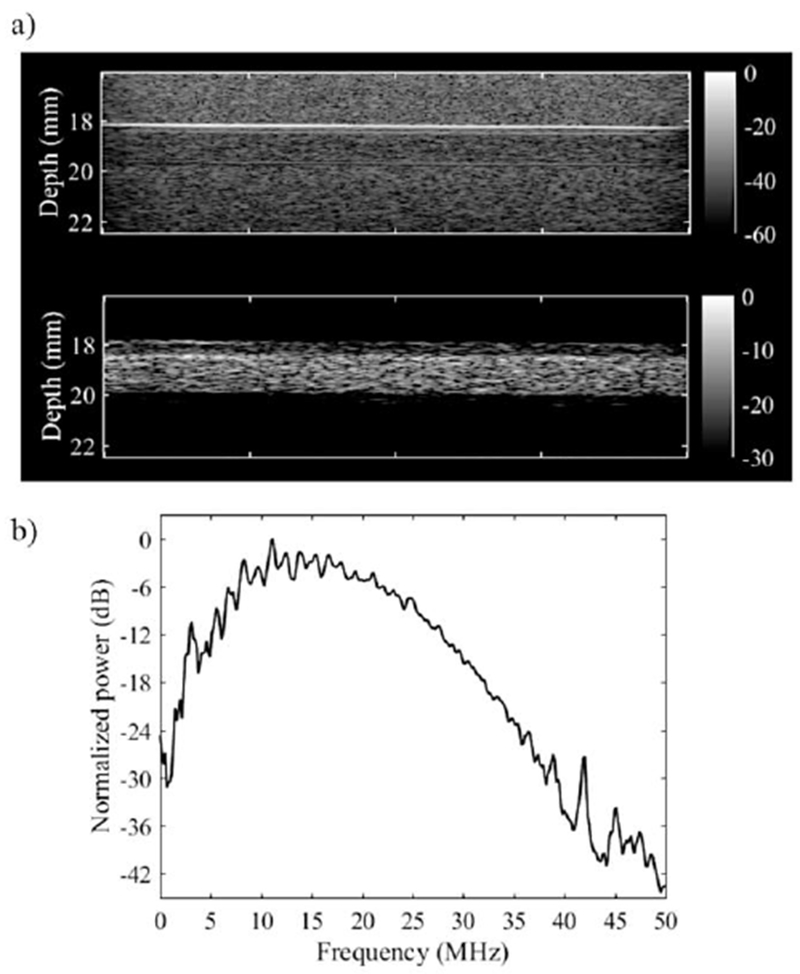
Comparison of images (first frame) of microbubbles in a wall-less agar/SiO₂ particles phantom: (a-top) 20 MHz B-mode; (a-bottom) SpHI-mode transmitting a 1-cycle 1.7-MHz pulse and receiving with the high frequency array; (b) average spectrum of the signals received in SpHI-mode.

The signal intensity $\overline{E_{SpHI}^c}$ measured in the first frame in SpHI-mode is shown in Fig.7-a as a function of peak pressure. At 40 kPa and below, the superharmonic signal generated by microbubbles, if any, was below the noise floor $\overline{E_{SpHI}^w}$ in our experimental conditions. Microbubble signals were detectable at a LF pressure of 78 kPa (for the 100%-BW excitation), and its amplitude in the first frame increased with LF pressure up to about 321 kPa (for the 50%-BW excitation). Above this pressure level, the microbubble signal amplitude started plateauing, potentially because as microbubble oscillations become more nonlinear, the increment in scattered energy is generated predominantly above the frequency range of the HF array. It is also interesting to note that the signal intensity is relatively independent of the bandwidth of the transmit excitation for peak pressure amplitudes below 130 kPa, whereas at higher transmit pressures the signal intensity measured with the 100%-BW excitation is about 3.5 to 4dB lower than that measured with the 50%-BW excitation. It could be that, above a pressure threshold, a larger microbubble subpopulation is generating signal in the bandwidth of the HF array when excited with a longer LF pulse, and/or that a higher number of cycles in the impinging pressure wave were above this pressure threshold, leading to a higher number of transients generated by the same microbubble subpopulation.

Figure 7:

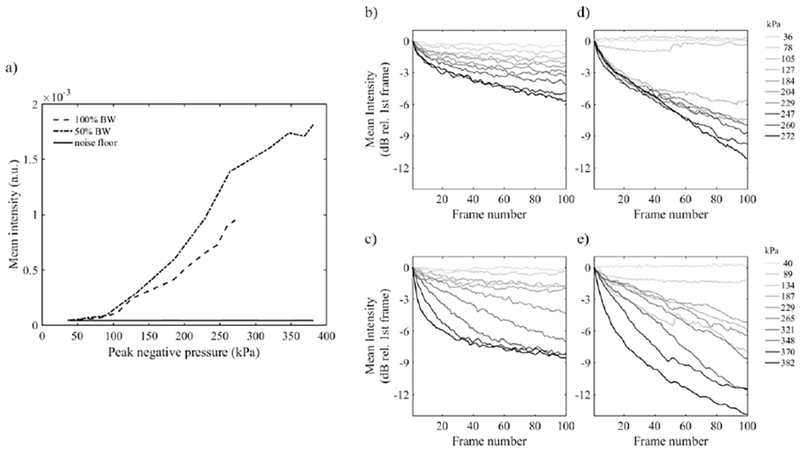
(a) Mean intensity of the signals in the first frame acquired in SpHI mode in the channel (microbubbles) and in water (noise floor) as a function of transmit peak pressure; Mean signal intensity (relative to the mean intensity in the first frame) measured in the interleaved HF B-mode frames following transmission of : (b) 100%-BW and (c) 50%-BW LF excitations. Mean signal intensity measured in SpHI-mode with: (d) 100%-BW and (e) 50%-BW excitations.

In following frames, the signal intensity in the channel decreases (relative to the intensity in the first frame) in both interleaved HF B-mode and SpHI-mode images. This decrease (Fig.7-b–e) is certainly associated with a progressive change in the microbubble population induced by LF excitations only, since HF transmit pressure is identical in all interleaved B-mode data acquisitions and the HF B-mode signal intensity does not vary with frame number at the lowest transmit LF amplitude. The variations of the relative signal intensity in Fig.7-b and Fig.7-c reflects changes in the bubble subpopulation interacting with the HF broadband excitation, whereas in Fig.7-d and Fig.7-e, it reflects the changes in the subpopulation of microbubbles generating superharmonic signal only. Therefore, it is not expected that the rates of change in signal intensity in HF B-mode and SpHI-mode would be equivalent, unless the two subpopulations are identical. Interestingly, whereas the signal intensity measured in HF B-mode decreases faster with increasing pressure amplitude for both 100%-BW and 50%-BW LF pulses (Fig.7-b and Fig.7-c, respectively), this is not the case for the 20 to 30 first frames acquired with the 100%-BW LF excitation (Fig.7-d), for which the decrease in signal intensity is independent of pressure amplitude above 105 kPa. This seems to indicate that, for the major contributors to the superharmonic signal in the microbubble subpopulation, the overall outcome to successive exposures is somewhat independent from impinging pressure above a given threshold. The same observation can be made in the 187 to 321 kPa pressure range, for the first 5 to 10 frames obtained with the 50%-BW excitation (Fig.7-e).

In the first frame acquired in SpHI-mode, the increase of the MB signal intensity with transmit LF pressure translates into an increase of the signal-to-noise ratio $SN{R}_{spHI}^c$ (Fig.8). On the other hand, $SN{R}_{SpHI}^m$ remains constant at 0 dB, reflecting the fact that no signal from the matrix could be detected above the noise floor, at all transmit LF pressure levels. In this circumstance, the contrast-to-signal CTR_SpHI ratio could not be estimated but must be superior to $SN{R}_{SpHI}^c$. In HF B-mode, both the signal from MBs and signal from the matrix are above the noise floor at the transmitted HF pressure amplitude, CTR_HFB could be estimated around 0 dB, but with a slight decrease with increasing LF pressure. This decrease originates from the four LF exposures (1 per receive aperture) that take place before the first HF B-mode frame is acquired and affect the MB population increasingly with increasing pressure amplitude. The lower limit of the CTR increase obtained in SpHI-mode relative to HF B-mode (i.e. $SN{R}_{SpHI}^c-CT{R}_{HFB}$) in the first acquired frame ranges from 4.2dB at 78kPa to 28.2 dB at 272 kPa for the 100%-BW LF excitation, and from 5.5 dB at 89 kPa to 32.2 dB at 382 kPa for the 50%-BW LF excitation. In the following frames, at any given transmit pressure, this lower limit decreases at the same rate as the contrast signal intensity in SpHI-mode (Fig.7-d, e).

Figure 8:

$SN{R}_{SpHI}^c$ and $SN{R}_{SpHI}^{ma}$ measured in the first frame in SpHI-mode as a function transmit LF peak pressure with (a) 100%-BW and (b) 50%-BW excitations, compared to CTR_HFB measured in the subsequent interleaved HF B-mode frame.

Multiple cellulose tube phantom

Maximum intensity projection (MIP) images of the cellulose tube phantom obtained in HF B-mode and SpHI-mode with the highest microbubble concentration, are compared in Fig.9. In HF B-mode, the strongest signals come from the walls of the tubes, which can be resolved (Fig.9-a, b). Consequently, the image intensity varies with the orientation of the tube relative to the impinging pressure pulse (Fig.9-a–c), due to the specular nature of this target. On the other hand, because the signal in SpHI-mode originates from microbubbles, it is insensitive to the tube orientation. Therefore, its intensity is relatively uniform over the 3-D volume (Fig.9-e, f). Axial (Fig.9-e) and lateral (Fig.9-f) resolution in SpHI-mode seem comparable to that in HF B-mode, although some blurring is visible in the lateral direction in SpHI-mode probably due to the lack of focusing on transmit. Also, ‘ghost’ signals running parallel to the cellulose tubes are visible in SpHI-mode (Fig.9-e), at a constant distance, as observed after beamforming, which corresponds to one LF wavelength. The presence of ‘ghost’ signals is therefore probably due to the limited bandwidth of the LF transducers which generate pressure waves more than one cycle in length (Fig.4-e) leading to the generation of lower “transient” signals prior to the middle of the transmitted pulse, which is used as reference for beamforming delays. This effect is also visible on Fig.6-a, where a lower intensity zone appears at the top of the channel. The thickness of this top layer is equivalent to the distance between the echoes from microbubbles in the cellulose tube and their ‘ghost’ echoes observed on Fig.9-e. Images obtained in the cellulose tube with lower microbubble concentrations were similar to those just described.

Figure 9:

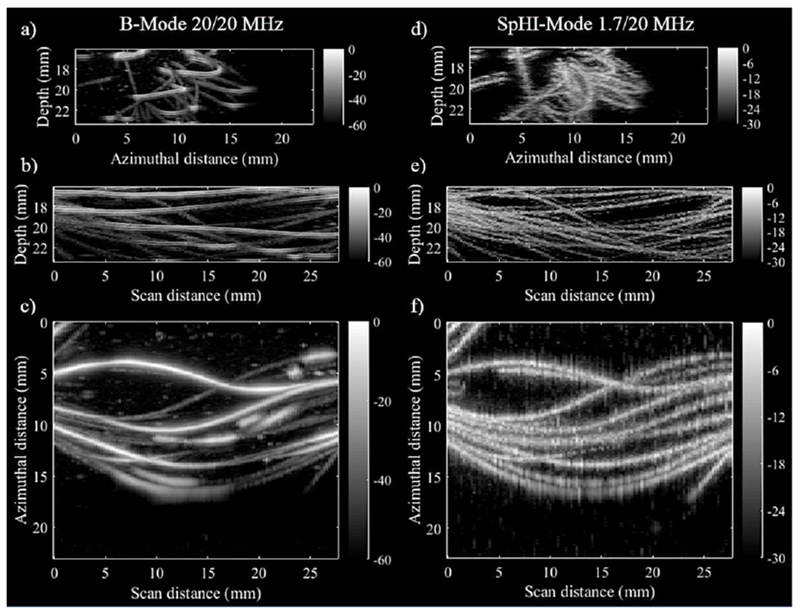
Maximum intensity projection images obtained from a 3D volume data set acquired in (left) HF B-mode and (right) SpHI-mode: projections are along, (top) the scan (i.e. elevation) direction, (middle) the azimuthal direction, and (bottom) the propagation direction.

Discussion

Hybrid dual frequency probe

In this study, we investigated the feasibility of implementing superharmonic imaging using two rectangular low frequency transducers assembled in a parallel geometry with a high frequency array. The most important advantages of this geometry are the relative ease of implementation and a complete electro-mechanical decoupling of the transmit and receive path allowing for the use of the HF array in traditional imaging modes without performance degradation. Our simulation work also demonstrated the flexibility in adjusting the transmit elevation beamwidth, focal position and depth-of-field, provided by the number of degrees of freedom in positioning of the LF transducers relative to the propagation axis of the HF array. However, the foot print of the dual frequency probe, which is about 2.5 cm for our assembly, might represent a limitation for applications where the contact surface dimension is small. The fixed focal region on transmit would also represent a limitation, for regions of interest located beyond the transmit focal zone. This geometry also requires the implementation of a beamforming algorithm specific to the geometry of the LF transmit source. The bandwidth of the LF transducers is a critical parameter as well. In our configuration, it determines the level of side-lobes which, if too high, would lead to changes in the MBs population outside of the imaging plane. This could be detrimental to 3-D imaging, where scanning along the elevation direction is performed, especially when perfusion rate is low such as in the microvasculature. Furthermore, LF excitations longer than one cycle can produce ‘ghost’ signals such as those observed in the present study, which could certainly impact negatively the ability to image the microvasculature accurately. This imaging artefact is probably related to the behavior of microbubbles in the LF field, which will be discussed next.

Contrast agent behavior

Micromarker™ microbubbles are constituted of a decafluorobutane/nitrogen core encapsulated in a phospholipid/polyethylene glycol/fatty acid shell. Their diameter ranges from below 1 to up 8 μm, with a volume-weighted size distribution peaking at around 2.3 μm (Raymond et al. 2014, Fig. 2; Sun et al. 2014, Fig. 3). Lindsey et al. (2015) investigated the behavior of a similar type of microbubbles when exposed to trains of 1.75 to 3.75 MHz singlecycle excitations of varying pressure amplitudes ranging from 100 to 500 kPa. Interleaved optical imaging allowed the observation of the fate of microbubbles between successive transmit excitations, and the categorization of the outcome into, no size change, shrinkage, or fragmentation. Over multiple pulse transmissions, diverse combinations of outcomes might be observed for a given bubble depending on factors including its size, pulse pressure and pulse length. However, the generation of signal in the superharmonic frequency range was associated with structural and/or oscillatory behavior leading to either fragmentation or shrinkage (Lindsey et al. 2015, Fig.6), with fragmenting bubbles generating a stronger signal than shrinking bubbles. Furthermore, fragmented bubble signal decreases drastically relative to pre-fragmentation, whereas little difference in signal intensity is observed between pre and post shrinkage.

These findings could shed some light on the variations of signal intensity with frame number and excitation amplitude in our experiments. For the 100% BW excitation (Fig.7-d), a definite threshold was observed between 105 and 127 kPa above which a rapid initial decrease in signal was observed with number of exposures (first 30 frames) most probably associated with bubble fragmentation. This threshold is lower than that found in Lindsey’s paper. This could be due to the differences in experimental conditions (200-μm rigid cellulose tube versus 1.5-mm square section wall less channel) and potential differences in microbubble size distribution and properties. It is also possible that the LF pressure amplitude was effectively lower in the cellulose tube than that measured in free-field. For the 50% BW excitation, the threshold was found a little lower at 89 kPa (Fig.7-e), probably due to an increase in likelihood of a fragmentation event occurring over the higher number of cycles in the excitation pulse. The rate of decrease in signal intensity at equivalent pressure, appears lower with the 50% BW excitation (−1.5 to 2 dB over 20 first frame) than with the 100% excitation (−3 to −4dB over 20 first frames). Such difference could potentially be explained by the behavior of shrinking bubbles, if we assume that they undergo stable cavitation. If this is the case the amount of energy scattered by these bubbles should increase with pulse duration in the first frame (Fig.7-a). For fragmenting bubbles on the other hand, this would be the case if and only if a transient fragmentation event occurs in every cycle of the transmitted excitation, which is possible, but unlikely for all fragmenting bubbles. Consequently, the contribution of shrinking bubbles to the overall received signal should increase with pulse duration in the first frame from which the signal intensity is used as normalization factor.

Contrast-to-tissue ratio

As previously mentioned, the CTRs measured in B-mode and SpHI-mode in the present paper depend on numerous factors that will certainly vary over different applications, e.g. contrast agent used, tissue type, and their respective interaction with ultrasound. On the “tissue” side in our experiments, the CTR_SpHI the depends on the interaction of the SiO₂ particles with 1.7 MHz transmit pulse, whereas CTR_HFB depends on the interaction of the same particles with a 21 MHz pulse. Assuming Rayleigh scattering, a decrease of 43dB in scattering cross-section is expected between 21-MHz and 1.7-MHz excitations, which will contribute to the increase in CTR_SpHI relative to CTR_HFB. To this should be added the difference between the LF (in SpHI-mode) and HF (in B-mode) transmit pressures which ranged from −21 to −1dB in our experiments (36-382 kPa for LF, relative to 425 kPa for HF), and the effect of bandpass filtering by the receive HF array. The latter set aside, tissue signal should drop by at least by 44 to 64dB in SpHI-mode relative to HF-B-mode, enough to bring it below the noise floor, as was observed in our experiments. For this reason alone, CTR_SpHI could not be estimated here, and its lower limit (represented by $SN{R}_{SpHI}^c$) is not to be taken as absolute value associated with the imaging technique itself. However, the difference between $SN{R}_{SpHI}^c$ and CTR_HFB for the same system {contrast agent, tissue, propagation characteristics}, should provide some indication of the minimum improvement in contrast to be expected in SpHI-mode relative to HF B-mode. It could also give some indications of the minimum improvement in contrast with other systems. For example, if specular reflectors, at both LF and HF frequencies simultaneously, are present in the tissue, the 43 dB difference in scattering cross-section would be eliminated from the difference in CTR between the two imaging methods.

SpHI-mode axial resolution

In our experiments with 200-μm diameter cellulose tubes, the broadband signal generated by the microbubble population spreads over an axial distance only slightly bigger than the diameter of the tube, and much smaller (1/4) than the transmit excitation wavelength (880 μm). For this to occur, two conditions are necessary. Firstly, the received broadband signal from a single microbubble must be concentrated in a relative short time window relative to the excitation pulse period and therefore associated with a transient event occurring during the MB oscillation. Such short duration signals have been observed by Kruse and Ferrara (2005,[Fig. 2]), and according to simulation could be generated by the MB rebound following maximum compression (Kruse and Ferrara, 2005, [fig. 1]), or by the MB destruction. And secondly, all microbubbles generating such broadband signal must oscillate somewhat in phase, which is most likely to occur if the damped resonance frequency of all microbubbles in the population is well above (or well below) the excitation frequency. This is probably the case for Micromarker™ MBs for which, the damped resonance frequency estimated using shell parameters from Helfield et al. (2013) and Eq. 6 in Goertz et al. (2007), ranges from about 3 MHz for 8-μm to 25 MHz for 1.5-μm diameter MBs. The use of short excitations (1 or 2 cycles) could also be contributing by preventing MBs from oscillating beyond the initial transient phase observed with longer excitations, and during which MB, independently from their resonance frequency, initiate their oscillation in phase with the excitation pressure. It is also possible that only a subpopulation of narrower size distribution produces transient broadband signals, increasing the likelihood of in-phase oscillations. All these hypotheses warrant further investigation.

SpHI plane wave imaging

Due to the lack of focusing in the azimuthal direction on transmit in SpHI-mode, which is inherent to the transmission of a single plane wave, the lateral resolution was expected to be lower in that mode than in HF B-mode, in which focusing is performed on both transmit and receive. This lower resolution probably explains the smearing in the azimuthal direction of the signal from microbubbles in the cellulose tubes that is observed (Fig.9-f). A potential way to improve resolution in SpHI-mode would be to compound coherently signals acquired successively using plane waves transmitted at different angles relative to the imaging depth axis. Montaldo et al. (2009) demonstrated that the lateral resolution obtained with traditional multiple focused transmits can be achieved using plane wave coherent compounding even with a limited number of angles (these results were recently replicated in the high-frequency range by Huang et al., 2017). They also showed a gain in SNR relative to one plane wave transmit, which can range from 11 to 18dB for a number of angles ranging from 12 to 71. This gain in SNR should theoretically be similar if plane wave coherent compounding was implemented in SpHI (because it simply arises from noise averaging). However, to fully benefit from coherent compounding, invariance of the tissue or contrast agent to be imaged is required over the time it takes to acquire signals with multiple transmit plane waves. In that respect, destruction of the contrast agent and the rate at which it occurs with number of exposures to LF transmits in our experiments could potentially mitigate the benefits of coherent plane wave compounding in terms of both SNR and resolution, warranting further investigations.

Conclusion and future work:

In summary, we developed a hybrid dual frequency probe comprising two rectangular 1.7-MHz stacks for transmit and a commercial 21-MHz array transducer on receive arranged in a parallel geometry. Superharmonic imaging of a MicroMarker™ was investigated using a single plane wave on transmit and dynamic focusing on receive. It was shown that, with this contrast agent, an increase in CTR of at least 36dB could be achieved using our SpHI implementation relative to traditional high frequency B-mode imaging, with a SNR above 30dB in some conditions. Apart from potential improvements in the bandwidth of the transmit transducer, the number of channels of the receive beamformer and a more thorough investigation of Micromarker™ microbubbles behavior when exposed to short LF pulses, all previously mentioned, our future investigations will focus on the evaluation of coherent plane wave compounding. This can be implemented by replacing the two LF transducers by two LF arrays in the same parallel geometry, or potentially by positioning a LF array behind the HF array in a vertical geometry.