Pulsed Excitation in Magnetic Particle Imaging

Abstract

Magnetic Particle Imaging (MPI) is a promising new tracer-based imaging modality. The steady-state, nonlinear magnetization physics most fundamental to MPI typically predicts improving resolution with increasing tracer magnetic core size. For larger tracers, and given typical excitation slew rates, this steady-state prediction is compromised by dynamic processes that induce a significant secondary blur and prevent us from achieving high resolution using larger tracers. Here we propose a new method of excitation and signal encoding in MPI we call pulsed MPI to overcome this phenomenon. Pulsed MPI allows us to directly encode the steady-state magnetic physics into the time-domain signal. This in turn gives rise to a simple reconstruction algorithm to obtain images free of secondary relaxation-induced blur. Here we provide a detailed description of our approach in 1D, discuss how it compares with alternative approaches, and show experimental data demonstrating better than 500 μm resolution (at 7 T/m) with large tracers. Finally we show experimental images from a 2D implementation.

I. INTRODUCTION

MAGNETIC particle imaging (MPI) is an emerging molecular imaging modality first described by Gleich et al. in 2005 [1] with applications in areas such as stem cell tracking [2], cancer imaging [3], gut bleed detection [4], lung imaging [5], [6], and stroke detection [7]. The fundamental basis of MPI is creation of a spatially sensitive region by exploiting nonlinear magnetic saturation of magnetic nanoparticles, typically superparamagnetic iron oxides (SPIOs). This sensitive ‘field-free’ region (FFR) can be moved through space to sample a volume of interest, inducing a magnetic signal linearly proportional to the mass of any present tracer [8], [9].

Since 2005, further work has described the physical and mathematical nature of the MPI signal [10], [11], the system matrix encoding and reconstruction approach [10], [12], the x-space encoding and reconstruction approach [13], [14], [15], and many other implementations of MPI [16], [17]. All are governed by magnetic saturation physics [13]. Both the M-H curve steepness and imaging resolution monotonically increase as a function of magnetic core size according to steady-state theory (e.g., the Langevin physics of SPIOs). Increasingly, however, the field has become aware of the impact tracer magnetic dynamics, or relaxation, has on the MPI signal and subsequent reconstructed images [18], [19], [20], [21], [22], [23], [24]. Steady-state models remain relevant only if the dynamic response of the tracer is much faster than the slew rates used in excitation. For small Néel-dominant tracers, this may be true. However, as the magnetic core size of a tracer increases, the magnetic response time does as well, regardless of mechanism (e.g., Néel or Brownian) [25], [26].

Fig. 1(a) describes how finite and non-negligible relaxation induces secondary blurring in x-space MPI. Intuitively, relaxation can be understood as a phase lag as the tracer struggles to keep up with a rapidly varying applied field. Regardless of the details, this can be modeled as convolution with a low-pass relaxation kernel. From an x-space MPI perspective, this temporal low-pass filter translates to an image domain low-pass filter due to the direct mapping between the two domains. From the Fourier domain or system matrix perspective, the higher order harmonics that contain high spatial resolution information are attenuated. As a result, relaxation manifests as a secondary blur in reconstructed images, compromising both resolution and signal-to-noise ratio (SNR). Using typical excitation parameters in canonical MPI (e.g., 25 kHz fundamental frequency and 20 mT amplitude), we have found that improved resolution with increasing magnetic core size follows the steady-state prediction up to approximately 25 nm at which point we encounter a ‘relaxation wall.’ We have assessed this phenomenon in detail in previous work [27].

Fig. 1. Current challenges to achieve the high resolution predicted by steady-state theory with larger tracers in MPI.

(a) Some MPI tracers have significant magnetic relaxation response times, and the tracer is observed to lag the excitation field. This blurs the time domain signal which maps to a blurring of the final image. (b) Experimental vs. theoretical (steady-state Langevin theory) 2D images of point sources using tracer with 18.5, 24.4, and 27.4 nm core sizes. The canonical steady-state Langevin theory predicts improving resolution with increased tracer core size, but this is not observed experimentally (c), where we observe improved resolution up to a certain size, after which resolution sharply degrades. We can shift the optimal curve by reducing the excitation slew rate (lower the drive frequency or amplitude – blue and red data points from our prior work [27] plotted here at 7 T/m) [28], [23]. However, we generally still hit a ‘relaxation wall’ that cannot be easily overcome.

Here we propose a new excitation approach for MPI using pulsed waveforms that allow for direct encoding of steady-state information into the acquired time domain signal in a way that is separable from relaxation dynamics. This enables reconstruction of images that asymptotically approach the theoretical steady-state resolution, even for large particles with significant magnetic response times.

Alternative approaches to try and achieve similar results include employing deconvolution or greatly slowing down standard sinusoidal excitation. For the latter, as the data of Fig. 1(c) shows, reducing excitation frequency or amplitude with canonical methods [28], [23], [27] can improve results, but it is not easy to fully mitigate the problem. We believe pulsed MPI can solve this problem while providing key advantages. These include retaining more raw signal energy due to temporal separation of feedthrough and signal, practical implementation advantages for producing arbitrary frequency waveforms to match a tracer’s relaxation behavior, and the ability to retain relaxation dynamic information in a way easily exploited for contrast or molecular imaging applications.

II. THE PULSED MPI APPROACH

The crux of pulsed MPI is use of piecewise-constant waveform components in MPI excitation trajectories. We make use of two primitive waveform components: 1) periods of temporally-invariant applied field and 2) periods of rapidly varying applied field. The former allows encoding of steady-state information in the raw signal while the latter provides high peak time domain SNR as well as temporal separability between the tracer signal and excitation feedthrough. These components can be assembled into larger periodic excitation waveforms or pulse sequences. One of the simplest cases is a square (trapezoidal) wave which we use in this work.

Pulsed MPI is a complete departure from typical continuous wave excitation sequences used in the field, requiring new transmit and receive electronics. However, as indicated in Fig. 2, other aspects of the typical MPI system infrastructure remain the same, such as the gradient-producing magnets and shift mechanisms that allow sampling of a large FOV over time in a canonical x-space acquisition [29].

Fig. 2. Depiction of pulsed encoding in MPI acquisition with a field-free line (FFL) scanner.

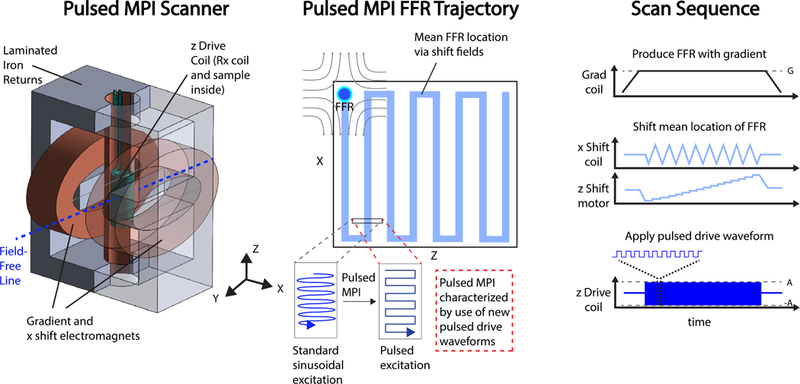
We can describe an MPI acquisition scheme in terms of a choice of fast excitation encoding waveform, FOV sampling strategy, and reconstruction formulation. Pulsed MPI replaces the canonical sinusoidal fast excitation encoding with pulsed waveforms (square, trapezoidal, etc.). The gradient and shift pulse sequences do not differ from standard continuous-wave x-space MPI.

Magnetic relaxation is complex and a very active area of research in MPI [18], [19], [20], [21], [22], [23], [24], but our approach requires only the assumption that magnetic relaxation processes have a finite step response, which is guaranteed for all real processes. The ramifications of pulsed encoding, therefore, should pertain for a great variety of tracers regardless of the specific nature of their magnetic relaxation physics. The simulated data of Fig. 3 and experimentally measured nanoparticle response in Supplementary Fig. 11(c) show the decaying MPI signal elicited after the rapid transitions of a typical square wave excitation.

Fig. 3. Pulsed MPI encoding with tracer relaxation.

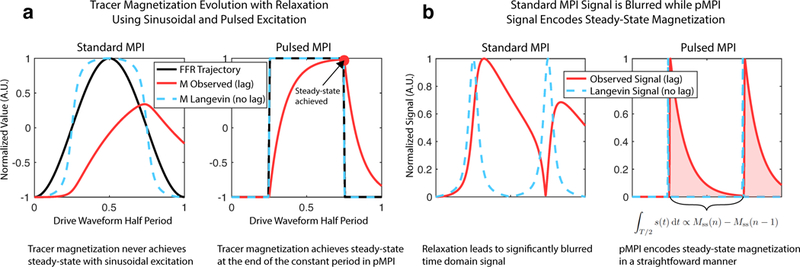
(a) In canonical sinusoidal MPI, the observed magnetization fails to keep up with the excitation waveform (FFR trajectory) for larger tracers. This leads to significant lag and blurring of the signal, and in general, at no point is steady-state achieved. Using a pulsed waveform such as a square wave, we can ensure steady-state magnetization is reached using sufficiently long stationary components. (b) The raw MPI signal associated with sinusoidal excitation is significantly blurred compared to the ideal. A square excitation waveform leads to an exponential decay-like signal for each half-period in which the area under the curve is directly proportional to the difference between the steady-state magnetization achieved at the end of successive half-periods. Steady-state and relaxation behavior are neatly separable, which is not the case in standard MPI.

A. Square Wave Excitation Signal and Imaging Equations

Here we develop the 1D signal and imaging equations for pulsed MPI with ideal square wave excitation and a tracer that obeys Langevin physics. We begin by defining the applied magnetic field in terms of the FFR in 1D [13]:

$$H(t,x)=\frac{G}{{\mu }_0}\cdot \left(x-x_{\text{s}}(t)\right)$$ (1)

where H(t,x) is the applied field in [Am⁻¹], G is the linear gradient strength in [T m⁻¹], μ₀ is the vacuum permeability in [Hm⁻¹], and x_s (t) is the center location of the FFR. The steady-state magnetization of a 1D tracer distribution is then:

$$M_{\text{ss}}(t,x)=m\rho (x)\mathcal{L}(kH(t,x))$$ (2)

where m is the tracer’s magnetic moment in [Am²], ρ(x) is the tracer distribution in [particles m⁻¹ ], $\mathcal{L}$ is the Langevin function, and k in [mA⁻¹] is a tracer-specific parameter.

We now consider excitation with an ideal square wave. To derive the signal equation, we assume use of an inductive receive coil with homogeneous sensitivity B₁ in [T A⁻¹]. The voltage on the receiver coil in 1D is then:

$$V(t)=B_1\frac{\text{d}}{\text{d}t}{\int }_{u}M(t,u)\text{d}u$$ (3)

We assume that non-instantaneous tracer magnetic relaxation can be described as a linear time-invariant (LTI) process with impulse response h_m(t,x) and associated step response r_m(t,x). These responses vary as a function of x because magnetic relaxation is a strong function of applied field which translates to a strong function of space in MPI due to our gradient fields. These expressions are normalized such that ${\overline{h}}_{\text{m}}={\int }_{-\infty }^{\infty }{h}_{\text{m}}(t,x)\text{d}t=1\forall x.$

The evolution of magnetization over each n-th square wave half-period is described by a scaled relaxation step response. As a crucial aspect of pulsed MPI, we consider a half-period that is long enough to achieve steady-state magnetization in the tracer distribution by the end of each half-period. We specify a signal equation s_n (t) as the receive coil voltage evaluated for each square wave half-period per index n:

$$\begin{array}{l}{s}_n(t)=V{(t)|}_{t_n}^{t_{n+1}}\\ =B_1{\int }_u\Delta M_n(u)h_{\text{m}}\left(t-t_n,u-u_n\right)\text{d}{u|}_{t_n}^{t_{n+1}}\end{array}$$ (4)

where $\Delta M_n(x)$ is the change in steady-state magnetization before and after a square wave jump and $h_{\text{m}}\left(t-t_n,x-x_n\right)$ indicates that the field-dependent relaxation impulse response is centered about the FFR location x_n after the n-th jump. The temporal derivative intrinsic to inductive reception converts the physical step response to an impulse response. See Appendix A-A and A-C for a complete derivation.

We now consider integrating this time-domain signal equation over each half-period. These values are then associated with the center location of the FFR for each half period:

$$\begin{array}{l}s(n)={\int }_{t_n}^{t_{n+1}}{s}_n(t)\text{d}t\\ =B_{1}m\rho (x)\underset{*}{x}\stackrel{.}{\mathcal{L}}(kGx)\underset{*}{x}\sqcap {\left(\frac{x}{2\Delta x}\right)|}_{x=x_n-\Delta x}\end{array}$$ (5)

where $2\Delta x=2A{G}^{-1}=x_n-x_{n-1}$ is the square wave step size, determined by the square wave magnetic field amplitude, A in [T], and the gradient strength. $\sqcap$ is the rectangular function (see [30] for a definition). See Appendix A-D for a complete derivation. We can use this discrete signal equation to form a 1D square wave pulsed MPI imaging equation:

$$\begin{array}{l}\widehat{\rho }(x)=\frac{s(n)}{B_{1}m}\\ =\rho (x)\underset{*}{x}\stackrel{.}{\mathcal{L}}(kGx)\underset{*}{x}\sqcap {\left(\frac{x}{2\Delta x}\right)|}_{x=x_n-\Delta x}\\ =\rho (x)\underset{*}{x}{\left(h_{\stackrel{.}{\mathcal{L}}}(x)\underset{*}{x}{h}_r(x)\right)|}_{x=x_n-\Delta x}\\ =\rho (x)\underset{*}{x}h{(x)|}_{x=x_n-\Delta x}\end{array}$$ (6)

Our 1D square wave point-spread function (PSF), h(x), is then the steady-state Langevin PSF, $h_{\stackrel{.}{\mathcal{L}}}(x),$ convolved with a rectangular function, h_r (x), defined by the excitation amplitude $\Delta x.$ To illustrate, Fig. 8(a) shows peak-normalized PSFs as a function of various excitation amplitudes. We summarize aspects and ramifications of this new imaging equation:

Fig. 8. Experimental relationships and theoretical expectations between pulsed waveform amplitude and pulsed MPI performance for 27.4 nm particles.

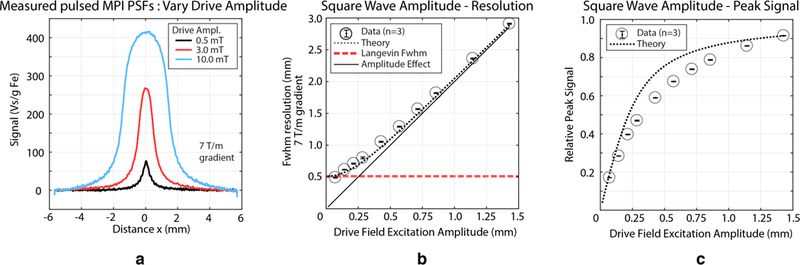
A 2.5 kHz square wave with varying amplitudes was used. (a) Pulsed MPI 1D point-spread functions show higher signal but worse resolution with increasing excitation amplitude. (b) Spatial resolution improves and approaches that of the Langevin model as the excitation amplitude → 0. The results match our theory as our approach to integrating the time domain signal for each half-period collapses all of the information of the half-period into a single value. Mathematically this presents as convolution of the ideal with a rectangular function. (c) Pulsed MPI peak signal improves with increasing excitation amplitude as a larger portion of the tracer’s M-H curve is covered per pulse. Amplitude is therefore a flexible way of trading off spatial resolution and SNR.

• This result is general for any LTI relaxation physics characterized with an impulse response that converges to zero, such as the Debye model [21], [23].

• The results are predicated on choosing a square wave half-period longer than some measure of the maximum observable impulse response time, such as $5\cdot {\tau }_{\max }$

• The results of (5) and (6) hold for non-square waveforms, such as a trapezoidal waveform, that contain a flat, timeinvariant section longer than the maximum observable impulse response time. In this case, however, (4) does not hold but a more general temporal convolution does.

• We obtain resolution related directly to the steady-state Langevin function and an excitation parameter under our direct control: the excitation amplitude.

• We can only asymptotically approach the steady-state resolution in the limit of small excitation amplitudes.

• The choice of excitation amplitude provides a convenient and continuous tradeoff between SNR and resolution.

B. Resolution

Rigorously, we can solve for the full-width-at-half-maximum (FWHM) of the square wave PSF in equation (6) by solving for x in the following expression (See Appendix A-D):

$$\mathcal{L}(kG(x+\Delta x))-\mathcal{L}(kG(x-\Delta x))=\frac{\mathcal{L}(kG\Delta x)-\mathcal{L}(-kG\Delta x)}{2}$$

This expression is difficult to solve analytically. Instead we note that the PSF is composed of two components: the derivative of the tracer’s Langevin function and a rectangular function with width equal to twice the square wave amplitude (the peak-to-peak amplitude). The FWHM of the derivative of the Langevin function has been reported [13] and the FWHM of a rectangular function is just its width. Fig. 8(a) shows how the PSF changes as a function of the excitation amplitude and Fig. 8(b) quantifies the FWHM resolution as a function of the excitation amplitude. Qualitatively we note:

$$\text{FWHM}\approx \{\begin{array}{ll}{\text{FWHM}}_{\stackrel{.}{\mathcal{L}}}\hfill & \text{if}\Delta x\ll {\text{FWHM}}_{{}_{\stackrel{.}{\mathcal{L}}}}\hfill \\ 2\Delta x\hfill & \text{if}\Delta x\gg {\text{FWHM}}_{\stackrel{.}{\mathcal{L}}}\hfill \\ {\text{FWHM}}_{\stackrel{.}{\mathcal{L}}}+\Delta x\hfill & \text{otherwise}\hfill \end{array}$$ (7)

With this approach, to significantly realize the gains in resolution that larger tracers promise, we must limit the square wave excitation amplitude.

C. SNR and Bandwidth

The signal and bandwidth of square wave pulsed MPI are both explicitly related to the tracer impulse response. Lacking a generic closed form expression for tracer impulse responses, we do not provide explicit expressions for SNR but can make a few observations.

Our time-domain signal equation (4) states that SNR at any given time is directly proportional to the tracer magnetic moment, mass of the tracer, and the difference between two points along a tracer’s steady-state M-H curve. Thus, as in standard MPI, tracers with steeper M-H curves provide better SNR [13]. Unlike standard MPI, reducing receive bandwidth can improve pulsed MPI resolution. A discussion of this mechanism is provided in the results section.

For optimal SNR and SNR-efficiency the excitation half-period should be no longer than needed to approach steady- state magnetization. We need to capture the signal but avoid including only noise after steady-state is reached. The equivalent of a $5\cdot \tau$ half-period may not be strictly necessary, and, as in standard MPI, resolution-SNR tradeoffs are manifest.

D. Comparison with Other Approaches

To accommodate the long relaxation times of larger tracers, we must tradeoff SNR or SNR efficiency in some form.

First we consider using standard high frequency excitation (e.g., 25–50 kHz, 15–30 mT) in tandem with deconvolution methods. This is not viable with the heavily relaxing large tracers that are the focus of this paper because relaxation effects both greatly reduce resolution and SNR at the same time (low-pass filter). However, one can consider using a smaller tracer, with relatively little relaxation, in this context. Deconvolution techniques could then be used to improve the intrinsically limited resolution. While this is a viable technique, deconvolution has several limitations. Aggressive deconvolution is a very expensive process in terms of SNR, and smaller tracers that exhibit little to no relaxation have less intrinsic MPI signal due to a less steep M-H curve. Additionally, if the PSF is not perfectly known, or the PSF varies spatially over the imaging FOV (both are typical in MPI), aggressive deconvolution can induce significant non-physical artifacts. Pulsed MPI methods, which require no a priori assumptions such as PSF shape, may navigate the SNR-resolution tradeoff space in a more robust manner.

Second, we consider pulsed excitation compared with low frequency standard MPI. We show some data for this approach in Fig. 1(c) as well as in our 2017 paper [27]. Ultimately, this is a similar approach to pulsed MPI – slowing slew rates to match relaxation times. The slowest slew rates of Fig. 1(c) that approach pulsed MPI methods used in this work still suffer from a noticeable relaxation wall, so it is not clear exactly how slow we must go with sinusoidal excitation to achieve resolution parity with pulsed methods. Additionally, because we can temporally separate excitation feedthrough from tracer signal using a square wave, we retain all or most of the raw tracer signal. With most single tone sinusoidal methods, the tracer signal at the fundamental harmonic is lost due to an inability to disambiguate it from excitation feedthrough. Since the majority of tracer signal is at the fundamental frequency, being able to retain this information is a significant boost in SNR for pulsed methods. This is especially true for low amplitude excitation, since this shifts more of the raw signal energy into the fundamental harmonic. Furthermore, we can easily tailor the square wave hold time per a tracer’s dynamic behavior. Standard sinusoidal excitation systems require resonant circuitry and modifying these systems to be arbitrarily frequency-flexible to accommodate arbitrary tracer dynamics is difficult. Finally, while the static hold-times of pulsed methods allow steady-state to be achieved, the rapid transitions allow us to encode the relaxation impulse response in the raw signal, available to be exploited for image contrast. A low frequency sinusoidal excitation will not retain relaxation information in this manner.

The biggest SNR drawback for pulsed methods described herein is the requirement for low amplitudes (e.g., 1–3 mT) to ensure high resolution. This reduces SNR potential compared to sinusoidal methods that use higher amplitudes. However, there are several ways to address this current limitation in the future. First, unlike the tracer PSF, blurring from higher amplitudes has a known closed form solution: a rectangular function that depends solely on the excitation amplitude. It should therefore be much more robust to deconvolution, should we choose to go that route. Second, we do not believe low amplitudes are intrinsic to pulsed methods, only to this first demonstration. For example, using a field-free line (FFL) MPI system, pulsed excitation along the line axis could use any achievable amplitude as information is already projected along this direction. We may also be able to bias the line to greatly reduce the time to steady-state and thus improve SNR efficiency.

Properly comparing various approaches is challenging but important. We anticipate much more analysis in future work.

III. EXPERIMENTAL METHODS

A. Implementation of Pulsed MPI Excitation Pulse Sequences

Implementation of a square wave, or more general pulsed MPI sequence, requires transmit and receive systems that differ from that used in standard sinusoidal MPI. Standard MPI typically uses resonant circuits in both the transmit and receive electronics. In pulsed MPI, we can use non-resonant systems, such as the arbitrary waveform relaxometer (AWR) [31] shown in shown in Supplementary Fig. 11. The AWR is a frequency-flexible (no resonant circuitry) tabletop MPI device with distinct excitation and bias coils capable of producing wideband excitation waveforms such as triangle, trapezoidal, or square waves in addition to single tone excitation (DC – 400 kHz). It is also capable of small FOV 2D projection imaging via an FFL generated by an attachable permanent magnet array. The accuracy and performance of the device was validated in prior work [37]. Fig. 4 describes temporal decoupling methods that address the wideband feedthrough encountered in pulsed MPI, as opposed to the monotonal feedthrough of conventional MPI. Further implementation details can be found in Appendix B-A.

Fig. 4. Receive chain modifications and direct feedthrough mitigation in pulsed MPI.

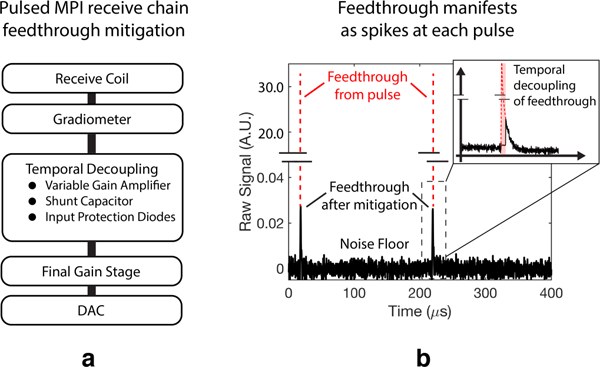
(a) Hardware modifications can be made to address the different nature of feedthrough in pulsed MPI. In addition to gradiometric attenuation, we can mitigate the temporally localized feedthrough spikes of pulsed MPI using tools such as variable gain amplifiers, shunt capacitors, and protection diodes. (b) Experimental feedthrough in pulsed MPI, which manifests as a narrow spike coinciding with each excitation pulse. Feedthrough not removed by fine gradiometric tuning [31] is significantly decoupled from the tracer signal decay. Time-domain baseline subtraction is not typically required using our AWR in pulsed MPI mode.

B. Reconstruction

In our x-space pulsed MPI implementation, we perform basic digital signal processing (DSP) on the digitized received voltage waveform. This includes application of a digital filter with a 200–500 Hz passband around each harmonic of the fundamental frequency (depending on the bias field slew rate), up to a frequency cutoff of 500 kHz.

With a fast slewing square wave excitation, the transmit feedthrough is limited to a few μs after each pulse. As Fig. 4 shows, this allows us to retain most of the tracer signal without need for complex feedthrough removal strategies or baseline subtraction. Feedthrough that does remain in the signal translates to a global DC offset in the reconstructed image (Supp. Fig. 12c), which is straightforward to remove using a robust and enforceable a priori assumption of zero signal at the edges of the imaging FOV. This also means that the DC recovery steps of canonical x-space MPI are not required such that we do not need overlapping FFR trajectories in x-space pulsed MPI [11].

Fig. 5 illustrates the square wave pulsed MPI reconstruction process, which consists of an integration step followed by a gridding step. After DSP, we fold the signal into half-period chunks, integrate each chunk, and grid this value to a location. In the AWR without a gradient this is a location in the magnetic field domain: H_n – ΔH where H_n is the value of the total applied field (including the bias field contribution) following a pulse and ΔH is the square wave amplitude. The result is a 1D PSF in the applied magnetic field space. We also note that the nature of pulsed excitation as well as the integration step simplify phase coherence methods required in x-space implementations. Precise identification of the initiation of each half-period excitation is self-evident in the raw data.

Fig. 5. Square wave data acquisition and image reconstruction using the AWR.

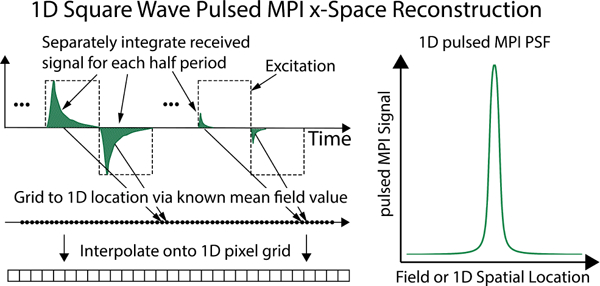
We integrate the signal for each square wave half-period and grid this value to the mean total applied field value. A slowly-varying bias field allows us to cover a large magnetic FOV. In this manner, we obtain a 1D square wave point-spread function (PSF). If we divide the applied field by a gradient strength (e.g., of a specific scanner) we can map to a 1D spatial PSF.

In AWR scans with no gradient, the system collapses the sample geometry to a virtual point and the resulting PSF is representative for the sample in aggregate. We have previously described theoretically and shown experimentally that this PSF, obtained with no gradient, corresponds directly to a 1D spatial PSF (a line, collinear with the excitation axis, through the center of a 2D point source image) after division by the gradient strength of the scanner [31], [23]. For spatial resolution values, we assume a 7 T m⁻¹ gradient, the gradient strength of our highest resolution scanner [29]. All SNR and signal calculations are normalized to tracer mass. In AWR scans with an FFL gradient, the same procedures are followed. Instead of gridding the signal to a mean magnetic field, we grid the value to the known mean location of the FFR.

C. Nanoparticles

For experiments, we used a set of monodisperse SPIO tracers purchased from the same supplier (Imagion Biosystems, Ltd., Albuquerque, NM, USA) with the following core sizes: 18.5 nm, 21.6 nm, 24.4 nm, 27.4 nm, and 32.1 nm. All samples are single core, crystalline magnetite with a polymer shell including an inner layer of oleic acid and outer layer of carboxylic acid-functionalized polymer. Detailed characterization and validation of these particles has been performed in previous work [27], [32]. All experimental samples consisted of 40 μL of stock tracer solution placed in small PCR vials. While stock solutions contained tracer at slightly different concentrations, all data is reported with signal normalized by the mass of iron in the sample for proper comparison.

D. Characterization of 1D pulsed MPI Performance

We subjected samples of each tracer to a number of different excitation conditions to build parametric data sets. These included amplitude (range: [1, 20] mT), steady-state hold time (range: [25, 750] μs), and rise time (range: [3, 380] μs).

All 1D excitation trajectories consisted of an (approximate) square wave, trapezoidal, or sinusoidal excitation superposed with a linear bias field to cover a magnetic FOV from −40 to 40 mT over a total single acquisition time of 0.5–0.7 seconds (consistent bias field waveforms ensured consistent total scan times, regardless of excitation waveform). To improve SNR, up to 25 single acquisitions were taken serially and averaged, for a maximum of 17.5 seconds total acquisition time per 1D trial or 2D line acquisition. Additionally, baseline scans with no sample present were taken for time domain baseline subtraction in some scans (e.g., sinusoidal excitation). In general, three replicate trials were performed in each experiment to report statistical variation in device performance.

E. Characterization of 2D pulsed MPI Performance

Conventional MPI FFL projection scans were obtained on the Berkeley FFL preclinical imager that has been validated in previous work [4]. In brief, this imager has a drive (excitation) coil along the z-axis and FFL oriented along the y-axis. Projection images in the x-z plane are obtained by raster scanning in which we shift the FFL along x via electromagnets and shift the sample along z through the vertical bore using a mechanical stage. The excitation sinusoid is 20 mT in amplitude at 20.25 kHz, and we set the electromagnet gradient strength to 3.5 Tm⁻¹ to match the 2D-enabled AWR.

We added magnets to the AWR to replicate the FFL imager in miniature for 2D projection imaging. The bias coil was replaced with a NdFeB permanent magnet array that generates a 3.5 Tm⁻¹ FFL. The geometries of the drive coil (along z) and gradient (along y) are the same as the preclinical imager. To shift the FFL in x, a Helmholtz electromagnet pair was installed. Full x-z projection images are obtained with raster scanning via shifting the FFL along x using the Helmholtz electromagnets and shifting the FFL in z using the frequency-flexible drive coil (a low frequency biasing field superposed with the pulsed drive waveform). A 1 mT square wave amplitude was used.

IV. EXPERIMENTAL RESULTS

A. Comparison of Pulsed MPI and Standard MPI

Fig. 6(a) shows 1D PSFs obtained with the AWR for each of the tracers but using conventional sinusoidal MPI excitation. Here we used the standard f₀ = 25 kHz and 20 mT excitation amplitude used in our scanning systems. The effects of magnetic relaxation are apparent in the data as blur and warping in the scanning direction. After approximately 25 nm, the PSFs greatly widen. Fig. 6(b) shows pulsed MPI PSFs obtained with the same samples using 1 mT square wave excitation. The steady-state encoding of pulsed MPI produces PSFs with no blurring or warping effects and PSFs narrow (better resolution) with increasing core size over the entire tested range. Fig. 6(c) plots the experimental FWHM resolution for sinusoidal MPI, square wave MPI, and the predictions from the theoretical Langevin model. We see the characteristic relaxation wall inflection point around 25 nm for sinusoidal excitation. In contrast, the square wave MPI data points follow the theoretical Langevin curve with only a slight offset. The effect of the excitation amplitude means, as predicted in our imaging equation (6), we only asymptotically approach the theoretical Langevin resolution.

Fig. 6. Experimental 1D comparison between conventional sinusoidal MPI at 25 kHz, 20 mT with square wave pulsed MPI at 2.5 kHz, 1 mT.

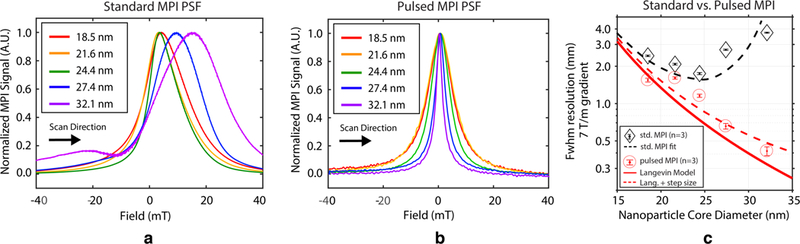
(a) Using standard sinusoidal excitation, resolution stops improving after approximately 25 nm (PSF widens) as relaxation-induced blurring becomes significant. (b) Pulsed MPI data for the same range of magnetic core sizes show constant improvement of resolution (PSF narrows) with increasing core size as predicted by the steady-state theory. (c) Comparison of experimental sinusoidal FWHM resolution, square wave FWHM resolution, and theoretical Langevin predictions as a function of tracer core size. Note the inflection point and worse resolution with the largest tracers in the sinusoidal MPI data while square wave MPI realizes the monotonic theoretical predictions (solid red line), with a small offset due to the contribution of the excitation amplitude to FWHM.

For the largest tracer we tested (32 nm core), our pulsed MPI PSF is equivalent to ≈ 450 μm FWHM resolution in a 7 Tm^–1 scanner. This is much better than the experimental sinusoidal data, both for the 32 nm core case (≈ 4 mm) and the the best performing 24.4 nm tracer (≈ 1.8 mm).

B. Effect of Drive Frequency (Half-Period) in Pulsed MPI

As described in theory section II, pulsed MPI relies on fully establishing steady-state tracer magnetization during the quiescent periods after pulsed excitation. For square waves, this means choosing a sufficiently long half-period. Practically, a value such as the time taken to reach 95% of the steady-state magnetization at 0 field may be used. The characteristic time constant varies significantly between tracers, and it is important that we wait no longer than required to maximize SNR efficiency. We again emphasize that we need not know anything about a tracer’s particular model of relaxation for pulsed methods to work or to optimize a scanning trajectory. We can simply observe the impulse response of the tracer with a fast scout scan or even a single gradient-less pulse and use this to set the half-period for subsequent acquisitions.

Fig. 7 shows the effects of hold time in experimental square wave MPI when testing the 27.4 nm tracer. Fig. 7(a) shows square wave MPI PSFs constructed from acquisitions with square wave half-periods of 25 μs, 100 μs, and 750 μs. For the shorter half-periods, steady-state is not achieved and we suffer relaxation-induced blurring quantified in Fig. 7(b), just as in standard MPI. In particular, we observe a phenomenon of ‘peak depression.’ At low field strengths the relaxation time is longest and unable to achieve steady-state conditions in, e.g., 25 or 100 μs. At higher field strengths, however, relaxation time constants are short and steady-state may be established. Fig. 7(b,c) show that both resolution and signal are compromised when half-periods are too short. We are able to effectively achieve steady-state and asymptotically approach the ideal Langevin resolution with a half-period/hold time of ≈300–400 μs. To achieve a true steady-state image in pulsed MPI, our hold time must be long enough to fully accommodate the worst case (0-field) relaxation time.

Fig. 7. Experimental relationships between pulsed waveform half-period (constant hold time) and pulsed MPI performance.

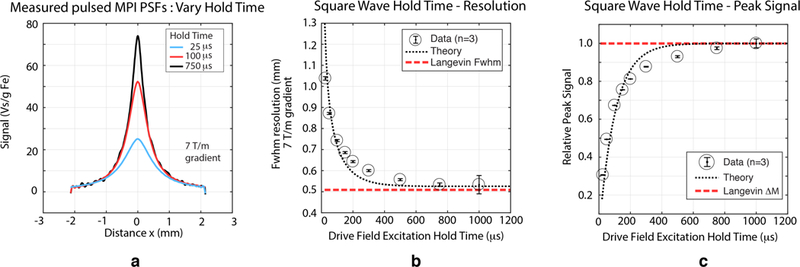
Here we show experimental results varying the half-period in square wave excitation of 27.4 nm particles with 1 mT excitation. Our theory states that the half-period must be sufficiently long to establish steady-state tracer magnetization and these data confirm. (a) 1D point-spread functions obtained with different half-periods. Without sufficiently long half-periods, the same relaxation-induced blurring occurs as in the case of sinusoidal MPI. We can also see how this process occurs in more detail: long relaxation times at low field strength lead to ‘peak depression’ of the PSF for shorter hold times. (b) Spatial resolution improves and approaches that of the Langevin model as hold time increases $\left(e.g.,T/2\gg 3{\tau }_{\text{max}}\right).$ (c) Relaxation is fundamentally a lossy process and pulsed MPI peak signal worsens with shorter hold times as the SPIO cannot reach steady-state magnetization. These results show that longer hold times that fully establish steady-state are desirable, but this must be traded-off against longer scan times and SNR efficiency.

C. Effect of Excitation Amplitude in Pulsed MPI

Fig. 8(a) shows experimental square wave PSFs for the 27.4 nm tracer excited with different amplitudes. As predicted by theory, the PSF shape, SNR, and resolution are strongly affected by the amplitude, with the characteristic rectangular blur apparent for the largest excitation. Fig. 8(b) experimentally quantifies the relationship between FWHM resolution and excitation amplitude, showing excellent agreement with theory, and Fig. 8(c) quantifies experimental peak signal as a function of amplitude, also agreeing well with theory.

D. Effect of Rise Time (Pulse Sharpness) in Pulsed MPI

The rise time has negligible effect on pulsed MPI as shown in Supplementary Fig. 13, where performance is maintained with more easily implemented trapezoidal waves. Therefore near perfect square waves are not required, which relaxes hardware (transmit power circuit) requirements. Downsides include reduced SNR efficiency and reduced separation of excitation feedthrough and tracer signal. More details can be found in Appendix C.

E. Harmonic and Resolution-Bandwidth Analysis

In Fig. 9 we experimentally explored the resolution-bandwidth relationship in square wave MPI. In particular, we modified the receive bandwidth by changing the number of harmonic bands used in reconstruction. Similar to standard MPI, our square wave pulsed MPI received data lives in bands around the harmonics of our fundamental square wave excitation. Fig. 9(a), shows reconstructed PSFs using only 1 (red) or 15 (blue) harmonics of the fundamental square wave excitation frequency. In Fig.9(b), we plot the FWHM resolution as a function of the number of harmonics used in reconstruction, and in Fig.9(c), we plot peak signal intensity as a function of the number of harmonics. Unlike in continuous wave MPI, resolution worsens with increasing receive bandwidth and the inclusion of more harmonics. Peak signal does, however, improve. This peculiar resolution-bandwidth relationship is a function of the temporo-spatial encoding of the signal due to the field dependence of the tracer magnetic relaxation. Tracer located farther from the FFR is characterized by fast relaxation due to the high field conditions while tracer nearer to the FFR is characterized by slower relaxation. Faster relaxation processes spread signal energy to higher harmonics, and signal from tracer near the FFR center is relatively concentrated at the lower harmonics. By selecting only lower harmonics, we can robustly boost resolution for a modest reduction in SNR. This tradeoff may be particularly favorable considering that, while the amount of signal energy captured is reduced, so is total noise due to the reduction in total bandwidth.

Fig. 9. Experimental resolution and signal bandwidth relationships.

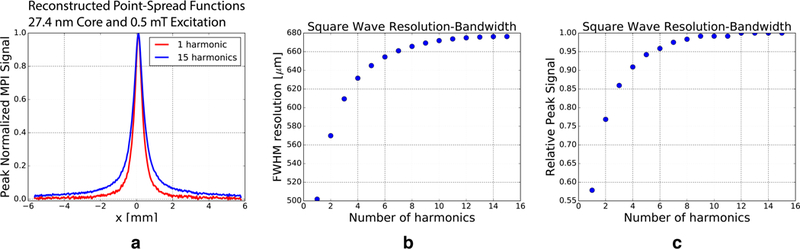
(a) PSFs constructed from the same dataset but using only 1 (red) or 15 (blue) harmonics of the fundamental square wave excitation frequency in reconstruction. (b) PSF FWHM resolution as a function of the number of harmonics used in reconstruction. (c) Peak signal intensity as a function of the number of harmonics used in reconstruction. Unlike in continuous wave MPI, resolution worsens with increasing receive bandwidth and the inclusion of more harmonics. Peak signal does, however, improve. This interesting resolution-bandwidth relationship is a function of the temporo-spatial encoding of the signal due to the field dependence of tracer magnetic relaxation.

F. Experimental 2D Pulsed MPI

To further verify and demonstrate pulsed MPI, we obtained 2D results by modifying the AWR with an FFL magnet and shift systems as previously described. Small line phantoms containing standard VivoTrax^™ MPI tracer and the 27.4 core monodisperse tracer were used as shown in Fig. 10. One phantom has a 0.6 mm spacing and another has a 1.5 mm spacing. We scanned these phantoms using both our preclinical FFL system (Fig. 10, center) and our AWR in 2D mode (Fig. 10, right). We also report the Langevin theoretical ideal (Fig. 10, right). The tabletop 2D AWR has a limited FOV as indicated by the red dashed lines in Fig. 10; we plot the AWR data in the same total FOV as that scanned by the preclinical system for visual comparison (the image area not sampled by the AWR was set to 0). The limited experimental FOV with the 2D AWR is why the hazy “wishbone” shape characteristic of single-axis x-space MPI is present in the simulation and standard MPI data but not observed in the pulsed MPI experimental data.

Fig. 10. Verification of pulsed MPI image resolution improvement using line phantoms in 2D imaging.

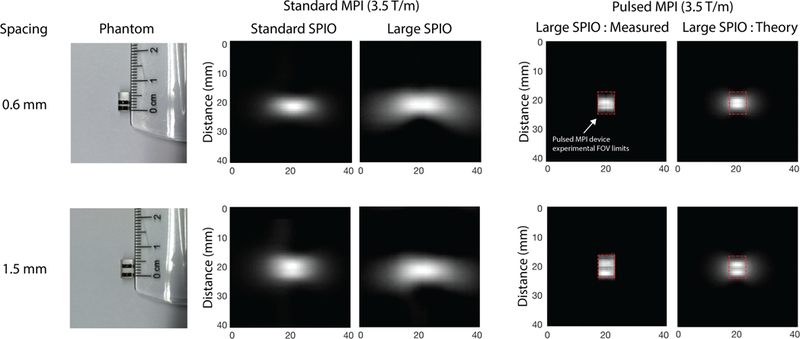
(Left) Line phantoms used; one is separated by 0.6 mm and the other by 1.5 mm. (Center) Standard MPI images line phantoms taken with our preclinical FFL system at 3.5 Tm⁻¹ with the current standard MPI tracer: (VivoTrax^™ ) and a monodisperse large core (27.4 nm) tracer. With standard MPI, the large core tracer shows more blurring than the standard tracer. (Right) Pulsed MPI data using the large core tracer. Our tabletop AWR in 2D mode has a limited FOV denoted by the dashed red lines. For visual comparison with the preclinical, standard MPI results, we display the pulsed MPI images in the larger total FOV by filling in the unsampled regions with the zeros (black). The experimental results are in good agreement with simulated, Langevin-ideal images. The halo in simulated images is not apparent in the experimental images due to the field-of-view limitation of the small pulsed MPI scanner (marked by the red dashed outline). In general, the standard MPI images are significantly blurred for both standard and large core tracers and neither phantom is resolved. The pulsed MPI experimental results, in contrast, are much sharper. In particular, we obtain improved performance with large core tracers compared to conventional MPI with standard or larger tracer. This demonstrates our ability to unlock the cubic improvement of resolution with core size promised by steady-state theory. We are able to resolve the 1.5 mm phantom with our 3.5 Tm⁻¹ setup, which translates to less than 750 micron resolution in a 7 Tm⁻¹ system, thus matching the 1D results of Fig. 6.

The results of Fig. 10 show that, in the case of the larger tracer, the standard MPI images are significantly blurred and it is not possible to resolve the two lines. But when using pulsed MPI, we see sharp images and are able to resolve the two lines. In addition, the measured experimental pulsed MPI images are very similar to the simulated images derived from ideal Langevin theory in the small FOV that was sampled. This verifies that pulsed MPI approaches the spatial resolution predicted by the ideal Langevin model in 2D as in the 1D case. The results also show a significant resolution gain of almost 8-fold when comparing standard MPI and pulsed MPI results using the 27.4 nm tracer. In the pulsed MPI case, we can resolve 1.5 mm spaced lines with the 3.5 Tm⁻¹ system used, which translates to better than 0.75 mm in a 7 Tm⁻¹ system. This matches the 1D data of Fig. 6 and illustrates how the large amount of relaxation-induced blurring present in standard MPI for large tracers can be circumvented by the pulsed MPI strategy in an imaging format.

V. DISCUSSION

A. Magnetostimulation and SAR Safety Considerations

Our analysis with reference to Saritas et al. [33] shows that optimal pulsed MPI waveforms are safe as shown in Supplementary Fig. 14. A detailed analysis can be found in Appendix D-A.

B. Spatial resolution and SNR Efficiency Tradeoff

As in conventional MPI, image resolution and SNR efficiency can be traded off in pulsed MPI. First, we can choose hold times that do not allow for full steady-state magnetization, but do allow for faster scanning. Second, high amplitudes increase total SNR per pulsed acquisition, but worsen image resolution due to the rect-function convolution term in the signal equation. One advantage of pulsed MPI in this context is the frequency-flexibility, which allows us to optimize this tradeoff for different scan situations and tracer types. For example, if we want to prioritize speed and SNR over resolution, we can simply program the drive waveform/sequences to have higher amplitudes and shorter hold times.

C. Hardware and Bandwidth Challenges

While the current study was performed on a low-inductance small bore setup, translation to practical in vivo imaging scenarios will require larger bores and higher inductance transmit coils that need much more power and may have challenges with self-resonance. Fortunately, our results in Supplementary Fig. 13 show that pulsed MPI does not require perfect square waves and also works well with trapezoidal waveforms. This greatly reduces the transmit hardware and bandwidth requirements.

D. Maximum Theoretical Resolution Gain with Pulsed MPI

While pulsed MPI has been shown to enable the improvement of resolution with core size for much larger tracers than before, new limits will pertain. First, with increasing core size we will eventually transition from superparamagnetic to ferromagnetic behavior. While in theory pulsed MPI should still be able to image ferromagnetic nanoparticles, they pose a host of other problems such as aggregation, mechanical motion, and poor colloidal stability.

Another issue is that relaxation time constants should continue to increase with core size, requiring scan times to become longer and longer. At some point, there will be diminishing returns and the tradeoff between resolution and scan time/SNR efficiency will become untenable, especially with inductive sensing. At low frequency drive fields, other magnetometers such as SQUIDs [34], [35] may be advantageous.

The effect of the excitation amplitude in our pulsed MPI implementation is also limiting. As shown in the theory section and in our experimental results, the actual spatial resolution is offset from the Langevin value by approximately the excitation amplitude. As the SPIO Langevin resolution approaches the lowest amplitude that can be implemented (from an SNR-limited perspective), gains in resolution from using larger SPIOs will have rapidly diminishing returns. As we previously discussed, however, we believe the low amplitude limitations of this first demonstration can be circumvented in the future.

Other new opportunities made possibly by pulsed MPI, such as the resolution-bandwidth tradeoff (see Fig. 9), where bandwidth reduction improves resolution, may yet allow us to go further. However, in view of these issues we anticipate that pulsed MPI, per the methods described in this paper, will have a practical resolution limit of around 200 microns. For example, this may be achieved with tracer on the order of 40 nm with an approximate FWHM resolution of 0.5 mT (excitation) + 1 mT (Langevin physics) ≈ 1.5 mT. This is about 200 μm resolution with a 7 Tm⁻¹ gradient.

VI. CONCLUSION

In this work, we demonstrate a novel pulsed method of signal excitation and encoding in MPI. We have termed this pulsed MPI, in contrast to canonical continuous wave (sinusoid) MPI. We present 1D and 2D experimental results showing significant improvement in MPI spatial resolution with this new scanning strategy. Most importantly, we demonstrate that we can approach the ideal steady-state resolution for large tracers (e.g., > 25 nm) which has previously eluded us due to magnetic relaxation effects. Pulsed MPI allows us to break down this ‘relaxation wall’ by allowing even heavily relaxing tracers to achieve steady-state magnetization when scanning. In this manner, relaxation behavior is directly encoded in the raw signal waveform in a way that is separable from steady-state information. More generally, we believe pulsed MPI may lead to many new interesting pulse sequencing strategies in MPI. The ability to quantify relaxation dynamics, even as we remove negative effects on image quality, could greatly advance MPI image contrast possibilities in applications such as color MPI.