Abstract
Our brains must maintain a representation of the world over a period of time much longer than the typical lifetime of the biological components producing that representation. For example, recent research suggests that dendritic spines in the adult mouse hippocampus are transient with an average lifetime of ~10 days. If this is true, and if turnover is equally likely for all spines, ~95% of excitatory synapses onto a particular neuron will turn over within 30 days; however, a neuron’s receptive field can be relatively stable over this period. Here, we use computational modeling to ask how memories can persist in neural circuits such as the hippocampus and visual cortex in the face of synapse turnover. We demonstrate that Hebbian plasticity during replay of presynaptic activity patterns can integrate newly formed synapses into pre-existing memories. Furthermore, we find that Hebbian plasticity during replay is sufficient to stabilize the receptive fields of hippocampal place cells in a model of the grid-cell-to-place-cell transformation in CA1 and of orientation-selective cells in a model of the center-surround-to-simple-cell transformation in V1. Together, these data suggest that a simple plasticity rule, correlative Hebbian plasticity of synaptic strengths, is sufficient to preserve neural representations in the face of synapse turnover, even in the absence of activity-dependent structural plasticity.
NEW & NOTEWORTHY Recent research suggests that synapses turn over rapidly in some brain structures; however, memories seem to persist for much longer. We show that Hebbian plasticity of synaptic strengths during reactivation events can preserve memory in computational models of hippocampal and cortical networks despite turnover of all synapses. Our results suggest that memory can be stored in the correlation structure of a network undergoing rapid synaptic remodeling.
Keywords: Hebbian, memory, place cell, structural plasticity, synapse turnover
INTRODUCTION
Synapses are sites of communication between neurons. In mammals, dendritic spines are the major sites of excitatory synapses (Nimchinsky et al. 2002). Dendritic spines in adult mammals can be eliminated or grow in new locations (Grutzendler et al. 2002; Trachtenberg et al. 2002). The reported degree of spine turnover in adult mice varies considerably by brain area. In cortex, most spines appear to be relatively stable once the critical period is over (Attardo et al. 2015; Grutzendler et al. 2002; Holtmaat et al. 2005). In contrast, most spines in hippocampal area CA1 seem to be transient with a mean lifetime of ~10 days (Attardo et al. 2015; Pfeiffer et al. 2018). Thus the hippocampus is expected to undergo dramatic structural remodeling with ~95% replacement of the CA1 spine population every 30 days (Attardo et al. 2015).
In light of such rapid and extensive restructuring of the hippocampal network, it is surprising that spatial memories can persist for ≥1 mo in mice (Guskjolen et al. 2017). Although these memories might not be entirely hippocampus dependent, Abraham and colleagues (2002) found that multiafferent long-term potentiation (LTP) can persist for ≤1 yr following stimulation in the rat dentate gyrus, suggesting that stable memories can be supported within the hippocampus. Furthermore, place fields of CA1 or dentate place cells are remarkably stable in mice and rats (Agnihotri et al. 2004; Cholvin et al. 2018; Hainmueller and Bartos 2018; Kentros et al. 2004; Leutgeb et al. 2005, 2006; Thompson and Best 1990; Ziv et al. 2013). Rats studies generally agree that place fields are stable (Cholvin et al. 2018; Leutgeb et al. 2005, 2006; Thompson and Best 1990) with some CA1 receptive fields persisting for months (Thompson and Best 1990). In mice, a set of studies suggests that although most place cells lose their location preference between exposures to an environment, some retain their place fields (Rubin et al. 2015; Ziv et al. 2013). The centroids of recurring place fields display little drift compared with their positions on earlier exposures (Rubin et al. 2015; Ziv et al. 2013). Most surprisingly, drift magnitude does not appear to increase over time, i.e., mean drift is no different after 30 days than after 5 days (Ziv et al. 2013).
Several proposed mechanisms might account for receptive-field persistence in structurally unstable networks. One idea is that a subset of spines is stable, and this subset is sufficient to maintain the receptive fields of a neuron (Chambers and Rumpel 2017; Mongillo et al. 2017). This hypothesis appears to hold true in some cortical regions, where a fraction of spines may persist throughout the lifetime of the animal (Yang et al. 2009). A second possibility is that spine stability is regulated by activity-dependent structural plasticity (synapse formation, stabilization, or deletion that depends on correlations between presynaptic and postsynaptic activity; Bourjaily and Miller 2011). Supporting this view, Hill and Zito (2013) found that LTP stabilizes nascent spines in hippocampal slices from neonatal mice. A third hypothesis is that plasticity of synaptic strengths can compensate for destabilization caused by activity-independent structural plasticity. Corrective plasticity could be mediated by feedback error signals (Chambers and Rumpel 2017). Alternatively, Hebbian plasticity, an increase in strength of synapses from those presynaptic neurons for which spikes often occur just before a postsynaptic spike, could lead to reinforcement of pre-existing activity patterns (Chambers and Rumpel 2017), a process we investigate here.
Specifically, we use a modeling approach to explore the hypothesis that the computations generating a neuron’s receptive field, and hence the resulting memories, can be embedded at the network level in a manner that is robust to the incessant rearrangement of the connections between neurons (Chambers and Rumpel 2017; Mongillo et al. 2017). We posit that the inevitable destabilization of circuits and resulting changes in neural responses caused by turnover of synapses is counteracted by Hebbian synaptic plasticity, particularly that which arises as a result of network dynamics during replay events.
The mechanism for stabilization relies on two general features essential to any type of pattern stability and identity preservation in the midst of change. First, a degree of robustness is essential so that small changes do not destroy the pattern. In the case of neural receptive fields, the loss of a few inputs does not significantly alter a neuron’s response pattern because there is some redundancy among the original inputs. Second, naïve components must be able to respond to the state of the system and replace lost redundancy. Hebbian plasticity, here, an increase in connection strength when the pre- and postsynaptic neurons are coactive, achieves this by specifically strengthening any new synapses from upstream neurons for which receptive fields overlap with that of the downstream neuron. Once a new synapse is strengthened, the corresponding upstream neuron supports the original receptive field. In so doing, it adds new redundancy so that the original receptive field can persist when more of the original synapses are lost.
To evaluate how effectively Hebbian plasticity of synaptic strengths could prevent drift in receptive fields due to connectivity changes, we measured the effects of synapse turnover on memory stability in a firing rate model of the grid-cell-to-place-cell transformation in CA1 (Brun et al. 2002, 2008; de Almeida et al. 2009b, 2012). CA1 place cells are thought to depend on input from place cells in CA3 and spatially tuned cells including grid cells in layer III of entorhinal cortex (Brun et al. 2008). Place fields in CA1 have separately been shown to form in the absence of CA3 input (Brun et al. 2002) and in the absence of input from layer III of entorhinal cortex (Brun et al. 2008). Our model focuses on the grid-cell-to-place-cell transformation, ignoring CA3 input because of the observation that spines are relatively stable in adult cortex (Attardo et al. 2015; Grutzendler et al. 2002; Holtmaat et al. 2005), suggesting that grid-cell receptive fields might not be subject to turnover noise. Stable grid-cell inputs would provide a clean information path from body position to the CA1 network. With the use of this model, we demonstrate that plasticity during reactivation of grid-cell activity stabilizes place fields over biologically relevant time scales in the presence of random synapse turnover.
We further asked whether our model could account for functional stability in nonhippocampal neural networks undergoing synapse turnover. In primary visual cortex (V1), orientation-preference maps appear to be stable over time (Stevens et al. 2013), whereas dendritic spines (Holtmaat et al. 2005; Tropea et al. 2010; Yu et al. 2011) and axonal boutons (Stettler et al. 2006) turn over throughout the life of the animal. To evaluate the effect of activity-independent rewiring of lateral geniculate nucleus (LGN)-to-V1 synapses on orientation-tuning stability, we simulated the center-surround-cell-to-simple-cell transformation in V1. In this model, we observed that orientation preferences in individual V1 cells survive complete rearrangement of input connections when visual stimuli were paired with Hebbian plasticity. Taken together, our results suggest mechanisms by which activity patterns can remain stable, thus maintaining a stability of identity at the single-neuron level, even when all of the connections providing input to the neuron have changed.
MATERIALS AND METHODS
We use three separate neural firing rate models to test our hypothesis. Models 1 and 2 represent the transformation of grid-cell inputs from entorhinal cortex (through the temporoammonic tract and perforant path) into the place fields of CA1 pyramidal cells. Model 1 includes only a single pyramidal cell in CA1, whereas model 2 expands the representation of CA1 to include 2,000 pyramidal cells and feedback inhibition. Model 3 represents the transformation of center-surround cell inputs from LGN into the orientation tuning of V1 simple cells. Overviews of the hippocampal and visual cortex models can be found in Supplemental Tables S1 and S2, respectively (all supplemental material is available at https://doi.org/10.5281/zenodo.2613088).
Models 1 and 2: Grid-Cell-to-Place-Cell Transformation
A summary of models 1 and 2 is provided in Supplemental Table S1.
Grid cells.
Data were simulated by assuming a 1-m linear enclosure divided into 1-cm bins. The activity of each cell was characterized by its firing rate in each bin. We simulated a library of 10,000 grid-cell responses according to a method described by Blair et al. (2007) (Eq. 1). With the use of this method, a grid cell’s firing rate varies in a hexagonal grid across the enclosure, and the orientation, phase, and offset of the grid are parameters selected randomly from a uniform distribution within the ranges given below.
| (1) |
In Eq. 1, G is a grid cell’s firing rate, r is the animal’s position in two-dimensional space, λ is the distance between grid vertices and ranged from 30 to 100 cm, θ is the angular offset and ranged from 0 to 60°, and c is the offset in two-dimensional space and ranged from 0 to 100 cm in both dimensions. g Is a gain function, g(x) = exp[a(x − b)] − 1, where a modulates the spatial decay and was set to 0.3 and b modulates the minimum firing rate and was set to −3/2. The hexagonal grid is created by summing cosine gratings angled at θ1 = −30°, θ2 = 30°, and θ3 = 90°. u Is the function u(θk) = [cos(θk),sin(θk)]. Grid parameters were assumed to be the same as for grid cells at the same position on the dorsal-ventral axis innervating dentate (Moser et al. 2014) and were adapted from de Almeida et al. (2009b).
Place cells.
We simulated place cells as described by de Almeida et al. (2009b). Each cell received and summed excitatory input from 1,200 randomly selected grid cells out of the library of 10,000 grid cells. This number of grid-cell inputs was chosen to approximate the total number of spatially modulated cells from entorhinal cortex that form synapses on the spines of a CA1 pyramidal cell. CA1 pyramidal neurons receive synaptic input from layer III of entorhinal cortex on dendrites in stratum lacunosum-moleculare. The number of inputs, 1,200, was obtained by taking the average number of spines per CA1 pyramidal cell on dendrites in stratum lacunosum-moleculare [~1,500 spines (Megías et al. 2001)] and multiplying by the fraction of neurons with spatial tuning in layer III of entorhinal cortex [~80% (Sargolini et al. 2006)]. We disregarded noncortical inputs because place fields can be observed in CA1 after the removal of all input from CA3 (Brun et al. 2002).
The activity of each place cell was determined in each 1-cm bin of the 1-m linear enclosure. The sum of synaptic input to a place cell was calculated as:
| (2) |
where is the input to the ith place cell at position r, is the synaptic strength vector representing grid-cell synapses onto the ith place cell, and is the vector of all grid-cell firing rates at position r.
In the case of model 1, where there was only 1 place cell, the firing rate was given by , which is the sum of synaptic inputs to the place cell at position r as shown in Eq. 3. Furthermore, the place cell’s firing rate was set to 0 at all locations except for the 10 where excitation was greatest. This procedure was not intended to be realistic but to assure that the single place cell in model 1 consistently had a defined place field. A more realistic approach to the same problem is used in model 2.
In model 2, there were 2,000 place cells. In this case, place-cell firing rates were modulated by feedback inhibition. This population model makes three assumptions about feedback inhibition: 1) pyramidal cells form convergent, excitatory synapses onto interneurons (English et al. 2017; Paz and Huguenard 2015), which, in turn, form divergent, inhibitory synapses onto pyramidal cells (Bezaire and Soltesz 2013); 2) interneurons fire in response to a single excitatory synaptic potential (de Almeida et al. 2009b); and 3) interneuron-to-place-cell synapses are strong enough to suppress pyramidal cell firing consistently (de Almeida et al. 2009b). These assumptions imply that, for a given cycle of the γ-oscillation, the first CA1 pyramidal neuron to fire will cause an interneuron to fire, which will, in turn, suppress the activity of any pyramidal neurons that do not fire before receiving synaptic input from the interneuron (de Almeida et al. 2009b). Since the neurons receiving the greater excitatory input will overcome the initially decaying inhibition and fire earlier in a γ-cycle, we can approximate this interneuron-pyramidal neuron interaction with a rule stating that CA1 pyramidal cells are only able to fire if they are excited to within some fraction (k) of the excitation received by the most excited cell (de Almeida et al. 2009b). Therefore, the firing rate of a place cell was calculated as:
| (3) |
where Fi(r) is the place cell’s firing rate at position r, H is the Heaviside function, and is the sum of excitatory input received by the most strongly excited place cell at position r. The parameter k determines the fraction, (1 − k), of to which a place cell must be excited to fire. We set k = 0.10, the approximate ratio of feedback delay [the time between a pyramidal cell spike and the arrival of feedback inhibition (2–3 ms; Miles 1990)] to the membrane time constant [~23 ms in pyramidal cells (Turner and Schwartzkroin 1983); de Almeida et al. 2009b, 2012].
Synaptic plasticity.
Synaptic strengths were updated once per running session within the linear enclosure. The strengths of realized synapses were updated according to Hebb’s rule (Eq. 4). After each strength update, we scaled the total strength of synapses converging onto each place cell by dividing by the sum of synaptic strengths and multiplying by the expected value of the sum of 1,200 random draws from the empirical distribution of synaptic strengths. This procedure represents the homeostatic scaling response seen in biological neurons (Turrigiano 2008).
| (4) |
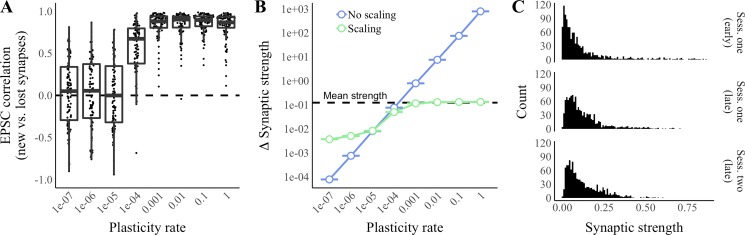
In Eq. 4, wij is the strength of the synapse connecting grid cell i and place cell j, Gi(r) is the firing rate of grid cell i at position r, and Fj(r) is the firing rate of place cell j at position r. The plasticity rate, η, in units of normalized quantal current per square frequency, influences the relative contribution of the pre-existing synaptic strength and the change in strength induced by plasticity. At high values of η, the change in strength will eclipse the preexisting strength, although scaling will cause the overall distribution of strengths to be largely unchanged. Unless otherwise stated, the plasticity rate was 1e−4, as determined in Fig. 4A.
Fig. 4.
Effects of plasticity rate on the training of nascent synapses. Activity in a single-place-cell model of the grid-cell-to-place-cell transformation was simulated over 2 sessions (Sess.) in a linear enclosure. Hebbian plasticity occurred during sessions, and 10% of synapses turned over between sessions. A: excitatory postsynaptic current (EPSC) correlation (Pearson’s correlation between the sum of synaptic inputs by position during the late phase of session 1 at synapses removed due to turnover between sessions and the sum of synaptic inputs by position during the late phase of session 2 at synapses formed due to turnover between sessions) vs. the plasticity rate. n = 100 Simulations per condition. B: absolute changes in synaptic strength from the early to the late phase of session 1 vs. plasticity rate in the presence or absence of scaling. Error bars represent means ± SE across the strengths of synapses pooled from 10 simulations. Dashed line represents the overall mean synaptic strength before plasticity. C: representative distributions of synaptic strengths across all synapses by experimental stage in 1 simulation with a plasticity rate of 1e−4.
Initial synaptic strengths.
Synaptic strength was assumed to be a function of synaptic size (Eq. 5; de Almeida et al. 2009b), and the distribution of synaptic sizes was assumed to be the same as that empirically determined for dentate (Eq. 6; de Almeida et al. 2009b, 2012).
| (5) |
| (6) |
In Eq. 5, W(s) is the synaptic strength of a synapse of size s. The synaptic size was an area value that could range from 0 to 0.2 μm2. In Eq. 6, P(s) is the probability density function of the distribution of synaptic sizes. The values of constants were obtained from Trommald and Hulleberg (1997) and were A = 100.7, B = 0.02, σ1 = 0.022 μm2, σ2 = 0.018 μm2, and σ3 = 0.15 μm2.
Synapse turnover.
Synapse turnover occurred before each running session in the linear enclosure. In the case of model 1, between 10 and 100% of the active grid-cell inputs were replaced each time between sessions. In the case of model 2, a random 114 of the 1,200 active grid-cell inputs per place cell were replaced each time between sessions. The number 114 corresponds to N0 − N(T) in the exponential decay model (Eq. 7) assuming a mean synapse lifetime (τ) of 10 days (Attardo et al. 2015) with the intertrial time (T) taken to be 1 day. This is derived from the exponential decay model:
| (7) |
where N(t) is the number of original synapses remaining after t days, N0 = 1,200 is the number of synapses on day 0, and t = T. Synapse turnover resulted in the erasure of learned synaptic strengths, with newly formed synapses taking random values sampled from the empirically determined distribution described above.
Place-field analysis.
Place cells were said to have a place field on a given trial if there was exactly one continuous region in the enclosure, ≥5 cm in length, where their firing rate was within 80% of their maximum firing rate on the same trial. The place-field drift on a given trial (Ωt) was calculated for all place cells with place fields both on trial t and trial 0 as the absolute centroid offset Ωt = |Ct − C0|, where Ct is the cell’s place-field centroid position on trial t and C0 is the position on day 0.
Model 3: LGN Inputs to Orientation-Selective Neurons in V1
A summary of model 3 is provided in Supplemental Table S2.
Grating stimulus.
Data were simulated by assuming a square visual field. Visual input consisted of a series of static gratings presented at a variety of orientations and phases. The grating was defined with 100- × 100-pixel resolution. The luminosity at each pixel was determined as:
| (8) |
where x and y are a grid of values covering the range (−1, 1) in both dimensions. The grid orientation, θ, was sampled evenly in the range of 0–180°, and the grid offset, ϕ, was sampled evenly in the range of 0 to 2π − 0.1 in steps of 0.1. The parameter α controls the spatial period and was set to 10.
LGN center-surround cells.
We simulated the activities of 20,000 LGN center-surround cells (10,000 on-center and 10,000 off-center). The input to each LGN cell was calculated at each position according to a difference-of-Gaussians function (Eq. 9).
| (9) |
In Eq. 9, is the input to LGN cell i at position x,y (pixel units). The parameter ai is +1 for on-center cells and −1 for off-center cells. The parameters and are, respectively, the x- and y-coordinates of the receptive-field centroid of cell i. Receptive-field centroids were randomly chosen positions from a uniform distribution on the visual field. G is the Gaussian , where σ is the standard deviation, set to 5 pixels, and the parameter s scales the standard deviation. D is the difference-of-Gaussians , where the standard deviation of the inner Gaussian is half that of the outer.
The firing rate of each LGN cell was determined at each orientation and phase of the grating stimulus as the rectified sum of input across all positions on the visual field (Eq. 10).
| (10) |
V1 simple cells.
We simulated the activities of 1,000 V1 simple cells. Real V1 cells are estimated to receive between 50 and 150 inputs from LGN cells (Van Hooser et al. 2014). In our model, V1 cells initially received synaptic input from 130 LGN cells. Simple cells in tree shrews are characterized by a single dark receptive field flanked by 2 light fields (Lee et al. 2016). Therefore, for each V1 cell, we selected the 130 inputs from LGN to best match an ideal V1 receptive field defined as an “off” bar flanked by two parallel “on” bars. For each V1 cell, bars were spaced 15 pixels apart. The off bar was 60 pixels in length, and the on bars were 40 pixels in length. Bars were centered on the randomly positioned receptive-field centroid of the V1 cell. Bars were oriented at a randomly chosen angle of between 0 and 180°. Specifically, 33 on-center LGN inputs were selected to align with each on bar, and 64 off-center LGN inputs were selected to align with the off bar. Selection of inputs was according to the minimum distance from the receptive field of the LGN input and the centroid of the corresponding bar representing the ideal V1 receptive field.
The sum of synaptic inputs to each V1 cell was determined as:
| (11) |
where wi,j is the strength of the synapse between LGN cell i and V1 cell j. V1 cell firing rates were modulated by lateral inhibition similar to that described for place cells in model 2. The firing rate of a V1 cell was calculated as:
| (12) |
where is the V1 cell’s firing rate at particular grating orientation and phase. The Heaviside function, H, is used to set the firing rate to 0 if the cell is not receiving input above a fraction, (1 − k) of , which is the sum of excitatory input received by the most strongly excited V1 cell at orientation θ and phase ϕ. We set k = 0.10, as estimated for V1 (de Almeida et al. 2009a).
Synaptic plasticity.
Each simulated recording session consisted of monitoring V1 cell activity as the grating stimulus rotated through 180°. Following each full rotation, synaptic strengths at realized synapses between LGN and V1 cells were updated as , where the plasticity rate, η, equals 1. After each strength update, we scaled the total strength of synapses converging onto each V1 cell by dividing by the sum of synaptic strengths and multiplying by the expected value of the sum of 130 random draws from the distribution of synaptic strengths.
Synaptic strengths and turnover.
The initial strengths of LGN-cell-to-V1-cell synapses were sampled from the distribution described above for grid-cell-to-place-cell synapses in model 1 (Eqs. 5 and 6). Synapse turnover occurred following each full rotation of the stimulus grating. On average, 10% of active LGN cell inputs per V1 cell were replaced during each turnover event. This turnover rate was chosen because Tropea et al. (2010) (mouse, layer 5) and Yu et al. (2011) (ferret, layer 2/3) observed that ~10% of V1 spines were replaced over a 2-day interval. In our model, all realized synapses had an equal probability of removal. In contrast, the probability of a synapse forming between a particular LGN cell and a V1 cell was modulated by a Gaussian function Ssyn (Eq. 13) so that synapses were more likely to form between neuron pairs with nearby receptive-field centroids.
| (13) |
In Eq. 13, , , and are the receptive-field centroids of V1 cell j and LGN cell i, respectively, and σ = 10. The probability of a synapse forming between a particular pre- and postsynaptic neuron pair was determined as:
| (14) |
where N is the number of realized synapses onto the postsynaptic neuron. Thus the average number of new synapses would be equivalent to the number of synapses removed per turnover event. Newly formed synapses took on random synaptic strength values sampled from the distribution described above.
Receptive-field analysis.
On and Off stimulus patterns were generated as images with a single pixel set to one (On) or zero (Off) and all other pixels set to zero (On) or one (Off). One On and one Off stimulus were generated for each position in the 100- × 100-pixel visual field. For each V1 cell, separate On and Off receptive fields were calculated as a two-dimensional map of synaptic input received by the cell when On and Off stimuli corresponding to each visual field position were presented to the network.
Orientation-preference analysis.
V1 cell firing rates were averaged across grating phases for each grating angle. Each V1 cell’s preferred orientation was determined as the angle at which it exhibited the maximum average firing rate. The orientation-preference shift on a given trial was calculated for all V1 cells as the difference angle between the cell’s preferred orientation on trial 0 and a later trial.
RESULTS
Nascent Synapses are Recruited into Spatial Memories
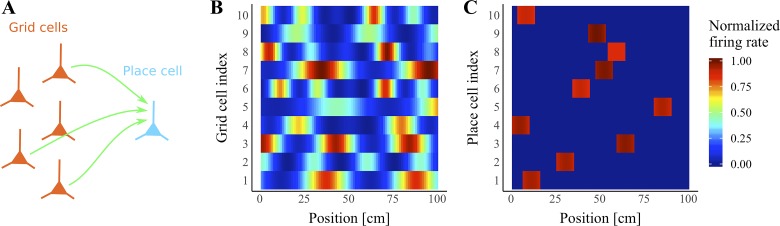
The crux of our hypothesis is that synapses that survive turnover provide a teaching signal for newly formed synapses. To illustrate this process, we first constructed a simple firing rate model (Fig. 1A) of a single place cell in CA1 driven by many grid cells in entorhinal cortex as a simulated animal runs in a linear track environment. In rodents, grid cells are active in evenly spaced grids across an environment, and the orientation and width of the grid vary by cell (de Almeida et al. 2009b). To capture these characteristics, we simulated grid-cell firing rates as positive periodic functions of position (Fig. 1B; Eq. 1) and assigned each grid cell a different grid rotation, phase, and period. When a simulation was run, the linear environment was divided into 100 equally spaced discrete positions, and the place cell’s total synaptic input was calculated at each position (Eq. 2). To ensure that the place cell would always have a place field (Fig. 1C), we set the place cell’s threshold dynamically such that the cell would be active at the 10 positions where it received the greatest synaptic input.
Fig. 1.
Feedforward convergent place-cell model of the grid-to-place-cell transformation. A: each individual place cell (blue) in CA1 receives synaptic input (green arrows) from many grid cells (orange) in entorhinal cortex. B: as the simulated animal moves through a linear enclosure, the firing rates of the grid cells vary as periodic functions of position such that most grid cells have multiple peak firing locations. Each row depicts the activity of a single representative grid cell. C: as the simulated animal moves, each place cell’s firing rate varies as the thresholded sum of its synaptic inputs from grid cells. The result of this process is that most place cells have a single firing field in the enclosure. Each row depicts the activity of a single place cell receiving inputs as shown in A.
Each simulation included 2 sessions on the linear track, and sessions were separated by between 1 and 30 days. Each session was subdivided into an early phase and a late phase. The early phase was used to inform plasticity, and the late phase was used to measure place fields after initial plasticity but before synapse turnover. During both phases, the animal visited each position on the track with equal frequency. At the end of each early phase, we updated the strengths of synapses onto the place cell according to Hebb’s rule (Eq. 6). This plasticity rule implies potentiation of synapses between coactive grid and place cells, regardless of whether the synapse is newly formed. We further implemented homeostatic scaling by divisive normalization (see materials and methods). We chose to have plasticity occur in the middle of each session because place-cell firing can induce LTP within minutes (Isaac et al. 2009). In addition, the spatial firing patterns of place cells in N-methyl-d-aspartate receptor subunit 1 knockout mice are less stable than those in wild-type mice in novel environments (Cabral et al. 2014), suggesting that the synaptic plasticity contributing to maintenance of receptive fields normally occurs early during exploration.
Synapse turnover occurred during the time between sessions. To simulate synapse turnover, we removed between 10% (~1 day of turnover; Attardo et al. 2015) and 100% (≥30 days of turnover; Attardo et al. 2015) of the existing grid-cell-to-place-cell synapses, and we created an equal number of new synapses to the place cell from randomly selected, previously unconnected grid cells.
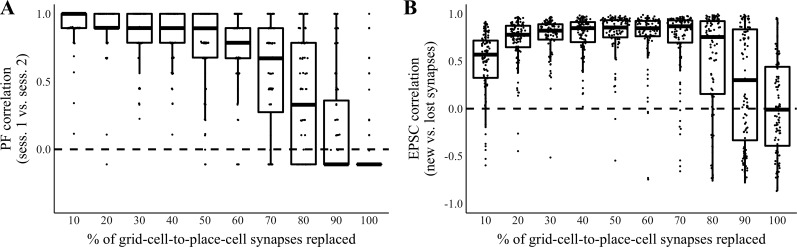
To assess the effect of synapse turnover on the integrity of a place cell’s firing field, we measured place-field (PF) correlations, spatial Pearson’s correlation between the place cell’s response during the late phase of session 1 and its response during the late phase of session 2. We performed 1,000 separate simulations, varying the amount of synapse turnover, and found that PF correlation was high (with a median >0.5) when ≤70% of synapses were replaced during turnover (Fig. 2A). These data suggest that a place cell can maintain its firing field after the majority of its original synaptic inputs are turned over.
Fig. 2.
Retained synapses provide a teaching signal to nascent synapses. Activity in a single-place-cell model of the grid-cell-to-place-cell transformation was simulated over 2 sessions (sess.) in a linear enclosure. Hebbian plasticity occurred during sessions, and 10–100% of synapses turned over between sessions. A: place-field (PF) correlation (Pearson’s correlation between the cell’s responses during the late phases of sessions 1 and 2) vs. the percentage of synapses replaced between sessions. In these and all box plots, the extent of the rectangle represents the interquartile range, the thick bar represents the median, and the extent of the whiskers represents 3 times the interquartile range. Whisker range is truncated to the minimum or maximum value if that is within 3 times the interquartile range. n = 100 Simulations per condition. B: excitatory postsynaptic current (EPSC) correlation (Pearson’s correlation between the sum of synaptic inputs by position during the late phase of session 1 at synapses removed due to turnover between sessions and the sum of synaptic inputs by position during the late phase of session 2 at synapses formed due to turnover between sessions) vs. the percentage of synapses replaced between sessions. n = 100 Simulations per condition.
Importantly, if retained synapses provide a teaching signal for new synapses, we expect that newly formed synapses will be functionally similar to synapses lost during turnover. To test functional similarity between new and lost synapses, we took the sum of synaptic input per position at a subset (ranging from 10 to 100%) of grid-cell-to-place-cell synapses during the late phase of session 1. We removed these synapses after session 1 and created an equal number of new synapses. We then took the sum of synaptic input per position at these new synapses during the late phase of session 2. We determined an excitatory postsynaptic current (EPSC) correlation score by taking the spatial Pearson’s correlation between these sums of synaptic input at new and lost synapses. We found that EPSC correlation was high when ≤80% of synapses were replaced during turnover (Fig. 2B). These data suggest that a place cell’s latent position selectivity can provide a teaching signal for new synapses even after substantial synapse turnover. Notably, we observed a nonmonotonic relation between EPSC correlation and the percentage of synapses replaced. On the one hand, if too many synapses are removed, the place field is immediately corrupted or destroyed and no teaching signal remains to strengthen new synapses that could support the prior place field. On the other hand, if too few synapses are removed, there is a good chance that none of the new synapses provides input that aligns with the place field, in which case no amount of training (i.e., strengthening of the appropriate new synapses) can match the new input to the removed input. In this latter case, the place field remains intact as few supporting synapses are lost.
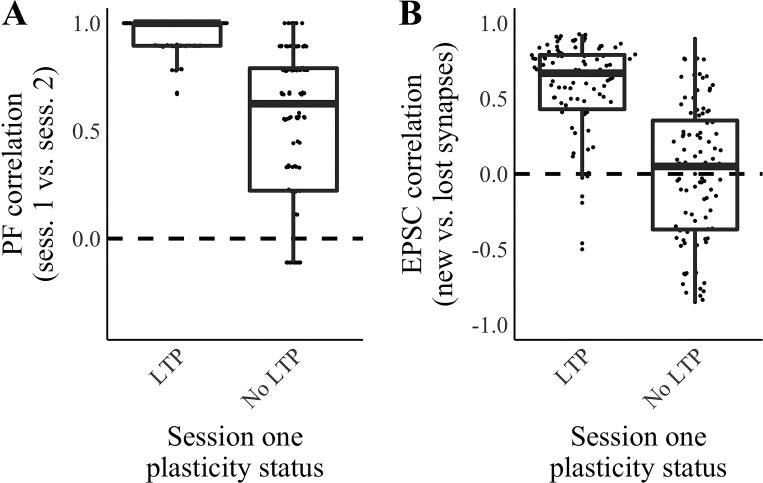
In mice, blocking of the processes necessary for long-term potentiation when the animal investigates a novel environment disrupts the long-term stability of place fields associated with that environment (Agnihotri et al. 2004; Kentros et al. 1998). We, therefore, asked whether plasticity in the novel environment (session 1 of our paradigm) is required for the training of new synapses that is necessary for place-field stability in our model. To test this, we performed 200 additional simulations, in half of which we omitted the Hebbian plasticity step in session 1. Omitting the Hebbian plasticity condition imitates the administration of a protein synthesis blocker or N-methyl-d-aspartate receptor antagonist in the novel environment. In these simulations, 10% of synapses were replaced between sessions 1 and 2. Similar to in vivo reports (Agnihotri et al. 2004; Kentros et al. 1998), we observed a decline in place-field correlations on session 2 when plasticity did not occur previously in the novel environment (P < 0.001, Wilcoxon rank sum test; Fig. 3A) even though Hebbian plasticity could occur for the new synapses present in session 2. In a further 200 simulations, we measured the functional similarity between new and lost synapses as described. We again omitted the Hebbian plasticity step in session 1 in half of the simulations. We found that without plasticity during session 1, EPSC correlations were not significantly different from zero (P = 0.887, Wilcoxon rank sum test; Fig. 3B). Taken together, these data show that our model reproduces the experimental finding that an initial period of plasticity in a novel environment is required for the later recruitment and training of nascent synapses, leading to a robust long-term place-field representation.
Fig. 3.
Training nascent synapses requires prior plasticity in the novel environment. Activity in a single-place-cell model of the grid-cell-to-place-cell transformation was simulated over 2 sessions (sess.) in a linear enclosure. Hebbian plasticity occurred during sessions, and 10% of synapses turned over between sessions. In 50% of the simulations, Hebbian plasticity was omitted during session 1 while still present for all synapses in session 2. A: place-field (PF) correlation (Pearson’s correlation between the cell’s responses during the late phases of sessions 1 and 2) vs. a Boolean value indicating whether plasticity occurred during session 1 of each simulation. n = 100 Simulations per condition. B: excitatory postsynaptic current (EPSC) correlation (Pearson’s correlation between the sum of synaptic inputs by position during the late phase of session 1 at synapses removed due to turnover between sessions and the sum of synaptic inputs by position during the late phase of session 2 at synapses formed due to turnover between sessions) vs. a Boolean value indicating whether plasticity occurred during session 1 of each simulation. n = 100 Simulations per condition. LTP, long-term potentiation.
As Hebbian plasticity is critical to the training of nascent synapses in our model, we decided to perform a parameter check to determine the range of plasticity rates over which such training is possible. To do this, we performed additional, two-session simulations as described above while varying the plasticity rate (η in Eq. 6) over a ten millionfold range. Ten percent of synapses were replaced between sessions. We evaluated the functional similarity between new and lost synapses by determining EPSC correlations as previously described. We found that EPSC correlation increased rapidly as the plasticity rate increased from 1e−5 to 1e−3 (Fig. 4A). We chose to use a plasticity rate of 1e−4 for simulations described in this manuscript because 1e−4 was the smallest tested value that resulted in an EPSC correlation significantly different from zero (P < 0.001, Wilcoxon rank sum test with Bonferroni corrections for multiple comparisons). In Fig. 4B, we show the average absolute change in synaptic strength from the early to the late phase of session 1 at a variety of plasticity rates in the presence or absence of synaptic scaling. At plasticity rates below 1e−5, changes in synaptic strength are dominated by scaling. At a plasticity rate of 1e−4, the average change in synaptic strength is ~50% (41% with scaling; 62% without scaling) of the mean synaptic strength before plasticity. At plasticity rates >1e−3, with scaling, the average change in strength saturates at ~107% of the mean synaptic strength before plasticity. Changes in synaptic strength of 50–100% are consistent with biological data indicating that 10 stimulations of the presynaptic terminal can trigger a 100% increase in the average strength of CA3-CA1 synapses (Murthy 1998). Furthermore, we find that synaptic plasticity over 2 running sessions at a plasticity rate of 1e−4 preserves key properties of the synaptic strength distribution: unimodality and heavy-tailedness (Fig. 4C).
Hebbian Plasticity Stabilizes Place Fields
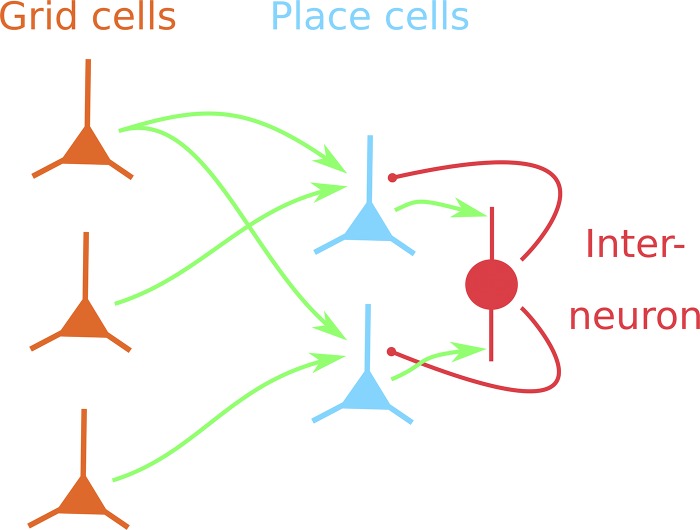
It is important to evaluate place-code stability in the context of the larger CA1 network because interneuron-mediated feedback inhibition may control which cells fire in a particular environment and location (de Almeida et al. 2009b). To simulate the CA1 network, we turned to a previously established model defined by de Almeida et al. (2009b). This model is identical to the single-place-cell model we described in the previous section, except for the addition of feedback inhibition (see materials and methods) and an expanded pyramidal cell population (2,000 cells) in CA1 (Fig. 5).
Fig. 5.
Multi-place-cell, feedback-inhibition model of the grid-cell-to-place-cell transformation. Many place cells (blue) in CA1 receive synaptic input (green arrows) from many grid cells (orange) in entorhinal cortex. Place cells in CA1 form convergent, excitatory connections (green arrows) onto interneurons in CA1, which, in turn, form divergent, inhibitory connections (red arrows) onto the place cells. Interneuron-mediated feedback inhibition controls which cells fire at particular locations in an enclosure.
Each of our simulations included 61 running sessions in the linear enclosure representing 61 days. The 1st running session is analogous to an experience in a novel environment. Subsequent sessions can be considered either as repeated experiences in the same environment or as offline events during which the original sequence of grid-cell activity is replayed. As before, sessions were divided into an early phase and late phase with plasticity occurring at the transition between phases according to Hebb’s rule (Eq. 6). To constrain synaptic strengths, we simulated homeostatic synaptic scaling (see materials and methods). Synapse turnover occurred at the end of each session. The rate of turnover was set at 9.5% (see materials and methods), the amount of synapse turnover expected during 1 day in mouse CA1 (Attardo et al. 2015). During the late phase of each session, we extracted the place-field centroids of all CA1 cells with place fields, excluding cells with more than one place field.
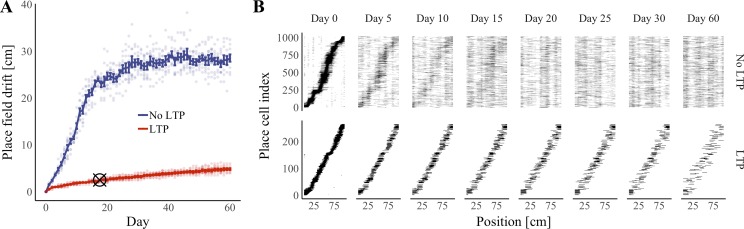
To measure the effect of synapse turnover on place-code stability, we compared the centroids of place fields found on the first session with the centroids of place fields found on later sessions. Comparisons were made within each cell so that we were able to measure the drift (see materials and methods) in the position of an individual place cell’s place field. We ran 10 independent simulations and found that mean place-field drift on the final session was significantly and dramatically reduced compared with 10 control simulations in which Hebbian plasticity steps were omitted (P < 0.001, Wilcoxon rank sum test; Fig. 6, A and B). These data suggest that Hebbian plasticity of synaptic strengths is sufficient to stabilize the place fields of individual place cells in a network, even after all original synapses are replaced.
Fig. 6.
Hebbian plasticity improves place-field stability. Activity in a feedback-inhibition, grid-cell-to-place-cell model was simulated over a period of 61 days with both Hebbian plasticity and synapse turnover. A: median place-field drift from day 0 vs. time and plasticity condition. Hebbian plasticity steps were omitted in the “No LTP” condition. Error bars represent means ± the standard error of the mean for median drift across simulations. Points represent median drift in individual simulations. Cross hairs indicate the experimentally determined median drift across days 5–30 in 5-day increments; cross hairs are positioned on the x-axis at the center of this time window (17.5 days). n = 10 Simulations per condition. B: representative place-cell firing fields sorted by place-field centroid on day 0. Black areas represent regions of the enclosure in which a cell was active. LTP, long-term potentiation.
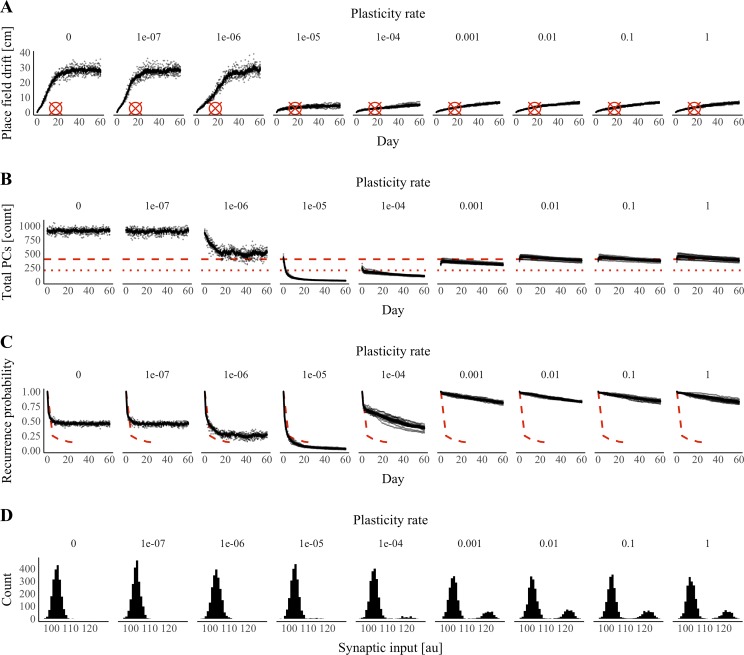
As our choice of plasticity rate (1e−4) was motivated by a parameter check (Fig. 3A) rather than biological data, we decided to investigate the robustness of our model to changes in the plasticity rate. In our model, the overall distribution of synaptic strengths is relatively unchanged by plasticity (Fig. 3B). Therefore, the plasticity rate can be seen as modulating the degree to which a synapse’s strength after plasticity depends on its strength before plasticity. We performed an additional 80 simulations as described above while varying the plasticity rate (η in Eq. 6) over a 10 million-fold range. We found that increasing the plasticity rate from 1e−6 to 1e−5 produced a dramatic increase in stability as measured by the rate of place-field drift (Fig. 7A) and PF correlation compared with the 1st day (Supplemental Fig. S1). All examined plasticity rates >1e−5 resulted in <10 cm of average drift over 61 sessions (Fig. 7A). Our simulated results compare favorably to calcium imaging data showing 3.5 cm of median drift when aggregating data from days 5 to 30 in 5-day increments (Ziv et al. 2013). Performing the same calculations over simulations performed at a plasticity rate of 1e−4, we observed 2.9 cm of median drift.
Fig. 7.
Effects of plasticity rate on place-code properties. Activity in a feedback-inhibition, grid-cell-to-place-cell model was simulated over a period of 61 days with both Hebbian plasticity and synapse turnover. Plasticity rate varied over a 10-million-fold range across simulations. A: median place-field drift from day 0 vs. time and the plasticity rate taken during the late phase (after plasticity) on each day. Cross hairs indicate the experimentally determined median drift over days 5–30 in 5-day increments. Cross hairs are positioned on the x-axis at the center of this time window (17.5 days). B: total number of place cells (PCs; CA1 cells with place fields) vs. time and the plasticity rate taken during the late phase (after plasticity) on each day. Dashed lines indicate the experimentally determined number of place cells per 2,000 cells when the animal is moving in 1 direction (small dashes, 10%) or either direction (large dashes, 20%). C: probability of place-cell recurrence (the fraction of CA1 cells with place fields on both day 0 and a later date) vs. the time and the plasticity rate taken during the late phase (after plasticity) on each day. Dashed lines indicate experimentally determined values from Ziv et al. (2013). A–C: n = 10 simulations per plasticity rate; data from the same set of simulations were used across panels; error bars represent means ± the standard error of the mean across simulations, and points represent values from individual simulations. D: histograms of mean synaptic input per cell across positions on day 60 at several plasticity rates. au, Arbitrary units.
To evaluate further the effect of plasticity rate on place-field properties, we measured the total number of place cells with place fields on each day (Fig. 7B) as well as the probability of place-cell recurrence (Fig. 7C). We defined the probability of recurrence as the fraction of place cells with place fields during both session 1 and a later session. We found that the total number of place cells and the number of recurring place cells followed a similar trend, decreasing as the plasticity rate increased from 1e−7 to 1e−5 and then increasing toward an apparent asymptote as the plasticity rate increased from 1e−5 to 1. Calcium imaging data indicate that ~20% of CA1 cells have a place field on a given session, whereas dividing the session into left and right moving trajectories reveals that ~10% of CA1 cells have a place field along a particular trajectory (Ziv et al. 2013). In our simulations, with a plasticity rate of 1e−4, an average of 7% of cells have place fields each day, an amount that is comparable with the experimentally determined percentage of cells with place fields along one trajectory.
To interpret the nonmonotonic relation between the total number of place cells and the plasticity rate, we inspected the distribution of total synaptic input across CA1 cells in our model at each plasticity rate (Fig. 7D). Without plasticity, total input followed a Gaussian distribution. When plasticity was introduced, two clusters emerged in the distribution of total input. The first cluster included the majority of cells and followed the initial Gaussian distribution, whereas the second cluster exhibited greater total synaptic input. The emergence of the second cluster corresponds to an increase in the excitation of the most excited cell. Thus fewer cells fired before the arrival of feedback inhibition, reducing the number of active place cells. With higher plasticity rates, the number of units in the second cluster increased. Thus more cells received a similar amount of excitation to the most excited cell, and more cells were able to fire before the arrival of feedback inhibition.
In the above-described simulations, different grid cells were assigned different orientations because grid cells are organized in modules at a given position on the dorsoventral axis, and orientation is shared within but not across modules (Stensola et al. 2012). We hypothesized that our results would not be impacted qualitatively if we fixed a single orientation for all grid fields because the basis is still overcomplete with a range of offsets and spatial frequencies. This means that with appropriately weighted inputs any desired place field could be generated with redundancy. We performed additional simulations in which grid orientation and spatial frequency among grid cells was sequentially fixed (identical for all cells) or varied (randomly assigned for each cell as previously described). As expected, we found that our results hold when CA1 cells receive inputs from grid cells with varied grid orientations (originating from multiple modules) and/or spatial frequencies (originating from different positions along the dorsoventral axis of medial entorhinal cortex; Supplemental Fig. S2A). Our place-cell model fails when neither orientation nor period varies between grid cells as the total number of place cells is reduced in the condition without LTP and rapidly falls to 1% of the CA1 population with LTP (Supplemental Fig. S2B).
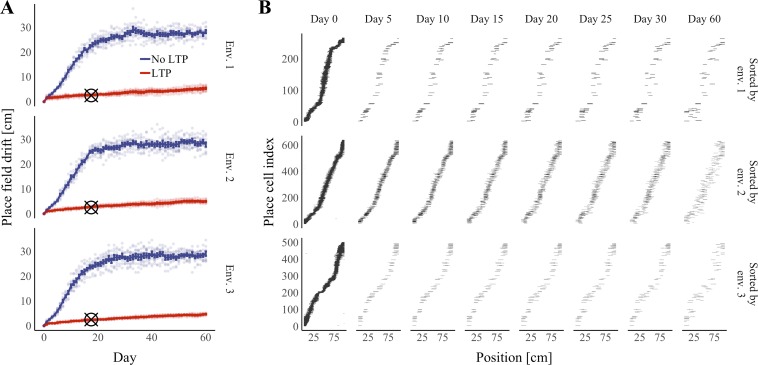
One caveat of our modeling approach thus far is that we did not account for the effects of irrelevant learning. For example, between running sessions, a mouse could be exposed to additional environments. Learning in these environments might interfere with previously stored memories. To address this complication, we asked whether our model would be able to sustain place fields across multiple enclosures or whether synaptic plasticity in a new environment would disrupt previously established place codes. To create a new linear enclosure, we shuffled the periodic firing rate functions associated with the grid cells. This procedure was motivated by the assumption that the firing fields of a grid cell in two environments are unrelated (de Almeida et al. 2009b). Our simulations in multiple enclosures were identical to our simulations in a single enclosure except that three running sessions, in three separate environments, were experienced before each synapse turnover event. The order in which environments were experienced was randomly reassigned each day. As before, plasticity occurred in the middle of each session. To assess place-field stability across multiple environments, we quantified place-field drift in each enclosure independently. We found that drift on the final session was significantly reduced in all three environments compared with control simulations with no plasticity (all P < 0.001, Wilcoxon rank sum tests with Bonferroni corrections for multiple comparisons; Fig. 8). Averaging median drift across all three environments, drift on the final session did not differ significantly from drift in experiments without interference (LTP in Fig. 6; P = 0.404, Wilcoxon rank sum test). Furthermore, the median drift over days 5–30 in 5-day increments was 3.2 cm, similar to the biological value of 3.5 cm (Ziv et al. 2013). These results suggest that Hebbian plasticity is sufficient to preserve place codes despite both irrelevant learning and synapse turnover.
Fig. 8.
Hebbian plasticity improves place-field stability across multiple environments (Env.). Activity in a feedback-inhibition, grid-cell-to-place-cell model was simulated in 3 separate linear enclosure environments over a period of 61 days with both Hebbian plasticity and synapse turnover. A: median place-field drift from day 0 vs. time in each environment. Hebbian plasticity steps were omitted in the “No LTP” condition. Error bars represent means ± the standard error of the mean for median drift across simulations. Points represent median drift in individual simulations. Cross hairs indicate the experimentally determined median drift across days 5–30 in 5-day increments; cross hairs are positioned on the x-axis at the center of this time window (17.5 days). n = 10 Simulations per condition. B: representative place-cell firing fields from the “LTP” condition sorted by place-field centroid on day 0 in each of the 3 environments. Black areas represent regions of the enclosure in which a cell was active. LTP, long-term potentiation.
Stable Orientation Tuning Despite Synapse Turnover in an LGN-to-V1 Model
So far, we have shown that Hebbian plasticity stabilizes the neural activity patterns believed to underlie place memory in models of hippocampal function. However, our model may also help explain the stability of computation in nonhippocampal networks such as the mammalian visual system. For example, in V1, many cells firing selectively in response to visual stimuli presented at a particular orientation (Bonhoeffer and Grinvald 1991). V1 cells with similar orientation preferences are clustered in pinwheel-patterned retinotopic maps (Bonhoeffer and Grinvald 1991). Furthermore, although synapses in V1 turn over in both developing and adult mammals (Holtmaat et al. 2005; Stettler et al. 2006; Tropea et al. 2010; Yu et al. 2011), retinotopic maps can be stable throughout this period (Stevens et al. 2013).
To ask how activity-independent synapse turnover might affect the stability of orientation selectivity in V1, we constructed a simplified model of the LGN-center-surround-cell-to-V1-simple-cell transformation. In our model, visual stimuli were presented as a set of static sinusoidal gratings, across a square section of visual field, with gratings differing in their phase and angle of orientation. Visual input was received by 20,000 LGN cells with on- or off-center difference-of-Gaussians receptive fields with random field centroids (see materials and methods). Each of 1,000 V1 cells initially received excitatory synaptic input from 130 LGN cells. LGN inputs were initially arranged such that each V1 cell had a simple-cell-like receptive field consisting of an inhibitory central bar and 2 flanking excitatory bars (Fig. 9A, top; Lee et al. 2016; see materials and methods). The centroids and rotations of V1 cell receptive fields were assigned randomly. The firing rates of V1 cells were further modulated by lateral inhibition (see materials and methods).
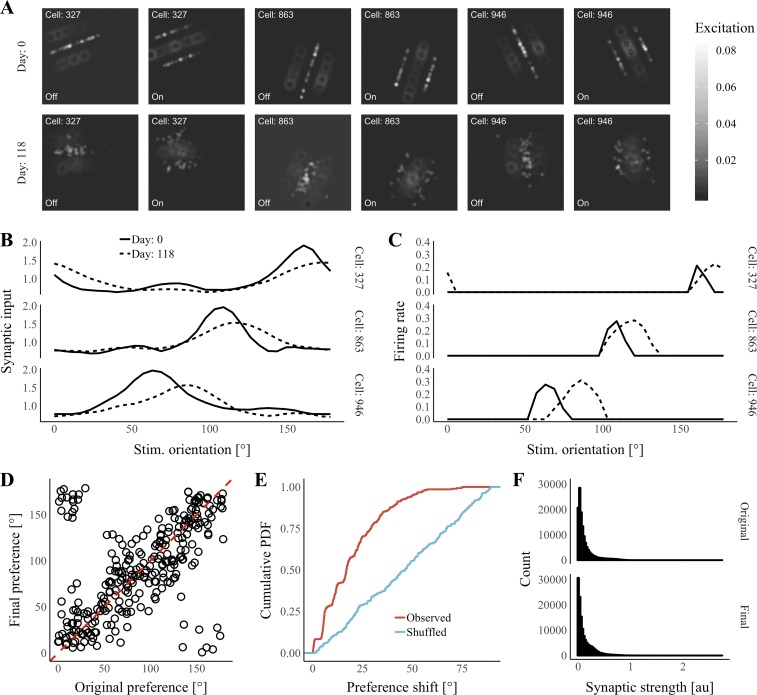
Fig. 9.
Persistent orientation tuning in a lateral geniculate nucleus-to-V1 model. A: visual receptive fields of 3 representative V1 cells on days 0 and 118. Excitation is the amount of synaptic input received by the V1 cell in response to bright (“On”) or dark (“Off”) spot on the visual field. B: synaptic input received by cells in A at their most excited phase across orientations on days 0 (solid lines) and 118 (dashed lines). C: firing rates of cells in A at their most-excited phase across orientations on days 0 (solid lines) and 118 (dashed lines). D: original vs. final preferred orientation for all V1 cells. E: cumulative probability density plot of observed orientation-preference shifts (red) and a shuffled condition (blue). F: histograms of original and final synaptic strengths at realized synapses across all cells. au, Arbitrary units; PDF, probability density function; Stim., stimulus.
We simulated network activity in sessions during which the static grating stimulus was presented at a set of angles sampled evenly over a 180° range. After each session, the strengths of LGN-to-V1 synapses were updated according to Hebb’s rule (see materials and methods), and an average of 10% of synapses were replaced (see materials and methods). In mice, spine turnover in V1 seems to be partially activity-dependent (Tropea et al. 2010); however, for simplicity, we assume that all rewiring is activity-independent. In addition, in mice, there appears to be a sizable population of stable spines in V1 (Holtmaat et al. 2005); however, we assume only a single population of unstable spines. In our model, the probability of removal was identical across all synapses, whereas the probability of synapse formation between 2 units was determined by a function that fell off with the distance between receptive-field centroids. In total, we simulated 60 sessions, representing network activity over 120 days in 2-day increments.
We visualized the receptive fields of individual V1 cells observing synaptic input at V1 in response to individual bright- or dark-spot stimuli at positions sampled evenly across the visual field (Fig. 9A). V1 receptive fields largely maintained their three-bar structure after 120 days. We also visualized the spatial tuning of synaptic inputs (Fig. 9B) and firing rates (Fig. 9C) for individual V1 cells across stimulus orientations at their preferred stimulus phase. We observed little change over time in the visual orientations producing peak synaptic input (Fig. 9B) and firing rates (Fig. 9, C and D) for individual V1 cells. To quantify within-cell shift in orientation preference, we took the angle between the orientations of peak firing during the first and final session (Fig. 9E). In our model, mean shift was significantly reduced compared with a control in which final orientation preferences were shuffled (P < 0.001, Wilcoxon rank sum test). Meanwhile, the range of synaptic strengths remained similar across the simulated period (Fig. 9F). These data suggest that our model can help to explain stable neural representations in extrahippocampal networks.
DISCUSSION
Recent research suggests that the neuronal connectomes of adult mammals are not as stable as once thought (DeBello and Zito 2017). In regions such as the hippocampus, the majority of the synaptic architecture might be rewired in a period as short as 1 mo (Attardo et al. 2015). Under these conditions, it is not clear whether or how memories and computational properties could be preserved in the long term. Although complete synaptic turnover may take longer in cortical regions, the many decades of an animal’s lifetime are likely to prove to be too long for the set of connections formed during an early critical period to remain. However, for us to recognize a person we met or place we lived many decades earlier, a fraction of the original cortical representation should remain intact.
Therefore, we sought to address the question of how representations could remain in the face of a long-term overhaul in the connectivity of a circuit, using a modeling approach. We found that Hebbian plasticity of synaptic strengths, in particular when combined with network reactivation, is sufficient to maintain network memory and function in the midst of random synapse turnover.
Specifically, in a network with many varying inputs, our model predicts that the synapses that survive turnover will provide a teaching signal to newly formed synapses. In time, all original synapses may turn over, but synapses that received the teaching signal will continue to pass that signal on as more new synapses are formed. Consistent with in vivo observations (Ziv et al. 2013), we found that reactivation of grid-cell activity patterns and Hebbian plasticity led to stable place fields in models of hippocampal place cell networks. These results suggest that random synapse turnover does not preclude long-term memory. To assess the generalizability of our model to nonhippocampal systems, we examined the stability of orientation tuning in a network model of V1 simple cells. In this model, we observed persistent orientation preferences despite activity-independent synapse turnover. This result suggests that, once established, simple plasticity rules may counteract effects of rewiring noise on orientation-tuning maps.
Several pre-existing models suggest that memory and computation can outlive individual synapses (Eppler et al. 2015; Fauth et al. 2015; Gallinaro and Rotter 2017; Hopfield and Brody 2004; Knoblauch et al. 2014; Poirazi and Mel 2001); our model is unique in two ways. First, in our model, synapse stability and the location of new synapses are random. This is in contrast to models created by Poirazi and Mel (2001), Hopfield and Brody (2004), Knoblauch et al. (2014), and Fauth et al. (2015), all of which involve activity-dependent synapse formation and/or elimination. Because we leave the control of synapse turnover to chance, our model is generalizable to neural structures such as the adult hippocampus in which mechanisms for activity-dependent wiring are poorly characterized. Second, our model requires only monosynaptic connections. This is in contrast to the model by Fauth et al. (2015) in which information is represented by the number of synapses connecting neuron pairs. Because our model does not rely on compound connections, it can be extended to represent a variety of circuits with few potential connections per neuron pair.
An important open question is whether synapse turnover in the hippocampus is truly random. For example, it is possible that spine stability increases with spine size and synaptic potentiation: LTP might lead to an expansion of the postsynaptic density and actin polymerization, resulting in an enlarged spine that is unlikely to collapse into the dendritic shaft (Bramham et al. 2010; Lüscher and Malenka 2012). In agreement with this hypothesis, Pfeiffer and colleagues (2018) showed a small but significant relationship between spine lifetime and spine volume in adult mouse CA1. However, the high density of dendritic spines in the region, as compared with cortex, might lead to optical merging of nearby spines, increasing uncertainty around volume estimates during in vivo imaging (Attardo et al. 2015). Our models contribute to these discussions of hippocampal plasticity as we have shown that the place fields of individual place cells can be stable despite the ongoing, random replacement of grid-cell inputs. Our results suggest that neither activity-dependent synapse stabilization nor an inherently stable synapse population is necessary to explain the observed persistence of hippocampal representations.
Another question requiring further investigation is the degree of place-field stability in the mouse, as opposed to the rat, hippocampus. Whereas rat studies agree that CA1 place fields are stable (Cholvin et al. 2018; Leutgeb et al. 2005, 2006; Thompson and Best 1990), studies in mice have reached differing conclusions. As discussed above, Ziv et al. (2013) found that place fields in mouse CA1 display minimal drift across days. A study by Rubin et al. (2015) reached a similar conclusion. Furthermore, Attardo et al. (2018) found that a sparse collection of CA1 cells was repeatedly activated in the same environment for ≥31 days and that the ensemble was stabilized over time by repeated training. The cells comprising this stable ensemble may be place cells encoding environmental features that are salient across days (Attardo et al. 2018). In contrast to these results that support stability in CA1, experimentation by Hainmueller and Bartos (2018) suggests that place cells in mouse CA1 remap rapidly, whereas those in the dentate gyrus are stable. Future research will be required before consensus can be reached on place field stability in mouse CA1.
To date, long-term in vivo measurements of hippocampal spine stability have been performed in mice but not in rats (Attardo et al. 2015; Pfeiffer et al. 2018). Thus we do not know whether significant synapse turnover occurs in rat hippocampus, and uncovering the degree to which this occurs is another important direction for future research.
Our results generalize to any circuits of the brain undergoing synaptic turnover and Hebbian plasticity. Since some synapses appear to be stable, suggesting synaptic turnover is not a biological necessity, one can question whether there is any advantage to circuits possessing connections that are not robust. Within cortical regions, which extract the important correlations from their inputs, such rewiring allows an animal to retrain when input statistics change. Within the hippocampus, the rewiring may allow for selective maintenance of memories, ensuring that only important or revisited experiences are connected to produce long-lasting episodic memories. In support of this idea, one theory of hippocampal and cortical memory is that hippocampus both learns and forgets quickly, whereas cortex learns more slowly but retains information longer (Lisman and Morris 2001; Roxin and Fusi 2013). According to this view, memories in the hippocampus are slowly transferred to the cortex for long-term storage. These memories can then be cleared from the hippocampus, making way for new learning (Lisman and Grace 2005; Lisman and Morris 2001; Richards and Frankland 2017). The regional time scales of memory retention in this hippocampus-to-cortex model are correlated with the difference in apparent turnover dynamics between these structures. Our model predicts that hippocampal memories would eventually be cleared without reinforcement; however, plasticity during reactivation events could allow a memory to endure.
This model generates several experimentally testable predictions. Since place fields are reactivated during hippocampal sharp-wave ripples (Lee and Wilson 2002) and ripples support spatial memory (Jadhav et al. 2012), we expect that disruption of such ripples would lead to more rapid destabilization of the place fields. Interestingly, whereas ripples often contain replay of trajectories from remote environments (Karlsson and Frank 2009), the maximum remoteness of ripple content has not been tested. Since stability in our model requires ongoing reactivation of place cells, we predict that either ripples contain replay of very remote memories or that place-field stability requires relatively frequent exposure to the environment. An additional intriguing possibility is that stability is situational and may be actively regulated by saliency- or reward-induced changes to plasticity rate or replay frequency. Consistent with this hypothesis, ripple density increases following learning in rats (Eschenko et al. 2008). We, therefore, expect enhanced long-term stability in reward-associated environments.
It is important to note that our models lack several features known to impact learning and memory. For example, we simulate homosynaptic potentiation but not depression. Long-term depression (LTD) is critically implicated in hippocampal declarative memory (Kemp and Manahan-Vaughan 2007). A simple implementation of LTD reduces the strength of synapses between a neuron pair when one neuron is active while the other is inactive relative to a threshold firing rate (Linsker 1986). We predict that this implementation of LTD would not substantially alter our conclusions because rank changes in synaptic strength would be preserved. However, we hypothesize that LTD would increase the uniformity of ensemble representations among place cells in the context of multiple environments by further reducing the synaptic input to less active cells.
In addition to lacking homosynaptic depression, our models are rate-based and learn by correlative Hebbian plasticity; however, precise spike timing contributes to both computation and plasticity in many systems (Feldman 2012). In models 2 and 3, we approximate a winner-takes-all process whereby spike timing controls CA1-place-cell and V1-simple-cell firing rates (de Almeida et al. 2009a, 2009b). Thus we predict that our conclusions would hold if spike timing were simulated explicitly. A further limitation of our neuron models is the absence of dendrites. Synapses tend to cluster both anatomically and functionally along dendrites (Kastellakis et al. 2015). This clustering permits nonlinear synaptic integration, as coactivation of adjacent synapses can trigger dendritic spikes (Kastellakis et al. 2015). In such situations, each dendritic compartment acts similarly to the neuron model used in our simulations, so qualitatively the results would not change, but the precise quantitative behavior would depend on the number of correlated inputs required to produce a dendritic spike. A comprehensive comparison of the behavior of our conceptual model with that of more detailed implementations will require rigorous analysis of these additional factors.
In sum, we describe a model of memory preservation amidst synapse turnover that accounts for an apparent contradiction emerging from recent research on connectome stability and the persistence of memories encoded in neural ensembles. We show that memory and computation can be stabilized by Hebbian plasticity of synaptic strengths, even as the network is randomly rewired.
GRANTS
This work was supported by the NIH (National Institute on Drug Abuse) via award number R01-DA-043195 to P. Miller and the NIH (National Institute of Neurological Disorders and Stroke) via award number R01-NS-065856 to S. Paradis.
DISCLAIMERS
The results in this paper are those of the authors and do not imply endorsement by NIH.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
D.A. conceived and designed research; D.A. performed experiments; D.A. analyzed data; D.A. and P.M. interpreted results of experiments; D.A. prepared figures; D.A. drafted manuscript; D.A., S.P., and P.M. edited and revised manuscript; D.A., S.P., and P.M. approved final version of manuscript.
ENDNOTE
At the request of the authors, readers are herein alerted to the fact that additional materials related to this manuscript may be found at the Web site of the authors, which at the time of publication they indicate is: https://github.com/AckerDWM/Stable-memory-and-computation-in-randomly-rewiring-neural-networks. These materials are not a part of this manuscript and have not undergone peer review by the American Physiological Society (APS). APS and the journal editors take no responsibility for these materials, for the Web site address, or for any links to or from it.
ACKNOWLEDGMENTS
We thank the late Dr. John Lisman, who contributed to this work through enlightening discussion and feedback.
Preprint is available at https://www.biorxiv.org/content/10.1101/367011v1.full.
REFERENCES
- Abraham WC, Logan B, Greenwood JM, Dragunow M. Induction and experience-dependent consolidation of stable long-term potentiation lasting months in the hippocampus. J Neurosci 22: 9626–9634, 2002. doi: 10.1523/JNEUROSCI.22-21-09626.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agnihotri NT, Hawkins RD, Kandel ER, Kentros C. The long-term stability of new hippocampal place fields requires new protein synthesis. Proc Natl Acad Sci USA 101: 3656–3661, 2004. doi: 10.1073/pnas.0400385101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Attardo A, Fitzgerald JE, Schnitzer MJ. Impermanence of dendritic spines in live adult CA1 hippocampus. Nature 523: 592–596, 2015. doi: 10.1038/nature14467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Attardo A, Lu J, Kawashima T, Okuno H, Fitzgerald JE, Bito H, Schnitzer MJ. Long-term consolidation of ensemble neural plasticity patterns in hippocampal area CA1. Cell Rep 25: 640–650.e2, 2018. doi: 10.1016/j.celrep.2018.09.064. [DOI] [PubMed] [Google Scholar]
- Bezaire MJ, Soltesz I. Quantitative assessment of CA1 local circuits: knowledge base for interneuron-pyramidal cell connectivity. Hippocampus 23: 751–785, 2013. doi: 10.1002/hipo.22141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blair HT, Welday AC, Zhang K. Scale-invariant memory representations emerge from moiré interference between grid fields that produce theta oscillations: a computational model. J Neurosci 27: 3211–3229, 2007. doi: 10.1523/JNEUROSCI.4724-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonhoeffer T, Grinvald A. Iso-orientation domains in cat visual cortex are arranged in pinwheel-like patterns. Nature 353: 429–431, 1991. doi: 10.1038/353429a0. [DOI] [PubMed] [Google Scholar]
- Bourjaily MA, Miller P. Excitatory, inhibitory, and structural plasticity produce correlated connectivity in random networks trained to solve paired-stimulus tasks. Front Comput Neurosci 5: 37, 2011. doi: 10.3389/fncom.2011.00037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bramham CR, Alme MN, Bittins M, Kuipers SD, Nair RR, Pai B, Panja D, Schubert M, Soule J, Tiron A, Wibrand K. The Arc of synaptic memory. Exp Brain Res 200: 125–140, 2010. doi: 10.1007/s00221-009-1959-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brun VH, Leutgeb S, Wu HQ, Schwarcz R, Witter MP, Moser EI, Moser MB. Impaired spatial representation in CA1 after lesion of direct input from entorhinal cortex. Neuron 57: 290–302, 2008. doi: 10.1016/j.neuron.2007.11.034. [DOI] [PubMed] [Google Scholar]
- Brun VH, Otnass MK, Molden S, Steffenach HA, Witter MP, Moser MB, Moser EI. Place cells and place recognition maintained by direct entorhinal-hippocampal circuitry. Science 296: 2243–2246, 2002. doi: 10.1126/science.1071089. [DOI] [PubMed] [Google Scholar]
- Cabral HO, Fouquet C, Rondi-Reig L, Pennartz CM, Battaglia FP. Single-trial properties of place cells in control and CA1 NMDA receptor subunit 1-KO mice. J Neurosci 34: 15861–15869, 2014. doi: 10.1523/JNEUROSCI.5320-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chambers AR, Rumpel S. A stable brain from unstable components: emerging concepts and implications for neural computation. Neuroscience 357: 172–184, 2017. doi: 10.1016/j.neuroscience.2017.06.005. [DOI] [PubMed] [Google Scholar]
- Cholvin T, Hok V, Giorgi L, Chaillan FA, Poucet B. Ventral midline thalamus is necessary for hippocampal place field stability and cell firing modulation. J Neurosci 38: 158–172, 2018. doi: 10.1523/JNEUROSCI.2039-17.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Almeida L, Idiart M, Lisman JE. A second function of gamma frequency oscillations: an E%-max winner-take-all mechanism selects which cells fire. J Neurosci 29: 7497–7503, 2009a. doi: 10.1523/JNEUROSCI.6044-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Almeida L, Idiart M, Lisman JE. The input-output transformation of the hippocampal granule cells: from grid cells to place fields. J Neurosci 29: 7504–7512, 2009b. doi: 10.1523/JNEUROSCI.6048-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Almeida L, Idiart M, Lisman JE. The single place fields of CA3 cells: a two-stage transformation from grid cells. Hippocampus 22: 200–208, 2012. doi: 10.1002/hipo.20882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeBello W, Zito K. Within a spine’s reach. In: The Rewiring Brain: A Computational Approach to Structural Plasticity in the Adult Brain, edited by van Ooyen A and Butz-Istendorf M. Amsterdam, The Netherlands: Elsevier Science, 2017, p. 295–317. [Google Scholar]
- English DF, McKenzie S, Evans T, Kim K, Yoon E, Buzsáki G. Pyramidal cell-interneuron circuit architecture and dynamics in hippocampal networks. Neuron 96: 505–520.e7, 2017. doi: 10.1016/j.neuron.2017.09.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eppler B, Aschauer D, Rumpel S, Kaschube M. Discrete cortical representations and their stability in the presence of synaptic turnover. BMC Neurosci 16, Suppl 1: P114, 2015. doi: 10.1186/1471-2202-16-S1-P114. [DOI] [Google Scholar]
- Eschenko O, Ramadan W, Mölle M, Born J, Sara SJ. Sustained increase in hippocampal sharp-wave ripple activity during slow-wave sleep after learning. Learn Mem 15: 222–228, 2008. doi: 10.1101/lm.726008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fauth M, Wörgötter F, Tetzlaff C. Formation and maintenance of robust long-term information storage in the presence of synaptic turnover. PLoS Comput Biol 11: e1004684, 2015. doi: 10.1371/journal.pcbi.1004684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldman DE. The spike-timing dependence of plasticity. Neuron 75: 556–571, 2012. doi: 10.1016/j.neuron.2012.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallinaro JV, Rotter S. Associative properties of structural plasticity based on firing rate homeostasis in recurrent neuronal networks (Preprint). arXiv: 1706.02912v1, 2017. [DOI] [PMC free article] [PubMed]
- Grutzendler J, Kasthuri N, Gan WB. Long-term dendritic spine stability in the adult cortex. Nature 420: 812–816, 2002. doi: 10.1038/nature01276. [DOI] [PubMed] [Google Scholar]
- Guskjolen A, Josselyn SA, Frankland PW. Age-dependent changes in spatial memory retention and flexibility in mice. Neurobiol Learn Mem 143: 59–66, 2017. doi: 10.1016/j.nlm.2016.12.006. [DOI] [PubMed] [Google Scholar]
- Hainmueller T, Bartos M. Parallel emergence of stable and dynamic memory engrams in the hippocampus. Nature 558: 292–296, 2018. doi: 10.1038/s41586-018-0191-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill TC, Zito K. LTP-induced long-term stabilization of individual nascent dendritic spines. J Neurosci 33: 678–686, 2013. doi: 10.1523/JNEUROSCI.1404-12.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holtmaat AJ, Trachtenberg JT, Wilbrecht L, Shepherd GM, Zhang X, Knott GW, Svoboda K. Transient and persistent dendritic spines in the neocortex in vivo. Neuron 45: 279–291, 2005. doi: 10.1016/j.neuron.2005.01.003. [DOI] [PubMed] [Google Scholar]
- Hopfield JJ, Brody CD. Learning rules and network repair in spike-timing-based computation networks. Proc Natl Acad Sci USA 101: 337–342, 2004. doi: 10.1073/pnas.2536316100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isaac JT, Buchanan KA, Muller RU, Mellor JR. Hippocampal place cell firing patterns can induce long-term synaptic plasticity in vitro. J Neurosci 29: 6840–6850, 2009. doi: 10.1523/JNEUROSCI.0731-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jadhav SP, Kemere C, German PW, Frank LM. Awake hippocampal sharp-wave ripples support spatial memory. Science 336: 1454–1458, 2012. doi: 10.1126/science.1217230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karlsson MP, Frank LM. Awake replay of remote experiences in the hippocampus. Nat Neurosci 12: 913–918, 2009. doi: 10.1038/nn.2344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kastellakis G, Cai DJ, Mednick SC, Silva AJ, Poirazi P. Synaptic clustering within dendrites: an emerging theory of memory formation. Prog Neurobiol 126: 19–35, 2015. doi: 10.1016/j.pneurobio.2014.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kemp A, Manahan-Vaughan D. Hippocampal long-term depression: master or minion in declarative memory processes? Trends Neurosci 30: 111–118, 2007. doi: 10.1016/j.tins.2007.01.002. [DOI] [PubMed] [Google Scholar]
- Kentros C, Hargreaves E, Hawkins RD, Kandel ER, Shapiro M, Muller RV. Abolition of long-term stability of new hippocampal place cell maps by NMDA receptor blockade. Science 280: 2121–2126, 1998. doi: 10.1126/science.280.5372.2121. [DOI] [PubMed] [Google Scholar]
- Kentros CG, Agnihotri NT, Streater S, Hawkins RD, Kandel ER. Increased attention to spatial context increases both place field stability and spatial memory. Neuron 42: 283–295, 2004. doi: 10.1016/S0896-6273(04)00192-8. [DOI] [PubMed] [Google Scholar]
- Knoblauch A, Körner E, Körner U, Sommer FT. Structural synaptic plasticity has high memory capacity and can explain graded amnesia, catastrophic forgetting, and the spacing effect. PLoS One 9: e96485, 2014. [Correction in PLoS One 10: e0141382, 2015.] doi: 10.1371/journal.pone.0096485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee AK, Wilson MA. Memory of sequential experience in the hippocampus during slow wave sleep. Neuron 36: 1183–1194, 2002. doi: 10.1016/S0896-6273(02)01096-6. [DOI] [PubMed] [Google Scholar]
- Lee KS, Huang X, Fitzpatrick D. Topology of ON and OFF inputs in visual cortex enables an invariant columnar architecture. Nature 533: 90–94, 2016. doi: 10.1038/nature17941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leutgeb S, Leutgeb JK, Barnes CA, Moser EI, McNaughton BL, Moser MB. Independent codes for spatial and episodic memory in hippocampal neuronal ensembles. Science 309: 619–623, 2005. doi: 10.1126/science.1114037. [DOI] [PubMed] [Google Scholar]
- Leutgeb S, Leutgeb JK, Moser EI, Moser MB. Fast rate coding in hippocampal CA3 cell ensembles. Hippocampus 16: 765–774, 2006. doi: 10.1002/hipo.20201. [DOI] [PubMed] [Google Scholar]
- Linsker R. From basic network principles to neural architecture: emergence of orientation-selective cells. Proc Natl Acad Sci USA 83: 8390–8394, 1986. doi: 10.1073/pnas.83.21.8390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lisman J, Morris RG. Memory. Why is the cortex a slow learner? Nature 411: 248–249, 2001. doi: 10.1038/35077185. [DOI] [PubMed] [Google Scholar]
- Lisman JE, Grace AA. The hippocampal-VTA loop: controlling the entry of information into long-term memory. Neuron 46: 703–713, 2005. doi: 10.1016/j.neuron.2005.05.002. [DOI] [PubMed] [Google Scholar]
- Lüscher C, Malenka RC. NMDA receptor-dependent long-term potentiation and long-term depression (LTP/LTD). Cold Spring Harb Perspect Biol 4: a005710, 2012. doi: 10.1101/cshperspect.a005710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Megías M, Emri Z, Freund TF, Gulyás AI. Total number and distribution of inhibitory and excitatory synapses on hippocampal CA1 pyramidal cells. Neuroscience 102: 527–540, 2001. doi: 10.1016/S0306-4522(00)00496-6. [DOI] [PubMed] [Google Scholar]
- Miles R. Synaptic excitation of inhibitory cells by single CA3 hippocampal pyramidal cells of the guinea-pig in vitro. J Physiol 428: 61–77, 1990. doi: 10.1113/jphysiol.1990.sp018200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mongillo G, Rumpel S, Loewenstein Y. Intrinsic volatility of synaptic connections – a challenge to the synaptic trace theory of memory. Curr Opin Neurobiol 46: 7–13, 2017. doi: 10.1016/j.conb.2017.06.006. [DOI] [PubMed] [Google Scholar]
- Moser EI, Moser MB, Roudi Y. Network mechanisms of grid cells. Philos Trans R Soc Lond B Biol Sci 369: 20120511, 2014. doi: 10.1098/rstb.2012.0511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murthy VN. Synaptic plasticity: step-wise strengthening. Curr Biol 8: R650–R653, 1998. doi: 10.1016/S0960-9822(07)00414-9. [DOI] [PubMed] [Google Scholar]
- Nimchinsky EA, Sabatini BL, Svoboda K. Structure and function of dendritic spines. Annu Rev Physiol 64: 313–353, 2002. doi: 10.1146/annurev.physiol.64.081501.160008. [DOI] [PubMed] [Google Scholar]
- Paz JT, Huguenard JR. Microcircuits and their interactions in epilepsy: is the focus out of focus? Nat Neurosci 18: 351–359, 2015. doi: 10.1038/nn.3950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeiffer T, Poll S, Bancelin S, Angibaud J, Inavalli VK, Keppler K, Mittag M, Fuhrmann M, Nägerl UV. Chronic 2P-STED imaging reveals high turnover of dendritic spines in the hippocampus in vivo. eLife 7: e34700, 2018. doi: 10.7554/eLife.34700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poirazi P, Mel BW. Impact of active dendrites and structural plasticity on the memory capacity of neural tissue. Neuron 29: 779–796, 2001. doi: 10.1016/S0896-6273(01)00252-5. [DOI] [PubMed] [Google Scholar]
- Richards BA, Frankland PW. The persistence and transience of memory. Neuron 94: 1071–1084, 2017. doi: 10.1016/j.neuron.2017.04.037. [DOI] [PubMed] [Google Scholar]
- Roxin A, Fusi S. Efficient partitioning of memory systems and its importance for memory consolidation. PLOS Comput Biol 9: e1003146, 2013. doi: 10.1371/journal.pcbi.1003146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin A, Geva N, Sheintuch L, Ziv Y. Hippocampal ensemble dynamics timestamp events in long-term memory. eLife 4: e12247, 2015. doi: 10.7554/eLife.12247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sargolini F, Fyhn M, Hafting T, McNaughton BL, Witter MP, Moser MB, Moser EI. Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science 312: 758–762, 2006. doi: 10.1126/science.1125572. [DOI] [PubMed] [Google Scholar]
- Stensola H, Stensola T, Solstad T, Frøland K, Moser MB, Moser EI. The entorhinal grid map is discretized. Nature 492: 72–78, 2012. doi: 10.1038/nature11649. [DOI] [PubMed] [Google Scholar]
- Stettler DD, Yamahachi H, Li W, Denk W, Gilbert CD. Axons and synaptic boutons are highly dynamic in adult visual cortex. Neuron 49: 877–887, 2006. doi: 10.1016/j.neuron.2006.02.018. [DOI] [PubMed] [Google Scholar]
- Stevens JL, Law JS, Antolík J, Bednar JA. Mechanisms for stable, robust, and adaptive development of orientation maps in the primary visual cortex. J Neurosci 33: 15747–15766, 2013. doi: 10.1523/JNEUROSCI.1037-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson LT, Best PJ. Long-term stability of the place-field activity of single units recorded from the dorsal hippocampus of freely behaving rats. Brain Res 509: 299–308, 1990. doi: 10.1016/0006-8993(90)90555-P. [DOI] [PubMed] [Google Scholar]
- Trachtenberg JT, Chen BE, Knott GW, Feng G, Sanes JR, Welker E, Svoboda K. Long-term in vivo imaging of experience-dependent synaptic plasticity in adult cortex. Nature 420: 788–794, 2002. doi: 10.1038/nature01273. [DOI] [PubMed] [Google Scholar]
- Trommald M, Hulleberg G. Dimensions and density of dendritic spines from rat dentate granule cells based on reconstructions from serial electron micrographs. J Comp Neurol 377: 15–28, 1997. doi:. [DOI] [PubMed] [Google Scholar]
- Tropea D, Majewska AK, Garcia R, Sur M. Structural dynamics of synapses in vivo correlate with functional changes during experience-dependent plasticity in visual cortex. J Neurosci 30: 11086–11095, 2010. doi: 10.1523/JNEUROSCI.1661-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner DA, Schwartzkroin PA. Electrical characteristics of dendrites and dendritic spines in intracellularly stained CA3 and dentate hippocampal neurons. J Neurosci 3: 2381–2394, 1983. doi: 10.1523/JNEUROSCI.03-11-02381.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turrigiano GG. The self-tuning neuron: synaptic scaling of excitatory synapses. Cell 135: 422–435, 2008. doi: 10.1016/j.cell.2008.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Hooser SD, Escobar GM, Maffei A, Miller P. Emerging feed-forward inhibition allows the robust formation of direction selectivity in the developing ferret visual cortex. J Neurophysiol 111: 2355–2373, 2014. doi: 10.1152/jn.00891.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang G, Pan F, Gan WB. Stably maintained dendritic spines are associated with lifelong memories. Nature 462: 920–924, 2009. doi: 10.1038/nature08577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu H, Majewska AK, Sur M. Rapid experience-dependent plasticity of synapse function and structure in ferret visual cortex in vivo. Proc Natl Acad Sci USA 108: 21235–21240, 2011. doi: 10.1073/pnas.1108270109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ziv Y, Burns LD, Cocker ED, Hamel EO, Ghosh KK, Kitch LJ, El Gamal A, Schnitzer MJ. Long-term dynamics of CA1 hippocampal place codes. Nat Neurosci 16: 264–266, 2013. doi: 10.1038/nn.3329. [DOI] [PMC free article] [PubMed] [Google Scholar]