Significance
Hole hopping pathways consisting of redox-active amino acids are proposed to direct potentially damaging holes away from active sites of proteins to the protein surface where they may be neutralized. We developed an approach to rapidly identify hole hopping pathways and to quantify the timescale for their shepherding of holes to the protein surface. Using this theoretical methodology, we identify the dominant hopping pathways in cytochrome P450, cytochrome c peroxidase, and benzylsuccinate synthase (BSS). Hopping pathways that involve a high-potential [4Fe4S] cluster as the terminal hole acceptor in BSS were identified to be accessible on a millisecond timescale, highlighting a [4Fe4S] cluster that is kinetically poised to play an oxidative damage protective role in a protein.
Keywords: electron-hole transfer, protein, oxidative damage, redox hopping pathway
Abstract
A recently proposed oxidative damage protection mechanism in proteins relies on hole hopping escape routes formed by redox-active amino acids. We present a computational tool to identify the dominant charge hopping pathways through these residues based on the mean residence times of the transferring charge along these hopping pathways. The residence times are estimated by combining a kinetic model with well-known rate expressions for the charge-transfer steps in the pathways. We identify the most rapid hole hopping escape routes in cytochrome P450 monooxygenase, cytochrome c peroxidase, and benzylsuccinate synthase (BSS). This theoretical analysis supports the existence of hole hopping chains as a mechanism capable of providing hole escape from protein catalytic sites on biologically relevant timescales. Furthermore, we find that pathways involving the [4Fe4S] cluster as the terminal hole acceptor in BSS are accessible on the millisecond timescale, suggesting a potential protective role of redox-active cofactors for preventing protein oxidative damage.
Proteins that incorporate oxygen into organic substrates from molecular oxygen and other potent oxidants, such as H2O2, are vital to biological function. In fact, these oxidants are often short-lived products of cellular biochemical reactions. Redox reactions involving these oxidants are susceptible to forming reactive oxygen species (ROS), which can lead to oxidative damage of DNA and proteins (1). ROS damage in proteins can manifest as backbone oxidation (2), protein fragmentation (2), or amino acid side-chain oxidation; cysteine, methionine, tryptophan, and tyrosine are the most susceptible to oxidation (3, 4). For example, tyrosine oxidation can promote dityrosine-linked aggregate formation in the eye lens protein γβ-crystallin, tertiary structure destabilization, and cataractogenesis (5). Studies also link the effects of ROS damage to aging complications and to cancer (2). Protein oxidation can lead to unfolding and, ultimately, to the loss of function (6). Although proteasomes and lysosomes help to degrade damaged proteins (2), the accumulation of oxidized protein can contribute to Alzheimer’s disease and diabetes (7). Here, we describe a computational method to identify hole hopping chains and to estimate the timescale with which these pathways may convey otherwise damaging oxidizing equivalents to a protein surface where they may be reduced by diffusible reducing species.
Recent studies (3, 4, 8) investigated a ROS protective mechanism that may act within monooxygenases, dioxygenases, and peroxidases. The authors proposed that chains of redox-active amino acids, including Tyr, Trp, Cys, and Met (SI Appendix, Figs. S1 and S2), can support hole hopping to direct strongly oxidizing electron holes to the protein surface in the absence of the enzyme substrate (3, 9), thus preventing damage to the protein active site. Once the excess charge is diverted to the exterior of the protein, reductants within the cell may be able to fill the holes. This hypothesis regarding molecular approaches to “defusing redox bombs” (10) was supported by a study of the Research Collaboratory for Structural Bioinformatics Protein Data Bank (PDB) (3), which revealed that one-third of the surveyed proteins contained chains of 3 to 5 aromatic amino acids, with the highest occurrence in redox proteins such as oxidoreductases and hydrolases (3).
In addition to protecting redox-active sites from oxidative damage, hole hopping pathways could also act to safeguard proteins from labilized hemes that may be produced in overoxidized proteins like cytochrome c peroxidase (Ccp1). Labilized heme may be produced when H2O2 levels in Ccp1 (e.g., from Saccharomyces cerevisiae) increase ∼10-fold with yeast respiration; in this mechanism, Ccp1 is activated via irreversible oxidation of the axial H175 ligand to transfer its heme to apo-catalase A, after which apo-Ccp1 escapes the mitochondria (11, 12). Irreversible oxidation of heme can therefore take place when H2O2 levels are high and hole escape routes are absent (12).
Solvent-exposed high-potential [4Fe4S]2+/3+ clusters may serve as terminal hole acceptors for a through-protein oxidative damage protection chain (13). Although it was initially proposed that the Gly829• radical cofactor could be reduced by the [4Fe4S]2+ cluster in the glycyl radical enzyme benzylsuccinate synthase (BSS) (14), the 31.2-Å edge-to-edge separation between Gly829• and the cluster (PDB ID code 4PKF) suggested that this distance could not enable a hole transfer (HT)-based protective mechanism (15). Despite the large transfer distance, experimental studies of other proteins (4) indicate that this HT reaction may be accessible. Electron tunneling over distances of 15 to 20 Å can occur on a nanosecond to microsecond timescale in iron and copper proteins (3, 4), and hopping (multistep tunneling) can enable charge transfer (CT) over longer distances on a submillisecond timescale when the free-energy profile is favorable (16).
The informatic–computational approach described here is implemented in the EHPath Python code (see Materials and Methods and SI Appendix) and is used to identify the fastest hole hopping routes that may limit ROS formation in cytochrome P450 (from Bacillus megaterium, P450BM3), Ccp1, and BSS. This methodology can be used more broadly for rapid database screening in the context of oxidative protection pathways and can also be used to explore hole hopping in signaling pathways that are proposed in protein–nucleic acid complexes (17, 18).
Results and Discussion
We tested the EHPath code by replicating the hopping pathways and mean residence times identified in earlier analysis (see Table 1 of ref. 17). The computations also identified weaker hole hopping routes that can be accessed on biologically relevant timescales, highlighting the capability of EHPath to map charge hopping routes in proteins.
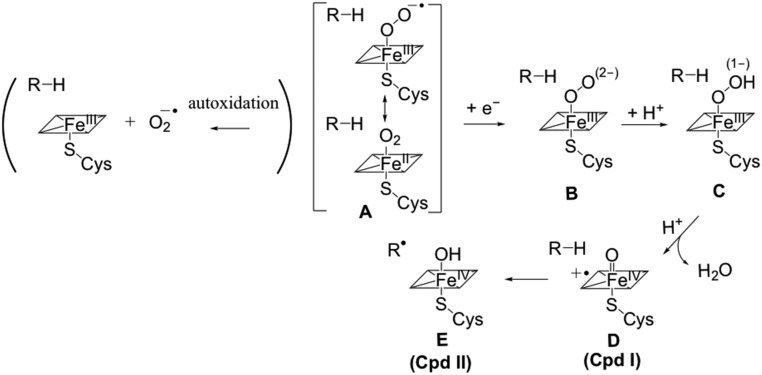
Next, we examined the hopping routes in the heme domain of P450BM3, a bacterial class II cytochrome P450 protein that catalyzes alkane hydroxylation. Cytochrome P450 is a known producer of ROS when the Fe-coordinated O2 remains in the oxidized state in the absence of a substrate (19, 20). In this protein, hole hopping pathways could divert holes from compound I (species D in Fig. 1) to the protein surface, thus preventing ROS formation. In the presence of a substrate, these hopping pathways should not enable hole escape on the timescale for the conversion of compound I to compound II (D to E, Fig. 1). Ab initio molecular dynamics simulations have found that D is converted to E in ∼ 0.1 ps (21). Thus, protective HT to the protein surface should not approach this timescale, lest it defeat normal enzyme function, but could be useful to prevent ROS formation from compound I in the absence of substrate (the R–H substrate shown in Fig. 1 is not considered explicitly in our analysis, as it is not involved in hole hopping pathways). Two hole hopping pathways to the protein surface were proposed in P450BM3 (PDB ID code 2IJ2) (4) (Fig. 2). Distance-based arguments suggested that Pathway 1 would support faster hole hopping (4).
Fig. 1.
Part of the catalytic cycle of cytochrome P450. The cycle begins with substrate entry to the active site (55), displacing an axial water, driving a low-to-high spin conversion at the metal center that causes the iron(III) center to dome the heme and enabling the heme’s action as an electron sink for the reductase domain (55). When the iron center is reduced from Fe(III) to Fe(II), O2 can bind to the iron center to generate the superoxy form of the enzyme, A (55). This species can undergo converting species A to a 5-coordinate Fe(III) complex and a superoxide anion at a rate of about 0.1 s−1 (55, 56) (indicated in the parentheses). Species A can avoid this fate by being converted into species B by electron transfer from the reductase domain at a rate faster than 99 s−1 in wild-type cytochrome P450BM3 (24, 55, 56). This step is followed by proton transfer to B, to form species C. A second proton transfer results in an iron-oxo radical cation D (compound I) and a water molecule. Then, D abstracts a hydrogen atom from the substrate to form a Fe(IV)-hydroxide intermediate E (57). The substrate radical subsequently abstracts hydroxyl radical from compound II, regenerating the resting [Fe(III)] state of the enzyme and oxidized substrate. The ligand-reduction step from A to B corresponds to the step from D to E in Figure 7 of ref. 55. The rate-determining step in the p450 catalytic cycle corresponds to the heme reduction step (i.e., the step from B to C in Figure 7 of ref. 55), which has a rate of 99 s−1 in the wild-type protein (see ref. 56). Therefore, the rate of the A-to-B step in Fig. 1 is larger than 99 s−1.
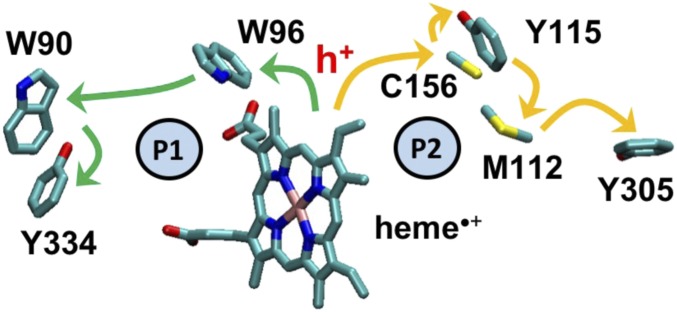
Fig. 2.
Probable routes for hole hopping from the active site of P450BM3 to the protein surface (4). Pathway 1 (P1, green arrows) is hemeW96W90Y334, with edge-to-edge distances (Ree) between the redox-active groups of 7.32 Å, 8.35 Å, and 4.45 Å, respectively, based on PDB structure 2IJ2. Ree was computed as the minimum distance between the heavy atoms for each redox-active site (i.e., porphyrin ring of heme, indole group of Trp, phenol group of Tyr, methanethiol moiety of Cys, and dimethyl sulfide in Met). Pathway 2 (P2, orange arrows) is hemeC156Y115M112Y305, with Ree values of 10.03 Å, 3.99 Å, 3.70 Å, and 5.19 Å, respectively. h+ denotes the hole that transfers from heme to W96 at the start of Pathway 1, or to C156 in Pathway 2, and the arrows indicate the direction of the protective hole transport.
EHPath was used to find the fastest predicted hole hopping routes with Y334 or Y305 as the terminal hole acceptor in P450BM3 (Fig. 2). The fastest HT route is established by Pathway 1 shown in Fig. 2 (the mean residence time of the charge on the route is τM = 3.7 × 10−2 s using Eqs. 1–3 and 5 in Materials and Methods). This HT route does not compete with the much faster conversion of D to E on the subpicosecond timescale (21) (Fig. 1). τM for Pathway 2 of Fig. 2 is 4.0 × 103 s (Table 1). Therefore, our results using EHPath exclude Pathway 2 (Fig. 2) as a plausible hole escape route.
Table 1.
Fastest 5 hole hopping routes in P450BM3
| Hole hopping pathways | τM, s | τSBT, s | τ′SBT, s |
| HEM-W96-W90-Y334 (P1) | 3.7 × 10−2 | 9.3 × 10−3 | 4.6 × 10−6 |
| HEM-Y115-Y305 | 6.1 × 10−2 | 1.9 × 10−2 | 6.1 × 10−6 |
| HEM-C156-Y115-Y305 | 1.4 × 10−1 | 7.7 × 10−2 | — |
| HEM-W96-Y334 | 4.2 × 10−1 | 5.7 × 10−2 | 9.6 × 10−6 |
| HEM-C156-Y305 | 1.5 × 101 | 6.7 | — |
| HEM-C156-Y115-M112-Y305 (P2) | 4.0 × 103 | 2.2 × 102 | — |
The heme is the hole donor and Y305 or Y334 is the terminal hole acceptor. The routes are ranked by the mean residence time τM (Eq. 5, with rates derived from Eq. 1 and from Eqs. 2 and 3). τSBT was similarly calculated using Eq. 4. τ′SBT also uses Eq. 4, but with the free-energy parameters of ref. 3.
Table 1 shows that the τ′SBT values (which are obtained using Eqs. 4 and 5, with the free-energy parameters suggested in ref. 3) differ from the corresponding τM values by 4 orders of magnitude, although both are in the range that would lead to protection on the relevant biological timescale. The difference is a consequence of the large differences between the individual forward HT rates (SI Appendix, Table S2), resulting from the use of different free-energy parameters in the 2 estimates of the timescale for hole escape. τM and τSBT, computed using rates derived from Eqs. 1 and 4 (Materials and Methods), respectively, use the same ∆G° and values and are therefore in much closer agreement; this reflects the similar conclusions derived from using Eqs. 1 and 4. Importantly, irrespective of the specific model used for the nearest-neighbor hopping rate, we reach the same conclusion that the fastest hole escape routes are predicted to function on reasonable biological timescales (probably within the ranges shown in Table 1) and will not interfere with the catalytic function. The closer agreement between the τM and τSBT values (compared with τM and τ′SBT values) results from using the same ∆G° and values in the expressions for the mean residence times. Our theoretical finding that path 1 is the most probable oxidative damage escape route is consistent with the experimental finding that W96•+ is a critical intermediate in the hole hopping of Ru-modified P450BM3 (8) [this amino acid is conserved in ∼75% of the cytochrome P450 species (3)].
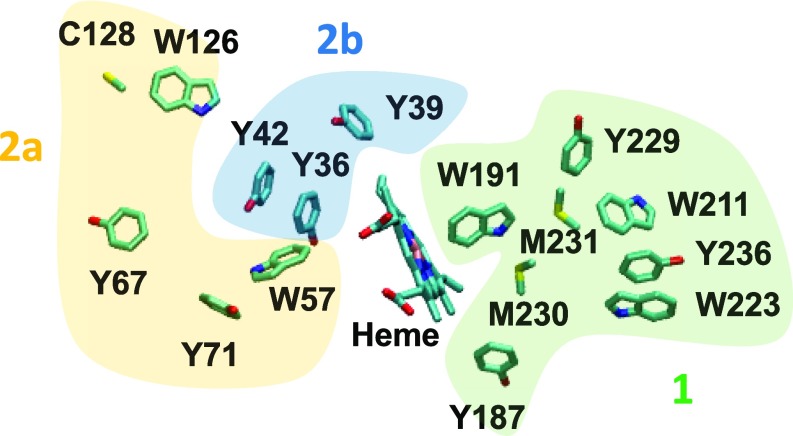
A recent experimental study (12) offers an excellent framework in which to analyze the hole hopping routes that may prevent oxidative damage to the heme in Ccp1 of S. cerevisiae [PDB ID code 1ZBY (22)]). Ref. 12 identifies protein zones with different densities of residues that can be oxidized by hole hopping from the heme. The 3 main zones are shown in Fig. 3: Zone 1 contains the highest percentage of oxidizable amino acid residues, followed by zones 2a and 2b.
Fig. 3.
Redox-active residues (C, M, W, Y) in zone 1 (green), 2a (yellow), and 2b (blue) of Ccp1 [PDB ID code 1ZBY (22)]. The zones lowest in oxidizable residues (zones 3 and 4 of ref. 12) are not shown.
We find that 17 of the 20 fastest hole hopping pathways terminate in zone 1 (SI Appendix, Table S3), providing theoretical support for the experimental data interpretation of ref. 12 (8 residues of the 24 oxidized residues in Ccp1 identified from liquid chromatography tandem mass spectrometry analysis were mapped into zone 1, while the 16 other residues were distributed across zones 2a, 2b, 3, and 4). We also identify W191 as a key residue in 4 of the top 5 hole hopping routes. Even using the large reorganization energies when estimating τM, we find that a hole can transfer from the heme to Y229, through W191, on a millisecond timescale (Table 2). This result is consistent with the experimental observation of a role for W191•+ in mediating CT between Ccp1 and cytochrome c (23), and the hypothesis that the charge would most likely migrate from W191•+ to a tyrosine residue (which is identified to be Y229 in our analysis) (24). Interestingly, comparisons of the hole hopping pathways listed in Tables 1 and 2 show that the fastest pathways in Ccp1 have smaller τM values than the fastest pathways in P450BM3. This difference may correlate with the differential functions of the 2 proteins. The main roles for Ccp1 are the oxidization of 2 ferrocytochrome c molecules through the initial 2-electron reduction of H2O2 (25), and the eventual transfer of its heme to catalase during respiration when large mitochondrial levels of H2O2 are present (11). In the absence of ferrocytochrome c molecules, the Ccp1 pathways listed in Table 2 can help protect the active site from irreversible oxidative damage (and heme cross-linking to W51) (26) produced by highly oxidizing H2O2; the protection of the active site integrity allows the subsequent transfer of undamaged heme to catalase A (12). The P450BM3 monooxygenase relies, instead, on the less strongly oxidizing O2 as the primary route to the hydroxylation of fatty acid substrates (27). Therefore, the reliance of P450BM3 on a weaker oxidant may require fewer and less rapid hole hopping routes for sufficient heme active site protection from oxidative damage in P450BM3 compared with the case with Ccp1.
Table 2.
Mean residence time τM of the hole for the 5 fastest hole hopping pathways in Ccp1 with selected terminal HT sites identified in ref. 12
| Hole hopping pathways | τM, s |
| HEM-W191-Y229 | 2.5 × 10−3 |
| HEM-W191-W211 | 2.5 × 10−3 |
| HEM-Y36 | 1.2 × 10−2 |
| HEM-Y187-W191-Y229 | 6.1 × 10−2 |
| HEM-Y187-W191-W211 | 6.1 × 10−2 |
Calculated using Eqs. 1 and 5 for the HT rates and Eqs. 2 and 3 for the free-energy parameters. Additional pathways are shown in SI Appendix, Table S3.
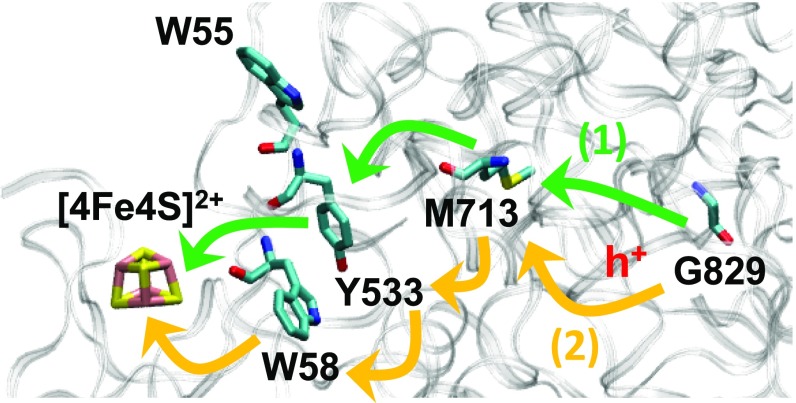
τM (Eq. 5 in Materials and Methods) and τM,approx (Eq. 6 in Materials and Methods) values for the top 5 hole hopping pathways between Gly829• and [4Fe4S]2+ in BSS appear in Table 3. These pathways involve the key residues highlighted in Fig. 4. Since the backward HT rates are negligible in these hopping pathways, Eq. 6 (Materials and Methods) provides an excellent approximation to the mean residence time (Table 3). The pathways from G829• to [4Fe4S]2+ via Y533, M713, and W58 are predicted to be traversed on a millisecond timescale (Table 3) despite their lengths (15), as a consequence of their downhill free-energy landscapes. Such landscapes dictate the unidirectional character of the hole transport to the iron–sulfur cluster, which is quantified by the very similar τM and τM,approx values in Table 3. Since our analysis demonstrates that [4Fe4S]2+ may reduce G829• [note that the G829• reduction potential used in our analysis accounts for the coupled proton transfer (28)], the iron–sulfur cluster could act as a reducing agent in other systems [e.g., in the experimentally observed reversible reduction of the Gly radical in pyruvate formate lyase, another glycyl radical enzyme (15, 29)]. The BSSβ small subunit of BSS can coordinate a [4Fe4S] cluster by adopting a local folding similar to that of high-potential [4Fe4S] proteins (15). However, in contrast to the latter, BSSβ does not provide the substantial shielding from the solvent that stabilizes [4Fe4S]3+ (15). This fact, and the thermodynamic driving force that prevents the hole from returning to the protein, might cause the iron–sulfur cluster to serve as a transient hole trap before hole delivery outside of a protein.
Table 3.
Mean residence times τM (Eq. 5) and τM,approx (Eq. 6) of the hole in the 5 fastest hole-hopping escape pathways of BSS, where Gly829• is the initial hole donor and [4Fe4S]2+ is the final hole acceptor
| Hole hopping pathways | τM, s | τM,approx, s |
| G829-M713-Y533-[4Fe4S] (1) | 4.5 × 10−3 | 4.5 × 10−3 |
| G829-M713-Y533-W58-[4Fe4S] (2) | 4.5 × 10−3 | 4.5 × 10−3 |
| G829-M713-W55-[4Fe4S] | 7.8 × 10−3 | 7.8 × 10−3 |
| G829-M713-W55-Y533-[4Fe4S] | 8.0 × 10−3 | 8.0 × 10−3 |
| G829-M713-W55-W531-[4Fe4S] | 1.0 × 10−2 | 9.1 × 10−3 |
Pathways 1 and 2 are delineated in Fig. 4.
Fig. 4.
Locations of the BSS redox-active residues involved in the 5 most rapid hole hopping routes from G829• to the terminal hole acceptor [4Fe4S]2+ (Table 3). The 2 fastest paths (1) and (2) are highlighted with green and orange arrows, respectively.
In a previous study, we showed that through-protein HT from an oxidized system (a nucleic acid double strand) to high-potential [4Fe4S] clusters may generally occur on a millisecond to microsecond timescale (17). This theoretical result agrees with previous experimental findings on the viability of redox signaling involving [4Fe4S] proteins relevant to DNA replication and repair (18, 30). The present analysis may indicate an (additional) example of ET function associated with iron–sulfur clusters.
Concluding Remarks
The HT kinetic modeling and analysis incorporated in the EHPath program allow us to identify, assess, and understand the role of hole hopping pathways as oxidative damage escape routes in 3 important biological systems, taking into account microscopic models for the HT rates among hopping stations. The quantitative results of this theoretical study support the general viability of the proposed hole-transfer protective mechanism in redox proteins (3, 4). Our analysis identifies the predicted dominant hole escape route in P450BM3. We find that the mean residence time computed for the charge on the fastest pathway is sufficiently rapid to be biologically relevant (and thus to help preventing ROS formation in the absence of substrate) and is longer than the timescale of the functional transition from the iron-oxo radical cation D to the Fe(IV)-hydroxide complex E in the presence of the substrate. The identification of W191 as a key site for hole hopping away from the active site in Ccp1 and the termination of the most rapid hopping are both consistent with the EPR spectral signature of W191•+ (12, 23). A [4Fe4S] cluster can serve as the terminal hole acceptor in BSS, reducing the Gly radical through hopping pathways that involve the M713, Y533, and W58 residues. The software and modeling described here provide a robust approach to map and to characterize CT hopping pathways.
Mutational studies of P450BM3, Ccp1, and BSS, combined with transient dynamical studies, would help to evaluate the hole escape routes explored here. For example, the Y533 residue in BSS, which is shared between the 2 fastest hole hopping pathways (Table 3), may be mutated to a structurally similar Phe residue to examine the robustness and detailed pathway of the oxidation protection mechanism in BSS. As well, W90, which appears in pathway P1 of P450BM3, may be mutated to His to explore the importance of the W90 residue for mediating hole escape.
Our approach should enable further studies of hopping pathways in proteins, DNA, and protein–DNA complexes, including the primase–polymerase complex (17, 18). Future applications of this approach to oxygen-utilizing/evolving proteins, including ribonucleotide reductase, cytochrome c oxidase, and photosystem II (3), may help to reveal how nature has evolved charge hopping protection mechanisms.
Materials and Methods
We investigated hopping routes for P450BM3, Ccp1, and BSS with transit times on biologically relevant timescales using the search program described here (EHPath). The program identifies hole hopping routes and estimates the timescale for hole hopping transfer or escape. The Python-based program implements a kinetic model (17) outlined below. EHPath allows the choice of electron transfer kinetic parameters. The fastest hole escape routes (or, more generally, CT routes) are identified, and the transit time is estimated. Estimates of these times allow us to resolve the outstanding question of whether such hopping paths could establish viable signaling or oxidative damage protection mechanisms. The viability of the [4Fe4S] clusters to serve as hole traps in BSS is addressed, and the biological relevance of the differences in the escape times for P450BM3 and Ccp1 are discussed.
The HT rate constant kDA for each donor (D)–acceptor (A) pair in an HT route was estimated using the nonadiabatic CT rate expression in the high-temperature (Marcus) limit (31):
| [1] |
Here, is the effective electronic coupling between the charge states localized on D and A, is the reaction free energy, is the reorganization energy, and is the temperature. The reorganization energy for each CT step was approximated as in refs. 32 and 33:
| [2] |
Here, and are the reorganization energies for nonadiabatic self-exchange weak-overlap reactions in the D–D and A–A redox pairs, respectively. The contribution of redox species S (S = D, A) to the reorganization energy, , is defined as half of the reorganization energy for self-exchange in the S–S system. The values for the redox-active residues and cofactors at the relevant center-to-center distances were derived from available literature values at selected center-to-center distances (summarized in SI Appendix, Table S1) (34) via the following equation (17):
| [3] |
Here, and are the optical [2.2 (35)] and static [4.0 (17, 35–37)] dielectric constants describing the environments of the D and A species, and is the transferring charge (equal to the magnitude of the electron charge here). To define the D and A moieties, the redox-active amino acids Cys, Met, Tyr, and Trp were truncated from their amide backbones and represented as methanethiol, thioether, phenol, and indole, respectively. Then, the D and A centers were defined as the averages of the heavy atom PDB coordinates in the truncated moieties. was calculated as the distance between the D and A centers.
∆G° for the HT step from D to A was computed from the difference of the A and D oxidation potentials (SI Appendix, Table S1). The oxidation potentials for the redox groups in this study were obtained as described in ref. 17, while the oxidation potential for heme was taken from ref. 3. was estimated using Hopfield’s equation 38 (SI Appendix, Eq. S2) for the amino acid residues and other semiempirical methods were used to estimate couplings for the heme (SI Appendix, Eq. S3) and iron–sulfur cluster (SI Appendix, Eq. S4) cofactors. Use of these semiempirical methods is justified and motivated by the following considerations: 1) the electronic coupling values previously obtained using semiempirical methods showed acceptable order of magnitude agreement with more accurate DFT results (17); 2) the aim here is to accomplish qualitative rapid screening of hopping pathways in large protein databases; and 3) the order of magnitude timescales computed for hole delivery to a protein surface do not depend strongly on the method used to compute the electronic couplings, while they can depend more critically on the free-energy parameters, as is shown in Table 1 (without changing the conclusions of our analysis).
Points 1 through 3, taken together, justify our use of semiempirical approaches to electronic coupling computations for rapid screening of vast databases with reasonable accuracy. However, more accurate evaluations of the CT parameters (including the electronic couplings) for specific systems are needed to discriminate between HT pathways relevant to the chemical function whose speeds differ by a few orders of magnitude. A starting point to improve on the coupling computation is proposed in ref. 17, where the ab initio calculation of the couplings for gas-phase redox-active groups is combined with a semiempirical treatment of the intervening medium.
Molecular motion may influence protein geometries and the nature of the predicted hopping pathways; if conformational changes are particularly large, these geometry changes may gate the hopping process, just as gating motions may limit single-step tunneling (39). Nonetheless, such motion is unlikely to affect the general conclusions on the feasibility of the identified charge-transport mechanisms, while the details of some pathways could change (17, 40).
We compared the kDA values of Eq. 1 with values obtained using the empirical square barrier tunneling (SBT) rate expression (3),
| [4] |
In Eq. 1, is a D–A contact distance of 3 Å, is the D–A edge-to-edge distance, and is the distance decay factor (1.1 Å−1) for the D–A electronic coupling (41). The prefactor of 1013 s−1 was fit to kinetic measurements in Ru-modified azurins (41–43). Rather than calculating the Marcus free-energy parameters for every HT step (SI Appendix, Eqs. 2–4 and Figs. S2–S4), ref. 3 used approximate values for Tyr and Trp hopping in heme proteins: = 0.8 eV, eV for HT from the heme to Trp or Tyr, eV for the intermediate HT step(s), and eV for the final HT to the terminal Trp or Tyr residue (3). This simple parameter choice was used with Eq. 4 to analyze Tyr/Trp hopping pathways. The simplicity of Eq. 4 enables the rapid evaluation of the CT rate constants. Comparing the results from different CT parameter choices and models (i.e., Eqs. 1 and 4), we will examine the robustness of the hopping pathway analysis.
Previous studies (34, 44) found that the reorganization energy for HT between redox-active residues can be much larger than 0.8 eV. One expects (45, 46) larger values because the size of the redox active groups is much smaller for amino acid residues than for most protein cofactors. Indeed, the values for HT between amino acids are computed to range from 1.38 eV to 2.04 eV (see the appendix Table S6 of ref. 17), while experimental estimates of for these systems are yet to be determined. We will explore the sensitivity of our conclusions regarding the dominant hole escape pathways and timescales as we change the reorganization energy from ∼0.8 eV to significantly higher values, up to ∼2 eV, predicted using Eq. 3 in conjunction with theoretical estimates in the literature (see refs. 34, 47, and 48 for further discussion of the reorganization energy parameters). The EHPath program allows the user to define in such ranges for all D–A pairs.
We calculated the mean residence time τ of the transferring charge in each pathway (i.e., the inverse of the effective start-to-finish transfer rate) by inserting the kDA or kSBT values into the expression (17)
| [5] |
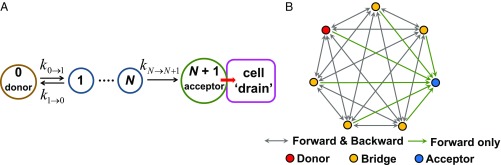
Eq. 5 is directly applied to the hole (i.e., hole occupation probabilities are used in the kinetic model). N is the total number of redox-active bridge sites in a pathway and is the rate constant for CT between consecutive redox sites for any given realization of Fig. 5B (i.e., for any given hopping pathway through a protein’s 3D network of possible hole hopping routes). = 0 denotes the initial charge donor, = 1 to N indicates intervening redox-active residues, and site = N + 1 is the terminal charge acceptor in contact with a charge “drain.” This kinetic model includes both forward and backward HT steps in the hopping pathway, except for the charge-transfer step between the last redox-active site in the protein and the terminal acceptor, which is irreversible due to rapid scavenging of the charge by redox agents in the cellular environment (17) (Fig. 5A). When all backward CT rates can be neglected (i.e., for 0 ≤ n < N), Eq. 5 reduces to the well-known expression (49)
| [6] |
Fig. 5.
(A) Kinetic model leading to Eq. 5 (17) (Materials and Methods). The cellular environment provides redox species that rapidly fill the hole that arrives at the final acceptor on the protein surface. Therefore, backward charge transfer from site N + 1 to site N cannot occur. (B) Structure of a directed graph representing hopping routes in a protein, where the nodes represent the initial charge donor site (red), the intermediate hopping sites (yellow), and the acceptor site (blue). As the acceptor is in contact with a charge “drain” in the kinetic model, there is no directed edge from acceptor to bridge (namely, no backward charge transfer to the bridge).
That is, the average time spent on the hopping chain by the transferring charge is approximately the sum of the mean residence times at the individual redox-active sites. Eq. 5 does not take into account the possibility of pathway branching, since the occupation probability of each redox group only depends on its coupling to the adjacent redox sites along a given HT pathway. We use this kinetic model since 1) the protein motion can decouple the HT pathways, so that a given escape route is realized each time and 2) branching would appreciably mix only the most rapid HT routes with similar mean residence times (through protein regions rich in redox-active amino acids) and would not change our assessment of the feasibility for oxidative damage protection on sufficiently rapid timescales. The kinetic model indicated in Fig. 5A (Eq. 5) and the pathway search indicated in Fig. 5B enable the fast screening of protein structural databases for proteins with possible protective structures and will identify the most probable hole escape route in most situations.
In the analysis, τM (τSBT) denotes the mean residence time (Eq. 5) obtained using the rate expression in Eq. 1 (Eq. 4), with the ∆G° values obtained from the oxidation potential differences and the reorganization energies of Eqs. 2 and 3. The mean residence times using the rate expression in Eq. 4, with free-energy parameters from ref. 3, are denoted τ′SBT. Since the estimates and analysis in ref. 3 were limited to pathways involving Tyr and Trp, we only calculated kSBT and τ′SBT for Tyr/Trp-based pathways.
The Pathways method to estimate bridge-mediated tunneling interactions uses graph theory to identify tunneling routes that maximize (50–52). Other CT pathway finders rely on quantum mechanics/molecular mechanics methods to identify tunneling pathways (53). EHPath focuses, instead, on the case of hopping transport. This hopping pathway finder 1) identifies bidirected graphs that correspond to specific protein structures, 2) estimates ΔG° and values for all hopping steps, and 3) calculates the mean times required for the charge hopping routes from D to A. The structure of a typical graph is shown in Fig. 5B. The rates for forward and reverse CT between nodes define the effective lengths of edges (in the 2 CT directions) in the corresponding graphs that are used in the minimum effective-length (minimum CT travel time) path search. The mean residence time for a charge hopping pathway is computed using Eq. 5 (Eq. 6 is also implemented) for user defined redox-active residues and cofactors (SI Appendix, section S4). The pathway search uses NetworkX, a python package for network analysis based on graph theory (54), to rank the hopping pathways based on mean residence time (SI Appendix, section S4).
Supplementary Material
Acknowledgments
This work was supported by National Institutes of Health Grant GM-48043, the Blue Waters sustained-petascale computing project (R.D.T.), National Science Foundation Awards OCI-0725070 and ACI-1238993, the State of Illinois, and National Science Foundation Grant CHE-1709497.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
Data deposition: The EHPath.py code can be accessed and downloaded at https://github.com/etransfer/EHPath.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1906394116/-/DCSupplemental.
References
- 1.Davies M. J., The oxidative environment and protein damage. Biochim. Biophys. Acta 1703, 93–109 (2005). [DOI] [PubMed] [Google Scholar]
- 2.Berlett B. S., Stadtman E. R., Protein oxidation in aging, disease, and oxidative stress. J. Biol. Chem. 272, 20313–20316 (1997). [DOI] [PubMed] [Google Scholar]
- 3.Gray H. B., Winkler J. R., Hole hopping through tyrosine/tryptophan chains protects proteins from oxidative damage. Proc. Natl. Acad. Sci. U.S.A. 112, 10920–10925 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Winkler J. R., Gray H. B., Electron flow through biological molecules: Does hole hopping protect proteins from oxidative damage? Q. Rev. Biophys. 48, 411–420 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kanwar R., Balasubramanian D., Structure and stability of the dityrosine-linked dimer of gammaB-crystallin. Exp. Eye Res. 68, 773–784 (1999). [DOI] [PubMed] [Google Scholar]
- 6.Hawkins C. L., Davies M. J., The role of aromatic amino acid oxidation, protein unfolding, and aggregation in the hypobromous acid-induced inactivation of trypsin inhibitor and lysozyme. Chem. Res. Toxicol. 18, 1669–1677 (2005). [DOI] [PubMed] [Google Scholar]
- 7.Stadtman E. R., Levine R. L., Free radical-mediated oxidation of free amino acids and amino acid residues in proteins. Amino Acids 25, 207–218 (2003). [DOI] [PubMed] [Google Scholar]
- 8.Ener M. E., Gray H. B., Winkler J. R., Hole hopping through tryptophan in cytochrome P450. Biochemistry 56, 3531–3538 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Choi M., Shin S., Davidson V. L., Characterization of electron tunneling and hole hopping reactions between different forms of MauG and methylamine dehydrogenase within a natural protein complex. Biochemistry 51, 6942–6949 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Polizzi N. F., Migliore A., Therien M. J., Beratan D. N., Defusing redox bombs? Proc. Natl. Acad. Sci. U.S.A. 112, 10821–10822 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kathiresan M., Martins D., English A. M., Respiration triggers heme transfer from cytochrome c peroxidase to catalase in yeast mitochondria. Proc. Natl. Acad. Sci. U.S.A. 111, 17468–17473 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kathiresan M., English A. M., LC-MS/MS suggests that hole hopping in cytochrome c peroxidase protects its heme from oxidative modification by excess H2O2. Chem. Sci. 8, 1152–1162 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Martins B. M., et al. , Structural basis for a Kolbe-type decarboxylation catalyzed by a glycyl radical enzyme. J. Am. Chem. Soc. 133, 14666–14674 (2011). [DOI] [PubMed] [Google Scholar]
- 14.Knappe J., Neugebauer F. A., Blaschkowski H. P., Gänzler M., Post-translational activation introduces a free radical into pyruvate formate-lyase. Proc. Natl. Acad. Sci. U.S.A. 81, 1332–1335 (1984). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Funk M. A., Judd E. T., Marsh E. N. G., Elliott S. J., Drennan C. L., Structures of benzylsuccinate synthase elucidate roles of accessory subunits in glycyl radical enzyme activation and activity. Proc. Natl. Acad. Sci. U.S.A. 111, 10161–10166 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gray H. B., Winkler J. R., Long-range electron transfer. Proc. Natl. Acad. Sci. U.S.A. 102, 3534–3539 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Teo R. D., et al. , Charge transfer between [4Fe4S] proteins and DNA is unidirectional: Implications for biomolecular signaling. Chem 5, 122–137 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.O’Brien E., et al. , The [4Fe4S] cluster of human DNA primase functions as a redox switch using DNA charge transport. Science 355, eaag1789 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gottlieb R. A., Cytochrome P450: Major player in reperfusion injury. Arch. Biochem. Biophys. 420, 262–267 (2003). [DOI] [PubMed] [Google Scholar]
- 20.Jezek P., Hlavatá L., Mitochondria in homeostasis of reactive oxygen species in cell, tissues, and organism. Int. J. Biochem. Cell Biol. 37, 2478–2503 (2005). [DOI] [PubMed] [Google Scholar]
- 21.Elenewski J. E., Hackett J. C., Ab initio dynamics of the cytochrome P450 hydroxylation reaction. J. Chem. Phys. 142, 064307 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bonagura C. A., et al. , High-resolution crystal structures and spectroscopy of native and compound I cytochrome c peroxidase. Biochemistry 42, 5600–5608 (2003). [DOI] [PubMed] [Google Scholar]
- 23.Payne T. M., Yee E. F., Dzikovski B., Crane B. R., Constraints on the radical cation center of cytochrome c peroxidase for electron transfer from cytochrome c. Biochemistry 55, 4807–4822 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Barrows T. P., Bhaskar B., Poulos T. L., Electrostatic control of the tryptophan radical in cytochrome c peroxidase. Biochemistry 43, 8826–8834 (2004). [DOI] [PubMed] [Google Scholar]
- 25.Volkov A. N., Nicholls P., Worrall J. A. R., The complex of cytochrome c and cytochrome c peroxidase: The end of the road? Biochim. Biophys. Acta 1807, 1482–1503 (2011). [DOI] [PubMed] [Google Scholar]
- 26.Murphy E. J., Metcalfe C. L., Basran J., Moody P. C. E., Raven E. L., Engineering the substrate specificity and reactivity of a heme protein: Creation of an ascorbate binding site in cytochrome c peroxidase. Biochemistry 47, 13933–13941 (2008). [DOI] [PubMed] [Google Scholar]
- 27.Lee D.-S., et al. , Substrate recognition and molecular mechanism of fatty acid hydroxylation by cytochrome P450 from Bacillus subtilis. Crystallographic, spectroscopic, and mutational studies. J. Biol. Chem. 278, 9761–9767 (2003). [DOI] [PubMed] [Google Scholar]
- 28.Armstrong D. A., Rank A., Yu D., Solution thermochemistry of the radicals of glycine. J. Chem. Soc. Perkin Trans. 2, 553–560 (1995). [Google Scholar]
- 29.Nnyepi M. R., Peng Y., Broderick J. B., Inactivation of E. coli pyruvate formate-lyase: Role of AdhE and small molecules. Arch. Biochem. Biophys. 459, 1–9 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Arnold A. R., Grodick M. A., Barton J. K., DNA charge transport: From chemical principles to the cell. Cell Chem. Biol. 23, 183–197 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Marcus R. A., Sutin N., Electron transfers in chemistry and biology. Biochim. Biophys. Acta 811, 265–322 (1985). [Google Scholar]
- 32.Marcus R. A., On the theory of oxidation-reduction reactions involving electron transfer. J. Chem. Phys. 67, 853–857 (1963). [Google Scholar]
- 33.Marcus R. A., Theoretical relations among rate constants, barriers, and Broensted slopes of chemical reactions. J. Phys. Chem. 72, 891–899 (1968). [Google Scholar]
- 34.Heck A., et al. , Charge transfer in model peptides: Obtaining Marcus parameters from molecular simulation. J. Phys. Chem. B 116, 2284–2293 (2012). [DOI] [PubMed] [Google Scholar]
- 35.Krishtalik L. I., Kuznetsov A. M., Mertz E. L., Electrostatics of proteins: Description in terms of two dielectric constants simultaneously. Proteins 28, 174–182 (1997). [PubMed] [Google Scholar]
- 36.Pethig R., Dielectric and Electronic Behavior of Biological Materials (John Wiley & Sons, New York, 1979). [Google Scholar]
- 37.Teo R. D., Smithwick E. R., Migliore A., Beratan D. N., A single AT-GC exchange can modulate charge transfer-induced p53-DNA dissociation. Chem. Commun. (Camb.) 55, 206–209 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hopfield J. J., Electron transfer between biological molecules by thermally activated tunneling. Proc. Natl. Acad. Sci. U.S.A. 71, 3640–3644 (1974). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Davidson V. L., Protein control of true, gated, and coupled electron transfer reactions. Acc. Chem. Res. 41, 730–738 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Goodpaster J. D., Theoretical chemistry answers bimolecular signaling debate in [4Fe4S] proteins. Chem 5, 12–14 (2019). [Google Scholar]
- 41.Langen R., et al. , Electron tunneling in proteins: Coupling through a beta strand. Science 268, 1733–1735 (1995). [DOI] [PubMed] [Google Scholar]
- 42.Winkler J. R., Gray H. B., Electron flow through metalloproteins. Chem. Rev. 114, 3369–3380 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Regan J. J., et al. , Electron tunneling in azurin: The coupling across a β-sheet. Chem. Biol. 2, 489–496 (1995). [DOI] [PubMed] [Google Scholar]
- 44.Zhao Y.-Y., Ma J.-Y., Zhao X.-J., Li X.-Y., Solvent reorganization energy of intramolecular electron transfer in peptides involving tryptophan and tyrosine. Chin. J. Chem. 26, 2003–2008 (2008). [Google Scholar]
- 45.Petersen R. A., Evans D. H., Heterogeneous electron-transfer kinetics for a variety of organic electrode-reactions at the mercury acetonitrile interface using either tetraethylammonium perchlorate or tetraheptylammonium perchlorate electrolyte. J. Electroanal. Chem. Interfacial Electrochem. 222, 129–150 (1987). [Google Scholar]
- 46.Migliore A., Nitzan A., Nonlinear charge transport in redox molecular junctions: A Marcus perspective. ACS Nano 5, 6669–6685 (2011). [DOI] [PubMed] [Google Scholar]
- 47.Kubar T., Elstner M., Solvent reorganization energy of hole transfer in DNA. J. Phys. Chem. B 113, 5653–5656 (2009). [DOI] [PubMed] [Google Scholar]
- 48.Khan A., Reorganization, activation and ionization energies for hole transfer reactions through inosine-cytosine, 2-aminopurine-thymine, adenine-thymine, and guanine-cytosine base pairs: A computational study. Comput. Theor. Chem. 1013, 136–139 (2013). [Google Scholar]
- 49.Leake M. C., Single-Molecule Cellular Biophysics (Cambridge University Press, 2013). [Google Scholar]
- 50.Balabin I. A., Hu X., Beratan D. N., Exploring biological electron transfer pathway dynamics with the Pathways plugin for VMD. J. Comput. Chem. 33, 906–910 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Beratan D. N., Betts J. N., Onuchic J. N., Protein electron transfer rates set by the bridging secondary and tertiary structure. Science 252, 1285–1288 (1991). [DOI] [PubMed] [Google Scholar]
- 52.Betts J. N., Beratan D. N., Onuchic J. N., Mapping electron-tunneling pathways–An algorithm that finds the minimum length maximum coupling pathway between electron-donors and acceptors in proteins. J. Am. Chem. Soc. 114, 4043–4046 (1992). [Google Scholar]
- 53.Guallar V., Wallrapp F., Mapping protein electron transfer pathways with QM/MM methods. J. R. Soc. Interface 5 (suppl. 3), S233–S239 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Hagberg A., Swart P., Schult D., “Exploring network structure, dynamics, and function using networkx” (Los Alamos National Laboratory, Los Alamos, NM, 2008).
- 55.Meunier B., de Visser S. P., Shaik S., Mechanism of oxidation reactions catalyzed by cytochrome p450 enzymes. Chem. Rev. 104, 3947–3980 (2004). [DOI] [PubMed] [Google Scholar]
- 56.Ost T. W. B., et al. , Oxygen activation and electron transfer in flavocytochrome P450 BM3. J. Am. Chem. Soc. 125, 15010–15020 (2003). [DOI] [PubMed] [Google Scholar]
- 57.Huang X., Groves J. T., Oxygen activation and radical transformations in heme proteins and metalloporphyrins. Chem. Rev. 118, 2491–2553 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.