Collective sinking promotes selective cell pairing in planktonic pennate diatoms

Significance

Planktonic pennate diatoms are a ubiquitous group of microalgae playing a major role as primary producers in aquatic ecosystems. Some species are also known to produce domoic acid, a neurotoxin that causes shellfish poisoning. Their reproduction is mostly accomplished through rapid clonal cell division, but eventual sexual exchange is required for population survival. How do nonswimming organisms find their partners in the water column? We demonstrate that planktonic pennate cells need to sink from surface turbulent waters to more stable environments where encounter rates, and thus pairing for sexual reproduction, are facilitated by viscous torques and collective interactions. This mechanism is key in our understanding of pennate diatom population dynamics and could help to improve prediction of some toxicity episodes.

Abstract

Finding a partner in an inherently unsteady 3-dimensional system, such as the planktonic marine environment, is a difficult task for nonswimming organisms with poor control over their orientation. We experimentally investigate the process of cell pairing in pennate marine diatoms and present field evidence of its occurrence in the ocean. We describe the mechanism as a 3-step process in which pennate diatoms (i) vertically reorient while sinking from surface turbulent waters to a more stable environment (i.e., under the seasonal pycnocline), (ii) segregate from incompatible partners (e.g., dead or different sized cells), and (iii) pair with other partners as a result of the hydrodynamic instabilities generated by collective cell sinking. This is, eminently, a cell abundance-dependent process, therefore being more effective when population sinking is synchronized. We suggest that this selective process, enabling matching of size-compatible healthy partners, could be fundamental in understanding sexual reproduction in pennate diatoms.

Diatoms are a ubiquitous nonmotile phytoplankton group present in most water bodies that play a fundamental role in ocean ecology and global biogeochemical cycles (1, 2). They are distinguished by being encased inside 2 ornamented silica cell shells (frustules) that conform to their body (3). Diatoms are by far the most successful lineages of eukaryotic phytoplankton, not only in numbers of species but also in amount of biomass and in their contribution to global inorganic carbon fixation in the ocean (4) due to their highly efficient CO₂ uptake mechanism (5). Indeed, it is estimated that this eukaryotic microalgal group is responsible for ∼20% of the net primary production in the ocean and up to 50% of the organic carbon exported to the ocean interior (6, 7).

Diatom populations undergo periods of rapid growth in turbulent and nutrient-rich environments, often dominating phytoplankton assemblages in high latitudes and coastal areas (8, 9). These “blooms” are normally terminated by rapid mass sinking when environmental conditions become unfavorable, contributing greatly to the vertical fluxes in the ocean (10). Opportunistic dominance of phytoplankton assemblages by diatoms is mostly accomplished through a prolonged period of vegetative cell division (asexual phase) when the parental cell produces 2 daughter cells (11). This clonal reproduction via mitosis is generally characterized by a progressive reduction in the mean cell size of a population imposed by their rigid frustule. Therefore, after successive vegetative divisions, the size decreases below a certain threshold known as the first cardinal point [30 to 75% of initial size (3, 12)]. To avoid mortality, the maximal size is typically restored by auxospore formation during obligated, but episodically occurring, sexual reproduction. This short sexual stage also has important benefits in terms of genetic recombination, elimination of deleterious mutations, and evolutionary adaptation (13, 14). Therefore, sporadic sexual mating events are a critical period determining the ecological dynamics of diatoms (11), and their failure during prolonged periods (i.e., a few years) can result in extinction of local populations (15).

Regarding the frustule morphology, 2 major morphological groups are prevalent: centric forms with disk-like bodies (radial symmetry) and elongated (bilaterally symmetrical) pennate diatoms (16, 17). Beyond their morphological differentiation, a major distinction between these groups is their pattern of sexual reproduction. Centric cells are characterized by oogamous reproduction, involving the formation of uniflagellate male gametes (sperms) that facilitate encounters with the nonmotile female gametes. Conversely, sexual reproduction in pennate diatoms depends on cell-to-cell interactions that involve valve-to-valve pairing. This implies that centric diatoms are capable of self-fertilization, while mating in most pennates promotes, per definition, cross-fertilization (18). An additional advantage is that pennates do not need to invest in many small flagellated gametes, most of which will go to waste (4). However, while the search for a partner and alignment for sex may be well suited for benthic environments, it is more puzzling to conceive for organisms suspended in a 3-dimensional system, such as the pelagic environment, without a cell encounter-facilitating mechanism.

Sexual mating events in marine diatoms are relatively rare and elusive, occurring at intervals of >1 y during highly constrained periods (3). Therefore, evidence of pairing events in the natural environment during these episodes is scarce, and, as a consequence, little is known about the way this critical mechanism occurs in the water column. It is speculated that pairing in pennate diatoms involves some sort of buoyancy-associated movement since, in the absence of a process that transports cells relative to each other, randomly distributed cells cannot form aggregations, even if turbulent dispersion is spatially variable (19, 20).

Based on previous theoretical analysis and experimental observations on high-aspect ratio particles (21), Botte et al. (22) proposed an original mechanism that would favor pennate diatom encounters in the marine environment: While sinking in calm hydrodynamic conditions, they should come closer to each other because of the specific hydrodynamic interactions that develop in such situations. In such case, the flow induced by the particles while sinking leads to a positive feedback between cell horizontal displacements and regions of high particle density (SI Appendix, Fig. S5), which, in turn, amplifies any minor inhomogeneity in their spatial distribution (23). Moreover, physical experiments on inert fibers (21) have shown that this clustering is accompanied by a preferential vertical alignment of the individual particles. However, a mechanistic demonstration of this process in pennate diatoms is lacking.

Results

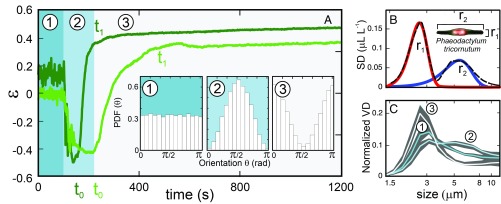
To understand the mechanism of cell pairing, we first analyzed the patterns of orientation of living and dead cells while sinking in seawater. The reorientation patterns were tracked in independent experiments using both laser diffractometry and videomicroscopy. We studied the existence of active mechanisms in the control of cell orientation and buoyancy using the fusiform morphotype of Phaeodactylum tricornutum as a model system. Reorientation and sinking were analyzed at a low Reynolds number (∼10⁻⁴) and in the dilute regime n(l/2)³ < 1, with n being the number of cells per unit volume and l their characteristic length. The particle size distribution of P. tricornutum from laser diffractometry measurements typically presents high variance at 2 differently sized bands: 1.89 to 3.11 μm (r₁) and 5.11 to 9.98 µm (r₂) (Fig. 1B). These size bands agree well with the apparent size of the transapical axis (2.3 ± 1 μm) and apical axis (10.6 ± 2.5 μm) of P. tricornutum (i.e., high optical contrast area), while the actual axes span 3.0 ± 0.3 μm and 22.5 ± 2.8 μm, respectively, as measured using microscopy. We used the relative variation of the bands in the diffractometer signal (R) (Fig. 1C) to infer the orientation parameter (ε).

Fig. 1.

Living and dead diatom orientation dynamics. (A) Progressive vertical orientation (ε) of living (light green) and dead (dark green) cells with changing shear (γ) conditions, as indicated by the different background colors. The expression ε ∼ 0 indicates random orientation of cells, while ε > 0 and ε < 0 indicate a preferential orientation in the vertical or horizontal axis, respectively. (Inset) Histograms for different ε values. PDF, probability density function. (B) SD of size spectrum of P. tricornutum cells during cell reorientation experiments (black line) and corresponding decomposed Gaussian peaks (red and blue lines). The symbols r₁ and r₂ indicate the dimensions of the apical axis (r₂) and transapical axis (r₁). (C) Variation in the size spectrum, as obtained from laser diffractometry, corresponding to each of the stages indicated in A. Gray areas indicate SD.

Fig. 1A shows the time evolution of cell orientation in our diffractometry experiments as depicted from ε values. Starting from a random cell orientation (ε = 0) generated by intense stirring (stage 1), P. tricornutum cells rapidly reorient horizontally (ε < 0) after stirring is ceased (stage 2). Cell reorientation during this stage is the result of alignment with the direction of remnant flow and lasts from 100 to t₀$\mathbf{\cong }$200 s in living cells and for a shorter period in the case of dead cells (t₀$\mathbf{\cong }$150 s). As the flow slows down even further due to viscous dissipation (stage 3), cells suddenly start to reorient parallel to gravity, with the major axis parallel to the incident beam (ε > 0, vertical orientation). This transition extends for nearly 450 s in living cells and 150 s in dead ones.

Fig. 2 shows the fluid conditions during these laser diffractometry experiments. Stage 1 is characterized by intense anomalies in the velocity field (δU) caused by vigorous stirring. These variations from the mean vortical flow (SI Appendix, Fig. S1), together with the overall high levels of shear present during stirring, are responsible for the sustained random orientation (ε = 0) of cells observed in Fig. 1. Surprisingly, dead cells present a slight vertical alignment during agitation (ε = 0.16), pointing to an anomalous response to local shear. Fluid flow (and the corresponding mean shear, γ) exponentially decrease due to viscous forces in stage 2 (no stirring), and the anomalies in the velocity field smear out. For sufficiently low γ, cells begin to reorient vertically. The observed critical shear, γ_c, is compatible with a simple balance of torques argument where displacement of the cell center of mass hinders the archetypical Jeffery orbits expected in the dynamics of ellipsoids under fluid shear (24, 25). For an ellipsoid of aspect ratio, AR, and characteristic reorientation time, τ_r, this balance is given by ${\gamma }_c=\left(A{R}^2+1\right)/2{\tau }_{\mathrm{\Upsilon }}$. With AR = 7.5 ± 1.2 and τ^a_r = 523 ± 5 for living cells (SI Appendix, Fig. S2), γ_c = 0.054 ± 0.028. As shown in Fig. 2, dead cells start orienting themselves at a higher critical shear value (γ_c = 0.1 ± 0.03) than living cells, which is, again, compatible with their shorter reorientation times (τ^d_r = 279 ± 1).

Fig. 2.

Critical shear conditions. (Upper) Anomalies in the velocity field (δU) at 2 different experimental times obtained using PIV during the orientation experiments shown in Fig. 1. (Lower) Temporal evolution of the mean shear (γ, dark blue) and adjustment of its exponential decay with time (magenta). The numbers correspond to the stages indicated in Fig. 1. Critical γ values for the initiation of vertical cell orientation of living and dead cells are indicated in light and dark green.

Videomicroscopy experiments corroborate cell reorientation with the apical axis parallel to the axis of gravity (SI Appendix, Fig. S2). In these experiments, vertical orientation not only occurs faster in dead cells (twice as fast) but is also more generalized (affects a larger percentage of the population). A similar response in both cell types indicates that reorientation is driven by a physical process rather than by cell behavior.

Pairing is tightly coupled to the orientation phenomenon, with both processes occurring consecutively during sinking (Fig. 3A). A principal component analysis of the size spectrum temporal variation in diffractometry experiments reveals that the first, and most significant, pattern corresponds to vertical cell reorientation (>80% of the variance). The second, and much weaker, mode (<10% of the variance) explains pairing between cells (aligned contact). Cell pairing is depicted from an increase in the peak of the 3- to 6-μm size band (twice the transapical size) that is observed at different coagulation times depending on cell abundance (SI Appendix, Fig. S3). Within a uniform distribution of ellipsoids sinking at speed V, any horizontal density perturbation drives a vertical shear flow. This flow field tends to increase even further the number of elongated particles drawn in the direction of higher particle density, thus causing a positive feedback, and concurrent growth, of the particle density perturbation (SI Appendix, Fig. S5) [i.e., a so-called hydrodynamic instability (21)]. This coagulation process occurs within a coagulation time, $\left(\zeta \right)$, derived from the corresponding linear stability analysis (23):

$$\zeta ={\left(\frac{V\sqrt{n{l}^3}}{l}\right)}^{-1}.$$ [1]

As shown in Fig. 3C, our experimental results fit exceptionally well with the expected scaling with cell concentration. Video microscopy experiments are also coherent with this theoretical prediction showing that coagulation time depends not only on cell concentration but also, inversely, on sinking speed [with $\zeta$ in dead cells, which consistently present a less stable response to physical forcing and show significant faster sinking speeds (Fig. 3B), fitting on the same scaling law when rescaled by V]. Cell clustering, as revealed by the structure function, g(r), increases with time (SI Appendix, Fig. S6), indicating that cell contacts are not merely a result of random spatial arrangements but, instead, are generated by fluid-mediated collective interactions.

Fig. 3.

Sinking velocity and cell coagulation. (A) Sketch of the different phases of the described cell-pairing mechanism. The arrow in the x axis indicates the approximate rate at which each phase takes place for living and dead P. tricornutum cells at 10⁵ cells per liter. A standard shear vertical profile is depicted as a dashed yellow line. It is only below γ_c that reorientation and pairing occur. g, direction of gravity. (B) Probability density functions (PDFs) of instantaneous sedimentation velocity for living cells (light green) and dead cells (dark green). (C) Coagulation time for diffractometry (circles) and videomicroscopy (squares) experiments. The filled square (■) indicates dead cells. The red line indicates the least-square fit to the measurements, and the dashed line is the theoretical model of Koch and Shaqfeh (23). (Inset) Evolution of the radial distribution function, g(r), obtained in videomicroscopy experiments. Line colors evolve with time from red to yellow. Dashed lines indicate the reference value [g(r) = 1] and the sampling uncertainties.

Field observations of cell orientation obtained using in situ laser diffractometry during a Pseudo-nitzschia bloom reveal a nonrandom cell orientation in the water column and an increase in cell pairing with enhanced vertical cell alignment. As shown in Fig. 4, Pseudo-nitzschia sp. cell abundances exceeding 10⁵ cells per liter were found at depths of 30 to 40 m, beneath the seasonal pycnocline. These pennate diatoms were characterized by an apical axis of 60 ± 12 μm and minor axis of 6 ± 3 μm. The depth variation of ε (Fig. 4B) displays a random orientation in cells at shallowest depths but progressive reorientation below 30 m to reach values consistent with unequivocal vertical alignment (ε > 0). At this depth, vertical shears did not exceed 0.007 s⁻¹. Both diffractometry measurements and visual microscopy counts revealed a higher proportion of paired cells (19%) at depths where increased vertical cell alignment was observed (Fig. 4D).

Fig. 4.

Field measurements of orientation and pairing. (A) Daily mean density (σ_t) profile and Pseudo-nitzschia sp. cell abundance obtained at Palma Bay (Balearic Islands). (B) Daily shear flow profile (γ) and cell orientation (ε) with its confidence interval shown with dashed lines. Cell orientation is only estimated where Pseudo-nitzschia sp. is dominant. (C) Variation of the in situ size spectrum obtained using laser diffractometry with depth (30 to 40 m). The darker color corresponds to larger depths. The peaks in VD at sizes corresponding to Pseudo-nitzschia sp. widths r₁ and 2r₁ indicate an increase in paired cells with depth. (D) Variation of VD with depth (solid line) and percentage of Pseudo-nitzschia sp. paired cells depicted from light microscopy samples (dots).

Discussion

Several studies have previously speculated that sinking of elongated cells at a low Reynolds number increases cell-to-cell contact probabilities, therefore favoring sexual reproduction in diatoms (13, 22, 26). However, experimental proof of the cell pairing mechanism and field evidence of its occurrence in the natural environment have been lacking. Here, we have experimentally demonstrated the existence of such a coagulation mechanism during sinking of pennate diatoms in the laboratory, and we have unambiguously provided its direct observation in the sea. Importantly, this pairing mechanism entails a preferential vertical orientation that favors cell-to-cell alignment along the apical axis, an obligate requirement for sexual exchange.

The conjecture of Botte et al. (22) is based on theoretical and experimental studies on dilute fiber suspensions settling at a low Reynolds number in unstratified fluids, showing concentration instabilities leading to particle clustering from their collective hydrodynamic interactions (21, 23, 27, 28). Nonetheless, most knowledge on the physics of coagulation emerges from experiments performed with inert particles of large sizes (10³ to 10⁴ μm). We have shown here that physical clustering also operates for significantly smaller elongated particles, therefore being relevant from tiny individual cells to long cell chains. As shown in Eq. 1 and Fig. 3C, clustering time is highly dependent on cell abundances. For example, at standard microphytoplankton cell abundances (i.e., 10³ cells per liter in the ocean), coagulation will be effective on the order of a few days, but during blooms, when cell abundances exceed 10⁶ cells per liter, coagulation time typically reduces to less than an hour. Accordingly, cell pairing is more likely to be successful at the end of a bloom period, when high cell numbers amplify collective effects on cell-to-cell encounters.

Besides this crucial clustering phenomenon, we have also established, both in the laboratory and in the field, that single pennate diatom cells have a clear tendency to orient along the gravity direction in the absence of external flows. This is at odds with the traditional view of phytoplankton cells being randomly oriented in the water column (17, 29). However, reports of cell orientation in the natural environment are scarce. The few available observations using in situ holography (30, 31) have established that, despite the accepted paradigm, nonrandom particle orientations in oceanic environments seem common. These studies have only reported preferential particle orientation in the horizontal direction in thin layers of highly stratified environments, where strong vertical density gradients (and, importantly, weak turbulence) exist (32). Such conclusions are not in contradiction to ours since we observe a transition to vertical orientation only below the pycnocline. This transition is consistent with a vertical orientation induced by a gravitational torque originating from density heterogeneities in the internal organization of cells. Hence, we conclude that these disparate cell orientations are revealing different stages of diatom dynamics in the water column.

Here, we propose that the combination of collective sinking and gravitational reorientation constitutes a robust mechanism for explaining pennate cell pairing in the sea. Crucially, such a mechanism is also very compatible with the life cycle and population dynamics of pennate diatoms. First, coagulation is a generic physical process solely driven by sinking, on which diatoms have a great control. Buoyancy regulation by osmotic variation of internal inorganic ion density (33, 34) is indeed a long-known mechanism by which diatoms physically control their interaction with the environment (35), influencing therefore their abundance and distribution in the water column. This ability helps notably regulating light and nutrient uptake (36–38). In fact, daily buoyancy-regulated migratory behavior has been observed in some diatoms that sink below the pycnocline to stock nutrients and then rise into the photic zone to photosynthesize, using up the nutrient stock (35), whereas a sinking response upon depletion of ambient nutrients is observed in different marine diatom species (39, 40). This vertical migration pattern following diatom blooms is thought to be a survival strategy whereby cells accumulate in darker, colder, and nutrient-rich water and are then ready to reenter the surface mixing layer, seeding a genetically renewed population when conditions become favorable.

Secondly, coagulation by sinking is an inherently selective process favoring interactions between healthy conspecific cells of similar size, which is a requirement for successful sexual reproduction. Because of the peculiarities of mitotic division, in which each daughter cell inherits a parental shell, variance in cell size on diatom populations increases over time. However, as illustrated in Fig. 3A, cell pairing is a sequential process in which a vertical segregation induced by sinking speed variability precedes pairing between cells sinking at similar rates. This is due to the fact that the velocity of vertical cell segregation depends on the concentration of cells and on their sedimentation rates. For usual cell abundances during a bloom (e.g., 10⁵ cells per liter) and with the sinking speeds measured in our experiments, the segregation time between living and dead P. tricornutum is 2 orders of magnitude faster than the estimated coagulation time. Only in the case of unusually high cell abundances (e.g., >10⁹ cells per liter in the case of Pseudo-nitzschia cells) would the segregation and coagulation times be similar. Consequently, cells of the same size are more likely to interact, provided that their sinking speed is similar.

For cells of similar size, changes in sedimentation velocity rely on several internal and external factors. For instance, nutrient-depleted cells sink more rapidly than nutrient-replete ones (41, 42). Likewise, other health-related factors also affect buoyancy; for example, parasitized cells are known to sink faster, hindering propagation of infections (43). These variations in sinking velocity may indeed selectively increase encounter rates among healthy cells.

Other physical coagulation processes, including Brownian motion and turbulent shear, can also bring suspended particles together, but they are slow (over 10⁴-fold slower at typical bloom conditions), nonspecific (enhancing the encounter between particles of different shapes, sizes, and sinking speeds), and do not preserve cell alignment. Hence, they constitute an unlikely mechanism for pairing and, instead, are mostly relevant for larger scale aggregations during the termination of diatom blooms and the formation of marine snow (44–46). Moreover, long-range turbulent transport (and its associated coherent structures) might also increase local cell abundance via, for example, preferential concentration, indirectly shaping encounter rates (47).

Lastly, coagulation during cell sinking also entails a high degree of synchronicity. This may be critical for sexual reproduction because gametes have to selectively interact with each other. In pennate diatoms, the main factor initiating sexualization is cell size (48), but density-dependent mechanisms have been also observed (49). Several other cues have been regarded to trigger synchronous sexualization, including irradiance, temperature, ambient nutrient concentrations, and chemical signals (50, 51).

Pairing success in diatoms might be eventually determined by other complex biological factors and selection mechanisms. For instance, chain-forming species, for which contacts are expected to be more frequent than for individual cells, are known to dramatically vary their sinking behavior (52). In addition, the existence of interlocking silica projections, spines, or tubes and the use of mucilage pads might all contribute to the ability of chains to retain proximity with compatible cells. Moreover, diatoms seem to have refined communication capabilities that can be used to vary the production of pheromones as well as other metabolites, such as allelopathic substances (53, 54). Therefore, although we have found pairing is greatly facilitated by collective cell–fluid interactions, it cannot be excluded that other active factors (Movie S2), such as chemical signaling, ultimately determine partner selection.

Methods

Cell Culture.

P. tricornutum cells were cultured in Erlenmeyer flasks containing 200 mL of Guillard’s f/2-medium + silica (15 mg⋅L⁻¹) at 20 °C under a 16-h/8-h light/dark cycle (OSRAM Fluora; 100 μmol⋅m⁻²⋅s⁻¹ photosynthetically available radiation). Cultures were transferred once a week (dilution factor ×200) to keep cells healthy and in the exponential growth phase.

Fluidic System and Microscopy.

Primary molds of the fluidic channels were created by gluing a flat capillary (CM Scientific no. 5012-050; inner dimensions: 0.10 × 2.00 mm, length: 5 cm) onto a glass slide with optical ultraviolet glue (Norland Optical Adhesive 81). Polydimethylsiloxane (PDMS) was then poured on the mold and cured for 30 min at 90 °C to create straight channels with final dimensions of ∼0.340 × 2.4 × 50 mm. Following the punching of holes at both ends of the channel, the piece of PDMS was irreversibly bonded to a glass slide using an air plasma etcher (CUTE; FemtoScience). The channel was then held vertically on an optical table (ScienceDesk B9090Ach; Thorlabs) at the focus point between a dark-field light-emitting diode (LED) ring (S80-55; Schott) and a continuously focusable microscope (InfiniVar GS, 160-mm tube lens; Infinity) set at 19× magnification on the back of which a 4-megapixel (MP) complementary metal-oxide semiconductor (CMOS) camera (UI-3370CP-NIR-GL R2; IDS) was fixed. The top inlet was then connected to a gas-tight syringe (500 μL, model 1750; Hamilton) attached to a syringe pump (Fusion 200; Chemyx), while the other end of the channel was connected to a 50-mL Falcon tube containing 10 to 20 mL of cell suspension. For all of the experiments, the cells contained in the Falcon tube were sucked into the PDMS channels at a flow rate of 50 μL⋅min⁻¹ for 2 min using the syringe pump. This process oriented the cells perpendicular to the flow (i.e., perpendicular to gravity) and produced relatively uniform cell distributions. Soon after stopping the flow, the sinking dynamics were recorded at 2 frames per second (fps) for 1 h (living cells) or 30 min (dead cells, killed by adding 1% [vol/vol] of Lugol’s iodine solution) to extract the evolution of both the distribution of cell orientation and suspension structure (i.e., radial distribution function). To get sufficient statistics, this operation was repeated between 10 and 20 times depending on the specific experiment. Cell trajectories were digitized using a standard MATLAB particle-tracking algorithm (http://site.physics.georgetown.edu/matlab/). Following tracking, cell orientation was obtained by analyzing the images further. This was done by cropping the images around the tracked features; thresholding and binarizing; and, finally, fitting the binary contours with ellipses. The radial distribution function, g(r), was directly computed from the diatom positions by counting, for all distance r, the number of particles within a distance r + dr (with dr being the discretization step) from a reference particle; averaging over all particles; and normalizing by what would be expected from a Poisson distribution. The experimental g(r) curves (SI Appendix, Fig. S6A), as a function of time, were all fitted with the function $f\left(r\right)=A_1\cos \left(\mathit{r}/{\mathit{A}}_3\right).e^{\left(-\text{r}/A_2\right)}+1$. Their evolution is encoded in the fitting parameter A₃ (while A₁ and A₂ remain constant), which shows an exponential decay (SI Appendix, Fig. S6C) with time. The coagulation process therefore exhibits a single characteristic time scale, the coagulation time. The numerical values of this time extracted from an exponential fit to A₃(t) are the ones reported in Fig. 3.

Laser Diffractometry.

Measurements were performed using a LISST-100× instrument (Sequoia Scientific, Inc.). This instrument obtains the particle volume concentration (VD) by size ranges (i.e., volume of particles in the seawater per unit volume of seawater) using a technique based on laser diffraction theory. The LISST instrument employed in this study uses a 670-nm collimated laser beam to illuminate the suspended particles, and a 32-ring detector measures the intensity of the scattered light, corresponding to 32 different size classes logarithmically spaced. The angular pattern of optical scattering depends on the physical characteristics of the particles (e.g., size, shape, orientation), and is used to calculate the particle volume concentration in these size classes (55).

The implemented inverse scattering transformation used by the LISST instrument to infer the particle volume concentration distribution from the laser diffraction pattern is based on Mie theory, strictly valid only for spherical particles. Diffraction patterns from nonspherical particles are complex and, even for simple spheroidal particles, a closed-form analytical solution to the inverse scattering problem is not generally available. Instead, different approximants better fitted for different size ranges (e.g., circle-pack and major axis length methods) have been proposed, which decompose particle shape into distinct combinations of equivalent spherical constituents (56).

We carried out a series of laboratory experiments in suspensions of the planktonic fusiform morphotype of P. tricornutum (57–59). The LISST-100× Small Volume Flow Through Chamber (Sequoia Scientific, Inc.) was precleaned and filled with the desired vol/vol concentration of cell culture in growth medium. Agitation was induced by a 2-cm-long magnetic bar powered by the built-in speed controller at minimum speed (Movie S1). Experiments consisted of an initial mixing phase (100 s), followed by a sedimentation phase in which the system was allowed to evolve without any external disturbance. Separate experiments were performed with living and dead cells to identify active cell mechanisms that contribute to these phenomena. In all our laser diffractometry experiments, the incident beam was parallel to the gravity axis.

In the present study, measurements from laser diffractometry of nearly spheroidal cells are interpreted in terms of the relative variation of the size bands (extracted from a Gaussian decomposition; Fig. 1) representing the known (measured from microscopy) major and minor cell axes (r₁ and r₂ in Fig. 1B). As cells orient in different directions, the signal in the size bands representing these axes presents an opposite behavior, with an inverse correlation between both groups (r = −0.97, P < 0.001) and direct correlation between sizes within the same size band (r = 0.98, P < 0.001). Hence, we can confidently compute the ratio between the signal from each of these 2 size bands, R(t) = (Σ VD₁)/(Σ VD₂), as a scalar proxy for cell orientation. The associated confidence interval for R(t) (and therefore ε, as discussed below) was estimated from the fitting errors of the Gaussian decomposition of the corresponding peaks.

The projection of each spheroidal particle onto the optical plane of the LISST sensor is then included as a linear superposition of the equivalent Circle-Pack and major axis length spherical equivalents with an a priori undetermined weight α₀, which serves as the single fitting parameter for the whole procedure. The function R(α_0, ε) is unique for a given particle size and aspect ratio, and it is shown for the measured r₁ and r₂ values in SI Appendix, Fig. S4. We set α₀ from the well-mixed stage (first 100 s) of our experiments, for which the distribution of cell orientations is assumed to be homogeneous (i.e., ε = 0), solving numerically for it in the equation R(α₀, 0) = R_measured. Once α₀ is known, it provides a functional route map for transforming size distributions into equivalent angular distributions; that is, it provides the unique inverse function ε(R, α₀) used throughout this paper.

Particle Image Velocimetry.

Measurements were performed using a commercial ultra-bright LED pulsing particle image velocimetry (PIV) system (LED Pulsing System; iLA5150 GmbH), with polyamide particles as flow tracers (mean diameter of 57 μm, density of 1.016 g⋅cm⁻³), a 5-MP uEye IDS CMOS camera with a 35-mm lens set at a 20-cm working distance, and double 100-μs-long green light pulses shifted 2 ms (overall period set to 10 fps). The LISST-100× Small Volume Flow Through Chamber was precleaned and filled with a 200 μL per 100 mL (vol/vol) microbeads solution in Milli-Q water. PIV multipass correlations analysis was run with 3 iterative steps and a minimum of 16 × 16 pixels window size. For long time series experiments, the extracted instantaneous velocity fields were further running-averaged over 1-s intervals to evaluate the mean shear rate.

Field Data.

Field data were obtained as part of a time series survey carried out during the spring to summer transition at Palma Bay at a station located at a depth of 40 m (39.4894° N, 2.6744° E). Herein, presented data correspond to April 23, on which date a Pseudo-nitzschia bloom was observed at depths of 30 to 40 m. Temperature, salinity, and depth were recorded hourly at the sampling site with a moored Aqualog wire-following profiler equipped with an SBE 19plus SeaCAT profiler CTD (conductivity, temperature, and depth). Current velocities were measured with a bottom-mounted Nortek Aquadopp, profiling at 1-m bins.

Water samples for pigment analysis and phytoplankton identification were collected at 5 depths (5, 10, 20, 30, and 40 m) throughout the water column with a 2.5-L Niskin bottle. Phytoplankton samples were preserved with Lugol’s iodine solution (1%). The general procedure for identifying and size-quantifying phytoplankton involved sedimentation (24 h) of a subsample in a 50-mL settling chamber, and subsequent counting of cells in an appropriate area (60) using a Leica-Leitz DM-IRB inverted microscope. For morphometric analysis, photographs were taken by a SEM videorecorder, and measurements (cell length and width) were obtained from the digital images using ImageJ software, version 1.51w (https://imagej.nih.gov/ij/) (61).

Suspended particle size distribution, including both phytoplankton and other nonalgal components, was measured using the LISST-100× instrument. The LISST instrument was lowered vertically and attached to the CTD cage, with the sensor looking down to avoid direct sunlight (62, 63). Algal and nonalgal components of the LISST-measured particle size spectra were separated using concurrent pigment concentration measurements (chlorophyll a, b, and c) as described by Font-Muñoz et al. (64).