A stepwise mechanism for aqueous two-phase system formation in concentrated antibody solutions

Significance

Concentrated liquid formulations of therapeutic antibodies are susceptible to colloidal instability, including liquid–liquid phase separation (LLPS). Herein, we measure the kinetics of aqueous two-phase system (ATPS) formation, the macroscopic stage of LLPS, along a linear temperature gradient device. These studies indicate that ATPS formation proceeds by the growth of protein-rich droplets and their subsequent coalescence. Droplet growth accelerates as the solution is cooled because protein–protein interactions become increasingly free energetically favorable. At lower temperatures, however, ATPS formation is rate-limited by a small barrier to droplet coalescence. A gel can form at the coldest temperatures, which arrest phase separation. We propose a simple 2-step model that relates these results to a reaction coordinate diagram for ATPS formation.

Abstract

Aqueous two-phase system (ATPS) formation is the macroscopic completion of liquid–liquid phase separation (LLPS), a process by which aqueous solutions demix into 2 distinct phases. We report the temperature-dependent kinetics of ATPS formation for solutions containing a monoclonal antibody and polyethylene glycol. Measurements are made by capturing dark-field images of protein-rich droplet suspensions as a function of time along a linear temperature gradient. The rate constants for ATPS formation fall into 3 kinetically distinct categories that are directly visualized along the temperature gradient. In the metastable region, just below the phase separation temperature, T_ph, ATPS formation is slow and has a large negative apparent activation energy. By contrast, ATPS formation proceeds more rapidly in the spinodal region, below the metastable temperature, T_meta, and a small positive apparent activation energy is observed. These region-specific apparent activation energies suggest that ATPS formation involves 2 steps with opposite temperature dependencies. Droplet growth is the first step, which accelerates with decreasing temperature as the solution becomes increasingly supersaturated. The second step, however, involves droplet coalescence and is proportional to temperature. It becomes the rate-limiting step in the spinodal region. At even colder temperatures, below a gelation temperature, T_gel, the proteins assemble into a kinetically trapped gel state that arrests ATPS formation. The kinetics of ATPS formation near T_gel is associated with a remarkably fragile solid-like gel structure, which can form below either the metastable or the spinodal region of the phase diagram.

Therapeutic monoclonal antibodies (mAbs) are often formulated in aqueous solutions at high concentrations, e.g., above 100 mg/mL, for small-volume subcutaneous injections. Concentrated protein solutions, however, are susceptible to colloidal instability, which includes crystallization, aggregation, and liquid–liquid phase separation (LLPS), all driven by attractive protein–protein interactions (1–7). Preventing these events from occurring at high concentrations is a critical challenge for improving the stability of liquid mAb formulations. The situation is particularly complex as temperature, pH, salts, surfactants, and crowders can each have a profound influence on mAb solution behavior (5, 8–11). As such, understanding the mechanisms involved in protein condensation requires a detailed characterization of both the kinetics and thermodynamics of mAb phase behavior under a variety of solution conditions.

LLPS occurs below the phase separation temperature, T_ph, and leads to an opaque suspension of protein-rich droplets. In the final stage of LLPS, the droplets macroscopically partition into an aqueous two-phase system (ATPS) consisting of protein-rich and protein-poor phases. The thermodynamics of LLPS provides a valuable tool for investigating protein–protein interactions (12). Some proteins, however, undergo LLPS well below the freezing point of water (13–16). This experimental limitation can be circumvented by elevating T_ph with nonionic crowding agents, like polyethylene glycol (PEG) (13–18). High molecular weight PEG is typically believed to be excluded from the protein surface at low concentrations and therefore induces attraction by depleted volume effects (13, 17–22). The values of T_ph have been routinely measured by the onset of turbidity as a solution is cooled (23–25). Alternatively, temperature quenching combined with centrifugation has also been employed (11). Unfortunately, such methods are impractical for temperature-dependent kinetic analysis, as they would require a very large number of cooling experiments to study the separation below T_ph. Instead, we apply temperature gradient microfluidics (26–29) to measure the kinetics of ATPS formation for mAb formulations in the presence of PEG.

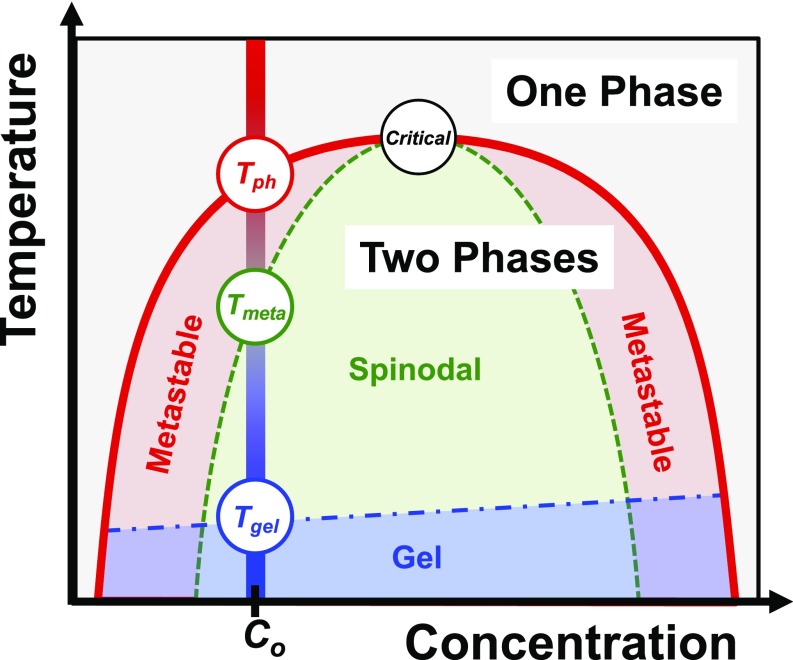
A model colloidal phase diagram displaying an upper critical solution temperature is shown in Fig. 1. Each of the experiments described herein provides continuous temperature-dependent information for a fixed mAb concentration, e.g., the vertical line at C = C_o in Fig. 1. The phase separation temperature is located on the binodal curve (red curve in Fig. 1), above which the solution is homogeneous. Below T_ph, LLPS is spontaneous and the solution separates into 2 phases. Just below T_ph, however, ATPS formation is slow because the homogeneous solution is metastable with respect to LLPS.* The lower temperature limit of the metastable region, T_meta, occurs on the spinodal curve (green curve in Fig. 1), below which ATPS formation proceeds more rapidly. At even cooler temperatures, below the gel line (blue line in Fig. 1), ATPS formation becomes arrested due to the assembly of proteins into a kinetically trapped gel state.

Fig. 1.

Schematic phase diagram of a colloidal system with attractive interactions displaying an upper critical solution temperature. The binodal (red), spinodal (green), and gelation (blue) curves delineate the various regions of the diagram. Temperature gradient experiments were performed at concentrations below the critical point (open black circle at the top of the binodal and spinodal curves), as illustrated by the vertical bar at C_o (red to blue gradient with decreasing temperature). T_ph, T_meta, and T_gel values were extracted from each experiment and are denoted by open colored circles.

By measuring ATPS formation along a temperature gradient, we simultaneously visualize the 3 regions of the colloidal phase diagram below T_ph. Each region can be identified by its unique kinetics for ATPS formation. The regions are quantitatively delineated by discontinuities in the line scans of light scattering intensity versus temperature, as well as in the temperature dependence of the rate constant for ATPS formation. Using the Arrhenius law, we determined an apparent activation energy, E_A,app, for ATPS formation in the metastable region (E_A,app ∼ −35 kcal mol⁻¹) and in the spinodal region (E_A,app ∼ 1 kcal mol⁻¹). A 2-step model, involving reversible droplet growth followed by irreversible droplet coalescence, is proposed to explain the effects of temperature on E_A,app. In fact, we demonstrate that the kinetics of ATPS formation is governed by the thermodynamics of supersaturation in the metastable region but becomes rate-limited by droplet coalescence in the spinodal region. Furthermore, we employ the Vogel–Fulcher–Tammann law to characterize the astoundingly fragile structure of the mAb gel state (fragility index value of D = 0.05), which is consistent with a fractal-like network held together by weak protein–protein interactions. Significantly, our measurements show that gelation can occur below either the metastable or the spinodal region of the colloidal phase diagram, depending on the mAb concentration. Such results contradict the notion that gelation can only occur via arrested spinodal decomposition.

Results

Measuring Phase Separation Along a Temperature Gradient.

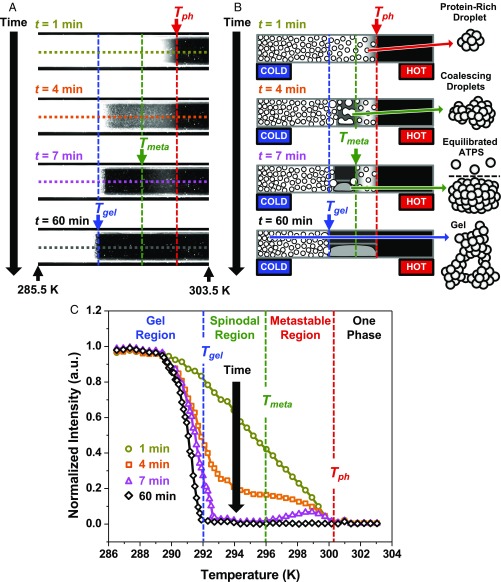
We investigated the phase behavior of a 90 mg/mL mAb solution containing 20 mg/mL PEG-3350, 15.5 mM NaCl, and 22.7 mM phosphate buffer at pH 6.8, which is below the antibody’s isoelectric point of 8.2. The experiment was initiated by introducing a clear, preheated sample (T = 318 K) onto a linear temperature gradient at a time designated as t = 0 min. Fig. 2A shows a set of dark-field images obtained at successive time points during the experiment. A schematic diagram from a side-on perspective of the rectangular sample capillary tube is provided in Fig. 2B to help illustrate the phase separation at each time point. A movie of the entire phase separation process (Movie S1) is provided in SI Appendix.

Fig. 2.

ATPS formation of a mAb solution on the temperature gradient device. (A) Dark-field images at time points ranging from t = 1 to t = 60 min during the experiment. The 2, short upward-pointing black arrows at the bottom of the image denote the temperatures at each of these 2 points, respectively, while the colored arrows denote the positions of the 3 transition temperatures. (B) Schematic diagrams of ATPS formation along the temperature gradient device corresponding to the time points in A. The schematics on the right are drawn from a side-on perspective of the rectangular capillary tube. The droplet cartoons on the far-right side depict more detailed structures corresponding, in descending order, to a protein-rich droplet, 2 coalescing droplets, an equilibrated ATPS, and the gel state, respectively. The protein molecules are depicted as gray spheres in each droplet cartoon. (C) Line scans of scattering intensity versus temperature. The line scans plotted in C correspond to the dashed horizontal lines in the images in A, which are color coded accordingly. The dashed vertical lines denote the 3 phase transition temperatures.

The cooler side of the sample became cloudy almost immediately as protein-rich droplets formed and scattered the light. The phase separation temperature, T_ph, was determined at t = 1 min from the onset of the scattering intensity near 300 K, marked by the red arrows in Fig. 2 A and B. A line scan of the scattering intensity versus temperature was measured from the dashed horizontal line in the t = 1 min image and plotted as gold data points in Fig. 2C. As can be seen in the orange line scan measured after 4 min, the scattering intensity decreased between 292 and 300 K due to droplet growth and coalescence. The pink line scan at t = 7 min showed when the intensity had just reached a minimum and stopped changing between 293 and 296 K because the droplets settled to the bottom of the capillary tube to form a transparent ATPS. The scattering intensity between 296 and 300 K, however, was still decreasing due to slow droplet growth near T_ph. Using this time point, we could define the metastable temperature, T_meta, indicated by the vertical green line in Fig. 2C. The value of T_meta divided the warmer, metastable region where ATPS formation was still occurring from the colder, spinodal region where it had just finished. We confirmed these interpretations for the decrease in light scattering by imaging ATPS formation in a larger sample, which is discussed further in SI Appendix, Fig. S1.

By t = 60 min, the separation yielded an equilibrated ATPS above a gelation temperature, T_gel. The equilibrated ATPS was optically homogeneous and did not scatter light. The line scans in Fig. 2C reveal that T_gel continued to shift subtly and ever more slowly toward colder temperature over time. The time-dependent shift of T_gel was consistent with a pseudo-phase transition, like a glass transition, which was kinetic rather than thermodynamic (30). Nonetheless, by t = 60 min, T_gel effectively stabilized on the timescale of the measurements and could be quantified by the onset of scattering relative to the completed ATPS, designated in Fig. 2C by the vertical blue line. The procedures for determining the precise transition temperatures (SI Appendix, Fig. S2) as well as for graphing the colloidal phase diagram as a function of mAb concentration (SI Appendix, Fig. S3) are provided in SI Appendix.

Modeling the Kinetics of ATPS Formation.

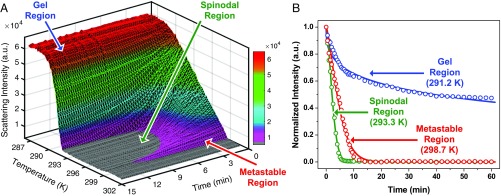
We analyzed the kinetics of ATPS formation as a function of temperature to probe the mechanism of the late stages of LLPS. Fig. 3A displays the scattering intensity as a function of both temperature and time from the data shown in Fig. 2. In the metastable region, slower ATPS formation gave rise to a low topographical ridge (magenta region in Fig. 3A), while the most rapid separation in the spinodal region produced a valley (gray region in Fig. 3A). Little or no scattering reduction was observed in the gel region at colder temperatures (red region in Fig. 3A). A characteristic scattering decay from each of the 3 kinetic regions is plotted in Fig. 3B. The procedure for measuring the scattering intensities is described in SI Appendix, Figs. S4 and S5. The normalized scattering intensity, I, for all temperatures was fit to the Kohlrausch–Williams–Watts (KWW) function provided in Eq. 1 (31, 32): The KWW fits to the data points are shown as solid curves in Fig. 3B.

$$I=\exp \left(-{\left(kt\right)}^{\beta }\right).$$ [1]

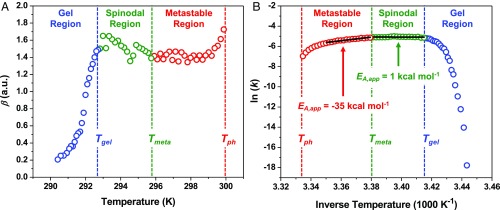
The KWW equation can be employed to empirically model the separation of a cloudy droplet dispersion into a clear, equilibrated ATPS over time, t, by using a cooperativity exponent, β, and an apparent ATPS formation rate constant, k. The fitted values of β are plotted as a function of temperature in Fig. 4A. As can be seen, ATPS formation was cooperative above T_gel with β = ∼1.5, indicating that the reduction of scattering intensity was faster than a regular exponential decay. ATPS formation for a solution containing a high concentration of droplets should follow a simple exponential decay (β = 1) if coalescence governs the separation, since the rate-limiting step is just the rupture of an interfacial water layer between 2 droplets (33). However, the high density of protein droplets relative to water should cause them to fall to the bottom of the capillary tube via gravitational sedimentation, as depicted in Fig. 2B; therefore, as the droplets grew larger with time, they should have settled ever faster (34). Thus, the observed cooperativity was consistent with ATPS formation governed by droplet coalescence, but accelerated by sedimentation.

Fig. 3.

Kinetic analysis of the light scattering data obtained in Fig. 2. (A) The scattering intensity is plotted as a function of both time and temperature. The data are shown at 15-s time intervals for clarity. (B) Three isothermal decays of the normalized scattering intensity as a function of time from the 3 distinct kinetic regions along the temperature gradient. The open circles are data points and the solid lines are fits to the data using Eq. 1.

Fig. 4.

Temperature-dependent KWW parameters for the kinetics of ATPS formation in a solution of 90 mg/mL mAb and 20 mg/mL PEG-3350. (A) The cooperativity exponent, β, is plotted as a function of temperature. The values of β are colored to indicate the gel region from 290.4 to 292.8 K (blue data points), the spinodal region from 293.0 to 295.8 K (green data points), and the metastable region from 295.9 to 299.9 K (red data points). (B) The natural log of the rate constants, ln(k), are presented in an Arrhenius plot. The ln(k) data points are colored according to the regions defined in A. The 2 solid black lines are linear fits to the data on either side of T_meta, which were used to determine the apparent activation energies, E_A,app, for ATPS formation in the metastable and spinodal regions.

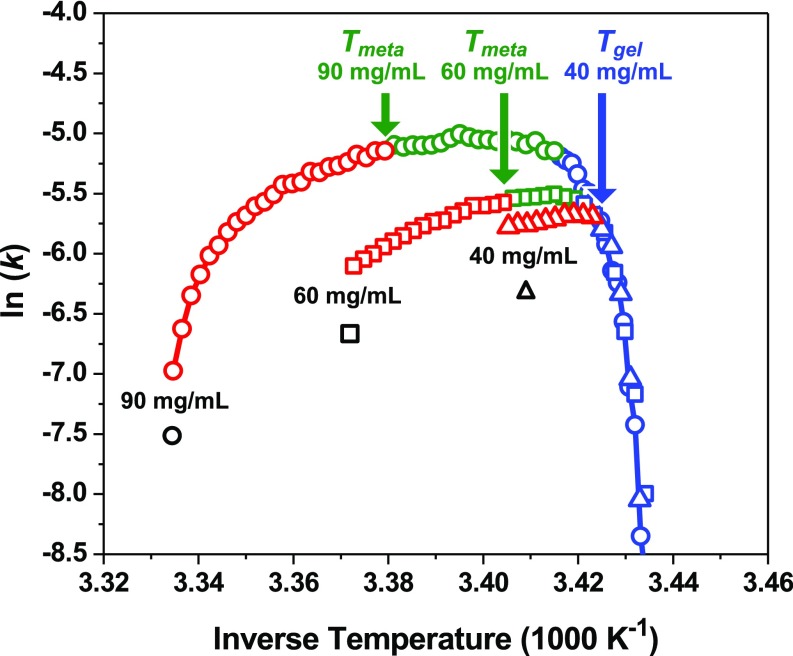
The temperature-dependent kinetics of ATPS formation provided further insight into the reaction mechanism. An Arrhenius plot of the fitted k values [ln(k) versus 1,000/T] is provided in Fig. 4B. As can be seen in the metastable region, ATPS formation accelerated as the temperature was lowered below T_ph. The fit to the Arrhenius law (solid black line over the red data points) revealed a negative apparent activation energy (E_A,app = −35 kcal mol⁻¹), which was inconsistent with the positive E_A,app expected for an elementary coalescence reaction. By contrast, ln(k) began to decrease modestly as the temperature was cooled below T_meta. The spinodal region could also be fit to the Arrhenius model (solid black line over the green data points), providing a slightly positive apparent activation energy (E_A,app = 1 kcal mol⁻¹) that was smaller than the dissociation energy of typical water–water hydrogen bonds (35, 36). The small, positive value of E_A,app in the spinodal region was consistent with the energy required to rupture the aqueous film between 2 droplets and initiate coalescence. We also observed distinct temperature-dependent regions in the kinetics of ATPS formation for 60 and 40 mg/mL mAb solutions, as shown in Fig. 5. A spinodal region, however, was not present in the 40 mg/mL mAb solution (triangle data points) as can be seen from the lack of a region characterized by a small, positive E_A,app. A detailed analysis of the effects of mAb concentration and temperature on the scattering decays, fitting parameters for the KWW model, and E_A,app values are provided in SI Appendix, Figs. S6–S8.

Fig. 5.

Arrhenius plots for the kinetics of ATPS formation in solutions containing 90 mg/mL (circle data points), 60 mg/mL (square data points), and 40 mg/mL (triangle data points) mAb in the presence of 20 mg/mL PEG-3350. The natural log of the rate constants, ln(k), for each mAb concentration versus inverse temperature is divided into metastable (red data points), spinodal (green data points), and gel (blue data points) regions. The solid red and blue curves are provided as guides to the eye.

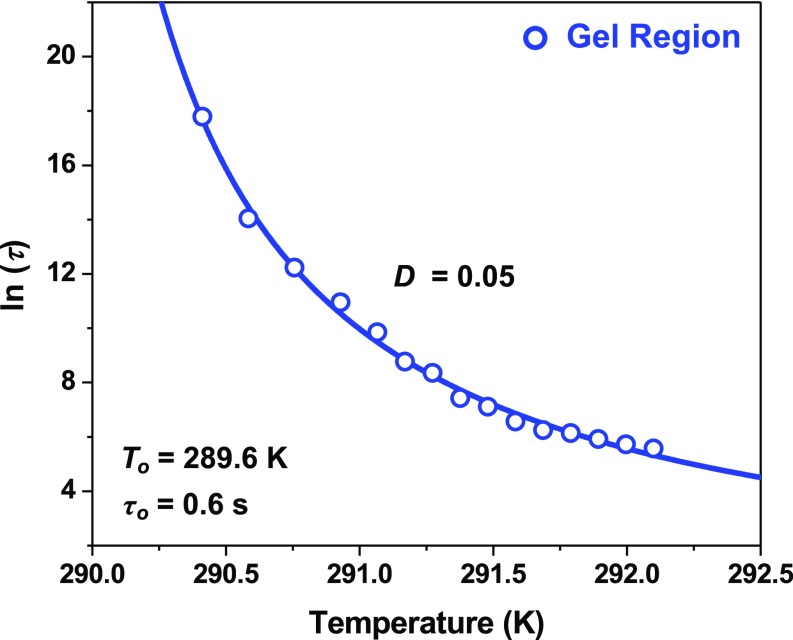
ATPS formation became anticooperative (β < 1) upon cooling below 292 K into the gel region, as can be seen in the blue data of Fig. 4A. This cross-over occurred concomitantly with a dramatic reduction in ln(k), as depicted by the blue data points in Figs. 4B and 5. As can be seen, ln(k) displayed an asymptotic decrease below T_gel that was reminiscent of changes in physical properties due to glass formation (37). To relate the abrupt deceleration of ATPS formation to the fragility of the arrested state formed below T_gel, the kinetics data in the gel region were converted to time constants, τ, by taking the reciprocal of k. The ln(τ) values for the 90 mg/mL mAb solution were plotted directly versus temperature in Fig. 6, which could be fit to the Vogel–Fulcher–Tammann (VFT) law provided in Eq. 2 (37): The VFT fit to the data points is shown as a solid blue curve in Fig. 6.

$$\ln \left(\tau \right)=\ln \left({\tau }_o\right)+\left(\frac{D{T}_o}{T-T_o}\right).$$ [2]

Here, the VFT law describes the melting of the kinetically arrested gel state by an ideal gelation temperature, T_o, an intrinsic ATPS formation time constant, τ_o, and a fragility index, D. The gel state formed below an ideal gelation temperature (T_o = 289.6 K) where ln(τ) approached infinity. As the temperature was increased toward the spinodal region, the ATPS formation time constants decreased rapidly and approached an intrinsic time constant (τ_o = 0.6 s) as T increased toward infinity. This extrapolated value for τ_o provides an estimation of the timescale for collective protein reorganization during droplet coalescence and is on the order of the coalescence time period measured for oil droplet dispersions in water (38). The fragility index (D = 0.05) quantifies the weak resistance of the gel structure to accelerated phase separation as the temperature was increased above T_o. Indeed, the measured fragility index was astoundingly weak in comparison with strong glass-forming liquids like SiO₂ (D ∼ 153) (39–41).

Fig. 6.

Time constants for ATPS formation as a function of temperature near T_gel for a solution of 90 mg/mL mAb and 20 mg/mL PEG-3350. The natural log values of the time constants, ln(τ), in the gel region, where β < 1, are plotted as blue data points along with the fit to the VFT model, shown as a solid blue curve.

Discussion

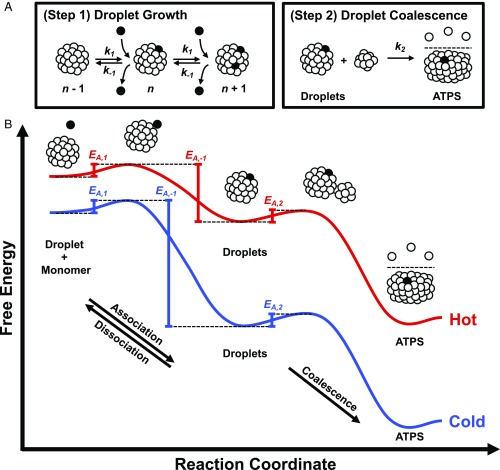
The thermodynamics of colloidal phase diagrams has been measured for numerous systems that undergo LLPS and gelation (3, 12, 23, 42–46). By measuring ATPS formation as a function of time along a temperature gradient, we directly visualized the metastable, spinodal, and gel regions of the phase diagram for mAb solutions containing PEG. This was possible because the temperature gradient measurements allowed the kinetics of ATPS formation to be extracted in parallel over a range of temperatures. The kinetics measurements suggest a 2-step mechanism for ATPS formation that is depicted schematically in Fig. 7A. After droplet nucleation has taken place, ATPS formation should continue via the first step of droplet growth, which involves the sequential, reversible addition of monomers into growing droplets (Fig. 7A, Step 1). Subsequently, ATPS formation is completed by the second step of irreversible droplet coalescence (Fig. 7A, Step 2). The rates of these 2 steps should have opposite temperature dependencies, which leads to a cross-over in the rate-limiting step at T_meta. The distinct apparent activation energies measured in the metastable and spinodal regions (Fig. 4B) can be related to the effects of temperature on the elementary activation energies of the 2-step mechanism. This idea is depicted by the 2 reaction coordinate diagrams in Fig. 7B that represent different temperatures below T_ph.

Fig. 7.

Two-step mechanism for ATPS formation. (A) ATPS formation begins with droplet growth (Step 1 in A) involving the sequential, reversible association of protein monomers with protein-rich droplets, characterized by the association, k₁, and dissociation, k₋₁. The circles represent folded protein monomers, several of which have been colored in black to highlight the growth mechanism. The number of monomers in the droplets, n, are not drawn to scale. The final stage of ATPS formation is the irreversible coalescence of droplets (Step 2 in A), characterized by the coalescence rate constant, k₂. (B) The reaction coordinate diagrams for ATPS formation at hot (red curve) and cold (blue curve) temperatures relate the apparent activation energies measured in Fig. 4B to the 2-step mechanism in A. The activation energies for the elementary steps are not drawn to scale in B.

When a protein solution is cooled below T_ph, it rapidly becomes turbid as protein-rich droplets form within seconds (42). The cloudy droplet suspension slowly becomes transparent via ATPS formation on the order of minutes (28, 29). Once a clear, macroscopic protein-rich phase forms, the system has reached equilibrium. The process of ATPS formation (depicted in Fig. 7A) is reminiscent of a simple consecutive reaction with a reversible first step and an irreversible second step, as described by Eq. 3:

$$A\begin{array}{c}\stackrel{k_1}{\to }\\ \underset{k_{-1}}{\leftarrow }\end{array}B\begin{array}{c}\stackrel{k_2}{\to }\end{array}C,$$ [3]

where A represents the initial droplet suspension. Over time, these droplets grow by reversible monomer addition into larger droplets, denoted by B. The larger droplets irreversibly coalesce to form an ATPS, represented by C. As growth and coalescence occur, the intensity of the light scattered by the initial droplet suspension decreases. Our analysis shows that the kinetics of ATPS formation in mAb solutions is well described by cooperative exponential decays with an apparent rate constant, k (Fig. 3B). Based on Eq. 3, however, k should be influenced by the elementary rate constants for monomer addition, k₁, and dissociation, k₋₁, as well as the elementary rate constant of coalescence, k₂. The exact relationship of k to k₁, k₋₁, and k₂ is complex in these experiments because Eq. 3 represents a simplification of the proposed mechanism illustrated in Fig. 7A, as discussed further in SI Appendix. Nevertheless, the 2-step mechanism provides a useful simplification for understanding the effects of temperature on the apparent value of k.

The fact that ATPS formation slows down upon cooling below T_meta (i.e., the green data points decrease very slightly from left to right in Fig. 4B) suggests that spinodal decomposition is rate-limited by the second step of coalescence (Fig. 7A, Step 2). Indeed, the rate constant for coalescence has previously been shown to be proportional to temperature (28, 29). Based on this similarity, we assign the E_A,app value for spinodal decomposition (black line over the green data in Fig. 4B) to the activation energy for coalescence, E_A,2. This assignment is depicted schematically in Fig. 7B. The acceleration of ATPS formation upon cooling through the metastable region (i.e., the red data points increase from left to right in Fig. 4B), however, is distinct from coalescence. In fact, the negative E_A,app value in the metastable region (black line over the red data in Fig. 4B) indicates that ATPS formation is rate-limited by the first step of droplet growth and that there should be 3 activation energies to take into account: the first 2 corresponding to the reversible steps of the droplet growth (E_A,1 and E_A,−1 in Fig. 7B) and the third for droplet coalescence in the forward direction (E_A,2 in Fig. 7B). We expect the value of E_A,2 to be independent of temperature. Moreover, if droplet growth is diffusion-limited, then E_A,1 should also have a temperature-independent value (47, 48). Based on these assumptions, the negative E_A,app in the metastable region should reflect the influence of temperature on the activation energy required to dissociate protein monomers from the surface of growing droplets (E_A,−1).

Upon cooling below T_ph, the solution becomes supersaturated, i.e., the initial protein concentration is higher than the concentration in the protein-poor phase of the equilibrated ATPS. This concentration difference can be related to the degree of supersaturation, which quantifies the thermodynamic driving force for LLPS (49). At warmer temperatures near T_ph, the addition of a monomer to a droplet should be free energy favorable, but the absolute change in free energy should be small (red curve in Fig. 7B). As the temperature is lowered, the supersaturation increases and the free energy difference for droplet growth becomes larger (blue curve in Fig. 7B). As a consequence, E_A,−1 becomes higher at colder temperatures and droplet growth accelerates. This idea is supported by the linear dependence of k on supersaturation in the metastable region, which was estimated from the colloidal phase diagram in SI Appendix, Fig. S9 (49–52). Although droplets grow ever more rapidly at lower temperatures, the value of k begins to decrease below T_meta (dashed vertical green line in Fig. 4B) because droplet coalescence becomes the rate-limiting step. The gradual and continuous transition from the metastable region into the spinodal region (red to green data points in Fig. 4B) should occur because droplet growth becomes faster at lower temperatures, while droplet coalescence is proportional to temperature. Also, droplet growth could become diffusion-limited upon cooling into the spinodal region. In fact, monomer diffusion to the surface of droplets should decrease with temperature, thereby promoting slower droplet growth. These ideas are consistent with the observation that T_meta is the first temperature at which ATPS formation comes to completion. Moreover, the 2-step mechanism provides a simple framework for modeling the kinetics of both the metastable and spinodal regions.

At even colder temperatures, ATPS formation becomes arrested by the formation of a kinetically trapped gel (blue data points in Fig. 4B). Gelation should occur under conditions where the proteins assemble into an expansive fractal-like network of poorly packed protein clusters that cannot undergo coalescence to complete ATPS formation, as depicted in the droplet cartoon at 60 min in Fig. 2B (53). Indeed, the extremely fragile structure of the gel, as determined by the VFT model in Fig. 6 (D = 0.05), is consistent with a fractal-like network held together by a collection of weak and poorly optimized protein–protein interactions. The value of T_gel is rather insensitive to the concentration of the protein, as shown by the blue data points in Fig. 5. T_gel occurs below the spinodal curve at high mAb concentration (e.g., C = 90 mg/mL mAb in Fig. 2), which is consistent with previously proposed gelation mechanisms involving arrested spinodal decomposition (44–46, 54). The phase diagram provided in SI Appendix, Fig. S3, however, demonstrates that gelation can also occur below the metastable region at lower mAb concentrations. In fact, the location of T_gel relative to T_meta as a function of mAb concentration can be directly observed in the 3 Arrhenius plots provided in Fig. 5. The fastest rate of ATPS formation occurs near T_meta (green arrows in Fig. 5) for both the 90 and 60 mg/mL mAb samples, where T_meta is above T_gel (blue data points). The 40 mg/mL mAb solution, however, shows a maximum value for ln(k) at T_gel (blue arrow in Fig. 5). This result demonstrates that T_gel can occur at the boundary of the metastable and gel regions of the phase diagram. As such, gelation in mAb solutions may occur by diffusion-limited cluster aggregation in the metastable region as opposed to arrested spinodal decomposition (55).

Conclusion

Herein, it was shown that the kinetics of ATPS formation in mAb solutions containing PEG exhibits unique temperature-dependent signatures that correspond to distinct regions of a colloidal phase diagram. Analysis of these signatures suggests that the late stages of phase separation proceed in 2 steps, beginning with droplet growth and ending with droplet coalescence. The kinetics of ATPS formation is controlled by droplet growth in the metastable region, which accelerates with decreasing temperature due to a growing activation energy required for dissociating a protein from the surface of a droplet. The kinetics for spinodal decomposition, however, is distinct because the reaction pathway is limited by the second step of coalescence. The ability to explore the reaction coordinate diagram for ATPS formation via temperature gradient microfluidics may help to provide insights into the effects of solution conditions (e.g., crowders, salts, surfactants, buffers, and pH) and protein properties on the phase behavior of mAb formulations. In a broader sense, the 2-step mechanism should help provide insight into the phase behavior of colloids and polymers, as well as the phase separation of biomacromolecules inside living cells (56).

Materials and Methods

SI Appendix describes the details of the sample preparation, the phase separation measurements on the temperature gradient device, the transition temperature determinations, a colloidal phase diagram, the kinetic modeling, and a more detailed discussion of the proposed 2-step mechanism for ATPS formation.