Summary
Meta-analysis is widely popular for synthesizing information on common parameters of interest across multiple studies because of its logistical convenience and statistical efficiency. We develop a generalized meta-analysis approach to combining information on multivariate regression parameters across multiple studies that have varying levels of covariate information. Using algebraic relationships among regression parameters in different dimensions, we specify a set of moment equations for estimating parameters of a maximal model through information available from sets of parameter estimates for a series of reduced models from the different studies. The specification of the equations requires a reference dataset for estimating the joint distribution of the covariates. We propose to solve these equations using the generalized method of moments approach, with the optimal weighting of the equations taking into account uncertainty associated with estimates of the parameters of the reduced models. We describe extensions of the iterated reweighted least-squares algorithm for fitting generalized linear regression models using the proposed framework. Based on the same moment equations, we also develop a diagnostic test for detecting violations of underlying model assumptions, such as those arising from heterogeneity in the underlying study populations. The proposed methods are illustrated with extensive simulation studies and a real-data example involving the development of a breast cancer risk prediction model using disparate risk factor information from multiple studies.
Keywords: Data integration, Empirical likelihood, Generalized method of moments, Meta-analysis, Missing data, Semiparametric inference
1. Introduction
In many areas of applications, including observational epidemiological studies, clinical trials and modern genome-wide association studies, meta-analysis is widely used to synthesize information on underlying common parameters of interest across multiple studies (Dersimonian & Laird, 1986, 2015; Ioannidis, 2005; Kavvoura & Ioannidis, 2008). The popularity of meta-analysis stems from the fact that it can be performed based only on estimates of model parameters and standard errors, avoiding various logistical, ethical and privacy concerns associated with accessing the individual-level data required in pooled analysis. Moreover, in many common settings, it can be shown that under reasonable assumptions, meta-analysed estimates of model parameters are asymptotically as efficient as those obtained from pooled analysis (Olkin & Sampson, 1998; Mathew & Nordstrom, 1999; Lin & Zeng, 2010). In fact, meta-analysis methods are now being used in divide-and-conquer approaches to big data, even when individual-level data are potentially available, because of the daunting computational task of model fitting with extremely large sample sizes (Jordan, 2013; Fan et al., 2014; Chun et al., 2015).
In this article, we study the problem of multivariate meta-analysis in the setting of parametric regression modelling of an outcome given a set of covariates. In standard settings, if estimates of multivariate parameters for an underlying common regression model and their associated covariances are available across all the studies, then meta-analysis can be performed by taking the inverse variance-covariance weighted average of the vector of regression coefficients (van Houwelingen et al., 2002; Ritz et al., 2008; Jackson et al., 2011). In many applications, a typical problem is that different studies include different, but possibly overlapping, sets of covariates. In a large consortium of epidemiological studies, for example, some key risk factors will be measured across all the studies, but inevitably there will be potentially important covariates that are measured only in some, but not all, of the studies. It is also possible that some covariates will be measured at a more detailed level or with a finer instrument in some studies than in others. Disparate sets of covariates across studies mean that standard meta-analysis is applicable only to the development of models limited to a core set of variables that are measured in the same way across all the studies.
We propose a generalized meta-analysis method, which we call genmeta, for building rich models using information on model parameters across studies with disparate covariate information. Our approach is built upon a fundamental mathematical relationship, presented in our recent work (Chatterjee et al., 2016), between parameters of two regression models in different dimensions. In the present article, we use this mathematical relationship to develop a general framework for combining information on parameters of various models of different dimensions within the generalized method of moments framework (Hansen, 1982; Imbens, 2002). We develop an iterated reweighted least-squares algorithm that allows stable and speedy computation of estimates. The proposed method requires access to a reference dataset for estimating the joint distribution of the covariates in a nonparametric fashion. We show how the reference dataset can be used to derive an optimal estimator and the associated variances and covariances, even when entire variance-covariance matrices for model parameter estimates may not be obtainable from individual studies.
2. Models and methods
2.1. Model formulation
Suppose that we have parameter estimates  and associated estimates of their covariance matrices
and associated estimates of their covariance matrices  from
from  independent studies that have fitted reduced regression models, of the form
independent studies that have fitted reduced regression models, of the form 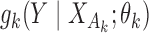 , where
, where 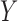 is a common underlying outcome of interest, but the vector of covariates
is a common underlying outcome of interest, but the vector of covariates 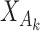 is potentially distinct across different studies. Let
is potentially distinct across different studies. Let 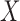 be the set of covariates used in at least one study, and assume that the true distribution of
be the set of covariates used in at least one study, and assume that the true distribution of 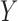 given
given 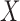 can be specified by a maximal regression model
can be specified by a maximal regression model 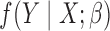 . Our goal is to estimate and make inference about
. Our goal is to estimate and make inference about 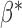 , the true value of
, the true value of 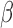 , based on summary-level information,
, based on summary-level information, 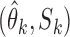 , from the
, from the 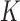 studies.
studies.
In the proposed set-up it is possible, but not necessary, that some of the studies will have information on all covariates to fit the maximal model by themselves. Under certain study designs, such as multi-phase designs (Breslow & Cain, 1988; Breslow & Holubkov, 1997; Scott & Wild, 1997; Whittemore, 1997) and the partial questionnaire design (Wacholder & Carroll, 1994), data could be partitioned into independent sets such that the maximal model can be fitted on some sets and various reduced models fitted on others. The maximal model 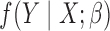 and the reduced models
and the reduced models 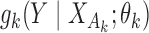 may have different parametric forms, such as logistic and probit models when
may have different parametric forms, such as logistic and probit models when 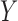 is a binary disease outcome. This set-up also allows incorporation of covariates which may be measured more accurately, or in a more refined manner in some studies than in others. For example, different studies may include two types of measurements, say
is a binary disease outcome. This set-up also allows incorporation of covariates which may be measured more accurately, or in a more refined manner in some studies than in others. For example, different studies may include two types of measurements, say  and
and  , for the same covariate, with
, for the same covariate, with 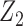 being a more refined measurement. In this case the different reduced models may include
being a more refined measurement. In this case the different reduced models may include 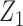 or
or 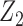 , but we require that the reference dataset include both
, but we require that the reference dataset include both 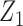 and
and 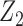 . In the maximal model, we can force
. In the maximal model, we can force 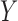 to be independent of
to be independent of 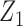 given
given 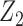 by setting the regression parameters associated with
by setting the regression parameters associated with 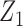 to zero.
to zero.
If all of the reduced models are the same, i.e., all the studies have the same covariate information, then 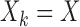 ,
, 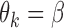 and
and 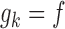 for each
for each 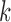 , and the common parameter of interest
, and the common parameter of interest 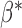 can be efficiently estimated by the fixed-effect meta-analysis estimator
can be efficiently estimated by the fixed-effect meta-analysis estimator 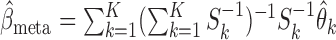 , the variance of which can in turn be estimated by
, the variance of which can in turn be estimated by 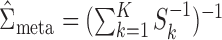 (van Houwelingen et al., 2002; Ritz et al., 2008; Jackson et al., 2011).
(van Houwelingen et al., 2002; Ritz et al., 2008; Jackson et al., 2011).
2.2. A special case involving the linear regression model
As readers may have difficulty comprehending how it is possible to estimate parameters of the maximal model when no single study may have ascertained 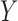 and all components of
and all components of 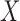 simultaneously, here we give a linear model example to help develop insight into the problem. Suppose that one is interested in developing a multiple linear regression model for
simultaneously, here we give a linear model example to help develop insight into the problem. Suppose that one is interested in developing a multiple linear regression model for 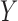 based on a set of covariates
based on a set of covariates 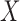 in the form
in the form
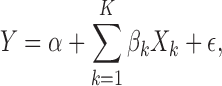 |
where it is further assumed that 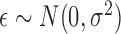 . Without loss of generality, we assume that all the variables
. Without loss of generality, we assume that all the variables 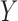 ,
, 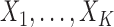 are standardized to have mean 0 and variance 1. Under this model, the population parameter
are standardized to have mean 0 and variance 1. Under this model, the population parameter 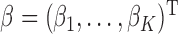 can be expressed as
can be expressed as 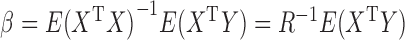 , where
, where 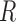 is the population correlation matrix of
is the population correlation matrix of 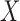 . Now, suppose we have no data available on
. Now, suppose we have no data available on 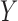 and multivariate
and multivariate 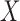 on the same sample, but we do have estimates available for parameters
on the same sample, but we do have estimates available for parameters 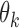 (
(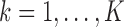 ) for univariate linear regression models of the form
) for univariate linear regression models of the form
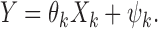 |
From above, 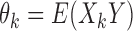 , and so
, and so 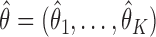 provides an estimate of the cross product terms
provides an estimate of the cross product terms 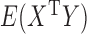 , which are required in estimating
, which are required in estimating 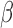 . Further, if we have a reference dataset which contains information on multivariate
. Further, if we have a reference dataset which contains information on multivariate 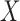 , but is not required to be linked to
, but is not required to be linked to 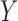 , it can be used to estimate
, it can be used to estimate 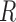 , as
, as 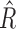 say, and a consistent estimate of
say, and a consistent estimate of 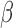 can then be obtained simply as
can then be obtained simply as 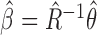 . Thus, it is possible to estimate parameters of a multiple regression model using information on parameters of a series of univariate regression models and a reference dataset. In fact, this observation that information on univariate regression parameters, known as summary-level statistics, can be used to reconstruct estimates of parameters of multivariate regression models has revolutionized the field of statistical genetics. Recently, a great variety of methods have been developed for inference on parameters underlying multivariate regression models that utilize widely available summary-level results from large genome-wide association studies and reference datasets to estimate linkage disequlibrium across genetic markers (Yang et al., 2012; Bulik-Sullivan et al., 2015; Zhu et al., 2016; Pasaniuc & Price, 2017). In the following, we describe a more general statistical formulation of the problem that allows consideration of nonlinear models and use of information from arbitrary types of reduced models, as opposed to simply univariate models.
. Thus, it is possible to estimate parameters of a multiple regression model using information on parameters of a series of univariate regression models and a reference dataset. In fact, this observation that information on univariate regression parameters, known as summary-level statistics, can be used to reconstruct estimates of parameters of multivariate regression models has revolutionized the field of statistical genetics. Recently, a great variety of methods have been developed for inference on parameters underlying multivariate regression models that utilize widely available summary-level results from large genome-wide association studies and reference datasets to estimate linkage disequlibrium across genetic markers (Yang et al., 2012; Bulik-Sullivan et al., 2015; Zhu et al., 2016; Pasaniuc & Price, 2017). In the following, we describe a more general statistical formulation of the problem that allows consideration of nonlinear models and use of information from arbitrary types of reduced models, as opposed to simply univariate models.
2.3. Generalized meta-analysis
The key idea underlying the proposed generalized meta-analysis is that we convert information on parameters from reduced models into a set of equations that are informative about the parameters of the maximal model. We will make the following assumptions: (i) the same probability law for 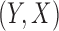 holds for all the underlying populations; (ii)
holds for all the underlying populations; (ii) 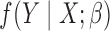 is a correctly specified model for the conditional distribution of
is a correctly specified model for the conditional distribution of 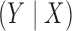 ; and (iii) we have a reference dataset to estimate empirically the joint distribution of all the factors included in
; and (iii) we have a reference dataset to estimate empirically the joint distribution of all the factors included in 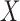 .
.
Here we assume that all the studies employ a random sampling design and that the same probability law for 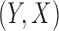 holds for all of the underlying populations. Let
holds for all of the underlying populations. Let 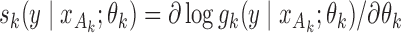 be the score function of the
be the score function of the 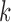 th reduced model, and write
th reduced model, and write 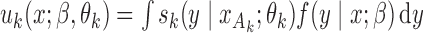 . Assume that
. Assume that 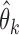 is the maximum likelihood estimator from the
is the maximum likelihood estimator from the 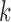 th study, and denote by
th study, and denote by 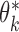 the asymptotic limit of
the asymptotic limit of 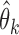 . Irrespective of whether the reduced models are correct,
. Irrespective of whether the reduced models are correct, 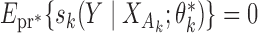 holds, where
holds, where 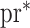 denotes the true probability law. Assuming that the maximal model is correctly specified, we can write
denotes the true probability law. Assuming that the maximal model is correctly specified, we can write 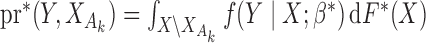 . Hence, a general equation describing the relationship between
. Hence, a general equation describing the relationship between 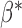 and
and 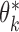 is of the form (Chatterjee et al., 2016)
is of the form (Chatterjee et al., 2016)
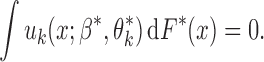 |
As we may not have individual-level data from the studies, these equations cannot be evaluated directly. Instead, we assume that we have a reference sample of size 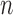 , independent of the study samples, on which measurements of
, independent of the study samples, on which measurements of 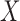 are available. The reference sample need not be linked with the outcome
are available. The reference sample need not be linked with the outcome 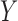 of interest, and its sample size can be fairly modest compared with the study sample sizes.
of interest, and its sample size can be fairly modest compared with the study sample sizes.
With 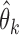 from the studies and the reference sample
from the studies and the reference sample  , we can set up the estimating equations
, we can set up the estimating equations 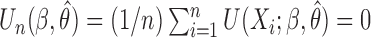 , where
, where 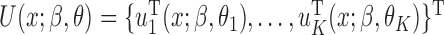 ,
, 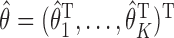 and
and 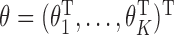 . Denote the dimensions of
. Denote the dimensions of 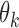 and
and 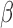 by
by 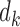 and
and 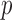 , respectively. Because the number of equations
, respectively. Because the number of equations 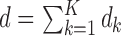 can be larger than the number of unknown parameters
can be larger than the number of unknown parameters  , it may be that the estimating equations cannot be solved exactly. Based on the generalized method of moments, we propose the following generalized meta-analysis estimator of
, it may be that the estimating equations cannot be solved exactly. Based on the generalized method of moments, we propose the following generalized meta-analysis estimator of 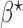 :
: 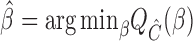 where
where 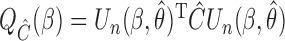 , with
, with 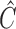 being a positive-semidefinite weighting matrix. Using the well-established theory of generalized method of moments (Hansen, 1982; Engle & McFadden, 1994), we derive the asymptotic properties of our estimator. Assume that the study summary statistics
being a positive-semidefinite weighting matrix. Using the well-established theory of generalized method of moments (Hansen, 1982; Engle & McFadden, 1994), we derive the asymptotic properties of our estimator. Assume that the study summary statistics 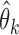 are independent across studies, that
are independent across studies, that 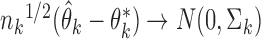 in distribution, that
in distribution, that 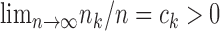 for each
for each 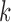 , and that the reference sample is independent of the study samples. Let
, and that the reference sample is independent of the study samples. Let 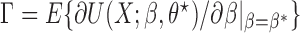 ,
, 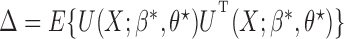 and
and  , where
, where 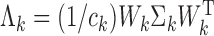 with
with 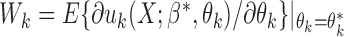 for
for 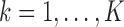 .
.
Theorem 1
(Consistency and asymptotic normality of
). Suppose that the positive-semidefinite weighting matrix
tends to
in probability. Then, under Assumptions A1–A4 in the Appendix,
in probability. Further, if
is an interior point, then under the additional Assumptions A5–A9 in the Appendix,
converges in distribution to the normal distribution
.
The optimal  that minimizes the above asymptotic covariance matrix is
that minimizes the above asymptotic covariance matrix is  , and the corresponding optimal asymptotic covariance matrix is
, and the corresponding optimal asymptotic covariance matrix is 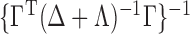 . Because
. Because 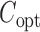 itself depends on unknown underlying parameters, it requires iterative evaluation. In our applications, we first evaluate an initial estimator with a simple choice of
itself depends on unknown underlying parameters, it requires iterative evaluation. In our applications, we first evaluate an initial estimator with a simple choice of 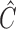 , such as the identity matrix. We then obtain the iterated estimator by continuing to set
, such as the identity matrix. We then obtain the iterated estimator by continuing to set 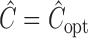 based on the latest parameter estimate until convergence. By Theorem 1,
based on the latest parameter estimate until convergence. By Theorem 1, 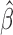 with
with 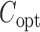 approximately follows a Gaussian distribution with mean
approximately follows a Gaussian distribution with mean 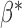 and covariance matrix
and covariance matrix
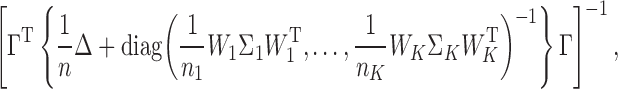 |
(1) |
which indicates that the precision of our estimator depends on the size of the reference sample, 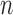 , as well as on the sample sizes of the studies,
, as well as on the sample sizes of the studies, 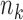 . However, as we will see in § 3, the study sample sizes are the dominant factor controlling the precision of our estimator, and with the
. However, as we will see in § 3, the study sample sizes are the dominant factor controlling the precision of our estimator, and with the 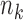 fixed the precision quickly reaches a plateau as a function of
fixed the precision quickly reaches a plateau as a function of 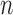 .
.
For the implementation of the optimal generalized meta-analysis and the variance estimation of any of the generalized meta-analysis estimators, one needs to have valid estimates of 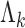 , which depend on
, which depend on 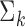 , the asymptotic covariance matrices of the estimates of the reduced model parameters. Ideally, the studies should provide robust estimates of the covariance matrices, such as the sandwich covariance estimators, so that they are valid irrespective of whether the underlying reduced models are correctly specified or not. In practice, however, while we expect some kind of estimate of standard errors of the individual parameters to be available from a study, obtaining the desired robust estimate of the entire covariance matrix can be difficult. When no estimate of
, the asymptotic covariance matrices of the estimates of the reduced model parameters. Ideally, the studies should provide robust estimates of the covariance matrices, such as the sandwich covariance estimators, so that they are valid irrespective of whether the underlying reduced models are correctly specified or not. In practice, however, while we expect some kind of estimate of standard errors of the individual parameters to be available from a study, obtaining the desired robust estimate of the entire covariance matrix can be difficult. When no estimate of 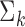 is available from the
is available from the 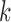 th study, one can take advantage of the reference sample to estimate it by
th study, one can take advantage of the reference sample to estimate it by 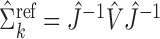 , where
, where  and
and 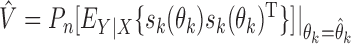 with
with 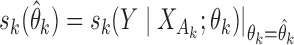 ; here
; here 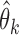 is a consistent estimator of
is a consistent estimator of  ,
, 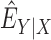 is the expectation with respect to the distribution of
is the expectation with respect to the distribution of 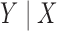 with
with 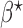 replaced by a consistent estimator
replaced by a consistent estimator 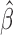 , and
, and 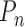 is the empirical measure with respect to the reference sample. Further, assuming
is the empirical measure with respect to the reference sample. Further, assuming 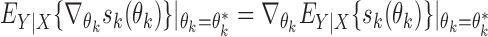 , it follows that
, it follows that 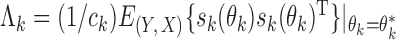 , which can be estimated by
, which can be estimated by 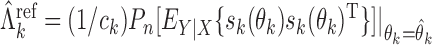 . For example, suppose that
. For example, suppose that 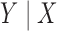 and
and 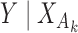 follow logistic distributions with parameters
follow logistic distributions with parameters 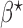 and
and 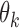 , respectively. Write
, respectively. Write 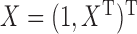 and
and 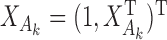 . Then
. Then
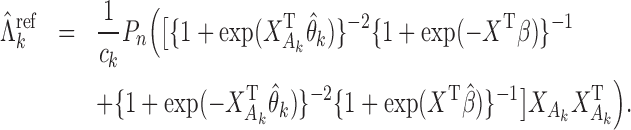 |
(2) |
In § 3 we will study the properties of our generalized meta-analysis estimators using either covariance matrices estimated from studies or the reference sample.
It is illuminating to explore the connection between our proposed approach and standard meta-analysis when all of the reduced models are identical to the maximal model, that is, when 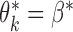 ,
, 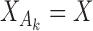 and
and 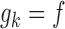 for each
for each 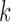 . In this set-up, the moment vector evaluated at the true parameters becomes zero for each study, i.e.,
. In this set-up, the moment vector evaluated at the true parameters becomes zero for each study, i.e., 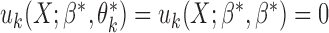 . This simplification implies
. This simplification implies 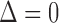 , and hence the optimal weighting matrix is
, and hence the optimal weighting matrix is 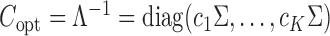 , where
, where 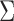 is the inverse of the Fisher’s information matrix of
is the inverse of the Fisher’s information matrix of  . Denote by
. Denote by 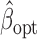 the genmeta estimator with a consistent estimator of
the genmeta estimator with a consistent estimator of  . Then, by arguments similar to those in the proof of Theorem 1,
. Then, by arguments similar to those in the proof of Theorem 1, 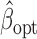 can be expressed as
can be expressed as
 |
which implies that 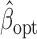 and
and 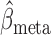 are asymptotically equivalent in terms of limiting distributions.
are asymptotically equivalent in terms of limiting distributions.
2.4. Generalized linear model and iterated reweighted least-squares algorithm
Our generalized meta-analysis computation involves minimization of a quadratic form, 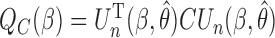 , with a known weighting matrix
, with a known weighting matrix 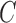 . In this subsection we derive the iterated reweighted least-squares algorithm for minimizing the quadratic form, assuming that the maximal and reduced models belong to the class of generalized linear models (McCullagh & Nelder, 1989). Specifically, the densities of
. In this subsection we derive the iterated reweighted least-squares algorithm for minimizing the quadratic form, assuming that the maximal and reduced models belong to the class of generalized linear models (McCullagh & Nelder, 1989). Specifically, the densities of 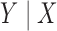 and
and 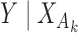 are of the forms
are of the forms 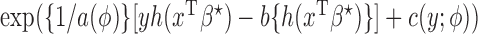 and
and 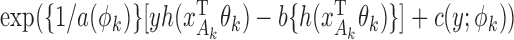 , respectively, where
, respectively, where 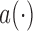 ,
, 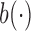 and
and 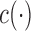 are known functions,
are known functions, 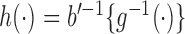 with
with  a monotone and differentiable link function, and
a monotone and differentiable link function, and 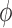 and
and 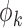 are the dispersion parameters of the maximal and the
are the dispersion parameters of the maximal and the 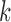 th reduced models, respectively.
th reduced models, respectively.
First we assume that the dispersion parameters, 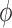 and the
and the 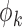 , are known; later we will relax this assumption. In this case it follows that for each
, are known; later we will relax this assumption. In this case it follows that for each 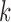 ,
,
 |
(3) |
where 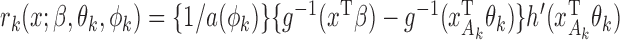 . Then the empirical moment vector is
. Then the empirical moment vector is 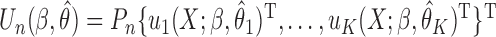 . The Newton–Raphson method for seeking the minimizer of
. The Newton–Raphson method for seeking the minimizer of 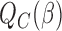 can be written as
can be written as
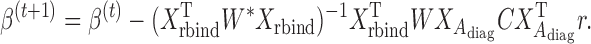 |
(4) |
In (4), 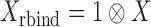 where
where 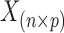 is the reference data matrix;
is the reference data matrix; 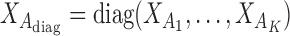 where
where 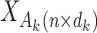 is the reference data matrix for the
is the reference data matrix for the 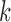 th study;
th study; 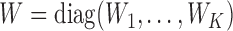 with
with 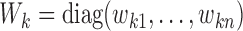 and
and 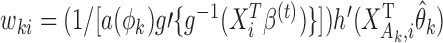 (
(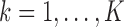 ;
; 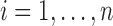 );
); 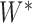 is the sum of
is the sum of 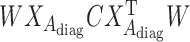 and
and 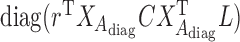 , a diagonalized matrix from a vector;
, a diagonalized matrix from a vector; 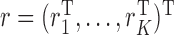 with
with 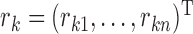 and
and 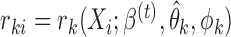 ; and
; and 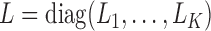 with
with 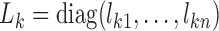 and
and 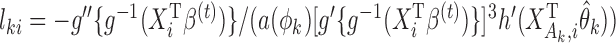 . Equation (4) implies that the Newton–Raphson method is an iterated reweighted least-squares algorithm.
. Equation (4) implies that the Newton–Raphson method is an iterated reweighted least-squares algorithm.
When 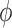 and the
and the 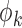 are unknown, we propose to first obtain the estimator
are unknown, we propose to first obtain the estimator 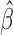 of
of 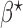 as above with
as above with 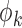 replaced by
replaced by  . Next, we consider the estimation of
. Next, we consider the estimation of  , the true value of
, the true value of 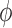 . For the
. For the 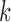 th reduced model, we have an additional score function with respect to
th reduced model, we have an additional score function with respect to 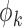 , from which we can obtain, similar to equation (3),
, from which we can obtain, similar to equation (3),
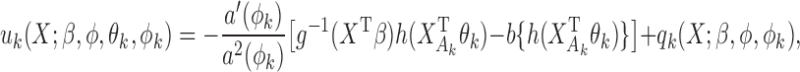 |
with 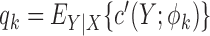 where
where 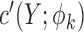 is the derivative of
is the derivative of 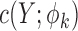 with respect to
with respect to 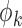 . Then the empirical moment vector for
. Then the empirical moment vector for 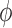 is
is 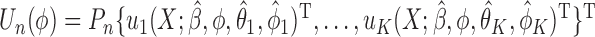 . To estimate
. To estimate 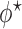 , we need to compute the minimizer of
, we need to compute the minimizer of 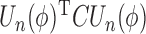 , where
, where 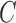 is a known weighting matrix. The Newton–Raphson steps can be written as
is a known weighting matrix. The Newton–Raphson steps can be written as
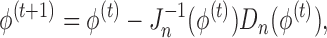 |
(5) |
where  ,
, 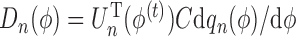 and
and 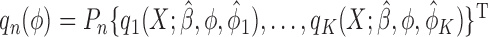 . In brief, when
. In brief, when 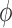 and
and 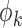 (
( ) are unknown, we first choose initial estimates
) are unknown, we first choose initial estimates 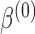 and
and 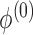 . Then we obtain the estimator
. Then we obtain the estimator 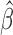 by iterating (4) until a stopping rule is reached. Subsequently
by iterating (4) until a stopping rule is reached. Subsequently 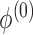 ,
, 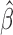 and the study estimates are inserted into (5), and the process is repeated until a stopping rule is reached, giving the genmeta estimator of
and the study estimates are inserted into (5), and the process is repeated until a stopping rule is reached, giving the genmeta estimator of 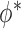 . In each Newton–Raphson step, the weighting matrix
. In each Newton–Raphson step, the weighting matrix 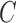 is estimated by the estimates from the previous step.
is estimated by the estimates from the previous step.
2.5. Diagnostic test for model violation
Our generalized meta-analysis approach relies on several modelling assumptions, including homogeneity of the underlying populations with respect to the distribution of covariates and regression parameters, and correct specification of the maximal model. In the absence of individual-level data from the different studies, these assumptions cannot be tested in the usual manner using traditional diagnostic tests. However, even with summary-level data, some diagnostic testing is possible. In particular, from an intuitive perspective, departure of the genmeta estimating equations, when evaluated at estimated parameter values, from their expected null value will be indicative of disagreement between the model and the observed data, i.e., the estimates of the parameters for the reduced models from different studies. For example, if the regression parameters underlying the maximal model are highly heterogeneous across studies, then the assumption of a common 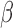 in genmeta will not be able to explain the heterogeneity that is expected to be present in overlapping reduced model parameters across the studies. Specifically, we propose to use the score test based on the statistic
in genmeta will not be able to explain the heterogeneity that is expected to be present in overlapping reduced model parameters across the studies. Specifically, we propose to use the score test based on the statistic 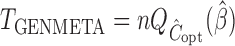 , where
, where 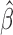 is the genmeta estimate. When all the underlying assumptions are correct, by the standard generalized method of moments theory,
is the genmeta estimate. When all the underlying assumptions are correct, by the standard generalized method of moments theory, 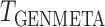 converges in distribution to a
converges in distribution to a 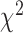 distribution with
distribution with 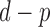 degrees of freedom, where
degrees of freedom, where 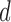 is the total number of genmeta equations and
is the total number of genmeta equations and 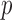 is the total number of underlying parameters that are being estimated. The test is applicable only when
is the total number of underlying parameters that are being estimated. The test is applicable only when 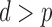 , which is the case when different studies have overlapping covariates.
, which is the case when different studies have overlapping covariates.
3. Simulations
3.1. Set-up
We study the performance of our estimators through simulation studies in both idealized and non-idealized settings. In all simulations, we assume that the relationship between a binary outcome variable 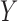 and three covariates
and three covariates 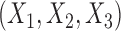 can be described with a logistic regression model of the form
can be described with a logistic regression model of the form
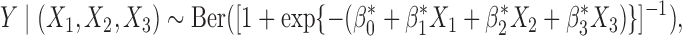 |
(6) |
where 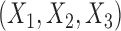 follows a multivariate normal distribution with mean
follows a multivariate normal distribution with mean 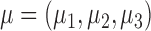 , variance
, variance 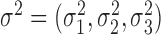 and underlying correlations
and underlying correlations 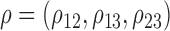 . We choose
. We choose 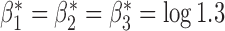 to reflect a moderate degree of association of the outcome with each covariate after adjusting for the others. We assume that there are three separate studies, where each study fits a reduced logistic model for the outcome
to reflect a moderate degree of association of the outcome with each covariate after adjusting for the others. We assume that there are three separate studies, where each study fits a reduced logistic model for the outcome 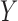 on two of the covariates in the form
on two of the covariates in the form
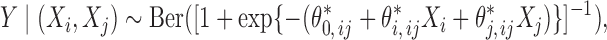 |
(7) |
with 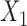 and
and 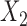 included in study I,
included in study I,  and
and 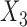 in study II, and
in study II, and 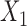 and
and 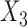 in study III. Here, as the data for each study are generated using the maximal model, the reduced models are by definition incompatible due to the non-collapsibility of the logistic model. We fix the sample size of the studies at
in study III. Here, as the data for each study are generated using the maximal model, the reduced models are by definition incompatible due to the non-collapsibility of the logistic model. We fix the sample size of the studies at 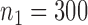 ,
, 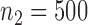 and
and  , and vary the sample size of the reference dataset.
, and vary the sample size of the reference dataset.
3.2. Homogeneous population
We assume that the studies are conducted in the same underlying population from which the reference sample is drawn. In this setting, there exists a common mean vector 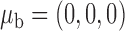 , a common variance vector
, a common variance vector 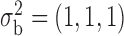 and a common correlation vector
and a common correlation vector 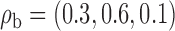 , which describes the joint distribution of the three covariates across all the underlying populations. In the first set of simulations, we assume a fixed sample size
, which describes the joint distribution of the three covariates across all the underlying populations. In the first set of simulations, we assume a fixed sample size 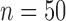 for the reference dataset. In all settings, we simulate data
for the reference dataset. In all settings, we simulate data 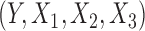 for the underlying studies based on the data-generating models as described above, and we fit the respective reduced models to obtain estimates of the reduced model parameters. For each set of simulated data, we obtain estimates of covariance matrices of the reduced model parameters using robust sandwich estimators based on either the study datasets themselves or the reference dataset; see (2). We consider three estimators: genmeta.0, which is the initial genmeta estimator with identity weighting matrix, and genmeta.1 and genmeta.2, which use covariance estimates from the reference dataset and from the studies, respectively.
for the underlying studies based on the data-generating models as described above, and we fit the respective reduced models to obtain estimates of the reduced model parameters. For each set of simulated data, we obtain estimates of covariance matrices of the reduced model parameters using robust sandwich estimators based on either the study datasets themselves or the reference dataset; see (2). We consider three estimators: genmeta.0, which is the initial genmeta estimator with identity weighting matrix, and genmeta.1 and genmeta.2, which use covariance estimates from the reference dataset and from the studies, respectively.
From the results shown in Table 1, we see that all three estimators are nearly unbiased. The standard error estimates, irrespective of whether 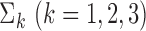 were estimated using the study datasets or the reference sample, accurately reflect the true standard errors of the genmeta parameter estimates across different simulations. As a result, the 95% confidence intervals maintain the coverage probability at the nominal level. Among the three estimators considered, clearly genmeta.0, which uses the non-optimal choice of
were estimated using the study datasets or the reference sample, accurately reflect the true standard errors of the genmeta parameter estimates across different simulations. As a result, the 95% confidence intervals maintain the coverage probability at the nominal level. Among the three estimators considered, clearly genmeta.0, which uses the non-optimal choice of 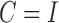 , is less efficient than genmeta.1 and genmeta.2, which had comparable efficiency.
, is less efficient than genmeta.1 and genmeta.2, which had comparable efficiency.
Table 1.
Simulation results for our generalized meta-analysis estimators in the logistic regression setting; estimated standard deviations were obtained by taking averages over simulated datasets and were used to construct 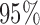 confidence intervals, whose coverage rates and average lengths are reported
confidence intervals, whose coverage rates and average lengths are reported
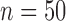
|
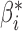
|
Bias | SD (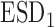 , , 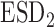 ) ) |
RMSE | CR | AL |
|---|---|---|---|---|---|---|
| genmeta.0 |
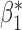
|
0.010 | 0.161 (0.161, 0.162) | 0.161 | 0.968, 0.964 | 0.642, 0.636 |
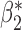
|
0.005 | 0.110 (0.111, 0.108) | 0.110 | 0.958, 0.960 | 0.434, 0.423 | |
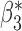
|
 0.001 0.001 |
0.138 (0.143, 0.142) | 0.138 | 0.963, 0.964 | 0.559, 0.556 | |
| genmeta.1 |
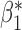
|
0.005 | 0.117 (0.116, 0.110) | 0.117 | 0.976, 0.966 | 0.455, 0.433 |
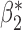
|
 0.003 0.003 |
0.101 (0.105, 0.099) | 0.101 | 0.964, 0.955 | 0.411, 0.386 | |
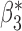
|
0.001 | 0.099 (0.102, 0.097) | 0.099 | 0.973, 0.961 | 0.402, 0.381 | |
| genmeta.2 |
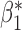
|
0.007 | 0.115 (0.116, 0.111) | 0.115 | 0.971, 0.964 | 0.455, 0.435 |
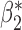
|
 0.003 0.003 |
0.102 (0.105, 0.099) | 0.102 | 0.960, 0.959 | 0.413, 0.388 | |
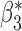
|
0.003 | 0.098 (0.103, 0.098) | 0.098 | 0.957, 0.957 | 0.403, 0.383 |
SD, standard deviation; ESD , estimated standard deviation using the reference sample; ESD
, estimated standard deviation using the reference sample; ESD , estimated standard deviation using the covariance estimates of reduced model parameters from the studies; RMSE, square root of mean square error; CR, coverage rate of 95% confidence intervals; AL, average length of 95% confidence intervals.
, estimated standard deviation using the covariance estimates of reduced model parameters from the studies; RMSE, square root of mean square error; CR, coverage rate of 95% confidence intervals; AL, average length of 95% confidence intervals.
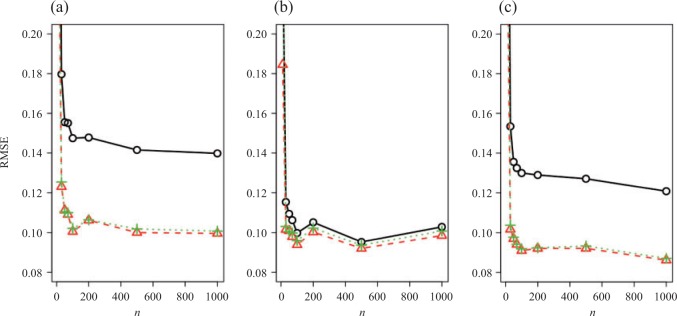
In the same setting as above, when we vary 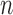 from 10 up to a maximum of 1000, we observe that the precision of the genmeta estimates does not increase with
from 10 up to a maximum of 1000, we observe that the precision of the genmeta estimates does not increase with 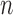 once it reaches a threshold of around 100, which is one-third of the minimum of the study sample sizes (
once it reaches a threshold of around 100, which is one-third of the minimum of the study sample sizes (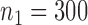 ); see Fig. 1. The thresholds were even lower for estimation of coefficients associated with
); see Fig. 1. The thresholds were even lower for estimation of coefficients associated with 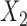 , which had weak to moderate correlation with the other covariates in the model. That the reference dataset can be substantially smaller than the study datasets without having much impact on the precision of our estimator is encouraging, given that accessing a reference dataset with a large sample size may be difficult in practice.
, which had weak to moderate correlation with the other covariates in the model. That the reference dataset can be substantially smaller than the study datasets without having much impact on the precision of our estimator is encouraging, given that accessing a reference dataset with a large sample size may be difficult in practice.
Fig. 1.
Root mean square errors, RMSE, of the of genmeta estimators for (a) 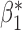 , (b)
, (b) 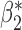 and (c)
and (c) 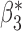 with fixed study sample sizes
with fixed study sample sizes 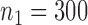 ,
, 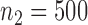 and
and 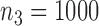 and varying reference sample size
and varying reference sample size 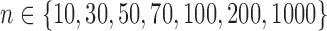 : genmeta.0, circles and solid line; genmeta.1, triangles and dashed line; genmeta.2, plus signs and dotted line.
: genmeta.0, circles and solid line; genmeta.1, triangles and dashed line; genmeta.2, plus signs and dotted line.
Finally, we conduct additional simulation studies to gain more insight into results from the real-data analysis. The settings are similar to those described above, except that we assume there are only two studies: study I fits the maximal logistic regression model involving all three covariates, while study II involves only two covariates, 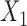 and
and 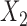 . We assume
. We assume 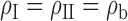 . In our estimation, we further incorporated an added complexity to account for study-specific intercept terms for the maximal logistic regression model,
. In our estimation, we further incorporated an added complexity to account for study-specific intercept terms for the maximal logistic regression model,
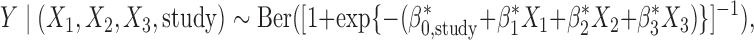 |
so that the prevalence of the outcome, 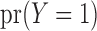 , could be different across the two studies. In this setting, the maximal set of parameters that are to be estimated through genmeta can be defined as
, could be different across the two studies. In this setting, the maximal set of parameters that are to be estimated through genmeta can be defined as 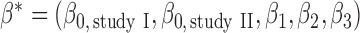 . We simulated data using values of intercept parameters that are identical for the two models, but for estimation we allowed the intercept parameters to be different. For the sake of comparison, we also fitted a reduced model for study I and conducted a standard multivariate meta-analysis of the underlying common parameters associated with
. We simulated data using values of intercept parameters that are identical for the two models, but for estimation we allowed the intercept parameters to be different. For the sake of comparison, we also fitted a reduced model for study I and conducted a standard multivariate meta-analysis of the underlying common parameters associated with 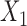 and
and 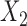 across the two studies. We took the sample sizes for the two studies to be
across the two studies. We took the sample sizes for the two studies to be 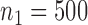 and
and 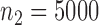 , and that for the reference dataset to be
, and that for the reference dataset to be 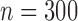 .
.
Table 2 shows that in this simulation setting the reduced models produce biased estimates for 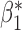 , but not for
, but not for 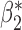 . The result is intuitive given that the omitted covariate
. The result is intuitive given that the omitted covariate 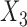 is primarily correlated with
is primarily correlated with 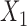 . As a result, standard meta-analysis was nearly unbiased for
. As a result, standard meta-analysis was nearly unbiased for 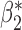 , but not for
, but not for 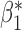 . Parameter estimates from the maximal model in study I are unbiased for all parameters, but have much larger standard errors compared to those obtained from meta-analysis for estimation of
. Parameter estimates from the maximal model in study I are unbiased for all parameters, but have much larger standard errors compared to those obtained from meta-analysis for estimation of 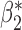 . Our generalized meta-anlysis estimator produced unbiased estimates for all the parameters and, at the same time, has efficiency comparable to standard meta-analysis for estimation of
. Our generalized meta-anlysis estimator produced unbiased estimates for all the parameters and, at the same time, has efficiency comparable to standard meta-analysis for estimation of 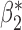 . These results highlight a desirable feature of our estimator, namely that it can effectively combine information across studies to minimize bias due to omitted covariates, and yet utilize all the information available across the partially informative studies.
. These results highlight a desirable feature of our estimator, namely that it can effectively combine information across studies to minimize bias due to omitted covariates, and yet utilize all the information available across the partially informative studies.
Table 2.
A simulation for understanding the real-data analysis: point estimates and standard deviations from logistic regression with reduced and maximal models, meta-analysis, and genmeta estimation with 
| Study I | Study II | Meta-analysis | genmeta | |||
|---|---|---|---|---|---|---|
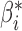
|
Maximal PE (SD) | Reduced PE (SD) | Reduced PE (SD) | Reduced PE (SD) | Reduced PE (SD) | Maximal PE (SD) |
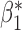
|
0.270 (0.149) | 0.429 (0.116) | 0.424 (0.037) | 0.424 (0.035) | 0.425 (0.035) | 0.268 (0.088) |
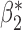
|
0.263 (0.111) | 0.243 (0.112) | 0.236 (0.035) | 0.236 (0.034) | 0.237 (0.034) | 0.263 (0.039) |
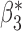
|
0.258 (0.136) | NA | NA | NA | NA | 0.255 (0.135) |
PE, point estimate; SD, standard deviation; NA, no corresponding estimator.
3.3. Heterogeneous population
We now conduct simulation studies where the underlying assumption of homogeneity of the covariate distribution across populations may be violated in various ways. As a benchmark for comparison, setting (I) will be the same as the one we simulated under the homogeneous population. In setting (II), we allow the means and/or variances to vary across the populations, underlying the studies and the reference sample, while keeping the correlations constant. Specifically, the mean vector for the three covariates can take one of three possible values: 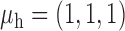 ,
, 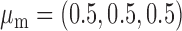 and
and 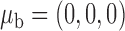 . Similarly, the variance vector is allowed to vary across three possible sets of values:
. Similarly, the variance vector is allowed to vary across three possible sets of values: 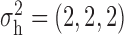 ,
,  and
and 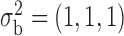 . In setting (III), we allow the correlations among the covariates to vary across populations; here we also consider three possible sets of correlation vectors, namely
. In setting (III), we allow the correlations among the covariates to vary across populations; here we also consider three possible sets of correlation vectors, namely  ,
, 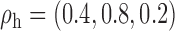 and
and 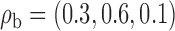 . In simulation setting (IV), we allow for potentially different inclusion criteria across studies, leading to possible violations of the assumption of homogeneity of the covariate distribution. Specifically, we first simulate an underlying study base using the set-up described in simulation setting (I), and then for study I we keep only individuals with
. In simulation setting (IV), we allow for potentially different inclusion criteria across studies, leading to possible violations of the assumption of homogeneity of the covariate distribution. Specifically, we first simulate an underlying study base using the set-up described in simulation setting (I), and then for study I we keep only individuals with 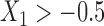 and
and 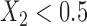 , while in study II we keep individuals with
, while in study II we keep individuals with 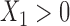 . Finally, we consider an alternative simulation scenario where we assume that the covariates are log-normally distributed by defining
. Finally, we consider an alternative simulation scenario where we assume that the covariates are log-normally distributed by defining 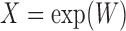 , where
, where  is generated from a multivariate normal distribution following the same settings as in (I)–(IV) above.
is generated from a multivariate normal distribution following the same settings as in (I)–(IV) above.
When the covariates are normally distributed, we observe that the proposed method is not very sensitive to the underlying assumption of homogeneity of the covariate distribution; see Table 3. In setting (II), where the means and/or variances of the covariates vary across the populations, but the correlations are fixed, there is virtually no bias. In setting (III), where the correlations are varied, we observe more noticeable, but still small, biases in the parameter estimates. In setting (IV), where the inclusion criteria vary across studies, there is also very minimal bias. When the covariates are log-normally distributed, however, the method can be more sensitive to violation of the underlying homogeneity assumption; see the Supplementary Material. In particular, when the inclusion criteria varied across studies in setting (IV), large bias in point estimates and low coverage probability were observed for estimation of the coefficient associated with 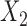 , the covariate which is used to define fairly non-overlapping inclusion criteria across two studies. Notably, even in this scenario, minimal bias is observed for estimation of the other covariates in the model.
, the covariate which is used to define fairly non-overlapping inclusion criteria across two studies. Notably, even in this scenario, minimal bias is observed for estimation of the other covariates in the model.
Table 3.
Robustness of generalized meta-analysis estimation: results for the genmeta estimates using the study covariance estimators in the setting of logistic regression. In setting (I), data are simulated in the ideal setting where the covariate distribution, characterized by the mean, standard deviation and correlation of normal variates, is the same across all populations. In settings (II)–(IV), the assumption is violated by creating variations in means and/or standard deviations, correlations, and selection criteria across the studies and the reference sample. The vectors of covariate means, variances and correlations are denoted by 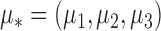 ,
, 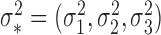 and
and 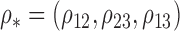 for
for 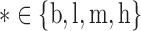 , where
, where 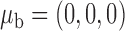 ,
, 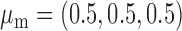 ,
, 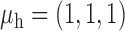 ,
, 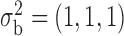 ,
, 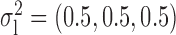 ,
, 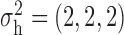 ,
, 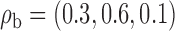 ,
, 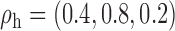 and
and 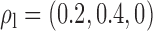 . Estimated standard deviation is obtained from the asymptotic formula (1) and used to construct
. Estimated standard deviation is obtained from the asymptotic formula (1) and used to construct 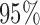 confidence intervals
confidence intervals
| Setting | Study I | Study II | Study III | Reference |
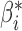
|
Bias | SD (ESD) | RMSE | CR | AL |
|---|---|---|---|---|---|---|---|---|---|---|
| I |
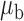
|
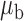
|
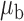
|
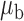
|
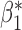
|
0.001 | 0.111 (0.112) | 0.111 | 0.947 | 0.437 |
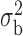
|
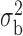
|
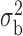
|
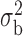
|
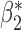
|
 0.002 0.002 |
0.098 (0.099) | 0.098 | 0.956 | 0.389 | |
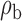
|
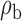
|
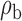
|
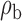
|
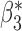
|
0.005 | 0.096 (0.098) | 0.096 | 0.954 | 0.382 | |
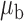
|
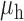
|

|

|
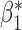
|
0.010 | 0.103 (0.104) | 0.103 | 0.952 | 0.405 | |
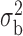
|
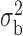
|
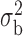
|

|
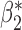
|
 0.006 0.006 |
0.083 (0.083) | 0.083 | 0.954 | 0.324 | |
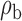
|
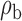
|
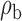
|
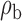
|

|
0.005 | 0.085 (0.088) | 0.085 | 0.956 | 0.343 | |
| II |
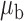
|
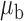
|
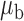
|
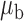
|
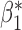
|
0.003 | 0.139 (0.136) | 0.139 | 0.939 | 0.529 |
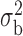
|
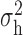
|
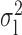
|
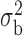
|
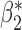
|
 0.003 0.003 |
0.084 (0.086) | 0.084 | 0.956 | 0.335 | |
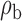
|
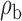
|
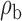
|
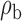
|
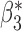
|
0.003 | 0.112 (0.111) | 0.112 | 0.949 | 0.431 | |
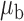
|
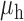
|
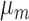
|
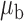
|
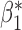
|
0.013 | 0.124 (0.126) | 0.125 | 0.946 | 0.493 | |
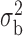
|
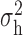
|
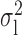
|
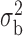
|
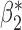
|
 0.006 0.006 |
0.073 (0.075) | 0.073 | 0.958 | 0.291 | |
|
|
|
|
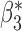
|
0.005 | 0.097 (0.100) | 0.097 | 0.949 | 0.391 | |
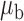
|
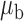
|
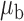
|
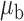
|
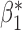
|
 0.092 0.092 |
0.142 (0.151) | 0.169 | 0.958 | 0.579 | |
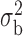
|
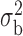
|
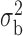
|
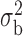
|
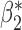
|
0.019 | 0.105 (0.109) | 0.107 | 0.963 | 0.423 | |
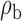
|
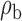
|
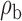
|
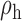
|
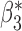
|
0.053 | 0.120 (0.129) | 0.131 | 0.971 | 0.495 | |
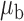
|
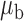
|
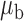
|
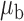
|

|
0.035 | 0.099 (0.099) | 0.106 | 0.917 | 0.385 | |
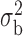
|
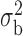
|
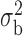
|
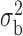
|
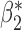
|
0.002 | 0.096 (0.096) | 0.096 | 0.954 | 0.377 | |
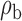
|
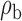
|
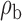
|
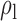
|
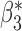
|
0.012 | 0.087 (0.087) | 0.088 | 0.944 | 0.343 | |
| III |
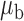
|
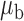
|
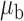
|
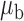
|
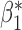
|
0.060 | 0.113 (0.113) | 0.128 | 0.916 | 0.443 |
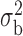
|
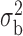
|
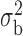
|
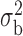
|
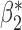
|
 0.001 0.001 |
0.096 (0.097) | 0.096 | 0.955 | 0.379 | |
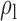
|
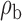
|
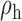
|
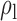
|
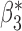
|
 0.006 0.006 |
0.103 (0.102) | 0.104 | 0.944 | 0.398 | |
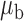
|
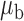
|
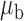
|
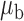
|
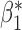
|
0.039 | 0.130 (0.132) | 0.135 | 0.939 | 0.515 | |
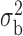
|
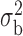
|
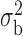
|

|
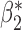
|
 0.006 0.006 |
0.097 (0.100) | 0.097 | 0.958 | 0.392 | |
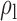
|
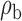
|

|
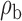
|
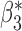
|
 0.027 0.027 |
0.116 (0.118) | 0.119 | 0.944 | 0.461 | |
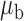
|
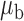
|

|
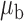
|
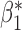
|
 0.036 0.036 |
0.165 (0.173) | 0.169 | 0.957 | 0.671 | |
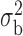
|
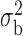
|
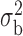
|
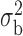
|
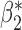
|
0.013 | 0.103 (0.109) | 0.104 | 0.962 | 0.424 | |
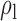
|
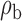
|
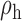
|
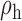
|
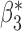
|
0.003 | 0.143 (0.153) | 0.143 | 0.959 | 0.591 | |
| IV |
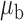
|
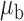
|
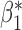
|
0.014 | 0.123 (0.127) | 0.124 | 0.961 | 0.494 | ||
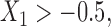
|
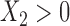
|
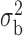
|
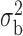
|
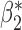
|
 0.008 0.008 |
0.105 (0.109) | 0.105 | 0.965 | 0.428 | |
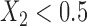
|
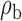
|
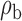
|
|
 0.001 0.001 |
0.094 (0.093) | 0.093 | 0.958 | 0.366 |
SD, standard deviation; ESD, estimated standard deviation; RMSE, square root of mean square error; CR, coverage rate of 95% confidence intervals; AL, average length of 95% confidence intervals.
3.4. Power evaluation of the diagnostic test
We assess the power of the proposed test statistic,  , in the presence of heterogeneity in the regression parameters,
, in the presence of heterogeneity in the regression parameters, 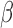 , across the studies. In the context of standard multivariate meta-analysis, where it is assumed that all the studies ascertain the same set of covariates, the test for heterogeneity is performed using the standard multivariate Cochran’s test-statistic
, across the studies. In the context of standard multivariate meta-analysis, where it is assumed that all the studies ascertain the same set of covariates, the test for heterogeneity is performed using the standard multivariate Cochran’s test-statistic
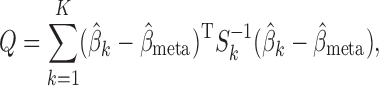 |
where 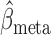 is the usual multivariate meta-analysis estimate and
is the usual multivariate meta-analysis estimate and 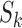 is the standard error of
is the standard error of 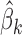 for
for 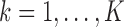 . We will use
. We will use 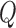 as a benchmark to evaluate the power of
as a benchmark to evaluate the power of 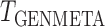 .
.
In all simulations, as before, we assume that there are three separate studies, and that the relationship between a binary outcome variable 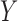 and three covariates
and three covariates 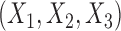 in each study follows the same logistic regression model of the form (6). However, instead of assuming a fixed set of
in each study follows the same logistic regression model of the form (6). However, instead of assuming a fixed set of 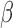 across all studies, we simulate different values of
across all studies, we simulate different values of 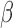 from a normal distribution with mean
from a normal distribution with mean 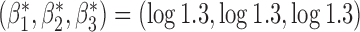 and variance
and variance 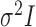 , where the parameter
, where the parameter 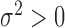 is varied to control the degree of heterogeneity across studies. As before, we assume that
is varied to control the degree of heterogeneity across studies. As before, we assume that 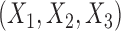 follows a multivariate normal distribution with zero mean, unit variance and underlying correlations
follows a multivariate normal distribution with zero mean, unit variance and underlying correlations 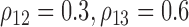 and
and  for the three studies. We simulate data for the different studies from the above random-effects logistic regression model and then fit reduced models of the form (7) to the three studies. In particular, we assume that
for the three studies. We simulate data for the different studies from the above random-effects logistic regression model and then fit reduced models of the form (7) to the three studies. In particular, we assume that 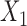 and
and 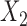 are included in study I,
are included in study I, 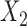 and
and 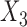 in study II, and
in study II, and 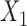 and
and 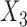 in study III. We fix the sample sizes of the studies at
in study III. We fix the sample sizes of the studies at 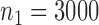 ,
, 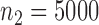 and
and 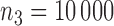 , and vary the sample size of the reference dataset. The level of the test is set to 5%. For comparison, we also fit the maximal model to each study involving all three covariates and apply the standard
, and vary the sample size of the reference dataset. The level of the test is set to 5%. For comparison, we also fit the maximal model to each study involving all three covariates and apply the standard 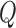 -statistic for testing heterogeneity.
-statistic for testing heterogeneity.
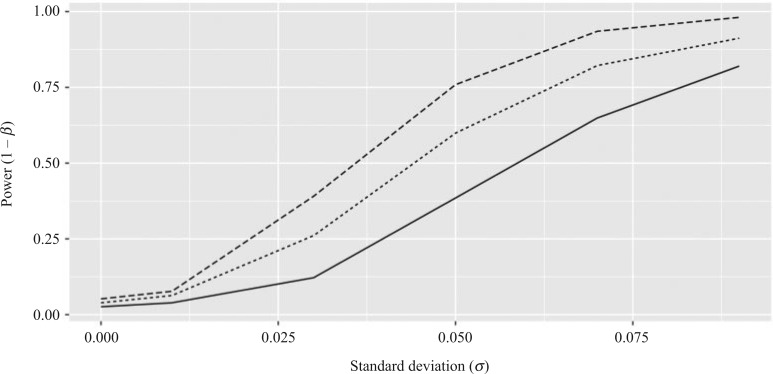
Comparison of the power of 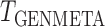 and of the
and of the 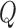 -statistic shows that, as expected, the power for both tests increases as a function of the degree of heterogeneity,
-statistic shows that, as expected, the power for both tests increases as a function of the degree of heterogeneity, 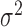 ; see Fig. 2. Clearly,
; see Fig. 2. Clearly, 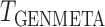 suffers some loss of power as it deals with the missing covariates, but it retains enough power, even with a small reference dataset (
suffers some loss of power as it deals with the missing covariates, but it retains enough power, even with a small reference dataset (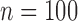 ), to remain practically useful.
), to remain practically useful.
Fig. 2.
Power curves of the simple multivariate meta-analysis test statistic, 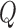 , and
, and 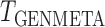 for simulated datasets: the simple meta-analysis estimator (dashed) and genmeta estimators with reference data sample sizes of 100 (solid) and 500 (dotted). The level of the test is set to 0.05.
for simulated datasets: the simple meta-analysis estimator (dashed) and genmeta estimators with reference data sample sizes of 100 (solid) and 500 (dotted). The level of the test is set to 0.05.
4. Real-data analysis
In this section we illustrate application of the proposed method by developing a model for predicting the risk of breast cancer using a combination of different risk factors based on data from multiple studies. The first study, the Breast Prostate Colorectal Cancer Cohort, BPC3, study, includes a total of 7448 cases and 8812 controls, drawn from eight different underlying cohorts. Details of the study, including its recent application to the development of a breast cancer risk prediction model, can be found in Mass et al. (2016). Here we focus on the analysis of breast cancer risk associated with a selected set of factors, including family history, age at menarche, age at first birth, and body weight. The second study is the Breast Cancer Detection and Demonstration Project, BCDDP, with a dataset containing 1217 cases and 1616 controls. The study has previously been used to develop an updated version of the widely popular Breast Cancer Risk Assessment tool (Chen et al., 2006) that incorporates mammographic density, the areal proportion of breast tissue that is radiographically dense, which is known to be a strong risk factor for breast cancer. The dataset from the BCDDP study contains mammographic density and the number of previous breast biopsies, in addition to all the factors considered in the BPC3 data analysis. Let 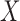 denote the common set of covariates measured across both studies, and let
denote the common set of covariates measured across both studies, and let  represent the factors available only in BCDDP. The goal is to estimate parameters associated with an underlying logistic regression model that includes all of the different factors. While the BPC3 study is large in size and represents multiple populations, it has information on a more limited number of risk factors. The BCDDP study, on the other hand, has information on an extended set of risk factors, but is much smaller in size. A combined analysis of these two studies can potentially yield more generalizable and precise estimates of risk parameters.
represent the factors available only in BCDDP. The goal is to estimate parameters associated with an underlying logistic regression model that includes all of the different factors. While the BPC3 study is large in size and represents multiple populations, it has information on a more limited number of risk factors. The BCDDP study, on the other hand, has information on an extended set of risk factors, but is much smaller in size. A combined analysis of these two studies can potentially yield more generalizable and precise estimates of risk parameters.
Throughout the analysis, we use a sample of 137 cases and 163 controls from the BCDDP study as the reference sample, based on which the distribution of covariates is estimated. To maintain independence of the reference and study samples, we exclude the reference sample from the primary analysis of the BCDDP study, which involves estimation of the log-odds-ratio parameters. Further, both of the studies involve case-control sampling with similar case-control proportions. In general, if nonrandom sampling is used for selection of subjects in any of the studies, then the covariate distribution underlying the genmeta estimating equation needs to be adjusted to account for the study design. In this application, because we had access to the BCDDP study, we could adjust for the design effect by simply selecting a reference sample that includes cases and controls in a similar ratio to that in the main studies. In general, however, the effect of nonrandom sampling design for the main studies may need to be accounted for through careful weighting of subjects in the reference sample.
For each of the eight cohorts in the BPC3 study and for the BCCDP study, we first fit a reduced logistic regression model including 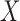 . All models include age as an additional cofactor as well as study-specific intercept parameters and age effects. Specifically, we consider underlying models of the form
. All models include age as an additional cofactor as well as study-specific intercept parameters and age effects. Specifically, we consider underlying models of the form
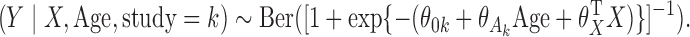 |
(8) |
We applied the diagnostic test for model violation to these datasets. We found the value of the test-statistic, 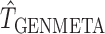 , to be 59.01 and the corresponding
, to be 59.01 and the corresponding 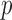 -value to be 0.366 under a
-value to be 0.366 under a 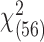 distribution. Hence, it appears that the underlying model assumptions are unlikely to be grossly violated in this application.
distribution. Hence, it appears that the underlying model assumptions are unlikely to be grossly violated in this application.
First, to illustrate how our proposed estimator compares with the standard meta-analysis method, we estimate the common underlying parameters of interest 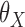 using these two methods. We fitted model (8) separately for each study and obtained estimates of the parameters and covariance matrices. Then, for the underlying common parameter of interest
using these two methods. We fitted model (8) separately for each study and obtained estimates of the parameters and covariance matrices. Then, for the underlying common parameter of interest 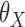 , we conducted a standard multivariate meta-analysis using the corresponding subset of parameter estimates and covariance matrices. Alternatively, using the parameter estimates and variance-covariance matrices from the individual studies, and using the BCDDP sample that was set aside as the reference dataset to estimate the joint distribution of
, we conducted a standard multivariate meta-analysis using the corresponding subset of parameter estimates and covariance matrices. Alternatively, using the parameter estimates and variance-covariance matrices from the individual studies, and using the BCDDP sample that was set aside as the reference dataset to estimate the joint distribution of 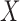 and Age, we estimated all the parameters of model (8) using our procedure. From the results reported in Table 4, it can be seen that in this setting the meta-analysis and our estimators produce similar estimates and corresponding standard errors across all the different risk factors of interest. In one of the results stated earlier, we saw theoretically that in an idealized setting, where all the models and underlying populations are identical, the two estimators are asymptotically equivalent. It is encouraging to observe the close correspondence between the estimators in the data analysis, which involves a diverse set of studies that are likely to have significant heterogeneity across the underlying populations. In particular, for a number of the risk factors, such as family history, coefficient estimates were noticeably different for the two studies. When significant heterogeneity existed, the meta-analysed estimates were pooled closer to those from the BPC3 study because of its large sample size.
and Age, we estimated all the parameters of model (8) using our procedure. From the results reported in Table 4, it can be seen that in this setting the meta-analysis and our estimators produce similar estimates and corresponding standard errors across all the different risk factors of interest. In one of the results stated earlier, we saw theoretically that in an idealized setting, where all the models and underlying populations are identical, the two estimators are asymptotically equivalent. It is encouraging to observe the close correspondence between the estimators in the data analysis, which involves a diverse set of studies that are likely to have significant heterogeneity across the underlying populations. In particular, for a number of the risk factors, such as family history, coefficient estimates were noticeably different for the two studies. When significant heterogeneity existed, the meta-analysed estimates were pooled closer to those from the BPC3 study because of its large sample size.
Table 4.
Real-data analysis results comparing meta-analysis and our generalized meta-analysis method: combined analysis of the BCDDP and BPC3 studies to develop a multivariate logistic regression model for breast cancer risk. For each cohort within BPC3 and for BCDDP, the standard logistic regression model is used to fit reduced models; parameter estimates of the reduced models across studies are then combined using standard meta-analysis or genmeta. For the BCDDP study, a maximal logistic model is fitted including two additional covariates. These estimates are then combined with estimates of reduced model parameters from BPC3 to obtain genmeta estimates of the maximal model
| BPC3 | ||||||||
|---|---|---|---|---|---|---|---|---|
| CPS2 | EPIC | MCCS | MEC | NHS | PLCO | WHI | WHS | |
| Risk factors | cohort PE (SE) | cohort PE (SE) | cohort PE (SE) | cohort PE (SE) | cohort PE (SE) | cohort PE (SE) | cohort PE (SE) | cohort PE (SE) |
| FH | 0.47 (0.13) | 0.29 (0.15) | 0.56 (0.19) | 0.41 (0.28) | 0.48 (0.08) | 0.39 (0.13) | 0.30 (0.06) | 0.28 (0.19) |
| AMEN1 |
 0.03 (0.14) 0.03 (0.14) |
0.02 (0.09) |
 0.19 (0.17) 0.19 (0.17) |
 0.09 (0.24) 0.09 (0.24) |
0.06 (0.09) |
 0.05 (0.12) 0.05 (0.12) |
0.13 (0.08) | 0.03 (0.17) |
| AMEN2 |
 0.09 (0.17) 0.09 (0.17) |
0.04 (0.12) |
 0.44 (0.23) 0.44 (0.23) |
0.35 (0.35) | 0.19 (0.10) | 0.03 (0.15) | 0.19 (0.09) | 0.14 (0.19) |
| AFB1 | 0.28 (0.17) | 0.12 (0.14) |
 0.08 (0.25) 0.08 (0.25) |
0.06 (0.17) | 0.39 (0.20) | 0.16 (0.14) | 0.19 (0.09) | 0.92 (0.23) |
| AFB2 | 0.73 (0.24) | 0.24 (0.17) | 0.35 (0.30) | 0.05 (0.26) | 0.36 (0.22) | 0.52 (0.22) | 0.44 (0.13) | 0.96 (0.28) |
| WT1 | 0.09 (0.14) |
 0.01 (0.09) 0.01 (0.09) |
0.22 (0.18) | 0.09 (0.17) | 0.21 (0.08) | 0.09 (0.13) |
 0.03 (0.08) 0.03 (0.08) |
 0.01 (0.14) 0.01 (0.14) |
| WT2 | 0.16 (0.14) | 0.24 (0.11) | 0.45 (0.19) |
 0.08 (0.18) 0.08 (0.18) |
0.10 (0.08) | 0.09 (0.13) | 0.18 (0.08) |
 0.16(0.15) 0.16(0.15) |
| BCDDP | Meta-analysis | GENMETA | |||
|---|---|---|---|---|---|
| Risk factors | Maximal model PE (SE) | Reduced model PE (SE) | Reduced model PE (SE) | Reduced model PE (SE) | Maximal model PE (SE) |
| FH | 0.80 (0.14) | 0.80 (0.14) | 0.40 (0.04) | 0.42 (0.04) | 0.37 (0.08) |
| AMEN1 | 0.11 (0.10) | 0.07 (0.10) | 0.04 (0.04) | 0.03 (0.04) | 0.04 (0.06) |
| AMEN2 | 0.55 (0.15) | 0.45 (0.15) | 0.13 (0.05) | 0.13 (0.05) | 0.32 (0.08) |
| AFB1 | 0.06 (0.14) | 0.18 (0.15) | 0.21 (0.05) | 0.20 (0.05) | 0.05 (0.09) |
| AFB2 | 0.29 (0.20) | 0.46 (0.20) | 0.38 (0.06) | 0.38 (0.07) | 0.21 (0.12) |
| WT1 | 0.29 (0.11) | 0.09 (0.11) | 0.08 (0.04) | 0.08 (0.04) | 0.31 (0.07) |
| WT2 | 0.52 (0.13) | 0.10 (0.13) | 0.14 (0.04) | 0.14 (0.04) | 0.63 (0.09) |
| NBIOPS | 0.13 (0.09) | NA | NA | NA | 0.13 (0.10) |
| MD | 0.46 (0.05) | NA | NA | NA | 0.43 (0.06) |
FH, binary indicator of family history; AMEN, age at menarche; AMEN1 and AMEN2, dummy variables associated with age-at-menarche categories 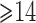 ,
, 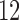 –
–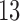 and
and 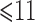 ; AFB, age at first live birth; AFB1 and AFB2, dummy variables associated with age-at-first-live-birth categories
; AFB, age at first live birth; AFB1 and AFB2, dummy variables associated with age-at-first-live-birth categories 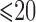 ,
, 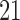 –
–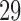 and
and 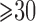 ; WT, weight; WT1 and WT2, dummy variables associated with weight categories
; WT, weight; WT1 and WT2, dummy variables associated with weight categories 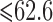 ,
, 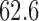 –
–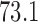 and
and 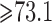 in kilograms; NBIOPS, number of previous biopsies coded as a continuous variable; MD, standardized mammographic density coded as a continuous variable; PE, point estimate; SE, standard error; NA, no corresponding estimator. CPS2, EPIC, MCCS, MEC, NHS, PLCO, WHI and WHS, abbreviated names of the eight cohorts of BPC3.
in kilograms; NBIOPS, number of previous biopsies coded as a continuous variable; MD, standardized mammographic density coded as a continuous variable; PE, point estimate; SE, standard error; NA, no corresponding estimator. CPS2, EPIC, MCCS, MEC, NHS, PLCO, WHI and WHS, abbreviated names of the eight cohorts of BPC3.
Next, we turn our attention to the analysis of data from the BCDDP study using a maximal model that includes 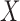 and the additional covariates, mammographic density and number of previous breast biopsies. Comparison of the parameter estimates associated with
and the additional covariates, mammographic density and number of previous breast biopsies. Comparison of the parameter estimates associated with  across the maximal and reduced models within the BCDDP study indicates major differences in the estimates of the coefficients associated with weight. In the maximal model, higher weight is found to be much more strongly associated with increased risk of breast cancer. The unmasking of the effect of weight in the maximal model is intuitive, given that body weight and mammographic density are known to have a strong negative correlation. Although not as dramatic, there are some differences in the effects of age at menarche and age at first birth between the maximal and reduced models, also possibly due to the modest correlation of these factors with mammographic density and the number of previous breast biopsies. The effect of family history, however, is almost identical across the two models.
across the maximal and reduced models within the BCDDP study indicates major differences in the estimates of the coefficients associated with weight. In the maximal model, higher weight is found to be much more strongly associated with increased risk of breast cancer. The unmasking of the effect of weight in the maximal model is intuitive, given that body weight and mammographic density are known to have a strong negative correlation. Although not as dramatic, there are some differences in the effects of age at menarche and age at first birth between the maximal and reduced models, also possibly due to the modest correlation of these factors with mammographic density and the number of previous breast biopsies. The effect of family history, however, is almost identical across the two models.
Finally, we used our generalized meta-anlysis method to combine estimates of the parameters of the maximal model from the BCDDP study and those from the reduced models for the eight BPC3 cohorts. We assumed an underlying maximal model of interest across the nine studies:
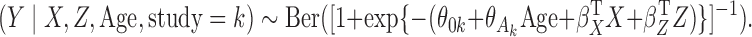 |
We observe that our generalized meta-analysis approach produces estimates of the effect of family history and associated standard error that are very similar to those based on standard meta-analysis of the reduced models across the nine cohorts. The estimate is pooled heavily towards the BPC3 study due to its large sample size. In contrast, the genmeta estimates for weight are very similar to those obtained from the maximal model only within the BCDDP study. These results are consistent with the simulation studies, in which genmeta behaves similarly to reduced-model meta-analysis when omitted covariates do not cause notable bias. In contrast, when omitted covariates cause considerable bias, our estimator is pooled towards estimates from maximal or more complete models that may be available from a restricted set of studies. The behaviour of genmeta for the other two covariates, age at menarche and age at first birth, was in between, which is also intuitive given that we observed their coefficients to have changed notably, but less dramatically, in the maximal model as compared to the reduced model within the BCDDP study. The genmeta parameter estimates and standard errors for the additional variables of mammographic density and number of previous breast biopsies were similar to those observed for the maximal model in the BCDDP study, the only study for which information was available on these two factors. Thus, overall the data analysis demonstrates that our estimator behaves in a similar manner to meta-analysis for combining information across multiple possibly heterogeneous studies, but it has added flexibility to effectively combine information from disparate models.
5. Discussion
The proposed method can be viewed as a natural extension of the traditional fixed-effect meta-analysis method that is widely used in practice. Our simulation studies and data analysis demonstrate that the method not only provides theoretically valid and efficient inference in idealized conditions, but also can perform robustly in non-idealized settings. A critical element of the proposed method is access to a reference dataset. While the ideal choice of reference dataset will vary by application, publicly available survey data, which contain information on a wide variety of factors, can be useful broadly. In fact, in large-scale genetic association studies, reference samples such as the 1000 Genomes Project are commonly used for estimating correlation parameters across genetic markers in the genome (The 1000 Genomes Project Consortium, 2012, 2015; Lee et al., 2013). For epidemiological studies, good sources of a reference dataset for the U.S. population include the National Health Interview Survey (Adams et al., 1999; Botman & Moriarity, 2000; Bloom et al., 2010) and the National Health and Nutrional Examination Survey (Fang & Alderman, 2000; He et al., 2001; de Ferranti et al., 2006; Idler & Angel, 2011; LaKind et al., 2012), which routinely collect data on a wide range of health- and lifestyle-related factors. If multiple studies coordinate through a consortium effort, which is becoming increasingly common in biomedical applications, then studies that have the most complete information, at least on some subsamples, can provide a reference sample.
When information on all covariates is not available in a single reference sample, one may have to consider using simulation to generate such data by combining information from multiple studies under some modelling assumptions. As access to large reference datasets can be difficult, researchers may find two aspects of our approach appealing. First, the sample size for the reference dataset can be small relative to the study datasets, and yet our generalized meta-analysis approach can have reasonable efficiency. In fact, increasing the sample size for the reference dataset beyond a certain threshold does not have an impact on the efficiency of our method. Secondly, although technically our method requires all the populations underlying the studies and the reference dataset to be the same, in practice the method can be robust against a reasonable degree of heterogeneity in the distribution of covariates. However, it is possible to have a large bias when estimating coefficients associated with covariates that have been used to define widely varying inclusion criteria. When different studies follow very different designs, it is best to obtain study-specific reference samples for estimating the underlying moment equations. Alternatively, it may be possible to modify a large reference sample by using study-specific sampling weights or inclusion criteria when estimating the moment equations. Dealing with study-specific covariates, such as centres within a study, can also pose challenges, as information on such variables is not expected to be available from a common reference sample. We have illustrated in our data example that it is possible to deal with such variables by imposing additional independence assumptions from other factors. In general, such complications need to be dealt with on a case-by-case basis, and some study-specific reference samples may be needed to avoid making strong assumptions. Further research is merited to explore these and other practical challenges in implementation of the proposed method.
In general, we believe that caution is needed for interpretations and applications of models developed by combining information from disparate models across multiple studies. A model developed from a single study with complete information may be inefficient and lack generalizability, but it is more likely to be internally consistent and thus can provide valid etiologic inference even if it is not representative of the general population. On the other hand, etiologic interpretation of parameters can be difficult when the underlying model is developed using information across multiple studies that are potentially heterogeneous. For predictive models, where the focus is not so much on parameter interpretation, development of rich models by combining information across multiple studies and then validating such models in independent studies can be an appealing strategy. These and other practical issues related to model development using multiple data sources have also been discussed in several recent articles (Wang et al., 2015; Han & Lawless, 2017; Cheng et al., 2019; Estes et al., 2018).
In this article we have used generalized method of moments as the underlying inferential framework. Alternatively, inference could be performed using empirical likelihood theory (Qin & Lawless, 1994; Qin, 2000; Chatterjee et al., 2016), exploiting the same set of moment equations as we propose. While in small samples empirical likelihood estimators may perform better, their implementation can be substantially more complex. Recently, a simulation-based method has also been proposed for combining information on model parameters across disparate studies (Rahmandad et al., 2017). Computationally, our method may enjoy substantial advantages in dealing with complex models, such as those in high-dimensional settings, where repeated model fitting on simulated data is extensive. Further research is needed in multiple directions to increase the practical utility of genmeta. It is possible that in some applications we may have information only on subsets of parameters underlying the fitted reduced models. It is an open question as to how such partial information can be used to set up the underlying moment equations in the genmeta procedure. Ideally, to increase robustness of inference, the procedure should use study-specific reference samples for setting up the moment equations. For this purpose, it may be useful to develop strategies to combine information on a common reference sample with complete covariate information and data from individual studies that have partial covariate information.
Supplementary Material
Acknowledgement
This research was funded through a Patient-Centered Outcomes Research Institute Award, and the National Institutes of Health. The statements and opinions in this article are solely the responsibility of the authors and do not necessarily represent the views of the Patient-Centered Outcomes Research Institute, its Board of Governors or its Methodology Committee. Chatterjee is also affiliated with the Department of Oncology at Johns Hopkins University.
Appendix
Assumptions of Theorem 1
Assumptions A1–A4 are for consistency, and Assumptions A5–A9 are for asymptotic normality:
Assumption A1.
is positive semidefinite and
if and only if
;
Assumption A2.
, which is compact;
Assumption A3.
is continuous for each
with probability 1, where
is a neighbourhood of
for
;
Assumption A4.
for
;
Assumption A5.
is continuous at each
with probability 1, where
is a neighbourhood of
;
Assumption A6.
;
Assumption A7.
is continuous at each
with probability 1;
Assumption A8.
;
Assumption A9.
exists and is finite, and
is of full rank.
Details of Assumption A1
In practice it is sometimes difficult to check the global identification condition. This motivates us to investigate conditions for local identifiability or, equivalently, the invertibility of the matrix of second derivatives at the true parameter, i.e.,  (Rothenberg, 1971; Engle & McFadden, 1994), assuming
(Rothenberg, 1971; Engle & McFadden, 1994), assuming 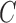 is a positive-definite matrix. The condition can be stated in terms of the equivalent sample version of the matrix, given by
is a positive-definite matrix. The condition can be stated in terms of the equivalent sample version of the matrix, given by 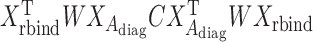 . As
. As  is a positive-definite matrix, the entire local identifiability condition for the sample version then boils down to
is a positive-definite matrix, the entire local identifiability condition for the sample version then boils down to 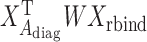 being a matrix of full column rank. A sufficient condition for this is the matrix
being a matrix of full column rank. A sufficient condition for this is the matrix 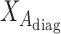 to have information on all the covariates of the maximal model. In other words, the individual covariates in the maximal model have to be part of at least one of the reduced models.
to have information on all the covariates of the maximal model. In other words, the individual covariates in the maximal model have to be part of at least one of the reduced models.
Supplementary material
Supplementary material available at Biometrika online includes all the derivations, the proof of Theorem 1, and a table containing the simulation results for log-normally distributed covariates. The R (R Development Core Team, 2019) package GENMETA is available on CRAN at https://cran.r-project.org/package=GENMETA.
References
- Adams, P. F., Hendershot, G. E. & Marano, M. A. (1999). Current estimates from the National Health Interview Survey, 1996. Vital Health Statist. 10, 1–203. [PubMed] [Google Scholar]
- Bloom, B., Cohen, R. & Freeman, G. (2010). Summary health statistics for U.S. children: National Health Interview Survey, 2009. Vital Health Statist. 10, 1–82. [PubMed] [Google Scholar]
- Botman, S. & Moriarity, C. L. (2000). Design and estimation for the National Health Interview Survey, 1995–2004. Vital Health Statist. 2, 1–31. [PubMed] [Google Scholar]
- Breslow, N. E. & Cain, K. C. (1988). Logistic regression for two-stage case control data. Biometrika 75, 11–20. [Google Scholar]
- Breslow, N. E. & Holubkov, R. (1997). Maximum likelihood estimation for logistic regression parameters under two-phase, outcome-dependent sampling. J. R. Statist. Soc. B 59, 447–61. [Google Scholar]
- Bulik-Sullivan, B. K., Loh, P.-R., Finucane, H., Ripke, S., Yang, J., Patterson, N., Daly, M. J., Price, A. L. & Neale, B. M. (2015). LD score regression distinguishes confounding from polygenicity in genome-wide association studies. Nature Genet. 47, 291–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatterjee, N., Chen, Y. H., Mass, P. & Carroll, R. (2016). Constrained maximum likelihood estimation for model calibration using summary-level information from external big data sources. J. Am. Statist. Assoc. 111, 891–921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, J., Pee, D., Ayyagari, R., Graubard, B., Schairer, C., Byrne, C., Benichou, J. & Gail, M. H. (2006). Projecting absolute invasive breast cancer risk in white women with a model that includes mammographic density. J. Nat. Cancer Inst. 98, 1215–26. [DOI] [PubMed] [Google Scholar]
- Cheng, W., Taylor, J. M. G., Gu, T., Tomlins, S. A. & Mukherjee, B. (2019). Informing a risk prediction model for binary outcomes with external coefficient information. Appl. Statist. 68, 121–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chun, W., Chen, M. & Schifano, E. (2015). Statistical methods and computing for big data. arXiv: 1502.07989v2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Ferranti, S. D., Gauvreau, K., Ludwig, D. S., Newburger, J. W. & Rifai, N. (2006). Inflammation and changes in metabolic syndrome abnormalities in US adolescents: Findings from the 1988–1994 and 1999–2000 National Health and Nutrition Examination Surveys. Clin. Chem. 52, 1325–30. [DOI] [PubMed] [Google Scholar]
- Dersimonian, R. & Laird, N. (1986). Meta-analysis in clinical-trials. Contr. Clin. Trials 7, 177–88. [DOI] [PubMed] [Google Scholar]
- Dersimonian, R. & Laird, N. (2015). Meta-analysis in clinical trials revisited. Contemp. Clin. Trials 45, 139–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engle, R. & McFadden, D. (1994). Handbook of Econometrics. Amsterdam: North Holland. [Google Scholar]
- Estes, J. P., Mukherjee, B. & Taylor, J. M. G. (2018). Empirical Bayes estimation and prediction using summary-level information from external big data sources adjusting for violations of transportability. Statist. Biosci. 10, 568–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan, J., Han, F. & Liu, H. (2014). Challenges of big data analysis. Nat. Sci. Rev. 1, 293–314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang, J. & Alderman, M. (2000). Serum uric acid and cardiovascular mortality: The NHANES I epidemiologic follow-up study, 1971–1992. J. Am. Med. Assoc. 283, 2404–10. [DOI] [PubMed] [Google Scholar]
- Han, P. & Lawless, J. F. (2017). Empirical likelihood estimation using auxiliary summary information with different covariate distributions. Statist. Sinica, DOI: 10.5705/ss.202017.0308. [DOI] [Google Scholar]
- Hansen, L. P. (1982). Large sample properties of generalized method of moments estimators. Econometrica 50, 1029–54. [Google Scholar]
- He, J., Ogden, L., Bazzano, L., Vupputuri, S., Loria, C. & Whelton, P. (2001). Risk factors for congestive heart failure in US men and women: NHANES I epidemiologic follow-up study. Arch. Intern. Med. 161, 996–1002. [DOI] [PubMed] [Google Scholar]
- Idler, E. L. & Angel, R. J. (2011). Self-rated health and mortality in the NHANES-I epidemiologic follow-up study. Am. J. Public Health 80, 446–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Imbens, G. W. (2002). Generalized method of moments and empirical likelihood. J. Bus. Econ. Statist. 20, 493–506. [Google Scholar]
- Ioannidis, J. P. A. (2005). Meta-analysis in public health: Potentials and problems. Eur. J. Public Health 15, 60–1. [Google Scholar]
- Jackson, D., Riley, R. & White, I. R. (2011). Multivariate meta-analysis: Potential and promise. Statist. Med. 30, 2481–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan, M. I. (2013). On statistics, computation and scalability. Bernoulli 19, 1378–90. [Google Scholar]
- Kavvoura, F. K. & Ioannidis, J. P. A. (2008). Methods for meta-analysis in genetic association studies: A review of their potential and pitfalls. Hum. Genet. 123, 1–14. [DOI] [PubMed] [Google Scholar]
- LaKind, J. S., Goodman, M. & Naiman, D. Q. (2012). Use of NHANES data to link chemical exposures to chronic diseases: A cautionary tale. PLoS One 8, 1295–302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee, S. H.,, Yang, J.,, Chen, G. B.,, Ripke, S.,, Stahl, E. A.,, Hultman, C. M.,, Sklar, P.,, Visscher, P. M.,, Sullivan, P. F.,, Goddard, M. E., et al. (2013). Estimation of SNP heritability from dense genotype data. Am. J. Hum. Genet. 93, 1151–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin, D. Y. & Zeng, D. (2010). On the relative efficiency of using summary statistics versus individual-level data in meta-analysis. Biometrika 97, 321–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mass, P.,, Barrdahl, M.,, Joshi, A. D.,, Auer, P. L.,, Gaudet, M. M.,, Milne, R. L.,, Schumacher, F. R.,, Anderson, W. F.,, Check, D.,, Chattopadhyay, S., et al. (2016). Breast cancer risk from modifiable and nonmodifiable risk factors among white women in the United States. JAMA Oncol. 2, 1295–302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathew, T. & Nordstrom, K. (1999). On the equivalence of meta-analysis using literature and using individual patient data. Biometrics 55, 1221–3. [DOI] [PubMed] [Google Scholar]
- McCullagh, P. & Nelder, J. A. (1989). Generalized Linear Models. Boca Raton, Florida: Chapman & Hall/CRC, 2nd ed. [Google Scholar]
- Olkin, I. & Sampson, A. (1998). Comparison of meta-analysis versus analysis of variance of individual patient data. Biometrics 54, 317–22. [PubMed] [Google Scholar]
- Pasaniuc, B. & Price, A. L. (2017). Dissecting the genetics of complex traits using summary association statistics. Nature Rev. Genet. 18, 117–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qin, J. (2000). Combining parametric and empirical likelihoods. Biometrika 87, 484–90. [Google Scholar]
- Qin, J. & Lawless, J. (1994). Empirical likelihood and general estimating equations. Ann. Statist. 22, 300–25. [Google Scholar]
- R Development Core Team (2019). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria: ISBN 3-900051-07-0. http://www.R-project.org. [Google Scholar]
- Rahmandad, H., Jalali, M. S. & Paynabar, K. (2017). A flexible method for aggregation of prior statistical findings. PloS One 12, e0175111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritz, J., Demidenko, E. & Spiegelman, D. (2008). Multivariate meta-analysis for data consortia, individual patient meta-analysis, and pooling projects. J. Statist. Plan. Infer. 138, 1919–33. [Google Scholar]
- Rothenberg, T. (1971). Identification in parametric models. Econometrica 39, 577–91. [Google Scholar]
- Scott, A. J. & Wild, C. J. (1997). Fitting regression models to case-control data by maximum likelihood. Biometrika 84, 705–17. [Google Scholar]
- The 1000 Genomes Project Consortium (2012). An integrated map of genetic variation from 1,092 human genomes. Nature 491, 56–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The 1000 Genomes Project Consortium (2015). A global reference for human genetic variation. Nature 526, 68–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Houwelingen, H. C., Arends, L. R. & Stijnen, T. (2002). Advanced methods in meta-analysis: Multivariate approach and meta-regression. Statist. Med. 21, 589–624. [DOI] [PubMed] [Google Scholar]
- Wacholder, S. & Carroll, R. J. (1994). The partial questionnaire design for case-control studies. Statist. Med. 13, 623–34. [DOI] [PubMed] [Google Scholar]
- Wang, F., Song, P. X.-K. & Wang, L. (2015). Merging multiple longitudinal studies with study-specific missing covariates: A joint estimating function approach. Biometrics 71, 929–40. [DOI] [PubMed] [Google Scholar]
- Whittemore, A. (1997). Multistage sampling designs and estimating equations. J. R. Statist. Soc. B 59, 589–602. [Google Scholar]
- Yang, J., Ferreira, T., Morris, A. P., Medland, S. E., Madden, P. A., Heath, A. C., Martin, N. G., Montgomery, G. W., Weedon, M. N. & Loos, R. J. (2012). Conditional and joint multiple-SNP analysis of GWAS summary statistics identifies additional variants influencing complex traits. Nature Genet. 44, 369–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu, Z.,, Zhang, F.,, Hu, H.,, Bakshi, A.,, Robinson, M. R.,, Powell, J. E.,, Montgomery, G. W.,, Goddard, M. E.,, Wray, N. R.,, Visscher, P. M., et al. (2016). Integration of summary data from GWAS and eQTL studies predicts complex trait gene targets. Nature Genet. 48, 481–7. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.