Tuning the “Violin” of Protein Kinases: The Role of Dynamics-Based Allostery

Abstract

The intricacies of allosteric regulation of protein kinases continue to engage the research community. Allostery, or control from a distance, is seen as a fundamental biomolecular mechanism for proteins. From the traditional methods of conformational selection and induced fit, the field has grown to include the role of protein motions in defining a dynamics-based allosteric approach. Harnessing of these continuous motions in the protein to exert allosteric effects can be defined by a “violin” model that focuses on distributions of protein vibrations as opposed to concerted pathways. According to this model, binding of an allosteric modifier causes global redistribution of dynamics in the protein kinase domain that leads to changes in its catalytic properties. This model is consistent with the “entropy-driven allostery” mechanism proposed by Cooper and Dryden in 1984 and does not require, but does not exclude, any major structural changes. We provide an overview of practical implementation of the violin model and how it stands amidst the other known models of protein allostery. Protein kinases have been described as the biomolecules of interest. © 2019 IUBMB Life, 71(6):685–696, 2019

Protein function especially in the context of signaling enzymes like protein kinases requires careful molecular control and regulation (1). Allostery plays a crucial role in this regard, and the field has seen considerable growth with an exponential expansion of structural data being available. Allosteric mechanisms of protein regulation presently include the role of various post-translational modifications, protein–protein interaction, and distal amino acid variations, as well as the classic binding of small molecule effectors at sites “other” than the active site (2, 3). Various experimental and theoretical methods have been developed to study the allosteric regulation of proteins, and specific cases show increasing levels of complexity. Although the role of allostery cannot be emphasized enough, it has been difficult to agree upon a unified theory of allostery that may be applicable across all protein forms (4) (Table 1).

TABLE 1.

Comparing conformation-based and dynamics-based allostery

Conformation-based allostery

Dynamics-based allostery

Defined by two distinct end states/conformations in the free energy landscape Defined by the “enthalpic” component of free energy allosteric effector binding Two models used to describe this allostery include the classical MWC (conformational selection) and KNF (induced fit) models “Ensemble model” aims to include the role of dynamics in conformation-based allostery Hydrophobic “spines” of protein kinases provide a way to harness conformation-based allostery to trap selective activation states

Defined by molecular fluctuations and protein dynamics around a defined conformation in the same free energy well Defined by the “entropic” component of the free energy allosteric effector binding Two models used to describe this allostery include description of pathways of (domino) model and “violin” model Dynamics-based allostery in context of enzymes is critical for understanding the molecular workings of distal sites in the context of their catalytic cycles “Community maps” of protein kinases allow for exploration of dynamics-based allostery and its impact on the kinase catalytic cycle

CONFORMATION-BASED ALLOSTERY

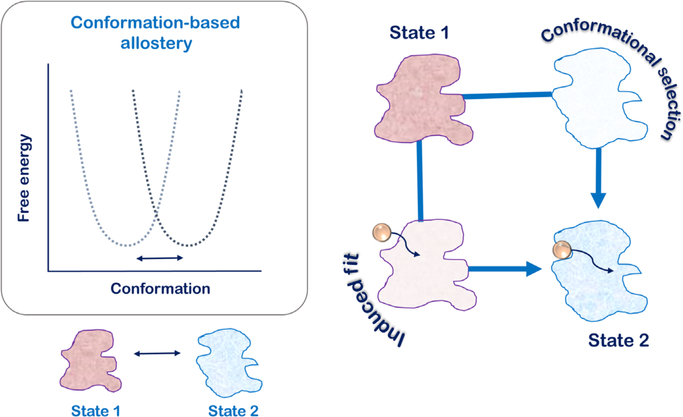
The central idea of allostery emphasizes that molecular alterations in the protein albeit away from the active site allow for maneuvering of its active site and mechanistic functions. This first concept of allosteric regulation was described in 1957 for L-threonine deaminase using feedback inhibition by L-isoleucine as an allosteric control (5). The exact term “allostery” was however introduced by Changeux and coworkers while describing the switching of the quaternary structure of oligomeric proteins between two T- and R-states (6, 7). This classical concept relied on switching of protein oligomers between two predefined states that formed two distinct basins in the free-energy landscape of the protein (Fig. 1). The transiting pathways that allowed for this conformational switching were defined by two discrete models. The first model was of “conformational selection,” also popularly known as the “population-shift model” was described by Monod, Wyman, and Changeux (hence also called the MWC model) (8). In this model, protein oligomers simultaneously populated the two T- and R-states and the allosteric effector selected for a particular state and stabilized it over the other. As the equilibrium fluctuated to accommodate allosteric effector binding, more and more protein oligomer populations shifted from one basin to the other in the free-energy landscape (9). The second model of transitions between the T- and R-states relies on sequential changes in the protein’s quaternary structure as determined by alterations in the protein–protein interfaces of the subunits. This model known as the “induced fit model” defined by Koshland, Nemethy, and Filmer (hence also called the KNF model) explains that allosteric effectors and protein conformational change from one to the other are sequential and continuous (Fig. 1).

FIG 1.

The classical model of allostery is based on structural descriptions of two end states that are defined by two discrete basins in the free energy landscape of the protein. Transition between the two states defines conformation-based allostery into paths: the “induced-fit”/KNF model and the “conformation-selection”/MWC model. As decided by the allosteric effector, one path may be taken over the other, but at any given time, significant flux is expected to be present in both pathways.

In both scenarios of the classical MWC and KNF models, the thermodynamic processes of the allosteric mechanism are defined by two end states and every conformation is argued to have an equilibrium probability in accordance with the Boltzmann equation (10). The models are defined by distinct kinetic intermediates such that the relative contributions of the two models in maneuvering the properties of the protein are decided by the rate of conformational switching between the two states as well as the rate of allosteric effects (11). In the KNF model, the allosteric effector initiates a conformational change in the protein such that the kinetic intermediate is apoprotein-like with a loosely bound effector. In contrast, the intermediate of the MWC model is the bound conformation that is eventually stabilized by effector binding (Fig. 1). Depending on the molecular scenario, one kinetic intermediate may be chosen over the other, but a significant fraction of flux is expected to occur through both pathways (11). In this way, this definition of allostery is purely structural and only depends on the end states with little emphasis on the exact pathways that may be connecting them.

CONFORMATION-BASED ALLOSTERY IN PROTEIN KINASES: THE ROLE OF HYDROPHOBIC “SPINES”

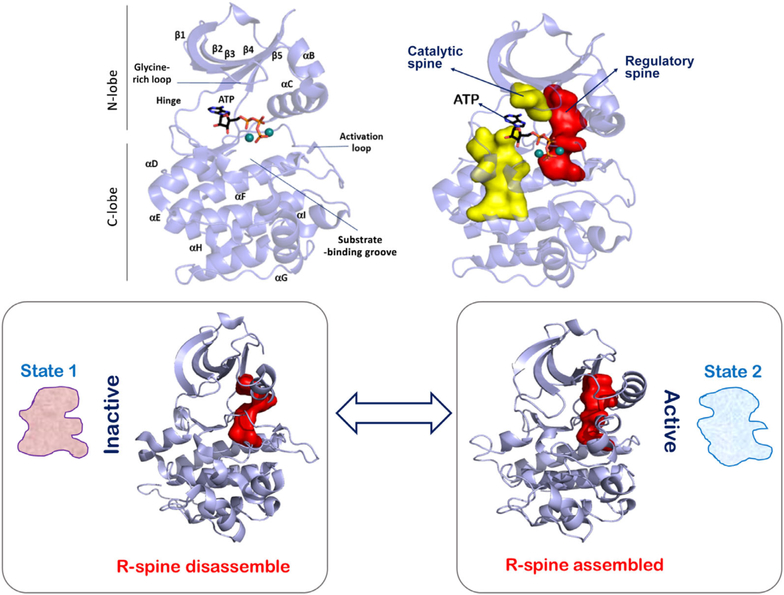
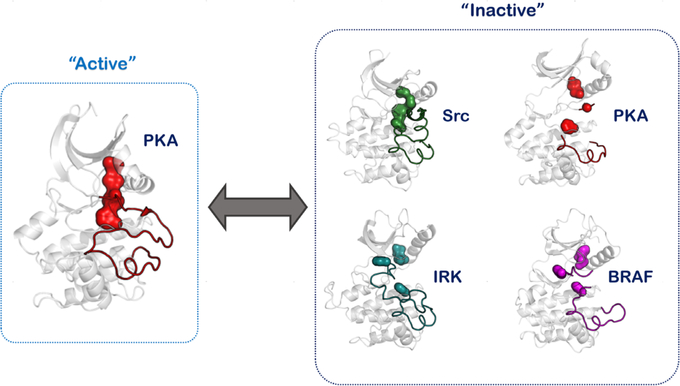
Conformation-based allostery can be defined for protein kinases using their “inactive” versus “active” conformations (12). The catalytic domain of protein kinases is a 250 amino acid bilobal structure that has a small N-lobe and a larger C-lobe (Fig. 2). A deep cleft between the two lobes forms the nucleotide-binding pocket with residues from both lobes contributing to ATP binding (13). Flexibility between the N- and C-lobes allows for nucleotide exchange at the kinase active site as ATP is used up and ADP is generated in each catalytic cycle (14, 15). Interlobal flexibility and maneuvering are mediated by two hydrophobic motifs that span the two lobes and rest on the large αF-helix of the large C-lobe (16, 17). These hydrophobic motifs have been defined as the “spines” in being analogous to the spinal cord of vertebrates that provides both support and flexibility to the animal anatomy. Comparison of the structural kinome provides a deep-seated link between these spines and the activation switch of protein kinases. Essentially, as the active conformations of protein kinases are necessarily similar and require the optimal orientation of their active site residues, the hydrophobic spine of the active structure is similar and unique to the conformation. The spine that is associated with activation is referred to as the regulatory spine (R-spine), and the assembled R-spine is a signature of the “active” kinase state. The second kinase spine is referred to as the catalytic spine (C-spine) as it completes upon nucleotide binding and primes the kinase for phosphotransfer reactions (18). It is worth appreciating that while the R-spine can be disassembled in various ways (that are typically specific to the inactive states of the particular kinase), the assembled R-spine is virtually conserved in all kinase-active structures (Fig. 3) (19). In this simplification, the conformational allostery between the inactive and active kinase states can be narrowed down to the conformational signature of the assembly of the R-spine residues at the core of the kinase domain.

FIG 2.

The conserved kinase core harbors a hydrophobic motif known as the regulatory or R-spine. An assembled R-spine is the signature of the “active” kinase conformation. This assembly and disassembly of the R-spine in accordance with effects like activation loop phosphorylation and kinase dimerization forms a conformation-based allosteric descriptor of protein kinase activation.

FIG 3.

The kinase R-spine can be disassembled in many ways, indicating that the “inactive” state is specific to the kinase. The R-spine-assembled conformation defines the “active” conformation that is conserved for the superfamily of proteins.

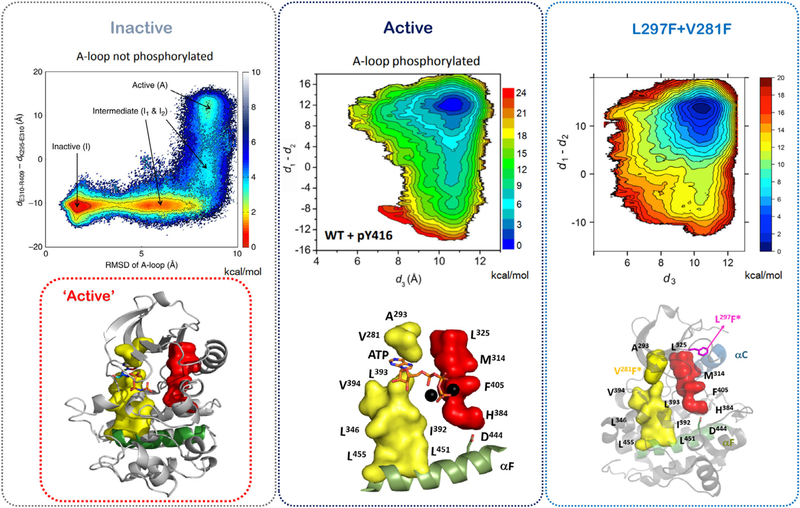
A clear example of this conformational allostery in the conserved kinase core is available for the nonreceptor tyrosine kinase, Src, which plays a crucial role in regulating many cellular processes (20–22). The conformational transition between the inactive and active states of the Src catalytic domain has been assessed by unbiased long MD simulations that use the theoretical framework of transition pathway theory (TPT) and Markov state modeling (MSM) to map out the conformational landscape of the protein (20, 23). The two-dimensional energy landscape of Src shows the presence of two intermediates I₁ and I₂ that connect the active and inactive states (Fig. 4). In the first intermediate I₁, the activation loop of the catalytic domain is unfolded and the conserved salt bridges Lys295 and Glu310 are not fully formed. The second intermediate I₂ resembles the active conformation more closely, but has the αC helix in the outward inactive conformation. Interestingly, this intermediate explains the atypical targeting of kinases by small molecules like 8-anilino-1-napthalene sulfonate (ANS) that can bind between the αC helix and the β4 element to trap a partially active kinase conformation (24). At the core of the kinase, this free energy landscape essentially means that there are two energy basins in which one is the inactive R-spine disassembled form and the other is the active R-spine assembled form (21,22). An allosteric effect like the phosphorylation of the activation loop of Src at Tyr416 is thought to shift the equilibrium to favor the population of catalytically capable Src (Fig. 4). Further studies try to recapitulate the effect of this allosteric effect by a direct manipulation of the hydrophobic spines (21, 22). By increasing the hydrophobicity of the R-spine with the L295F mutant and fusing the C-spine by using a bulky V281F mutation, structurally one is able to switch the equilibrium to favor the active conformation/basin in the free energy landscape (Fig. 4). Allosterically, it means that a core motif in the catalytic domain allows for selection of the two conformational states of any given kinase. Biochemical studies have shown this to be true for constitutive activation of Braf, Craf, protein kinase A (PKA), RIP2, Abl, and many more kinases (19, 25–27).

FIG 4.

Computational umbrella-sampling-based assessment of conformation-based allostery in the Src kinase domain. The free energy landscape shows the presence of “inactive” and “active” conformation basins and also two intermediates. Assembly of the R-spine by activation loop phosphorylation or the L297F/V281F double mutant shifts the Src populations into the “active” basin of the free energy landscape. Data are adapted from references 21–23.

DYNAMICS-BASED ALLOSTERY

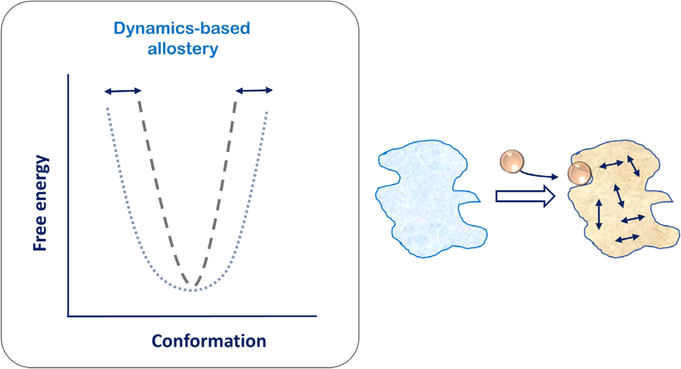
In 1970, Perutz introduced an early model for communication between the allosteric site and active site of proteins (28). This model as proposed for hemoglobin was based on structure-function correlations and tried to explain how oxygen binding to the heme group would trigger movements in neighboring helices and allow for switching of hemoglobin conformation from one state to the other. Though not explicitly obvious at that time, these studies paved the way for understanding the dynamics-based approach for allostery that was distinct from the conformational paradigm (29, 30). This concept as popularized by Cooper and Dryden relies on dynamic changes or fluctuations in the protein conformational state that are limited to the basin of the free energy landscape of the protein (Fig. 5). They postulated that dynamic allostery can be primarily an entropic effect that could be experimentally examined using the protein normal modes or mean-square atomic displacements (30). They noted that dynamic changes around the average structure of a protein could account for intramolecular communication between distinct binding sites. Moreover, this communication held true even in situations of the apoprotein where no ligand may be present bound to any sites. This concept of entropy-based dynamic allostery attracted exponential interest from the research community as it was increasingly realized that allostery is not a characteristic of oligomeric proteins alone (31,32). Monomeric proteins also show functionally important allosteric regulation (33, 34) and demonstrate that the concept of allostery is not limited to ligand binding but also includes distal mutations, protein–protein interactions, and covalent modifications that can serve as crucial allosteric effectors (35, 36).

FIG 5.

Internal motions of the protein allow for dynamics-based allostery wherein the conformation of the protein is limited to the same free energy basin. Reorganization of internal motions of the protein allow for allosteric effects that are entropically driven.

Various approaches have been harnessed to explore the role of protein dynamics in the context of allostery. Dynamic properties of proteins can be defined by time-dependent processes such as timescale, amplitudes, and spatiotemporal correlations of internal motions (37), and different NMR experimental setups can help analyze conformational dynamics at various timescales (38). An increased complementarity between MD simulations and protein NMR has allowed for a greater appreciation of this concept in recent times. While clear evidence emerged that dynamics plays a crucial role in allostery of proteins (39), it was also difficult to demonstrate with certainty that allosteric effects were carried out by dynamics alone (40). Hence, a more cohesive model integrating dynamics with structural allostery was introduced with the understanding that there may be changes in structure (due to dynamic fluctuations) that evade experimental exploration. This model of allostery is the “ensemble model” where dynamics here conservatively refers to the fluctuations of the structure of the protein under equilibrium conditions. As the protein samples an ensemble of conformations in the same energy basin, there are structural conformations at play that determine the shape of the said basin (33, 41). The extent of conformational sampling is limited by the allosteric effectors that allow for stabilizing the ensemble in a particular population that is a subpart of the bigger population of the free energy basin. The relative stability of the various conformations in the ensemble in turn decides the extent of communication between the allosteric effector and the active site (42). As described for Src kinase previously, this approach links the classical models of allostery to the internal fluctuations of the protein (21, 22). The model substantiates how protein dynamics lies at the center of classic understanding of conformational switching, but is a more statistical approach as opposed to the deterministic MWC or KNF models (43). In this way, the free energy landscape of the protein is also considered dynamic, indicating that allostery can be explained by both enthalpic and entropic contributions (10, 44). MD simulation-based Markov state modeling is used to generate microstates based on structural similarity, and the rates of switching between these microstates can be calculated from the simulation trajectory (45,46). However, strictly speaking, the ensemble model of allostery is not entirely entropy based. Although fluctuations in the protein structure giving rise to a dynamic ensemble are a reflection of entropy, the reverse is not necessarily true. Binding of ligands or substrate to a protein can lead to entropic changes with release of water molecules from these binding sites providing an entropic gain to the system but not necessarily to the protein. Also, this model does not account for entropic compensation in proteins where regions of a protein can become rigidified in places where ligands bind but become more flexible in other regions (47).

Given the recent literature on dynamics-based allostery, three lines of thought emerge that substantiate the link between dynamics and allostery. The first thought process determines that allosteric effects are purely thermodynamic in nature and dynamics is a by-product of allosteric effects. In this way, an allosteric effector will increase substrate binding to the protein by reducing the flexibility of the active site residues, thereby priming the protein to bind the substrate better. This pre-organization of the protein active site leads to a lower entropic cost for the reaction process (41, 48). The opposite thought process argues that while protein dynamics may not provide for a defined thermodynamic end state, the rate of conformational transitions can determine allostery (49). In this view, configurational entropy of the side chains of proteins, which are essentially the fast timescale motions of the protein, is responsible for the allosteric communication between various sites in the protein (39). For enzymatic proteins, a third view emerges that extends the role conformational dynamics of enzyme to participation in their reaction pathways. As the enzymatic reaction can be described by three rate constants of substrate binding, formation of products, and product release, it becomes imperative to understand that protein dynamics influences these three steps. Allosteric effectors can influence the millisecond timescale dynamics of enzymes and directly affect their kinetic constants (50–52).

The origin of dynamics-based allosteric effects has been explained by perturbations caused in the interiors of the protein as the allosteric effector exerts it function. These perturbations are then dissipated through the entire protein leading to dynamic and/or structural changes in the protein (53, 54). It has been suggested that the dynamic communication between the allosteric effects and the active site is defined via molecular pathways in the interior of proteins (42, 55, 56). Moreover, there are speculations that these pathways are predefined and evolutionarily conserved in protein families (56). The major criticism of this approach is a bit fundamental as it ignores the thermodynamics of reciprocity in binding of an allosteric effector and substrate to the protein. The free energy change for the formation of a ternary complex (protein with substrate and allosteric ligand) from the apoprotein form is the same whether the substrate binds first or the binding of allosteric ligand precedes substrate binding. This implies that these two binding events if connected by a pathway should have a bidirectional allosteric communication between them. Hence, any predefined path that connects the substrate binding and allosteric binding site should allow for bidirectional information transfer. Indeed, it has been very difficult to prove this bidirectionality, and mostly the described allosteric pathways are unidirectional (57, 58). Recently, it has also been demonstrated that the choice of methods used to explore these allosteric pathways can influence the outcomes such that only the sought-after pathways become visible in the examined context (59). This indicates that residue interaction networks in the protein interior are too complex to be explained by a simplistic connectivity of linear pathways.

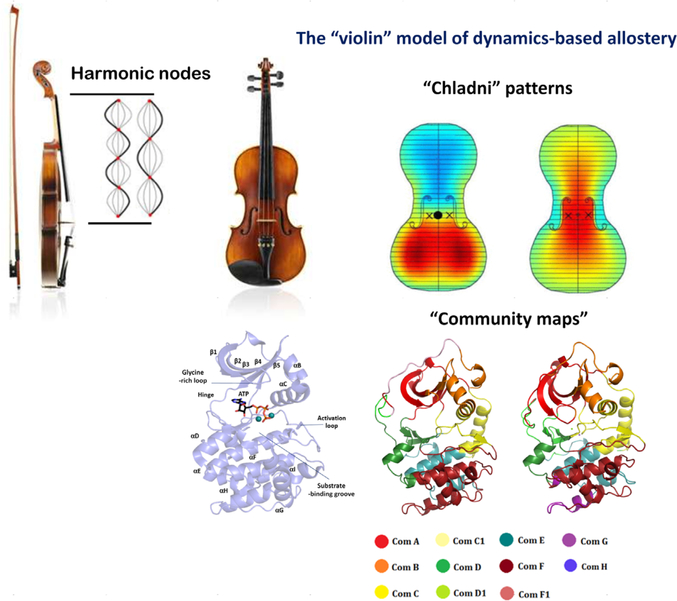
In light of elusive explanations but growing importance of dynamics allostery, we introduced the “violin” model of dynamics-based allostery with the premise that protein dynamics is robust, malleable to perturbation, and prone to remodeling/redistribution (Fig. 6) (3, 61). It can be argued that this phenomenon can be derived from the fundamental properties of proteins that can be viewed as a set of interacting oscillators (62). In the case of violin as a music instrument, a bow is used to excite the strings into vibrations and generate a harmonic note (63). The strength of each such harmonic note is transferred to the body of the violin such that the entire violin plate vibrates with the note. Parts of the violin plate move synchronously, while others not so much. These vibrations create an acoustic pattern on the violin plates called a “Chladni pattern” (Fig. 6) (63). Each harmonic frequency as played on the violin registers a specific Chladni pattern on the top and bottom plates (64). In this way, the entire violin plate vibrates with the note being played, and changing the pitch of the node by altering the pressure on the fingerboard is realized by the body of the violin that redistributes vibration patterns to develop another Chladni pattern (60). Using this analogy, we argue that the protein kinase domain functions like the plates of the violin and reorganizes its dynamics in accordance with the allosteric signal, much like the violin plates reorganize their vibrations with the note played on the stem. Mathematically, as the Chladni patterns show the redistribution of vibrations on the violin plate, our “community map” analysis allows for studying the redistribution of dynamics in the protein kinase domain (Fig. 6) (3, 61). In this way, the violin model recapitulates the founding argument of Cooper and Dryden where vibrations/fluctuations from the entire protein would participate in allosteric communication (30). In the context of protein kinases in particular, this method has been very fruitful in understanding the role of distal regions/mutations in the catalytic domain and how these regions alter dynamics-based allosterics of the kinase core to change its kinetic properties (61, 65, 66). Recently, our violin model has been used to understand dynamics-based allostery in protein families other than kinases. Examples include exploration of red light–sensing bacteriophytochromes associated with cyclic dimeric guanosine monophosphate–producing diguanylyl cyclases (67) and the zinc metallopeptidase neurolysin (68).

FIG 6.

The “violin” model of dynamics-based allostery. Harmonic nodes at the stem of the violin create a “Chladni pattern” on the body of the violin. These Chladni patterns are descriptors of parts of the body of the violin that vibrate in sync or out of sync. Each harmonic creates a distinct Chladni pattern. Using this analogy, we argue that a protein kinase domain works like the body of a violin wherein the internal vibrations/motions of the protein are remodeled based on the allosteric effector. Every effector creates a distinct “community map” much like a distinct Chladni pattern for each harmonic of the violin. Chladni patterns were taken from reference 60. Colored regions of the violin denote the regions that vibrate together. This is analogous to the “communities” of residues in the protein structure that share the same dynamics-based information.

COMPUTATIONAL METHODOLOGY FOR EXPLORING THE VIOLIN MODEL: THE “COMMUNITY MAPS”

The reductionist approach simplifies proteins into “ball-and-spring” models, where each residue of the protein is defined only by its Cα atom and each such “ball” is connected to other balls of the protein by harmonic springs (69). This elastic network model (ENM) (or the Gaussian network model (GNM)) in combination with the analysis of the normal mode vibration analysis of the proteins neatly describes long-range allosteric communication in the interiors of proteins (70). The active and inactive conformations of the insulin receptor kinase, ABL tyro-sine kinase, RAC-alpha serine/threonine-protein kinase B (PKB), and cyclin-dependent protein kinase (CDK2) have been explored using these coarse-grained approaches (71). This study describes the kinase core to be formed by “blocks” of residues that serve as semirigid bodies. The number and distributions of these blocks decide the allosteric activation of these kinases from the inactive to the active form. Active kinase structures of three of the mentioned kinases have central “loop” block that includes residues of the R-spine.

The more complex models borrow and expand upon the concepts of graph-theory based methods. A protein composed of N residues is denoted by the same number of nodes and mapped onto a weighted graph. Then two aspects of this graph become relevant in this network analysis. The first being the connections between the nodes and the second concerns the exchange of information between these connections. The simplest methods used static structures of proteins with a resolution-based cutoff to define an adjacency matrix such that the edge weight of a connection is considered as 1 when within the cutoff and 0 when outside (72). In this approach, as the value of 1 is assumed for each path length of every edge, the total path length connecting any two nodes is simply the number of edges that connect them (72, 73). Indeed the allosteric site and active site can be connected by multiple paths, and in this context, the shortest path connecting them is deemed most relevant (73). The authors of these studies also found a direct correlation between the positions of the thermal fluctuations of the residues as predicted by the Gaussian model and the average shortest path connecting one residue to the other. The more complex models of making these matrixes use interresidue interaction strength instead of a distance cutoff (74). Another approach uses “messenger nodes” to understand the allosteric communication wherein certain nodes with high entropies are shared in the network with higher probabilities (75). As MD simulations have gained popularity, some of the best methods now use the quasiequilibrium states of proteins that are limited around a single conformation basin (76). Mutual information or contact maps are used to create residue information matrices from submicrosecond MD trajectories (77, 78). The Girvan–Newman algorithm (79) of social networks has been employed to divide the matrices/graph into “communities” (3, 78). Essentially, the method partitions the graph into groups based on nodes that are densely connected by the edges from those that are sparsely connected. The “betweenness” of the intercommunity edge is high as all the intercommunity paths must be contained in it. The algorithm is iterative and systematically chooses for edges at every step until every node becomes isolated and becomes a community of its own. However, partitioning of the graph in proteins is carefully chosen based on a “modularity” where intuitively the fraction of intracommunity edges maximally exceed the number or random connection paths in the graph. The major advantage of this MD simulation-based method is that it takes into account the role of both main-chain and side-chain dynamics of each residue of the protein. This is critical for understanding of allosteric coupling between the communities (80).

THE “COMMUNITY NETWORK” OF PROTEIN KINASES

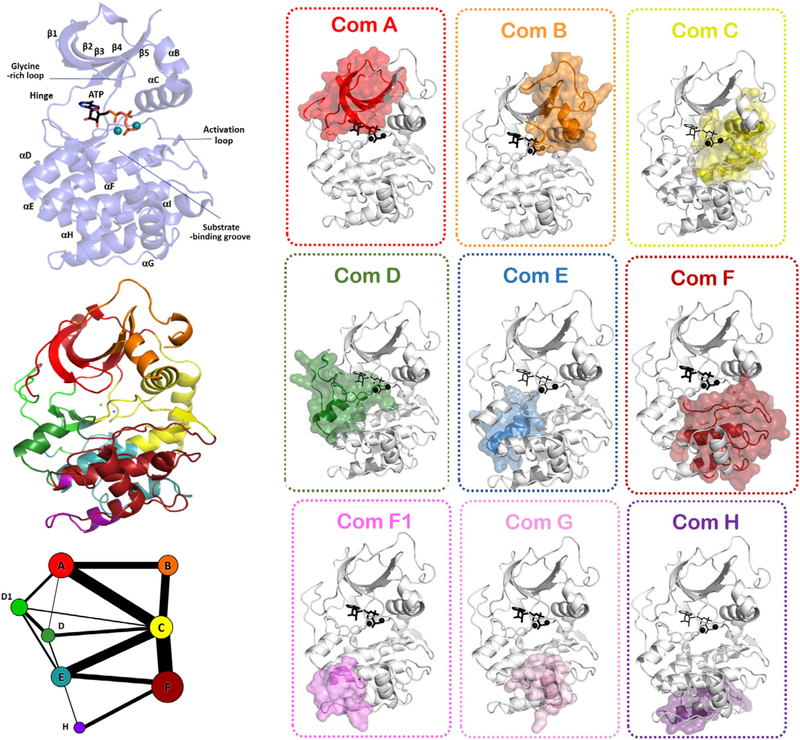
Multiple microsecond molecular dynamics (MD) simulations on PKA have allowed for exploration of the community map of its dynamics-based allostery (Fig. 7) (61, 78). Essentially, each such community map of the protein is a Chladni pattern for violin frequencies as described above in the violin model (Fig. 6). Using the most appropriate modularity cutoffs, PKA can be described to be made of about eight communities of 40–60 amino acid residues. The expansive structural and biochemical data on PKA have also allowed for attributing these communities with biological functions. Community A has the amino acid residues that orchestrate ATP binding at the active site, while community B has residues surrounding the α-C helix that help its appropriate positioning. Communities C and C1 are responsible for providing support to the R-spine and hence participate in activation of the kinase domain. Community D supports the C-spine. Community E orchestrates the optimal arrangement of the active site residues in synchronization with communities F and F1 that control substrate peptide binding. Communities G, H, and I are responsible for binding of small molecule effectors or interactions with the regulatory subunit of PKA. As these communities have allowed for a direct correspondence with molecular function of the conserved kinase core, it is increasingly understood that this community-based approach can explain the workings of other kinases. One such example is the case of Bruton’s tyrosine kinase (Btk) (65). In accordance with the violin model of allostery, every dynamic state of the kinase that responds to a stimulus shows a distinct community map. The community map of the apoprotein is distinct from that of the nucleotide-bound forms (78). The sensitivity of community maps in capturing the reorganized entropy of the kinase is evident in the altered graphs for ATP forms of PKA with two metal ions or one metal ion (61, 78). As the binding of the second metal serves as a “lynch pin” for the catalytic cycle, the dynamics of the protein changes to accommodate the metal ion for optimal catalytic turnover.

FIG 7.

Girvan–Newman algorithm-based “community map” of protein kinase A (PKA) describes the sets of 40–60 amino acid large communities that share the maximum mutual information. Each community is mapped onto the structure to explore its biological function. Graph theory-based representation shows each the community map a 2D graph where communities as circles are connected to each other by edges. Sizes of the community circle are indicative of the number of residues contained in them. Thickness of edges connecting the communities denotes the strength of interaction.

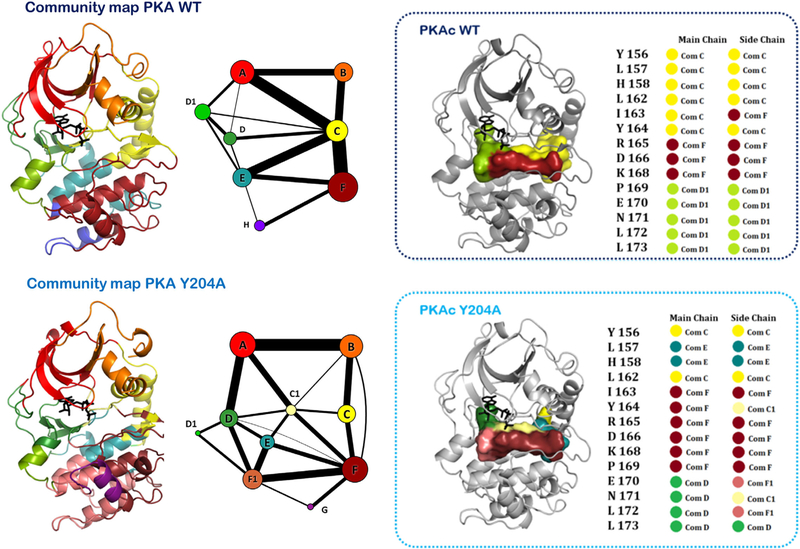
A detailed analysis for exploring the allosteric communication between distal sites and the kinase active site is available for the Y204A mutation of PKA (Fig. 8) (61). This mutation was identified from a pep-tag assay-based screen that lacks catalytic activity, although the site was about 8 Å away from the kinase active site (81). The crystal structure of the Y204A mutant was found to be almost identical to that of the wild-type protein (82). Although the mutant showed the ability to transfer the γ-phosphate of ATP to water molecules (ATPase activity) (61, 82), it did not show the ability to do so on peptide substrates (61). While NMR spectra of the mutant showed considerable alterations, the exact allosteric effect of the mutation remained elusive (83). Community map analysis of the Y204A mutant in the catalytically competent ATP–Mg bound form and its comparison with the community map of the wild type in the identical state provided these answers (Fig. 8). The distal Y204A mutation reorganized the dynamics of the protein, pertinently around the active sit region such that communities C, D, and E were most affected. Moreover, the small molecule-binding community H disappeared from the protein and a distinct community G appeared. The peptide-binding community was also split into communities F and F1. A thorough analysis of this community network in the ATP-binding and peptide-binding regions provided a rationale toward designing a fluorescence polarization-based assay for substrate cooperativity. These biochemical assays validated that while the Y204A mutant was able to bind both ATP and substrate peptides with optimal affinity, it was unable to synchronize the two at the active site for phosphotransfer (61). In this way, reorganization of the community networks around the kinase sites of interest allowed for its detailed biochemical exploration and provided clues to its regulation that were earlier elusive to traditional explanations of protein allostery.

FIG 8.

Community map of PKA explored in the context of a distal Y204A mutation. The mutation about 8 Å away from the active site debilitates the kinetics of the kinase. Comparison of the community maps of the mutant and the wild-type PKA allow for understanding the dynamic allostery-based modulations that effect kinase activity. As shown in the active-site cleft, the distal Y204A mutation alters the distribution of the dynamics of the protein and reorganizes its community map. As a result, the mutant is unable to synchronize the nucleotide and peptide substrates optimally at the active site.

CONCLUDING REMARKS

Dynamics-based allosteric descriptors are critical to our understanding of protein regulation, more so in the case of protein kinases that regulate some of the most crucial biological processes. Structure–function assays have provided insights into the conformation-based allostery of these proteins, much of which finds relevance even till date. Dynamics-based allostery has been a more challenging area and extremely difficult to validate. The “violin” model of dynamics-based allostery encapsulates the basic tenants of entropy-driven allostery and focuses on changes in internal motions of the protein in a global context. Community maps provide a mathematical/computational descriptor of the violin model and have been successful in explaining the role of distal sites in the regulation of protein kinase function.

Abbreviations:

ANS

8-anilino-1-napthalene sulfonate

ATP

adenosine triphosphate

CDK2

cyclin-dependent protein kinase 2

C-Spine

catalytic spine

ENM

elastic network model

GNM

gaussian network model

KNF

koshland, nemethy, and filmer

MD Simulation

molecular dynamics simulation

MSM

markov state model

MWC

monod, wyman, and changeux

NMR

nuclear magnetic resonance

PKA

protein kinase A

R-spine

regulatory spine

TPT

transition pathway theory