Comparative Study of Confidence Intervals for Proportions in Complex Sample Surveys

Abstract

The most widespread method of computing confidence intervals (CIs) in complex surveys is to add and subtract the margin of error (MOE) from the point estimate, where the MOE is the estimated standard error multiplied by the suitable Gaussian quantile. This Wald-type interval is used by the American Community Survey (ACS), the largest US household sample survey. For inferences on small proportions with moderate sample sizes, this method often results in marked under-coverage and lower CI endpoint less than 0. We assess via simulation the coverage and width, in complex sample surveys, of seven alternatives to the Wald interval for a binomial proportion with sample size replaced by the ‘effective sample size,’ that is, the sample size divided by the design effect. Building on previous work by the present authors, our simulations address the impact of clustering, stratification, different stratum sampling fractions, and stratum-specific proportions. We show that all intervals undercover when there is clustering and design effects are computed from a simple design-based estimator of sampling variance. Coverage can be better calibrated for the alternatives to Wald by improving estimation of the effective sample size through superpopulation modeling. This approach is more effective in our simulations than previously proposed modifications of effective sample size. We recommend intervals of the Wilson or Bayes uniform prior form, with the Jeffreys prior interval not far behind.

1. INTRODUCTION

Constructing well-calibrated confidence intervals (CIs) for population proportions based on survey data is challenging, unless the sample size is very large. With a simple random sample (SRS) from a large population where the sampling fraction is negligible, the data are approximately binomial, and CIs that guarantee at least nominal coverage are available (Clopper and Pearson 1934; Blyth and Still 1983; Casella 1986). These CIs tend to be conservative (exceed the nominal coverage) and wide. However, methods that guarantee nominal coverage for the binomial case do not necessarily do so when applied to complex survey data. Intervals based on randomized tests (that is, tests based on exact discrete distributions with auxiliary randomization to produce rejection regions of exact size α under the null hypothesis) exist in the SRS case (see, for instance, Wright 1997). Such tests would be very difficult to construct in more complex settings, and we focus only on nonrandomized intervals.

Many surveys use intervals of the form $\widehat{p}\pm z_{\alpha /2}·\widehat{SE}$, or equivalently $\widehat{p}\pm \text{MOE}$, where $\widehat{p}$ is an estimate of the proportion, $\widehat{SE}$ is an estimate of its standard error, $z_{\alpha /2}$ is the $(1-\alpha /2)$ quantile of the normal distribution, sometimes replaced by a corresponding t-quantile, and MOE is the margin of error. The Wald interval is the most basic, with $\widehat{SE}=\sqrt{\widehat{p}(1-\widehat{p})/n}$, but it can perform poorly even in the SRS case. An improvement is provided by replacing the sample size with the effective sample size (e.g., Korn and Graubard 1998; Liu and Kott 2009; Dean and Pagano 2015), but the Wald interval still performs poorly.

We conduct an extensive simulation study to evaluate and compare coverage and width of the Wald and seven other candidate intervals and the performance of three different approaches to estimating the effective sample size. The three approaches include a simple design-based approach, a modification of this design-based estimate recommended by Dean and Pagano (2015), and the use of an improved method to estimate the sampling variance based on super-population model assumptions. The intervals considered are the Wald, Agresti-Coull (1998), Clopper-Pearson (1934), Wilson (1927), Arcsine Square Root (Sokal and Rohlf 1994, as modified by Gilary, Maples, and Slud 2012), and two quasi-Bayesian intervals using the Jeffreys and the uniform priors. We also study the CI for the logit-transformed proportion, which was previously considered in Liu and Kott (2009) and Dean and Pagano (2015). Results for the logit-transformed method, or Logit interval, are limited to the online supplementary material, because its performance was less promising than competitors. Our results are consistent with those of Brown, Cai, and DasGupta (2001), who find that it can produce very wide intervals in the binomial case. The Agresti-Coull, Wilson, and Jeffreys and uniform prior intervals previously performed well in the SRS setting (Brown et al. 2001; Carlin and Louis 2009). The Clopper-Pearson always meets or exceeds the nominal coverage in the SRS setting and was recommended by Korn and Graubard (1998) for settings with small expected numbers of successes. Performance of the Arcsine Square Root interval was compared by simulation with a cell-based version in Gilary et al. (2012) in a small-area (Fay-Herriot) model setting. A modified Arcsine Square Root interval was used to produce the Census Bureau’s May 2012 publicly released confidence bounds for estimates of 2010 census erroneous enumeration rates. For all these intervals, in complex surveys, we replace the sample size by an estimate of the effective sample size. The quasi-Bayesian intervals are based on the Beta prior and posterior distribution from the SRS case, with sample size and observed proportion replaced by effective sample size and design-weighted estimated proportion.

This work builds on the simulation studies in Franco, Little, Louis, and Slud (2014) and Dean and Pagano (2015). We evaluate the joint distribution of coverage and width in the context of clustering and stratification of several degrees of heterogeneity within and between clusters and among strata and of uncertainty in estimating sampling variances. We set aside samples for which the estimated sampling variance is zero, and so our results are conditional on a positive estimated variance. Our primary objective is to find intervals that have well-calibrated coverage and controlled width. We treat a wide range of scenarios and aim to find intervals that work well across all scenarios rather than prescribing criteria for the use of particular intervals, because the determining factors will generally not be known to the analyst.

For intervals that perform well in the SRS context, our results suggest that the principal cause of undercoverage in complex surveys is uncertainty in estimating the effective sample size. Hence, we have improved estimation of the sampling variance and consequently of the design effect and effective sample size. These improvements come by making basic assumptions about the superpopulation. We then take the expectation both with respect to the sampling design and the superpopulation model when computing the variance of the survey weighted estimator (i.e., the “anticipated variance” of Isaki and Fuller 1982). Chen and Rust (2017) also use superpopulation models to improve variance estimates based on the well-known design effect formula by Kish (1987).

Our study is motivated by the American Community Survey (ACS), the largest household sample survey in the United States, sampling approximately 3.5 million addresses annually and producing billions of estimates (US Census Bureau 2014). The American Community Survey publishes CIs of the form $\widehat{p}\pm z_{\alpha /2}·\widehat{SE}$, with $\widehat{SE}$ based on the successive difference replication (SDR) method (Fay and Train 1995; see US Census Bureau 2014, Chapter 12). Despite its large overall sample size, the extensive cross-classification of its many demographic, personal, and economic questions can generate domains with small sample sizes. Due to the sheer quantity and diversity of estimates, we consider only basic CI methods that are easy to implement and depend only on sample size, the survey-weighted estimate of the proportion, and a sampling variance estimate used to estimate the design effect and effective sample size. Three different approaches to estimating the sampling variance and effective sample size are considered.

Other authors have conducted related simulations for complex surveys. Liu and Kott (2009) and Kott and Liu (2009) compared one-sided intervals for proportions in stratified SRS surveys; we focus on two-sided intervals. Korn and Graubard (1998) studied CIs for small proportions in surveys including clusters (of sizes ten or one hundred) and unequal weights by simulation and data analysis, comparing intervals based on design-effect modifications, including replacement of Gaussian by t quantiles in Wald-type intervals. Dean and Pagano (2015) considered essentially the same intervals we do (excluding the Arcsine Square Root interval), varying overall prevalence p and intracluster correlations (ICCs) within a design of thirty primary and seven secondary sampling units. They also have limited results related to stratification, including a case with two strata in their sampling design. Their modification of effective sample size resembles Korn and Graubard’s (1998), except that in their adjustment factor—our formula (20)—they replace the t quantile by a z quantile in the numerator. Kott, Andersson, and Nerman (2001) also discuss confidence intervals for complex surveys, but their simulations are carried out under SRS.

The sampling design in our simulations is that of a single-stage, stratified SRS sample of all-or-none clusters of identical size. The strata sampling fractions, the cluster sizes, and the relationship between the sample sizes and the true stratum proportions vary among runs. Although this is more basic than the complex designs common in practice, our setup is more complex than those of previously published simulation studies. Moreover, single-stage SRS samples of appropriately chosen “ultimate clusters” can be used to approximate more complex epsem or stratified epsem-within-stratum designs (for example, see Kalton 1979). In an epsem design, each unit in the population has an equal probability of selection.

Our research builds on previous work by (1) using a more elaborate, multi-factorial, simulation design that allows estimation of the main effects of scenario components and interactions, (2) assessing the impact of uncertainty in estimating the effective sample size by comparing results to those using the true effective sample size, and (3) applying superpopulation models to improve performance by better estimation of the sampling variance and, hence, of the effective sample size.

Section 2 defines the eight intervals we study, and section 3 develops estimation of the effective sample size. Section 4 provides simulation specifications. Section 5 presents results, and section 6 draws conclusions and formulates recommendations and promising avenues for future research. The appendix includes mathematical proofs, additional details of the simulations, and a brief description of the R code and workspace (R Core Team 2017) for computing design effect estimates and CIs that are included in the online supplementary material.

2. CANDIDATE INTERVALS

We consider seven alternatives to the basic Wald interval for a binomial proportion: Jeffreys and uniform prior quasi-Bayesian intervals, Clopper-Pearson, Wilson, Agresti-Coull, Arcsine Square Root, and Logit intervals. Each of these interval methods is in turn treated in three ways: using a simple design-based estimate of the effective sample size, adjusting this estimate as recommended by Dean and Pagano (2015), and estimating the design effect using superpopulation model assumptions.

Here, we describe the interval construction methods first for Bernoulli sampling, with n trials and X successes; the intervals for complex surveys are obtained by replacing n by an estimate of the effective sample size $n_{\text{eff}}$ and X by an estimate of $n_{\text{eff}}·p$, where p is estimated by the survey-weighted proportion.

The different methods of estimating the effective sample size are discussed in section 3.

2.1 Wald Interval

The Wald interval is

$$\widehat{p}\pm z_{\alpha /2}·\sqrt{\widehat{p}(1-\widehat{p})/n},$$ (1)

with $\widehat{p}=X/n$ and $z_{\alpha /2}$ the quantile of the standard normal distribution. This is a special case of what we refer to as “Wald-type intervals” for general complex surveys,

$$\widehat{p}\pm z_{\alpha /2}·\widehat{SE},$$ (2)

where $\widehat{p}$ is possibly survey weighted, and $\widehat{SE}$ is an estimate of its standard error.

The normal quantiles are sometimes replaced by t quantiles, with the degrees of freedom depending on the amount of clustering and stratification (Korn and Graubard 1998). This adjustment is based on empirical evidence (Frankel 1971, Chapter 7), with some formal justification under strong assumptions (Korn and Graubard 1990).

2.2 Quasi-Bayesian Intervals: Jeffreys and Uniform

With the prior $[p|a,b]=\text{Beta}(a,b);a,b>0$ and data distributed as $[X|p,n]=\text{Binomial}(n,p)$, the posterior distribution is $[p|X,n]=\text{Beta}(X+a,n-X+b)$. With $qbeta(r;·,·)$ denoting the r quantile of a Beta distribution, the $(1-\alpha )*100\%$ equal-tail credible interval is

$$\begin{array}{c}L(X,n)=qbeta(\alpha /2;X+a,n-X+b)\\ U(X,n)=qbeta(1-\alpha /2;X+a,n-X+b)\end{array}$$ (3)

The Jeffreys interval (“JeffPr”) uses $a=b=0.5$, and the uniform interval (“UnifPr”) uses $a=b=1$. Carlin and Louis (2009) show that these have excellent frequentist properties for SRS sampling, making them attractive candidates in the survey context.

2.3 Clopper-Pearson Interval

The Clopper-Pearson interval (“ClPe” or “CP”) is based on exact binomial tails and can be expressed as,

$$\begin{array}{c}L(X,n)=\frac{v_1{F}_{v_1,v_2}(\alpha /2)}{v_2+v_1{F}_{v_1,v_2}(\alpha /2)}=qbeta(\alpha /2;X,n-X+1)\\ U(X,n)=\frac{v_3{F}_{v_3,v_4}(1-\alpha /2)}{v_4+v_3{F}_{v_3,v_4}(1-\alpha /2)}=qbeta(1-\alpha /2;X+1,n-X),\end{array}$$ (4)

where $v_1=2X,\hspace{0.17em}{v}_2=2(n-X+1),\hspace{0.17em}{v}_3=2(X+1),\hspace{0.17em}{v}_4=2(n-X)$, and $F_{d_1,d_2}(\beta )$ is the β quantile of an F distribution with d₁ and d₂ degrees of freedom (Korn and Graubard 1998). Interval endpoints in (4) are very similar to those of Jeffreys and uniform, shown in (3), but demonstrably wider (see Appendix A for a proof).

2.4 Wilson Interval

Like the Wald interval (1), the Wilson interval (“Wils”) can be derived from an asymptotic pivot. In place of the Wald pivot $(p-\widehat{p})/\sqrt{\widehat{p}(1-\widehat{p})/n}$, the Wilson interval uses $(p-\widehat{p})/\sqrt{p(1-p)/n}$, producing CI limits,

$$\frac{X+z^2/2}{n+z^2}\pm \frac{z{n}^{1/2}}{n+z^2}{\left\{\widehat{p}\widehat{q}+z^2/(4n)\right\}}^{1/2},$$ (5)

where $z=z_{\alpha /2}$ from now on.

2.5 Agresti-Coull Interval

The Agresti-Coull Interval (“AgCo” or “AC”) uses the same form as the Wald interval (2), replacing $\widehat{p}$ with the center of the Wilson interval $\tilde{p}=(X+z^2/2)/(n+z^2)$ and n with the denominator of $\tilde{p}$ (i.e., $\tilde{n}=n+z^2$). The interval is then,

$$\tilde{p}\hspace{0.17em}\pm \hspace{0.17em}z\sqrt{\tilde{p}(1-\tilde{p})/\tilde{n}}.$$ (6)

Agresti and Coull (1998) deal with the case of a 95 percent CI, pointing out that at this confidence level, this is approximately the same as adding two successes and two failures and then applying the Wald interval. They also show that the center of the Wilson interval is a weighted average between $\widehat{p}$ and 0.5. They note that the interval is simpler in form than the Wilson interval, is not as conservative as the Clopper-Pearson interval, and performs better than the Wald interval in the SRS case.

2.6 Arcsine Square Root Interval

The Arcsine Square Root Interval (“Assqr”) uses $\text{arcsine}\sqrt{p}$ as variance stabilizing transformation, along with $\widehat{p}=(X+1/2)/(n+1)$ (as in Jeffreys) to correct the marked anticonservatism of the Wald interval (Gilary et al. 2012). The Wald formula (2) produces endpoints in the transformed scale, which are back-transformed to produce CI limits,

$$\begin{array}{c}L(X,n)=\hspace{0.17em}{\text{sin}}^2\left\{\max \left(0,\arcsin \sqrt{\frac{X+.5}{n+1}}-\hspace{0.17em}\frac{z}{\sqrt{4n}}\right)\right\}\\ U(X,n)=\hspace{0.17em}{\text{sin}}^2\left\{\min \left(\frac{\pi }{2},\arcsin \sqrt{\frac{X+.5}{n+1}}+\frac{z}{\sqrt{4n}}\right)\right\}\end{array}$$ (7)

2.7 Logit Interval

The Logit interval applies a logit transformation, then produces a Wald-type interval, and then back-transforms to the original scale, yielding the following:

$$\begin{array}{c}L(X,n)=\frac{e^{{\lambda }_l}}{1+e^{{\lambda }_l}}\\ U(X,n)=\frac{e^{{\lambda }_u}}{1+e^{{\lambda }_u}},\end{array}$$ (8)

where ${\lambda }_l=\widehat{\lambda }-z\sqrt{\widehat{V}}$, and ${\lambda }_u=\widehat{\lambda }+z\sqrt{\widehat{V}}$ with $\widehat{\lambda }=\hspace{0.17em}\text{log}(\widehat{p}/(1-\widehat{p}))$, and $\widehat{V}=n/(X(n-X))$. Note that (8) is undefined when $\widehat{p}=0$ or $\widehat{p}=1$. We define $\widehat{\lambda }$ to be $-\infty$ when $\widehat{p}=0$, $\infty$ when $\widehat{p}=1$, and $\text{log}(\widehat{p}/(1-\widehat{p}))$ otherwise. Such a definition does not affect our results since we condition on positive estimated variance.

2.8 Discussion of Candidate Intervals

Brown et al. (2001, 2002) proposed alternative methods that ameliorate the erratic coverage of the standard Wald interval, recommending Jeffreys and Wilson for small sample sizes and Agresti-Coull for large sample sizes (Brown et al. 2001, Section 5). These intervals are appropriate for survey data with SRS designs where the sampling fraction is small or the sampling is with replacement, but they are not designed to accommodate the clustering, stratification, or unequal weights of more complex sample surveys.

A common approach to constructing confidence intervals for proportions from complex sample survey data is to modify the inputs to binomial intervals, such as the Wald interval (section 2.1), to account for survey weighting and the design effect. The survey-weighted, estimated proportion, $\widehat{p}$, is used along with a consistent design-based estimate, $\widehat{\text{Var}}(\widehat{p})$, of its variance. These combine to estimate the design effect (Kish 1965) and effective sample size,

$$\begin{array}{c}\widehat{Deff}=\frac{\widehat{\text{Var}}(\widehat{p})}{\widehat{p}(1-\widehat{p})/n}\\ {\widehat{n}}_{\text{eff}}=\frac{n}{\widehat{\mathit{Deff}}}=\frac{\widehat{p}(1-\widehat{p})}{\widehat{\text{Var}}(\widehat{p})}.\end{array}$$ (9)

For simplicity, we ignore the finite population correction in the SRS variance expression in the denominator of (9). In CI expressions, n is replaced by ${\widehat{n}}_{\text{eff}}$ and X by $\widehat{p}·{\widehat{n}}_{\text{eff}}$ without rounding (e.g., Korn and Graubard 1998; Liu and Kott 2009; Dean and Pagano 2015). The effective sample size $n_{\text{eff}}$ can be interpreted as the sample size needed under an SRS design to obtain the same large-sample CI width obtained under the complex sampling scheme. Applying the design-effect modifications to the Wald interval produces $\widehat{p}\pm z_{\alpha /2}\sqrt{\widehat{Var}(\widehat{p})}$.

3. ESTIMATING THE EFFECTIVE SAMPLE SIZE

Let Y_hki be the (binary) response for individual i in cluster k in stratum h. Denote the population count in stratum h and cluster k by $Y_{hk+}$ and the population count in stratum h by $Y_{h++}$. That is,

$$Y_{hk+}=\sum _{i\in C_{hk}}{Y}_{hki},Y_{h++}=\sum _{k=1}^{K_h}{Y}_{hk+}=\sum _{k=1}^{K_h}\sum _{i\in C_{hk}}{Y}_{hki},$$

where C_hk denotes the set of units or individuals i belonging to cluster k in stratum h, and K_h is the number of clusters in stratum h. The population total is denoted by Y, and the corresponding sample weighted estimator is

$$\widehat{Y}=\sum _{h=1}^H{\widehat{Y}}_{h++},{\widehat{Y}}_{h++}=\frac{K_h}{n_h^C}\sum _{k\in S_h}{Y}_{hk+},$$ (10)

where S_h and $n_h^C$ are the set and number of sampled clusters in stratum h, and H is the number of strata. For future reference, also define N_h to be the population size in stratum h, and denote by c the size of each cluster in the population.

The population proportion $\overline{Y}=Y/N$ has expectation $E(\overline{Y})=\theta$, and confidence intervals for it are based on (10), together with the “working model” $n_{\text{eff}}·(\widehat{Y}/N)\sim \text{Binom}(n_{\text{eff}},\overline{Y})$, where $n_{\text{eff}}$ is a suitable effective sample size. It is permissible for values of $n_{\text{eff}}·(\widehat{Y}/N)$ and $n_{\text{eff}}$ to be noninteger within likelihood-based methods such as those implemented in R.

We evaluate the performance of CIs for the overall proportion $\overline{Y}$ of successes within a survey assumed to have the sampling design of an SRS of clusters, with clusters sampled all-or-none. Generalizations of design- and model-based estimators to the case of cluster sampling with unequal cluster sizes and weights within strata are given in Appendix B.

We compare coverages and widths of the intervals using the “true” effective sample size based on the actual simulated (frame) population and using “estimated” effective sample sizes computed from sampled data. For the former, we compare two approaches: one with no superpopulation model assumptions and one that makes some basic assumptions. We incorporate finite population corrections, although the sampling fractions we consider are small.

3.1 Design-Based Estimate of the Design Effect

Let $f=c{n}^C/N$ denote the overall sampling fraction, with n^C the number of clusters sampled, and $f_h=c{n}_h^C/N_h=n_h^C/K_h$ the sampling fraction within the h’th stratum. The design variance $\widehat{Y}$ of the survey estimator (for stratumwise SRS cluster samples) is

$$\text{Var}(\widehat{Y})\hspace{0.17em}=\hspace{0.17em}\sum _{h=1}^H\frac{K_h^2(1-f_h)}{n_h^{\mathcal{C}}}\hspace{0.17em}{s}_{Y_{h·+}}^2\hspace{0.17em}\hspace{0.17em},s_{Y_{h·+}}^2\hspace{0.17em}=\hspace{0.17em}\frac{1}{K_h-1}\sum _{k=1}^{K_h}{\left(Y_{hk+}-\frac{Y_{h++}}{K_h}\right)}^2.$$ (11)

So the true design effect and true effective sample size are

$$Deff\hspace{0.17em}=\hspace{0.17em}\frac{n\hspace{0.17em}\text{Var}(\widehat{Y})}{Y(N-Y)(1-f)},n_{\text{eff}}\hspace{0.17em}=\hspace{0.17em}n/Deff.$$ (12)

Superpopulation model-free estimates of the design effect and effective sample size, denoted $\widehat{Deff}$ and ${\widehat{n}}_{\text{eff}}$, are

$$\widehat{\text{Var}}(\widehat{Y})\hspace{0.17em}=\hspace{0.17em}\sum _{h=1}^H\frac{K_h^2(1-f_h)}{n_h^{\mathcal{C}}}\hspace{0.17em}{\widehat{s}}_{Y_{h·+}}^2,$$ (13)

$${\widehat{s}}_{Y_{h·+}}^2\hspace{0.17em}=\hspace{0.17em}\frac{1}{n_h^C-1}\sum _{k\in S_h}{\left(Y_{hk+}-\frac{1}{n_h^C}\sum _{l\in S_h}{Y}_{hl+}\right)}^2,$$

$$\widehat{\text{Var}}=\frac{n\hspace{0.17em}\widehat{\text{Var}}(\widehat{Y})}{\widehat{Y}(N-\widehat{Y})(1-f)},{\widehat{n}}_{\text{eff}}=n/\widehat{Deff}.$$ (14)

3.2 Model-Based Estimate of the Design Effect

The method that Kish (1987) used to derive his famous approximate formula for design effects in terms of intracluster correlations (ICCs) and unit-level attribute variances can be viewed as an attempt to combine design-based variance formulas with simple modeling assumptions about the superpopulation. Like Gabler, Haeder, and Lahiri (1999) and Chen and Rust (2017), we extend this method (in Appendix B) to obtain a model-based estimator of Deff under somewhat more general assumptions. The assumptions that we consider here are as follows:

• (A.i): $E(Y_{hki})={\tau }_h$ for all clusters k and individuals i in stratum h,

• (A.ii): $\text{Var}(Y_{hki})={\sigma }_h^2$ for all $k$ in stratum h and i in cluster $C_{kh}$,

• (A.iii): $\text{Corr}(Y_{hki},Y_{hk\prime j})\hspace{0.17em}=\hspace{0.17em}\rho$ when $i,j\in C_{kh}$ and $k=k\prime$, and $\text{Corr}\hspace{0.17em}=0$ otherwise.

Assumption (A.iii) is restrictive in assuming constancy of ICCs across strata, and assumptions (A.i) and (A.ii) might also oversimplify in assuming distributional parameters of all attributes within stratum to be the same. Although a superpopulation model based on these assumptions is too simple to be realistic, we find that the reduction in variability of the estimated design effect more than compensates for potential bias.

In our setting of binary Y_hki, assumptions (A.i) and (A.ii) are redundant, since ${\sigma }_h^2={\tau }_h(1-{\tau }_h)$ for all h. For this reason, the parameter estimates ${\widehat{\sigma }}_h^2$ are defined to be $(n_h/(n_h-1)){\widehat{\tau }}_h(1-{\widehat{\tau }}_h)$, as in (16), or as actually implemented in our simulations, by the formula $(n_h^C/(n_h^C-1)){\widehat{\tau }}_h(1-{\widehat{\tau }}_h)$, which inflates variances in a helpful way.

As justified in Appendix B, the model-based estimation formula derived from assumptions (A.i)–(A.iii) for $\text{Var}(\widehat{Y})$ that we implement in our simulations (specifically for the stratumwise SRS cluster sampling of equal-sized clusters of binary attributes) is closely related to Kish’s formula. The variance formula is

$${\widehat{\text{Var}}}^{*}(\widehat{Y})=\sum _{h=1}^H{\widehat{\sigma }}_h^2\hspace{0.17em}\frac{K_h-n_h^C}{n_h^C}\hspace{0.17em}{N}_h(1+(c-1)\widehat{\rho }),$$ (15)

with ${\sigma }_h^2$ and ρ parameters estimated according to the formulas ${\widehat{\tau }}_h=\sum _{k\in S_h}{Y}_{hk+}/n_h$ and

$${\widehat{\sigma }}_h^2=\frac{1}{c{n}_h^C-1}\sum _{k\in S_h}\sum _{i\in C_{kh}}{(Y_{hki}-{\widehat{\tau }}_h)}^2\hspace{0.17em}=\hspace{0.17em}\frac{n_h}{n_h-1}{\widehat{\tau }}_h(1-{\widehat{\tau }}_h)$$ (16)

$$1-\widehat{\rho }=\frac{n-H}{2n(c-1)}\sum _{h=1}^H\sum _{k\in S_h}\sum _{i,j\in C_{kh}}{(Y_{hki}-Y_{hkj})}^2/\sum _{h=1}^H(c{n}_h^C-1){\widehat{\sigma }}_h^2$$ (17)

But $\widehat{\rho }$ is defined as zero when c = 1, and in the simulations, $\widehat{\rho }$ was set to zero whenever it was negative in (17). For the more realistic case of unequal-sized clusters and unknown cluster sizes for unsampled clusters, see (26) in Appendix B.

The corresponding estimated design effect and effective sample size are

$${\widehat{Deff}}^{*}\hspace{0.17em}=\hspace{0.17em}\frac{n\hspace{0.17em}{\widehat{\text{Var}}}^{*}(\widehat{Y})}{\widehat{Y}(N-\widehat{Y})(1-f)},{\widehat{n}}_{\text{eff}}^{\ast }\hspace{0.17em}=\hspace{0.17em}n/{\widehat{Deff}}^{*}.$$ (18)

These formulas have analogs, justified and developed more generally in Appendix B, for more complex designs. Our broader point is that generalized, model-based formulas such as (18) yield CIs with better coverage properties than CIs from purely design-based estimates of effective sample size.

3.3 Adjustments to Estimated Effective Sample Size

Korn and Graubard (1998) suggested multiplying the effective sample size by a factor,

$${\widehat{n}}_{\text{eff}}^{df}={\widehat{n}}_{\text{eff}}·{\left\{\frac{t_{n-1}(1-\alpha /2)}{t_d(1-\alpha /2)}\right\}}^2,$$ (19)

where the design degrees of freedom are $d=$ #{sampled clusters} - #{strata} for a multi-stage design with stratified selection of clusters at the first stage, and ${\widehat{n}}_{\text{eff}}$ is an estimate of the effective sample size. If $n-1<d$, as when there is significant clustering, the bracketed ratio is less than one. The effective sample size is reduced, resulting in wider intervals, counteracting to a degree the undercoverage typically associated with clustering.

Dean and Pagano (2015) similarly define adjusted estimated effective sample size as,

$${\widehat{n}}_{\text{eff}}^{dfDP}={\widehat{n}}_{\text{eff}}·{\left\{\frac{z(1-\alpha /2)}{t_d(1-\alpha /2)}\right\}}^2\hspace{0.17em},$$ (20)

which is (19) with a normal quantile in the numerator in place of the t quantile. This replacement yields a smaller ratio, smaller effective sample size, wider confidence intervals, and higher coverage.

4. SIMULATION STUDY

We simulate one population for each parameter configuration, then implement sampling designs, analyze the data, and summarize results.

4.1 Simulating the Population

First, we create a population of size N = 10,000 with H = 4 strata. In the h^th stratum, there are $K_h=K$ clusters, each of size c, and N_h units with $N_h=c·K_h$. We allow different sampling fractions in different strata. In separate runs, c = 1, 3, 5, or 7. The expected population proportion, $E(\overline{Y})=\theta$, is specified for each simulation, where $\overline{Y}$ is the population mean of the binary attribute. Scenarios jointly specify the dependence on the stratum-specific samples n_h and population proportions of the form ${\theta }_h=\theta +b·(h-2.5)$, ensuring that $\overline{\theta }=\theta$ for various choices of b, including b = 0 (see section 4.2) where $\overline{\theta }$ denotes the average across strata of the stratum proportions.

A “success” or “failure,” $Y_{hki}\in \{0,1\}$ for unit i in cluster k in stratum h is generated from the model,

$$\begin{array}{c}[p_{hk}|{\theta }_h]\sim \text{Beta}(\frac{1-\rho }{\rho }{\theta }_h,\hspace{0.17em}\frac{1-\rho }{\rho }(1-{\theta }_h))\\ [Y_{hki}|p_{hk}]\sim \text{Bernoulli}(p_{hk}).\end{array}$$ (21)

As described in section 4.3, parameter configurations $(\rho ,{\left\{{\theta }_h\right\}}_{h=1}^H,c)$ for model (21), “scenario,” and sample size n are specified once for each simulated frame population. Here ρ is the ICC for the binary attribute, which measures within-cluster heterogeneity when c > 1.

4.2 Simulating the Sampling Design

After generating the population, it is sampled R = 10,000 times for each simulation configuration. As discussed in the introduction, the sampling design is a single-stage stratified SRS sample of all-or-none clusters of identical size, where the objective is inference about the proportion Y/N.

An alternative to generating each population once and sampling repeatedly is to generate 10,000 populations and sample each once. Our approach is consistent with the design-based philosophy prevalent among survey practitioners, in which the finite population is viewed as fixed, and all randomness is ascribed to the sampling process. In our simulations, the large number of frame populations generated for different factorial combinations prevent anomalous characteristics in any single-frame population from distorting the results.

With $f=n/N$ the overall sampling fraction, and $f_h=n_h/N_h$ the stratum-specific fractions for $h=1,\dots ,4$, we study four scenarios:

• Scenario C: ${\theta }_h\equiv \theta ,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{f}_h\equiv f$

• Scenario I: f_h increases as θ_h increases

• Scenario D: f_h decreases as θ_h increases

• Scenario H: the relation between f_h and θ_h is quadratic and concave

For example, if $\theta =0.3,\hspace{0.17em}c=1$, and the sampling fraction $f$ is such that n = 80, then under scenario C, the vector of stratum sample sizes is $\mathbf{n}=(20,20,20,20)$, and $\theta =({\theta }_1,\dots ,{\theta }_4)=(0.3,0.3,0.3,0.3)$; under scenario D, it is $\mathbf{n}=(28,22,18,12),\hspace{0.17em}\theta =(0.1875,0.2625,0.3375,0.4125)$. With no clustering, scenario C closely resembles an SRS design. By contrast, scenario D yields large variability among stratum sample sizes. For some simulation configurations, rounding of stratum sample sizes may cause actual total sample sizes to differ slightly from the nominal n. For more details on rounding and other aspects of the simulation design, see Appendix C.

4.3 Factorial Design

Each simulation parameter can take on several values, creating a factorial design shown in Table 0. The combinations number 648, after excluding configurations with $n\le 50$ and $c\ge 5$ because of problems such as undefined stratum sample variances due to strata with one or zero clusters.

Table 1.

Average Ratio of Estimated Effective Sample Size (18) Divided by True Effective Sample Size, Based on 10,000 Replications and Averaged Across Scenarios, with $N=\mathrm{10,000},n=200$

	$\rho =0.001$			$\rho =0.25$
Clus-Size	$\theta =0.1$	$\theta =0.2$	$\theta =0.3$	$\theta =0.1$	$\theta =0.2$	$\theta =0.3$
c=1	1.07	1.02	1.01	1.07	1.02	1.01
c=3	0.98	0.93	0.90	1.16	1.03	1.00
c=5	0.89	0.86	0.86	1.27	1.02	1.02
c=7	0.82	0.78	0.79	1.33	1.10	1.00

Table 0.

Factors, Notations and Levels for Factorial Simulation Study.

Factor	Symbol	Levels
Cluster size	c	$1,3,5,7$
Sample size$\ast$	n	$30,40,50,84,196,280$
Scenario	–	C, I, D, H
Expected Proportion	$\theta =E(Y/N)$	$0.05,0.10,0.30$
Intra-Cluster Correlation	ρ	$0.001,0.10,0.25$

^*Sample sizes $n\le 50$ excluded when $c\ge 5$. Case c = 1 represents no clustering.

For each element in the factorial design, R = 10,000 replicated samples are drawn. In each simulated sample for which $\widehat{V}(\widehat{p})\ne 0$, the coverage indicator and interval width are computed for the Wald and seven other 95 percent CI methods described in section 2, using both $n_{\text{eff}}$ and ${\widehat{n}}_{\text{eff}}$, where the latter is computed from three different variance estimates: the purely design-based estimator (13), the modification by the reciprocal of the effective sample size factor of Dean and Pagano (2015) in (20), or the Kish-type formula (15) derived from superpopulation model assumptions. Empirical coverage in each simulation configuration is the percentage of replicate samples with $\widehat{V}(\widehat{p})\ne 0$ for which the interval contains the true proportion Y/N. Noncoverage is (100 - coverage)%. Width is computed as the average of widths of CIs intersected with $[0,1]$ (needed for Wald, Wilson, and Agresti-Coull).

5. SIMULATION RESULTS

We present results on CI performance in four steps. First in section 5.1, we compare coverage of the Wald CI with coverage of the other CI methods. The clearly inferior CI coverage of Wald eliminates this method from further consideration. Second, we summarize the performance of methods other than Wald across all simulation configurations, first with design-based estimated effective sample size and then with true effective sample size $n_{\text{eff}}$. Third in section 5.2, we compare the Dean and Pagano estimated effective sample size (20) with the Kish-type estimates ${\widehat{n}}_{\text{eff}}^{\ast }$ in (18). Finally in section 5.3, we compare the relative merits of the seven non-Wald intervals based on ${\widehat{n}}_{\text{eff}}^{\ast }$, with results for the Logit method discussed separately in section 5.3.1 and illustrated in the online supplementary material.

5.1 Coverage with Design-Based Sampling Variance Estimate

We first examine in figure 1 seven intervals (Wald, Jeffreys, uniform, Clopper Pearson, Wilson, Agresti-Coull, and Arcsine Square Root) computed from estimated (in the left panel) or true (in the right panel) effective sample size, given by (14) and (12), respectively. Figure 1 plots coverage based on this design-based estimate of design effect against “effective expected number of successes” $(n_{\text{eff}}·\theta )$, a feature which increases with n/c and θ. There are seven plotted points for each element of our factorial design, plotted separately for the Wald interval, and each point summarizes 10,000 samples.

Figure 1.

Left Panel: Coverage of seven CIs (all of those in section 2 except Logit) using effective sample size estimate (14), plotted against effective expected number of successes $({\mathit{n}}_{\text{eff}}·\theta$, plotted on the log scale), for each simulation configuration where the Wald points are plotted separately from the others. Right Panel: Analogous to left panel, using the true effective sample size (12) instead of (14).

All intervals with estimated effective sample size undercover, especially for small $n_{\text{eff}}·\theta$, but the lesser coverage of the Wald CI relative to others is evident (figure 1, left panel). For CIs other than Wald, undercoverage is rarely a major problem when the true design effect is known. The Wald interval does very poorly even when the design effect is known (in the right panel), and figure 1 sufficiently justifies eliminating it from consideration.

The format of plots in figure 2 is the same as that of figure 1 but with coverage plotted for only one CI method in each row and the Wald interval excluded. All six CIs tend to be conservative when based on the true design effect (right panel of figure 2). The Clopper-Pearson interval with estimated $n_{\text{eff}}$ tends to overcover at the expense of very large width (see Section 5.3). For all methods, coverage tends to the nominal as $n_{\text{eff}}·\theta$ increases, but convergence can be slow. (Note the log scale on the horizontal axis.)

Figure 2.

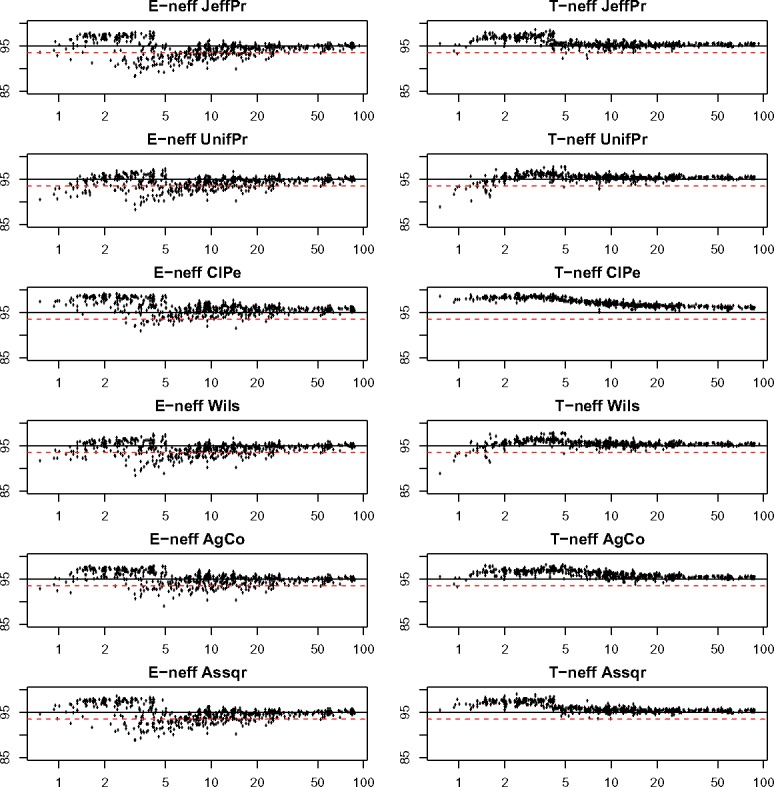
Left Panels: Coverage of six CIs using design-based effective sample size estimate, plotted against effective expected number of successes $({\mathit{n}}_{\text{eff}}·\theta$, plotted on the log scale), for each simulation configuration. JeffPr refers to Jeffreys interval, UniPr to uniform, ClPe to Clopper-Pearson, Wils to Wilson, AgCo to Agresti-Coull, and Assqr to Arcsine Square Root interval. Solid line at 95 represents nominal coverage, and dashed line at 93.5 undercoverage by 1.5 percent. Right panels: Analogous to left panels, using the true effective sample size (12) instead of (14).

In practice, the true sampling variance (11) is unknown, and comparison of the left and right panels of figure 2 suggests that variance estimation is the primary source of undercoverage in CIs from complex surveys, so that improving the estimate of variance (and hence of the effective sample size) will improve CI coverage.

5.2 Adjustments & Alternatives to Design-Based Estimates

Motivated by the good coverage properties of all CIs other than Wald with true effective sample size in the right panels of figure 2, the next subsection directly examines the improved mean-squared error (MSE) achieved by estimating sampling variance with (15) in place of (13). We compare in subsection 5.2.2 the performance of non-Wald intervals using the Dean-Pagano modification to the estimated effective sample size versus CIs based on (15).

5.2.1 Properties of the alternative design effect estimator.

The Kish-type formula (15) exploits a superpopulation model. Although the design-effect estimator in (14) is essentially unbiased, the corresponding effective sample size estimator is not. The effective sample size estimator (18) corresponding to the model-based variance estimator (15) has some biases that vary systematically with cluster size θ and ICC ρ. Table 1 displays within the simulation design of section 4, for n = 200, the simulation-averaged ratio of the estimated effective sample size (18) divided by the true effective sample size (12) averaged across scenarios.

The biases of estimated effective sample size (18) turn out to be very slight when $\rho =0.1$ (not shown) or when c = 1, are negative by up to 22 percent when $\rho =0.001$ and $c\ge 3$ and can be quite positive when $\rho =0.25$ and $\theta =0.1$. These biases are tolerable because the MSE of the effective sample size estimator (18) is low compared to that of (14).

The biases in estimated effective sample size illustrated in table 1 and those not shown are generally associated with upward bias in the corresponding design effect estimates (18). However, these biases in estimating design effect and effective sample size in the Kish method are generally accompanied by a notable decrease in RMSE by comparison with the purely design-based estimators. Table 2 shows the ratio of RMSE for estimated effective sample size (18) over the RMSE of the corresponding design-based estimate in (14) for ICC $\rho =0.25$ and n = 200, by scenario. Parameter combinations with c = 1 are not shown, since in those cases, the Kish and design-based estimators are algebraically equivalent. The table shows the considerable improvements in RMSEs when using the Kish method relative to the design-based method. For other values of n, the pattern is the same as that shown, with RMSE ratios often even smaller (many in the range 0.3–0.7). The favorable performance of the Kish method in confidence interval construction appears to be due to its reduced RMSE in combination with its positive biases in estimated design effect, which increase with cluster size.

Table 2.

Ratio of RMSE for Estimated Effective Sample Size (18) over RMSE for Design-Based Estimated Effective Sample Size (14) for ICC $\rho =0.25$ and n = 200, by Scenario, Based on N = 10,000 and 10,000 Replications.

	$\theta =0.1$			$\theta =0.2$			$\theta =0.3$
Scen.	c=3	c=5	c=7	c=3	c=5	c=7	c=3	c=5	c=7
C	0.92	0.88	0.85	0.94	0.90	0.86	0.94	0.90	0.87
I	0.89	0.83	0.83	0.84	0.83	0.77	0.82	0.78	0.72
D	0.83	0.83	0.73	0.68	0.54	0.58	0.58	0.49	0.44
H	0.88	0.85	0.81	0.88	0.81	0.79	0.91	0.82	0.81

It should be noted that in the exhibits of this subsection, as elsewhere in the displays of simulation results, a new and independent random population of size N is generated for each simulation configuration. Accordingly, each cell in the tables and point in the figures has inherent variability in repeated runs due to finite population differences. Nevertheless, the patterns described in the article are fairly consistent, stable, and support general conclusions.

5.2.2 Comparison of Kish-type formula CIs to Dean-Pagano CIs.

We now discuss CI results for the Kish-formula (15)–(18) method of estimating effective sample size—which we refer to as the Kish $n_{\text{eff}}$ method—versus the Dean and Pagano (DP) method applying the modification (20) to the design-based effective sample size (14).

Briefly, the two methods are broadly similar in their coverage rates, although the Kish method tends to have slightly higher coverage. When there is no clustering (i.e., c = 1), undercoverage is not a big problem, and the Kish method is essentially the same as the design-based method. For c = 3, undercoverage is frequent when using the design-based method, and both the DP modification and the Kish methods reduce it to a similar extent. In configurations with $c\ge 3$, there are slightly more configurations aggregated across the six non-Wald intervals considered in this subsection in which DP coverage falls below 93.5 percent, 94 percent, or 94.5 percent as compared with Kish, and this comparison holds for almost every combination of θ and ρ when c > 1 and n > 50 (tables shown in the online supplementary material).

For large cluster-size c and ICC ρ, undercoverage for either the DP or Kish method is common. The most problematic setting is c = 7, and figure 3 contrasts the methods in this case. In each panel labeled by a CI method, the ratio of average interval lengths with effective sample size estimated by the Kish method over the DP method is plotted against the noncoverage ratio under the two $n_{\text{eff}}$ methods. For all CI types, most points have one ratio > 1 and one < 1. Among points with width ratios > 1 and noncoverage ratios < 1, the cyan (gray in print version) ones for which DP coverage was below nominal can be viewed as favorable for the Kish method, and perhaps so are the black points with width-ratios < 1 and noncoverage ratios > 1 and above-nominal DP coverage. The points in the lower-left quadrant in each panel are very favorable to the Kish method because they reflect settings in which Kish-method coverage is larger than for DP while width is smaller. Notably, none of the CI types show any upper-right quadrant configurations in which the DP method would have smaller average width but larger coverage. Similar pictures for c = 3 and c = 5, included in the online supplementary material, show a similar pattern but not quite so strikingly favorable to the Kish $n_{\text{eff}}$ method over the DP method.

Figure 3.

Comparison of Metrics for Kish Versus DP $n_{\text{eff}}$ Methods, for Each of Six CIs Under 108 Simulation Settings with c = 7. Plotted points are y = 100 times ratio of widths for Kish ${\mathit{n}}_{\text{eff}}$ method over DP, versus x = 100 times ratio of noncoverage for Kish ${\mathit{n}}_{\text{eff}}$ method over noncoverage for DP. Points with below-nominal DP coverage plotted in cyan (gray in print version). Vertical line indicates coverage ratio 1, horizontal line width-ratio 1.

Figure 4 presents another view of the coverage of the same six CI types as figure 3 computed with the Kish versus DP $n_{\text{eff}}$ method. In each of these six panels, which correspond to the case c = 7, the middle range of DP points with near-nominal (94 percent–96 percent) coverage correspond to a range 94 percent–97.5 percent of Kish-method coverage. This observation is consistent with the width-comparisons from figure 3. Analogous figures for the cases c = 3, 5 are presented in the online Supplementary Material.

Figure 4.

Coverage for Six CI Types, for the Kish and DP $n_{\mathbf{e}\mathbf{f}\mathbf{f}}$ Methods in 108 Simulation Configurations with c = 7. Equal coverage is indicated by ${45}^{°}$ line, nominal 95 percent coverage by black solid lines, and extreme $(93.5\%)$ undercoverage by black dashed lines.

Both the DP and the Kish methods have increased width over all (non-Wald) types compared to the design-based method of estimating sampling variance and $n_{\text{eff}}$. In fact, for the six intervals considered in this subsection, the Kish method increases width 0–41.1 percent with a mean increase of 6.9 percent, and the DP modification increases width 0.4–50.6 percent with a mean of 6.8 percent. Figure 4 indicates the somewhat higher coverage for the Kish versus DP method for each interval type. The increased coverage is acceptable because the overall message from the Kish versus DP comparisons is that the Kish method makes more effective use than DP of CI widths, with slightly better success at mitigating undercoverage in the presence of clustering.

5.3 Comparison of Alternative Intervals

We now highlight relative advantages among the non-Wald CI types of section 2. In this comparison, we examine results using the Kish method (18) of $n_{\text{eff}}$ estimation. Considering first the rather good coverage properties of these CI types based on true $n_{\text{eff}}$ in the right-most panels of figure 2, the coverage performance of the Jeffreys, uniform prior and Wilson intervals seem most favorable to us: Clopper-Pearson is excessively conservative, with systematically above-nominal coverage also for Agresti-Coull and Arcsine Square Root. When $n_{\text{eff}}$ is estimated, the left-most panels in figure 2 show Clopper-Pearson to be overly conservative and Arcsine Square Root erratic and dominated across the range of $\theta ·n_{\text{eff}}$ by the Jeffreys prior interval, but it is rather hard to choose among the Jeffreys, uniform, Wilson, and Agresti-Coull alternatives. In the presence of extensive clustering (c = 7), figure 4 shows somewhat more detail but also does not provide a compelling reason to prefer any of the Jeffreys, uniform, Wilson, and Agresti-Coull to the others, although Jeffreys has a slightly wider range of coverage and Agresti-Coull a more systematically conservative tendency than the others in this group.

Width and coverage are shown simultaneously for the six CI types in a further pictorial display in figures 5 and 6. In these, we plot the ratio of each interval width to that of Clopper-Pearson (since that CI is typically the widest and has highest coverage) multiplied by 100 versus the noncoverage, plotting a separate panel for each level of clustering and within each c for each overall proportion θ. Points in the lower left of each panel have high coverage and small widths. The definition of relative width removes much of the dependence on θ and n. Figure 5 contains the three θ panels for c = 1 and figure 6 for c = 5. The other cases, c = 3 and c = 7, can be found in the online supplementary material.

Figure 5.

Relative Width (ratio of width of Jeffreys, uniform, Clopper-Pearson, Wilson, and Agresti-Coull interval to that of the Clopper-Pearson, multiplied by 100) Versus Noncoverage for 72 Configurations with No Clustering (c = 1) and (a)$\theta =0.05$, (b)$\theta =0.1$, (c)$\theta =0.3$. The solid vertical line represents nominal noncoverage. The dotted line, given for reference, represents undercoverage of 1.5 percentage points.

Figure 6.

Ratio of Width of Jeffreys, Uniform, Clopper-Pearson, Wilson, Agresti-Coull, and Arcsine Square Root to That of the Clopper-Pearson, Multiplied by 100, Plotted Versus Noncoverage for 36 Simulation Configurations with c = 5 and (a)$\theta =0.05$, (b)$\theta =0.1$, (c)$\theta =0.3$. The solid vertical line represents nominal noncoverage. The dotted line, given for reference, represents undercoverage of 1.5 percentage points.

Some patterns are common to all these plots: the Agresti-Coull and Clopper-Pearson tend to be the widest for $\theta =0.05,0.1$ and also tend to have higher coverage, typically overcovering. The other intervals are comparable to each other in coverage, with the Jeffreys being the shortest, though having slightly more cases of marked undercoverage, especially for ICC ρ of 0.25. For $\theta =0.3$, the Clopper Pearson is the widest and most conservative. The other intervals are comparable in coverage, with the Wilson and uniform tending to be the shortest.

In figure 5, there is a general tendency towards overcoverage and few cases of pronounced undercoverage. Panels (a) and (b), respectively for $\theta =.05$ and 0.1, show that the Clopper-Pearson (CP), Agresti-Coull (AC), Jeffreys, and Arcsine Square Root intervals all have many overcoverage events in the region where noncoverage is less than 4 percent, but CP and AC are widest in this region, achieving overcoverage at the cost of increased width. Agresti-Coull can be wider than CP for $\theta =0.05$. Among other CIs, Jeffreys strikes a good width/coverage trade-off but not in all situations (showing marked undercoverage $\theta =0.1$ and n = 50). The Wilson and uniform CIs are calibrated relatively well, though there are a few instances of noncoverage beyond 7 percent for $\theta =0.05$ and n = 30, most of them for the uniform. For $\theta =0.3$, the Wilson and the uniform intervals tend to be shortest, with Jeffreys the shortest for $\theta =0.05$ and $\theta =0.1$.

In figure 6, many of the same comments apply, including the excessive width of Agresti-Coull and Clopper-Pearson for $\theta =0.05$, the well-calibrated uniform and Wilson, the short but occasionally severely undercovering Jeffreys, and the somewhat erratic Arcsine Square Root.

The most pronounced undercoverage for all intervals occurs when c = 7 and $\rho =0.25$. Even the Clopper-Pearson undercovers there, although not more than 1.5 percent.

Some of the width relationships among interval widths can be proved analytically. Specifically, both the uniform and the Jeffreys intervals are contained in the Clopper-Pearson interval (see Brown et al. 2001). A proof is supplied in Appendix A. Though the proof does not cover the relationship between the Jeffreys and the uniform, we have verified numerically that for $\alpha =0.10,0.05,0.01$ and $n=2,\dots ,10,000$, the Jeffreys interval’s lower endpoint is always smaller than that of the uniform’s when the binomial count $Y<n/2$. That is, qbeta $(\alpha /2,y+1/2,n-y+1/2)<$ qbeta $(\alpha /2,y+1,n-y+1)$ for $y<n/2$.

5.3.1 The Logit interval (see the online supplementary material).

In our simulations, the Logit interval shows a similar performance to the Agresti-Coull, but in some cases, it is extremely wide, as shown in figures S7–S11 of the online supplementary material. Figure S7 in the online Supplementary Material is analogous to figure 2 in the article but also includes the Logit interval. Figures S8–S11 in the online supplementary material are analogous to figure 5–6 in the main article, covering the cases c = 1, 3, 5 and 7, but plotting points corresponding to the Logit in cyan, the Agresti-Coull in blue, the Clopper-Pearson in black, and all others in gray to highlight the similar pattern of behavior of the Agresti-Coull and Logit. The strikingly high widths in some cases, seen mostly for $\theta =0.05$ and sometimes for $\theta =0.01$, are consistent with the finding by Brown et al. (2001) that the Logit interval is “unnecessarily long” in the binomial case.

6. CONCLUSIONS AND FUTURE WORK

We have seen that the Wald CI is badly flawed for estimating proportions in complex surveys due to its severe undercoverage in a variety of situations. Improving the estimation of sampling variance does not salvage the Wald interval, which performs poorly even when the true sampling variance is known. Since the alternative methods studied are straightforward to implement and clearly superior, the Wald approach should not be used—especially not in complex surveys.

For the other intervals considered, notable undercoverage can also occur when there is clustering. Improving the estimation of sampling variance by using simple superpopulation model assumptions can greatly enhance the performance of these intervals. This approach worked well throughout our factorial design, was better than the modification of effective sample size by Dean and Pagano (2015), and can be applied more generally. This approach to improving coverage by improving estimation of the effective sample size is perhaps our main methodological contribution.

Among the CI methods studied, there was no clear winner with respect to coverage or length. Our comparisons of coverage and lengths suggest the Wilson, uniform, and Jeffreys intervals tend to have shorter lengths (the former two especially for larger θ such as $\theta =0.3$ and the latter for smaller θ) and coverage closest to nominal. The Clopper-Pearson interval, recommended by Korn and Graubard (1998) and by Dean and Pagano (2015) in cases with high clustering and extreme proportions, tends to be much longer and should only be used if conservative coverage is paramount.

Our method of estimating the effective sample size has been developed and tested for the Horvitz-Thompson estimator under stratified one-stage sampling of clusters of equal sizes. The appendix extends the method to unequal cluster sizes (24) and to the case where the weights might not be inverse inclusion probabilities, but design-consistent variance estimates of the stratum totals are available (25) and may come, for instance, from random groups, Balanced Repeated Replication (Wolter 1985), jackknife, or bootstrap (Shao and Tu 1995). Future research will extend and test the method using other designs and other types of estimators. The ratio estimator or combined ratio estimator will be particularly relevant, as these are frequently used in surveys to achieve gains in precision in estimating proportions when the cluster sizes are not equal or when a good auxiliary variable is available (see Lohr 2010). We expect that under moderate misspecification of the sampling design or the model, the method will still perform well. Further research about the impact of model misspecification is recommended. In particular, our simulations do not test the performance of the method in settings with cross-cluster correlation. Sampling variance estimators can also be developed using the same ideas under other superpopulation model assumptions (e.g., allowing for other correlation structures), but care must be taken that the number of parameters to be estimated is not too large given the sample size.

In the case where a data user is only provided with replicate weights in a public-use data file with no information about clustering, our method of estimating sampling variances will not apply. Even when our method cannot be used, a strong recommendation still emerges from our simulations: the Wald interval is not to be used and should be replaced by the preferred non-Wald method, where the best available sampling variance estimate is used to compute the effective sample size and effective sample count as described in section 2.8, and the effective sample count and effective sample size are then used in the confidence interval formulas (equations (3)–(7) in sections 2.2–2.6). Possible variance estimators include those based directly on supplied weight-replicates or random-group or jackknife estimators in which weights and replicates are used to define the groups or others, such as bootstrap variances in complex surveys when those can be justified as consistent (see Rust and Rao 1996 for a review of replication techniques for variance estimation in complex surveys).

Several other lines of investigation of CI performance for proportions based on complex survey data deserve attention. Coverage of all of the intervals tends to fall below nominal as cluster sizes increase, and variants of these intervals—or more urgently, of the underlying estimation of effective sample size, which mitigate this tendency—are needed. In particular, a full Bayesian approach with weakly informative prior distributions, which incorporates complex design features like clustering and stratification through a hierarchical Bayes model appropriate for a binary outcome, deserves consideration. We did not assess this approach since we confined attention to simple computational approaches that are more readily implemented in ACS-type settings. Indeed, further research is needed to confirm that any method performs well consistently across designs with widely varying (nonconstant) cluster sizes and other sorts of inhomogeneity, and it is in such settings where we believe the model-based approach introduced here shows greatest promise.

Supplementary Materials

Supplementary materials are available online at academic.oup.com/jssam.

Appendix

A. ORDERING OF CLOPPER-PEARSON, JEFFREYS, AND UNIFORM INTERVALS

Theorem:

Let $[L_J(X,n),U_J(X,n)],\hspace{0.17em}[L_{UNI}(X,n),U_{UNI}(X,n)],\hspace{0.17em}[L_{CP}(X,n),U_{CP}(X,n)]$ be the lower and upper bounds of the Jeffreys, uniform, and Clopper-Pearson Intervals, respectively. Then

$$[L_J(X,n),U_J(X,n)]\subset [L_{CP}(X,n),U_{CP}(X,n)]$$

$$[L_{UNI}(X,n),U_{UNI}(X,n)]\subset [L_{CP}(X,n),U_{CP}(X,n)]$$

Proof:

The result follows from the fact that if f and g are densities for random variables W and Z with cdf’s F and G, respectively, such that f/g is increasing, then W is stochastically bigger than Z. To show this, write

$$\frac{d}{du}[F(u)-G(u)]=g(u)(\frac{f(u)}{g(u)}-1).$$

Because the ratio $f(u)/g(u)$ is increasing, the derivative on the left-hand side can only change from negative to positive. Hence, the function $F(u)-G(u)$ can have only one local minimum, and its value is zero at $\infty$ and $-\infty$. Hence $F(u)-G(u)\le 0$. The Jeffreys, and Clopper-Pearson endpoints can all be expressed from the quantiles of the beta distribution, as described in section 2. The result follows by taking the ratios of the beta densities for each of the interval endpoints and showing that each is decreasing or increasing. For instance, in terms of the Beta function $\beta (a,b)$

$$f(u)=\frac{\text{dbeta}(u,X+1/2,n-X+1/2)}{\text{dbeta}(u,X,n-X+1)}=\frac{\beta (X+1/2,n-X+1/2)}{\beta (X,n-X+1)}{\{u/(1-u)\}}^{1/2}.$$

It is easy to check that $f\prime (u)>0$, so f(u) is increasing. This implies $L_J(X,n)>L_{CP}(X,n).$ The relationships between the other endpoints are proved analogously.

B. JUSTIFICATION OF MODEL-BASED ESTIMATION FORMULAS

Consider the survey-weighted estimator of Y applicable in survey settings with stratification and single-stage cluster sampling but not necessarily equal-sized clusters or stratumwise SRS single-stage cluster sampling. In terms of single and joint inclusion probabilities ${\pi }_{hki},{\pi }_{hki,hk\prime j}$, the general survey-weighted (Horvitz-Thompson) estimator of Y becomes

$$\widehat{Y}\hspace{0.17em}=\hspace{0.17em}{\widehat{Y}}^{\text{HT}}\hspace{0.17em}=\hspace{0.17em}\sum _{h=1}^H\sum _{k\in S_h}\sum _{i\in C_{kh}}{Y}_{khi}/{\pi }_{hki},$$ (22)

and a general expression for the anticipated variance of (22) (Isaki and Fuller, 1982), where the expectation is taken with respect to both the sampling design and the super population model, is

$$\text{AV}({\widehat{Y}}^{HT})\hspace{0.17em}=\hspace{0.17em}\sum _{h=1}^H\hspace{0.17em}\sum _{k,k\prime \in {\mathcal{U}}_h}\hspace{0.17em}\sum _{i\in C_{kh},j\in C_{k\prime h}}\frac{{\pi }_{hki,hk\prime j}-{\pi }_{hki}{\pi }_{hk\prime j}}{{\pi }_{hki}{\pi }_{hk\prime j}}[E(Y_{hki})E(Y_{hk\prime j})+\text{Cov}(Y_{hki},Y_{hk\prime j})],$$ (23)

where ${\mathcal{U}}_h$ is the set of clusters in stratum h of the population.

Our blanket assumption is that

(A.o) clusters are sampled all-or-none

which implies that the single and double inclusion probabilities are constant over clusters, so we drop the indices i, j from their notation. Let M_kh denote the number of units i in cluster C_kh. Then the extra assumptions underlying the formula simplifications in sections 3.1 and 3.2 are that all $M_{kh}$ are equal to $c$ and that

(A.iv) the single and pairwise inclusion probabilities are equal to those of stratified SRS cluster sampling:

$${\pi }_{hk}=\frac{n_h^C}{K_h},{\pi }_{hk,hk\prime }=\frac{n_h^C(n_h^C-1)}{K_h(K_h-1)}\hspace{0.17em}\text{for}\hspace{0.17em}k\in U_h,k\prime \ne k$$

Under assumptions (A.o)–(A.iii), the mean and variance of the cluster-attribute $Y_{kh+}=\sum _{i\in C_{kh}}{Y}_{khi}$ are given by

$$E(Y_{kh+})=M_{kh}{\tau }_h\hspace{0.17em}\hspace{0.17em},V(Y_{kh+})=\{M_{kh}+M_{kh}(M_{kh}-1)\rho \}{\sigma }_h^2$$

Then (23) simplifies to

$$\text{AV}({\widehat{Y}}^{HT})=\sum _{h=1}^H{\tau }_h^2\sum _{k,k\prime =1}^{K_h}\frac{{\pi }_{hk,hk}-{\pi }_{hk}{\pi }_{hk\prime }}{{\pi }_{hk}{\pi }_{hk\prime }}{M}_{kh}{M}_{k\prime h}+\sum _{h=1}^H\sum _{k=1}^{K_h}\frac{1-{\pi }_{hk}}{{\pi }_{hk}}\{M_{kh}+M_{kh}(M_{kh}-1)\rho \}{\sigma }_h^2$$ (24)

However, in many real surveys where the weights w_i are based on calibration, raking, nonresponse adjustment, and/or weight-trimming steps, the fiction that these weights are inverse inclusion probabilities cannot be maintained, and therefore, anticipated-variance formulas like (23) must be replaced by some off-the-shelf, design-consistent, variance estimation method such as random-groups or Balanced Repeated Replication (Wolter 1985), jackknife, or bootstrap (Shao and Tu 1995). Let ${\widehat{V}}_h(\mathbf{z})={\widehat{V}}_h({\left\{z_k\right\}}_k)$ denote the estimated variance in stratum h by any of these methods applicable to the total of a cluster-level attribute z_k for $k\in \{1,\dots ,K_h\}$. Then, under assumptions (A.i), (A.ii), and (A.iii), the anticipated variance AV in (23) or (24) is estimated by

$$\widehat{\text{AV}}({\widehat{Y}}^{HT})=\sum _{h=1}^H{\widehat{\tau }}_h^2\hspace{0.17em}{\widehat{V}}_h({\left\{M_{kh}\right\}}_k)+\sum _{h=1}^H{\widehat{\sigma }}_h^2\sum _{k\in S_h}\frac{M_{kh}}{{\pi }_{kh}}\left(\frac{1-{\pi }_{kh}}{{\pi }_{kh}}\right)(1+(M_{kh}-1)\widehat{\rho }),$$ (25)

where ${\widehat{\tau }}_h,{\widehat{\sigma }}_h^2,\widehat{\rho }$ are design-based estimators derived from sample-weighted moments. Natural formulas for such estimators are

$$1-\widehat{\rho }\hspace{0.17em}=\hspace{0.17em}\frac{n-H}{n}\hspace{0.17em}·\hspace{0.17em}\frac{{\sum }_{h=1}^H\sum _{k\in S_h}\sum _{i,j\in C_{kh}}{(Y_{hki}-Y_{hkj})}^2/2}{{\sum }_{h=1}^H{\widehat{\tau }}_h(1-{\widehat{\tau }}_h)\hspace{0.17em}\sum _{k\in S_h}{M}_{kh}(M_{kh}-1)}$$

$${\widehat{\sigma }}_h^2\hspace{0.17em}=\hspace{0.17em}\frac{1}{n_h-1}\sum _{k\in S_h}\sum _{i\in C_{kh}}{(Y_{hki}-{\widehat{\tau }}_h)}^2,{\widehat{\tau }}_h\hspace{0.17em}=\hspace{0.17em}\frac{1}{n_h}\hspace{0.17em}\sum _{k\in S_h}{Y}_{hk+},$$

where $n_h=\sum _{k\in S_h}{M}_{kh}$. In a complex survey with stratification and take-all clusters, (25) provides a general variance estimator as part of our proposed design-effect and CI estimators. If assumption (A.iv) also holds, then these variance-estimation formulas take the explicit form,

$${\widehat{\text{AV}}}^{\ast }(\widehat{Y})=\sum _{h=1}^H\frac{K_h-n_h^C}{n_h^C}\{{\widehat{\tau }}_h^2\frac{K_h}{n_h^C-1}\sum _{k\in S_h}{(M_{kh}-\frac{n_h}{n_h^C})}^2\hspace{0.17em}+\hspace{0.17em}{\widehat{\sigma }}_h^2\hspace{0.17em}\frac{K_h}{n_h^C}(n_h(1-\widehat{\rho })+\widehat{\rho }\sum _{k\in S_h}{M}_{kh}^2)\},$$ (26)

where ${\widehat{\tau }}_h,{\widehat{\sigma }}_h^2$ and $\widehat{\rho }$ are as above. Then the expressions for estimated design effect and effective sample size are as in (18).

Note that in the further restricted setting of section 3.2, where $M_{kh}=c$ is constant, (26) reduces to (15), which in the main text we denote as ${\widehat{\text{Var}}}^{\ast }(\widehat{Y})$ for simplicity of exposition. This formula would imply the usual Kish formula $\text{Deff}=1+\widehat{\rho }(c-1)$ under the further assumption of proportional allocation with cluster sample sizes $n_h^C$ to stratum h, if ${\widehat{\sigma }}_h^2$ were changed to a variance assumed not to depend on stratum. With proportional allocation, the design-based estimated sampling variance $\widehat{\text{Var}}(\widehat{Y})$ in (13) is essentially equal to ${\widehat{\text{Var}}}^{\ast }(\widehat{Y})$, the only difference being the $K_h-1$ terms instead of K_h in the denominators of stratum sample variances in (13).

The idea of this section has been that approximately design-based estimators of the variance of survey-weighted estimates of proportions, with anticipated variance calculated on the basis of slightly misspecified models expressed in terms of a few unknown parameters to be estimated, can be an effective and numerically stable way to produce estimated design effects.

C. ADDITIONAL SIMULATION DETAILS

Patterns of joint variation of stratum sampling fractions $f_h=n_h/N_h$ and stratum proportions θ_h are given by

$${\theta }_h=\theta (1+b_0(h-\frac{H+1}{2})),{\overline{f}}_h\propto {\theta }_h^{a_1}\hspace{0.17em}{(2\theta -{\theta }_h)}^{a_2},1\le h\le H$$ (27)

Initially we consider four patterns of parameters for the pair of H-vectors:

C: $b_0=a_1=a_2=0$ level θ’s, $\overline{f}$’s

I: $b_0=3/(4H-4),a_1=1,a_2=0$$\nearrow \theta$’s, $\nearrow \hspace{0.17em}\overline{f}$’s

D: $b_0=3/(4H-4),a_1=0,a_2=1$$\nearrow \theta$’s, $\searrow \hspace{0.17em}\overline{f}$’s

H: $b_0=3/(4H-4),a_1=1,a_2=1$$\nearrow \theta$’s, $\cap$ shaped $\overline{f}$’s

The purpose of the choice $b_0=3/(4H-4)$ in the scenarios I, D, and H with H = 4 strata is to fix the smallest of the ratios ${\theta }_h/\theta$ as 5/8, and the largest as 11/8. Of course, other choices are possible: to set the minimum value ${\theta }_1/\theta$ of these ratios to ${\beta }_0<1/2$, fix $b_0=2(1-{\beta }_0)/(H-1)$. The intent was to choose values that would allow for differences between the scenarios while avoiding extreme values that would lead to poorly behaved and unusual results.

Rounding of Stratum Sample Sizes

Stratum sample sizes to be calculated following the rules given previously need to be rounded to become integers, and the corresponding proportions are changed to reflect the integer population and sample sizes. Thus, with round denoting the operation of rounding a number to the nearest integer, $n=round(fN/c)$, then $f\equiv cn/N$; then $N_h=round(N{\lambda }_h),\hspace{0.17em}\hspace{0.17em}{\lambda }_h\equiv N_h/N$, then from the values ${\overline{f}}_h$ defined by (27), $n_h^C=round({\overline{f}}_h{N}_h/c),\hspace{0.17em}\hspace{0.17em}{f}_h\equiv n_h^{C}c/N_h$.

D. R CODE FOR DESIGN EFFECT AND CI CALCULATIONS

In section S1 of the online supplementary material, we describe the use of two functions coded in R (R Core Team, 2017) adapted from those used in the simulations of section 4, VarKish and CIarrFcn, and provide an illustrated example based on simulated data. The R function VarKish calculates the design-based and Kish-type variances for a survey-weighted total of a binary attribute Y_hki in the setting of a stratified, single-stage, cluster-sample (in which all units are taken from each sampled cluster). The R function CIarrFcn encodes the calculation of all eight types of confidence intervals studied in this article. These functions along with parameter values and data objects used in the illustration are contained in the supplementary R workspace RSupp.RData, where function listings and the data objects can be found. After explaining in successive subsections of section 2 of the online supplementary material the inputs and outputs of these R functions, the online supplementary material also provides a detailed example of the use of these functions similar to the way they were applied in the simulations of sections 4 and 5.

This work was supported partially by the funding provided by International Centers of Excellence for Malaria Research: “Malaria Transmission and the Impact of Control Efforts in Southern Africa.” NIH-NIAID, U19-AI089680.