Closed Loop Spatial and Temporal Control of Cavitation Activity with Passive Acoustic Mapping

Abstract

Ultrasonically actuated microbubble oscillations hold great promise for minimally invasive therapeutic interventions. While several preclinical studies have demonstrated the potential of this technology, real-time methods to control the amplitude and type of microbubble oscillations (stable vs inertial acoustic cavitation) and ensure that cavitation occurs within the targeted region are needed for their successful translation to the clinic. In this paper, we propose a real-time nonlinear state controller that uses specific frequency bands of the microbubble acoustic emissions (harmonic, ultra-harmonic, etc.) to control cavitation activity (observer states). To attain both spatial and temporal control of cavitation activity with high signal to noise ratio, we implement a controller using fast frequency-selective passive acoustic mapping (PAM) based on the angular spectrum approach. The controller includes safety states based on the recorded broadband signal level and is able to reduce sensing inaccuracies with the inclusion of multiple frequency bands. In its simplest implementation the controller uses the peak intensity of the passive acoustic maps, reconstructed using the 3^rd harmonic (4.896 ± 0.019 MHz) of the excitation frequency. Our results show that the proposed real-time nonlinear state controller based on PAM is able to reach the targeted level of observer state (harmonic emissions) in less than 6 seconds and remain within 10 % of tolerance for the duration of the experiment (45 seconds). Similar response was observed using the acoustic emissions from single element passive cavitation detection, albeit with higher susceptibility to background noise and lack of spatial information. Importantly, the proposed PAM-based controller was able to control cavitation activity with spatial selectivity when cavitation existed simultaneously in multiple regions. The robustness of the controller is demonstrated using a range of controller parameters, multiple observer states concurrently (harmonic, ultra-harmonic, and broadband), noise levels (−6 to 12 dB SNR), and bubble concentrations (0.3 to 180 × 10³ bubbles per microliter). More research in this direction under preclinical and clinical conditions is warranted.

I. Introduction

Utrasonically actuated microbubble oscillations are a promising technology for minimally invasive therapeutic interventions. Microbubble oscillations (acoustic cavitation) are generally categorized into two types, stable volumetric oscillations (stable cavitation) that are associated with harmonic, ultra-harmonic and sub-harmonic acoustic emissions, and inertial oscillations (inertial cavitation) that are accompanied by broadband emissions [1]–[3]. Extensive research over the past years has linked these types of oscillations to a range of therapeutically relevant effects. For stable cavitation these effects include dissolution of blood clots (sonothrombolysis)[4]–[6] and transient disruption of cellular (sonoporation) and vascular barriers (e.g. blood brain barrier) [7]–[9], whereas for inertial cavitation, in addition to enhancing cellular permeability and extravasation [9]—[11], they include activation of mechanosensitive ion channels [12], [13], mechanical ablation [14], [15], and enhancement of thermal ablation [16], [17]. While some of these effects could be obtained using innate cavitation nuclei [15], their onset is more reproducible and, potentially, controlled in the presence of stabilized micron scale bubbles (e.g. phospholipid microbubbles [18], [19]). Moreover, when stabilized microbubbles are loaded with therapeutic agents, ultrasonic actuation can be used for targeted release and delivery of their cargo [20]. Considering that weak oscillations might not be able to promote the desired effect or attain effective cargo release and the narrow range of excitation pressures (tens of kilopascals) for transition from stable to inertial cavitation [14], real-time methods to control the level, type, and location of cavitation activity are essential for promoting the desired interaction and ensuring safe implementation.

To attain acoustic exposure level for safe and effective cavitation activity, control methods should be i) fast in order to adapt to the fast dynamics of the bubble oscillations and be amenable to clinical implementation, ii) able to account for non-modelled dynamics using feedback methods (i.e. account for the unpredictable nature of bubble dynamics), iii) robust to tuning and sensing inaccuracies, and iv) be able to accommodate broad ranges of errors and sensitivities that can be used to parameterize the control law. To date several methods have been developed to control acoustic cavitation (see Supplementary Table I). These can be broadly categorized to direct and indirect methods, which can then be subdivided to open and closed-loop controllers.

Direct controllers use control theory to control directly the system states (i.e. variables that are used to describe the mathematical “state” of a dynamical system), namely the bubble radius R and its derivatives $\dot{R}$ and $\ddot{R}$ [21], [22]. These approaches, which use Rayleigh-Plesset-type models, are able to control the bubble dynamics to any desired trajectory (i.e. the performance of the system states as function of time). Such controllers assume complete knowledge of the system states at all times and thus do not require observer states (i.e. metrics to infer the system states). The system states are constantly evaluated based on the underlying model and used as feedback for next step (i.e. closed loop controllers). An additional class of direct controllers are controllers based on chaos theory [23], [24], which unlike the above controllers have the advantage that they do not require knowledge of the system states.

While direct controllers demonstrate the possibility of controlling the bubble dynamics even under extreme conditions, the underlying assumptions made by these controllers make experimental realization impractical. This is because these controllers are i) based on an idealized bubble dynamics model, ii) assume no sensing and transmission latency, and iii) impose no limits on controller actuations (unrealistic for physical systems), which limits their implementation (Supplementary Table I).

To overcome these challenges and enable practical realizations, controllers that use the acoustic emissions from microbubble oscillations as observer states have been recently proposed (Supplementary Table I) [25]–[33]. In these controller implementations, the observer state, which is used to control the ultrasound exposure level, is based on the spectral content of the acoustic emissions recorded by a single element passive cavitation detector (PCD). Open loop (i.e. input is not updated throughout the experiment) implementations of this type of controller are primarily threshold based [25]–[28], [30], wherein after attaining a predefined threshold [34], the ultrasound exposure can be fixed to a certain predefined level. To date, harmonic [25], sub-harmonic [27], [30], [35] broadband [28] and ultra-harmonic emissions [26] [36], have been used as observer states.

Additional work has been performed using PCD for finding excitation parameters and techniques that optimize the desired effect, including heating [36], sonoluminescence [37] and spatially-selective adjustment of the cavitation threshold [38]. On the other hand closed-loop implementations, which use harmonics [29], ultra- and sub-harmonics [31], or broadband emissions as an observer of temperature [32], monitor the acoustic emissions throughout the duration of the experiment and adjust the ultrasound exposure level using the previous state of the controller and a desired target state (e.g. level of harmonic signal).

While the above controllers have demonstrated the potential for attaining safe and, to some extent, effective therapy, they have several limitations that may limit their clinical implementation. In particular, open-loop controllers lack realtime control, which may hinder their ability to attain acoustic exposure level for effective cavitation activity, whereas existing closed-loop controllers are sensitive to parameter gain tuning, bubble concentration, and do not include safety states in their design for safe execution during instabilities of the controller (especially since the change in applied pressure relies on single observer recordings). Finally, incorporation to the controller states of spatially selective control of cavitation activity has yet to be demonstrated.

To overcome the above limitations, in this paper, we propose a closed-loop real-time nonlinear state controller (the control law is used to control nonlinear dynamics) based on harmonic, ultra-harmonic, and broadband frequency bands as observer states to control the acoustic exposure level and maintain desired levels of acoustic emissions and by extension of cavitation activity. The controller introduces the use of spatially specific measurement of cavitation activity, and tunable control laws to enable stable behavior around a target level. In the present implementation, the controller i) adjusts the pressure change (ΔP) from the initial value (P₀) according to the level of the harmonic (or ultra-harmonic) signal, ii) selects the sign of the applied pressure (increase or decrease: ±ΔAP) according to the level of the harmonic signal, and iii) incorporates a switch state that is based on the broadband emissions to ensure a predefined level of broadband emissions is not exceeded (i.e. safety state). Its ability to control cavitation activity is tested with both single-channel PCD and frequency-selective passive acoustic mapping (PAM) based on the angular spectrum approach (ASA) [39].

Here, we employed ASA-PAM as it provides i) extremely fast reconstructions of the acoustic field (>3 orders of magnitude faster than time domain methods) [39], ii) frequency selectivity (e.g., harmonics, ultra-harmonics, etc.) that allows the localization of different types of cavitation activity, and iii) high signal-to-noise ratio (SNR) as compared to single element PCD (i.e. SNR is proportional to √N, where N is the number of elements used in the reconstruction) [39]. According to our workflow, we obtain training data to determine the performance of the different observer states and then we compare different control laws and parameters to determine their effect on reaching the desired state at specific location. Finally, we examine the effects of signal, noise, and bubble concentration on the controller’s performance.

II. Methods

A. Controller Design

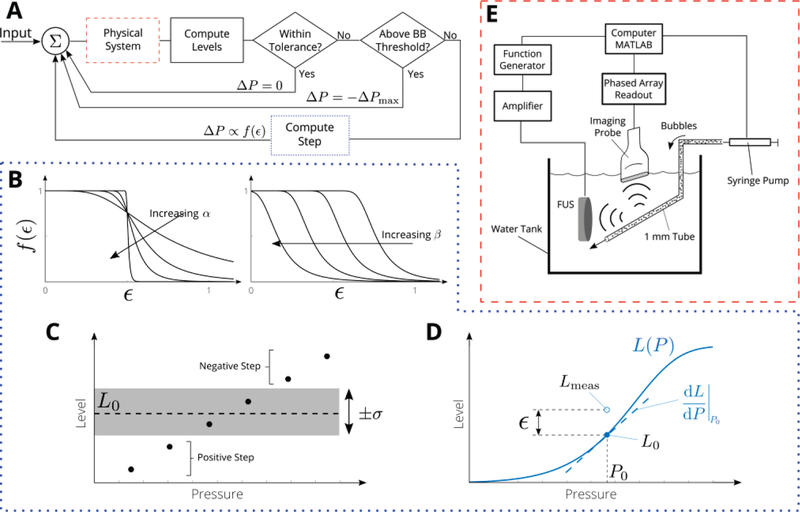
To control the level of cavitation activity we developed a nonlinear state controller based on multiple observer states [harmonic, ultra-harmonic, and broadband emissions; Fig. 1(A)]. The controller uses as input the first observer state to adjust the step size. When the measured level L_meas of the first observer state is sufficiently close to its desired value L₀ there is no change in the output pressure. When the measured level L_meas of the first observer state differs from its desired value L₀ by more than the tolerance level σ, the change in the applied pressure (ΔP) is computed according to the following control law:

$$\Delta P=\mathrm{sgn}(L_0-L_{\text{meas}})\Delta P_{\max }\tanh [{(\in \text{+}\beta )}^{-a}$$ (1)

where sgn is the sign function, α and β are parameters, and ε is the normalized error magnitude as in Fig. 1(D):

$$\in \equiv \frac{\left|L_{\text{meas}}-L(P)\right|}{L(P)}.$$ (2)

Here, L(P) is the model for the observer state, i.e., the training data; see Section II(E). The form of Eq. (1) was chosen to enable tenability and ensure stability; other control law shapes could be used, provided they decrease from a maximum at 0 and vanish for large errors ε. The effect of α and β on the control law is shown in Fig. 1(B). The maximum step size was computed from the slope of the model equation near the target value L₀ = L(P₀) as follows

$$\Delta P_{\max }=A\sigma {\left({\left.\frac{\text{d}L}{\text{d}P}\right|}_{P_0}\right)}^{-1}$$ (3)

To avoid overshoot (i.e. going past), the target range was set according to L₀(1 ± σ). Here A is a chosen multiplier that is of order 1. The increase or decrease in applied pressure (second state) is based on whether the measured level L is above or below the desired target range L₀ (1 ± σ) [negative if above target and positive if below, Fig. 1(C)]. An additional observer state (third state) can be incorporated to the controller as a (safety) switch condition (e.g. if it is above a threshold, then a maximum negative step is applied). Note that in the proposed controller the step, the sign, and the switch can be controlled by any observer state described above, including sub-harmonics.

Fig. 1.

Design of passive acoustic cavitation controller. (A) Controller logic flow (B) Effect of controller parameters α and β on the shape of the control law, which is a function of the normalized error ε. In the proposed controller implementation the step (ε) , the sign (± ΔP), and the (safety) switch (±ΔP_max), can be controlled by any observer state described including, harmonics, ultraharmonics, subharmonics and broadband emissions. (C) The applied pressure is decreased if the measured level is above the target level L₀, increased if the measured level is below L₀, and maintained (i.e. ΔP = 0) if the measured level is within L₀(l ± σ). (D) The magnitude of the step is determined by the normalized error ε, i.e., the difference between the measured level L_meas and the level predicted by the model L(P). (E) Microbubbles were flowed through a 1 mm tube (channel mimicking vessel) with a syringe pump and excited by FUS pulse (center frequency 1.662 MHz). Microbubble emissions were recorded by imaging probe connected to a 128-channel acquisition system. All systems were controlled and synchronized with MATLAB.

B. Passive Acoustic Mapping using the Angular Spectrum Method

While active methods have been used for microbubble imaging [40]–[42], PAM allows capture of data during the sonication without interfering with the therapy pulse [35], [39], [43]–[51]. Here we employed the angular spectrum approach, which performs computations in the frequency domain allowing reconstructions created with selected frequencies to be fed directly to the controller. The angular spectrum, due to the extensive use of the fast Fourier transform, offers a marked reduction in computation time compared to time domain methods [39], which is essential for real-time controllers.

For completeness, the ASA algorithm is described briefly here. Let p be the harmonic pressure field with p = p(x)e^-iωt and denote its spatial Fourier transform (or “angular spectrum”) by $\widehat{p}$(k_x), where k_x is the spatial frequency (the transform variable). If p₀(x) is measured along the face of the receiving transducer at position z₀, then the angular spectrum is ${\widehat{p}}_0$ = F_x(${\widehat{p}}_0$), where F_x denotes the spatial Fourier transform. Then, $\widehat{p}$ at an arbitrary axial distance z can be found via multiplication with a transfer function $\widehat{p}={\widehat{p}}_0\exp \left[i\sqrt{{\omega }^2/c_0^2-k_x^2}(z-z_0)\right]$ [52], where ω is the angular frequency and i is the imaginary unit. PAMs were created by computing the intensity I at each point (x, z) within the field of interest, i.e.,

$$I(x,z)={\left|{\mathcal{F}}_x^{-1}\left\{{\widehat{p}}_0\exp \left[i\sqrt{{\omega }^2/c_0^2-k_x^2}(z-z_0)\right]\right\}\right|}^2,$$ (4)

where ${\mathcal{F}}_x^{-1}$ is the inverse spatial transform. Linear acoustic propagation is assumed, and thus more complicated fields with multiple frequencies (i.e. microbubble emissions) can be expressed as a summation of the individual frequency components.

C. Experimental Setup

The excitation waveform (sinusoidal excitation: 1.662 MHz; pulse duration: 60 µs; pulse repetition frequency: 1 Hz) was sent from a waveform generator (Keysight, Santa Rosa, CA, USA) whose output was passed through a 43 dB amplifier (Mini-Circuits, Brooklyn, NY, USA) before applied to the FUS transducer (built in house, central frequency 1.662 MHz; curvature 30 mm and diameter 40 mm); see Fig. 1(E). The transducer was focused on a 1 mm channel submerged in a water tank by maximizing the echo recorded by a pulser-receiver (Olympus, Waltham, MA USA).

Optison microbubbles (GE Healthcare, USA) were diluted to approximately 6000 bubbles per microliter in a 10 ml syringe (unless otherwise stated), and manually agitated before injection into the channel. A syringe pump (KD Scientific, Holliston, MA, USA) was programmed to infuse bubbles continuously during all experiments (sonications) shown in the current paper at approximately 16 mm/s. A 256 element linear array transducer (GE L3–12D, 200 μm element spacing, 50 mm total aperture) was positioned at a right angle to the incident beam. The array was connected to a research ultrasound system (Vantage 256, Verasonics, Kirkland, WA, USA) that was programmed to operate in passive mode (center 128 channels, 20 MHz sampling frequency) to record microbubble emissions [Fig. 1(E)]. The recorded bubble emissions were used to create PAMs from emissions in the harmonic, ultra-harmonic, and broadband frequency ranges (see next section specific frequency bands) using the above ASA algorithm [Eq. (4)]. The current PAM implementation used axial resolution of 0.5 mm, pad factor of 4, frequency bin width of 5, and reconstruction region 100 mm (509 pixels) transverse by 35 mm (71 pixels) axial. For these settings, the reconstruction time was approximately 40 ms per level. All hardware was synchronized and controlled with custom MATLAB code (MathWorks, Natick, MA, USA). All reported pressures were determined using a calibrated a hydrophone (Onda, Sunnyvale, CA, USA) with a reported uncertainty of ±10 % in the frequency range of the excitation.

D. Controller Implementation

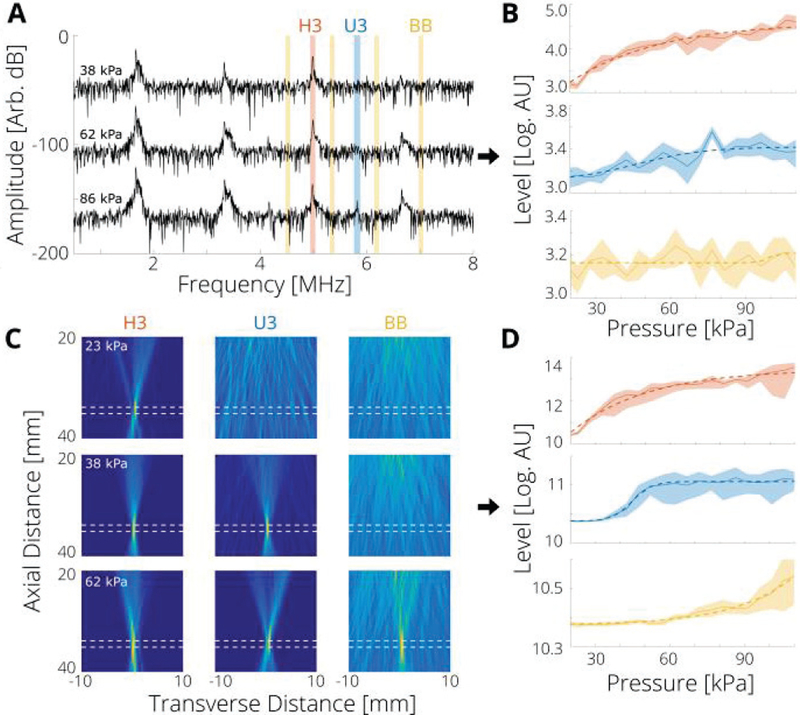
In the current controller implementation, the third harmonic is used as a control state and to determine the step of ΔP, the third harmonic or the third ultra-harmonic as a second observer state that is used to determine the sign of ΔP (we tested both implementations), and the broadband emissions as switch third state [safety condition; Fig. 1(A)]. Acoustic emission levels based on PAM were calculated by integrating the intensity of the PAM at each frequency: 3f₀ (4.986 ± 0.019 MHz) for the harmonic (H3), 3.5f₀ (5.817 ± 0.019 MHz) for ultra-harmonic (U3), and 2.72f₀, 3.22f₀, 3.72f₀, and 4.22f₀ (4.52, 5.35, 6.18, 7.01 ± 0.019 MHz), for the broadband (BB; these values were chosen to avoid harmonic and ultra-harmonic contributions). We chose these frequencies, because i) they are clinically relevant, ii) in this range our array had its highest sensitivity, and iii) they are associated only with cavitation activity; when no bubbles were present in the tube, the levels of these frequencies did not change for the pressure range used (20 to 110 kPa). In single channel PCD levels reported here, their values were computed from the center channel only using the same frequency bins used in the PAM. The threshold for the broadband emissions (safety condition) was taken to be about 1 % above the baseline broadband level. To assess the performance of the controller at different noise levels, zero mean, normally distributed noise (via MATLAB’s randn function) was added to the data before processing.

Two general controller shapes were chosen for comparison based on preliminary testing using a range of parameters. These were termed “sharp” and “smooth” based on the shape of their control laws (Fig. 1B) and represent reasonable but distinct controller performance. The parameters for each are listed in Table I. In the current implementation each controller loop, which included the emissions recording, the PAM reconstruction, the parameter extraction, and updating the pressure value based on the controller decision, required approximately 500 ms. This computation time could be reduced for other applications as needed, perhaps to a few tens of milliseconds, by use of lower spatial resolution for the PAMs, smaller sampling frequencies, narrower bandwidth, shorter acquisition times, or by use of parallel computing or use of GPUs.

TABLE I.

Parameters for the control laws [from Eq. (1)] used for the experiments

Name	A	α	β
Smooth	2	7	0.99
Sharp	1	10	0.8

E. Controller Calibration

The target state of the controller was determined from training data collected by monotonically increasing the applied pressure (20 to 110 kPa) to determine thresholds for the onset of harmonic and ultra-harmonic (stable), and broadband (inertial) cavitation. From the training data, nonlinear fits of the expected level L as a function of applied pressure P were computed for U3, H3 and BB according to

$$L(P)=a_1\tanh (a_{2}P+a_3)+a_4$$ (5)

where the a_i are constants optimized to fit the data. While a range of functions can be used (e.g. polynomial, power law, etc.), the form of Eq. (5) was chosen because it provides a single fitting function that enables reasonable fits of the differing nonlinear data trends for each frequency component (e.g. H3, BB). Six measurements were made at each applied pressure, and their mean value was fit with Eq. (5). Results for the level fits of the single channel data are shown in Fig. 2(B) and for the PAM in Fig. 2(D). For the PAM, the computed level was found not to depend strongly on the region over which the intensity was summed (provided the bubble region was included) or the axial resolution used (Supplementary Fig. 1). Therefore, for simplicity, in all PAM values presented here we used a reconstruction region that was 35 mm in transverse and 35 mm in axial direction respectively.

Fig. 2.

Cavitation thresholds measured by PAM have smaller uncertainty compared with single element passive cavitation detection. (A) Representative measured single channel (center channel of imaging array) spectra for the indicated applied pressure. The range from which the acoustic emission level of each component—third harmonic (H3), third ultra-harmonic (U3), and broadband (BB)—was taken is shaded as red, blue and yellow respectively. (B) Measured single channel levels as a function of applied pressure for each frequency: 3f₀ (4.986 ± 0.019 MHz) for the harmonic (H3), 3.5f₀ (5.817 ± 0.019 MHz) for ultra-harmonic (U3), and 2.72f₀, 3.22f₀, 3.72f₀, and 4.22f₀ (4.52, 5.35, 6.18, 7.01 ± 0.019 MHz), for the broadband. (C) Representative PAMs at the indicated applied pressure for each frequency range; dashed white lines represent the approximate position of the tube. (D) Measured PAM levels as a function of applied pressure. In the current set up, localization was accurate to within 1 mm. In (B) and (D), shaded range is standard deviation across 6 measurements, and dashed lines are models computed from Eq. (5).

F. Controller Performance Metrics

To quantify the performance of the controllers, we define the following metrics.

Rise Time:

Number of steps before H3 reaches or exceeds target value (smaller is better). The rise time measures how quickly the desired state can be achieved; while only the step number was recorded during experiments, successive sonications were found to be separated by 970±40 ms; according to this estimation the rise times were converted to seconds.

Proximity Ratio $\chi$:

Fraction of measured levels within the tolerance of the target level (larger is better)

$$\chi \equiv \frac{\text{No}.\hspace{0.17em}\text{of}\hspace{0.17em}\text{Seps}\hspace{0.17em}\text{within}\hspace{0.17em}\text{Tolerance}}{\text{Total}\hspace{0.17em}\text{Steps}}$$ (6)

The proximity ratio is a measure of how often the controller maintains the level of H3 to within the specified tolerance σ.

Normalized Variability ϛ:

One standard deviation of the measured H3 levels were within ϛ percent of the target level (smaller is better):

$$\text{ς}\equiv 100\times \frac{\text{Std}.\hspace{0.17em}\text{Deviation}\hspace{0.17em}\text{of}\hspace{0.17em}\text{Proximity}}{\text{Target}\hspace{0.17em}\text{Level}}$$ (7)

The normalized variability measures how closely overall the level of H3 is kept to the target level. A perfect controller has a small rise time, proximity ratio of unity ($\chi \to 1$), and a vanishing normalized variability (ϛ → 0).

III. Results

A. Cavitation Threshold Measurements with PAM and PCD

The training data for the proposed nonlinear state controller were collected from multiple measurements with linearly increasing applied pressure using FUS excitation and concurrent recording of acoustic emissions of bubbles that were flowing through a plastic tube with a linear array operated in passive mode [Fig. 1(E) and Fig. 2]. With a single channel recordings from the center element of the imaging array the threshold for the detection of third harmonic (H3) was at 33 ± 3 kPa (i.e., the pressure level at which the harmonic level was 5 standard deviations above its baseline value). The third ultraharmonic (U3) and broadband (BB) emissions level did not exceed the detection threshold (5 standard deviations above baseline value) for the pressure levels applied. Inspection of the plots indicates that the threshold for the onset of U3 and BB were on the order of 70 kPa and 100 kPa, respectively [Fig. 2(A) and (B)]. Computing the levels with all elements acting as a single active surface gave a moderate improvement in detection of the acoustic emissions. This is because the size of the array is significantly longer than a wavelength and comparable to the distance from the source, which limits the increase in sensitivity due to the larger effective area used (Supplementary Fig. 2). When no bubbles were present, the levels for H3, U3, and BB emissions did not deviate from the baseline in this pressure range, indicating the absence of finite amplitude propagation effects in the pressures employed in this study (Supplementary Fig. 3). With PAM at H3, U3, and BB frequency bands (see Methods, Section D) a well localized peak [Fig. 2(C)] was observed at pressure levels of 23 ± 3 kPa, 38 ± 5 kPa, and 73 ± 5 kPa respectively [Fig. 2(D)]. As compared to the single channel values, the higher sensitivity PAM allowed detecting cavitation activity more consistently, in addition to providing spatial information. Therefore, unless otherwise stated, PAM was selected as the H3, U3 and BB detection method to test performance of the controller.

B. Controller Performance with a Single Observer State

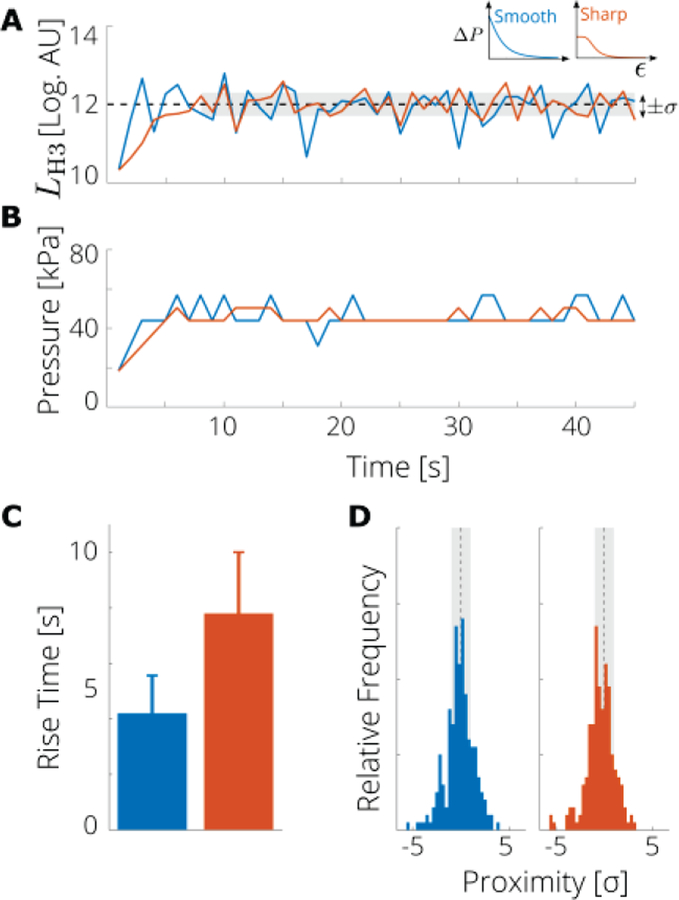
After we characterized the system using the cavitation threshold measurements, we examined the performance of the controller with a single observer state, namely the level of H3, for two representative controller shapes: smooth and sharp [Fig. 1(B) and Fig. 3]. The control law parameters (i.e. controller shapes) were chosen based on preliminary testing in which the control laws resulted in controllers with different rise times and normalized variabilities (Table I). Using single observer state, the step size was determined by the difference between the measured and modeled level of H3; that is, the level L in the definition of the normalized error ε in Eq. (2) was the level of the third harmonic. The rise time was generally shorter for the smooth controller (4.2 ± 1.2 s) than for the sharp controller (7.8 ± 1.9 s), as the maximum step size was larger for the smooth case [Fig. 3 (D)]. The proximity ratio [Fig. 3 (C)], the normalized variability, and the mean applied pressure were very similar for both control laws (Χ = 0.56 and 0.57, ϛ = 3.7 and 3.6; 53 ± 7 kPa and 55 ± 6 kPa, for smooth and sharp respectively). The difference between the two shapes suggest that the controller is relatively insensitive to the specific parameter values, however the smooth control law is slightly better due to shorter rise time.

Fig. 3.

A nonlinear state controller based on PAM with the step size determined by the emission level of the third harmonic (H3) can attain and sustain a desired level of cavitation activity. (A) Measured acoustic emission level of the H3 compared with target value (dashed black line) and tolerance (gray region) a representative run of each controller. (B) Applied pressure at each step for a representative run with the smooth (blue) and sharp (orange) control laws. (C) Rise times; error bar represents the standard error (5 runs). (D) Histogram of proximity of H3 level to target value, i.e., the difference between all measured levels (after the target level was first reached) and the target value (dashed black line) in terms of the tolerance σ.Vertical scale is 40 counts.

C. Controller Performance with Multiple Observer States

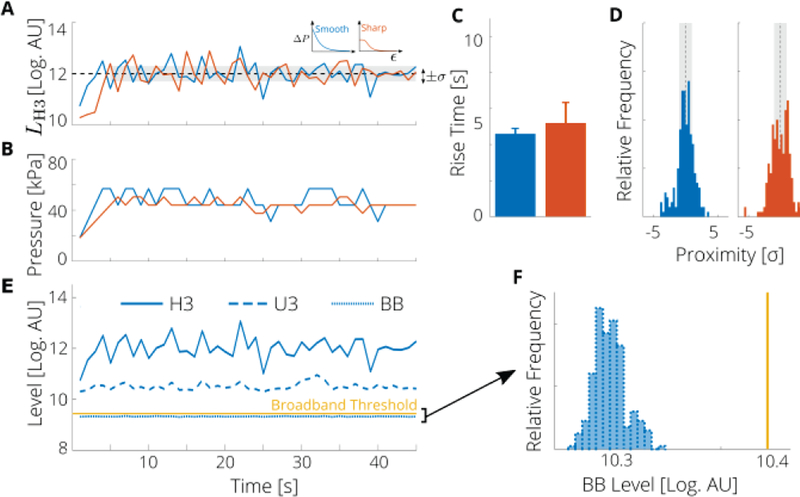
We next sought to determine the controller performance by incorporating an additional observer state: that is the level of the third ultra-harmonic (U3) was used to control the size of the step (the magnitude of ΔP; Fig. 4). While, the two controller shapes had similar rise times (4.6 ± 0.2 s for the smooth and 5.2 ± 1.0 s for the sharp) and normalized variability (ϛ = 3.3 vs ϛ = 3.5), the smooth control law had a larger proximity ratio than did the sharp control law [Χ = 0.63 vs x = 0.49; Fig. 4(C)]. As compared to single observer state controller (H3) the multiple observer states controller (H3/U3) had similar rise time but larger proximity ratio. The increased performance is directly related to the multiple independent states used (H3 and U3). Thus, the smooth control law, with U3 as the level controlling the step size resulted in the largest fraction of time spent within the tolerance of the desired level, indicating that this combination provides the best performance. This implementation was used as a reference controller for the remaining experiments (nominal condition). Note that in the above implementations, an additional switch state based on BB emissions was active, but the BB level never exceeded the specified threshold (1 % higher than the baseline), indicating that throughout the experiment a desired level of stable cavitation was achieved [i.e., there were no detectable BB emissions; Fig. 4(E) and (F)].

Fig. 4.

A nonlinear state controller based on PAM with the step size determined by the emission level of the third ultra-harmonic (U3) can attain and sustain a desired level of cavitation activity. (A) Measured level of the third harmonic (H3) compared with target value (dashed black line) and tolerance (gray region). (B) Applied pressure at each step for a representative run with the smooth (blue) and sharp (orange) control laws. (C) Rise times; error bar represents the standard error (5 runs). (D) Histogram of proximity of H3 level to target value, i.e., the difference between all measured levels (after the target level was first reached) and the target value (dashed black line) in terms of the tolerance σ. Vertical scale is 40 counts. (E) Measured acoustic emission levels of the third harmonic (H3), third ultra-harmonic (U3), and broadband (BB) components for the smooth control law. BB level has been lowered by 1.5 dB for clarity. (F) Histogram of all measured BB levels across all runs compared to threshold value (solid yellow line).

D. Effect of Noise on Controller Performance

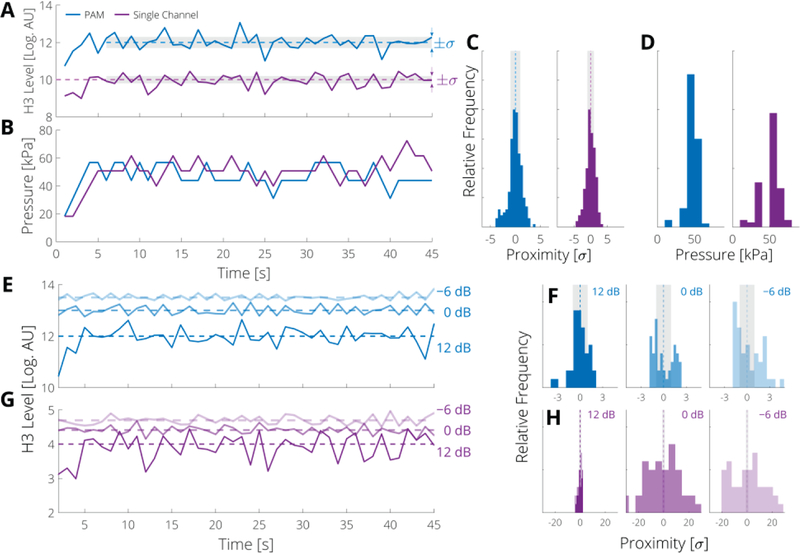
To assess the impact of the noise level of the controller we conducted two different experiments. In the first experiment, we compared the performance of the controller between PAM and a single channel PCD using identical frequency bands and in the second, we assessed the performance of the controller using different levels of added white noise. In the first set of experiments, our results indicate that both acoustic emission detection methods had similar performance (at nominal controller conditions), although the PAM controllers had mean applied pressures that were lower by approximately 3 kPa [Fig. 5(D)]. The addition of Gaussian noise had a stronger effect on the single channel PCD controllers than the PAM [Fig. 5(E–H)], as is reflected by the lower proximity ratio for increasing noise levels (PCD: Χ = 0.52 to 0.38 to 0.04; and PAM: χ = 0.63, 0.34, and 0.27). These data suggest that PAM is better suited for monitoring the observer state in high noise and/or low sensitivity environments, as under these conditions it will attain the largest fraction of time spent within the tolerance of the desired level.

Fig. 5.

PAM and single channel controllers perform similarly, but the PAM controller is less susceptible to noise. (A) Measured levels of the third harmonic (H3) due to PAM (blue) and single channel (purple) controllers for the smooth control law for a representative run (note the single channel level has been shifted up by 6 dB for ease of comparison. (B) Applied pressure at each step. (C) Histogram of proximity of acoustic emission level of the third harmonic (H3) to target level for PAM and single channel controllers in terms of controller tolerance σ, and (D) applied pressures over all runs; vertical scale is 60 counts. (E) Level of H3 due to the smooth PAM controller and (G) single channel controller with the indicated SNR (− 6, 0, and 12 dB). (F) Histogram of proximity of H3 level to level for PAM and (H) single channel controller with indicated SNR; vertical scale is 12 counts.

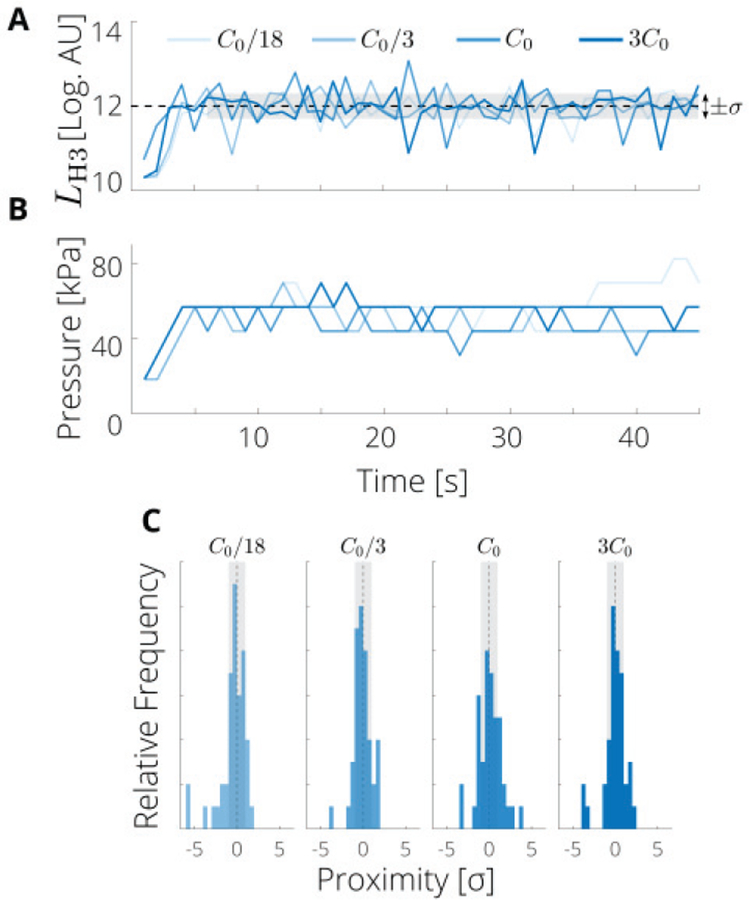
E. Effect of Bubble Concentration on Controller Performance

Next, we assessed the impact of bubble concentration on the performance of the controller. The performance was relatively consistent for concentrations around C₀ = 6000 bubbles per microliter (C₀/3, and 3C₀), however for much lower concentrations (C₀/18 or about 300 bubbles per microliter), the normalized variability, ϛ, of the proximity of H3 values increased from about 3 to 4 (Fig. 6). As expected, the applied pressure was more consistent (i.e., the applied pressures had a lower standard deviation) as the bubble concentration increased, whereas slightly higher mean pressures were required to obtain the same level for H3 for the lowest bubble concentration (Table II). Thus, for the bubble concentrations tested, the PAM controller was somewhat insensitive to change in bubble concentration, though the lowest concentrations gave less consistent performance.

Fig. 6.

PAM controller performance is not strongly affected by bubble concentrations from 2000 to 18000 bubbles per microliter. (A) Measured levels of the third harmonic (H3) for a representative run of the smooth PAM controller at the indicated concentrations. (B) Corresponding applied pressures. (C) Proximity histograms of H3 to the target level for each concentration. The default concentration was C₀= 6000 bubbles per microliter. Vertical scale is 12 counts.

TABLE II.

Range of applied pressures different bubble concentrations for the smooth PAM controller (see also Fig. 6).

Concentration	Pressure Level [kPa]
C0/18	57.0 ± 12.7
C0/3	46.3 ± 6.8
C0	46.3 ± 7.0
3C0	54.3 ± 4.5

F. Controller Spatial Selectivity

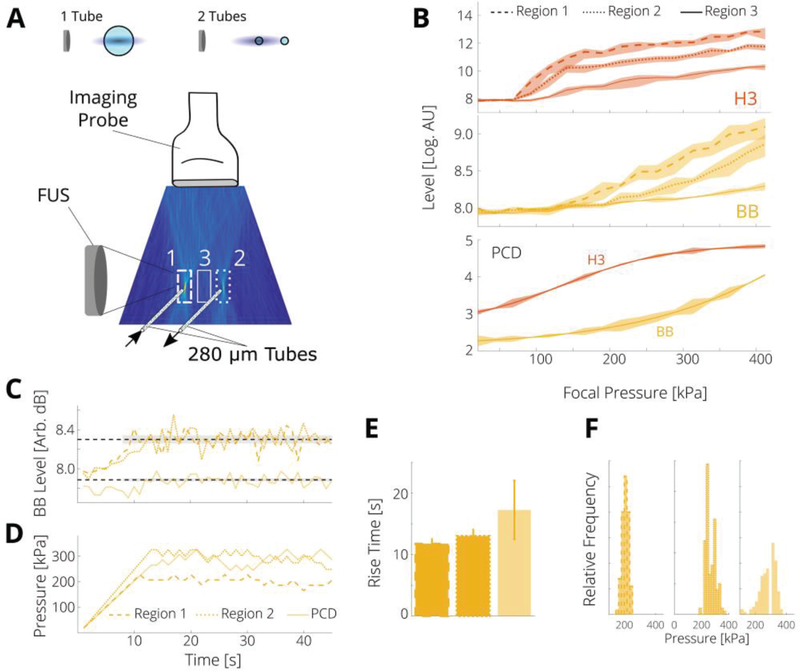
Finally, as a demonstration of the controller’s ability to control cavitation activity with spatial specificity, we modified the setup to include two smaller tubes (280 μm inner diameter) containing microbubbles [Fig. 7(A)]. We selceted three regions of the PAM (2 mm transverse by 6 mm axial) and the total intensity within each region was used to cumpute the controller levels. As shown in Fig. 7(A), Region 1 included a tube that was in the focus of the FUS, Region 2 contained the second tube that was at the edge of the FUS focus, and Region 3 contained no bubbles. From Fig. 7(B) it is seen that the onset of H3 and BB emissions now depends on the region selected, as the local pressure is higher in the focus. To minimize interference betwenn the three regions, the distacne of the two tubes was 30 times the trasverese resolution in the PAM. Higher pressures were required for this setup, as the volume of bubbles insonified in the smaller tubes was reduced by a factor of 16. In these experiments, we aimed to attain cavitation activity in both tubes concurrently, while controlling for the activity in only one. This inevitably resulted in inertial cavitation activity in the tube that was in the focus. Note that this is an experimental constraint and not a limitation of the controller, which can use any input and control both stable and inertial cavitation.

Fig. 7.

PAM controller enables spatial selectivity. (A) Bubbles were flowed through 2 parallel tubes, one was placed in the focal region of the FUS and the other at the edge. Relative sizes of tubes are shown at top (FUS not to scale). (B) The level in Region 1 (dashed lines) was generally higher than Region 2 (dotted lines) as Region 1 is in the focus, and Region 3 (solid lines), which contained no cavitation activity. PCD levels from a single channel are shown for comparison. These data have no regional selectivity. (C) Control of the level of BB emissions was achieved in Regions 1 and 2, and with single channel PCD (level shifted upward for ease of comparison). (D) Control required lower applied pressures for Region 1, as this includes the focal region. (E) Rise times were longer for this case. (F) The applied pressures were generally lower for Region 1 than for Region 2, though both regions had lower variance in pressure than the PCD controller; vertical scale is 40 counts.

The smooth controller parameters was used to maintain a target level of BB emissions for both regions containing bubbles [Fig. 7(C)]; the BB level was chosen as the target state, as its PAM level depended most distinctly on region and had a trend very similar to the PCD level [Fig. 7(B)]. Controlling cavitation in Region 1 (the FUS focus region) reqiured lower pressures (205 ± 23 kPa) than Region 2 (268 ± 34 kPa), demonstrating the importacne of spatial selectivity to attain desirable cavitation activity in either tube. For control via PCD, which is responsive to cavitation activity in either tube, the pressures were higher and more variable (268 ± 71 kPa) [Fig. 7(D, F)], presumably due to lower sensitivity. The PAM controller in both regions had improved proximity over the PCD controller (x = 0.311 for Region 1, 0.308 for Region 2, and 0.050 for PCD), which is similar to the cases of very noisy data [Sec. III(D)]. Finally the rise times were smaller for the PAM controllers (11.8 ± 0.9 s for Region 1, 13.0 ± 1.1 s for Region 2) than the PCD controller (17.25 ± 4.77 s). The rise times were longer than for the stable cavitation case, as higher pressures (and thus more steps) were required; these times could be reduced by adjusting ΔP_max.

IV. Discussion

The design of our controller was motivated by the need for a clinically relevant solution to control cavitation activity. Our solution, shown in Fig. 1 and summarized in Table III, is a nonlinear state controller of cavitation activity based on PAM to adjust the acoustic exposure level for safe and effective cavitation activity. The proposed controller uses three parameters, A, α, and β to modify the maximum step size, error sensitivity, and error range, respectively, which offers significant flexibility for parameterizing the control law. The proposed controller was able to consistently achieve desirable states (i.e. control oscillations) under a range of tests (changes in observer states, controller parameters, external noise, and varying bubble concentration Figs. 3–6), demonstrating robustness to tuning and sensing inaccuracies. By centralizing the software and hardware interface to facilitate the transmission, acquisition, processing, and control of acoustic emissions, we were able to achieve total processing times less than 1 s. Moreover, the controller was able to achieve the targeted level of the observer state (harmonic emissions) within 7 s, and maintain it to within 10 % tolerance at pressure levels (50 kPa ± 5 kPa) that are consistent with stable cavitation activity [53]. Importantly, the controller enables control of cavitation activity within a targeted region (Fig. 7).

TABLE III.

Performance of previously presented pcd based controllers (in vivo and in vitro experiments)

Controller	Rise Time [s]	Pressure [kPa]
Arvanitis et al. [25]	not real-time	140–440
O’Reilly & Hynynen [26]	~27	180–400
Tsai et al. [27]	10	440–820
Kamimura et al. [28]	16	185–266
Sun et al. [29]*	2	500
Huang et al. [30]	10	500
Hockham et al. [32]	6	5–10 ×103
Bing et al. [31]	15	400
Cornu et al. [33]	0.1	580

^*χ=0.7

As compared to direct controllers [21]–[24], we used experimental data rather than idealized models of bubble dynamics to train the controller, which allowed us to incorporate effects of complex bubble behaviors, as indicated by the robust performance of the controller for a range of bubble concentrations (Fig. 6), and via feedback to account for nonmodelled system changes. However, unlike direct controllers, our controller cannot guarantee stability using control theory and aims to control the acoustic emissions level (observers), instead of directly controlling the bubble dynamics (e.g. bubble radius).

Compared to indirect controllers, which were the basis for this work (Table III) [25]—[33], the rise time of the proposed controller for stable cavitation compares favorably with in vivo open loop methods and has similar response with closed loop methods (less than 4 s compared with averages of 14.6 s for open loop [25]–[28], [30], and 5.8 s for closed loop [29], [31]–[33]). A targeted level of inertial cavitation was achieved and maintained with spatial selectivity with a rise time of 11 s, though this time could be lessened via adjustment of the controller step size. In addition to the fast rise time and spatial selectivity, the proposed controller has the additional advantage of incorporating switch (safety) states, to ensure safe application in case of instability that may be encountered during clinical operation. While the controller was demonstrated with harmonics, ultra-harmonics, and broadband components relative to a 1.662 MHz excitation frequency, the algorithm can in principle use any combination of harmonics, ultraharmonics, and sub-harmonics as the application and hardware require.

Future research to demonstrate that the controller enables, for example, effective BBB disruption without tissue damage due to inertial cavitation is warranted. Moreover, tuning the controller parameters and control laws, as well as potential modification of the time dependence of the model fits to account for in vivo conditions, including microbubble concentration decay due to clearance from the circulation, should be further investigated.

V. Conclusion

A PAM-based feedback loop controller was developed and demonstrated to maintain target levels of stable and inertial cavitation experimentally. PAM with the angular spectrum method was found to be a fast and sensitive method for measuring microbubble emissions with improved reproducibility over single element feedback. The PAM-based controller allowed us to perform spatial and temporal control over cavitation activity, including the ability to achieve stable cavitation activity within 6 s and maintain this level within a 10 % tolerance. Importantly, we demonstrated the ability to control inertial cavitation activity with spatial selectivity in the presence of multiple cavitation sources. These data highlight the importance of spatial selectivity for attaining desirable cavitation activity, which is crucial to optimizing treatment efficacy whilst maintaining safety. Further work during therapeutic intervention in preclinical and clinical investigations is merited.