The hippocampal code for space in Mongolian gerbils

Abstract

Large parts of our knowledge about the physiology of the hippocampus in the intact brain are derived from studies in rats and mice. While many of those findings fit well to the limited data available from humans and primates, there are also marked differences, for example in hippocampal oscillation frequencies and in the persistence of theta oscillations. To test whether the distinct sensory specializations of the visual and auditory system of primates play a key role in explaining these differences, we recorded basic hippocampal physiological properties in Mongolian gerbils, a rodent species with high visual acuity and good low-frequency hearing, similar to humans. We found that gerbils show only minor differences to rats regarding hippocampal place field activity, theta properties (frequency, persistence, phase precession, theta compression), and sharp wave ripple events. The only major difference between rats and gerbils was a considerably higher degree of head direction selectivity of gerbil place fields, which may be explained by their visual system being able to better resolve distant cues. Thus, differences in sensory specializations between rodent species only affect hippocampal circuit dynamics to a minor extent, which implies that differences to other mammalian lineages, such as bats and primates, cannot be solely explained by specialization in the auditory or visual system.

Introduction

The formation of autobiographic episodic memories in humans critically depends on an intact hippocampal formation (Scoville & Milner, 1957; Squire, 1982; Squire & Zola-Morgan, 1991). Knowledge of hippocampal cellular and circuit mechanisms is therefore crucial to understand the neurobiology of human memory function and dysfunction (Buzsaki, 2005). The vast majority of physiological studies in behaving animals are performed in rodents, more specifically in mice and rats, and it has generally been a challenge to link the hallmark findings in rodent hippocampus, such as place fields (O’Keefe & Dostrovsky, 1971) and theta oscillations (Buzsaki & Draguhn, 2004), to human memory function. For example, hippocampal recordings in non-rodent mammals have revealed striking differences from rodent species. In particular, theta oscillations have been reported to occur predominantly in short bouts in bats (Ulanovsky & Moss, 2007), non-human primates (Jutras et al., 2013; Leonard et al., 2015), and humans (Watrous et al., 2013; Aghajan et al., 2016; Bohbot et al., 2017). It is therefore necessary to critically evaluate which of the physiological and anatomical features discovered in rats and mice pertain across most mammals and which ones are species-specific evolutionary adaptations. A complementary approach to recordings in non-rodent mammals, such as bats and primates, is to determine the hippocampal physiology across diverse rodent species and, in particular, include species that share sensory specializations with primates.

While rats and mice are nocturnal animals with low visual acuity and only high-frequency hearing (Grothe & Pecka, 2014), Mongolian gerbils (Meriones unguiculatus) are a rodent species that possesses a unique set of sensory specializations, including low-frequency hearing (Schmiedt, 1989) and daylight vision (Pietrewicz et al., 1982) with an acuity of about 1.5 – 2 cycles per degree (Ingle, 1981; Baker & Emerson, 1983). As such, gerbils are evolutionarily separated from rats and mice by only about 25 million years (Figure 1A, cf. Fabre et al., 2012) but utilize a sensory repertoire that shares properties of that of primates. In addition, gerbils are a traditional model animal in ischemia (Dam, 1992) and epilepsy research (Buchhalter, 1993), which has provided multiple accounts for their general hippocampal anatomy matching that of other rodents (Loskota et al., 1974; Salter, 1975). Thus anatomical factors are unlikely to explain potential large differences in physiology. We therefore considered gerbils an ideal species for examining to what extent sensory specializations, as opposed to lineage, determine hippocampal physiology, and performed recordings in the gerbil hippocampus during tasks that have commonly been used for studying hippocampal physiology in freely-behaving rats and mice.

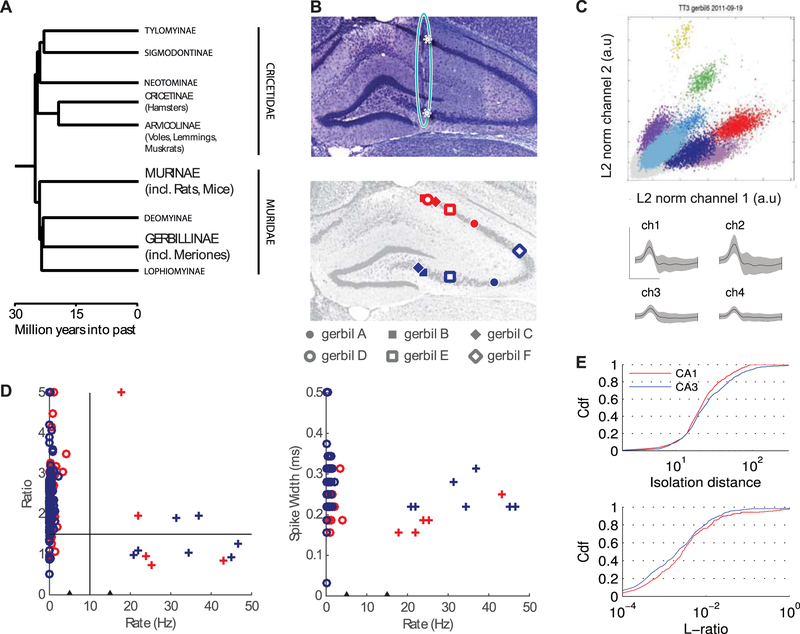
Figure 1.

Basic hippocampal anatomy and physiology of the Mongolian Gerbil. (A) Phylogeny tree. Gerbillinae, which include gerbils, diverged from Murinae, which include rats and mice, over 25 million years ago (Fabre et al., 2012). (B) Top panel: a coronal slice from gerbil hippocampus, stained with Cresyl Violet. The teal oval highlights tissue damage left by the implanted tetrodes. These tracks were used to identify the recording locations from each animal. In each animal, we recorded for several days while tetrodes were in CA1 (red) and then moved the tetrodes further ventral to record from CA3 (blue). Red stars mark the points where the tetrode passed through CA1 and terminated in CA3. Bottom panel: The approximate recording positions in CA1 and CA3 of each tetrode bundle are projected onto a single representative slice. In 6 out of 7 animals such histological verification was possible. Data from all gerbils was collected from the linear track and during sleep. Gerbils A-C, shown as filled symbols, also performed random foraging in the open field. (C) Top: Result of cluster-cutting of one tetrode in an exemple linear track session with 8 identifiable pyramidal cell (different colors). Bottom: mean (black) and standard deviation (grey) of all four tetrode channels of the light blue cluster in the front (Scale bars: up 1 mV, right 0.5ms). (D) Mean firing rate vs. peak-to trough ratio (Ewell et al. 2015) of the average wave (left) and mean firing rate vs. spike widths (right) for each cell recorded during open field sessions. Clusters with ratios above 5 were plotted at ratio = 5 and clusters with width exceeding 0.5 ms were plotted at width = 0.5 ms, because they had no well identifiable trough in the 1 ms time interval used for analysis. Black triangles on the rate axis at 5 Hz and 15 Hz mark the lack of cells with firing rates between 5 and 15 Hz. Since there was no apparent clustering along both the ratio and the spike widths dimensions, cells below 5 Hz were identified as putative pyramidal neurons (circles). Cells above 15 Hz were identified as interneurons (crosses). Red and blues colors correspond to CA1 and CA3, respectively. (E) Cumulative distributions of cluster quality measures (Top: isolation distance, Bottom: L-ratio; computed as in Mankin et al. 2012) for all units from open field recordings and those from linear track sessions in animals that were not tested in an open field.

Methods

Experimental Methods

Animals.

Experiments were conducted with 4 female and 3 male wild-type adult Mongolian gerbils with at least four months of age at the beginning of the experiments. Animals were set on a diet to maintain them at about 85–95% of their free feeding weight. After surgery, gerbils were housed individually on a 12-h light/dark cycle. Behavioral training and recordings were performed in the light phase. Experiments were approved either according to German and European guidelines on animal welfare (Reg. von Oberbayern, AZ 55.2-1-54-2532-10-11) or as approved by the Institutional Animal Care and Use Committee at the University of California, San Diego.

Behavioral paradigm and training.

Gerbils were trained to run between the two ends of a linear track of 100, 130, or 150 cm length. Animals were given food reward when they reached either end of the track. Naive animals were first implanted and then trained on the track for about ten sessions until their performance reached a threshold performance level of 40 runs in 20 min. One experimental session was typically 15 to 30 min long and a maximum of two sessions were conducted per day. In 3 of the 7 animals this training was interspersed with training in a 2-dimensional enclosure, where animals had to forage for randomly distributed food pellets. Animals were exposed to at least 5 days of training (26,5,5) before recording. The enclosure could be shaped as either a square (80 cm sides) or a 16-sided polygon (referred to as a circle, diameter = 100 cm), and a polarizing white cue card (20 cm wide) was placed on an inside wall of the black enclosure (Leutgeb et al., 2005). To more closely match task demands between linear track and open field, training on the linear track for these animals consisted of one to three 10-minute sessions.

Electrodes and microdrives.

Microdrives (Axona Ltd., St. Albans, UK) with 4 tetrodes were chronically implanted above the dorsal hippocampus. With these drives, all tetrodes could be moved together as a bundle. Tetrodes were constructed of 17-μm diameter platinum-iridium wire (California Fine Wire Co.).

Surgery.

Animals were anesthetized using either a continuous stream of isoflurane gas (2–2.5% in O₂) or a subcutaneous injection of medetomidine-midazolam-fentanyl (MMF; initial dose: 0.15 mg/kg, 7.5 mg/kg, 0.03 mg/kg; subsequent doses of 2/3 the amount of the initial dose were administered every 2h to maintain surgical anesthesia levels). To keep their body temperature at 37° C, animals were placed on a heating pad within a stereotactic unit. For tetrode placement above the dorsal hippocampus, a hole was drilled at 2.5 mm AP and 2.5 mm ML (Loskota et a., 1974). Tetrodes were inserted 0.8 mm DV into the cortex. Alginate (0.5\% sodium alginate and 10\% calcium chloride, Sigma-Aldrich) was used to shield the unprotected brain in the screw hole. To hold the microdrive in place, screws were placed in the frontal, parietal and occipital bone and bonded to the microdrive using dental acrylic (iBond Etch, Heraeus Kulzer GmbH, Germany; Simplex Rapid, Kemdent, UK). The electrical ground of the microdrive was connected to one of the screws. For animals receiving MMF, anesthesia was antagonized using atipamezole-flumazenil-naloxone (0.4 mg/kg, 0.4 mg/kg, 0.5 mg/kg, s.c.) and animals received analgesia via meloxicam (0.2 mg/kg, s.c.) or buprenorphine (0.02 mg/kg, s.c.) once during surgery and every day for three post-surgical days afterwards. Antibiotics (enrofloxacin, 10 mg/kg, s.c.) were additionally given as necessary for five to seven post-surgical days. Animals were given at least two days of recovery after surgery before recordings started.

Recording procedures.

Signals were passed through a 16-channel head-mounted preamplifier and were passed into a digital data acquisition system connected to a personal computer (Neuralynx Inc.). The x-y position of light-emitting diodes on the preamplifier was tracked at 30 Hz by processing video images. We recorded unit activity with a sampling rate of 32 kHz, which was amplified and band-pass filtered in the range of 600 Hz to 6 kHz. We used one channel of each of the 4 Tetrodes to record LFPs at a rate of 2 kHz, which were band-pass filtered at 1 to 500 Hz. To adjust the placement of tetrodes, we used the microdrive screw to initially move tetrodes 100 μm per day. As soon as spatially selective units were observable in recordings, the sites were considered as putatively located in either subfield CA1 or CA3 and recording sessions were started. Tetrodes were then moved 25–50 μm per day, after recording sessions, to target new units the next day.

Owing to our experimental protocol, CA3 recordings always occurred after CA1 recordings. Differences reported between the two subregions may therefore also have experience-dependent components. However, our recordings in the CA1 region of gerbils in open field environments were taken after at least 5 days of training, where—at least for rats—no further experience-dependent changes have been reported for either place field size and stability (Leutgeb et al., 2006) or head direction selectivity (Leutgeb et al., 2004). Thus experience-dependent contributions to the reported differences would probably be small, if gerbils were similar to rats in this respect.

To rule out the possibility that our results were unduly influenced by recording the same units over multiple days, we redid our analysis applying the more stringent criterion of analyzing units from each tetrode only once per animal. Using the session with most place cells or cell pairs, we found that most results remained unchanged, except that CA3 theta phase locking (Figure 4 C bottom; reduced data set, CA1: p = 0.0063, CA3: p = 0.11; full data set, CA1: p = 8.7 10⁻⁶, CA3: p = 0.0095) and and pooled CA3 phase precession slopes (Figure 6 D pooled; reduced data set, p = 0.11; full data set, p = 0.044) were no longer significant, but trends remained. There were also too few CA3 cell pairs to analyze spike-timing correlations in the reduced data set on the linear track. Moreover, the CA1-CA3 difference in shape preference (Figure 3C; reduced data set, CA1: median = 0.26, CA3: median = 0.17, Mann-Whitney U test, p = 0.16507; full data set medians, CA1: 0.29, CA3: 0.16, p = 0.036) and in spatial information (Figure 4C; reduced data set medians (bits), CA1: 1.15, CA3: 1.47, Mann-Whitney U test, p = 0.19; full data set medians 1.29, CA3: 1.51, p = 0.019) was lost, although their medians remained similar.

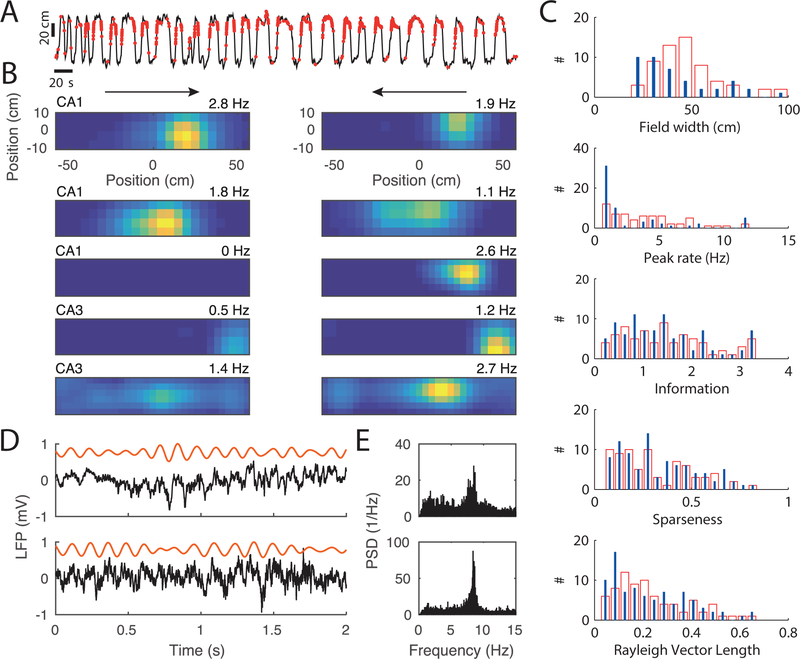
Figure 4.

Place field activity on the linear track. (A) Trajectory (black) and spike locations (red) on the linear track for one example cell. (B) Firing rate maps of five example cells from 4 different animals (the two upper examples are from the same animal), with the two running directions plotted separately in the two columns (arrows). Top most plots are derived from the data in A. The color code is normalized to the maximum peak rate of the two running directions, and the peak rate for each direction is indicated on the top right of each firing map. (C) Field properties from 72 CA1 place fields (red bars) and 66 CA3 place fields (blue lines). (D) Two example traces of the local field potential during running. Each row is a different animal. Raw signal is in black and theta band filtered signal in orange. (E) Power spectral density of one recording session from the animals in D.

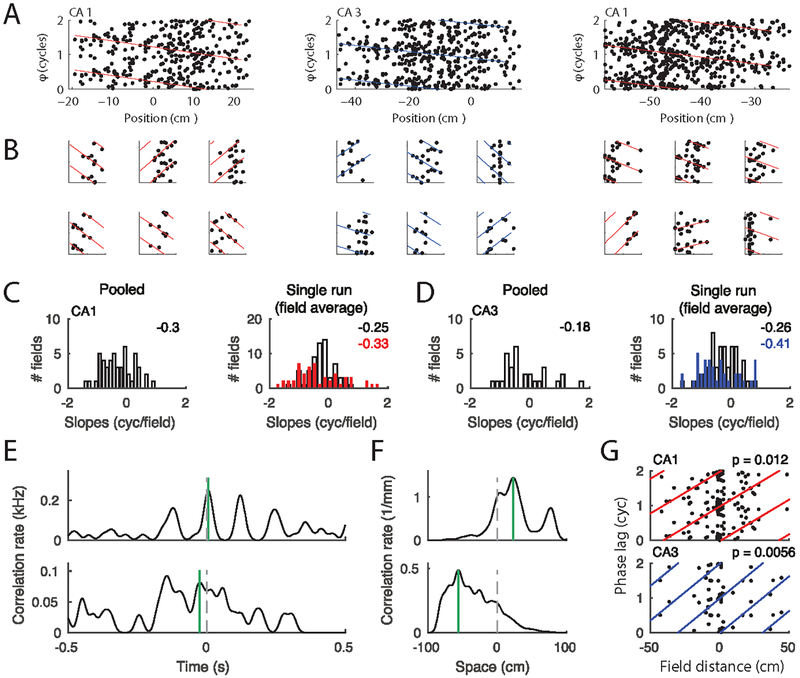
Figure 6.

Phase precession and theta compression. (A) Phase precession in three example place fields (from three animals) pooled over all runs in a session. Position is normalized to place field width. Colored lines indicate the best circular-linear fit to the data. The phase axes show two cycles, and every spike as well as the fitted lines are thus plotted twice. (B) Spike phases from six single paths per field from the three fields in A. The four left-most single trials showed significant phase precession (p < 0.05). The two right most examples show trials with non-significant precession (p>0.05). P values were obtain using circular-linear regression (Kempter et al., 2012).(C) Left: Histogram of slopes of circular-linear fits to pooled data (as in A) for the whole population of CA1 place fields. Right: Slopes of fits to single passes. Open bars include the average of all slopes per field and red bars include the average of the significant single trial slopes through each field. The numbers on the right upper corners indicate the means of the distributions. (D) as C, but for CA3 data (blue). (E) Spike cross-correlation functions provide an estimate of temporal separation within a theta cycle. Two example place cell pairs are shown. Stippled vertical lines depict zero and green vertical lines depict the peak closest to zero. (F) Cross-correlations (in units of spike pairs per spatial bin) between firing rates along the track provide an estimate of place field distance (Colors as in E). (G) Theta phase lag (time lag as shown in E translated to the Hilbert phase of the theta band LFP) as a function of place field distance for CA1 (top) and CA3 (bottom) fields. Colored lines indicate circular linear fits, and P-values indicate significance of circular linear correlation. The circular linear correlations (Kempter et al., 2012) are R = 0.37 for CA1 (n = 81) and R = 0.58 for CA3 (n = 42).

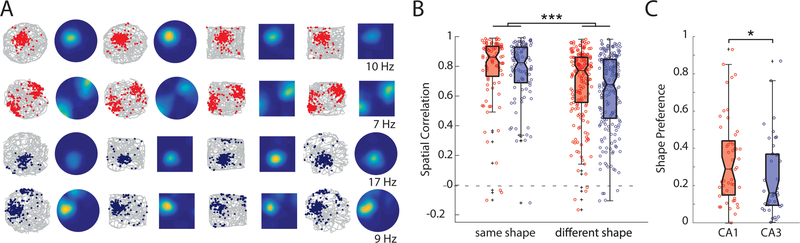
Figure 3.

Comparison of firing patterns in distinct enclosure shapes. (A) Each row represents the activity of a single cell recorded across four 10-minute sessions in the open field. The top two rows show cells from CA1, and the bottom two rows show two cells recorded simultaneously from CA3. Each session is presented as both the animal’s trajectory (gray line) with locations of each individual spikes (colored dots) and a heat map of mean firing rates (scaled in dark blue to bright yellow from 0 Hz to the peak firing rate across all 4 sessions, noted at the end of each row). (B) For each cell, we computed the spatial correlation between each pair of 10-minute sessions, and then grouped the correlations by whether the comparison was between sessions of the same shape (square-square or circle-circle) or different shapes (square-circle). Data is summarized as box plots, with individual comparisons shown as small circles. CA1 is red, and CA3 is blue. We found that spatial correlations were lower for different-shape than same-shape comparisons, but there were no differences between subregions. (C) For each place field identified on a reference map, we computed the degree to which firing in that field was selective for one box shape over the other (absolute shape preference score). Identical firing rates between box shape would result in a shape preference score of 0, while firing that was exclusive to only one shape would result in a score of 1. CA1 showed moderately larger shape preference than CA3, with a larger fraction of cells showing significant shape preference.

Histology and tetrode position reconstruction.

To verify tetrode position, animals received an overdose of sodium pentobarbital. After perfusion (intracardially using 4% formaldehyde or paraformaldehyde), brains were sliced coronally (40 or 80 μm thickness) and stained with Nissl, Neutralred, or Cresyl Violet (Figure 1B). If the deepest tetrode position was in the CA1 or CA3 pyramidal cell layer, recordings were included in our analysis. Recordings at higher positions were assigned to either CA1 or CA3 by matching the record of recording depth to the reconstruction of the electrode tracks in the histological material.

Owing to the relatively coarse anatomical approach, our data set does not allow statements about the sampling of the specific regions along the transverse axis of the cornu ammonis. Reported differences between areas CA1 and CA3 may thus be, to a certain extent, confounded by regional differences. At least CA1 recordings, however, were relatively constrained to the proximal regions.

A summary of all recorded cells and behavioral sessions in provided in Table 1.

Table 1.

Summary of recorded units

Gerbil	Session	CA1 Principal					CA1 Interneurons					CA3 Principal					CA3 Interneurons
		TT1	TT2	TT3	TT4	Total	TT1	TT2	TT3	TT4	Total	TT1	TT2	TT3	TT4	Total	TT1	TT2	TT3	TT4	Total
5	1 Box & Track	3	2	1	2	8	2	0	1	0	3					0					0
5	2 Box	1	3	3	4	11	0	1	0	0	1					0					0
5	3 Track & Sleep	2	4	3	7	16	0	1	0	0	1					0					0
5	4 Box & Track					0					0	8	8	8	0	24	0	1	2	0	3
5	5 Box & Track					0					0	4	8	4	9	25	0	0	2	0	2
6	1 Box, Track & Sleep	0	2	11	1	14	0	0	1	0	1					0					0
6	2 Box & Track	0	1	3	3	7	0	0	0	0	0					0					0
6	3 Box, Track & Sleep					0					0	8	6	7	13	34					0
6	4 Box, Track & Sleep					0					0	4	4	6	8	22	1	0	1	0	2
6	5 Track					0					0	5	1	16	11	33					0
16	1 Box	1	0	7	0	8					0					0					0
16	2 Track	0	0	5	0	5					0					0					0
16	3 Box	1	0	4	0	5					0					0					0
16	4 Track	5	0	0	0	5					0	0	0	8	5	13					0
16	5 Box	7	0	0	0	7					0	0	0	5	5	10					0
16	6 Track	7	0	0	0	7					0	0	0	4	5	9					0
16	7 Box	10	0	0	0	10					0	0	0	6	5	11					0
7602	1 Track	2	0	0	0	2					0					0					0
8981	1 Track	1	0	0	0	1					0					0					0
8981	2 Track	0	1	0	0	1					0					0					0
8978	1 Track	0	0	2	0	2					0					0					0
8978	2 Track	0	0	1	0	1					0					0					0
8978	3 Track					0					0	1	0	0	0	1					0
8978	4 Track					0					0	1	0	0	0	1					0
8978	5 Track					0					0	1	0	0	0	1					0
8978	6 Track					0					0	0	2	0	0	2					0
8978	7 Track					0					0	0	1	0	0	1					0
10353	1 Track	1	0	0	0	1					0					0					0
10353	2 Track	1	0	0	0	1					0					0					0
10353	3 Track	1	0	0	0	1					0					0					0
10353	4 Track	0	0	0	1	1					0					0					0
10353	5 Track	0	1	0	0	1					0					0					0
10353	6 Track	0	0	0	1	1					0					0					0
10353	7 Track	1	0	1	0	2					0					0					0
Total across all						118					6					187					7

Size of the data set. Data was collected from 7 gerbils in three different behaviors: on the linear track (Track), during free foraging in the open fields with two box shapes (Box), and during quiet wakefulness or sleep (Rest).

Data analysis.

Single unit isolation.

Spike sorting was performed manually offline using a customized version of MClust (Redish, A.D. MClust. http://redishlab.neuroscience.umn.edu/MClust/MClust.html, Mankin et al., 2012; Figure 1C). The quality of the clusters were checked using Isolation distance and L-ratio measures (Figure 1E; Schmitzer-Torbert et al., 2005, Mankin et al., 2012). Sleep periods before and after behavioral sessions were examined to ensure stability of recorded cells and to identify cells that were active during rest but silent during behavior.

Firing rate maps.

For each well-isolated neuron, a spatial firing rate distribution was constructed in the standard manner by summing the total number of spikes that occurred in a given location bin (5 cm by 5 cm), dividing by the amount of time that the animal spent in that location, and smoothing with a Gaussian centered on each bin (Koenig et al., 2011). Spatial correlation was calculated as the Pearson correlation coefficient between firing rates in each 5-cm² bin that was common to the square and circular enclosures. Place maps on linear tracks were calculated using the same 2D procedure as in the open field. Linear-track field widths were determined from the 1D projections of the 2D rate maps with fields defined as the spatial intervals in which the firing rate was above 10% peak rate.

Spatial information, Sparseness.

Spatial Information (SI) was computed from spatially binned firing rates r_i according to (Skaggs et al., 1993) as SI = Σ_i p_i r_i/R log2(r_i/R), with i indicating the spatial bin and R = (Σ_i r_i p_i)/(Σ_i p_i) denoting the expected value of the firing rate (p_i: occupancy of spatial bin i). Sparseness was computed as R² divided by the expected value of r_i² (Treves & Rolls, 1992).

Field boundaries and passes through fields.

Place field boundaries for each cell were calculated as described previously (Mankin et al., 2012). Briefly, the firing rate maps were interpolated to 1-cm by 1-cm bins, and then firing rate contour maps were created. The contour at 20% of the peak rate of the field was selected as the outer field boundary. Contours shared by multiple place fields were divided based on the shape of the contours and their proximity to field centers. These smoothed maps are displayed in Figures 2 and 3. In order to define uniform field boundaries across square and circle, we computed the place field map across the 100×100 cm square that contained the entire circle and entire square. Because we applied smoothing to the rate maps, the field boundaries sometimes extend beyond the border of the apparatus. The area outside the apparatus, however, did not enter into further analysis.

Figure 2.

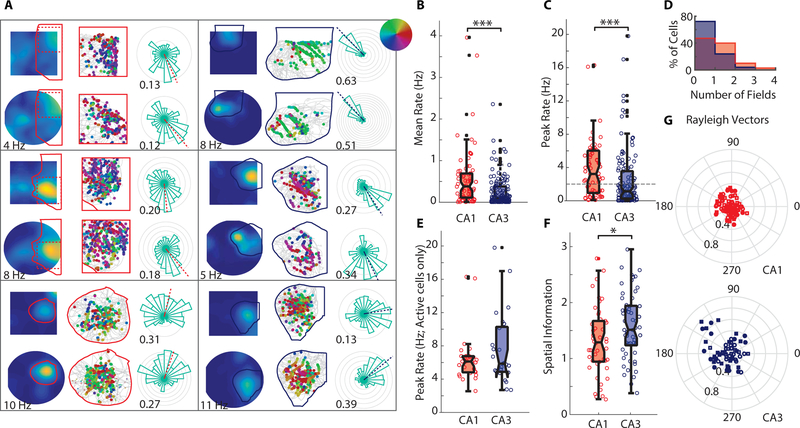
Firing properties of putative pyramidal cells during random foraging in an open field. (A) Six example cells recorded from either CA1 (left hand panels) or CA3 (right hand panels). In each panel, the top row summarizes data from a single session in a square-shaped enclosure, while the bottom row shows the same from a single session in a circular enclosure. Leftmost column: Firing rate maps with colors representing the mean firing rate at that location, scaled from dark blue (no firing) to bright yellow (max rate across 4 sessions; noted below the firing rate maps for each cell). Individual place fields were identified on a reference map (average across 4 sessions in the open field) with a contour-based approach, and one field is outlined on each map (solid lines). Center column: Outlined fields are shown enlarged (for the two cells with fields that stretched the height of the enclosure, only the area [marked dashed] with densest spiking is shown). The animal’s trajectory is shown in gray, with spikes shown as dots in the location of the animal at the time of the spike. Spikes are color-coded by the animal’s heading-direction, as indicated by the inset in the upper right of panel A. Rightmost column: Occupancy-normalized firing rate in each of 24 directional bins. Each gray circle represents 1 Hz. Dashed line indicates the direction of the Rayleigh Vector (RV) derived from the MLM procedure (Cacucci et al., 2004; see Methods) and the numbers by each plot note the length of the RV (RVL; 0 indicates a uniform firing rate at all head directions, 1 indicates perfect directional tuning). (B) Average firing rates of CA1 and CA3 cells. For each cell, the mean firing rate across each 10-minute session was computed, and sessions were averaged to yield a single data point per cell. The box plot extends from the 25^th-75^th percentile. Medians are marked as black lines. (C) Peak firing rates from each hippocampal subregion. Data are presented as in B. Dashed horizontal line at 2 Hz indicates the cutoff to define place fields. (D) Normalized histograms of the mean number of fields exhibited by cells in each region (CA1, red; CA3, blue). Field boundaries were computed separately in each 10-minute session, and total number of fields was averaged to yield one data point per cell. The maximum number of fields identified in any single session was 5 in CA1 and 4 in CA3. (E) Peak firing rates of cells with fields. Medians are not significantly different between CA1 and CA3. (F) Spatial information of cells with fields. (G) Rayleigh Vectors, which were computed on individual fields (directional tuning appeared to be modulated independently in cells with multiple fields). Filled dots represent RVLs greater than 95% of shuffled data.

Directionality analysis.

The trajectory of the animal was first smoothed using a Kalman filter. Instantaneous heading direction at any moment was calculated as the direction of movement on the smoothed trajectory. For each place field, we identified the heading direction at the time of each in-field spike, as well as at each time point during each pass through the field. Head direction sensitivity was then derived using the maximum likelihood model (MLM) described in Cacucci et al. (2004), which estimates spike probability as a product of a spatial and a directional distribution and thereby reduces biases induced by running statistics. The directional distribution was discretized in 36 angular bins. To compute the directional Rayleigh Vector for each field, we took the vector sum of the vectors defined by the midpoint of each circular histogram bin and normalized by the sum of the length of those vectors. To define significant directional selectivity, we compared the length of the Rayleigh Vector to the length found by shuffling the assignment of spike timing to trajectories through the field 200 times. A place field was said to be significantly modulated if the Rayleigh Vector length for the actual data was greater than for 95% of shuffles. To avoid confounds from rate remapping between shapes, directionality was computed separately for square and circle, and fields were only included if there were 200 spikes or more in that shape. Spikes from sessions in the same shape were combined to compute the RV. Confidence intervals for the proportion of directionally selective place fields were computed using the Clopper-Pearson interval method for binomial confidence intervals.

Comparison to rat data.

To compare the degree of directionality modulation observed in gerbils to rats, we used the dataset from Mankin et al., 2015. In this dataset, rats completed several blocks of 4 10-minute sessions, and a single block of 4 sessions was comparable to the 4 sessions that gerbils completed each day. To analyze matching data segments between rats and gerbils, we therefore included only the first block of 4 sessions from the rat data in the directionality analysis.

The difference between our findings in rats (6.8% directional place fields in CA1) and those of Acharya et al. 2016 (27% directional place cells in CA1) could be related to methodological differences in the experimental design. Our environments were about 1 m diameter, while theirs were 2m; we provided a proximal visual cue card on box walls, while their animals ran on a table without walls but with rich distal visual cues. We also used a different analysis method for head directional selectivity.

Shape preference.

To measure whether neuronal firing within a place field occurred preferentially in one enclosure shape, we calculated a shape preference score as described previously (Mankin et al., 2015). For each field and each experimental session, the path segments inside of field boundaries were identified. Time periods when the path segments were continuously inside the field boundary for at least 200 ms were considered a pass through the field if the path crossed inside of the contour at 50% of the field’s peak value. The average firing rate for a pass was calculated as the number of spikes during the pass divided by the duration of the pass. For each field, the rates from the individual passes were combined to yield a distribution of firing rates for the square enclosure and a distribution of firing rates for the circular enclosure. The degree to which these distributions overlapped was calculated as the area under the receiver operating characteristic curve for the distribution in the square compared with the distribution in the circle. If all firing rates in the square enclosure were higher than in the circle enclosure, the area under the curve was 1. If all firing rates in the square enclosure were smaller than in the circle enclosure, the area was 0. If the distributions were identical, the area was 0.5. We then did a linear transformation on this measure (subtracting 0.5 and multiplying by 2), so that the shape preference score would vary between −1 and 1, with 0 indicating no shape preference. The signed value of this score provides a nonparametric estimate of preferred firing in the square enclosure shape compared with the circle enclosure shape. The absolute value of the score gives an indication of the extent of firing preference for either shape.

To test whether a field exhibited higher absolute shape preference than expected by chance, for each field we created a null distribution of absolute shape preference scores by randomly assigning shape labels to each pass through the field and recomputing a shuffled score, 1000 times. We considered a field to exhibit significant shape preference if its true shape preference score exceeded the 95% quantile of the shuffled values.

(P-)episodes of locomotion-dependent theta.

Oscillatory local field potentials are generally noisy and the periods in time at which a specific rhythm is present are sometimes hard to detect. Recently a method has been developed to identify periods during which a specific frequency is significantly present in the LFP. Such p-episodes were detected using the BOSC (Better Oscillation Detection) Method described in Hughes et al., 2012. In brief, the LFP spectrum in a linear frequency range between 0.1 Hz and 40 Hz is obtained by a wavelet transform (Morlet with width 6). In each time bin, the power in a frequency band is then considered significant if it exceeds the 95% quantile of a χ²(2) distribution based on the mean power in this frequency band.

Phase precession analysis.

We analyzed phase precession using circular linear regression as outlined in Kempter et al., 2012. In brief, the theta band component (6–10 Hz) of the local field potential was Hilbert transformed, and each spike (n) was assigned a phase φ _n with respect to the theta oscillation. Circular-linear slopes a of phase position pairs (φ _n, x_n) were obtained by maximizing

$$\text{R}\left(\text{a}\right)=\left|{\sum }_{\text{n}}\text{exp}\left[\text{i}\left(\phi {\text{n}}^{-\text{a\hspace{1em}}}{\mathrm{x}}_n\right)\right]\right|$$

on field-normalized spatial coordinates 0<x<1. The phase offset (start phase) φ was calculated by maximizing U(φ) = |Σ_n cos[(φ_n-a x_n-φ)]|. P values were obtained using circular linear statistics as described in Kempter et al., 2012.

Theta compression analysis.

Place field pairs that co-fired within one theta cycle 25 times or more were used to correlate theta phase difference with place field difference. Since theta phase difference is a circular variable, we also used circular-linear regression (see Phase precession analysis). To obtain theta phase difference we computed the cross-correlation function of the smoothed spike trains (normalized Gaussian kernel, σ = 10 ms) and derived the phase difference from the correlation peak closest to zero lag. Place field differences were obtained from the peak positions of the two place maps. Note that because the Gaussian smoothing kernels are normalized, the correlation integrals have units of 1/time and 1/space, respectively, and are thus termed correlation rate.

Sharp wave analysis.

Sharp wave analysis was performed in the two animals with the longest rest sessions (26 sessions from 6 days). Sharp waves were detected while animals were in the rest box before and after linear track running or random foraging. We visually inspected all recording channels, in both time and frequency domains. In each session, the least noisy and most stable channels with an apparent increase in ripple band (150–200 Hz) power was selected for further analysis. To separate theta from non-theta episodes, we only considered periods in which the animal was not moving according to the video tracking. We then applied a second order autoregressive (AR,2) model to whiten the hippocampal LFP (using python package statsmodels; http://statsmodels.sourceforge.net/). The relative spectral power of delta (0–5), theta (6–10) and gamma (12–20 Hz) bands were subsequently compared by visual inspection to identify periods with dominant theta oscillation from non-theta periods. Periods lasting less than 10s were discarded from further analysis (Montgomery et al., 2008). Applying this procedure, we analysed 4407 high-frequency events during 107.8 minutes of non-theta LFP in total. Sharp-wave ripple candidate events were detected from the LFP during non-theta periods using a threshold on the absolute value of the Hilbert transform in the 100–200 Hz range. Peaks exceeding 3 standard deviations above the mean (SD) were recorded as candidate events. Event extent was defined as continuous times where Hilbert transform was above 1 SD levels.

All candidate SWR events were Fourier transformed to build corresponding spectral power vectors (10–300 Hz), with frequency resolution of 10 Hz. Principal component analysis (PCA) was applied to the power vectors and clustering was performed on the first five PC components by fitting Gaussian mixture models via the masked EM algorithm implemented in the KlustaKwik (v. 2.0.1–1) software (Kadir et al., 2014). As a control, the same procedure was repeated on the principal components after whitening. Since the identity of the group label (SWR/FGB) should be independent of noise we discarded any event that showed inconsistent cluster labels. The number of such discarded events were below 5% of the total number of candidates in each session.

The duration of each event was calculated as the time difference between moments in which the modulus of the Hilbert transform of the band passed signal crossed the 1 SD line. Inter-event intervals were calculated as the time difference between peaks in each group.

To finally control how well our algorithm identified individual HFEs, we visually inspected the spectrogram of the HFEs over time in an interval of 600 ms around the ripple band peak using a wavelet transformation (Torrence & Compo, 1998). Our results showed that detected events were indeed confined in both time and frequency domain.

Results

We performed extracellular tetrode recordings from the hippocampal CA1 and CA3 subregions (Figure 1B) in 7 gerbils (3 male/4 female) on a linear track. CA1 recordings were confined to proximal region along the transversal axis, CA3 recordings were dispersed along the whole extent of the transversal axis. In addition, we recorded from 3 of the gerbils during random foraging in an open field. All experimental sessions included recordings of at least 10 minutes of sleep or quiet rest in the beginning and in the end, which allowed us to identify cells that were active during sleep but silent during the behavioral tasks (Figure 1 C). Mean firing rates of recorded cells in the open field were either below 5 Hz or above 15 Hz, and we used the gap between 5 and 15 Hz (Figure 1D) as a criterion to separate putative pyramidal cells (mean rates < 5 Hz) from putative interneurons (mean rates > 15 Hz).

Most hippocampal pyramidal cells in rats and mice, but also in bats, are known to have well-defined spatial firing fields (O’Keefe & Dostrovsky, 1971; Ulanovsky & Moss, 2007). Moreover, since gerbils were reported to show place fields in virtual reality (Haas et al., 2018), we also had a strong expectation to find similar place fields in gerbils during random foraging in an open field. As expected, we observed standard place fields in both the hippocampal CA1 and CA3 subregions (Figure 2A, examples). Overall, CA1 pyramidal cells exhibited higher average and peak rates than CA3 pyramidal cells (average rates: median CA1: 0.38 Hz, median CA3 0.11 Hz, Mann-Whitney U-test, p=1.0 10⁻⁵; peak rates: median CA1 3.22 Hz, median CA3 1.14 Hz, Mann-Whitney U-test, p = 1.0 10^−4, Figure 2B–C). However, when only cells with peak rates of more than 2 Hz were considered, CA1 and CA3 no longer showed significant differences in peak firing rate (median CA1: 5.31 Hz; median CA3: 4.8 Hz, Mann-Whitney U-test, p = 0.18, Figure 2E). This indicates that it is more common for CA3 cells to be silent during behavior or show low rate firing, which results in fewer cells functioning as place cells (32.1% in CA3 compared to 56.1% in CA1). However, within the place cell populations, many properties did not substantially differ. The number of place fields per cell was not significantly different (Figure 2D; median CA1: 1.33; median CA3: 1.00; Mann-Whitney U-test, p = 0.29) and spatial information was only moderately higher in CA3 compared to CA1 (CA1:1.29, CA3: 1.51, Mann-Whitney U-test, p = 0.019, Figure 2F).

A further hallmark of the hippocampal code for space is its invariance with respect to heading direction in open fields. Full directional invariance has recently been challenged by observations that some place fields are directionally modulated in rats (Acharya et al, 2016). We tested the degree to which place fields in gerbil CA1 and CA3 showed directional tuning during running in an open field using the maximum likelihood model (MLM) method proposed in Cacucci et al., 2004. We found directional selectivity in 20.0% of CA1 place fields (17/85, 95 % confidence interval: [12.1, 30.1]) and 46.0 % of CA3 fields (29/63, 95 % confidence interval: [33.4, 59.1]) (Figure 2A, G), each of which is more than would be expected by chance (p-values of binomial tests: CA1, p=9.3 10⁻⁷; CA3, p < 10⁻⁸). Furthermore, a significantly larger proportion of place fields were directionally modulated in CA3 compared to CA1 (Chi-square test, χ²= 11.45, p = 0.00072), and the directional modulation in CA3 was more robust, as reflected in the higher Rayleigh Vector Length values of significantly modulated fields (Figure 2G; CA1: median RVL = 0.27; CA3, median RVL = 0.32; Mann-Whitney U-test, p = 0.0036).

For a direct comparison of directional selectivity between gerbils and rats, we reanalyzed the dataset from Mankin et al. (2015). Using identical analysis methods as in gerbils revealed that 6.8% of rat CA1 fields (12/176, CI = [3.6, 11.6]) and 14.0% of rat CA3 fields (8/57. CI = [6.3, 25.8]) were significantly directionally selective and that only directional selectivity in CA3 exceeded the proportion expected by chance (p-values binomial tests: CA1, p=0. 173; CA3, p=0.0072). This finding is also consistent with higher directionality in CA3 reported for rats in Leutgeb et al., (2004). The proportion of place fields with significant directional modulation in gerbil exceeded that of rat both for CA3 (Chi-square test, χ ²= 14.37, p = 1.51 10⁻⁴), and also for CA1 (Chi-square test, χ ²= 10.08, p = 0.0015).

To then test the effects of non-spatial visual cues on place field firing, we recorded hippocampal activity in two differently shaped enclosures (circular and rectangular). Each day, gerbils completed four 10-minute sessions of running in the enclosures, two in the circle and two in the square (Figure 3A). The order of shapes was selected randomly. In rats, changing the box shape has been shown to induce remapping of place fields in CA1 and CA3 (Lever et al., 2002; Leutgeb et al., 2005; Mankin et al., 2012). In our gerbil data we observed mostly rate remapping, as indicated by a moderately reduced spatial correlation of firing fields when comparing between different box shapes as opposed to comparing between the same box shape in the same laboratory environment (Figure 3B). To assess the magnitude of the responses to box shape, we calculated a shape preference score (as described previously; Mankin et al., 2012) to measure how much individual place fields changed their firing rate between shapes. Significant fractions of fields had shape preference scores exceeding the 95% quantile of the score distribution obtained from shuffling shape labels (binomial tests: CA1: 24/49, p = 5.8 10⁻²⁰; CA3: 14/38, p = 1.6 10⁻¹⁰). Also shape preference scores were larger in CA1 than in CA3 (median CA1: 0.29; median CA3: 0.16; Mann-Whitney U-test, p = 0.036) but with a high degree of variability within each hippocampal subregion (Figure 3C). Shape preference values in rats were generally larger than in gerbils, and there was no difference between subregions for shape preference in rats (Mankin et al. 2012). We thus conclude that there are quantitative differences in the extent of the shape preference, but that gerbils, similar to other rodents, respond with mostly rate remapping to changes within environments.

In rats and mice, hippocampal activity has been found to represent sequences on different time scales. For example, the sequence of place fields along the path of the animal corresponds to the sequence of active cells within a theta cycle. A prerequisite for sequences on the theta scale is the temporal organization of spike timing while traversing the place field, including both phase precession (O’Keefe & Recce, 1993; Skaggs et al., 1996; Mehta et al., 2002; Feng et al., 2015) and theta compression (Dragoi & Buzsaki, 2006; Geisler et al., 2010). To test whether phase precession occurs in gerbils, we recorded hippocampal activity while gerbils were running back and forth on linear tracks and were thus frequently traversing place fields along the same trajectory. When analyzing these trajectories, we found robust place field activity (Figure 4A, B) without a difference in peak rates between CA1 and CA3 (medians: 1.4 Hz vs. 1.3 Hz; ranksum test, p = 0.41; Figure 4C). However, peak firing rates were lower than in the open field and we therefore employed a threshold for peak rate at 0.5 Hz to identify place fields. Using this criterion, we found that place fields were on average larger in CA1 than in CA3 (medians: 36 cm vs. 27 cm; ranksum test, p = 0.027; Figure 4C), but we could otherwise not find differences between CA1 and CA3 in sparseness and spatial information (ranksum test, sparseness: p = 0.12, spatial information, p = 0.23 Figure 4C)

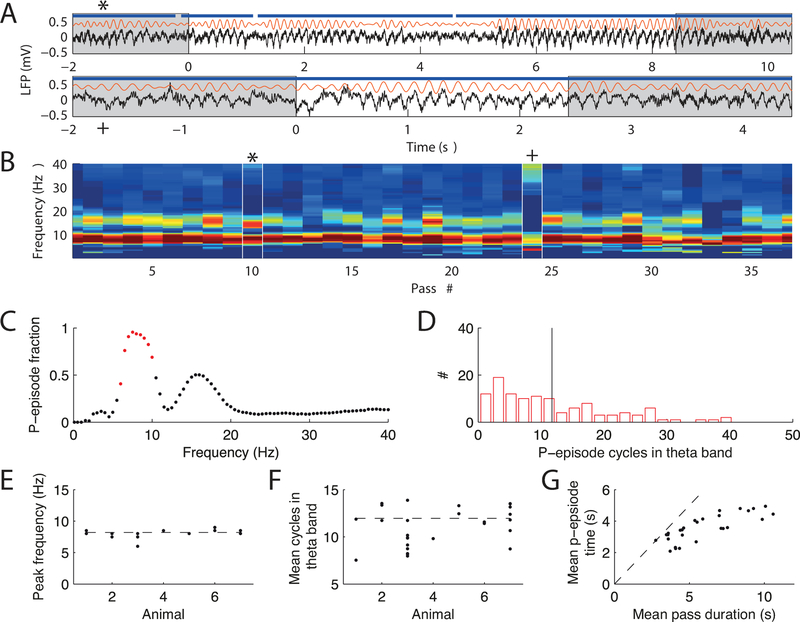
We next tested whether we could identify theta oscillations in gerbils that were similar to theta oscillations in rats and mice. Similar to other rodent species, the local field potential in gerbils exhibited persistent hippocampal theta rhythmicity in a frequency range of 7 to 9 Hz during locomotion (Figure 4D, E; see also Whishaw, 1972), and pyramidal cell activity was significantly phase locked to these oscillations (Rayleigh test, CA1: p = 8.75 10⁻⁶, CA3: p = 0.0095; Figure 4 C). To quantify the persistence of theta oscillations, we adopted an approach by Hughes et al. (2012) and computed the fraction of time spent in a state with significant theta power called p-episodes (see Methods and Figure 5A–D). In all animals and experimental sessions the peak frequency of significant theta episodes (Figure 5C) was at approximately 8 Hz (Figure 5E). The mean number of consecutive significant theta cycles was approximately 12 but showed variability between sessions (Figure 5F). We reasoned that some of the variability may arise from the average duration of running between reward locations, and found that the mean duration of p-episodes linearly increased with the average time of a pass on a linear track (Figure 5G; Pearson’s r = 0.80, p = 3.1 10⁻⁷). However, the time in p-episodes only corresponded to the entire length of the pass for short pass durations, which is expected because periods during which the animals moved slowly—leading to longer passes—would interrupt the continuity of movement-related theta oscillations (Figure 5G). We thus conclude that gerbils exhibited persistent locomotion-dependent theta oscillations.

Figure 5.

Episodes of locomotion-dependent theta. (A) Two examples of raw LFP (black) and theta band filtered LFP (orange). The white background indicates one pass (starting at t = 0) from reward location to reward location. Blue line indicates significant episodes (p-episodes) of sustained theta. (B) Fraction of time spent in significant p-episodes (color code is from 0 % in blue to 100 % in red) for each frequency band. An example recording session with 37 passes is shown, and the white marks indicate the passes shown in A. (C) Fraction of p-episodes averaged over all passes in B. Red dots indicate the theta band. The second peak corresponds to the theta harmonic at 16 Hz. (D) Histogram of p-episode lengths from the theta band in B. Black line indicates the mean. (E) Frequency at highest p-episode fraction (determined from analysis shown in C) for all sessions and animals (each dot is a recording session). Dashed line indicates the mean. (F) Mean p-episode length for each session and animal. Dashed line indicates the mean. (G) Mean time within a p-episode vs. mean duration of a pass. Each dot marks a recording session on the linear track. The bisecting line (dashed) is shown for comparison. For short passes with continuous running, the p-episode lengths are comparable to the run time. There is a decrease in p-episode length for longer passes because theta periods become interrupted at slow movement speeds that typically involve pauses.

After we had verified that place fields and continuous theta occurred on the track, we were able to perform standard phase precession analysis. Phase precession is a phenomenon in which spikes at the beginning of a place field occur at late theta phases and precess to earlier phases as the animal moves through the place field (O’Keefe & Recce, 1993). This relation results in a negative slope in circular-linear fits of phase vs. position (Schmidt et al., 2009; Kempter et al., 2012). As in rats and mice, we found that place cells in gerbils showed theta phase precession, which could be detected in the pooled data as well as in individual runs (Figure 6A, B). Phase precession slopes were significantly negative (Wilcoxon’s signed rank test; CA1 mean slope, p = 1.6 10⁻⁴, field-averaged slopes, p = 2.2 10⁻⁵, field averaged significant slopes p = 0.0019; CA3 mean slope, p = 0.044, field-averaged slopes, p = 1.8 10⁻⁴, field averaged significant slopes p = 9.6 10⁻⁴) and did not differ significantly between areas CA1 and CA3 (ranksum test; mean slope: p = 0.71, field-average single run slopes: p = 0.82, field-averaged significant single run slopes: p = 0.57, Figure 6C, D). The magnitude of slopes was generally similar to that reported in rats (Schmidt et al., 2009; Schlesiger et al., 2015).

To more directly assess spike timing relations of place field pairs, we also performed analysis that compares the distance of fields on the maze to the time difference of spikes within a theta cycle (i.e., theta compression; Dragoi & Buzsaki (2006)). The presence of theta sequences (Foster & Wilson, 2007) would predict that place field pairs that are more separated in space will also be more separated in time within the theta cycle. We were able to correlate 87 pairs of CA1 place cells from 4 animals and 43 pairs of CA3 place cells from 3 animals. In both hippocampal subregions, theta phases showed a significant circular-linear correlation with place field distance (Figure 6E–G), showing theta compression in gerbils and therefore arguing for theta sequences as a general phenomenon in the rodent hippocampus.

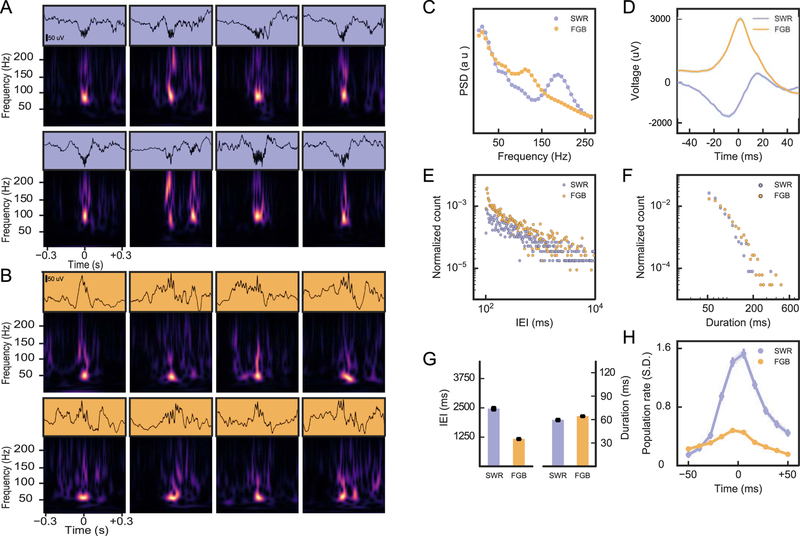
Finally, we considered LFP signatures beyond the theta state (Figure 7). Here, analyses in rats and mice have particularly focused on sharp-wave ripple complexes that occur during slow wave sleep and quiet wakefulness. They are thought to originate from intrahippocampal synaptic connectivity (Ylinen et al.,1995; Csicsvari et al.,2000) and to underlie certain forms of memory consolidation (Buzsaki, 1989). For our analysis, we used the electrodes with largest power in the ripple band, indicating that the tetrode was positioned close to CA1 stratum pyramidale. We focused on resting periods before and after the animal was in a behavioral session during which we had no theta band power (see Methods). We then selected for events with high power at frequencies between 100 and 200 Hz and observed two distinct types of LFP signatures (Sullivan et al., 2011). One signature corresponded to the classical sharp-wave ripple complex (SWR) with substantial power at high (200 Hz) frequencies (Figure 7A,C). The second signature contained frequency components below 150 Hz (Figure 7 B,C) and is thus referred to as fast gamma burst (FGB). The low frequency components of the SWRs showed the expected bimodal shape where a negativity is followed by a positivity (Figure 7D, Buzsaki et al., 1992), whereas FGBs exhibited rather unimodal, mostly positive low frequency components (Figure 7D). On average, FGBs occurred in a more burst-like fashion than SWRs, i.e., at lower inter-event intervals (IEIs) than SWRs (Figure 7E, G) (ranksum test; p = 3.4 10⁻²⁹). Both SWRs and FGBs are typically shorter than 200 ms and their median durations were not significantly different (ranksum test, p = 0.67, Figure 7 F, G). Only less than 1% of the high frequency events detected by our algorithm exhibits longer duration (Figure 7F), indicating a good performance of the detection algorithm. Finally, we analyzed the increase in population activity during the two types of LFP events (Figure 7H). During FGBs we observed only a moderate increase in population activity of less than one half of a standard deviation of the baseline activity, while during SWRs, unit activity was about four times larger (~1.6 standard deviations), indicating that during SWRs, CA1 generates a much more prominent population output than during FGBs. We thus conclude that gerbils exhibit CA1 SWRs of similar frequency content as rats, and in addition, show clear signs of a second type of CA1 populations bursts in the fast gamma range, similar to a phenomenon that has been observed in rats (Sullivan et al., 2011) and macaque monkeys (Ramirez-Villegas et al., 2015).

Figure 7.

High frequency events in the LFP. (A) LFP traces (top) and spectrograms of 8 exemplary SWRs during non-theta rest periods. Spectral power in the high-frequency band (150–200 Hz) coincides with a spectral peak at around 100 Hz. (B) Same as in A for FGBs. Spectral power in the high frequency band (100–150 Hz) coincides with a spectral peak at around 50 Hz. (C) Power spectrum of SWRs and FGBs from one example animal. (D) Average time domain profile of FGB and SWR event envelopes from the animal in D. Data from the two gerbils with most sleep data are shown in E-H. (E) Inter-event-interval (IEI) distribution of SWR and FGBs. (F) Event durations. (G) Comparison of average IEI and duration for the two types of high-frequency events. Error bars indicate standard error of the mean (SEM). (H) LFP peak triggered population firing rates for FGB and SWRs.

Discussion

Mongolian gerbils (Meriones unguiculatus) are a rodent species evolutionarily separated from rats and mice by about 25 million years, and phylogenetically ascribed to the murid subfamily of Gerbillinae (Fabre et al., 2012). Some authors even consider the gerbil as a member of the non-murid family of Cricetidae (Wissdorf & Irmer, 1980). Despite the phylogenetic differences to more commonly used rodent species, the hippocampal activity patterns of gerbils and rats/mice are very similar. Not only did we find prototypical place field activity in CA1 and CA3 (see Figures 2–4), as was expected from reports in non-rodent species (Ulanovsky & Moss, 2007), but also evidence for rate remapping and context selectivity (see Figure 3). In addition to the similarity in spatial tuning between rodent species, we also found numerous similarities in the temporal organization of hippocampal neuronal activity. As in rats and mice, theta rhythmicity was persistently observable in gerbils during locomotion, and the theta frequency range of 7 to 9 Hz was not different from that reported for mice and rats (Vanderwolf, 1969; Bland, 1986). Along with the pronounced theta rhythmicity, we found phase precession and theta compression (Figures 4, 5).

Gerbils and rats/mice exhibit marked differences in their sensory apparatus as well as in their habitat and behavior. Most importantly, gerbils have well-developed daylight vision and low-frequency hearing. Their well-developed visual system allows gerbils to leave their burrows in the morning and evening when they forage for food in the desert within a radius of up to 20 m from the nest (Agren et al. 1989). By choosing this niche they might have been able to avoid their mostly nocturnally active predators, such as larger mammals (foxes, weasels) and owls (Agren et al. 1989), and to escape extreme temperature conditions in the Mongolian desert (−40°C in winter to +50°C in summer; Agren et al. 1989). The reason for the development of their low-frequency hearing may also arise from having to sense approaching large predators. Furthermore, heavy rain conditions in the summer Mongolian desert have been observed to make gerbils leave their burrows to avoid drowning (Agren et al. 1989), which requires them to detect the (probably mostly low frequency) sounds related to these weather conditions. These adaptations could have resulted in changes in hippocampal processing, but we found remarkably few functional differences in basic hippocampal physiology between gerbils and rats/mice. Thus, we propose that the basic hippocampal computations in rodents are evolutionarily preserved and that higher specialization for vision does not necessarily result in differences in hippocampal network function. The only hint for a difference between gerbils and rats is that gerbils exhibit considerably stronger directional tuning within hippocampal CA3 place fields, which could be a result of the well-developed visual system of gerbils facilitating heading-direction modulation of place fields. The fact that sensory specializations of the gerbil do not lead to major differences in the organization of hippocampal place maps is consistent with results from ultrasound sensation in bats, where basic hippocampal place field activity also shares many similarities with rodents (Geva-Sagiv et al., 2016).

While the presence of hippocampal place maps appears to be uniform despite species-specific variations, there is considerable variability in the presence and role of awake (i.e., atropine resistant, type I) theta oscillations across species. In contrast to rodents, for example, several bat species seem to exhibit awake theta only in short bouts during stationary ultra-sonic exploration, and it is generally not visible during ground-borne locomotion (Ulanovsky & Moss, 2007) or flight (Yartsev & Ulanovsky, 2013). Conversely, non-movement related long-lasting awake theta activity is present in hamsters (Macrides, 1975), which are members of the rodent family of Cricetidae, and also in pigs (Forslid et al., 1986) and cats (Grastyan et al., 1959; Brown, 1968), which are species that are more closely related to bats than to rodents (Springer et al. 2003). These variations in theta oscillations may reflect family-specific adaptations in distinct species, but could also reflect that behavioral tasks typically used in rodent experiments are different than those used in primates, cats and bats. The latter either include strong memory components or are conducted when the animal is not moving at high speeds. The variability in the way different species are tested experimentally thus could also probe different types of theta serving different computational purposes. For example, the short theta bouts in bats may hint towards a purpose of the theta state that is not generally linked to locomotion, such as attention or active sensing (Bennett & French, 1977; Geva-Sagiv et al., 2015). Consistent with this idea, a congenitally-blind human has been shown to have much more persistent movement-related theta than sighted counterparts, suggesting that the persistence of theta may reflect a “mode-of-exploration” that relies more on self-motion cues than on visually sampling the environment (Aghajan et al., 2016). Despite these variations across mammalian species and behavioral tasks, our data corroborates that at least in rodents, stable movement-related theta is a general feature independent of the specific sensory specializations of each species, perhaps suggesting that despite their superior vision, gerbils still explore their environment in a mode predominantly similar to other rodents.

In contrast to awake theta oscillations, the ability to generate stable long-lasting theta activity during REM sleep seems to be universal among all mammals, including bats (Zhao et al., 2010), and may even be universal among all amniotes (Shein-Idelson et al., 2016; Lesku et al., 2011). These findings indicate that it is predominantly the association of theta with specific behavioral states that varies across species, but that the theta state per se may nonetheless impose a computationally essential oscillation in all mammalian species.

The phylogenetic relation between rodents and primates is closer than that between rodents and bats (about 85Myrs vs. 95Myrs; Springer et al. 2003) and thus primates and rodents might share particularly many similarities in hippocampal physiology. Indeed, theta oscillations appear to be more robust in humans and monkeys than in bats (Jutras et a., 2013, Zhang & Jacobs, 2015; Vass et al., 2016; Bohbot et al., 2017), and sharp-wave ripples show very similar features between rodents and humans (Ramirez-Villegas et al., 2015, Leonard et al., 2015). Also, strongly invariant single unit activity in humans, in which only a small portion of cells code for a person or item (Quian Quiroga et al., 2005), could resemble the low proportion of active place cells in rodents. Similar to rats and mice, our hippocampal recordings in gerbils also show these commonalities to primates and thus further corroborate the hypothesis that common oscillation patterns and sparse single cell firing reflect evolutionary invariants of hippocampal function.