Abstract
We present the results of the atomistic molecular dynamics modeling of different protonation states of Nafion at varying hydration levels. Previous experiments have shown that the degree of deprotonation (DDP) of the sulfonic acid groups in a Nafion membrane varies significantly upon hydration. Our goal is to provide insights into the effects of variable protonation states and water content on the internal structure and vehicular transport inside the Nafion membrane. The Nafion side chain lengths showed a weak increasing trend with increasing DDP at all hydration levels, exposing more of the sulfonic acid groups to the hydrophilic/water phase. The water-phase characteristic size/diameter decreased with increasing DDP, but, interestingly, the average number of water molecules per cluster increased. The probability of water–hydronium hydrogen bond formation decreased with increasing DDP, despite an increase in the total number of such hydrogen bonds. The water diffusion was largely unaffected by the state of deprotonation. In contrast to that, the hydronium ion diffusion slowed down with increasing DDP in the overall membrane. The hydronium ion residence times around the sulfonic acid group increased with increasing DDP. Our simulations show a strong connection between the morphology of the water domains and protonation states of Nafion. Such a connection can also be expected in polyelectrolyte membranes similar to Nafion.
Introduction
Fuel cells are very promising devices for energy generation.1 The most common type of such fuel cells uses hydrogen or methanol as the fuel. In addition, energy storage is becoming of utmost importance in the renewable energy revolution. In this respect, the flow batteries are being proposed as one of the solutions for large-scale energy storage.2
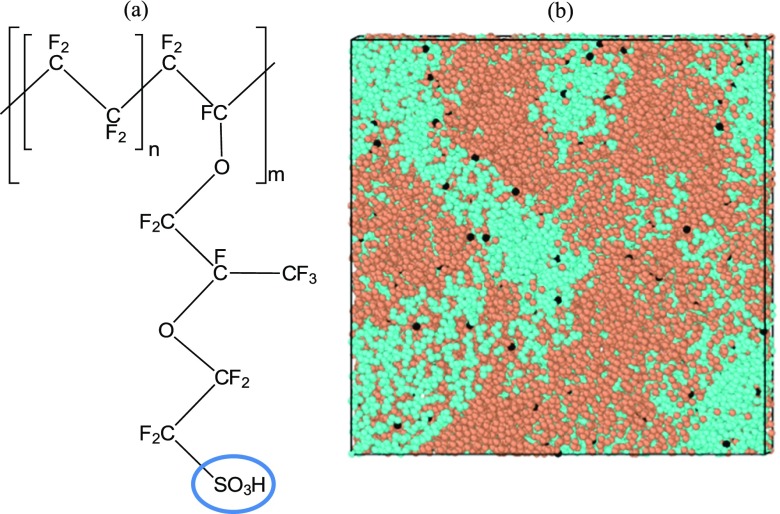
Nafion, see Figure 1a for the chemical structure, is a commonly used polymer electrolyte membrane (PEM) material in flow batteries and in PEM fuel cells.3,4 The main purpose of the PEM is to allow proton transport through it. Additionally, it prevents the electrolytes from mixing in a flow battery and the air and fuel streams from mixing in a fuel cell.
Figure 1.
(a) Single Nafion chain (n = 7, m = 10) for EW of 1100; n represents the length of the monomer and m represents the degree of polymerization; the blue oval encircles the side chain protogenic group. (b) Hydrated Nafion simulated sample, where blue color is used for the water/hydrophilic phase, orange—for hydrophobic phase, and black—for the sulfonic acid groups.
Spry and Fayer5 measured the proton concentrations in Nafion at various hydration levels using different molecules like 8-hydroxypyrene-1,3,6-trisulfonic acid trisodium salt (HPTS) and rhodamine-6G, by means of the time-resolved fluorescence anisotropy. HPTS molecules measured the amount of proton transfer in bulk water channels, whereas rhodamine-6G molecules measured it at the water interface. The fluorescence anisotropy decay times showed significant changes from the hydration level of λ = 22a to λ = 5. The proton concentration using HPTS molecules at a high hydration level (λ = 22) corresponded to 0.54 M, whereas a complete dissociation of all of the protons at this hydration level would correspond to a concentration of 2.5 M. In fact, the amount of proton transfer at λ = 12 and 22 were found to be 22 and 44%, respectively. Using rhodamine-6G, the proton concentration at the water interface was found to be 1.4 M which is still less than the 2.5 M expected concentration for complete dissociation of all of the protons. It was concluded, contrary to the common notion, that Nafion was not a superacid, that is, not all of the sulfonic acid groups are deprotonated for hydrated Nafion, even at high hydration levels.
The equivalent proton concentrations at the water interface measured using rhodamine-6G for λ = 7.5 and 12 were 1.8 and 1.4 M, respectively. These concentrations were lower than what would be expected by keeping the number of dissociated protons constant and just reducing the amount of water. The water present had reduced to a third and to a half, respectively, at λ = 7.5 and 12, as compared to that at λ = 22, which implies that the proton concentration should have roughly tripled and doubled at λ = 7.5 and 12, respectively. Because this was not the case, it meant that the proton dissociation at the water interface was lowered with reduction in hydration levels. This was also reflected in small changes of the fluorescence anisotropy decay time of rhodamine-6G from λ = 22 to λ = 5.
Gruger et al.6 measured the different hydrated species present in Nafion using spectroscopy techniques. At high hydration levels of λ = 20, the sulfonic acid was completely dissociated and the dissociated proton was found to be associated with water molecules. At a lower dehydration level of λ = 10, there was an emergence of a new species in which the hydronium ions were associated with the sulfonate groups. This species was even more abundant at lower hydration states. Singhal and Datta7 found that the concentration of protons decreased with decreasing thickness in Nafion films which was attributed to the increased association of the protons to the sulfonate ions with decreasing thickness.
Such experimental observations gain importance in light of other measurements made inside a Nafion membrane in a fuel cell under operating conditions. Patil et al.8 found that the water content inside the Nafion membrane went down with the increasing fuel cell current. This could create regions of varying water content and, consequently, varying proton dissociation inside the membrane.
Classical molecular dynamics (MD) simulations have been used to study the variable protonation states for a variety of materials. Simulations of graphene oxide (GO) flakes showed aggregation at low pH, if the carboxyl groups were mainly protonated, whereas the GO flakes dissolved in water at high pH, with the deprotonated carboxyl groups.9 This also agreed well with experiments.9 Polyamidoamine (PAMAM) dendrimers in the presence and absence of linear polyethylene oxide (PEO) chain were studied using different protonation states of the amines in the PAMAM molecule.10 Conformational states and hydrogen bonding were studied, and good agreements with experiments were found.10
Classical MD simulations have also been performed for Nafion to study the water-phase structure and diffusion within the membrane.3,11−13 Other techniques such as ReaxFF,14 MS-EVB,15 and ab initio MD16 simulations have also been used to study Nafion and other PEMs to better understand the proton hopping transport mechanism in such materials. Classical MD techniques enable the study of large system sizes (>10 000 atoms) which is important for understanding the internal water-phase structure in these PEM materials.
Previous classical MD simulation studies of Nafion had assumed that it is a superacid and, consequently, all of the sulfonic acid groups had been deprotonated.3,11,12 There have been experiments17 which have shown that Nafion is a very strong acid comparable to 95% sulfuric acid solution. Calculations using the pKa database have shown Nafion to have a pKa = −6.18 Previous density functional theory (DFT) studies19 had shown that the sulfonic acid groups were deprotonated at λ ≥ 3 which was the reason behind deprotonating all of the sulfonic acid groups in the classical MD simulations. However, there are other experiments,5,6 as discussed before, which have shown the existence of different protonation states even at very high hydration levels. Therefore, we think that it is important to provide some insights, using classical MD, for both structural and dynamical properties of Nafion for various degrees of deprotonation (DDPs) at different hydration levels. Our results show that the sulfur–sulfur radial distribution functions (RDFs) peak heights showed similar trends as the neighboring intramolecular/intrachain sulfur–sulfur (S–S) distance, although the first peak distance and the intramolecular S–S distance are noticeably different. The hydrophilic cluster characteristic size and number of water molecules per cluster were analyzed using structure factors and cluster distributions, respectively. Both these parameters showed a visible correlation with DDP. The water molecules and hydronium dynamics were also analyzed using translational diffusion coefficients and residence times around the sulfonic acid group. It is important to note that properties like characteristic size of the water phase, residence time, and diffusion can be measured in experiments and provide support for our simulation studies. The visible dependence of the water cluster morphology on the Nafion protonation states could have a bearing on the efficiency of fuel cells.
Materials and Methods
Simulation Details
The Nafion monomer chemical structure is shown in Figure 1a, where n represents the number of repeat [−CF2–CF2−] units in a monomer and m represents the degree of polymerization. The value of n = 7 has been chosen which corresponds to an equivalent weight (EW) of 1100. EW is defined as the molecular weight of the polymer divided by the number of protogenic/sulfonic acid groups. EW of 1100 is a very commonly used variety of Nafion and, hence, has been chosen for this study.3,20 Please refer to our previous study for Nafion chain construction details.21
Figure 1b shows a typical simulated snapshot of a hydrated Nafion sample. The water phase, shown in blue, forms a continuous phase at sufficiently high hydration levels and so does the hydrophobic phase, shown in orange, at low or high hydration levels. The black dots are the sulfonic acid groups which are situated at the water-phase–hydrophobic-phase interface.
A combination of polymer consistent force field22 and condensed-phase optimized molecular potentials for atomistic simulation studies23 force fields has been used for our study. Details about the force field used and the validation of our choice are provided in the main text and the Supporting Information of our previous study.21
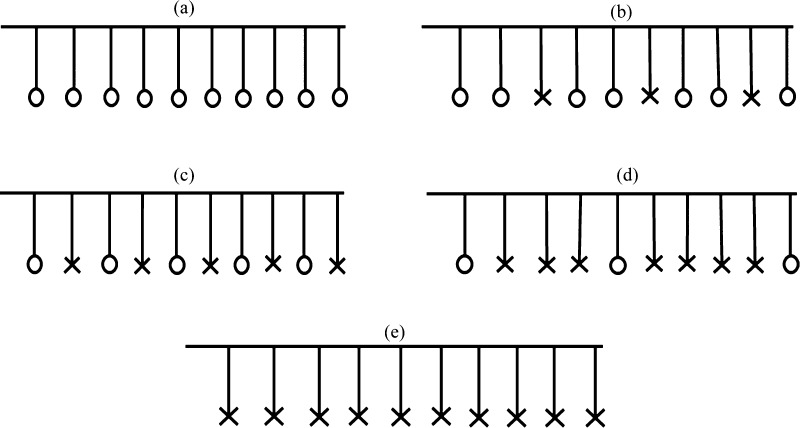
Five different DDPs were chosen, corresponding to 0, 3, 5, 7, and 10, as seen in Figure 2. The zero DDP corresponds to the case where all of the sulfonic acid groups in a single Nafion chain have the proton attached to them. At DDP = 10, all of the sulfonic acid groups in a Nafion chain have the protons detached. The intermediate DDP = 3, 5, 7 correspond to 3, 5, and 7 deprotonated sulfonic acid groups in a Nafion chain, respectively. For the 3 and 7 DDP cases, the deprotonated groups have been distributed as uniformly as possible throughout the chain. This was done to negate additional effects from clustering of the sulfonic acid groups which have been observed in previous simulations.3
Figure 2.
Different DDPs for a Nafion chain (a) DDP = 0, (b) DDP = 3, (c) DDP = 5, (d) DDP = 7, and (e) DDP = 10. “O” represents a protonated sulfonic acid group and “X” represents a deprotonated sulfonic acid group.
Four different hydration levels corresponding to λ = 5, 10, 15, 20 were simulated at a temperature of T = 353 K, common operating temperature of fuel cells. Hydration level (λ) is defined as the number of water molecules present per sulfonic acid group. Thus, a total of 20 different state points, corresponding to different choices of DDP and λ, were used. All these different state points started from a different and independent initial configuration.
Therefore in summary, five different DDP values, DDP = 0, 3, 5, 7, 10 at four different hydration levels of λ = 5, 10, 15, 20 were simulated in our study. A total of 20 different simulation boxes were constructed using the amorphous cell module of Materials Studio.24 Each simulation box had Nch = 20 Nafion chains. There were NH = 0, 60, 100, 140, 200 hydronium ions present in simulation boxes for DDP = 0, 3, 5, 7, and 10, respectively. The number of water molecules present is equal to Nch × 10 × λ – NH, where the factor 10 is due to the number of sulfonic acid groups per Nafion chain corresponding to the chain degree of polymerization. The total number of atoms were in the range of 17 000–26 000, and the simulation box sizes were in the range of 58–66 Å.
The boundary conditions were periodic in all three directions. In addition, Nafion simulations were also performed in 3D periodic boxes for DDP = 10 and for λ = 5, 10, 15, 20 having 7 and 20 Nafion chains. No finite size effects have been observed on comparing the density, RDFs, and water and hydronium diffusion coefficients. All of the simulation results shown in the present paper are for a 20 chain Nafion system.
The simulations were run for a total of 9 ns, and the last 3 ns of the production runs was used for analysis. Six independent additional simulations were run corresponding to DDP = 0, 3, 5 and λ = 5, 20 for 12 ns. The analysis was done for these independent simulations by sampling from a production run corresponding to the last 6 ns. In addition, the original simulations, which had a production run of 3 ns, were also extended to have a production run of 6 ns from which the analysis was performed for these six state points. There were no noticeable differences found between the independent and the extended simulation runs. Therefore, all of the results provided here are from sampling production runs corresponding to the last 3 ns in 9 ns simulation runs.
The density with variation less than 0.05% was close to experimental values,b and the energies had stabilized after around 2.5 ns from the start of the simulation. Moreover, the water phase also stabilized within this simulation period as evidenced by the simulated water structure factor peak wave numbers and water diffusion coefficients being close to the experimental values.c Residence times for hydronium ions were also comparable to experimental values.d The duration of the present simulations and the implemented system sizes are consistent with the previous simulation studies.3,11,12,25−27 Each simulation consumed around 50 CPU hours on 32 cores of the Lisa computing cluster in SurfSara (Amsterdam). A detailed description of the model construction and simulation protocol has been presented in the Supporting Information (sections I and II).
Analysis Techniques
From the production runs, structural and dynamic characteristics like chain radius of gyration (Rg), side chain lengths, RDFs, intramolecular sulfur–sulfur (S–S) distance, characteristic size/diameter of hydrophilic/water domains, cluster distribution of water molecules and/or hydronium ions, hydrogen bond count in the water phase, diffusion coefficients, and residence time of water molecules and hydronium ions have been analyzed. The effect of DDP and hydration levels on all these characteristics will be discussed in detail later.
The RDF g(r) is proportional to the probability of finding an atom B at a distance r from the reference atom A inside a shell of thickness dr.20 The sulfur–sulfur RDF has been analyzed to check for any significant changes in the distance between the side chain protogenic groups. The average Nafion chain radius of gyration (⟨Rg⟩)28 and Nafion side chain lengths have been calculated for all different DDPs and all hydration levels (λ). The side chain length is defined as the distance between the carbon, connecting the backbone of Nafion to the side chain, and the sulfur in the sulfonic acid group. The intramolecular S–S distance is the distance between two adjacent sulfonic acid groups in a Nafion chain.
The structure factor for the hydrophilic/water phase is computed by the Fourier transform of the oxygen (water and hydronium)–oxygen (water and hydronium) RDF,
| 1 |
where ρ is the density, g(r) is the RDF value at distance r, q is the corresponding wave number, and rm is the maximum distance up to which RDF is calculated.
The structure factor S(q) has a peak at a particular wave number (qmax) which corresponds to the characteristic size, dmax = 2π/qmax, of the water/hydrophilic phase. The RDF is computed using VMD29g(r) plugin which uses a special normalization function30 to compute RDFs up to 3L/2, where L is the box size with periodic boundaries in all three dimensions.31 The minimum box size for our simulations is about L = 58 Å. The RDFs are computed up to rm = 40 Å which is smaller than the maximum allowable distance of 3L/2 = 50.2 Å. Using the standard method, the RDFs can only be computed up to a maximum distance of L/2 under periodic boundary conditions. However, the method used in the present study allows us to simulate RDFs at larger distances, thus improving the resolution of the structure factors at lower wave numbers. The structure factor calculated using eq 1 allows computation up to a minimum wave number,32qmin = π/rm = 0.0785 Å–1.
The cluster distribution of water molecules was computed for the different hydration levels (λ) using the OVITO software.33 A cluster is defined as a group of atoms in which each atom is within a particular predefined cutoff distance of at least another atom within that group. The oxygen atom in a water molecule and in a hydronium ion was used for computing cluster sizes. For example, cluster of 5 oxygen atoms is assumed to represent the cluster of 5 water molecules and/or hydronium molecules. The cluster distribution plots number of clusters, averaged over a time interval of 3 ns, versus the cluster size. Cluster size is the number of water and/or hydronium molecules present in a cluster, as defined in a previous simulation study.11 The average number of clusters for any particular cluster size is the occurrence frequency of that particular cluster size divided by the total number of trajectory snapshots during the 3 ns production period. The total cluster count and average number of water molecules and/or hydronium ions per cluster at all hydration levels and DDP have been extracted from the cluster distributions and analyzed.
Hydrogen bond count was computed for hydrogen bonds between water molecules and also between water molecules and hydronium ions using the criteria introduced in previous simulation studies.34,35 The normalized hydrogen bond counts were computed by dividing the actual count by the maximum possible number of hydrogen bonds at a particular hydration level and DDP.
The translational diffusion coefficients for the center of masses of water molecules and hydronium ions were computed by analyzing their mean square displacements (MSD) using the Einstein relation in the diffusive regime.28 Diffusion coefficients were computed for water molecules and hydronium ions averaged over the entire simulation box. The diffusion coefficients were also computed in the first residence shell around the sulfur atoms by tracking the molecules present within 4.2 Å of the sulfur atom of the sulfonic acid group for 3 ns using the method prescribed in a previous simulation study.36
The residence time was calculated for water molecules and hydronium atoms in the first residence shell around sulfur using the procedure suggested before.37,38 In essence, a correlation function, C(t), was introduced as
| 2 |
where vi is the Boolean variable whose value is 1 if the oxygen atom of a water molecule/hydronium ion is within 4.2 Å of a sulfur of the sulfonic acid group or else the value is zero, N is the total number of water molecules/hydronium ions, offset time (th) = hΔt, h—0, 1, ..., 1800, Δt = 1 ps is the sampling interval, and M is the total number of samples (M = 2000 corresponding to 2000 ps).
A correlation function C(t), as introduced in eq 2, is computed for each sulfur atom in the system. The residence time (τ) has been calculated using the stretched exponential fit,
| 3 |
Each correlation function C(t) fitted with eq 3 yielded a residence time (τ). All these residence times were averaged. There were a few very high residence time values due to some water molecules/hydronium ions getting stuck near some sulfur atoms. These high residence times were filtered out before averaging by a commonly used outlier elimination method.39 Outliers were adjudged to be all those residence times for which the median absolute deviation was greater than 1.5 times the interquartile range.
Results and Discussion
Structural Properties
Density of Hydrated Nafion
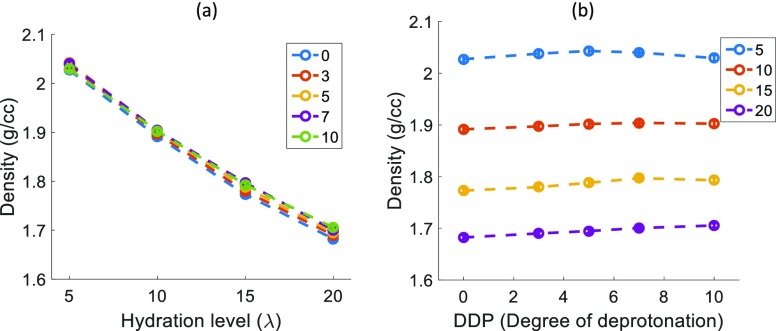
Figure 3 shows the density of the simulated Nafion samples at various DDPs and different hydration levels at T = 353 K. The density values are within 5–7% of the previously reported experimental data40,41 at T = 300 K and simulated values12 at T = 353 K. The simulated density decreases with increasing hydration at any particular DDP (Figure 3a), as more water causes the sample to swell. However, the density does not show any considerable trend with varying DDP at any hydration level (Figure 3b). This means that DDP does not affect the amount of swelling of Nafion.
Figure 3.
Hydrated Nafion density values for (a) λ = 5, 10, 15, 20 at DDP = 0, 3, 5, 7, 10 and (b) for DDP = 0, 3, 5, 7, 10 at λ = 5, 10, 15, 20. The error bars are very small and are located within the circular symbols.
Radial Distribution Functions
The distance between the protogenic sulfonic acid groups is an important property to understand the structural changes in the Nafion membrane. Previous DFT-based simulation studies42 have shown that the sulfur–sulfur distance less than 6.5 Å increased water binding to sulfonic acid groups and also affected the ease of the proton dissociation. Hence, the sulfur–sulfur (S–S) RDF at small atomic separations (<8 Å) have been analyzed in the present study to check for any significant trends.
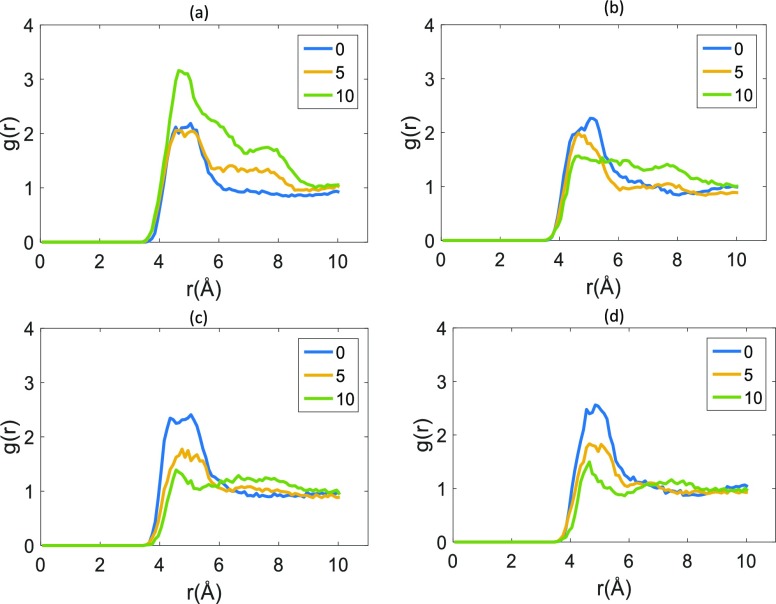
Figure 4 shows the S–S RDFs for a range of DDPs and hydration levels. The position of the first peak of the S–S RDF, at around 5 Å, does not show any noticeable trend with varying DDP at any particular hydration level. However, the RDF values at the first maximum, for low hydration level of λ = 5, increase with the increasing DDP, whereas the same RDF values decrease with the increasing DDP at higher hydration levels of λ = 10, 15, 20. Increasing DDP creates more negatively charged sulfonic acid groups which increase the repulsion between these groups and reduce the RDF values at a shorter distance. This explains the trend at higher hydration levels of λ ≥ 10 but not for λ = 5. A similar reversal of trend from λ = 5 to λ = 20 is also observed in intramolecular sulfonic acid group separation distances, which are analyzed below. Later, we will provide an explanation for this interesting similar trend of two different metrics.
Figure 4.
Sulfur–sulfur (S–S) RDF dependence on DDP = 0, 5, and 10 for different hydration levels (λ) of (a) λ = 5, (b) λ = 10, (c) λ = 15, and (d) λ = 20.
The sulfur–oxygen (water) (S–Ow) and sulfur–oxygen (hydronium) (S–Oh) RDF first peak values increase with the increasing DDP at all hydration levels (Figures S1 and S2). The reason being that the number of charged sulfonic acid groups increase with the increasing DDP, resulting in more attraction between the water molecules/hydronium ions and sulfonic acid groups. This effect also reduces the small distance correlation in between water molecules, as reflected in the decreasing first peak oxygen (water)–oxygen (water) RDF values with the increasing DDP (Figure S3).
Chain Length Statistics
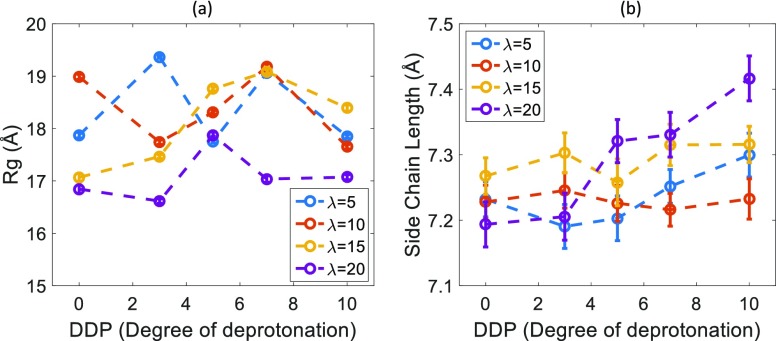
The radius of gyration (Rg) as shown in Figure 5a, is an important statistical property because it can be measured in experiments like dynamic light scattering and small-angle neutron scattering.43 No observable trend can be seen for Rg values upon changing DDP, in contrast with the weakly increasing trend of side chain length, as shown in Figure 5b. As was already noticed earlier, increasing DDP increases the number of charged sulfonic acid groups. This increased charge consequently increases the affinity of the side chains for the polar water phase, which causes them to stretch toward the hydrophilic/water phase.
Figure 5.
(a) Radius of gyration (Rg) for Nafion chain, error bars are within the symbols. (b) Nafion side chain length dependence on DDP for different hydration levels (λ).
As opposed to the side chain lengths, the Rg does not show any trend with DDP simply because Nafion is mostly composed of hydrophobic components which form a separate hydrophobic phase. Slight changes in side chain lengths are unlikely to have an effect on the conformations of this largely hydrophobic molecule.
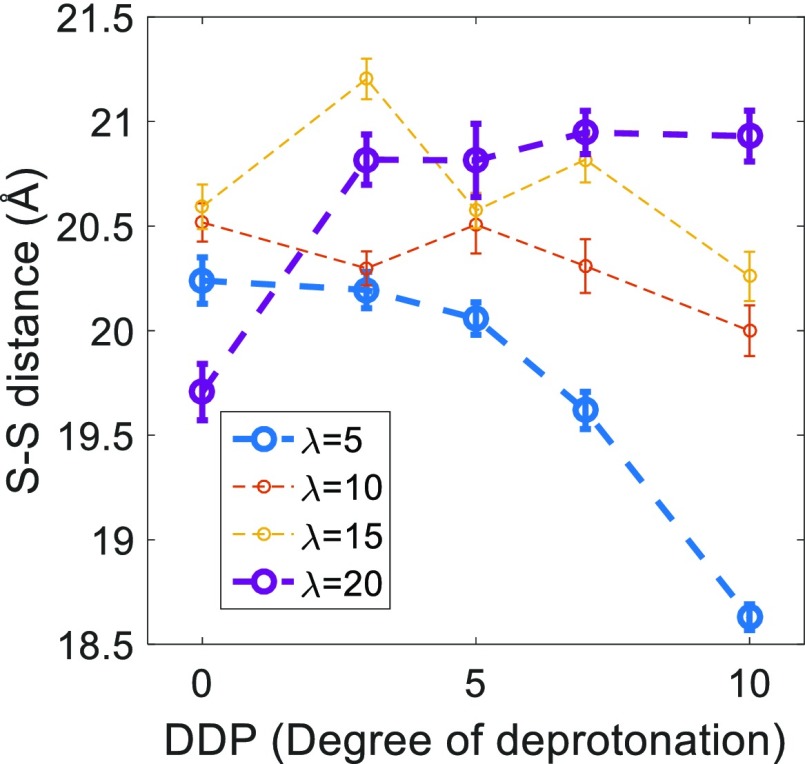
Figure 6 shows the intramolecular distance between the neighboring sulfur atoms, in the sulfonic acid groups. This distance goes down sharply with the increasing DDP for λ = 5, while it remains unchanged for λ = 10 and 15 and increases gradually for λ = 20. The neighboring intramolecular S–S distances are much higher than the first peak distances observed in the S–S RDF. However, a similar reversal of trend has been noticed, as seen before for the S–S RDF first maximum values, from a low hydration level to higher hydration levels. We believe that this trend is connected to the preferable interactions of increasingly hydrophilic sulfonic acid groups with existing water domains. The side chains stretch and move toward the hydrophilic/water phase with the increasing DDP at all hydration levels. At higher hydration levels, larger water clusters allow easier movement of the sulfonic acid groups which increases separation between these groups. However, at a low hydration level of λ = 5, large water clusters are absent which restricts the free movement of the sulfonic acid groups and, hence, reduces the distance between them on average.
Figure 6.
Intramolecular neighboring sulfur–sulfur (S–S) distance dependence on the DDP for different hydration levels (λ).
Structure Factor and Cluster Distribution
Hydrophobic and hydrophilic parts of Nafion tend to phase separate upon hydration. The hydrophilic phase is made up of water clusters. At sufficiently high hydration levels, these water clusters join together to form a percolated hydrophilic/water domain,44 allowing the transport of protons through it. The characteristic size/diameter of the water domains, comprising of water molecules and hydronium ions, in the water phase has been analyzed by computing the structure factor using eq 1, as demonstrated in a previous study.45 In addition, the water cluster analysis has been performed to calculate the number of water molecules and/or hydronium ions in different water clusters of varying sizes. All of the water cluster analyses shown here are for a cutoff distance of 3.7 Å. This cutoff distance was chosen because it is well beyond the first maximum of the RDFs of oxygen (water)–oxygen (water) and oxygen (hydronium)–oxygen (water), as shown in Figures S3 and S4. Hence, this distance will include majority of the water molecules and hydronium ions. We here refer to our previous study21 for further justification of this cutoff distance.
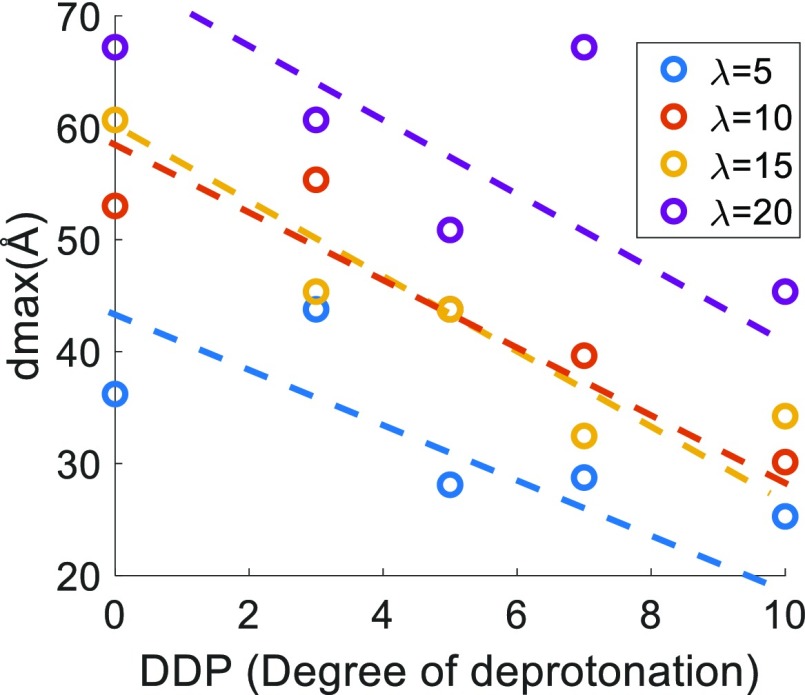
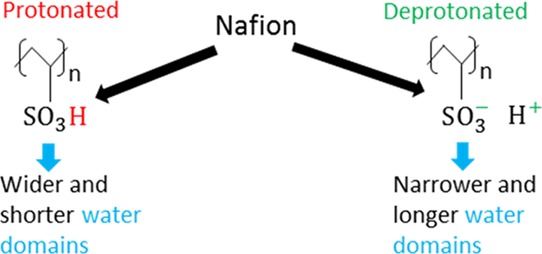
Figure 7 shows the characteristic water phase, composed of water molecules and hydronium ions, channel size/diameter (dmax)e for various DDPs at different hydration levels. The corresponding structure factors, calculated using eq 1, for each of these DDPs and hydration levels are shown in Figure S5. The wave numbers corresponding to the first peak of the structure factors are very close to the experimental values46 and previous simulated values for a smaller system size.3 We can see that dmax shows a noticeable decreasing trend with the increasing DDP at all hydration levels, which means that the water domains are becoming narrower with the increasing DDP. It is important to note that DDP can be connected to solution pH, that is, higher DDP corresponds to higher solution pH and vice versa. Cluster distributions for water molecules and/or hydronium ions have been analyzed next to get further insights into the hydrophilic/water-phase morphology.
Figure 7.
Characteristic water/hydrophilic phase channel size (dmax) dependence on the DDP for different hydration levels (λ). The circular symbols are the actual data points and the dashed lines are only a guide to the eye.
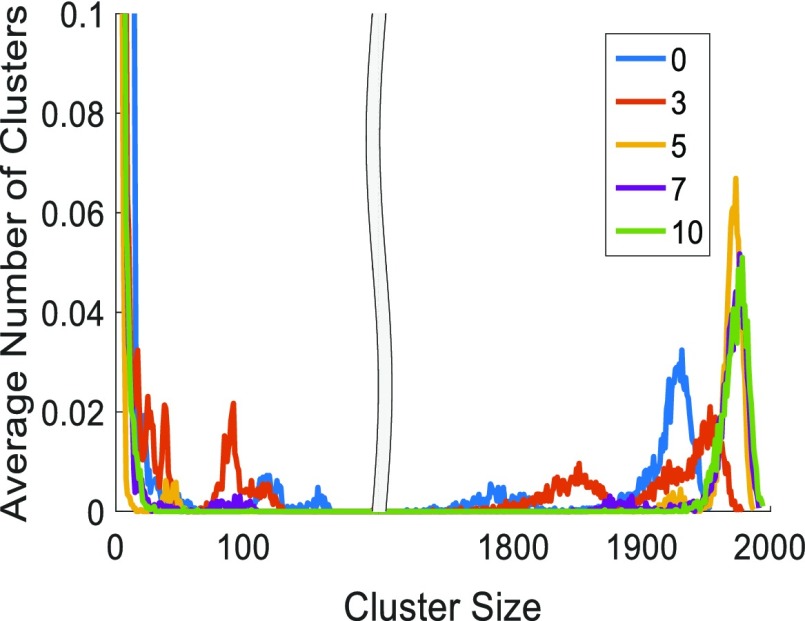
Figure 8 shows the water cluster distributionf for λ = 10 at the different DDPs chosen for this study. We can see a peak forming in the size range of 1800–2000 for various DDPs representative of a large connected water cluster. This large cluster peak is moving toward bigger water cluster sizes with the increasing DDP. This pattern is repeated for higher hydration levels of λ = 15 and 20 (Figure S6). However, for λ = 5 no such trend is observed because only a limited amount of water is present.
Figure 8.
Hydrophilic/water-phase cluster distribution for DDP = 0, 3, 5, 7, 10 at a hydration level of λ = 10. The average number of clusters for cluster sizes <10 is well beyond the vertical scales. The average number of clusters is directly proportional to the occurrence frequency of a particular cluster size in the averaging interval of 3 ns. Hydrophilic/water phase contains both water molecules and hydronium ions.
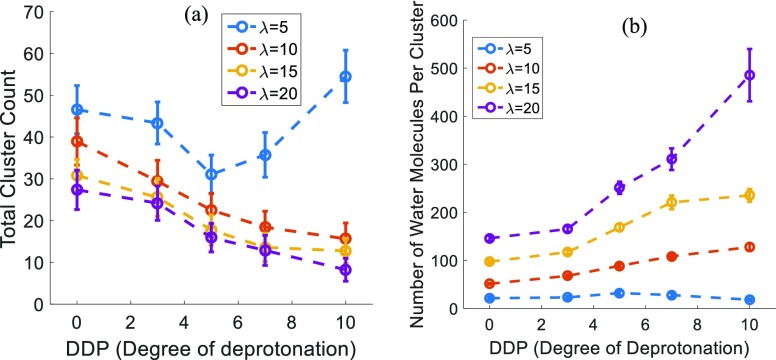
Figure 9a shows the total number of water clusters/cluster count for different DDPs at various hydration levels. The total cluster count decreases with the increasing DDP for λ ≥ 10. This observation indicates a more dispersed water phase with the decreasing DDP at higher hydration levels. No such trend is observed for λ = 5 because of the absence of any large connected water phase.
Figure 9.
Hydrophilic/water phase (a) total cluster count and (b) average number of water and/or hydronium ions per cluster, dependence on the DDP for different hydration levels (λ). Hydrophilic/water phase contains both water molecules and hydronium ions.
The average number of water and/or hydronium ions per cluster, as shown in Figure 9b, is the weighted average of cluster sizes where the weights are the average number of clusters corresponding to the different cluster sizes. This is effectively the area under the cluster distributions, as shown in Figures 8 and S6. We can see a trend that matches with the visual interpretation of cluster distributions discussed above. The average number of water and/or hydronium ions per cluster increases with the increasing DDP at large enough hydration levels of λ ≥ 10. The reason for such a trend could be that higher DDP creates more charged sulfonic acid groups which, in turn, attracts more water in the vicinity of such groups and aids in the formation of bigger water clusters.
Concluding this part, we can see that the water cluster distributions and water channel characteristic sizes are significantly affected by changes in DDP. Water domains are getting narrower with the increasing DDP at any given hydration level, as seen in Figure 7. However, the average number of water molecules per cluster is increasing with DDP, as seen in Figure 9b, which means that the domains are also becoming longer or more connected over larger distances with the increasing DDP.
We provide a conceptual picture behind such morphological changes of the water domains/channels. The number of water molecules, considering the ones present in hydronium ions, is constant at any given hydration level. The water molecules and hydronium ions get distributed in the vicinity of a larger number of charged sulfonic acid groups with the increasing DDP at any particular hydration level. Consequently, the water molecules and hydronium ions are distributed over a larger volume with the increasing DDP which causes the water domains to stretch out and become narrower. To conserve the volume of the water molecules and hydronium ions, the water domains should become longer with the increasing DDP, even if the average number of water molecules and/or hydronium ions per cluster is constant with DDP. However, the average number of water molecules and/or hydronium ions per cluster increases with DDP which implies that water domains are further elongated than what would be expected by just volume conservation.
Hydrogen Bond Count
The water molecules present in the system form hydrogen bonds with themselves and with the hydronium ions. The protons can hop across these hydrogen bonds and diffuse through membrane. Therefore, the number of such hydrogen bonds existing in the system at various DDPs and hydration levels is important for proton transport and has been analyzed in our study.
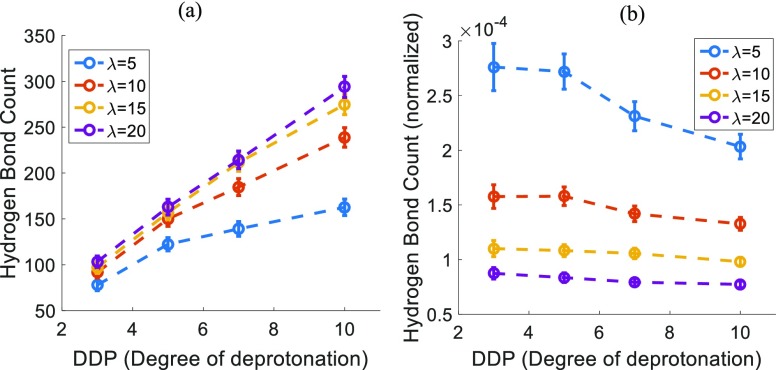
Figure 10a shows the number of hydrogen bonds existing between water molecules and hydronium ions. The total number of such hydrogen bonds increases considerably with the increasing DDP at any particular hydration level. This is expected because the number of hydronium molecules present in the system is increasing with the increasing DDP. The normalized hydrogen bond count is computed by normalizing the total count by the maximum possible number of hydrogen bonds (between water and hydronium) at any particular DDP and hydration level. Interestingly, this normalized hydrogen bond count (Figure 10b) shows a decreasing trend with the increasing DDP at all hydration levels. This implies that the probability of forming a hydrogen bond between water molecule and hydronium ion decreases, despite the increasing availability of hydronium ions upon the increasing DDP. The reason for this could be that the hydronium molecules reside close to the sulfonic acid group and, hence, do not participate in hydrogen bonding with water molecules despite increasing number of hydronium ions. Such a change in trend is not observed for hydrogen bonds formed between water molecules (Figure S7).
Figure 10.
Dependence on the DDP for (a) actual hydrogen bond count and (b) normalized hydrogen bond count between water molecules and hydronium ions for different hydration levels (λ).
Dynamical Properties
Translational Diffusion of Water and Hydronium
Water diffusion through the membrane in a fuel cell or flow battery is important for the functioning of these devices. The vehicular diffusion mechanism describes a process in which the proton attaches to the water molecules and diffuses through the membrane.47 There exists another proton transport process known as the Grotthuss mechanism, which describes the proton jumps across the hydrogen bonds present in the network.47 Here, we will be analyzing only the vehicular diffusion of both water molecules and hydronium ions across various DDP and hydration levels.
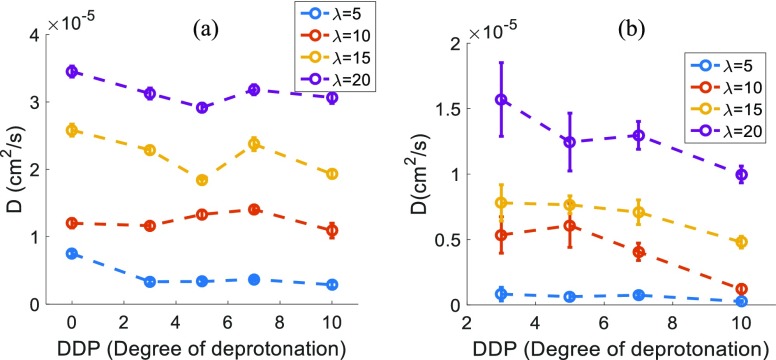
The average water molecules and hydronium ion center of mass diffusion coefficients have been computed using the Einstein relation in a diffusive regime (Figures S8 and S9). Figure 11 shows the simulated diffusion coefficients of the water molecules and hydronium ions for various DDPs at different hydration levels (λ). The diffusion coefficients decrease with the decreasing hydration level because of the decreasing average number of water molecules and/or hydronium ions per cluster, as expected. The diffusion coefficients for hydronium ions are 2–3 times smaller than those of water molecules, at any given DDP and hydration level. This is due to the stronger electrostatic attraction between the hydronium ions and sulfonic acid groups, as compared to that for water molecules.
Figure 11.
Diffusion coefficients for the center of mass of all (a) water molecules and (b) hydronium ions, as functions of the DDP for different hydration levels (λ).
The water diffusion coefficients show a very weak, almost negligible decreasing trend with DDP at all hydration levels. This can be explained analyzing the corresponding structural changes of the hydrophilic/water domains. The water domain characteristic size/diameter (dmax) grows with the decreasing DDP, whereas the average number of water molecules and/or hydronium ions per cluster goes down with the decreasing DDP. Both these effects counteract each other and, hence, the water diffusion remains largely unaffected by the DDP.
On the other hand, the hydronium ion vehicular diffusion rates are showing a significant downward trend with the increasing DDP, despite the counteracting effects discussed in the preceding paragraph. The electrostatic attraction between the positively charged hydronium ions and the negatively charged sulfonic acid groups increases with the increasing DDP, which hinders significantly the free diffusion of the hydronium ions. It can be concluded that the electrostatic interaction is the dominant factor in the vehicular diffusion of hydronium ions, as compared to any morphological changes of the water domains induced by the DDP variation.
The sulfonic acid group forms hydrogen bonds with water molecules and this helps in the deprotonation of this group. Therefore, both the diffusion and residence time of water molecules and hydronium ions have been analyzed within a distance of 4.2 Å around the sulfur atoms of sulfonic acid group. This is the distance up to the first maximum of the S (sulfur)–Ow (oxygen of water) and S (sulfur)–Oh (oxygen of hydronium) RDFs (Figures S1 and S2). Figures S10 and S11 show the MSDs of the water molecules and hydronium ions within this distance. The diffusion coefficients have been extracted from these MSDs, as shown in Figure S12. Both the water molecules and hydronium ion diffusion follow a similar trend, as observed for the average values discussed earlier. The reason for this similarity of trend is that a large percentage of the water molecules and hydronium ions are found within the 4.2 Å of the sulfur atoms of the sulfonic acid groups. This first maximum of the S–Ow and S–Oh RDFs is the most prominent maxima in the RDFs by far, hence encompassing a majority of the water molecules and hydronium ions.
Residence Time
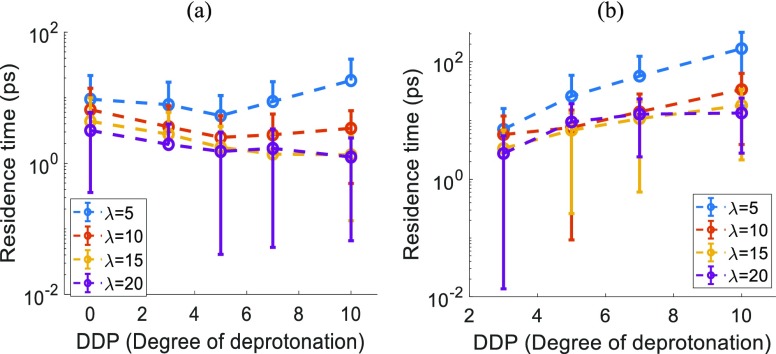
Figure 12 shows the residence times extracted from the relaxation of the corresponding correlation function, eq 2, using a stretched exponential fit, eq 3, for water molecules and hydronium ions within a distance of 4.2 Å from the sulfur in the sulfonic acid group, respectively. This is the distance near the first up to the first maximum of the S (sulfur)–Ow (oxygen of water) and S (sulfur)–Oh (oxygen of hydronium) RDFs (Figures S1 and S2). The residence times extracted with an exponential fit,37 β = 1 in eq 3, are shown in Figure S13. Both these fits show the same qualitative trend, but the residence times are larger for exponential fit as compared to those from the stretched exponential fit. The adjusted R2 of the stretched exponential fit values is always higher than that for the exponential fit, which is why we have chosen to show only the stretched exponential fit parameters here.
Figure 12.
Residence time for (a) oxygen (water molecules) (b) oxygen (hydronium ions) as a function of the DDP for different hydration levels of (λ).
The residence times for hydronium ions are higher than those of water molecules because of the stronger electrostatic attraction between hydronium ions and sulfonic acid groups. These observations also match qualitatively with the previous simulation results.37 It is important to note here the quasielastic neutron scattering spectra analysis of hydrated Nafion,46 which showed the existence of slow and fast protons at all hydration levels. The number of fast protons was significantly bigger than that of slow protons at higher hydration levels of λ ≥ 10,46 which means the residence time of protons at higher hydration levels will be biased toward the residence time of the fast protons. Our simulated residence time for hydronium ions matches very well with the experimental residence time46 of fast protons at higher hydration levels of λ ≥ 10.
The residence times for water molecules, shown in Figure 12a, show no visible trend with the varying DDP at all hydration levels. This correlates well with water diffusion coefficients in the whole system, as well as in the vicinity of the sulfonic acid group. In contrast to that, the residence time for hydronium ions increases with DDP, especially for a low hydration level of λ = 5 (Figure 12b). This is due to the lack of connected water clusters at λ = 5 which hinders the hydronium ion movement away from the charged sulfonic acid groups. For higher hydration levels, the hydronium ion residence time also shows a noticeable increase with the DDP. This increasing trend is in agreement with the hydronium ion diffusion trends observed previously. The diffusion slows down with the increasing DDP because the hydronium ions spend more time in the vicinity of the sulfonic acid groups.
In conclusion, the water molecule diffusion is not affected by the DDP, despite changes taking place in the structure of the hydrophilic phase. The hydronium ion diffusion slows down with the increasing DDP because of the electrostatic interactions, which overrides any effects caused by changes in the shape and size of the water/hydrophilic domains.
Conclusions
Previous experiments5 of Nafion have shown less than 50% deprotonation even at very high hydration levels (λ = 22). Other experiments6,7 have shown the existence of protons associated with the sulfonate groups at moderate hydration levels (λ = 10) and also with decreasing film thickness. Therefore, in the present study, Nafion was simulated using classical MD for varying levels of degree of deprotonation (DDP) at four different hydration levels of λ = 5, 10, 15, 20 at T = 353 K, to understand its structure and dynamics.
The position of the first maximum of the simulated sulfur–sulfur RDFs did not show any noticeable trend with varying DDP. However, the first maximum height reduced with the increasing DDP for higher hydration levels (λ = 10, 15, and 20), whereas it increased with the increasing DDP for a low hydration level (λ = 5).
The Nafion side chain lengths increased with the increasing DDP at all hydration levels because of the increasing attraction between the charged sulfonic acid groups and the hydrophilic phase. The intramolecular neighboring sulfur–sulfur (S–S) distance reduced with the increasing DDP for λ = 5, whereas it stayed the same or increased for higher hydration levels (λ ≥ 10). This trend was similar to the peak heights observed in the S–S RDF, although the distances for both these metrics were quite different. It was hypothesized that the longer side chain lengths with the increasing DDP allowed the side chains to move freely in bigger water clusters at higher hydration levels. In contrast, the longer side chain lengths at a low hydration level had reduced ability to move freely because of the absence of large water clusters which, in turn, induced more order and regularity in the spacing of the side chains.
The characteristic size/diameter of the hydrophilic phase decreased with the increasing DDP. At the same time, the average number of water molecules per cluster increased with the increasing DDP. Therefore, it was concluded that the water domains became narrower and longer with the increasing DDP.
The probability of formation of hydrogen bonds between a water molecule and a hydronium ion decreased with the increasing DDP at all hydration levels, despite the increasing total number of such hydrogen bonds. The increased residence time of hydronium ions near the sulfonic acid groups with the increasing DDP was found to be the reason behind this trend.
The water vehicular diffusion coefficients showed no considerable changes with the DDP. This effect correlated well with the structural changes observed in the water phase/domains. The water domains became narrower with the increasing DDP, but this narrowness was compensated by a larger amount of water molecules per cluster which provided longer water domains. Despite these counteracting effects, the hydronium ions showed a significantly decreasing vehicular diffusion with the increasing DDP across all hydration levels. This was attributed to the strong electrostatic attraction between the hydronium ions and sulfonic acid groups. The residence time trends for both the water molecules and hydronium ions were in agreement with the vehicular diffusion trends. The water residence time was almost invariant with the DDP, whereas the hydronium residence showed considerable increase with DDP.
The varying DDP had a significant effect on the morphology of the water domains. This changing morphology of water domains can be measured experimentally using scattering techniques to provide information about structure factors. The present simulation study can definitely be important to provide insights to such experiments. Also, the changes in morphology of the water domains will have a bearing on the efficiency of fuel cells because the water content in the membrane changes8 during the operation of fuel cells.
Acknowledgments
This study was done as a part of the FOM-SHELL 15CSER13 project. This work was carried out on the Dutch national e-infrastructure with the support of SURF Cooperative. SHELL-NWO CSER (Computational Science for Energy Research) project 15CSER13 funds were used for performing this study.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.9b04534.
Simulation protocol, S–Ow RDF, S–Oh RDF, Ow–Ow RDF, Oh–Ow RDF, water structure factor, cluster distribution, water–water hydrogen bond count, MSD (overall and within 4.2 Å of sulfur for water molecules and hydronium ions), diffusion coefficients for water molecules and hydronium ions within 4.2 Å of sulfur, residence time for water molecules and hydronium ions extracted from exponential model fit, and β coefficients for water molecules and hydronium ions extracted from the stretched exponential model fit (PDF)
Author Contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
The authors declare no competing financial interest.
Footnotes
Please refer to the “Simulation Details” section for the definition of hydration level (λ).
Please refer to the “Density of Hydrated Nafion” section.
Simulated water diffusion coefficients have been compared to the experimental values in the Supporting Information of our previous study.21 Comparison of simulated and experimental structure factors is provided in the “Structure Factor and Cluster Distribution” section.
Please refer to the “Residence Time” section.
The maximum dmax value is around 70 Å. dmax is the characteristic diameter of the water channels. So, the maximum radius of these water channels would be 35 Å which is well within the maximum distance of 40 Å up to which the RDFs are calculated. RDFs assume spherical symmetry and therefore features with radius of 35 Å can be detected for the maximum distance of RDF computation of 40 Å.
Please refer to the “Analysis Techniques” section for understanding calculation of water cluster distribution.
Supplementary Material
References
- Carrette L.; Friedrich K. A.; Stimming U. Fuel Cells - Fundamentals and Applications. Fuel Cells 2001, 1, 5–39. . [DOI] [PubMed] [Google Scholar]
- Skyllas-Kazacos M.; Chakrabarti M. H.; Hajimolana S. A.; Mjalli F. S.; Saleem M. Progress in Flow Battery Research and Development. J. Electrochem. Soc. 2011, 158, R55–R79. 10.1149/1.3599565. [DOI] [Google Scholar]
- Jang S. S.; Molinero V.; Çaǧın T.; Goddard W. A. III Nanophase-Segregation and Transport in Nafion 117 from Molecular Dynamics Simulations: Effect of Monomeric Sequence. J. Phys. Chem. B 2004, 108, 3149–3157. 10.1021/jp036842c. [DOI] [Google Scholar]
- Devanathan R.; Venkatnathan A.; Dupuis M. Atomistic Simulation of Nafion Membrane: I. Effect of Hydration on Membrane Nanostructure. J. Phys. Chem. B 2007, 111, 8069–8079. 10.1021/jp0726992. [DOI] [PubMed] [Google Scholar]
- Spry D. B.; Fayer M. D. Proton Transfer and Proton Concentrations in Protonated Nafion Fuel Cell Membranes. J. Phys. Chem. B 2009, 113, 10210–10221. 10.1021/jp9036777. [DOI] [PubMed] [Google Scholar]
- Gruger A.; Régis A.; Schmatko T.; Colomban P. Nanostructure of Nafion membranes at different states of hydration. Vib. Spectrosc. 2001, 26, 215–225. 10.1016/s0924-2031(01)00116-3. [DOI] [Google Scholar]
- Singhal N.; Datta A. Thickness Dependence of Acidity and Microstructure in Nafion Films. ChemistrySelect 2016, 1, 2277–2283. 10.1002/slct.201600189. [DOI] [Google Scholar]
- Patil Y. P.; Seery T. A. P.; Shaw M. T.; Parnas R. S. In Situ Water Sensing in a Nafion Membrane by Fluorescence Spectroscopy. Ind. Eng. Chem. Res. 2005, 44, 6141–6147. 10.1021/ie0491286. [DOI] [Google Scholar]
- Shih C.-J.; Lin S.; Sharma R.; Strano M. S.; Blankschtein D. Understanding the PH-Dependent Behavior of Graphene Oxide Aqueous Solutions: A Comparative Experimental and Molecular Dynamics Simulation Study. Langmuir 2012, 28, 235–241. 10.1021/la203607w. [DOI] [PubMed] [Google Scholar]
- Tanis I.; Karatasos K. Molecular Dynamics Simulations of Polyamidoamine Dendrimers and Their Complexes with Linear Poly(Ethylene Oxide) at Different PH Conditions: Static Properties and Hydrogen Bonding. Phys. Chem. Chem. Phys. 2009, 11, 10017–10028. 10.1039/b913986a. [DOI] [PubMed] [Google Scholar]
- Cui S.; Liu J.; Selvan M. E.; Keffer D. J.; Edwards B. J.; Steele W. V. A Molecular Dynamics Study of a Nafion Polyelectrolyte Membrane and the Aqueous Phase Structure for Proton Transport. J. Phys. Chem. B 2007, 111, 2208–2218. 10.1021/jp066388n. [DOI] [PubMed] [Google Scholar]
- Karo J.; Aabloo A.; Thomas J. O.; Brandell D. Molecular Dynamics Modeling of Proton Transport in Nafion and Hyflon Nanostructures. J. Phys. Chem. B 2010, 114, 6056–6064. 10.1021/jp903288y. [DOI] [PubMed] [Google Scholar]
- Urata S.; Irisawa J.; Takada A.; Shinoda W.; Tsuzuki S.; Mikami M. Molecular Dynamics Simulation of Swollen Membrane of Perfluorinated Ionomer. J. Phys. Chem. B 2005, 109, 4269–4278. 10.1021/jp046434o. [DOI] [PubMed] [Google Scholar]
- Goddard W.; Merinov B.; van Duin A.; Jacob T.; Blanco M.; Molinero V.; Jang S. S.; Jang Y. H. Multi-Paradigm Multi-Scale Simulations for Fuel Cell Catalysts and Membranes. Mol. Simul. 2006, 32, 251–268. 10.1080/08927020600599709. [DOI] [Google Scholar]
- Jorn R.; Savage J.; Voth G. A. Proton Conduction in Exchange Membranes across Multiple Length Scales. Acc. Chem. Res. 2012, 45, 2002–2010. 10.1021/ar200323q. [DOI] [PubMed] [Google Scholar]
- Devanathan R.; Idupulapati N.; Baer M. D.; Mundy C. J.; Dupuis M. Ab Initio Molecular Dynamics Simulation of Proton Hopping in a Model Polymer Membrane. J. Phys. Chem. B 2013, 117, 16522–16529. 10.1021/jp410229u. [DOI] [PubMed] [Google Scholar]
- Sondheimer S. J.; Bunce N. J.; Lemke M. E.; Fyfe C. A. Acidity and Catalytic Activity of Nafion-H. Macromolecules 1986, 19, 339–343. 10.1021/ma00156a016. [DOI] [Google Scholar]
- Kreuer K. D. On the Development of Proton Conducting Polymer Membranes for Hydrogen and Methanol Fuel Cells. J. Membr. Sci. 2001, 185, 29–39. 10.1016/s0376-7388(00)00632-3. [DOI] [Google Scholar]
- Paddison S. J.; Elliott J. A. Molecular Modeling of the Short-Side-Chain Perfluorosulfonic Acid Membrane. J. Phys. Chem. A 2005, 109, 7583–7593. 10.1021/jp0524734. [DOI] [PubMed] [Google Scholar]
- Venkatnathan A.; Devanathan R.; Dupuis M. Atomistic Simulations of Hydrated Nafion and Temperature Effects on Hydronium Ion Mobility. J. Phys. Chem. B 2007, 111, 7234–7244. 10.1021/jp0700276. [DOI] [PubMed] [Google Scholar]
- Sengupta S.; Lyulin A. V. Molecular Dynamics Simulations of Substrate Hydrophilicity and Confinement Effects in Capped Nafion Films. J. Phys. Chem. B 2018, 122, 6107–6119. 10.1021/acs.jpcb.8b03257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun H.; Mumby S. J.; Maple J. R.; Hagler A. T. An Ab Initio CFF93 All-Atom Force Field for Polycarbonates. J. Am. Chem. Soc. 1994, 116, 2978–2987. 10.1021/ja00086a030. [DOI] [Google Scholar]
- Sun H. COMPASS: An ab Initio Force-Field Optimized for Condensed-Phase ApplicationsOverview with Details on Alkane and Benzene Compounds. J. Phys. Chem. B 1998, 102, 7338–7364. 10.1021/jp980939v. [DOI] [Google Scholar]
- Materials Studio, version 7.0; Accelrys Inc.: San Diego, CA, 2013.
- Tripathy M.; Kumar P. B. S.; Deshpande A. P. Molecular Structuring and Percolation Transition in Hydrated Sulfonated Poly(ether ether ketone) Membranes. J. Phys. Chem. B 2017, 121, 4873–4884. 10.1021/acs.jpcb.7b01045. [DOI] [PubMed] [Google Scholar]
- Zhang R.; Duan X.; Ding M.; Shi T. Molecular Dynamics Simulation of Salt Diffusion in Polyelectrolyte Assemblies. J. Phys. Chem. B 2018, 122, 6656–6665. 10.1021/acs.jpcb.8b02644. [DOI] [PubMed] [Google Scholar]
- Sengupta S.; Pant R.; Komarov P.; Venkatnathan A.; Lyulin A. V. Atomistic Simulation Study of the Hydrated Structure and Transport Dynamics of a Novel Multi Acid Side Chain Polyelectrolyte Membrane. Int. J. Hydrogen Energy 2017, 42, 27254–27268. 10.1016/j.ijhydene.2017.09.078. [DOI] [Google Scholar]
- Sunda A. P.; Venkatnathan A. Atomistic Simulations of Structure and Dynamics of Hydrated Aciplex Polymer Electrolyte Membrane. Soft Matter 2012, 8, 10827–10836. 10.1039/c2sm26561c. [DOI] [Google Scholar]
- Humphrey W.; Dalke A.; Schulten K. VMD: Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- Deserno M.How to Calculate a Three-Dimensional g(r) under Periodic Boundary Conditions. https://www.cmu.edu/biolphys/deserno/pdf/gr_periodic.pdf, (accessed Feb 14, 2019).
- Kohlmeyer A.VMD-L Mailing List. https://www.ks.uiuc.edu/Research/vmd/mailing_list/vmd-l/24654.html, (accessed Feb 14, 2019).
- Hasmy A.; Foret M.; Anglaret E.; Pelous J.; Vacher R.; Jullien R. Small-Angle Neutron Scattering of Aerogels: Simulations and Experiments. J. Non-Cryst. Solids 1995, 186, 118–130. 10.1016/0022-3093(95)00046-1. [DOI] [Google Scholar]
- Stukowski A. Visualization and Analysis of Atomistic Simulation Data with OVITO-the Open Visualization Tool. Modell. Simul. Mater. Sci. Eng. 2010, 18, 015012. 10.1088/0965-0393/18/1/015012. [DOI] [Google Scholar]
- Pan Z.; Chen J.; Lü G.; Geng Y.-Z.; Zhang H.; Ji Q. An Ab Initio Molecular Dynamics Study on Hydrogen Bonds between Water Molecules. J. Chem. Phys. 2012, 136, 164313. 10.1063/1.4705371. [DOI] [PubMed] [Google Scholar]
- Kuo I.-F. W.; Mundy C. J. An Ab Initio Molecular Dynamics Study of the Aqueous Liquid-Vapor Interface. Science 2004, 303, 658–660. 10.1126/science.1092787. [DOI] [PubMed] [Google Scholar]
- Damasceno Borges D.; Franco A. A.; Malek K.; Gebel G.; Mossa S. Inhomogeneous Transport in Model Hydrated Polymer Electrolyte Supported Ultrathin Films. ACS Nano 2013, 7, 6767–6773. 10.1021/nn401624p. [DOI] [PubMed] [Google Scholar]
- Devanathan R.; Venkatnathan A.; Dupuis M. Atomistic Simulation of Nafion Membrane. 2. Dynamics of Water Molecules and Hydronium Ions. J. Phys. Chem. B 2007, 111, 13006–13013. 10.1021/jp0761057. [DOI] [PubMed] [Google Scholar]
- Brunne R. M.; Liepinsh E.; Otting G.; Wüthrich K.; van Gunsteren W. F. Hydration of Proteins. J. Mol. Biol. 1993, 231, 1040–1048. 10.1006/jmbi.1993.1350. [DOI] [PubMed] [Google Scholar]
- Hubert M.; Van der Veeken S. Outlier Detection for Skewed Data. J. Chemom. 2008, 22, 235–246. 10.1002/cem.1123. [DOI] [Google Scholar]
- Morris D. R.; Sun X. Water-Sorption and Transport Properties of Nafion 117 H. J. Appl. Polym. Sci. 1993, 50, 1445–1452. 10.1002/app.1993.070500816. [DOI] [Google Scholar]
- Takamatsu T.; Eisenberg A. Densities and Expansion Coefficients of Nafion Polymers. J. Appl. Polym. Sci. 1979, 24, 2221–2235. 10.1002/app.1979.070241102. [DOI] [Google Scholar]
- Elliott J. A.; Paddison S. J. Modelling of Morphology and Proton Transport in PFSA Membranes. Phys. Chem. Chem. Phys. 2007, 9, 2602–2618. 10.1039/b701234a. [DOI] [PubMed] [Google Scholar]
- Linegar K. L.; Adeniran A. E.; Kostko A. F.; Anisimov M. A. Hydrodynamic Radius of Polyethylene Glycol in Solution Obtained by Dynamic Light Scattering. Colloid J. 2010, 72, 279–281. 10.1134/s1061933x10020195. [DOI] [Google Scholar]
- Devanathan R.; Venkatnathan A.; Rousseau R.; Dupuis M.; Frigato T.; Gu W.; Helms V. Atomistic Simulation of Water Percolation and Proton Hopping in Nafion Fuel Cell Membrane. J. Phys. Chem. B 2010, 114, 13681–13690. 10.1021/jp103398b. [DOI] [PubMed] [Google Scholar]
- Schmidt-Rohr K.; Chen Q. Parallel Cylindrical Water Nanochannels in Nafion Fuel-Cell Membranes. Nat. Mater. 2008, 7, 75–83. 10.1038/nmat2074. [DOI] [PubMed] [Google Scholar]
- Perrin J.-C.; Lyonnard S.; Volino F. Quasielastic Neutron Scattering Study of Water Dynamics in Hydrated Nafion Membranes. J. Phys. Chem. C 2007, 111, 3393–3404. 10.1021/jp065039q. [DOI] [Google Scholar]
- Dutta K.; Kumar P.; Das S.; Kundu P. P. Utilization of Conducting Polymers in Fabricating Polymer Electrolyte Membranes for Application in Direct Methanol Fuel Cells. Polym. Rev. 2014, 54, 1–32. 10.1080/15583724.2013.839566. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.