Abstract
As a bubble-based ablative therapy, the efficacy of histotripsy has been demonstrated in healthy or acutely diseased models. Chronic conditions associated with stiff tissues may require additional bubble activity prior to histotripsy liquefaction. In this study, histotripsy pulses were generated in agarose phantoms of Young’s moduli ranging from 12.3 to 142 kPa, and in vitro clot models with mild and strong platelet-activated retraction. Bubble cloud emissions were tracked with passive cavitation imaging, and the threshold acoustic power associated with phantom liquefaction was extracted with receiver operator characteristic analysis. The power of histotripsy-generated emissions and the degree of liquefaction were tabulated for both clot models. For the agarose phantoms, the acoustic power associated with liquefaction increased with Young’s modulus. When grouped based on agarose concentration, only two arms displayed a significant difference in the liquefaction threshold acoustic power (22.1 kPa versus 142 kPa Young’s modulus). The bubble cloud dynamics tracked with passive cavitation imaging indicated no strong changes in the bubble dynamics based on the phantom stiffness. For identical histotripsy exposure, the power of acoustic emissions and degree of clot lysis did not vary based on the clot model. Overall, these results indicate that a fixed threshold acoustic power mapped with passive cavitation imaging can be utilized for predicting histotripsy liquefaction over a wide range of tissue stiffness.
Keywords: focused ultrasound, histotripsy, passive cavitation imaging, phantom, deep vein thrombosis
Introduction
Histotripsy is an ablative ultrasound therapy under development for the treatment of several pathological conditions (Khokhlova et al 2015). Tissue is liquefied not as a direct result of the incident pulse, but due to the nucleation and resultant mechanical action of bubble clouds (Xu et al 2004). The type of mechanical activity that can be initiated is dependent on the type of histotripsy pulse (Bader et al 2019b). For shock-scattering histotripsy, a bubble cloud is formed when the nonlinear, multi-cycle pulse scatters from a microbubble activated within the focal zone (Maxwell et al 2011). Expansion of bubbles within the focal zone imparts lethal strain on the surrounding cellular and extracellular tissue components (Vlaisavljevich et al 2016, Bader 2018). Pre-clinical studies have demonstrated the efficacy of histotripsy ablation for heathy tissues (Khokhlova et al 2015). Chronically pathologic tissue, including deep vein thrombosis (Hirsh and Hoak 1996), is stiff compared to heathy tissue (Samani et al 2007, Duck et al 2013). The medium stiffness can have a significant influence on histotripsy-induced bubble dynamics (Vlaisavljevich et al 2015, Bader 2018), and therefore ablation efficacy. Thus, it is important to understand the influence of medium stiffness on the bubble cloud activity necessary for uniform tissue liquefaction.
Passive cavitation imaging (PCI) maps the power of acoustic emissions generated by the mechanical oscillations of bubbles (Gyöngy et al 2008, Salgaonkar et al 2009). Previous studies have employed passive ultrasound imaging techniques to monitor thermal ablation with focused ultrasound (Jensen et al 2012, Arvanitis and McDannold 2013, Haworth et al 2015), ultrasound-mediated drug delivery (Choi et al 2014, Coviello et al 2015, Kwan et al 2015, Haworth et al 2016), histotripsy bubble clouds (Gateau et al 2011), and clot liquefaction with histotripsy (Bader et al 2016b). In a recent study, PCI provided a better predictor for histotripsy liquefaction than plane wave B-mode hyperechogenicity in a tissue-mimicking phantom with a fixed stiffness (Bader et al 2018).
The objective of this study was to determine the medium stiffness dependence of the bubble cloud activity necessary for liquefaction in vitro. Acoustic emissions generated by histotripsy-induced bubble clouds in agarose phantoms of varied Young’s moduli were processed to form passive cavitation images. Additionally, the bubble cloud grayscale was also tracked with plane wave B-mode images. The threshold acoustic emissions or grayscale for phantoms were assessed via receiver operating characteristic (ROC) curve analysis. Bubble activity was also assessed in clots formed in vitro with varying degrees of retraction, and therefore varying clot stiffnesses (Mercado-Shekhar et al 2018). The degree of clot liquefaction was assessed histologically, and the power of bubble cloud emissions generated by the histotripsy pulse was recorded. Finally, an analytic model developed by Bader (2018) was utilized to assess the influence of medium stiffness on histotripsy-induced bubble expansion for the conditions considered in this study.
Methods and materials
Porcine red blood cell phantom preparation
Red blood cell phantoms composed of alternating layers of agarose and porcine red blood cell/agarose mixtures were manufactured following Maxwell et al (2010). Briefly, 50 ml of unspecified CPD porcine blood was obtained from a commercial vendor (Lampire, Pipersville, PA) and centrifuged at 3000 RPM for 10 min. The plasma and buffy coat supernatant were removed, leaving behind a volume of red blood cells. Agarose powder (1.48, 2.00, 3.60, 4.00, or 5.80 g) and 3.6 g NaCl (Sigma-Aldrich, St. Louis, MO, USA) were dissolved into 400 ml of 0.2 μm filtered, deionized water by heating in a microwave (700 W power) in 30 s increments until clear. The resulting concentrations of agarose reported in w/v (g/ml) were 0.37%, 0.50%, 0.90%, 1.00%, and 1.45%. The agarose mixture was then transferred to an ultrasonic cleaning bath heated to 55 °C while continuously evacuating (50 kPa) over the course of 30 min. After degassing, approximately 47 ml of the agarose mixture was poured into a rectangular acrylic phantom mold and allowed to solidify. A 5% v/v red blood cell/agarose mixture was pipetted onto the solidified agarose slab to form a layer approximately 500 μm thick. This process was repeated to generate three red blood cell layers separated by 1.5 cm, after which the phantom was placed in a 4 °C refrigerator overnight.
Human blood clot phantom production
Human whole blood clots were manufactured following an established protocol (Sutton et al 2013, Mercado-Shekhar et al 2018). After local institutional review board approval and informed written consent, venous human whole blood was drawn from five patients undergoing invasive catheterization procedures at the University of Chicago Medicine cardiac catheterization laboratory (patient demographics in table 1). Patients on medications that would alter the clotting cascade (e.g. platelet inhibitors, etc) were screened out of the study a priori. Blood aliquots of 2 ml were transferred to Pasteur pipettes composed of either borosilicate or flint glass (14.6 cm length, 2 ml capacity, Fisher Scientific, Hanover Park, IL, USA) to produce clots of high or mild retraction, respectively (Sutton et al 2013, Mercado-Shekhar et al 2018). The pipettes were submerged in a water bath at 37 °C for 3 h, and allowed to retract over the course of three days at 4 °C. After three days, the clots were suspended in a 2% w/v low-gelling temperature agarose (product number A0701, Sigma-Aldrich, St. Louis, MO, USA) prior to histotripsy insonation, or retained for assessment of elastic properties.
Table 1.
Demographics for the five patients from whom blood was drawn.
| Clot number | Sex | Age | Race |
|---|---|---|---|
| 1 | F | 61 | African American |
| 2 | F | 72 | White |
| 3 | M | 77 | African American |
| 4 | M | 64 | White |
| 5 | M | 56 | White |
Young’s modulus measurements
The Young’s modulus of each phantom layer was determined with a shear-wave elastography imaging sequence using an L11–4v imaging array (Verasonics, Inc., Kirkland, WA, USA) driven by a research ultrasound system (Vantage 128, Verasonics, Inc. Kirkland, WA, USA) (Nightingale 2011). Images were processed offline as described by Deng et al (2017) to assess the shear wave speed. The Young’s modulus was related to the shear wave speed assuming an isotropic material:
| (1) |
where S is the shear wave speed, E is the elastic or Young’s modulus, and ρ is the density.
The shear wave elastography ultrasound sequence was compared to measured stiffnesses of agarose phantoms with a dynamic mechanical analyzer (DMA) (RSA-G2, TA Instruments, New Castle, DE, USA). Uniform cylindrical phantoms of varying concentrations of agarose were made for this dynamic mechanical analysis. The test comprised a uniaxial stress–strain compression measurement assuming cylindrical geometry with a constant linear compression rate of 0.02 mm s−1. Stress–strain data were analyzed using commercial software (Trios, TA Instruments, New Castle, DE, USA). The linear slope of the stress–strain curves was reported as the Young’s modulus. Over the range of stiffnesses considered (12.3–142 kPa) the two measurements agreed on average within 15 kPa. Soft tissues such as lung, fat, muscle, prostate and kidney have Young’s moduli ranging from 1 to 30 kPa (Duck 1990, Vlaisavljevich et al 2014, Liu et al 2015, Glybochko et al 2016). Diseased pathologies such as chronic thrombus can be considerably stiffer than healthy tissues due to the infiltration of calcification and collagen (Czaplicki et al 2017).
In comparison to the red blood cell layers, the clot specimen have a finite area whose assessment of stiffness may be confounded by the shear wave elastography technique. Therefore, the stiffness of clots formed from each donor’s blood were assessed via the dynamic mechanical analysis protocol as outlined above. For each donor, the Young’s modulus was measured on three clots (n = 15 total for each clot type).
Histotripsy insonation
A 1 MHz annular array with a 10 cm aperture and a 9 cm focal length was used to generate histotripsy pulses (Imasonic, Voray sur l’Ognon, France). Each element was driven in parallel by a custom-built class D amplifier and matching network (Hall 2006). A total of 4000 histotripsy pulses of 5 μs duration were delivered to each phantom layer or clot location at a pulse repetition frequency (PRF) of 100 Hz (20 ms total histotripsy exposure time). The focal peak negative pressure of the pulse was 12, 18, or 24 MPa for phantom studies (Bader and Holland 2016). These acoustic parameters conditions are consistent with previous studies that successfully generated bubble activity via shock scattering histotripsy pulses (Maxwell et al 2011, Vlaisavljevich et al 2014, 2016, Darnell et al 2015, Khokhlova et al 2015, Mancia et al 2017, Zhang et al 2017, Bader et al 2018). For the pulse repetition frequency utilized here, bubble clouds will likely persist between the application of pulses (Wang et al 2012, Bader et al 2019a). For the clot study, a fixed peak negative pressure of 18 MPa was employed.
Passive cavitation and plane wave B-mode imaging
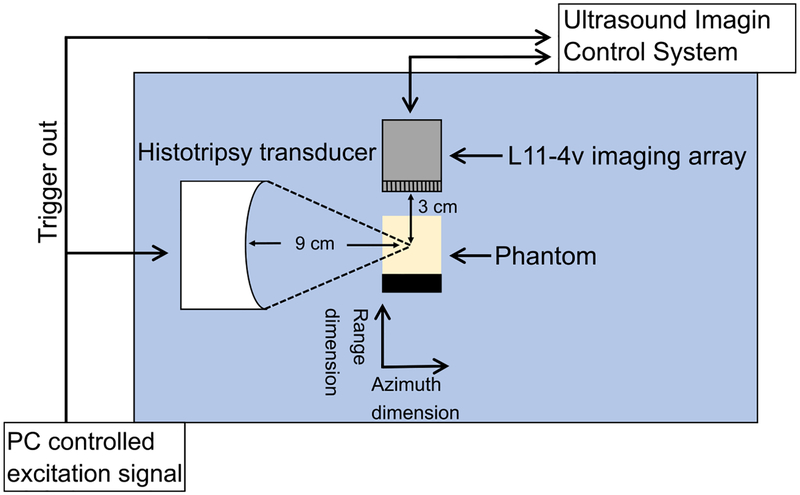
Passive cavitation images were used to map the power of acoustic emissions generated by histotripsy-induced bubble clouds. Emissions were passively recorded during the histotripsy insonation with a 128-element L11–4v imaging array connected to an ultrasound research scanner (Vantage 128, Verasonics, Inc., Kirkland, WA, USA). The imaging array was oriented to monitor cavitation activity along the acoustic axis of the histotripsy transducer (azimuthal axis of the imaging array, figure 1). The received passive cavitation waveforms were processed offline with a frequency-domain delay, sum, and integrate beamformer (Haworth et al 2017). A cosine apodization function was applied a priori to the steered spectra prior to integration. To assess bubble cloud echogenicity, the same imaging array was employed to acquire plane wave B-mode images 1 ms following the histotripsy excitation (Szabo 2014). The delay duration was chosen to minimize constructive interference between the imaging and therapy pulses (Bader et al 2018). All elements of the array were excited in parallel to generate the plane wave imaging pulse. The peak negative pressure of the plane wave B-mode imaging pulse was 420 kPa in the histotripsy focal zone, as assessed with a needle hydrophone (HNP-0400, Onda Corporation, Sunnyvale, CA, USA). Due to the data transfer acquisition rate, passive cavitation and plane wave images were acquired every 10th histotripsy pulse (10 Hz acquisition rate, 400 total frames per data set). For a given data set, the acoustic power or grayscale was summed pixel-wise across all frames to generate cumulative passive cavitation or plane wave images, respectively.
Figure 1.
Side view of the experimental set up for histotripsy insonation of the agarose phantom, or the clot embedded in the agarose phantom. The L11–4v imaging array was oriented to monitor bubble cloud activity along the azimuthal axis of the histotripsy source.
Experimental protocol
Phantoms were degassed for two hours in an isotonic solution at a partial pressure of 50 kPa, after which they were affixed to a three-axis position system (Thorlabs Inc. Newton, New Jersey, United States) immersed in a tank of degassed (20% dissolved oxygen), filtered (10 μm pore size) deionized water, as noted in figure 1. The distance between the histotripsy focus and the imaging array was fixed at 3 cm. The histotripsy source focal location was determined in the imaging plane by visualizing bubble cloud generation in degassed water. Once located, the focus was then positioned at a depth of 2 cm into the phantom along one of the red blood cell layers (three layers per phantom). For each phantom, the exposure conditions were randomized for each layer. For clot samples, test pulses were applied to locations lateral (into or out of page for figure 1) to the target zone to ensure uniform bubble activity within the clot. In total, 75 liquefaction zones were generated in 25 different phantoms, and 30 liquefaction zones were generated in ten clots.
Phantom liquefaction and bubble dynamics analysis
After insonification, the phantoms were sectioned and photographed with a DSLR camera (Nikon D3400, 24 MP resolution, Minato, Tokyo, Japan) to visualize liquefaction. Gross images were converted to grayscale and segmented using a grayscale thresholding algorithm (Otsu 1979) to delineate liquefied and intact regions. Cumulative passive cavitation and plane wave B-mode images were co-registered with the gross phantom observation using a custom geometric transformation in MATLAB based on hyperechoic nylon filaments embedded in the phantom (figure 2). Receiver operator characteristic (ROC) analysis was performed to compare passive cavitation and plane wave B-mode images to gross observation of the phantom. The analysis was performed for all pixels in the image at a fixed depth location of 30 mm. Data was only analyzed across this central line due to the documented limited range resolution of the delay, sum, and integrate beamformer for a linear array geometry (see bottom panel, figure 2) (Haworth et al 2017).
Figure 2.
(a) The blue colormap overlay represents the PCI power registered with processed phantom image. The liquefaction zone is outlined in yellow. The phantom image was analyzed along the entire azimuth through the liquefaction zone (black dashed line) (b) comparison of PCI acoustic power and plane wave B-mode image grayscale along the dashed line in panel (a) and binary phantom image. For the phantom, values of 1 indicate liquefaction, and values of 0 indicate intact phantom. The histotripsy pulse was propagating from left to right in the image. The geometric focal distance of the source is 90 mm.
The delay, sum, and integrate beamforming algorithm used to form the passive cavitation images in this study is diffraction limited (Haworth et al 2017, Anthony et al 2019), causing emission artifacts along the range dimension for a linear imaging array. For this reason, pixels corresponding to a fixed range depth of 30 mm were employed to calculate ROC statistics. For the ROC analysis, a pixel was assigned true positive (false positive) when it corresponded to a location with liquefied phantom and the acoustic power or grayscale value was greater than (less than) a pre-defined threshold value. A pixel was assigned a true negative (false negative) value when it corresponded to intact phantom and the acoustic power or grayscale value was less than (greater than) a pre-defined threshold value (Jensen et al 2012, Haworth et al 2015) (figure 2(b)). The optimal liquefaction classification based on grayscale or acoustic power was extracted from the ROC curve at the point following Zweig and Campbell (1993) for each phantom.
For each phantom layer, the area of the liquefaction zone was tabulated. To quantify the histotripsy bubble dynamics, the maximum pixel value (i.e. acoustic power or grayscale) and the azimuthal location of the maximum pixel were extracted for each data set. Differences in these values were assessed via a one-way analysis of variance test utilizing a Bonferroni correction.
Blood clot analysis
Following histotripsy exposure, agarose/clot samples were stained with hematoxylin and eosin (H&E) to identify locations of clot liquefaction. Scanned processed slides were assessed via Otsu’s method (Otsu 1979) to identify intact and ablated clot. During processing, agarose and liquefied clot sections lost their in situ orientation which prohibited registration of processed sections with passive cavitation or plane wave images. Therefore, qualitative analysis was performed of the influence of clot structure on histotripsy ablation. The degree of clot liquefaction was computed as:
| (2) |
where AT is the area of the residual, treated clot, and AC is the area adjacent to the histotripsy focal zone (i.e. control sample). A one-sample Student’s t-test was used to test if clot loss was significantly greater than 0% (a fully intact clot). The averaged acoustic power or grayscale of the bubble cloud within the clot was assessed with passive cavitation or plane wave imaging, respectively. Clot area loss and averaged acoustic power/grayscale were also analyzed via a paired-sample Student’s t-test for differences between clot types.
Statistical analysis
A one-way ANOVA multiple comparisons test using the Bonferroni method was applied to identify significant differences between phantom stiffnesses for maximum passive cavitation/plane wave B-mode values, the location of maximum passive cavitation/plane wave B-mode values, and liquefaction areas. The Pearson’s correlation coefficient and its level of statistical significance were calculated for passive cavitation and plane wave B-mode liquefaction threshold values as a function of phantom stiffness. The area under the curve was tabulated for each arm, and the significance relative to 0.5 (i.e. guessing) was determined according to DeLong et al (1988). The sensitivity, specificity, positive predictive value, and negative predictive value were extracted from the ROC curve at the optimal operating point. Paired-sample t-tests were used to test for significant differences in clot metrics (area loss, area-averaged plane wave B-mode value, and area-averaged acoustic emissions) between clot types.
Analytic model
The maximum size of a bubble nucleus exposed to a shocked histotripsy pulse of one cycle duration in an elastic medium can be computed as (Bader 2018):
| (3) |
where P0 is the ambient pressure of the medium (0.1 MPa) and ρ is the fluid density (1000 kg m−3). The parameters ξ and τ incorporate the effects of surface tension, viscosity, and medium inertia (Holland and Apfel 1989). The medium stiffness is also incorporated into these terms assuming a Kelvin–Voight model, which has been validated for soft tissues in the 3–13 MHz range (Madsen et al 1983). The initial bubble radius R0 was set to 20 nm, which will provide an upper estimate to the maximum bubble size (Bader and Holland 2016). For a shock-scattering pulse, the effective pressure, pEFF, can be defined as the magnitude of the peak negative pressure, |pN|(Bader and Holland 2016).
Results
Phantom liquefaction
For all insonation conditions, phantom liquefaction was initiated (figure 3(a)). The liquefaction zone was continuous, resembling a tadpole shape with a large head and a tail that narrows distally (Haworth et al 2015, Bader et al 2018). For a given phantom stiffness, the liquefaction area increased with peak negative pressure of the histotripsy pulse (p < 0.05). The area of liquefaction was independent of the phantom Young’s modulus for a given peak negative pressure of the histotripsy pulse (p > 0.05) (figure 4).
Figure 3.
(a) Phantom liquefaction zone (white) generated by histotripsy insonation. (b) Comparison of co-registered plane wave B-mode image (black and white colormap overlay) and processed phantom image. (c) Comparison of co-registered PCI and processed phantom image. Both the passive cavitation and plane wave B-mode images were summed over the duration of the histotripsy insonation to create cumulative images. For panels (b) and (c), the liquefaction zone borders are outlined in yellow. The histotripsy pulse (24 MPa peak negative pressure) propagated from left to right in the image. The bar in the lower left corner of each image corresponds to 1 mm.
Figure 4.
Area of phantom liquefaction as a function of peak negative pressure and phantom stiffness. No significant differences were observed between liquefaction areas for a given peak negative pressure.
Correlation of imaging with phantom liquefaction
The resulting ROC curves comparing the ability of plane wave B-mode image (grayscale) or PCI (acoustic power) to predict the phantom liquefaction zone are shown in figure 5. For each phantom stiffness, the area under the ROC curve (AUROC) was significantly greater than 0.5 for both plane wave and PCI. The AUROC generally increased with increasing stiffness.
Figure 5.
Receiver operator characteristic curve across stiffnesses for plane wave B-mode imaging (left) and PCI (right). The legend applies for both sub-figures and denotes the Young’s modulus for each phantom.
Statistics extracted from the ROC curves at the optimal operating point (e.g. AUROC, sensitivity, specificity, accuracy, positive predictive value, and negative predictive value) are shown in table 2. The predictive ability of passive cavitation and plane wave B-mode imaging for phantom liquefaction were similar for most categories. A strong increase in liquefaction sensitivity was observed with the phantom stiffness, from 0.512 to 0.877 for plane wave B-mode imaging and from 0.582 to 0.915 for PCI.
Table 2.
Comparison of statistics extracted from receiver operator characteristics for plane wave B-mode (top) and (PCI, bottom) grouped by stiffness (all peak negative pressures), including the area under the receiver operator characteristic (AUROC), accuracy, sensitivity, specificity, positive predictive value (PPV), and negative predictive value.
| B-mode | ||||||
|---|---|---|---|---|---|---|
| Young’s modulus | AUROC | Accuracy | Sensitivity | Specificity | PPV | NPV |
| 12.3 ± 3.7 kPa | 0.940 ± 0.041 | 0.939 ± 0.020 | 0.512 ± 0.181 | 0.990 ± 0.007 | 0.845 ± 0.126 | 0.945 ± 0.020 |
| 22.1 ± 7.7 kPa | 0.975 ± 0.027 | 0.963 ± 0.018 | 0.772 ± 0.209 | 0.986 ± 0.006 | 0.858 ± 0.025 | 0.974 ± 0.024 |
| 65.3 ± 8.5 kPa | 0.976 ± 0.012 | 0.968 ± 0.009 | 0.718 ± 0.071 | 0.992 ± 0.005 | 0.891 ± 0.057 | 0.974 ± 0.009 |
| 85.8 ± 11.9 kPa | 0.982 ± 0.015 | 0.972 ± 0.016 | 0.698 ± 0.328 | 0.994 ± 0.005 | 0.948 ± 0.048 | 0.975 ± 0.015 |
| 142 ± 22 kPa | 0.993 ± 0.006 | 0.986 ± 0.006 | 0.877 ± 0.036 | 0.995 ± 0.003 | 0.935 ± 0.034 | 0.990 ± 0.004 |
| PCI | ||||||
| Young’s modulus | AUROC | Accuracy | Sensitivity | Specificity | PPV | NPV |
| 12.3 ± 3.7 kPa | 0.958 ± 0.021 | 0.948 ± 0.015 | 0.582 ± 0.090 | 0.991 ± 0.006 | 0.884 ± 0.094 | 0.952 ± 0.010 |
| 22.1 ± 7.7 kPa | 0.958 ± 0.026 | 0.959 ± 0.014 | 0.657 ± 0.098 | 0.993 ± 0.003 | 0.918 ± 0.028 | 0.962 ± 0.014 |
| 65.3 ± 8.5 kPa | 0.985 ± 0.007 | 0.978 ± 0.004 | 0.799 ± 0.033 | 0.994 ± 0.004 | 0.929 ± 0.044 | 0.982 ± 0.003 |
| 85.8 ± 11.9 kPa | 0.980 ± 0.011 | 0.967 ± 0.006 | 0.727 ± 0.117 | 0.992 ± 0.007 | 0.886 ± 0.145 | 0.972 ± 0.012 |
| 142 ± 22 kPa | 0.994 ± 0.006 | 0.991 ± 0.005 | 0.915 ± 0.055 | 0.998 ± 0.002 | 0.968 ± 0.026 | 0.993 ± 0.006 |
The optimal operating point on the ROC curve used to determine the threshold acoustic power or grayscale for phantom liquefaction is reported in figure 6. No trend was observed in the grayscale value with the phantom stiffness (p > 0.05), and there was no difference in the threshold when grouped by agarose concentration. For PCI, a weak but significant trend was observed in the acoustic power threshold for phantom liquefaction (ρ = 0.522, p = 0.01). When grouped by agarose concentration, only two arms displayed a significant difference in the liquefaction threshold based on acoustic power (142 and 22.1 kPa, figure 6).
Figure 6.
(Top) Plane wave B-mode grayscale and (bottom) PCI acoustic power liquefaction threshold as a function of Young’s modulus. Circles denote thresholds for individual phantoms, and squares denote the average for a given concentration of agarose. The legend is the same for both panels. The bar with asterisk denotes a significant difference between threshold values for different stiffness groups.
Phantom bubble cloud activity
Within the liquefaction zone, bubble cloud activity indicated by hyperechogenicity and acoustic emissions was observed for all experimental conditions (figures 3(b) and (c)). For the 12 MPa peak negative pressure histotripsy exposures, bubble activity was noted to be more sporadic than for larger peak negative pressure pulses. Limited trends were observed between the bubble cloud activity and the phantom stiffness. For a given peak negative pressure, no significant difference was observed in peak acoustic power or peak grayscale value across stiffnesses except in two instances, as noted in figure 7 (grayscale values generated in phantoms with 12.3 kPa and 142 kPa Young’s modulus for the 12 MPa peak negative pressure insonations, and acoustic emissions generated in phantoms with 22.1 and 142 kPa Young’s modulus for the 18 MPa peak negative pressure insonations).
Figure 7.
(Left) Maximum plane wave B-mode grayscale and (right) maximum PCI acoustic power as a function of peak negative pressure and stiffness. Asterisk with bar denotes statistically significant difference between the maxima of two stiffnesses within a pressure group. The legend denoting phantom stiffness is the same for both panels.
The azimuthal positions of the maximum bubble cloud emissions and maximum plane wave B-mode values were independent of the phantom stiffness for a given peak negative pressure of the histotripsy pulse (figure 8). For a given phantom stiffness, the location of maximum bubble cloud emissions shifted closer to the histotripsy source as the peak negative pressure increased. The most hyperechoic portions of the bubble cloud were not dependent on the peak negative pressure of the histotripsy source.
Figure 8.
Azimuthal location of (left) plane wave B-mode grayscale and (right) PCI acoustic power maxima. Horizontal lines denote the median. Smaller values indicate positions closer to the histotripsy source while larger values indicate positions farther from the histotripsy source. The legend denotes phantom stiffness. The geometric focus corresponds to 90 mm.
In vitro clot histotripsy exposure
The Young’s modulus of mildly-retracted and well-retracted clots was found to be 2.94 ± 0.95 kPa and 4.26 ± 1.30 kPa, respectively. Histotripsy exposed sections of both clot models were characterized by a marked reduction in red blood cells and moderate reduction in the extent of the fibrin mesh and platelets (figure 9). There was no observed difference in the area of histotripsy ablation between the clot models (table 3) (p > 0.05).
Figure 9.
Hematoxylin and eosin stained clot sections. (a) Flint clot sample; (b) flint clot sample with passive cavitation image overlay; (c) borosilicate clot sample; (d) borosilicate clot sample with PCI overlay. The black bars denote a length of 1 mm. The histotripsy pulse propagated from left to right in the image. The black arrows mark representative areas of residual fibrin, and the green arrows mark areas of complete liquefaction. The purple areas outside of the clot in subfigures (a) and (b) are histological artifacts.
Table 3.
Clot area loss measured for flint clots and borosilicate clots, and area-averaged grayscale value and acoustic emissions contained within the clot. A clot loss of 0% signifies the clot was unaffected by the histotripsy pulse relative to control samples. Bold font indicates a significant difference between clot types.
| Clot type | Clot loss (% area) | Grayscale averaged over area (grayscale mm−2) | Emissions averaged over area (V2/μs mm2) |
|---|---|---|---|
| Flint glass | 32.8 ± 23.4 | 189 ± 9 | 9.59 × 107 ± 0.56 × 107 |
| Borosilicate glass | 33.1 ± 12.8 | 177 ± 17 | 9.15 × 107 ± 2.69 × 107 |
Strong bubble activity was noted inside the clot for all insonifications (figure 9). On occasion, bubble activity was also noted in the agarose surrounding the clot. The area-averaged power of acoustic emissions for bubble cloud activity within the clot cross section was not significantly different between the two models (p > 0.05). An increase in bubble cloud echogenicity was noted in the flint glass (mildly retracted) clots relative to the borosilicate glass (well retracted) clots (p < 0.05) (table 3).
In silico model
Analytic computations of the maximum bubble size as a function of the medium stiffness are shown in figure 10. As the medium stiffness increased beyond 20 MPa, the maximum bubble size decreased rapidly as a function of the Young’s modulus for a fixed peak negative pressure of the histotripsy pulse. For medium stiffnesses between 1 and 142 kPa (the range of phantom stiffness considered in this study), the maximum bubble size is predicted to decrease by 0.46%, 0.31%, and 0.23% at 12 MPa, 18 MPa, and 24 MPa peak negative pressure, respectively.
Figure 10.
Analytic computation for the maximum bubble diameter as a function of Young’s modulus and peak negative pressure.
Discussion
Liquefaction threshold dependence on material stiffness
In this study, the histotripsy bubble activity necessary for liquefaction was only mildly dependent on agarose stiffness. Over the Young’s modulus range 12.3–85.8 kPa, there was no change in the bubble activity necessary for phantom liquefaction. No change was observed in the degree of liquefaction for well and mildly-retracted clots, despite the variation in stiffness between the two models. These results are consistent with a previous study that found minimal changes in the degree of histotripsy-induced erosion over the range of Young’s moduli considered here (Vlaisavljevich et al 2014). The lack of change in the bubble dynamics for less-stiff phantoms may be in part due to the shocked pulses employed in this study. If the medium’s Young’s modulus is less than 1.5 MPa, analytic computations indicate the positive pressure of the shock wave has a larger influence on bubble expansion than the medium elastic properties (Bader 2018). The observations in this study may not extend to the intrinsic-threshold regime of histotripsy where the compressional phase of the acoustic excitation has little influence on the bubble dynamics (Maxwell et al 2013, Lin et al 2014).
Only two groups of phantoms displayed a significant difference in the emission threshold associated with liquefaction tracked with PCI (142 ± 22 kPa and 22.1 ± 7.7 kPa phantoms). A weak but significant correlation was noted between the phantom stiffness and the liquefaction threshold tracked with PCI (p < 0.05). These observations may reveal that the material stiffness has a mild influence on the overall outcome for histotripsy therapy over the range of Young’s moduli considered in these studies. Analytic calculations of bubble expansion indicated that the medium stiffness has a small, but observable, influence on the bubble dynamics (figure 10). The increase in liquefaction threshold with phantom stiffness may be a reflection of the ultimate tensile strength dependence on agarose concentration (Normand et al 2000, Barrangou et al 2006). The relationship between true tensile stress and agarose concentration has a steeper slope for low-frequency assessment than that observed here (1.2 slope for low frequency assessment of true strain (Normand et al 2000) versus agarose concentration in comparison to 0.5 for acoustic power liquefaction threshold versus agarose concentration observed here). The variation in slopes may reveal the difference in behavior of the agarose between the high strain rates induced by the microsecond time scale of the bubble cloud and the aforementioned low-frequency assessment of stress and strain.
It is important to make a distinction between the threshold peak negative pressure for bubble cloud nucleation and the acoustic emission threshold associated with liquefaction measured in this study. The peak negative pressure necessary for bubble cloud formation increases significantly over the Young’s modulus range of 1.5–38 kPa (Vlaisavljevich et al 2014). In contrast, the acoustic power threshold for phantom liquefaction did not change significantly for Young’s moduli less than 85.8 kPa in this study. The power of acoustic emissions can be taken as an indication of the bubble cloud mechanical activity. Previous studies have noted that the peak negative pressure threshold for bubble cloud nucleation is stiffness-dependent for shock scattering pulses (Vlaisavljevich et al 2014, 2015). The findings here indicate that, following nucleation, the degree of bubble cloud mechanical activity necessary for liquefaction is largely independent of the material stiffness.
Imaging modality for prediction of histotripsy liquefaction
The AUROC values were similar for passive cavitation and plane wave B-mode imaging, in contrast to previous observations (Jensen et al 2012), Bader et al 2018. The discrepancy between the two studies may in part be due to the experimental design. The current study used an agarose phantom with a thin red blood cell layer, whereas studies demonstrating better prediction of liquefaction with PCI utilized ex vivo liver or an evaporated milk phantom (Jensen et al 2012, Bader et al 2018). The latter materials are more attenuating compared to the agarose phantoms in this study which will reduce bubble cloud visualization on plane wave images (Szabo 2014, Bader et al 2016a). Medium attenuation also altered the shape of the structure of histotripsy bubble activity. Liquefaction zones appeared continuous in this study, whereas two disjoint zones were generated in the attenuating phantom (Bader et al 2018). A lower pulse repetition frequency was used in the previous study in comparison to this study (20 Hz versus 100 Hz), which would minimize the likelihood of persistent bubble clouds (Wang et al 2012). The application of histotripsy pulses at a high rate would initiate mechanical activity at discrete locations in the focal zone. While passive cavitation and plane wave B-mode imaging had similar predicative abilities in this phantom study, PCI maintains robust liquefaction prediction in clinically relevant attenuating media.
The strongest bubble cloud emissions tracked with PCI translated towards the acoustic source with increasing peak negative pressure of the histotripsy pulse. In contrast, no trend with pressure was observed with plane wave imaging in the position of the most hyperechoic portion of the bubble cloud. This observation is consistent with a previous study by Bader et al (2018). The discrepancy in trends may reflect the different features of bubble activity that each modality monitors. Plane wave B-mode imaging signifies the size and density of bubbles within the cloud (e.g. echogenicity), whereas PCI denotes the strength of bubble cloud mechanical oscillations. The observed trend in maximum pixel intensity position with peak negative pressure may also be reflective of the relative timing of image acquisition. Bubble cloud emissions used to form passive cavitation images were recorded during the histotripsy excitation. To avoid artifacts due to constructive interference between the imaging and therapy pulses, plane wave images were acquired 1 ms after the histotripsy excitation.
For both PCI and plane wave B-mode imaging, the AUROC and sensitivity for predicting phantom liquefaction increased with the Young’s modulus. The increased sensitivity to liquefaction can be attributed to a decrease in the number of false negatives with increasing phantom stiffness (figure 11). It is unknown why the false negatives decreased with the phantom stiffness. A more uniform distribution of acoustic emissions throughout the liquefaction zone would lead to a decrease in false negatives, although no strong changes are observed in the bubble cloud dynamics with the phantom stiffness (figures 7 and 8). Nevertheless, these data indicate both PCI and plane wave imaging are sensitive to the to the bubble activity associated with liquefaction of stiff tissues.
Figure 11.
Number of true positives, true negatives, false positives, and false negatives detected by plane wave B-mode (top) and PCI (bottom) as a function of Young’s modulus (blue dots) with a best fit line (red line). Only the PCI false negative trend (noted with asterisk) was significantly correlated with elasticity, with a Pearson’s correlation coefficient of −0.9230 (p < 0.05). There was no significant trend with plane wave B-mode imaging (p > 0.05).
Due to variant response of the agarose and clot, reliable registration between passive cavitation images and clot samples could not be performed. Therefore, qualitative parameters were extracted to gain insight on the bubble response in a varying stiffness tissue model. There was no difference in the clot loss metric or the area-averaged acoustic emissions between the clot models. This indicates that the degree of bubble cloud mechanical activity necessary for liquefaction is similar between the two clot models. A significant difference was observed in the area-averaged grayscale values between mildly and well-retracted clots (table 3).
The variation in bubble cloud echogenicity may be in part due to the structural differences between the clots, rather than a change in bubble dynamics. Indeed, a significant difference was observed in the clot stiffness between the two models, indicating structural differences which may be reflected as changes in echogenicity on the plane wave B-mode images. Chronic thrombi with collagen or calcifications would further alter the clot echogenicity (Rubin et al 2006), heightening the need for a medium-independent assessment of ablation with a modality like PCI.
Limitations
Agarose phantoms were used to provide consistent, specified mechanical and acoustic properties. However, there are important differences between agarose and tissue. Agarose phantoms were degassed prior to histotripsy exposure. Thus, the total amount of dissolved gases, and therefore bubble dynamics, within the agarose phantoms may not be representative of in vivo conditions (Bader and Bollen 2018). Likewise, the clots for this study were formed in vitro. While medium stiffness can be used as a criterion in delineating acute from chronic clots, the clotting cascade and formation of stiff, chronic thrombi is a complex process (Palta et al 2014, Czaplicki et al 2017). With the current in vitro model, there is neither fibroblast infiltration for collagen nor calcification present to model a chronic thrombus (Czaplicki et al 2017). Features of chronic clots should be investigated further.
The agarose gels employed in this study would not fully congeal for concentrations lower than 0.37% (w/v). Consequently, phantoms in this study had Young’s moduli greater than 12.3 ± 3.7 kPa, whereas the stiffness of soft tissues can be less than 1 kPa (Weickenmeier et al 2016). The propagation of shear waves could not be resolved with our system when the agarose concentration exceeded 1.45%, coincident with a phantom stiffness of 142 ± 22 kPa. Thus, stiff tissues such as arterial walls and mineralized samples (e.g. bone) were not modeled in this study (Duck 1990).
Ultrasound images and gross observations of liquefaction were analyzed in a 2D plane, whereas the liquefaction zone occupies a 3D volume. Furthermore, the range resolution of the delay, sum, and integrate algorithm is limited, and ROC curves were constructed based on phantom, passive cavitation, and plane wave B-mode data at a fixed range position. Future studies should consider a modified receiver geometry or an alternative beamforming algorithm for improved resolution of the passive cavitation image (O’Reilly et al 2014, Coviello et al 2015). The acoustic power or grayscale threshold for phantom liquefaction reported here will vary based on the array sensitivity and the depth of the histotripsy excitation. Such issues can be overcome with system-independent assessment of the acoustic power based on the element-by-element sensitivity (Rich and Mast 2015) or by com-pensating for the attenuation of the acoustic path (Gray and Coussios 2018). Current approaches to quantitate scattering also do not account for dense bubble clouds, such as those generated during histotripsy (Coviello et al 2015). In addition, the optimal operating points may vary between the phantom and living tissue due to differences in structural composition, and may be tissue specific.
In this study, phantom liquefaction occurred over the course of approximately 40 s (4000 pulses delivered at 100 Hz). This may be excessive for complete liquefaction of the focal zone. PCI in the future may be used to monitor cavitation emissions, which can then be used as a decision-making tool to determine the optimum treatment length. Preventing excessive liquefaction will reduce treatment time and mitigate off-target or critical structure damage.
Conclusion
In this study, histotripsy pulses were generated in agarose phantoms of Young’s moduli ranging from 12.3 to 142 kPa, and in vitro clot models with mild and strong platelet-activated retraction. PCI indicated there was a weak correlation between phantom stiffness and the degree of bubble cloud activity necessary for phantom liquefaction (figure 6). Minimal changes were observed in the bubble cloud dynamics, tracked with passive cavitation and plane wave imaging, with material stiffness (figures 7 and 8). Despite the variation in clot retraction, there was no change in the bubble cloud dynamics or degree of liquefaction between the two clot models. Overall, these results indicate that a fixed dose of bubble activity can be utilized to predict histotripsy liquefaction over a wide range of media stiffnesses.
Acknowledgments
Parts of this work were carried out at the Soft Matter Characterization Facility of the University of Chicago. The authors gratefully acknowledge the discussions of passive cavitation imaging with Kevin J. Haworth, and Adam D. Maxwell for his assistance calibrating the histotripsy source. This work was funded in part by the National Institutes of Health, Grant R01HL13334.
References
- Anthony GJ, Bollen V, Hendley S, Antic T, Sammet S and Bader KB 2019. Assessment of histotripsy-induced liquefaction with diagnostic ultrasound and magnetic resonance imaging in vitro and ex vivo Phys. Med. Biol 64 095023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arvanitis CD and McDannold N 2013. Integrated ultrasound and magnetic resonance imaging for simultaneous temperature and cavitation monitoring during focused ultrasound therapies: Simultaneous temperature and cavitation mapping Med. Phys 40 112901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bader KB. The influence of medium elasticity on the prediction of histotripsy-induced bubble expansion and erythrocyte viability. Phys. Med. Biol. 2018;63:095010. doi: 10.1088/1361-6560/aab79b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bader KB and Bollen V 2018. The influence of gas diffusion on bubble persistence in shock-scattering histotripsy J. Acoust. Soc. Am 143 EL481–6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bader KB, Crowe MJ, Raymond JL and Holland CK 2016a. Effect of frequency-dependent attenuation on predicted histotripsy waveforms in tissue-mimicking phantoms Ultrasound Med. Biol 42 1701–5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bader KB, Haworth KJ, Maxwell AD and Holland CK 2018. Post hoc analysis of passive cavitation imaging for classification of histotripsy-induced liquefaction in vitro IEEE Trans. Med. Imaging 37 106–15 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bader KB, Haworth KJ, Shekhar H, Maxwell AD, Peng T, McPherson DD and Holland CK 2016b. Efficacy of histotripsy combined with rt-PA in vitro Phys. Med. Biol 61 5253–74 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bader KB, Hendley SA, Anthony GJ and Bollen V 2019a. Observation and modulation of the dissolution of histotripsy-induced bubble clouds with high-frame rate plane wave imaging Phys. Med. Biol 64 115012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bader KB, Vlaisavljevich E and Maxwell AD 2019b. For whom the bubble grows: physical principles of bubble nucleation and dynamics in histotripsy ultrasound therapy Ultrasound Med. Biol 45 1056–80 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bader KB and Holland CK 2016. Predicting the growth of nanoscale nuclei by histotripsy pulses Phys. Med. Biol 61 2947–66 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrangou LM, Daubert CR and Allen Foegeding E 2006. Textural properties of agarose gels. I. Rheological and fracture properties Food Hydrocolloids 20 184–95 [Google Scholar]
- Choi JJ, Carlisle RC, Coviello C, Seymour L and Coussios C-C 2014. Non-invasive and real-time passive acoustic mapping of ultrasound-mediated drug delivery Phys. Med. Biol 59 4861–77 [DOI] [PubMed] [Google Scholar]
- Coviello C, Kozick R, Choi J, Gyöngy M, Jensen C, Smith PP and Coussios C-C 2015. Passive acoustic mapping utilizing optimal beamforming in ultrasound therapy monitoring J. Acoust. Soc. Am 137 2573–85 [DOI] [PubMed] [Google Scholar]
- Czaplicki C, Albadawi H, Partovi S, Gandhi RT, Quencer K, Deipolyi AR and Oklu R 2017. Can thrombus age guide thrombolytic therapy? Cardiovasc. Diagn. Ther 7 S186–96 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darnell SE, Hall TL, Tomlins SA, Cheng X, Ives KA and Roberts WW 2015. Histotripsy of the prostate in a canine model: characterization of post-therapy inflammation and fibrosis J. Endourol 29 810–5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeLong ER, DeLong DM and Clarke-Pearson DL 1988. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach Biometrics 44 837–45 [PubMed] [Google Scholar]
- Deng Y, Rouze NC, Palmeri ML and Nightingale KR 2017. Ultrasonic shear wave elasticity imaging sequencing and data processing using a verasonics research scanner IEEE Trans. Ultrason. Ferroelectr. Freq. Control 64 164–76 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duck FA 1990. Physical Properties of Tissue: a Comprehensive Reference Book (London: Academic; ) [Google Scholar]
- Duck FA, TotalBoox and TBX 2013. Physical Properties of Tissues (New York: Elsevier; ) (www.totalboox.com/book/id-5258306496708787708) [Google Scholar]
- Gateau J, Aubry J-F, Pernot M, Fink M and Tanter M 2011. Combined passive detection and ultrafast active imaging of cavitation events induced by short pulses of high-intensity ultrasound IEEE Trans. Ultrason. Ferroelectr. Freq. Control 58 517–32 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glybochko PV, Alyaev YG, Amosov AV, Krupinov GE, Ganzha TM, Vorobev AV, Lumpov IS and Semendyaev RI 2016. Prostate cancer detection by assessing stiffness of different tissues using shear wave ultrasound elastography Urologiia 56–61 [PubMed] [Google Scholar]
- Gray MD and Coussios CC 2018. Broadband ultrasonic attenuation estimation and compensation with passive acoustic mapping IEEE Trans. Ultrason. Ferroelectr. Freq. Control 65 1997–2011 [DOI] [PubMed] [Google Scholar]
- Gyöngy M, Arora M, Noble JA and Coussios CC 2008. Use of passive arrays for characterization and mapping of cavitation activity during HIFU exposure 2008 IEEE Ultrasonics Symp (Beijing: IEEE; ) pp 871–4 (http://ieeexplore.ieee.org/document/4803435/) [Google Scholar]
- Hall T 2006. A low cost compact 512 channel therapeutic ultrasound system for transcutaneous ultrasound surgery AIP Conf. Proc 829 445–9 [Google Scholar]
- Haworth KJ, Bader KB, Rich KT, Holland CK and Mast TD 2017. Quantitative frequency-domain passive cavitation imaging IEEE Trans. Ultrason. Ferroelectr. Freq. Control 64 177–91 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haworth KJ, Raymond JL, Radhakrishnan K, Moody MR, Huang S-L, Peng T, Shekhar H, Klegerman ME, Kim H, McPherson DD and Holland CK 2016. Trans-Stent B-Mode Ultrasound and Passive Cavitation Imaging Ultrasound Med. Biol 42 518–27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haworth KJ, Salgaonkar VA, Corregan NM, Holland CK and Mast TD 2015. Using passive cavitation images to classify high-intensity focused ultrasound lesions Ultrasound Med. Biol 41 2420–34 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirsh J and Hoak J 1996. Management of deep vein thrombosis and pulmonary embolism : a statement for healthcare professionals from the council on thrombosis (in consultation with the Council on Cardiovascular Radiology), American Heart Association Circulation 93 2212–45 [DOI] [PubMed] [Google Scholar]
- Holland CK and Apfel RE 1989. An improved theory for the prediction of microcavitation thresholds IEEE Trans. Ultrason. Ferroelectr. Freq. Control 36 204–8 [DOI] [PubMed] [Google Scholar]
- Jensen CR, Ritchie RW, Gyöngy M, Collin JRT, Leslie T and Coussios C-C 2012. Spatiotemporal monitoring of high-intensity focused ultrasound therapy with passive acoustic mapping Radiology 262 252–61 [DOI] [PubMed] [Google Scholar]
- Khokhlova VA, Fowlkes JB, Roberts WW, Schade GR, Xu Z, Khokhlova TD, Hall TL, Maxwell AD, Wang Y-N and Cain CA 2015. Histotripsy methods in mechanical disintegration of tissue: towards clinical applications Int. J. Hyperth 31 145–62 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwan JJ, Myers R, Coviello CM, Graham SM, Shah AR, Stride E, Carlisle RC and Coussios CC 2015. Ultrasound-propelled nanocups for drug delivery Small 11 5305–14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin K-W, Kim Y, Maxwell AD, Wang T-Y, Hall TL, Xu Z, Fowlkes JB and Cain CA 2014. Histotripsy beyond the intrinsic cavitation threshold using very short ultrasound pulses: microtripsy IEEE Trans. Ultrason. Ferroelectr. Freq. Control 61 251–65 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Zheng H, Poh P, Machens H-G and Schilling A 2015. Hydrogels for engineering of perfusable vascular networks Int. J. Mol. Sci 16 15997–6016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madsen EL, Sathoff HJ and Zagzebski JA 1983. Ultrasonic shear wave properties of soft tissues and tissuelike materials J. Acoust. Soc. Am 74 1346–55 [DOI] [PubMed] [Google Scholar]
- Mancia L, Vlaisavljevich E, Xu Z and Johnsen E 2017. Predicting tissue susceptibility to mechanical cavitation damage in therapeutic ultrasound Ultrasound Med. Biol 43 1421–40 [DOI] [PubMed] [Google Scholar]
- Maxwell AD, Cain CA, Hall TL, Fowlkes JB and Xu Z 2013. Probability of cavitation for single ultrasound pulses applied to tissues and tissue-mimicking materials Ultrasound Med. Biol 39 449–65 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maxwell AD, Wang T-Y, Cain CA, Fowlkes JB, Sapozhnikov OA, Bailey MR and Xu Z 2011. Cavitation clouds created by shock scattering from bubbles during histotripsy J. Acoust. Soc. Am 130 1888–98 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maxwell AD, Wang T-Y, Yuan L, Duryea AP, Xu Z and Cain CA 2010. A tissue phantom for visualization and measurement of ultrasound-induced cavitation damage Ultrasound Med. Biol 36 2132–43 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mercado-Shekhar KP, Kleven RT, Aponte Rivera H, Lewis R, Karani KB, Vos HJ, Abruzzo TA, Haworth KJ and Holland CK 2018. Effect of clot stiffness on recombinant tissue plasminogen activator lytic susceptibility in vitro Ultrasound Med. Biol 44 2710–27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nightingale K 2011. Acoustic radiation force impulse (ARFI) imaging: a review Curr. Med. Imaging Rev 7 328–39 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Normand V, Lootens DL, Amici E, Plucknett KP and Aymard P 2000. New insight into agarose gel mechanical properties Biomacromolecules 1 730–8 [DOI] [PubMed] [Google Scholar]
- O’Reilly MA, Jones RM and Hynynen K 2014. Three-dimensional transcranial ultrasound imaging of microbubble clouds using a sparse hemispherical array IEEE Trans. Biomed. Eng 61 1285–94 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otsu N 1979. A threshold selection method from gray-level histograms IEEE Trans. Syst. Man Cybern 9 62–6 [Google Scholar]
- Palta S, Saroa R and Palta A 2014. Overview of the coagulation system Indian J. Anaesthesia 58 515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rich KT and Mast TD 2015. Methods to calibrate the absolute receive sensitivity of single-element, focused transducers J. Acoust. Soc. Am 138 EL193–8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin JM, Xie H, Kim K, Weitzel WF, Emelianov SY, Aglyamov SR, Wakefield TW, Urquhart AG and O’Donnell M 2006. Sonographic elasticity imaging of acute and chronic deep venous thrombosis in humans J. Ultrasound Med 25 1179–86 [DOI] [PubMed] [Google Scholar]
- Salgaonkar VA, Datta S, Holland CK and Mast TD 2009. Passive cavitation imaging with ultrasound arrays J. Acoust. Soc. Am 126 3071–83 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samani A, Zubovits J and Plewes D 2007. Elastic moduli of normal and pathological human breast tissues: an inversion-technique-based investigation of 169 samples Phys. Med. Biol 52 1565–76 [DOI] [PubMed] [Google Scholar]
- Sutton JT, Ivancevich NM, Perrin SR, Vela DC and Holland CK 2013. Clot retraction affects the extent of ultrasound-enhanced thrombolysis in an ex vivo porcine thrombosis model Ultrasound Med. Biol 39 813–24 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szabo TL 2014. Diagnostic Ultrasound Imaging: Inside Out (Amsterdam: Elsevier; ) [Google Scholar]
- Vlaisavljevich E, Kim Y, Owens G, Roberts W, Cain C and Xu Z 2014. Effects of tissue mechanical properties on susceptibility to histotripsy-induced tissue damage Phys. Med. Biol 59 253–70 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vlaisavljevich E, Lin K-W, Warnez MT, Singh R, Mancia L, Putnam AJ, Johnsen E, Cain C and Xu Z 2015. Effects of tissue stiffness, ultrasound frequency, and pressure on histotripsy-induced cavitation bubble behavior Phys. Med. Biol 60 2271–92 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vlaisavljevich E, Maxwell A, Mancia L, Johnsen E, Cain C and Xu Z 2016. Visualizing the histotripsy process: bubble cloud-cancer cell interactions in a tissue-mimicking environment Ultrasound Med. Biol 42 2466–77 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang T-Y, Xu Z, Hall TL, Fowlkes JB and Cain CA 2012. An efficient treatment strategy for histotripsy by removing cavitation memory Ultrasound Med. Biol 38 753–66 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weickenmeier J, de Rooij R, Budday S, Steinmann P, Ovaert TC and Kuhl E 2016. Brain stiffness increases with myelin content Acta Biomater 42 265–72 [DOI] [PubMed] [Google Scholar]
- Xu Z, Ludomirsky A, Eun LY, Hall TL, Tran BC, Fowlkes B and Cain CA 2004. Controlled ultrasound tissue erosion IEEE Trans. Ultrason. Ferroelectr. Freq. Control 51 726–36 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X, Macoskey JJ, Ives K, Owens GE, Gurm HS, Shi J, Pizzuto M, Cain CA and Xu Z 2017. Non-invasive thrombolysis using microtripsy in a porcine deep vein thrombosis model Ultrasound Med. Biol 43 1378–90 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zweig MH and Campbell G 1993. Receiver-operating characteristic (ROC) plots: a fundamental evaluation tool in clinical medicine Clin. Chem 39 561–77 [PubMed] [Google Scholar]