Abstract
Purpose
Dose conformality and robustness are equally important in intensity modulated proton therapy (IMPT). Despite the obvious implication of beam orientation on both dosimetry and robustness, an automated, robust beam orientation optimization algorithm has not been incorporated due to the problem complexity and paramount computational challenge. In this study, we developed a novel IMPT framework that integrates robust beam orientation optimization (BOO) and robust fluence map optimization (FMO) in a unified framework.
Methods
The unified framework is formulated to include a dose fidelity term, a heterogeneity‐weighted group sparsity term, and a sensitivity regularization term. The L2, 1/2‐norm group sparsity is used to reduce the number of active beams from the initial 1162 evenly distributed noncoplanar candidate beams, to between two and four. A heterogeneity index, which evaluates the lateral tissue heterogeneity of a beam, is used to weigh the group sparsity term. With this index, beams more resilient to setup uncertainties are encouraged. There is a symbiotic relationship between the heterogeneity index and the sensitivity regularization; the integrated optimization framework further improves beam robustness against both range and setup uncertainties. This Sensitivity regularization and Heterogeneity weighting based BOO and FMO framework (SHBOO‐FMO) was tested on two skull‐base tumor (SBT) patients and two bilateral head‐and‐neck (H&N) patients. The conventional CTV‐based optimized plans (Conv) with SHBOO‐FMO beams (SHBOO‐Conv) and manual beams (MAN‐Conv) were compared to investigate the beam robustness of the proposed method. The dosimetry and robustness of SHBOO‐FMO plan were compared against the manual beam plan with CTV‐based voxel‐wise worst‐case scenario approach (MAN‐WC).
Results
With SHBOO‐FMO method, the beams with superior range robustness over manual beams were selected while the setup robustness was maintained or improved. On average, the lowest [D95%, V95%, V100%] of CTV were increased from [93.85%, 91.06%, 70.64%] in MAN‐Conv plans, to [98.62%, 98.61%, 96.17%] in SHBOO‐Conv plans with range uncertainties. With setup uncertainties, the average lowest [D98%, D95%, V95%, V100%] of CTV were increased from [92.06%, 94.83%, 94.31%, 78.93%] in MAN‐Conv plans, to [93.54%, 96.61%, 97.01%, 91.98%] in SHBOO‐Conv plans. Compared with the MAN‐WC plans, the final SHBOO‐FMO plans achieved comparable plan robustness and better OAR sparing, with an average reduction of [Dmean, Dmax] of [6.31, 6.55] GyRBE for the SBT cases and [1.89, 5.08] GyRBE for the H&N cases from the MAN‐WC plans.
Conclusion
We developed a novel method to integrate robust BOO and robust FMO into IMPT optimization for a unified solution of both BOO and FMO, generating plans with superior dosimetry and good robustness.
Keywords: beam orientation optimization, integrated, intensity modulation, proton, robustness
Short abstract

1. Introduction
Multifield optimized intensity‐modulated proton therapy (MFO‐IMPT) is the state‐of‐the‐art delivery technique of radiation therapy. It utilizes the spot scanning technique1 and three‐dimensional (3D) modulation2 of pencil beams from multiple fields to achieve high target dose conformality and superior organs at risk (OARs) sparing. Since MFO‐IMPT is exclusively investigated in this study, we will refer to it as IMPT in the remainder of the paper for brevity.
In general, both plan robustness and plan quality/conformality depend on beam angle selection. An ideal IMPT treatment planning process should include beam angle selection and fluence map optimization (FMO) simultaneously. In current clinical practice, the proton beam angles are manually selected first by a planner. Different from x‐ray therapy where equiangular or arc beams are often acceptable, the proton beam orientations are typically asymmetric, and need to be more carefully considered for factors such as the water‐equivalent thickness to the target, nearby OAR sparing, heterogeneity of tissues in the beam path, and setup robustness etc.3, 4, 5 To minimize low dose regions and speed up treatment delivery, there are practically fewer beam angles in a typical proton plan, which makes the selection of proton beam angle particularly important. Planners' experience and skill can heavily influence the final treatment plan quality. For complicated patient cases, tedious trial‐and‐error attempts may be needed to find better beam configurations. Yet, human operators cannot effectively search the enormous coplanar and noncoplanar beam space, resulting in inconsistent planning results. Beam orientation optimization (BOO) using a computational model is therefore essential for improving IMPT.
The Intensity Modulated Photon Therapy (IMXT) BOO problem has been extensively researched using stochastic and analytical methods,6, 7, 8, 9, 10, 11, 12 but there have been limited IMPT BOO studies. Cao et al.13 applied a local neighborhood search (LNS) algorithm to the IMPT BOO problem and implemented it on prostate cancer to improve beam arrangement.14 The LNS is confined to be within a small search space near the initial condition, which still has to be manually selected. Later Lim et al.15 used global search methods, such as branch‐and‐bound and simulated annealing, to find a good feasible solution as the initial condition for LNS but these stochastic methods were only demonstrated on much smaller coplanar IMPT problems. In our previous work,16 we developed an integrated BOO and FMO framework for noncoplanar IMPT. Based on group sparsity regularization, this algorithm efficiently performs a global search on noncoplanar candidate beams and finds a dosimetrically optimal solution.
Besides plan dosimetric quality, uncertainty or plan robustness is important for IMPT. The dose of a proton pencil beam is mostly deposited around the Bragg peak,17 whose location is sensitive to both patient positioning and range estimation uncertainties.18, 19, 20, 21, 22 The former is caused by the misalignment between proton beam and patient anatomy, and the latter due to the error of converting CT number to stopping power ratio, CT image artifacts, and patient anatomy changes. The proton dose uncertainties can lead to severely under‐dosed target and over‐dosed OARs yet the geometrical margin used in x‐ray therapy is ineffective to mitigate the problem. For IMPT, a commonly used method to reduce the effect of uncertainties is worst‐case optimization method,21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40 where the estimated worst situations are sparsely sampled in the optimization problem to maintain the dose distribution even with uncertainties above. The plan robustness is better maintained at the cost of substantially increased computational cost.21, 34 To avoid the additional burden of calculating the worst cases and provide the robustness consideration as a soft constraint, we recently modeled the scanning spot sensitivity concerning range and positioning uncertainties as a regularization term in the optimization.41 We showed improved dosimetry, robustness to larger range uncertainties, and an order of magnitude faster optimization time than the worst case approach.
In our previous IMPT frameworks, robustness and BOO were studied separately, despite their obvious inter‐dependence. For instance, beams passing through highly heterogeneous tissues are likely more sensitive to range and positioning uncertainties than beams passing through homogeneous tissues. It may cause more dosimetric compromise to achieve robustness for these beams. The robustness consideration complicates beam selection in manual IMPT planning, making integrated robust BOO and FMO even more urgently needed. Pflugfelder et al.20 modeled the interdependence of beam orientation and robustness as a lateral tissue heterogeneity across the proton pencil beams. Their heterogeneity number, is then used to guide beam angle selection.42, 43 After evaluating the heterogeneity of each beam, Bueno et al.42 recommended to change the beam direction if the heterogeneity exceeded a threshold, and Toramatsu et al.43 proposed to use the beams with minimum heterogeneity in single field uniform dose (SFUD) plans. These heuristic heterogeneity‐guided beam angle selection methods have not quantitatively incorporated the robustness consideration in IMPT optimization and potentially dismiss dosimetrically superior beam orientations. Cao et al.13, 14, 15 combines the worst‐case approach and local neighborhood search algorithm to achieve robust beam angle selection. However, in addition to the limitations above being confined to the local search, in each search step, a subproblem of worst‐case FMO is solved, making the method impractically slow.
In this work, we develop a novel unified robust optimization framework for IMPT, that integrates robust beam orientation selection and robust fluence map optimization in a single problem and then solve this global optimization problem. The BOO is achieved by group sparsity regularization, and robustness is promoted by the lateral tissue heterogeneity penalty and dose sensitivity regularization.
2. Materials and methods
The integrated robust BOO and FMO framework is formulated with a dose fidelity term, a heterogeneity‐weighted group sparsity term, and a dose sensitivity regularization term. The details are described as follows.
2.A. Group sparsity‐based BOO
Assume is the set containing all the feasible candidate beams. As proposed in our previous work,16 the selection of a small number of beams from the set by group sparsity regularization is formulated as the following optimization problem:
| (1) |
where x b is a vector representing the intensities of scanning spots from the candidate beam b, and x is the concatenation of all the vectors . A is the dose calculation matrix including all candidate beams, with each column being the vectorized doses delivered to the patient from one unit intensity spot. The first term in problem (1) is the dose fidelity term on target and critical organs, to penalize dose deviation from the ideal distribution. The second term is an L2,1/2‐norm group sparsity term. Most candidate beams are turned off with a proper value of weighting hyperparameter for each beam b, denoted as . A small number (e.g., 2–4) of beams, remain active. The weighting parameter of beam b is set to be:
| (2) |
where is the dose calculation matrix of the target volume for beam b, nb is the number of scanning spots in beam b, 1 is a vector with every element being one, and c is a regularization parameter. The aim of (2) is to use a single parameter c to control the number of active beams while the beams of different ranges and spot numbers are unbiasedly weighted.
2.B. Heterogeneity‐weighted group sparsity
The group sparsity‐based BOO (GSBOO) method presented in problem (1) is designed to select beams for good dosimetry, and the robustness is not considered yet. In order to select beams with less sensitivity to setup uncertainties, we incorporate lateral tissue heterogeneity into the current group sparsity term, to encourage the algorithm to choose beams with less lateral tissue heterogeneity. The lateral tissue heterogeneity observed along beam b is quantified by its heterogeneity index hb , which is defined as follows.
First, as shown in Fig. 1, a coordinate system is created for each pencil beam (scanning spot) in beam b, with the z axis along the central axis of the pencil beam and pointing from the source to the patient. The central axis of ith pencil beam is located at (xi , yi ), and the position of (xi , yi , 0) is where the pencil beam enters the patient.
Figure 1.
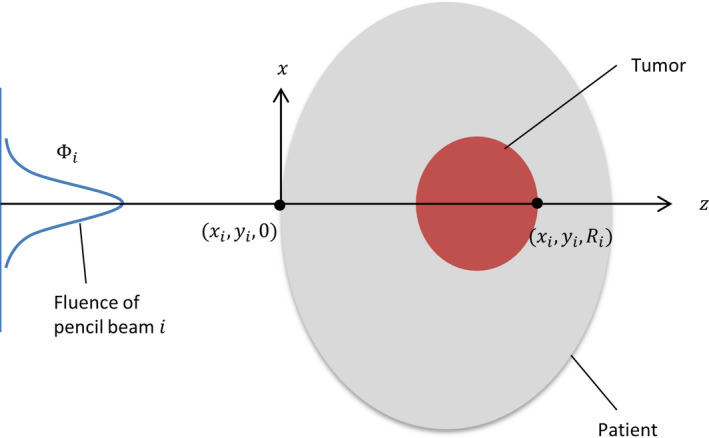
Diagram showing the coordinates used in heterogeneity index calculation for a specific pencil beam. [Color figure can be viewed at wileyonlinelibrary.com]
With discrete sampling, the heterogeneity index of ith pencil beam in beam b at the depth zk , denoted as , is defined as:
| (3) |
where is the relative stopping power ratio at the voxel , and is the particle fluence at for the ith pencil beam. The sampling set of lateral voxels at depth zk is written as . In the analytical model, the lateral dose distribution of pencil beam i is approximated as a single Gaussian distribution, with a standard deviation of at depth zk . The sampling set at each depth is selected to include the voxels within from the central axis.
The depth‐specific is evaluated and summed up from , which is the path spanning from where the pencil beam enters the patient to the end of its range. The sum generates a single metric to indicate the lateral heterogeneity affecting the ith pencil beam in beam b:
| (4) |
The heterogeneity index values of all scanning spots in the same beam b are then averaged to represent the beam heterogeneity. Therefore, the heterogeneity index of beam b, denoted as hb , is calculated as:
| (5) |
where nb is the number of scanning spots in beam b.
Then hb is evaluated for each candidate beam and used to weigh the group sparsity in problem (1). The heterogeneity‐weighted group sparsity BOO (HBOO) is thus formulated as:
| (6) |
In this algorithm, the beams with higher lateral heterogeneity are more heavily penalized in the group sparsity term, resulting in selecting beams with higher dose fidelity and less sensitivity to setup errors.
2.C. Sensitivity regularization and robust BOO‐FMO
Even though the beams more resilient to setup errors are preferred in problem (6), the range uncertainty has not been considered in FMO. Sensitivity regularization41 is thus incorporated into the framework to achieve simultaneous robust beam angle selection and robust fluence map optimization. We now describe the formulation of the sensitivity vector.
As shown in Fig. 2, a coordinate system ( u b , v b , w b ) is first designated for the beam b, with the origin centered at the isocenter. u b represents the beam direction pointing from the source to the isocenter, and v b and w b are orthogonal vectors in the plane perpendicular to the beam direction. We define p b,i as the spatial position of scanning‐spot i from beam b, which points from the isocenter to the position of its Bragg peak in the patient. a b,i is the full dosimetric contribution of spot i in beam b to all voxels of the patient, embedded as a column vector in the dose calculation matrix A, and a b is the submatrix of A that contains only the a b,i for all the spots in the same beam b. Then we evaluate the gradient field of a b,i with respect to the spot position p , and denote its directional derivatives along u b , v b , and w b in the respective functional forms:
| (7) |
Figure 2.
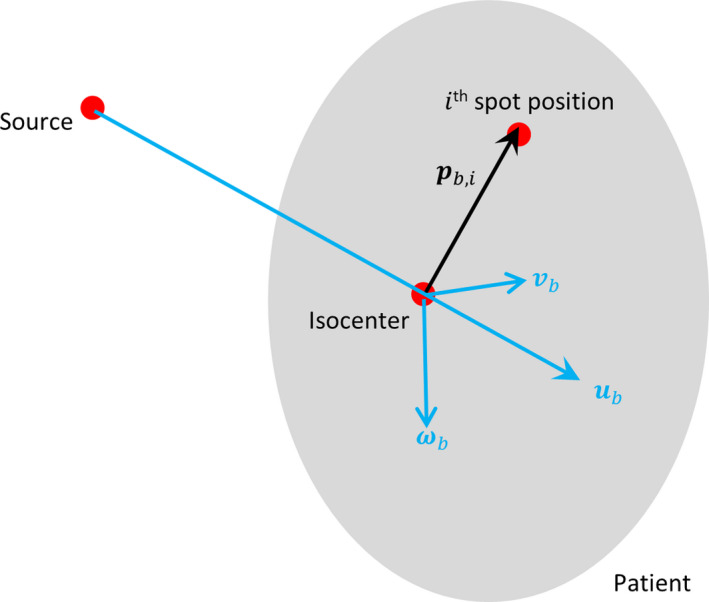
Diagram showing the coordinates and the vectors used in spot sensitivity calculation. The beam divergence due to spot lateral distance to the isocenter is exaggerated for illustration purposes. The actual proton system source‐to‐axis distance is substantially greater than the target size and the individual pencil beams in the same beam direction are nearly parallel. [Color figure can be viewed at wileyonlinelibrary.com]
This equation set evaluates the dose sensitivity level at each voxel from a specific scanning spot along the longitudinal direction (beam direction) and the lateral directions (orthogonal to beam direction). Since both and represent the lateral sensitivity, only and are used for optimization in the following sections.
We can obtain the vector specific to spot i of beam b in each direction, u b or v b , by simply extracting column i from or , respectively. After performing this operation on every beam‐specific submatrix of the A, we can obtain two sensitivity matrices, written as DuA and DvA. The absolute values of the rows of DuA and DvA are summed up, and the two resulting row vectors are transposed to produce the longitudinal and lateral sensitivity vectors, denoted as su and sv , respectively.
After acquiring the sensitivity vectors, the sensitivity regularization term is added to problem (6), to formulate the final integrated robust BOO and FMO framework, which is written as:
| (8) |
where and are the sensitivity regularization parameters. This Sensitivity regularization and Heterogeneity weighting based BOO and FMO framework (SHBOO‐FMO), allows robust beams to be selected and robust fluence map to be generated in a single equation. SHBOO will be used in place of SHBOO‐FMO for the rest of the paper when referring to the BOO algorithm and the selected beams for brevity.
In this study, a one‐sided quadratic function is used for dose fidelity term, which is formulated as:
| (9) |
where is the structure set of the target volumes, with lj being the prescription dose to jth target, and is the dose‐limiting structure set which includes the OARs as well as the target to suppress its maximum dose, with dj being the prescribed maximal allowed dose to the jth structure. Aj is the dose calculation matrix block for structure j, and wj is the structure weighting parameter.
Problem (8) is a nondifferentiable problem due to the presence of L2, 1/2‐norm group sparsity. However, it can be efficiently solved by FISTA, an accelerated proximal gradient method known as the Fast Iterative Shrinkage‐Thresholding Algorithm.44 The details of solving problem (8) using FISTA are shown in Appendix A.
2.D. Evaluations
This SHBOO‐FMO method was tested on two patients with skull base tumor (SBT) and two bilateral head‐and‐neck (H&N) patients. Four beams were selected for the SBT patients and three beams for the H&N patients. For each patient, there were originally 1162 noncoplanar beams in the candidate set, which were evenly distributed across the 4 space with 6° separation. Geometrically undesired beams and beams of infeasible energies, such as those directed through the feet to the head, were manually excluded from the candidate set, resulting in about 700 to 800 candidate beams for each patient. More accurate beam screening can be performed for a specific proton gantry but should not affect the generality of the current study. For each candidate beam, dose calculation for the scanning spots covering the CTV and a 5 mm margin was performed by matRad,45, 46 a MATLAB‐based 3D treatment planning toolkit. In matRad, the lateral beam width is calculated as the root sum square of the initial beam width from Safai et al.47 and the lateral broadening from Gottschalk et al.48 The performance of analytical dose calculation for IMPT optimization was compared with Monte Carlo in our previous paper41 and found to be acceptable for pencil beam dose calculation and robust planning. The spot spacing was 3 mm in the beam direction, 5 mm in the lateral direction for the H&N patients and 4 mm in the lateral direction for the SBT patients. The dose calculation resolution was 2.5 × 2.5 × 2.5 mm. The CTV was set as the optimization target. The prescription dose, target volume, and average spot count per beam for each patient are shown in Table 1.
Table 1.
Prescription doses, CTV volumes and average number of spots per beam for each patient.
| Case | Prescription dose (GyRBE) | CTV volume (cc) | Average spots per beam |
|---|---|---|---|
| SBT #1 | 56 | 33.7 | 2537 |
| SBT #2 | 70 | 36.8 | 2650 |
| H&N #1 | |||
| CTV54 | 54 | 108.0 | 10 077 |
| CTV60 | 60 | 127.3 | |
| H&N #2 | |||
| CTV54 | 54 | 110.4 | 9433 |
| CTV60 | 60 | 99.0 | |
| CTV63 | 63 | 10.2 | |
The dosimetry and plan robustness of the proposed SHBOO‐FMO method was compared against (a) the voxel‐wise worst‐case FMO method with manually selected beams (MAN‐WC), and (b) sensitivity‐regularized FMO method with the same manual beams (MAN‐SenR). The voxel‐wise worst‐case optimization considered nine scenarios, including one nominal scenario and the following eight worst‐case scenarios: (a) six setup uncertainty scenarios, defined by shifting the beam isocenter by ± 3 mm along anteroposterior, superior‐inferior, and mediolateral directions; (b) two range uncertainty scenarios, by scaling the CT number by ± 3%. The SenR robust FMO method described in our previous work41 consists of dose fidelity term and a sensitivity regularization term, which has been described in Section 2.C. The same quadratic loss function as Eq. (9) was used in the WC method and the SenR method.
In addition to the robustness of the final plan, the sole robustness of the selected beams by SHBOO‐FMO, was also evaluated and compared with the following beam sets: (a) manually selected beams, (b) GSBOO beams, and (c) HBOO beams. The comparison was performed by creating plans using the same conventional CTV‐based FMO method (Conv), using the aforementioned beam sets. Same candidate beam set, spot population, and dose calculation scheme were used for different BOO algorithms. The acronym used for each method and its definition can be found in Table 2.
Table 2.
Acronym of each method and its definition.
| Acronym | Definition |
|---|---|
| SHBOO‐FMO | Group sparsity‐based integrated BOO and FMO framework with sensitivity regularization and heterogeneity weighting |
| SHBOO | Short for SHBOO‐FMO when referring to the BOO algorithm and the beams selected by SHBOO‐FMO |
| MAN | Manually selected beams |
| GSBOO | Group sparsity‐based BOO algorithm |
| HBOO | Heterogeneity‐weighted group sparsity BOO algorithm |
| Conv | Conventional CTV‐based FMO method |
|
MAN‐Conv GSBOO‐Conv HBOO‐Conv SHBOO‐Conv |
Conventional CTV‐based FMO plan with MAN, GSBOO, HBOO, and SHBOO beams, respectively |
| MAN‐WC | CTV‐based voxel‐wise worst‐case FMO method with manually selected beams |
| MAN‐SenR | Sensitivity‐regularized FMO method with manually selected beams |
CTV homogeneity, D95%, D98%, and maximum dose were evaluated under the nominal condition. CTV homogeneity is defined as D95%/D5%. The maximum dose is defined as the dose to 2% of the structure volume, D2%, following the recommendation by IRCU‐83.49 The mean and maximum doses for OARs were also evaluated. The robustness of a plan was evaluated by the DVH band plot,50 as well as the worst dose metrics occurred among uncertainties scenarios. The robustness analysis considered the same nine scenarios as the WC method.
3. Results
3.A. Runtime and selected beams
The dose, sensitivity, and heterogeneity calculation for all the candidate beams were performed on a Xeon 20‐core CPU server operating at 3.10 GHz clock, with Matlab and its Parallel Computing Toolbox. The averaged time per beam to calculate the three data is listed in Table 3. The most time‐consuming step during preparation is the evaluation of the sensitivity vector. The averaged runtime for GSBOO, HBOO, and SHBOO, on an i7 CPU desktop, is also shown in Table 3. Depending on the target size, these BOO process took about 6–75 min to complete. With the additional heterogeneity weighting and sensitivity regularization, the SHBOO method reduced the runtime from the original GSBOO method approximately by half.
Table 3.
Preparation time and runtime of each BOO method for the tested patients.
| Case | Calculation time per beam (s) | BOO runtime (s) | ||||
|---|---|---|---|---|---|---|
| Dose | Sensitivity | Heterogeneity | GSBOO | HBOO | SHBOO | |
| SBT #1 | 0.4 | 1.5 | 1.5 | 804 | 745 | 362 |
| SBT #2 | 0.6 | 2.0 | 1.6 | 1102 | 999 | 682 |
| H&N #1 | 1.9 | 24.0 | 8.2 | 3214 | 2978 | 1446 |
| H&N #2 | 1.4 | 14.9 | 7.2 | 4407 | 3996 | 2728 |
The couch and gantry angles for the beams from manual selection, GSBOO, HBOO, and SHBOO, are listed in Table 4. The angle notation follows IEC 61217 coordinate conventions. Figure 3 also shows the beam arrangement by the four methods of the SBT #1 and H&N #1 patients. It is observed in the four tested cases that the SHBOO algorithm tends to select more aggregated beams while GSBOO and HBOO prefer more scattered beams.
Table 4.
Beam angles (gantry and couch angle) selected in each method.
| Patient | MAN | GSBOO | HBOO | SHBOO |
|---|---|---|---|---|
| SBT #1 | (60, 273), (270, 0), (90, 0), (180, 0) | (84, 312), (80, 323), (30, 272), (289, 25) | (252, 45), (206, 69), (96, 342), (96, 348) | (78, 348), (96, 348), (96, 354), (96, 0) |
| SBT #2 | (60, 273), (270, 0), (90, 0), (180, 0) | (285, 80), (270, 342), (62, 21), (37, 43) | (262, 81), (126, 270), (72, 354), (67, 20). | (66, 353), (72, 354), (62, 21), (67, 20) |
| H&N #1 | (0, 0), (162, 0), (198, 0) | (153, 332), (197, 46), (37, 57) | (167, 296), (197, 46), (32, 23) | (36, 0), (328, 291), (33, 66) |
| H&N #2 | (0, 0), (162, 0), (198, 0) | (145, 327), (49, 344), (192, 270) | (188, 45), (180, 0), (324, 301) | (32, 23), (30, 39), (324, 301) |
Figure 3.
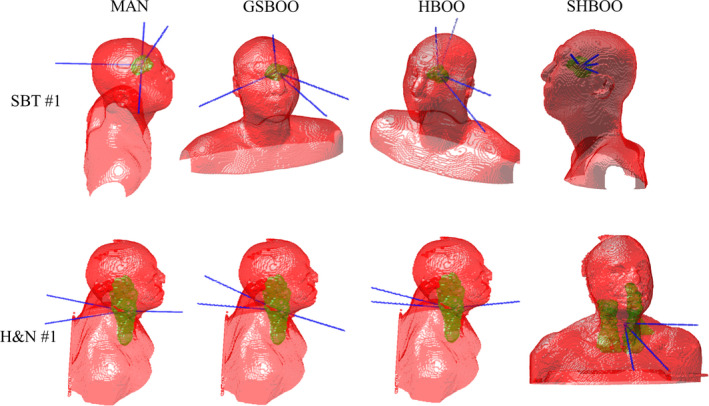
The beam arrangement of each method for the SBT #1 patient (top row) and H&N #1 patient (bottom row). From left to right, each column is MAN, GSBOO, HBOO, and SHBOO beams, respectively. [Color figure can be viewed at wileyonlinelibrary.com]
3.B. Beam robustness
The beam robustness was compared among the plans using different BOO methods but the same conventional CTV‐based approach (Conv) for fluence map optimization.
Figure 4 shows the DVH bands of the CTVs of these Conv plans with range uncertainty and setup uncertainty for the SBT patients and H&N patients. In these DVH band plots, the solid lines are the nominal DVHs without uncertainties, the dotted lines and bands bound the worst‐case dose distributions, and the horizontal and vertical lines label the worst D95% of each method for each CTV. For the tested cases, the beam robustness of the GSBOO method is not maintained. For example, the GSBOO beams lead to wide DVH bands under range uncertainties for the SBT #2 and H&N #2 patients, and wide bands under setup uncertainties for the two SBT patients. With heterogeneity‐weighted group sparsity, the beam robustness against setup uncertainty is improved from the GSBOO beams for the four tested patients, while the robustness against range uncertainty varies among patients. With SHBOO method, the beams with superior range robustness over manual beams and HBOO beams are selected while the setup robustness is maintained or improved.
Figure 4.
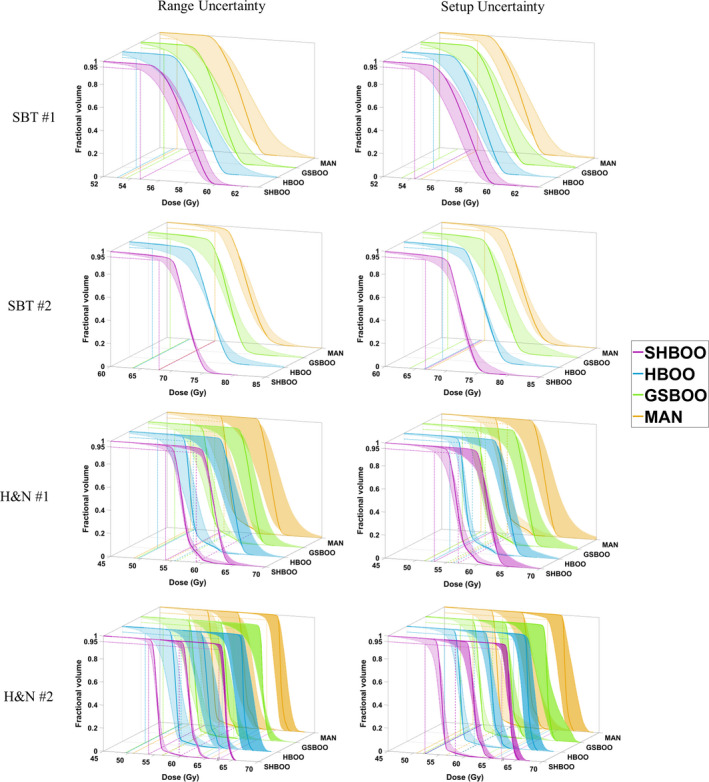
CTV DVH bands of the four patients, indicating the robustness of the beams chosen by different methods. The situation with only range uncertainty is shown on the left and situation with only setup uncertainty is shown on the right. The worst D95% of each method is labeled by reference lines in the x‐y plane. The two CTVs in the H&N #1 patient are plotted together in the third row, and the three CTVs in the H&N #2 patient are plotted together in the fourth row, with different transparencies. [Color figure can be viewed at wileyonlinelibrary.com]
The lowest (worst) D98%, D95%, V95%, and V100% of each CTV with range uncertainties and setup uncertainties were evaluated and plotted in Fig. 5. Compared with the manual selection, the D98%, D95%, V95%, and V100% were improved by the SHBOO method. On average, the lowest [D98%, D95%, V95%, V100%] of CTV increased from [90.85%, 93.85%, 91.06%, 70.64%] in MAN beams, to [96.05%, 98.62%, 98.61%, 96.17%] in SHBOO beams. Under setup uncertainties, the average lowest [D98%, D95%, V95%, V100%] of CTV increased from [92.06%, 94.83%, 94.31%, 78.93%] in MAN beams, to [93.54%, 96.61%, 97.01%, 91.98%] in SHBOO beams.
Figure 5.
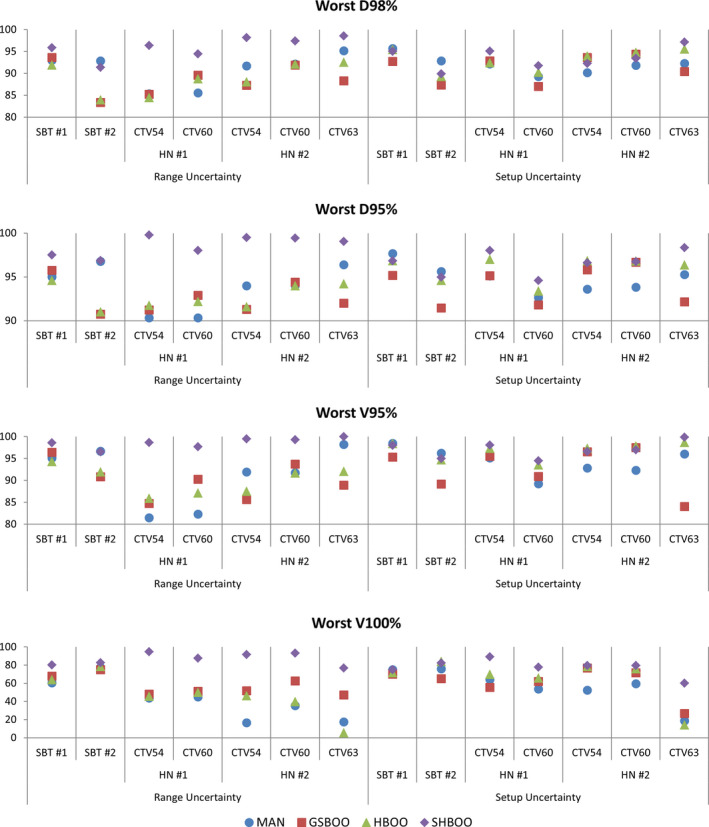
The comparison of worst D98% (top row), D95% (second row), V95% (third row), and V100% (bottom row) of the CTVs as a percentage of prescription doses, for every patient, between the plans with Conv FMO and MAN, GSBOO, HBOO and SHBOO beams, respectively. The situation with only range uncertainty is shown on the left and situation with only setup uncertainty is shown on the right in each plot. [Color figure can be viewed at wileyonlinelibrary.com]
3.C. Plan robustness
The plan robustness of SHBOO‐FMO method was compared with the plan with manual beams and voxel‐wise worst‐case FMO (MAN‐WC) as well as that with manual beams and SenR FMO (MAN‐SenR). The CTV DVH bands of the three methods are shown in Fig. 6 for the SBT patients and the H&N patients. Under range uncertainties, narrower DVH bands were observed in the SHBOO‐FMO plans compared with the MAN‐WC plans, and the CTV underdosage in the MAN‐SenR plans was also improved by the SHBOO‐FMO method. Under setup uncertainties, the SHBOO‐FMO method was less robust than MAN‐WC but comparable with or more robust than MAN‐SenR.
Figure 6.
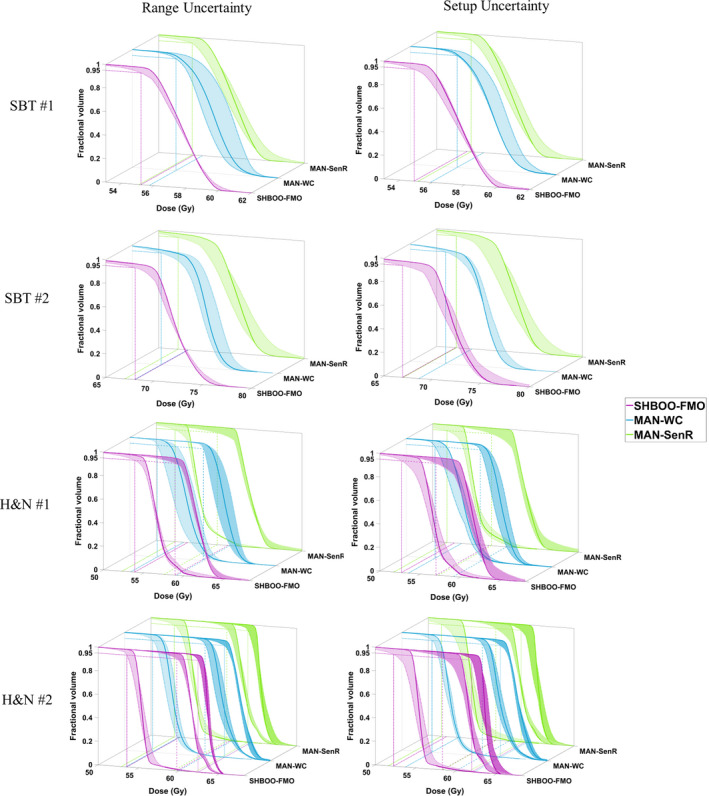
CTV DVH bands of the four patients, indicating the robustness of the plans generated by SHBOO‐FMO, MAN‐WC and MAN‐SenR. Situation with only range uncertainty is shown on the left and situation with only setup uncertainty is shown on the right. The two CTVs in the H&N #1 patient are plotted together in the third row, and the three CTVs in the H&N #2 patient are plotted together in two figures in the fourth row. The worst D95% of each method is labeled by reference lines in the x‐y plane. [Color figure can be viewed at wileyonlinelibrary.com]
The lowest (worst) D98%, D95%, V95%, and V100% of each CTV with range uncertainties and setup uncertainties were also evaluated and plotted in Fig. 7. Compared with MAN‐SenR, the D98%, D95%, V95%, and V100% were improved by the SHBOO‐FMO method. On average, the lowest [D98%, D95%, V95%, V100%] of CTV were increased from [93.95%, 97.42%, 97.64%, 94.60%] in MAN‐SenR plans, to [96.18%, 98.75%, 98.68%, 96.68%] in SHBOO‐FMO plans. Under setup uncertainties, the averaged lowest [D98%, D95%, V95%, V100%] of CTV were increased from [93.10%, 96.54%, 96.93%, 92.01%] in MAN‐SenR plans, to [93.80%, 96.89%, 97.29%, 92.99%] in SHBOO‐FMO plans. Overall the MAN‐WC method achieved the best CTV metrics, with the averaged lowest [D98%, D95%, V95%, V100%] of [97.53%, 98.82%, 99.36%, 97.44%] under range uncertainties and [97.86%, 99.10%, 99.59%, 97.90%] under setup uncertainties.
Figure 7.
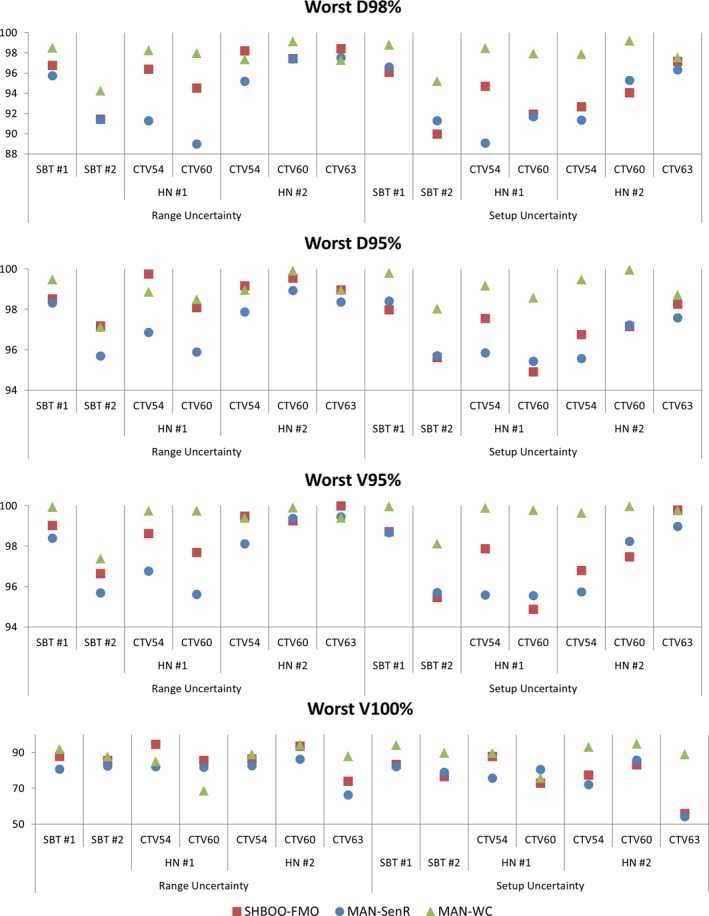
The comparison of worst D98% (top row), D95% (second row), V95% (third row), and V100% (bottom row) of the CTVs as a percentage of prescription doses, for every patient, between the MAN‐WC plan, MAN‐SenR plan and SHBOO‐FMO plan Situation with only range uncertainty is shown on the left and situation with only setup uncertainty is shown on the right. [Color figure can be viewed at wileyonlinelibrary.com]
3.D. Nominal dose comparison
Table 5 compares the nominal CTV statistics of each patient between the MAN‐WC, MAN‐SenR, and SHBOO‐FMO methods. Without uncertainties, the three methods achieved similar CTV dose coverage. Several OARs are selected for the SBT and H&N sites, respectively, and the differences of their mean and maximum doses between the SHBOO plans and the MAN plans are presented in Tables 6, and 7. Figure 8 shows the nominal DVHs comparison between the SHBOO‐FMO method and MAN‐WC method for the four tested patients.
Table 5.
CTV statistic comparison between three methods for all patients under the nominal situation.
| Case | Dmax | D95% | D98% | Heterogeneity | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAN‐WC | MAN‐SenR | SHBOO‐FMO | MAN‐WC | MAN‐SenR | SHBOO‐ FMO | MAN‐WC | MAN‐SenR | SHBOO‐ FMO | MAN‐WC | MAN‐SenR | SHBOO‐ FMO | |
| SBT #1 | 106.8 | 106.2 | 106.8 | 100.0 | 100.0 | 100.0 | 99.1 | 99.6 | 99.5 | 94.4 | 94.6 | 94.0 |
| SBT #2 | 108.7 | 108.5 | 108.3 | 100.0 | 100.0 | 100.0 | 97.0 | 96.4 | 98.2 | 92.7 | 92.8 | 93.1 |
| HN #1 | ||||||||||||
| CTV54 | 112.0 | 110.4 | 111.4 | 101.9 | 100.0 | 102.1 | 101.0 | 99.7 | 101.4 | 92.2 | 91.9 | 92.8 |
| CTV60 | 107.2 | 106.4 | 106.6 | 100.0 | 100.0 | 100.0 | 99.3 | 99.7 | 99.5 | 94.0 | 94.5 | 94.5 |
| HN #2 | ||||||||||||
| CTV54 | 108.0 | 108.6 | 108.3 | 101.1 | 100.7 | 101.0 | 100.6 | 100.3 | 100.6 | 95.2 | 95.6 | 96.6 |
| CTV60 | 108.4 | 106.8 | 106.8 | 101.1 | 100.7 | 101.0 | 100.5 | 100.4 | 100.7 | 94.4 | 95.0 | 95.3 |
| CTV63 | 105.2 | 103.2 | 103.3 | 100.0 | 100.0 | 100.0 | 99.6 | 99.8 | 99.7 | 95.7 | 97.4 | 97.3 |
Table 6.
OAR mean dose and max dose reduction of the SHBOO‐FMO plans from the MAN‐WC plans and MAN‐SenR, for the SBT cases under nominal situation.
| SBT case | SHBOO‐FMO — MAN‐WC (GyRBE) | SHBOO‐FMO — MAN‐SenR (GyRBE) | ||||||
|---|---|---|---|---|---|---|---|---|
| Dmean | Dmax | Dmean | Dmax | |||||
| #1 | #2 | #1 | #2 | #1 | #2 | #1 | #2 | |
| Left optic nerve | −5.06 | −15.12 | −1.40 | −0.90 | +0.07 | −10.05 | +0.83 | +1.40 |
| Right optic nerve | −13.93 | −1.80 | −4.57 | −11.20 | −2.07 | −0.18 | −2.00 | −4.60 |
| Chiasm | −2.35 | −13.72 | −0.76 | −7.18 | −2.07 | −5.14 | +0.24 | −4.18 |
| Brainstem | −1.45 | −4.63 | −5.75 | −7.32 | −0.37 | −0.39 | −3.33 | +2.34 |
| Left eye | −0.57 | −13.65 | −5.42 | −25.63 | +0.50 | −6.01 | −2.23 | −16.66 |
| Right eye | −1.21 | 0.00 | −8.38 | 0.00 | −0.13 | 0.00 | −0.72 | 0.00 |
| Left cochlea | 0.00 | −3.59 | 0.00 | 0.00 | 0.00 | 0.79 | 0.00 | +1.20 |
| Right cochlea | 0.00 | −4.89 | 0.00 | −6.72 | 0.00 | −2.06 | 0.00 | −3.52 |
Table 7.
OAR mean dose and max dose reduction of the SHBOO‐FMO plans from the MAN‐WC plans and MAN‐SenR, for the H&N cases under the nominal situation.
| H&N case | SHBOO‐FMO — MAN‐WC(GyRBE) | SHBOO‐FMO — MAN‐SenR(GyRBE) | ||||||
|---|---|---|---|---|---|---|---|---|
| Dmean | Dmax | Dmean | Dmax | |||||
| #1 | #2 | #1 | #2 | #1 | #2 | #1 | #2 | |
| Right submandibular gland | −6.76 | +11.48 | −5.25 | −0.33 | +9.22 | +10.31 | −1.60 | +0.76 |
| Left parotid | −3.79 | −0.42 | −1.85 | −0.27 | +5.67 | +0.94 | +0.25 | +0.07 |
| Right parotid | −1.45 | −3.33 | 0.00 | −4.27 | −0.79 | −3.22 | +0.22 | −3.99 |
| Larynx | −3.18 | −2.28 | −5.39 | −9.63 | −1.30 | +0.04 | −0.48 | −3.91 |
| Spinal cord | −1.56 | −2.33 | −5.88 | −8.68 | −0.49 | −0.30 | −3.58 | −2.75 |
| BrainStem | −1.77 | −0.35 | −13.57 | −4.11 | −0.68 | −0.06 | −8.82 | −0.79 |
| Oral cavity | +0.12 | −3.28 | +2.86 | −9.20 | 1.91 | −0.41 | +5.46 | +1.52 |
| Constrictors | −3.37 | −1.24 | −6.28 | −2.17 | −0.20 | +0.98 | −3.15 | −0.04 |
| Left middle ear | −3.40 | −5.33 | −10.05 | −9.06 | −1.77 | −10.51 | −4.78 | −16.46 |
| Esophagus | −1.82 | −3.36 | −6.80 | −11.89 | −0.80 | −1.34 | −2.02 | −7.73 |
| Mandible | +0.68 | −4.87 | +0.15 | −0.05 | 4.02 | −3.48 | +2.98 | −5.96 |
Figure 8.
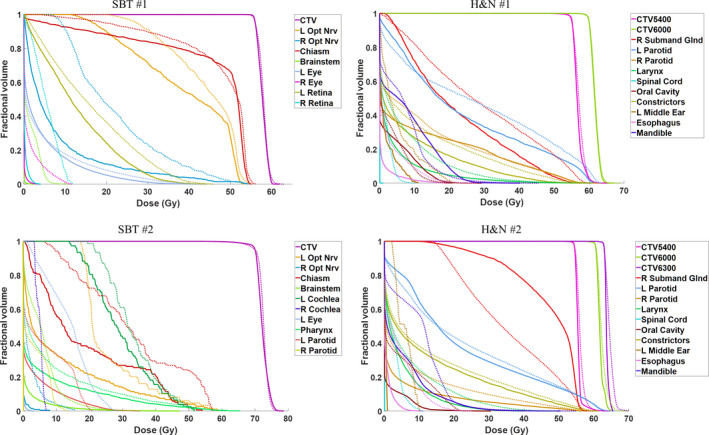
Comparison of nominal DVHs for four patients between the SHBOO‐FMO method (solid) and MAN‐WC method (dotted). [Color figure can be viewed at wileyonlinelibrary.com]
The SHBOO‐FMO plans achieved substantially better OAR sparing compared with the MAN‐WC plans. For example, in the SBT cases, the dose sparing of all the OARs was improved. In the SBT #2 patient, the SHBOO‐FMO plan reduced the max dose to the right optical nerve and left eye by 13.93 and 25.63 GyRBE from the MAN‐WC plan. In the H&N cases, the overall OAR sparing was also improved by SHBOO‐FMO method from MAN‐WC method, except for the increase in mean dose to the right submandibular gland. The average reduction of [Dmean, Dmax] of the SHBOO‐FMO plans from the MAN‐WC plans were [6.31, 6.55] GyRBE for the SBT cases and [1.89, 5.08] GyRBE for the H&N cases.
From Tables 6, and 7, the overall OAR sparing of SHBOO‐FMO was better than MAN‐SenR in the SBT cases and comparable with the MAN‐SenR in the H&N cases. The average reduction of [Dmean, Dmax] of the SHBOO‐FMO plans from the MAN‐SenR plans were of [2.09, 2.40] GyRBE for the SBT cases, and [−0.35, 2.49] GyRBE for the H&N cases.
4. Discussion
To the best of our knowledge, this work describes the first integrated IMPT optimization method that optimizes beam orientation and scanning‐spot intensities for both nominal dose conformality and robustness. It is known that the beam orientation directly impacts the IMPT dose conformality and robustness, requiring substantial manual effort from the dosimetrists in clinical IMPT planning to find better beam angles. However, a manual search is ineffective to identify beams from the enormous noncoplanar space for both dosimetry and robustness goals. The combination of group sparsity, lateral heterogeneity, and sensitivity into a formulation that allows global search on all feasible candidate beams is a major contribution of this study.
Proton beam has a unique feature that protons stop at the end of its Bragg Peak. This is different from photon beam. As a result, the experience in beam angle selection is different from the photon experience, in particular for noncoplanar beams. The results on tested patients show that the proposed robust BOO algorithm selects beams that are more resilient to range and setup uncertainties. The final SHBOO‐FMO plans better spared the OAR sparing compared with the voxel‐wise worst‐case method on the manual beams while maintaining similar robustness. Compared with the plans using manually selected beams and SenR FMO, the proposed method achieved better target coverage under simulated uncertainties.
Furthermore, the sensitivity regularization term helps to directly generate the fluence map which is more robust to range and setup uncertainties. In the limited existing IMPT BOO studies, the FMO is a nested subproblem that is solved post hoc, which not only is inefficient but also compromises plan optimality as the FMO results could influence the selected beams. Our algorithm integrates FMO and BOO in a single function to ensure that both the beam orientations and the spot intensities are matched for the desired dosimetry and robustness. The second important aspect of our study is that rather than the commonly used worst‐case scenario optimization method for FMO, we apply sensitivity regularization to improve the plan robustness against errors. This nonscenario‐based method can be easily and efficiently incorporated into the optimization framework and provides the flexibility between the dosimetry and the robustness. Our previous study41 showed that the sensitivity regularization is more effective to mitigate range uncertainties than setup uncertainties. The latter weakness is largely remedied in the current framework by incorporating lateral tissue heterogeneity in the BOO.
Compared with GSBOO16 or SenR41 alone, the planning time of SHBOO‐FMO is longer. The computational cost of the proposed method attributes to two main components: the preoptimization calculation and optimization of the objective function. Preoptimization includes calculating a dose calculation matrix, heterogeneity index, and sensitivity vector for each candidate beam. Under the analytical calculation model, the dose calculation and heterogeneity evaluation, in theory, could have shared the same ray tracing step to reduce the calculation time shown in Table 3. Calculation of the sensitivity is more time‐consuming. However, this parallel calculation process can be accelerated using the modern graphics processing unit (GPU) platform. Further acceleration is expected using a nonuniform sampling of the dose matrix to have a higher resolution in the CTV and its vicinity and lower resolution elsewhere.
For the optimization step, the problem (8) itself is a large‐scale problem due to the extra freedom of proton energy in IMPT and a large number of noncoplanar candidate beams used in this study. With the linear formulation of the sensitivity regularization term and the proximal operators derived in our previous work,16 we are able to efficiently solve the problem with FISTA, which converges at a rate of O(1/k 2) among the first‐order methods.44 Moreover, by adding the sensitivity regularization term, the time spent on beam pruning within the SHBOO method is reduced to approximately half of the initial group sparsity‐based BOO method.
It is necessary to clarify that the study only handles range uncertainties and setup errors from interfractional setup variations. Other sources of uncertainties such as intrafractional respiratory motion and anatomy changes, which heavily affect the beam selection process, require separate approaches to tackle. Biological effect is another important factor to consider in BOO. In our future work, linear energy transfer (LET) will be included in this framework to encourage selecting beams with a higher biological effect on the target and lower biological risk on the OARs.
5. Conclusions
We developed a novel IMPT robust optimization method, which efficiently solved robust BOO and FMO in a unified framework, generating plans with superior dosimetry and good robustness.
Conflict of interest
The authors have no relevant conflict of interest to disclose.
Acknowledgment
This research is supported by NIH Grants Nos. R44CA183390, R43CA183390, R01CA188300 and R01CA230278.
Appendix A.
To solve an optimization problem using FISTA, the problem needs to be formulated in the following form:
| (A1) |
where f is a smooth convex function, which is continuously differentiable with Lipschitz continuous gradient (); g is a function which is possibly nonsmooth, but has a proximal operator that can be evaluated efficiently. The proximal operator with step size t> 0 for function g is defined by:
| (A2) |
Once the optimization problem is formulated as in Equation (A1) and the conditions for f( x ) and g( x ) are satisfied, FISTA is relatively straightforward to implement as it only involves elementary matrix‐vector arithmetic operations and inexpensive proximal operator evaluations. FISTA with line search is used in this work, which follows the steps shown in Table A1.
Table A1.
Pseudo code for FISTA with line search.
| FISTA with line search | ||
|---|---|---|
| Initialize x 0:= 0, v 0:= x 0, t 0> 0, 0 < r < 1 | ||
| for k = 1,2,…,n, do | ||
|
| ||
| Repeat | ||
|
| ||
|
| ||
|
| ||
| break if | ||
|
| ||
|
| ||
|
| ||
|
| ||
| end | ||
| return x |
In the problem (8), the objective function can be rewritten in the following format:
| (A3) |
where is an indicator function on non‐negative orthant, with its th element equal to 0 if and otherwise.
For the quadratic fidelity formulation, the gradient of is given by:
| (A4) |
is a separable sum: , where
| (A5) |
Following the separable sum rule, the problem evaluating the proximal operator of reduces to independently evaluating the proximal operators of the functions . To simplify notation, we derive an expression for the proximal operator of the function . The proximal operator of function is.16
| (A6) |
The form of proximal operator for L2, 1/2‐norm is known41:
| (A7) |
Using these formulas for the gradient of the function and the proximal operator of function , the problem (8) is readily solved using FISTA.
Reference
- 1. Kanai T, Kawachi K, Kumamoto Y, et al. Spot scanning system for proton radiotherapy. Med Phys. 1980;7:365–369. [DOI] [PubMed] [Google Scholar]
- 2. Lomax A. Intensity modulation methods for proton radiotherapy. Phys Med Biol. 1999;44:185–205. [DOI] [PubMed] [Google Scholar]
- 3. Jäkel O, Debus J. Selection of beam angles for radiotherapy of skull base tumours using charged particles. Phys Med Biol. 2000;45:1229–1241. [DOI] [PubMed] [Google Scholar]
- 4. Trofimov A, Nguyen PL, Coen JJ, et al. Radiotherapy treatment of early‐stage prostate cancer with IMRT and protons: a treatment planning comparison. Int J Radiat Oncol Biol Phys. 2007;69:444–453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Kase Y, Yamashita H, Fuji H, et al. A treatment planning comparison of passive‐scattering and intensity‐modulated proton therapy for typical tumor sites. J Radiat Res. 2012;53:272–280. [DOI] [PubMed] [Google Scholar]
- 6. Bortfeld T, Schlegel W. Optimization of beam orientations in radiation therapy: some theoretical considerations. Phys Med Biol. 1993;38:291–304. [DOI] [PubMed] [Google Scholar]
- 7. Li Y, Yao J, Yao D. Automatic beam angle selection in IMRT planning using genetic algorithm. Phys Med Biol. 2004;49:1915–1932. [DOI] [PubMed] [Google Scholar]
- 8. Pugachev A, Li JG, Boyer AL, et al. Role of beam orientation optimization in intensity‐modulated radiation therapy. Int J Radiat Oncol Biol Phys. 2001;50:551–560. [DOI] [PubMed] [Google Scholar]
- 9. Li Y, Yao D, Yao J, Chen W. A particle swarm optimization algorithm for beam angle selection in intensity‐modulated radiotherapy planning. Phys Med Biol. 2005;50:3491–3514. [DOI] [PubMed] [Google Scholar]
- 10. Djajaputra D, Wu Q, Wu Y, Mohan R. Algorithm and performance of a clinical IMRT beam‐angle optimization system. Phys Med Biol. 2003;48:3191–3212. [DOI] [PubMed] [Google Scholar]
- 11. Wang X, Zhang X, Dong L, Liu H, Wu Q, Mohan R. Development of methods for beam angle optimization for IMRT using an accelerated exhaustive search strategy. Int J Radiat Oncol Biol Phys. 2004;60:1325–1337. [DOI] [PubMed] [Google Scholar]
- 12. Dias J, Rocha H, Ferreira B, Lopes MC. IMRT beam angle optimization using dynamically dimensioned search. IFMBE Proceedings. 2014;42:1–4. [Google Scholar]
- 13. Cao W, Lim GJ, Lee A, et al. Uncertainty incorporated beam angle optimization for IMPT treatment planning. Med Phys. 2012;39:5248–5256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Cao W, Lim GJ, Li Y, Zhu XR, Zhang X. Improved beam angle arrangement in intensity modulated proton therapy treatment planning for localized prostate cancer. Cancers (Basel). 2015;7:574–584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Lim GJ, Kardar L, Cao W. A hybrid framework for optimizing beam angles in radiation therapy planning. Ann Oper Res. 2014;217:357–383. [Google Scholar]
- 16. Gu W, O'Connor D, Nguyen D, et al. Integrated beam orientation and scanning‐spot optimization in intensity‐modulated proton therapy for brain and unilateral head and neck tumors. Med Phys. 2018;45:1338–1350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Wilson RR. Radiological use of fast protons. Radiology. 1946;47:487–491. [DOI] [PubMed] [Google Scholar]
- 18. Lomax AJ, Boehringer T, Coray A, et al. Intensity modulated proton therapy: a clinical example. Med Phys. 2001;28:317–324. [DOI] [PubMed] [Google Scholar]
- 19. Lomax AJ. Intensity modulated proton therapy and its sensitivity to treatment uncertainties 2: the potential effects of inter‐fraction and inter‐field motions. Phys Med Biol. 2008;53:1043–1056. [DOI] [PubMed] [Google Scholar]
- 20. Pflugfelder D, Wilkens JJ, Szymanowski H, Oelfke U. Quantifying lateral tissue heterogeneities in hadron therapy. Med Phys. 2007;34:1506–1513. [DOI] [PubMed] [Google Scholar]
- 21. Unkelbach J, Chan TCY, Bortfeld T. Accounting for range uncertainties in the optimization of intensity modulated proton therapy. Phys Med Biol. 2007;52:2755–2773. [DOI] [PubMed] [Google Scholar]
- 22. Liu W, Zhang X, Li Y, Mohan R. Robust optimization of intensity modulated proton therapy. Med Phys. 2012;39:1079–1091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Liao L, Lim GJ, Li Y, et al. Robust optimization for intensity modulated proton therapy plans with multi‐isocenter large fields. Int J Part Ther. 2016;3:305–311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Liu W, Li Y, Li X, Cao W, Zhang X. Influence of robust optimization in intensity‐modulated proton therapy with different dose delivery techniques. Med Phys. 2012;39:3089–3101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Liu W, Mohan R, Park P, et al. Dosimetric benefits of robust treatment planning for intensity modulated proton therapy for base‐of‐skull cancers. Pract Radiat Oncol. 2014;4:384–391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Unkelbach J, Alber M, Bangert M, et al. Robust radiotherapy planning. Phys Med Biol. 2018;63:22TR02. [DOI] [PubMed] [Google Scholar]
- 27. Liu W, Frank SJ, Li X, et al. Effectiveness of robust optimization in intensity‐modulated proton therapy planning for head and neck cancers. Med Phys. 2013;40:051711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Liu W, Liao Z, Schild SE, et al. Impact of respiratory motion on worst‐case scenario optimized intensity modulated proton therapy for lung cancers. Pract Radiat Oncol. 2015;5:e77–e86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Li H, Zhang X, Park P, et al. Robust optimization in intensity‐modulated proton therapy to account for anatomy changes in lung cancer patients. Radiother Oncol. 2015;114:367–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. van der Voort S, van de Water S, Perkó Z, Heijmen B, Lathouwers D, Hoogeman M. Robustness recipes for minimax robust optimization in intensity modulated proton therapy for oropharyngeal cancer patients. Int J Radiat Oncol Biol Phys. 2016;95:163–170. [DOI] [PubMed] [Google Scholar]
- 31. van de Water S, van Dam I, Schaart DR, Al‐Mamgani A, Heijmen BJM, Hoogeman MS. The price of robustness; impact of worst‐case optimization on organ‐at‐risk dose and complication probability in intensity‐modulated proton therapy for oropharyngeal cancer patients. Radiother Oncol. 2016;120:56–62. [DOI] [PubMed] [Google Scholar]
- 32. van Dijk LV, Steenbakkers RJHM, ten Haken B, et al. Robust Intensity Modulated Proton Therapy (IMPT) increases estimated clinical benefit in head and neck cancer patients. PLoS ONE. 2016;11(3):e0152477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Pflugfelder D, Wilkens JJ, Oelfke U. Worst case optimization: A method to account for uncertainties in the optimization of intensity modulated proton therapy. Phys Med Biol. 2008;53:1689–1700. [DOI] [PubMed] [Google Scholar]
- 34. Fredriksson A, Forsgren A, Hårdemark B. Minimax optimization for handling range and setup uncertainties in proton therapy. Med Phys. 2011;38:1672–1684. [DOI] [PubMed] [Google Scholar]
- 35. Fredriksson A, Bokrantz R. A critical evaluation of worst case optimization methods for robust intensity‐modulated proton therapy planning. Med Phys. 2014;41:081701. [DOI] [PubMed] [Google Scholar]
- 36. Liu W, Frank SJ, Li X, Li Y, Zhu RX, Mohan R. PTV‐based IMPT optimization incorporating planning risk volumes vs robust optimization. Med Phys. 2013;40:021709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Chen W, Unkelbach J, Trofimov A, et al. Including robustness in multi‐criteria optimization for intensity‐modulated proton therapy. Phys Med Biol. 2012;57:591–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Stuschke M, Kaiser A, Pöttgen C, Lübcke W, Farr J. Potentials of robust intensity modulated scanning proton plans for locally advanced lung cancer in comparison to intensity modulated photon plans. Radiother Oncol. 2012;104:45–51. [DOI] [PubMed] [Google Scholar]
- 39. Casiraghi M, Albertini F, Lomax AJ. Advantages and limitations of the “worst case scenario” approach in IMPT treatment planning. Phys Med Biol. 2013;58:1323–1339. [DOI] [PubMed] [Google Scholar]
- 40. Li Y, Niemela P, Liao L, et al. Selective robust optimization: a new intensity‐modulated proton therapy optimization strategy. Med Phys. 2015;42:4840–4847. [DOI] [PubMed] [Google Scholar]
- 41. Gu W, Ruan D, O'Connor D, et al. Robust optimization for intensity‐modulated proton therapy with soft spot sensitivity regularization. Med Phys. 2019;46:1408–1425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Bueno M, Paganetti H, Duch MA, Schuemann J. An algorithm to assess the need for clinical Monte Carlo dose calculation for small proton therapy fields based on quantification of tissue heterogeneity. Med Phys. 2013;40:081704. [DOI] [PubMed] [Google Scholar]
- 43. Toramatsu C, Inaniwa T. Beam angle selection incorporation of anatomical heterogeneities for pencil beam scanning charged‐particle therapy. Phys Med Biol. 2016;61:8664–8675. [DOI] [PubMed] [Google Scholar]
- 44. Beck A, Teboulle M. A fast iterative shrinkage‐thresholding algorithm for linear inverse problems. SIAM J Imaging Sci. 2009;2:183–202. 10.1137/080716542. [DOI] [Google Scholar]
- 45. Cisternas E, Mairani A, Ziegenhein P, Jäkel O, Bangert M. matRad – a multi‐modality open source 3D treatment planning toolkit. IFMBE Proc. 2015;51:1608–1611. [Google Scholar]
- 46. Wieser HP, Cisternas E, Wahl N, et al. Development of the open‐source dose calculation and optimization toolkit matRad. Med Phys. 2017;44:2556–2568. [DOI] [PubMed] [Google Scholar]
- 47. Safai S, Bula C, Meer D, Pedroni E. Improving the precision and performance of proton pencil beam scanning. Transl. Cancer Res. 2012;1(3). http://tcr.amegroups.com/article/view/599
- 48. Gottschalk B, Koehler AM, Schneider RJ, Sisterson JM, Wagner MS. Multiple Coulomb scattering of 160 MeV protons. Nucl Inst Methods Phys Res B. 1993;74:467–490. [Google Scholar]
- 49. Grégoire V, Mackie TR. State of the art on dose prescription, reporting and recording in intensity‐modulated radiation therapy (ICRU report No. 83). Cancer/Radiothérapie. 2011;15:555–559. 10.1016/j.canrad.2011.04.003. [DOI] [PubMed] [Google Scholar]
- 50. Trofimov A, Unkelbach J, DeLaney TF, Bortfeld T. Visualization of a variety of possible dosimetric outcomes in radiation therapy using dose‐volume histogram bands. Pract Radiat Oncol. 2012;2:164–171. [DOI] [PMC free article] [PubMed] [Google Scholar]


