Residual structures and transient long-range interactions of p53 transactivation domain: Assessment of explicit solvent protein force fields

Abstract

Molecular dynamics simulations using physics-based atomistic force fields have been increasingly used to characterize the heterogeneous structural ensembles of intrinsically disordered proteins (IDPs). To evaluate the accuracy of latest atomistic explicit-solvent force fields in modelling larger IDPs with non-trivial structural features, we focus on the 61-residue N-terminal transactivation domain (TAD) of tumor suppressor p53, an important protein in cancer biology that has been extensively studied and abundant experimental data is available for evaluation of simulated ensembles. We performed extensive replica exchange with solute tempering simulations, in excess of 1.0 μs/replica, to generate disordered structural ensembles of p53-TAD using six latest explicit solvent protein force fields. Multiple local and long-range structural properties, including chain dimension, residual secondary structures, and transient long-range contacts, were analyzed and compared against available experimental data. The results show that IDPs such as p53-TAD remains highly challenging for atomistic simulations due to conformational complexity and difficulty in achieving adequate convergence. Structural ensembles of p53-TAD generated using various force fields differ significantly from each other. The a99SB-disp force field demonstrates the best agreement with experimental data at all levels, and proves to be suitable for simulating unbound p53-TAD and how its conformational properties may be modulated by phosphorylation and other cellular signals or cancer-associated mutations. Feasibility of such detailed structural characterization is a key step towards establishing the sequence-disordered ensemble-function-disease relationship of p53 and other biologically important IDPs.

Graphical Abstract

Introduction

Lacking well-defined three-dimensional structures under physiological conditions, intrinsically disordered proteins (IDPs) are functional proteins that deviate from the traditional protein structure-function paradigm^1–10. Sequence analysis have shown that nearly one half of eukaryotic proteins contain disordered regions whose lengths are least 30 amino acids¹¹, which implies that many proteins may rely on intrinsic disorder to perform biological functions. Indeed, IDPs could specifically interact with many cellular targets under different conditions, thus playing critical roles in cellular signaling and regulation^{5, 7, 8, 11–13}. Missense mutation of IDPs, changes in IDP concentration, or aggregation of IDPs are frequently associated with human diseases, including cancers, cardiovascular diseases, diabetes, and neurodegenerative diseases^{11, 13–16}. Thus, there is a great need to characterize the detailed structural and dynamic properties of IDPs in order to better understand the functional mechanisms of IDPs in many biological processes.

The highly dynamic and heterogeneous conformations of IDPs pose great challenges in their experimental characterization. They must be described using ensembles of diverse structures that does not lend themselves to description using traditional methods that are geared toward describing a coherent set of similar structures. For a disordered protein state, only ensemble-averaged properties can be measured in most cases^17–21, which alone are insufficient to uniquely define the heterogeneous ensemble^{17, 22, 23}. In contrast, molecular dynamics (MD) simulations using physics-based atomistic force fields could provide high temporal and spatial resolution information for the system of interest, thus offering a powerful tool in characterizing the detailed structures of IDPs. Properly validated using experimental data, the simulated ensemble could provide the much needed basis for establishing how intrinsic conformational disorder mediates protein function and how such functional mechanism may be altered in diseases.

Nevertheless, challenges still exist in atomistic simulations of IDPs. First of all, IDPs usually are more expanded than folded proteins with the same number of residues, requiring larger explicit solvent simulation boxes and significantly increasing the computational cost. Efficient enhanced sampling techniques^24–27 and/or implicit treatment of solvent^28–31 are often needed to reduce the computational cost of adequate sampling of the large conformational space of IDPs. However, a more fundamental challenge lies in the accuracy of current protein force fields, since the quality of force field ultimately determines the reliability of simulated ensembles. The free energy landscape of an IDP often displays a multitude of comparably shallow minima^{32, 33}, and accurate description of relative prevalence of these important sub-states has pushed the limit of protein force fields. In fact, the need for accurate simulation of IDPs has prompted intensive efforts towards developing improved atomistic force fields^{28, 34–42}.

It has been shown that many modern atomistic force fields could describe folded proteins and some small IDPs quite well. For example, 12 structurally distinct proteins have been shown⁴³ to reversibly fold into their native states using the CHARMM22* force field³⁹. By systematic comparison against 524 NMR measurements on very short peptides (≤ 4 residues) and a folded protein, ubiquitin⁴⁴, ff99sb-ildn-phi⁴⁵ or ff99sb-ildn-NMR⁴⁶ force fields were found to yield errors that are comparable to the experimental uncertainty. In another benchmark study⁴⁷, both ff99SB*-ILDN^{42, 48, 49} and CHARMM22*³⁹ were found to reproduce experimental data on folded proteins and small IDPs (10–15 residues) quite well. As for slightly larger IDPs, for instance, the 24-residue arginine/serine (RS) peptide, CHARMM 22*³⁹ was observed to agree best with experimental measurement⁵⁰. However, it has also been increasingly recognized that most explicit solvent atomistic force fields often generate overly compact conformations for the unfolded state of proteins and larger IDPs^{37, 38, 51}. Several strategies then have been proposed to alleviate this problem. For example, a new water force field, TIP4P-D³⁷, has been developed, where water dispersion interaction was increased by approximately 50% compared with the TIP3P water force field⁵². Another approach was to scale up the Lennard-Jones (LJ) interactions between protein and water, such as in the Amber ff03ws force field³⁸. More recently, the CHARMM36m³⁵ and a99SB-disp³⁴ force fields were developed based on extensive simulations of tens of folded and disordered proteins and peptides, demonstrating impressive levels of accuracy in simulating both folded and intrinsically disordered proteins.

These exciting developments in protein force field optimization have now paved the way for broader application of atomistic simulations to larger and more complex IDPs of biological and biomedical interest. In this work, we focus on the N-terminal transactivation domain of tumor suppressor p53 (p53-TAD, residues 1–61), one of the most frequently mutated proteins in human cancers^{53, 54}. The stability and activity of p53 are tightly controlled by its interactions with key regulators, such as the E3 ubiquitin ligase MDM2 and transcriptional coactivator CBP/p300⁵⁵. These interactions are mediated through the intrinsically disordered TAD domain of p53, which can specifically recognize these targets and often gain stable secondary and tertiary structures upon binding. Under normal cellular conditions, p53-TAD binds more tightly to MDM2, leading to polyubiquitination and degradation of p53^{56, 57}. Under prolonged genotoxic stress, p53-TAD accumulates phosphorylation at multiple sites, which reduces binding affinity to MDM2 and enhances binding to the CBP/p300, resulting in stabilization and activation of p53^58–62. So far, the molecular mechanisms of how phosphorylation modulates binding affinity to MDM2 and CBP/p300 is not obvious. The effects of phosphorylation on binding is typically understood by examining how it may provide additional interaction sites or disrupt the existing binding interface in the complex state. However, available structures of p53-TAD complexes^63–66 suggest that most phosphorylation sites are outside of the binding interface. Instead, the effects of p53-TAD phosphorylation are likely achieved through modulation of the unbound state, where the disordered ensemble is poised to respond sensitive to posttranslational modifications and mutations. Altered level of partially formed secondary structures and/or tertiary contacts may lead to different folding conformational entropy cost upon specific binding and modulate the binding affinity^{67, 68}. Therefore, the disordered ensemble of p53-TAD is likely a central conduit of p53 regulation, and its detailed characterization will be critical for establishing the sequence-disordered ensemble-function-disease relationship of p53.

As a key step towards detailed characterization of the structural ensembles of p53-TAD using MD simulations, one needs to carefully examine if the current protein force field could accurately recapitulate key structural features revealed by available experimental measurements. Due to its biological and biomedical significance, p53-TAD has been extensively characterized using several experimental techniques^69–74, including NMR, single-molecule FRET (smFRET), and time-resolved FRET (TR-FRET). These studies have reveal that p53-TAD contains non-trivial structural features, including multiple residual helical elements^{69, 72, 74} and transient long-range contact formation^{73, 75}. The conformational complexity and availability of large amount of experimental data also makes p53-TAD an ideal model system for evaluating the quality of current protein force fields for simulating of increasingly complex IDPs of biological interest.

In the present work, we evaluate six of the latest protein force fields including CHARMM36m³⁵ (herein termed c36m), CHARMM36m³⁵ with an alternative water force field³⁵ (herein termed c36mw), CHARMM22*^{39, 76, 77} (herein termed c22*), ff99SB-ILDN^{48, 49}, ff99SB-ILDN⁴⁹ with TIP4P-D water force field³⁷ (herein termed ff99SB-ILDN-TIP4P-D), and a99SB-disp³⁴. To obtain sufficient sampling of relevant conformational space for the 61-residue p53-TAD peptide, we deployed the replica exchange with solute tempering (REST2) enhanced sampling technique^{27, 78}, which allows tempering on only the region of interest (e.g., protein) and dramatically reduce the computational cost of replica exchange types of simulations in explicit solvent^79–82. Two independent REST2 simulations were performed starting from distinct conformations for each force field examined, to allow rigorous evaluation of the convergence of simulated ensembles. The aggregated simulation time is over 192 μs. A wide range of local and long-range structural features of p53-TAD were carefully analyzed and compared directly against available experimental measurements.

Methods

Simulation details

The p53-TAD domain (residues 1–61: MEEPQ SDPSV EPPLS QETFS DLWKL LPENN VLSPL PSQAM DDLML SPDDI EQWFT EDPGP D) was studied in this work. The N- and C- termini were capped with an acetyl group and N-methyl amide, respectively. Six latest protein force fields were examined, including c36m³⁵, c36mw³⁵, c22*^{39, 76, 77}, ff99SB-ILDN^{48, 49}, ff99SB-ILDN-TIP4P-D^{37, 49}, and a99SB-disp³⁴. For each force field, two independent REST2 simulations were performed, one starting from a highly helical state (i.e., control run) and the other one starting from an extended state (i.e., folding run). This allows rigorous evaluation of simulation convergence. The protein was simulated in a truncated octahedron box containing ~24,000 water molecules. The shortest distance between two opposite hexagons was ~ 9.8 nm. 14 Na⁺ were added to neutralize the system.

All simulations were carried out using GROMACS 5.1.4^{83, 84} patched with PLUMED 2.3.0^{81, 85, 86}. The initial conformation was first energy minimized using a steepest descent algorithm for 6000 steps. NVT simulation at 298 K was then performed for 100 ps, following by 1 ns of NPT simulation at 298 K and 1 atm, during which the position of protein heavy atoms was restrained using harmonic potentials with force constants of 1000 kJ/mol/nm². The system was then equilibrated under the same NPT condition for another 1 ns, removing all restraints on the protein. From this NPT simulation, the mean volume of the simulation box was calculated, and one conformation was selected with its volume closest to the mean volume. This conformation was then used as the initial structure for the production NVT run at 298 K. Only the protein was subjected to tempering, which was achieved by scaling the solute-solute and solute-solvent interactions by λ and $\sqrt{\lambda }$, respectively. 16 replicas were used in all cases, with λ values set to 1.00, 0.97, 0.93, 0.90, 0.87, 0.84, 0.81, 0.79, 0.76, 0.73, 0.71, 0.68, 0.66, 0.64, 0.62 and 0.60, respectively. They correspond to 16 exponentially spaced effective temperatures of the protein, ranging from 298 K to 500 K. Replica exchange was attempted every 2 ps, and the averaged exchange acceptance ratio was ~25%. Each simulation lasted for ~1 μs/replica. In simulations using c36m³⁵, c36mw³⁵, or c22*^{39, 76, 77} force field, van der Waals interactions were truncated at 1.2 nm, with the force smoothly switched to zero starting from 1.0 nm and the neighboring list updated every 10 steps. When ff99SB-ILDN⁴⁹, ff99SB-ILDN-TIP4P-D, or a99SB-disp³⁴ was used, the van der Waals interactions were cut off at 1.0 nm with the neighboring list updated every 5 steps. For all simulations, long-range electrostatic interactions were treated using the Particle Mesh Ewald (PME) method⁸⁷. Lengths of all bonds involving hydrogen atoms were constrained using the LINCS algorithm⁸⁸, which allows for an integration time step of 2 fs.

Analysis

By examining the evolution of secondary structure and radius of gyration of p53-TAD, the first 300 ns trajectories of each REST2 simulation were excluded from all analysis to remove the initial condition dependence. Simulated structure ensembles were constructed by collecting conformations sampled in the replica of λ = 1.00. Unless otherwise specified, all structural analysis were performed using the GROMACS toolset^{83, 84} and in-house scripts. Chemical shifts of simulated structures were calculated using SHIFTX2⁸⁹, and the ensemble-averaged values were compared with experimental data⁹⁰. For secondary chemical shift analysis, random coil values^{91, 92} were subtracted from both calculated and experimental⁹⁰ chemical shifts. For conformational clustering analysis, trajectories from independent control and folding simulations were combined. For such a large and highly dynamic system, the root-mean-square deviation (RMSD) in the Cartesian coordinate space is not an optimal distance metric. Therefore, featurization was first performed using the DRID algorithm, distribution of reciprocal of interatomic distances⁹³, implemented in MSMBuilder 3.6.1⁹⁴, with only Cα atoms selected in this calculation. K-means clustering was then performed in the DRID space. Different numbers of total clusters were tested, including 50, 100, 500, 1000, 5000, and 10000. Final results were reported for 1000 total clusters, because smaller values would result in large clustering error, while larger values do not significantly decrease the clustering error, i.e., sum of squared distances of samples to their closest cluster center (see Fig. S1).

The paramagnetic relaxation enhancement (PRE) effects of four sites (D7, E28, A39 and D61) were calculated for simulated ensembles, and directly compared with previously published experimental results⁷¹. The ratios of peak intensities of oxidized (paramagnetic) and reduced (diamagnetic) resonances were calculated according to $\frac{I_{Ox}}{I_{red}}=\frac{R_{2}exp\left(-R_2^{sp}t\right)}{R_2+R_2^{sp}}$ where $R_2^{sp}=K<r^{-6}>\left(4{\tau }_c+\frac{3{\tau }_c}{1+{\omega }_H^2{\tau }_c^2}\right)$^95,96 Here r is the distance between spin label and residue; K is 1.23×10⁻³² cm⁶s⁻²; and <> indicates ensemble averaging. Consistent with experimental conditions⁷¹, Larmor frequency ω_H is 600 MHz; the correlation time τ_c is 3.3 ns; the intrinsic R₂ relaxation rate is 16 s⁻¹; and the INEPT evolution time t is set to 9.8 ms. Since our simulations didn’t include the paramagnetic spin labels used in the actual NMR measurement⁷¹, Cα-Cα distances were used to approximate the electron-proton distances.

Results and Discussion

Evaluation of self-consistency of simulated ensembles

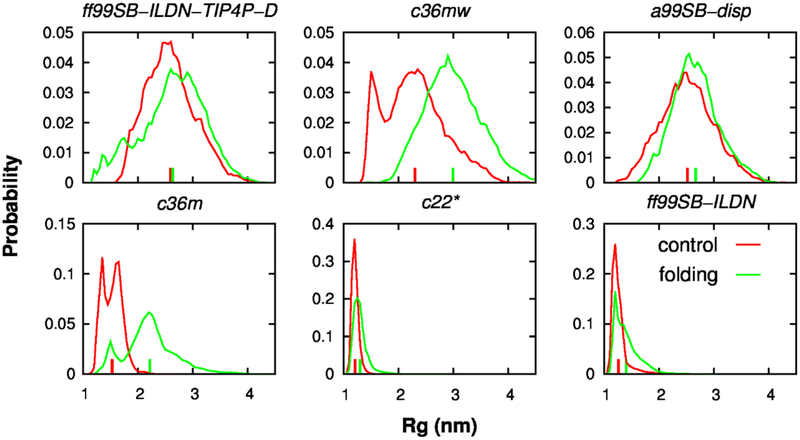
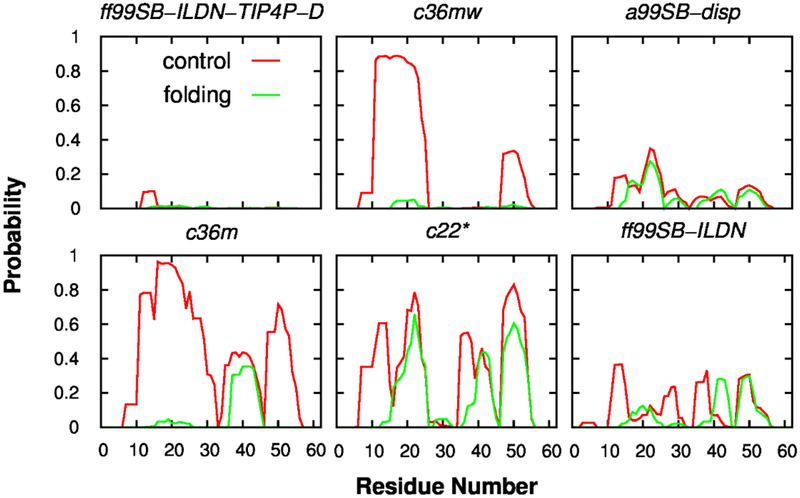
The p53-TAD peptide provides an exceptional model system to understand the sequence-disordered ensemble-function-disease relationship of IDPs. In order to reliably simulate the disordered ensembles of p53-TAD using de novo simulations, the first, and probably one of the most important steps is to generate well-converged simulations. Here, the convergence of our REST2 simulations was mainly assessed by comparing the structural ensembles generated from the independent control and folding runs (see Methods). As shown in Fig. 1, the overall dimension of p53-TAD (indicated by the radius of gyration, R_g) appears well-converged in c22*, ff99SB-ILDN, ff99SB-ILDN-TIP4P-D, and a99SB-disp simulations. Similar observations could be made for the distributions of end-to-end distance (Fig. S2). Acceptable convergence at the level of secondary structure is also found for the REST2 simulations using these four force fields (Fig. 2). This was further supported by comparing the results calculated from different segments of each trajectory, demonstrating the self-consistency of each individual simulation (Fig. S3 and S4).

Figure 1.

Probability distributions of R_g of p53-TAD calculated from independent control (red) and folding (green) simulations, for all six force fields examined in this work. The corresponding ensemble averaged values are indicated using vertical bars on the x-axis.

Figure 2.

Residue helicity profiles of p53-TAD calculated from independent control (red) and folding (green) simulations using six force fields.

However, it seems challenging to obtain convergence for c36m and c36mw simulations, as reflected by the distributions of R_g (Fig. 1), end-to-end distance (Fig. S2) and residue helicity profiles (Fig. 2). For example, as shown in Fig. 2, residues 10–25 barely unfolded in the control simulations (where initial structures were highly helical), while it remained full disordered in the folding simulations (where initial structures were highly extended). As a result, REST2 simulations as configured were not able to generate converged ensembles when these two force fields were used to study p53-TAD. We note that both sets of simulations appeared to reach steady states, where distributions for individual control or folding REST2 runs stopped changing (Fig. S3 and S4). This again highlights the importance of using independent runs with drastically different initial conformations to rigorously evaluate convergence in IDP simulations. Two factors may contribute to slow convergence of c36m and c36mw simulations. The free energy barrier separating helical and unfolded coil states may be higher in these two force fields such that longer helix-coil transition timescales may have significantly slowed down the convergence of REST2 simulations. On the other hand, the apparent difficulty of achieving convergence with REST2 simulations using c36m and c36mw may also be due to imperfect compensation between the scaled solute-solute and solute-solvent interaction energies, which will hinder the sampling efficiency of REST type of simulations⁷⁸. To further understand this issue, we extracted the last conformations at the λ = 1.00 condition from the four REST2 simulations to initiate four multi-μs MD simulations at 298 K. After about another 1 μs, the seemingly long-lived helical states for residues 10–25 from control REST2 simulations became unfolded in both c36m and c36mw force folds; yet partial helix refolding was not observed in any of these 7 μs simulations (see Fig. S5). This suggests that lack of convergence of REST2 simulations in c36m and c36mw is likely attributed to the force field characteristics instead of the REST2 protocol. Due to a lack of convergence, the quality of c36m and c36mw will not be reliably evaluated based on the current REST2 and constant temperature simulations. Therefore, we will mainly focus on evaluating c22*, ff99SB-ILDN, ff99SB-ILDN-TIP4P-D, and a99SB-disp in the remainder of this study, where well-converged structural ensembles are available from REST2 simulations.

Overall dimension of p53-TAD varies significantly among different force fields

Previous NMR study has shown that under normal cellular conditions, p53-TAD could interact simultaneously with HDM2 (the human homolog of MDM2) and CBP domains, thus forming ternary complexes⁵⁹. The fate of these ternary complexes can be regulated by many cellular events, such as phosphorylation of p53-TAD, thus affecting the stability and activity of p53. According to this model, the compactness of p53-TAD may have a consequence in its availability to these regulatory proteins and in coordinating various interactions, as proposed previously⁷⁵. Therefore, in order to study the “structure”-function relationship of p53-TAD using de novo simulations, it is very important to model its overall dimension correctly. Here we examine if these six force fields could describe the level of compaction of p53-TAD. The results show that chain dimensions of simulated p53-TAD ensembles depend strongly on the force field used. For instance, simulations using c22* and ff99SB-ILDN yield significantly more compact ensembles compared to those generated by ff99SB-ILDN-TIP4P-D and a99SB-disp simulations (Fig. 1 and Fig. S2). The ensemble averaged R_g values were 1.26, 1.33, 2.61, and 2.60 nm in c22*, ff99SB-ILDN, ff99SB-ILDN-TIP4P-D and a99SB-disp simulations, respectively. This is not surprising as both of the latter two force fields have been parameterized specifically to overcome the over compaction bias of earlier force fields^{34, 37}. Despite a lack of convergence, scaling up protein-water interactions in the c36mw force field clearly leads to more expanded structural ensembles, which appears more in-line with results from ff99SB-ILDN-TIP4P-D and a99SB-disp simulations (Fig. 1 and S2). The Stokes radius of a slightly longer p53-TAD peptide (residues 1–73) was found to be 2.38 nm based on size exclusion chromatography⁷¹. Therefore, both c22* and ff99SB-ILDN, and likely c36m, overestimate the compaction of p53-TAD.

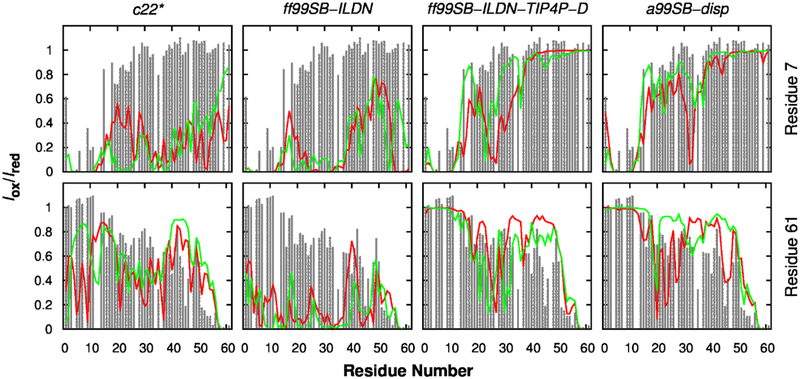
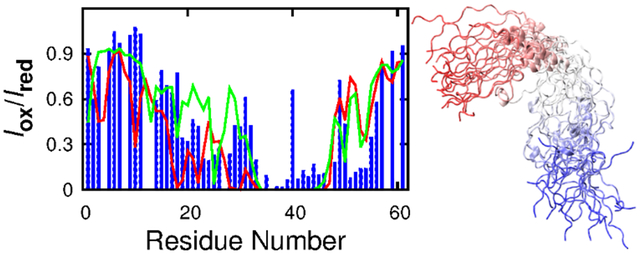
We further assess the ability of these force fields to correctly describe the overall compactness of p53-TAD as well as transient long-range ordering by comparing the back-calculated PRE effects with experimental measurements. PRE measurement provides ensemble-averaged distance information between the paramagnetic spin label at a specific residue location and all protons throughout the rest of the protein; it provides unparallelly rich information to examine the presence (and absence) of transient long-range ordering of the simulated ensembles. In Fig. 3, we compare the back-calculated PRE effects with experimental results on labelling at residues 7 and 61, where the terminal locations of the spin label provide particularly useful information on the peptide chain dimension. Quantitative comparison of experimental and back-calculated PRE effects is summarized in Table 1. These results clearly confirm that the simulated ensemble generated using c22* and ff99SB-ILDN are overly compact, leading to global over-estimation of PRE effects (Fig. 3). As for c36m and c36mw simulations, although not converged, better agreement with experimental PRE measurements appear to be achieved compared to the older c22* force field (Fig. S6 and Table 1), demonstrating their improvement in describing the overall dimension of IDPs. Moreover, ff99SB-ILDN-TIP4P-D and a99SB-disp simulations are able to reliably capture the chain dimension and long-range ordering of p53-TAD, generating conformational ensembles with minimal over-estimation of PRE effects (Fig. 3 and Table 1).

Figure 3.

Calculated (lines) and experimental (grey bars) PRE effects induced by paramagnetic spin labelling at residues 7 (top row) and 61 (bottom row). Red and green traces are calculated from independent control and folding simulations, respectively.

Table 1.

Root-mean-square (RMS) error of PRE effects of simulated ensembles in comparison with experimental measurements.

		c22*	ff99SB-ILDN	ff99SB-ILDN-TIP4P-D	a99SB-disp	c36m	36mw
Residue 7	Control	0.68	0.71	0.35	0.29	0.38	0.21
	Folding	0.69	0.70	0.23	0.19	0.50	0.35
Residue 28	Control	0.36	0.42	0.31	0.32	0.27	0.34
	Folding	0.34	0.39	0.24	0.34	0.35	0.43
Residue 39	Control	0.48	0.50	0.28	0.31	0.36	0.32
	Folding	0.49	0.48	0.26	0.24	0.37	0.31
Residue 61	Control	0.37	0.55	0.23	0.21	0.25	0.31
	Folding	0.34	0.60	0.26	0.22	0.32	0.34
Overall RMS error		0.49	0.56	0.27	0.27	0.36	0.33

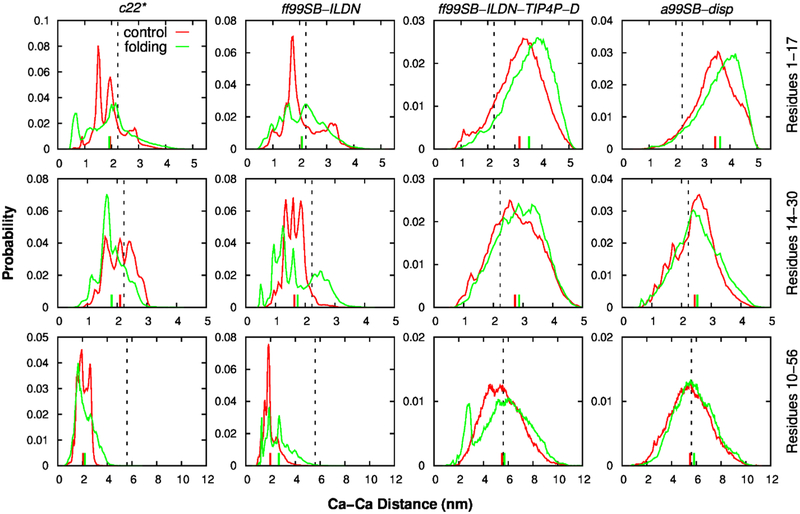
Ensemble-averaged distances between several pairs of residues of p53-TAD have also been determined previously using smFRET and TR-FRET measurement⁷⁰ (see Figs. 4 and S7). For the distances between residues 1 and 17 (Fig. 4 top row), results from c22* and Amber ff99SB-ILDN simulations agreed well with experimental values, while ff99SB-ILDN-TIP4P-D and a99SB-disp appeared to slightly overestimate this distance. For another residue pair, 14 and 30 (Fig. 4 middle row), all four force fields showed reasonable agreement with the experimental data. However, caution needs to be taken to interpret the absolute distance estimation from smFRET and TR-FRET experiments, since fluorescence properties and energy transfer also depends on environment and orientation of the dye⁹⁷. Therefore, the distances between these two residue pairs calculated from all simulations didn’t seem to qualitatively different from experimental measurement. On the other hand, the distance between residues 10 and 56 was significantly underestimated in c22* and ff99SB-ILDN simulations, while better agreement was observed for ff99SB-ILDN-TIP4P-D and a99SB-disp force fields (Fig. 4 bottom row). Since these two residues are close to N- and C-termini, respectively, in the primary sequence, it may be used to approximate the end-to-end distance and thus overall dimension of the peptide. The results again suggest that c22* and ff99SB-ILDN-derived structures are too collapsed and that ff99SB-ILDN-TIP4P-D and a99SB-disp can faithfully predict the chain dimension of p53-TAD.

Figure 4.

Probability distributions of distances between three pairs of residues, 1 and 17 (top row), 14 and 30 (middle row), and 10 and 56 (bottom row), calculated from independent control (red) and folding (green) simulations using four force fields. The corresponding ensemble averages were indicated as vertical bars. The vertical black line indicated experimental values from smFRET and TR-FRET measurements⁷⁰.

Dependence of p53-TAD secondary structure on force field

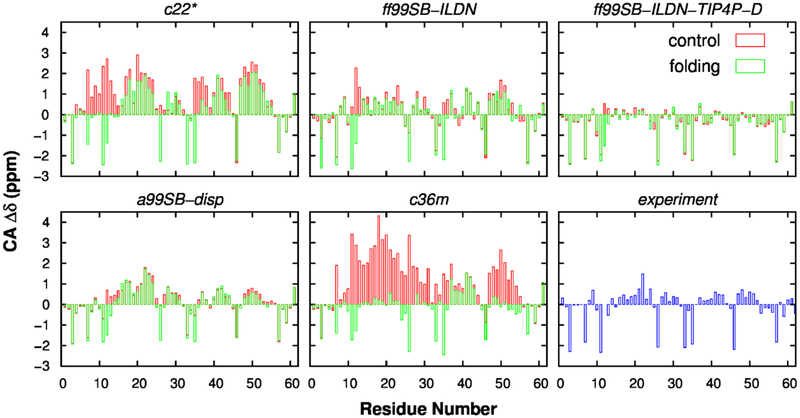
The level of secondary structure of IDPs is often finely tuned by their sequences, which is critical for signaling fidelity⁸. Many disease mutations in IDPs have been predicted to alter secondary structure with higher probabilities than functionally neutral mutations¹⁵, which may perturb the protein interaction network and lead to mis-regulation. Multiple partial helices have also been identified in p53-TAD^{69, 74} and suggested to play roles in mediating p53’s interactions with key regulators including MDM2 and CBP/p300⁵⁵. Cancer associated p53-TAD mutant K24N has been shown to reduce the helicity of residues 18–27⁷⁴. Therefore, it’s very important to evaluate how well current force fields can capture residual secondary structures. Like chain dimension, secondary structure content of p53-TAD also depends strongly on the chosen force field. The helical content in c22* simulations seemed to be the highest among these four force fields, where three segments (residues 15–25, 35–45 and 45–55) constantly showed helical propensity of at least 40% (Fig. 2). In contrast, there was almost no residual helical structure in both control and folding simulations using ff99SB-ILDN-TIP4P-D force field (Fig. 2). The residual helicities for the other two force fields, ff99SB-ILDN and a99SB-disp, were in between these two extremes. Previous NMR studies have shown that residues 17–29 were ~10% helical, and two turns were assigned to the regions of 40–44 and 48–52, respectively^{69, 74}. Nonetheless, continual sequential d_NN NOEs and negative secondary Hα chemical shifts were found in the latter two regions⁶⁹, implying that partial helical elements may exist. Results from a99SB-disp force field appear the most consistent with these experimental observations (see Fig. 2).

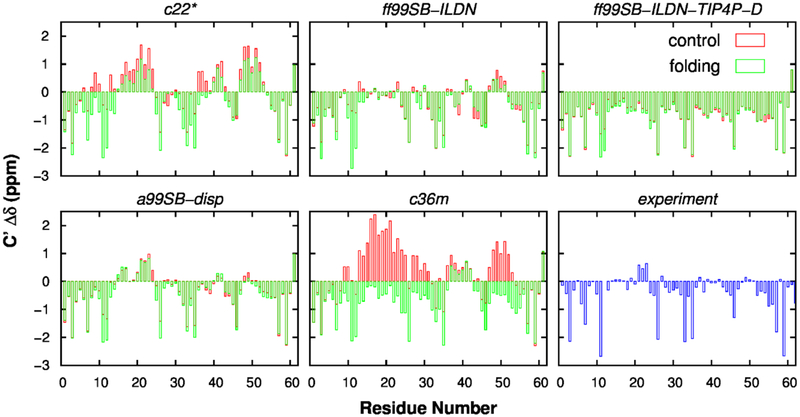
To better quantify the level of agreement of simulated ensembles with NMR results, we calculated the secondary chemical shifts of Cα and C’ atoms, which are sensitive to the secondary structure. The profiles of secondary chemical shift are shown in Figs. 5 and 6, and quantitative comparison between simulated and experimental results is summarized in Table 2. These results demonstrate that secondary chemical shifts of Cα and C’ atoms from a99SB-disp simulations agreed the best with experimental measurements, suggesting that this force field could properly describe the secondary structure propensity of p53-TAD. Note that SHIFTX2 could predict chemical shifts for folded proteins with RMS errors of 0.4412 and 0.5330 ppm for Cα and C’ atoms, respectively⁸⁹. Therefore, according to Table 2, results from ff99SB-ILDN force field also seem in reasonable agreement with experimental values. In contrast, the content of helical structure is significantly underestimated by ff99SB-ILDN-TIP4P-D and over-estimated by c22* (Figs. 5 and 6).

Figure 5.

Secondary chemical shift analysis for Cα atoms in p53-TAD. Calculations were performed using independent control (red) and folding (green) simulations for five force fields. Experimental results were obtained from previously published work⁹⁰.

Figure 6.

Secondary chemical shift analysis for C’ atoms in p53-TAD. Calculations were performed using independent control (red) and folding (green) simulations for five force fields. Experimental results were obtained from previously published work⁹⁰.

Table 2.

RMS error of Cα and C’ chemical shifts for simulated ensembles in comparison with experimental values. The values within the SHIFTX2 prediction errors were shown in italics.

		c22*	ff99SB-ILDN	ff99SB-ILDN-TIP4P-D	a99SB-disp
Cα (ppm)	Control	1.429	0.734	0.479	0.554
	Folding	0.665	0.375	0.473	0.367
C’ (ppm)	Control	0.824	0.481	0.591	0.417
	Folding	0.544	0.376	0.578	0.345

We note a curious observation regarding the propensity of forming 3₁₀ helices from multiple fore fields. As summarized in Fig. S8, the 3₁₀ helical content in simulations using three CHARMM force fields was low, and significantly lower than the corresponding α-helical content (Fig. 2). This can be directly attributed to the CMAP term used in CHARMM force fields, which was designed to rebalance the propensities of forming α, 3₁₀ and π helices⁷⁶. In contrast, the Amber family of force fields appears to generate significant 3₁₀ helices. The only exception was ff99SB-ILDN-TIP4P-D, but this may be a direct result of increased water dispersion in TIP4P-D water force field that destabilizes both α (e.g., Fig. 2) and 3₁₀ helices. As shown in Fig. S8, the 3₁₀ helical propensity is comparable to the α-helical content for residues 20–25 in both ff99SB-ILDN and a99SB-disp simulations. Similar observations have also been reported previously for ff99SB*-ILDN^{42, 48, 49}, a force field modified from ff99SB-ILDN by rebalancing the backbone helix-coil propensity, where the probability of forming 3₁₀ helix is higher in ff99SB*-ILDN simulations than in those using other force fields (see Figure 2 in reference⁵⁰). Nevertheless, it is not clear how such an apparent systematic bias may affect IDP simulations using these force fields.

Detection of transient long-range contact formation using different force fields

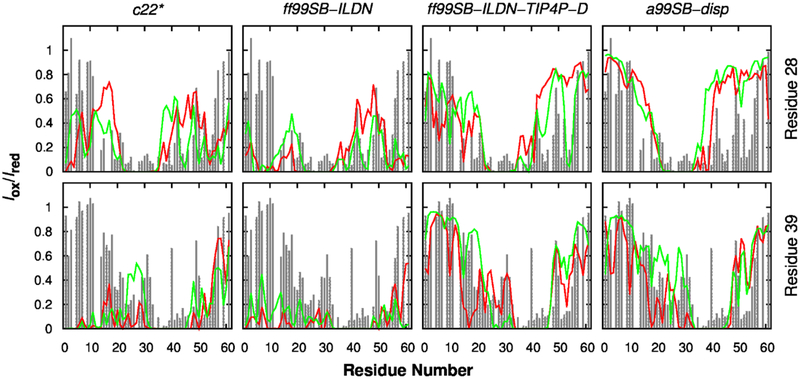
Transient long-range interactions in IDPs are known to have important functional implication^98–100. For example, previous NMR study has shown that loss of transient long-range interactions in α-synuclein, an IDP associated with Parkinson’s disease, could lead to completely unfolded conformations that aggregate more rapidly¹⁰⁰. Such transient long-range interactions have also been found in p53-TAD^{73, 75}, and they can be modulated both locally and remotely by binding of regulatory proteins or post-translational modification⁷³. Thus, in order to obtain reliable simulated structural ensembles of p53-TAD, the force field also needs to be able to capture such important structural features. Experimentally, PRE in combination with site-specific spin labelling provides a powerful tool in detecting transient long-range contact formation for IDPs^{75, 101–103}. The increase in relaxation rate of a proton is proportional to 1/r⁶, where r is the distance between proton and the unpaired electron in a spin label. Because of this 1/r⁶ dependence, PRE effect is suitable for identifying transient long-range contacts and insensitive to conformations with large proton-electron distance. Since PRE measurement could detect contact formation between unpaired electron and all amide protons in a protein, it provides valuable information for globally validating our simulation ensembles. Experimental PRE measurement⁷⁵ found that residue 28 could become close to many residues ranging from 16 to 55 (see Fig. 7 top row). This feature could be captured by all simulations, although c22* and ff99SB-ILDN simulations seemed to underestimate the distances to both N- and C-termini, and a99SB-disp may overestimate the distances between residue 28 and residues 45–55 (Fig. 7 top row). Similar observations could also be found for PRE induced by spin labelling at residue 39 (Fig. 7 bottom row). Notably, a99SB-disp and ff99SB-ILDN-TIP4P-D force fields could even recapitulate some fine features in the experimental PRE profiles (Figs. 3 and 7). Taken together, transient long-range interactions from ff99SB-ILDN-TIP4P-D and a99SB-disp simulations agreed the best with experimental PRE (Table 1).

Figure 7.

Calculated (lines) and experimental (grey bars) PRE effects induced by paramagnetic spin labelling at residues 28 (top row) and 39 (bottom row). Red and green traces are calculated from independent control and folding simulations, respectively.

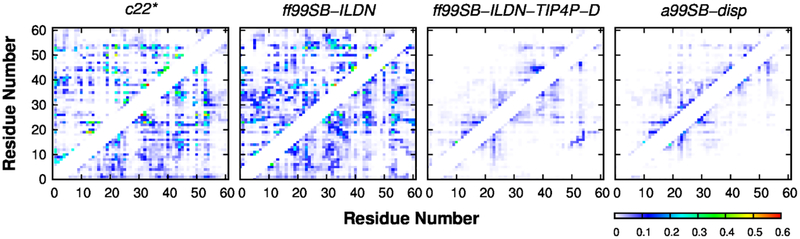
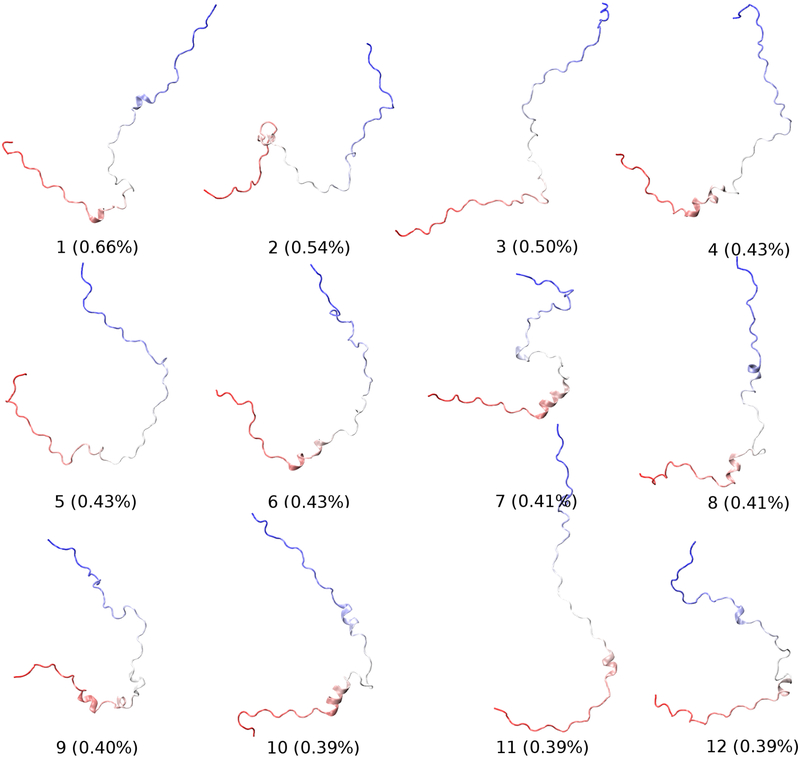
The presence of long-range contacts can be more directly and systematically examined using the contact probability map. As shown in Fig. 8, c22* and ff99SB-ILDN force fields generate significantly more transient interactions than ff99SB-ILDN-TIP4P-D and a99SB-disp force fields, consistent with the above observation that they may over-estimate the compactness of p53-TAD (e.g., Fig. 1). Nevertheless, many weakly populated tertiary contacts were also constantly observed in both ff99SB-ILDN-TIP4P-D and a99SB-disp simulations (Fig. 8), implying that the structural ensemble is highly heterogeneous. This can be illustrated by conformational clustering analysis shown in Figs. 9 and S9–S11, where no major cluster with over 2% occupancy was identified (see Methods for details). Since many of these long-range contacts involve the regions important for binding to MDM2 or CBP domains (e.g., residues 16–26, 48–55, see Fig. 8), in the future it would be interesting to study how these transient long-range contacts are modulated by mutation or post-translational modification, thus shedding light on the molecular mechanisms of p53 regulation.

Figure 8.

Contact probability maps calculated from independent control (top left) and folding (bottom right) simulations using four force fields. A contact is considered formed if the minimum distance between heavy atoms of two residues is less than or equal to 0.42 nm. Local and intermediate range contacts between residues separated by ≤ 4 residues were not shown for clarity.

Figure 9.

Centroid structures and populations of the top 12 most populated clusters for the structural ensemble derived from a99SB-disp control and folding simulations. The p53-TAD peptide is shown in Cartoon, with the color changing from red (at N-terminus) to blue (at C-terminus).

Conclusions

Accurate description of various local and long-range structural features of large, complex IDPs using empirical force fields is crucial for successful application of de novo simulations to characterize the disordered structure ensembles of IDPs and understand their sequence-disordered ensemble-function-disease relationships. We have explored the 61-residue p53-TAD as an exceptional model system to assess the ability of six latest protein force fields to describe non-trivial structural features within the disordered ensemble. Structural ensembles generated using μs-timescale REST2 enhanced sampling simulations were carefully analyzed and compared to a wide-range of experimental measurements derived from NMR, smFRET, and TR-FRET experiments. The results show that complex IDPs like p53-TAD remain very challenging for atomistic explicit solvent simulations, not only in achieving adequate level of convergence but also in proper description of local and long-range structural properties. Results from different force fields can vary significantly. Both c36m and c36mw fail to generate converged ensembles despite multiple μs simulation timescales. c22* generated overly compact structural ensembles, and residual helicity is also slightly over-estimated. Similar problem of over-compactness was also observed in ff99SB-ILDN simulations, but the helical propensity agreed well NMR measurement. More expanded structures can be obtained by combining ff99SB-ILDN force field with the TIP4P-D water force field; this seems to be achieved at the expense of over-destabilizing protein-protein interactions, leading to significant under-estimation of residual secondary structures in p53-TAD. Encouragingly, the latest a99SB-disp force field seems capable of faithfully recapitulating virtually all experimental measurements examined, including the overall chain dimension, residual secondary structures, and transient long-range ordering. As such, we anticipate that atomistic simulations using a99SB-disp will provide a viable approach for understanding how the disordered state of p53-TAD may be modulated by multi-site phosphorylations and/or many cancer-associated mutations in biology and cancers. Such structural insights will pave the way for establishing the sequence-disordered ensemble-function-disease relationships of p53-TAD and other regulatory IDPs.