Deep Learning for Fast and Spatially-Constrained Tissue Quantification from Highly-Accelerated Data in Magnetic Resonance Fingerprinting

Abstract

Magnetic resonance fingerprinting (MRF) is a quantitative imaging technique that can simultaneously measure multiple important tissue properties of human body. Although MRF has demonstrated improved scan efficiency as compared to conventional techniques, further acceleration is still desired for translation into routine clinical practice. The purpose of this work is to accelerate MRF acquisition by developing a new tissue quantification method for MRF that allows accurate quantification with fewer sampling data. Most of existing approaches use the MRF signal evolution at each individual pixel to estimate tissue properties, without considering the spatial association among neighboring pixels. In this work, we propose a spatially-constrained quantification method that uses the signals at multiple neighboring pixels to better estimate tissue properties at the central pixel. Specifically, we design a unique two-step deep learning model that learns the mapping from the observed signals to the desired properties for tissue quantification, i.e., 1) with a feature extraction module for reducing the dimension of signals by extracting a low-dimensional feature vector from the high-dimensional signal evolution and 2) a spatially-constrained quantification module for exploiting the spatial information from the extracted feature maps to generate the final tissue property map. A corresponding two-step training strategy is developed for the network training. The proposed method is tested on highly undersampled MRF data acquired from human brains. Experimental results demonstrate that our method can achieve accurate quantification for T1 and T2 relaxation times by using only 1/4 time points of the original sequence (i.e., four times of acceleration for MRF acquisition).

I. Introduction

QUANTITATIVE imaging, i.e., quantification of important tissue properties in human body such as the T1 and T2 relaxation times, is desired for both clinical and research purposes. Compared with conventional qualitative imaging techniques, e.g., T1- and T2-weighted imaging, quantitative imaging can provide more accurate and unbiased information of tissue properties and enable objective comparison of scans acquired in longitudinal studies [1]–[3]. However, one of the major barriers to translate conventional quantitative imaging techniques [4]–[7] for clinical applications is the prohibitively long time for data acquisition.

Recently, magnetic resonance fingerprinting (MRF) [8], a new approach for MR image acquisition and post-processing, has been introduced, which can significantly reduce the acquisition time for quantitative imaging. Compared with conventional MR imaging methods, the MRF framework uses pseudo-randomized imaging parameters to generate a unique signal evolution for each tissue type. Multiple tissue properties can be estimated by matching the observed signal evolution to a precomputed MRF dictionary using a template matching algorithm. The parallel measurement of multiple tissue properties using highly undersampled data acquisition enables fast quantitative imaging within the MRF framework. The efficacy of MRF for quantification of various tissue properties in multiple organs has been demonstrated in recent studies [9]–[13].

Although MRF has demonstrated better scan efficiency than conventional quantitative imaging techniques, further acceleration is still needed to improve spatial resolution/coverage and translate MRF into routine clinical practice, especially for pediatric and body imaging. Further reduction of acquisition time is of great benefit to clinical practice as it allows reduction of motion artifact, improvement of efficiency and throughput, and alleviation of patient discomfort during the MRF scan. In this work, we aim to shorten the acquisition time of MRF by acquiring fewer time points for each scan. However, acquiring fewer time points will result in fewer sampled data available for tissue quantification and thus degraded quantification accuracy. Thus, a robust tissue quantification method that can accurately estimate tissue properties from fewer time points is needed for further acceleration of MRF acquisition.

In the literature, various methods have been proposed for tissue quantification in MRF. The original framework [8] uses a template matching method, where the signal evolution at each pixel is matched to a precomputed dictionary containing signal evolutions corresponding to a wide range of tissue types. The tissue properties used to generate the best matching entry in the dictionary are then assigned to the corresponding pixel. McGivney et al. [14] propose to use singular value decomposition (SVD) to reduce the dictionary dimension, thus improving the computational efficiency. Cauley et al. [15] has introduced a fast group matching algorithm that assigns dictionary entries to several highly-clustered groups to further accelerate the matching process. Yang et al. [16] has developed randomized SVD and dictionary polynomial fitting to largely reduce the memory requirement of calculating low-rank approximations for large-scale dictionaries. In [17], the authors combine the dictionary matching technique with the compressed sensing (CS) framework by iteratively performing MR image reconstruction and tissue quantification to improve the quantification accuracy. Furthermore, the CS-based method is improved by adding certain constraints (i.e., low-rank constraint [18] and wavelet domain sparsity [19]) on the reconstructed MR images and reconstructing the MR images at different resolution levels to suppress the noise in the reconstructed images [20]. However, these methods only use the signal at a single pixel to estimate tissue properties, without considering spatial information of the whole image. To incorporate spatial information, [21] introduces a spatiotemporal dictionary, with each entry containing signals at multiple neighboring pixels. However, this method dramatically increases the dimension of each dictionary entry and thus could only exploit spatial information from a small neighborhood (e.g., 7 × 7 pixels) due to its high computation load.

Besides the aforementioned dictionary-based methods, other methods that do not involve dictionary matching have also been developed for the tissue quantification process. These methods can be roughly divided into two categories: 1) model-based and 2) learning-based methods. The model-based methods [22], [23] usually employ mathematical models to simulate the signal generation and acquisition process of MRF, and then obtain an statistically optimal estimation of the tissue property maps from the observed signals. Although the model-based methods provide new theoretical insights into the MRF framework, they are subject to unavoidable mismatches between mathematical models and the real-world non-ideal imaging systems [24], and also need complex algorithms to solve the statistical optimization problem. In the second category, the learning-based methods [25]–[28] use deep learning models to approximate a direct mapping from MRF signals to the underlying tissue properties. These methods have demonstrated improved computation efficiency since they perform tissue quantification with feed-forward neural networks without iterative computations. The performance of some learning-based methods has been evaluated on in vivo human brain data [27], [28]. However, previous learning-based methods rely on signal evolution acquired from single pixel for tissue quantification, without exploiting spatial context information of images. Moreover, these methods aim at improving computation efficiency, while the potential for further acceleration of MRF acquisition has not been evaluated in these approaches.

In this work, we propose a learning-based method for tissue quantification in MRF. Our method exploits spatial context information by using a deep learning model to learn the mapping from the signals at multiple neighboring pixels to the tissue properties at the central pixel. We hypothesize that the spatial context information is helpful for accurate quantification for two reasons. First, there is correlation between tissue properties at neighboring pixels. For example, the tissue properties at adjacent pixels in a homogeneous region are likely to be similar. Therefore, information from neighboring pixels could be utilized as spatial constraint to regularize the estimation at the central target pixel for improving the accuracy of tissue quantification. Second, signals at the target pixel are distributed to its neighboring pixels due to the aliasing effect caused by undersampling in k-space during MRF acquisition. Therefore, using spatial information can help recover the scattered signals and achieve a better quantification with MRF.

A major challenge here is the high dimension of the observed signal evolution at each pixel due to the large number of acquired time points. To this end, we develop a unique two-step deep learning model for spatially-constrained tissue quantification, including 1) a feature extraction module in the first step used to reduce the dimension of signals by extracting a low-dimensional feature vector from the high-dimensional signal evolution, and 2) a spatially-constrained quantification module used to exploit the spatial information from the extracted feature maps to generate the final tissue property map. We further design a two-step training strategy for learning this two-step model. Moreover, a relative-difference-based loss function is adopted to tackle with the large range of the tissue property values to be estimated. Experiments on 6 subjects demonstrate that our method is superior to several state-of-the-art methods.

The rest of this paper is organized as follows. We first present materials used in this work and our proposed method in Section II, and then introduce experimental results and related analysis in Section III. In Section IV, we compare quantification results for T1 and T2, compare our method with previous studies, and present the limitations of the current work and future research direction. We finally conclude this paper in Section V.

II. Materials and Method

In this section, we first describe the data acquisition and preprocessing approach used in this work. We then present our proposed tissue quantification method in detail, including our proposed two-step deep learning model, two-step training strategy, and implementation details.

A. Data Acquisition and Preprocessing

All imaging was performed on a Siemens 3T Prisma scanner. A 32-channel head coil was used for signal reception. MRF data of axial human brain slices were acquired using the fast imaging with steady state precession (FISP) sequence [29]. A total of 2,304 time points were acquired for each scan, and data from only one spiral readout was acquired for each time point (reduction factor = 48). Other imaging parameters used in this study included: field of view (FOV) = 30 cm; matrix size = 256 × 256; slice thickness = 5 mm; flip angle = 5°~12°. A constant TR of 7.0 msec was used and the acquisition time for each 2D MRF dataset was ~23 seconds.

The MRF dictionary used in this study contains 13,123 combinations of T1 (60 ~ 5000 ms, with an increment of 10 ms below 2000 ms, an increment of 20 ms between 2000 ms and 3000 ms, an increment of 50 ms between 3000 ms and 3500 ms, and an increment of 500 ms above 3500 ms) and T2 (10 ~ 500 ms, with an increment of 5 ms below 200 ms, an increment of 10 ms between 200 ms and 300 ms, and an increment of 50 ms above 300 ms). The signal evolution corresponding to each combination was simulated using Bloch equations.

The ground-truth tissue property maps were obtained from the acquired MRF data of all 2,304 time points by using the dictionary matching method as introduced in the original MRF framework [8]. Specifically, MR images are first reconstructed using non-uniform Fast Fourier Transform (NUFFT) [30]. Next, the signal evolution in the dictionary that best matches the observed signal evolution at each pixel is selected by using the cross correlation as similarity metric. The T1 and T2 values corresponding to the best-matching entry are assigned to that pixel. Repeated over the entire image, this process yields quantitative T1 and T2 maps simultaneously. The obtained tissue property maps are then used as the ground truth in the following experiments. Since the magnitudes of MRF signal evolutions vary largely across different subjects, the MRF signal is normalized to a common range for better generalization of the deep learning model. Specifically, we normalize the energy (i.e., the sum of squared magnitudes) of each signal evolution to one, which is similar to the normalization performed when calculating cross correlation in the dictionary matching method [8].

For simplicity, denote the normalized MRF signals of an axial slice as X ∈ ℂ^M×N×T, where M × N is the size of the imaging matrix, i.e., 256 × 256 in this study, and T is the number of time points used for tissue quantification. Denote the signal evolution at the pixel (m, n) as x_m,n ∈ ℂ^T. Denote the ground-truth tissue property (T1 or T2) map of that axial slice as Θ ∈ ℝ^M×N.

B. Proposed Model

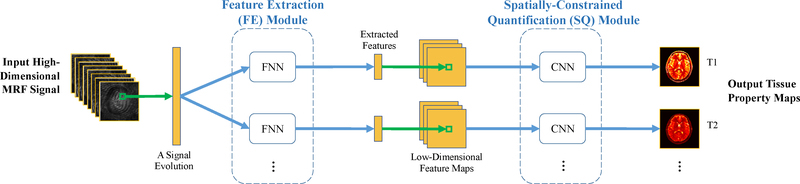
We design a two-step deep learning model to learn the mapping from the MRF signals X to the tissue property map Θ. Our model contains two sequential components, i.e., 1) a feature extraction (FE) module for reducing the dimension of signal evolutions, and 2) a spatially-constrained quantification (SQ) module for estimating the tissue property maps from the extracted feature map. The schematic overview of our proposed model is shown in Fig. 1, with Figs. 2 and 3 showing the detailed network structure for each of the two modules. The structures of FE and SQ modules are described in details in the following sections.

Fig. 1.

Schematic overview of our proposed two-step deep learning model for spatially-constrained tissue quantification in MRF. FNN: fully-connected neural network. CNN: convolutional neural network. The number of channels (each with paired FNN and CNN) is equal to the number of tissue properties to be estimated (i.e., 2 in this study).

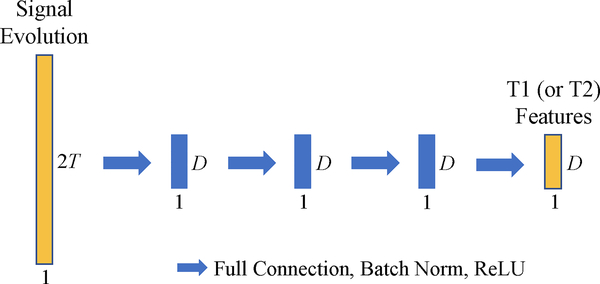
Fig. 2.

Network structure of the fully-connected neural network (FNN) in our proposed feature extraction (FE) module. Each blue arrow represents a fully-connected (FC) layer, and each blue block represents the output of an FC layer.

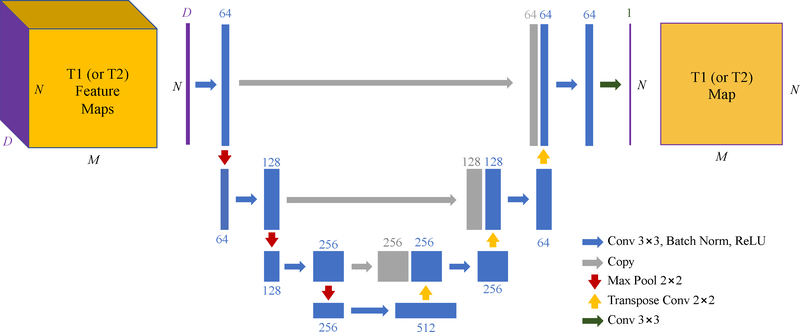
Fig. 3.

Network structure of the convolutional neural network (CNN) in our proposed spatially-constrained quantification (SQ) module, i.e., U-Net. The blue blocks represent spatial feature maps obtained from spatial convolutions, and gray blocks represent feature maps copied from previous layers. Each feature map has one feature dimension and two spatial dimensions, while only one feature dimension and one spatial dimension are shown for simplicity. The feature dimension is labeled on the top of each block.

1). Feature Extraction Module:

In the feature extraction (FE) module, fully-connected neural networks (FNNs) are used to convert the input high-dimensional signal evolution into a low-dimensional feature vector which contains useful information for tissue property estimation. One FNN is used to extract the features useful for estimation of one specific tissue property. In total, our FE module contains two FNNs for estimation of two tissue properties, i.e., T1 and T2 relaxation times. Specifically, each FNN learns a nonlinear mapping f from the signal evolution at a certain pixel x_m,n ∈ ℂ^T, to the feature vector at that pixel y_m,n ∈ ℝ^D:

$$y_{m,n}=f\left(x_{m,n}\right)$$ (1)

where T is the number of time points used for tissue quantification and D (D = 46 in this study) is the number of features extracted. Applying the FE module to all the pixels in the axial slice yields a low-dimensional feature map Y ∈ ℝ^M×N×D corresponding to the high-dimensional MRF signals X:

$$Y=f\left(X\right)$$ (2)

The FE module is needed for the following reasons. First, MRF implementation usually acquires a large number of time points, such as 2,304 in the FISP sequence and 576 after 4 times of acceleration. In this case, directly feeding such high-dimensional data into the subsequent spatially-constrained quantification module will lead to large network size and challenges in efficient network training. Besides, the FE module can provide a better representation of the original signal for tissue quantification, by extracting only the essential information for estimation of the target tissue property while filtering out the noise and unrelated information in the original signal.

Previous studies [14], [18], [23], [31] used singular value decomposition (SVD) to reduce the dimension of signal evolutions. The advantage of using deep neural networks, i.e., FNN in this study, instead of SVD is twofold. First, the deep neural network learns a multilayer nonlinear mapping from the original signal to the extracted features, whereas SVD learns only a single-layer linear mapping. Therefore, the deep neural network can extract more abstract and higher-level information from the input signal, which can be used to improve the robustness and accuracy of tissue quantification. Second, the combination of neural networks for both FE and SQ modules allows end-to-end training of the entire two-step model through back propagation, which further improves the compatibility between two modules and thus the performance of our method.

There are various choices for the structure of FNN in the FE module. The particular structure adopted in this study is composed of 4 fully-connected (FC) layers (as shown in Fig. 2), where each FC layer includes a full connection followed by batch normalization and ReLU activation. The output dimensions of all the FC layers are the same (i.e., D = 46). The input of FNN, i.e., a signal evolution x_m,n ∈ ℂ^T, is transformed to a real vector by splitting the real and imaginary parts, thus the input dimension of FNN is 2T.

2). Spatially-Constrained Quantification Module:

In the spatially-constrained quantification (SQ) module, convolutional neural networks (CNNs) are used to capture spatial information of the feature map Y and finally generate the estimated tissue property map $\widehat{\mathrm{\Theta }}\in {ℝ}^{M\times N}$. One CNN is used for the estimation of one tissue property. In total, our SQ module contains two CNNs for estimation of two tissue properties, i.e., T1 and T2 relaxation times. Specifically, each CNN learns a nonlinear mapping s from the feature map Y to the estimated tissue property map $\widehat{\mathrm{\Theta }}$:

$$\widehat{\mathrm{\Theta }}=s(Y)$$ (3)

There are also various choices for the structure of CNN in the SQ module. In this study, we use U-Net [32], [33] (as shown in Fig. 3) to capture both local and global spatial information of feature map Y. This network includes an encoder sub-network (i.e., left part of Fig. 3) to extract spatial features at multiple resolution levels from the input feature map, and a subsequent decoder sub-network (i.e., right part of Fig. 3) to estimate the output tissue property (T1 or T2) map based on the extracted spatial features from encoder subnetwork.

In the encoder sub-network, the spatial context information is incorporated into the extracted feature maps by feature extraction (with convolution) and 2× down-sampling (with max pooling). Specifically, each convolution layer incorporates spatial information from 3×3 neighboring pixels by applying 3×3 convolution kernels to the input feature map. Moreover, each max pooling layer incorporates information from 2×2 pixels by retaining the max value of 2×2 subregion in the input. Spatial sharing further increases with the concatenation of convolution layers and pooling layers.

In the subsequent decoder sub-network, the feature maps at different spatial scales are up-sampled (with transpose convolution), concatenated, and merged (with convolution), to combine global context knowledge with complementary local details and generate the final tissue property maps with spatial context information from different scales. The U-Net shown in Fig. 3 has a receptive field size of 54×54 pixels, which means that the signals from 54×54 neighboring pixels in the input MRF images are used for estimation of tissue property at one pixel in the output tissue property map.

C. Two-Step Training Strategy

To better train the proposed two-step model, we design a two-step training strategy, including 1) pretraining of the FE module by signals and tissue properties at individual pixels, and 2) end-to-end training of the entire model by signals and tissue property maps of whole axial slices.

1). Pretraining of the Feature Extraction (FE) Module:

As there is no ground truth for the output features of FE module, we extend each FNN with one FC layer and trains the extended FNN to estimate the desired tissue property (corresponding to the input signal evolution). Therefore, the features extracted by the original FNN will capture useful information for estimation of the desired tissue property. Denote the mapping learned by the added FC layer as f_a and the mapping learned by the extended FNN as $f_a\circ f$. The objective function of pretraining of the FE module can be formulated as the following:

$${\xi }_f,{\xi }_{f_a}=\arg \underset{{}_{{\xi }_f,{\xi }_{f_a}}}{\min }{\mathbb{E}}_{x,\theta }\left[\left|\frac{{\theta }_{m,n}-f_a\circ f\left(x_{m,n}\right)}{{\theta }_{m,n}}\right|\right]$$ (4)

where θ_m,n ∈ ℝ is the ground-truth tissue property at the pixel (m, n), f_a ∘ f(x_m,n) ∈ ℝ is the output of extended FNN for input signal evolution x_m,n, ξ_f and ${\xi }_{f_a}$ are the network parameters of the original FNN and the added FC layer respectively, and E[] represents mathematical expectation.

Note that we use relative difference between the ground truth θ_m,n and the network output f_a ∘ f(x_m,n) as the loss function, instead of the absolute difference which is commonly used for regression problems. The main reason is that T1 and T2 measures in human body span a large range, and thus the loss function based on the conventional absolute difference will be dominated by the pixels with high tissue properties. Therefore, we use relative difference as the loss function to balance across tissues with different ranges in our proposed method.

The pretraining of FE module is helpful in providing better initial parameters of FE module for the subsequent end-to-end training of the entire model. Besides, during pretraining, more data can be used to better train the FE module since the signal and tissue property at each individual pixel can be used as training data. However, during the subsequent end-to-end training, only the whole images or image patches can be used as training data, to provide the spatial context information needed for spatially-constrained tissue quantification.

2). End-to-End Training of the Entire Model:

After pretraining of the FE module, the end-to-end training is performed to train the SQ module and fine-tune the FE module. During the end-to-end training, the parameters in both the FE and SQ modules are tuned together, so that the two modules are more compatible and the performance of the entire model can be improved. The objective function of end-to-end training can be formulated as the following:

$${\xi }_s,{\xi }_f=\arg \underset{{}_{{\xi }_s,{\xi }_f}}{\min }{\mathbb{E}}_{X,\mathrm{\Theta }}\left[{\Vert \frac{\mathrm{\Theta }-s\circ f(X)}{\mathrm{\Theta }}\Vert }_1\right]$$ (5)

where s and f are the mappings learned by SQ and FE modules, respectively, while ξ_s and ξ_f are the network parameters of SQ and FE modules, respectively. Also, s ∘ f(X) ∈ ℝ^M×N is the output of entire model for the input MRF signals X, and ∥·∥₁ stands for the entry-wise L₁-norm.

3). Training Details:

For both training stages, we used ADAM optimizer [34] with a batch size of 32 and an initial learning rate of 0.0002. At each stage, we trained the networks for 400 epochs, by keeping the learning rate the same for the first 200 epochs and linearly decaying it to zero over the next 200 epochs. For end-to-end training, we extracted image patches of 64×64 pixels as training data. Network weights were initialized from a Gaussian distribution with mean 0 and standard deviation 0.02. We implemented the algorithm in Python with PyTorch library and trained the models on a GeForce GTX TITAN XP GPU.

D. Implementation

When the training is completed, the model can be applied to new testing data for tissue quantification. Specifically, the model calculates the desired tissue property map $\widehat{\mathrm{\Theta }}\in {ℝ}^{M\times N}$ for the input MRF signals of an axial slice Z ∈ ℂ^M×N×T by:

$$\widehat{\mathrm{\Theta }}=s\circ f(Z)$$ (6)

Note that the tissue quantification is performed by a direct mapping from the observed signals to the tissue property map, i.e., s ∘ f, thus our method is much more computationally efficient than the dictionary-based or model-based methods that require iterative computations.

III. Experiments

In this section, we first present experimental settings and competing methods, then report experimental results achieved by our method and competing methods, and finally investigate the influence of several key components of our method.

A. Experimental Settings

Our dataset contains axial brain slices from 6 human subjects. Among the 6 subjects, 5 subjects were acquired with 12 slices per subject and one subject was acquired with 10 slices. The MRF image series and ground-truth T1 and T2 maps of each slice were obtained through the method described in Section II.A.

In this work, we accelerate MRF acquisition by using fewer time points for tissue quantification. Specifically, for the acceleration rate ar, we only use the first 1/ar · T_a of all T_a (T_a = 2,304 in this study) time points. For example, when ar = 4, T (i.e., the number of time points used for tissue quantification) = 1/4 × 2,304 = 576.

In our experiments, we use the relative error to measure the quantification accuracy achieved by different methods: $e_{m,n}=\left|({\theta }_{m,n}-{\widehat{\theta }}_{m,n})/{\theta }_{m,n}\right|$, where e_m,n ∈ ℝ is the quantification error at the pixel (m, n), and θ_m,n ∈ ℝ and ${\widehat{\theta }}_{m,n}\in ℝ$ are the ground-truth and estimated tissue properties at that pixel, respectively. The relative error of an axial slice is calculated by averaging the relative errors across all brain tissues (excluding background) in the slice. The mean and standard deviation of relative errors of all testing slices are calculated for quantitative comparison between different methods.

B. Competing Methods

We first compare our proposed spatially-constrained tissue quantification (SCQ) method with the baseline dictionary matching (DM) method proposed in the original MRF frame-work [8]. In the DM method, we use the same dictionary as that used to calculate the ground truth (as described in Section II.A). Specifically, the dictionary is generated using the Bloch equations and contains 13,123 entries corresponding to different combinations of T1 and T2 values.

Besides, we further compare our SCQ method with three state-of-the-art methods, including 1) SVD-compressed dictionary matching (SDM) [14], 2) compressed sensing multiresolution reconstruction (CSMR) [20], and 3) conventional deep learning (DL) method [28]. The details of these state-of-the-art methods are listed as follows.

1). SVD-Compressed Dictionary Matching (SDM) [14]:

A variant of DM that uses SVD to compress the dictionary, which is reported to have better computation efficiency than DM. Specifically, in SDM, SVD is applied to all the entries in the dictionary used in DM. Then, each entry is projected to a lower dimensional subspace spanned by the singular vectors. The dimension of the subspace is set as 17, which corresponds to 99.9% of the total energy of all singular values.

2). Compressed Sensing Multi-resolution Reconstruction (CSMR) [20]:

A compressed-sensing-based method that uses multi-resolution reconstruction for MR images, which is reported to have good quantification accuracy for accelerated data with fewer time points. Specifically, in the CSMR method, MR image reconstruction is performed iteratively at different resolution levels, and tissue quantification is performed at each iteration through dictionary matching. The number of iterations is set as 14, and the tissue property maps obtained from the last (i.e., 14th) iteration are used as the final quantification results.

3). Conventional Deep Learning (DL) Method [28]:

A non-spatially-constrained deep-learning-based method, which is reported to have better computation efficiency than DM. Specifically, the DL method treats each observed signal evolution as a time sequence and feeds it into a CNN with six 1-D temporal convolution layers followed by six fully-connected layers. The network then outputs the desired tissue properties.

It is worth noting that DM, SDM, and CSMR are dictionary-matching-based methods, while DL and our SCQ method are deep-learning-based methods.

C. Comparison with Baseline Method

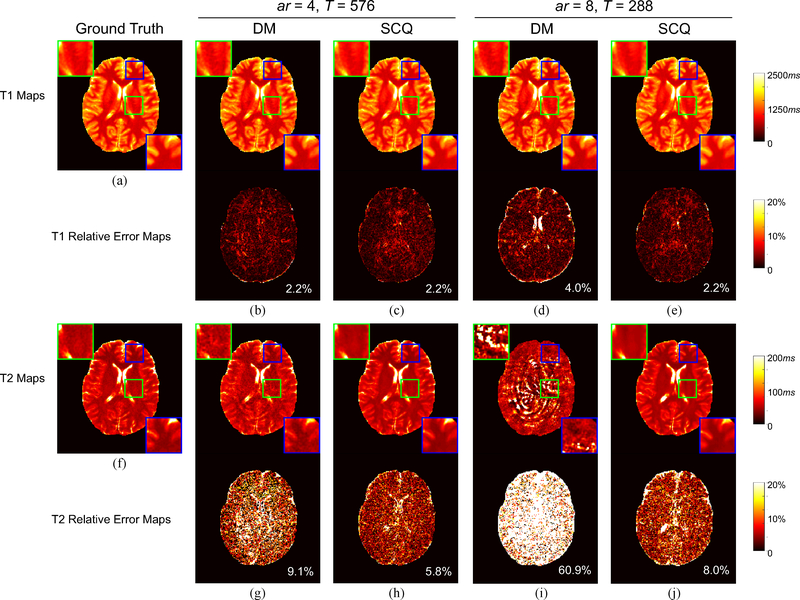
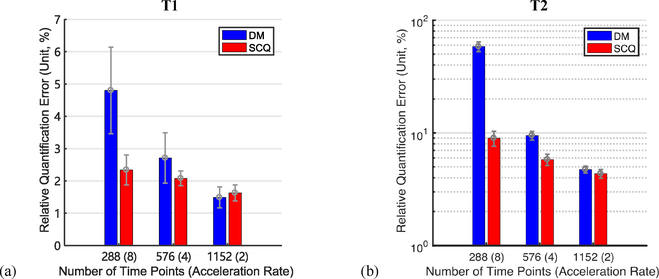
In this group of experiments, we compare our SCQ method with the baseline DM method with 3 acceleration rates: 1) ar = 2, T = 1152; 2) ar = 4, T = 576; and 3) ar = 8, T = 288. Here, we use slices of 5 randomly selected subjects as the training data, and slices of the remaining one subject as the test data. The quantification results for a representative slice in the test dataset yielded by the two methods are shown in Fig. 4. In general, our method achieves more accurate quantification results than the baseline DM method. Notably, with ar = 8 for T2 quantification, our method yields a reasonable result (error = 8.0%), while DM nearly fails to estimate the T2 map (error = 60.9%).

Fig. 4.

Visual results of T1 and T2 quantification by our method (SCQ) and the baseline method (DM). (a) Ground-truth T1 map. (b)-(e): Estimated T1 maps and associated relative error maps. (f) Ground-truth T2 map. (g)-(j): Estimated T2 maps and associated relative error maps. The overall error is labeled at the lower right corner of each error map. ar: acceleration rate; T: number of time points used for tissue quantification.

The means and standard deviations of the relative errors calculated from all slices in the test data are summarized in Fig. 5. As shown in Fig. 5, our method yields lower error than the baseline method for T2 quantification when ar = 8, 4, and 2, and also for T1 quantification when ar = 8 and 4. In addition, the improvement is more evident when the acceleration rate is higher, i.e., the acquisition time is shorter.

Fig. 5.

Quantification errors of (a) T1 and (b) T2 (mean ± standard deviation, unit: %) yielded by our method (SCQ) and the baseline method (DM) for different acceleration rates.

Besides, we also compared the SCQ method with DM for the data with no acceleration. Note that the DM results with no acceleration are used as the ground-truth tissue property maps in this study. The quantification errors yielded by SCQ are 1.00% ± 0.19% for T1 and 2.82% ± 0.19% for T2, which suggests a good agreement between the quantification results of SCQ and DM with no data acceleration.

D. Comparison with State-of-the-art Methods

In this group of experiments, we compare our method with three state-of-the-art methods in terms of quantification accuracy and processing time, with ar = 4. Here, we performed subject-level leave-one-out cross validation. Specifically, each time we used the slices of one subject as test data and slices of all the remaining 5 subjects as training data. This process was repeated 6 times until all subjects were alternatively used as test data. The quantification errors yielded by different methods for each test subject are summarized in Table I. For comparison, we also show the errors of DM in Table I.

TABLE I:

Quantification errors of T1 and T2 (mean ± standard deviation, unit: %) yielded by our method (SCQ), the baseline method (DM) and the state-of-the-art methods (SDM, CSMR, AND DL) for each test subject. Here, ar = 4.

	Subject	DM	SDM	CSMR	DL	SCQ (ours)
T1	1	2.39 ± 0.24	2.78 ± 0.29	2.61 ± 0.29	1.86 ± 0.18	1.87 ± 0.23
	2	2.40 ± 0.80	2.89 ± 0.93	2.65 ± 0.67	1.78 ± 0.36	1.83 ± 0.27
	3	2.75 ± 0.77	3.17 ± 0.86	2.91 ± 0.79	2.04 ± 0.30	2.07 ± 0.27
	4	2.90 ± 0.74	3.51 ± 0.97	4.38 ± 0.97	2.17 ± 0.46	1.85 ± 0.28
	5	2.71 ± 0.78	3.15 ± 0.96	3.34 ± 0.83	2.12 ± 0.46	2.08 ± 0.23
	6	2.13 ± 0.39	2.53 ± 0.58	2.29 ± 0.47	1.72 ± 0.20	1.64 ± 0.15
	Overall	2.55 ± 0.62	3.00 ± 0.76	3.03 ± 0.67	1.95 ± 0.33	1.89 ± 0.24
T2	1	10.06 ± 0.75	13.99 ± 1.52	10.40 ± 0.93	6.46 ± 0.95	5.73 ± 0.71
	2	8.69 ± 0.68	11.87 ± 1.44	8.57 ± 0.59	6.35 ± 1.04	5.47 ± 0.60
	3	9.96 ± 1.52	13.96 ± 2.23	9.60 ± 1.43	6.68 ± 1.13	6.29 ± 0.89
	4	9.81 ± 0.58	14.16 ± 1.37	14.89 ± 4.91	6.65 ± 0.85	5.88 ± 0.56
	5	9.48±0.84	13.46 ± 1.38	9.36±0.65	7.00±1.51	5.81±0.66
	6	8.82±0.87	13.34 ± 1.41	8.78±1.57	5.69±0.77	5.45±0.70
	overall	9.47 ± 0.87	13.46 ± 1.56	10.27 ± 1.68	6.47 ± 1.04	5.77 ± 0.69

From Table I, we can observe that our SCQ method consistently achieves superior accuracy for T1 and T2 quantification compared to the four competing methods. Also, compared with the conventional deep-learning-based method (i.e., DL), our method achieves higher T2 quantification accuracy because our method can exploit spatial context information through CNNs in its SQ module, while the DL method cannot exploit that information through its network. On the other hand, compared with the dictionary-based methods (i.e., DM, SDM, and CSMR), our method learns a multilayer nonlinear mapping from the signal to the underlying tissue properties, which is potentially more noise-robust than the simple cross-correlation-based template matching procedure performed in the dictionary-based methods. Also, the dictionary-based methods perform tissue quantification for each pixel separately, without considering the spatial context information.

In addition, we also report the average testing times for one axial slice required by different methods in Table II. The testing time includes all computations performed using the reconstructed MRF image series for the quantification of T1 and T2 maps. Specifically, both signal compression time and matching time are included for SDM. From Table II, we can clearly see that our SCQ method achieves the shortest testing time, i.e., 2.3 seconds for quantification of T1 and T2 for an axial slice with a matrix size of 256 × 256, while the second fastest method (i.e., SDM) needs 14.2s. These results suggest that, compared with the competing methods, our method is more efficient in tissue quantification, which is particularly useful in practice.

TABLE II:

Average testing time required by our method (SCQ), the baseline method (DM) and the state-of-the-art methods (SDM, CSMR, AND DL) for T1 and T2 quantification for an axial slice with a matrix size of 256 × 256. Units: second (S) and hour (H). Here, ar = 4.

DM	SDM	CSMR	DL	SCQ (ours)
26.2s	14.2s	∼2h	18.0s	2.3s

Experiments were performed on an iMac (2017) desktop, with CPU: 4.2 GHz Intel Core i7, and memory: 16 GB 2400 MHz DDR4. DM, SDM, DL, and SCQ were implemented in Python, and CSMR was implemented in Matlab R2017a. Testing time is defined as the time for all computations performed using the reconstructed MRF image series for the quantification of both T1 and T2 maps. Specifically, the testing time of SDM includes both signal compression time and matching time.

E. Effects of Important Components in Our Method

In this subsection, we study the effect of three essential components in our method for tissue quantification. All the experiments in this subsection were performed with ar = 4 and D = 46 unless stated otherwise. In the Supplementary Materials, we further analyze the influence of another two components (i.e., network architecture and data normalization) in SCQ, with results shown in Fig. S1 and Tables SI–SIII.

1). Influence of Feature Number, and Comparison between FNN and SVD:

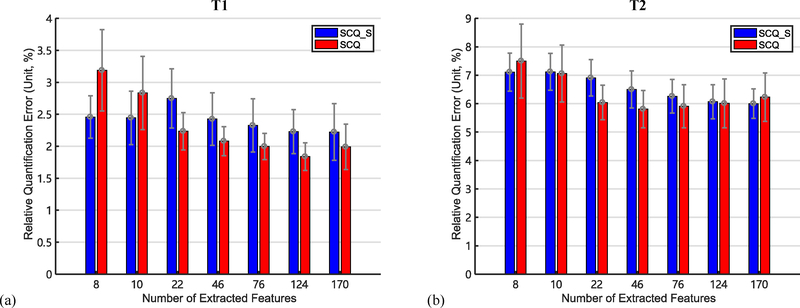
We evaluate the influence of the number of features extracted by the FE module, i.e., D. To estimate possible values for D, we first apply SVD to the MRF dictionary using the method in [14]. Multiple numbers of singular values corresponding to certain energy thresholds are then selected as the D values. Specifically, we select D = 8, 10, 22, 46, 76, 124, and 170, corresponding to the energy thresholds of 90%, 95%, 99%, 99.9%, 99.99%, 99.999%, and 99.9999%, respectively.

We also compare our method (SCQ) with its variant SCQ_S which uses SVD (instead of FNN) for feature extraction in the FE module. We use the method proposed in [14] to apply SVD to the MRF signal evolutions.

The quantification errors yielded by SCQ and SCQ_S with different numbers of extracted features are summarized in Fig. 6. As shown in Fig. 6, SCQ generally yields lower quantification error than SCQ_S. Besides, the quantification error of SCQ first drops then rises when the number of extracted features increases. Specifically, the error of SCQ reaches the minimum for T1 when D = 124, and for T2 when D = 46. It is worth noting that the quantification error is lower from SCQ_S than SCQ when the number of extracted features is around 10. To further study this case, we examine the visual results for D = 10 and D = 46 in Section I.C and Fig. S2 in the Supplementary Materials.

Fig. 6.

Quantification errors of (a) T1 and (b) T2 (mean ± standard deviation, unit: %) yielded by our method (SCQ) and its variant (SCQ S) which uses SVD (instead of FNN) for feature extraction in the FE module, with different numbers of extracted features. Here, ar = 4.

2). Influence of the FE and SQ Modules:

In this group of experiments, we study the importance of the FE module and the SQ module, respectively, by removing each of them from the original SCQ model.

Specifically, we compare SCQ with its two degraded variants. In the first variant (denoted as SQ-only), we feed the high-dimensional MRF signals directly into the SQ module, without using the FE module for dimension reduction. In SQ-only, the number of input channels for the CNN in SQ module increases from D to 2T, with each channel corresponding to the real or imaginary part of the signal at one time point. In the second variant (called FE-only), we use the extended FNN obtained from the pretraining of FE module to estimate the tissue property from individual signal evolutions, without using the SQ module to exploit spatial context information.

The results yielded by our SCQ method and its two variants (i.e., SQ-only and FE-only) are summarized in Table III. As shown in Table III, removing the FE module (in SQ-only) increases the quantification errors, which is likely due to the over-fitting problem caused by the increased network size in SQ module. Removing the SQ module (in FE-only) increases quantification errors, demonstrating the importance of the proposed SQ module and the spatial context information it extracts for accurate tissue quantification.

TABLE III:

Quantification errors of T1 and T2 (mean ± standard deviation, unit: %) yielded by our method (SCQ) and its variants (SQ-only and FE-only) where only one of the modules exists. Here, ar = 4.

	SQ-only	FE-only	SCQ (ours)
T1	2.34 ± 0.40	2.41 ± 0.49	2.08 ± 0.23
T2	6.42 ± 0.64	7.02 ± 0.78	5.81 ± 0.66

3). Importance of the Phase Information in MRF Signals:

In our SCQ method, both the real and imaginary parts of the complex MRF signals are inputted to our model for tissue quantification. In the previous work that applies deep learning to MRF [26], [28], only the magnitude of signals (without any phase information) is inputted. In this group of experiments, we study whether the phase in MRF signals provides valuable information for tissue quantification, by comparing our method (SCQ) with its another variant, called SCQ_M, which uses only the magnitude of signals as input. The results are summarized in Table IV. As shown in Table IV, SCQ_M yields much higher quantification errors than SCQ, suggesting that both magnitude and phase values in MRF signals contain useful information for tissue quantification. It is worth noting that the error increase due to removing phase information is much higher than that due to removing FE or SQ module (as shown in Table III), which further demonstrates the importance of phase information in MRF signals for accurate tissue quantification. This result is consistent with recent findings in the literature [35].

TABLE IV:

Quantification errors of T1 and T2 (mean ± standard deviation, unit: %) yielded by our method (SCQ) which uses both the real and imaginary parts of mrf signals as input, and its variant (SCQ_M) which uses only the magnitude of signals as input. Here, ar = 4.

	SCQ_M	SCQ (ours)
T1	10.82 ± 2.12	2.08 ± 0.23
T2	13.71 ± 2.11	5.81 ± 0.66

IV. Discussion

A. Difference between T1 and T2

It has been observed in Figs. 4, 5, and 6 and Tables I, III, and IV that both our SCQ method and the existing methods yield higher accuracy for T1 quantification than for T2 quantification. Previous studies have also observed this difference for longer acquisitions [22], which indicates that the FISP sequence is not as sensitive to T2 as to T1. Moreover, the FISP sequence applies an inversion preparation pulse at the beginning of the acquisition, stimulating T1-recovery-like dynamics that dominate the early portion of signal evolutions [22]. Therefore, the early portion of signal evolutions, which is used for tissue quantification in this study, contains more information of T1 than of T2, resulting in higher accuracy in T1 quantification. This also explains why the optimal number of extracted features for T1 (i.e., 124) is greater than that for T2 (i.e., 46), as shown in Section III.E.1, as more features are needed to encode the information of T1 contained in the MRF signals used for tissue quantification.

B. Flexibility of SCQ Framework

As demonstrated by the experiments with different acceleration rates, our framework is flexible with different acquisition lengths. Moreover, the framework can also be applied to various other acquisition protocols, including different MRF pulse sequences, under-sampling designs, and 3D imaging. When applying our framework to a new acquisition protocol, a new set of training dataset is likely needed to train the deep neural networks (i.e., FNN and CNN in our framework) and the model can then be applied to the data acquired with the corresponding protocol.

Compared to the standard dictionary matching approach, our framework could potentially provide more flexibility in the estimation of tissue properties. Specifically, the MRF dictionary only covers a limited range of discrete tissue property values, which limits the precision of quantification and leads to partial volume problems. In comparison, our framework learns an unbounded and continuous mapping from MRF signals to underlying tissue properties, which could potentially improve the performance of tissue quantification.

C. Comparison with Previous Studies

Compared with the baseline DM method [8], our method can significantly improve the quantification accuracy for highly-accelerated data, as shown in Figs. 4 and 5. However, it is worth noting that some blurring effects can be observed in the quantitative maps estimated by our method with 8 times of acceleration (see Fig. 4). In the Supplementary Materials, we further study this blurriness through frequency-domain representations of the quantitative maps. The blurring effect of our method potentially degrades spatial resolution and hinders application for high-resolution imaging [36]–[39]. To tackle with this problem, a loss function can be added to enhance the high frequency details of our output tissue property map, such as a discriminative loss within generative adversarial networks (GAN) [40]–[42], or a gradient loss that minimizes the difference between the gradient maps of network output and the ground-truth tissue property map [42], [43].

Compared with three state-of-the-art methods (i.e., SDM, CSMR, and DL), our method achieves higher quantification accuracy with a shorter processing time, as shown in Tables I and II. Among the state-of-the-art methods, SDM reduces the processing time of the baseline DM method by 46% but achieves poorer quantification accuracy than DM. DL shortens the processing time of DM by 31% while simultaneously achieving higher accuracy. CSMR can achieve higher quantification accuracy than the baseline DM method in certain cases for T2, but at a cost of longer processing time. On the other hand, our method can improve both the quantification accuracy and the processing speed of the baseline DM method. Furthermore, the dictionary-based methods, i.e., DM, SDM, and CSMR, all have a testing time that grows exponentially with the number of tissue properties to be estimated, since the dictionary dimension grows exponentially with the number of tissue properties [22], [25]. However, the testing time of our method only grows linearly with the number of tissue properties, as the number of networks used in our method grows linearly with the number of tissue properties. Given these relationships, our method is potentially superior to the dictionary-based methods in computation efficiency when more tissue properties are quantified with MRF in future work.

D. Limitations and Future Work

There are several limitations in the current method. First, our method, like other deep-learning-based methods, needs large amounts of training data for network learning. All the training data used in this study are acquired from in vivo subjects at our institution, while the number of subjects (i.e., 6) is not large enough. In the future work, simulation data, obtained from computer simulation based on the mathematical models of the data generation and acquisition process, will also be used for training to increase the training data size and further optimize our model. Second, our method only exploits the spatial context information inside an axial slice, without considering the spatial information from neighboring slices. Inspired by [44]–[47] that extend the MRF framework from 2D to 3D, we will extend our 2D model for 3D application to exploit the spatial information from all 3 spatial dimensions. Third, our method estimates different tissue properties separately, ignoring the inherent relationship among different tissue properties, e.g., T1 and T2. We plan to explicitly exploit this correlation through a multi-target joint estimation network [48] to improve the quantification accuracy. Finally, other advanced convolutional neural networks besides the U-Net [32], e.g., ResNet [49], DenseNet [50] and others [51]–[53], can also be used in SQ module to capture spatial context information in MRF signals in future work.

Besides the aforementioned improvements in methodology, more experiments can be also conducted to better evaluate our method. First, in this work, we only test our method with the FISP sequence. The performance of our method on other MRF sequences, e.g., bSSFP [8], [54], is worth evaluating. Second, we only examine two tissue properties, i.e., T1 and T2 relaxation times, while other properties, e.g., spin density and T2^∗ relaxation time, are also worth evaluating. Third, our dataset contains only healthy subjects with no brain lesions. In the future work, data from subjects with brain lesions or other brain diseases can be also used for testing, to better evaluate our method’s potential for clinical usage.

V. Conclusion

In this paper, we have introduced a deep-learning-based spatially-constrained tissue quantification method for magnetic resonance fingerprinting (MRF). A unique two-step deep learning model is proposed to tackle with the high dimensionality of MRF data, including a feature extraction module and a spatially-constrained quantification module. A two-step training strategy and a relative-difference-based loss function are used to optimize the performance of our model. Based on the experimental results, our method can 1) achieve accurate quantification of T1 and T2 relaxation times from highly undersampled in vivo brain data, and 2) allow at least four times of acceleration for MRF data acquisition without significant loss of accuracy in tissue quantification.