The Interactions of Composition and Stress in Crystalline Solids

Abstract

The thermodynamics of stressed crystals that can change phase and composition is examined with particular attention to hypotheses used and approximations made, Bulk and surface conditions are obtained and for each of them practical expressions are given in terms of experimentally measurable quantities. The concept of open-system elastic constants leads to the reformulation of internal elastochemical equilibrium problems into purely elastic problems, whose solutions are then used to compute the composition distribution. The atmosphere around a dislocation in a cubic crystal is one of several examples that are completely worked out. The effects of vacancies and their equilibrium within a solid and near surfaces are critically examined, and previous formulas are found to be first order approximations. Consequences of the boundary equations that govern phase changes are studied with several examples. Finally, problems connected with diffusional kinetics and diffusional creep are discussed.

Introduction

The literature of the thermodynamics of solids spans more than a century and has appeared in many fields. It has been marked by long controversies, some even regarding the very existence of equilibrium under conditions of nonhydrostatic stress. The resulting concepts and relations have been used in applications to global equilibrium problems, and as local equilibrium conditions in nonequilibrium problems of diffusion, creep, electrochemistry, and phase changes. The formulations have been gradually generalized to include multi-component anisotropic solids, containing vacancies and other defects, that are nonhydrostatically and non-uniformly stressed. Considerable attention has been given to multi-phase systems and to conditions of equilibrium at interfaces between phases that are in mechanical and thermal contact, that can exchange matter and under conditions of slip or no slip (incoherent and coherent, resp.). In view of the importance of the field, a clarification of the controversies seems in order.

Thermodynamics lends itself to many formulations based on different definitions, conventions and notations. When properly done, all these formulations should identify the same measurable quantities and give identical relationships among them. Discrepancies arise when the formulations differ in assumptions made about the behaviour of matter. There are also many simplifications that may not be valid or necessary. Invalid assumptions have been made about the laws of thermodynamics and about the conditions for equilibrium. We will examine the main formulations for their assumptions to find their range of validity. Whenever possible we will identify the most general formulation and show how the other formulations follow as special cases, compare predictions, and identify sources of discrepancies. But since general formulations are often more cumbersome to apply, we will examine a set of simple applications to display how one uses the main results in this field.

It may be worthwhile to categorize broadly the main controversies and to illustrate with one simple example how they arise. These center around: 1) the question of the existence of equilibrium if diffusion is permitted; 2) the various methods of distinguishing solids from fluids in a formulation, these involving models of solids and constraints on the variations that can occur in solids; 3) the definitions of chemical potential of species inside solids, since in some formulations one cannot arbitrarily add atoms to the interior of a crystal without removing other atoms or destroying vacancies; 4) how one formulates the conditions for equilibrium when the familiar minimum Gibbs-free energy which works only for constant hydrostatic pressure is inapplicable, and when so many different chemical potential conventions have been proposed; and 5) clear distinctions between the accretions that can occur at surfaces and at interior defects, such as climbing dislocations, and the addition of atoms to sites inside of crystals.

In addition, there are a variety of simplifications with obvious limitations on the applicability of the results. Among them is one, homogeneity, which has led to major misconceptions. Many situations will lead to homogeneous systems at equilibrium, but if one requires in tests for equilibrium that all variations keep the system homogeneous, one may constrain the system unnecessarily.

With these controversies in mind, let us examine the simple example of a solid cylinder containing one or more components and a straight axial dislocation. Let us first ignore surface effects and let the cylinder be infinite in all directions. Let there be no restriction on diffusion. If the solid is crystalline, an equilibrium will be reached with the dislocation retained in which the solid is heterogeneously and nonhydrostatically stressed. If the solid is multicomponent, it will also be compositionally heterogeneous. The system can reach an equilibrium which of course means that all diffusional flow has ceased, in spite of the shear stresses and the heterogeneity.

If the cylinder had been a highly viscous liquid in which the dislocation had been introduced by a cutting, displacing, and welding procedure, the dislocation would disappear on annealing. Equilibrium would not be compatible with shear stress or heterogeneity. It is apparent that crystallinity imposes restrictions on the variations that lead to a different type of equilibrium.

Even in a one component solid, there will be a gradient in the Helmholtz-free energy density at equilibrium. Any definition of a chemical potential, which for a one-component system reduces to the local free energy per atom, cannot subsequently be used by asserting that such chemical potentials must be constant at equilibrium or, if not constant, will lead to diffusional fluxes. Care must be exercised in the definition of chemical potentials in one or multicomponent systems to ensure that they are useful.

The constraint which crystallinity imposes in this example is that some of the atoms cannot be moved at will without a counterflux of some other species, including vacancies, to take their place in the crystal structure. At the surface and at the core of dislocations capable of climbing, this constraint does not apply and atoms can be inserted or removed at will.

To illustrate the importance of separate equilibrium conditions at surfaces, let the cylinder in our example have a finite radius and permit surface rearrangement. An equilibrium shape could be reached where transfer of small amounts of any species of atoms from one surface location to another does not change the appropriate free energy. This would be a thermodynamically stationary state in which all fluxes would cease, but it would be metastable or possibly unstable equilibrium because moving the dislocation out of the cylinder would lead to a lowered energy.

2. What Is a Solid?

Formulations of thermodynamics differ considerably in how the essential aspects of solidity are represented mathematically. Many authors purporting to deal specifically with solids reach conclusions that are the same as for very viscous liquids that may take a long time to reach an equilibrium that does not support shears.

Various models, composed of springs and dashpots, have been proposed to represent the viscoelastic behavior of matter. Whereas the Maxwell model creeps continuously under load, the Meyer-Kelvin-Voigt [1]¹ solid reaches a mechanical equilibrium when the load is entirely carried by the spring. The elements of these solids do not dissolve or diffuse, and Gibbs [2] devised a model of a solid that did both.

Gibbs introduced the idea of a solid component which does not diffuse. Like Mayer-Kelvin-Voigt’s solid, it can deform elastically but it always retains its connectivity. In addition Gibbs considered surfaces, where he did permit the solid to grow by accretion or to shrink by vaporization, to melt or to dissolve into contacting fluids. He also incorporated the concept of a fluid component which can diffuse and distort the solid. He fully developed the thermodynamic properties of such a solid, including its equilibria, and revealed a variety of surprising properties. Since the solid component was not involved in any chemical variations except at the surface, there was no need to define a chemical potential in the solid. When the solid was equilibrated with a fluid, the chemical potential of this solid component in the fluid was readily calculated. One important result was that the chemical potential in the saturated fluids in contact with a homogeneously stressed solid depends on the orientation of the surface. There is thus not only no need to define a chemical potential of the solid component, but it does not seem to be definable. The fluid component on the other hand has a defined chemical potential that is constant at equilibrium throughout all phases even if they are heterogeneously stressed. Gibbs’ solid is therefore quite active chemically and yet it is different from a fluid. The key was the solid component. Even though this component can dissolve, essential solid properties are obtained.

Gibbs was strongly influenced by the law of definite proportions and required his solid component to be a single element or a stoichiometric compound. If it was a compound, the chemical potential in the saturated fluids is calculated even if the compound dissociates or reacts with the solvent. Modern examples of Gibbs solids are polymer fibers which also can absorb solvent molecules, and silicate glasses in which the silicate network is the solid component while modifier ions can diffuse about. A very good example of the kind of equilibrium Gibbs was able to calculate is the bending of a damp wooden beam in which the water redistributes at equilibrium and affects the compliance. Li, Darken, and Oriani [3] pointed out that mobile interstitials in metals at temperatures where the substitutional atoms did not move was a valid metallurgical example of a Gibbs solid with a fluid component. An example of the equilibria of a dissolving Gibbs solid occurs in stressed electrodes. The equations predict the effect of elastic stress on the electrode potential [4].

Solid state diffusion of every component is counter to the strict definition of Gibbs’ solid component. As a result most thermodynamic formulations that permit unrestricted diffusion to take place do not ascribe to the solid any property that differs from a viscous fluid. As the example in the introduction points out, unrestricted diffusion consistent with our knowledge of the solid does permit new kinds of equilibria.

Gibbs’ solid component, because it did not diffuse, served as network for defining displacement and hence strain, as well as the local composition of the fluid component. The local energy and entropy density were functions of the local strain and composition. What was needed was a network which continued to define unambiguously the same place in the solid even if all atoms were capable of diffusing. In crystalline structures, the lattice serves this function, and a thermodynamics has been developed. Robin [5] has simply let the lattice itself be the solid component, and has found that “component differences” become the exact analogues of Gibbs’ fluid components. Instead of modifying Gibbs’ concept we have defined a network solid as one in which there is an unambiguous method of locating the same place after diffusion, and where the thermodynamic properties are functions of the strain and local composition defined by this network [6]. Gibbs solid component is one example of such a network; the lattice is another example.

Most of our work has been with simple crystal structures in which there is one type of substitutional site and one type of interstitial side. Atoms of a given species are assumed to be either substitutional or interstitial. The substitutional sites served as a network. Bravais solids where lattice sites are occupied by substitutional atoms are an example. Recently attention has focused on species which could occupy both interstitial or substitutional sites [7], and this has led to the generalization of structures in which many different sites are occupied in a unit cell and where a particular species can occupy several sites. One can even include the case where no species occupies the origin in the unit cell which serves as network marker.

In crystal structures, the network imposes what we have called the network restriction. A site exists, regardles of the species that occupies it, or even if it is empty. Atoms exchange among sites

$$A_{\mathrm{I}}+B_{\text{J}}=A_{\text{J}}+B_{\text{I}}$$ (2.1)

where I and J are different types of sites: Sites that are mostly filled are occupied by what are called substitutional atoms, while sites that are mostly vacant are occupied by what are called interstitial atoms.²

Vacancies are capable of diffusing or reacting with atoms on other sites. Letting B be a vacancy, (2.1) becomes

$$V_{\mathrm{I}}+A_{\text{J}}=A_{\mathrm{I}}+V_{\text{J}}$$ (2.2)

where I and J are different sites. If I is an interstitial site, this can also be written

$$A_{\text{J}}=A_{\mathrm{I}}+V_{\mathrm{J}}.$$ (2.3)

One of the main results of the network restriction is that there is no need to define separate chemical potentials of individual network species. Within the crystal only their differences are ever needed.

The network is unambiguously defined only as long as the structure is not severely distorted. The network can be modified at surfaces and dislocations and these have led to special equilibrium conditions. Of particular interest is the fact that there are differences between solid-fluid interfaces and solid-solid interfaces regarding equilibrium conditions. Two types of solid-solid boundaries have been treated [10]: incoherent interfaces where there are two independent networks with no relationship between them and coherent interfaces where there is an exact correspondence between network sites in the two crystals, and a connectivity across the interface that survives the distortions of a phase change that transfers sites from one crystal to the other. Thus many restrictions in Gibbs’ solid have been eliminated. Modern understanding of solid solutions, crystalline defects, and diffusion have been incorporated. In addition, solidsolid equilibria, interfaces, and phase changes have been considered.

3. Derivations of Usable Equilibrium Conditions

3.1. Thermodynamic Formulation

The basic two laws of thermodynamics are quite general and applicable not only to all equilibrium conditions but also in specifying what cannot happen in non-equilibrium conditions. They often are cumbersome to use, but from them special conditions have been derived (such as constant temperature at equilibrium) that are easier to apply. In addition, there are certain restrictions or constraints that occur commonly that permit even simpler specialized but rigorously applicable procedures to be developed. A good example is the Gibbs free energy. Under the special restriction that temperature, pressure, and the mass of various species be held constant, it can be shown that the laws of thermodynamics reduce to the simple condition that the Gibbs free energy monotonically decreases to a minimum. For these common restrictions, it is not longer necessary to start from the basic laws. For equilibrium, one begins with the minimization of Gibbs free energy knowing that this is fully equivalent to the basic laws. The procedure is a general one, subject only to the easily verifiable restrictions on temperature, pressure, and mass. The restrictions are important. When temperature decreases (as in an endothermic reaction held adiabatically), pressure increases or mass is added, the Gibbs free energy can increase and has lost it usefulness as a simple condition for equilibrium.

Whenever we encounter new restrictions or constraints, it is necessary to return to the two basic laws to find new conditions for equilibrium that are general, subject only to the restrictions or constraints. It is important that the restrictions or constraints are verifiable and that they be general enough to include many important situations, but not so general as to lead to cumbersome conditions. The procedures for finding simpler equilibrium conditions subject to new restrictions or constraints are straightforward and if done with mathematical rigor, need only be done once. Applications then follow from these derived conditions. The derivation often identifies the useful free energy. It is dangerous to assert conditions for equilibrium under new restrictions (some type of free energy to be minimized or some potential to be constant) without a derivation that begins with the basic two laws.

There are various derivations in the literature. They differ in the model of “what is a solid” expressed in terms of restrictions on possible variations. They also differ on whether or not they require homogeneity. They differ on whether they begin with the basic two laws, or with some derived law.

It is not difficult to start with the basic laws used by Gibbs: “For the equilibrium of any isolated system, it is necessary and sufficient that in all possible variations in the state of the system which do not alter its entropy, the variation of its energy shall either vanish or be positive” [9, p. 56]. It is quite straightforward to permit the system to be heterogeneous.

Since the general state of a solid is heterogeneous, the energy, entropy and mass of its various components will be integrals over the volume, and the minimization procedure is done by standard variational calculus. Such a formulation permits the solid to change its shape by elastic deformation or by a process of network modification which we will call either accretion, dissolution, or phase change.

These methods of variational calculus were used by Gibbs every time the system under consideration was not homogeneous; the influence of gravity [9, p. 144], stressed solids [2], surfaces [9, p. 238], multiphase systems [9, p. 64], etc. A variational statement of the first and second laws of thermodynamics for the multicomponent network solid has been carried out [6]. It very neatly produces all the conditions for equilibrium—mechanical, thermal, and chemical—in the bulk and at the interfaces. There is usually no need to assume linearity, ideality, or isotropy. The derived equations identify and define important functions and usually can be manipulated to suggest methods of measurement.

The imposed constraints are incorporated into the formulation as Lagrange multipliers and this introduces quantities which must be constant throughout the system at equilibrium. Since sites in a unit cell or a network exist whether occupied by atoms or not, vacancies appear as a conserved species within a network. We formulated three different rules for the transfer of material across an interface [10]. Network sites could be added or subtracted to the solid at solid-fluid and at incoherent solid-solid interfaces. At a coherent solid-solid interface, a single network describes both solids, and during phase changes, sites are transferred but do not change their relative locations.

3.2. State Variables and Notations

The procedure outlined can be followed once the state variables have been identified. With network solids, a strain can be defined. The energy density is assumed to be a function of that strain (either the usual small strain, or the deformation gradient to include the cases of large strains), of the entropy density, and of the density of the various atomic or molecular species.

The choice of the strain or deformation gradient as a state variable that describes the mechanical state of the solid by no means exhausts the possible choices. Continuum mechanicians and others [11–14] have described much more complex solids, where higher gradients of displacement or composition come in the picture. We feel that our choice is sufficient to describe many metallurgical materials. In any case, thermodynamics uses as input data the results of measurements of mechanical and thermal properties, and inadequate specification of state variables would become apparent.

Only small strain theory will be explicitly used here. The relations that are valid without this approximation have been derived [10, 15], and effects that might modify the small strain results will be mentioned and discussed in the course of this article.

The reference state for strain in the solid is quite arbitrary. It can be at zero stress, or under hydrostatic pressure, and at any arbitrary constant composition. It merely serves to identify the same point x′ in a solid after composition change and strain. For many elastic energy equations, a convenient reference state is zero stress. There are also useful standard states for thermodynamic quantities. These are often at hydrostatic stress that is not zero and at definite compositions. As a result there are advantages to be flexible about the reference state for strain. We will try to point out in each application which reference state we have used.

When the point x′ of a solid is displaced by u, the small strain is defined by³

$$E_{ij}=1/2\left(u_{i,j}+u_{j,i}\right).$$ (3.1)

A change of reference state from x′ to x″(x′) where x″− x′=v leads in the small strain approximation to a new strain $E_{ij}^{″}$ given by

$$E_{ij}^{″}=E_{ij}+1/2\left(v_{i,j}+v_{j,i}\right).$$ (3.2)

The density of energy, entropy and component I are respectively denoted by ϵ, s, and ρ_I. Because the elementary volume of solid is affected by its state of strain, densities per unit volume in the deformed state always contain a strain effect. As such they are not very convenient to use. Much better variables are the densities per unit volume in the reference state. These will be noted by primed symbols. The relations between primed and unprimed densities are

$${ϵ}^{\prime }/ϵ=s^{\prime }/s={\rho }_{\mathrm{I}}^{\prime }/{\rho }_{\mathrm{I}}={\rho }_0^{\prime }/{\rho }_0=\dots$$ (3.3)

$$=V_0/V_0^{\prime }=1+E_{kk}$$ (3.4)

where ρ₀ is the molar density of lattice sites, and its inverse V₀ is the molar volume of lattice sites.

All of our chemical densities ρ_I and ${\rho }_{\text{I}}^{\prime }$ will be atomic or molar densities (moles/volume). This is especially preferred to mass densities when we consider vacancies as a species. It is useful to introduce dimensionless composition variables

$$c_{\mathrm{I}}={\rho }_{\mathrm{I}}^{\prime }/{\rho }_0^{\prime }={\rho }_{\mathrm{I}}/{\rho }_0.$$

This is the classical mole fraction for single-site substitutional alloys. For an interstitial alloy with no vacancies on the substitutional sites, c_I given above is the molal composition. The mole fraction ${\tilde{c}}_I$ is then

$${\tilde{c}}_{\mathrm{I}}={\rho }_{\mathrm{I}}/\left({\rho }_0+{\rho }_{\mathrm{I}}\right)=c_{\mathrm{I}}/\left(1+c_{\mathrm{I}}\right).$$

which reduces to c_I at small concentration. We will drop the distinction between c_I and ${\tilde{c}}_I$.

3.3. Lagrange Multipliers

From the entropy constraint comes the standard condition that the temperature is everywhere equal to a Lagrange multiplier, and is therefore constant. It allows us to define a Helmholtz free energy density by a Legendre transform

$$f^{\prime }={ϵ}^{\prime }-\theta s^{\prime }$$ (3.5)

which we subsequently use because it is more convenient in many practical applications.

From the conservation of mass conditions come Lagrange multipliers that differ substantially from standard fluid equilibrium, a direct consequence of the network constraint. As with fluids, conservation of N chemical components lead to N Lagrange multipliers that are constants at equilibrium. Whereas for fluids they can be identified with N chemical potentials, for a system consisting of a network solid containing N substitutional species only N-1 quantities can be identified with physical processes replacing one specie with another on a site. The quantities thus identified with Lagrange multiplier differences we have called diffusion potentials. The notation is M_IK, where K is the dependent species. Vacancies are considered a species that can be ignored in some applications. Because of their definition as Lagrange multipliers, the M_IK, like the temperature are constants, and take on a precise local meaning everywhere within the system

M_IK = constant everywhere within the system.

$$=\left(1/{\rho }_0^{\prime }\right){\left(\partial f^{\prime }/\partial c_{\text{IK}}\right)}_{\theta ,E_{ij}}.$$ (3.6)

Since the c_I are not independent, we have introduced the differential operator

$$\left(\partial /\partial c_{\text{IK}}\right)={\left(\partial /\partial c_{\text{I}}\right)}_{c_J\ne \mathrm{I},\text{K}}$$ (3.7)

for a unit composition increase of species I, an equal decrease in species K, holding the composition of all other substitutional species on that site fixed. For binaries we drop the subscripts and adopt the convention c = c₁ and (∂/∂c₁₂)=(∂/∂c).

From this definition we have

$$M_{\text{IJ}}+M_{\text{JK}}+M_{\text{KI}}=0$$ (3.8)

$$M_{\text{IJ}}=-M_{\text{JI}};M_{\text{II}}=0.$$ (3.9)

In the case of equilibrium with a fluid, M_IK is equal to the difference in chemical potential of I and K in the fluid

$$M_{\text{IK}}={\mathrm{\mu }}_{\mathrm{I}}^L-{\mathrm{\mu }}_{\text{K}}^L$$ (3.10)

If the vacancy is chosen as K, we have

$$M_{\mathrm{I}v}={\mathrm{\mu }}_{\mathrm{I}}^L.$$ (3.11)

It might seem natural to use the M_Iv, and keep the formalism of hydrostatic thermodynamics. This has been done in a number of formulations [7]. However, it has practical drawbacks (see sect. 5.5), and we have found it preferable to keep the flexibility of choice for the dependent species K.

The Nth Lagrange multiplier which we will call μ_K cannot be identified in many problems. It is eliminated from all equilibrium calculations for internal equilibrium of a crystal away from surfaces and dislocations that can climb. It also is eliminated from all equilibrium calculations at coherent boundaries. Only in fluids, at incoherent boundaries and climbable dislocations can we identify μ _K with the chemical potential of the K specie.

The chemical potentials of interstitials are constant and equal to the chemical potentials of the corresponding species in the other phases,

$$M_{\mathrm{I}}={\mathrm{\mu }}_{\mathrm{I}}^L.$$ (3.12)

We shall see in section 5, where multisite solids are considered, that there is no need to differentiate between substitutional and interstitial sites. An increase of composition of the interstitial species I, holding the composition of all other interstitial species fixed, results in an equivalent decrease of vacancies on interstitial sites. But unlike vacancies on substitutional sites, vacancies on interstitial sites always have a concentration close to the total number of possible sites and can be dropped from consideration. In order to standardize and simplify the notation, we also call these chemical potentials diffusion potentials, and in order to simplify the notation in the various expressions, M_IK is understood to represent all diffusion potentials.

The restriction in the number of potentials necessary to calculate an equilibrium is a direct consequence of the crystalline nature of the solid and therefore should apply to the same solid under hydrostatic stress. In this case it can be shown (Appendix 1) that the previous equations, together with the boundary conditions to be discussed thereafter, are strictly equivalent to the standard conditions for equilibrium between fluids.

3.4. Mechanical Equilibrium

The variational calculus gives us [6,10] the very standard form of the mechanical equilibrium equation. It states that the divergence of the stress tensor is zero

$$T_{ij,j}=0.$$ (3.13)

This equation is also true for the large strain case, but the derivative is with respect to variables x rather than x′, distinction that is not made in the small strain approximation. Large strain forms involving x′ have been obtained [15].

3.5. Interface Conditions

Along each interface, there are conditions for mechanical equilibrium, and a condition for phase change equilibrium. They both depend on the nature of this interface.

3.5.1. Solid-Fluid Interfaces

For solid-fluid interfaces, the mechanical equations state that the normal is a principal direction of stress. The principal value associated with it is equal in magnitude to the pressure in the liquid and opposite in sign. The pressure is here the classical thermodynamic pressure, which is positive in fluids, and the convention for stress is such that the stress corresponding to a tension is positive.

The phase change equation can be written

$$f-\mathrm{\Sigma }{\mathrm{\mu }}_{\mathrm{I}}^L{\rho }_{\mathrm{I}}=-P$$ (3.14)

where ${\mathrm{\mu }}_{\mathrm{I}}^L$ are the chemical potentials in the fluid, while the ρ_I and f pertain to the solid. Because of the (N-1) equalities (3.10)

$$f-\sum _{\mathrm{I}\ne \mathrm{K}}{M}_{\mathrm{IK}}{\rho }_{\mathrm{I}}-{\mathrm{\mu }}_{\mathrm{K}}^L{\rho }_0=-P.$$ (3.15)

Because M_KK=0 the summation over all species is the same as the summation over all species but K. We can therefore drop the restriction and adopt the notation that Σ without any qualification means summation over all species I. To simplify notation it is convenient to define the ω function as

$$\omega \equiv f-\mathrm{\Sigma }{M}_{\text{IK}}{\rho }_{\mathrm{I}}-{\mathrm{\mu }}_{\text{K}}{\rho }_0$$ (3.16)

where μ_K is the Lagrange multiplier associated with the K^th species. At this stage neither ω nor μ_K has physical meaning. Once all the equilibrium equations are written they will have a specific meaning, or are eliminated. In a fluid ω is equal to minus the pressure, and thus because ${\mathrm{\mu }}_{\text{K}}={\mathrm{\mu }}_{\text{K}}^L$ eq (3.15) could be rewritten

$${\omega }^s={\omega }^L.$$ (3.17)

We should emphasize that these equations are between unprimed quantities, that are usually not convenient to use for solids. The conversion follows eq (3.4) and gives

$${\omega }^{\prime s}=-P\left(1+E_{kk}\right).$$ (3.18)

3.5.2. Incoherent Interfaces

Along an incoherent solid-solid boundary, the equilibrium equations are

$$T_{ij}^{\alpha }{n}_j^{\alpha }={\omega }^{\alpha }{n}_i^{\alpha }$$ (3.19)

$$T_{ij}^{\beta }{n}_j^{\beta }={\omega }^{\beta }{n}_i^{\beta }$$ (3.20)

$${\omega }^{\alpha }={\omega }^{\beta }$$ (3.21)

where $n_i^{\alpha }$ (resp. $n_i^{\beta }$) are the components of the normal to the interface oriented from α to β (resp. β to α). They all contain ω and hence the Lagrange multiplier μ_K.

Equations (3.19) and (3.20) imply that the normal is a principal stress axis and that in this case ω is the value of that principal stress. Multiplication of (3.19) by $n_i^{\alpha }$ and summation over i gives

$${\omega }^{\alpha }=T_{ij}^{\alpha }{n}_i^{\alpha }{n}_j^{\alpha }.$$ (3.22)

From (3.20) we can obtain a similar expression for ω^β. Therefore ω^α and ω^β are identified for this problem.

Using the definition of ω we obtain

$${\mathrm{\mu }}_{\text{K}}=V_0^{\beta }(f^{\beta }-\mathrm{\Sigma }{M}_{\text{IK}}{\rho }_{\mathrm{I}}^{\beta }-T_{ij}^{\beta }{n}_i^{\beta }{n}_j^{\beta }).$$ (3.23)

Substituting this value of μ_K in (3.21) and (3.19) gives the equivalent system of equations

$$\begin{gathered} {\mathrm{\mu }}_{\text{K}}=V_0^{\alpha }(f^{\alpha }-\mathrm{\Sigma }{M}_{\text{IK}}{\rho }_{\mathrm{I}}^{\alpha }-T_{ij}^{\alpha }{n}_i^{\alpha }{n}_j^{\alpha }) \\ =V_0^{\beta }(f^{\beta }-\mathrm{\Sigma }{M}_{\text{IK}}{\rho }_{\text{I}}^{\beta }-T_{ij}^{\beta }{n}_i^{\beta }{n}_j^{\beta }) \end{gathered}$$ (3.24)

$$T_{ij}^{\alpha }{n}_j^{\alpha }=-T_{ij}^{\beta }{n}_j^{\beta }=T_{kl}^{\alpha }{n}_k^{\alpha }{n}_l^{\alpha }{n}_i^{\alpha }$$ (3.25)

Equations (3.24) and (3.25) contain only known quantities and are the usable ones. Equation (3.23) can be interpreted as a definition for the chemical potential of the K species and this potential is constant along the interface. Along an incoherent interface we can then calculate a chemical potential for every specie, something which is not possible at any other location within the bulk of the α and β phase. Let us note that each side of eq (3.24) depends on what specie is chosen for K. Because the expression

$$\mathrm{\Sigma }{M}_{\mathrm{IK}}\left(\frac{{\rho }_{\mathrm{I}}^{\alpha }}{{\rho }_0^{\alpha }}-\frac{{\rho }_{\mathrm{I}}^{\beta }}{{\rho }_0^{\beta }}\right)=\mathrm{\Sigma }{M}_{\mathrm{IK}}(c_{\mathrm{I}}^{\alpha }-c_{\mathrm{I}}^{\beta })$$

is independent of K, the equation itself is independent of this choice. A comparison of (3.23) and (3.15) shows the similarities between solid-fluid and incoherent solid-solid equilibria.

3.5.3. Coherent Solid Interfaces

In a coherent solid-solid equilibrium, the mechanical boundary conditions

$$T_{ij}^{\alpha }{n}_j^{\alpha }=-T_{ij}^{\beta }{n}_j^{\beta }$$ (3.26)

indicate that the tractions (but not necessarily the stress tensor) are continuous across the interface. If the same reference state for strain is chosen for α and β the phase change equation (Appendix 2) reads

$$\begin{gathered} V_0^{\prime }{f}^{\alpha }-\mathrm{\Sigma }{M}_{\text{IK}}{c}_{\text{I}}^{\alpha }+V_0^{\prime }(-T_{ij}^{\alpha }{n}_i^{\prime \alpha }{n}_j^{\prime \alpha }+2{\mathrm{\Omega }}_{ij}^{\alpha }{T}_{jk}^{\alpha }{n}_i^{\prime \alpha }{n}_k^{\prime \alpha }) \\ =V_0^{\prime }{f}^{\beta }-\mathrm{\Sigma }{M}_{\text{IK}}{c}_{\text{I}}^{\beta }+V_0^{\prime }(-T_{ij}^{\beta }{n}_i^{\prime \beta }{n}_j^{\prime \beta } \\ +2{\mathrm{\Omega }}_{ij}^{\beta }{T}_{jk}^{\beta }{n}_i^{\prime \beta }{n}_k^{\prime \beta }) \end{gathered}$$ (3.27)

where Ω_ij is the small rotation tensor

$${\mathrm{\Omega }}_{ij}=\frac{1}{2}\left(u_{i,j}-u_{j,i}\right).$$ (3.28)

For this type of interface equilibrium, the Lagrange multiplier μ_K has disappeared from the equations. In contrast to the two cases treated before, no definition of individual chemical potentials for each species arises, even at the interface. As we will see none are needed to solve problems. This is a direct consequence of the restrictions in a fully coherent phase change, where no network site is created or destroyed.

4. The Data Base

We have identified a number of important thermodynamic quantities that determine the state of a system, and a number of functions of these state variables that enter into the equations of equilibrium. We now examine how one might determine these quantities from the usual quantities that are measured and available in compilations. They turn out to be identical to those used in ordinary solution thermodynamics and elasticity.

4.1. Geometric Variables

The lattice constants are readily-determined nonlinear functions of composition, temperature, and stress. From the lattice constants in the reference state we can compute ${\rho }_0^{\prime }$. From a comparison of the lattice shape in the actual state and the reference state, we can compute the strain, or, if the strain is large, the deformation gradient. Since the actual state and the reference state are usually chosen to be at the same temperature but not necessarily at the same composition, the strain E_ij is a sum of a contribution due to composition change with no change in stress, $E_{ij}^c$, and one due to stress. The general case when neither contribution is isotropic has been treated [15]. The tensor $E_{ij}^c$ is subject to the same crystal symmetry restrictions as the thermal expansion tensor [17]. For the present we will concentrate mostly on the isotropic case. Defining k such that

$$E_{ij}^c=k{\mathrm{\delta }}_{ij}$$ (4.1)

and assuming Hooke’s law of linear elasticity we can write

$$E_{ij}=\left(k-\frac{\nu }{E}{T}_{kk}\right){\mathrm{\delta }}_{ij}+\frac{1+\nu }{E}{T}_{ij}.$$ (4.2)

The dilatation E_kk is given by

$$E_{kk}=\frac{1-2\nu }{E}{T}_{kk}+3k.$$ (4.3)

In cubic crystals, $E_{ij}^c$ is also isotropic, so that the formula in eq (4.1) is still valid.

The constant ${\rho }_0^{\prime }$ appears repeatedly in various formulas because elastic energy naturally appears as energy per unit volume, whereas other energies will be per mole, ${\rho }_0^{\prime }$ is the conversion factor that transforms one into the other. Its inverse $V_0^{\prime }$ is the molar volume of the lattice sites. Combining (3.3), (3.4) and (4.3) we have for isotropic solids

$$V_0/V_0^{\prime }={\rho }_0^{\prime }/{\rho }_0=1+\frac{1-2\nu }{E}{T}_{kk}+3k.$$ (4.4)

The derivative of $E_{ij}^c$ with respect to composition in binary allows also occurs commonly

$${\eta }_{ij}=\text{d}{E}_{ij}^c/\text{d}c.$$ (4.5)

For systems with orthogonal axes

$${\eta }_{ii}=\left(\partial 1n{a}_i/\partial c\right)(\text{no}\text{summation})$$ (4.6)

where the a_i are the lattice parameters. When $E_{ij}^c$ is isotropic

$${\eta }_{ij}=(\text{d}k/\text{d}c){\mathrm{\delta }}_{ij}=\eta {\mathrm{\delta }}_{ij}.$$ (4.7)

In binary isotropic and cubic systems η is also related to the partial molar volumes

$$\eta =\left({\overline{V}}_1-{\overline{V}}_2\right)/3V_0^{\prime }.$$ (4.8)

If η is constant

$$k=\left(c-c_0\right)({\overline{V}}_1-{\overline{V}}_2)/3V_0^{\prime }$$ (4.9)

where c₀ is the composition of the reference state chosen to measure the strain. It is to be emphasized that the anisotropic and nonlinear versions of these equations are readily available [15].

4.2. Thermochemical Quantities

The two important quantities to be determined are f′ and M_IK. There are several convenient paths of integration from a hydrostatic state, where these quantities can be determined with standard thermodynamic methods, to the actual stressed state. We begin with the differential of f′

$$\text{d}{f}^{\prime }=T_{ij}\text{d}{E}_{ij}-s^{\prime }\text{d}\theta +{\rho }_0^{\prime }\mathrm{\Sigma }{M}_{\text{IK}}\text{d}{c}_{\text{I}}.$$ (4.10)

The function ϕ′, defined by a Legendre transform

$${\mathrm{\varphi }}^{\prime }=f^{\prime }-T_{ij}{E}_{ij}$$ (4.11)

proves to be useful. Its differential

$$\text{d}{\mathrm{\varphi }}^{\prime }=-E_{ij}\text{d}{T}_{ij}-s^{\prime }\text{d}\theta +{\rho }_0^{\prime }\mathrm{\Sigma }{M}_{\text{IK}}\text{d}{c}_{\text{I}}$$ (4.12)

permits us to deduce the following Maxwell relation

$$-{\rho }_0^{\prime }{\left(\partial M_{\text{IK}}/\partial T_{ij}\right)}_{c_J}={\left(\partial E_{ij}/\partial c_{\text{IK}}\right)}_{T_{kl}}.$$ (4.13)

Hooke’s law at constant composition is

$$T_{ij}=C_{ijkl}\left(E_{kl}-E_{kl}^c\right)$$ (4.14)

or

$$E_{ij}=E_{ij}^c+S_{ijkl}{T}_{kl}$$ (4.15)

where the C_ijkl are moduli of elasticity, and the S_ijkl compliances. Both are composition and temperature dependent. From (4.15) we deduce

$${\left(\frac{\partial E_{ij}}{\partial c_{\text{IK}}}\right)}_{T_{kl}}=\left(\frac{\partial E_{ij}^c}{\partial c_{\text{IK}}}\right)+\left(\frac{\partial S_{ijkl}}{\partial c_{\text{IK}}}\right)T_{kl}.$$ (4.16)

Chemical potentials are assumed known at a hydrostatic pressure P, and composition c₁, c₂, …

$$\begin{gathered} M_{\text{IK}}\left(P,c_1,c_2,\dots .\right)={\mathrm{\mu }}_{\text{l}}\left(P,c_{\text{l}},c_2,\dots .\right) \\ -{\mathrm{\mu }}_{\mathrm{K}}\left(P,c_1,c_2,\dots .\right). \end{gathered}$$ (4.17)

It is customary to define standard chemical potentials ${\mathrm{\mu }}_I^0$ and activity coefficients such that

$${\mathrm{\mu }}_{\mathrm{I}}(P,c)={\mathrm{\mu }}_{\mathrm{I}}^0(P)+R\theta \ln {\gamma }_{\text{I}}{c}_{\text{I}}$$ (4.18)

where γ₁ is chosen for convenience. Depending on the problem, it is chosen to approach 1 either for dilute or concentrated solution. Vacancy potentials also are fit to this convention. Since ${\mathrm{\mu }}_{\text{v}}\left(P,{\overline{c}}_{\text{v}}\right)=0$, where ${\overline{c}}_{\text{v}}$ is the equilibrium vacancy concentration at P,

$${\mathrm{\mu }}_{\text{v}}^0(P)=-R\theta \ln {\gamma }_{\text{v}}{\overline{c}}_{\text{v}}$$ (4.19)

where γ_v is the vacancy activity coefficient. If it is constant, the chemical potential of vacancies under pressure P can also be written

$${\mathrm{\mu }}_{\text{v}}\left(P,c_{\text{v}}\right)=R\theta \ln \left(c_{\text{v}}/{\overline{c}}_{\text{v}}\right)$$ (4.20)

The expressions for the chemical potentials are introduced into eq (4.13) and the resulting expression integrated along a constant composition path to the stress T_ij. For a binary solution

$$\begin{gathered} M_{12}\left(T_{ij},c\right)={\mathrm{\mu }}_1^0(P)-{\mathrm{\mu }}_2^0(P)+R\theta \ln \frac{{\gamma }_{1}c}{{\gamma }_2(1-c)} \\ -V_0^{\prime }{\eta }_{ij}{T}_{ij}-\frac{V_0^{\prime }}{2}\frac{\text{d}{S}_{ijkl}}{\text{d}c}{T}_{ij}{T}_{kl}+\frac{V_0^{\prime }}{2}\frac{\text{d}{S}_{jjkk}}{dc}{P}^2-V_0^{\prime }{\eta }_{kk}P. \end{gathered}$$ (4.21)

If the solid is isotropic, this expression becomes

$$\begin{gathered} M_{12}\left(T_{ij},c\right)={\mathrm{\mu }}_1^0(P)-{\mathrm{\mu }}_2^0(P)+R\theta \ln \frac{{\gamma }_{1}c}{{\gamma }_2(1-c)}-V_0^{\prime }\eta T_{kk} \\ +\frac{V_0^{\prime }}{2}\frac{\text{d}}{\text{d}c}\left(\frac{\nu }{E}\right){\left(T_{kk}\right)}^2-\frac{V_0^{\prime }}{2}\frac{\text{d}}{\text{d}c}\left(\frac{1+\nu }{E}\right)T_{ij}{T}_{ij}-3V_0^{\prime }\eta P \\ +\frac{3V_0^{\prime }}{2}\frac{\text{d}}{\text{d}c}\left(\frac{1-2\nu }{E}\right)P^2. \end{gathered}$$ (4.22)

These expressions contain terms both linear and quadratic in stress. They simplify considerably when the elastic coefficients are not composition dependent. Equation (4.22) for instance becomes

$$\begin{gathered} M_{12}\left(T_{ij},c\right)={\mathrm{\mu }}_1^0(P)-{\mathrm{\mu }}_2^0(P)+R\theta \ln \frac{{\gamma }_{1}c}{{\gamma }_2(1-c)} \\ -V_0^{\prime }\eta \left(T_{kk}+3P\right). \end{gathered}$$ (4.23)

To obtain f′ we calculate ϕ′ with eq (4.12). It is First integrated along a path of constant composition, from pressure P to stress T_ij. Using Hooke’s law (4.15), this gives

$$\begin{gathered} {\mathrm{\varphi }}^{\prime }\left(T_{ij},c\right)-{\mathrm{\varphi }}^{\prime }(P,c)=-\frac{1}{2}{S}_{ijkl}{T}_{ij}{T}_{kl}-E_{kl}^c{T}_{kl} \\ +\frac{1}{2}{S}_{jjkk}{P}^2-E_{kk}^{c}P \end{gathered}$$ (4.24)

and using (4.11)

$$f^{\prime }\left(T_{ij},c\right)-f^{\prime }(P,c)=\frac{1}{2}{S}_{ijkl}{T}_{ij}{T}_{kl}-\frac{1}{2}{S}_{jjkk}{P}^2$$ (4.25)

Since under hydrostatic stress, the familiar liquid thermodynamics is valid, the Helmholtz free energy f′(P,c) is known. It may be obtained from the more commonly tabulated molar Gibbs free energy G_m by subtracting PV₀ and dividing by $V_0^{\prime }$. This gives

$$f^{\prime }(P,c)={\rho }_0^{\prime }{G}_{\text{m}}-P{\rho }_0^{\prime }/{\rho }_0.$$ (4.26)

Since

$${\rho }_0^{\prime }/{\rho }_0=1+E_{kk}=1+E_{kk}^c-S_{jjkk}P$$ (4.27)

one obtains, after replacement of G_m by its value as a function of composition

$$\begin{gathered} f^{\prime }(P,c)={\rho }_0^{\prime }\{c\left[{\mathrm{\mu }}_1^0(P)+R\theta \ln {\gamma }_{1}c\right]+(1-c)[{\mathrm{\mu }}_2^0(P) \\ +R\theta \ln {\gamma }_2(1-c)]\}-P\left(1+E_{kk}^c\right)+S_{jjkk}{P}^2. \end{gathered}$$ (4.28)

Combination of (4.25) and (4.28) gives the final result

$$\begin{gathered} f^{\prime }\left(T_{ij},c\right)={\rho }_0^{\prime }\{c\left[{\mathrm{\mu }}_1^0(P)+R\theta \ln {\gamma }_{1}c\right]+(1-c)[{\mathrm{\mu }}_2^0(P) \\ +R\theta \ln {\gamma }_2(1-c)]\}-P\left(1+E_{kk}^c\right) \\ +\frac{1}{2}{S}_{ijkl}{T}_{ij}{T}_{kl}-\frac{1}{2}{S}_{jjkk}{P}^2. \end{gathered}$$ (4.29)

For an isotropic solid, this relation becomes

$$\begin{gathered} f^{\prime }\left(T_{ij},c\right)=p_0^{\prime }\{c\left[{\mathrm{\mu }}_1^0(P)+R\theta \ln {\gamma }_{1}c\right]+(1-c)[{\mathrm{\mu }}_2^0(P) \\ +R\theta \ln {\gamma }_2(1-c)]\}-P(1+3k)-\frac{\nu }{2E}{\left(T_{kk}\right)}^2 \\ +\frac{1+\nu }{2E}{T}_{ij}{T}_{ij}-\frac{3(1-2\nu )}{2E}{P}^2. \end{gathered}$$ (4.30)

Because it always appears in the boundary conditions, the expression for the quantity $V_0^{\prime }{f}^{\prime }-M_{12}c$ is useful. Combining (4.22) and (4.30) we get, in the isotropic case

$$\begin{gathered} V_0^{\prime }{f}^{\prime }-M_{12}c={\mathrm{\mu }}_2^0(P)+R\theta \ln {\gamma }_2(1-c)+V_0^{\prime }[-P(1+3k) \\ -\frac{\nu }{2E}{\left(T_{kk}\right)}^2+\frac{1+\nu }{2E}{T}_{ij}{T}_{ij}+c\eta \left(T_{kk}+3P\right)-\frac{3(1-2\nu )}{2E}{P}^2 \\ -\frac{c}{2}\frac{\text{d}}{\text{d}c}\left(\frac{\nu }{E}\right){\left(T_{kk}\right)}^2+\frac{c}{2}\frac{\text{d}}{\text{d}c}\left(\frac{1+\nu }{E}\right)T_{ij}{T}_{ij} \\ -\frac{3c}{2}\frac{\text{d}}{\text{d}c}\left(\frac{1-2\nu }{E}\right)P^2]. \end{gathered}$$ (4.31)

When the elastic coefficients are not composition dependent, this becomes

$$\begin{gathered} V_0^{\prime }{f}^{\prime }-M_{12}c={\mathrm{\mu }}_2^0(P)+R\theta \ln {\gamma }_2(1-c)+V_0^{\prime }[-P(1+3k) \\ -\frac{\nu }{2E}{\left(T_{kk}\right)}^2+\frac{1+\nu }{2E}{T}_{ij}{T}_{ij}-\frac{3(1-2\nu )}{2E}{P}^2 \\ +c\eta \left(T_{kk}+3P\right)]. \end{gathered}$$ (4.32)

In a crystal of arbitrary symmetry, this expression is

$$\begin{gathered} V_0^{\prime }{f}^{\prime }-M_{12}c={\mathrm{\mu }}_2^0(P)+R\theta \ln {\gamma }_2(1-c)+V_0^{\prime }[-P\left(1+E_{kk}^c\right) \\ +\frac{1}{2}{S}_{ijkl}{T}_{ij}{T}_{kl}-\frac{1}{2}{S}_{jjkk}{P}^2+c{\eta }_{\mathrm{ij}}{T}_{ij} \\ +\frac{c}{2}\frac{\text{d}{S}_{ijkl}}{\text{d}c}{T}_{ij}{T}_{kl}+c{\eta }_{kk}P-\frac{c}{2}\frac{\text{d}{S}_{jjkk}}{\text{d}c}{P}^2]. \end{gathered}$$ (4.33)

Expressions (4.21) to (4.23) apply to substitutional binary solutions. For interstitial binary solutions the integration along a constant composition path from the hydrostatic stress to the stress T_ij using (4.13) gives the elastic terms identical to those in (4.21) to (4.23). Because there is no network constraint or interstitial concentration we use (3.12) for M_I and obtain for dilute interstitial solutions

$$\begin{gathered} M_{\mathrm{I}}\left(T_{ij}/c\right)={\mathrm{\mu }}_0^{\prime }(P)+R\theta \ln {\gamma }_{1}c-V_0^{\prime }{\eta }_{ij}{T}_{ij} \\ -\frac{V_0^{\prime }}{2}\frac{\text{d}{S}_{ijkl}}{\text{d}c}{T}_{ij}{T}_{kl}-V_0^{\prime }{\eta }_{kk}P+\frac{V_0^{\prime }}{2}\frac{\text{d}{S}_{jjkk}}{\text{d}c}{P}^2. \end{gathered}$$ (4.34)

Equations for the special cases of isotropy and constant elastic coefficients are like (4.34) except that the elastic terms take the forms they have in (4.22) and (4.23). We will see in section 5.7 that there is no need to distinguish between interstitial and substitutional solutions. Had we chosen the vacancy on the interstitial site as component 2 we could have obtained (4.34) directly from (4.21) by noting that ${\mathrm{\mu }}_2^0=0$ for the vacancy.

5. Internal Equilibrium

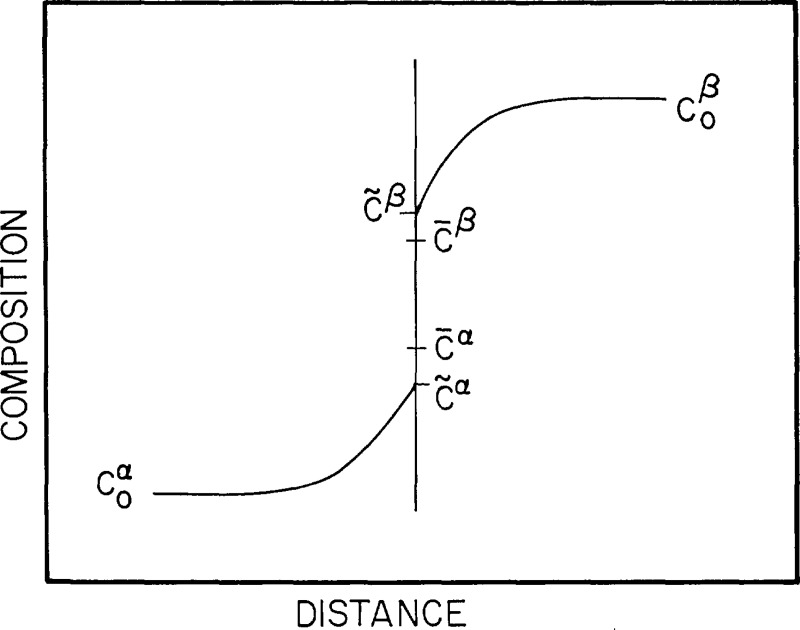
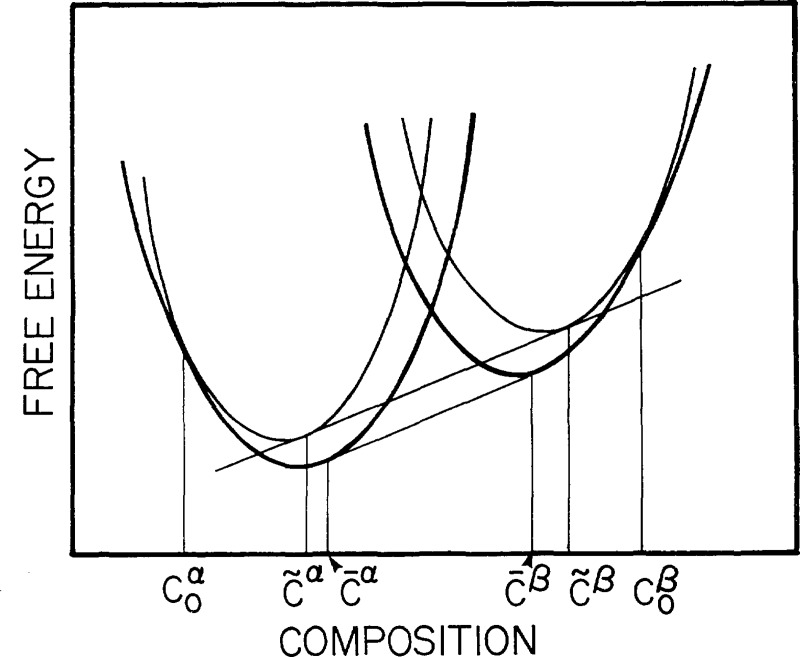
The study of internal equilibrium requires the simultaneous solution of the equations of elasticity and those of chemical equilibrium. The method we have found useful recognizes that the strain is a function of stress and composition. But the composition at equilibrium with a given diffusion potential is determined by the local stress alone. Thus the strain at a given diffusion potential is a function of stress alone. If we obtain this stress-strain function, we can solve these problems as if they were ordinary elastic problems, without any further regard to chemical problems whose effects are now implicitly accounted for.

There are several derivations. The simplest and most easily generalized for large strains and nonlinear effects parallels in its first steps the thermodynamic methods used to derive the relationships between isotropic (adiabatic) and isothermal elasticity. In the first section we review the main results and then apply them to various problems.

5.1. Open-System Elastic Constants

After a straightforward manipulation of partial derivatives, the following expression, valid for a two-component solid, is obtained (Appendix 3)

$${\left(\frac{\partial E_{ij}}{\partial T_{kl}}\right)}_{M_{12}}={\left(\frac{\partial E_{ij}}{\partial T_{kl}}\right)}_c+V_0^{\prime }{\eta }_{ij}{\eta }_{kl}/{\left(\frac{\partial M_{12}}{\partial c}\right)}_{T_{mn}}.$$ (5.1)

Making the usual small strain approximations, and an expansion of the strain around T_ij = 0 produces the constant chemical-potential form of Hooke’s law

$$E_{ij}=S_{ijkl}^{*}{T}_{kl}.$$ (5.2)

The coefficients of the stress have been called open-system compliances, S* and are related to the constant composition compliances S by

$$S_{ijkl}^{*}=S_{ijkl}+V_0^{\prime }{\eta }_{ij}{\eta }_{kl}/{\left(\frac{\partial M_{12}}{\partial c}\right)}_{T_{mn}}$$ (5.3)

where (∂M₁₂/∂c)_Tmn is evaluated at T_mn = 0 and where all the quantities except $V_0^{\prime }$ are functions of c. The second order terms that are neglected in this expansion have been discussed [15]. Introducing the notation

$$1/\chi ={\rho }_0^{\prime }{\left(\frac{\partial M_{12}}{\partial c}\right)}_{T_{ij}=0}$$ (5.4)

i.e.,

$$1/\chi =\frac{{\rho }_0^{\prime }R\theta }{c}\left(1+\frac{\partial \ln {\gamma }_1}{\partial \ln c}\right)$$ (5.5)

for interstitial solutions, and

$$1/\chi =\frac{{\rho }_0^{\prime }R\theta }{c(1-c)}\left(1+\frac{\partial \ln {\gamma }_1}{\partial \ln c}\right)$$

for substitutional binary solutions, the open systems compliances, for isotropic solids are given by

$$\begin{gathered} E^{*}=E/\left(1+\chi {\eta }^{2}E\right) \\ {\nu }^{*}=\left(\nu -\chi {\eta }^{2}E\right)/\left(1+\chi {\eta }^{2}E\right) \\ {\left(K^{-1}\right)}^{*}=3\left(1-2{\nu }^{*}\right)/E^{*}=K^{-1}+9\chi {\eta }^2 \\ {G}^{*}=G \end{gathered}$$ (5.6)

where K is the bulk modulus and G the shear modulus.

Far away from spinodals and critical points, the expression (5.3) is not very sensitive to the composition. It is then appropriate to use the values of the open-system constants, at a composition near the average composition of the specimen. The elastic coefficients become constants, and the elastic part of the problem is now independent of the compositional part. For a closed system, the obvious choice is the average composition. For a system that is in contact with a chemical reservoir, the composition at equilibrium under zero stress is usually a good choice. In the case of a very high average stress, the equilibrium composition at some high pressure may be more appropriate. With such replacement of the composition in (5.3) or (5.4) to (5.6), all the solutions of ordinary linear elasticity become directly applicable to elasto-chemical problems.

5.2. Finding the Composition Field

Finally, even though we have eliminated the composition to solve the elastochemical problem, the composition field is easily obtained from the solution. At constant diffusion potential, composition is uniquely determined by the local stress. For a binary for example (4.21) can be solved for the composition

$$\frac{{\gamma }_{1}c}{{\gamma }_2(1-c)}=\text{constant}\times \text{exp}[\text{elastic}\text{terms}/R\theta ]$$ (5.7)

$$\text{where}\text{constant}=\exp \left[\left\{M_{12}-\left({\mathrm{\mu }}_1^0-{\mathrm{\mu }}_2^0\right)\right\}/R\theta \right].$$ (5.8)

A useful linearized version of eq (5.7) is obtained by linearizing the elastic terms of that equation or of (4.21) to (4.23) and differentiating at constant M₁₂, P, and θ. Using (5.5) this gives

$$\text{d}c/\chi ={\eta }_{ij}\text{d}{T}_{ij}$$ (5.9)

or

$$c=c_0+\chi {\eta }_{ij}{T}_{ij}$$ (5.10)

where c₀ is a constant of integration and is the composition that an element of unstressed solid would have if it were in equilibrium with the system.

For the isotropic case this becomes

$$c-c_0=\chi \eta T_{kk}$$ (5.11)

Had we linearized about a hydrostatic pressure P the result would have been

$$c-c(P)=\chi \eta \left(T_{kk}+3P\right)$$ (5.12)

There are several ways of evaluating the constants in (5.8) or (5.10), but basically they are all methods of evaluating M₁₂ at equilibrium. If the system is in contact with a materials reservoir with specified M₁₂ the answer is straightforward. If it is equilibrated with a fluid phase, eq (3.10) applies. If the composition and stress are specified at some point in the system, eq (4.21) can be used. This occurs in some problems where almost all of the solid acts as a reservoir in the sense that most of it is homogeneous in composition and stress, and that transfer of components to small inhomogeneously stressed parts of thè system hardly affects the composition of the homogeneous part.

For the typical case of a closed heterogeneous system the overall composition is specified. At equilibrium the diffusion potentials become a constant whose value must be determined as part of the solution. This is a standard procedure in the method of Lagrange multipliers. Equation (5.7) is a one-parameter family of composition profiles. For each assumed value of the parameter M₁₂, we can determine the overall composition by integration. The one that satisfies the specified composition is the solution and this fixes M₁₂.

This procedure is simplified if linearization of (5.7) to give (5.10) is valid. Using this to obtain c₀ from which we can obtain M₁₂. We use the conservation of mass for the entire solid of total volume Ω′ in the reference state and average composition $\overline{c}$

$${\int }_{{\mathrm{\Omega }}^{\prime }}c\text{d}{V}^{\prime }={\mathrm{\Omega }}^{\prime }\overline{c}.$$ (5.13)

Substituting (5.10) we obtain

$$c_0=\overline{c}-\frac{X{\eta }_{ij}}{{\mathrm{\Omega }}^{\prime }}{\int }_{{\mathrm{\Omega }}^{\prime }}{T}_{ij}\text{d}{V}^{\prime }$$ (5.14)

which can be substituted into (4.21) to (4.23) to obtain M₁₂. Once c₀ is known we have the composition profile of the inhomogeneously stressed system

$$c-\overline{c}=\chi {\eta }_{ij}(T_{ij}-\frac{1}{{\mathrm{\Omega }}^{\prime }}\int T_{ij}\text{d}{V}^{\prime })$$ (5.15)

or

$$c-\overline{c}=\chi {\eta }_{ij}\left(T_{ij}-{\overline{T}}_{ij}\right)$$

where ${\overline{T}}_{ij}$ is a component of the volume averaged stress, and χ and η_ij are evaluated at c. This is the linearized equation for composition in a closed system.

5.3. Internal Equilibrium of Vacancies

We consider a single component solid with vacancies as the second component. If, as is often assumed [18], there is no relaxation around a single vacancy at any level of applied stress and the elastic constants do not depend on vacancy concentrations, the diffusion potential M_v1, given by eq (4.23), is a function of composition only. Therefore a constant diffusion potential would imply a vacancy composition field that is constant regardless of the stress distribution. Even with these assumptions we will later see (sec. 6.2) that the local equilibrium vacancy concentration at the interface does depend on stress at the interface.

A more realistic model assumes relaxation. Let the partial molar volume of vacancies differ from the molar volume of the species. If the elastic constants do not depend on vacancy concentration, eq (4.23) yields with P = 0

$$M_{v1}=M_{v1}^0+R\theta \ln \frac{c_v}{1-c_v}-\left({\overline{V}}_v-{\overline{V}}_1\right)T_{kk}/3$$ (5.16)

At equilibrium, this is constant, leading to a vacancy concentration field given by (with c_v ⪡ 1)

$$c_v={\overline{c}}_v\exp \left(\frac{{\overline{V}}_v-{\overline{V}}_1}{3R\theta }{T}_{kk}\right)$$ (5.17)

where ${\overline{c}}_v$ is the equilibrium concentration of vacancies at P = 0.

5.4. Dislocation Atmospheres

5.4.1. Atmosphere Around a Dislocation in an Isotropic Solid

Let us consider a substitutional two-component infinite isotropic solid, with a negligible concentration of vacancies. A straight edge dislocation with a Burgers vector of magnitude b is located in the solid along the z axis. If the sizes of components 1 and 2 are different, there will be a segregation around the dislocation. This problem has been solved, considering one of the atoms as a defect [19]. This means that its concentration has to be relatively small. Indeed in many cases only vacancies or interstitials are considered. These are unnecessary restrictions as we shall see.

Far from the dislocation, the solid is at composition c₀, and is stress-free. Therefore we can think of this faraway solid as a chemical reservoir. The solid with the dislocation and its atmosphere has the same diffusion potential as the stress-free solid at c₀. For convenience, we choose the solid at c₀ as the reference for strain. Since we have shown that under small strain approximation, the elastic part of the problem is equivalent to a constant composition problem with the open-system elastic coefficients, eq (5.6), the stress field, with the atmosphere present, is given by

$$\begin{gathered} T_{rr}=T_{\mathrm{\varphi }\mathrm{\varphi }}=\frac{-Gb\sin \mathrm{\varphi }}{2\pi \left(1-{\nu }^{*}\right)r} \\ {T}_{r\mathrm{\varphi }}=\frac{Gb\cos \mathrm{\varphi }}{2\pi \left(1-{\nu }^{*}\right)r} \\ {T}_{zz}=\frac{-Gb{\nu }^{*}\sin \mathrm{\varphi }}{\pi \left(1-{\nu }^{*}\right)r} \end{gathered}$$ (5.18)

and the composition field is, to a first approximation, using eqs (5.11) and (5.18)

$$\mathrm{\Delta }c=-\chi \eta \frac{\left(1+{\nu }^{*}\right)Gb\sin \mathrm{\varphi }}{\left(1-{\nu }^{*}\right)\pi r}.$$ (5.19)

(These equations correct an algebraic error in reference [6].) Replacing the open systems constant by their values, we finally obtain

$$\begin{gathered} T_{rr}=T_{\mathrm{\varphi }\mathrm{\varphi }}=\frac{-Gb\left(1+\chi {\eta }^{2}E\right)\sin \mathrm{\varphi }}{2\pi \left(1-\nu +2\chi {\eta }^{2}E\right)r} \\ {T}_{r\mathrm{\varphi }}=\frac{Gb\left(1+\chi {\eta }^{2}E\right)\cos \mathrm{\varphi }}{2\pi \left(1-\nu +2\chi {\eta }^{2}E\right)r} \\ {T}_{zz}=\frac{-Gb\left(\nu -\chi {\eta }^{2}E\right)\sin \mathrm{\varphi }}{\pi \left(1-\nu +2\chi {\eta }^{2}E\right)r} \\ \mathrm{\Delta }c=\frac{-\chi \eta (1+\nu )Gb\sin \mathrm{\varphi }}{\pi \left(1-\nu +2\chi {\eta }^{2}E\right)r} \end{gathered}$$ (5.20)

where the subscript 0 has been dropped from all the variables since all of them have to be evaluated at composition c₀, including the Burgers vector magnitude. In our case (substitutional solution), χ is given by eq (5.5) and η by (4.7) and (4.8).

We first note that, since χ is positive for a stable solid solution, the stresses are decreased, by a fraction of the order of χη²E. This factor tends to zero for highly dilute solutions. But for a concentrated solution, it can be significant. Taking an ideal solution, c₀=0.5, ${\rho }_0^{\prime }={10}^5$ mol m⁻³, Rθ = 10⁴J mol⁻¹, E = 10¹¹ Nm⁻², and η=0.1 gives a value of 0.25 for χη²E. This change in the stress field, which is readily obtained here, has, to our knowledge, not been calculated within the framework of the defects model.

At low concentration, the following approximation holds

$$\chi \simeq c_0{V}_0^{\prime }/R\theta$$

and

$$\chi \eta \simeq \frac{c_0\left({\overline{V}}_1-{\overline{V}}_2\right)}{3R\theta }$$

and we can neglect 2χη² E in comparison to (1 − v) obtaining thereby the classical point-defect solution

$$\mathrm{\Delta }c\simeq \frac{-c_0\left({\overline{V}}_1-{\overline{V}}_2\right)(1+\nu )Gb\sin \mathrm{\varphi }}{3\pi R\theta (1-\nu )r}.$$

But it is to be emphasized that the composition eq (5.7) can be solved exactly by numerical methods. Our result is more general in that it includes in a self-consistent way all the interactions that may be present, specifically in concentrated solutions, between the defects themselves and the defects and the matrix. In particular, it takes into account the nonideality of the solid solutions in a phenomenological way that is model independent. If no measured value is available for the activity coefficient function γ₁, specific statistical mechanical models [20–22] can of course be used and the result directly introduced in the value of χ.

5.4.2. Dislocation Atmosphere in a Cubic Crystal

Analytic expressions are rarely known for the elastic fields caused by point-forces in a medium of arbitrary symmetry [23]. Hence the usual integral methods for calculating atmospheres cannot be used. On the other hand the introduction of open system compliances is not restricted to isotropic solids, and formulas have been developed for the most general elastic solids [15]. Because the elastic field has been found for several cases of dislocations in these non-isotropic single-component crystals, the concept is most valuable.

By a simple substitution of the open-system elastic coefficients, the same elastic calculations are valid for solid solutions equilibrated to constant diffusion potentials. The composition fields are given to first order by eq (5.10) or more exactly from the solution of eq (5.7). We shall treat the case of a [111] screw dislocation in a cubic crystal. The x₃ axis is along the dislocation, the x₂ axis is along [110] and x_l along [112]. The stress field has been given by Steeds [24]. Because the equations are rather long, we shall derive only the composition field. In cubic crystals, the change in composition with stress is given to first order by

$$\mathrm{\Delta }c=\chi \eta T_{kk}$$ (5.21)

as for the isotropic case. At constant composition, T_kk has the value

$$T_{kk}=\frac{Gb\mathrm{\delta }{\mathrm{s}}_{44}\sin 3\mathrm{\varphi }}{4\sqrt{2}\pi r\left(1-\mathrm{\delta }{\cos }^{3}3\mathrm{\varphi }\right){(1-\mathrm{\delta })}^{1/2}S\left(3s_{11}-2S\right)}$$ (5.22)

with

$$S=s_{11}-s_{12}-s_{44}/2$$

a factor which is zero for isotropic crystals,

$$\mathrm{\delta }=\frac{2S^2}{9\left(s_{11}+s_{44}+5S/6\right)}$$

and the s_ij are the standard two indices compliances, referred to the cube axis. For cubic crystals, the open system compliances are

$$\begin{gathered} s_{ij}^{*}=s_{ij}+\chi {\eta }^{2}i\text{and}j<3 \\ {s}_{ij}^{*}=s_{ij}i\text{and}j>3 \end{gathered}$$ (5.23)

therefore

$$S^{*}=S$$

and

$${\mathrm{\delta }}^{*}=\frac{2S^2}{9\left(s_{11}^{*}+s_{44}+5S/6\right)}.$$

Combining (5.21), (5.22), and (5.23), we obtain the composition field

$$\mathrm{\Delta }c=\frac{9\chi \eta b{\mathrm{\delta }}^{*}{s}_4\sin 3\mathrm{\varphi }}{4\sqrt{2}\pi r\left(1-{\mathrm{\delta }}^{*}{\cos }^{2}3\mathrm{\varphi }\right){\left(1-{\mathrm{\delta }}^{*}\right)}^{1/2}S\left(3s_{11}^{*}-2S\right)}$$ (5.24)

where all the constants that depend on the material have to be taken at c₀, the composition far away from the dislocation. This result, obtained by a simple algebraic manipulation, has, to our knowledge, never been obtained by other methods.

5.4.3. Dislocation Atmospheres: Nonlinear Effects

At constant diffusion potentials, when the composition changes from the unstressed to the stressed state are small, we have shown that the strain is linearly related to the stress, as in the usual theory of elasticity. But this law has a smaller range of applicability than in the constant composition case. The thermodynamics of solutions introduce nonlinear terms in the stress-strain law. When the strain is expanded as a function of stress, we have identified four second-order effects [15]: (a) non-linear stress-strain laws at constant composition, due, for instance, to rearrangement of interstitial atoms into sites that become nonequivalent under stress; (b) change of compliances with composition; (c) deviation from Vegard’s law; and (d) non-linearity of the solution thermodynamics. The first two effects have been considered within the framework of defects theories. It does not seem that the two others have been treated [25]. Since solutions of non-linear elastic problems have been found [26], they can be used, with the second-order open-system compliances, to find second-order effects on dislocation atmospheres.

5.5. Internal Equilibrium of a Binary Substitutional Solid With Vacancies

We have seen in section 4 that, for a binary substitutional solid with vacancies, in equilibrium with a fluid, the following is true

$$M_{1v}={\mathrm{\mu }}_1^L$$ (5.25)

$$M_{2v}={\mathrm{\mu }}_2^L$$ (5.26)

where ${\mathrm{\mu }}_1^L$ and ${\mathrm{\mu }}_2^L$ are the chemical potentials of species 1 and 2 in the fluid. It seemed therefore rather natural to use these equations, which have the same form as those for fluid equilibrium, rather than the mathematically equivalent

$$M_{12}={\mathrm{\mu }}_1^L-{\mathrm{\mu }}_2^L$$ (5.27)

$$M_{v2}=-{\mathrm{\mu }}_2^L.$$ (5.28)

From a theoretical point of view, there is no difference. Although these equations are valid for nonlinear inhomogeneous and anisotropic solids, we give as an example expressions for constant elastic coefficients and isotropy

$$M_{1v}=M_{1v}^0+R\theta \ln \frac{{\gamma }_1{c}_1}{{\gamma }_v{c}_v}-\frac{{\overline{V}}_1-{\overline{V}}_v}{3V_0^{\prime }}{T}_{kk}$$ (5.29)

$$M_{12}=M_{12}^0+R\theta \ln \frac{{\gamma }_1{c}_1}{{\gamma }_2{c}_2}-\frac{{\overline{V}}_1-{\overline{V}}_2}{3V_0^{\prime }}{T}_{kk}.$$ (5.30)

The concentration of vacancies is small compared to c₁ and c₂. Measurement of c_v, γ_v and ${\overline{V}}_v$ are therefore subject to potentially large errors. These affect eqs (5.25), (5.26), and (5.28) but not (5.27). For computational purposes, it is then better to use the second formulation. Besides, if we are only interested in the composition c₁ and c₂, we can neglect the vacancies and use only eq (5.30) for equilibrium calculations. By keeping the flexibility of choice for the dependent substitutional species, we can eliminate species whose concentration has been found to have a negligible effect on the chemical behavior of the solid solutions, including vacancies, even if they are essential to the mechanisms by which chemical equilibrium is attained.

5.6. Multisite Solids

Up to this point, we have focused our attention on crystalline solids that are most common in the metallurgical world, where there is only one substitutional site, that is highly occupied, and an interstitial site that is lightly occupied. But in many instances crystals have several non-equivalent sites, occupied by mixed species of atoms or molecules or vacancies. The fraction of empty sites can vary for each type of site from 0 to 1. In the description we can of course eliminate sites that are and remain empty. They don’t contribute to the energy or entropy of the system. For all other sites, we can describe their status by the densities of the atoms and the densities of vacancies on each of them. As for the substitutional site with which we have been dealing in the preceding section, there will be a constraint condition: the total density of atoms and vacancies is constant for each site. Using the method described in section 4, it can be shown that at equilibrium, the diffusion potentials are constant, equal on all sites, and equal to the corresponding difference in chemical potentials when equilibrated with a fluid

$$M_{\text{IK}}^1=M_{\text{IK}}^2\dots =M_{\text{IK}}^v={\mathrm{\mu }}_{\mathrm{I}}^L-{\mathrm{\mu }}_{\text{K}}^L$$ (5.31)

where the superscripts label the different sites. There are cases where there is no species K that is present on all sites, or where it is not convenient to use the same K-species for all sites. The formulas can easily be transformed, using eqs (3.8) and (3.9)

$$M_{\text{IK}}+M_{\text{KJ}}=M_{\mathrm{IJ}}.$$ (5.32)

If a species is not present on one site, it cannot be used as the dependent species on that site, and its diffusion potential equation drops from the set of eqs (5.31). The vacancies are to be considered as a species, since an exchange of an i-site vacancy for a j-site vacancy produces no change of state, exactly as the exchange of a K atom on an i-site with a K atom on a j-site.

Equations (5.31) govern the equilibrium partitioning of I atoms on the different sites. If only the total density is of interest, one can interpret eqs (5.31) differently. They state that along an equilibrium path, the Helmoltz free energy density is only a function of the total density of the (N-1) independent species.⁴ Calling M_IK the common value of the diffusion potential for each site, we have

$$\text{d}{f}^{\prime }=s^{\prime }\text{d}\theta +\mathrm{\Sigma }{M}_{\text{IK}}\text{d}{\rho }_{\mathrm{I}}^{\prime }.$$ (5.33)

Equation (5.33) shows that the formulas developed in the preceding section can also be applied, with the total density of each species as composition variables (or the ratio ${\rho }_{\mathrm{I}}^{\prime }/{\rho }_0^{\prime }$, ${\rho }_0^{\prime }$ being a chosen total density, like the total density of sites, or the density of sites I, (I = 1, …, v) whatever is most useful).

In the equations used in section 5, the interstitial site was sparsely occupied, and we used eq (4.34) for the diffusion potential of this species. But rigorously its diffusion potential is M_1v where v represents the vacancies on interstitial sites

$$M_{1v}=M_{1v}^0+R\theta \ln \frac{{\gamma }_1{c}_1}{{\gamma }_v{c}_v}+\text{elastic}\text{terms}.$$ (5.34)

If there are v interstitial sites per substitutional site, γ_vc_v tends to one as c_v tends to v. Therefore, in dilute interstitial solutions

$$M_{1v}\simeq {\mathrm{\mu }}_1^0+R\theta \ln {\gamma }_1{c}_1+\text{elastic}\text{terms}$$ (5.35)

which is the expression we have used. In almost all cases, site occupancy is either high or low. Phase transformations occur before intermediate occupancy is reached. But hydrogen in metals is an important case where the occupancy can span all the possible composition field without a phase change. In such cases, the rigorous diffusion potential has to be used. Equations for the internal equilibrium between sites have been given, with the preceding approximation by Li et al. [27]. It is clear that there is no need to make the distinction between interstitial and substitutional atoms. A single formalism with multisite occupation is possible and avoids the confusion that can arise if a specie occupies both substitutional and interstitial sites [7]. For most metallurgical examples, species do seem to occupy only one site.

We next turn to phase change equilibrium at solid-fluid interfaces. The case of a stoichiometric compound already illustrates the principal features. Let species A completely occupy a equivalent sites α per unit cell, species B b equivalent sites β, etc. Because there is only one species on each site we cannot define a diffusion potential. In the liquid each species has a well defined chemical potential. The equation for equilibrium is

$$f-\left(\mathbf{a}{\mathrm{\mu }}_{\text{A}}^L+\mathbf{b}{\mathrm{\mu }}_{\text{B}}^L+\mathbf{c}{\mathrm{\mu }}_{\text{C}}^L\dots \right){\rho }_0=-P$$ (5.36)

where ρ₀ is the total density of sites in a unit cell. This is a straightforward expression of chemical equilibrium for the dissolution of the compound A_aB_bC_c …, which continues to hold under stress. It is Gibbs’ eq (393) [9] since he quite clearly considered solids to be compounds (CP) and defined a single chemical potential μ^CP for them in the fluid even if they dissociated

$${\mathrm{\mu }}^{\text{CP}}=\mathbf{a}{\mathrm{\mu }}_{\text{A}}+\mathbf{b}{\mathrm{\mu }}_{\text{B}}+\mathbf{c}{\mathrm{\mu }}_{\text{C}}+\dots .$$ (5.37)

In defining μ^CP there is a rigid adherence to a law of definite proportions dictated by the numbers of equivalent sites fully occupied in the crystal structure.

If we now let the α sites be occupied by several species I, J, K including vacancies we obtain diffusion potentials. Choosing species K as the counterspecies the equilibrium equation is

$$f-{\rho }_0\mathrm{\Sigma }{M}_{\text{IK}}{c}_{\mathrm{I}}^{\alpha }-{\rho }_0\left(\mathbf{a}{\mathrm{\mu }}_{\text{K}}^L+\mathbf{b}{\mathrm{\mu }}_{\text{B}}^L\dots \right)=-P.$$ (5.38)

The term in the parenthesis is the chemical potential for the stoichiometric compound K_aB_bC_c …. There are obvious advantages to choosing K to be the major species on site α. If site α is a lightly occupied interstitial site the compound is B_bC_c … and μ_K is set to zero.

If several sites are each occupied by more than one species the equations are not changed if a different species is chosen as counter species for each site. If the same species is chosen as counter species of several sites the terms combine. In particular if the same counter species K is used for all sites we obtain

$$f-{\rho }_0\sum _{\mathrm{I}}\sum _{\alpha }{M}_{\mathrm{IK}}{c}_{\mathrm{I}}^{\alpha }-(\mathbf{a}+\mathbf{b}+\mathbf{c}+\dots ){\mathrm{\mu }}_{\text{K}}{\rho }_0=-P.$$ (5.39)

Summing over all sites we obtain

$$f-{\rho }_0\mathrm{\Sigma }{M}_{\mathrm{IK}}{c}_{\mathrm{I}}-(\mathbf{a}+\mathbf{b}+\mathbf{c}+\mathrm{...}){\mathrm{\mu }}_{\text{K}}{\rho }_0=-P.$$ (5.40)

This is identical with eq (3.15) if we redefine ρ₀ in terms of atom site density instead of unit cell densities.

6. Interface Equilibria

In this section we illustrate various aspects of equilibria involving three kinds of interfaces that stressed solids can have but ignoring capillary effects. Most of our examples will be uniformly stressed, and have only as many components as are necessary to illustrate the points to be made. When the solid is multicomponent and nonuniformly stressed, the interior equilibria can be solved by the methods of the open-system elastic constants of the previous section. This converts a multicomponent elastic and thermochemical problem into an elastic problem alone, although possibly a nonlinear one.

6.1. Change of Solubility With Stress

Our first example is a Gibbs solid—a pure substance for instance—in equilibrium at pressure P with a fluid in which it can dissolve along a flat interface. Forces are applied to the solid so that its state of stress is now T_ij. To maintain mechanical equilibrium, one of the principal values of T_ij is −P, and the corresponding principal direction of stress is normal to the fluid-solid interface. What is the change in the chemical potential of the fluid necessary to keep the system in chemical equilibrium? The only equation, besides mechanical equation, is the boundary conditions, eq (3.18) which becomes for a one component linear elastic solid

$$f^{\prime }-{\mathrm{\mu }}^L{\rho }_0^{\prime }=-P\left(1+E_{kk}\right).$$ (6.1)

Following Gibbs [9, p. 196], we compare this equilibrium with that of the same solid phase equilibrated under hydrostatic stress with the same fluid. Using bars to indicate the values of the thermodynamic quantities in this equilibrium we write

$${\overline{f}}^{\prime }-{\overline{\mathrm{\mu }}}^L{\rho }_0^{\prime }=-P\left(1+{\overline{E}}_{kk}\right).$$ (6.2)

Subtracting these two equations, we obtain

$$f^{\prime }-{\overline{f}}^{\prime }+P\left(E_{kk}-{\overline{E}}_{kk}\right)={\rho }_0^{\prime }\left({\mathrm{\mu }}^L-{\overline{\mathrm{\mu }}}^L\right)$$ (6.3)

$(f^{\prime }-{\overline{f}}^{\prime })$ is the elastic energy stored in the solid on going from pressure P to stress state T_ij and $P\left(E_{kk}-{\overline{E}}_{kk}\right)$ is the work done on the solid by the liquid. The l.h.s. of eq (6.3) is thus the work that has to be done to bring a hydrostatically stressed solid to the nonhydrostatic state while surrounded by the liquid. It is necessarily positive, and the fluid in equilibrium with a nonhydrostatically stressed solid is always supersaturated with respect to precipitating a hydrostatically stressed solid by the amount given in (6.3). If we let c_L and ${\overline{c}}_L$ be the concentration of the solid component in the fluid in equilibrium with respect to the nonhydrostatically and hydrostatically stressed solid, we can use eq (4.32) to obtain

$$\begin{gathered} {\rho }_0^{\prime }R\theta \ln \left({\gamma }_L{c}_L/{\overline{\gamma }}_L{\overline{c}}_L\right)=-\frac{\nu }{2E}{\left(T_{kk}\right)}^2+\frac{1+\nu }{2E}{T}_{ij}{T}_{ij} \\ +\frac{3(1-2\nu )}{2E}{P}^2+\frac{1-2\nu }{E}{T}_{kk}P. \end{gathered}$$ (6.4)

Let t₁, t₂, and −P be the principal values of stress. If the change in solubility is small, and the solution is dilute or ideal, we get

$$\begin{gathered} \frac{c_L-{\overline{c}}_L}{{\overline{c}}_L}=\frac{1}{2{\rho }_0^{\prime }R\theta E} \\ \times \left[t_1^2+t_2^2-2\nu t_1{t}_2+2(1-\nu )\left(t_1+t_2+P\right)P\right]. \end{gathered}$$ (6.5)

Because −1 < v < 1/2, the right hand side of eq (6.5) is positive, except of course when t₁ = t₂ = −P, where it is zero. The solubility of the solid in the liquid is always increased when a stress is applied to the solid. The solution is supersaturated with respect to a hydrostatically stressed solid at pressure P, a classical result that was derived by Gibbs.

We now turn to the case of a two-component solid in equilibrium with a melt. We have two conditions for equilibrium

$$f^{\prime }-{\mathrm{\mu }}_1^L{\rho }_1^{\prime }-{\mathrm{\mu }}_2^L{\rho }_2^{\prime }=-P\left(1+E_{kk}\right)$$ (6.6)

$$M_{12}={\mathrm{\mu }}_1^L-{\mathrm{\mu }}_2^L.$$ (6.7)

We compare again to the equilibrium of the solid with the fluid under pressure P.

$${\overline{f}}^{\prime }-{\overline{\mathrm{\mu }}}_1^{\mathrm{L}}{\overline{\rho }}_1^{\prime }-{\overline{\mathrm{\mu }}}_2^L{\overline{\rho }}_2^{\prime }=-P\left(1+{\overline{E}}_{kk}\right)$$ (6.8)

$${\overline{M}}_{12}={\overline{\mathrm{\mu }}}_1^L-{\overline{\mathrm{\mu }}}_2^L.$$ (6.9)

Subtraction of (6.8) from (6.6) and (6.9) from (6.7) gives two equations for the change of composition in the fluid and the solid to maintain equilibrium under stress.

Assuming for simplicity (i) P = 0, (ii) terminal solutions (i.e., both solid and liquid are dilute solutions), (iii) no change in elastic coefficients with composition, we get

$$\begin{gathered} R\theta \ln \left(\frac{1-c}{1-\overline{c}}\right)+V_0^{\prime }[-\frac{1}{2}\frac{\nu }{E}{\left(t_1+t_2\right)}^2+\frac{1+\nu }{2E}\left(t_1^2+t_2^2\right) \\ +c\eta \left(t_1+t_2\right)]=R\theta \ln \left(\frac{1-c_{\text{L}}}{1-{\overline{c}}_{\text{L}}}\right) \end{gathered}$$ (6.10)

$$R\theta \ln \frac{c(1-\overline{c})}{\overline{c}(1-c)}-V_0^{\prime }\eta \left(t_1+t_2\right)=R\theta \ln \frac{c_{\text{L}}\left(1-{\overline{c}}_{\mathrm{L}}\right)}{{\overline{c}}_L\left(1-c_{\text{L}}\right)}.$$ (6.11)

As usual, this system of equations can be solved numerically, or, if the changes are small, we can linearize the equations and solve with Cramer’s rule.

6.2. Vacancies Equilibrium in a One-Component Solid

Consider a cylinder of isotropic hydrostatically stressed solid in contact with a fluid in which it cannot dissolve at pressure P, with an equilibrium concentration of vacancies ${\overline{c}}_v$. A load is applied that produces a stress whose components are T_zz, T_rr = T_θθ. We want to calculate the equilibrium concentration of vacancies along the surfaces S_r and S_z. Since the components of the solid don’t appear in the fluid, there is no equation like (3.12). But the phase change eq (3.15) applies, and in this case since μ_K is identified with ${\mathrm{\mu }}_v^L=0$, the equation becomes

$$V_0^{\prime }{f}^{\prime }-\left(1-c_v\right)M_{1v}=-P{V}_0^{\prime }\left(1+E_{kk}\right)$$ (6.12)

where −P is the normal traction. Let us first adopt Herring’s simplifying assumptions that (a) there is no volume relaxation around vacancies, (b) there is no change in elastic constants with vacancy concentration, and (c) the solid obeys the law of dilute solutions. Using (4.32) we get (i) under pressure $\overline{P}$

$${\mathrm{\mu }}_v^0(\overline{P})+R\theta \ln {\overline{c}}_v=0$$ (6.13)

(ii) under stress, along S_z

$$\begin{gathered} {\mathrm{\mu }}_0^v(\overline{P})+R\theta \ln c_v^z+V_0^{\prime }[-\overline{P}-\frac{1}{2}\frac{v}{E}{\left(2T_{rr}+T_{zz}\right)}^2 \\ +\frac{1+v}{2E}\left(2T_{rr}^2+T_{zz}^2\right)+\frac{3(1-2\nu )}{2E}{\overline{P}}^2] \\ =V_0^{\prime }{T}_{zz}\left[1+\frac{1-2\nu }{E}\left(2T_{rr}+T_{zz}\right)\right] \end{gathered}$$ (6.14)

(iii) under stress, along S_r

$$\begin{gathered} {\mathrm{\mu }}_v^0(\overline{P})+R\theta \ln c_v^r+V_0^{\prime }[-\overline{P}-\frac{1}{2}\frac{\nu }{E}{\left(2T_{\mathit{rr}}+T_{\mathit{zz}}\right)}^2 \\ +\frac{1+\nu }{2E}\left(2T_{rr}^2+T_{zz}^2\right)+\frac{3(1-2\nu )}{2E}{\overline{P}}^2] \\ =V_0^{\prime }{T}_{rr}\left[1+\frac{1-2\nu }{E}\left(2T_{rr}+T_{zz}\right)\right]. \end{gathered}$$ (6.15)

It is quite clear that $c_v^r$ and $c_v^z$ are different, unless T_rr = T_zz, i.e., when the system is under hydrostatic stress. Since we have assumed no relaxation around vacancies, η = 0, and therefore according to eq (4.23), M_1v is different on S_z and S_r. As a result, a vacancy flux will appear. This is further discussed in section 8.4.

Making the further assumption that P = 0, and neglecting quadratic terms in stress, subtraction of (6.13) from (6.14) and (6.15) gives

$$\begin{gathered} \ln \left(c_v^r/{\overline{c}}_v\right)=V_0^{\prime }{T}_{rr}/R\theta \\ \ln \left(c_v^z/{\overline{c}}_v\right)=V_0^{\prime }{T}_{zz}/R\theta . \end{gathered}$$ (6.16)

This is Herring’s [18, 28] well-known formula: to first order in stress, only the normal pressure affects the equilibrium vacancy concentration at an interface. We will get the same results, whether this interface is a solidfluid interface or an incoherent solid-solid interface.

The order of magnitude of the quadratic terms can be easily obtained by making T_rr = 0 so that linear terms disappear in (6.15). We obtain, along S_r

$$\ln \left(c_v^r/{\overline{c}}_v\right)=V_0^{\prime }{T}_{zz}^2/2ER\theta .$$ (6.17)

Within the small strain approximation, this effect is less than 1% of the effect on S_z. But there are cases where it might be significant (cf. sec. 8.4).

Conditions (a), (b), and (c) can easily be removed through the use of the general formulas developed in section 4. As an example we treat the case where there is a volume relaxation around a vacancy. Using (4.32), assuming P = 0, and following the above procedure, we get, to first order in stress

$$\ln \left(c_v^r/{\overline{c}}_v\right)=\frac{V_0^{\prime }}{R\theta }\left[T_{rr}-\eta \left(2T_{rr}+T_{zz}\right)\right]$$ (6.18)

$$\ln \left(c_v^z/{\overline{c}}_v\right)=\frac{V_0^{\prime }}{R\theta }\left[T_{\mathit{zz}}-\eta \left(2T_{rr}+T_{zz}\right)\right].$$ (6.19)

The corrective term, proportional to η, contains the trace of the stress tensor. As such other components than the normal pressure influence the vacancy concentration at a particular interface, if elastic relaxation around vacancies are taken into account.

6.3. Using Open-System Elastic Constants for Multicomponent Phase Equilibrium

For the general multicomponent phase-equilibrium under stress, the fact that the M_IK are constant gives (N-1) relationships between stress and composition. As shown earlier, it is possible to solve these equations for composition as a function of stress and obtain the strain $E_{ij}^c$ at results from composition changes. The result is a stress-strain relation at constant M_IK. This relationship was used to solve elastic problems within a single phase as if it were composed of a single component.

These same relationships apply to each individual phase in a multiphase equilibrium, but the phase change boundary conditions of section 3.5 contain a similar coupling between stress and composition. In the present section we shall demonstrate that by using open-system-elastic constants, the compositional part of these equations can also be eliminated. In fact this method allows us to treat multicomponent equilibrium as if each phase were a one-component purely elastic part of the system, and that for such a solid, the ω function is equal to the elastic energy apart from a constant (cf. eq (3.16)). Finally once the elastic problem has been solved, the composition field is obtained by the methods of section 5.2.

We will use as an example binary isotropic linear solids, although the proof can be made for a multicomponent anisotropic system. We shall further assume constant elastic coefficients, and that, at zero stress and potential M₁₂, the composition is c. Let Δc be the change of composition due to a change of stress. Expanding f′ around the unstressed state we find using (3.6) and (5.4)

$$\begin{gathered} f^{\prime }\left(T_{ij},c+\mathrm{\Delta }c\right)=f^{\prime }(0,c)+{\rho }_0^{\prime }{M}_{12}\mathrm{\Delta }c+{\left(\mathrm{\Delta }c\right)}^2/\chi \\ -\frac{\nu }{2E}{\left(T_{kk}\right)}^2+\frac{1+\nu }{2E}{T}_{ij}{T}_{ij}. \end{gathered}$$ (6.20)

Let us consider the function

$$f^{\prime *}=f^{\prime }(0,c)-\frac{{\nu }^{*}}{2E^{*}}{\left(T_{kk}\right)}^2+\frac{1+{\nu }^{*}}{2E^{*}}{T}_{ij}{T}_{ij}$$ (6.21)

where we have added to the free energy of the solid under zero stress and at potential M₁₂, an elastic energy computed with open-system elastic constants at M₁₂. Replacing these constants by their values (5.6) we obtain

$$f^{\prime *}=f^{\prime }(0,c)+\frac{1+\nu }{2E}{T}_{ij}{T}_{ij}-\frac{\nu }{2E}{\left(T_{kk}\right)}^2+\frac{1}{2}\chi {\eta }^2{\left(T_{kk}\right)}^2.$$ (6.22)

But the change in composition Δc is given by (5.11) so that (6.22) can be written

$$f^{\prime *}=f^{\prime }(0,c)+\frac{1+\nu }{2E}{T}_{ij}{T}_{ij}-\frac{\nu }{2E}{\left(T_{kk}\right)}^2+{(\mathrm{\Delta }c)}^2/2\chi .$$ (6.23)

The function $[f^{\prime }-{\rho }_0^{\prime }(c+\mathrm{\Delta }c)M_{12}]$ that appears repeatedly in the phase change boundary equations (cf. (3.24) and (3.27)) is thus obtained as

$$f^{\prime }-{\rho }_0^{\prime }(c+\mathrm{\Delta }c)M_{12}=f^{\prime *}-{\rho }_0^{\prime }c{M}_{12}$$ (6.24)

Or, if we replace M₁₂ and f′(0,c)

$$\begin{gathered} f^{\prime }-{\rho }_0^{\prime }(c+\mathrm{\Delta }c)M_{12}=-\frac{{\nu }^{*}}{2E^{*}}{\left(T_{kk}\right)}^2 \\ +\frac{1+{\nu }^{*}}{2E^{*}}{T}_{ij}{T}_{ij}-{\rho }_0^{\prime }{\mathrm{\mu }}_2(0,c). \end{gathered}$$ (6.25)

Thus the various phase change boundary conditions are expressed in terms of an open-system Helmholtz free energy for each phase. This free energy has the same form as a Helmholtz free energy of a one-component phase. Its elastic constants are the open-system elastic constants of section 5.1. The reference state of each phase is the unstressed multicomponent phase with the same value of M. Its composition is c in (6.24) and (6.25), its lattice parameter is used to define strain, and its constant composition elastic constants are to be used in eqs (5.3) or (5.6) to calculate the open-system constants.

By examination of (6.25), we can see that the use of these open-system constants allows us to treat, as far as the stress is concerned, any multicomponent system just as if it were a one-component system. Thus elastic solutions developed for one component inclusions, for instance [23], can now be used for similar multicomponent inclusions.

After finding the stress field, the results of section 5.2 can be used to obtain the composition field.

An interesting consequence of the preceding results occurs in a binary system in which both phases have the same conventional elastic constants. In an infinite single component system the Bitter-Crum theorem [16] holds. There is no elastic interaction between particles. The system is degenerate with respect to particle shape and dispersion. In a binary system if the χ or η’s differ, the open system elastic constants would differ even if the conventional elastic constants did not. As a result there is now elastic interaction between particles that is entirely the result of the compliance due to composition changes.

7. Partial Equilibrium—Local Equilibrium

When the general conditions for equilibrium are not satisfied, the system will tend to equilibrium. The rates of various processes are usually so different that in the time scale of an experiment we may often assume that some processes have reached equilibrium while others have not occurred at all. In this section we briefly discuss these partial equilibria. When processes are too fast for thermal and chemical relaxation, we obtain the results of classical adiabatic elasticity. The relation between isothermal constant composition elastic coefficients $S_{ijkl}^{\theta }$ and adiabatic elastic coefficients $S_{ijkl}^s$ is a well known thermodynamic result [17]

$$\begin{gathered} S_{ijkl}^{\theta }=S_{ijkl}^s+{\alpha }_{ij}{\alpha }_{kl}{\left(\frac{\partial \theta }{\partial s}\right)}_{T_{ij}} \\ =S_{ijkl}^s+{\alpha }_{ij}{\alpha }_{kl}\theta /C^T \end{gathered}$$ (7.1)

α_ij is the thermal expansion coefficient, and C^T the heat capacity, both at constant stress.

When thermal and elastic equilibration occur but without diffusion or interface motion, we have classical isothermal elasticity. Comparing eqs (5.3) and (7.1) we note that they are quite similar except that temperatures instead of compositional derivatives are used. Thus the relationship between adiabatic, isothermal, and open-system elastic constants is one of increasing equilibration first with thermal and then with materials reservoirs.

Diffusion of some species, e.g., interstitials, often is orders of magnitude faster than that of other species. Such a partial equilibrium, called paraequilibrium [29], is often reached in phase transformations of multicomponent alloys. Only hydrostatic cases seem to have been treated. When stresses are important the modification from corresponding binary interstitial alloy problems seems straightforward.

Interface processes, crystal growth or dissolution and grain growth all involve network modification processes that may be quite slow. Grain boundary sliding may not occur. For calculation of such partial equilibria, the corresponding equilibrium equations must be suppressed. Polycrystalline averages of the properties can be used to obtain corresponding averages for stress and composition fields.

The most common partial equilibrium occurs when all processes except diffusion have relaxed to equilibrium. The only suppressed condition is that M_IK need be constant, but M_IK remains continuous across all interfaces that have reached equilibrium. This partial equilibrium is called local equilibrium at interfaces.

Many experiments are done under conditions where partial equilibrium is maintained while some or all of the remaining variables are observed while they relax to equilibrium. The laws of most of the relaxation processes have been studied. Interface relaxation is complicated and often nonlinear. On the other hand, heat flow in response to thermal gradients is coupled with elasticity and constitutes the subject of thermoelasticity. Diffusion in response to nonuniformity of the M_IK is also well understood, regardless of whether the origin of the gradients in M_IK are from composition gradients, stress gradients or interface conditions. The next section examines a set of problems involving diffusional equilibration under isothermal conditions with local equilibrium assumed.

8. Diffusional Kinetics and Creep

Many problems of diffusion involve stress. In diffusional creep the applied stress is the motivating force for the diffusion. Compositional heterogeneity results in a self-stress that affects diffusion in a way that is too often ignored in the diffusion calculation. As we have seen, stress affects the diffusion potential and interface equilibrium conditions. It has an effect both on the rate and direction of the diffusional flux within each grain and on the boundary conditions to the diffusion equations at each interface.

Often only some of the effects of stress have been considered, or approximations have been made that ignored effects of the same order or larger than the effects considered. In this section we will examine the effects of stress on-diffusion and creep, inside the grains and at interfaces, and with both applied stresses and the self-stresses that arise from the compositional inhomogeneity.

We begin with a formulation for multicomponent diffusion that is consistent with our thermodynamic formulation and has the proper invariances with respect to arbitrary choices of the species K. We then examine problems of inhomogeneous stress when the network is unaltered. Much of this was the subject of a recent overview [30] in which a hierarchy of increasingly difficult problems was discussed. We next turn our attention to diffusional network alteration phenomena, such as creep and phase change, both under applied stress and self-stress. Because of the importance of vacancies in this problem, interesting phenomena occur even in one-component systems. We reformulate and simplify the general equations to examine a few problems of diffusional creep in a one-component system with vacancies.

8.1. Multicomponent Diffusion in Isothermal Network Solids

As shown in [31] the invariant formulation of substitutional multicomponent diffusion flux J_I in an isothermal isotropic or cubic network solid⁵ is given by

$$-{\underset{˜}{\mathrm{J}}}_{\mathrm{I}}=\sum _{\mathrm{J}=1}^N{B}_{\mathrm{IJ}}\mathrm{grad}{M}_{\text{JK}}\text{I}=1,\dots N.$$ (8.1)

B_IJ is a mobility, function of composition and stress at a given temperature. It has been shown that the B_IJ are independent of the choice of the species K. There are (N-1) chemical species plus vacancies. There are (2N-1) independent network restrictions on the B_IJ

$$\sum _{\mathrm{I}}{B}_{\mathrm{IJ}}=0\text{J}=1,\dots N$$ (8.2)

$$\sum _{\mathrm{J}}{B}_{\mathrm{IJ}}=0\text{I}=1,\dots N.$$ (8.3)

As a result there are (N-1)² independent coefficients which is the expected number of phenomenological coefficients for the diffusion of (N-1) interacting species without a network constraint. It is also the number expected for (N-1) interstitial species. For a one-component solid with vacancies there is only one term

$${\underset{˜}{\mathrm{J}}}_1=-{\underset{˜}{\mathrm{J}}}_v=B_{v1}\mathrm{grad}{M}_{v1}.$$ (8.4)

Similarly for the diffusion of a single interstitial species there is one term

$$-{\underset{˜}{\mathrm{J}}}_1=B_1\mathrm{grad}{M}_1.$$ (8.5)

For a two-component substitutional solution there are four independent B. With vacancies as the K species the M_vv terms disappear and we have

$$\begin{gathered} -{\underset{˜}{\mathrm{J}}}_1=B_{11}\text{grad}{M}_{1v}+B_{12}\text{grad}{M}_{2v} \\ -{\underset{˜}{\mathrm{J}}}_2=B_{21}\mathrm{grad}{M}_{1v}+B_{22}\mathrm{grad}{M}_{2v} \\ -{\underset{˜}{\mathrm{J}}}_v=B_{v1}\mathrm{grad}{M}_{1v}+B_{v2}\mathrm{grad}{M}_{2v} \end{gathered}$$ (8.6)

with the restrictions that

$$\begin{gathered} B_{11}+B_{21}+B_{v1}=0 \\ {B}_{12}+B_{22}+B_{v2}=0. \end{gathered}$$

Using species 2 as the K species we have the same coefficients in different combinations with the diffusion potential M

$$\begin{gathered} -{\underset{˜}{\mathrm{J}}}_1=B_{11}\text{grad}{M}_{12}+B_{1v}\text{grad}{M}_{v2} \\ -{\underset{˜}{\mathrm{J}}}_2=B_{21}\mathrm{grad}{M}_{12}+B_{2v}\mathrm{grad}{M}_{v2} \\ -{\underset{˜}{\mathrm{J}}}_{\mathrm{v}}=B_{v1}\mathrm{grad}{M}_{12}+B_{vv}\mathrm{grad}{M}_{v2}. \end{gathered}$$ (8.7)

The knowledge that B remains the same in various formulations should permit flexibility both in gathering data and in formulating and applications.

Stress affects both B and M in the flux equations. B is affected by the level of stress alone. We expand about a stress state which can be either zero

$$B_{\text{JK}ij}=B_{\text{JK}ij}^0(c,\theta )+B_{\text{JK}ijkl}^1(c,\theta )T_{kl}+\mathrm{...}$$ (8.8)

or some other convenient state T⁰

$$\begin{gathered} B_{JKij}(c,\theta ,T)=B_{JKij}^0\left(c,\theta ,T^0\right) \\ +B_{\text{JK}ijkl}^{\mathrm{I}}\left(c,\theta ,T^0\right)\left(T_{kl}-T_{kl}^0\right). \end{gathered}$$ (8.9)

The gradient of M depends on the stress and the stress gradient. From the Maxwell eq (4.13) the coefficient of the stress gradient is the strain produced by a unit composition change

$$\left(\frac{\partial M_{\text{JK}}}{\partial T_{ij}}\right)=-V_0^{\prime }{\left(\frac{\partial E_{ij}}{\partial c_{\text{JK}}}\right)}_{T_{kl}}$$ (8.10)

which is precisely defined and readily estimated from lattice parameter-composition data. For cubic or isotropic cases

$$\partial M_{\text{JK}}/\partial T_{ij}=-V_0^{\prime }{\eta }_{\text{JK}}{\mathrm{\delta }}_{ij}$$ (8.11)

and

$$\nabla M_{\text{JK}}=R\theta \left[\left(\nabla c_{\text{J}}/c_{\text{J}}\right)-\left(\nabla c_{\text{K}}/c_{\text{K}}\right)\right]-V_0^{\prime }{\eta }_{\text{JK}}\nabla (trT).$$ (8.12)

Strictly this should be at the actual stress, but in most cases data for unstressed crystals should be adequate, and lead to a linear formulation. Combining (8.1) with (8.12) and retaining only terms linear in T we obtain for cubic or isotropic cases

$$-J_{\mathrm{I}}=-A_1(\nabla trT)+{\rho }_0^{\prime }\sum _{\mathrm{J}\ne \mathrm{K}}{D}_{\text{IJ}(\text{K})}\nabla c_{\text{J}}.$$ (8.13)

The factor ${\rho }_0^{\prime }$ needs to be introduced since the c are defined to be dimensionless rather than molar densities, where

$$\begin{gathered} A_1=V_0^{\prime }\sum _{\mathrm{J}}{B}_{\mathrm{I}\mathrm{J}}{\eta }_{\text{JK}} \\ {D}_{\text{IJ}(\text{K})}=V_0^{\prime }R\theta B_{\text{IJ}}\left(\frac{1}{c_{\text{J}}}+\frac{1}{c_{\text{K}}}\right) \end{gathered}$$ (8.14)

Because diffusion fluxes and gradients are independent of the choice of K, A_I and the B_IJ can be shown also to be independent of that choice, but to be consistent the D_IJ(K) must depend on the choice in the way shown in (8.14). To avoid large uncertainties in the D_IJ(K) it is again clearly advantageous to choose K to be the major species, rather than vacancies.

8.2. Diffusion Without Network Changes

Conservation of matter is expressed by the equation

$${\rho }_0^{\prime }\frac{\partial c_{\text{I}}}{\partial t}+\mathrm{div}{\underset{˜}{\mathrm{J}}}_{\text{I}}=0.$$ (8.15)

Compositional heterogeneity produces a long-range stress field and changing compositions change this field. Since stress and stress gradients affect B and M, the stress and diffusion equations have to be solved simultaneously. It has been common to ignore this mutual interaction and to study either the stress resulting from diffusion or the effect of stress on diffusion alone. When the ignored effects are small, this is valid, but for most cases it is not.

A straightforward technique for solving the stress and diffusion equations has been developed [30]. As in section 5 the relationship between elastic stress and an arbitrary composition field often remains solvable and can be used to eliminate stress from the diffusion equation. Plastic stress accommodation would render this technique invalid.

A hierarchy of increasingly complicated problems was examined for cases of diffusion in binary alloys in which there was no applied stress. All stress was due to compositional heterogeneity alone.

The mutual interaction in most cases is a major factor. In the case of spinodal decomposition, it can change the sign of the diffusional flux and is responsible for the metastability between the chemical and coherent spinodal [32]. The stress effect is so long ranged that compositional heterogeneity can affect diffusion elsewhere. Fick’s law which states that the flux depends only on local gradients is often not valid. Because this stress effect is proportional to the local concentration it can be neglected in dilute solutions.

Interface boundary conditions for diffusion in interstitial solutions have been examined for cases in which the network is chemically inactive. The boundary condition is a simple continuity of M at a fixed location in the reference state. It depends on the level of stress at the boundary. For local equilibrium eq (5.7) is applicable.

8.3. Diffusion with Self-stress and Phase-change at the Boundary

In our previous work [30] on the effect of self-stress on diffusion the network was conserved at the boundary. There are many metallurgical problems, such as diffusion controlled phase growth, where the network is not conserved, but where equilibrium prevails at the interface. This equilibrium is governed by eq (5.7) and a phase-change equation that depends on the nature of the boundary.

Self-stress is what we call the stress that is the result of sample heterogeneity. Generally its value at a point is a function of the composition distribution everywhere. For special geometries its value becomes a simple expression involving principally the local composition, and the effects of self-stress on the thermodynamic variables can be expressed in terms of the local composition only reducing self-stress problems to composition problems.

One such geometry is the semi-infinite solid with concentration fields that are functions only of the distance from the surface. We will consider the case of a semi-infinite couple, with diffusion in α and β, and an incoherent boundary. Under pressure P, the equilibrium compositions are ${\overline{c}}^{\alpha }$ and ${\overline{c}}^{\beta }$. When diffusion takes place, the compositions are $c_0^{\alpha }$ and $c_0^{\beta }$ far away from the boundary, and ${\tilde{c}}^{\alpha }$ and ${\tilde{c}}^{\beta }$ at the boundary (fig. 1). We shall further assume, for simplicity, that the pressure P is zero, and that the diffusing sample is under zero external pressure. This implies that the tractions are zero at the α-β boundary. We also assume no change of elastic constant with composition for either phase. Under these hypotheses, the mechanical equilibrium at the interface, eq (3.25), is always fulfilled. Equations (5.7) and (3.24) become, using (4.22) and (4.32)

$$\begin{gathered} {\mathrm{\mu }}_1^{0\alpha }-{\mathrm{\mu }}_2^{0\alpha }+R\theta \ln \frac{{\tilde{\gamma }}_1^{\alpha }{\tilde{c}}^{\alpha }}{{\tilde{\gamma }}_2^{\alpha }\left(1-{\tilde{c}}^{\alpha }\right)}-V_0^{\prime \alpha }{\eta }^{\alpha }{T}_{kk}^{\alpha } \\ ={\mathrm{\mu }}_1^{0\beta }-{\mathrm{\mu }}_2^{0\beta }+R\theta \ln \frac{{\tilde{\gamma }}_1^{\beta }{\tilde{c}}^{\beta }}{{\tilde{\gamma }}_2^{\beta }(1-{\tilde{c}}^{\beta })}-V_0^{\prime \beta }{\eta }^{\beta }{T}_{kk}^{\beta } \end{gathered}$$ (8.16)

and

$$\begin{gathered} {\mathrm{\mu }}_2^{0\alpha }+R\theta \ln \left[{\tilde{\gamma }}_2^{\alpha }\left(1-{\tilde{c}}^{\alpha }\right)\right]+V_0^{\prime \alpha }[-\frac{1}{2}\frac{{\nu }^{\alpha }}{E^{\alpha }}{\left(T_{kk}^{\alpha }\right)}^2 \\ +\frac{1+v^{\alpha }}{2E^{\alpha }}{T}_{ij}^{\alpha }{T}_{ij}^{\alpha }+{\tilde{c}}^{\alpha }{\eta }^{\alpha }{T}_{kk}^{\alpha }] \\ ={\mathrm{\mu }}_2^{0\beta }+R\theta \ln [{\tilde{\gamma }}_2^{\beta }\left(1-{\tilde{c}}^{\beta }\right)] \\ +V_0^{\prime \beta }\left[-\frac{1}{2}\frac{{\nu }^{\beta }}{E^{\beta }}{(T_{kk}^{\beta })}^2+\frac{1+{\nu }^{\beta }}{2E^{\beta }}{T}_{ij}^{\beta }{T}_{ij}^{\beta }+{\tilde{c}}^{\beta }{\eta }^{\beta }{T}_{kk}^{\beta }\right]. \end{gathered}$$ (8.17)

Figure 1–

Compositions in a self-stressed diffusion couple with an incoherent interface. The compositions far away from the interface are $c_0^{\alpha }$ and $c_0^{\beta }$. The self-stress generated by the composition gradient has shifted the equilibrium composition at the boundary to ${\tilde{c}}^{\alpha }$, ${\tilde{c}}^{\beta }$ from their unstressed phase diagram values of ${\overline{c}}^{\alpha }$, ${\overline{c}}^{\beta }$.

At equilibrium under zero pressure, these equations become

$$\begin{gathered} {\mathrm{\mu }}_1^{0\alpha }-{\mathrm{\mu }}_2^{0\alpha }+R\theta \ln \frac{{\overline{\gamma }}_1^{\alpha }{\overline{c}}^{\alpha }}{{\overline{\gamma }}_2^{\alpha }\left(1-{\overline{c}}^{\alpha }\right)}={\mathrm{\mu }}_1^{0\beta }-{\mathrm{\mu }}_2^{0\beta } \\ +R\theta \ln \frac{{\overline{\gamma }}_1^{\beta }{\overline{c}}^{\beta }}{{\overline{\gamma }}_2^{\beta }\left(1-{\overline{c}}^{\beta }\right)} \end{gathered}$$ (8.18)

$${\mathrm{\mu }}_2^{0\alpha }+R\theta \ln \left[{\overline{\gamma }}_2^{\alpha }\left(1-{\overline{c}}^{\alpha }\right)\right]={\mathrm{\mu }}_2^{0\beta }+R\theta \ln [{\overline{\gamma }}_2^{\beta }\left(1-{\overline{c}}^{\beta }\right)].$$ (8.19)

We first have to find the stress field. In a half-space specimen, we have found [30] that its trace depends only on the local composition

$$T_{kk}^{\alpha }=-2Y^{\alpha }{\eta }^{\alpha }\left({\overline{c}}^{\alpha }-c_0^{\alpha }\right)$$ (8.20)

$$T_{kk}^{\beta }=-2Y^{\beta }{\eta }^{\beta }({\tilde{c}}^{\beta }-c_0^{\beta }).$$ (8.21)

Where Y = E/(1 − v). Introducing these values in (8.16) and (8.17), and after subtraction of (8.18) from (8.16) and (8.19) from (8.17), we obtain the system of equations to solve for ${\tilde{c}}^{\alpha }$ and ${\tilde{c}}^{\beta }$. As we have seen before, it can be solved numerically or, if $({\tilde{c}}^{\alpha }-c_0^{\alpha })$ and $({\tilde{c}}^{\beta }-c_0^{\beta })$ are small, it can be linearized, and the resulting system of equations solved by Cramer’s rule.

Under the assumption that there is no normal stress across the α-β interface, a common tangent construction is possible (see Appendix 4 for the demonstration). To the Helmholtz free energy per mole we have to add the elastic energy per mole, which is just a function of the local composition. Its value is

$${\widehat{f}}_{\text{el}}=\frac{V_0^{\prime }E}{1-\nu }{\eta }^2{\left({\tilde{c}}^{\alpha }-c_0^{\alpha }\right)}^2$$ (8.22)

where $V_0^{\prime }$ is the molar volume at composition c₀. The construction is shown in figure 2. This type of construction has been used by Hillert [33] for the case of massive transformation, in which it is proper to assume that the phase which is forming is homogeneous, and by Purdy et al. [34] for diffusion-induced grain boundary migration.

Figure 2–

Common tangent construction that gives the composition of figure 1. The unstressed free energies (heavy lines) are shifted by an amount equal to the elastic energy $V_0^{\prime }E{\mathrm{\eta }}^2{\left(c-c_0\right)}^2/(1-v)$ to give the light curves. The common tangent construction gives ${\tilde{c}}^{\alpha }$ and ${\tilde{c}}^{\beta }$.

8.4. Effect of Vacancies: General Formulation

When vacancies, in addition to providing a mechanism for diffusion, also interact with the stress, and provide a means for creating or destroying network at an interface, new phenomena appear, in particular diffusional creep. In this section, we consider only one-component systems, where these effects are not obscured by the phenomena previously described in this chapter. We first formulate the creep as a boundary value problem and then turn our attention to specific creep problems.

The Partial Differential Equation

The flux of vacancies J is given by

$$-J_i=B_{ij}{\left(M_{v1}\right)}_{,j}$$ (8.23)

where B_ij is a tensor function of the temperature θ, c_v (the concentration of vacancies) and the stress. An expansion around T = 0 gives

$$B_{ij}=B_{ij}^0\left(c_v,\theta \right)+B_{ijkl}^1\left(c_v,\theta \right)T_{kl}+\dots$$ (8.24)

The coefficient of order 0 is given by

$$B_{ij}^0=D_{ij}{c}_v\left(1-c_v\right)/R\theta {\rho }_0^{\prime }$$ (8.25)

where D_ij is the self-diffusion matrix. Usually it is not very much dependent on the vacancy concentration.

The tensors $B_{ij}^0$ and $B_{ij}^1$ being properties of a crystalline material follow the rules of crystalline symmetries. For isotropic materials

$$B_{ij}^0=B^0{\mathrm{\delta }}_{ij}$$ (8.26)

and

$$B^0=c_v\left(1-c_v\right)D/R\theta {\rho }_0^{\prime }.$$ (8.27)

The tensor $B_{ijkl}^1$ has the same form as an elastic tensor for an isotropic material

$$B_{ijkl}^1{T}_{kl}=\beta T_{kk}{\mathrm{\delta }}_{ij}+\gamma T_{ij}$$ (8.28)

where β and γ are two constants. This equation reveals that if the tensor B_ij is stress dependent, it introduces a stress-coupled anisotropy in an otherwise isotropic diffusion coefficient.

Neglecting second order effects in stress in M_v1, that is assuming that the elastic coefficients do not depend on vacancy concentration, the gradient of the vacancies diffusion potential can be written

$${\left(M_{v1}\right)}_{,j}=\frac{R\theta }{c_{v}1-c_v)}\left[1+\frac{\partial \ln {\gamma }_v}{\partial \ln c_v}\right]{\left(c_v\right)}_{,j}-V_0^{\prime }{\eta }_{kl}{T}_{kl,j}.$$ (8.29)

If dilute solution laws apply, this equation simplifies into

$${\left(M_{v1}\right)}_{.j}=\frac{R\theta }{c_v}{\left(c_v\right)}_{,j}-V_0^{\prime }{\eta }_{kl}{T}_{kl,j}$$ (8.30)

which, for isotropic material becomes

$$\nabla M_{v1}=\left(R\theta /c_v\right)\nabla c_v-V_0^{\prime }\eta \nabla (trT).$$ (8.31)

The conservation equation is expressed as usual

$${\rho }_0^{\prime }\frac{\partial c_v}{\partial t}+J_{i,i}=s{\rho }_0^{\prime }.$$ (8.32)

The source and sink terms, which is the number of vacancies created per unit volume, come, for instance, from the vacancy source at a moving dislocation. The complete diffusion equation for vacancies is obtained by combining [8.23] with [8.32]

$${\rho }_0^{\prime }\frac{\partial c_v}{\partial t}={\rho }_0^{\prime }s+{[B_{ij}{\left(M_{v1}\right)}_{,j}]}_{,i}.$$ (8.33)

In an isotropic solution, one gets

$$\frac{\partial c_v}{\partial t}=s+D{\nabla }_{c_v}^2-\frac{D{V}_0^{\prime }\eta }{R\theta }\nabla c_v\cdot \nabla T_{kk}-\frac{c_{v}D{V}_0^{\prime }\eta }{R\theta }{\nabla }^2{T}_{kk}$$ (8.34)

where we have neglected the stress dependence of B_ij. When the relaxation of the lattice around a vacancy can be neglected, the last two terms of the r.h.s. disappear, and one obtains the simple equation

$$\frac{\partial c_v}{\partial t}=s+D{\nabla }^2{c}_v.$$ (8.35)

Initial Conditions

The initial conditions consist in a given vacancy concentration field. For steady state, these conditions are not needed. They are unimportant at long times, as long as a steady state can be reached. Boundary Conditions. The boundary conditions depend of course on the problem that is treated. The most useful seems to be given by an equilibrium condition along all surfaces of the solid. Written for an isotropic solid, constant elastic coefficients, a reference pressure P = 0 (with an equilibrium vacancy concentration c_v), dilute solution behavior, and a reference composition c_v = 0 for strain, this reads (eqs (3.18) and (4.31))

$$\begin{gathered} {\mathrm{\mu }}_v^0(\text{o})+R\theta \ln c_v=-P{V}_0^{\prime }\left(1+\frac{1-2\nu }{E}{T}_{kk}+3c_v{\eta }_v\right) \\ -V_0^{\prime }\left[-\frac{1}{2}\frac{\nu }{E}{\left(T_{kk}\right)}^2+\frac{1+\nu }{2E}{T}_{ij}{T}_{ij}-\left(1-c_v\right){\eta }_v{T}_{kk}\right] \end{gathered}$$ (8.36)

or

$$\begin{gathered} R\theta \ln \left(c_v/{\overline{c}}_v\right)=-P{V}_0^{\prime }\left(1+\frac{1-2\nu }{E}{T}_{kk}+3c_v{\eta }_v\right) \\ -V_0^{\prime }\left[-\frac{1}{2}\frac{\nu }{E}{\left(T_{kk}\right)}^2+\frac{1+\nu }{2E}{T}_{ij}{T}_{ij}-\left(1-c_v\right){\eta }_v{T}_{kk}\right]. \end{gathered}$$ (8.37)

Since c_v ⪡ 1, these equations can be simplified into

$$\begin{gathered} {\mathrm{\mu }}_v^0(\text{o})+R\theta \ln c_v=-P{V}_0^{\prime }\left(1+\frac{1-2\nu }{E}{T}_{kk}\right) \\ -V_0^{\prime }\left[-\frac{1}{2}\frac{\nu }{E}{\left(T_{kk}\right)}^2+\frac{1+\nu }{2E}{T}_{ij}{T}_{ij}-{\eta }_v{T}_{kk}\right]. \end{gathered}$$ (8.38)

Because it is the dominant term linear in stress, the r.h.s. is usually $-P{V}_0^{\prime }$. Only this term was taken into account in Herring’s theory of diffusional creep. We shall see in the next section cases where the quadratic terms are important for new effects.

Network modification along the surfaces due to the vacancy flux is simply given by

$$n_i^{\prime }\left(\frac{\partial x_i^{\prime }}{\partial t}+V_0{J}_i\right)=0$$ (8.39)

where the $x_i^{\prime }$ are the coordinates of a point of the interface. This equation tells us that the shape of the specimen changes as diffusion takes place, due to the vacancy creation and annihilation at the surfaces.

Stress Equilibrium

Up to now we have been concerned with the diffusion equation. Stress equilibrium in this quasi-static model obeys the partial differential equation (3.13)

$$T_{ij,j}=0$$ (8.40)

with proper boundary conditions. In most problems they will be given in terms of tractions along the surface. It is important to note that, because of the network modifications there, they are specified on a changing (and usually unknown) surface.

To specify the problem fully in term of stress, we need the Beltrami-Mitchell equations [11,30]. For isotropic materials, the expression is

$$(1+\nu )T_{ij,kk}+T_{kk,ij}+E\eta \left[\frac{1+\nu }{1-\nu }{\mathrm{\delta }}_{ij}\left(c_v\right){,}_{kk}+\left(c_v\right){,}_{ij}\right]=0.$$ (8.41)

8.5. Some Creep Problems

8.5.1. Herring’s Classical Problems: Diffusional Viscosity of a Polycrystalline Solid

Let us first show that with Herring’s assumptions and approximations [18] the equations presented in section 8.4 become identical to his starting equations. Only steady state is considered. There is no volume change associated with a vacancy (i.e., the average volume of a vacancy is equal to the atomic volume). This implies η = 0; therefore the interactions between stress and composition appear only in the boundary condition pertaining to network modification. Furthermore all terms nonlinear in stress are neglected, and the reference pressure is zero. The solution of atoms and vacancies is ideal (i.e., there is no interaction with vacancies and their concentration is very small). Finally, there is no source term within a grain.

With these approximations, the diffusion eq (8.33) becomes

$${\nabla }^2{M}_{v1}=0.$$ (8.42)

The expression for the diffusion potential is

$$M_{1v}={\mathrm{\mu }}_1^0(0)-{\mathrm{\mu }}_v^0(0)+R\theta \ln \left[\left(1-c_v\right)/c_v\right]$$ (8.43)

and the boundary condition (8.29) becomes

$${\mathrm{\mu }}_v^0(0)+R\theta \ln c_v=-P{V}_0^{\prime }.$$ (8.44)

Subtracting (8.44) from (8.43), and neglecting ln(1 − c_v), one gets

$$M_{1v}={\mathrm{\mu }}_1^0+P{V}_0^{\prime }.$$ (8.45)

This is the boundary condition used by Herring (his eq (2)) for the partial differential eq (8.42) since our P equals his −P_zz. The stress equilibrium equation is the same, and he implicitly used condition (8.37) to get the rate of displacement of the interface (e.g., to go from (3) to (4) in his paper). Thus within the assumptions explicitly spelled out at the beginning of this section, we recover Herring’s equations and boundary conditions.

His solutions combined a mean field (the average of the stress tensor within a grain is equal to the applied stress) and a perturbation analysis (the shape of the grain does not change as diffusion proceeds).

The formulation of the problem with fewer assumptions is possible using the equations of the previous section which contains important additional terms in the diffusion eq (8.33) and boundary conditions (8.29). We next explore a few problems chosen to illustrate the physical consequences of these additional terms.

8.5.2. Quadratic Effects

Usually the linear term of the r.h.s. of (8.36) is the dominant one, but, whenever the specimen surfaces are all immersed in a fluid of constant pressure, this term is constant and at steady state does not contribute any gradient. Under these conditions the higher order terms are the only ones present. We consider two examples in which we approximate condition for which P is constant over the surfaces of interest.

The first treated by Roitburd [35] is a pore in a specimen under uniaxial stress in which he examined the shape change by vacancy fluxes that redistributed material around the pore. Other vacancy sinks and sources were assumed so far away that fluxes between them and pores could be neglected. Because P in the pore is constant, the effects depend entirely on the quadratic terms. The result of the calculation is that a spherical pore will distort to an oblate spheroid with the minor axis along the stress axis. Because this conclusion arises from quadratic terms the same result is obtained regardless of whether the specimen is under tension or compression.

A closely related problem is a long single crystal rod of nonuniform cross section under a uniaxial load applied at the ends. If the characteristic length of the nonuniformities is short compared to the specimen length, we may examine the redistribution of material along the lateral surfaces by vacancy flux and ignore the fluxes between these surfaces and the specimen ends. Along the surface P is again constant. If we assume η_v = 0 and that the elastic constants are independent of c_v, (8.36) becomes

$${\mathrm{\mu }}_v^0(\text{o})+R\theta \ln c_v=-V_0^{\prime }\left[-\frac{1}{2}\frac{\nu }{E}{\left(T_{kk}\right)}^2+\frac{1+\nu }{2E}{T}_{ij}{T}_{ij}\right].$$ (8.46)

The r.h.s. is minus the elastic energy of the solid. Let us note that the rod is unstable to necking. A small indentation (or any change in cross section) will produce a higher stress at its root (or at the minimum cross section). Vacancy flux will remove material from the root (or at minimum cross section) and deposit it nearby at a place of lowered elastic energy. The rod is unstable to necking by diffusion creep regardless of whether it is under tension or compression. This is the same result as Roitburd’s pore,which can be considered an internal notch.

This counterintuitive result is consistent with thermodynamics. Consider the work done by the loading system, applied force times distance moved. The compliance of a rod with nonuniform cross section increases if the rod necks down, and thus the load system does work on the specimen. Conversely if the rod were to become more uniform under load, its compliance would decrease and it would have to do work on the load system. This would be in violation of thermodynamic principles.

Another interesting result of eq (8.46) is the case of a uniform rod, in which we again can ignore the ends as vacancy sources or sinks. The equation states that for η_v = 0 and elastic constants independent of c_v the equilibrium vacancy concentration is a maximum at zero stress, and is lowered equally by tensile and compressive stresses. This result is again understood if we realize that the cross-section will be reduced if vacancies leave the system, increasing the specimen’s compliance. The result will be modified if we assume that the elastic constants are a function of c_v and if we let η_v differ from zero, but for small changes it will not affect the sign.

8.5.3. Balancing Quadratic and Linear Effects. The 2π Wedge Disclination

Linear effects do not automatically dominate quadratic effects. An interesting example where both are present and cancel identically is a hollow tube composed of a 2π wedge disclination in which there is a pressure difference between the inside and outside of the tube.

To form the 2π wedge disclination we take a rectangular sheet of a perfect single crystal, bend it into a tube and weld the seam to insure perfect matching of lattice planes (fig. 3).

Figure 3–

Radial vacancy fluxes that remove layers from the inner surfaces and deposit them on the outer surface of a 2π wedge disclination do not enlarge the disclination and therefore no work is done by any pressure difference. To see this, consider the cross section (c) of 2π wedge disclination made by elastically bending the perfect crystal (a) into a circular cylindrical shell and joining the ends. The 2π wedge disclination after radial diffusion is unchanged because it can be made from (b) which is identical to (a) except for translation of bottom layers to top. It will therefore reach the same equilibrium geometry in the presence of the pressure differences.

At this stage there are tangential compressive stresses at the inner surface and tensile stresses at the outer surfaces. M_1v at the two surfaces is the same because the stresses at the two surfaces have the same magnitude. Because of this the system reaches a vacancy equilibrium in this heterogeneously stressed system in which vacancy gradients and stress gradients combine to give a constant M_1v throughout.

Now apply a pressure difference between the inside and outside and permit vacancy flow. It is readily shown that in spite of the pressure difference the value of M_1v at the inner surface equals that at the outer surface. In the presence of the higher pressure at the inside there is a change in elastic free energy density, a reduction at the inner surface and an increase at the outer surface, and vice versa if the sign of the pressure difference is changed. The elastic energy is quadratic in the stress, but the change in stress due to the imposed pressure difference is linear in ΔP. The result is that the linear terms in P in M_1v cancel identically the changes in the quadratic terms in the tangential stresses. The linear and quadratic terms balance identically to give the same M_1v at the two surfaces. Again an equilibrium is reached in which M_1v is constant throughout and vacancy concentration gradients compensate for stress gradients.

This surprising result that the 2π wedge disclination will not creep by vacancy flow even when there is a pressure difference can also be understood by considering the consequence of the transfer of an entire plane of atoms from the inside to the outside. If we start with either of the flat single crystal plates and create the disclination we see that the tube is the same whether the atom layer is transferred or not (fig. 3).

9. Summary and Conclusions

We have reviewed and applied the thermodynamics that has been developed for multicomponent multiphase stressed crystalline solids. We have found equilibria in which the solids were neither homogeneous in stress nor in composition. We have considered equilibria for three types of multiphase contact: solid-fluid, incoherent, and coherent solid-solid. We have also examined simple non-equilibrium cases where potential gradients determine diffusion. Diffusional creep in particular was used to illustrate the importance of a full thermodynamic treatment.

Crystalline solids differ fundamentally from liquids in that they posses long range three-dimensional translational order. This implies that we can define a lattice and site occupancy. The number density and type of sites is known, and a local change in composition can only be made by redistributing atoms and vacancies among these sites. This fundamental restriction in the interior of a crystalline solid introduces important differences between the thermodynamics of solids and those of liquids. Because these restrictions apply at coherent boundaries but not at other boundaries, we find different equilibrium conditions at the various boundaries.

The equations that result from the thermodynamics consists of a set of coupled partial differential equations, algebraic equations and boundary conditions for stress and composition. For the kinetics, the diffusion equations are added. Although full nonlinear and large strain formulations exist, we have concentrated on examples where the essential features were displayed with small-strain approximations and linearized thermodynamics.

The thermodynamics has resulted in identifying and precisely defining the important phenomenological quantities needed for predictive calculation. The definitions in particular are important and much of the controversy in the literature is judged to be the result of inadequate definitions of quantities. Furthermore the necessary data needed for evaluating the equations turn out to be computable from classically measured quantities, such as free energies of hydrostatically stressed solid solutions, elastic coefficients, and lattice parameters.

One important method for solving the equilibrium equations uses the notion of open-system elasticity. This method eliminates the composition variable from the system of equations, and leaves a purely elastic problem to be solved. Central to the method are the open-system elastic constants, and in this paper we show that the same technique applies to multiphase solid equilibria. With this technique a large number of elastochemical problems are now solved because they become identical to solved problems of chemically homogeneous elastic solids. Once the stress field is known, only algebraic equations have to be solved to obtain the composition in the solid. As an example of the use of this concept, we have solved the dislocation atmosphere (stress field and composition field) in an isotropic and a cubic solid, automatically taking into account in a self-consistent way the thermodynamics of the solid solutions. Another example is the inclusion problem, although we have not found in the literature the shapes that satisfy the phase equilibrium boundary condition other than sphere, circular rod, and plate.

The question of the need for defining separate chemical potentials for each chemical species inside the solid has been a subject of controversy ever since Gibbs. We hope that we have shown that problems of equilibria can be solved without defining or using them. Gibb’s famous example of a homogeneously stressed solid which gave three different chemical potentials when equilibrated with three fluids each at a pressure equal to minus a principal stress should alert everyone to the danger of attempting a definition. Of course our M_1v could be construed to be a chemical potential of the Ith specie, but we prefer for clarity to retain the vacancy as the counter specie.

Questions of species that occupy more than one site needed to be addressed. As our section 5.6 shows, the classical notion of chemical reactions among species on different sites very nicely resolves any confusion. Treating interstitials as atoms occupying sites that are mostly empty resulted in a unified treatment and clearly demonstrated the principle. From this more general treatment we showed it is possible to develop a treatment in which interstitials require a different and more convenient formulation.

We have supplemented an earlier overview on the effect of self-stress on diffusion by adding boundary conditions that permit phases to grow or shrink at the interface.

Diffusional creep is an important field in which the linearized and simplified treatment of Herring was an important first step. However Herring’s definitions were not precise and this has led to much later confusion. We have presented a detailed derivation of a fuller treatment in which each term is fully defined and related to the data base. To emphasize the importance of the nonlinear terms, which Herring alluded to, but discarded, we gave two examples each of which seems counterintuitive but thermodynamically correct: a long rod which in compression is unstable to necking by diffusional creep, and a tube composed of a perfect 2π wedge disclination which does not bulge by radial vacancy flux even when there is a pressure difference between the interior and exterior. The former is a case where Herring’s linear term is zero and we must resort to the quadratic terms, and the latter is a case where the linear term identically cancels changes in the quadratic terms. The fuller equation contains several other terms usually ignored in creep theories that also can become important.

Capillary effects (surface strain and surface free energy) are not included. A formulation exists for some types of interfaces or specific geometries [36,37]. Theories of equilibrium of stressed solids with capillarity effects for the three types of interfaces considered here are being developed [38].

Although the elastic energy is usually small compared to the free energy change resulting from a composition change, there are domains where the interactions of composition and stresses are likely to be important. Self-stresses resulting from the presence of defects or heterogeneity of the material can have sizable consequences. The depression of the consolute critical point and the spinodal is a well known example. In systems without critical points coherent equilibrium is also strongly affected. Coherent phase diagram features have recently been found [39,40] that differ markedly from incoherent phase diagrams. The equations that could be used to calculate these phase diagrams have been obtained in sections 3 and 4.

Interesting consequences originate from the long range nature of the elastic forces. For instance this introduces non-local effects in the diffusion equation. Under hydrostatic pressure, a multi-phase incoherent dispersion at equilibrium is degenerate with respect to the shape of the phases, i.e., the equilibrium is independent of the shape of the precipitates. Under a more general state of stress (coherent precipitates, for instance), this simple result is no longer valid. The equilibrium equations have to be solved on an unknown boundary and the equilibrium shape is to be determined as part of the solution (a so-called free boundary problem). With the use of the open-system elastic constants such problems can be expressed as a purely elastic problem. The phase equilibrium boundary condition is the one that makes the problem different from classical elastic inclusion problems for which a shape is imposed. The solutions of the elastic equation of general shape will not be consistent with the phase equilibrium boundary condition. The catalog of the shapes that produce an elastic field that in turn satisfies this condition has not yet been found. The introduction of capillarity would modify this condition. Work has been done on the subject [41].

Biography

About the Authors, Paper: F. C. Larché, a member of the faculty at the Université de Montpellier, and J. W. Cahn, who is with NBS’ Center for Materials Science, are frequent collaborators in scientific papers. This paper, which is also appearing in Acta Metallurgica, is presented here through the courtesy of Acta Metallurgica and its publisher, Pergamon Press.

Appendix 1. Solid-Liquid Equilibrium Under Hydrostatic Stress

We consider the case of a substitutional binary solid. In equilibrium with a fluid under hydrostatic stress (for instance if it is entirely surrounded by the fluid), the mechanical equilibrium eqs (3.13) and (3.14) implies that the stress is equal to

$$T_{ij}=-P{\mathrm{\delta }}_{ij}$$ (A1.1)

where P is the pressure in the fluid. The stress being uniform, the constancy of the diffusion potential implies that the composition is uniform. Therefore the solid is uniform. The boundary condition

$$f-{\mathrm{\mu }}_1^L{\rho }_1-{\mathrm{\mu }}_2^L{\rho }_2=-P$$ (A1.2)

can be combined with the equation for the diffusion potential

$$M_{12}={\mathrm{\mu }}_1^L-{\mathrm{\mu }}_2^L$$ (A1.3)

to give

$${\mathrm{\mu }}_1^L=\left(f+P+{\rho }_2{M}_{12}\right)V_0$$ (A1.4)

$${\mathrm{\mu }}_2^L=\left(f+P+{\rho }_1{M}_{12}\right)V_0$$ (A1.5)

Because the solid is uniform, these expressions are valid everywhere. The quantities on the right hand side of (A1.4) and (A1.5) depend only on the value of the state variables. Let us call them ${\mathrm{\mu }}_1^s$ and ${\mathrm{\mu }}_2^s$.

$${\mathrm{\mu }}_1^s\equiv \left(f+P+{\rho }_2{M}_{12}\right)V_0$$ (A1.6)

$${\mathrm{\mu }}_2^s\equiv \left(f+P-{\rho }_1{M}_{12}\right)V_0$$ (A1.7)

Elimination of M₁₂ between these two equations gives

$$f=-P+{\rho }_1{\mathrm{\mu }}_1^s+{\rho }_2{\mathrm{\mu }}_2^s$$

and, because of the uniformity, we can multiply by V₀ to get the total Helmholtz free energy

$$F=-P{V}_0+N_1{\mathrm{\mu }}_1^s+N_2{\mathrm{\mu }}_2^s$$

where N₁ and N₂ are the total number of moles of components 1 and 2 respectively. The differential of f′ is

$$\text{d}{f}^{\prime }=T_{ij}\text{d}{E}_{ij}+M_{12}\text{d}{\rho }_1^{\prime }$$

M₁₂ is replaced by its value obtained from (A 1.6) and (A 1.7). Using the definition of ${\rho }_1^{\prime }$, and after multiplication by $V_0^{\prime }$, one obtains

$$\text{d}F=-P\text{d}{V}_0+{\mathrm{\mu }}_1^s\text{d}{N}_1+{\mathrm{\mu }}_2^s\text{d}{N}_2$$

Therefore

$$\begin{gathered} {\mathrm{\mu }}_1^s\equiv {\left(\frac{\partial F}{\partial N_1}\right)}_{V,N_2} \\ {\mathrm{\mu }}_2^s\equiv {\left(\frac{\partial F}{\partial N_2}\right)}_{V,N_1} \end{gathered}$$

We have recovered all the classical formula for fluid-fluid equilibrium. Despite network constraints, a solid under hydrostatic stress behaves as if it were a fluid.

Appendix 2. The Boundary Conditions for Coherent Phase Change: Small Strain Approximation

The full large strain boundary condition for coherent phase change is [15]

$${\omega }^{\prime \alpha }-{\omega }^{\prime \beta }-{\mathbf{n}}^{\prime \alpha }•\left({\mathbf{F}}^{\alpha \mathrm{T}}-{\mathbf{F}}^{\beta \mathrm{T}}\right)•\left(\partial {\mathbf{f}}^{\prime \alpha }/\partial \mathbf{F}\right)•{\mathbf{n}}^{\prime \alpha }=0$$ (A2.1)

where the same reference state is chosen for both phases. The superscript T stands for transpose and F is the deformation gradient. (∂f′/∂F) is the first Piola-Kirchoff tensor T_R. It is related to the Cauchy stress tensor T by

$${\mathbf{T}}_R=J\mathbf{T}•{\left({\mathbf{F}}^{-1}\right)}^T$$ (A2.2)

where J is the determinant of F. In the small strain approximation, the displacement tensor is given, to first order in the derivatives by u_j,i, by [11]

$$\mathbf{F}=I+E+\mathrm{\Omega }+0(u_{i,j}^2)$$ (A2.3)

where E is the small strain tensor, (eq (3.1)), Ω the small rotation tensor, and I the unit tensor. To the same approximation, its inverse is given by

$${\mathbf{F}}^{-1}=\mathbf{I}-\mathbf{E}-\mathrm{\Omega }+0(u_{i,j}^2)$$ (A2.4)

Using these equations we get

$$\begin{gathered} {\mathbf{n}}^{\prime }•\left({\mathbf{F}}^{\mathrm{T}}•T_R\right)•{\mathbf{n}}^{\prime }={\mathbf{n}}^{\prime }•(\mathbf{I}+\mathbf{E}-\mathrm{\Omega })•\mathbf{T}•(\mathbf{I}-\mathbf{E}+\mathbf{\Omega })•{\mathbf{n}}^{\prime } \\ +0({\mathrm{u}}_{i,j}^2) \end{gathered}$$ (A2.5)

Dropping terms of order $u_{i,j}^2$, and since, for an arbitrary 3×3 tensor

$${\mathbf{n}}^{\prime }•\mathbf{A}•{\mathbf{n}}^{\prime }={\mathbf{n}}^{\prime }•{\mathbf{A}}^T•{\mathbf{n}}^{\prime }$$

we finally obtain

$${\mathbf{n}}^{\prime }•\left({\mathbf{F}}^{\mathrm{T}}•{\mathbf{T}}_{\text{R}}\right)•{\mathbf{n}}^{\prime }={\mathbf{n}}^{\prime }•\mathbf{T}•{\mathbf{n}}^{\prime }-2{\mathbf{n}}^{\prime }•\mathrm{\Omega }•\mathbf{T}•{\mathbf{n}}^{\prime }$$ (A2.6)

Since the same reference state has been chosen for α and β, the following equalities hold

$$\begin{gathered} {\rho }_{\mathrm{I}}^{\prime }={\rho }_0^{\prime }{c}_{\mathrm{I}}^{\alpha };{\rho }_{\mathrm{I}}^{\prime \beta }={\rho }_0^{\prime }{c}_{\mathrm{I}}^{\beta } \\ {J}^{\alpha }={\rho }_0^{\prime }/{\rho }_0^{\alpha }{J}^{\beta }={\rho }_0^{\prime }/{\rho }_0^{\beta } \end{gathered}$$ (A2.7)

Using (A2.7), (A2.6), and (A2.1) we finally obtain

$$\begin{gathered} V_0^{\prime }{f}^{\prime \alpha }-\mathrm{\Sigma }{M}_{\text{IK}}{c}_{\mathrm{I}}^{\alpha }+V_0^{\prime }[-T_{ij}^{\alpha }{n}_i^{\prime \alpha }{n}_j^{\prime \alpha }+2{\mathrm{\Omega }}_{ij}^{\alpha }{T}_{jk}^{\alpha }{n}_i^{\prime \alpha }{n}_k^{\prime \alpha }] \\ =V_0^{\prime }{f}^{\prime \beta }-\mathrm{\Sigma }{M}_{\text{IK}}{c}_{\mathrm{I}}^{\beta }+V_0^{\prime }[-T_{ij}^{\beta }{n}_i^{\prime \beta }{n}_j^{\prime \beta }+2{\mathrm{\Omega }}_{ij}^{\beta }{T}_{jk}^{\beta }{n}_i^{\prime \beta }{n}_k^{\prime \beta }] \end{gathered}$$ (A2.8)

The various terms are seen to be energies per mole of lattice sites. It is then easy to make a change of reference volume (like the stress free state for each phase). To the level of approximation used in linear elasticity this won’t affect the $V_0^{\prime }{f}^{\prime }$ terms. But it does affect the terms linear in T_ij.

Appendix 3. Derivation of the Open-System Elastic Stiffness and Compliance Tensor

All the calculations are done at constant temperature, so that all the partial derivatives are understood to be at constant temperature. We first treat the case of a binary solid, then generalize to a multicomponent solid.

A3.1. Binary Solid

To simplify the notation we take ρ′ to be ${\rho }_1^{\prime }$. The differential of the stress can be written

$$\text{d}{T}_{ij}={\left(\frac{\partial T_{ij}}{\partial E_{kl}}\right)}_{{\rho }^{\prime }}\text{d}{E}_{kl}+{\left(\frac{\partial T_{ij}}{\partial {\rho }^{\prime }}\right)}_{E_{kl}}\text{d}{\rho }^{\prime }$$ (A3.1)

or

$$\text{d}{T}_{ij}={\left(\frac{\partial T_{ij}}{\partial E_{kl}}\right)}_{M_{12}}\text{d}{E}_{kl}+{\left(\frac{\partial T_{ij}}{\partial M_{12}}\right)}_{E_{kl}}d{M}_{12}$$ (A3.2)

The differential of the diffusion potential is

$$\text{d}{M}_{12}={\left(\frac{\partial M_{12}}{\partial {\rho }^{\prime }}\right)}_{E_{ij}}\text{d}{\rho }^{\prime }+{\left(\frac{\partial M_{\text{l}2}}{\partial E_{ij}}\right)}_{p^{\prime }}\text{d}{E}_{ij}$$ (A3.3)

Replacing dρ′ from (A3.3) into (A3.1) yields

$$\begin{gathered} \text{d}{T}_{ij}=\left[{\left(\frac{\partial T_{ij}}{\partial E_{kl}}\right)}_{{\rho }^{\prime }}-{\left(\frac{\partial T_{ij}}{\partial {\rho }^{\prime }}\right)}_{E_{kl}}{\left(\frac{\partial M_{12}}{\partial E_{ij}}\right)}_{{\rho }^{\prime }}/{\left(\frac{\partial M_{12}}{\partial {\rho }^{\prime }}\right)}_{E_{ij}}\right]\text{d}{E}_{kl} \\ +\left[{\left(\frac{\partial T_{ij}}{\partial {\rho }^{\prime }}\right)}_{E_{kl}}/{\left(\frac{\partial M_{12}}{\partial {\rho }^{\prime }}\right)}_{E_{kl}}\right]\text{d}{M}_{12} \end{gathered}$$ (A3.4)

and the coefficient of the term dE_kl is the (ijkl) component of the open-system stiffness tensor.

Using the stress-strain relationship (4.14) and the Maxwell relation

$${\left(\frac{\partial T_{ij}}{\partial {\rho }^{\prime }}\right)}_{E_{kl}}={\left(\frac{\partial M_{12}}{\partial E_{ij}}\right)}_{{\rho }^{\prime }}$$ (A3.5)

one gets

$${\left(\frac{\partial M_{12}}{\partial E_{ij}}\right)}_{{\rho }^{\prime }}=-C_{ijkl}{\eta }_{kl}+\frac{\text{d}{C}_{ijkl}}{\text{d}{\rho }^{\prime }}\left(E_{kl}-E_{kl}^c\right)$$ (A3.6)

The value of M₁₂ as a function of E_ij rather than T_ij is obtained from (4.14) by using

$$S_{ijkl}{C}_{klmn}={\mathrm{\delta }}_{im}{\mathrm{\delta }}_{jn}$$ (A3.7)

Neglecting strain dependent terms, we finally get

$$C_{ijkl}^{*}=C_{ijkl}-\frac{1}{{\rho }_0^{\prime }\chi }{C}_{ijmn}{C}_{klpq}{\eta }_{mn}{\eta }_{\text{pq}}$$ (A3.8)

Because of the linearity, we have

$$S_{ijkl}^{*}{C}_{klmn}^{*}={\mathrm{\delta }}_{im}{\mathrm{\delta }}_{jn}$$ (A3.9)

where $S_{ijkl}^{*}$ are the open-system compliances. Combining (A3.8) and (A3.9) gives

$$S_{ijkl}^{*}=S_{ijkl}+{\rho }_0^{\prime }\chi {\mathrm{\eta }}_{ij}{\eta }_{kl}$$ (A3.10)

where η_ij are defined by (4.4).

A3.2. Multicomponent Solids

We follow the same derivation as above. The differential of the stress tensor is

$$\text{d}{T}_{ij}={\left(\frac{\partial T_{ij}}{\partial E_{kl}}\right)}_{{\rho }_{\mathrm{I}}^{\prime }}\text{d}{E}_{kl}+\sum _{\mathrm{I}\ne \mathrm{K}}\left(\frac{\partial T_{ij}}{\partial {\rho }_{\text{IK}}^{\prime }}\right)\text{d}{\rho }_{\mathrm{I}}^{\prime }$$ (A3.11)

The differentials of the potentials are

$$\text{d}{M}_{\text{IK}}=\sum _{\mathrm{J}\ne \mathrm{K}}\left(\frac{\partial M_{\text{IK}}}{\partial {\rho }_{\text{J K}}^{\prime }}\right)\text{d}{\rho }_{\mathrm{J}}^{\prime }+{\left(\frac{\partial M_{\text{IK}}}{\partial E_{ij}}\right)}_{{\rho }_{\mathrm{I}}^{\prime }}\text{d}{E}_{ij}$$ (A3.12)

$\text{d}{\rho }_J^{\prime }$ can be obtained from this system of linear equation by Kramer’s rule

$$\mathrm{d}{\rho }_{\text{J}}^{\prime }=\left[\sum _{\mathrm{I}\ne \text{K}}\left(\text{d}{M}_{\text{IK}}-{\left(\frac{\partial M_{\text{IK}}}{\partial E_{ij}}\right)}_{{\rho }_L^{\prime }}\text{d}{E}_{ij}\right)A_{\text{IJ}}\right]/D$$ (A3.13)

where D is the determinant

$$D=\left|\frac{\partial M_{\text{IK}}}{\partial {\rho }_{\text{JK}}^{\prime }}\right|$$

and A_IJ is the minor of the $\left(\partial M_{\mathrm{IK}}/\partial {\rho }_{\mathrm{JK}}^{\prime }\right)$ term of D. Replacing $\text{d}{\rho }_I^{\prime }$ by its value in (A3.11) and using the Maxwell relation

$${\left(\frac{\partial T_{ij}}{\partial {\rho }_{\mathrm{I}}^{\prime }}\right)}_{E_{kl}}={\left(\frac{\partial M_{\mathrm{IK}}}{\partial E_{ij}}\right)}_{{\rho }_L^{\prime }}$$ (A3.14)

we get

$${\left(\frac{\partial T_{ij}}{\partial E_{kl}}\right)}_{M_{\mathrm{IK}}}={\left(\frac{\partial T_{ij}}{\partial E_{kl}}\right)}_{{\rho }_{\mathrm{I}}^{\prime }}-\frac{1}{D}\sum _{\mathrm{I}\ne \text{K}}\sum _{\text{J}\ne \text{K}}{\left(\frac{\partial T_{ij}}{\partial {\rho }_{\mathrm{I}}^{\prime }}\right)}_{E_{\text{p}q}}{\left(\frac{\partial T_{ij}}{\partial {\rho }_{\text{J}}^{\prime }}\right)}_{E_{\text{p}q}}{A}_{\text{IJ}}$$ (A3.15)

Using (A3.9), Hooke’s law, and neglecting strain dependent terms we finally get

$$S_{ijkl}^{*}=S_{ijkl}+\frac{1}{\chi }\sum _{\mathrm{I},\mathrm{J}\ne \mathrm{K}}\left(\frac{\partial E_{ij}^c}{\partial c_{\mathrm{I}}}\right)\left(\frac{\partial E_{ij}^c}{\partial c_{\mathrm{J}}}\right)A_{\mathrm{IJ}}$$ (A3.16)

where χ is the determinant

$$\chi ={\rho }_0^{\prime }\left|\frac{\partial M_{\mathrm{IK}}}{\partial c_{\mathrm{J}}}\right|$$

and A_IJ the minor of the (IJ) term of $\chi /{\rho }_0^{\prime }$.

Appendix 4. A Common Tangent Construction

Let ξ^k be three unit vectors normal to each other, such that ξ³ is the normal to the interface, with components ${\xi }_i^k$. The vectors λ^k are defined by

$${\mathrm{\lambda }}_i^k=E_{ij}{\xi }_j^k$$ (A4.1)

Since the determinant $\left|{\xi }_j^k\right|$ has the value 1 the system of equations (A4.1) constitute a valid linear change of variable. Using the chain rule, we obtain, considering the ξ^k as fixed

$${\left(\frac{\partial f^{\prime }}{\partial E_{ij}}\right)}_{E_{kl},\rho \mathrm{j}}=T_{ij}={\left(\frac{\partial f^{\prime }}{\partial {\mathrm{\lambda }}_i^k}\right)}_{{\mathrm{\lambda }}_m^n}{\xi }_j^k$$ (A4.2)

After multiplication by ${\xi }_j^k$ and summation on j one gets

$$T_{ij}{\xi }_j^k={\left(\frac{\partial f^{\prime }}{\partial {\mathrm{\lambda }}_i^k}\right)}_{{\mathrm{\lambda }}_m^n}$$ (A4.3)

Let us define the free energy ζ′ by

$${\zeta }^{\prime }=f^{\prime }-{\mathrm{\lambda }}_i^3\left(\frac{\partial f^{\prime }}{\partial {\mathrm{\lambda }}_i^3}\right)$$ (A4.4)

$$=f^{\prime }-T_{ij}{n}_j{E}_{ik}{n}_k$$ (A4.5)

and it is easy to show that

$$M_{\text{IK}}={\left(\frac{\partial f^{\prime }}{\partial {\rho }_{\mathrm{IK}}^{\prime }}\right)}_{E_{ij}}={\left(\frac{\partial {\zeta }^{\prime }}{\partial {\rho }_{\text{IK}}^{\prime }}\right)}_{{\mathrm{\lambda }}_i^1,{\mathrm{\lambda }}_i^2,T_{ij}{n}_j}$$ (A4.6)

The conditions for equilibrium at an incoherent interface (eq (3.24)) can be written

$$\begin{gathered} {\widehat{f}}^{\alpha }-\mathrm{\Sigma }{\text{c}}_{\mathrm{I}}^{\alpha }\left(\frac{\partial {\widehat{f}}^{\alpha }}{\partial c_{\mathrm{I}}}\right)-T_{ij}^{\alpha }{n}_i^{\alpha }{n}_j^{\alpha }{V}_0^{\prime \alpha } \\ ={\widehat{f}}^{\beta }-\mathrm{\Sigma }{c}_{\mathrm{I}}^{\beta }\left(\frac{\partial {\widehat{f}}^{\beta }}{\partial c_{\mathrm{I}}}\right)-T_{ij}^{\beta }{n}_i^{\beta }{n}_j^{\beta }{V}_0^{\prime \beta } \end{gathered}$$ (A4.7)

where quantities such as $\widehat{f}$ are just $f^{\prime }{V}_0^{\prime }$, i.e., quantities per mole of lattice sites. If the normal pressure is zero, so that T_ijn_j = 0 it becomes equivalent to

$${\widehat{\zeta }}^{\alpha }-\sum c_{\mathrm{I}}^{\alpha }{\left(\frac{\partial {\widehat{\zeta }}^{\alpha }}{\partial c_{\mathrm{I}}}\right)}_{{\mathrm{\lambda }}_i^1,{\mathrm{\lambda }}_i^2}=\widehat{\zeta }-\sum c_{\mathrm{I}}^{\beta }{\left(\frac{\partial {\widehat{\zeta }}^{\beta }}{\partial c_{\mathrm{I}}}\right)}_{{\mathrm{\lambda }}_i^1,{\mathrm{\lambda }}_i^2}$$ (A4.8)

which together with

$$M_{\text{IK}}^{\alpha }=M_{\text{IK}}^{\beta }$$

which can then be written

$${\left(\frac{\partial {\widehat{\zeta }}^{\alpha }}{\partial c_{\mathrm{I}}}\right)}_{{\mathrm{\lambda }}_i^1,{\mathrm{\lambda }}_i^2}=={\left(\frac{\partial {\widehat{\zeta }}^{\beta }}{\partial c_{\text{I}}}\right)}_{{\mathrm{\lambda }}_i^1,{\mathrm{\lambda }}_i^2}$$ (A4.9)

show that c_IK can be obtained by a tangent construction to $\widehat{\zeta }$, which, in this case is just equal to $\widehat{f}$.