Decomposition of the Total Effect in the Presence of Multiple Mediators and Interactions

Abstract

Mediation analysis allows decomposing a total effect into a direct effect of the exposure on the outcome and an indirect effect operating through a number of possible hypothesized pathways. Recent studies have provided formal definitions of direct and indirect effects when multiple mediators are of interest and have described parametric and semiparametric methods for their estimation. Investigating direct and indirect effects with multiple mediators, however, can be challenging in the presence of multiple exposure-mediator and mediator-mediator interactions. In this paper we derive a decomposition of the total effect that unifies mediation and interaction when multiple mediators are present. We illustrate the properties of the proposed framework in a secondary analysis of a pragmatic trial for the treatment of schizophrenia. The decomposition is employed to investigate the interplay of side effects and psychiatric symptoms in explaining the effect of antipsychotic medication on quality of life in schizophrenia patients. Our result offers a valuable tool to identify the proportions of total effect due to mediation and interaction when more than one mediator is present, providing the finest decomposition of the total effect that unifies multiple mediators and interactions.

Mediation analysis allows decomposing a given exposure-outcome association (total effect (TE)) into the effect that operates through one or more intermediate variables of interest (indirect effect) and the effect that is due to other independent mechanisms (direct effect) (1). Defining direct and indirect effects in counterfactual terms has been crucial for overcoming major limitations of the classical approaches to mediation, and the field of causal mediation analysis has rapidly expanded over the last decades (2). Most of the current literature has focused on the situation where one single mediator is of interest. It may often be the case, however, that multiple mediators are simultaneously contributing to the exposure-outcome effect. Daniel et al. (3) have presented the counterfactual definition of all direct and indirect effects that can be theoretically defined when multiple mediators are of interest, and the identification of path-specific effects has been discussed (4). Two alternative estimation procedures, one based on weighting and one based on regression, have been also presented (5).

Investigating direct and indirect effects with multiple mediators can be particularly challenging when multiple exposure-mediator and mediator-mediator interactions are also present. A framework that incorporates multiple mediators together with multiple and potentially high-dimensional interactions has not been fully investigated, and a decomposition that separates interaction and mediation effects in this context is not available. While several papers have investigated path-specific effects and multiple mediators (3–5), none of them have formally included terms of causal interactions between the different components. In the context of one single mediator, VanderWeele (6) showed that the TE can be decomposed into a direct effect, an indirect effect, a proportion due to the exposure-mediator interaction alone, and a proportion due to both interaction and mediation. This finest decomposition of the TE provides the maximum insight to identify and separate the contribution of interaction and mediation when these are simultaneously present in explaining an exposure-outcome effect. We aimed to derive a decomposition of the TE that unifies mediation and interaction when multiple mediators and interactions are present.

We first revise the counterfactual definitions of total, direct, indirect, and interaction effects, in the context of multiple mediators. Next, we introduce a decomposition of the TE that unifies mediation and interaction with 2 mediators. The decomposition is provided for both binary and continuous mediators and exposures. We proceed by discussing the assumptions required for the identification of these effects and presenting the nonparametric empirical analogues for each of the components. We illustrate the properties of the proposed framework for multiple mediators and interactions in a secondary analysis of a pragmatic trial for the treatment of schizophrenia. Finally, we provide an extension of these results to the general situation with more than 2 mediators.

COUNTERFACTUAL DEFINITIONS OF EFFECTS AND INTERACTIONS

Potential outcomes

Let A denote the exposure of interest, Y the outcome, and M₁ and M₂ 2 mediators that may be on the pathway from A to Y and are conditionally independent given a baseline factor C, a potential confounder of the mediators-outcome relationships. Figure 1 depicts the possible causal pathways through which A has an effect on Y.

Figure 1.

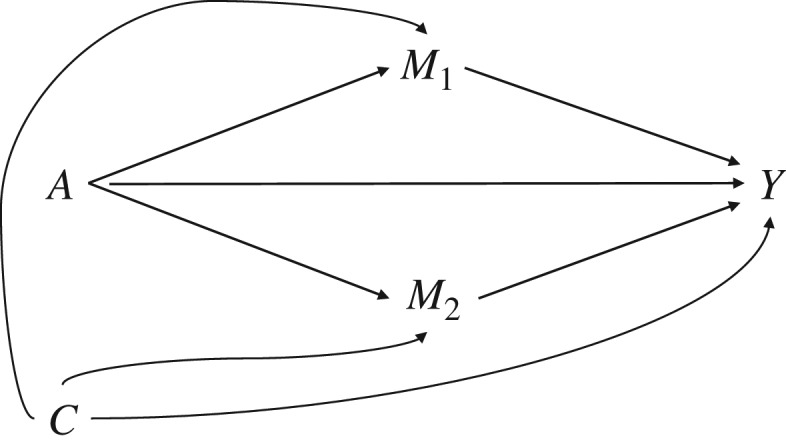
An illustration of mediation analysis with 2 mediators conditionally independent given a baseline factor C.

The generic counterfactuals of interest for the outcome and the mediators can be written as M₁(a), M₂(a), and Y(aM₁(a)M₂(a)), representing, respectively, the value M₁ would take were A set to a, the value M₂ would take were A set to a, and the value Y would take were A set to a, M₁ to M₁(a), and M₂ to M₂(a). In the simplified case of binary exposure and mediators, there is a total of 8 composite outcomes [Y(1M₁(1)M₂(1)), Y(1M₁(1)M₂(0)), Y(1M₁(0)M₂(1)), Y(1M₁(0)M₂(0)), Y(0M₁(1)M₂(1)), Y(0M₁ (1)M₂(0)), Y(0M₁(0)M₂(1)), Y(0M₁(0)M₂(0))] and 8 potential outcomes [Y(111), Y(110), Y(101), Y(001), Y(100), Y(010), Y(001), Y(000)] that could be defined.

Effects definitions

We review here the definitions of mediation contrasts and interaction terms in the case of 2 binary mediators and 1 binary exposure. Extension of these definitions to the general case of continuous exposure and mediators is straightforward, and it only requires setting specific reference values a^*, m₁^*, m₂^*. By following the definition and notation introduced in the context of one single mediator (6–8), we can define the TE of A on Y as:

$$\begin{array}{c}\mathrm{TE}=Y(1)-Y(0)=Y(\mathrm{1}{M}_{\mathrm{1}}(1)M_{\mathrm{2}}(1))\hfill \\ -Y(\mathrm{0}{M}_{\mathrm{1}}(0)M_{\mathrm{2}}(0))\mathrm{.}\hfill \end{array}$$

The controlled direct effect (CDE), regardless of the number of mediators involved, retains its interpretation as the effect of A on Y if both the mediators are fixed to a specific value. In the binary case, CDE can be defined across 4 different strata. Throughout the paper we will refer to the strata where both binary mediators are set to the referent value 0:

$$\mathrm{CDE}\left(\mathrm{0},\mathrm{0}\right)=Y(\mathrm{100})-Y(\mathrm{000})\mathrm{.}$$

In terms of differences in composite potential outcomes, the pure natural direct effect (PNDE) can be defined as the effect of A on Y if both the mediators are set on the value they would naturally take at the referent value of the exposure (i.e., 0):

$$\mathrm{PNDE}=Y(\mathrm{1}{M}_{\mathrm{1}}(0)M_{\mathrm{2}}(0))-Y(\mathrm{0}{M}_{\mathrm{1}}(0)M_{\mathrm{2}}(0))\mathrm{.}$$

The pure natural indirect effect (PNIE) is intuitively defined as the effect of the mediator in the absence of exposure. When 2 independent mediators are of interest, it can be further divided into 3 components. The effect of M₁ in the absence of both A and M₂:

$${\mathrm{PNIE}}_{M_1}=Y(\mathrm{0}{M}_{\mathrm{1}}(1)M_{\mathrm{2}}(0))-Y(\mathrm{0}{M}_{\mathrm{1}}(0)M_{\mathrm{2}}(0))\mathrm{.}$$

The effect of M₂ in the absence of both A and M₁:

$${\mathrm{PNIE}}_{M_{\mathrm{2}}}=Y(\mathrm{0}{M}_{\mathrm{1}}(0)M_{\mathrm{2}}(1))-Y(\mathrm{0}{M}_{\mathrm{1}}(0)M_{\mathrm{2}}(0))\mathrm{.}$$

The combined effect of M₂ and M₁ in the absence of A:

$${\mathrm{PNIE}}_{M_{\mathrm{1}}{M}_{\mathrm{2}}}=Y(\mathrm{0}{M}_{\mathrm{1}}(1)M_{\mathrm{2}}(1))-Y(\mathrm{0}{M}_{\mathrm{1}}(0)M_{\mathrm{2}}(0))\mathrm{.}$$

PNDE, ${\mathrm{PNIE}}_{M_1}$, ${\mathrm{PNIE}}_{M_2}$ are defined by changing one of the 3 arguments (A, M₁(a), M₂(a), respectively) from the reference value, while leaving the other 2 arguments fixed. ${\mathrm{PNIE}}_{M_{\mathrm{1}}{M}_{\mathrm{2}}}$ is defined by changing 2 of the arguments (M₁ and M₂) and leaving the other (A) fixed. Fixed arguments could be set either to the referent or to the alternative value, if binary, or to any potential value if continuous. Here we are showing, and in the next sections using, the definitions of PNDE and PNIE where the fixed arguments are left to the reference value. We refer to previous publications for the description of all other possible definitions in the context of multiple mediators (3).

Interaction definitions

Evaluating a mediation model with 2 potential mediators increases the number of interactions that need to be assessed. The exposure can interact with the first mediator or with the second mediator, and the 2 mediators can interact within each other, thus requiring the specification of 3 2-way interactions (i.e., A·M₁, A·M₂, and M₁·M₂). In addition, all components can interact within each other, so that a measure of 3-way interaction (i.e., A·M₁·M₂) must be specified. Following the classical notation, measures of 2-way interactions, on the additive scale, can be defined by taking the differences between the combined effect and the sum of the 2 main effects of interest (9). Each of these measures can be further specified in both the presence and the absence of the third component (Table 1).

Table 1.

Illustration of the Possible Definitions of 2-Way Interactions With 1 Binary Exposure and 2 Binary Mediators

Varying Argument	Interaction Definition
A·M1 varying, M2 = 1	p(111) − p(101) − p(011) + p(001)
A·M1 varying, M2 = 0	p(110) − p(100) − p(010) + p(000)
A·M2 varying, M1 = 1	p(111) − p(110) − p(011) + p(010)
A·M2 varying, M1 = 0	p(101) − p(100) − p(001) + p(000)
M1·M2 varying, A = 1	p(111) − p(110) − p(101) + p(100)
M1·M2 varying, A = 0	p(011) − p(010) − p(001) + p(000)

Abbreviations: A, exposure of interest; M, potential mediator.

A measure of additive 3-way interaction can be defined in 3 different ways:

• the change in the product A·M₁ when M₂ goes from absent to present: (p(111) – p(101) – p(011) + p(001) > p(110) – p(100) – p(010) + p(000));

• the change in the product A·M₂ when M₁ goes from absent to present: (p(111) – p(110) – p(011) + p(010) > p(101) – p(100) – p(001) + p(000)); or

• the change in the product M₁·M₂ when A goes from absent to present: (p(111) – p(110) – p(101) + p(100) > p(011) – p(010) – p(001) + p(000)).

All these definitions yield the same measure of 3-way interaction on the additive scale:

$$\begin{array}{c}p(111)-p(110)-p(101)+p(100)+p(011)\hfill \\ -p(010)-p(001)+p(000).\hfill \end{array}$$

As for the classical 2-way interaction on the additive scale, depending on whether this measure is smaller than, equal to, or larger than 0, we can define a situation of 3-way subadditivity, additivity, or superadditivity, respectively.

DECOMPOSITION OF THE TOTAL EFFECT

When one single mediator M is evaluated, it has been shown that the TE can be decomposed into 4 components that detect mediation mechanisms through M and interactive effects between M and the exposure (6). Specifically, the TE can be decomposed into a component that is due neither to interaction nor to mediation (corresponding to the CDE), a component due only to mediation (corresponding to the PNIE), a component due only to the additive interaction between the exposure and the mediator (defined reference interaction, or INTref), and a component due to both mediation and interaction, defined as an additive interaction that operates only if the mediator has an effect on the outcome (defined mediated interaction, or INTmed). When moving to the situation of 2 mediators simultaneously contributing to the A-Y association (Figure 1), a 4-way decomposition of the TE is still valid. In such context, however, the PNIE, the INTref, and the INTmed, can be additionally decomposed into 3 components each, capturing effects that operate through specific pathways and interactions. Specifically:

$$\begin{array}{c}\mathrm{TE}{=\mathrm{CDE}+\mathrm{PNIE}}_{M_{\mathrm{1}}}{+\mathrm{PNIE}}_{M_{\mathrm{2}}}{+\mathrm{PNIE}}_{M_{\mathrm{1}}{M}_{\mathrm{2}}}\hfill \\ +\mathrm{INT}re{f}_A{\cdot }_{M_{\mathrm{1}}}+\mathrm{INT}re{f}_A{\cdot }_{M_{\mathrm{2}}}+\mathrm{INT}re{f}_A{\cdot }_{M_{\mathrm{1}}}{\cdot }_{M_{\mathrm{2}}}\hfill \\ +\mathrm{INT}me{d}_A{\cdot }_{M_{\mathrm{1}}}+\mathrm{INT}me{d}_A{\cdot }_{M_{\mathrm{2}}}+\mathrm{INT}me{d}_A{\cdot }_{M_{\mathrm{1}}}{\cdot }_{M_{\mathrm{2}}}\hfill \end{array}.$$ (1)

The definition of each component is presented in Table 2. A complete proof of the derivation of equation 1 is provided in Web Appendix 1 (available at https://academic.oup.com/aje). In brief, the derivation uses PNDE and ${\mathrm{PNIE}}_{M_{\mathrm{1}}{M}_2}$, as defined earlier in the text in terms of differences of composite potential outcomes, and calculates the operationalized version of all effects in terms of differences of potential outcomes, operating only under specific scenarios.

Table 2.

Illustration of the Decomposition of the Total Effect of a Binary Exposure on an Outcome, in the Presence of 2 Binary Mediators, Exposure-Mediators, and Mediator-Mediator Interactions

Component	Definition
CDE	(Y(100)) − Y(000))
${\mathrm{PNIE}}_{M_{\mathrm{1}}}$	(Y(010)) − Y(000)) [M1(1)) − M1(0)]a
${\mathrm{PNIE}}_{M_{\mathrm{2}}}$	(Y(001)) − Y(000)) [M2(1)) − M2(0)]b
${\mathrm{PNIE}}_{M_{\mathrm{1}}{M}_{\mathrm{2}}}$	(Y(011)) − Y(010)) − Y(001) + Y(000)) [M1(1)M2(1)) − M1(0)M2(0)]
$\mathrm{INT}re{f}_A{\cdot }_{M_{\mathrm{1}}}$	(Y(110)) − Y(100)) − Y(010) + Y(000)) [M1(0)]
$\mathrm{INT}re{f}_A{\cdot }_{M_{\mathrm{2}}}$	(Y(101)) − Y(100)) − Y(001) + Y(000)) [M2(0)]
$\mathrm{INT}re{f}_A{\cdot }_{M_{\mathrm{1}}}{\cdot }_{M_{\mathrm{2}}}$	(Y(111)) − Y(110)) − Y(101)) − Y(011) + Y(001) + Y(010) + Y(100)) − Y(000)) [M1(0)M2(0)]
$\mathrm{INT}me{d}_A{\cdot }_{M_{\mathrm{1}}}$	(Y(110)) − Y(100)) − Y(010) + Y(000)) [M1(1)) − M1(0)]
$\mathrm{INT}me{d}_A{\cdot }_{M_{\mathrm{2}}}$	(Y(101)) − Y(100)) − Y(001) + Y(000)) [M2(1)) − M2(0)]
$\mathrm{INT}me{d}_A{\cdot }_{M_{\mathrm{1}}}{\cdot }_{M_{\mathrm{2}}}$	(Y(111)) − Y(110)) − Y(101)) − Y(011) + Y(001) + Y(010) + Y(100)) − Y(000)) [M1(1)M2(1)) − M1(0)M2(0)]

Abbreviations: A, exposure of interest; CDE, controlled direct effect; INTref, defined reference interaction; INTmed, defined mediated interaction; M, possible mediator; PNIE, pure natural indirect effect; Y, outcome.

^aM₁(1) = I[M₁(1) = m₁], M₁(0) = I[M₁(0) = m₁].

^bM₂(1) = I[M₂(1) = m₂], M₂(0) = I[M₂(0) = m₂].

The first component of the decomposition is the CDE. The component of the effect due only to mediation (PNIE) is divided into: 1) the effect of M₁ when both A and M₂ are absent $\left({\mathrm{PNIE}}_{M_{\mathrm{1}}}\right)$ and A has an effect on M₁ so that change in M₁ captures an exposure-induced change; 2) the effect of M₂ when both A and M₁ are absent $\left({\mathrm{PNIE}}_{M_{\mathrm{2}}}\right)$ and A has an effect on M₂ so that change in M₂ captures an exposure-induced change; and 3) an additional component of the indirect effect (taking the form of an additive interaction between M₁ and M₂) that is active only when both M₁ and M₂ have an effect in the absence of the exposure. The component due to interaction alone (INTref) is divided into: 1) the 2-way interaction between A and M₁ when M₂ is absent $\left(\mathrm{INT}{\mathit{\text{ref}}}_A{\cdot }_{M_{\mathrm{1}}}\right)$; 2) the 2-way interaction between A and M₂ when M₁ is absent $\left(\mathrm{INT}re{f}_A{\cdot }_{M_{\mathrm{2}}}\right)$; and 3) the 3-way interaction between A, M₁, and M₂$\left(\mathrm{INT}re{f}_A{\cdot }_{M_{\mathrm{1}}}{\cdot }_{M_{\mathrm{2}}}\right)$. These components, respectively, operate only when the first mediator is present in the absence of exposure (i.e., M₁(0) = 1), when the second mediator is present in the absence of exposure (i.e., M₂(0) = 1), and when both mediators are present in the absence of exposure (i.e., M₁(0) = 1 and M₂(0) = 1). The component due to both mediation and interaction (INTmed) is divided into the same 3 components of INTref. However, these, respectively, are active only when M₁ affects the outcome when A is absent and A itself affects M₁, when M₂ affects the outcome when A is absent and A itself affects M₂, and when M₁ and M₂ have a combined effect on the outcome when A is absent and A itself affects both M₁ and M₂.

Definition of the components in the case of continuous exposure and mediators is also provided in Web Appendix 2 and Web Table 1.

It is straightforward to observe that the decomposition presented here is a natural extension of the 4-way decomposition introduced by VanderWeele (6) in the single mediator setting. With one single mediator, say M₁, all components including M₂ would be null, and the decomposition would reduce to $\mathrm{TE}=\mathrm{CDE}+{\mathrm{PNIE}}_{M_1}+\mathrm{INT}re{f}_A{\cdot }_{M_{\mathrm{1}}}+\mathrm{INT}me{d}_A{\cdot }_{M_{\mathrm{1}}}$. Additional decompositions presented in the context of a single mediator can also be extended to our setting. For example, we could calculate the proportion of effect attributable to interaction (PAI = INTref + INTmed), and the total indirect effect (TIE = INTmed + PNIE) (10, 11). Both of these measures could be further decomposed if we were interested in the proportion attributable to the interaction between the exposure and one specific mediator (e.g., ${\mathrm{PAI}}_A{\cdot }_{M_{\mathrm{1}}}=\mathrm{INT}re{f}_A{\cdot }_{M_{\mathrm{1}}}+\mathrm{INT}me{d}_A{\cdot }_{M_{\mathrm{1}}}$). It is also of interest to note that, while previous studies obtained multiple decompositions of the TEs (3), by accounting for the possible interactions between exposure and mediators, we obtained a single unique decomposition.

IDENTIFICATION OF THE EFFECTS

Individual values for each component, as they are defined within the counterfactual framework, cannot be estimated. However, all components of equation (1) can be correctly identified and estimated at the population level under specific assumptions (12).

To identify the CDE, control must be made for a covariate set C that includes all confounders of not only the exposure-outcome relationship but also the mediator-outcome relationships. We formally require that, conditional on C, there be no unmeasured confounding for the exposure-outcome relationship (assumption 1), and no unmeasured confounding for the mediator-outcome relationship conditional on (A, C) (assumption 2). Identification of natural direct and indirect effects requires 2 additional assumptions to hold. First, conditional on C, there must be no unmeasured confounding of the exposure-mediator relationships (assumption 3). Second, there must be no effect of exposure A that itself affects both M and Y (i.e., no mediator-outcome confounder that is itself affected by the exposure) (assumption 4) (13, 14). Assumptions 2, 3, and 4 are required to hold for all mediators included in the analysis. Formally we can write the assumptions as: 1) Y(am₁m₂)⊥A|C; 2) Y(am₁m₂)⊥M₁|[A,C], Y(am₁m₂)⊥M₂|[A,C]; 3) M₁⊥A|C, M₂⊥A|C; 4) Y(am₁m₂)⊥M₁(a)^*|C, Y(am₁m₂)⊥ M₂(a)^*|C.

When these assumptions hold, the average value of each component of the decomposition is given by the empirical expressions presented in Table 3. In Web Appendix 3, we present a simulation study empirically proving the results of our decomposition and the calculation of these empirical analogues. The Web Material also includes the empirical analogues for the nonparametric estimation of the components with continuous exposure and mediators (Web Table 2).

Table 3.

Illustration of the Empirical Analogues for the Components of the Total Effect Decomposition With 1 Binary Exposure and 2 Binary Mediators

Component	Empirical Analogues
CDE	(p(100) − p(000))a
${\mathrm{PNIE}}_{M_{\mathrm{1}}}$	(p(010) − p(000)) [P(M1 = 1|A = 1) − P(M1 = 1|A = 0)]
${\mathrm{PNIE}}_{M_{\mathrm{2}}}$	(p(001) − p(000)) [P(M2 = 1|A = 1) − P(M2 = 1|A = 0)]
${\mathrm{PNIE}}_{M_{\mathrm{1}}{M}_{\mathrm{2}}}$	(p(011) − p(010) − p(001) + p(000)) [P(M2 = 1, M2 = 1|A = 1) − P(M1 = 1, M2 = 1|A = 0)]
$\mathrm{INT}re{f}_A{\cdot }_{M_{\mathrm{1}}}$	(p(110) − p(100) − p(010) + p(000))P(M2 = 1|A = 0)
$\mathrm{INT}re{f}_A{\cdot }_{M_{\mathrm{2}}}$	(p(101) − p(100) − p(001) + p(000))P(M2 = 1|A = 0)
$\mathrm{INT}re{f}_A{\cdot }_{M_{\mathrm{1}}}{\cdot }_{M_{\mathrm{2}}}$	(p(111) − p(110) − p(101) + p(100) + p(011) − p(010) − p(001) + p(000))P(M1 = 1, M2 = 1|A = 0)
$\mathrm{INT}me{d}_A{\cdot }_{M_{\mathrm{1}}}$	(p(110) − p(100) − p(010) + p(000)) [P(M1 = 1|A = 1) − P(M1 = 1|A = 0)]
$\mathrm{INT}me{d}_A{\cdot }_{M_{\mathrm{2}}}$	(p(101) − p(100) − p(001) + p(000)) [P(M2 = 1|A = 1) − P(M2 = 1|A = 0)]
$\mathrm{INT}me{d}_A{\cdot }_{M_{\mathrm{1}}}{\cdot }_{M_{\mathrm{2}}}$	(p(111) − p(110) − p(101) + p(100) + p(011) − p(010) − p(001) + p(000))[P(M1 = 1, M2 = 1|A = 1) − P(M1 = 1, M2 = 1|A = 0)]

Abbreviations: A, exposure of interest; CDE, controlled direct effect; INTref, defined reference interaction; INTmed, defined mediated interaction; M, possible mediator; PNIE, pure natural indirect effect; Y, outcome.

^ap_am1m2 = E(Y|A = a; M₁ = m₁; M₂ = m₂).

ILLUSTRATION

To illustrate the concepts and methods presented above we used an example from psychiatric epidemiology. Antipsychotic treatments are generally divided into first-generation (typical) and second-generation (atypical) medications. Several observational and clinical studies have attempted to elucidate the efficacy and effectiveness of atypical antipsychotics in comparison both with placebo and with first-generation antipsychotics (15). Moderate improvement in schizophrenia symptoms, such as those assessed by the Positive and Negative Syndrome Scale (PANSS) (16), have been observed (17), but new-generation medications also showed consistently higher rates of side effects such as excessive weight gain (18). Among patients affected by psychotic disorders, schizophrenia patients display the highest deficit in social functioning. The ability of typical and atypical agents to improve social functioning has not been fully explored. To take into account the complex effects of antipsychotics and clarify the relative effect on patients’ social functioning, it is critical to investigate the interplay of treatment, symptoms, and side effects over the course of treatment. Here we focused on a specific atypical medication (olanzapine), which has been claimed to be the most effective antipsychotic medication but is also associated with the most severe metabolic side effects, especially in terms of weight gain (19, 20). We used data from the Clinical Antipsychotic Trials of Intervention Effectiveness (CATIE) (21) to evaluate the effect of olanzapine as compared to a typical agent (perphenazine), on individual quality-of-life scores that capture level of social activity, involvement in social network, and social initiatives. We employed the effect decomposition to assess the mediating and interactive role of percent weight gain, PANSS symptoms, and extrapyramidal symptoms (EPS, the most frequent neurological adverse events induced by first-generation antipsychotics).

For this example, we included data from 497 patients in the CATIE trial assigned to either olanzapine (n = 336) or perphenazine (n = 161). The continuous outcome (quality-of-life score, ranging from 0 to 18 with higher score representing better condition) was assessed 9 months after the beginning of the study. The 3 continuous mediators (weight gain (in pounds), EPS symptoms (ranging from 0 to 1.67), and PANSS total score (ranging from 30 to 116)) were assessed after 6 months from the beginning of the study. Analyses were adjusted for sex, age, race/ethnicity, education, employment, marital status, systolic and diastolic blood pressure, prior treatment, hospitalization, waist-hip ratio, body mass index, PANSS total score, and EPS symptoms measured at baseline. We used the parametric procedure for multiple mediators as presented by VanderWeele and Vansteelandt (5), using linear regression models for both outcome and mediators, and used R (R Foundation for Statistical Computing, Vienna, Austria) to implement our decomposition.

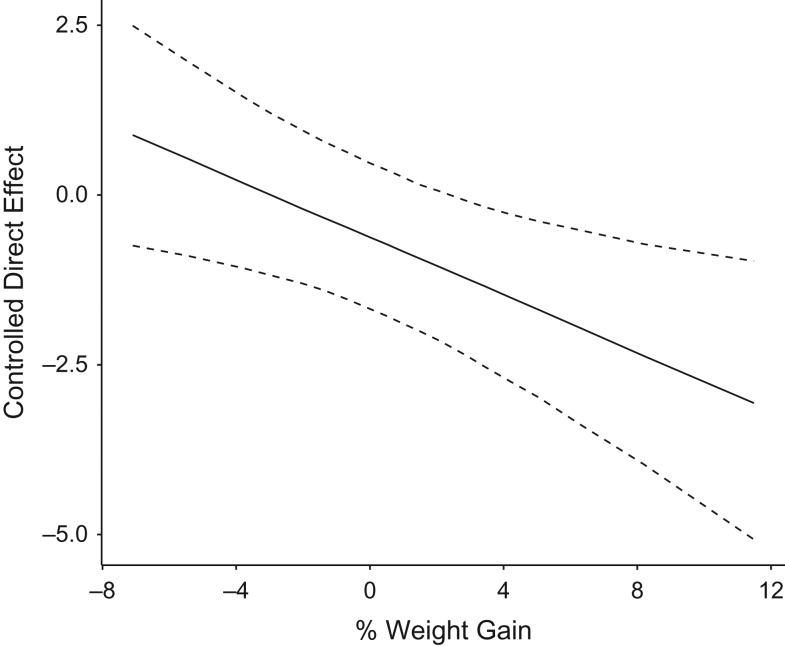
Overall, in the exposure-outcome model not adjusting for the mediators (TE), a nonsignificant lower quality-of-life score at 9 months was observed (TE = −0.45, 95% CI: −1.45, 0.51) between patients treated with olanzapine and those with perphenazine. Results from the 4-way decomposition are presented in Table 4. We found a significant interaction between weight gain and treatment, whereby increase in weight appeared to increase quality of life among patients treated with perphenazine while it reduced quality of life among patients treated with olanzapine. Interactive and mediated effects summed up to the TE previously estimated and are suggestive of a complex interplay among the factors under study. The CDE showed that had the patient experienced no weight gain and no PANSS or EPS symptoms, the atypical treatment’s effect on quality of life score would still not be significantly different from the typical antipsychotic (CDE = −0.63, 95% CI: −1.68, 0.41). However, if we still assumed that the patient did not experience any positive PANSS or EPS symptoms, but that the patient experienced moderate to severe weight gain (>4% increase), olanzapine would yield a significantly lower quality of life (Figure 2). The relationship between weight gain and treatment also appears to be complex. While the indirect effect is positive and significant (PNIE_WG = 0.81, 95% CI: 0.20, 1.58), the mediated interaction is significant and negative (INTmed_WG = −0.85, 95% CI: −1.67, −0.20). This indicates that mediating and interactive mechanisms operate in opposite directions. Perhaps this result is due to the fact that weight gain is a proxy of treatment efficacy through neurological pathways related to glucose metabolism.

Table 4.

Decomposition of the Treatment Effect on Quality of Life Scores for Social Functioning Into Direct Effect and Mediated and Interactive Effects Due to Weight Gain (M₁), Positive and Negative Syndrome Scale Total Symptoms (M₂), and Extrapyramidal Symptoms (M₃), Using Data From the Clinical Antipsychotic Trials of Intervention Effectiveness, United States, 2000–2004

Component	Estimate	95% CI
CDE	−0.63	−1.68, 0.41
PNIEWG	0.81	0.20, 1.58
PNIEPANSS+	0.00	0.16, 0.17
PNIEEPS	0.35	0.05, 1.11
INTrefA·WGb	−0.18	−0.90, 0.33
INTmedA·WGb	−0.85	−1.67, −0.20
NDE	−0.81	−2.10, 0.34
NIE	0.35	−0.26, 1.20
TE	−0.45	−1.45, 0.51

Abbreviations: CDE, controlled direct effect; CI: confidence interval; EPS, extrapyramidal symptoms; INTref, defined reference interaction; INTmed, defined mediated interaction; NDE, natural direct effect; NIE, natural indirect effect; PANSS, Positive and Negative Syndrome Scale; PNIE, pure natural indirect effect; TE, total effect.

^a Bootstrap 95th percentile CI.

^b PNIE_WG·_PANSS+, PNIE_WG·_EPS, PNIE_PANSS+·_EPS, PNIE_WG·_PANSS+·_EPS null because no mediator-mediator interaction. INTref_A·_PANSS+, INTref_A·_EPS, INTref_A·_WG·_PANSS+, INTref_A·_WG·_EPS, INTref_A·_PANSS+·_EPS, INTref_A·_WG·_PANSS+·_M3, INTmed_A·_PANSS+, INTmed_A·_EPS, INTmed_A·_WG·_PANSS+, INTmed_A·_WG·_EPS, INTmed_A·_PANSS+·_EPS, INTmed_A·_WG·_PANSS+·_EPS null because no interaction between treatment and positive PANSS and EPS symptoms and no 3- or 4-way interactions.

^c NDE = CDE + INTref term.

^d NIE = PNIE terms + INTmed term.

^e TE = NDE + NIE.

Figure 2.

An illustration of the controlled direct effect of olanzapine relative to perphenazine on quality-of-life score, fixing Positive and Negative Syndrome Scale total score and extrapyramidal symptoms score at zero, while fixing percent weight gain from −7% to 11%, using data from the Clinical Antipsychotic Trials of Intervention Effectiveness, United States, 2000–2004. Dashed lines represent 95% confidence intervals.

Symptoms do not appear to play a major role, given that no differences between first- and second-generation antipsychotics were observed (PNIE_{Positive symptoms} = 0.00, 95% CI: −0.16, 0.17). EPS symptoms significantly mediate the association between treatment and quality of life, whereby reduction in EPS symptoms in patients treated with olanzapine leads to an improvement in quality of life (PNIE_EPS = 0.35, 95% CI: 0.05, 1.11). By combining pure indirect effect and mediated interaction, we obtain a positive indirect effect, which is driven mostly by the pathway through reduction in EPS symptoms.

EXTENSION TO THE GENERAL CASE OF n MEDIATORS

Extending the 4-way decomposition of the TE to the general case of more than 2 mediators is theoretically straightforward but requires defining an increasingly higher number of components. In the Web Material, we provide the illustration of such decomposition in the case of 3 mediators (Web Table 3). A decomposition of the TEs into the 4 components can always be identified. The CDE(0, . . . ,0) always retains its interpretation as the effect of the exposure by setting all n mediators at 0 (or at their reference values if continuous). The 3 other components are further divided into 2ⁿ − 1 parts detecting effects operating through all the specific pathways. The scenario previously presented, with n = 2 mediators, may be seen as a special case of this general decomposition (with PNIE, INTref, and INTmed, divided into 2² − 1 = 3 components each). The main caveat in extending the decomposition to the general case of n mediators is that a measure of n-way interaction on the additive scale should be defined. This can be done by fixing n − 1 components and evaluating the change when the nth component moves from present to absent. For instance, with 3 mediators we can evaluate the change in A·M₁·M₂ when M₃ goes from present to absent as p(1111) − p(1101) − p(1011) p(0111) + p(1001) + p(0101) + p(0011) − p(0001) > p(1110) − p(1100) − p(1010) − p(0110) + p(1000) + p(0100) + p(0010) − p(0000). Regardless of which of the n components is let to vary, these comparisons will always yield the same measure of n-way interaction. In the case of 3 mediators, this is equal to p(1111) − p(1101) − p(1011) − p(0111) + p(1001) + p(0101) + p(0011) − p(0001) + p(1110) − p(1100) − p(1010) − p(0110) + p(1000) + p(0100) + p(0010) − p(0000).

The decomposition that we described in the context of 2 mediators assumes that M₁ and M₂ are conditionally independent given a baseline factor C. As the number of mediators increases, finding a set of confounders that satisfies this assumption may not be feasible, and assuming dependency (i.e., sequentially) between sets of mediators may be required. Evaluating sequential mediators, however, poses critical challenges for the identifiability of the components of the decomposition (with the exception of the CDE, which is always identifiable), because mediator-outcome confounding induced by the exposure is introduced, thus violating assumption 4. Methods for the identification of path-specific effects in the context of sequential mediators, including the use and definition of randomized interventional analogues (22), have been recently described (4). Extending these methods to take high-dimension interactions into account is beyond the scope of this work and is a primary goal of future work.

FINAL REMARKS

In this work, we derived a decomposition of the TE that unifies mediation and interaction when multiple mediators are present. We showed that a 4-way decomposition of the TE into 1) a direct effect, 2) an indirect effect, 3) a component due to interaction, and 4) a component due to mediation and interaction can always be derived. Components 2–4 are further divided into subcomponents that identify indirect effects and interactions that operate through specific pathways. This decomposition provides useful advantages for practical application because it allows the investigator, given a TE, to distinguish the proportion due to mediation effects and the proportion due to interaction components. As shown in our illustration, this decomposition may be a valuable tool for situations in which several interactions, both synergistic and antagonistic, may be hypothesized on the evaluated causal pathway.

This decomposition is a natural extension of the 4-way decomposition presented in the context of a single mediator, which can be viewed as a particular case of that presented here. The classical assumptions for the identification of direct and indirect effects are also required for identification of the components of the 4-way decomposition, and they should be assessed for every newly included mediator. We showed that currently available parametric regression approaches can easily be extended to estimate the decomposition (see code in the Web Material). As the number of mediators increases, the definition, identification, and estimation of the components become challenging. Future studies focusing on high-dimension mediation and interaction are required and would represent a major contribution to the field. Also, the high number of mediators may hamper the efficiency of currently available estimation methods for multiple mediators. Alternative procedures, especially semiparametric methods, should be developed and integrated into statistical software. Additional research is also needed to evaluate the robustness of the components to residual confounding, extending current sensitivity-analysis techniques (23, 24) to the specific components of the decomposition.

In conclusion, we have presented a decomposition that identifies the proportions of TE due to mediation and interaction when more than 1 mediator is present. The decomposition can be used to identify the extent to which the TE would be changed by intervening on 1 or more mediators, and to exploit the mechanism through which the TE is generated, thus providing a valuable tool to understand the interplay of multiple factors in explaining a given exposure-outcome effect.

Abbreviations

CDE

controlled direct effect

EPS

extrapyramidal symptoms

PANSS

Positive and Negative Syndrome Scale

PNDE

pure natural direct effect

PNIE

pure natural indirect effect

TE

total effect