Inferring time-dependent migration and coalescence patterns from genetic sequence and predictor data in structured populations

Abstract

Population dynamics can be inferred from genetic sequence data by using phylodynamic methods. These methods typically quantify the dynamics in unstructured populations or assume migration rates and effective population sizes to be constant through time in structured populations. When considering rates to vary through time in structured populations, the number of parameters to infer increases rapidly and the available data might not be sufficient to inform these. Additionally, it is often of interest to know what predicts these parameters rather than knowing the parameters themselves. Here, we introduce a method to  infer the predictors for time-varying migration rates and effective population sizes by using a generalized linear model (GLM) approach under the marginal approximation of the structured coalescent. Using simulations, we show that our approach is able to reliably infer the model parameters and its predictors from phylogenetic trees. Furthermore, when simulating trees under the structured coalescent, we show that our new approach outperforms the discrete trait GLM model. We then apply our framework to a previously described Ebola virus dataset, where we infer the parameters and its predictors from genome sequences while accounting for phylogenetic uncertainty. We infer weekly cases to be the strongest predictor for effective population size and geographic distance the strongest predictor for migration. This approach is implemented as part of the BEAST2 package MASCOT, which allows us to jointly infer population dynamics, i.e. the parameters and predictors, within structured populations, the phylogenetic tree, and evolutionary parameters.

1. Introduction

Genetic sequence data can be used to reconstruct the shared evolutionary history, i.e. the phylogenetic tree, of pathogens. These trees are shaped by migration and transmission dynamics, and thus these dynamics should be quantifiable from the trees by using phylodynamic methods. Phylodynamic methods, however, typically assume that all sequences are from the same well-mixed population.

Methods that account for population structure, such as the structured coalescent (Takahata 1988; Hudson 1990; Notohara 1990), allow us to infer how lineages coalesce within and migrate between sub-populations. This is done by inferring effective population sizes and migration rates, with the effective population sizes being related to transmission dynamics (Volz et al. 2009). Even when only considering constant parameters through time, the number of parameters to estimate grows quadratically with the number of sub-populations. When additionally allowing these parameters to change through time by using piecewise constant rate approaches (also referred to as skyline approaches), this number has to be multiplied by the number of time intervals considered. However, the information encoded within a single phylogenetic tree can be too limited to inform all these parameters. This problem is not only limited to the structured coalescent process but also applies to structured birth-death models (Stadler and Bonhoeffer 2013; Kühnert et al. 2016).

Alternatively, one can make use of additional data, such as transportation data, that potentially predict these parameters by using generalized linear models (GLMs) in a discrete trait analysis (DTA), which we call DTA–GLM in this paper (Lemey et al. 2014). This has, for example, been done to study the cross-species transmission of bat rabies virus (Faria et al. 2013) or the spatial spread of dog rabies virus through rural Tanzania (Brunker et al. 2017). It was further used to study Ebola virus dissemination throughout West Africa (Dudas et al. 2017) or the spread of Dengue virus in the Americas (Nunes et al. 2014). The same approach has also been used to inform effective population sizes through time in unstructured populations (Gill et al. 2016).

The underlying migration model (Lemey et al. 2009) used in these structured models, although computationally feasible, relies on simplifying assumptions of the tree generating process. Namely, it is assumed that the process which generated the phylogenetic tree is independent from the migration process. This in turn can lead to biased estimates of migration rates, e.g. when sampling is biased (De Maio et al. 2015). Additionally, since only the migration process is modelled, the coalescent process and thus the transmission dynamics in different sub-populations cannot be quantified.

The structured coalescent (Takahata 1988; Hudson 1990; Notohara 1990) does not make this independence assumption. This enables us to model the tree generating process by using coalescence within and migration between sub-populations. It, however, only allows considering a very limited number of different sub-populations (Vaughan et al. 2014), due to computational issues (De Maio et al. 2015). The GLM approach can therefore not be readily used within the structured coalescent framework.

In order to allow for structured models with many different sub-populations and parameters that change through time, approximations to the structured coalescent have been developed (Volz 2012). Such approaches avoid the sampling of migration histories by formally integrating over every possible migration history, allowing to consider scenarios with more parameters (De Maio et al. 2015). They have, however, been subject to strong biases due to simplifying assumptions that were initially not accounted for (Müller, Rasmussen, and Stadler 2017). The marginal approximation of the structured coalescent (MASCOT) on the other hand allows integrating over every possible migration history, avoiding such biases (Müller, Rasmussen, and Stadler 2017, 2018). This marginal approximation allows us to consider datasets with many different sub-populations.

Here, we introduce a GLM approach similar to Lemey et al. (2014) coupled with the marginal approximation of the structured coalescent (MASCOT-GLM). We infer the time varying effective population sizes of and the migration rates between different sub-populations from predictor and sequence data, with predictor data characterizing one location (e.g. population size, location) or how two locations are connected (e.g. transportation, distance). These predictors may describe differences of effective population sizes of different sub-populations or migration rate differences between sub-populations. Similar to Lemey et al. (2014), we define the migration rates as log-linear combinations of coefficients, indicators and time varying predictors. We further employ the same definition for the effective population sizes. Some previously used predictors for migration rates include air traffic data between different locations (Lemey et al. 2014; Nunes et al. 2014) and distances between them (Dudas et al. 2017). The indicators and coefficients quantify if and to what degree each predictor contributes in predicting effective population size or migration rate differences across different sub-populations and points in time. Whereas the use of indicators is not strictly necessary, they allow us to use priors on the number of active predictors, thereby helping to reduce over-fitting. We implemented this approach as part of the BEAST2 (Bouckaert et al. 2012) package MASCOT (Müller et al. 2018). This implementation allows us to co-infer indicators and coefficients from genetic sequence and predictor data alongside phylogenetic trees and evolutionary parameters.

By using simulations, we show that we are able to retrieve the extent to which each predictor informs the population dynamics parameters. We then apply our GLM approach to a subset of sequence data from the West African Ebola virus (EBOV) dataset (Dudas et al. 2017). This subset is comprised of lineages descended from the major introduction of EBOV into Sierra Leone (Dudas et al. 2017), further down-sampled to only sequences collected in 2014. The Sierra Leonean lineage was sustained via intense endemic transmission, making it the dominant EBOV lineage in the entire epidemic (Dudas et al. 2017). Following its introduction into Sierra Leone this lineage was also the source of EBOV in neighbouring Liberia and Guinea in the late stages of the epidemic (Dudas et al. 2017). Using the example of Ebola, we demonstrate that our approach is able to retrieve reasonable predictors for the migration rates and effective population sizes.

2. Results

2.1 Inference of predictor contributions from phylogenetic trees

We first tested how well indicators and coefficients can be inferred from phylogenetic trees. To do so, we randomly simulated ten time-varying migration rate and ten time-varying effective population size predictors for five different sub-populations. Each value of each predictor at every point in time was drawn from a normal distribution with mean = 0 and σ = 1. This means that different values of the predictors were sampled independently of one another. As in Lemey et al. (2014), we standardized each predictor to have mean 0 and standard deviation 1. Next, we randomly sampled the number of active migration rate and effective population size predictors, i.e. predictors for which the indicator is 1, from a Poisson distribution with λ = 0.693. This puts 50% of the weight on no predictor predicting migration rates or effective population sizes. Having only few predictors explaining migration patterns is common. Lemey et al. (2014), for example, inferred sample numbers and air traffic as the most likely predictors of the global migration patterns of influenza when having air communities as discrete locations. Additionally, having many different predictors explaining rates can lead to very large differences in rates across sub-populations and time. Since MASCOT is using ODE calculations to compute the probability of a tip labelled tree under the marginal approximation of the structured coalescent, large differences in rates requires very small integration time steps to compute this probability. This in turn can lead to very slow run times.

All other predictors are considered inactive and are used only to see if inactive predictors can be reliably identified as such. By using equations (1) and (2), we then calculated the migration rates between every sub-population and the effective population size in every sub-population at any point in time from the active predictors and coefficients. We then used these parameters to simulate 500 phylogenetic trees in MASTER (Vaughan and Drummond 2013) under the exact structured coalescent with 400 serially sampled tips. The location of these tips were sampled uniformly at random, allowing for different sample numbers across these sub-populations. Additionally, we simulated sequence alignments of 1,000 nucleotides in length using the Jukes–Cantor model on top of each phylogenetic tree using Seq-Gen (Rambaut and Grassly 1997).

We next inferred which predictors explained patterns of migration and effective population size (indicators) in simulated phylogenies and their relative contributions (coefficients). This inference was done using MASCOT (Müller et al. 2018) (see Section 4). We did this once using fixed phylogenetic trees, and once where we co-inferred phylogenetic trees. We assessed convergence by calculating the effective samples size of each Markov chain Monte Carlo (MCMC) run by using coda (Plummer et al. 2006). If either the inference on fixed trees or the joint inference with the phylogenetic tree had an effective sample size of any parameter of <50, the run was not used in the analysis. This removed ∼10% of all runs from the further analysis.

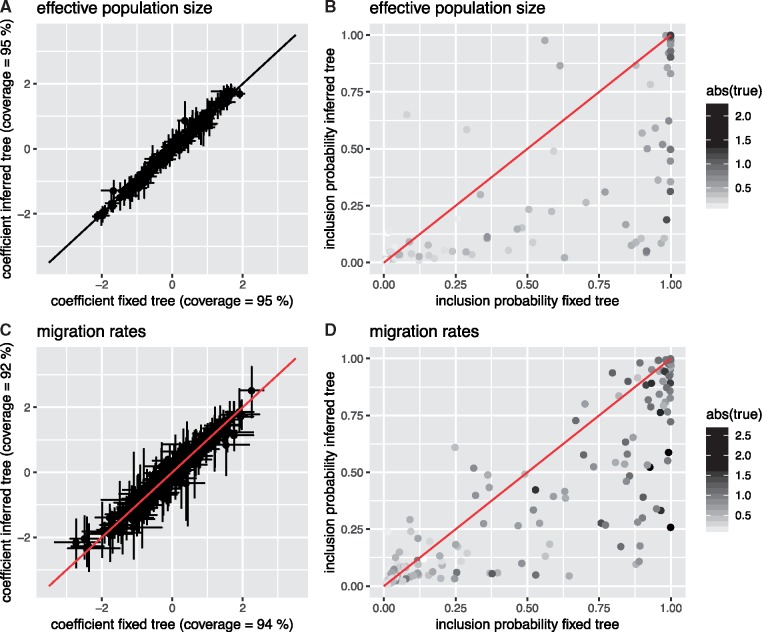
In Fig. 1, we compare the inferred coefficient values of active predictors as well as the probability that active predictors are identified as such between the analyses when fixing and when inferring the phylogenetic tree. The coefficients are inferred well for both migration rate and effective population size predictors when fixing and when inferring the phylogenetic tree (see Fig. 1A and C;Supplementary Figs S1 and S2 that compare estimated to simulated values). When fixing the phylogenetic tree, active migration rate, and effective population size predictors are inferred to be active more reliably than when inferring the phylogenetic tree (Fig. 1B and D). While inactive predictors are reliably excluded and predictors with strong effects (large coefficients) are reliably included, predictors with only minor effects (small coefficients) can be falsely excluded (see also Supplementary Figs S1 and S2). This is, however, expected due to a small effect size.

Figure 1.

Comparison in inference of coefficients and indicators from fixed phylogenetic trees and when jointly inferring them. (A) Inferred active coefficients when inferring the phylogenetic tree (y-axis) versus the inferred active coefficients when fixing the phylogenetic tree (x-axis) for the effective population size predictors. The coverage denotes how often the 95% highest posterior density interval includes the true values of the coefficient, which describe the effect size of active predictors. (B) Probability of the indicator of active effective population size predictors to be 1 when inferring the phylogenetic tree (y-axis) versus it being 1 when fixing the phylogenetic tree (x-axis). The effect size of a predictor is given by the grey scale. Predictors with a smaller effect size (brighter) are included less often as active predictors. (C) Inferred active coefficients when inferring the phylogenetic tree (y-axis) versus the inferred active coefficients when fixing the phylogenetic tree (x-axis) for the migration rate predictors. (D) Probability of the indicator of active migration rate predictors to be 1 when inferring the phylogenetic tree (y-axis) versus it being 1 when fixing the phylogenetic tree (x-axis).

The 95% highest posterior density (HPD) interval contains the true parameter values in 92–95% of cases. Additionally, the HPD interval of the number of predictors that are active contain the true number of active predictors well (see Supplementary Fig. S3). The coverage is especially good considering that the simulations are performed under the exact structured coalescent, while the inference is done using the marginal approximation of the structured coalescent (Müller et al. 2018).

We next compared the performance of the structured coalescent GLM with the DTA-GLM approach introduced in Lemey et al. (2014) using time invariant predictors. Since we used predictor data that change through time in the simulation study above, we re-simulated datasets with ten effective population size and ten migration rate predictors for ten different sub-populations. We simulated 500 trees using MASTER (Vaughan and Drummond 2013) under the exact structured coalescent with 1,000 serially sampled tips. We next inferred which predictors explained migration and effective population sizes from these simulated phylogenies as well as their coefficients. Since biased sampling has been shown to bias inferences of the underlying migration model of Lemey et al. (2014), we additionally used the sample numbers in each sub-population as predictors for migration into or out of a state. As above, we assessed convergence by calculating the effective sample size of each MCMC run by using coda (Plummer et al. 2006). If either the run using DTA or MASCOT had an effective sample size any parameter of <50, the run was not used in the analysis. This removed ∼10% of all runs from further analysis.

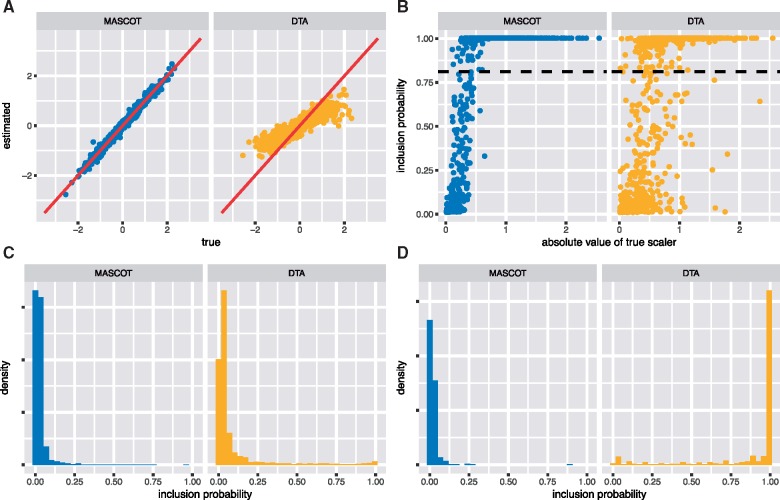
Figure 2 and Supplementary Fig. S4 shows how the inference of predictors and their contribution compares between the two different methods. DTA-GLM underestimates the contribution of active predictors, but correctly infers if they positively or negatively predict migration rates. In particular, the relationship between true and estimate contribution is linear. When we compare the power of the two methods to infer active predictors to be active, we find that DTA-GLM often does not correctly identify predictors. This is not only the case for predictors with a small effect size, but also seems to be the case for predictors with larger effect sizes. Additionally, DTA is more likely to infer random predictors that are not active to be predicting migration rates. Consistent with the findings in De Maio et al. (2015), we find that sample numbers are inferred to be a strong predictor of migration rates into a sub-population by DTA. MASCOT on the other hand does not put strong weight on sample numbers as predictors when they are not actually predicting migration rates.

Figure 2.

Inference of coefficients and indicators using the generalized linear model versions of MASCOT and DTA based on fixed phylogenetic trees. (A) Inferred active coefficients (y-axis) versus the true coefficients for migration rate predictors using MASCOT (left) and DTA (right). (B) Probability of the indicator of active migration rate predictors to be 1 (y-axis) for the effective population size. The dashed line corresponds to a Bayes Factor of 10 for the predictor being included. (C) Histogram of inclusion probabilities from predictors that are not predicting migration rates. Therefore, the true value of these inclusion probabilities is 0 and predictors with large inclusion probabilities might be falsely considered as predicting migration rates. (D) Histogram of inclusion probabilities of indicators for sample number predictors. That is, the predictor that predicts migration into a state being proportional to the number of samples from that state. These predictors were not used to predict migration rates.

2.2 2014 Ebola epidemic in Sierra Leone

We next apply the MASCOT-GLM approach to a previously described Ebola virus dataset. We used EBOV sequences sampled in fourteen different regions of Sierra Leone in 2014 (Dudas et al. 2017). As migration rate predictors, we used the same time invariant predictors as Dudas et al. (2017). Namely, we used mean travel time to the nearest major settlement of at least 100,000 inhabitants, gridded economic output, population size and density, mean annual temperature and precipitation, and index of precipitation and temperature seasonality. All these predictors can either inform migration rates from or to a particular district and are therefore called origin/destination predictors.

To account for potentially missing predictors, we added predictors that only predict the migration rate from or to one individual district. We also included the sample numbers, whether two districts neighbour each other and the ratio of weekly cases between two districts as a migration rate predictor. Additionally, we used the great circle distances between the different districts as a migration rate predictor.

For effective population sizes we used the origin/destination predictors from Dudas et al. (2017), i.e. the ones we listed above being used for migration rates. Effective population size predictors could not be used previously, since information about the coalescent process in different sub-populations cannot be incorporated into previous approaches (Lemey et al. 2014). Additionally, we incorporated the weekly case data of each location as a time-varying predictor of the effective population size. Instead of using 0 for weeks with no reported cases, we used 0.01 in order to not completely exclude lineages to be in a location if there are no reported cases there. This also avoids computational issues arising from predictors being log(0). We further added eight predictors for which we changed the weekly case data such that we assume that every case happened 1, 3, 6 and 9 weeks later or earlier. This allows us to test on real data if the approach is sensitive to changes in the time scale.

We then jointly inferred the phylogenetic tree and the indicators and predictors of effective population sizes and migration rates from the genetic sequence data. As an evolutionary model, we used a strict clock and a separate HKY + Γ₄ site model on the three codon positions as well as a separate HKY + Γ₄ site model on the non-coding regions. We fixed the evolutionary rates of the site models to the mean inferred rates of Dudas et al. (2017) to save computation time. We analysed the data by running three independent coupled MCMC (Altekar et al. 2004; Müller and Bouckaert 2019) chains, each with twelve chains for around forty-five million iterations. Then, we combined the three chains after a burn-in of 5% and calculated effective sample size values and potential scale reduction factors (PSRF) (Brooks and Gelman 1998) for each inferred parameter to assess convergence using coda (Plummer et al. 2006). The PSRF values on the posterior, prior and likelihood values was below 1.01 and below 1.05 for most parameters. For parameters with a PSRF larger than 1.05, the ESS of the combined chain was always >700.

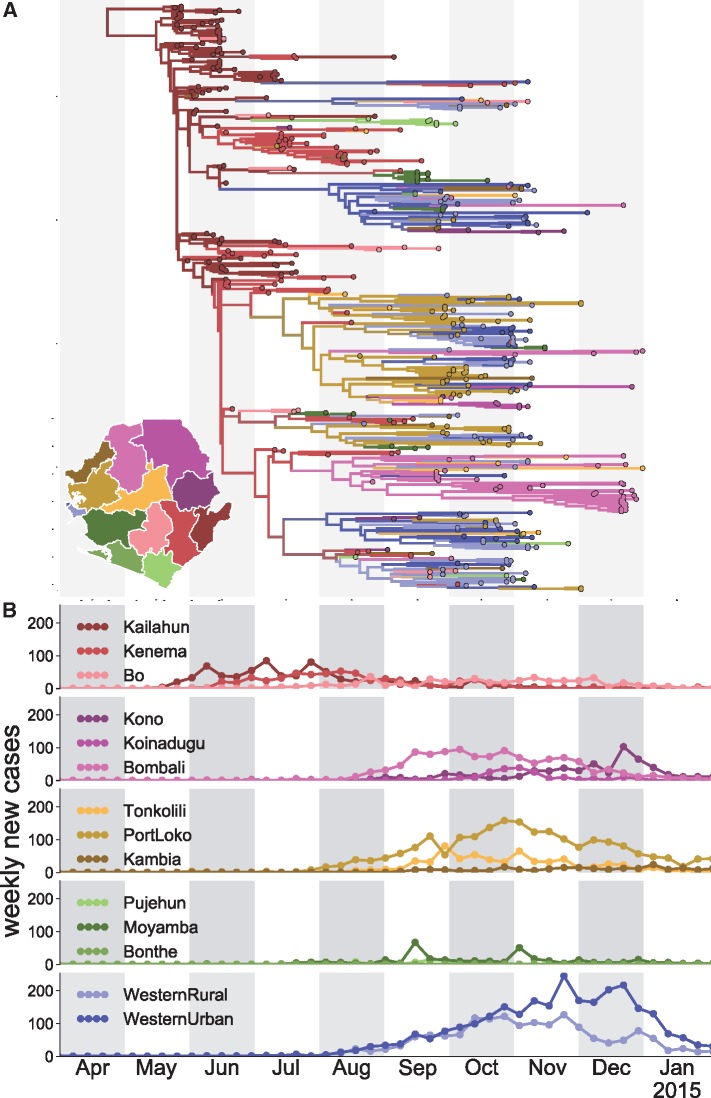
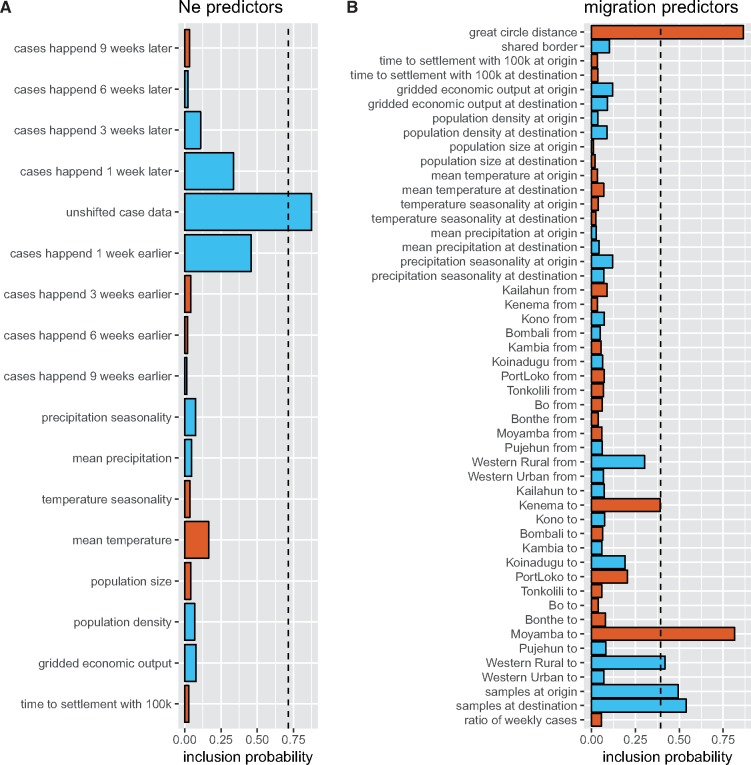
Figure 3 shows the inferred maximum clade credibility tree with the different colours denoting the inferred locations of the nodes. Location inference is done as described in Müller et al. (2018). Figure 4 shows the inferred predictors for the migration rates and the effective population sizes. The distribution of the number of active predictors is shown in Supplementary Fig. S5. Weekly case data is inferred to be the strongest predictor of effective population size. This is to be expected since weekly cases should be approximately proportional to viral effective population sizes in each location given the probability of EBOV being transmitted is similar across different locations (Volz et al. 2009). Weekly case data offset by 3, 6, or 9 weeks is excluded from predicting effective population sizes. Weekly case data where we assume all cases to have happened 1 week later or earlier, have higher support than the predictors shifted by more weeks, but are still less supported than the un-shifted weekly case data.

Figure 3.

Analysis of data from the 2014 Ebola epidemic in Sierra Leone. (A) Inferred maximum clade credibility tree from the 2014 Sierra Leone EBOV sequences. Colours denote the most likely inferred district for each node, and branches are coloured as their descendant node. District colour scheme is shown on the map. (B) Weekly incidence by district. The x-axis denotes time in months and acts as a scale for both incidence data as well as the phylogenetic tree.

Figure 4.

Inferred predictors of the effective population sizes and migration rates for the Ebola analysis. (A) Inferred effective population size predictors. The x-axis shows the probability of the predictors being included in predicting the effective population sizes. Red bars are predictors for which the median value of the coefficient is negative and blue bars are predictors for which the median value of the coefficient is positive. The magnitude of the coefficient from a standardized predictor does not have a direct meaning or dimension. We therefore only plotted if a coefficient was inferred to be positive or negative, i.e. if the relationship between a predictor and the effective population size or migration rates is inverse or not. The case data predictor include the number of cases per week in a location. We additionally added eight predictors where the cases are assumed to have happened 1, 3, 6, and 9 weeks earlier or later. These are not inferred to strongly predict effective population sizes. (B) Inferred migration rate predictors. The x-axis shows the probability of the predictors being included in the migration model. ‘Origin’ and ‘from’ predictors predict the migration rate from a location. ‘Destination’ and ‘to’ predictors predict the migration rate into a location. The dashed line corresponds to a Bayes Factor of 10 for the predictor being included.

We infer great circle distances between population centroids of districts to be the strongest predictor for migration rates. This means that migration rates are inversely proportional to the distance between population centroids of districts. The root of the tree is inferred to be in Kailahun with 62% probability, with the rest of the probability mass approximately evenly distributed across the other locations.

3. Discussion

We here introduce a new approach that is able to jointly infer time varying effective population sizes and migration rates using predictor data and sequencing data. Previous GLM approaches were restricted to time invariant (Lemey et al. 2014) and time variant (Bielejec et al. 2014) migration rates in models that treat the migration and coalescent process as independent processes and thus do not model effective population sizes across sub-populations. Other approaches were using the GLM framework to inform effective population sizes through time in unstructured populations (Gill et al. 2016), but none allowed to jointly model these processes. While Lemey et al. (2014) has significant computational advantages over MASCOT, it cannot model the effective population size and thus the transmission dynamics within a sub-population. Approximated structured coalescent approaches accounting for effective population sizes within sub-populations, such as BASTA (De Maio et al. 2015), potentially also have speed advantages compared with MASCOT. They have, however, been shown to be significantly biased in the presence of asymmetric effective population sizes or non-uniform sampling (Müller, Rasmussen, and Stadler 2017).

By using simulations, we show that indicators and coefficients of predictors can be inferred reliably using MASCOT-GLM. Predictors that do not explain migration rates or effective population sizes are reliably excluded. This, however, also applies to predictors with small effect size. These are often inferred to not predict effective population sizes or migration rates at all. We further showed that at least for phylogenetic trees simulated under the structured coalescent, MASCOT-GLM outperforms DTA-GLM. Sample numbers are not used as migration rate predictors in our simulations. Sample numbers are correctly excluded by MASCOT, but not by DTA. It remains open how the different methods perform under more realistic simulation scenarios or when some of the active predictors are missing.

In contrast to, for example, Gill et al. (2016), we currently do not allow for error terms in the GLM equation. We therefore essentially assume that all or a subset of the predictors fully explain the migration rates and the effective population sizes through time. Future improvements could fill that gap by allowing for such error terms. This would, however, require efficient operators to sample the error terms. Furthermore, it would require to develop reasonable priors on these error terms, similar to the ones used for skyline methods (see, e.g. Drummond et al. (2005) or Minin, Bloomquist, and Suchard (2008)).

Similar GLM approaches as presented here could be applied to inform birth, death, migration, and sampling rates through time for structured birth-death models (Stadler and Bonhoeffer 2013; Kühnert et al. 2016).

By using the example of the 2014 Sierra Leone Ebola virus disease (EVD) outbreak, we show that our approach is able to infer the effect size of predictors reasonably from real data as well. We infer weekly case numbers to predict effective population sizes best. We further exclude weekly case numbers offset forwards or backwards in time as effective population size predictors. For migration rate predictors, the distances between population-weighted centres of different locations is inferred to be the strongest predictor. Previously, distances have been identified as an important predictor of geographic spread for Ebola virus in West Africa, by both phylodynamic (Dudas et al. 2017) and epidemiological approaches (Kramer et al. 2016), even when only Sierra Leone is considered (Gustafson and Proctor 2017). Overall, we infer similar migration rate predictors as Dudas et al. (2017) that used the panmictic and time invariant model described in Lemey et al. (2014). We expect the greatest differences in the inference of migration rate predictors between the two approaches when sampling is strongly biased (De Maio et al. 2015).

Sampling of Ebola cases was fairly dense during the outbreak. Whilst Ebola virus sequencing in West Africa has generally kept up well with increasing numbers of cases (Dudas et al. 2017), numerous locations are, however, known to have been under-sampled or un-sampled altogether. For example, an EBOV lineage established early in Conakry prefecture of Guinea resurfaced at least three times during the epidemic (Carroll et al. 2015; Simon-Loriere et al. 2015; Quick et al. 2016). This suggests the presence of a substantial, yet cryptic, localised transmission chain not seen outside of Conakry. It remains unclear how to treat entirely un-sampled locations and what their effect might be on internal node state reconstruction or inference of predictors. Future research will need to investigate the effects of ghost states (Slatkin 2004) on the GLM approach.

Overall, this newly introduced method allows including predictor data, such as transportation or incidence data, into phylodynamic analyses. This allows us to infer population dynamic parameters as well as the location of ancestral nodes more reliably in a computationally tractable way. Predictor data, such as the movement of people using mobile phone data (Deville et al. 2014; Wesolowski et al. 2015) or the social mixing of different age groups (Mossong et al. 2008), are increasingly being gathered. This in turn means that methods that are able to combine various sources of information in a computationally feasible way will be playing an ever increasing role in epidemiology.

4. Materials and Methods

4.1 Effective population sizes and migration rates as GLMs

Instead of inferring the effective population size $N{e}_{\mathrm{a}}\left(t\right)N{e}_a\left(t\right)$ of state a at time t directly, we define it as a linear combination of c different predictors $p_{N_e}\left(t\right)$, coefficients ${\beta }_{N_e}$, and indicators ${\sigma }_{N_e}$:

$$N{e}_{\mathrm{a}}\left(t\right)={\beta }_{\mathit{Ne}}\mathrm{e}\mathrm{xp}\left({\sum }_{i=1}^c{\beta }_{N_{\mathrm{e}}}^i{\sigma }_{N_{\mathrm{e}}}^i{p}_{N{e}_{\mathrm{a}}}^i\right(t\left)\right).$$ (1)

The coefficients ${\beta }_{N_{\mathrm{e}}}^i$ can be between $-\infty$ and $\infty$ and denote the extent to which each predictor contributes in predicting effective population sizes. We typically use a normal distribution as a prior distribution on these coefficients. The values of the coefficients are sampled during the MCMC by using a random walk operator independent of the value of the corresponding indicator. This means that if the corresponding indicator to a coefficient is 0, the operator samples the value of a coefficient from the prior distribution.

The indicators ${\sigma }_{N_e}^i$ can be 0 or 1 and denote if a predictor contributes at all. We sample these indicators by using an operator that randomly switches the values of indicators between 0 and 1 with a hastings ratio such that the total number of indicators that is 1 is distributed as given by some prior distribution, for example, a Poisson distribution. We therefore perform model selection on which predictors are active, as described for phylogenetic approaches in Lemey et al. (2009, 2014). In other words, the sum of active predictors is a random variable which is distributed according to some prior distribution. This prior distribution is typically chosen such that lower numbers of active predictors are favoured. That means, more weight is put on less predictors explaining the observed migration and coalescent patterns.

β_Ne denotes a scaling parameter, scaling every effective population size at every point in time with the same value. This means that if every indicator in the effective population size or migration rate GLM is 0, every effective population size or migration rate will be equal to the scaling parameter. As a prior distribution on the scaling parameters, we here used an inverse-uniform distribution. The different predictors are in log space and in order to have comparable predictors, they are typically standardized, such that their mean is 0 and their standard deviation is 1. The values of these predictors vary across different states a as well as different time points t. This parametrization of the GLM is the same as described in Lemey et al. (2014).

We apply the same framework for the forward-in-time varying migration rates $m_{\mathrm{ab}}^{\mathrm{f}}\left(t\right)$ at time t between states a and b:

$$m_{\mathrm{ab}}^{\mathrm{f}}={\beta }_m^{}\mathrm{e}\mathrm{xp}\left({\sum }_{i=1}^c{\beta }_m^i{\sigma }_m^i{p}_{m_{\mathrm{ab}}}^i\right(t\left)\right)$$ (2)

where β_m is the overall rate scaler, describing the overall magnitude of migration. Since the structured coalescent uses backwards in time migration rates, we define the backwards in time rates as:

$$m_{\mathrm{ba}}^{\mathrm{b}}\left(t\right)\approx \frac{N{e}_{\mathrm{a}}\left(t\right)}{N{e}_{\mathrm{b}}\left(t\right)}{m}_{\mathrm{ab}}^{\mathrm{f}}\left(t\right).$$

The ‘$\approx$’ becomes ‘=’ for the case when ${\alpha }_{\mathrm{a}}={\alpha }_{\mathrm{b}}$ such that $N{e}_{\mathrm{a}}\left(t\right)={\alpha }_{\mathrm{a}}{I}_{\mathrm{a}}\left(t\right)$ and $N{e}_{\mathrm{b}}\left(t\right)={\alpha }_{\mathrm{b}}{I}_{\mathrm{b}}\left(t\right)$ with $I_{\mathrm{a}}\left(t\right)$ denoting the number of infected individuals in population a at time t (Volz 2012). This is the case when the ratio of effective population sizes between states is equal to the ratio of number of infected individuals between states.

4.2 Ebola sequence and incidence data

Sequences belonging to the major Sierra Leonean Ebola virus lineage that dominated the country’s epidemic (Dudas et al. 2017) were extracted and down-sampled to sequences collected up to 31 December 2014, leaving 473 taxa. Stretches of putative hypermutation tracts corresponding to hypothesised ADAR edits were identified and masked as described in Dudas et al. (2017).

Incidence data were compiled from the latest WHO report on EVD cases in Sierra Leone: http://apps.who.int/gho/data/view.ebola-sitrep.ebola-country-SLE-new-conf-prob-districs-20160511-data?lang=en. These data report the number of new EVD cases for each subnational division of Sierra Leone (district) and epi week, split by whether the cases are confirmed or probable. Additionally, due to the scale of the epidemic across the region, there are two databases (an earlier patient database and later situation reports) for EVD incidence that overlap by around a year (September 2014–September 2015) with slightly different reported incidences. Available data are likely underestimates of the true burden of EVD in Sierra Leone, and thus we combine confirmed and probable cases, and keep the higher number for each epi week for when the reporting of patient and situation report databases overlap (Dudas et al. 2017).

4.3 Software

The method above is implemented into our BEAST2 package MASCOT (Marginal Approximation of the Structured COalsescenT). Simulations were performed using a backwards in time stochastic simulation algorithm of the structured coalescent process using MASTER 5.0.2 (Vaughan and Drummond 2013) and BEAST 2.5.2 (Bouckaert et al. 2014). Script generation and post-processing were performed in Matlab R2015b. Plotting was done in R 3.2.3 using ggplot2 (Wickham 2009). Plotting of the EBOV analysis was done by using baltic (https://github.com/blab/baltic) and matplotlib (Hunter 2007). Effective sample sizes and PSRF for MCMC runs were calculated using coda version 0.18-1 (Plummer et al. 2006).