Evaluation of Some High-Temperature Platinum Resistance Thermometers

Abstract

Two sets of high-temperature platinum resistance thermometers of different design have been tested in the temperature range 0 to 1100 °C. One set was constructed at the National Institute of Metrology, in the People’s Republic of China, and the other at the National Bureau of Standards. The results of the tests provide information on long- and short-time thermometer stability, and on other characteristics such as temperature coefficient, immersion, self-heating effect, electrical leakage, and durability. The results also show that the behavior of the two sets is similar enough to allow them to be considered as a single set of thermometers, and that the sets perform as well as, or better than, other sets of thermometers tested earlier. It is expected that this information will aid in the evaluation of the high-temperature platinum resistance thermometer as an interpolating instrument for a practical temperature scale up to the gold point.

1. Introduction

The high-temperature platinum resistance thermometer has long been advocated as a standard interpolating instrument for a practical temperature scale up to the gold point, in place of the standard thermocouple. Acceptance of the resistance thermometer for this purpose is likely to come only when sufficient information is available for careful evaluation of thermometer characteristics and performance as they relate to the definition of a practical temperature scale.

The experiments and results reported here are intended to provide some of the needed information on the behavior of high-temperature resistance thermometers; specifically on the following characteristics:

1. Long-time stability at high temperature

2. Short-time stability upon temperature cycling

3. Temperature coefficient of resistance

4. Immersion characteristics

5. Heating effect of measuring current

6. Electrical leakage of thermometer supporting parts

7. Thermometer durability

8. Agreement among thermometers of derived temperature values.

Another purpose of this paper is to describe some experimental procedures that have proved useful in evaluating thermometer performance. The procedures require little in the way of apparatus beyond what is needed for routine thermometer measurement, calibration, and conditioning.

A third purpose of this paper is to report on the behavior of two sets of high-temperature platinum resistance thermometers from different sources and of different design. One set was constructed at the National Institute of Metrology (NIM), Beijing, People’s Republic of China; the thermometers were lent to the National Bureau of Standards (NBS) for testing. The other set was constructed at the NBS. Both types of thermometers have been described in the literature [1–6].¹

2. General Methods and Equipment

The general methods and equipment that were used to test the thermometers also have been described [3]. The descriptions are repeated in the following sections for convenience and completeness; they have been updated, where necessary, to apply to the lower resistance thermometers that were used in the present experiments.

2.1. Thermometer Heat-treating Furnace

Thermometers are heat-treated in a vertical annealing furnace capable of reaching 1100 °C. The furnace contains a relatively short cylindrical electrical heater near the center that heats only the resistor and a short section (a few centimeters) of adjacent leads to the selected heating temperature. During heat treatment, the thermometers are inserted into closed-end, silica-glass furnace wells, with the resistors situated in the hottest region of the furnace. The space between the wells and the heater contains only air. Six thermometers can be heated at one time.

The furnace is controlled by a Type B thermocouple (Pt – 30%Rh/Pt – 6%Rh), and it is monitored by a Type S thermocouple (Pt – 10%Rh/Pt). A calibrated test thermometer can also be used for monitoring. The control system is capable of maintaining the furnace at a desired temperature within about 2 K, and is also capable of controlling furnace cooling at a uniform rate of 80 K/h.

For heat treatment, the thermometer sheaths are first thoroughly cleaned by appropriate means (e.g., acids or solvents) to remove dirt and fingerprints. The thermometers are then inserted into the furnace described above, which has been set to control at the desired temperature. At the end of the heating period, the control system is set to reduce the furnace temperature at the programmed rate of 80 K/h so as to avoid quenching in lattice-site vacancies [7]. When the furnace temperature reaches about 520 °C, the thermometers are removed. This procedure avoids the effects of the platinum oxidation that could occur if thermometers were allowed to cool slowly to room temperature [8].

2.2. Fixed Points

The triple point of water is realized in a conventional sealed glass cell. The ice mantle is prepared using a special immersion cooler [9] at least 24 h before measurements are to be made, and the cell is stored in an ice bath. During use, the ice mantle is free to rotate within the cell, the annulus between the cell well and the thermometer contains an aluminum bushing and water, and the cell is shielded from ambient radiation. When a thermometer is fully immersed in a triple-point cell, the bottom tip of its sheath is about 275 mm below the surface of the liquid water.

The metal freezing points are also realized in sealed cells. The high-purity metal is contained in a graphite crucible with a re-entrant graphite well, and the graphite is surrounded by a sealed glass envelope. Before the cell is sealed, it is evacuated and filled with enough pure argon to provide a pressure of 1 atm at the freezing point. The cell is similar to the type 1 cell described by Furukawa [10].

The freezing points of all the cells have been found to be sufficiently constant during a single freeze, and sufficiently reproducible from freeze to freeze, to serve the requirements of thermometer testing. The tin, zinc, and silver cells contain Standard Reference Material metals (SRM 741, 740, and 748, respectively) obtained from the NBS Office of Standard Reference Materials. The materials are known to be of high purity (less than 1 ppm total impurity content), and the freezing points of the tin and zinc cells have been established to be well within 1 mK of the freezing points maintained in the NBS Thermometer Calibration Laboratory. The aluminum cell contains metal obtained from a commercial supplier who reported the impurity content to be less than 1 ppm. The gold cell contains a sample used in an earlier cell [11]. From the results of tests conducted with the earlier cell, including a comparison with the freezing point of a sample of known high purity, the freezing point of the present cell is believed to be within about 10 mK of the gold point. All of the cells except the gold cell provide a depth of thermometer immersion, from the top of the liquid metal to the inside bottom of the graphite well, of about 17 cm. The immersion in the gold cell is about 15 cm.

The metal freezing-point cells are heated in vertical electrical furnaces different from the annealing furnace. These furnaces are similar to those described earlier [11], but the present furnaces employ only a single long heating zone, and temperature equalization is achieved with aluminum cylinders or heat pipes. The tin and zinc cells are encased in aluminum cylinders located near the center of the zone; the cylinder walls are about 2 cm thick. The aluminum, silver, and gold cells are centered in coaxial heat pipes, about 10 cm o.d., 5 cm i.d., and 45 cm long, made of Inconel and containing sodium as the working fluid. The cylinders and heat pipes serve to establish for the cells a uniform temperature environment that is maintained about 1 K below the freezing point by control systems during freezing.

The metal freezing points are established by induced freezing. Except for tin, the molten metals are allowed to cool slowly through the supercooled region until they recalesce. A solid mantle of metal is then induced on the cell well by inserting a cool rod. For tin, the freeze is induced in the supercooled metal by blowing air down the cell well, recalescence being detected by a thermocouple wrapped around the glass envelope.

Test thermometers are first preheated for about 5 min in the furnace just above the freezing point cell, and then measurements at full thermometer immersion are started after the system has come to thermal equilibrium. Except for special tests, the measurement process takes about 30 min, and at least five thermometers can be tested in a single freeze at the tin, zinc, and aluminum points. The gold and silver are remelted after each thermometer test. After testing at the gold, silver, or aluminum points, thermometers are placed in the annealing furnace, held at a temperature near the fixed point for 30 minutes, and then cooled at the programmed rate to 520 °C to anneal out lattice site defects. Following this, and also after tin- and zinc-point measurements, the resistance at the triple point of water is determined.

2.3. Electrical Measurements

Measurements of thermometer resistance are made with an automatic self-balancing bridge [12], and a computer is used to control the operation of the bridge and record the data. The bridge utilizes square-wave excitation, normally at 30 Hz, though 15 Hz can be selected. It also has provision for selecting thermometer measuring current of 1, 2, 4, or 8 mA and one of four resistor input channels. It can resolve resistance to less than 1 micro-ohm with a linearity of 1 part in 10⁷.

Thermometer resistance is determined from a sequence of measurements of both the thermometer and a relatively stable (20 micro-ohm per year drift) 10-ohm standard resistor located in a temperature-controlled oil bath. When a thermometer, carrying a normal measuring current of 4 mA, has come to thermal equilibrium in a fixed-point cell, 10 readings of its resistance are recorded. The system then switches to the standard resistor and records 10 readings at the same current. Immediately thereafter, the thermometer is reconnected to the bridge and the measuring current is doubled. When the thermometer has come to thermal equilibrium at this higher current (a period of 3 min is usually allowed), additional sets of 10 readings are recorded for the thermometer and standard resistor. The entire process takes about 7 min. From these data, a mean value of the ratio of thermometer resistance to standard-resistor resistance, extrapolated to zero measuring current, is computed and stored. The computer also calculates the heating effect of the normal measuring current, and the estimated standard deviation of the computed mean ratio value. This standard deviation seldom exceeds the equivalent of 0.2 micro-ohm.

3. Thermometers

The thermometers used in the experiments were in some ways similar to other high-temperature platinum resistance thermometers that have been described in recent years [3,5,11]. The temperature sensing resistors were 1 to 3 cm long and about 0.5 cm in diameter, they were connected to four platinum leads, and they were sealed in long (70 – 80 cm) silica-glass tubes. Thermometer resistance at 0 °C was small—less than 1 ohm.

In other ways the thermometers were novel. The resistors in the NIM thermometers were of the single-layer, bifilar helix design, but the support for the resistor wire consisted of a single notched silica-glass blade, rather than the customary cross. The NBS thermometers employed newly-designed “toroidal” resistors and guarded leads. Detailed features of the thermometers are presented in tables 1 and 2.

Table 1.

General features of thermometers.

	NIM	NBS
Overall length (including header)	805 mm	885 mm
Header length	85 mm	125 mm
External tube length	720 mm	760 mm
Nominal tube diameter	7 mm	7 mm
Header diameter	20 mm	19 mm
Resistor type	Single layer helix	Toroidal (straight wire)
Resistor former	Notched silica	Notched-end
	blade	silica tube
Former length	40 mm	15 mm
Resistor coil length	30 mm	10 mm
Resistor wire diameter	0.4 mm	0.25 mm
Nominal resistance at 0 °C	0.25 ohm	0.37 ohm
Lead insulator type	Silica tube and disk	Long silica tubes with internal guard
Lead wire diameter	0.3 mm	0.25 mm
Length of roughened sheath surface	350 mm	500 mm
External connection	Permanent copper lead wire cable	Separable five-pin connector on header

Table 2.

Features of individual thermometers.

Thermometer number	Nominal resistance at 0 °C, ohm	Initial stabilization, h at 1100 °C	Alpha coefficient,α, at beginning of test, × 106, K−1	Distance in mm, bottom of former to bottom of sheath at room temperature
NIM thermometers
80179	0.244	350	3927.1	1.0
18227	0.260	350	3926.9	0.5
18236	0.257	350	3926.8	0
18237	0.263	500	3926.8	1.5
NBS thermometers
8202	0.373	400	3926.9	7.5
8204	0.361	400	3927.0	7.0
8205	0.378	400	3926.8	7.5

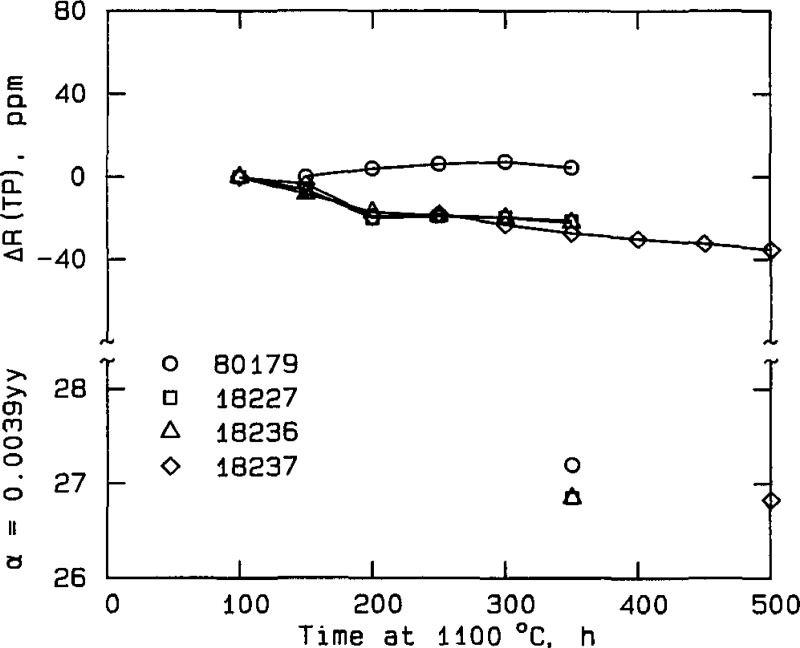
The NIM thermometers had been stabilized by heat treatment, as indicated in table 2, before they were transported to NBS. Properties of the thermometers measured at the NIM during the stabilization are shown in figure 1. Upon their arrival at the NBS the four NIM thermometers were inspected. It was observed that three thermometers (18227, 18236, 18237) had bent sheaths, and that in two of the thermometers (18227 and 18236), the resistor support blade was bent. It was believed that these minor defects would not introduce unwanted biases into the experiments, so all four thermometers were prepared for testing by annealing them for 30 min at or near the gold point, and then slow-cooling them to about 520 °C.

Figure 1.

Change in characteristics of NIM thermometers during stabilization. The measurements were made at the National Institute of Metrology, Beijing. Both the relative change in thermometer resistance at the triple point of water (parts in 10⁶, ppm) and the alpha coefficient, α, are shown.

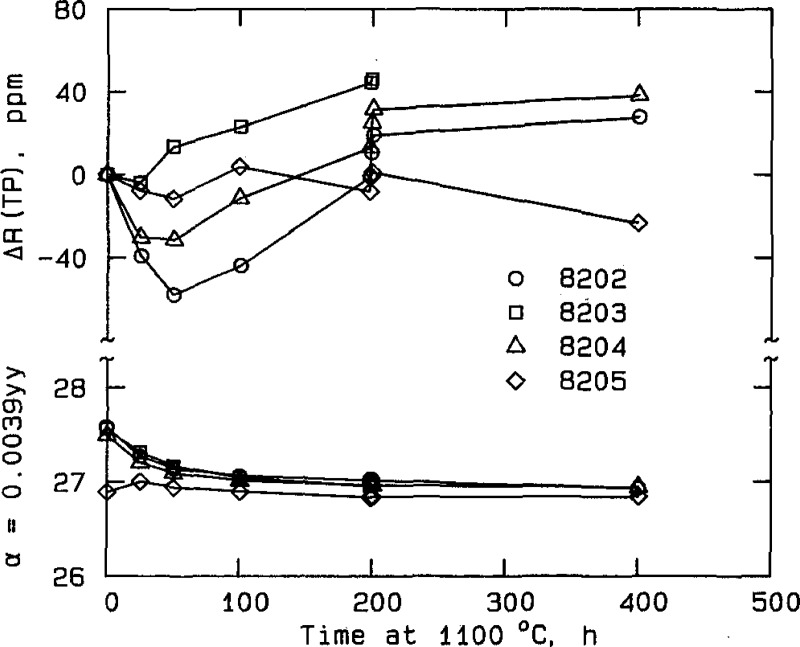
The NBS thermometers had also been stabilized by heat treatment, as indicated in table 2 and figure 2. One of the four thermometers originally made for the investigation (8203) failed during the stabilization process because of internal lead separation. It therefore could not be included in any of the experiments.

Figure 2.

Change in characteristics of NBS thermometers during stabilization. Both the relative change in thermometer resistance at the triple point of water (parts in 10⁶, ppm) and the alpha coefficient, α, are shown.

4. Experimental Procedures and Results

Unless otherwise indicated, the general methods and equipment described above were used throughout the experiments. The internal guard of the guarded lead thermometers was connected to the bridge guard circuit during measurement [13], except for special tests. All experimental results are reported in the appendix tables. The values of resistance in the tables are given by

$$R=10\times R(\text{th})/R(\text{sr}),$$ (1)

where R (th) is the value of the thermometer and R (sr) is the value of the standard resistor, as measured by the bridge. The factor 10 in eq (1) is the nominal resistance of the standard resistor; it is included so that R is approximately in ohms. If the factor were to be replaced by the actual value of the standard resistor in absolute ohms, then R would also be in absolute ohms. This was not considered necessary for the present investigation because all results were derived from ratios of R values. In the time required to obtain the values of R for a single ratio, the standard resistor did not change significantly.

The first experiment consisted of two runs (series of measurements of thermometer resistance at fixed points) with an intervening exposure of the thermometers to high temperature. In the first run, the resistance of a thermometer was determined at thermometric fixed points in the sequence TP, AU, TP, AG, TP, AL, TP, ZN, TP, SN, TP, where TP designates the triple point of water and AU, AG, AL, ZN, SN designate the freezing points of gold, silver, aluminum, zinc, and tin, respectively. Three or four thermometers were measured in a single freeze at the tin, zinc, and aluminum points, but at the gold and silver points, separate freezes were used for each thermometer. The measurements were made with the thermometer fully immersed in the freezing-point cells and in the triple-point cell. Thermometer resistance was determined both with the normal measuring current and with twice the normal current; the value of resistance for zero power dissipation was calculated from these two determinations. The thermometer was then heated in a vertical position at 1100 °C for 100 h and cooled slowly as described above (sec. 2.1), and the measurement sequence was repeated for the second run. The results are given in tables A1a–g of the appendix.

The second experiment was conducted at the silver point. A “mesh” made of 0.25 mm diameter platinum wire was placed around the sheath of a thermometer before it was inserted into the silver freezing-point cell. Upon insertion, the mesh was situated in the small annulus between the silica-glass sheath of the thermometer and the silica-glass cell guide tube and cell well, thus preventing direct contact between the sheath and the guide tube and well. The mesh extended all the way from the bottom of the thermometer to the top of the cell guide tube at room temperature, where it was connected electrically to the bridge guard circuit, forming an external electrical thermometer guard. Thermometer resistance determinations were made, with the normal measuring current, at 5 min intervals as the silver was allowed to freeze slowly. From time to time the connection between the bridge guard circuit and the thermometer guards was changed, or the guard circuit was disconnected completely. Results for all thermometers except No. 18227 (NIM) are given in tables A2a–f of the appendix.

Thermometer No. 18227 was not tested in the second experiment because the slightly larger diameter of its sheath did not leave enough room in the cell well to accommodate the wire mesh. Similarly, the slightly smaller diameter of the gold-point cell well prevented the use of the external guard with any of the thermometers at the gold point.

In the third experiment the immersion characteristics of the thermometers were compared at the freezing point of zinc. The zinc point was chosen for this experiment because electrical leakage effects were negligible, and because it was easy to establish long periods of constant temperature. Only the normal measuring current was used; precise determination of variations in thermometer self-heating would have been obscured by the limited bridge resolution of the thermometers′ low resistance. Measurements were made at 5 min intervals at various vertical stations (in cm) in the cell well. The results are given in tables A3a–b of the appendix. At station 0, the thermometer sheath was fully immersed in and resting on the bottom of the cell well.

5. Analysis of Data

5.1. First Experiment

The data obtained in the first experiment may be analyzed by deriving the resistance ratio at each fixed point from the resistance values given in tables Ala–g. The resistance ratio at a fixed point, designated by W(FP), is defined by

$$W(\text{FP})=R(\text{FP})/R(0).$$ (2)

R (FP) is the resistance at the fixed point taken from the tables. R (0) is the associated value of thermometer resistance at 0 °C; it is derived from the mean of the values of R (TP) immediately preceding and following R (FP) in the tables, taking into account a correction for the depth of immersion of the thermometer in the triple-point cell. The values of W(FP) are listed in table 3.

Table 3.

Resistance ratios at fixed points.^1,2

Run	W(AU)	W(AG)	W(AL)	W(ZN)	W(SN)
RT no. 80179
1	4.57174066	4.28647159	3.37604256	2.56895487	1.89283568
2	4.57168631	4.28642060	3.37600925	2.56893131	1.89282128
RT no. 18227
1	4.57157254	4.28629894	3.37591813	2.56886467	1.89278068
2	4.57151496	4.28623733	3.37587016	2.56883989	1.89276336
RT no. 18236
1	4.57148343	4.28625191	3.37588957	2.56884678	1.89277435
2	4.57147650	4.28622095	3.37585840	2.56882739	1.89275797
RT no. 18237
1	4.57149741	4.28628074	3.37591249	2.56886121	1.89277637
2	4.57145197	4.28622217	3.37586485	2.56883266	1.89276204
RT no. 8202
1	4.57150591	4.28624231	3.37592544	2.56888096	1.89279537
2	4.57147188	4.28622642	3.37590991	2.56887218	1.89279135
RT no. 8204
1	4.57152289	4.28627237	3.37594233	2.56888153	1.89279772
2	4.57153108	4.28627577	3.37594331	2.56887922	1.89279320
RT no. 8205
1	4.57137553	4.28617237	3.37587835	2.56884607	1.89277446
2	4.57136712	4.28614094	3.37586420	2.56884047	1.89277239

¹Values derived from resistance values given in tables A1a-g.

²W(FP)= R(FP)/R(0), where R(0) is derived from the mean of the values of R(TP) before and after R(FP).

It is convenient to interpret resistance ratios and their differences in terms of temperature values. To do this, we define a simple “temperature scale” on which values of temperature (designated by t′) lie close to values on ordinary scales. The resistance ratio of a thermometer is related to a value on the scale by

$$W\left(t^{\prime }\right)=1+A{t}^{\prime }+B{t}^{\prime 2}.$$ (3)

The coefficients A and B are determined from the values of W(SN) and W(ZN) in table 3 using the IPTS-68 assigned values of t′ at the tin and zinc points, but taking into account corrections due to thermometer immersion. The values of A and B are listed in table 4, along with values of the coefficients alpha, α, and delta, δ, related to A and B by

$$\alpha =A+100B;\delta =-{10}^{4}B/(A+100B).$$ (4)

Table 4.

Calibration coefficients.^1,2

Run	A	B	α	δ
RT no. 80179
1	3985.8728E-63	−0.58756370E-6	3927.1164E-6	1.4961708
2	3985.8033E-6	−0.58753192E-6	3927.0502E-6	1.4961151
RT no. 18227
1	3985.6083E-6	−0.58744562E-6	3926.8637E-6	1.4959664
2	3985.5143E-6	−0.58736232E-6	3926.7781E-6	1.4957869
RT no. 18236
1	3985.6000E-6	−0.58752738E-6	3926.8472E-6	1.4961809
2	3985.4992E-6	−0.58739730E-6	3926.7594E-6	1.4958831
RT no. 18237
1	3985.5769E-6	−0.58739055E-6	3926.8379E-6	1.4958360
2	3985.5229E-6	−0.58742386E-6	3926.7805E-6	1.4959427
RT no. 8202
1	3985.7019E-6	−0.58757620E-6	3926.9443E-6	1.4962682
2	3985.6890E-6	−0.58759525E-6	3926.9295E-6	1.4963224
RT no. 8204
1	3985.7229E-6	−0.58762304E-6	3926.9606E-6	1.4963813
2	3985.6862E-6	−0.58754853E-6	3926.9313E-6	1.4962027
RT no. 8205
1	3985.6031E-6	−0.58753878E-6	3926.8492E-6	1.4962092
2	3985.5996E-6	−0.58756233E-6	3926.8434E-6	1.4962714

¹W(t′) = 1 + At′ + Bt′².

²Coefficients derived from values of W(ZN) and W(SN) and IPTS-68 assigned values of t′(ZN) and t′(SN).

³The notation E-6 signifies multiplication by 10⁻⁶.

The values of t′ calculated from the values of W(AL), W(AG), and W(AU) in table 3, using eq (3), represent values of temperature in the respective metal freezing point cells during freezing experiments, specifically at the mid-point of the resistor of a fully immersed thermometer. The values obtained from runs 1 and 2 are listed in table 5.

Table 5.

Derived values of t′ at AU, AG, and AL.^1,2

	t′(AU)		t′(AG)		t′(AL)
RT no.	Run 1	Run 2	Run 1	Run 2	Run 1	Run 2
80179	1062.5201	1062.5141	960.5363	960.5315	660.4079	660.4075
18227	1062.5127	1062.4938	960.5266	960.5098	660.4075	660.4006
18236	1062.5171	1062.5004	960.5394	960.5204	660.4114	660.4048
18237	1062,4747	1062.4928	960.5130	960.5215	660.4047	660.4055
8202	1062.5059	1062.5063	960.5175	960.5225	660.4082	660.4086
8204	1062.5232	1062.5098	960.5361	960.5256	660.4155	660.4133
8205	1062.4812	1062.4892	960.5142	960.5120	660.4088	660.4083

¹W(t′)= 1 +At′ + Bt′2.

²Values of t′ derived from values of W(FP) in table 3 and values of the coefficients in table 4.

Table 6 summarizes pertinent statistics of the values in table 5. The data are analyzed in various subsets and combinations of subsets as indicated. “Mean” is the arithmetic mean of the equally weighted values in the subset. “SD” is the estimate of the standard deviation of one value in the subset derived from the data in the subset. “Range” is the difference between the maximum and minimum values in the subset. All values are given in “degrees” on the “temperature scale”—close to degrees C or kelvins on ordinary scales.

Table 6.

Statistics of t′.¹

RT set		Run 1	Run 2	Combined runs
at gold point (Au)
NIM	Mean	1062.5062	1062.5003	1062.5032
	SD2	0.0212	0.0098	0.0156
	Range	0.0454	0.0213	0.0454
NBS	Mean	1062.5034	1062.5018	1062.5026
	SD	0.0211	0.0110	0.0151
	Range	0.0420	0.0206	0.0420
Combined Set	Mean	1062.5050	1062.5009	1062.5030
	SD	0.0194	0.0094	0.0148
	Range	0.0485	0.0249	0.0485
at silver point (AG)
NIM	Mean	960.5288	960.5208	960.5248
	SD	0.0119	0.0089	0.0106
	Range	0.0264	0.0217	0.0296
NBS	Mean	960.5226	960.5200	960.5213
	SD	0.0118	0.0071	0.0088
	Range	0.0219	0.0136	0.0241
Combined set	Mean	960.5262	960.5205	960.5233
	SD	0.0113	0.0075	0.0097
	Range	0.0264	0.0217	0.0296
at aluminum point (AL)
NIM	Mean	660.4079	660.4046	660.4062
	SD	0.0027	0.0029	0.0031
	Range	0.0067	0.0069	0.0108
NBS	Mean	660.4108	660.4101	660.4104
	SD	0.0041	0.0028	0.0031
	Range	0.0073	0.0050	0.0073
Combined set	Mean	660.4091	660.4069	660.4080
	SD	0.0034	0.0039	0.0037
	Range	0.0108	0.0127	0.0149

¹Statistics derived from values of t′ in table 5.

²SD: estimate of standard deviation of one value in indicated set.

Table 7 gives the temperature equivalents of the resistance ratio changes between run 1 and run 2. The temperature differences are estimated from

$$\mathrm{\Delta }t=\mathrm{\Delta }W/(\text{d}W/\text{d}t),$$ (5)

where ΔW = W(run 2) − W(run 1), and W(run 1) is the value of W(FP) determined in run 1 at a fixed point, and W(run 2) is the value of W(FP) at the same fixed point determined during run 2, both taken from table 3. The derivative dW/dT, obtained by differentiating eq (3), is evaluated using the coefficients from table 4 and the mean value of t′ at the fixed point given in table 6 or the value of t′ assigned to the fixed point.

Table 7.

Temperature equivalent of resistance ratio changes.^1,2

RT no.	AU	AG	AL	ZN	SN
80179	−0.0199	−0.0179	−0.0104	−0.0068	−0.0039
18227	−0.0211	−0.0216	−0.0149	−0.0071	−0.0047
18236	−0.0025	−0.0109	−0.0097	−0.0056	−0.0044
18237	−0.0166	−0.0206	−0.0148	−0.0082	−0.0039
Mean	−0.0150	−0.0177	−0.0125	−0.0069	−0.0042
8202	−0.0125	−0.0056	−0.0048	−0.0025	−0.0011
8204	0.0030	0.0012	0.0003	−0.0007	−0.0012
8205	−0.0031	−0.0110	−0.0044	−0.0016	−0.0006
Mean	−0.0042	−0.0051	−0.0030	−0.0016	−0.0010
Combined
Mean	−0.0104	−0.0123	−0.0084

¹Values derived from difference (run 2—run 1) in resistance ratio values given in table 3.

²Values expressed in terms of t′.

It is instructive to evaluate t′ from the values of W(AU), W(AG), and W(AL) determined in run 2 using the values of the coefficients determined in run 1. The results of this procedure are given in table 8; these values are to be compared with the original run 1 values in tables 5 and 6. It can be seen that the temperature differences are the same as the temperature equivalent changes shown in table 7. This is to be expected, since both evaluations are based on the same “calibration coefficients”; the changes are thus due only to the changes in W(AU), W(AG), and W(AL) between the two runs. A comparison of the statistics in table 8 with those in table 6 show that upon prolonged heating at high temperature the thermometers may change, resulting in changes in temperature values and increases in standard deviation and range if the thermometers are not recalibrated. Table 8 also shows similar results using run 2 coefficients and run 1 resistance ratios.

Table 8.

Derived values of t′ at AU, AG, and AL.^1,2

Run 1 coefficients; run 2 W(AU), W(AG), W(AL)
RT no.	t′(AU)	t′(AG)	t′(AL)
80179	1062.5003	960.5184	660.3975
18227	1062.4917	960.5051	660.3925
18236	1062.5146	960.5286	660.4017
18237	1062.4581	960.4925	660.3898
8202	1062.4934	960.5120	660.4034
8204	1062.5262	960.5373	660.4158
8205	1062.4781	960.5032	660.4052
Mean	1062.4946	960.5139	660.4008
SD3	0.0225	0.0155	0.0087
Range	0.0681	0.0448	0.0260
Run 2 coefficients; run 1 W(AU), W(AG), W(AL)
RT no.	t′(AU)	t′(AG)	t′(AL)
80179	1062.5340	960.5494	660.4178
18227	1062.5148	960.5314	660.4155
18236	1062.5026	960.5313	660.4145
18237	1062.5094	960.5420	660.4203
8202	1062.5188	960.5280	660.4135
8204	1062.5068	960.5244	660.4130
8205	1062.4922	960.5230	660.4127
Mean	1062.5112	960.5328	660.4153
SD	0.0132	0.0096	0.0028
Range	0.0418	0.0264	0.0076

¹W(t′)= l+ At′ + Bt′².

²Values of t′ derived from indicated values of W(FP) in table 3 and indicated values of the coefficients in table 4.

³SD: estimate of standard deviation of one value in set.

The results of an analysis at the silver point using a different “temperature scale” formulation are given in table 9. In this case, t″ is defined in terms of a quadratic relation between W(t″) and t″, as in eq (3), but with the coefficients determined at the aluminum and gold points (and at 0 °C). The coefficients are determined from the values of W(AL) and W(AU) given in table 3; the values of t″ assigned to these points, t″(AL)=660.408 and t″ (AU)= 1062.503, are the means of the combined sets and runs at the aluminum and gold points given in table 6. The statistics in table 9 are analogous to the statistics for t′ at the silver point given in table 6.

Table 9.

Statistics of t′ at silver point.^1,2

RT set		Run 1	Run 2	Combined runs
NIM	Mean	960.5269	960.5240	960.5254
	SD3	0.0052	0.0042	0.0046
	Range	0.0121	0.0103	0.0139
NBS	Mean	960.5211	960.5200	960.5206
	SD	0.0063	0.0009	0.0041
	Range	0.0124	0.0018	0.0124
Combined set	Mean	960.5244	960.5223	960.5233
	SD	0.0060	0.0038	0.0049
	Range	0.0171	0.0103	0.0171

¹W(t″)= 1+at″ +bt″² , where the coefficients a and b are determined from values of W(AL) and W(AU) given in table 6, and t″(AL)=660.408, t″(AU)=1062.503 (see table 6).

²Values of t″(AG) derived from values of W(AG) given in table 3 using the above equation.

³SD: estimate of standard deviation of one value in indicated set.

The value of R (TP) was determined six times for each thermometer during each of the two runs, as indicated in tables A1a–g. Table 10 presents a summary of the changes that occurred in R (TP). The numbers in the table give relative, or fractional, changes in parts per million (parts in 10⁶). The “Range” for a thermometer is the difference between the largest and the smallest of its six R(TP) values in a run. The other two statistics, “Max” and “RMS,” deal with successive differences between values of R(TP) in a given run. These successive differences are of interest because the value of W(FP) is calculated from the mean of successive values of R(TP) bracketing a value of R(FP). “Max” is the largest of such successive differences in a run, without regard to sign of the difference. “RMS” is the square root of the mean of the squares of such successive differences.

Table 10.

Variations in R(TP).¹ (Values given are parts in 10⁶)²

	Run 1			Run 2
RT no.	Range3	Max4	RMS5	Range	Max	RMS
80179	5.6	4.8	3.2	7.6	5.0	3.0
18227	2.8	2.5	1.4	2.0	2.0	1.6
18236	4.8	4.8	2.9	2.6	1.7	1.1
18237	3.2	3.2	2.3	6.1	2.9	1.9
8202	8.3	5.5	2.9	2.5	2.5	1.9
8204	7.0	4.0	2.3	5.7	5.0	3.2
8205	3.8	2.3	1.4	9.5	5.5	3.1

¹Values derived from values of R(TP) in tables A1a-g.

²A fractional difference in R(TP) of 4×10⁻⁶ is equivalent to a temperature interval of about 1 mK at the triple point of water.

³Range: fractional difference between largest and smallest value of R(TP) in a single run.

⁴Max: magnitude of largest fractional difference between two successive values of R(TP) in a single run.

⁵RMS: root-mean-square of fractional differences between successive values of R(TP) in a single run.

5.2. Second Experiment

The data obtained in the second experiment may be examined by plotting thermometer resistance as a func-tion of time. Figures 3 — 8 are plots of the data given in tables A2a–f. The data points show results of the various electrical guard configurations; the data for each are connected by solid lines to form “freezing curves” of the silver as it solidified. For the NIM thermometers, the only possible guard configurations were with the external guard connected to or disconnected from the bridge guard driving circuit, since the thermometers had no internal guarding system. The NBS thermometers were measured with both the internal and external guards connected to the drive circuit, with only the external guard connected, with only the internal guard connected, or with neither guard connected. The various configurations are labeled in the figures. The temperature scaling brackets shown in the figures are estimated from the relation

$$\mathrm{\Delta }t=(\mathrm{\Delta }R/R)\times W/(\text{d}W/\text{d}t),$$ (6)

where R is thermometer resistance at the silver point, W is W(AG) taken from table 3, and the derivative dW/dt, found by differentiating eq (3), is evaluated at the silver point using the coefficients in table 4 and the mean value of t′(AG) in table 6.

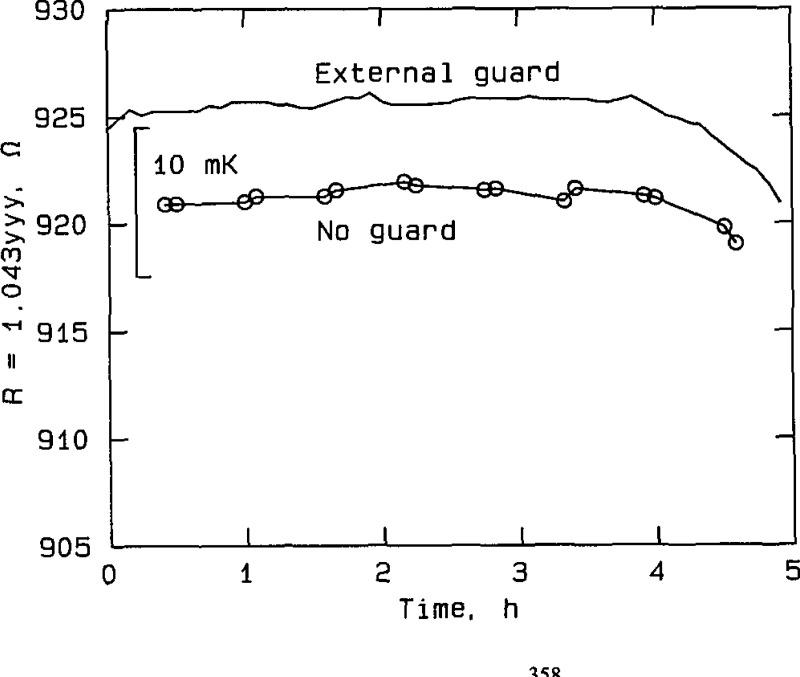
Figure 3.

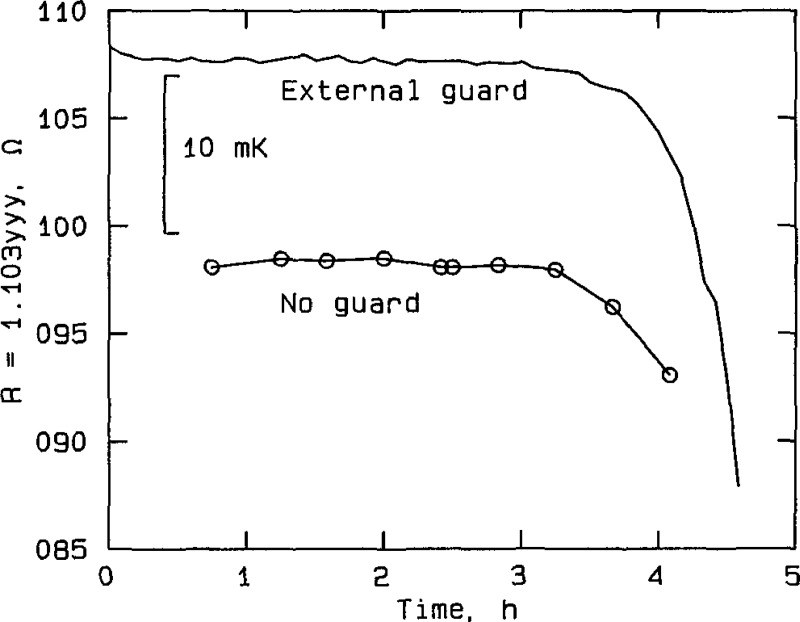
Effect of guarding at silver point, RT No. 80179, plotted from the data in table A2a. The curve labeled “External guard” represents measurements taken with the external guard connected to the bridge guard circuit. The curve labeled “No guard” represents measurements taken with the guard disconnected.

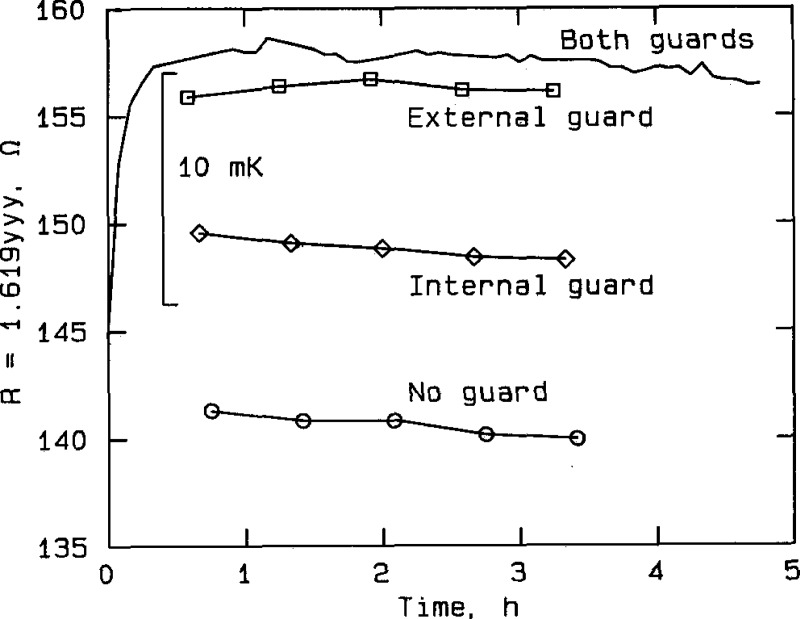
Figure 8.

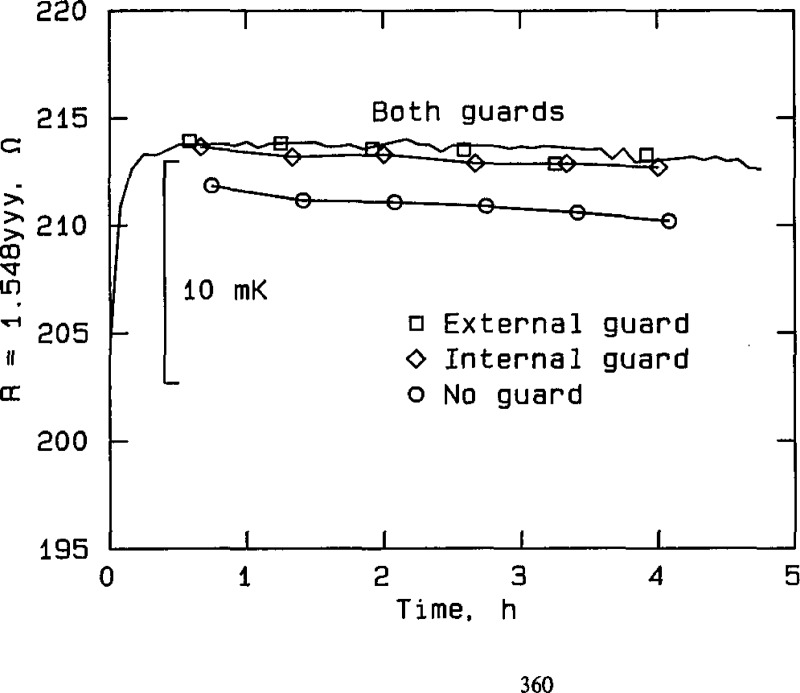
Effect of guarding at silver point, RT No. 8205, plotted from the data in table A2f. The curve labeled “Both guards” represents measurements taken with both the external guard and the internal thermometer guard connected to the bridge guard circuit. The curve labeled “External guard” represents measurements taken with only the external guard connected, and the curve labeled “Internal guard” represents measurements taken with only the internal guard connected. The curve labeled “No guard” represents measurements taken with neither guard connected to the bridge guard circuit.

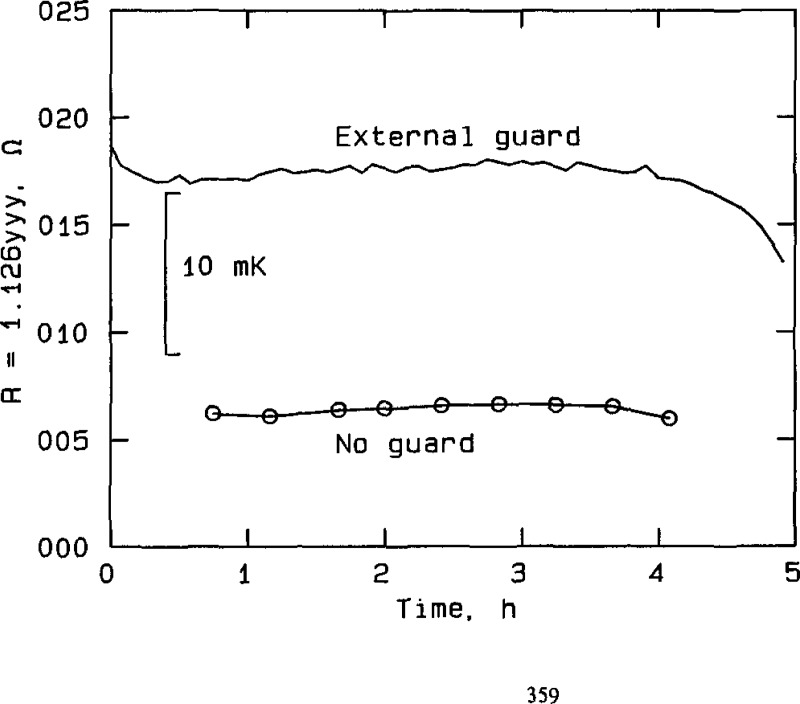
Figure 4.

Effect of guarding at silver point, RT No. 18236, plotted from the data in table A2b. The curve labeled “External guard” represents measurements taken with the external guard connected to the bridge guard circuit. The curve labeled “No guard” represents measurements taken with the guard discon

Figure 5.

Effect of guarding at silver point, RT No. 18237, plotted from the data in table A2c. The curve labeled “External guard” represents measurements taken with the external guard connected to the bridge guard circuit. The curve labeled “No guard” represents measurements taken with the guard disconnected.

Figure 6.

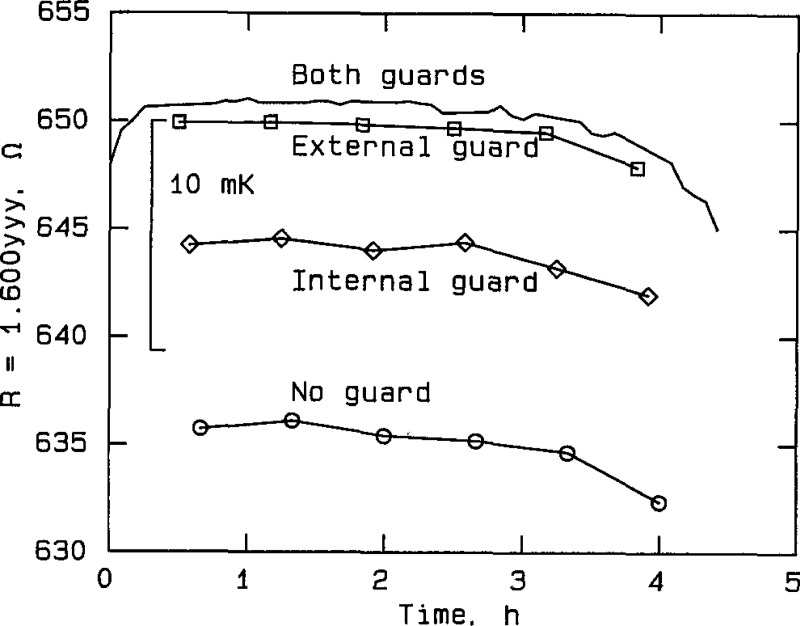
Effect of guarding at silver point, RT No. 8202, plotted from the data in table A2d. The curve labeled “Both guards” represents measurements taken with both the external guard and the internal thermometer guard connected to the bridge guard circuit. The curve labeled “External guard” represents measurements taken with only the external guard connected, and the curve labeled “Internal guard” represents measurements taken with only the internal guard connected. The curve labeled “No guard” represents measurements taken with neither guard connected to the bridge guard circuit.

Figure 7.

Effect of guarding at silver point, RT No. 8204, plotted from the data in table A2e. The curve labeled “Both guards” represents measurements taken with both the external guard and the internal thermometer guard connected to the bridge guard circuit. The unlabeled points lying on or close to the curve, designated by unconnected open symbols, represent measurements taken with only the external guard connected. The curve labeled “Internal guard” represents measurements taken with only the internal guard connected. The curve labeled “No guard” represents measurements taken with neither guard connected to the bridge guard circuit.

5.3. Third Experiment

The data obtained in the third experiment may also be examined by plotting. In this case the differences between thermometer indications at full immersion and at reduced immersion are plotted as a function of immersion. We start by computing for each thermometer the resistance differences,

$$\mathrm{\Delta }R=R(\text{station}x)-R(\text{station}0),$$ (7)

from the data in tables A3a and A3b. R (station x) is the resistance measured when the thermometer is at one of the stations above station 0. R (station 0) is the average of resistance measurements at station 0 before and after the measurement at station x. The resistance differences are then converted to equivalent temperature differences using eq (6), but with the second term evaluated for the zinc point. The resulting temperature differences are plotted as a function of immersion station up to station 10 in figures 9 and 10. The straight line with intercept at Δt = 0 in the plots represents the expected decrease in temperature with immersion due to the hydrostatic pressure of the liquid metal.

Figure 9.

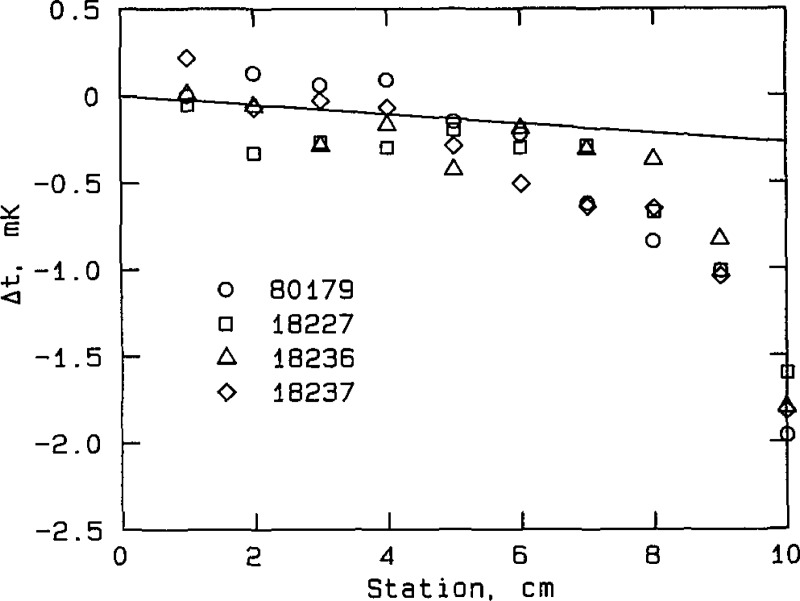
Effect of immersion in zinc cell at the freezing point, NIM thermometers, plotted from the data in table A3a. “Station” is the vertical location of the thermometer in the cell well; it represents the elevation of the thermometer, in cm, above full immersion. The thermometer is fully immersed and resting on the bottom of the cell well at station 0. Δ t is the temperature equivalent of the difference in thermometer resistance, measured when the thermometer is fully immersed at station 0 and when it is elevated to the indicated station. The straight line represents the expected temperature gradient due to the hydrostatic pressure of the liquid zinc.

Figure 10.

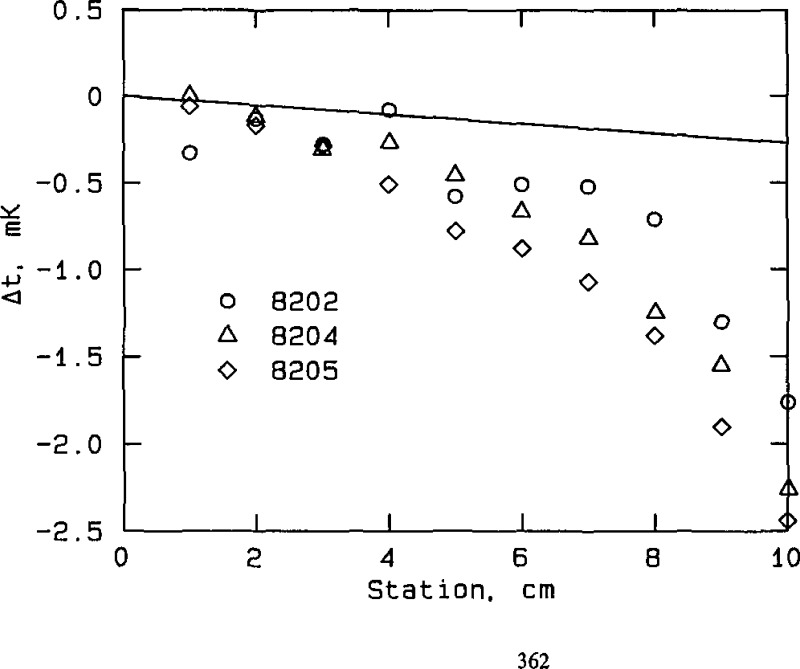
Effect of immersion in zinc cell at the freezing point, NBS thermometers, plotted from the data in table A3b. “Station” is the vertical location of the thermometer in the cell well; it represents the elevation of the thermometer, in cm, above full immersion. The thermometer is fully immersed and resting on the bottom of the cell well at station 0. Δ t is the temperature equivalent of the difference in thermometer resistance, measured when the thermometer is fully immersed at station 0 and when it is elevated to the indicated station. The straight line represents the expected temperature gradient due to the hydrostatic pressure of the liquid zinc.

6. Evaluation of Thermometer Characteristics

6.1. Long-Time Stability at High Temperature

The effect of 100 h exposure at 1100 °C upon the thermometers may be judged from the results presented in tables 3–10. Changes in derived values can be observed, and the group of thermometers as a whole tends to exhibit a downward drift in resistance ratio upon exposure (see tables 3 and 7). The results in table 7 show average changes for the group as a whole to be equivalent to 10.4 mK at the gold point, 12.3 mK at the silver point, and 8.4 mK at the aluminum point after the 100 h exposure. A comparison of the results in table 6 and 8, based on run 1 “calibration coefficients,” shows an increase in the variability of extrapolated values of t′ after the exposure.

However, the thermometers are apparently not degraded in their ability to measure values on the designated “temperature scale” because of the exposure, as shown by a comparison of the statistics for run 1 and run 2 in table 6. Upon “recalibration” at the tin and zinc points, the mean extrapolated values of t′ at the gold, silver, and aluminum points in run 2 differ little from the values obtained in run 1; the differences are 4.1, 5.7, and 2.3 mK respectively. Similarly, the statistics in table 9 show a change of only 2.1 mK in the mean value of t″ at the silver point. As to thermometer variability, the statistics show the variability of t′, after recalibration, actually to be less in run 2 than in run 1. This is attributed more to a somewhat better precision in measurements in run 2 than to an effect of the exposure. Table 10 shows little difference in the variability of R(TP) due to exposure.

6.2. Short-Time Stability upon Temperature Cycling

The short-time stability of a thermometer subjected to the temperature cycling of either run in the first experiment, which is assumed to be typical for a thermometer calibration procedure, may be partially assessed from variations in the thermometer resistance at the triple point of water. The results are given in table 10. The variability of resistance ratios will depend in part on the variability of R (TP), since a resistance ratio is derived from the mean of before and after R (TP) determinations. Thus, the root-mean-square variations of R (TP) given in the table could be expected to contribute the following temperature equivalents to the standard deviation of a determination of W(FP): 0.9 to 2.7 mK at the gold point, 0.8 to 2.4 mK at the silver point, 0.6 to 1.7 mK at the aluminum point.

6.3. Temperature Coefficient of Resistance

The high values of the alpha coefficient given in table 4 show that the platinum in all of the thermometers is very pure and in a well defined physical state. The changes in alpha coefficients produced by the 100 h exposure at 1100 °C are consistent with the changes observed in resistance ratios at the fixed points.

6.4. Immersion Characteristics

The results of the third experiment provide some information about thermometer immersion characteristics. It must be emphasized that immersion behavior depends not only on thermometer characteristics, but also on details of the environment surrounding the thermometer. Figures 9 and 10 show the immersion behavior of the thermometers in the zinc cell.

The set of NIM thermometers appears to “track” the temperature gradient produced by hydrostatic pressure over the bottom 4 cm of immersion, while the set of NBS thermometers probably tracks the gradient over the bottom 2 cm of immersion. Consequently, immersion losses at the zinc point are probably not a major source of error in the temperature determinations with any of the thermometers. While it is believed that immersion losses at other fixed points used in the experiments are not a limiting source of error, a more thorough examination of thermometer immersion behavior in all of the fixed-point cells would be highly desirable, if measurements could be made with adequate precision (see below).

6.5. Heating Effect of Measuring Current

Heating effects at all Fixed points are listed in tables Ala through Alg. It may be noted that the heating effect in the NIM thermometers due to the 4 mA measuring current is small and almost negligible. The larger heating effect in the NBS thermometers (and also the poorer immersion characteristic noted above) is attributable to resistor design; half the resistor wire is remote from the wall of the thermometer sheath in the toroidal resistor.

6.6. Electrical Leakage of Thermometer Supporting Parts

The results of the second experiment, plotted in figures 3 through 8, provide some information about the effects of electrical leakage in the thermometers. The experiment takes advantage of the electrical guard driving circuit available in the automatic bridge used. The internal guard system in the guarded lead thermometers (NBS) reduces the error due to electrical leakage from lead to lead in the thermometer, and from the thermometer leads to the bridge through ground. It does not, however, prevent leakage at the unguarded resistor. The external guard temporarily installed on the thermometers reduces only the effects due to leakage through ground between the thermometer and the grounded bridge.

It is evident from the data that leakage through ground is a major source of error in all of the thermometers when they are measured with a grounded instrument, and that the internal guard system used only partially eliminates the error. Without any guarding, leakage effects at the silver point can amount to 20 mK or more. In other preliminary tests with internally guarded thermometers, it has been found that the effect is even greater at the gold point, but may be very small at the aluminum point. The data do not reveal whether the external guard completely eliminates the leakage through ground.

The data show that the effect can vary considerably from thermometer to thermometer. The effect may also vary from time to time in a particular thermometer. It has been observed that in some thermometers, in the absence of an external guard, a small movement of the thermometer during measurement in a high temperature fixed-point cell can alter the electrical leakage. The effect thus adds to the imprecision of measurements, and, in experiments such as immersion tests in the cells, may obscure results.

6.7. Thermometer Durability

The thermometers experienced no catastrophic failures and no obvious mechanical degradation during the course of the experiments. The bending of support blades in two of the NIM thermometers and the separation of a lead in one of the NBS thermometers during initial stabilization suggest potential problem areas in the two designs.

6.8. Agreement Among Thermometers of Derived Temperature Values

The agreement among thermometers has been tested by means of two “temperature scales.” For one scale, on which values of temperature are designated by the symbol t′, the thermometers are “calibrated” at the tin and zinc points, and then the values of temperature are determined at the aluminum, silver, and gold points by extrapolation. For the other scale, on which the thermometers are “calibrated” at the aluminum and gold points, the values of temperature (designated by the symbol t″) at the silver point are determined by interpolation. These procedures allow comparison of derived values at the available constant-temperature fixed points, and the measures of variability given in tables 6 and 9 describe the agreement among thermometers using the procedures.

It is unlikely that a practical temperature scale at high temperatures would be defined by extrapolation from lower temperatures, as in the case of the “t′ scale.” Such a procedure exaggerates the variability in derived temperature values due to propagation of normal and unavoidable calibration errors. It is more likely that a practical scale will be devised so that values of temperature can be derived by interpolation between adjacent defining fixed points, as in the case of the “t″ scale”. Table 9 shows a smaller variability in t″ at the silver point (an interpolated value) than is shown, in table 6 for t′ at the silver point (an extrapolated value). A practical temperature scale utilizing all of the fixed points, including the silver point, could be expected to exhibit even less variability in derived temperature values. Therefore, the variations among thermometers reported here are larger than would be expected with the use of a well-designed temperature scale; the variations should be considered as upper bounds on thermometer variability.

Despite its limitations, the “t′ scale” is useful for comparison purposes because of its simplicity and because the data necessary for deriving values on it are often available. In the present case, it reveals little difference between the two groups of thermometers, and in fact, all seven thermometers may be considered as a single set. It is interesting to compare these results with results obtained earlier using other sets of thermometers. This is done in table 11, where the results obtained with 2.5-ohm guarded-lead thermometers measured with the grounded automatic bridge [3], and the results obtained with 0.25-ohm unguarded “birdcage” thermometers measured with isolated dc instrumentation [11], are summarized along with the present results. The summary shows differences between mean values at the fixed points that may be attributable, at least in part, to leakage problems. The summary also shows a decreasing variability in measurements in the past decade, though the decrease is not very dramatic.

Table 11.

Statistics of t′ at fixed points.

RT set		AU	AG	AL
NIM/NBS1	Mean	1062.5030	960.5233	660.4080
(14/7)	SD4	0.0148	0.0097	0.0037
1984	Range	0.0485	0.0296	0.0149
NBS 2.5 ohm2	Mean	1062.4898	960.5154	660.4127
(11,16/8)	SD	0.0114	0.0079	0.0024
1982	Range	0.0341	0.0243	0.0088
Birdcage3	Mean	1062.5308	960.5230	- - - -
(27/9)	SD	0.0191	0.0132	(0.0032)
1971	Range	0.0816	0.0541	(0.0087)

¹NIM/NBS: 14 independent determinations at each of the fixed points with 7 thermometers, this report.

²NBS 2.5 ohm: 11 independent determinations at AU, 16 independent determinations at AG and AL with 8 thermometers, reported [3] in 1982.

³Birdcage: 27 independent determinations at AU, AG, and the antimony point with 9 thermometers, reported [11] in 1971.

⁴SD: estimate of standard deviation of one value in indicated set.

7. Summary and Conclusions

The results of the experiments reported here show that the two sets of high-temperature platinum, resistance thermometers tested, thermometers from different sources and of different design, behaved in a similar manner. The thermometers proved to be enough alike in their characteristics and performance that they could be considered as a single class.

It was found that upon prolonged exposure to high temperature the resistance ratios of the thermometers, on the average, changed by the equivalent of only 8 to 12 mK at high temperature fixed points. The exposure (100 h at 1100 °C) was probably more severe than that to which thermometers would normally be subjected.

The thermometers were subjected to cycling between high temperatures and room temperature, comparable to cycling that would be encountered in normal use and calibration. The variability in thermometer resistance at the triple point of water with such cycling, expressed as a root-mean-square relative change in resistance per cycle, was found to range from about 1 to 3 parts in 10⁶, This variability in resistance is equivalent to temperature increments of 0.3 to 0.8 mK at the triple point; it would contribute the equivalent of about 1 to 3 mk to the variability of resistance ratios at the gold point derived from the mean of bracketing triple-point determinations.

The thermometers proved to be durable; the 100-h exposure produced no pronounced mechanical change in them, and throughout the tests their alpha coefficients remained greater than 0.0039268 K⁻¹. Self-heating effects and immersion characteristics of the thermometers were found to be commensurate with thermometer design and not to be accuracy-limiting sources of error. When the thermometers were calibrated on a simple quadratic “temperature scale” and values determined by extrapolation to high temperatures, the standard deviation of a single thermometer measurement was estimated to be about 4 mK at the aluminum point, 10 mK at the silver point, and 15 mK at the gold point. These values were found to compare favorably with values determined in the past by other sets of low resistance thermometers.

In contrast, it was found that electrical leakage through ground, between a thermometer at high temperature and a grounded measuring instrument, introduced large errors. Errors equivalent to 20 mK or more were observed at the silver point, and even greater errors were indicated at the gold point. Internal guarding of thermometer leads only partially eliminated the leakage, while the use of an electrical guard outside the thermometer appeared to be more effective. Consequently, the results reported here are probably biased by errors due to leakage effects, and variations in the leakage have also probably contributed to measurement imprecision. Electrical leakage through ground is believed to be the single largest source of error in the experiments.

Despite the problems with electrical leakage, it may be concluded from the results of the experiments that the thermometers tested are as good as or better than other thermometers tested in the past. A prior assessment has placed an uncertainty of about 10 mK on “state-of-the-art” resistance thermometer measurements up to the gold point [14]. In view of their exceptional long-time stability, agreement in derived temperature values, and other favorable characteristics, the present thermometers could be expected to perform equally as well, or better, if they were used so as to eliminate biases due to leakage.

Biography

About the Author: J. P. Evans is a physicist in the Temperature and Pressure Division of NBS’ Center for Basic Standards.

APPENDIX

Table A1a.

Resistance of thermometer 80179 at fixed points.

	Run 1				Run 2
FP1	R(TP)2	R (FF)3	HE(4)4		R(TP)	R(FP)	HE(4)
TP	0,24354530		10		0.24355153		23
AU		1.11338142		17		1.11339495		30
TP	0.24354484		37		0.24355032		19
AG		1.04390980		22		1.04391980		11
TP	0.24354602		10		0.24355100		4
AL		0.82218768		15		0.82219719		20
TP	0.24354487		19		0.24355033		1
ZN		0.62563109		15		0.62563938		9
TP	0.24354467		22		0.24355013		8
SN		0.46097202		24		0.46097844		28
TP	0.24354465		16		0.24354968		14

¹Measurements taken in order indicated.

²R (TP): thermometer resistance (ohms) at triple point of water for zero measuring current.

³R(FP): thermometer resistance (ohms) at indicated metal freezing point for zero measuring current.

⁴HE(4): increase in resistance of thermometer (ohms × 10⁻⁸) due to heating effect of 4 mA measuring current.

Table A1b.

Resistllnce of thermometer 18227 at fixed points.

	Run 1				Run 2
FP1	R (TP)2	R(FP)3	HE(4)4		R (TP)	R (FP)	HE(4)
TP	0.26036578		17		0.26036839		23
AU		1.19023546		41		1.19023032		24
TP	0.26036617		8		0.26036787		29
AG		1.11596340		14		1.11595591		6
TP	0.26036605		15		0.26036834		4
AL		0.87894006		14		0.87893466		19
TP	0.26036600		27		0.26036791		11
ZN		0.66881872		38		0.66881738		6
TP	0.26036586		10		0.26036793		16
SN		0.49279685		26		0.49279604		24
TP	0.26036652		19		0.26036836		5

^1,2,3,4See footnotes of Table A1a.

Table A1c.

Resistance of thermometer 18236 at fixed points.

	Run 1				Run 2
FP1	R(TP)2	R(FP)3	HE(4)4		R(TP)	R (FP)	HE(4)
TP	0.25736827		1		0.25737145		17
AU		1.17651167		38		1.17652127		27
TP	0.25736951		17		0.25737131		16
AG		1.10310634		20		1.10310718		14
TP	0.25736898		21		0.25737129		18
AL		0.86881563		23		0.86881446		42
TP	0.25736916		10		0.25737091		17
ZN		0.66111513		26		0.66111592		14
TP	0.25736839		18		0.25737114		13
SN		0.48712186		19		0.48712267		24
TP	0.25736902		4		0.25737158		11

^1,2,3,4See footnotes of Table A1a.

Table A1d.

Resistance of thermometer 18237 at fixed points.

	Run 1				Run 2
FP1	R(TP)2	R(FP)3	HE(4)4		R(TP)	R(FP)	HE(4)
TP	0.26271185		20		0–26271457		0
AU		1.20094154		45		1.20093838		42
TP	0.26271268		5		0.26271380		7
AG		1.12601457		23		1.12600557		14
TP	0.26271186		16		0.26271372		2
AL		0.88685765		35		0.88685013		14
TP	0.26271188		14		0.26271298		18
ZN		0.67484408		23		0.67483947		20
TP	0.26271194		9		0.26271309		19
SN		0.49723614		30		0.49723423		20
TP	0.26271258		4		0.26271339		10

^1,2,3,4See footnotes of Table A1a.

Table A1e.

Resistance of thermometer 8202 at fixed points.

	Run 1				Run 2
FP1	R(TP)2	R (FP)3	HE(4)4		R(TP)	R(FP)	HE(4)
TP	0.37344847		82		0.37345575		77
AU		1.70715643		123		1.70717762		121
TP	0.37344900		72		0.37345655		87
AG		1.60063481		87		1.60065483		89
TP	0.37345106		67		0.37345562		102
AL		1.26069404		98		1.26070485		100
TP	0.37345126		70		0.37345654		92
ZN		0.95931356		117		0.95932446		84
TP	0.37345063		84		0.37345639		84
SN		0.70683891		120		0.70684723		92
TP	0.37345157		69		0.37345619		86

^l,2,3,4See footnotes of Table A1a.

Table A1f.

Resistance of thermometer 8204 at fixed points.

	Run 1				Run 2
FP1	R(TP)2	R(FP)3	HE(4)4		R(TP)	R(FP)	HE(4)
TP	0.36121077		58		0.36121424		50
AU		1.65121770		97		1.65124068		86
TP	0.36121028		72		0.36121557		56
AG		1.54818827		90		1.54820525		64
TP	0.36121172		55		0.36121378		65
AL		1.21938181		82		1.21938917		91
TP	0.36121142		66		0.36121351		64
ZN		0.92787383		94		0.92787912		104
TP	0.36121198		74		0.36121466		72
SN		0.68367531		88		0.68367855		102
TP	0.36121282		59		0.36121529		62

^1,2,3,4See footnotes of Table A1a.

Table A1g.

Resistance of thermometer 8205 at fixed points.

	Run 1				Run 2
FP1	R(TP)2	R(FP)3	HE(4)4		R(TP)	R (FP)	HE(4)
TP	0.37777464		77		0.37777391		94
AU		1.72688249		105		1.72688057		103
TP	0.37777472		80		0.37777600		77
AG		1.61914245		88		1.61913827		89
TP	0.37777384		87		0.37777615		85
AL		1.27526979		106		1.27527344		97
TP	0.37777447		89		0.37777749		62
ZN		0.97040708		124		0.97041140		102
TP	0.37777487		85		0.37777686		84
SN		0.71501507		117		0.71501814		111
TP	0.37777526		75		0.37777734		80

^1,2,3,4See footnote of Table A1a.

Table A2a.

Effect of guarding at silver point, thermometer 80179.

No.1	Thermometer resistance2		No.	Thermometer resistance
	External Guard	No Guard		External Guard	No Guard
1	1.04392444		31	1.04392563
2	1.04392494		32	1.04392576
3	1.04392533		33	1.04392535
4	1.04392506		34		1.04392155
5	1.04392526		35		1.04392162
6		1.04392090	36	1.04392582
7		1.04392092	37	1.04392580
8	1.04392524		38	1.04392595
9	1.04392531		39	1.04392578
10	1.04392552		40	1.04392577
11	1.04392542		41		1.04392101
12	1.04392569		42		1.04392163
13		1.04392100	43	1.04392580
14		1.04392127	44	1.04392567
15	1.04392567		45	1.04392564
16	1.04392553		46	1.04392575
17	1.04392556		47	1.04392592
18	1.04392541		48		1.04392127
19	1.04392533		49		1.04392115
20		1.04392126	50	1.04392502
21		1.04392155	51	1.04392489
22	1.04392592		52	1.04392467
23	1.04392583		53	1.04392454
24	1.04392610		54	1.04392402
25	1.04392569		55		1.04391980
26	1.04392554		56		1.04391904
27		1.04392194	57	1.04392274
28		1.04392176	58	1.04392240
29	1.04392554		59	1.04392180
30	1.04392560		60	1.04392091

¹No: sequence number of reading. Resistance determinations made at 5 min intervals.

²All determinations made with normal measuring current.

Table A2b.

Effect of guarding at silver point, thermometer 18236.

No.1	Thermometer resistance2		No.	Thermometer resistance
	External Guard	No Guard		External Guard	No Guard
1	1.10310830		36	1.10310753
2	1.10310798		37	1.10310762
3	1.10310787		38	1.10310730
4	1.10310773		39	1.10310727
5	1.10310780		40		1.10309795
6	1.10310777		41	1.10310717
7	1.10310766		42	1.10310708
8	1.10310783		43	1.10310663
9	1.10310764		44	1.10310644
10		1.10309809	45		1.10309621
11	1.10310763		46	1.10310619
12	1.10310782		47	1.10310571
13	1.10310777		48	1.10310504
14	1.10310757		49	1.10310429
15	1.10310767		50		1.10309304
16		1.10309847	51	1.10310223
17	1.10310786		52	1.10310018
18	1.10310796		53	1.10309737
19	1.10310766		54	1.10309643
20		1.10309836	55	1.10309299
21	1.10310790		56	1.10308788
22	1.10310762		57	1.10307519
23	1.10310756		58	1.10300411
24	1.10310779		59	1.10234670
25		1.10309850	60	1.10218298
26	1.10310748		61	1.10208952
27	1.10310777		62	1.10228282
28	1.10310760		63	1.10229746
29	1.10310764		64	1.10229948
30		1.10309806	65	1.10228864
31		1.10309806	66	1.10227829
32	1.10310766		67	1.10225154
33	1.10310748		68	1.10226344
34	1.10310761		69	1.10225939
35		1.10309818	70	1.10224858

^1,2See footnotes of Table A2a.

Table A2c.

Effect of guarding at silver point, thermometer 18237.

No.1	Thermometer resistance2		No.	Thermometer resistance
	External Guard	No Guard		External Guard	No Guard
1	1.12601866		13	1.12601706
2	1.12601772		14	1.12601735
3	1.12601741		15		1.12600610
4	1.12601719		16	1.12601762
5	1.12601699		17	1.12601739
6	1.12601702		18	1.12601746
7	1.12601732		19	1.12601757
8	1.12601692		20	1.12601742
9	1.12601711		21		1.12600639
10		1.12600623	22	1.12601775
11	1.12601713		23	1.12601739
12	1.12601717		24	1.12601781
25		1.12600647	49	1.12601716
26	1.12601744		50		1.12600598
27	1.12601768		51	1.12601704
28	1.12601773		52	1.12601684
29	1.12601745		53	1.12601655
30		1.12600659	54	1.12601641
31	1.12601764		55	1.12601612
32	1.12601779		56	1.12601584
33	1.12601781		57	1.12601543
34	1.12601807		58	1.12601487
35		1.12600667	59	1.12601409
36	1.12601779		60	1.12601322
37	1.12601796		61	1.12601211
38	1.12601778		62	1.12601112
39	1.12601790		63	1.12601050
40		1.12600662	64	1.12600944
41	1.12601752		65	1.12600784
42	1.12601792		66	1.12600536
43	1.12601777		67	1.12600135
44	1.12601760		68	1.12599782
45		1.12600655	69	1.12599122
46	1.12601740		70	1.12597467
47	1.12601745		71	1.12561508
48	1.12601774		72	1.12534593

^1,2See footnotes of Table A2a.

Table A2d.

Effect of guarding at silver point, thermometer 8202.

No.1	Thermometer resistance2				No.	Thermometer resistance
	Both Guards	External Guard	Internal Guard	No Guard		Both Guards	External Guard	Internal Guard	No Guard
1	1.60064788				25				1.60063539
2	1.60064955				26	1.60065087
3	1.60065002				27	1.60065094
4	1.60065063				28	1.60065082
5	1.60065065				29	1.60065076
6	1.60065069				30	1.60065037
7		1.60064992			31		1.60064967
8			1.60064424		32			1.60064438
9				1.60063572	33				1.60063516
10	1.60065077				34	1.60065044
11	1.60065091				35	1.60065075
12	1.60065091				36	1.60065028
13	1.60065105				37	1.60065012
14	1.60065082				38	1.60065039
15		1.60064994			39		1.60064949
16			1.60064455		40			1.60064320
17				1.60063609	41				1.60063464
18	1.60065083				42	1.60065000
19	1.60065093				43	1.60064946
20	1.60065089				44	1.60064935
21	1.60065073				45	1.60064951
22	1.60065092				46	1.60064924
23		1.60064983			47		1.60064788
24			1.60064400		48			1.60064197
49				1.60063237	52	1.60064660
50	1.60064810				53	1.60064631
51	1.60064700				54	1.60064501

^1,2See footnote of Table A2a.

Table A2e.

Effect of guarding at silver point, thermometer 8204.

No.1	Thermometer resistance2				No.	Thermometer resistance
	Both Guards	External Guard	Internal Guard	No Guard		Both Guards	External Guard	Internal Guard	No Guard
1	1.54820421				30	1.54821341
2	1.54821086				31	1.54821373
3	1.54821266				32		1.54821351
4	1.54821332				33			1.54821288
5	1.54821325				34				1.54821089
6	1.54821350				35	1.54821369
7	1.54821376				36	1.54821357
8		1.54821392			37	1.54821368
9			1.54821365		38	1.54821359
10				1.54821185	39	1.54821371
11	1.54821378				40		1.54821286
12	1.54821371				41			1.54821287
13	1.54821390				42				1.54821059
14	1.54821361				43	1.54821350
15	1.54821382				44	1.54821356
16		1.54821381			45	1.54821305
17			1.54821318		46	1.54821356
18				1.54821116	47	1.54821293
19	1.54821386				48		1.54821328
20	1.54821364				49			1.54821270
21	1.54821367				50				1.54821020
22	1.54821375				51	1.54821312
23	1.54821354				52	1.54821318
24		1.54821355			53	1.54821301
25			1.54821331		54	1.54821318
26				1.54821108	55	1.54821297
27	1.54821401				56	1.54821306
28	1.54821376				57	1.54821263
29	1.54821373				58	1.54821261

^1,2See footnotes of Table A2a.

Table A2f.

Effect of guarding at silver point, thermometer 8205.

No.1	Thermometer resistance2				No.	Thermometer resistance
	Both Guards	External Guard	Internal Guard	No Guard		Both Guards	External Guard	Internal Guard	No Guard
1	1.61914472				9			1.61914954
2	1.61915280				10				1.61914129
3	1.61915553				11	1.61915803
4	1.61915653				12	1.61915813
5	1.61915731				13	1.61915796
6	1.61915743				14	1.61915798
7	1.61915755				15	1.61915860
8		1.61915587			16		1.61915636
17			1.61914904		38	1,61915773
18				1.61914080	39	1.61915751
19	1.61915808				40		1.61915609
20	1.61915782				41			1.61914825
21	1.61915737				42				1.61913994
22	1.61915749				43	1.61915756
23	1.61915748				44	1.61915748
24		1.61915669			45	1.61915719
25			1.61914880		46	1.61915722
26				1.61914080	47	1.61915693
27	1.61915787				48	1.61915708
28	1.61915801				49	1.61915726
29	1.61915779				50	1.61915712
30	1.61915791				51	1.61915721
31	1.61915779				52	1.61915681
32		1.61915617			53	1.61915736
33			1.61914839		54	1.61915669
34				1.61914015	55	1.61915660
35	1.61915767				56	1.61915658
36	1.61915781				57	1.61915638
37	1.61915745				58	1.61915644

^1,2See footnotes of Table A2a.

Table A3a.

Immersion characteristics of thermometers in zinc cell. ^1,3

Station2	Resistance of thermometer number				Station	Resistance of thermometer number
cm	80179	18227	18236	18237	cm	80179	18227	18236	18237
0	0.62564094	0.66881727	0.66111506	0.67483970	7	0.62563817	0.66881563	0.66111550	0.67483869
0	0.62564009	0.66881635	0.66111560	0.67483926	6	0.62563851	0.66881562	0.66111561	0.67483881
0	0.62563969	0.66881612	0.66111562	0.67483920	0	0.62563869	0.66881598	0.66111585	0.67483930
0	0.62563923	0.66881629	0.66111546	0.67483921	0	0.62563858	0.66881588	0.66111580	0.67483918
18	0.62469878	0.66772854	0.65999691	0.67377628	0	0.62563850	0.66881599	0.66111593	0.67483931
18	0.62468420	0.66769737	0.65997147	0.67371738	5	0.62563830	0.66881572	0.66111552	0.67483899
16	0.62532066	0.66845569	0.66074723	0.67446863	4	0.62563851	0.66881563	0.66111576	0.67483919
14	0.62555932	0.66871951	0.66101985	0.67474217	3	0.62563848	0.66881566	0.66111565	0.67483923
12	0.62562814	0.66880302	0.66110364	0.67482532	2	0.62563854	0.66881561	0.66111586	0.67483919
10	0.62563737	0.66881433	0.66111437	0.67483735	1	0.62563843	0.66881586	0.66111592	0.67483946
0	0.62563886	0.66881583	0.66111589	0.67483939	0	0.62563836	0.66881582	0.66111589	0.67483920
0	0.62563878	0.66881593	0.66111572	0.67483913	0	0.62563841	0.66881591	0.66111581	0.67483919
0	0.62563872	0.66881580	0.66111571	0.67483926	0	0.62563846	0.66881569	0.66111578	0.67483930
10	0.62563703	0.66881444	0.66111416	0.67483761	0	0.62563843	0.66881570	0.66111577	0.67483935
9	0.62563784	0.66881497	0.66111503	0.67483833	0	0.62563840	0.66881587	0.66111591	0.67483913
8	0.62563799	0.66881528	0.66111545	0.67483868

¹Resistance determinations made at 5 min intervals.

²Station: distance (cm) thermometer raised above full immersion.

³All determinations made with normal measuring current.

Table A3b.

Immersion characteristics of thermometers in zinc cell.^1,3

Station2	Resistance of thermometer number
cm	8202	8204	8205
0	0.95931822	0.92788595	0.97041322
0	0.95931846	0.92788611	0.97041326
0	0.95931850	0.92788615	0.97041342
0	0.95931844	0.92788625	0.97041309
18	0.95818532	0.92679249	0.96920870
18	0.95816807	0.92676693	0.96918238
16	0.95884974	0.92745293	0.96990494
14	0.95922028	0.92779867	0.97029903
12	0.95930572	0.92787549	0.97039663
10	0.95931639	0.92788322	0.97040958
0	0.95931885	0.92788618	0.97041311
0	0.95931879	0.92788625	0.97041361
0	0.95931866	0.92788612	0.97041344
0	0.95931875	0.92788634	0.97041330
10	0.95931649	0.92788339	0.97041009
9	0.95931708	0.92788429	0.97041080
8	0.95931786	0.92788468	0.97041149
7	0.95931810	0.92788521	0.97041190
6	0.95931812	0.92788541	0.97041214
0	0.95931881	0.92788616	0.97041331
0	0.95931876	0.92788638	0.97041326
0	0.95931920	0.92788636	0.97041333
0	0.95931870	0.92788626	0.97041335
5	0.95931818	0.92788564	0.97041231
4	0.95931882	0.92788588	0.97041266
3	0.95931856	0.92788584	0.97041295
2	0.95931876	0.92788607	0.97041311
1	0.95931850	0.92788622	0.97041325
0	0.95931916	0.92788619	0.97041332
0	0.95931833	0.92788620	0.97041322
0	0.95931903	0.92788607	0.97041312
0	0.95931882	0.92788632	0.97041306
0	0.95931895	0.92788615	0.97041351

^1,2,3See footnotes of Table A3a.