Influence of life history tactics on transient dynamics: a comparative analysis across mammalian populations

Abstract

Most mammalian populations suffer from natural or human-induced disturbances; populations are no longer at the equilibrium (i.e. at stable (st)age distribution) and exhibit transient dynamics. From a literature survey, we studied patterns of transient dynamics for mammalian species spanning a large range of life history tactics and population growth rates. For each population, we built an age-structured matrix and calculated six metrics of transient dynamics. After having controlled for possible confounding effects of the phylogenetic relatedness among species using a Phylogenetic Principal Component Analysis and Phylogenetic Generalized Least-Squares models, we found that short-term demographic responses of mammalian populations to disturbance are shaped by generation time and growth rate. Species with a slow pace of life (i.e. species with a late maturity, a low fecundity, and a long lifespan) displayed decreases in population size after a disturbance, whereas fast-living species increased in population size. The magnitude of short-term variation in population size increased with asymptotic population growth, being buffered in slow-growing species (i.e. species with a low population growth rate), but large in fast-growing species. By demonstrating direct links between transient dynamics, life history (generation time), and ecology (demographic regime), our comparative analysis of transient dynamics clearly improves our understanding of population dynamics in variable environments and has clear implications for future studies of the interplay between evolutionary and ecological dynamics. As most populations in the wild are not at equilibrium, we recommend analyses of transient dynamics to be performed when studying population dynamics in variable environments.

Introduction

Natural or human-induced disturbances can affect population structure through demographic parameters such as survival or reproduction. For instance, diseases have been shown to affect mammalian survival (e.g., pneumonia in bighorn sheep Ovis canadensis (Jorgenson et al. 1997), keratoconjunctivitis epizootics in chamois Rupicapra rupicapra (Loison et al. 1996), facial tumor disease in Tasmanian devil Sarcophilus harrisii (Lachish et al. 2007), tularemia in hares Lepus europaeus (Runge et al. 2011) and canine distemper virus in spotted hyena Crocuta crocuta (Honer et al. 2012)). Extreme climatic events, such as El-Niño-Southern Oscillation, can impact population dynamics (e.g., Bradshaw et al. 2003 in New Zealand fur seals Arctocephalus forsteri and Cubaynes et al. 2011 in red-footed booby Sula sula). Finally, human-induced factors like translocations (Koons et al. 2005) or hunting (Servanty et al. 2011 in wild boar Sus scrofa) have also been shown to influence markedly population dynamics.

Even though disturbances often act on mammalian population dynamics, they are often ignored by biologists who often make the assumption of a stable population structure. Indeed, to study population dynamics, demographic parameters such as survival and reproduction are integrated into population projection models (PPM) from which the population growth rate, the stable (st)age distribution, the reproductive values, the sensitivities and the elasticities can be estimated (see Caswell 2001 for details about the procedures). These quantities are useful tools for biologists to predict the future of a population in a management or conservation context (Morris and Doak 2002; Mills 2007). These so-called asymptotic analyses, however, rely on the strong assumption that the population structure (for instance the age structure) is at equilibrium and remains stable over time. However, after a disturbance, a regime shift occurs (Hastings 2004) and the assumption of a stable population structure rarely holds in free-ranging populations. Some time is needed before a new equilibrium is reached, which is usually referred as the transient period (Stott et al. 2011). By ignoring this regime shift, management efforts may fail to achieve desired goals. For instance, in the desert tortoise Gopherus agassizii,Stott et al. (2012a) showed that in some cases, an asymptotic analysis would markedly underestimate the short-term decline. Likewise, Koons et al (2005) found that after 5 years of projection, transient population growth rates could differ from asymptotic growth rates by as much as 59 % and transient sensitivities by as much as 200 %.

There has recently been increasing interest in analyses relaxing the assumption of equilibrium, i.e., analyses of transient dynamics (Ellis and Crone 2013; Ezard et al. 2010; Koons et al. 2005; Townley et al. 2007). These applications have been stimulated by the development of methodologies to quantify transient dynamics. The damping ratio is a standard metric used to study the rate of convergence to the stable population structure (Caswell 2001). However, other metrics of transience have been developed (Neubert and Caswell 1997; Townley and Hodgson 2008; Ezard et al. 2010). These metrics can be split into two groups that quantify amplification (i.e., short-term increases in population size) or attenuation (i.e., short-term decreases in population size) of differences between initial and stable distributions (Ezard et al. 2010; Stott et al. 2011). In their recent review, Stott et al. (2011) highlighted these new tools and their use in population dynamics. In a pioneering work, Koons et al. (2005) performed a first preliminary analysis of transient dynamics in 6 mammal and bird species by studying short-term population growth rate and sensitivity. More recently, Stott et al. (2010) used different metrics to investigate how life history influences the transient dynamics of 108 plant species. They found that species at opposite ends of the scale of ecological succession (i.e., monocarps and trees) had large short-term variation in population size after a disturbance, in contrast to species with intermediate life history complexity (i.e., perennial herbs and shrubs).

To date, however, there has been no study of transient dynamics of age-structured populations covering a large range of life histories and demographic regimes. We aim here to fill the gap. Mammals have both large variability among life history tactics and a large number of available demographic data. Mammalian life history tactics are distributed along a continuum of generation times, a metric that provides the position of a given species on the slow-fast continuum (Gaillard et al. 2005), which is a major axis of variation in life history tactics in mammals (Gaillard et al. 1989; Bielby et al. 2007; Jeschke and Kokko 2009). The slow-fast continuum contrasts species characterized with an early maturity, a high fecundity, and a short lifespan to species with opposite characteristics (Stearns 1983; Gaillard et al. 1989). As a consequence, a fast species will be characterized by a short generation time and a slow species will be characterized by a long generation time. The large range of mammalian generation times (here from 2.6 years for Gunnison’s prairie dog Cynomys gunnisoni to 102.9 years for Indian rhinoceros Rhinoceros unicornis) along the slow-fast continuum provides a unique opportunity to investigate how life history tactics influence the magnitude of transient dynamics. Moreover, from a management and conservation viewpoints, a better understanding of short-term population responses to disturbances could allow managers to develop more appropriate strategies for these species (Ezard et al. 2010).

Here, we evaluate the effect on transient dynamics of both generation time and asymptotic growth rate (λ), the latter providing a measure of the demographic regime of a population and allowing a comparison of short-term dynamics across different growth regimes. More precisely, for 111 mammalian species for which the required demographic data were available, we investigate both the effects of generation time and of asymptotic population growth rate on six metrics of transient dynamics, after having accounted for the phylogenetic non-independence among species.

Methods

Data collection

Data on age at first reproduction, age-specific fecundity (i.e., average number of females produced by females of a given age) and age-specific survival were collected from the literature for 111 species of mammals with contrasting life histories (Table A1). When information was available for several populations of the same species, we retained the least perturbed population (i.e., not harvested, not facing predation or disease) as the most representative population for the species.

For each species, we built an age-structured matrix involving a pre-breeding census female-dominant model (Caswell 2001), in which mature individuals are grouped into a single age class whose members die at a fixed rate per projection interval. We standardized the matrix dimension using the age at first reproduction. We opted for the age at first reproduction over the observed longevity that is often used to measure the pace of life (e.g., Baudisch 2011); by doing so, we parametrized matrices that were not larger than necessary to incorporate the published age-specific differences in vital rates (Koons et al. 2005). For example, a density-independent time-invariant PPM for a species starting to breed at 4 years of age corresponds to:

$$\left(\begin{array}{cccc}0& 0& 0& S0.F4\\ S1& 0& 0& 0\\ 0& S2& 0& 0\\ 0& 0& S3& S4\end{array}\right)$$

where S0 is juvenile survival (between birth and 1 year of age), S_i, is survival between ages i and i+1, and F_i, is fecundity of individuals of age i. From 4 years of age onwards, the annual survival is S4. For each species, the generation time Tc, corresponding to mean age of the parents of the offspring produced by a cohort over its lifetime (Caswell 2001), was calculated as $T_c=\left(\sum _{i}i.S_i\cdot m_i\right)/\left(\sum _i{S}_i.m_i\right)$ with m_i, the number of female offspring born to a female of age i. The dominant eigenvalue of the matrix λ was also calculated. The λ value provides an assessment of the demographic regime of the population with λ of 1 when the population is stationary, λ<1 when the population is decreasing, and λ>1 when the population is increasing. As the slow-fast continuum of mammalian life histories has been shown to occur both with and without accounting for body size (Stearns 1983; Gaillard et al. 1989), we did not include species body size as a potential driver of transient dynamics.

Analysis of transient dynamics

Six metrics of transient dynamics, requiring no prior knowledge of the population’s demographic distribution, were calculated (see Table 1 for a list of these metrics and their biological meaning) using the package R “popdemo” (Stott et al. 2012a). Two groups of metrics were considered: amplification indices bringing together reactivity, Kreiss bounds on amplification and maximum amplification metrics and attenuation indexes bringing together first time step attenuation, Kreiss bounds on attenuation, and maximum attenuation metrics (Table 1). Reactivity and first time step attenuation are the maximal possible amplification and attenuation in the first time step. Maximal amplification and maximal attenuation are the largest possible amplification and attenuation that may be achieved at any time point of population projection. Finally, Kreiss bounds on amplification and Kreiss bounds on attenuation are time-independent. Those metrics were calculated from standardized PPM (i.e., PPM divided by λ) allowing direct comparison of both amplified and attenuated dynamics across species and allowing inferring relationships between those metrics and λ (see below). We did not use other well established indices of transient dynamics such as population momentum or inertia, because, even if they are strongly correlated with transient amplification/attenuation metrics (Stott et al. 2011), they are useful to demographers who have information on current population structure and who aim at comparing transient dynamics patterns within rather than between populations (Stott et al. 2010).

Table 1:

The six metrics of transient dynamics analyzed and their associated biological meaning.

Index	Amplification index	Biological meaning	Attenuation index	Biological meaning
One-time step transient	Reactivity (Reactivity)	The largest possible density (relative to asymptotic dynamics) that may be reached by the population in the first time-step after disturbance	First-time step attenuation (Firststepatt)	The smallest possible density (relative to asymptotic dynamics) that may be reached by the population in first time-step after disturbance
Kreiss bound	Kreiss bounds on amplification (Kmax)	The density a population must amplify (relative to asymptotic dynamics) before reaching its maximum overall size	Kreiss bounds on attenuation (Kmin)	The density a population must attenuate (relative to asymptotic dynamics) before reaching its minimum overall size
Maximum transient index	Maximum amplification (Rhomax)	The largest density (relative to asymptotic dynamics) that may be reached by the population overall	Maximum attenuation (Rhomin)	The smallest density (relative to asymptotic dynamics) that may be reached by the population overall

We performed a Phylogenetic Principal Component Analysis (PPCA) on these metrics (after log-transformation to describe more accurately the multiplicative nature of these indices) because the transience indices were highly interrelated (Table 2). However, species may share similar values in terms of transient dynamics as a result of common ancestry (Harvey and Pagel 1991). This problem generates dependency among the data, which, when not accounted for, may lead to the detection of spurious effects (Ives and Zhu 2006). To control for this non-independence among species, a phylogeny was derived from the phylogenetic supertree of mammals with topology and branch length provided by Bininda-Emonds et al. (2007) (see Figure A1). Because the complete mammalian supertree lacks direct estimates of ancestral dates based on the empirical data, relative branch lengths should be viewed with some caution and could contribute error to subsequent analyses. However, Barraclough (2010) has shown that while lacks of empirical estimates of dates can limit the application of specific tests, the comparative methods we used here are robust to error in branch lengths. From this phylogenetic supertree, we thus performed a PPCA using the procedure implemented in R (package phytools, Revell 2009). The PPCA allowed reducing the 6 correlated metrics into two uncorrelated Principal Components (PPCs) (see Results).

Table 2:

Sperman’s rank correlation matrix for the log-transformed metrics of transient dynamics used in the analyses. All p-values are < 0.01.

	Log10-Rhomax	Log10-Kmax	Log10-Reactivity	Log10-Rhomin	Log10-Kmin
Log10-Kmax	0.99
Log10-Reactivity	0.91	0.90
Log10-Rhomin	−0.64	−0.66	−0.50
Log10-Kmin	−0.60	−0.63	−0.46	0.99
Log10-Firststepatt	−0.54	−0.53	−0.67	0.63	0.61

Statistical analyses

We investigated the effect of generation time (on an identity scale) and λ (on a log-scale) on the two first PPCs. As λ (on a log-scale) is inversely proportional to generation time for a given reproductive rate (Caswell 2001), we looked for possible multi-collinearity among explanatory variables, which can lead to high standard errors and difficulties in interpreting parameter estimates in regressions (Graham 2003). We calculated Spearman pairwise correlation coefficient (ρ) and used the rule ρ < 0.5 to determine whether generation time and λ could be included in the same model (Price et al. 2009, 2010). As recommended by Revell (2009), we controlled for non-independence among species by fitting Phylogenetic Generalized Least-Squares models (PGLS) to link PPC1 and PPC2 as response variables with the two explanatory life history metrics previously defined (i.e., generation time (on a an identity scale) and λ (on a log-scale)). We estimated an index varying from 0 (corresponding to the complete absence of phylogenetic structure) to 1 (when the phylogenetic structure can be represented by the previously constructed tree) (Freckleton et al. 2002), which was then incorporated in the model to control for the phylogenetic effect (Freckleton et al. 2002, procedure implemented in R by Gage and Freckleton 2003).

The Akaike Information Criterion corrected for small sample size (AlCc) was used for model selection (Burnham and Anderson 2002).

Using PGLS, we did the same analyses on the six original log-transformed metrics of transient dynamics (i.e., not combined into two synthetic PPCs).

All these analyses were performed with the R software (R Development Core Team 2011).

Results

Database

The database included 111 mammalian species having generation times ranging from 2.6 years for Gunnison’s prairie dog Cynomys gunnisoni to 102.9 years for Indian rhinoceros Rhinoceros unicornis (Table A1). Population growth rates ranged from 0.63 for the Gunnison’s prairie dog Cynomys gunnisoni, to 1.48 for the Painted Hunting Dog Lycaon pictus. The number of years involved in case studies ranged from 1 year for the chamois Rupicapra rupicapra, to 51 years for the European bison Bison bonasus (Table A1) but only 5 studies covered more than 30 years. This variation in study duration had no effect on the transient metrics (results not shown here).

Analysis of transient dynamics

PPC1 accounted for 75.6 % of the overall variation in transient dynamics and PPC2 18.5 %. Other PPCs only accounted for a small part of the variation (Figure A2). Hereafter we only retained PPC1 and PPC2 (that explained 94.1 % of the total variation observed in transient dynamics).

Amplification indices (i.e., reactivity, Kreiss bounds on amplification, and maximum amplification), corresponding to short-term increases in population size after a disturbance, were all positively associated with PPC1 while attenuation indices (i.e., first-time step attenuation, Kreiss bounds on attenuation and maximum attenuation), corresponding to short-term decreases in population density, were all negatively correlated with PPC1 (Table 3, Fig. 1). All metrics of transient dynamics (i.e., amplification and attenuation indexes) were negatively correlated with PPC2 (Table 3, Fig. 1). PPC1 corresponded to a continuum of increasing magnitude of transience. A large value on PPC1 corresponded to populations with large short-term variation in population size after a disturbance (see e.g. the coyote Canis latrans (n^o15, Fig. 1)). A small value on PPC1 corresponded to populations with small short-term variation in population size after a disturbance (see e.g. the Virginia opossum Didelphis virginiana (n^o37, Fig. 1)).

Table 3:

Log10-transformed metrics and their contribution on PPC1 and PPC2.

	PC1	PC2
Log10-Kmax	0.92	−0.37
Log10-Kmin	−0.84	−0.47
Log10-Rhomax	0.92	−0.38
Log10-Rhomin	−0.93	−0.30
Log10-Reactivity	0.88	−0.43
Log10-Firststepatt	−0.70	−0.57

Figure 1:

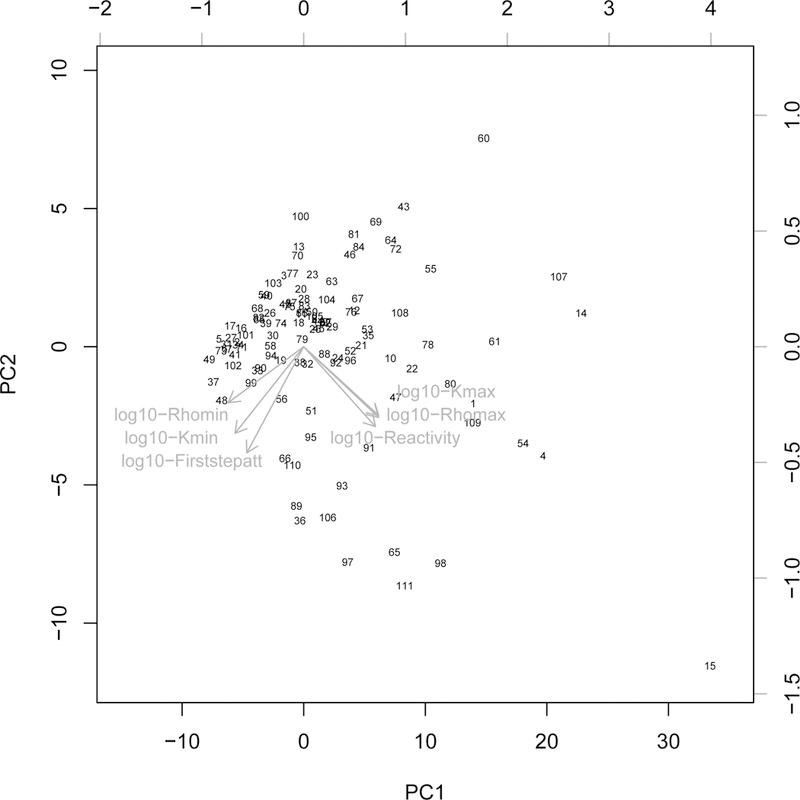
First factorial plan of the phylogenetic principal component analysis performed on 6 log-10 transformed transient metrics measured in 111 mammalian species (numbered from 1 to 111). The correspondence between number and species name is given in Table A1. The six log10-transformed transient metrics are displayed in red and their meanings are presented in Table 1.

For a given magnitude of transience, PPC2 confronted populations that increased in size after a disturbance (with small values on PPC2 like the wild boar Sus scrofa (n^o98, Fig. 1)) with populations that decreased in size after a disturbance (with high values on PPC2 like the toque macaque Macaca sinica (n^o60, Fig. 1)).

Drivers of transient dynamics

The correlation between λ and generation time was 0.466, so that both variables could be included into a same model.

In all models linking PPC1 to explanatory variables (Table 4A), the best one only included an effect of λ (on a log-scale) on PPC1. The higher the λ is, the higher is the ranking on PPC1 (slope = 15.817 (SE: 4.307), Fig. 2). Species with high λ thus had transience of large magnitude, involving either increased or decreased population size after a disturbance. On the contrary, species with low λ had transience of small magnitude, leading them to be buffered against disturbance. Generation time did not influence the magnitude of transience, either directly (slope = 0.072 (SE: 0.047)) or through interactive effects with λ (slope of log(λ)*generation time = 0.269 (SE: 0.369)).

Table 4:

Model selection results. Displayed are the AlCc of each model, the difference in AlCc between each tested model and the best model (ΔAICc) and the phylogenetic signal. Additive effects of asymptotic population growth rate (λ) (on a log-scale) and generation time (Tc) were tested on (A) PPC1 and (B) PPC2. The best models retained are in bold.

Model	AICc	ΔAICc	Phylogenetic signal
A
PPC1(log(λ))	720.58	0	0.43
PPC1(log(λ)+Tc)	723.48	2.90	0.44
PPC1(log(λ)+Tc+Tc2)	725.80	5.22	0.45
PPC1(1)	730.39	9.81	0.40
PPC1(Tc)	731.20	10.62	0.44
PPC1(Tc+Tc2)	731.29	10.71	0.46
B
PPC2(Tc+Tc2)	539.43	0	0.40
PPC2(Tc)	541.25	1.82	0.46
PPC2(log(λ)+Tc+Tc2)	541.98	2.55	0.41
PPC2(1)	542.07	2.64	0.52
PPC2(log(λ)+Tc)	544.36	4.93	0.46
PPC2(log(λ))	544.98	5.55	0.51

Figure 2:

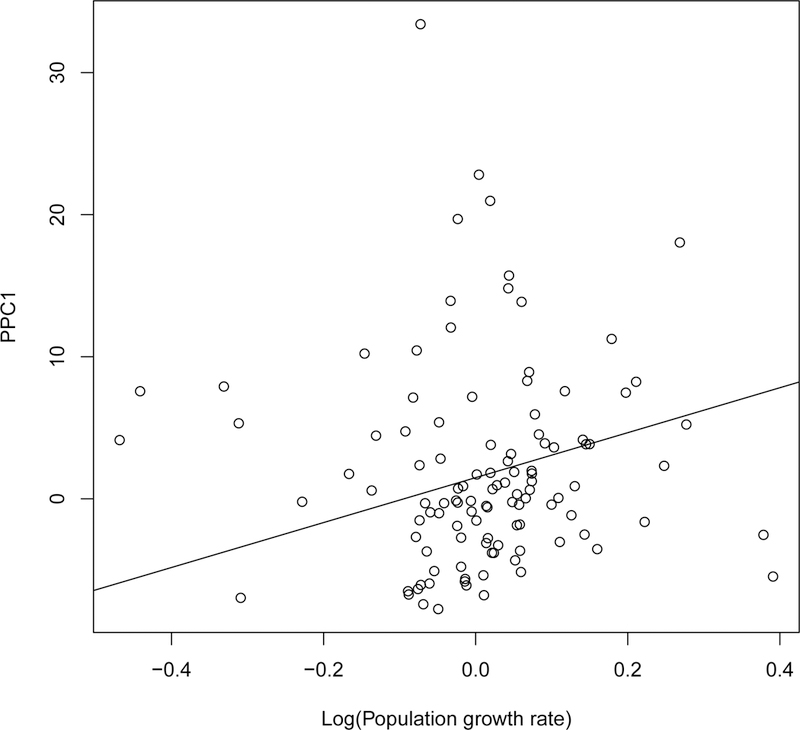
Relationship between PPC1 and the asymptotic population growth rate λ (on a log-scale). The solid line corresponds to the best model retained (Table 4A).

The best model accounting for observed variation in PPC2 (Table 4B) included a quadratic effect of generation time (linear term = 0.130 (SE: 0.044); quadratic term = −0.001 (SE: 0.0005)). More specifically, the longer the generation time is, the higher is the ranking on PPC2 (Fig. 3). Nevertheless, for very long generation times (>60 years), PPC2 did not increase with generation time anymore.

Figure 3:

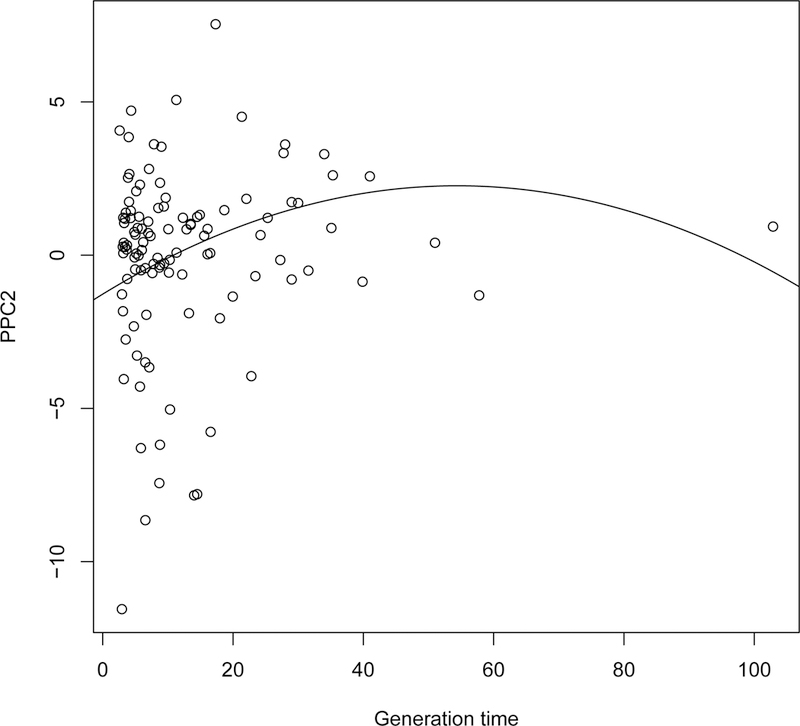
Relationship between PPC2 and the generation time Tc. The solid line corresponds to the best model retained (Table 4B).

The same analyses done on the six log-transformed metrics of transient dynamics are provided in Table A2. The same results as those obtained using PPCs were obtained when each metric was tested separately: a strong effect of λ (on a log-scale) was detected on all metrics that quantify amplification and on two of three metrics that quantify attenuation. In addition, an effect of generation time was detected on all metrics that quantify attenuation.

Discussion

We investigated how life history tactics in mammals influence the magnitude of transient dynamics. We used an extensive database including 111 mammalian species ranging widely along the slow-fast continuum of life histories. To date, the influence of life history tactics on the transient dynamics has only been studied in plant species from stage-structured models. We thus provide here the first comprehensive study of transient dynamics in age-structured populations, after having standardized the matrix dimension using the age at first reproduction and after controlling for the non-independence among species. We found that transient dynamical properties of mammalian populations are shaped by both generation time and λ, indicating that the pace of life (i.e. life history) and the demographic regime (i.e. ecology) shape patterns of transient dynamics.

PPM standardization and transient dynamics

In the hypothetical case in which the matrices would have been built as a function of data availability without any standardization, the dimension of the matrices would not reflect the life cycle of the species but would instead be arbitrarily set by the availability of age-specific estimates of demographic parameters in published case studies. Thus, the largest matrices would not correspond necessarily to longest-lived species, but would simply reflect the level of detail that was available on age-specific variation in demographic parameters, with high matrix dimension for species for which fully age-dependent demographic estimates are available and low matrix dimension for species for which estimates of demographic parameters are only available for broad age-classes (i.e., less than one year of age vs. older animals). For these latter cases, individuals are brought into an absorbing age class with average values of survival and fertility, which does not take into account further age-specific variation. Stott et al. (2010) explicitly included the effect of matrix dimension in their models linking PPC1 and PPC2 to explanatory variables. They interpreted the averaging effect as a parsimonious explanation for an increase in transient magnitude with increasing matrix dimension in the case of stage-structured populations. However, Stott et al. (2010) analyzed stage-structured populations, and simply including the “matrix dimension” effect in the analyses of age-structured populations analyzed here is not satisfactory because the dimension of age-structured matrices is a compound between the life cycle and the level of details available on the age-specific variation in demographic parameters, hence preventing a clear interpretation from a biological viewpoint. Likewise, by standardizing the matrix dimension across species by using the age at first reproduction, matrix dimension would reflect the pace of life of a given species.

Even if a standardization of the PPM was required in our comparative analysis, this standardization assumed an age-independent and constant fecundity through the entire reproductive life. Indeed, all reproductive stages are lumped together. However, it is well known that fecundity is age-specific in most vertebrates (Emlen 1970), including mammals (Caughley 1976). As a rule, fecundity varies with age according to a hump-shaped curve, with younger and older females having lower reproductive output than prime-age ones. Likewise, actuarial senescence is pervasive in mammalian populations (see Nussey et al. 2013 for a recent review) and neglecting it leads to overestimate the proportion of animals reaching very old ages. Whether the intensity of transient dynamics depends on the strength of the difference in reproductive performance and/or in survival across life stages remains an open question. In addition, recent work has highlighted the need to model the demographic age structure accurately when considering transient metrics (Tenhumberg et al. 2009). Further investigations would be required to test whether the number of life-history stages included in the PPM influences transient metrics.

Effect of generation time

Our analyses involved a large range of generation times. From a biological viewpoint, the cohort generation time corresponds to the average age of females at reproduction in a cohort. A generation time of 102.9 years is thus biologically impossible. The obvious overestimation of Tc was likely due to the assumption of no senescence in demographic parameters we made for all species to standardize the matrices because accurate estimates of age-specific survival and reproductive parameters beyond the prime-age stage was often lacking. Tc seems to be especially sensitive to this assumption. For instance, in their comparative demographic analyses among primates based on age-structured population matrices, Morris et al. (2011) also reported very high value of Tc for some long-lived species with high prime-age survival (e.g., 70.1 years for Muriqui, Brachyteles hypoxanthus). Nevertheless, the standardization of demographic matrices we performed alleviates the problem in the context of a comparative analysis.

We showed that generation time, which measures the position of a given mammalian species on the slow-fast continuum, influenced the transient dynamics of mammalian species (Fig. 3). Right after a disturbance, species with a long generation time decrease in population size, whereas species with a short generation time increase in population size. Consequently, species with long generation time, which have a slow pace of life, are not expected to counterbalance the negative effects of stochastic disturbances (such as hunting) by increasing population growth. This pattern of transient dynamics explains why the conservation status deteriorates with increasing generation time (Lebreton et al. 2012). These findings thus provide a direct support for the “malediction” (sensu Lebreton 2006) of long-lived species, a great concern in a conservation context, and are in line with the greater sensitivity of slow-living species to transient dynamics. Koons et al. (2006) also reported similar findings in their analyses of variation in population momentum in relation to generation time. In most vertebrates (including 10 species of mammals), these authors found that a sudden decrease in fecundity that would shift from 1.1 to 1 generated increasingly negative population momentum with increasing generation time.

Effect of population growth rate

Species represented by populations with high growth rate had short-term increases and decreases in population size of large magnitude (Fig. 2). For these species, after a disturbance, the magnitude between the increases and the decreases in population size is thus large. In contrast, species represented by populations with low growth rate (including 48 species with decreasing populations) exhibited short-term increases and decreases in population size of small magnitude. Importantly, population growth rate is shaped by processes involved at two different scales of the biological organization.

First, at the inter-specific level, the maximum population growth rate (r-max sensu Caughley 1977) is a life history trait that decreases with increasing body mass according to allometric rules (Fenchel 1974; Hennemann 1983). In a transient dynamics context, for a given demographic regime, smaller species (which are generally short-lived) with higher maximal population growth rates thus exhibit both increases and decreases in population size of large magnitude. On the contrary, larger species (which are generally long-lived) with lower maximal population growth rates exhibit buffered short-term variation in population size. This result echoes to both Caughley and Krebs (1983)’s and Sinclair (1996)’s analyses indicating that species with high population growth rates have highly fluctuating population abundance. This result also provides direct support for the dampening effect of large species (which are generally long-lived) on demographic variation (Sinclair 1996). Likewise, Morris et al. (2008) showed that short-lived species (which are generally small species) are more affected by increasing variation in demographic parameters than large and long-lived species. Our results thus provide a direct support for the dampening effect of large species on the demographic variation.

We thus showed that depending on their pace of life, species exhibit different patterns of transient dynamics. At the intra-specific level, population growth rate provides an assessment of the demographic regime of a population. For a given species, populations with different demographic regime will not have the same responses to disturbances. Decreasing populations exhibited buffered variation to disturbances, whereas increasing populations had large variation in population size. This is an important finding for conservation.

Consequently, in contrast with Koons et al. (2005, 2006) who did not include asymptotic population growth rate in their analyses of short-term dynamics, we showed that the demographic regime of a population, as represented by λ, is tightly associated with short-term variation in population size. Indeed, fast-growing populations by having both increases and decreases in population size of large magnitude, will be able to take advantage of positive disturbances while minimizing the effects of negative disturbances, and therefore to persist in variable environments. However, this high risk-high benefit short-term demographic pattern might lead the population to extinction when an extreme negative event occurs. On the other hand, slow-growing or declining populations have both amplified and attenuated dynamics of small magnitude. These populations will be able to resist to disturbances of small magnitude, but will be led to extinction when the negative disturbances will occur. As a negative disturbance will lead to decrease the already low growth rate of slow-growing populations and will thereby make them more susceptible to the next disturbance, transient dynamics can create a “vortex of extinction” (sensu Lacy and Lindenmayer 1995) for such populations, assuming the PPM remains unchanged.

Conclusions

Species currently face a changing environment so that a better understanding of the consequences of environmental variation on population dynamics has become of great interest in evolutionary ecology (Lande et al. 2003). Ecologists used to build population projection models to capture the key features of population demography, but as rightly stated by Ellis and Crone (2013), these models are of course over-simplifications of systems occurring in nature. The development of demography in stochastic environments has launched both theoretical concepts and metrics to address the question of demography in variable environments (Tuljapurkar 1982, 1989; Caswell 2001; Morris and Doak 2002; Lande et al. 2003), and explicit links with life history strategies have been investigated (Tuljapurkar et al. 2009; Saether et al. 2013). However, such analyses have focused on populations at stable age or stage structure, whereas there is an increasing literature documenting the importance of focusing on short-term dynamics via the study of transient dynamics (see Stott et al. 2011 for a review). This study, through a large-scale analysis across mammals, provides a first attempt to link life history with transient dynamics, and our findings demonstrate that both the speed of the life cycle and the population growth shape patterns of transient dynamics. We thus came to the same conclusion as Koons et al. (2006) that transient dynamics may be an especially important aspect of population dynamics for long-lived vertebrates characterized with a slow pace of life. After Koons et al. (2006) reported that population momentum has a larger effect on long-term population size for slow-living species than for fast-living species, we found that the short-term responses of slow-living species after a disturbance involve decreasing population size, whereas fast-living species respond by increasing population size. These patterns of transient dynamics might explain why slow-living species are more vulnerable than fast-living ones in highly variable environments. However, the positive association between the population growth rate and the magnitude of transient dynamics indicates that slow-living species are buffered against disturbance, as slow-living species are also slow-growing species. This buffering effect of a slow growth rate on short-term variation in population size echoes the results obtained by Stott et al. (2010) on plants. However, while large (and thereby often slow-living) species generally live at much lower population density than small (and thereby often fast-living species) (Damuth 1981), the influence of population density on transient dynamics remains unknown. Whatever the transient metrics considered, it is noteworthy that current methods developed in analyses of transient dynamics are based on the assumption of density-independent time-invariant PPM, and the development of transient analyses for density-dependent and stochastic PPM models is required to assess the potential role of population density on transient dynamics.

Our empirical study of transient dynamics across mammals has clear implication for future studies of the interplay between evolutionary and ecological dynamics (Schoener 2011). For instance, Lande (1982) and van Tienderen (2000) have shown that population dynamics and selection can be related by coupling PPM and analyses of selection gradients. This approach, which has been applied to empirical case studies (Smekens and van Tienderen 2001; Coulson et al. 2003; Gamelon et al. 2011), is based on populations at demographic equilibrium. An investigation of this approach in a context of transient dynamics would allow assessing whether transient dynamics influence the selection gradients. Our analysis of short-term dynamics also has important implications in conservation and management. Indeed, populations often suffer from natural or human-induced disturbances, and management strategies should not be based on asymptotic analyses that ignore these disturbances. Moreover, the time-scale of transient effects is often similar to the length of many management or conservation projects (Ezard et al. 2010). From a management and conservation points of view, the assumption of equilibrium, generally made by biologists, is therefore hardly applicable to species suffering from disturbances and the study of transient dynamics appears as a more realistic tool to manage populations. Short-term (transient) and long-term (equilibrium) population dynamics should be considered simultaneously (Stott et al. 2012b) to help predict the future of a population.