Generalizing the per-protocol treatment effect: The case of ACTG A5095

Abstract

Background

Intention-to-treat comparisons of randomized trials provide asymptotically consistent estimators of the effect of treatment assignment, without regard to compliance. However, decision makers often wish to know the effect of a per-protocol comparison. Moreover, decision makers may also wish to know the effect of treatment assignment or treatment protocol in a user-specified target population other than the sample in which the trial was fielded. Here, we aimed to generalize results from the ACTG A5095 trial to the US recently HIV-diagnosed target population.

Methods

We first replicated the published conventional intention-to-treat estimate (2-year risk difference and hazard ratio) comparing a four-drug antiretroviral regimen to a three-drug regimen in the A5095 trial. We then estimated the intention-to-treat effect that accounted for informative dropout and the per-protocol effect that additionally accounted for protocol deviations by constructing inverse probability weights. Furthermore, we employed inverse odds of sampling weights to generalize both intention-to-treat and per-protocol effects to a target population comprising US individuals with HIV diagnosed during 2008–2014.

Results

Of 761 subjects in the analysis, 82 dropouts (36 in the three-drug arm and 46 in the four-drug arm) and 59 protocol deviations (25 in the three-drug arm and 34 in the four-drug arm) occurred during the first 2 years of follow-up. A total of 169 subjects incurred virologic failure or death. The 2-year risks were similar both in the trial and in the US HIV-diagnosed target population for estimates from the conventional intention-to-treat, dropout-weighted intention-to-treat, and per-protocol analyses. In the US target population, the 2-year conventional intention-to-treat risk difference (unit: %) for virologic failure or death comparing the four-drug arm to the three-drug arm was −0.4 (95% confidence interval: −6.2, 5.1), while the hazard ratio was 0.97 (95% confidence interval: 0.70, 1.34); the 2-year risk difference was −0.9 (95% confidence interval: −6.9, 5.3) for the dropout-weighted intention-to-treat comparison (hazard ratio = 0.95, 95% confidence interval: 0.68, 1.32) and −0.7 (95% confidence interval: −6.7, 5.5) for the per-protocol comparison (hazard ratio = 0.96, 95% confidence interval: 0.69, 1.34).

Conclusion

No benefit of four-drug antiretroviral regimen over three-drug regimen was found from the conventional intention-to-treat, dropout-weighted intention-to-treat or per-protocol estimates in the trial sample or target population.

Introduction

Randomized controlled trials are considered the gold standard for causal inference in medical interventions. This is primarily because randomization eliminates confounding by design and therefore helps to ensure internal validity by making treatment groups comparable (or exchangeable) in expectation. The standard approach to the analysis of randomized trials, the intention-to-treat (ITT) comparison, provides an asymptotically consistent effect estimate of the treatment assignment.^1–3 Yet, those making treatment decisions often want to know the effect of the treatment assigned under adherence to the treatment protocol (i.e. the per-protocol comparison).^4,5 Asymptotically consistent estimates of the per-protocol effect (accounting for protocol deviations (e.g. non-compliance)) can be obtained by censoring patients at protocol deviation and using inverse probability (IP) weights under the additional assumption that the common causes of the endpoint and protocol deviations are measured and the model correctly specified.⁶ For example, recently Murray and Hernán⁷ estimated a per-protocol effect on mortality in the placebo arm of the Coronary Drug Project by standardizing on pre- and post-randomization covariates using IP weighting.

In addition, lack of external validity is a major concern in medical research and randomized trials.^8,9 External validity refers to the extent that results generalize to a specified target population. In a randomized trial, generalizability is often limited, and external validity is constrained due to restrictive inclusion and exclusion criteria. Recently, there have been several quantitative methods developed to enhance external validity.^10–16 Asymptotically consistent estimates of the generalized treatment effect can be obtained also using IP of sampling weights under the additional assumption that the common causes of the endpoint and determinants of sampling into the trial are measured and the model correctly specified.^9,13,17

The AIDS Clinical Trials Group (ACTG), established in 1987, is a paragon of modern clinical trial research. ACTG studies have made major contributions to optimizing HIV treatment. One exemplar ACTG study is the A5095 trial, which compared the efficacy and safety of a standard three-drug antiretroviral therapy (ART) regimen (zidovudine, lamivudine, efavirenz) versus adjuvant therapy regimen with abacavir (zidovudine, lamivudine, efavirenz, and abacavir) among HIV-infected adults with viral load of at least 400 copies/mL at randomization.¹⁸ An ITT analysis found no significant difference in time to virologic failure between three-drug and four-drug regimens (hazard ratio = 0.95; 97.5% confidence interval (CI): 0.69, 1.33). However, like many randomized trials, the A5095 trial suffered from 20% dropout and 17% protocol deviations (i.e. non-compliance to the assigned treatment).¹⁸ In this setting, an ITT estimator may produce biased estimates of the per-protocol effect (i.e. the effect if everyone initiated and followed the protocol over the entire follow-up) and may be inadequate for the assessment of comparative effectiveness.^4,19,20 Therefore, a per-protocol analysis that accounts for protocol deviations would complement the published ITT results. In addition, the existing A5095 ITT results and perprotocol results may not generalize to the target population of US HIV-diagnosed persons. For example, the A5095 study sample included 35% African American patients and 9% patients under 26 years of age compared with about 45% and 20%, respectively, in the annual HIV-diagnosed population in the United States as defined using national HIV surveillance data by the Centers for Disease Control and Prevention (CDC).²¹ If race and age are potential modifiers of the treatment effect on virologic failure, we may be concerned about such covariate imbalances, as they may pose a threat to the external validity of the trial results.

Here, we first replicate the ITT estimate for the effect of assigned treatment published with the A5095 results.¹⁸ Next, we estimate the per-protocol effect of the treatment plan. Then, we generalize both the ITT and per-protocol effect estimates to persons diagnosed with HIV in the United States during 2008–2014 as defined by CDC national surveillance data.

Methods

The ACTG A5095 study

The ACTG A5095 study was a three-arm randomized double-blind, placebo-controlled clinical trial designed to compare three antiretroviral regimens for treatment of HIV-1 infection.^18,22 Between March 2001 and November 2002, 1147 HIV-1-infected patients were enrolled and randomly assigned 1:1:1 to one of three antiretroviral regimens: a triple-nucleoside regimen (i.e. zidovudine, lamivudine, and abacavir), a three-drug standard-of-care-regimen (i.e. zidovudine, lamivudine, and efavirenz), or a novel four-drug regimen (i.e. zidovudine, lamivudine, efavirenz, and abacavir). Eligible patients had received no previous ART and had a plasma HIV-1 RNA level of at least 400 copies/mL. Excluded patients had received immunomodulatory or investigational therapy or vaccines within the previous month, weighed <40 kg, or were pregnant or breastfeeding. In 2003, the triple-nucleoside regimen was discontinued due to inferiority.²² As in the primary report,¹⁸ here we disregard the triple-nucleoside regimen and compare the novel four-drug regimen to the three-drug standard-of-care regimen. For the present analysis, we used the public A5095 data set available from the National Technical Information Service (NTIS) (http://www.ntis.gov/).

In the published study, the primary endpoint was time from randomization to virologic failure; here, we take the primary endpoint to be time to virologic failure or death from any cause. Virologic failure was defined as the time of the first of two successive HIV-1 RNA levels of 200 or more copies/mL, at least 16 weeks after randomization. Follow-up visits occurred at weeks 2, 4, 8, 12, 16, 20, and 24 and then every 8 weeks until end of study in March 2005. While the longest recorded follow-up was 204 weeks, here we administratively censor patients at 2 years (730 days). Four patients were excluded from analysis because of inconsistencies in the public-use data. This work was judged not to be human subjects research by the University of North Carolina Institutional Review Board.

Intention-to-Treat Effect

Let uppercase letters represent random variables, and lowercase letters represent possible realizations of random variables or constants. Let i index the n study patients and t index the up to 2 years (730 days) from randomization. Let R_i = 1 denote that patient i was randomized to the four-drug regimen, and R_i = 0 denote randomization to the three-drug regimen. Let Δ_it = 1 indicate the primary endpoint for patient i by day t from randomization. Let D_it = 1 indicate dropout (i.e. defined as loss to follow-up before completing the study protocol) for patient i by day t from randomization. The conventional ITT hazard ratio assumes independent censoring (i.e. the censoring mechanism is independent of the survival time given treatment assignment). It was estimated from standard Cox proportional hazards model.²³ The parameters of this Cox model were estimated by maximizing the partial likelihood.²⁴ Assuming no tied survival times, the partial likelihood corresponding to patient i experiencing endpoint on day t is

$$\frac{\exp \left({\widehat{\beta }}_{ITT,S}{R}_i\right)}{{\sum }_{j\in J(t)}\exp \left({\widehat{\beta }}_{ITT,S}{R}_j\right)}$$

where J(t) is the risk set on day t, $\exp ({\widehat{\beta }}_{ITT,S})$ is the estimator of the conventional sample ITT hazard ratio of virologic failure or death comparing assignment to the four-drug regimen to assignment to the three-drug regimen in the A5095 trial. We used Efron’s method for tied survival times.²⁵

Next, to account for potential dependent censoring due to dropout (i.e. informative dropout), we standardized the ITT hazard ratio to the study sample at randomization (i.e. before dropouts occurred) using IP of censoring weights.^6,26 Let W_it be a vector of time-fixed (i.e. where t = 0) and time-varying covariates. Time-fixed covariates included sex, age at randomization, baseline hepatitis B virus/hepatitis C virus (HBV/HCV) infection status, and baseline viral load (copies/mL) and baseline CD4 cell count (cells/mm³). Time-varying covariates, used to account for informative dropout, included CD4 counts, viral load, first diagnosis of an HIV-related disease, and the presence of severe or life-threatening adverse events (i.e. National Institute of Allergy and Infectious Diseases Division of AIDS toxicity scale grade 3 or 4²⁷) during the follow-up visits. Restricted quadratic splines with four knots at 5th, 35th, 65th, and 95th percentiles were used to model CD4 cell count and viral load.^28,29

Let ${\overline{W}}_{it}=\left\{W_{i0},W_{i1},\dots ,W_{it}\right\}$ be the covariate history through day t. We estimated stabilized inverse probability-of-dropout weights as

$${\widehat{\pi }}_{it}^D=\prod _{k=0}^t\frac{P\left(D_{ik}=0|D_{i(k-1)}=0,R_i\right)}{P\left(D_{ik}=0|D_{i(k-1)}=0,R_i,{\overline{W}}_{i(k-1)}\right)}$$

where D_i(−1) and W_i(−1) are defined to be D_i0 and W_i0.³⁰ Here, we did not include baseline covariates in the numerator of the weight and solely stabilized on the probability of treatment so as to allow presentation of marginal survival functions. The numerator and denominator of these stabilized weights were estimated by pooled logistic regression fit by maximum likelihood with models

$$\begin{gathered} \mathrm{logit}P\left(D_{it}=0|D_{i(t-1)}=0,R_i\right)={\alpha }_{0t}+{\alpha }_1{R}_i\text{and} \\ \mathrm{logit}P\left(D_{it}=0|D_{i(t-1)}=0,R_i,{\overline{W}}_{i(t-1)}\right) \\ ={{\alpha }^{\prime }}_{0t}+{{\alpha }^{\prime }}_1{R}_i+{{\alpha }^{\prime }}_2{\overline{W}}_{i(t-1)} \end{gathered}$$

where ${\alpha }_2^{\prime }$ is the transpose of column vector of log odds ratios for the covariate history ${\overline{W}}_{i(t-1)}$. Specifically, in a pooled logistic regression, each person-visit was considered as an observation, and the model was fit using person-visits.³¹ The denominator of each term in ${\widehat{\pi }}_{it}^D$ is the probability that a patient i remained uncensored at time t given his or her past exposure and covariate history and that he or she remained uncensored in the previous visits.

Then the ITT hazard ratio was estimated by partial likelihood, IP weighted to account for informative dropout.³¹ The weighted partial likelihood was maximized, where patient i who incurred virologic failure or death at day t from randomization contributed the term

$${\left\{\frac{\exp \left({\tilde{\beta }}_{ITT,S}{R}_i\right)}{{\sum }_{j\in J(t)}{\widehat{\pi }}_{jt}^D\exp \left({\tilde{\beta }}_{ITT,S}{R}_j\right)}\right\}}^{{\widehat{\pi }}_{it}^D}$$

where $\exp ({\tilde{\beta }}_{ITT,S})$ is the estimator of the ITT hazard ratio of virologic failure or death comparing assignment to the four-drug regimen to assignment to the three-drug regimen in the trial sample. This estimator accounts for potential informative dropout, under the assumption that the patients who dropped out on day t are exchangeable with those who remained in the study on day t conditional on prognostic factors W_it.³⁰ Here and below, we also assume positivity, namely, there is a nonzero probability of being observed for every combination of values of treatment and covariate histories.³² Throughout, for identification of effects, we also assume that there is no interference between subjects,^33,34 that any versions of treatment are irrelevant,³⁵ negligible measurement error, and that models are correctly specified. The standard error for IP-weighted hazard ratio was estimated using robust sandwich variance.

In addition, for each study arm, conventional ITT risks and dropout-weighted ITT risks of the primary endpoint (i.e. virologic failure or death) were estimated using the Kaplan–Meier method³⁶ and the inverse probability-weighted Kaplan–Meier method.³⁷ The two arms were also compared using a 2-year risk difference. The CIs for risks, weighted risks, and risk difference were obtained with the standard error estimated by the standard deviation of 200 nonparametric bootstrap samples with replacement of the total study sample size n.³⁸

Per-protocol effect

To estimate the per-protocol effect for continuous use of the four-drug regimen compared with the continuous use of the three-drug regimen, we account for protocol deviations as well as informative dropout.^6,39 The estimation of the per-protocol effect was similar to that for the ITT effect accounting for informative dropout, except that C_it is used to denote censoring at the minimum of dropout or a protocol deviation by day t from randomization, rather than D_it denoting censoring at dropout alone previously. Then, we estimated stabilized IP weights for dropout and protocol deviations as

$${\widehat{\pi }}_{it}^C=\prod _{k=0}^t\frac{P\left(C_{ik}=0|C_{i(k-1)}=0,R_i\right)}{P\left(C_{ik}=0|C_{i(k-1)}=0,R_i,{\overline{W}}_{i(k-1)}\right)}$$

where C_i(−1) and W_i(−1) are defined to be C_i0 and W_i0. The numerator and denominator of these stabilized weights were estimated by pooled logistic regression fit by maximum likelihood with models

$$\begin{gathered} \mathrm{logit}P\left(C_{it}=0|C_{i(t-1)}=0,R_i\right)={\gamma }_{0t}+{\gamma }_1{R}_i\text{and} \\ \mathrm{logit}P\left(C_{it}=0|C_{i(t-1)}=0,R,{\overline{W}}_{i(t-1)}\right)={{\gamma }^{\prime }}_{0t}+{{\gamma }^{\prime }}_1{R}_i+{{\gamma }^{\prime }}_2{\overline{W}}_{i(t-1)} \end{gathered}$$

where ${\gamma }_2^{\prime }$ is the transpose of column vector of log odds ratios for the covariate history ${\overline{W}}_{i(t-1)}$.

The per-protocol hazard ratio was estimated by partial likelihood, IP weighted to account for potential informative dropout and protocol deviations.³¹ The weighted partial likelihood was maximized, where patient i who incurred virologic failure or death at day t from randomization contributed the term

$${\left\{\frac{\exp \left({\widehat{\beta }}_{PP,S}{R}_i\right)}{{\sum }_{j\in J(t)}{\widehat{\pi }}_{jt}^C\exp \left({\widehat{\beta }}_{PP,S}{R}_j\right)}\right\}}^{{\widehat{\pi }}_{jt}^C}$$

where $\exp ({\widehat{\beta }}_{PP,S})$ is now the per-protocol hazard ratio of virologic failure or death comparing continually received four-drug regimen to continually received three-drug regimen in the trial sample. This estimator is consistent under the assumption that the patients who incurred protocol deviations on day t are exchangeable with those who complied with the study protocol on day t conditional on prognostic factors W_it.^6,30 The perprotocol risks were also estimated using the IP-weighted Kaplan–Meier method and risk difference estimated at year 2 from baseline.

Generalizing effects to a US target population

The target population of size m was defined as the recently HIV-diagnosed population in the United States in 2008–2014 based on CDC data.⁴⁰ To account for the potential differences between the trial sample and the specified target population, we employed inverse odds-of-sampling weights.⁹ Let i now index the n + m subjects in the concatenated study sample and target population (of size m). Let S_i = 1 denote selection into the trial sample of Σ_i S_i patients, and S_i = 0 denote those in the target population. Let V_i be an (n + m)-by-p matrix of discrete variables that describe the composition of the sample and target population, including age, sex, and injection drug use (ever versus never). Stabilized inverse odds-of-sampling weights for patient i that was selected into the trial sample were defined as

$${\widehat{\pi }}_i^S=\{\begin{array}{cc}\frac{P\left(S_i=0|V_i\right)}{P\left(S_i=1|V_i\right)}\times \frac{P\left(S_i=1\right)}{P\left(S_i=0\right)}& S_i=1\\ 0& S_i=0\end{array}$$

as described by Westreich et al.¹⁶ The odds weights allow us to estimate the effect in the target population rather than in the combined population. Here, we use odds weights because we wish to estimate the effect in the target population uncorrupted by the trial sample.¹⁶ If standard IP of sampling weights¹⁰ were employed as opposed to the odds weights, the estimator would be standardized to the combination of the target population and the trial sample. The numerator and denominator of these stabilized weights were estimated by logistic regression fit by maximum likelihood with models

$$\begin{gathered} \mathrm{logit}P\left(S_i=1\right)={\delta }_0\text{and} \\ \mathrm{logit}P\left(S_i=1|V_i\right)={\delta }_0^{\prime }+{\delta }_1^{\prime }{V}_i \end{gathered}$$

where ${\delta }_1^{\prime }$ is the transpose of column vector of log odds ratios for the composition of the population V_i. Then, for each subject in the trial sample, we created the total IP weight

$${\widehat{\pi }}_{it}^{D\times S}={\widehat{\pi }}_{it}^D\times {\widehat{\pi }}_i^S$$

that accounted for informative dropout and sampling bias for the dropout-weighted ITT hazard ratio estimation in the target US recently HIV-diagnosed population and total IP weight

$${\widehat{\pi }}_{it}^{C\times S}={\widehat{\pi }}_{it}^C\times {\widehat{\pi }}_i^S$$

that accounted for informative dropout, protocol deviations, and sampling bias for the per-protocol hazard ratio estimation in the target population (as well as the IP weight ${\widehat{\pi }}_i^S$ that only accounted for sampling bias for the conventional ITT hazard ratio estimation in the target population). Both dropout-weighted ITT and per-protocol hazard ratios were estimated by IP-weighted partial likelihood. The partial likelihood was maximized, where patient i who incurred virologic failure or death at day t from randomization contributed the terms

$${\left\{\frac{\exp \left({\widehat{\beta }}_{ITT}{R}_i\right)}{{\sum }_{j\in J(t)}{\widehat{\pi }}_i^S\exp \left({\widehat{\beta }}_{ITT}{R}_j\right)}\right\}}^{{\widehat{\pi }}_i^S}$$

where $\exp ({\widehat{\beta }}_{ITT})$ is the conventional ITT hazard ratio of virologic failure or death in the target population

$${\left\{\frac{\exp \left({\tilde{\beta }}_{ITT}{R}_i\right)}{{\sum }_{j\in J(t)}{\widehat{\pi }}_{jt}^{D\times S}\exp \left({\tilde{\beta }}_{ITT}{R}_j\right)}\right\}}^{{\widehat{\pi }}_{jt}^{D\times S}}$$

where $\exp ({\tilde{\beta }}_{ITT})$ is the ITT hazard ratio of virologic failure or death accounting for informative dropout in the target population, and

$${\left\{\frac{\exp \left({\widehat{\beta }}_{PP}{R}_i\right)}{{\sum }_{j\in J(t)}{\widehat{\pi }}_{jt}^{C\times S}\exp \left({\widehat{\beta }}_{PP}{R}_j\right)}\right\}}^{{\widehat{\pi }}_{it}^{C\times S}}$$

where $\exp ({\widehat{\beta }}_{PP})$ is the per-protocol hazard ratio of virologic failure or death in the target population under the additional assumption that the patients who were sampled in the trial are exchangeable with those who were not sampled conditional on pretreatment covariates V_i.⁹ We also assume a form of positivity, that is, within strata of V_i, all subjects in the population have a nonzero probability of being sampled into the trial.⁹

Results

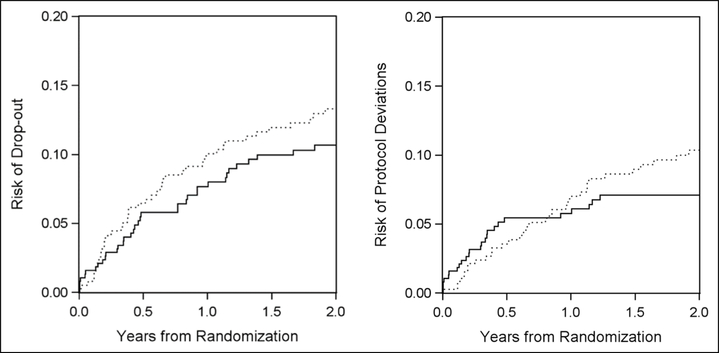
Data for 761 of the 765 patients were available in the public-use data set (380 were randomized to the three-drug arm and 381 to the four-drug arm). The descriptive statistics of baseline characteristics are reported in Table 1 along with the characteristics of the US recently HIV-diagnosed population in 2008–2014 from CDC national surveillance data. ACTG A5095 included fewer aged <26 years compared with that of the recently HIV-diagnosed persons in the United States. Of the 761 patients, 169 experienced virologic failure or death (161 virologic failures and 8 deaths) during the 2-year follow-up (88 in the three-drug arm and 81 in the four-drug arm). There were 82 dropouts during 2-year follow-up. Of the 761 patients, 59 stopped their assigned therapy for reasons other than toxicity (25 in the three-drug arm and 34 in the four-drug arm), and an additional 7 patients stopped their assigned therapy due to toxicity defined by protocol. It was inappropriate to treat these patients who stopped therapy due to toxicity as protocol deviations because these toxicities were considered to be unavoidable deviations. Thus, only those 59 patients who stopped therapy for reasons other than toxicity were considered as protocol deviations during follow-up. The risks for dropout and protocol deviations are depicted in Figure 1 separately. In addition, the distribution of estimated weights is described in Table 2.

Table 1.

Characteristics of patients in the ACTG A5095 trial, and persons with HIV diagnosed in the United States during 2008–2014.

Characteristics	ZDV/3TC + EFV	ZDV/3TC/ABC + EFV	Total	Recently HIV-diagnosed persons in the USA, 2008–2014
Total N	380	381	761	296,073
Sex, no. (%)
Men	314 (83)	302 (79)	616 (81)	232,933 (79)
Age group, no. (%), y
<26	32 (8)	36 (9)	68 (9)	59,274 (20)
26–50	318 (84)	310 (81)	628 (83)	209,289 (70)a
>50	30 (8)	35 (9)	65 (9)	27,510 (9)
Intravenous drug useb, no. (%)
Ever	37 (9)	46 (12)	82 (11)	23,134 (8)
HIV-1 RNA (copies/mL)
log10
Median (IQR)	4.75 (4.43–5.43)	4.78 (4.33–5.38)	4.77 (4.38–5.41)
No. (%)
<10,000	30 (9)	41 (11)	71 (9)
10,000–100,000	201 (53)	188 (49)	389 (51)
>100,000	149 (39)	152 (40)	301 (40)
CD4 cell count, cells/mm3
Median (IQR)	209 (77–331)	223 (79–339)	214 (78–334)
No. (%)
0–50	80 (21)	72 (19)	152 (20)
51–200	102 (27)	104 (27)	206 (27)
201–500	165 (43)	168 (44)	333 (44)
>500	33 (9)	37 (10)	70 (9)
HBV/HCV infectionc, no. (%)
Positive	50 (13)	48 (13)	98 (14)

HIV, human immunodeficiency virus; IQR, interquartile range; SD, standard deviation; ZDV, zidovudine; 3TC, lamivudine; ABC, abacavir; EFV, efavirenz; HBV, hepatitis B virus; HCV; hepatitis C virus.

^aThe number and percentage of persons at age 25–54 years in the US recently HIV-diagnosed population.

^bOnly one patient in ZDV/3TC + EFV arm was current intravenous drug user.

^cHBV infection was defined as the presence of hepatitis B surface antigen; HCV infection was defined as the presence of hepatitis C antibody.

Figure 1.

Risks of dropout and protocol deviations over 2 years by arm in the trial, respectively.

Solid line represents the three-drug arm, and dotted line represents the four-drug arm. The upper panel represents risks of dropout (hazard ratio = 1.27, 95% CI: 0.82, 1.96 (comparing four-drug arm to three-drug arm)). The lower panel represents risks of protocol deviations (hazard ratio = 1.35, 95% CI: 0.80, 2.26 (comparing four-drug arm to three-drug arm)).

Table 2.

Distribution of estimated weights.

Weights	Mean	Standard deviation	Minimum	Maximum
${\widehat{\pi }}_t^D$	0.998	0.070	0.885	4.163
${\widehat{\pi }}_t^C$	0.997	0.066	0.878	3.235
${\widehat{\pi }}^S$	1.002	0.417	0.630	3.279
${\widehat{\pi }}_t^{D\times S}$	0.994	0.434	0.592	8.999
${\widehat{\pi }}_t^{C\times S}$	0.992	0.434	0.585	6.992

${\widehat{\pi }}_t^D$ represents the estimated weight that accounts for informative dropout.

${\widehat{\pi }}_t^C$ represents the estimated weight that accounts for informative dropout and protocol deviations.

${\widehat{\pi }}^S$ represents the estimated weight that accounts for sampling bias.

${\widehat{\pi }}_t^{D\times S}$ represents the estimated weight that accounts for informative dropout and sampling bias.

${\widehat{\pi }}_t^{C\times S}$ represents the estimated weight that accounts for informative dropout, protocol deviations and sampling bias.

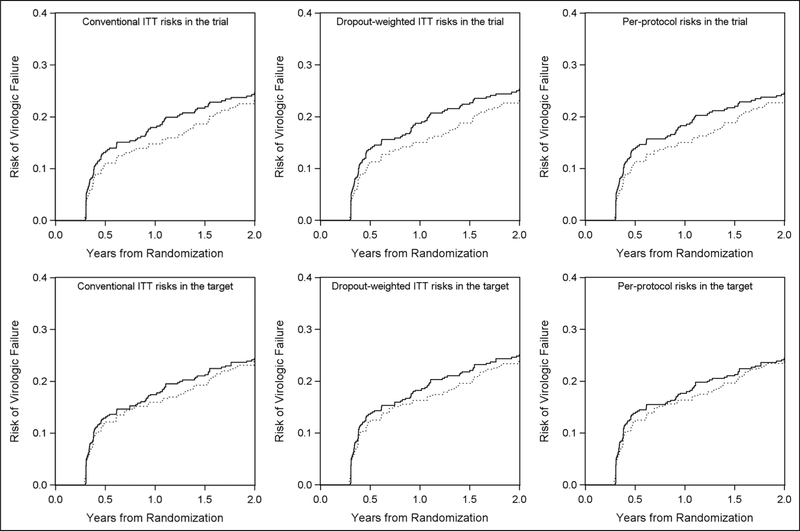
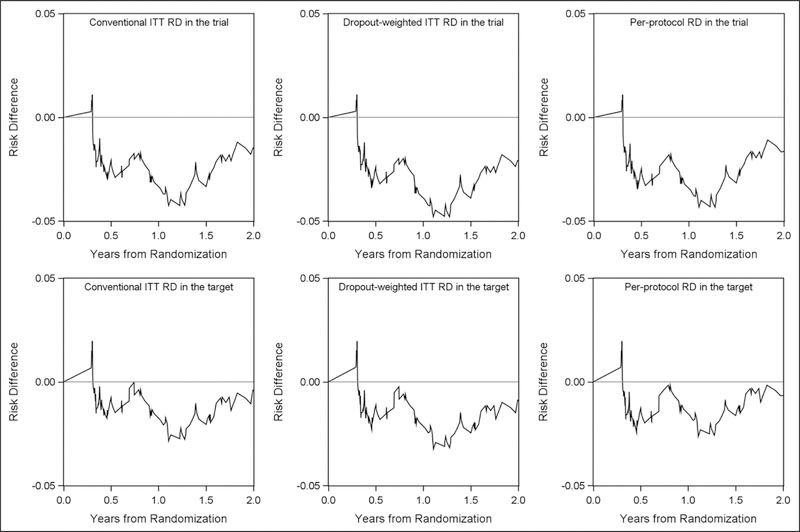
The conventional ITT 2-year risk (unit: %) of virologic failure or death from any cause in the trial was 24.5 among those who were assigned to the three-drug arm and 23.1 among those assigned to the four-drug arm (shown in upper left panel of Figure 2). The conventional ITT 2-year risk difference (unit: %) comparing the four-drug arm to the three-drug arm was −1.4 (95% CI: −8.0, 5.1), and the hazard ratio was 0.91 (95% CI: 0.68, 1.24), as shown in Table 3. The risk difference as a function of time from randomization is depicted in the upper left panel of Figure 3, with lower bound at −4.3. The IP-weighted ITT risk difference that accounted for informative dropout in the trial was −2.1 (95% CI: −8.8, 4.6), and the hazard ratio was 0.89 (95% CI: 0.66, 1.20). That is, the 2-year risk of virologic failure or death if everyone in the trial were to initiate four-drug regimen was 2.1 percentage points lower than the risk if everyone were to initiate three-drug regimen.

Figure 2.

Risk of virologic failure or death by arms over 2 years (conventional ITT risks, dropout-weighted ITT risks, per-protocol risks that accounted for informative dropout and protocol deviations in the A5095 trial and in the target population). ITT: intention-to-treat; target: target population.

Solid line represents the three-drug arm, and dotted line represents the four-drug arm. Upper panels represent risks in the trial with the left panel depicting the conventional ITT results under the independent censoring assumption, middle panel depicting the ITT results that accounted for informative dropout, and the right panel depicting per-protocol results that accounted for informative dropout and protocol deviation. Lower panels represent risks in the target US recently HIV-diagnosed population with the left panel depicting the conventional ITT results that only accounted for sampling bias, middle panel depicting the ITT results that accounted for informative dropout and sampling bias, and the right panel depicting per-protocol results that accounted for informative dropout, protocol deviation and sampling bias.

Table 3.

Risk of virologic failure or death over 2 years in the trial and in persons with HIV diagnosed in the United States during 2008–2014.

		ACTG A5095 trial			Target population
		2-year risk (%)	2-year RD (%) (95% CI)	HR (95% CI)	2-year risk (%)	2-year RD (%) (95% CI)	HR (95% CI)
Conventional ITT effecta	Three-drug armb	24.5	0 (REF)	1 (REF)	24.4	0 (REF)	1 (REF)
	Four-drug armc	23.1	−1.4 (−8.0, 5.1)	0.91 (0.68, 1.24)	24.0	−0.4 (−6.2, 5.1)	0.97 (0.70, 1.34)
Dropout-weighted ITT effect	Three-drug arm	25.3	0 (REF)	1 (REF)	25.1	0 (REF)	1 (REF)
	Four-drug arm	23.2	−2.1 (−8.8, 4.6)	0.89 (0.66, 1.20)	24.2	−0.9 (−6.9, 5.3)	0.95 (0.68, 1.32)
Per-protocol effectd	Three-drug arm	24.6	0 (REF)	1 (REF)	24.4	0 (REF)	1 (REF)
	Four-drug arm	23.0	−1.7 (−8.2, 5.9)	0.90 (0.67, 1.23)	23.7	−0.7 (−6.7, 5.5)	0.96 (0.69, 1.34)

RD, risk difference; CI, confidence interval.

^aAssuming independent censoring.

^bThree-drug standard-of-care-regimen included zidovudine, lamivudine, and efavirenz.

^cFour-drug regimen including zidovudine, lamivudine, efavirenz, and abacavir.

^dEffect accounted for informative dropout, protocol deviation in the trial, and additionally accounted for sampling bias in the target population.

Figure 3.

Risk difference comparing four-drug arm to three-drug arm over 2 years (naïve ITT risks, dropout-weighted ITT risks, per-protocol risks that accounted for dropout and protocol deviations in the A5095 trial and in the target population). ITT: intention-to-treat; RD: risk difference; target: target population.

Upper panels represent risk differences over 2 years in the A5095 trial with the left panel depicting the conventional ITT risk difference under the independent censoring assumption, middle panel depicting the ITT risk difference that accounted for dropout, and the right panel depicting per-protocol risk difference that accounted for dropout and protocol deviation. Lower panels represent risk differences over 2 years in the target US recently HIV-diagnosed population with the left panel depicting the conventional ITT risk difference that only accounted for sampling bias, middle panel depicting the ITT risk difference that accounted for dropout and sampling bias, and the right panel depicting per-protocol risk difference that accounted for dropout, protocol deviation, and sampling bias.

After accounting for protocol deviations in addition to informative dropout, the IP-weighted per-protocol 2-year risk of virologic failure or death in the trial was 24.6 among the three-drug arm and 23.0 among the four-drug arm. The per-protocol 2-year risk difference in the trial was −1.7 (95% CI: −8.2, 5.9), and the hazard ratio was 0.90 (95% CI: 0.67, 1.23), as shown in Table 3. That is, the 2-year risk of virologic failure or death if everyone in the trial were to initiate and stay on four-drug regimen was 1.7 percentage points lower than the risk if everyone were to initiate and stay on three-drug regimen.

When generalizing the ITT and per-protocol effects to the US recently HIV-diagnosed population, all the estimates were closer to the null. The conventional ITT 2-year risk difference in the target population was −0.4 (95% CI: −6.2, 5.1), and the hazard ratio was 0.97 (95% CI: 0.70, 1.34); the IP-weighted ITT 2-year risk difference that accounted for informative dropout in the target population was −0.9 (95% CI: −6.9, 5.3), and the hazard ratio was 0.95 (95% CI: 0.68, 1.32). That is, the 2-year risk of virologic failure or death if everyone in the US target population were to initiate four-drug regimen was 0.9 percentage points lower than the risk if everyone were to initiate three-drug regimen. Accounting for protocol deviations in addition to informative dropout, the IP-weighted per-protocol 2-year risk of virologic failure or death in the target population was 24.4 in the three-drug arm and 23.7 in the four-drug arm. The per-protocol 2-year risk difference in the target population was −0.7 (95% CI: −6.7, 5.5), and the hazard ratio was 0.96 (95% CI: 0.69, 1.34). That is, the 2-year risk of virologic failure or death if everyone in the US target population were to initiate and stay on four-drug regimen was 0.7 percentage points lower than the risk if everyone were to initiate and stay three-drug regimen.

Discussion

In this study, we reanalyzed the ACTG A5095 trial by (1) estimating the ITT effect accounting for potential informative dropout and (2) estimating the per-protocol effect that accounted for informative dropout and protocol deviations, and then (3) generalizing these estimates to the US recently HIV-diagnosed target population. We found that there was no significant benefit of the four-drug regimen (containing zidovudine, lamivudine, efavirenz, and abacavir) over the three-drug regimen (containing zidovudine, lamivudine, and efavirenz) with regard to both effects in the trial and in the target population. Our results also suggest the adjusted ITT and per-protocol results were similar to the conventional ITT effect, which may be due to the relatively balanced dropout and protocol deviations in the two arms. To our knowledge, this is the first example of generalizing the per-protocol effect from a randomized trial to a specified target population.

For this study, as a first step, we employed inverse probability weighting^6,39 (one of the g-methods) to adjust for dependent censoring that may potentially arise from informative dropout when estimating ITT effect and additionally to adjust for protocol deviations for the per-protocol effect. The dropout-weighted ITT and per-protocol estimates are likely to differ from the conventional ITT estimates when dropout and protocol deviations differ by treatment arm. The mechanism of inverse probability weighting reweights the population over time based on the sequential weighting estimated from time-fixed as well as time-varying prognostic factors. Such methods have been adopted in previous work such as to estimate the per-protocol effect in the Women’s Health Initiative estrogen-plus-progestin trial.⁴¹ Alternative methods can also be applied to per-protocol effect estimation. Lodi et al.⁴² used g-computation (another g-method) to analyze the per-protocol effect of immediate ART initiation versus deferred initiation in the Strategic Timing of Antiretroviral Treatment (START) trial and found a potential underestimate of the benefit of immediate initiation by conventional ITT estimation. In addition, instrumental variable methods, which do not require measurement of all confounders (as do inverse-probability weighting and g-computation) is an option for per-protocol effect estimation.^43,44 In double-blind randomized trials, the randomization indicator is an instrumental variable where the exclusion restriction criteria is expected to be met (i.e. the effect of randomly assigned treatment on the outcome is entirely mediated through the received treatment). However, the instrumental variable approach requires another unverifiable assumption of no “defiers” in the trial (also as known as the monotonicity assumption).⁴⁵ Furthermore, even when these assumptions are met, instrumental variable methods estimate the per-protocol effect among “compliers” which may not be representative of the total study population.

In the second step, we also adopted inverse odds weighting (a version of inverse probability weighting) to generalize the adjusted ITT and per-protocol effect to the US target population. Target population estimates are expected to differ from trial estimates when the distributions of effect modifiers differ in the trial and the target population. That is, the external validity of randomized trial results is influenced substantially by the extent to which the prevalence of effect modifiers differs in the trial and the target population. Similar work has been done in previous studies. Cole and Stuart¹⁰ used IP weighting to transport the ACTG 320 trial results to the US HIV-infected target population.

In our analyses, we used a composite endpoint of virologic failure and death rather than the sole virologic failure endpoint which was used in the original published study. We chose not to censor the deaths because they are a competing risk,⁴⁶ and we chose to make a composite endpoint rather than model the competing risk because there were only eight deaths.

Our results are subject to several limitations. First, in the per-protocol effect estimation, we only accounted for the observed protocol deviations from the publicly available A5095 trial data. However, there is no guarantee that all the protocol deviations were captured. To obtain a valid per-protocol effect, any protocol deviations from assigned treatment therapy, except for clinical reasons such as toxicity, should be accounted for.⁵ Second, it is not possible to verify the assumption that all prognostic factors are measured. We may not capture all the common causes of protocol deviations and outcomes, which can lead to residual confounding. However, the trial data are of high quality, and many important baseline and time-varying covariates were measured. This limitation suggests that to ensure the validity of per-protocol analyses, clinical trials should record detailed and high-quality data on prognostic factors. Third, race, an important factor that potentially modifies the effect of antiretroviral treatment, is unavailable in the public A5095 data, limiting our ability to address external validity. Fourth, we assume correct model specification, especially for the models used to construct weights. To enhance model robustness, further analyses that adopt double robust estimation can be conducted.⁴⁷ Finally, we censored patients at the minimum of dropout or a protocol deviation for the per-protocol analysis. Creating weights based on a combination of dropout and protocol deviation assumes a common set of variables and association between dropout, protocol deviation, and outcome of interest.²⁶ However, the results that the parameter estimates for predictors of the combined dropout and protocol deviation were similar to those for dropout alone make such assumption plausible.

In conclusion, our analyses of the ACTG A5095 trial serve as an example of using inverse probability weighting to generalize the per-protocol effect as well as the ITT effects to a specified target population. We recommend conducting generalized per-protocol analyses to complement conventional ITT comparisons, even though in this case study there was little difference between ITT and per-protocol effects, either in the sample or in the target population. There is some evidence that protocol deviations for this trial did not matter and that results were valid for recently HIV-diagnosed individuals. One may argue reasonably that if subgroup effects are strong enough to make a difference for generalizability, then we should report results by subgroups. However, covariates which individually do not yield notable subgroup effects may combine as detailed by Lesko et al.,⁹ and population-level planning may require population-level effect estimates summarized over subgroups. However, as long as positivity³² is met and key covariates are measured, one can generalize results.