Deep generative models of genetic variation capture the effects of mutations

Abstract

The functions of proteins and RNAs are defined by the collective interactions of many residues, and yet most statistical models of biological sequences consider sites nearly independently. Recent approaches have demonstrated benefits of including interactions to capture pairwise covariation, but leave higher-order dependencies out of reach. Here we show how it is possible to capture higher-order, context-dependent constraints in biological sequences via latent variable models with nonlinear dependencies. We found that DeepSequence (https://github.com/debbiemarkslab/DeepSequence), a probabilistic model for sequence families, predicted the effects of mutations across a variety of deep mutational scanning experiments substantially better than existing methods based on the same evolutionary data. The model, learned in an unsupervised manner solely on the basis of sequence information, is grounded with biologically motivated priors, reveals the latent organization of sequence families, and can be used to explore new parts of sequence space.

Amajor unanswered question in biological research, clinical medicine, and biotechnology is how to decipher and exploit the effects of mutations on biomolecules. For efforts ranging from the identification of genetic variants underlying human disease, to the development of modified proteins with useful properties, to the synthesis of large molecular libraries that are enriched with functional sequences, there is a need to be able to rapidly assess whether a given mutation in a protein or RNA will disrupt function^1,2. Although high-throughput technologies can now simultaneously assess the effects of thousands of mutations in parallel^1,3–27, sequence space is exponentially large and experiments are resource intensive. Accurate computational methods are thus an important component of high-throughput sequence annotation and design.

Most improvements to computational predictions of mutation effects have been driven by leveraging of the signal of evolutionary conservation among homologous sequences^28–33. Historically, these tools have been used to analyze the conservation of single sites in proteins in a background-independent manner. Recent work has demonstrated that the incorporation of intersite dependencies in a pairwise interaction model of genetic variation can lead to more accurate prediction of the effects of mutations in high-throughput mutational scans^34–37. However, numerous lines of evidence suggest that higher-order epistasis pervades the evolution of proteins and RNAs^38–41, and pairwise models are unable to capture this. Naive extension of pairwise models with third or higher terms is statistically unfeasible, as even third-order interaction models for a protein of 100 amino acids will have approximately 1 billion parameters. Even if such a model could be engineered or coarse-grained⁴² to be computationally and statistically tractable, it would only marginally improve the fraction of higher-order terms considered, leaving fourth and higher-order interactions out of reach.

Direct parameterization of sequence-variation models with all possible interactions of order k leads to an intractable combinatorial explosion in the number of parameters to consider. An alternative to this fully observed approach for modeling data—in which the correlations between positions are explained directly in terms of position-position couplings—is to model variations in terms of ‘hidden’ variables to which the observed positions are coupled. Two widely used models for the analysis of genetic data, principal component analysis and admixture analysis^43–45, can be cast as latent-variable (i.e., hidden-variable) models in which the visible data (genotypes) depend on hidden variables (factors or populations) in a linear way. In principle, the replacement of those linear dependencies with flexible nonlinear transformations could facilitate the modeling of arbitrary-order correlations in an observed genotype, but the development of tractable inference algorithms for them is more complex. Recent advances in approximate inference^46,47 have made these kinds of nonlinear latent-variable models tractable for the modeling of complex distributions for many kinds of data, including text, audio, and even chemical structures⁴⁸, but their application to genetic data remains in its infancy.

Here we developed nonlinear latent-variable models for biological sequence families and leveraged approximate inference techniques to infer the families from large multiple-sequence alignments. We show how a Bayesian deep latent-variable model can be used to reveal latent structure in sequence families and predict the effects of mutations with accuracies exceeding those of site-independent or pairwise-interaction models.

Results

A deep generative model captures latent structure in sequence families.

The genes observed across species today are the results of long-term evolutionary processes that select for functional molecules. We sought to model the constraints underlying the evolutionary processes of these sequences and to use those constraints to make reasonable inferences about what other mutations may be plausible. If we approximate the evolutionary process as a ‘sequence generator’ that generates a sequence x with probability p(x\θ) and parameters θ that are fit to reproduce the statistics of evolutionary data, we can use the probabilities that the model assigns to any given sequence as a proxy for the relative plausibility of a molecule satisfying functional constraints. We consider the log-ratio

$$\log \frac{p\left({\mathbf{x}}^{(\text{Mutant})}|\mathit{\theta }\right)}{p\left({\mathbf{x}}^{(\text{Wild-type})}|\mathit{\theta }\right)}$$

as a heuristic metric for the relative favorability of a mutated sequence, x^(Mutant), compared with that of a wild-type sequence, x^(wiid-type). This log-ratio heuristic has been shown to accurately predict the effects of mutations across multiple kinds of generative models p(x|θ)³⁴. Our innovation here is to consider a nonlinear latent-variable model for p(x|θ) that is capable of capturing higher-order constraints (Fig. 1a and Methods). This approach is fully unsupervised, as we do not train on observed mutation-effect data but rather use the statistical patterns in observed sequences as a signal of selective constraint.

Fig. 1 |. A nonlinear latent-variable model captures higher-order dependencies in proteins and RNAs.

a, Comparison of a nonlinear latent-variable model with site-independent and pairwise models. b, The dependency p(x|z) (blue) of the sequence x on the latent variable z is modeled by a neural network, and inference and learning are made tractable by joint training with an approximate inference network q(z|x) (pink). This combination of model and inference is also known as a variational autoencoder. The size of the latent variables z and hidden dimensions of the neural network are shown.

We introduce a nonlinear latent-variable model p(x|θ) to implicitly capture higher-order interactions between positions in a sequence. We imagine that when the data are generated, a hidden variable z is sampled from a prior distribution p(z), in our case a standard multivariate normal, and a sequence x is in turn generated on the basis of a conditional distribution p(x|z,θ) that is parameterized by a neural network. If the system were fully observed, the probability of data would be simple to compute as p(x|z,θ)p(z), but when z is hidden we must contend with the marginal likelihood,

$$p(\mathbf{x}|\mathit{\theta })=\int p(\mathbf{x}|\mathbf{z},\mathit{\theta })p(\mathbf{z})d\mathbf{z}$$

which considers all possible explanations for the hidden variables z by integrating them out. Direct computation of this probability is intractable in the general case, but we can use variational inference⁴⁹ to form a lower bound on the (log) probability. This bound, known as the evidence lower bound (ELBO), $\mathcal{L}(\mathit{\varphi };\mathbf{x})$ takes the form

$$\log p(\mathbf{x}|\mathit{\theta })\ge \mathcal{L}(\mathit{\varphi };\mathbf{x})\triangleq {\mathbb{E}}_q[\log p(\mathbf{x}|\mathbf{z},\mathit{\theta })]-D_{\text{KL}}(q(\mathbf{z}|\mathbf{x},\mathit{\varphi })\Vert p(\mathbf{z}))$$

where q(z|x,ϕ) is a variational approximation for the posterior distribution p(z|x,θ) of hidden variables given the observed variables. We model both the conditional distribution p(x|z,θ) of the generative model and the approximate posterior q(z|x,ϕ) with neural networks, which results in a flexible model-inference combination known as a variational autoencoder (VAE)^46,47 (Fig. 1b). After the model is fit to a given family through optimization of the variational parameters ϕ, it can be readily applied to predict the effects of arbitrary types and numbers of mutations. We quantify effects with an approximation to the log-ratio by replacing each log probability with the ELBO (Fig. 2).

Fig. 2 |. Mutation effects can be quantified by likelihood ratios.

After fitting a probabilistic model to a family of homologous sequences, we heuristically quantified the effect of mutation as the log-ratio of mutant likelihood to wild-type likelihood (as approximated by the ELBO; Methods). Bottom: mutation-effect scores for positions 310–393 in the PDZ domain.

We use a particular combination of priors, parameterizations, and learning algorithms to make the model more interpretable and more likely to generalize. First, we encourage sparse interactions⁵⁰ with a group sparsity prior on the last layer of the neural network for p(x|z,θ). This prior encourages small subgroups of hidden units in the network to influence only a few positions at a time. Second, we encourage correlation between amino acid usage by transforming all local predictions of the amino acids at each position with a shared a linear map C, which we refer to as a dictionary. Finally, and in deviation from standard practice for VAEs, we learn distributions over the weights of the neural network for p(x|z,θ) with a variational approximation over both the global model parameters and the per-datum hidden variables. This means that rather than learning a single neural network for p(x|z,θ), we learn an infinite ensemble of networks.

We optimized the joint variational approximation over global and local parameters by stochastic gradient ascent on the ELBO to obtain a fully trained model (Methods). Because this is a nonconvex optimization problem with multiple solutions, we fit five replicas of the model from different initial conditions. Throughout the analysis, we considered both the average performance across these five fits and the performance of the ensemble prediction that averaged the predictions together.

Model probabilities correlate with experimental mutation effects.

We compared predictions from DeepSequence to a collection of 42 high-throughput mutational scans (712,218 mutations across 108 sets of experiments on 34 proteins and a tRNA; Methods, Supplementary Tables 1 and 2, Supplementary Fig. 1). We found that the predictions of the DeepSequence ensemble correlated equally as well or better with experimental mutation effects across a majority of the datasets, compared with predictions from both a pairwise interaction model (EVmutation³⁴; 33/42 datasets; median difference in rank correlation Δρ = 0.036) and a siteindependent model (34/42 datasets; median Δρ = 0.063) trained on the same data (Fig. 3, Supplementary Table 3). The average performance of DeepSequence without ensembling reproduced this overall advantage over EVmutation (32/42 datasets; median Δρ = 0.024) and the site-independent model (3¼2 datasets; median Δρ = 0.055). The clear exceptions to the overall superiority of DeepSequence were the comparisons to the viral protein mutation experiment effects, and especially the two HIV env experiments, which suggests that the VAE approach is more dependent on a larger diversity of fit sequences on which to train the model. When compared against a subset of the data that was previously analyzed³⁴, the DeepSequence predictions were consistently more accurate than those of other commonly used methods, such as BLOSUM62 (20/20; median Δρ = 0.32), SIFT³² (20/20; median Δρ = 0.24), and Polyphen2³¹ (19/20; median Δρ = 0.20) (Supplementary Table 4).

Fig. 3 |. A deep latent-variable model predicts the effects of mutations better than site-independent or pairwise models.

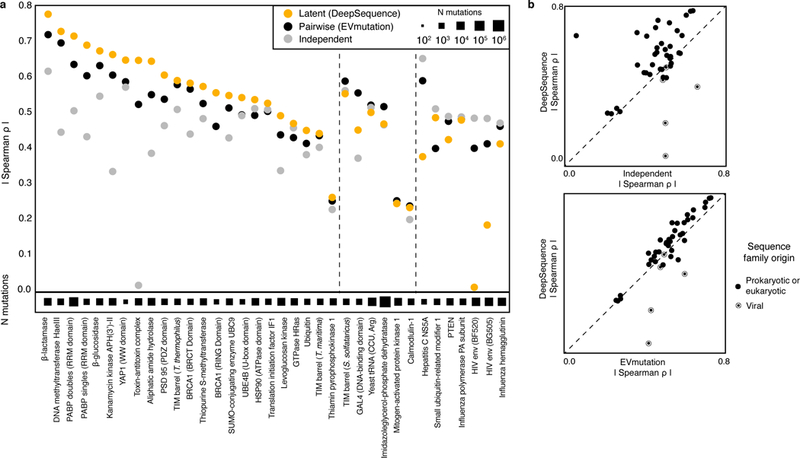
a, DeepSequence captures the effects of mutations across deep mutational scanning experiments as measured by rank correlation. b, Comparison of prediction accuracy of DeepSequence to that of a site-independent model (top) and EVmutation (bottom).

The deep mutational scans that we analyzed typically involved only one or a few mutational steps from assayed sequences (‘test set’) to the sequences that the model was trained on, which raised the question of how well the model can generalize when the number of steps is larger. To test this, we reran the experiments for TEM1 P-lactamase with artificially purged training sets in which sequences with 35%, 60%, 80%, 95%, or 100% identity to wild-type TEM1 were removed. We found that DeepSequence continued to outperform pairwise and site-independent models even when all sequences within 60% sequence identity were purged. The Spearman correlation decreased by only 0.07, despite the fact that all mutated test sequences were ~100 mutational steps away from the training set (Methods, Supplementary Fig. 2).

We observed a consistent amino acid bias in the prediction accuracy of all three evolutionary models (independent, EVmutation, and DeepSequence) when we compared the residuals of the rankings of the predictions with the experimental data for each amino acid transition (Supplementary Fig. 2), but we were unable to find consistent patterns for this discrepancy. For instance, we could not explain the observed bias by codon usage. Accounting for this bias by fitting a linear model on top of the predictions improved DeepSequence, but the improvements were small (Supplementary Fig. 3, Methods).

Sequence space in latent space.

Examining the low-dimensional latent spaces learned by a latent-variable model can give insight into relationships between data points (sequences). To gain insight into the organization of latent space directly, we fit an otherwise identical copy of the model with 2-dimensional rather than 30-dimensional z to β-lactamase (Fig. 4). This visualization illustrated the comparative shallowness of deep mutational scans: all mutated sequences from the deep mutational scans of β-lactamase were tightly concentrated in a small region of latent space. We also observed an uneven distribution in latent space with phylogenetically coherent structure; however, we caution against overinterpreting this distribution, because it will depend strongly on the choice of prior and the variational approximations⁵¹.

Fig. 4 |. Latent variables capture the organization of sequence space.

The β-lactamase family shown in two-dimensional latent space; a single deep mutational scanning experiment with variants (center: pink) is shown.

Bayesian learning prevents overfitting and facilitates interpretation.

To test the importance of our specific choices for the architecture and learning algorithm, we carried out an ablation study of model design decisions across a subset of proteins. We found that all of the major design decisions contributed to improved performance, including the use of sparse priors on the last layer, a learned dictionary of amino acid correlations, a global inverse-temperature parameter, and a Bayesian variational approximation for the weights (Supplementary Table 5, Fig. 5, and Methods). The largest improvement seemed to result from the use of variational Bayes to learn distributions over the weights of the network rather than point estimates, even when point estimation was combined with group sparsity priors⁵² or Dropout⁵³ regularization (Supplementary Table 5).

Fig. 5 |. Structured priors over weights capture biological assumptions.

Top: traditional fully connected layer that outputs per-position logits over different letters (A, B, C, D) at each position. Center: a group-sparsity prior over the weights encourages block sparsity such that groups of k hidden units tend to influence all the logits at a small number of positions. Bottom: an additional global transform at every position in the sequence by a shared weight matrix captures correlations between letter usage.

We considered two kinds of structured correlations in multiple-sequence alignments in the design of the final layer. The first was correlated bias in amino acid usage, where hydrophobic or polar amino acids tend to have correlated liability at a given position. We captured this with a shared linear transformation C that was tied across all positions and found that its implicit correlation structure (C^TC) reflected well-known amino acid similarities (Fig. 6a, Supplementary Table 6). The second kind of correlation in multiple-sequence alignments is between positions, and often coincides with structural proximity^54–57. Our group sparsity prior captured these correlations by learning 500 soft subgroups of positions that were each connected to four hidden units. We computed the average pairwise distance between positions in each subgroup using representative structures from the Protein Data Bank (Methods) and found that most distances were less than a null expectation (Methods, Fig. 6a, Supplementary Tables 7 and 8), with subsets of residues close in 3D.

Fig. 6 |. Interpretation of model and effect predictions.

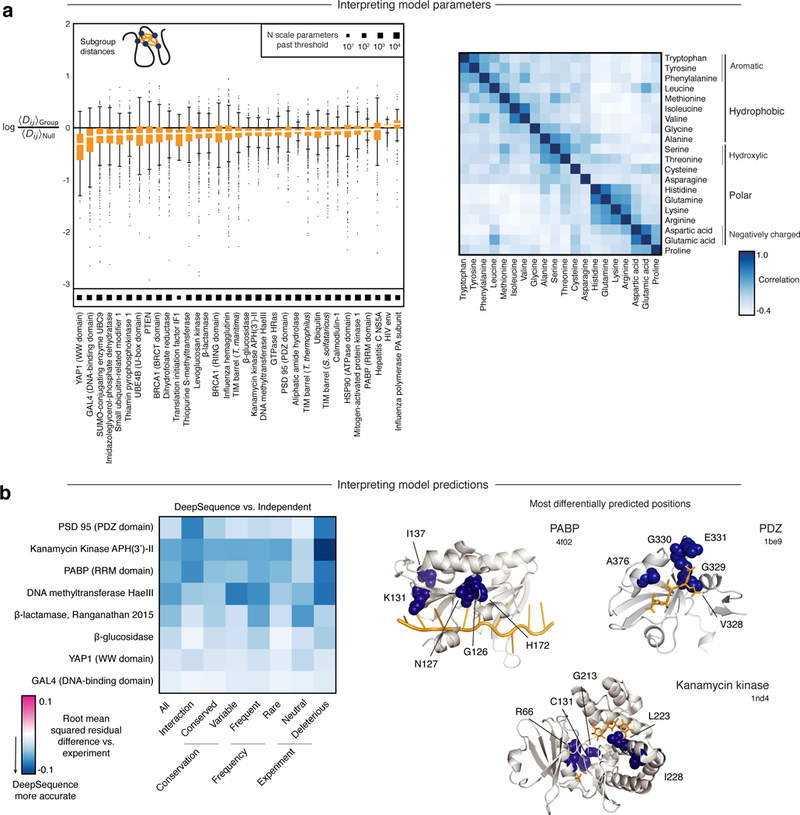
a, Left: log enrichment of 3D distances between residues that make up the sparse factors compared to a null distance (Methods). Box plots show the median (center line), interquartile range (hinges), and 1.5 times the interquartile range (whiskers); outliers are plotted as individual points. Right: correlations in the weights of the final width - 1 convolution taken across all models reflect known amino acid correlations and are correlated with a well-known substitution matrix BLOSUM62 (Spearman p = 0.83, N = 210). b, Left: comparison of relative rank error between DeepSequence and a position-independent conservation model across different positions and mutation attributes. Right: top five positions with the greatest reduction in rank error from the site-independent model to DeepSequence.

Interpretation of mutation-effect predictions.

We then explored which sets of mutations were most differentially predicted by DeepSequence (using a subset of eight experiments with large overall differences from the independent methods; Supplementary Fig. 5, Supplementary Table 9, Methods). DeepSequence was most accurate for all proteins across all residue classifications that we explored, including both evolutionary (‘conservation, ‘frequency’) and structural features (‘interaction’) (Fig. 6b). The overall increased accuracy of the latent model predictions was particularly strong for mutations that were deleterious in the experiment, and often where these deleterious sites were variable or proximal to interacting ligands. For example, in the RNA-recognition-motif domain of the poly(A) binding protein and the PDZ domain in PSD95 and kanamycin kinase, residues close to their ligands or cofactors are the most differentially accurate. These include a residue position involved in specificity switching G330 in the PDZ domain and RNA interaction sites in the RNA recognition motif (Fig. 6b). These results are consistent with the idea that the latent model makes better predictions for sites sensitive to change but still varied across evolution, and hence context dependent.

Discussion

We have presented a deep latent-variable model that can capture higher-order correlations in biological sequence families and shown how it can be applied to predict the effects of mutations across diverse classes of proteins and RNAs. We found that the predictions of the deep latent-variable model were more accurate than those of a previously published pairwise-interaction approach to model epistasis^34,36, which in turn was more accurate than commonly used supervised methods^58,59. In addition, both latent variables and global variables of the model learned interpretable structure for both macrovariation and phylogeny, as well as the structural proximity of residues.

Deep latent-variable models introduce additional flexibility for modeling of higher-order constraints, but at the cost of reduced interpretability and increased potential for overfitting. Indeed, we found that even traditional approaches for regularization, such as Dropout⁵³ and sparsity priors, were often worse than the already-established pairwise models. While this work was in progress, other nonlinear latent-variable models were proposed for sequence families^60,61, evidencing the benefits of more parametrically powerful models for sequence variation. A key aspect of this work distinguishing it from both those and other models in our ablation study is its use of approximate Bayesian inference, whereby we estimated distributions over model parameters and propagated that uncertainty into model predictions. Although we found that mean-field approximate variational inference and group sparsity priors were sufficient to exceed the performance of a wide range of models, it is likely that future work would benefit from other biologically motivated priors, as well as more accurate approximations for variational inference^62,63. Additionally, the incorporation of more rigidly structured probabilistic graphical models in model dependencies between latent variables could improve generality and interpretability⁶⁴.

Lastly, the efficacy of DeepSequence for predicting experimental mutational scans will be contingent on both the quality and the relevance of the evolutionary sequence data in two ways. First, DeepSequence and other mutation-effect-prediction methods train on multiple-sequence alignments^{34,55,65–67}, for which the quality of the available data may vary across families and for which decisions on inclusion thresholds are somewhat ad hoc. Second, the premise that evolutionary data can be applied to predict outcomes of an experiment is highly contingent on the relevance of the experimental assay to long-term selective forces in the family. A mutation may be damaging with regard to some measurable protein feature—for example, enzyme efficiency—but harmless for stability or even organism fitness, as others and we have previously discussed^13,34,68. Both of these issues could be partially addressed by the incorporation of DeepSequence predictions as features in a supervised learning framework.

Despite the challenges for deep models of sequence variation and data used to train them, they are likely to be of increasing importance for the high-throughput design and annotation of biological sequences. Evolution has conducted and continues to conduct an unthinkably large number of protein experiments, and deep generative models can begin to identify the statistical patterns of constraint that characterize essential functions of molecules.

Methods

Datasets.

We constructed a dataset of deep mutational scans that combined those analyzed in EVmutation^{3–12,14–18,20–22,24,69} with additional studies published later^25,70–80. Data underlying Fig. 3 include 41 measurements across 35 protein or RNA domains. The conditions, assay, references, maps to data for specific figures, and criteria for disambiguating multiple available measurements are listed in Supplementary Table 1.

Alignments.

We repeated the same alignment-generation protocol used for EVmutation³⁴. Briefly, for each protein (target sequence), we obtained multiple-sequence alignments of the corresponding protein family in five search iterations of the profile HMM homology search tool jackhmmer⁸¹ against the UniRef100 database of nonredundant protein sequences⁸² (release 11/2017 for the main analysis and 11/2015 for the ablation study). We used a bit score of 0.5 bits per residue as a threshold for inclusion unless the alignment yielded <80% coverage of the length of the target domain, or if there were not enough sequences (redundancy-reduced number of sequences ≥ 10L, where L is the sequence length). For <10L sequences, we decreased the required average bit score until satisfied, and when the coverage was <80% we increased the bit score until satisfied. Proteins with <2L sequences at <70% coverage were excluded from the analysis. See previous work for ParE-ParD toxin-antitoxin and tRNA alignment protocols.

Sequence weights.

The distributions of protein and RNA sequences in genomic databases are biased by both (i) human sampling, as some parts of a phylogeny may be more studied and sequenced than others, and (ii) evolutionary sampling, as some groups of species have arisen from large radiations and will have proteins that are over-represented. We aim to reduce these biases by reweighting the data distribution. We use the previously established procedure⁸³ of computing each sequence weight π_s as the reciprocal of the number of sequences within a given Hamming distance cutoff. If D_H(x^(s), x^(t)) is the normalized Hamming distance between the query sequence x^(s) and another sequence in the alignment x^(t) and θ_ID is a predefined neighborhood size (percent divergence), the sequence weight is

$${\pi }_s={\left(\sum _t^{N}I\left[D_H\left({\mathbf{x}}^{(s)},{\mathbf{x}}^{(t)}\right)<{\theta }_{ID}\right]\right)}^{-1}$$

The effective sample size of a multiple-sequence alignment can then be computed as the sum of these weights as

$$N_{\text{eff}}=\sum _t^N{\pi }_t$$

To fit a model to reweighted data, there are two common approaches. First, as was done previously⁸³, one can reweight every log-likelihood in the objective by its sequence weight π_s. Although this works well for batch optimization, we found that it led to high-variance gradient estimates with mini-batch optimization that made stochastic gradient descent unstable. We instead used the approach of sampling data points for each mini-batch with probability p_s proportional to their weight as $p_s={\pi }_s/N_{\text{eff}}$.

Following prior work³⁴, we set θ_ID = 0.2 for all multiple-sequence alignment sequences (80% sequence identity) except those for viral proteins, where we set θ_ID = 0.01 (99% sequence identity) owing to limited sequence diversity and the expectation that small differences in viral sequences will have a higher probability of containing constraint information than the same diversity might from a sample of mammals, for instance.

Background: latent factor models.

Probabilistic latent-variable models reveal structure in data by positing a partially unobserved generative process that created the data and then conducting inference to learn the parameters of the generative process. We focus on models in which an unobserved set of factors z are drawn from an independent distribution and each data point arises according to a conditional distribution p(x|z,θ) that is parameterized by θ. This process can be written as

$$\mathbf{z}~\mathcal{N}\left(0,{\mathbf{I}}_D\right)$$

$$\mathbf{x}~p(\mathbf{x}|\mathbf{z},\mathit{\theta })$$

Principal component analysis (PCA) has been a foundational model for the analysis of genetic variation and can be realized in this probabilistic framework as the zero-noise limit of probabilistic PCA^43,84. With linear conditional dependencies p(x|z,θ), PCA can model only additive interactions between the latent factors z. This limitation could in principle be remedied through the use of a conditional model p(x|z,θ) with nonlinear dependencies on z.

Here we consider a conditional model for sequences p(x|z,θ) that differs from PCA in two ways. First, the conditional distribution of the data p(x|z,θ) will be categorical rather than Gaussian to model discrete characters. Second, the conditional distribution p(x|z,θ) will be parameterized by a neural network rather than a linear map. In this sense, our latent-variable model may be thought of as a discrete, nonlinear analog of PCA.

Nonlinear categorical factor model.

Our probabilistic model is specified by two components: a prior distribution p(z) that specifies the marginal distribution of the hidden variables z, and a conditional distribution p(x|z,θ) that specifies how a sequence x is generated given the hidden variables. In our model, the sequence x is a string of letters of length L drawn from an alphabet of size q, and the hidden variables z are a vector of real numbers with length D.

In this work, we structure our prior and conditional distribution similarly to original versions of the VAE⁴⁶. That is, we model the prior distribution p(z) as a multivariate normal of dimension D with mean 0 and identity covariance, and we model the conditional distribution p(x|z,θ) as a simple fully connected neural network with two hidden layers. Thus, the generative process for the joint distribution p(z)p(x|z,θ) can be written as

$$\mathbf{z}~\mathcal{N}\left(0,{\mathbf{I}}_D\right)$$

$${\mathbf{h}}^{(1)}=f_1\left({\mathbf{W}}^{(1)}\mathbf{z}+{\mathbf{b}}^{(1)}\right)$$

$${\mathbf{h}}^{(2)}=f_2\left({\mathbf{W}}^{(2)}{\mathbf{h}}^{(1)}+{\mathbf{b}}^{(2)}\right)$$

$${\mathbf{h}}^{(3,i)}={\mathbf{W}}^{(3,i)}{\mathbf{h}}^{(2)}+{\mathbf{b}}^{(3,i)}\text{for}i=1\dots L$$

$$p\left(x_i=a|\mathbf{z}\right)=\frac{e^{h_a^{(3,i)}}}{\sum _b{e}^{h_b^{(3,i)}}}\text{for}i=1\dots L$$

where the nonlinearities are rectified linear units (ReLU) f₁ = max(0, u) on the first layer and sigmoidal f₂ = 1/(1 + e^−u) on the second. The sigmoidal nonlinearity was introduced to bound the magnitude of the preactivations that are multiplied by the structured matrix W^(3,i) (discussed in the next section). It is important to note that each letter x_i is conditionally independent of every other position given the hidden variables z and, as a result, all correlations between letters must be mediated by correlations with the hidden variables.

Structured parameterization.

All biologically motivated aspects of our model are captured in a structured parameterization of the final weight matrix. Our parameterization is motived by three assumptions. (i) Sparsely interacting subsystems: hidden factors influence small subsystems of positions at a time, rather than jointly affecting the entire sequence. (ii) Correlated amino acid usage: certain amino acids are more likely to functionally substitute other amino acids in the same position on the basis of biochemistry. (iii) Selective uncertainty: differences in the strength of selection may lead to varying effective ‘temperatures’ of the constraint distribution. To capture these constraints, we parameterize at each position i as

$${\mathbf{W}}^{(3,i)}=\lambda \mathbf{C}{\tilde{\mathbf{W}}}^{(3,i)}\text{diag}\left({\mathbf{S}}_{\mathbf{i}}\right)$$

where W^(3,i) is a [q × H] matrix that linearly combines the H activations in the final hidden h⁽²⁾ layer to q multinomial logits for the different characters (for example, amino acids) at position i. The parameterization consists of four terms: a matrix C that captures amino acid correlations, a matrix S with elements on (0,1) that gates which hidden units can affect which positions, a scalar constant λ capturing the overall selective constraint shared across all positions (inverse temperature), and underlying parameters ${\tilde{\mathbf{W}}}^{(3,i)}$ that combine with the other terms to capture site-specific constraints. We describe these elements in turn.

To capture correlations in amino acid usage, we split the weights themselves into a combination of local weights at each position ${\tilde{\mathbf{W}}}^{(3,i)}$ plus a global ‘dictionary’ matrix C. The inner dimension of the product $\text{C}{\tilde{\mathbf{W}}}^{(3,i)}$ is a hyperparameter E such that C is a global [q × E] matrix that left multiplies each of the ${\tilde{\mathbf{W}}}^{(3,i)}$ matrices, which are [E × H], to transform to the alphabet of the model (for example, the amino acids).

To capture sparsely depending subsystems, we learn an [H × L] matrix S that masks which neurons in the final hidden layer h⁽²⁾ can influence which positions in the sequence. Each column vector S_i captures the hidden units in h⁽²⁾ that affect position i in the sequence. We constrain the values of this matrix to be between 0 and 1, and also to tie some of the rows of S to be equal (Fig. 5; see parameterization below). In the above expression we write diag(S_i) to indicate the [H × H] matrix containing the column vector s_i along its diagonal, which allows us to frame the matrix S as a component of the parameterization of W^(3,i). In practice, we actually compute the effect of S with broadcasting as $h^{(3,i)}=\lambda \mathbf{C}{\tilde{\mathbf{W}}}^{(3,i)}\left({\mathbf{S}}_{\mathbf{i}}\odot {\mathbf{h}}^{(2)}\right)+{\mathbf{b}}^{(3,i)}$.

Lastly, a positive scalar λ captures the overall strength of the constraints. Typically, including a scalar prefactor in a weight matrix is fully redundant, but placing a prior over this parameter and then modeling uncertainty with a variational approximation can capture global, sequence-wide correlations in the selective strength.

We parameterize the constrained parameters S and λ with unconstrained forms $\tilde{\mathbf{S}}$ and $\tilde{\lambda }$ that can be optimized by gradient descent. The global ‘inverse temperature’ λ is parameterized by the softplus function as $\lambda =\log \left(1+e^{\tilde{\lambda }}\right)$. The sparsity matrix S is constrained to both (i) have elements on (0,1) and (ii) have H/k blocks of k identical rows. To accomplish this, we parameterize it in terms of an [H/k × L] matrix $\tilde{\mathbf{S}}$, transform it by a sigmoid, and tile the rows of $\tilde{\mathbf{S}}$ k times with the transform $S_{ji}={\left(1+\exp \left({\tilde{\mathbf{S}}}_{j\mathrm{mod}(H/k),i}\right)\right)}^{-1}$. When paired with a Gaussian prior over $\tilde{\mathbf{S}}$ and ${\tilde{\mathbf{W}}}^{(3,i)}$, the scale parameters S will be a priori logit-normally distributed, and the resulting product ${\tilde{\mathbf{W}}}^{(3,i)}$ diag $\left({\mathbf{S}}_i\right)$ can be seen as a continuous relaxation of a spike and slab prior (where it would be exact if the elements of S were Bernoulli).

Priors.

We place Gaussian priors over all unconstrained parameters as ${\tilde{W}}_{ij}~\mathcal{N}(0,1),C_{ij}~\mathcal{N}(0,1),{\tilde{S}}_{ij}~\mathcal{N}\left({\mu }_s,{\sigma }_s^2\right)$, and $\tilde{\lambda }~\mathcal{N}(0,1)$. To set the hyperparameters ${\mu }_s,{\sigma }_s^2$, we consider the effective logit-normal prior over s, which can be thought of as a smooth relaxation of a Bernoulli that can be made sharper by an increase in the variance ${\sigma }_s^2$. We set ${\mu }_s=-12.36$ and ${\sigma }_s^2$ = 16.

Background: variational inference.

Nonlinear latent factor models are difficult to infer. Because the latent variables z are not observed, computation of the marginal likelihood of the data requires that they be integrated out as

$$\log p(\mathbf{x}|\mathit{\theta })=\log \int p(\mathbf{x}|\mathbf{z},\mathit{\theta })p(\mathbf{z})d\mathbf{z}$$

We must apply this integral because we do not know a priori which z is responsible for each data point x, and so we average over all possible explanations weighted by their relative probability. When this integral over z cannot be simplified, optimization of the marginal likelihood log p(x|θ) to fit a model to data will be intractable.

Variational inference forms a lower bound on log p(x|θ) that is easier to optimize. First, we introduce q(z|x,ϕ), an approximate distribution for z given x that is flexibly parameterized by variational parameters ϕ. By Jensen’s inequality, we can lower-bound the intractable marginal likelihood log p(x|θ) as

$$\log p(\mathbf{x}|\mathit{\theta })=\log \int p(\mathbf{x}|\mathbf{z},\mathit{\theta })p(\mathbf{z})d\mathbf{z}$$

$$=\log \int \frac{p(\mathbf{x}|\mathbf{z},\mathit{\theta })p(\mathbf{z})}{q(\mathbf{z}|\mathbf{x},\mathit{\varphi })}q(\mathbf{z}|\mathbf{x},\mathit{\varphi })d\mathbf{z}$$

$$\ge \int \log \frac{p(\mathbf{x}|\mathbf{z},\mathit{\theta })p(\mathbf{z})}{q(\mathbf{z}|\mathbf{x},\mathit{\varphi })}q(\mathbf{z}|\mathbf{x},\mathit{\varphi })d\mathbf{z}$$

We write this lower bound as

$$\log p(\mathbf{x}|\mathit{\theta })\ge \mathcal{L}(\mathit{\varphi })\stackrel{\mathit{\Delta }}{=}{\mathbb{E}}_q[\log p(\mathbf{x}|\mathbf{z},\mathit{\theta })]-D_{\text{KL}}(q(\mathbf{z}|\mathbf{x},\mathit{\varphi })\Vert p(\mathbf{z}))$$

which we refer to as the evidence lower bound (ELBO). Maximizing the ELBO has the side effect of minimizing the Kullback-Leibler (KL) divergence between the variational approximation q(z|x,ϕ) and the true posterior distribution for z given x,

$$p(\mathbf{z}|\mathbf{x},\mathit{\theta })=\frac{p(\mathbf{x}|\mathbf{z},\mathit{\theta })p(\mathbf{z})}{\int p\left(\mathbf{x}|{\mathbf{z}}^{\prime },\mathit{\theta }\right)p\left({\mathbf{z}}^{\prime }\right)d{\mathbf{z}}^{\prime }}$$

Variational approximation for local posteriors p(z|x,θ). We structure the functional form of the variational approximation for z as

$${\mathbf{g}}^{(1)}=f_1\left({\mathbf{W}}_q^{(1)}\mathbf{x}+{\mathbf{b}}_q^{(1)}\right)$$

$${\mathbf{g}}^{(2)}=f_1\left({\mathbf{W}}_q^{(2)}{\mathbf{g}}^{(1)}+{\mathbf{b}}_q^{(2)}\right)$$

$$\mathit{\mu }={\mathbf{W}}_{\mu }^{(3)}{\mathbf{g}}^{(2)}+{\mathbf{b}}_{\mu }^{(3)}$$

$$\mathit{\sigma }=\exp \left({\mathbf{W}}_{\sigma }^{(3)}{\mathbf{g}}^{(2)}+{\mathbf{b}}_{\sigma }^{(3)}\right)$$

$$q(\mathbf{z}|\mathbf{x},\varphi )=\mathcal{N}\left(\mathit{\mu },\text{diag}\left({\mathit{\sigma }}^2\right)\right)$$

We apply the ‘reparameterization trick’ of Kingma and Welling⁴⁶ and Rezende et al.⁴⁷ to write the latent variables z as deterministic transforms of a noise source $\mathit{ϵ}~\mathcal{N}\left(0,{\mathbf{I}}_D\right)\text{as}\mathbf{z}=\mathit{\mu }+\mathit{\sigma }\odot \mathit{ϵ}$, where the symbol $\odot$ is an element-wise product.

Variational approximation for global posteriors $p(\mathit{\theta }|\mathbf{X})$. We briefly review^46,47 how to extend variational approximations to include both the latent variables z and the global parameters θ^46,47. Because the posterior for the global parameters is conditioned on the entire dataset, we must consider the marginal likelihood of the full dataset $\mathbf{X}=\left\{{\mathbf{x}}^{(1)},\dots ,{\mathbf{x}}^{(N)}\right\}$, which integrates out all of the corresponding latent factors $\mathbf{Z}=\left\{{\mathbf{z}}^{(1)},\dots ,{\mathbf{z}}^{(N)}\right\}$. The likelihood of the entire dataset log p(X) can be lower-bounded by

$$\log p(\mathbf{X})=\log \iint p(\mathbf{X}|\mathbf{Z},\mathit{\theta })p(\mathbf{Z})p(\mathit{\theta })d\mathbf{Z}d\mathit{\theta }$$

$$=\log \iint \frac{p(\mathbf{X}|\mathbf{Z},\mathit{\theta })p(\mathbf{Z})p(\mathit{\theta })}{q(\mathbf{Z},\mathit{\theta }|\mathbf{X},\mathit{\varphi })}q(\mathbf{Z},\mathit{\theta }|\mathbf{X},\mathit{\varphi })d\mathbf{Z}d\mathit{\theta }$$

$$\ge \iint \log \frac{p(\mathbf{X}|\mathbf{Z},\mathbf{\theta })p(\mathbf{Z})p(\mathbf{\theta })}{q(\mathbf{Z},\mathbf{\theta }|\mathbf{X},\varphi )}q(\mathbf{Z},\mathbf{\theta }|\mathbf{X},\varphi )d\mathbf{Z}d\mathbf{\theta }$$

The ELBO can then be written as

$$\begin{gathered} \log p(\mathbf{X})\ge \mathcal{L}(\mathit{\varphi }) \\ \triangleq N{\mathbb{E}}_{\mathbf{x}\in \mathbf{X}}\left[{\mathbb{E}}_{q(\mathit{\theta })q(\mathbf{z}|\mathbf{x})}(\log p(\mathbf{x}|\mathbf{z},\mathit{\theta }))-D_{\text{KL}}(q(\mathbf{z}|\mathbf{x},\mathit{\varphi })\Vert p(\mathbf{z}))\right] \\ -\sum _{{\mathit{\theta }}^{(i)}}{D}_{\text{KL}}\left(q\left({\mathit{\theta }}^{(i)}\right)\Vert p\left({\mathit{\theta }}^{(i)}\right)\right) \end{gathered}$$

We model all variational distributions over the parameters with fully factorized mean-field Gaussian distributions. We factorize the variational approximation across the global and local parameters as $q(\mathbf{Z},\mathit{\theta }|\mathbf{X},\mathit{\varphi })=q(\mathbf{Z}|\mathbf{X},\mathit{\varphi })q(\mathit{\theta }|\varphi )$ across Z as $q(\mathbf{Z}|\mathbf{X},\mathit{\varphi })=\prod q\left({\mathbf{z}}^{(i)}|{\mathbf{x}}^{(i)},\mathit{\varphi }\right)$, and across the model parameters as $q(\mathit{\theta }|\mathit{\varphi })=\prod \left({\mathit{\theta }}^{(i)}|\mathit{\varphi }\right)$. In accordance with our data-reweighting scheme, we set N = N_eff, the effective number of sequences that is the sum of the sequence weights.

Model hyperparameters.

We used a fixed architecture across all sequence families. The encoder has architecture 1500–1500-(30×2) with fully connected layers and ReLU nonlinearities. The decoder has two hidden layers: the first with size 100 and a ReLU nonlinearity, and the second with size 2,000 with a sigmoid nonlinearity. The dictionary C is a q × 40 matrix where the alphabet size q is 20 for proteins and 4 for nucleic acids. We tied rows of the S matrix into groups of size k = 4. Dropout⁵³ was set to 0.5 when used in ablation studies. Models were optimized with Adam⁸⁵ with default parameters and a batch size of 100 until convergence, completing 300,000 updates.

Each model was fit five times to the same multiple-sequence alignment using a different random seed. We calculated the mutation effect prediction (ΔE) by taking the difference of the mean of 2,000 ELBO samples of the wild-type and a given mutated sequence.

Site-independent and pairwise model.

We compared the VAE with two other kinds of probabilistic models, both of which can be characterized as undirected graphical models with probability

$$P(\mathbf{x}|\mathit{\theta })=\frac{1}{Z}\exp (E(\mathbf{x}))$$

For these distributions, E(x) is the log-potential that describes the favorability of a sequence, and Z normalizes the distribution over sequence space. A site-independent model has site-additive terms for each amino acid in each position as

$$E_{\text{site}}(\mathbf{x})=\sum _i{\mathbf{h}}_i\left(x_i\right)$$

while the pairwise model includes additional parameters for every pairwise combination of amino acids as

$$E_{\text{pair}}(\mathbf{x})=\sum _i{\mathbf{h}}_i\left(x_i\right)+\sum _{i<j}{\mathbf{J}}_{ij}\left(x_i,x_j\right)$$

We estimated these models using the same methods previously described for EVmutation³⁴ (L₂-penalized maximum pseudolikelihood). To compute the effects of mutations, we again use the log-ratio

$$\log \frac{p\left({\mathbf{x}}^{(\text{Mutant})}|\mathit{\theta }\right)}{p\left({\mathbf{x}}^{(\text{Wild-type})}|\mathit{\theta }\right)}$$

which reduces to the difference of the (negative) energy values E(x) for the mutated and wild-type sequence.

Predictors for non-epistatic mutation effects.

We also compared a subset of protein datasets with three commonly used mutation-effect predictors—a BLOSUM62 matrix, SIFT³², and Polyphen2³¹—as previously described for EVmutation³⁴.

Group sparsity analysis.

We aimed to test whether positional activations driven by specific neurons in the last hidden layer corresponded to structural proximity. We gathered ground-truth distance data from the PDB⁸⁶ records of homologous sequences that were found via Jackhmmer (Supplementary Table 8). To aggregate distance information across multiple structures from the same family, we computed the median (across PDBs) of the minimum atom distances (across all atom pairs per position pair) for both intra- and homo-oligomer distances. The final aggregated distance matrix was the element-wise minimum of the intra- and homo-oligomeric distance matrices.

To identify the dominant connections between the last hidden layer of neurons and specific positions in the sequence, we consider the (approximate) sparsity structure of the matrix S. The row vectors ${\mathit{S}}_{a,:}$ represent positions in the sequence that are affected by the hidden unit $h_a^{\left(2\right)}$. We quantify the ‘typical’ distances in these groupings by means of a weighted average of the distances, where the weighting within each group is computed as $w_{ij}^{(a)}=S_{ai}{S}_{aj}$. The ‘typical’ distance within a group a is then

$${\widehat{D}}^{(a)}=\frac{{\sum }_{i<j}{w}_{ij}^{(a)}{D}_{ij}}{{\sum }_{i<j}{w}_{ij}^{(a)}}$$

The null expectation for each ${\widehat{D}}^{(a)}$ is the expected average distance under permuted groups, which is simply the average pairwise distance across the whole structure. We discarded any ‘disconnected’ hidden units for which the entire row of S had a negligible value $\left(\forall j,S_{ij}<0.001\right)$.

Residual analysis.

We calculated the Spearman ρ by transforming paired data to ranked quantiles and then computing the Pearson correlation between the ranks. To determine where the model over- or underpredicted the ΔE for each mutation, we transformed the experimental measurements and mutation-effect predictions to normalized ranks on the interval [0,1].

To quantify the error between predictions, we fit a least-squares linear fit from the normalized ranks of the predictions to the normalized ranks of the data for each method and then measured the residuals of this fit. Thus, we define the residual effects as the residuals of a least-squares linear fit between the normalized ranks. Given a least-squares fit with slope and bias m and b, respectively, the residuals are then

$${\epsilon }_{\Delta \text{E}}=d_{\text{Experiment}}-\left(m{d}_{\Delta \text{E}}+b\right)$$

Thus positive residuals ε_ΔE > 0 represent underprediction of the rank of the experimental effect (and thus overprediction of deleteriousness), whereas negative ε_ΔE values represent overprediction of the experimental rank (and thus underprediction of deleteriousness). We analyzed deep mutational scans with only single mutations, using the most recent experimental data for each protein. Residuals were grouped by the identity of the amino acid either before mutation (wild-type) or after mutation (mutant).

Bias correction.

To correct for biases between mutation-effect predictions and experimental measurements, we created a feature matrix for each mutation that included ΔE, amino acid identity before and after mutation, alignment column statistics (conservation and amino acid frequency), and residue hydrophobicity⁸⁷. We used leave-one-out cross-validation (LOOCV) to correct the bias for each dataset. Using the most recent deep mutational scan (DMS) experiment as the representative of that protein family (28 DMS datasets), we used the mutants of 27 datasets to fit a regression model to predict the residuals of each known mutation, ε_ΔE, given the feature matrix. After this model was fit, it was used to predict ${\epsilon }_{\mathrm{\Delta }E}$ for the mutants in the test dataset. This predicted residual bias ${\widehat{\epsilon }}_{\Delta E}$ was subtracted from the normalized predicted rank ${\widehat{d}}_{\Delta E}=d_{\Delta E}-{\widehat{\epsilon }}_{\Delta E}$. These corrected predictions were then reranked and compared to the experimental results for calculation of the corrected Spearman ρ. To predict the effects of mutations solely from DMS data, we used the same LOOCV procedure but excluded all evolutionary information in the feature matrix for each mutation. In this case, the feature matrix was used to directly compute a rank ${\widehat{d}}_{\text{DMS}}$. We subsequently reranked these values and compared them to the ranked experimental results to calculate a corrected Spearman ρ.

Generalizability analysis.

We focused on the alignment and mutation effects of β-lactamase as a case study to test the generalizability of evolutionary models for the prediction of mutation effects (Supplementary Fig. 2). We first made four reduced alignments by removing the query sequence (BLAT_ECOLX) and all sequences with a normalized hamming distance greater than 0.95, 0.8, 0.6, and 0.35 to the query, respectively. Five latent variable models were fit to each alignment, as well as a pairwise and independent model using the same sequence weighting and model fitting techniques.