Abstract
We employ an advanced 3D computational model of the head with high anatomical fidelity, together with measured tissue properties, to assess the consequences of dynamic loading to the head in two distinct modes: head rotation and head extension. We use a subject-specific computational head model, using the material point method, built from T1 magnetic resonance images, and considering the anisotropic properties of the white matter which can predict strains in the brain under large rotational accelerations. The material model now includes the shear anisotropy of the white matter. We validate the model under head rotation and head extension motions using live human data, and advance a prior version of the model to include biofidelic falx and tentorium. We then examine the consequences of incorporating the falx and tentorium in terms of the predictions from the computational head model.
Introduction
Traumatic brain injury (TBI) is a major public health problem in the United States1. Sports-related concussions are widely discussed in the media, but brain injury is also the leading cause of morbidity and mortality in road accidents, and in addition has significant psychological and economic costs. Each year, approximately 1.7 million people in the United States suffer from TBI.2 In Europe, the incidence rate and mortality rate are about 235 and 15.4 per 100,000 of the population each year, respectively.3 Similar rates have been shown in France and China.4,5 Improvements in understanding and prevention of TBI can thus have tremendous impact on society. Our focus in this study is to investigate in vivo brain deformation under mild angular accelerations, with a view towards eventually understanding mild TBI, which is a large subset of the reported injuries.
Understanding the biomechanical mechanisms of TBI is critical for establishing injury tolerance criteria as well as for developing protective devices to prevent injury. Several injury threshold criteria have been proposed, at the level of the whole head (e.g., critical linear and rotational accelerations, critical impulse), at the level of the tissues (e.g., relative motion between the brain and the skull, the development of positive and negative pressure in coup and contrecoup injuries)6–9 and at the level of individual neurons or fibers (e.g. critical axonal strains). While many of these mechanisms have been shown to be associated with injury, the inability to perform controlled experiments makes it difficult to obtain the quantitative estimates of injury needed to establish validated injury criteria. Our approach is therefore to employ computational models of the head with high anatomical fidelity together with measured tissue properties to assess the consequences of dynamic loading to the head. We have developed a subject-specific computational head model which can predict strains in the brain under large rotational accelerations.10 In this study, we validate the model under additional rotational acceleration modes using live human data, and advance the model to include biofidelic falx and tentorium. We then examine the consequences of incorporating the falx and tentorium in terms of the predictions of the computational model.
Prior work on modeling brain deformations
Numerous methods have been employed over the years to investigate brain injury mechanisms, including animal tests, cadaver studies, anthropomorphic test devices, and computational models.11 Many investigations have been conducted using cadaver heads, animal heads, physical head models, and in vitro models throughout the world.8,12–20 These experiments, together with the development of efficient computational techniques, have subsequently led to the development of computational head models to allow in-depth biomechanical studies. Computer simulations using models such as finite element (FE) models are increasingly used to study TBI,13,17,25,31,35,39,44 and also for modeling and simulation of neurosurgical procedures. Such computational simulations are widely accepted as a good way to supplement and provide an alternative to physical tests. With the help of numerical models, internal biomechanical responses (such as intracranial pressure, stress, and strain of brain tissues) can be calculated, and the causes of TBI and locations of injury can be further assessed. The computational models provide a way to relate external head-scale loading conditions to internal tissue-scale deformations and responses. The models have varying levels of anatomical and material fidelity, and questions of what degree of anatomical fidelity is relevant remain important questions in this research community. More generally, the broad issue of how we should calibrate and validate these computational models remains a critical question, particularly as modelers must make choices about what to include in their models in order to manage the computational costs associated with high-resolution simulations.
The key experimental datasets on brain deformation have recently been developed for non-injurious cases. The mechanical properties of the human brain have been examined extensively in vitro, where postmortem time and dissection degradation are likely to change the properties. However, in vivo experimental data is limited because of the difficulty of making non-invasive measurements.21 One of the most effective approaches to obtaining in vivo data on human brains is tagged MRI, a noninvasive approach for quantifying motion in vivo, and this has been applied to evaluate regional brain deformation in live human subjects. The scanned tagging lines can be analyzed by a few image analysis techniques, such as harmonic phase (HARP) analysis20 and active geometrytechnique.12,22 For example, Bayly et al. investigated the brain deformation of the head extension motion under mild acceleration using tagged MRI and found that measured strains of 0.02–0.05 were typical during the motion.23 That study provided the first quantitative images of in vivo acceleration-induced strain fields in the human brain. Each tagged image required more than 72 rotations to complete the acquisition of the lines in the spatial frequency domain (“k-space”).23
Knutsen et al. designed a novel double-trigger tagged MRI pulse sequence, which can dramatically reduce temporal variability in imaging of human head motion and applied the technique to investigate brain motions during head axial rotation.20 The approach reduces the number of rotations down to 4 drops for each tagged image and increased the conformity of subjects during MR scanning, leading to the ability of scanning multiple brain slices. We utilize this novel design to acquire experimental data and calculate in vivo brain deformation during the head motions, and use these experimental datasets for validation of the computational model.
Objectives of this work
We investigate the strains generated in the human brain using an experimental protocol that enables quantification of whole brain deformation, together with a high-fidelity 3D computational model that captures the detailed subject-specific brain anatomy while incorporating generic (i.e., non-subject-specific) material properties for the brain tissues. In previous work, we have used a similar computational approach to validate our head models using in vivo head rotation data. In this work, we have extended the prior model to incorporate the shear anisotropy of the white matter, and to validate against a second mode of loading (head extension). The falx cerebri (or falx) is a scythe-shaped band of dura matter that separates the left and right hemispheres of the brain.24,25 Its inferior boundary is defined by the inferior sagittal sinus and straight sinus. The tentorium cerebelli (or tentorium) separates the cerebrum and cerebellum. While it is known that the falx and tentorium are stiffer than the brain and pia, their roles in constraining brain motion and dampening deformation across brain regions remain poorly understood.25,26 For example, Ho et al.25 examined the effect of the falx and tentorium on a 3D head model, but their model was validated using cadaveric heads, and both membrane properties and tissue properties are known to change after death. Our effort here further analyzes the effects of these membranes, using a model that is validated in vivo.
In this study, we compare two different brain motions, head rotation and head extension, by acquiring a series of MR scans of a healthy volunteer. The acquired image data are analyzed to obtain in vivo strains and are compared to the subject-specific simulation results. The numerical simulations use three-dimensional material point method (MPM) models built from T1 MR images, incorporating white matter anisotropy and realistic anatomy of falx and tentorium structures. The MPM model is validated using the in vivo measurements for both head rotation and head extension motions under mild angular acceleration. Furthermore, simulations of models with and without falx and tentorium are conducted to assess the importance of and the role of the falx and tentorium during such head motions.
Materials and Methods
In vivo experiments on human subjects
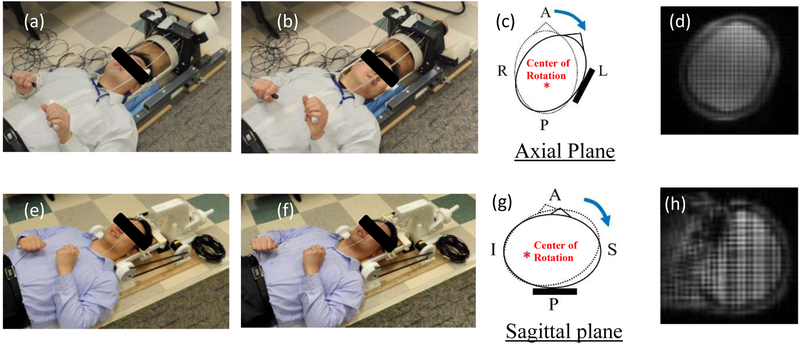
Experiments to measure brain deformation in vivo were conducted with the help of healthy human subjects recruited by the Center for Neuroscience and Regenerative Medicine (CNRM) under a study approved by the Combined NeuroScience Institutional Review Board (CNS IRB) at the National Institutes of Health. Two custom devices were designed and built to support and constrain the head motion (rotation and extension) of a human subject within the MRI scanner (Fig. 1). In the experiments, a mild angular head deceleration in this human subject is generated after being initiated by voluntarily releasing a latch and coming to a rigid stop within the head support devices. For the head rotation device, a rotation of approximately 32 degrees about the inferior-superior axis toward the left shoulder was performed (Fig. 1a–c), while for the head extension device, the head was rotated in the frontal-occipital direction, constituting a neck extension of about 4 degrees (Fig. 1e–g).
Figure 1.
a) The head rotation device (rest position): b) The head rotation device (stop position): c) Schematic of head at rest (dotted line) and stop (solid line) positions for head rotation test: d) A tagged image of head rotation test: e) The head extension device (rest position): f) The head extension device (stop position): g) Schematic of head at rest (dotted line) and stop (solid line) positions for head extension test: h) A tagged image of head extension test. A: Anterior: P: Posterior: R: Right: L: Left: S: Superior: I: Infereior.
In this study, a male adult (45 yrs age, 175.3 cm height, and 94.7 kg weight) performed consistent mild accelerations of the head inside the imaging coil of a clinical MRI scanner (3T Siemens mMR Biograph) using each of the two devices. The subject had no known TBI history, but it must be noted upfront that mTBI is difficult to detect. The subject was chosen to represent the 50th percentile male around age 40 in terms of height and weight among American males.27 The MRI acquisition was similar to the protocol utilized by Knutsen et al.20, employing a SPAMM tagging sequence optimized for acquisition speed. The angular position for each drop was measured in real-time by an optical sensor20. Images with two orthogonal tag line directions for measuring plane displacements were acquired in the axial plane for rotation and in the sagittal plane for extension (tag spacing=8 mm) (Fig. 1d & Fig. 1h). Phase oversampling (14%) was applied to sagittal acquisitions to eliminate wrap artifacts. Using 4 repetitions of the head motion, a time series of a tagged MR slice with 18.06 ms temporal resolution was acquired. Motion was tracked between image frames using HARP analysis with the shortest-path HARP refinement algorithm20. The Lagrangian strain tensor (E) was computed from the displacement vectors, and the radial-circumferential strain (Ert) and the maximum shear strain (Gmax) was calculated from the Lagrangian strain tensors for each slice.
Subject-specific computational models
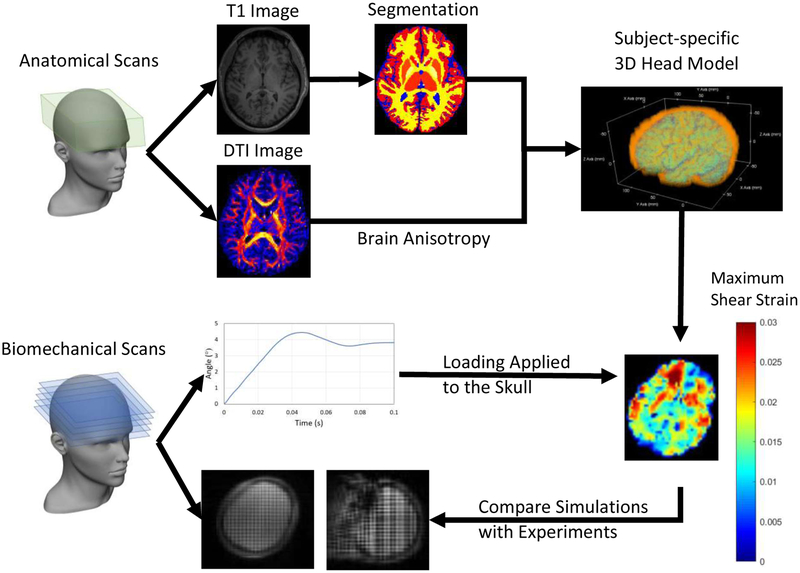
There are four parts that are required for an effective biomechanics simulation: first, the anatomical details of the head and brain at the resolution appropriate for the computations; second, the material properties associated with each material or tissue that is included in the simulation; and third, the initial values and boundary conditions appropriate for the simulations. Finally, robust experimental measurements are required to first calibrate and then validate such computational models. The source of this last dataset was described earlier. We obtain the first (anatomical fidelity) primarily through magnetic resonance imaging (MRI). The second (material properties) are described in the next section. The third (initial and boundary conditions) are extracted directly from experimental measurements.
The subject-specific head model was built for the recruited subject. The 3D computational model of the brain was constructed from T1-weighted images with a uniform spatial resolution of 1 × 1 × 1 mm3 and diffusion MR images. The cortical and subcortical structures were found using a multi-atlas segmentation algorithm and refined based on the reconstructed inner and outer cortical surfaces24. The falx and tentorium were localized by fast marching the cortical labels into the longitudinal and transverse fissures. The shape of the falx was refined using a multi-atlas boundary fusion algorithm. The structure included white matter, grey matter, caudate, putamen, thalamus, ventricles, cerebrospinal fluid (CSF), subarachnoid space (SAS), and brainstem. Image processing (dilation of a brain mask) is used to generate an approximate, artificial “skull.” The uniform spatial resolution of the model was further reduced to 2 × 2 × 2 mm3, keeping the spatial resolution of the falx and tentorium unchanged (i.e. 1 × 1 × 1 mm3) to accurately simulate the thickness and the resulting bending stiffness of the substructure. These data, which carried with its subject-specific anatomy of the brain, were imported to the 3D head model with each voxel now representing a physical material volume. Adjacent material volumes were integrated to represent the structure of the brain (assumed to be a continuum). The deformation response of the brain was computed with the help of a numerical method, called MPM, to solve governing equations of motion, supplemented with initial conditions, boundary conditions, and material constitutive responses. The MPM approach is extremely easily coupled to voxelated anatomical information, and has the advantage of excellent scalability with respect to high-performance computing. Our MPM implementation is performed using the Uintah platform that is supported by the University of Utah, and is available in the public domain.
Segmentation of brain falx and tentorium
The falx cerebri and tentorium cerebelli are the two largest dural folds in the brain 26. The falx cerebri is a large, crescent-shaped fold of meningeal layer of dura mater that descends vertically in the longitudinal fissure between the cerebral hemispheres of the human brain. The tentorium cerebelli lies in the axial plane attached perpendicularly to the falx cerebri and divides the cranial cavity into supratentorial and infratentorial compartments. While the anatomical structures and pathological functions28 of the falx and tentorium have been widely studied, these structures were sometimes simplified in brain computational models due to the difficulty of accurate segmentation from MR images.24 Recently, Glaister et al. proposed an automatic segmentation algorithm to find the falx and tentorium which uses the results of a multi-atlas segmentation and cortical reconstruction algorithm.24 This promising improvement of the segmentation enables the finer structures of the falx and tentorium. In this study we utilize this novel segmentation technique to build computational models with falx and tentorium and compare the results with the models which ignored the falx and tentorium structures to demonstrate the importance of the incorporation of these structures in computational biomechanics simulations.
Material properties for brain tissues
The two major components of brain tissue are grey matter and white matter. The grey matter of the brain contains the cell bodies of neurons and the white matter consists of bundles of myelinated axons, which connect various grey matter areas (the locations of nerve cell bodies) of the brain to each other and carry nerve impulses between neurons (Table 1).18,19,29–33 Grey matter is commonly considered to be essentially isotropic, and some studies have considered the white matter also to be isotropic.17,31,34,35 However, the presence of fiber tracts in the white matter generates a degree of anisotropy, and a number of previous studies have found that this anisotropy (because of preferential fiber orientations) is important for capturing brain deformations and in particular for estimating the likelihood of injury (using an injury criterion based on critical axonal strains).21,36,37,39,40 The degree of anisotropy can be quantified by the axonal fiber orientation and fiber dispersion of the neural axons using diffusion tensor imaging (DTI). In this study, the grey matter tissue was considered isotropic, while the white matter tissue was considered anisotropic.11,40
Table 1.
Material properties of the brain substructures.
| Substructure | Properties | Reference |
|---|---|---|
| Skull | E = 8000 MPa; ν = 0.22; ρ = 2070 kg/m3 | McElhaney 1966 |
| Cerebrospinal fluid/Ventricles |
κ = 2.190 MPa; η = 0.001 Pa s; γ = 7.15; ρ = 1004 kg/m3 | Goldsmith 1972 |
| Subarachnoid Space | E = 9.85 MPa; ν = 0.45; ρ= 1133 kg/m3 | Jin et al 2006 |
| Gray Matter | G∞ = 385 Pa; g1 = 0.625; g2 = 0.05; g3 =0.182; τ1 =2 s; τ2 = 11 s; τ3 = 47.5 s | Lee et al. 2014 |
| Thalamus | G∞ = 1.2 kPa; g1 = 0.8; τ1 = 0.0125 s | Mao et al. 2013 |
| Caudate, Putameu | G∞ = 110 Pa; g1 = 0.61; g2 = 0.135; g3 = 0.103; τ1 = 1.45 s; τ2 = 10 s; τ3 = 110 s | Lee et al. 2014 |
| White Matter | G∞ = 286 Pa; g1 = 0.81; τ1 = 0.00143 s | Velardi et al. 2006 |
| Brain Stem | G∞ = 4.5 kPa; g1 = 0.8; τ1 = 0.0125 s | Zhang et al. 2001 |
| Falx and Tentorium | E = 31.5 MPa; ν = 0.45; ρ =1133 kg/m3 | Nahum et al. 1977 |
| Common Properties | κ= 2.19 GPa; ρ = 1040 kg/m3 |
We incorporate the Holzapfel–Gasser–Ogden (HGO) anisotropic model41 for the white matter in these simulations, incorporating anisotropy through the fiber-reinforced nature of the material. Most studies use the HGO strain energy function as a function of the strain invariants Il and I4 only, together with the incorporation of fiber dispersion parameter κ, where the pseudo-invariant I4 is the square of the stretch ratio in the fiber direction10,39. Recently, Feng et al.40 proposed an alternative strain energy function (we will refer to this as the “Feng-Bayly model” or “FB model”), which includes both I4 and I5 invariants in the isochoric component. The pseudo-invariant I5 captures the contributions of shear strain in planes parallel to the fiber axis. Feng et al. pointed out that models in which the strain energy depends on I4 but not I5 can capture differences in Young’s moduli (tensile) but will not exhibit differences in shear moduli for loading parallel and normal to the mean direction of axons. Thus, in this study, we incorporate both I4 and I5 invariants in the strain energy function for the white matter using the FB model. Definitions of the invariants are presented by Feng et al.40
The deformation gradient can be decomposed into a spherical (dilatational) and a unimodular (distortional) part as:
where I is the second order identity tensor and is associated to the part of the total deformation gradient that does not produce any change of volume42. The isochoric right and left Cauchy–Green deformation tensors can then be defined as
in terms of the traditional Cauchy-Green deformation tensors. The corresponding isochoric counterparts of the principal invariants are
The strain energy function can then be decomposed into volumetric change (Wv) and isochoric deformation parts, i.e.
The volumetric change (Wv) is a function of the effective bulk modulus K and the volume change ratio J, and is expressed as
The total elastic strain energy can be decomposed into the elastic energy associated to the deformation of the matrix (i.e. the non-fibrous isotropic part) plus the elastic energy associated to the deformation of the fibers (i.e. the fibrous anisotropic part). The complete strain energy function for the FB model is
where ζ and φ are parameters of the anisotropic model (here, ζ is 5.5 and φ is 0.4).40 Such “reinforcing” models for anisotropic hyperelasticity are established in the literature, and the case with φ = 0 (i.e., without the invariant) has been examined in prior brain models such as that of Wright and Ramesh48.
The corresponding Cauchy stress tensor is then obtained as
where .
All other brain substructures were modeled using isotropic constitutive functions. The time-dependent response is incorporated using a linear viscoelastic function for the relaxation of shear modulus, expressed through a Prony series.
where G0 is the instantaneous shear modulus, gi are constant parameters, τi are time constants. The value of N = 1 is chosen for white matter and thalamus31,39, and N = 3 is chosen for grey matter, caudate, putamen and brainstem30,34.
The CSF was modeled as a fluid using the Tait equation of state:
where P is the pressure, K is the bulk modulus, and ρ is the density. The subscript “0” indicates the density at zero pressure. For fluids similar in composition and viscosity to that of water, the value of constant n is set to 7.1514. In addition, simple Newtonian behavior is assumed for shear, with a viscosity of 0.001 Pa-s.
The falx and tentorium were modelled as an isotropic linear elastic material with a constant bulk modulus of 31.5 MPa and Poisson ratio of 0.4533. The skull was modelled as a rigid body. Finally, the bulk modulus of the brain tissue was assumed to be 2.19 GPa, a value that is widely used in the literature (Table 1)31,34,43.
Finally, our model idealizes the dura mater, the sub-arachnoid matter, and pia mater as a homogenized single structural layer with a single set of material properties to represent their combined viscous and softening response towards modulating the incoming rotational accelerations from the skull. Clinically, the dura is tightly adherent to the skull and it is difficult to mechanically distinguish it from the skull, and we effectively assume that the dura and the pia act as relatively rigid membranes compared to the soft sub-arachnoid structure (SAS) and the cerebrospinal fluid (CSF) that flows through the SAS (the effective properties assumed for the SAS are provided also in Table I, and are assumed similar to those of the CSF). The mechanical properties of these layers is poorly known, particularly in shear, and thus most previous studies have made similar approximations when investigating the shear motions of the brain during mild accelerations.10,44
Loading and boundary conditions
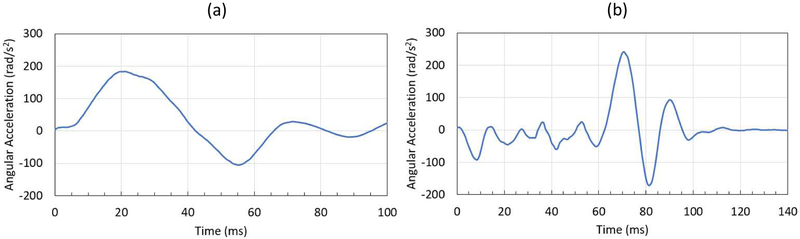
During the experiments, angular position histories were measured on the head rotation device and head extension device in real-time using an MRI-compatible angular position sensor (Micronor Inc., Camarillo, CA).20 Angular velocity and acceleration histories were computed from the recorded angular positions. The experimentally measured initial angular velocity and angular acceleration of the head acted as initial conditions and boundary conditions to the head model, respectively. For the head rotation motion, the head model has an initial angular velocity of ω0=2.13 rad/sec at t = 0 ms, after which the motion followed the recorded angular acceleration history (Fig. 3a). For the head extension motion, the head model has an initial angular velocity of ω0=0 rad/sec at t = 0 ms, after which the motion followed the corresponding angular acceleration history (Fig. 3b).
Figure 3.
Loading conditions for material point method (MPM) models for head rotation and head extension motions (a) angular acceleration (rad/s2) for head rotation motion: (b) angular acceleration (rad/s2) for head extension motion.
Material Point Method
The Material Point Method (MPM) is a numerical method that was developed to treat large deformations of history–dependent materials, especially those involving complex geometries and contact boundaries. Unlike Lagrangian-based methods like the FE method, the MPM has material particles that convect over a grid that can be reset independently of the particle position, field variables, and material state variables. As a result, the background grid in MPM does not encounter mesh entanglement and element degeneracy errors that are encountered in large shear deformation problems. The method also has the advantage of easy translation from segmented biomedical imaging. A representative volume element is represented using a material volume (referred to as a point), which stores all physical properties of the material, including field and history variables. Note that all the material points from the different sub-structures of the brain are updated using a single velocity field on the background grid—this models no-slip contact without a need for an additional contact algorithm. The Uintah package (University of Utah, Salt Lake City, Utah, https://uintah.utah.edu) was utilized to perform high-performance simulations on the MARCC computing cluster (https://www.marcc.jhu.edu/). During the computation, the explicit time integrator was utilized with a time step of 1 ms, and the convected particle domain interpolation (CPDI) was used for interpolation between grid nodes and material points. The number of material points for the model without falx and tentorium was 227,745, and the number of material points for the model with falx and tentorium was 253,340. The computational times for the models with and without falx and tentorium under head rotation motion were 56 and 49 hours respectively, while the computational times for the models with and without falx and tentorium under head extension motion were 79 and 62 hours. For further details on MPM, readers are referred to Sadeghirad et al 2011 and Daphalapurkar et al (2007).49,50
Validation of the computational model
We compare the computed Lagrangian strain tensor with the Lagrangian strains calculated directly from the in vivo brain tagged MRI measurements. Specifically, we compare Ert and Gmax. The latter can be calculated from the principal strains:
The direction of Gmax is always oriented at an angle of 45° with respect to the principal directions of strain. In each case the strains are calculated for each material point and compared to the corresponding in-plane (2D) strain calculated from tagging images.10 We then use three specific measures to validate the full spatial field model with the experimental measurements. Such measures are needed because the two datasets are non-commensurate, and are 3D in space with evolving time histories. Note that there are uncertainties in the measured data, but we assume that the measured data is the ground truth for comparison with our simulated results.10
First, we use an Error Measure (EM), defined as:43
Here, the variables P and 0 represent the Predicted spatially varying simulated data and the Observed experimentally measured data, respectively. Note that in order to use this measure, we need spatially equivalent data (possible with the MPM), and that this is a measure taken at a given time.
Next, the Correlation Score (CS) is calculated based on EM as follows43:
Hence, the CS values range from 0 to 100. According to the biofidelity rating,15 the CS value was categorized into five rating classifications:
Excellent: 86 ≤ CS < 100
Good:65 ≤ CS < 86
Fair: 44 ≤ CS<65
Marginal: 26 ≤ CS < 44
Unacceptable: 0 ≤ CS < 26
A higher value of this statistical measure indicates a better agreement between the simulated and measured data sets.
Finally, for a more traditional measure, the peak Gmax in each slice and the area fraction of this over all slices were also determined. The area fraction (φA) of all slices that have Gmax within a specified range m to n, is defined by
That is, the area fractions of the strain field in which Gmax was within the pre-defined ranges (e.g. 0–0.01 and 0.01–0.02 etc.) are determined for both the simulations and the experiments, and these area fractions are compared10,20,23.
Results
Dynamics of the live human brain
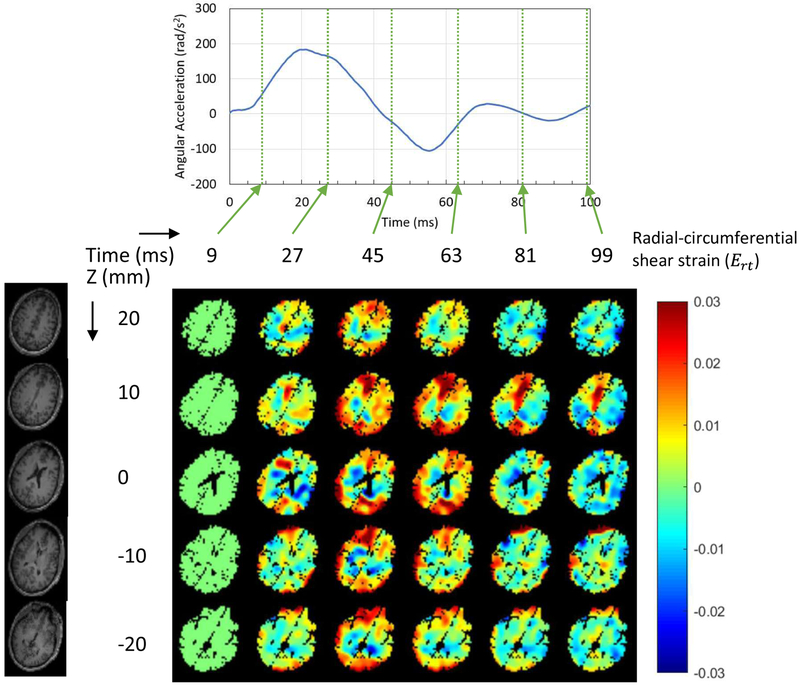
The dynamics of brain deformation was investigated by the measured experimental tagging images of the live human head during a mild angular acceleration. The average peak angular acceleration (rad/s2) was 186.2±24.3 for head rotation tests (11 axial plane slices with 88 rotations) and 239.5±22.8 for head extension tests (13 sagittal plane slices with 104 rotations). Figures 4 and 5 show the measured Ert during head rotation and head extension motions respectively for rapid deceleration for this subject. We note that head rotations of the first type were also studied by Ganpule et al. (2017), but we are considering a different subject, and both motions here are presented For the one subject (thus we can validate using one motion and predict for the other). For the head rotation motion, five axial plane slices of the brain were selected (the rows in Fig. 4), while for the head extension motion, five sagittal plane slices of the brain were selected (the rows in Fig. 5). Six time points for the head rotation motion and eight time points for the head extension motion are presented (the columns in each figure), corresponding to the times of measured data from experiments.
Figure 4.
Dynamics of wave propagation of the measured radial-circumferential shear strain distribution in a human brain subjected to axial plane rotation within the first 100 ms.
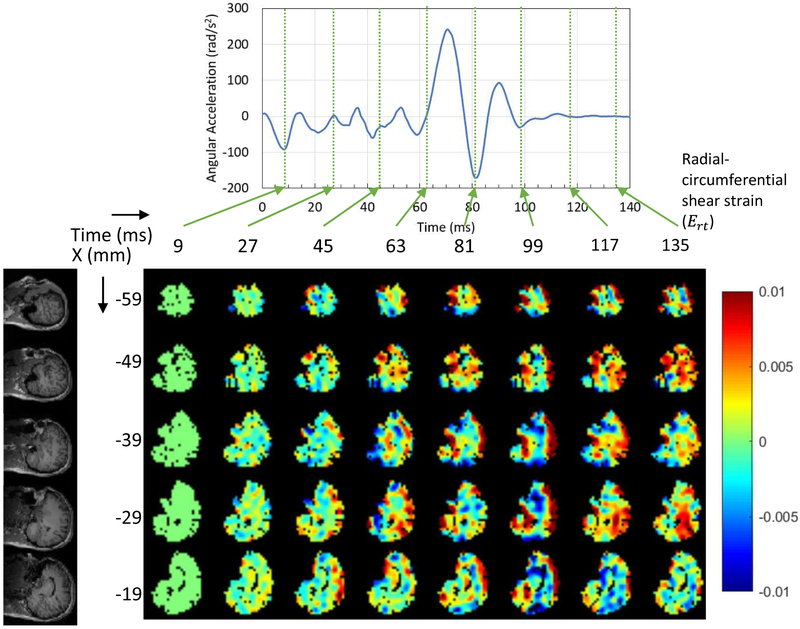
Figure 5.
Dynamics of wave propagation of the measured radial-circumferential shear strain distribution in a human brain subjected to sagittal plane rotation within the first 140 ms.
For the head rotation motion, during the deceleration process, the shear wave propagated from the exterior boundary toward the center of the brain in terms of the Ert (Fig. 4). The center of rotation was along the longitudinal axis (head-foot axis) inside the brain. As time proceeds, the shearing wave reflects from the center of the head and propagates back outward. Afterwards, the strain fields consist of a combination of reflected waves from the center traveling toward the external boundary and release waves traveling from the exterior boundary toward the center. By the time of ~100 ms the angular acceleration was close to zero, but the kinetic energies in the system were still non-zero. It is also noted that the motion of the brain lagged behind the motion of the skull, and this lag in motion causes the brain to deform dynamically during deceleration.
For the head extension motion, a total of eight time points corresponding to experimental measurements are presented (Fig. 5). The higher Ert occurred at the boundary of the cerebrum, after the initiation of the deceleration. The peak positive Ert occurred at time 99 ms, and the shear wave then propagated from exterior boundary toward the inner brain because the center of rotation was along the horizontal axis (right-left axis) and was close to the neck. Afterwards, the shear strain decreased. Similar to the head rotation motion, by the time of ~100ms the angular acceleration was close to zero, but the kinetic energies in the system were still non-zero. In addition, the motion of the brain lagged behind the motion of the skull.
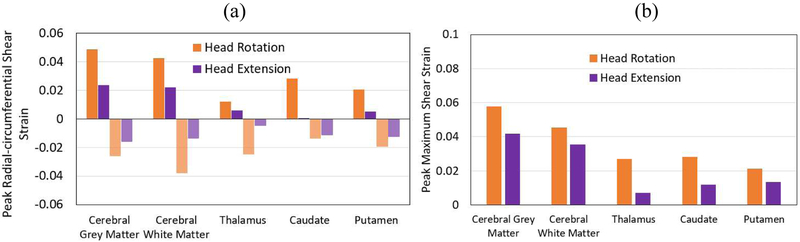
The peak Ert and peak Gmax of all slices measured from experiments were determined within each of five brain substructures (cerebral grey matter, cerebral white matter, thalamus, caudate, and putamen) (Fig. 6). Note that negative strains in this plot imply shear in the opposite direction. It was found that the cerebral grey matter experienced higher peak Ert (0.048) than other substructures. In addition, it was observed that the deep grey matter substructures (thalamus, caudate, and putamen) experienced lower peak Ert for both motion types. Overall, peak positive and peak negative Ert were higher in the head rotation motion than the strain in the head extension motion. Similarly, the cerebral grey matter experienced the highest peak Gmax (0.058 for head rotation and 0.042 for head extension), followed by cerebral white matter (0.045 for head rotation and 0.035 for head extension). The peak Gmax among all deep grey matter substructures (thalamus, caudate, and putamen) were 0.028 for head rotation and 0.013 for head extension. Overall, the peak Gmax was higher for the head rotation than the peak Gmax For the head extension by the brain substructures.
Figure 6.
(a) Comparison of peak positive and peak negative radial-circumferential shear strain (Ert) between head rotation and head extension motions in each substructure, (b) Comparison of the peak maximum shear strain (Gmax) between head rotation and head extension motions in each substructure.
Validation of simulations, and predictions
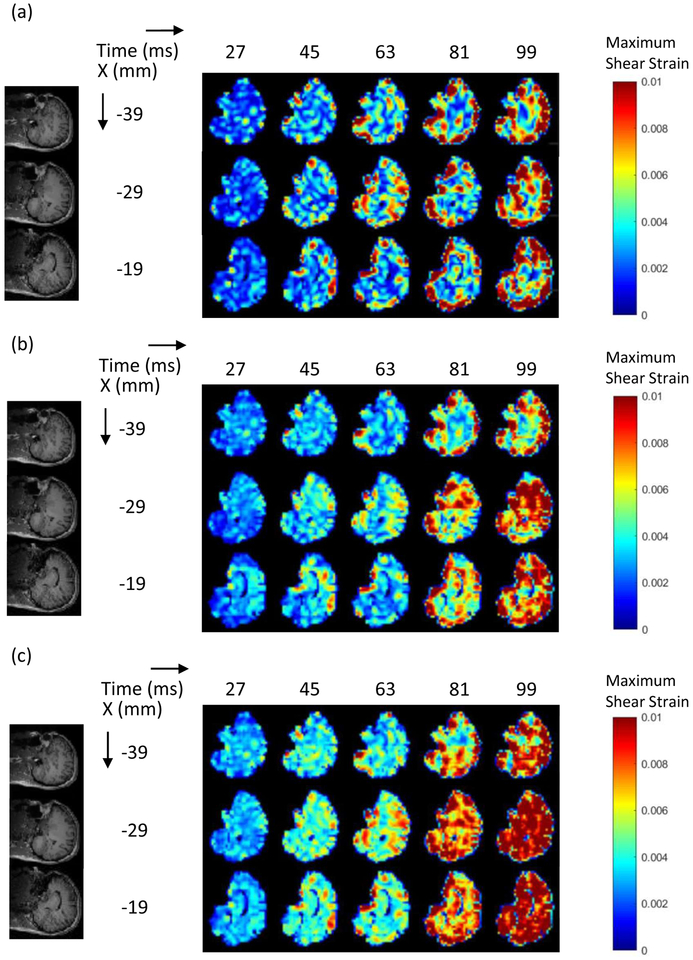
The subject-specific computational head models were validated against corresponding full-field live human brain data with a focus on Gmax. Experiments were performed with slice thickness and temporal resolutions of 8 mm and 18 ms, respectively. The strain fields for specific slices (corresponding to the tagging images) from the simulations performed on the subject-specific head models with identical input accelerations were extracted at each time step. The full experimental and simulation data sets are enormous, and, thus, a set of representative slices are selected and presented. For the head rotation motion, three slices were selected, which are the midaxial slice z = 0 mm and the slices at z = −10 and 10 mm for a range of times (t = 27, 45, 63, 81, and 99 ms, dictated by the temporal resolution of the experiment) to provide the comparison. For the head extension motion, three slices were selected (x = −39, −29, −19 mms) for a range of times (t = 27, 45, 63, 81, and 99 ms) to provide the comparison.
The direct image-based comparison is shown in Figure 7 (for head rotations) and in Figure 8 (for head extension). The computational model that incorporated the falx and tentorium (Fig. 7b) was able to capture the approximate magnitudes and dynamics of the experimentally observed strain fields (Gmax) in the live human brain (Fig. 7a), providing the qualitative validation of subject-specific computational models against live human brain data. Figure 7 shows that in both experiments and the simulations, higher Gmax occurred on the outer boundary of the brain after the deceleration (time=45 ms) and dissipated afterwards.
Figure 7.
Representative results of strain distribution for head rotation motion (a) experiments: (b) stimulations with falx and tentorium; (c) stimulations without falx and tentorium.
Figure 8.
Representative results of strain distribution for head extension motion (a) experiments; (b) stimulations with falx and tentorium; (c) stimulations without falx and tentorium.
We could consider Figure 7 to provide validation of the computational model. Since the simulations are based on the same parameters, anatomy and computational structure, the comparisons made in Figure 8 then represent a comparison of the predictions of the model with the measurements from the experiments. Figure 8 shows that higher strains distributed at the boundary of the cerebrum are observed in both the experiments and the simulations for the head extension motion. Our 3D MPM computational model is therefore able to predict the in vivo observations, at least from the image-based semi-quantitative viewpoint. We note that these comparisons are for the simulations that include the falx and tentorium.
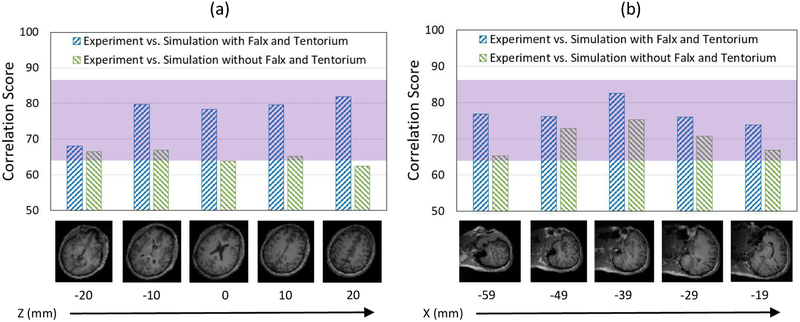
A more robust, quantitative way to compare full-field data between the model and the experiment is to use statistical measures for model evaluation. The statistical measure, CS, which was commonly used for validating brain computational models, was utilized to estimate the degree of agreement between the simulations and the experiments. The degree of model performance was evaluated based on pointwise spatial variations at fixed time steps. The five selected slices for each type of motions with their corresponding CS comparing Gmax are presented at specific time steps (45 ms for head rotation and 99 ms for head extension) in Figure 9. For the five selected slices for head rotation motion, CS was ranging from 68 to 82 when comparing experiment versus simulation with falx and tentorium, which were within the “Good” match range (65 ≤ CS < 86) (Fig. 9a). Thus, the quantitative comparison based on overall statistics at discrete spatial points shows that the simulations with falx and tentorium matched the strain fields reasonably to the measured experimental data. We consider this to be an effective validation.
Figure 9:
The five selected slices for each type of motions with their corresponding correlation scores (a) head rotation motion at time 45 ms; (b) head extension motion at time 99 ms.
Using the same model For the head extension motion, we compare the predictions of the model with the observations of the in vivo experiments. CS range from 74 to 83 when comparing experiment versus simulation, which were also within the “Good” match range (65 ≤ CS < 86) (Fig. 9b). We conclude that the model is predictive within a satisfactory range.
Comparison between head rotation and head extension motions
The experimental measurements of head rotation and head extension were compared by the quantities of the peak Ert and the peak Gmax (Fig. 6). Within the 100 ms, either peak positive or peak negative Ert was higher for head rotation motion than the head extension motion by the brain regions (Fig. 6a). Similarly, the peak Gmax measured in the head rotation tests was higher than the strain measured in the head extension tests by about 0.8% to 2% strain (Fig. 6b).
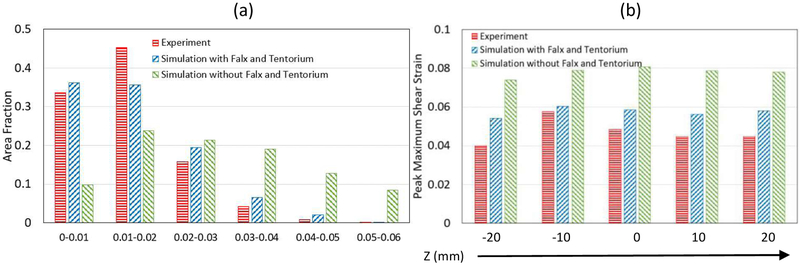
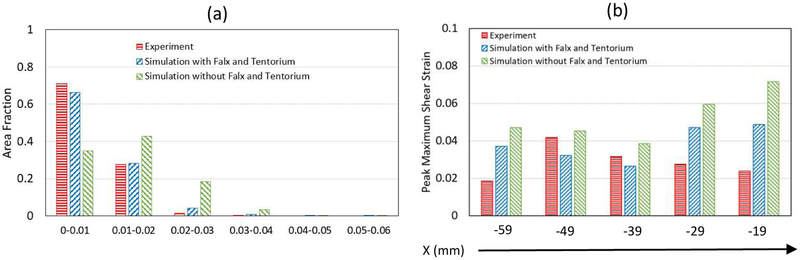
The quantitative comparisons of the measured head rotation and head extension motions in terms of area fractions and peak Gmax are presented in Figures 10 and 11. For head rotation, the area fraction of the brain with Gmax greater than 0.01 was 0.664 for experiment and 0.638 for simulation (with falx and tentorium) (Fig. 10a), while for head extension, the area fraction of the brain with Gmax greater than 0.01 was only 0.290 for experiment and 0.336 for simulation (with falx and tentorium) (Fig. 11a), which is less than the area fractions observed in the head rotation tests. Furthermore, the measured peak Gmax by slices was all greater than 0.04 for head rotation (Fig. 10b), while most measured peak Gmax by slices for head extension was less than 0.04 (Fig. 11b). The measured strain was higher in head rotation than in head extension in both the experiments and simulations.
Figure 10.
Comparison between the experiments and the simulations for the head rotation motion at time 45 ms. (a) Area fraction of the maximum shear strain of the entire brain: (b) Peak maximum shear strain by slices.
Figure 11.
Comparison between the experiment: and the simulations for the head extension motion at time 99 ms. (a) Area friction of the maximum shear strain of the entire brain. (b) Peak maximum shear strain by slices.
Comparison of simulations with and without falx and tentorium
Now that we have some confidence in the ability of the simulations to describe brain deformations, we compare simulations with and without the falx and tentorium membrane structures to investigate the role of falx and tentorium during brain motions and their mechanisms. The falx obstructs the strain propagation between the left and right hemispheres of the brain during head rotation motion (Fig. 7). When the falx is absent, the shear stress wave propagates across the two hemispheres, resulting in higher shear strains in the cerebrum. On the other hand, the tentorium obstructs the strain propagation from the cerebrum to the cerebellum during the head extension motion (Fig. 8), causing the reduced strain in the cerebellum. When the tentorium is absent, the strain wave propagates to the cerebellum, resulting in higher shear strain in the cerebellum.
As noted earlier, CS used for comparing the experimental measurements and simulated data showed a good correlation in the scenario of the simulations with falx and tentorium for both head rotation and head extension motions (Fig. 9). However, simulations without the falx and tentorium had significantly lower CS ranging from 63 to 67 when comparing with the experimental data. In some regions, the simulations that ignored the falx and tentorium structures had CS that decrease by as much as 20 points (e.g. Fig. 9a, Z=20 mm) in comparison to the more biofidelic model. Similarly, the simulation without falx and tentorium produces lower CS than the simulation with falx and tentorium for the head extension motion (Fig. 9b). Overall, we conclude that effective biomechanical simulations should include the falx and tentorium.
The area fractions of the Gmax of the entire brain are compared between the simulations with and without falx and tentorium in Fig. 10. For the head rotation motion, the fraction of Gmax between 0 and 0.02 was 0.718 for the simulation with falx and tentorium, while the fraction of Gmax between 0 and 0.02 for the simulation without falx and tentorium was only 0.337 (Fig. 10a). Similarly, for the head extension motion, the fraction of the Gmax between 0 and 0.02 was 0.948 for the simulation with falx and tentorium, while the fraction for the simulation without falx and tentorium was 0.777 (Fig. 11a). These indicate that the simulations without falx and tentorium will over-estimate the strain field over the entire brain. In addition, the computed peak Gmax on each brain slices showed that the simulation without falx and tentorium predicted higher strains, while the simulations with falx and tentorium predicted peak Gmax closer to the experimental measurements for both head rotation and head extension motions.
Discussion
Comparison with previous experimental studies
The experimental measurements from the current study are comparable to a few findings in previous studies. Knutsen et al. conducted head rotation tests on three healthy volunteers using the same device, two male and one female, and found that the peak angular acceleration could range from 173 to 246 rad/s2 20. The range of the peak angular acceleration of the head rotation tests in the current study is 148 to 229 rad/s2. The measured peak Gmax in Knutsen’s study was 0.048±0.007 (mean±s.d.), which is close to the measured peak Gmax 0.047±0.007 (mean±s.d.) observed in the current study. The shear wave speeds that we measure in the head rotation motion are comparable to the recent study of Ganpule et al.10, who utilized the same head rotation device with six subjects. Those authors also reported that the peak positive Ert was higher for the cerebral grey matter, followed by the white matter and the deep grey matter (thalamus, caudate, putamen), similar to the observations in the current study.
For the head extension motion, Bayly et al. investigated head extension motion on three healthy subjects using the tagged MRI technique,23 and showed that the high strain areas (maximum principal strain) were the peripheral region of the cerebrum. This finding is similar to the observations in the current study. However, one major difference between this work and Bayly et al.23 is that the head extension motion had to be repeated through 72 drops to obtain a single tagging image data matrix at the temporal resolution of 6 ms in the Bayly et al. study, while the current study utilized only 4 drops to acquire the central 24 lines in the k-space for each tagging image with the temporal resolution of 18.06 ms, taking advantage of the work of Knutsen et al.20.
Higher strains for head rotation than head extension
This study compared brain deformations between the head rotation and head extension motions, and higher strains were observed in the head rotation than in head extension. Although both motions involved the same head, the range of motions is quite different, and so this is perhaps to be expected. However, the difference of deformations observed in these two motions could also be partly due to the neck musculature. The muscle forces of the head/neck motions have been measured in a few studies. Salo et al. measured the cervical flexor, extensor, and rotator muscles in 220 healthy females aged 20 to 59 years old and found that neck muscle forces for head extension could reach as high as 250 N (average=190 N)45. In addition, Snijders et al. found that axial rotations of less than 35 degrees do not need great muscle forces, while axial rotations further than 35 degrees cause muscle forces and joint reaction forces to increase rapidly46. Therefore, the brain may experience larger movement without the muscle force constraint in the low-angle head rotation motions in our study. A similar study comparing the brain deformation between head flexion and head extension conducted by Hansson et al. reported that neck flexion induces larger deformation of the brain than extension at a sagittal rotational acceleration due to the muscle force constraint mechanism.16
Another point to note is that the calculated 2D strain was in the axial plane for head rotation motion while it was in the sagittal plane for head extension rotation. While we observe the brain deformation mainly along its rotated direction for each motion, the off-plane deformations are ignored for both motions. Future studies on the comparison of the 3D strain will be performed with the consideration of the off-plane deformation.
Need to incorporate falx and tentorium
We find that a computational brain model with falx and tentorium membranes is better able to predict the observed strain fields than a model without falx and tentorium for these axial and sagittal rotations under mild angular acceleration. Some other studies have also indicated the importance of the falx and tentorium and the increased strain in simulations without falx and tentorium under different types of loadings. For example, Ho et al. constructed a subject-specific FE brain model from a healthy subject and the loadings to the head models were based on combined translational and angular movements of sporting events, considering both non-injurious and injurious loading applications.25 The authors found that for both non-injurious and injurious loadings, the maximum principal strains were higher in the peripheral regions (frontal, occipital and parietal) in the model without falx and tentorium compared with the model with falx and tentorium. Those results are consistent with our observations. Belingardi et al. also developed a FE head model13, validated by experimental tests carried out by Nahum et al. in 1977,33 and noted that the absence of falx and tentorium membranes leads to higher pressure peaks confirming an important protective effect for these tissues. However, while these studies all provided insights of the importance of the falx and tentorium, they used computational models under different types of loadings and validated by separate sets of experimental data (and not in vivo data).
Limitations
There are several limitations in the current study. First, the consequence of including the I5 term in the strain energy function (through the Feng-Bayly model) is essentially that of enhancing the shear response of the brain tissue, but, it is not possible to draw simple conclusions about the cases with and without l5. This is because the I4 invariant couples into that reinforcing term, and we have not performed detailed sensitivity analyses with respect to this additional term. Second, while both invariants I4 and I5 were considered, the fiber dispersion of the white matter was not incorporated in the strain energy function in the current study. The degree of fiber dispersion can be measured from the fractional anisotropy (FA) map from DTI39. Further studies are suggested to quantitatively investigate the real effect of the fiber dispersion on the brain deformation simulations.
Third, the voxel resolutions of the MPM models in the current study was 2 mm3 for all brain substructures except the falx and tentorium (1 mm3). While the resolution of the T1 weighted images, which were used for constructing the MPM models, was 1 mm3, this study reduced the resolution in order to reduce the computational burden. A pilot convergence study using the gelatin gel instead of live human subjects showed that the model with material point resolution of 2 mm3 would be sufficient to match the strain results calculated from the model with material point resolution of 1 mm3. In addition, according to a recent study47, a mesh convergence study was conducted on specimen-specific MPM brain models similar to our brain models, and it was found that a material point resolution of 2 mm3 was sufficient to achieve the spatial convergence in terms of Gmax. Therefore, the voxel resolutions of the MPM models were coarsened to 2 mm3 for reducing the computational wall-clock time. Third, since the focus of the current study was to compare the different head motions and the structural differences of the brain in computational simulations but not to determine the strain variations across subjects in human population, the current study reported the analysis based on only one live human subject test. This subject has been chosen since his body type was close to the midsize male in terms of the height and weight.27. More subjects are required to obtain statistically meaningful results in future studies and to better address the inter-subject variations during head rotation and extension motions.
The choice of material properties for the different substructures in the brain continues to be a major challenge. Variations in each individual material parameter may influence the brain deformations, but these influences require much more detailed studies. For instance, a recent study [Ganpule et al. 2018] investigated the consequence of variations in the assumed bulk modulus of the brain ranging from ~106 to ~109 Pa, and showed that this would have significant impact on the computed volumetric strain in head rotation problems.47 The specific sets of properties that we chose are determined by a combination of the extremely limited availability of experimental data for individual anatomical regions (substructures) and the fact that some of these parameters are consistently used in recent brain simulation studies10,26,35 (making it easier to compare results).
Experimental characterization of brain substructures is difficult, and is affected by moisture content, tissue handling, in situ vs ex situ measurements, other protocols, kind of stress state used to characterize the material properties, and so forth. Currently, there is a wide range of properties reported for the brain, and reconciling all the reported brain data will continue to be challenging. Recent biomechanical material tests emphasize the viscoelastic properties of the brain and therefore the updated brain tissue properties (grey matter, white matter, deep grey matter and brain stem) were reported after year 2000. Thus, the elastic and fluid-like properties such as skull, falx, tentorium and ventricles measured in the 1970s are still widely accepted in recent brain computational models.10,16,26,35,44 We hope to add primary laboratory data in the near future.
Figure 2.
Computational modeling procedure. The 3D head model was constructed based on T1 and DTI images. The initial angular velocity and angular position profile measured from experiments were served as loading conditions. The simulation results were compared with experimental results calculated from tagging images.
Acknowledgements
Funding was this research was provided by NIH Grant NS055951 from the National Institute of Neurological Disorders and Stroke. This work was partially supported by the Department of Defense in the Center for Neuroscience and Regenerative Medicine (CNRM), and by the Intramural Research Program of the Clinical Center of the National Institutes of Health.
Footnotes
Publisher's Disclaimer: This Author Accepted Manuscript is a PDF file of an unedited peer-reviewed manuscript that has been accepted for publication but has not been copyedited or corrected. The official version of record that is published in the journal is kept up to date and so may therefore differ from this version.
References
- 1.Hyder AA, Wunderlich CA, Puvanachandra P, Gururaj G, Kobusingye OC. The impact of traumatic brain injuries: a global perspective. NeuroRehabilitation. 2007;22(5):341–353. [PubMed] [Google Scholar]
- 2.Faul M, Xu L, Wald MM, Coronado VG. Traumatic Brain lnjuryin the United States: Emergency Department Visits, Hospitalizations and Deaths 2002–2006. Centers for Disease Control and Prevention; 2010. [Google Scholar]
- 3.Tagliaferri F, Compagnone C, Korsic M, Servadei F, Kraus J. A systematic review of brain injury epidemiology in Europe. Acta Neurochir (Wien). 2006;148(3):255–68; discussion 268. doi: 10.1007/s00701-005-0651-y. [DOI] [PubMed] [Google Scholar]
- 4.Masson F, Thicoipe M, Aye P, et al. Epidemiology of severe brain injuries: a prospective population-based study. J Trauma. 2001;51(3):481–489. [DOI] [PubMed] [Google Scholar]
- 5.Wu X, Hu J, Zhuo L, et al. Epidemiology of traumatic brain injury in eastern China, 2004: a prospective large case study. J Trauma. 2008;64(5):1313–1319. doi: 10.1097/TA.0b013e318165c803. [DOI] [PubMed] [Google Scholar]
- 6.Holbourn AHS. MECHANICS OF HEAD INJURIES. Lancet. 1943;242(6267):438–441. doi: 10.1016/S0140-6736(00)87453-X. [DOI] [Google Scholar]
- 7.Pudenz RH, Shelden CH. The lucite calvarium; a method for direct observation of the brain; cranial trauma and brain movement. J Neurosurg. 1946;3(6):487–505. doi: 10.3171/jns.1946.3.6.0487. [DOI] [PubMed] [Google Scholar]
- 8.Gross AG. Impact thresholds of brain concussion. J Aviat Med. 1958;29(10):725–732. [PubMed] [Google Scholar]
- 9.Hodgson VR, Thomas LM, Gurdjian ES, Fernando OU, Greenberg SW, Chason J. Advances in understanding of experimental concussion mechanisms. Soc Automot Eng. 1969:387–406. [Google Scholar]
- 10.Ganpule S, Daphalapurkar NP, Ramesh KT, et al. A Three-Dimensional Computational Human Head Model That Captures Live Human Brain Dynamics. J Neurotrauma. 2017;34(13):2154–2166. doi: 10.1089/neu.2016.4744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Takhounts EG, Eppinger RH, Campbell JQ, Tannous RE, Power ED, Shook LS. On the Development of the SIMon Finite Element Head Model. Stapp Car Crash J. 2003;47:107–133. [DOI] [PubMed] [Google Scholar]
- 12.Amini AA, Chen Y, Curwen RW, Mani V, Sun J. Coupled B-snake grids and constrained thin-plate splines for analysis of 2-D tissue deformations from tagged MRI. IEEE Trans Med Imaging. 1998;17(3):344–356. doi: 10.1109/42.712124. [DOI] [PubMed] [Google Scholar]
- 13.Belingardi G, Chiandussi G, Gaviglio I. Development and Validation of a New Finite Element Model of Human Head. In: 19th International Technical Conference on the Enhanced Safety of Vehicles.; 2005. [Google Scholar]
- 14.Cole RH, Weller R. Underwater Explosions. Phys Today. 1948;1(6):35. [Google Scholar]
- 15.de Lange R, van Rooij L, Mooi H, Wismans J. Objective biofidelity rating of a numerical human occupant model in frontal to lateral impact. Stapp Car Crash J. 2005;49:457–479. [DOI] [PubMed] [Google Scholar]
- 16.Hansson H-A, Krave U, Höjer S, Davidsson J. Neck Flexion Induces Larger Deformation of the Brain Than Extension at a Rotational Acceleration, Closed Head Trauma. Adv Neurosci. 2014;2014(945869). [Google Scholar]
- 17.Horgan TJ, Gilchrist MD. Influence of FE model variability in predicting brain motion and intracranial pressure changes in head impact simulations. Int J Crashworthiness. 2004;9(4):401–418. doi: 10.1533/ijcr.2004.0299. [DOI] [Google Scholar]
- 18.McElhaney JH. Dynamic response of bone and muscle tissue. J Appl Physiol. 1966;21(4):1231–1236. doi: 10.1152/jappl.1966.21.4.1231. [DOI] [PubMed] [Google Scholar]
- 19.Velardi F, Fraternali F, Angelillo M. Anisotropic constitutive equations and experimental tensile behavior of brain tissue. Biomech Model Mechanobiol. 2006;5(1):53–61. doi: 10.1007/s10237-005-0007-9. [DOI] [PubMed] [Google Scholar]
- 20.Knutsen AK, Magrath E, McEntee JE, et al. Improved measurement of brain deformation during mild head acceleration using a novel tagged MRI sequence. J. Biomech 2014;47(14):3475–3481. doi: 10.1016/j.jbiomech.2014.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Green MA, Bilston LE, Sinkus R. In vivo brain viscoelastic properties measured by magnetic resonance elastography. NMR Biomed. 2008;21(7):755–764. doi: 10.1002/nbm.1254. [DOI] [PubMed] [Google Scholar]
- 22.Kumar S, Goldgof D. Automatic tracking of SPAMM grid and the estimation of deformation parameters from cardiac MR images. IEEE Trans Med lmaging. 1994;13(1):122–132. doi: 10.1109/42.276150. [DOI] [PubMed] [Google Scholar]
- 23.Bayly PV, Cohen TS, Leister EP, Ajo D, Leuthardt E, Genin GM. Deformation of the human brain induced by mild acceleration. J Neurotrauma. 2005;22(8):845–856. doi: 10.1089/neu.2005.22.845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Glaister J, Carass A, Pham DL, Butman JA, Prince JL. Automatic falx cerebri and tentorium cerebelli segmentation from Magnetic Resonance Images. Proc SPIE--the lnt Soc Opt Eng. 2017;10137. doi: 10.1117/12.2255640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ho J, Zhou Z, Li X, Kleiven S. The peculiar properties of the falx and tentorium in brain injury biomechanics. J Biomech. 2017;60:243–247. doi: 10.1016/j.jbiomech.2017.06.023. [DOI] [PubMed] [Google Scholar]
- 26.Joldes GR, Doyle B, Wittek A, Nielsen PMF, Miller K. Computational Biomechanics for Medicine: Imaging, Modeling and Computing. 1st ed. Springer International Publishing; 2016. doi: 10.1007/978-3-319-28329-6. [DOI] [Google Scholar]
- 27.Moss S, Wang Z, Salloum M, et al. Anthropometry for WorldSID, a World-Harmonized Midsize Male Side Impact Crash Dummy. 2000. [Google Scholar]
- 28.Daghighi MH, Rezaei V, Zarrintan S, Pourfathi H. Intracranial physiological calcifications in adults on computed tomography in Tabriz, Iran. Folia Morphol (Warsz) 2007;66(2):115–119. [PubMed] [Google Scholar]
- 29.Goldsmith W Biomechanics of Head Injury. In: Fung YC, ed. Biomechanics: Its Foundations and Objectives. Englewood Cliffs, NJ: Prentice Hall; 1972:585–634. [Google Scholar]
- 30.Lee SJ, King MA, Sun J, Xie HK, Subhash G, Sarntinoranont M. Measurement of viscoelastic properties in multiple anatomical regions of acute rat brain tissue slices. J Mech Behav Biomed Mater. 2014;29:213–224. doi: 10.1016/j.jmbbm.2013.08.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Mao H, Zhang L, Jiang B, et al. Development of a finite element human head model partially validated with thirty five experimental cases. J Biomech Eng. 2013;135(11):111002. doi: 10.1115/1.4025101. [DOI] [PubMed] [Google Scholar]
- 32.Zhang L, Yang KH, Dwarampudi R, et al. Recent advances in brain injury research: a new human head model development and validation. Stapp Car Crash J. 2001;45:369–394. [DOI] [PubMed] [Google Scholar]
- 33.Nahum AM, Ward CC, Smith R. Intracranial pressure dynamics during head impact. Stapp Car Crash Conf. 1977;21:337–366. [Google Scholar]
- 34.Zhang L, Yang KH, King AI. A proposed injury threshold for mild traumatic brain injury. J Biomech Eng. 2004;126(2):226–236. [DOI] [PubMed] [Google Scholar]
- 35.Song X, Wang C, Hu H, Huang T, Jin J. A Finite Element Study of the Dynamic Response of Brain Based on Two Parasagittal Slice Models. Comput Math Methods Med. 2015;2015(816405). doi: 10.1155/2015/816405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Karami G, Grundman N, Abolfathi N, Naik A, Ziejewski M. A micromechanical hyperelastic modeling of brain white matter under large deformation. J Mech Behav Biomed Mater. 2009;2(3):243–254. doi: 10.1016/j.jmbbm.2008.08.003. [DOI] [PubMed] [Google Scholar]
- 37.Labus KM, Puttlitz CM. An anisotropic hyperelastic constitutive model of brain white matter in biaxial tension and structural-mechanical relationships.VMech Behav Biomed Mater. 2016;62:195–208. doi: 10.1016/j.jmbbm.2016.05.003. [DOI] [PubMed] [Google Scholar]
- 38.Prange MT, Margulies SS. Regional, directional, and age-dependent properties of the brain undergoing large deformation.J Biomech Eng. 2002;124(2):244–252. [DOI] [PubMed] [Google Scholar]
- 39.Wright RM, Post A, Hoshizaki B, Ramesh KT. A multiscale computational approach to estimating axonal damage under inertial loading of the head. J Neurotrauma. 2013;30(2):102–118. doi: 10.1089/neu.2012.2418. [DOI] [PubMed] [Google Scholar]
- 40.Feng Y, Okamoto RJ, Namani R, Genin GM, Bayly PV. Measurements of mechanical anisotropy in brain tissue and implications for transversely isotropic material models of white matter. J Mech Behav Biomed Mater. 2013;23:117–132. doi: 10.1016/j.jmbbm.2013.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Gasser TC, Ogden RW, Holzapfel GA. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J R Soc Interface. 2006;3(6):15–35. doi: 10.1098/rsif.2005.0073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Nolan DR, Gower AL, Destrade M, Ogden RW, McGarry JP. A robust anisotropic hyperelastic formulation for the modelling of soft tissue. J Mech Behav Biomed Mater. 2014;39:48–60. doi: 10.1016/j.jmbbm.2014.06.016. [DOI] [PubMed] [Google Scholar]
- 43.Kimpara H, Nakahira Y, lwamoto M, et al. Investigation of anteroposterior head-neck responses during severe frontal impacts using a brain-spinal cord complex FE model. Stapp Car Crash J. 2006;50:509–544. [DOI] [PubMed] [Google Scholar]
- 44.Ji S, Ghadyani H, Bolander RP, et al. Parametric Comparisons of Intracranial Mechanical Responses from Three Validated Finite Element Models of the Human Head. Ann Biomed Eng. 2014;42(1):ll–24. doi: 10.1007/s10439-013-0907-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Salo PK, Ylinen JJ, Malkia EA, Kautiainen H, Hakkinen AH. Isometric strength of the cervical flexor, extensor, and rotator muscles in 220 healthy females aged 20 to 59 years. J Orthop Sports Phys Ther. 2006;36(7):495–502. doi: 10.2519/jospt.2006.2122. [DOI] [PubMed] [Google Scholar]
- 46.Snijders CJ, Hoek van Dijke GA, Roosch ER. A biomechanical model for the analysis of the cervical spine in static postures. J Biomech. 1991;24(9):783–792. [DOI] [PubMed] [Google Scholar]
- 47.Ganpule S, Daphalapurkar NP, Cetingul MP, Ramesh KT. Effect of bulk modulus on deformation of the brain under rotational accelerations. Shock Waves. 2018;28(1):127–139. doi: 10.1007/s00193-017-0791-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Wright RM and Ramesh KT An axonal strain injurycriterion fortraumatic brain injury. Biomechanics and Modeling in Mechanobiology. 2012;11:245–260. [DOI] [PubMed] [Google Scholar]
- 49.Sadeghirad A, Brannon RM and Burghardt J. A convected particle domain interpolation technique to extend applicability of the material point method for problems involving massive deformations. Int. J. Numer. Meth. Engng 2011; 86: 1435–1456 [Google Scholar]
- 50.Daphalapurkar NP, Lu H, Coker D, Komanduri R Simulation of dynamic crack growth using the generalized interpolation material point (GIMP) method. Int J Fracture. 2007;143:79 [Google Scholar]