A review of the mechanism by which exploding bridge-wire detonators function

Abstract

An introduction to exploding bridge-wire (EBW) detonators is given followed by an extensive critical review of open source literature pertaining to these devices. The aim is to better establish the mechanism of operation. Some authors state that the key mechanism is shock-to-detonation while others maintain it is more thermal in nature, or a complex combination of both. In addition to EBW detonators, arc detonators and direct optical initiation detonators are also reviewed, and it is demonstrated that in this manner the usually coupled effects from both shock and deflagration can be somewhat decoupled. As a result, it is hypothesized that the mechanism of operation in all three detonators is in fact the same: the formation of a hot plasma with a power of ≈1 MW and emission in the ultraviolet drives a thermal explosion process.

1. Introduction

(a). The detonator

The exploding bridge-wire (EBW) detonator was invented in Los Alamos towards the end of the Second World War [1]. The aim was to create a safe detonator with highly repeatable functioning time (less than 1 μs) coupled to a powerful explosive output booster.

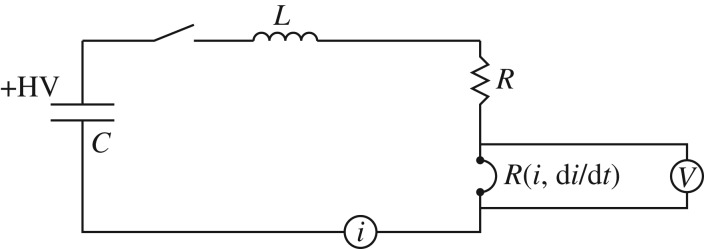
This was achieved by discharging a high voltage capacitor across a short, very fine, gold wire to create an air shock, gold plasma and arc next to a pellet of low-density (≈50% of theoretical maximum density, TMD) PETN (2,2-bis[(nitrooxy)methyl]propane-1,3-diyl dinitrate). The exploding of the wire, also called bridge-burst, was discovered to reproducibly detonate the low-density PETN by some mechanism and, by coupling this low-pressure detonation output to a higher-density booster pellet, a reliable, highly reproducible detonator was made containing only secondary explosives. A cutaway drawing of a typical EBW detonator is shown in figure 1.

Figure 1.

A cutaway drawing of a typical EBW detonator showing the fine gold wire, the low-density initial pressing (IP) and the powerful high-density output pellet (OP).

The low-density explosive material is commonly called the initial pressing (IP) and the higher-density booster material, the output pellet (OP). Initially, the IP was made exclusively from high surface area (SA) PETN (4000–12 000 cm² g⁻¹), but as time has passed it was discovered that other secondary explosives (e.g. RDX, 1,3,5-trinitro-1,3,5-triazinane, HMX, 1,3,5,7-tetranitro-1,3,5,7-tetrazocane) could be substituted so long as the powder morphology and SA were adequately large and the capacitor, cabling and bridge were appropriately sized [1]. As intuition would suggest, less-sensitive explosives (e.g. RDX and HMX) require larger diameter bridge-wires and greater electrical current than more sensitive PETN for reliable operation.

Studies have shown that contrary to intuition, generally lower SA (coarser) PETN is optimal for lower energy to be required for a specific bridge-wire length and diameter (3000–5000 cm² g⁻¹). However, higher SA PETN accelerates to full detonation more quickly after burst. Hence, to assist temporal accuracy in output time after bridge-burst, a higher SA PETN is usually used despite requiring slightly more electrical energy for reliable detonation (5000–12 000 cm² g⁻¹) [2,3].

To the knowledge of the authors, no one has produced a practical EBW from the explosive HNS (1,3,5-trinitro-2-[2-(2,4,6-trinitrophenyl)ethenyl]benzene) although it is commonly used for exploding foil initiated (EFI) detonators (also known as slapper detonators) where the function mechanism is prompt shock-to-detonation (SDT) in higher-density pressed material [1]. The possible significance of this will be discussed later.

Bridges made from gold are by far the most common, but other materials such as aluminum, copper, silver, iron, platinum and tungsten have all been used successfully. The most efficient EBW wire materials have low boiling points, low heats of vaporization and a high increase in resistance at burst [4]. Therefore, in order of efficiency, gold was found to be best, followed by silver, copper, aluminum, platinum, tungsten and finally iron [5,6]. This list does not consider the effects of corrosion during long-term storage, and thus in practical applications precious metals are generally preferred unless special care is taken to ensure that the explosive powder is free from residual acid or other contamination likely to produce slow chemical reactions with the very fine wires. It was discovered that the length of the wires needed to be optimized for the different metals in PETN IP for greatest operational efficiency [5]. Generally, less efficient metals required shorter lengths to produce detonation from the fixed electrical fireset.

It is remarkable that 75 years later and after literally millions of EBW detonators have been fired, there is still uncertainly about how they actually work. The following key events are generally agreed to occur:

• (i)Current flow from the charged capacitor heats the bridge conductor to plasma temperature. Initially, the resistance of the bridge increases somewhat linearly with temperature, but as melting, vaporization and expansion occur, the resistance increase becomes highly nonlinear [7].
• (ii)During vaporization and plasma formation of metal from the bridge, a series of shock waves are produced that couple to the low-density explosive powder. An initial weak shock is observed during vaporization followed by a stronger shock as plasma is made. Given the short timescales, distances and the complex physics, it is possible that these two observed shocks are a result of the shock collection of a number of smaller amplitude shocks [8,9].
• (iii)Subsequently, an arc is formed in some or all of the conductor plasma, the air, the IP and the IP reaction products. The resistance of this arc is significantly lower than the conductor at bridge-burst.
• (iv)By some action of the bridge-bursting, a building reaction wave forms in the IP. At some time later, a steady detonation is formed that consumes the rest of the IP.
• (v)The output shock from the IP detonates the OP by a prompt SDT process.

The uncertainty in function mechanisms occurs in item iv. If the current through the bridge, and voltage across it, are measured, the change in bridge resistance at burst and the inherent inductance of the electrical circuit create a clear signal corresponding to the moment of bridge-burst. That is, at burst the current is seen to plateau or even drop slightly while the voltage spikes as the circuit inductance acts to keep constant current in the increasing resistance of the bridge.

Thus, in detonators used in the laboratory, the onset of bridge-burst can be clearly identified. Additionally, the velocity of detonation (VOD) in the IP can be measured (it is approx. 5.0 km s⁻¹ for PETN at a density of 0.88 g cc⁻¹ [10]) as well as that of the OP. Therefore, by measuring the time from bridge-burst until the detonation arrives at the free face of the OP, an overall function time can be established. Further, if the time that steady-state detonation in both the IP and OP would have taken is calculated from the known geometry, any excess time can be identified. That is, if the function time is greater than the steady-state detonation time, then another process must have occurred in between.

When this calculation is performed for real EBWs, it is always found that the reaction build-up after bridge-burst until the onset of steady-state detonation indeed takes approximately 1 μm. That is, the mechanism of initiation of EBW detonators does not create steady-state detonation immediately after bridge-burst, but it could be delayed SDT occurring as a result of a building reaction shock.

This extra time is called variously in the literature the ‘excess transit time’, ‘lost time’ or ‘missing time’ [11]. In this paper, we shall term the time after bridge-burst until the onset of steady detonation the ‘excess transit time’ or ETT.

The ETT is found to be a function of capacitor voltage. As the charge voltage is increased, the ETT is found to asymptote to a steady value greater than zero [12]. This asymptotic firing region is termed a hard-fire and is essential if the maximum temporal reproducibility in detonators is required. As the voltage is decreased, the ETT is found to increase until a statistical go/no-go threshold is reached. The minimum voltage where reproducible detonation occurs is termed the all-fire voltage while the voltage where 50% of the detonators fire is termed the threshold voltage. The voltage range below the hard-fire voltage down to the all-fire voltage is termed the soft-fire range and can be used safely only if suboptimal timing is acceptable.

For most normally fired detonators, the excess time is 0.7–1.3 μs corresponding to a run-to-detonation distance of ≈1 mm if the apparent centre of initiation is reverse calculated from detonation breakout measurements [13]. These small time scales and distances contribute to the difficulty of studying these processes. For example, the commercial Teledyne RISI RP-80 detonator has a 40 mil (1.02 mm) long, 1.5 mil (38 μm) diameter gold bridge-wire welded to the electrical terminals. Prompt detonation would require a function time of 1.49 μs. The manufacturer's hard-fire asymptotic function time is 2.65 μs. This results in an ETT of 1.16 μs for the RP-80 under hard-fire conditions. The ETT for the RP-1, another RISI detonator, asymptotes to 0.7 μs even at burst currents of 2000 A [13]. Because of its significance, it is restated that even under the hardest fire situations possible, prompt SDT is never observed in EBWs.

Typically, the IP is pressed to 0.83–1.0 g cc⁻¹. The greater density reduces the sensitivity of the detonator and therefore requires a greater current at burst in the bridge [3]; however, some high-specific SA PETN materials have pour densities of almost 0.5 g cc⁻¹. As a result, it is sometimes chosen to press the IP to ≈1.0 g cc⁻¹ so that the powder is physically compressed to a moderate degree during manufacture. The alternative may result in uneven IP density during construction or even partial collapse of the IP during storage and handling leading to very unreliable detonator function. The approximate pour density of ≈3000 cm² g⁻¹ SA PETN is 0.3 g cc⁻¹ while ≈6000 cm² g⁻¹ is 0.4 g cc⁻¹ (Varosh J 2018, personal communication).

Typical IPs are cylindrical and can have widely varying dimensions between 2,5 and 7 mm in diameter and 2–6 mm in height. The sleeves into which the IP is pressed are typically metallic (brass or aluminum) for reasons of machining tolerance stability, but high-performance fibre reinforced polymers can also be used.

Although this review mainly relates to EBW detonators, a closely related variant, the arc detonator (AD), will also be reviewed [14,15]. The AD typically has a very similar construction to an EBW except that there is no conductor between the terminals (figure 2). To reduce the arc breakdown voltage required to make the AD function, the terminals are often closer than in an EBW, 10–20 mil (0.25–0.5 mm), although some EBWs also have bridges this short. Additionally, it is advantageous for the terminals to protrude slightly (≈0.5 mm) into the IP so that the effects of thermal cycling of the detonator are less severe. It is presumed that the thermal cycling causes the PETN to contract away from the header producing less coupling from the arc. Raising the terminals appears to help with this phenomenon by enabling the arc to transit the explosive. As with the EBW detonator, PETN is often used as the IP. ADs are fired in a similar manner to EBWs except the charge voltage is often slightly higher. It is found that the energy to fire the detonators is lower than with a comparable EBW [15,16] and that excellent temporal reproducibility is possible.

Figure 2.

A cutaway drawing of a typical arc detonator.

Two other detonator technologies that should be reviewed are EFI or ‘slapper’ detonators and direct optical initiation (DOI) detonators. A slapper detonator is so termed because a very high-velocity solid flyer disc of some material interacts with a high-density pellet (typically 1.5–1.6 g cc⁻¹) of pressed explosive and the shock (slap) from this flyer directly detonates the explosive pellet [1]. A generic EFI detonator design is shown in figure 3.

Figure 3.

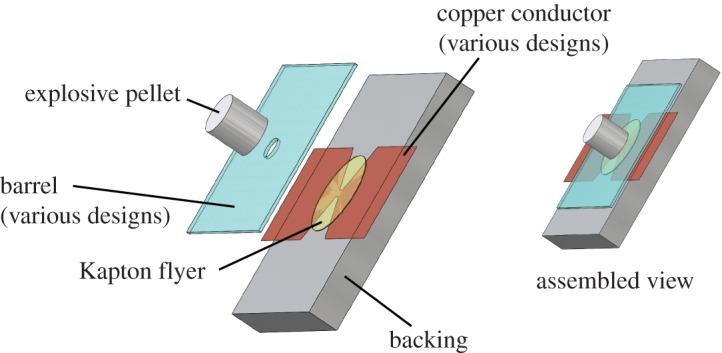
An annotated drawing of a typical EFI or slapper detonator. (Online version in colour.)

The EFI detonator is similar to the design of a EBW in that a thin foil is exploded by the discharge of a high voltage capacitor; however, the energy from the exploding conductive foil (often copper) drives a thin plastic disc (often Kapton) situated on top at 2–5 km s⁻¹. It is the shock from the polymer disc hitting the explosive that causes the detonator to function. To effectively drive the flyer, a rate of current rise of 10³–10⁴ A μs⁻¹ is required. This is an order of magnitude, or more, greater than that required for the functioning of EBW. To achieve this, an ultra low inductance CDU is required and only short flat transmission lines can be employed from the CDU to the EFI detonator. The impedance of the transmission line is of the order of 1 Ω and so the initial current from a 2000 V CDU is approximately 2000 A. This produces a sufficiently violent foil explosion that the polymer is accelerated in a few hundred micrometres of flight to the required velocity for prompt detonation to occur in the acceptor explosive pellet.

Before the more highly developed laser flyer detonator was optimized, a competing method of optical initiation was tried whereby a high-power laser pulse interacted directly with the explosive pellet to produce a detonation [17,18]. This was termed direct optical initiation (DOI). A drawing of a generic DOI detonator is shown in figure 4. It fell out of favour because it was discovered that the process could be made more efficient by either having the laser absorb onto a thin layer of material between the laser source and the explosive to create an enhanced plasma, or by directly ablating a flyer to form a slapper detonator. Nevertheless, this archaic technology is of interest because it is a pure optically initiated detonator where only a very short duration (≈20–30 ns) and unsupported ablation shock is initially generated and either direct photochemistry or thermal absorption produces chemical reaction.

Figure 4.

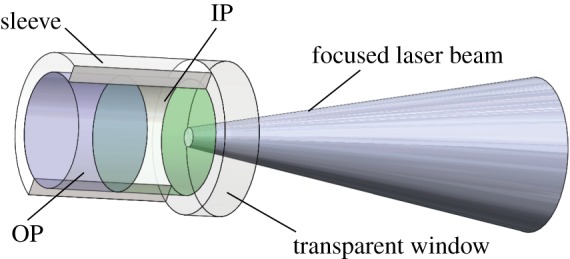
An annotated drawing of a generic DOI detonator. (Online version in colour.)

There is much debate about how detonation is produced in EBWs. Three broad hypotheses exist: (1) it is an SDT process with a short run-to-detonation as a result of the shocks from the bridge-burst and arc; (2) it is a DDT (deflagration-to-detonation transition) [19] event as a result of the thermal input from the wire burst process or (3) a complex mix of both, with fast SDT playing a bigger role at higher burst currents and DDT at lower ones.

Practical DDT detonators using PETN have not been made, but the violent reaction has been used to drive a high-velocity flyer capable of creating SDT in an OP [20].

The key problem is separating the hypotheses because typically the controlled variable in a CDU/EBW combination is the charge voltage. Usually, increasing the voltage increases the bridge current at burst, the power at burst and the energy available post-burst. As such, the voltage simultaneously affects the bridge-burst shock pressure and the arc energy and the power. It is therefore very difficult to decouple the shock input from the thermal one.

(b). Firesets

In practice, all EBW detonators are fired from capacitative discharge units (CDUs). Figure 5 shows the equivalent lumped circuit (inductor, capacitor, resistance, LCR). A high voltage capacitor is charged to specific voltage and a low-inductance fast switch is closed to fire the detonator. The circuit will have some parasitic inductance inherent to all elements within it. Generally, this inductance is minimized to ensure a rapid rise in current through the bridge (10²–10³ A μs⁻¹). However, as previously described, some inductance is beneficial to the operation of EBWs to prevent current being starved at the time of bridge-burst. This is particularly true if multiple detonators are placed in series.

Figure 5.

A lumped circuit representation of a CDU. Also shown is the bridge resistance that is a function of i and di/dt and the key measurement positions.

Additionally, the circuit will have a parasitic resistance that is generally minimized by design. A typical gold bridge-wire has an ambient resistance of 30–50 mΩ. The parasitic resistance is generally much greater than this (100–300 mΩ), but generally not enough to prevent ringing if the bridge is replaced by a dead-short at the output of the CDU.

Figure 6 shows the three classes (regions of bridge-burst location) for a CDU that may be used to detonate an EBW depending on CDU physical size and timing reliability trade-offs.

Figure 6.

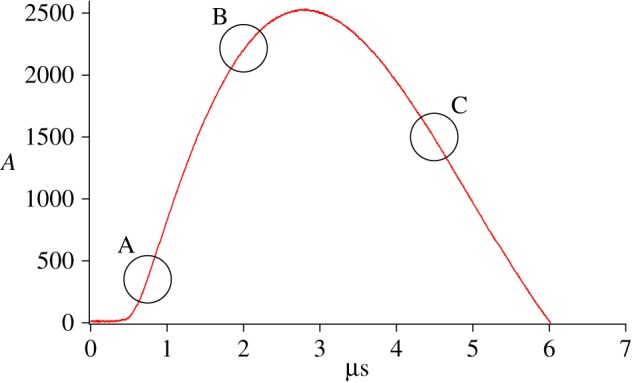
A typical current trace for a CDU discharge. Region A is the bridge-burst zone for a very conservative CDU. Region B represents the zone for an optimized CDU. Region C represents the zone for backside operation of a CDU. The magnitude of the peak current would be much lower for regions B and C than shown. (Online version in colour.)

Historically, for general use, LANL design ‘rules-of-thumb’ for parallel fired detonators recommended a CDU with 1 μF of capacitance per detonator charged to 2000–2400 V and a peak power at burst of more than 1 MW for more than 100 ns (corresponding to more than 100 mJ; Goforth J 2018, personal communication). As high voltage technology has improved, the recommended charge voltage has increased to 3500 V.

An analytic solution to the lumped LCR circuit model of a CDU is given in [21]. The highly nonlinear response of the gold bridge is challenging to model. For an example, Maninger [22] gives a good explanation of the several physical processes occurring during rapid heating.

In an effort to simplify the analysis of the bridge-burst process, a concept of the ‘action-integral’ was introduced [12,23–26]. It was noticed that for the charged coaxial-cable fireset used for basic research on detonators [23], the instant of bridge-burst, t_b, over a wide range of constant currents, could be calculated from a single number, G, that depended only on the bridge material and wire diameter using the equation

$$G={\int }_0^{t_b}i{(t)}^2\hspace{0.17em}\mathrm{d}t=g{A}^2,$$ 1.1

where i(t) is the instantaneous current, t the time, g a bridge material-dependent constant and A the original bridge-wire area.

Although this simplification is attractive, later experiments with CDU firesets have shown that the action-integral is not in fact constant [27,28], although this well-known fact in the detonator community has not been widely mentioned in the literature.

2. Background information

Before reviewing the many papers that discuss the mechanism of detonation in EBW detonators, it will be useful to review some mechanisms by which detonation is known to occur in other more defined circumstances. It will be necessary to keep the explanations brief and so it is inevitable that certain subtleties will need to be ignored.

(a). The DDT process

The DDT process is complicated and poorly understood in detail, particularly for low-density powdered explosives and in three-dimensional solid explosive geometries. From the application of some initial thermal stimulus, an exothermic reaction of the explosive begins. If that exothermic energy is greater than the heat loss, then reaction will grow. A flame front propagates, initially by conductive burning, but transitioning to convective burning resulting in greater propagation velocity [19]. In these initial stages, the permeability of the explosive bed and SA available to the reactions are critical to the rate of pressurization and burn velocity.

The DDT process has been broadly separated into two classes and is still the subject of active research. Type I DDT occurs in higher-density explosive fills and type II occurs in lower-density ones [19]. However, the transition from one class to the other is not unambiguous. Type I DDT has been more extensively studied because it is more applicable to how most explosives are actually used (i.e. at high density). Currently, Type I DDT is understood to be comprised of five stages: (a) a conductive burn that propagates to choked flow convective burning, (b) compression compaction of the powder bed, (c) the formation of a high-density plug, (d) volumetric thermal explosion (explained later) and (e) an SDT process (also explained later). It is inconceivable that as described these processes can occur on microsecond timescales and within 1 mm of displacement in EBW detonators. Therefore, if DDT is involved it will not be classical Type I DDT.

The DDT process in pseudo-one-dimensional columns of PETN and several other explosives have been studied both as a function of particle size and density. A convenient summary is reported in [29]. It is found that in fine-powder PETN pressing densities comparable with IP densities, the burn propagation distance up the confining tube prior to detonation breakout (distance-to-detonation) is minimized (typically 50–60% of TMD). That is, both greater and lesser pressing densities have greater distances-to-detonation. Significantly, the measured run distances are significantly greater (more than 10 mm) than those observed to occur in EBW detonators (≈1 mm). It appears therefore that the processes operating in an EBW detonator are fundamentally different from this type of DDT.

Although the data are sparse, the DDT response of varying both particle size and pressing density is more complex. It appears that for each particle size there is a different pressing density that minimizes the distance to detonation. Generally, larger particles (more than 200 μm) require a higher density (65–75% of TMD) than finer powder (≈20 μm) to minimize the distance (45–60% of TMD). It is unclear, owing to the limited studies, if the minimum distance to detonation is similar for all particle sizes, or if larger particles transition at shorter distances at optimal density. Specifically, the data for two different PETN particles sizes exhibit similar minima, while several other explosives exhibit minima that are significantly smaller at greater particle sizes. More research in this area with representative PETN particle sizes would clarify this.

In the broadest sense, the DDT process involves a principally thermally generated initial gradual ramping up of pressure in the explosive bed that culminates in a sufficiently strong shock being formed that detonation results. That is, a shock wave only results at the end of the process.

The term DDT is used by many explosive researchers without proper definition of what they understand the term to mean. Unfortunately, what many other researchers understand it to mean is sufficiently different that confusion results. Because there is no indication that classic type I DDT is operating in EBW detonators, and this is what most researchers think of when the term DDT is applied, the use of the term will be largely avoided in the rest of this review.

(b). The SDT process

There are two broad types of SDT. The build-up process to detonation in homogeneous explosives (liquids, very fine-pressed powders and solid explosives pressed to extremely close to theoretical maximum density (TMD)) and heterogeneous explosives (most solid cast or pressed explosives) is found to be very different under shock loading [30,31]. It is widely agreed that heterogeneous explosives build up from SDT because of hot spot formation.

It is easy to show that the bulk temperature rise associated with even a strong shock is too low to produce rapid reaction in most explosives of practical interest. Therefore, something must be localizing the shock energy into a much smaller volume that then can reach much higher temperatures (hot spots) and that these start separately but growing reaction sites coalesce into a single shock front at a formation rate that can support a steady-state detonation [32].

There is considerable debate about all of the imperfections in the explosive that can produce useful hot spots, but they include hydrodynamic pore jetting, adiabatic gas-filled pore collapse, adiabatic shear band formation, viscoplastic work at voids, shock wave interactions at impedance discontinuities, etc. [33]. It is thought that the first listed mechanism, hydrodynamic pore jetting, is the most significant for SDT and steady-state detonation in most pressed explosives, because the jet-tip velocity is of comparable velocity to the detonation wave and so provides for the production of hot spots contemporaneous with the detonation front rather than behind it, as with the other mechanisms.

Therefore, a moderate-strength shock acting on a pressed explosive is presumed to create localized burn sites some distance behind the shock by performing work on the imperfect explosive. The burn sites grow and coalesce to release energy that can feed forward towards the shock. This extra energy arriving at the lead shock initially increases its strength and thus propagation velocity, but at some point, the velocity of the shock asymptotically approaches the sound speed and particle velocity in gases behind the detonation front. Energy released behind this sonic locus (later-time reactions) can no longer reach the lead shock and so a steady-state supported shock (detonation) results.

The imperfections that can localize enough energy to be useful towards both SDT and DDT have a finite range of sizes (0.1–10 μm [33]). Those imperfections that are too small quench, owing to the heat required for expansion being greater than can be provided by the reaction volume. Hot spots that are too large produce energy that arrives too late to contribute practically in real-size explosive charges.

For homogeneous explosives, a different shock process occurs. In these explosives, there is nothing to localize the shock energy because there are no imperfections of appropriate size. Liquid homogeneous explosives such as nitromethane can be made into heterogeneous explosives by the addition of other ingredients and the mechanism of detonation is observed to alter when this is done [34]. Instead, the passage of a strong shock does raise the bulk temperature of the explosive sufficiently that exothermic energy begins to be released. While the shock continues to run into fresh explosive, a feedback reaction is initiated in the material already shocked where energy from the initial shock produces reaction energy that heats the explosive so that greater reaction occurs, releasing yet more energy. At some time later (tens of nanoseconds to microseconds depending on the explosive and shock strength), a thermal explosion occurs in the material that was shocked first [30]. The resulting detonation then forms a super-detonation that catches the initial strong shock because the partially reacted material behind the shock is at much higher than ambient pressure and so the shock velocity is greater. Once the super-detonation catches the lead shock, steady-state detonation at a lower velocity occurs after a decay period.

Normally, pressed explosives are considered to be heterogeneous; however, some powders used in IPs are so fine (less than 1 μm) that the pore size in a collapsed bed may be approaching the lower limit for traditional hot spot theory to operate (less than 0.1 μm) [33]. Hence the response to a strong shock may resemble a homogeneous thermal explosion rather than the more commonly observed heterogeneous mechanism. This will not be the case for coarser particles of the same explosive pressed to low or moderate density.

An example of this phenomenon is found in HNS [35]. Type 1 HNS (5–10 μm particle size, 2100 cm² g⁻¹) is found to behave as a heterogeneous explosive at approximately 92% TMD (1.6 g cc⁻¹). Very fine HNS-FP (1–2 μm particle size, 8000 cm² g⁻¹) at the same density behaves as a homogeneous explosive when shocked at low to moderate pressures (3–5 GPa). Presumably, this finer powder, when pressed, deforms to result in voids that are too small to form viable hot spots upon shock loading. When strongly shocked, the thermal explosion process is so rapid that the super-detonation is not resolved as it is at lower pressures.

For sustained shocks, it is found that, at constant material density, the smaller particles are more sensitive than larger under SDT conditions down to minimum size when the sensitivity decreases again. An investigation of RDX powder at 90% of TMD showed that in order of sensitivity 21 μm powder was more sensitive than 100, 138 and 250 μm, but that 3.9 μm powder was slightly less sensitive than 21 μm [36]. As noted before, this is probably a result of the efficacy of the hot spot forming imperfections being related to the particle size of the pressed powder.

A similar observation, but for slightly different reasons, occurs in short shock loading. In both PETN [37] and HNS [38], it was discovered that laser-driven thin-flyers that promptly detonated small particle size pressings did not detonate larger particle size ones. As noted by the authors, this is a result of the very short shock duration traversing several small particles and voids before pressure release and therefore initiating reaction, while not even traversing a single particle of the larger material and so effectively running into imperfection-free explosive and producing only modest bulk heading.

An important distinction between SDT and DDT is that detonation produced by SDT involves the passage of a shock, or shocks, from the start of the process. DDT transitions to SDT only at the end of the process. Therefore, observations of the particle velocity from building reactions in explosives can be distinguished because a DDT process will have a slow to fast, or perhaps just fast, ramping particle velocity versus time profile prior to the formation of a shock profile, while SDT will have weaker shock building in strength until a steady-state strong shock is formed. In the case of homogeneous explosives, a strong shock of greater than steady-state magnitude may be transiently observed in the pre-shocked region prior to steady-state detonation. Examples of the particle velocity versus time profiles from the SDT build-up to detonation in heterogeneous and homogeneous explosives can be seen in [34].

(c). Volumetric thermal explosion

Volumetric thermal explosion is a subset of the thermal runaway process possible in any exothermic chemical reaction where self-generated heat accelerates the reaction and therefore production of additional heat. Specifically, thermal explosion analysis calculates the kinetics of heat gain and heat loss for a particular geometry and explosive. In the case of explosives, the heat gain initially comes from some external source, but is increasingly driven by exothermic reaction of the explosive as heating progresses. The analytical study of thermal explosion predates the invention of the EBW detonator [39,40] and has been analysed at various levels of complexity.

In its simplest form, a hypothetical volume of explosive is heated by some outside means. This external source may deposit a defined amount of energy or continuously add heat to the volume. Thermal transport processes (conduction, convection and radiation) will remove energy from the heated volume at a rate defined by the boundary conditions. If the rate of heat input from the initial source and the specific explosive kinetics is greater than the heat loss processes then at some defined time thermal runaway will lead to explosion. Times to explosion have been calculated for some common explosives (e.g. [41]) for various starting temperatures. For PETN, it is found that thermal explosion will occur in a microsecond if a volume is heated to approximately 700°C by some means. This may have relevance to EBW detonator function and is consistent with the research presented in [11] where thermal explosion, termed ‘direct thermal initiation’, is found to be responsible for the ETT in EBW detonators.

The process by which thermal explosion leads to either deflagration or detonation is highly dependent on both the explosive and the effects of confinement (both mechanical and inertial). Obviously more sensitive explosives under greater confinement are more likely to detonate than vice versa. For the purposes of this article, it will be assumed that the mechanism of growth to detonation is not important, but that under some circumstances it can occur very promptly.

3. A review of previous exploding bridge-wire research

(a). The role of shock-to-detonation

The simplest explanation for the functioning of an EBW detonator is direct SDT from the action of the bridge-burst and indeed at least one researcher just states that as fact [12,13]. There is remarkably little literature on the sustained one-dimensional shock response of low-density PETN. Possibly, this is because the difficulty of manufacturing coherent test charges from this fragile material, the relative difficulty of generating strong shocks in a material with a very low impedance and the short run-to-detonation distances of interest at those pressures make diagnostics with adequate temporal resolution challenging to field.

There appears to only be one Pop-plot curve for PETN at densities relevant to EBW detonators (1 g cc⁻¹) [42] (figure 7). Seay & Seely [42] also suggests values for the shock velocity versus particle velocity response of unreacted PETN at that same density. This is often, but technically incorrectly, called the unreacted equation of state (EOS) because, with knowledge of the starting density, it allows the relationship between pressure and volume to be calculated for single shock processes. It does not predict temperature, isentropic or multi-shock behaviour without additional information [12]. As reported in [43], comparison of this EOS curve with others from higher density PETN leads to a simple variation in offset of the Y -axis intercept with respect to density (figure 8). That is, the gradient of the curve stays constant while the initial bulk sound speed is a function of density. However, closer observation reveals a problem with that extrapolation to densities below 1 g cc⁻¹; the bulk sound speed at 0.9 g cc⁻¹ would have to be less than zero and this is clearly not physical. Therefore, this simple Y -axis intercept approximation breaks down around PETN densities of interest for EBW detonators, if not before. Nevertheless, from ETT measurements it is known that the run-to-detonation distance back calculates to ≈1 mm. Consulting the Pop-plot, a sustained pressure of 0.4 GPa is required for this run distance in PETN at 1 g cc⁻¹. This is a very low shock pressure compared with most explosives. However, there is an important caveat to this that is seldom expanded upon in the literature exploring the operation of the EBW. That is, the Pop-plot is only valid for sustained steady shocks. If the initial shock releases before detonation breaks out, the insult is termed ‘short-shock’, and it is found that the pressure to produce detonation needs to be increased substantially over that required for sustained shocks. Indeed, this is the region in which slapper detonators operate where the very thin flyer fails to support the shock in most practical circumstances and, as a result, for adequate detonator function much higher flyer velocities are required than would be required from a thick flyer of the same impedance [44].

Figure 7.

The Pop-plot for PETN as a function of density. The numbers next to the linear regression fit lines are the density of the PETN in g cc⁻¹. Adapted from [43].

Figure 8.

The shock velocity versus particle velocity for PETN as a function of density. The numbers next to the linear regression fit lines are the density of the PETN (ρ) in g cc⁻¹. Adapted from [43].

Alternatively, the shock can release from the side or from the shock formation geometry (termed divergent flow). Given that the wire in an EBW is much longer than its diameter, any strong shock produced must be largely cylindrical. In fact, because the wire is located close to the polymer header, a semi-cylindrical outgoing shock is created that is somewhat supported by a complex reflection process from the header surface. The resulting divergent flow at small radius will also destroy the assumption required to use the Pop-plot data directly.

(b). The magnitude of a shock from an EBW

The magnitude of the shock from an EBW has been studied [45–47]. This is a difficult measurement to make and so generally some from of Schlieren high-speed photography of the shock has been used to estimate the shock pressure from the known properties of the transparent medium (air, water or siloxane rubber) into which the bridge-bursts occur. Earlier studies made use of air and close examination revealed two shocks from an EBW: an initial weak one followed by a second stronger one that caught the first [8,48]. However, it is known that wires that burst in air have a different resistance versus electrical current profile compared with wire burst in PETN and this will affect the shock(s) produced.

Measurements in water, or rubber, suffer from the difficulty that, although the density is approximately correct, the impedance of water is much higher than low-density PETN. That is, the bulk sound speed in water and rubber is almost two orders of magnitude greater than that measured for low-density PETN. Because the effective impedance of the EBW ‘piston’ is not known, the shock-matched pressure into PETN cannot readily be calculated from the value measured in water. Interestingly, only a single shock is typically observed. In water, this may be because the second stronger shock overtakes the initial weaker one at very small radius. An additional consideration is that both rubber and water are electrical insulators and so may affect the formation of the arc after bridge-burst which may be important to supporting a shock process.

Despite this, the peak calculated shock pressure in water from a typical EBW burst varies widely (0.3–1.5 GPa) [45,47,49,50] and is found to have a complex triangular structure of duration ≈100–200 ns [49,51]. It will be noted that this pressure is of the correct order of magnitude to explain the functioning of an EBW detonator if the significant caveats are ignored regarding the fact that the shock duration is too short to fully support the lead shock until detonation breaks out and that the divergent flow that results at small radii from bridge-burst also greatly complicates things. As an aside, the waveforms presented in [49] show a marked double shock, perhaps even a ramp, to a second peak. This feature is not reported by others.

Measurements reported in [50] are particularly significant because they measured the output pressure as a function of CDU energy and calculated values between 0.3 and 1.1 GPa. Pressures above 0.5–0.6 GPa corresponded to hard-fire conditions and so the ETT will have ceased to vary much in real detonators. The Pop-plot for low-density PETN suggests that the run-to-detonation will vary widely between those pressure values. This is not observed. The ETT for different detonators varies greatly and is ≈650 ns for the RP-1 [13], ≈300 ns for the ER-213 [27] and 1.16 μs for the RP-80 [51]. Even if the absolute shock pressure measurement value is in error, the over 50% increase in pressure should have had an effect on the ETT in the event that EBW detonator function is an SDT process.

This issue has received little comment regarding the asymptotic ETT value [13,27,28]. Unless another rate-limiting physical process occurs, it would be expected that larger and larger burst currents produce larger and larger shock pressures. From the Pop-plot, it is known that larger shock pressures produce shorter run-to-detonation in all explosives studied so far [52]. In fact since the Pop-plot is always plotted on a log–log plot, increased shock pressures produce much shorter run-to-detonation values.

Thermal explosions are a kinetic process that may not be able to occur above a certain rate. That is, there may be a finite limit to the physical rate of that process. SDT has no such limit observed in other aspects of explosives. A greater magnitude shock always results in faster build-up. In extreme cases, SDT can be overdriven and an increased VOD results until release processes drop the velocity down to the steady-state value.

The role of divergent flow in SDT is large. It has been shown that the velocity of a metal sphere impacting explosive must be three times the velocity of a flat plate of similar dimensions to produce SDT [53]. This is because the spherical geometry releases the equal magnitude initial shock pressure so quickly compared with a pseudo-one-dimensional flyer that releases from the rear. The effects of cylindrical shocks (two-dimensional) have not been studied experimentally, but it is reasonable to expect the release effect to lie between the sphere (three-dimensional) and flat plates (one-dimensional).

As a result of these caveats (the effect of short-shocks and cylindrical divergence), one might expect the measured shock pressure from an EBW to have to be much greater than the Pop-plot might suggest for SDT to cause the functioning of the detonator. From the experiments conducted so far, this appears not to be the case, although as explained, translating the shock pressures observed in water to porous PETN is not straightforward.

(c). Photographic observations of detonators

High-speed photography has been used for many years to observe the process of bridge-burst [8,48,54]. Most often the bursts were performed in air or in another gas with controlled pressure. It is known that the impedance of the medium surrounding the wire affects the expansion process. This in turn affects the resistance versus time and so affects the burst process itself [7]. Occasionally, bursts were photographed in water in order to radically change the impedance of the material surrounding the bridge [47,50].

X-Ray and other similar techniques such as proton radiography used to gather information about the internal processes have been limited in application up until recently owing to the low contrast obtained in low-density powder, the short timescales involved relative to realistic exposure times and interframe times and finite spot size effects or similar blurring phenomena. Some advances have been made, see [11], and more can be expected in the future.

Photographing the build-up to detonation is harder because most explosive powders are white, attenuate visible light and are highly scattering. For this reason, observations are usually performed at the transparent walls of special detonators designed for the purpose [2,5,55].

The most extensive study, [2], through very careful optical path design and illumination, observed shock waves propagating in the PETN crystals after burst. The magnitude of these shocks, determined from their velocity, increased as the CDU voltage increased. Further, by observing detonation breakout at the transparent walls, increased CDU voltage resulted in detonation breakout occurring closer to the original bridge location.

Additionally, increased PETN density required increased CDU voltage for the same breakout distance to be observed. Increased SA PETN reduced the breakout distance for otherwise the same initial conditions. Finally, it was noticed that close to the threshold voltage, detonation often started off-axis with respect to the bridge location. That is, a randomly located volume somewhere near the original bridge achieved conditions required for detonation to occur and reaction in the rest of the IP propagated from that location.

In summary, photographic observations resolve a shock in the IP bed and detonation breakout occurring some distance away, on-axis for hard-fired detonators, but often off-axis for very soft-fired detonators. It is clear that the detonation in PETN is not homogeneous SDT in nature since breakout does not occur in the material shocked first near the bridge and observation location. However, the mechanisms underway after bridge-burst until detonation breakout could equally well be SDT, thermal explosion or a mixture of both.

(d). Observations of cut-back detonators

The particle velocity of IP beds during detonator function has been measured by cutting back an assembled detonator to a known distance above the bridge [56,57]. The PETN output surface was placed against a ‘silvered’ stress-maintaining window that was thick enough to prevent rear surface motion over the short timescales of interest. Optical velocimetry was then used to measure the interface particle velocity versus time profile after the bridge-burst. By varying the distance from bridge to window, a pressure build-up history can be measured. In both cases, it was clearly shown that a ramp wave was present initially that transitioned into a steady-state detonation some distance later.

In [56], building pressure ramp waves were observed at 0.655 and 0.914 mm from the bridge, but by 1.181 mm a steady-state detonation had formed. In this detonator, the IP was 0.9 g cc⁻¹. The bridge geometry is not described, but the author describes the functioning as a hard-fire. In [57], a weak ramp wave is observed at 0.76 mm, a stronger ramp at 1.44 mm and steady-state detonation at 2.5 mm. In this case, the IP was 0.93 g cc⁻¹. Neither the bridge geometry nor the firing conditions are described. If the function of an EBW is SDT, a ramp wave should not have been observed at any stage, but rather only shocks of varying magnitude. This strongly indicates that the initiation process in a EBW is not SDT.

A shock wave may initially drive a shock compaction wave, but that will decay to a ramp wave if not supported. The estimates vary for the duration of the shock from an EBW, but are of order 100–200 ns [45,51]. The ETT is typically several times that and so it is probable that an unsupported shock situation occurs. Forced compaction waves have been shown to bypass the experimentally inconvenient initial stage of the DDT process allowing a more controlled experiment that observes the more interesting latter stages [19]. Thus, the bridge-burst shock could still play a significant role in the operation of an EBW detonator, but the underlying process would still be DDT or thermal explosion.

It has been shown that bridge-wire bursts in both inert powders, and PETN that failed to then detonate, result in approximately hemispherical cavities forming near the bridge location [58]. It is therefore clear that a compaction mechanism, driven by the bridge-burst, is operating at some time scale in these low melting point solids.

(e). The effects of interstitial gas

Further evidence of a thermal mechanism rather than an SDT process is provided by [45]. In this research, the type of interstitial gas and gas pressure were altered for a nominally fired fixed-design detonator. It was discovered that the probability of the detonator operating varied tremendously according to the gas fill in the PETN. When argon (a gas that readily ionizes) was used, detonation was assured at almost any fill pressure. When SF6 (a gas that is very difficult to ionize) was used, detonation only occurred at very low fill pressures where the Pashen curve suggested ionization was possible at the voltage potentials created in the header. The probability for fills of nitrogen (78% of air), a gas with an ionization threshold that is between argon and SF6, fell between the other gas values.

Previous SDT research using supported shocks has shown that the presence or the absence of gas in shocked PETN had no effect on the Pop-plot [42]. This observation, in conjunction with the observation about the role of gas pressure on EBW detonator functioning, further supports the idea of SDT not being the principal mechanism operating in EBW detonators. Additionally, whatever process operates in nominally fired EBW detonators requires some degree of ionization of the interstitial gas. It is notable that ionization aids the establishment of an arc after bridge-burst. Indeed reference [45] suggests that SDT is not the mechanism by which EBW detonators function, but instead proposes it is a coupling of shock and pre-sensitization of the PETN by the arcing process.

(f). Arc detonators

Examining the function of an AD may be important to understanding EBW detonators, for while a shock is associated with the discharge, it is an order of magnitude weaker than the action of bursting a wire [59], thereby removing one of the obstacles towards understanding discussed previously: that of coupled effects.

In ADs, it was discovered that the energy required for detonation decreased with increasing SA PETN. That is, the mechanism of initiation was more efficient with higher SA PETN (10 500 cm² g⁻¹) than lower (3500 cm² g⁻¹) [15]. It is reported that the stored energy on the CDU necessary for self-triggered discharges needed to be 40–90 mJ to assure detonation with an average value of ≈60 mJ. Detonation was observed occasionally at energies as low as 20 mJ under some configurations.

It was also reported that reliable functioning of ADs happened when the majority of the energy discharge occurred in the initial 30 ns of the arc. Equal total energy discharges, where the majority of the energy arrived later, more commonly resulted in failure to detonate.

The AD function energy values above are broadly supported by [58] for triggered discharges in both EBW and ADs. In this research, the threshold energy for arc was measured as 26 mJ and 34 mJ for the normally detonated EBW. The all-fire threshold was 42 mJ for the arc version and 100 mJ for the EBW. However, it should be noted that the activation volume for the arc version was substantially smaller (150 μm spark gap) than the detonators tested in [15] (500 μm spark gap) and, until some unknown lower limit, this may require less energy to initiate detonation.

The explanation and model presented in [15] assumes no surface tracking of the PETN crystal since it is often considered a good dielectric and the experimental results are therefore solely explained using the Paschen curve for air. Subsequent research has indicated that ionization of the surface of PETN occurs at high potentials per unit distance [45]; therefore, it is quite possible that ADs can be made to function adequately, even at intermediate air pressures, if the fireset is externally triggered after full voltage charging rather than from self-breakdown.

A modified SE-1 detonator (essentially the same design as the RP-1) has been used in arc mode [16] using very high SA PETN (14 000 cm² g⁻¹) in the IP. The gap that the arc had to jump was systematically varied; however, the go/no-go threshold was identified as 54 mJ with an all-fire threshold of 73 mJ. This is similar to the values found in [15,58].

The effect of melting the bridge-wires in EBW detonators by the application of a low voltage prior to attempting to fire them normally in arc mode has been studied [60]. An electrical current between 2 and 20 A was applied to melt the gold wire. As might be expected, melting at greater current resulted in a larger gap being formed between the wire ends.

In all cases, the results of test firing the now-damaged AD showed that significantly greater energy was required than to fire the original pristine gold bridged detonator. This is attributed to the wire heating process producing partial reaction in the PETN, including sintering of the remaining powder, and therefore creating a void between the residual wire ends and the PETN. The energy required to fire an AD is lower than a similar bridged detonator and so the required energy for the melted ADs would have been substantially greater than would be required for a pristine AD of similar design.

(g). Direct optical initiation

Another exception to the problem of coupled effects from increased voltage on an EBW CDU is direct optical initiation of the explosive powder, usually by laser [61]. In this case, the process produces only a weak shock from ablation and so is largely thermal or photo-chemical in nature. As with the electrical arc created after an EBW bridge-burst, high-power laser pulses are observed to create plasma. Presumably, this is from direct interaction with explosive crystals because it occurred even under vacuum [18].

Direct optical ignition was studied in PETN, HMX and HNS [17]. In this research, various frequencies of laser were used with a 10 ns pulse at a spot size of 1 mm diameter. An ETT of ≈100–150 ns was noticed in PETN. At a laser wavelength of 1064 nm, a pulse energy of 56 mJ was required for detonation PETN at 0.9 g cc⁻¹. This dropped to 40 mJ at 308 nm and 24 mJ at 266 nm. The author suggests that light in the ultra-violet range, below 350 nm, may directly break chemical bonds in molecular crystals such as PETN. It was also noticed that confinement was required for detonation to occur at 1064 nm, but not at the shorter wavelengths. The HMX could be made to detonate, but required greater pulse energy than for PETN.

A similar study was undertaken by different researchers [18]. They studied PETN, RDX and HNS. The effect of density and particle size on the response of PETN was reported using a 20 ns pulse and a spot size of 0.6 mm diameter. For the finest PETN used at a density of 0.9 g cc⁻¹, the threshold energy required at 1064 nm was 20 mJ with hard-firing occurring at 41 mJ. Using slightly coarser LANL type 12 PETN, the energy required for hard-fire increased to 53 mJ.

For a fixed density, the particle size had little effect on ETT. By contrast, it was found that the ETT increased with decreased powder density (from 1.4 to 0.9 g cc⁻¹) and the variability in ETT increased as well. It may be significant that the particle size of the fine PETN used for this segment of the study was abnormally fine (21 000 cm² g⁻¹) and so it is possible that, as discussed elsewhere, the hot spot formation was suppressed under compaction compared with most PETN reported so far. The study also reported that the effect of shorter laser wavelengths on sensitivity was not as dramatic as noted by Paisley [17], but also confirmed that confinement was no longer required for detonation to occur.

By observing the light emission from the window in contact with the PETN, and through which the laser entered, it was noticed that after the initial plasma formed in the PETN, the light intensity dropped to essentially zero for a period before rising again. This was attributed to the arrival of a retonation wave from the detonation starting somewhere in the interior of the pressing. For this reason, the idea of a detonation occurring because of a delayed thermal explosion immediately behind the window (indicative of a homogeneous response) was discounted. They report that the reaction transitioned to detonation between 0.4 and 2.5 mm into the powder bed depending on the conditions.

The addition of carbon to PETN lowered the power required for detonation [62]. This is attributed to reducing the scattering length in the translucent PETN and therefore concentrating the energy into a smaller volume of explosive.

No researchers have observed detonation in HNS at any achievable pulse energy despite reflectometery measurements showing that the energy absorbed at the laser wavelengths will be similar to PETN and HMX. Other researchers have been unable to detonate HNS despite the additions of dopants [62].

Extensive searches have revealed essentially no papers studying DDT in HNS and so its propensity to react violently under pure thermal excitation is unknown. The SDT sensitivity of HNS has been studied extensively, particularly related to its short shock response because of its use in EFI detonators [35,63]. At comparable density (≈1.6 g cc⁻¹) and particle size (≫1 μm), HNS is found to be less sensitive than both RDX and HMX under SDT conditions and very much less sensitive than PETN [64].

(h). The effect of post-bridge-burst energy

The effect of post-bridge-burst energy on the functioning of EBW detonators has been studied using modified CDU units with an additional fast-acting triggered current-shunt circuit to quickly remove the current flow from the bridge [51,65]. The disadvantage of this approach is that it is very difficult to cease the bridge current instantly in this manner and so some attenuated current flows for a period after the shunting occurs. This creates a more complex analysis problem.

In [65], the effects of post-burst energy on platinum and gold wires was studied in PETN. The researcher was clearly focusing on the effects of substantial energy after burst and so very few ‘no-go’ events were noticed. However, close inspection reveals that with a platinum wire, a ‘go’ occurred when the post-burst energy was ≈200 mJ and a ‘marginal’ and a ‘no-go’ occurred when the post-burst energy was ≈0 mJ. With a gold wire, a ‘go’ occurred when the post-burst energy was ≈200 mJ and ‘no-go’ occurred when the post-burst energy was ≈0 mJ. The post-burst energy was calculated from the time where sufficient energy had been delivered to totally vapourize the bridge.

In [51], an RP-80 was studied. Total failure to detonate occurred with a post-burst energy of less than 30 mJ and ≈50 mJ was required for a hard-fire. It is presumed that bridge-burst was defined in the usual manner: the time at which the peak bridge voltage was measured. In [66], the effect of post-bridge-burst energy on the velocity of the bridge debris and plasma cloud was measured. It is reported that the post-burst energy increased the velocity of the cloud over those without post-burst energy. Interestingly, when there was no post-burst energy, the burst was delayed by a short time, but still occurred. This delay is not enough to explain the accompanying change in ETT observed in a functioning detonator under those same lower energy conditions.

In most of the literature on EBW detonators, bridge-burst is assumed to have occurred when the voltage across the bridge is at maximum and a small inflection is observed in the current curve. The obvious role of post-burst energy on correct functioning suggests that although it is a very convenient timing metric for day-to-day discussions of EBWs (because it is easy to quantify), a better metric might be found elsewhere. Indeed Valancius et al. [28] suggests that comparison of EBW detonator performance is assisted by considering the energy until peak power, not peak voltage. That is, although the power is the instantaneous value of V I, neither the voltage across the bridge (V ), nor the current (I) drops immediately after the voltage spike. As a result of the rapid rate of current rise just prior to burst from most CDUs, the peak power occurs some time shortly after ‘voltage-indicated bridge-burst’. It is probable that this new suggested metric is correlated with the required post-burst energy for correct functioning of the detonator discussed previously.

(i). Light absorption in explosives

Estimates of the temperatures of arcs in air suggest a value of order 10 000 K [67]. By considering the Planck distribution of energy at such temperatures, the peak emission will occur in the soft to hard ultraviolet (350–280 nm), but with significant energy content down to 200 nm. Reliable light absorption data for PETN, and other explosives, have proven elusive. Two papers [68,69] agree qualitatively that PETN has little light absorption at wavelengths above 350 nm, but that it is highly absorbing at ultraviolet (UV) wavelengths below that. However, attempts to quantitatively compare the two papers failed. Nevertheless, it appears probable that for PETN, UV light from an arc would be largely absorbed (more than 90%) within 1 mm of transmission depth. It will be recalled that rapidly raising the temperature of a small volume of PETN by 700°C results in a thermal explosion in approximately 1 μs. This is the same timescale as the ETT in a typical EBW detonator.

High-temperature arcs and ultraviolet lasers have the advantage that their photons appear to result in a photochemical effect in the explosives commonly used in EBW detonators (i.e. PETN, RDX and HMX) and are therefore absorbed in a short distance [69–72]. It is unclear at this time if direct UV ignition chemistry occurs in PETN that results in exothermic breakdown, or if the volumetric thermal heating associated with photon absorption and subsequent thermal explosion and SDT process is assisted by the decomposition products produced from high-energy photons.

4. Discussion and conclusion

The mode of functioning in exploding bridge-wire (EBW) detonators is obviously complex. It is clear that they do not operate by prompt SDT because there is a measurable excess transit time (ETT), even under hard-fire conditions [13]

The fact that the ETT asymptotes to a non-zero time is important for considering traditional SDT with a run distance or run time. Measurements show that the shock produced by a bursting wire increases in strength with increasing voltage on the CDU [50]. In traditional SDT, increased pressure always reduces the run-to-detonation. Observations of cut-back detonators show that they produce ramped compression waves prior to the establishment of a steady-state detonation [56,57]. Again, this demonstrates that traditional SDT does not occur because by that mechanism a lead shock would be observed at all stages.

However, it is apparent from analysis of inert powder simulated EBW detonators and real PETN detonators that failed to detonate, that the bridge-burst shock does form a compaction wave that moves the IP powder away from the bridge location [58]. Energy in the form of PdV work will then heat the powder as well as form a compaction wave. This energy would augment any thermal explosion process also occurring although it is currently unclear on what time scale the compaction phenomenon operates (i.e. what the particle velocity is). It appears unlikely that the compaction occurring in an AD and a DOI would be similar to an EBW detonator.

Both the magnitude and duration of the shock from the bridge-burst are at best contested, and at worst unknown [45,47,49,50]. Without these data, it is not possible to assess the applicability of one-dimensional, sustained, shock strength input to run-to-detonation data for PETN (a Pop-plot). Because the EBW bridge produces a pseudo-hemi-cylindrical divergent shock, it is unlikely that the sparse Pop-plot for PETN has much applicability at all. Instead, an energy fluence approach, such as described in [53], and subsequent papers by the same author, is more likely to be successful in predicting response, if SDT is the ignition mechanism.

Additional evidence favouring a thermal explosion explanation comes from observations of the essential role that post-bridge-burst energy has on the likelihood of detonation occurring. It has been demonstrated that late-time arcing between the EBW electrodes is highly advantageous under normal operating conditions [45]. Further, it has been demonstrated that starving the arc of energies less than 30–200 mJ after burst prevents normal detonator function [51,65]. Since this energy arrives after the main shock from burst, it will serve to both slightly support the shock, but also provide a high-power high-temperature thermal flux (≈1 MW).

It is interesting that these magnitudes of the values required for function are also in agreement with the largely empirically developed conservative design rules-of-thumb used at LANL for 50 years. That is, an arc with a more than 1 MW for more than 100 ns (corresponding to more than 100 mJ) is required for reliable EBW detonator operation (Goforth J 2018, personal communication).

Experiments on PETN ADs have demonstrated that energies of between 26 and 90 mJ are required for normal functioning and that detonation was most likely if the energy was deposited in less than 30 ns [15,58]. Because there is no working fluid in an AD compared with a regular EBW detonator, the shock from a comparable energy discharge is weaker in the case of the arc, possibly by an order of magnitude [59]. This strongly suggests that the thermal input is more significant than shock input in functioning an AD.

Further evidence pointing to a heating, or at least heat flux, role in the operation of EBW detonators comes from direct optical ignition (DOI) studies of PETN [17,18]. Energies of between 20 and 56 mJ were required. Detonation was easier to achieve at laser wavelengths in the ultraviolet, and this was attributed to a likely photochemical effect at wavelengths below approximately 350 nm. Significantly, the laser pulse durations used were 10–20 ns in duration and the presence or the absence of air in the interstitial space between PETN crystals was found to be irrelevant.

Interestingly, Smit [68] also has absorption data for RDX, HMX and HNS. Both RDX and HMX show greater absorbency in the UV than HNS. Additionally, HNS is extremely stable at elevated temperature as well as being less shock sensitive than RDX, HMX and PETN. At a common rapid heating rate, the explosives have the following chemical breakdown temperatures: PETN 180°C, RDX 220°C, HMX 250°C and HNS 320°C. These observations may explain the apparent inability to make HNS-based EBW detonators.

The hypothesis is thus that the functioning of EBW detonators, ADs and DOI detonators are all related to the deposition of a suitable heat flux (20–90 mJ in 10–30 ns) and the formation of a plasma with spectral content well into the UV. The plasma can result from a high-temperature arc and associated bridge-wire gas, or be formed directly by the action of sufficient photon energy being absorbed by the explosive. The rapid expansion of the heated zone, and the release of energy from combustion, form a thermal explosion that promptly transitions to a detonation in the shock-sensitive IP. This hypothesis would appear as a volumetric explosion, although not one necessarily centred directly against the detonator header and has been suggested previously [10]. It is also consistent with the findings presented in [11].

This explanation also suggests that the bridge-wire is no more than a fuse to allow the CDU current to build from zero to a high enough value where a high energy arc is formed. This has been postulated before [14,58]. It also implies that the historically significant, and experimentally convenient, bridge-burst, indicated by the inflection in the current rise and the voltage spike, is the beginning of the thermal operation process, rather than the stimulus that directly results in detonation.

Confirming or disproving this hypothesis could be done in many ways. A few suggestions are made here.

Bridge current shunting tests on EBW detonators have been undertaken before [51,65]; however, stopping the current instantly in a CDU is extremely difficult and results in an inductive ‘tail’ current that complicates analysis. A charged coaxial-line fireset operates at a higher voltage that most CDUs. The ability to turn off the current, either by a true high-voltage on–off switch or trimming the length of the transmission line, offers the opportunity to control the total energy supplied post-burst. Additionally, the higher voltage would allow the same detonator geometry, without the gold bridge installed to function in AD mode. In that manner, the post-bridge-burst energy and the AD function energy could be compared.

A self-similar set of visible and UV absorption measurements on various explosives is clearly needed, as is some understanding of the DDT susceptibility of HNS.

Another experimental variant that may be possible along the same lines is a DOI electrically based detonator: coupling only the light output from a bursting wire onto a PETN IP to observe the results versus directly embedding the wire in the IP. Compensation for the inevitable losses with remote coupling would need to be carefully considered to interpret the results.

A good understanding of the role of the bridge, the arc, the plasma, light absorption behaviour in PETN, RDX, HMX and HNS and subsequent explosive combustion will go a long way toward demonstrating the validity, or otherwise, of the hypothesis presented above.

Data accessibility

This article has no additional data.

Authors' contributions

P.J.R. did most of the literature search and writing. P.M.D. provided significant advice and improvements to the text regarding the DDT, SDT, thermal explosion sections and assisted in improving the clarity of the arguments presented.

Competing interests

We declare we have no competing interests.

Funding

The research was funded by the US Department of Energy as part of our regular employment at Los Alamos National Laboratory. No funds from external organizations were used.