Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Jul 16;35(32):10374–10382. doi: 10.1021/acs.langmuir.9b01600

Initial Growth Study of Atomic-Layer Deposition of Al2O3 by Vibrational Sum-Frequency Generation

V Vandalon 1,*, W M M Erwin Kessels 1,*
PMCID: PMC6694409  PMID: 31310143

Abstract

graphic file with name la-2019-01600a_0007.jpg

The initial growth during the atomic-layer deposition (ALD) of Al2O3 using trimethylaluminum (TMA) and water was studied on two starting surfaces: SiO2 and −H-terminated Si(111) [H/Si(111)]. In situ spectroscopy ellipsometry (SE) showed virtually immediate growth of Al2O3 on both surfaces, although for H/Si(111) a reduced growth-per-cycle was observed in the initial 20 cycles. The underlying surface chemistry during the initial cycles of ALD was monitored with in situ broadband sum-frequency generation (BB-SFG) spectroscopy. For the SiO2 surface, the −CH3 surface groups were followed revealing that only the first TMA half-cycle deviates from the steady-growth regime. The reaction cross section of the initial TMA half-cycle (σTMA = 2.0 ± 0.2 × 10–18 cm2) was a factor of 3 lower than the cross section of the TMA half-cycle during the steady-growth regime of ALD (σTMA = 6.5 ± 0.6 × 10–18 cm2). All H2O half-cycles, including the first, showed steady-growth behavior with a corresponding reaction cross section (σH2O = 4.0 ± 0.4 × 10–20 cm2). Therefore, only the first ALD cycle was affected by initial growth effects on the SiO2 starting surface, in line with the SE data. For the H/Si(111) surface, the Si–H groups were monitored with BB-SFG spectroscopy, revealing a reaction cross section of σTMA = 3.1 ± 0.3 × 10–18 cm2 for the first TMA half-cycle on H/Si(111); a factor two lower than that during the steady regime of Al2O3. These results demonstrate that the chemistry during the initial growth regime of Al2O3 ALD on SiO2 and H/Si(111) shows subtle but measurable differences compared to the steady-growth regime.

Introduction

Ultrathin films grown by atomic-layer deposition (ALD) currently serve an enabling role in areas such as nanoelectronics,1−3 nanotechnology,4,5 and photovoltaics.6,7 Given the ever increasing demands in these fields for more control on the nanoscale, a fundamental understanding of the reaction mechanisms during ALD is essential. Two phases can be identified in the growth during an ALD deposition. Once the influence of the starting surface has subsided, typically the reaction mechanism stabilizes and, as a result, process characteristics such as the growth-per-cycle (GPC) are virtually constant. This phase of the ALD process is referred to as the steady-growth regime or in the ALD literature occasionally as “steady-state growth”. The primary focus of mechanistic ALD studies so far has been on characterizing the steady-growth regime.1,8−12 However, at the start of deposition, the growth is influenced by the starting surface and the process parameters can vary from cycle-to-cycle. This initial growth regime is commonly referred to as the “nucleation” phase in the ALD literature. Apart from a hand full of publications around the early 2000s,13−20 few works have focused on directly studying the surface chemistry during the initial growth phase. As a result of this lack of mechanistic studies of the initial growth phase, the surface chemistry during the initial growth is substantially less well understood than those during the well-studied steady-growth regime of ALD.

Because of new developments in the field of ALD, the initial growth phase has become more important in recent years. The demand for more complex materials has led to the adoption of complex multistep ALD schemes for the synthesis of doped or ternary materials. These materials can be grown by alternating two ALD processes triggering the initial growth phenomena after each switch between chemistries (typically after just 10 s of ALD cycles).21−23 The impact of initial growth on such materials is illustrated by, for example, combining a ZnO and an Al2O3 ALD process to synthesize Al-doped ZnO.21,22 For the resulting ALD process of Al-doped ZnO, a significant decrease in growth and even etching have been reported at the switch from the Al2O3 ALD process to the ZnO ALD process depending on the chemistry used.21,22 Area-selective ALD is a further example of a topic where initial-growth phase phenomena play a pivotal role. Area-selective ALD has recently attracted significant attention as a promising concept to reduce the total number of lithography-based process steps and, at the same time, mitigate alignment issues which have been identified as bottlenecks in the fabrication of (future) nanoelectronic devices.24 Several approaches for achieving area-selective ALD exploit (large) differences in the initial growth on different starting surfaces to selectively deposit material.24 This is illustrated by the area-selective growth of ZnO on −OH-terminated SiO2 versus −H-terminated Si; it turns out that the precursor does not chemisorb on the −H-terminated surface but does readily react with the −OH groups, leading to selective deposition of ZnO.25 The initial growth also plays a key role in the synthesis of 2D transition-metal dichalcogenides (TMDs) by ALD. Single and few atomic-layer thick films of these TMDs—grown by only 10 s of ALD cycles—are of interest because of their unique thickness-dependent properties.26 For example, the prototypical 2D-TMD MoS2 exhibits a direct band gap at 1.9 eV in the monolayer regime resulting in, for example, strong photo luminescence (PL), whereas bilayer or thicker films show an indirect band gap and negligible PL.26 A slight variation in growth during the initial ALD cycles can therefore have a large impact on the properties of the TMDs. To make significant and systematic advances in any of these topics, fundamental understanding of the growth mechanism during the initial growth phase is essential.

For the most common ALD processes, the surface chemistry during the steady-growth phase is understood qualitatively. Various different techniques have been used to study the growth mechanism of ALD including gas-phase and surface infrared absorption spectroscopy,11,27−29 quadrupole-mass spectrometry,30,31 and quartz-crystal microbalance.32,33 Most of these approaches indirectly study the surface chemistry ruling the growth mechanism of ALD and benefit from the repetitive nature of the ALD process. Direct observation of the surface chemistry requires highly sensitive in situ diagnostic techniques with sub-monolayer sensitivity. Such studies are not always feasible, and as a result, a qualitative picture is not always available. A quantitative understanding of the surface chemistry based on experimental data, that is, knowledge of the reaction kinetics and thermodynamics, and insights into nonidealities are limited to only a hand full of processes.

The prototypical metal-oxide ALD process of Al2O3 using Al(CH3)3 (trimethylaluminum, TMA) as a precursor and H2O as a coreactant is one of the few cases where a relatively complete picture is available. For this ALD process, the dominant reaction path in the steady-growth regime can be summarized as

graphic file with name la-2019-01600a_m001.jpg 1a
graphic file with name la-2019-01600a_m002.jpg 1b

where a hyphen (-) indicates a surface group and where all other molecules are in the gas or vapor phase.27,28,30,32,34−37 As one of the better studied processes, several secondary or alternative reaction paths and nonidealities have been reported. Furthermore, the surface chemistry has also been studied quantitatively looking at the reactivity (initial sticking probability or reaction cross section), reaction kinetics (activation energy), and reaction thermodynamics (potential energy change).35,36,38−42 However, for most ALD processes the growth mechanism is known at a qualitative level at best.

The fundamental understanding of the reaction mechanism during the initial growth phase of ALD is even more fragmented and limited than that of the steady-growth regime. For example, only a few studies investigated the growth mechanism during the initial growth of Al2O3 ALD qualitatively on the two common and relevant starting surfaces of c-Si/SiO2 and H-terminated c-Si.43−45 For the SiO2 surface, it is likely that the growth of Al2O3 by ALD occurs via the same reaction path as during the steady-growth regime, although the reactivity—and as a result the GPC—can differ.46 However, evidence for other reaction paths has been reported on specially prepared SiO2 surfaces: on SiO2 with low −OH density, for example, Si–CH3 can be formed during chemisorption, as will be discussed later.46 On the H-terminated c-Si surface, different chemisorption reactions must occur during the first TMA half-cycle because of the absence of −OH groups. Indeed, evidence for different reaction paths has been reported for this surface: for example, the formation of Si–Al(CH3)2 after TMA exposure has been observed on H-terminated c-Si.13,14 However, quantitative experimental data of the surface chemistry is lacking for both starting surfaces despite their relevance and ubiquity.

In this work, the surface chemistry during the initial growth on both SiO2 and H-terminated Si(111) (H/Si(111)) surface was studied directly using in situ vibrational broadband sum-frequency generation (BB-SFG) spectroscopy. The initial growth on the SiO2 surface was followed by monitoring the density of −CH3 surface groups during the first three ALD cycles as a function of the precursor and coreactant exposure. Emphasis was placed on the reaction kinetics of the ALD chemistry and the determination of the reaction cross section σ. The initial growth on the H/Si(111) surface was followed by measuring the relative density of Si–H on the surface as a function of TMA exposure. This revealed the reaction kinetics of the precursor chemisorption on H/Si(111) and allowed the determination of the initial sticking probability and the reaction cross section of TMA chemisorption on the H/Si(111) surface.

Experimental Details

ALD Setup and Substrate Preparation

The surface chemistry during thermal ALD of Al2O3 on the Si(100)/SiO2 and H/Si(111) starting surfaces was studied in a home-built ALD reactor. The ALD reactor consisted of a vacuum chamber which was equipped with two turbomolecular pumps (Pfeiffer TMU 261P) reaching a base pressure better than 1 × 10–6 mbar. The vapor drawn precursor and coreactant used in the ALD process were dosed using “fast ALD” valves (Swagelok 34C-A-GDFG-1KT) using pulse times of 20 ms for the SiO2 experiments and 10 ms for the H/Si(111) experiments with a TMA flux of ΓTMA ≈ 1.7 × 1019 cm–2 s–1 and a H2O flux of ΓH2O ≈ 3.5 × 1020 cm–2 s–1 in both experiments. The reactor walls were heated to 80 °C. The BB-SFG measurements were performed on a 2 in. c-Si wafer suspended in the middle of the reactor being clamped at the edges of the wafer. For the experiments at 100 °C, the sample was heated radiatively using a Boralectric heating element (GE Advanced Ceramics ACSF0073 HTR1002). The temperature of the sample was measured with a thermocouple (Thermocoax 2ABAc05/1m/TI/FIM.K) glued to the sample with thermally conductive adhesive (RS 186-3600) and controlled using custom electronics modulating the power dissipation in the heating element using the sample temperature as the input.

The samples for the initial growth studied with BB-SFG spectroscopy and spectroscopic ellipsometry (SE) experiments were prepared as follows: the Si(100)/SiO2 substrates were made by depositing 90 nm of SiO2 on the Si wafer with plasma-enhanced chemical-vapor deposition at 300 °C using a SiH4–O2 plasma. The H/Si(111) surfaces were prepared by the procedure as described by Higashi et al.47 In short, a Si(111) wafer with native oxide was immersed for 120 s in a buffered hydrofluoric acid (BHF) comprising of 40% NH4F and 49% HF mixed in a volume ratio of 7:1. After the BHF exposure, the wafer was rinsed in a flow of ultrapure water until the resistivity of the water down stream of the wafer reached a resistance > 5 MΩ cm. Exposing the Si(111) surface to BHF removed the native oxide and subsequently formed an atomically smooth, Si–H-terminated surface which is stable in water and ambient.47 The BB-SFG spectroscopy experiments on the H/Si(111) surface were performed at 80 °C and all other experiments were performed at 100 °C.

Vibrational BB-SFG

Vibrational BB-SFG spectroscopy is a nonlinear optical technique that is ideally suited for in situ studies of the surface chemistry during thin-film deposition. BB-SFG combines identification of surface groups with inherent surface selectivity, sub-monolayer sensitivity, and the flexibility of an all-optical technique. The surface selectivity of SFG spectroscopy is caused by the strict selection rules for the SFG process associated with a second-order nonlinear phenomena and, as a result, bulk contributions from centrosymmetic media are forbidden in the dipole approximation.48 For the substrates used in this study, this indeed leads to surface selectivity for BB-SFG spectroscopy. The surface selectivity is not only crucial in isolating the surface contribution from the bulk background that is typically dominant in linear optical techniques, but it can also greatly facilitate the interpretation of the results: as a consequence of the surface selectivity of BB-SFG spectroscopy, the total surface coverage can be measured directly which is more revealing than the change in coverage that is detected by differential techniques such as absorption spectroscopy often used to study surface chemistry.35,36

For the detection and identification of surface groups, BB-SFG spectroscopy relies on the enhancement of frequency mixing between visible and mid-IR laser pulses. This enhancement occurs when the photon energy of the mid-IR light is resonant with vibrational transitions of the surface groups. As a result, the spectral shape of the BB-SFG signal contains the vibrational signature of the surface groups, see also Figure 1. The degree to which the surface groups polarize, P⃗, in response to the simultaneous interaction with the electric field of a spectrally narrow visible pulse E⃗(ωvis) and the electric field associated with a broadband femtosecond mid-IR pulse E⃗(ωir) is described by their second-order susceptibility χ̿(ωvis,ωir).48 The resulting SFG intensity ISFG measured in BB-SFG spectroscopy for surface groups with areal density ρ therefore given by

graphic file with name la-2019-01600a_m003.jpg 2

Figure 1.

Figure 1

Open in a new tab

Vibrational transitions of the surface groups are probed with BB-SFG by exposing the surface groups simultaneously to a broadband femtosecond IR pulse and a narrowband visible pulse. The two pulses interact, resulting in the emission of a SFG signal. The efficiency of the mixing is resonantly enhanced by the vibrational transitions of the surface groups, and as a result, the vibrational signature is contained in the SFG signal situated in the visible part of the spectrum.

The resonances in the SFG signal can be used to identify the surface groups, but more importantly, the (relative) areal density ρ of these surface groups can be monitored in situ during, for example, an ALD process by following the amplitude of these resonances. To obtain information about the density of surface groups, the resonances in BB-SFG spectra have to be modeled. The spectral SFG response of a surface group with coverage ρ is given by a modified version of eq 2

graphic file with name la-2019-01600a_m004.jpg 3

where Ares is the cross section of the SFG process of a single surface group for a resonance at ωir and Γ is the broadening of the resonance. The parameter χ̿NR aggregates the nonresonant contributions to the SFG signal and ϕ describes the phase of the resonant contribution with respect to the nonresonant contribution. The relative density of the surface groups can be determined from a fit of this model to the data using the least-squares approach with a Levenberg–Marquardt algorithm. This procedure was used to obtain the relative densities reported in this work. See the Supporting Information for a more detailed discussion of the fitting of the data.

The optical setup for in situ BB-SFG spectroscopy—integrated into the ALD setup—was composed of three main components: the laser system, optical components used to tailor the beam, and detection system. The laser system generating the 90 fs pulses consisted of an optical oscillator (Spectra-Physics Tsunami) and amplifier (Spectra-Physics Spitfire) producing a 1.8 W beam of visible (795 nm) light with a repetition rate of 1 kHz. Of this visible signal, 70% was used to pump an optical-parametric amplifier (OPA, Light Conversion TOPAS-C), generating the tunable mid-IR signal (3–8 μm). The mid-IR beam generated in the OPA was directed toward the ALD system. The remaining 30% of the visible beam was made spectrally narrow by a spike filter (CVI F1.1-800 spike filter) which lengthened the pulses to ∼1 ps duration and significantly reduced its intensity. Both beams were focused onto the same spot on the substrate situated in the vacuum chamber in a noncollinear geometry. Either beam had an average power of 5 mW at the sample. To synchronize the visible and mid-IR pulses, a home-built delay line was incorporated into the visible beam path built around a computer-controlled motorized stage (Physik Instrumente M-014-D1). The BB-SFG signal generated at the sample was separated from the visible and mid-IR laser beams using spatial filtering (2 apertures of ∼2 mm placed ∼30 cm apart) and spectral filtering (4 Thorlabs FES0750 short-pass filters each with an optical density > 5). To select the polarization of the SFG light, the beam was passed through a Glan-laser polarizer (Thorlabs GL10A). The BB-SFG signal was focused onto the entrance slit of the spectrograph (Acton Research SP2500) and detected by a liquid nitrogen cooled CCD chip (Princeton Instruments Spec-10). The BB-SFG spectra were collected using an acquisition time of 120 s. The so-called “Ssp” polarization mode was used which is the strongest mode for −CH3 and Si–H groups. In this mode, p polarized mid-IR and s polarized visible light are used to drive the SFG process while the s component of the SFG (denoted as capital S) signal is detected.

In Situ SE Measurements and Modeling

The initial growth of the Al2O3 film by ALD was followed using in situ SE (J. A. Woollam Co. M2000X) on a half-cycle basis. To obtain the thickness of the deposited Al2O3 film from the SE spectra recorded during ALD, the optical response of the two samples was modeled. The bare Si(111)/H and Si(100)/SiO2 substrates were parameterized using the in situ SE spectra recorded before the start of the deposition. The optical constants of the Al2O3 film grown on the top of these substrates were described using the Cauchy model. The parameters of the Cauchy model were determined from the in situ SE spectrum recorded after 50 ALD cycles, that is, using the thickest film deposited in the experiment. The Al2O3 films had a refractive index of n = 1.6 at 2 eV which is typical for ALD Al2O3.49 Using this model, all of the intermediate SE spectra were fitted, yielding the thickness of the Al2O3 film as a function of ALD half-cycle as shown in Figure 2a.

Figure 2.

Figure 2

Open in a new tab

(a) Thickness of ALD grown Al2O3 film on a SiO2 and a H/Si(111) starting surface measured during growth at 100 °C with in situ SE plotted as a function of the number of ALD cycles. Data were collected after both the TMA (open markers) and H2O (solid markers) half-cycle. The inset shows the first four cycles in more detail. (b) Corresponding GPC plotted as a function of the ALD cycle number for ALD of Al2O3 on both the SiO2 and H/Si(111) surface.

To monitor how the GPC changes from cycle-to-cycle during the initial growth, the GPC needs to be determined from the increase in the film thickness after each individual ALD cycle. Typically, in the steady-growth regime, the GPC is calculated from the increase in film thickness over multiple (10 s) of ALD cycles. When measuring thickness changes with SE as small as those caused by a single ALD cycle, the role of the surface groups on the SE spectra has to be considered. A strategy similar to the one outlined by Langereis et al. to monitor the GPC during the steady-growth regime on a cycle-by-cycle basis was adopted here to study the initial growth.50 In short, the cycle-by-cycle GPC during the initial growth on both surfaces was calculated from the SE spectra recorded after each H2O half-cycle instead of the TMA half-cycle. This approach mitigates the complications arising due to changing surface functionalization to a large part, for a more detailed discussion see the Supporting Information.

Results

GPC during Initial Growth

Figure 2a shows the Al2O3 thickness measured with in situ SE during the first 50 ALD cycles on a SiO2 and a H/Si(111) starting surface. For the SiO2 surface, virtually no growth delay was observed, whereas for the H/Si(111) surface the growth starts out slower but eventually shows the same slope as the growth on the SiO2 surface. Figure 2b shows the GPC for the first 50 cycles calculated from the data in Figure 2a using the procedure discussed earlier. For the SiO2 surface, the first cycle shows a GPC of 2.7 Å, whereas all subsequent cycles exhibit a GPC of 0.8 Å. The subtle cycle-to-cycle variation observed in the GPC for cycle 2 up to ∼20 was considered too small to warrant further interpretation because it can easily be caused by, for example, minor variations in the optical constants of the <2 nm thin Al2O3 film. For the H/Si(111) surface, the first cycle shows a GPC of 1.1 Å. The subsequent cycles showed a GPC of 0.3 Å which gradually increased to 0.8 Å after approximately 20 cycles. The cause of the higher GPC in the first cycle will be addressed later. Comparing the measured GPC for the subsequent cycles to that of the steady regime (0.8 Å at 100 °C49) suggests that for the SiO2 surface the initial growth phenomena are mainly limited to the first cycle. For the H/Si(111) starting surface it is clear that approximately the first 20 cycles are affected by initial growth phenomena after which the steady-growth regime is reached. The significantly longer perturbation of the growth on the H/Si(111) starting surface indicates that the surface chemistry is indeed different to that on the SiO2 surface.

Methyl Coverage during Initial Growth on SiO2

The −CH3 groups that play a key role in the surface chemistry were monitored by BB-SFG spectroscopy during the initial three cycles of ALD on the SiO2 surface. Small amounts of the precursor or coreactant were dosed to reveal the reaction kinetics. A BB-SFG spectrum was recorded of the bare SiO2/c-Si substrate probing the spectral region around 3000 cm–1, see the Supporting Information, in which the C–H stretch mode of −CH3 groups is situated. Subsequently, the pristine SiO2 surface was exposed to 20 ms of TMA and after pumping away the precursor and gas-phase reaction products, a BB-SFG spectrum was collected, resulting in the spectrum (i) in Figure 3. Spectrum (i) in Figure 3 clearly shows the appearance of a resonant feature at 2890 cm–1 which is indicative of the −CH3 groups of chemisorbed TMA on the surface. This procedure was repeated several times and spectra (ii) up to (v) show an increase in the strength of the feature assigned to the −CH3 groups. From spectrum (v) onward, the feature related to the −CH3 groups no longer changes. This indicates that no additional TMA could adsorb on the surface and that saturation was reached. The H2O half-cycle following the TMA half-cycle was studied using the same procedure, exposing the surface to multiple sequential 20 ms of H2O doses and recording a BB-SFG spectrum after each exposure. A decrease in −CH3 coverage on the surface was observed as a function of H2O exposure (spectra not shown). This procedure was repeated, following the initial three ALD cycles on this surface. The generally weak C–H stretch mode could be observed on the SiO2 surface but not on the H/Si(111) because of the Fresnel coefficients in essence enhancing the BB-SFG signal strength on the SiO2/c-Si substrate and suppressing it on the H/Si(111) substrate, see also the Supporting Information.

Figure 3.

Figure 3

Open in a new tab

BB-SFG spectra of the C–H stretch region (i) after the first TMA exposure during ALD at 100 °C. The characteristic peak around 2890 cm–1 is indicative of the −CH3 groups of chemisorbed TMA on the surface. The amount of chemisorbed TMA increases for subsequent exposures (ii–iv) and eventually saturates (v–viii).

Figure 4 shows the −CH3 coverage as a function of precursor and coreactant exposure in the first three ALD cycles determined by fitting the BB-SFG spectra such as those shown in Figure 3, see also the Supporting Information. From Figure 4 it is clear that the reaction kinetics of the first TMA half-cycle deviates significantly from the reaction kinetics of the steady-growth regime in both the TMA uptake (i.e., the increase in θCH3 over a half-cycle) and reactivity (i.e. the time-constant of the change). Yet, the reaction kinetics of the TMA half-cycles for the second and third ALD cycle is virtually identical to the reaction kinetics observed during the steady-growth regime (also shown in Figure 4). Furthermore, Figure 4 shows that the final −CH3 coverage reached after saturation of the TMA half-cycle did not vary from cycle-to-cycle; the second and third TMA half-cycle reached a relative −CH3 coverage of 0.99 and 1.02 with reference to the first TMA half-cycle, respectively. For the H2O step, all of the half-cycles show reaction kinetics virtually identical to that seen in the steady-growth regime. Moreover, in each case persistent −CH3 groups were observed that are unreactive toward H2O at this temperature in line with earlier work for steady-growth of Al2O3 and related ALD processes.23,35,36 The relative coverage of the persistent −CH3 groups was ∼0.6 for all cycles, similar to what we have found for the steady-growth regime at 100 °C.35 The enhanced GPC in the first ALD cycle seen in Figure 2 is in part related to the presence of these persistent −CH3 groups. The GPC is proportional to the TMA uptake, that is, the change in θCH. For the first ALD cycle, θCH3 starts at 0 and reaches 1 at the end of the TMA half-cycle (the data set is normalized to this data point). In the H2O half-cycle, H2O is not reactive enough to remove all −CH3 leaving persistent −CH3 groups on the surface at this temperature. The subsequent cycles all start with θCH3 ≈ 0.6 and reach θCH3 ≈ 1 at the end of the TMA half-cycle. This indicates that the TMA uptake is significantly higher in the first ALD cycle compared to the subsequent cycles and is reflected in the GPC. To summarize, these data show that only the reaction kinetics of the first TMA half-cycle are significantly affected when growing ALD Al2O3 on a SiO2 surface. This is in line with the immediate growth observed for ALD of Al2O3 on the SiO2 surface shown in Figure 2 and in agreement with reports in the literature.28,53

Figure 4.

Figure 4

Open in a new tab

–CH3 coverage as a function of the TMA and H2O exposure for the first three cycles on the SiO2 surface for ALD of Al2O3 at 100 °C obtained from modeling the BB-SFG spectra. For comparison, the reaction kinetics for the steady-growth regime is also given in the figure. Only the −CH3 coverage after saturation of the first TMA half-cycle was normalized, all other spectra were scaled by the same factor so that relative coverage differences between the half-cycles can still be interpreted. The solid lines are fits to the data used to determine the reaction cross section.

The reactivity of TMA and H2O toward the surface can be quantified in terms of reaction cross sections. The reaction cross section σTMA (σOH) links the change in the −OH(−CH3) density θOH (θCH3) to the TMA (H2O) flux ΓTMA (ΓOH). The chemisorption of TMA and H2O can be described as reactions that are first order in −OH/–CH3 surface coverage, leading to the following differential equations

graphic file with name la-2019-01600a_m005.jpg 4a
graphic file with name la-2019-01600a_m006.jpg 4b

These equations can be expressed solely in −CH3 coverage using the relation θOH + θCH3 = 1. Furthermore, the Hertz–Knudsen equation was used to determine the flux of H2O (ΓH2O = 3.5 × 1020 cm–2 s–1) and TMA (ΓTMA = 1.7 × 1019 cm–2 s–1) toward the substrate from the pressure in the reactor during dosing. The reaction cross section was determined by fitting the solution of the differential equations—an exponential function—to the data in Figure 4. The main uncertainty in the cross section was caused by a systematic error in the absolute magnitude of the flux (based upon the pressure measurement with an absolute error less than an order of magnitude) which only introduces a scaling factor in the absolute value of the cross section. Therefore, this does not affect the interpretation of relative differences between the cross sections. The “random error” in the data is better than 10% which is a conservative estimate from the fluctuations in the strength of the SFG signal over time.

Table 1 lists the reaction cross sections obtained from the fits to the data in Figure 4 for both half-cycles during the first three ALD cycles. The reaction cross section of the initial TMA half-cycle, σTMA = 2.0 ± 0.2 × 10–18 cm2, was a factor of three lower than that during the steady-growth regime. The corresponding initial sticking probability S0TMA, related to the reaction cross section by S0 = σTMA·θOH, was calculated assuming an absolute −OH surface coverage of 6 × 1014 groups per cm2 for both the −OH-terminated SiO2 and Al2O3 surfaces.51,54 The initial sticking probability of S0TMA = 0.001 indicates that a TMA molecule has on average 1000 interactions with −OH groups on the SiO2 surface before the TMA molecule chemisorbs. The reaction cross section and initial sticking probability of the subsequent TMA half-cycles, σTMA = 6.0 × 10–18 cm2 and S0 = 0.004, were comparable to the reactivity found for the steady-growth regime within the time resolution of the experiment. During the H2O half-cycle, the reaction kinetics did not vary from cycle-to-cycle with a reaction cross section of σH2O = 4.0 ± 0.4 × 10–20 cm2, that is, virtually identical to the kinetics observed for the H2O half-cycle during the steady-growth regime. The corresponding initial sticking probability was Inline graphic, assuming a −CH3 coverage of 6 × 1014 cm–2.34

Table 1. Reaction Cross Sections σTMA and σH2O of the Reactions Taking Place in the TMA and H2O Half-Cyclesa.

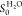starting surf. cycle σTMA (10–18 cm2) S0TMA (10–3) σH2O (10–20 cm2) Inline graphic (10–5)
SiO2 1st 2.0 ± 0.2 1.2 ± 0.1 4.0 ± 0.4 2.4 ± 0.2
SiO2 2nd 6.0 ± 0.6 3.6 ± 0.4 3.9 ± 0.4 2.3 ± 0.2
SiO2 3rd 6.0 ± 0.6 3.6 ± 0.4 4.0 ± 0.4 2.4 ± 0.2
H/Si(111) 1st 3.1 ± 0.3 1.9 ± 0.2    
steady growth ∞ 6.5 ± 0.6 3.9 ± 0.4 3.7 ± 0.4 2.2 ± 0.2
Open in a new tab
a

For the H/Si(111) surface, the first TMA half-cycle was monitored and for the SiO2 surface the first three ALD cycles were followed. The cross sections for the TMA/H2O process during the steady-growth regime are also listed for comparison. For the calculation of the sticking probability S0TMA and 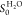Inline graphic, a surface coverage of θOH = θCH3 = 6.0 × 1014 cm–2 and θSiH = 7.8 × 1014 cm–2 was assumed.34,51,52 The “random error” is listed in the table, the systematic error might be larger due to uncertainties in ΓTMA and ΓH2O, but it only introduces a scaling factor and does not affect the trend in the data.

Si–H Coverage during the First TMA Half-Cycle on H/Si(111)

The initial chemisorption of TMA on the H/Si(111) surface was studied with BB-SFG spectroscopy by monitoring the stretching mode of the Si–H groups on the surface. It was not possible to detect the −CH3 groups on the H/Si(111) surface because of less favorable Fresnel coefficients, resulting in a reduced sensitivity on this surface, see also the Supporting Information. A BB-SFG spectrum of the pristine H/Si(111) surface in the vicinity of 2100 cm–1 was collected after the reactor was pumped down. Figure 5 does indeed show a sharp resonance at 2090 cm–1 which is characteristic for the stretch mode of Si–H groups on the H/Si(111) surface. In Fourier transform infrared spectroscopy, the Si–H stretch mode is known for its extremely narrow spectral width of ≈1 cm–1 at room temperature.13,43,47,55,56 The spectral width of the Si–H feature in the BB-SFG spectra is entirely due to the instrumental broadening, see the Supporting Information. To demonstrate repeatability of the BB-SFG measurement and the stability of the surface, a second spectrum is recorded after waiting 120 s. The overlap between the two spectra in Figure 5 shows the excellent repeatability of the measurement. After the collection of the BB-SFG spectra of the pristine surface, the sample was exposed to TMA by opening the ALD valve for a duration of 10 ms. After pumping down the vacuum chamber, a new BB-SFG spectrum was collected that indeed showed a decreased intensity of the Si–H mode. This indicated that TMA had reacted with the Si–H groups, in agreement with the observation of Frank et al.13 Again a second spectrum was collected after 120 s to verify the stability of the surface which showed virtually no change. This entire procedure of dosing TMA for 10 ms and recording two BB-SFG spectra was repeated until the Si–H feature could no longer be discerned resulting in spectra shown in Figure 5.

Figure 5.

Figure 5

Open in a new tab

(i) BB-SFG spectrum of a pristine H/Si(111) surface at 80 °C showing the typical Si–H stretch for this surface situated at 2900 cm–1. In (ii) through (viii) the Si–H signal decreases due to subsequent TMA exposures. The stability of the surface and reproducability of the measurement was verified by the overlap between the spectrum recorded directly after the TMA dose (solid lines) and the spectrum recorded after a dwell time of 120 s (dashed lines).

The Si–H coverage was determined from a fit to the BB-SFG spectra in Figure 5 using the procedure detailed in the previous section. The resulting Si–H coverage was plotted as a function of TMA exposure in Figure 6. An exponential decrease of the Si–H coverage was found as a function of TMA exposure (see also inset in Figure 6). This means that the reaction of TMA with the Si–H surface can be described as a first-order reaction in the TMA flux

graphic file with name la-2019-01600a_m008.jpg 5

where θSiH, is the Si–H coverage. The reaction cross section was determined from the exponential fit to the data in Figure 6. The reaction cross section of TMA chemisorption on H/Si(111) was found to be σTMA = 3.1 × 10–18 cm2 with a corresponding initial sticking probability of S0 = 2 × 10–3 using the TMA flux mentioned earlier and a Si–H density of 7.8 × 1014 cm–2.52 This reaction cross section is slightly smaller than the cross section of the steady-growth regime but larger than the reaction cross section of the initial chemisorption on a SiO2 surface.

Figure 6.

Figure 6

Open in a new tab

Si–H coverage of a H/Si(111) surface as a function of TMA exposure determined from the BB-SFG spectra. The inset shows the same data plotted on a logarithmic scale.

Discussion

The reaction mechanism of the initial growth of Al2O3 ALD on the −OH-terminated SiO2 surface has already been studied qualitative by others from an experimental standpoint and also by ab initio calculations.46,54,57−62 The initial growth on the −OH-terminated SiO2 surface exhibits a similar reaction mechanism as observed during the steady-growth regime involving chemisorption of TMA on −OH groups.54,57 However, alternative reaction paths can become important depending on the density of −OH groups on this surface. Growth on the starting SiO2 surface prepared with a reduced −OH density results in the formation of Si–CH3 groups as has been predicted using density functional theory (DFT) by Sandupatla et al. and observed experimentally by Levrau et al.46,54 The −OH density on a silica surface decreases rapidly when annealing the surface at high temperatures, as shown by Zhuravlev.51 However, the SiO2 surface used in this work was prepared at low temperatures using an oxygen plasma which results in a high −OH coverage; thus, the alternative reactions are not expected to play a prominent role in our work.

For initial growth on the SiO2 surface, a higher GPC was observed by SE during the first ALD cycle. This higher GPC can be explained in part by the higher TMA uptake on this surface seen in the BB-SFG spectra and it is also in line with the observations reported by Levrau et al.46 Turning toward the reaction cross sections determined in this work, the reactivity of Si–OH groups was found to be a factor of 3 lower than that of Al–OH. Bartram et al. reported a sticking probability S0 < 0.01 for chemisorption of TMA on a −OH-terminated silica surface.57 Although hardly a restrictive criterion, the sticking probabilities found in this work are indeed below 0.01 for TMA chemisorption in both the initial regime and steady-growth regime. The experimentally determined reaction cross section can be compared to the activation energy found by DFT. Sandupatla et al. reported an activation energy for TMA chemisorption on −OH-terminated silica of 0.76 eV, whereas Shirazi and Elliott reported an activation energy of 0.28 eV for TMA chemisorption on Al–OH.40,54 This difference in activation energy corresponds to a change in reactivity of a factor of 1.4 assuming Arrhenius behavior, in good agreement with the experimental result.

The surface chemistry of TMA chemisorption on a H/Si(111) has also been studied qualitatively, although to a lesser extent than the SiO2 surface.13,14,19,63,64 The reaction path for the chemisorption of TMA on the H/Si(111) has to be different from the mechanism in the steady-growth regime because of the absence of −OH groups. Frank et al. found O–Al–CH3 species but also Al directly bonded to Si in the form of Si–Al–(CH3)2 after exposing the H/Si(111) surface to TMA.13 They postulate that O from background H2O can insert itself into the Si–Al bond during the TMA half-cycle. On the other hand, a pristine H/Si(111) surface was shown by Frank et al. to be unreactive toward H2O vapor.13 Note that the kinetics of the TMA chemisorption was not discussed in the work by Frank et al. nor did they discuss a full reaction mechanism which would imply certain reaction kinetics.13 From our data, there is no evidence to assume more complex reaction kinetics than a first-order reaction in Si–H. The reaction cross section found for chemisorption of TMA on the H/Si(111) surface was a factor of 2 lower than that during the steady-growth regime. To our knowledge, no other experimental values have been reported. The recent ab initio studies are focused mainly on the H/Si(100) surface which is known to be more reactive than the H/Si(111) surface.19,20 Halls and Raghavachari report an activation energy for TMA chemisorption on H/Si(111) of 1.5 eV which is rather large, suggesting that chemisorption does not take place. However, because of computational limitations at the time, the model and methodology they used to determine activation energy was very basic compared to later modes used by, for example, Shirazi and Elliott and Longo et al. to study the other surfaces.19,40 As has been shown experimentally by us (see Figure 2) and others such as Frank et al.,13 Al2O3 ALD growth does occur on the H/Si(111) surface, and more elaborate DFT simulations would be required to understand the growth on this surface from an ab initio standpoint. A larger surface should be used (>10 Si atoms) giving greater freedom—allowing, for example, dissociative chemisorption of TMA—but also the presence of background H2O should be considered in such a simulation.

The apparent contradiction that the H/Si(111) surface is more reactive than the SiO2 despite showing a significant longer growth delay highlights that there is no universal relation between the reaction cross section and the number of ALD cycles affected by initial growth phenomena. The reaction cross section is a measure of how reactive the precursor is toward a specific surface, but this is only a part of the picture. During the initial growth phase, the type and areal density of the dominant surface groups are changing cycle-by-cycle. The differences in reaction cross section for TMA chemisorption on the two surfaces should be seen in this light. TMA chemisorbs more readily on H/Si(111) than it does on −OH groups on the SiO2 surface. However, the growth mechanism takes longer to reach the steady regime, especially considering the transition from a chemistry without −OH groups to the chemistry of the steady-growth regime which is dominated by TMA chemisorption on −OH sites.

Furthermore, these results show that especially studies providing quantitative insights into the reactions during initial growth are essential to gain a fundamental understanding. Such insights are needed to make systematic advances in, for example, area-selective ALD. Moreover, the comparison of experimental and ab initio results can result in improvements in simulations and steer experiments.

Conclusions

The subtle differences in the surface chemistry and reaction kinetics during the initial growth of Al2O3 by thermal ALD on the SiO2 surface and H/Si(111) surface were studied with in situ BB-SFG spectroscopy and spectroscopy ellipsometry.

For the SiO2 surface, the reaction cross section—and as a result the related initial sticking probability—of TMA chemisorption on the pristine SiO2 was found to be a factor of 3 lower than the reaction cross section of the steady-growth regime. For all subsequent TMA half-cycles and for all H2O half-cycles, the cross section was equal to that of its stead-state counterpart. Moreover, a higher GPC was observed by SE in the first cycle that can be directly linked to a higher TMA uptake, as is evidenced by the BB-SFG spectra.

The chemisorption of TMA onto the H/Si(111) surface during the first TMA half-cycle showed a smaller reaction cross section than that during the steady-growth regime. With in situ SE, immediate growth was observed, however, the first ∼20 cycles showed a lower GPC with respect to the steady regime. This is in line with the drastic change in surface chemistry that has to occur going from the initial growth regime in the first cycle to the steady-growth regime.

These results demonstrate that BB-SFG spectroscopy is well suited to study the initial growth of ALD revealing quantitative information such as the reaction cross sections and that it can easily be applied to other ALD processes of interest.

Acknowledgments

The authors thank J. J. A. Zeebrechts, J. J. L. M. Meulendijks, C. van Helvoirt, and C. O. van Bommel for their technical support. This work was supported by the Dutch Technology Foundation STW and the Netherlands Organization for scientific Research (NWO, VICI Program on “Nanomanufacturing”).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.langmuir.9b01600.

  • Nonresonant suppression in BB-SFG spectroscopy, spectral width of the Si–H stretch mode, influence of the (linear) optical properties of the sample/SiO2 film on the sensitivity of BB-SFG, and more detailed discussion on how to calculate the GPC from the subcycle SE data (PDF)

The authors declare no competing financial interest.

Supplementary Material

la9b01600_si_001.pdf (297.3KB, pdf)

References

  1. George S. M. Atomic layer deposition: an overview. Chem. Rev. 2010, 110, 111–131. 10.1021/cr900056b. [DOI] [PubMed] [Google Scholar]
  2. Choi J. H.; Mao Y.; Chang J. P. Development of hafnium based high-k materials - A review. Mater. Sci. Eng., R 2011, 72, 97–136. 10.1016/j.mser.2010.12.001. [DOI] [Google Scholar]
  3. Robertson J.; Wallace R. M. High-K materials and metal gates for CMOS applications. Mater. Sci. Eng., R 2015, 88, 1–41. 10.1016/j.mser.2014.11.001. [DOI] [Google Scholar]
  4. Mackus A. J. M.; Mulders J. J. L.; van de Sanden M. C. M.; Kessels W. M. M. Local deposition of high-purity Pt nanostructures by combining electron beam induced deposition and atomic layer deposition. J. Appl. Phys. 2010, 107, 116102. 10.1063/1.3431351. [DOI] [Google Scholar]
  5. Weber M. J.; MacKus A. J. M.; Verheijen M. a.; Van Der Marel C.; Kessels W. M. M. Supported core/shell bimetallic nanoparticles synthesis by atomic layer deposition. Chem. Mater. 2012, 24, 2973–2977. 10.1021/cm301206e. [DOI] [Google Scholar]
  6. van Delft J. a.; Garcia-Alonso D.; Kessels W. M. M. Atomic layer deposition for photovoltaics: applications and prospects for solar cell manufacturing. Semicond. Sci. Technol. 2012, 27, 074002. 10.1088/0268-1242/27/7/074002. [DOI] [Google Scholar]
  7. Hoex B.; Gielis J. J. H.; van de Sanden M. C. M.; Kessels W. M. M. On the c-Si surface passivation mechanism by the negative-charge-dielectric Al2O3. J. Appl. Phys. 2008, 104, 113703. 10.1063/1.3021091. [DOI] [Google Scholar]
  8. Rai V. R.; Vandalon V.; Agarwal S. Influence of surface temperature on the mechanism of atomic layer deposition of aluminum oxide using an oxygen plasma and ozone. Langmuir 2012, 28, 350–357. 10.1021/la201136k. [DOI] [PubMed] [Google Scholar]
  9. Sperling B. a.; Hoang J.; Kimes W. A.; Maslar J. E. Time-resolved surface infrared spectroscopy during atomic layer deposition. Appl. Spectrosc. 2013, 67, 1003–1012. 10.1366/13-06995. [DOI] [PubMed] [Google Scholar]
  10. Langereis E.; Keijmel J.; van de Sanden M. C. M.; Kessels W. M. M. Surface chemistry of plasma-assisted atomic layer deposition of Al2O3 studied by infrared spectroscopy. Appl. Phys. Lett. 2008, 92, 231904. 10.1063/1.2940598. [DOI] [Google Scholar]
  11. Elam J. W.; Routkevitch D.; Mardilovich P. P.; George S. M. Conformal coating on ultrahigh-aspect-ratio nanopores of anodic alumina by atomic layer deposition. Chem. Mater. 2003, 15, 3507–3517. 10.1021/cm0303080. [DOI] [Google Scholar]
  12. Yanguas-Gil A.; Libera J. a.; Elam J. W. Modulation of the Growth Per Cycle in Atomic Layer Deposition Using Reversible Surface Functionalization. Chem. Mater. 2013, 25, 4849–4860. 10.1021/cm4029098. [DOI] [Google Scholar]
  13. Frank M. M.; Chabal Y. J.; Wilk G. D. Nucleation and interface formation mechanisms in atomic layer deposition of gate oxides. Appl. Phys. Lett. 2003, 82, 4758. 10.1063/1.1585129. [DOI] [Google Scholar]
  14. Frank M. M.; Chabal Y. J.; Green M. L.; Delabie A.; Brijs B.; Wilk G. D.; Ho M.-Y.; da Rosa E. B. O.; Baumvol I. J. R.; Stedile F. C. Enhanced initial growth of atomic-layer-deposited metal oxides on hydrogen-terminated silicon. Appl. Phys. Lett. 2003, 83, 740. 10.1063/1.1595719. [DOI] [Google Scholar]
  15. Halls M. D.; Raghavachari K.; Frank M.; Chabal Y. Atomic layer deposition of Al2O3 on H-passivated Si: Al(CH3)2OH surface reactions with H/Si(100)-2×1. Phys. Rev. B: Condens. Matter Mater. Phys. 2003, 68, 161302. 10.1103/physrevb.68.161302. [DOI] [Google Scholar]
  16. Li M.; Dai M.; Chabal Y. J. Atomic layer deposition of aluminum oxide on carboxylic acid-terminated self-assembled monolayers. Langmuir 2009, 25, 1911–1914. 10.1021/la803581k. [DOI] [PubMed] [Google Scholar]
  17. Halls M. D.; Raghavachari K. Atomic layer deposition of Al2O3 on H-passivated Si. I. Initial surface reaction pathways with H/Si(100)-2×1. J. Chem. Phys. 2003, 118, 10221–10226. 10.1063/1.1571513. [DOI] [Google Scholar]
  18. Wilson C. A.; Grubbs R. K.; George S. M. Nucleation and Growth during Al2O3 Atomic Layer Deposition on Polymers. Chem. Mater. 2005, 17, 5625–5634. 10.1021/cm050704d. [DOI] [Google Scholar]
  19. Longo R. C.; Owen J. H. G.; McDonnell S.; Dick D.; Ballard J. B.; Randall J. N.; Wallace R. M.; Chabal Y. J.; Cho K. Toward Atomic-Scale Patterned Atomic Layer Deposition: Reactions of Al2O3 Precursors on a Si(001) Surface with Mixed Functionalizations. J. Phys. Chem. C 2016, 120, 2628–2641. 10.1021/acs.jpcc.5b09053. [DOI] [Google Scholar]
  20. Ghosh M. K.; Choi C. H. The initial mechanisms of Al2O3 atomic layer deposition on OH/Si(1 0 0)-2 ×1 surface by tri-methylaluminum and water. Chem. Phys. Lett. 2006, 426, 365–369. 10.1016/j.cplett.2006.05.126. [DOI] [Google Scholar]
  21. Elam J. W.; George S. M. Growth of ZnO/Al2O3 alloy films using atomic layer deposition techniques. Chem. Mater. 2003, 15, 1020–1028. 10.1021/cm020607+. [DOI] [Google Scholar]
  22. Wu Y.; Potts S. E.; Hermkens P. M.; Knoops H. C. M.; Roozeboom F.; Kessels W. M. M. Enhanced doping efficiency of al-doped ZnO by atomic layer deposition using dimethylaluminum isopropoxide as an alternative aluminum precursor. Chem. Mater. 2013, 25, 4619–4622. 10.1021/cm402974j. [DOI] [Google Scholar]
  23. Mackus A. J. M.; MacIsaac C.; Kim W.-H.; Bent S. F. Incomplete elimination of precursor ligands during atomic layer deposition of zinc-oxide, tin-oxide, and zinc-tin-oxide. J. Chem. Phys. 2017, 146, 052802. 10.1063/1.4961459. [DOI] [PubMed] [Google Scholar]
  24. Mackus A. J. M.; Merkx M. J. M.; Kessels W. M. M. From the Bottom-Up: Toward Area-Selective Atomic Layer Deposition with High Selectivity. Chem. Mater. 2019, 31, 2–12. 10.1021/acs.chemmater.8b03454. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Mameli A.; Karasulu B.; Verheijen M. A.; Barcones B.; Macco B.; Mackus A. J. M.; Kessels W. M. M. E.; Roozeboom F. Area-Selective Atomic Layer Deposition of ZnO by Area Activation Using Electron Beam-Induced Deposition. Chem. Mater. 2019, 31, 1250–1257. 10.1021/acs.chemmater.8b03165. [DOI] [Google Scholar]
  26. Mak K. F.; Lee C.; Hone J.; Shan J.; Heinz T. F. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 2010, 105, 136805. 10.1103/physrevlett.105.136805. [DOI] [PubMed] [Google Scholar]
  27. Dillon A. C.; Ott A. W.; Way J. D.; George S. M. Surface chemistry of Al2O3 deposition using Al(CH3)3 and H2O in a binary reaction sequence. Surf. Sci. 1995, 322, 230–242. 10.1016/0039-6028(95)90033-0. [DOI] [Google Scholar]
  28. Ott A. W.; McCarley K. C.; Klaus J. W.; Way J. D.; George S. M. Atomic layer controlled deposition of Al2O3 films using binary reaction sequence chemistry. Appl. Surf. Sci. 1996, 107, 128–136. 10.1016/s0169-4332(96)00503-x. [DOI] [Google Scholar]
  29. Bosch R. H. E. C.; Bloksma F. L.; Huijs J. M. M.; Verheijen M. A.; Kessels W. M. M. Surface Infrared Spectroscopy during Low Temperature Growth of Supported Pt Nanoparticles by Atomic Layer Deposition. J. Phys. Chem. C 2016, 120, 750. 10.1021/acs.jpcc.5b10839. [DOI] [Google Scholar]
  30. Rahtu A.; Alaranta T.; Ritala M. In Situ Quartz Crystal Microbalance and Quadrupole Mass Spectrometry Studies of Atomic Layer Deposition of Aluminum Oxide from Trimethylaluminum and Water. Langmuir 2001, 17, 6506–6509. 10.1021/la010103a. [DOI] [Google Scholar]
  31. Erkens I. J. M.; Mackus a. J. M.; Knoops H. C. M.; Smits P.; van de Ven T. H. M.; Roozeboom F.; Kessels W. M. M. Mass Spectrometry Study of the Temperature Dependence of Pt Film Growth by Atomic Layer Deposition. ECS J. Solid State Sci. Technol. 2012, 1, P255–P262. 10.1149/2.006206jss. [DOI] [Google Scholar]
  32. Elam J. W.; Groner M. D.; George S. M. Viscous flow reactor with quartz crystal microbalance for thin film growth by atomic layer deposition. Rev. Sci. Instrum. 2002, 73, 2981. 10.1063/1.1490410. [DOI] [Google Scholar]
  33. Aaltonen T.; Rahtu A.; Ritala M.; Leskelä M. Reaction Mechanism Studies on Atomic Layer Deposition of Ruthenium and Platinum. Electrochem. Solid-State Lett. 2003, 6, C130. 10.1149/1.1595312. [DOI] [Google Scholar]
  34. Ott A. W.; Klaus J. W.; Johnson J. M.; George S. M. Al3O3 thin film growth on Si(100) using binary reaction sequence chemistry. Thin Solid Films 1997, 292, 135–144. 10.1016/s0040-6090(96)08934-1. [DOI] [Google Scholar]
  35. Vandalon V.; Kessels W. M. M. What is limiting low-temperature atomic layer deposition of Al2O3? A vibrational sum-frequency generation study. Appl. Phys. Lett. 2016, 108, 011607. 10.1063/1.4939654. [DOI] [Google Scholar]
  36. Vandalon V.; Kessels W. M. M. Revisiting the growth mechanism for atomic layer deposition of Al2O3 : a vibrational sum-frequency generation study. J. Vac. Sci. Technol., A 2017, 35, 05C313. 10.1116/1.4993597. [DOI] [Google Scholar]
  37. Mitsui T.; Hill E.; Curtis R.; Ganz E. Initial stages of Al growth from dimethylaluminum hydride on silicon. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 8123–8127. 10.1103/physrevb.59.8123. [DOI] [Google Scholar]
  38. Gakis G. P.; Vergnes H.; Scheid E.; Vahlas C.; Boudouvis A. G.; Caussat B. Detailed investigation of the surface mechanisms and their interplay with transport phenomena in alumina atomic layer deposition from TMA and water. Chem. Eng. Sci. 2019, 195, 399–412. 10.1016/j.ces.2018.09.037. [DOI] [Google Scholar]
  39. Lownsbury J. M.; Gladden J. A.; Campbell C. T.; Kim I. S.; Martinson A. B. F. Direct Measurements of Half-Cycle Reaction Heats during Atomic Layer Deposition by Calorimetry. Chem. Mater. 2017, 29, 8566. 10.1021/acs.chemmater.7b01491. [DOI] [Google Scholar]
  40. Shirazi M.; Elliott S. D. Cooperation between adsorbates accounts for the activation of atomic layer deposition reactions. Nanoscale 2015, 7, 6311–6318. 10.1039/c5nr00900f. [DOI] [PubMed] [Google Scholar]
  41. Weckman T.; Laasonen K. First principles study of the atomic layer deposition of alumina by TMA-H2O-process. Phys. Chem. Chem. Phys. 2015, 17, 17322–17334. 10.1039/c5cp01912e. [DOI] [PubMed] [Google Scholar]
  42. Arts K.; Vandalon V.; Puurunen R. L.; Utriainen M.; Gao F.; Kessels W. M. M.; Knoops H. C. M. Sticking probabilities of H2O and Al(CH3)3 during atomic layer deposition of Al2O3 extracted from their impact on film conformality. J. Vac. Sci. Technol., A 2019, 37, 030908. 10.1116/1.5093620. [DOI] [Google Scholar]
  43. Tully J. C.; Chabal Y. J.; Raghavachari K.; Bowman J. M.; Lucchese R. R. Infrared linewidths and vibrational lifetimes at surfaces: H on Si(100). Phys. Rev. B: Condens. Matter Mater. Phys. 1985, 31, 1184–1186. 10.1103/physrevb.31.1184. [DOI] [PubMed] [Google Scholar]
  44. Deal B. E. The Current Understanding of Charges in the Thermally Oxidized Silicon Structure. J. Electrochem. Soc. 1974, 121, 198C. 10.1149/1.2402380. [DOI] [Google Scholar]
  45. Grunthaner F. J.; Grunthaner P. J. Chemical and electronic structure of the SiO 2/Si interface. Mater. Sci. Rep. 1986, 1, 65–160. 10.1016/s0920-2307(86)80001-9. [DOI] [Google Scholar]
  46. Levrau E.; Van De Kerckhove K.; Devloo-Casier K.; Pulinthanathu Sree S.; Martens J. A.; Detavernier C.; Dendooven J. In situ IR spectroscopic investigation of alumina ALD on porous silica films: Thermal versus plasma-enhanced ALD. J. Phys. Chem. C 2014, 118, 29854–29859. 10.1021/jp5088288. [DOI] [Google Scholar]
  47. Higashi G. S.; Chabal Y. J.; Trucks G. W.; Raghavachari K. Ideal hydrogen termination of the Si (111) surface. Appl. Phys. Lett. 1990, 56, 656. 10.1063/1.102728. [DOI] [Google Scholar]
  48. Boyd R. W.Nonlinear Optics, 2; Elsevier Science Publishing Co Inc., 1992. [Google Scholar]
  49. van Hemmen J. L.; Heil S. B. S.; Klootwijk J. H.; Roozeboom F.; Hodson C. J.; van de Sanden M. C. M.; Kessels W. M. M. Plasma and Thermal ALD of Al2O3 in a Commercial 200 mm ALD Reactor. J. Electrochem. Soc. 2007, 154, G165. 10.1149/1.2737629. [DOI] [Google Scholar]
  50. Langereis E.; Heil S. B. S.; Knoops H. C. M.; Keuning W.; van de Sanden M. C. M.; Kessels W. M. M. In situ spectroscopic ellipsometry as a versatile tool for studying atomic layer deposition. J. Phys. D: Appl. Phys. 2009, 42, 073001. 10.1088/0022-3727/42/7/073001. [DOI] [Google Scholar]
  51. Zhuravlev L. T. Concentration of hydroxyl groups on the surface of amorphous silicas. Langmuir 1987, 3, 316–318. 10.1021/la00075a004. [DOI] [Google Scholar]
  52. Dinger A.; Lutterloh C.; Küppers J. Interaction of hydrogen atoms with Si(111) surfaces: Adsorption, abstraction, and etching. J. Chem. Phys. 2001, 114, 5338. 10.1063/1.1351158. [DOI] [Google Scholar]
  53. Higashi G. S.; Fleming C. G. Sequential surface chemical-reaction limited growth of high-quality Al2O3 dielectrics. Appl. Phys. Lett. 1989, 55, 1963–1965. 10.1063/1.102337. [DOI] [Google Scholar]
  54. Sandupatla A. S.; Alexopoulos K.; Reyniers M.-F.; Marin G. B. DFT Investigation into Alumina ALD Growth Inhibition on Hydroxylated Amorphous Silica Surface. J. Phys. Chem. C 2015, 119, 18380–18388. 10.1021/acs.jpcc.5b05261. [DOI] [Google Scholar]
  55. Dumas P.; Chabal Y. J.; Higashi G. S. Coupling of an adsorbate vibration to a substrate surface phonon: H on Si(111). Phys. Rev. Lett. 1990, 65, 1124–1127. 10.1103/physrevlett.65.1124. [DOI] [PubMed] [Google Scholar]
  56. Jakob P.; Chabal Y. L.; Raghavachari K. Lineshape analysis of the Si-H stretching mode of the ideally H-terminated Si(111) surface: the role of dynamical dipole coupling. Chem. Phys. Lett. 1991, 187, 325–333. 10.1016/0009-2614(91)90433-a. [DOI] [Google Scholar]
  57. Bartram M. E.; Michalske T. A.; Rogers J. W. A reexamination of the chemisorption of trimethylaluminum on silica. J. Phys. Chem. 1991, 95, 4453–4463. 10.1021/j100164a054. [DOI] [Google Scholar]
  58. Puurunen R. L.; Root A.; Haukka S.; Iiskola E. I.; Lindblad M.; Krause A. O. I. IR and NMR Study of the Chemisorption of Ammonia on Trimethylaluminum-Modified Silica. J. Phys. Chem. B 2000, 104, 6599–6609. 10.1021/jp000454i. [DOI] [Google Scholar]
  59. Puurunen R. L.; Root A.; Sarv P.; Haukka S.; Iiskola E. I.; Lindblad M.; Krause A. O. I. Growth of aluminium nitride on porous silica by atomic layer chemical vapour deposition. Appl. Surf. Sci. 2000, 165, 193–202. 10.1016/s0169-4332(00)00440-2. [DOI] [Google Scholar]
  60. Puurunen R. L. Correlation between the growth-per-cycle and the surface hydroxyl group concentration in the atomic layer deposition of aluminum oxide from trimethylaluminum and water. Appl. Surf. Sci. 2005, 245, 6–10. 10.1016/j.apsusc.2004.10.003. [DOI] [Google Scholar]
  61. Puurunen R. L. Surface chemistry of atomic layer deposition: A case study for the trimethylaluminum/water process. J. Appl. Phys. 2005, 97, 121301. 10.1063/1.1940727. [DOI] [Google Scholar]
  62. Widjaja Y.; Musgrave C. B. Quantum chemical study of the mechanism of aluminum oxide atomic layer deposition. Appl. Phys. Lett. 2002, 80, 3304–3306. 10.1063/1.1473237. [DOI] [Google Scholar]
  63. Halls M. D.; Raghavachari K. Importance of Steric Effects in Cluster Models of Silicon Surface Chemistry: ONIOM Studies of the Atomic Layer Deposition (ALD) of Al2O3 on H/Si(111). J. Phys. Chem. A 2004, 108, 2982–2987. 10.1021/jp037014m. [DOI] [Google Scholar]
  64. Halls M. D.; Raghavachari K. Atomic Layer Deposition Growth Reactions of Al 2 O 3 on Si(100)-2×1. J. Phys. Chem. B 2004, 108, 4058–4062. 10.1021/jp0378079. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

la9b01600_si_001.pdf (297.3KB, pdf)

Articles from Langmuir are provided here courtesy of American Chemical Society

RESOURCES