Abstract
Relationships between interaction energy (Eint) and electron density properties at the X···X bond critical point or the d(X···X) distance were established for the large set of structures [(A)nY–X···X–Z(B)m] bearing the halogen bonds Cl···Cl, Br···Br, and I···I (640 structures in total). The best estimator of Eint is the kinetic energy density (Gb), which reasonably approximates the whole set of the structures as −Eint = 0.128Gb2 − 0.82Gb + 1.66 (R2 = 0.91, mean absolute deviation 0.39 kcal/mol) and demonstrates low dispersion. The potential and kinetic energy densities, electron density, and the d(X···X) distance behave similarly as estimators of Eint for the individual series Cl···Cl, Br···Br, and I···I. A number of the Eint(property) correlations are recommended for the practical application in the express estimates of the strength of the homo-halogen bonds.
Keywords: bond critical point properties, interaction energy, bond energy, bond strength, density functional theory, electron density, energy density, halogen bond, QTAIM
1. Introduction
Halogen bonds (XBs) belong to the most important type of non-covalent interactions (apart from hydrogen bonds) [1,2,3,4,5,6,7,8,9,10,11]. XB is usually formulated as an interaction of the Y–Hal···X–Z type where Hal is a halogen atom (Lewis acid, XB donor) bearing a region with the positive electrostatic potential directed toward the X atom (the co-called σ-hole) and X is a donor of electron density (Lewis base, XB acceptor) (X = N, O, S, Se, Hal, Hal−, etc.). Halogen bonds play a very important role in molecular recognition and crystal engineering, synthesis of functional solid materials [12,13,14,15,16,17,18,19,20,21,22], and drug design [23,24,25]. They have a broad application in the tuning of useful functional properties such as redox, magnetic [26,27], or catalytic [28,29,30] properties, and nonlinear optical (NLO) activity [31,32]. Non-covalent interactions, including XB, are involved in the control of various biochemical processes participating in the organization of the secondary, tertiary, and quaternary protein structures [33,34,35,36,37].
One of the most important characteristics of XB controlling its functional properties is the halogen bond energy (EXB). Experimental determination of EXB is usually associated with significant technical issues [38,39], while its direct theoretical calculations are not always possible or reliable (e.g., for the intramolecular XBs or molecular associates involving several non-covalent interactions, Watson-Crick base pairs being among them). One of the most attractive and sometimes the only possible methods of the approximate express estimate of the bond energy for weak interactions is the application of appropriate EXB(property) correlations [40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87]. This method has got an impulse after the publication of an article by Espinosa, Molins, and Lecomte [88]. It was found that the interaction energy (Eint) of hydrogen bonds of the X–H···O type correlates with the potential energy density at the bond critical point (BCP) of the electron density distribution, Vb, as Equation (1)
| Eint ≈ 0.5Vb | (1) |
(the co-called EML formula, the interaction energy between two fragments A and B is defined as Eint = EA–B − E{A} − E{B}, where EA–B is energy of the fully optimized molecule A–B, E{A}, and E{B} are energies of the fragments A and B with unrelaxed geometries corresponding to the equilibrium structure A–B).
Later, similar relationships between Eint and Vb or kinetic energy density at BCP (Gb) were deduced for the FH···FR hydrogen bonds [89,90] (Equation (2)) and for the Y–Hal···Z(B)m halogen bonds (Hal = Cl, Br, I; Z = N, S, O, C) [79] (Equations (3)–(5)).
| Eint ≈ −0.429Gb | (2) |
| Eint ≈ 0.49Vb ≈ −0.47Gb, for Hal = Cl | (3) |
| Eint ≈ 0.58Vb ≈ −0.57Gb, for Hal = Br | (4) |
| Eint ≈ 0.68Vb ≈ −0.67Gb, for Hal = I. | (5) |
Since the publication of the EML formula, numerous but usually not justified attempts to apply this relationship to different types of non-covalent interactions were undertaken. However, it was shown that these equations may not be universal, and their validity may be restricted only to the type of interactions for which they were deduced [91,92]. Thus, there is a great practical need to establish the reliable Eint(property) relationships for the most important types of non-covalent interactions others than the X–H···O, FH···FR, and Y–Hal···Z(B)m ones.
Recently, the author started the project aimed to establish the Eint(property) relationships for various types of non-covalent interactions. In the first publication of this research cycle [92], the halogen bonds of the [(A)nZ–Y···X]− type (X, Y = F, Cl, Br; Z = F, Cl, Br, I, C, N, O, H, S, P, Si, B, totally 441 structure) formed upon interaction of the neutral fragment (A)nZ–Y and the halide anion X− were considered. It was shown that the Eint(property) correlations are different for each particular type of the Y···X− interaction and they are also different from Equations (1)–(4). Several Eint(property) relationships practically important for express estimates of the interaction energy were recommended for each series of these structures.
In this work, the Eint(property) relationships are analyzed for the homo-halogen bonds of the [(A)nY–X···X–Z(B)m] type formed upon the interaction of two neutral fragments (A)nY–X and X–Z(B)m (X = Cl, Br, I; Y, Z = F, Cl, Br, C, N, O, H, S, P, Si, B). For the first time, the Eint(property) relationships were deduced for the Cl···Cl, Br···Br, and I···I homo-XBs based on a large, statistically significant set of structures (640 structures in total).
2. Computational Details
Full geometry optimization and energy calculations of all structures were carried out at the DFT level of theory by using the M06-2X functional [93] with the help of the Gaussian 09 [94] program package applying the tight optimization criteria and ultrafine integration grid. Cartesian d and f basis functions (6d, 10f) were used in all calculations. The M06-2X function reasonably describes weak dispersion forces and is widely and successfully used for the treatment of structures with non-covalent interactions. It was shown by Kozuch and Martin [95] for a set of 51 structures bearing XBs that the root-mean-square deviation, the mean signed error, and the maximum error of dissociation energy for M06-2X are 0.43, 0.01, and 1.58 kcal/mol, respectively, relative to the CCSD(T) method. Additionally, it was shown [92] that the Eint(Vb) correlation for structures of the [(A)nZ–Y···F]− type (Y = F, Cl, Br) at the M06-2X level of theory has similar parameters as that for the MP4, CCSD, and CCSD(T) methods (see Figure 7A in [90]).
Molecular systems of the medium and large dimension are usually computationally treated using double zeta quality basis sets with corresponding diffuse and polarization functions. Therefore, to ensure that the results of this work may be successfully transferred to larger molecular systems, the 6-31+G* basis set was used for structures of the Cl···Cl and Br···Br types and the all electron DZP basis set [96,97,98] was applied for all atoms of the I···I structures. Previously [92], it was shown that the 6-31+G* basis set performs similarly to the much more extended triple zeta basis set 6-311++G(3df,3pd) in the direct calculations of Eint and the electron density based properties of the [(A)nZ–Y···F]− structures. Coefficients of the Eint(Vb) correlations obtained for these two basis sets are also similar (see Figures 5C, 6C, and 7D in [90]). Meanwhile, the effect of the computational method and basis set is worthwhile to investigate but this should be the subject of separate work.
The Hessian matrix was calculated for all optimized structures to prove the location of correct minima. No symmetry operations were applied during the calculations. The stability test was performed and the stable solutions were achieved for all structures using the keyword STABLE(OPT). BSSE was corrected using the counterpoise (CP) method [99,100]. A detailed discussion of the BSSE effect for each Cl···Cl, Br···Br, and I···I series is provided in the Supplementary Material. The topological analysis of the electron density distribution was performed with the help of the AIM method developed by Bader [101] using the AIMAll program [102].
3. Computational Models
For this study, structures [(A)nY–X···X–Z(B)m] (X = Cl, Br, I; Y, Z = F, Cl, Br, C, N, O, H, S, P, Si, B) bearing the homo-halogen bonds Cl···Cl, Br···Br, and I···I and formed upon interaction of two neutral fragments (A)nY–X and X–Z(B)m were selected as computational models (640 structures in total, among them 210 structures of the Cl···Cl type, 216 structures of the Br···Br type, and 214 structures of the I···I type). In this work, the fragment (A)nY–X (at the left side of the complex formula) corresponds to the XB donor and the fragment X–Z(B)m (at the right side of the complex formula) corresponds to the XB acceptor.
For each type of halogen bonds, three series were considered, i.e., [(A)nY–X···X–F], [(A)nY–X···X–H], and [F–X···X–Z(B)m]. In the first two series, the XB donor part is variable while the XB acceptor part is fixed with the Z(B)m group being either a strong electron acceptor (Z(B)m = F) or an electron donor (Z(B)m = H). Series of the structures with even stronger electron donor groups Z(B)m = CMe3, CHMe2, or CH3 were also calculated. However, in most of cases, secondary X···H–C interactions were found and, therefore, the individual X···X halogen bonds cannot be isolated for the analysis.
In the third series, [F–X···X–Z(B)m], the XB acceptor part is variable whereas the XB donor part is fixed ((A)nY = F). Most of the attempts to calculate similar series with an electron donor group (A)nY = H failed because the σ-hole at the terminal X atom of the XB donor is not sufficiently pronounced in this case, and other interactions prevail in the resulting structures.
Ninety various groups (A)nY or Z(B)m were considered to analyze the effect of the second-order atoms Y and Z and remote groups A and B as well as the effects of the orbital hybridization and the oxidation state of the Y and Z atoms on the Eint(property) correlations. The groups A and B vary from strong electron donors to strong electron acceptors to ensure a broad interval of the interaction energies within each series (see Table S1 in the Supplementary Material for the complete list of the calculated structures).
There are two typical geometries of the fragments with halogen bonds [103]. The first one is characterized by the similar (or equal) angles θ (θ1 ≈ θ2) (type I, Figure 1). The second geometry corresponds to θ1 ≈ 180° and θ2 ≈ 90° (type II, Figure 1). In this work, only structures of type II are discussed since they are typically more stable than structures of type I. Indeed, 54 structures of type II and only 14 structures of type I were successfully optimized for the [(A)nY–Cl···Cl–H] series (90 various (A)nY groups were considered, Table S1).
Figure 1.
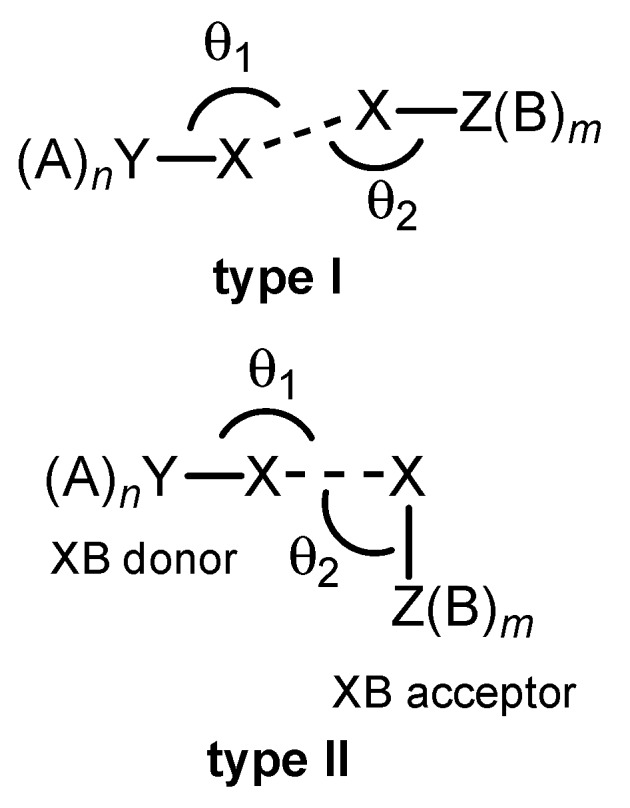
Two types of the halogen bond geometries.
Only structures which have no other contacts shorter than the sum of van der Waals radii between the (A)nY–X and X–Z(B)m fragments, apart from the X···X one, are included in the analysis. Additionally, only structures with θ2 ≥ 70° were analyzed because, in those with θ2 < 70°, the X···Z interaction may play a significant or even a predominant role compared to the X···X interaction (Sixty eight structures of the [F–X···X–Z(B)m] type with the X···Z contact shorter the sum of van der Waals radii but with θ2 ≥ 70° and with no other weak interactions were included in the analysis since no BCPs for the X···Z contacts were found). Effect of the angle θ2 on the correlations under study is discussed in Section 4.6. “Effect of angle θ2”.
Further in this work, the series [(A)nY–Cl···Cl–Z(B)m], [(A)nY–Br···Br–Z(B)m], and [(A)nY–I···I–Z(B)m] are called “large”, while the series [(A)nY–Cl···Cl–H], [(A)nY–Cl···Cl–F], [F–Cl···Cl–Z(B)m], [(A)nY–Br···Br–H], [(A)nY–Br···Br–F], [F–Br···Br–Z(B)m], [(A)nY–I···I–H], [(A)nY–I···I–F], and [F–I···I–Z(B)m] are called “small” series.
4. Results and Discussion
The calculated X···X interaction energy with the BSSE correction in the whole set of the structures varies from 0.34 to −9.24 kcal/mol. All three types of halogen bonds, Cl···Cl, Br···Br, and I···I, have comparable strengths. The dispersion of Eint increases along the row X = Cl < Br < I (−0.18 to −5.01, 0.08 to −7.10, and 0.34 to −9.24 kcal/mol, respectively). The Cl···Cl interaction is slightly weaker than the corresponding Br···Br and I···I bonds for the [(A)nY–X···X–H] and [F–X···X–Z(B)m] series (Table S2 in the Supplementary Material). The halogen bonds in the series [F–X···X–Z(B)m] are the strongest ones while the XBs in the series [(A)nY–X···X–F] are typically the weakest bonds.
In the next sections, the Eint(property) relationships are considered for each estimator [i.e., the electron density, ρb, its Laplacian, ∇2ρb, the curvature of ρ(r) which is parallel to the bond path direction (positive), λ||,b, potential, kinetic, and total energy densities, V, Gb, and Hb and the X···X distance, d(X···X)] within the whole set and various series of the structures.
4.1. Whole Set of Structures
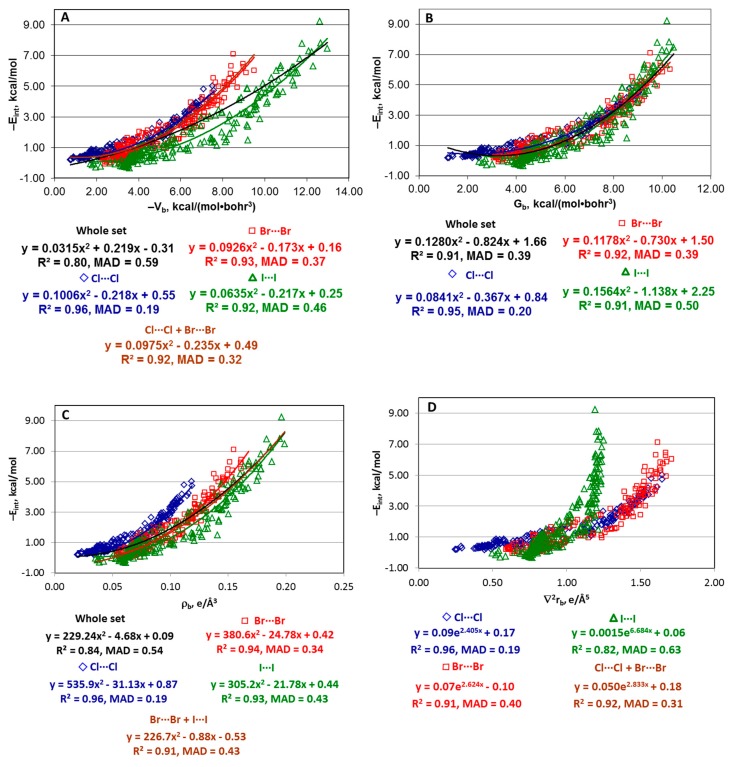
Potential energy density at BCP (Vb). A rough correlation between Eint and the potential energy density at the X···X BCP is observed for the whole set of the structures (Figure 2A). Very curiously, this dependence is obviously nonlinear and may be approximated with the similar quality by either a quadratic or an exponential function −Eint = 0.0315Vb2 − 0.219Vb − 0.31 or −Eint = 3.67e−0.09Vb − 4.19. Such behavior is unusual since most of the Eint(Vb) correlations reported in literature obey a linear law. The R2 values (0.80) indicate that the correlations are of rather poor quality. Meanwhile, the mean absolute deviation (MAD) for these fittings is ~0.60 kcal/mol. This value is well within the typical accuracy of the DFT methods (several kcal/mol) and this is almost three times less than the average interaction energy for this structural set (1.72 kcal/mol).
Figure 2.
Plots of −Eint against −Vb (A), Gb (B), ρb (C), ∇2ρb (D), λ||,b (E), Hb (F), and d(X···X) (G) for the whole set of the structures [(A)nY–X···X–Z(B)m] and the “large” series [(A)nY–Cl···Cl–Z(B)m], [(A)nY–Br···Br–Z(B)m], and [(A)nY–I···I–Z(B)m].
Thus, in the case of structures [(A)nY–X···X–Z(B)m] with the homo-halogen bonds formed upon interaction of the neutral fragment, Eint may be roughly estimated from Vb using a single formula for all X = Cl, Br, and I. This situation is very different from that found recently for the set of anionic structures [(A)nZ–Y···X]− (Y, X = F, Cl, Br) [92]. In the latter case, the Eint(Vb) relationship is much more sensitive to the nature of the interacting X and Y atoms, and there is no single dependence which could approximate Eint through Vb for the whole set.
Kinetic energy density at BCP (Gb). The quadratic and exponential relationships between Eint and Gb (−Eint = 0.1280Gb2 − 0.824Gb + 1.66 and − Eint = 0.144e0.39Gb − 0.13) display significantly lower dispersion and have noticeably better quality than the Eint(Vb) dependence (Figure 2B). The R2 value is quite reasonable (0.91) and MAD is 0.39 and 0.40 kcal/mol that is more than four times lower than the average interaction energy for this structural set (1.72 kcal/mol). Thus, the kinetic energy density at BCP is a better estimator of Eint compared to Vb, and a single function may be used for the reasonable approximation of interaction energy for the whole set of structures bearing the homo-halogen bonds Cl···Cl, Br···Br, and I···I. Meanwhile, both Eint(Vb) and Eint(Gb) correlations found here, being strongly nonlinear, are qualitatively different from the EML formula and other relationships published in the literature for other types of non-covalent interactions (Equations (1)–(5)) [79,88,89,90].
Electron density at BCP (ρb). The correlation of Eint against ρb is also clearly nonlinear that is different from most of the cases reported in the literature. Quality of the Eint(ρb) relationship is intermediate between the Eint(Vb) and Eint(Gb) dependencies (Figure 2C).
Other estimators. There are no single Eint(property) trends for other estimators [∇2ρb, λ||,b, Hb, and d(X···X)] which could describe the whole set of structures. At least two various dependencies are clearly visible on each Eint(property) plot (Figure 2D–G).
4.2. Series [(A)nY–Cl···Cl–Z(B)m], [(A)nY–Br···Br–Z(B)m], and [(A)nY–I···I–Z(B)m]
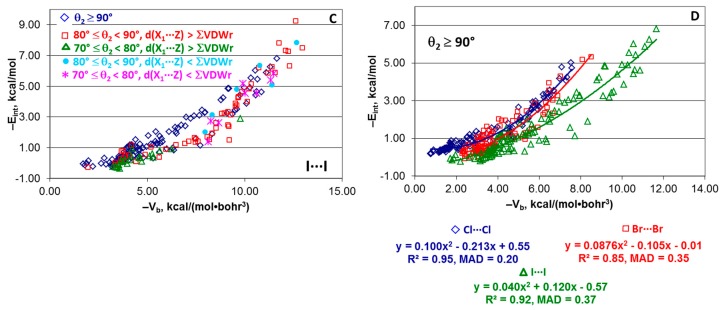
Potential energy density at BCP. The Eint(Vb) correlations for each specific type of the halogen bond are of significantly better quality than those for the whole set in terms of both R2 (0.92–0.96) and MAD (0.18–0.45 kcal/mol) (Figure 2A). The Cl···Cl structures are clearly better described than the Br···Br or I···I structures. Both series [(A)nY–Cl···Cl–Z(B)m] and [(A)nY–Br···Br–Z(B)m] may be well approximated by a single quadratic or exponential function, the former performing slightly better with R2 = 0.92 and MAD = 0.32 kcal/mol. The [(A)nY–I···I–Z(B)m] series lies below the series with the Cl···Cl and Br···Br bonds on the −Eint(–Vb) plot.
Kinetic energy density at BCP. The kinetic energy density behaves similarly to the potential energy density for the estimate of Eint within these series with the MAD values being only slightly worse (R2 = 0.92–0.96, MAD = 0.18–0.47 kcal/mol) (Figure 2B). However, Gb demonstrates lower dispersion compared to Vb. Indeed, the Eint(Gb) relationships for all series [(A)nY–Cl···Cl–Z(B)m], [(A)nY–Br···Br–Z(B)m] and [(A)nY–I···I–Z(B)m] have similar parameters despite the application of different basis sets (6-31+G* for the Cl···Cl and Br···Br structures and DZP for the I···I structures, although both these basis sets are of a double zeta quality). Meanwhile, the Eint(Vb) relationship for the iodine halogen bonds is quite different from those for the Cl···Cl and Br···Br structures. Thus, the application of Gb as an estimator of Eint is preferable over Vb also from this point of view.
Electron density at BCP. The Eint(ρb) relationships for these series are similar to Eint(Vb) and Eint(Gb) (Figure 2C). In contrast to Vb, both series [(A)nY–Br···Br–Z(B)m] and [(A)nY–I···I–Z(B)m] may be approximated by a single function (R2 = 0.91, MAD = 0.43 kcal/mol), while the fitting for the [(A)nY–Cl···Cl–Z(B)m] series has quite different parameters.
Laplacian and curvature of electron density distribution at BCP. Both Eint(∇2ρb) and Eint(λ||,b) relationships for these series have similar features and are described by either quadratic or exponential function (Figure 2D,E). Quality of the approximations for the Cl···Cl series is similar to the Vb, Gb, and ρb estimators. However, both ∇2ρb and λ||,b perform worse for the Br···Br and, in particular, I···I series. Both Cl···Cl and Br···Br series may be quite well treated by a single function, whereas the fitting parameters for the I···I series are very different. Various basis sets used for the Cl···Cl + Br···Br and I···I structures are conceivably responsible for this effect.
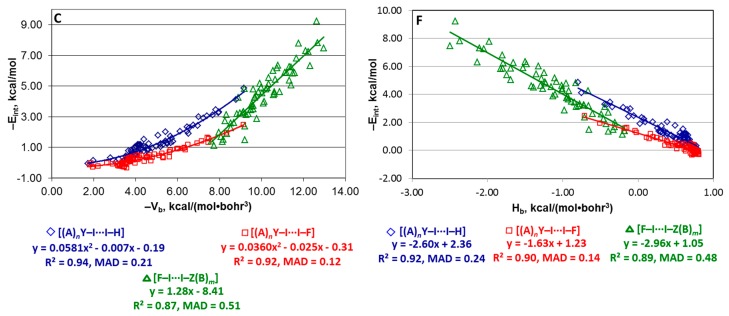
Total energy density at BCP. The Eint(Hb) relationships demonstrate different behavior for the Cl···Cl and Br···Br series, on one side, and for the I···I series, on the other side (Figure 2F). For the Cl···Cl series, the negative interaction energy increases with the enhancement of Hb. This series may be approximated by a single exponential function but with rather poor quality for this type of the halogen bond (R2 = 0.87 and MAD = 0.31 kcal/mol). For the Br···Br series, the Eint(Hb) function is not well-defined. Finally, for the I···I structures, −Eint increases with the decrease of Hb. The −Eint(Hb) relationship is nearly linear with R2 = 0.93 and MAD = 0.42 kcal/mol and may be used for the estimate of Eint for this type of halogen bonds.
Internuclear distance d(X···X). The −Eint(d(X···X)) dependencies are exponential with rather different parameters for the Cl···Cl, Br···Br, and, in particular, I···I structures (Figure 2G). The quality of this estimator is similar to Vb, Gb, and ρb.
4.3. Series [(A)nY–X···X–H], [(A)nY–X···X–F], and [F–X···X–Z(B)m]
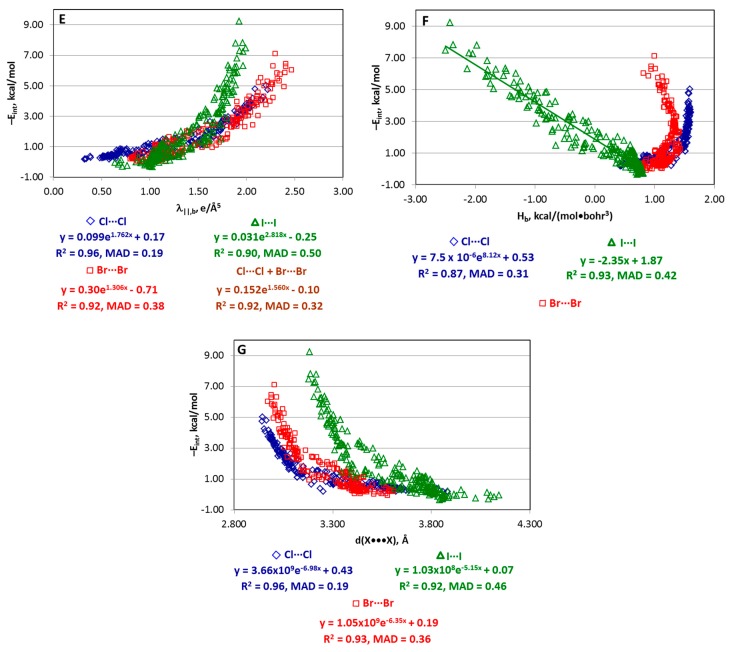
Typically, there are no statistically meaningful trends describing these series (Figure S1 in the Supplementary Material). Several dependencies corresponding to the “small” series with quite different parameters are clearly visible on the Eint(property) plots. The best Eint(Gb) approximation was found for the [F–X···X–Z(B)m] series with R2 = 0.86 and MAD = 0.44 kcal/mol (Figure 3A). The Eint(ρb) function also reasonably describes each of the pairs “[(A)nY–Br···Br–H] + [(A)nY–I···I–H] and “[(A)nY–Br···Br–F] + [(A)nY–I···I–F] (Figure 3B) but the fitting parameters for the corresponding Cl···Cl series are quite different. This situation demonstrates that the Eint(property) relationships significantly depend on the nature of the interacting atoms X.
Figure 3.
Plots of −Eint against Gb for the series [F–X···X–Z(B)m] (A) and against ρb for the series [(A)nY–{Br,I}···{Br,I}–H] and [(A)nY–{Br,I}···{Br,I}–F] (B).
4.4. “Small” Series
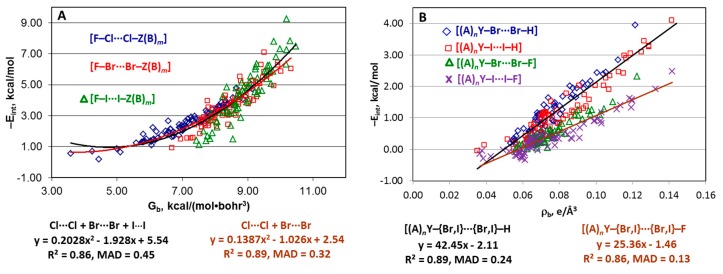
Potential energy density at BCP. The Eint(Vb) relationship for each of nine “small” series may be reasonably approximated by a linear function. The quadratic fitting is noticeably better than the linear one only for the [F–Cl···Cl–Z(B)m], [(A)nY–I···I–H], and [(A)nY–I···I–F] series (Figure 4A–C). The points corresponding to Br–Cl···Cl–H and Br–Cl···Cl–F are clearly out of the trends and they were excluded from the further analysis. Analysis of the correlations indicates the following.
Figure 4.
Plots of −Eint against –Vb (A–C) and Hb (D–F) for the “small” series. Points corresponding to structures Br–Cl···Cl–H, Br–Cl···Cl–F, and F–Br···Br–F are not included in the fitting in parts A, D, and E.
First, the slope and negative interception of the −Eint(−Vb) relationships for the [F–Cl···Cl–Z(B)m], [F–Br···Br–Z(B)m], and [F–I···I–Z(B)m] series are significantly higher than for the other series, whereas those for the [(A)nY–Cl···Cl–F], [(A)nY–Br···Br–F], and [(A)nY–I···I–F] structures are the lowest.
Second, quality of the dependencies for the “small” series is usually worse than for the “large” ones in terms of R2. However, the MAD values for the [(A)nY–{Cl,Br,I}···{Cl,Br,I}–{H,F}] “small” series (0.05–0.21 kcal/mol) are significantly lower than for the corresponding “large” series (0.18–0.45 kcal/mol). The estimate of Eint for the structures [F–Br···Br–Z(B)m] and [F–I···I–Z(B)m] is preferable using equations for the “large” series because both MAD and R2 parameters are worse for these “small” series than for the corresponding “large” ones.
Third, among all “small” series, only one, [(A)nY–Cl···Cl–H], is described by an equation similar to the EML formula (Eint = 0.47Vb + 0.27). Equations (3)–(5) obtained for the halogen bonds of the X···D type (X = Cl, Br, I; D = N, S, O, C) [79] are also not applicable to structures of the [(A)nY–X···X–Z(B)m] type discussed in this work (except the same [(A)nY–Cl···Cl–H] series).
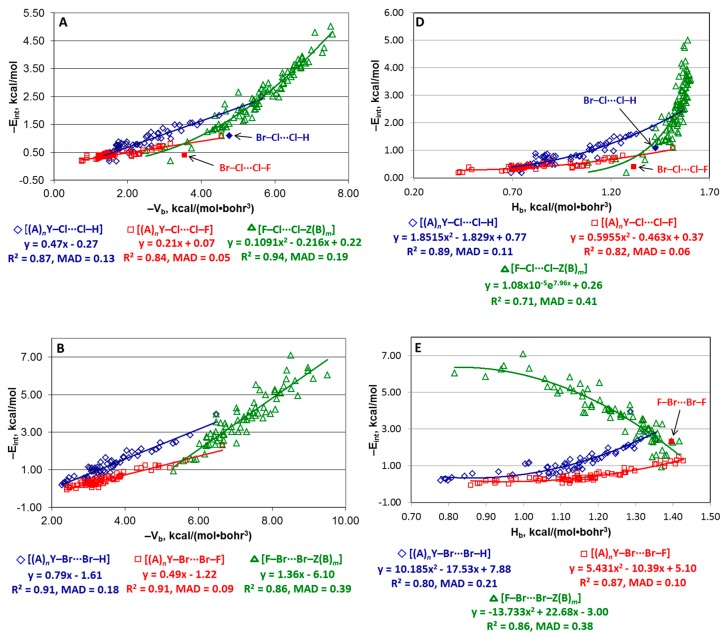
Total energy density at BCP. For the Cl···Cl structures, the −Eint(Hb) function shows similar quadratic or exponential behavior for all three “small” series [(A)nY–Cl···Cl–H], [(A)nY–Cl···Cl–F] and [F–Cl···Cl–Z(B)m] (Figure 4D) although with quite different parameters: interaction energy −Eint increases with the enhancement of Hb. For the Br···Br structures, the −Eint(Hb) relationship is of the same type for [(A)nY–Br···Br–H] and [(A)nY–Br···Br–F] (Figure 4E). However, −Eint increases with the reduction of Hb as a quadratic/exponential function for [F–Br···Br–Z(B)m] and as a linear function for the I...I structures (Figure 4F). The quality of all Eint(Hb) dependencies for the “small” series is worse than for the other estimators.
Other estimators. The main features of the Eint(Gb), Eint(ρb), Eint(∇2ρb), Eint(λ||,b), and Eint(d(X···X)) relationships for the “small” series are similar to the corresponding Eint(Vb) dependencies (Figure S2 in Supplementary Material). Laplacian describes the series [F–I···I–Z(B)m] particularly poor.
4.5. Estimate of Eint from an Integral of Electronic Virial over Interatomic Zero-Flux Surface (IAS)
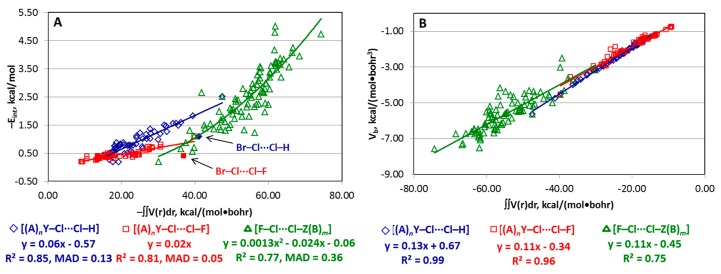
Recently, Romanova, Lyssenko, and Ananyev [104] reported that the integral of electronic virial V(r) over IAS (, r ∈ IAS) may be a better estimator of Eint than the potential energy density at BCP (Vb). This result was obtained for a set of 50 structures with very different types of non-covalent interactions. Here, the quality of this estimator was verified for structures of the [(A)nY–Cl···Cl–Z(B)m] type. The calculations indicated that the IAS integral of electronic virial field behaves similarly as Vb for the [(A)nY–Cl···Cl–H] and [(A)nY–Cl···Cl–F] series (compare Figure 4A and Figure 5A). However, the former estimator works much worse for the [F–Cl···Cl–Z(B)m] series providing unacceptably poor R2 value (0.77) and relatively high MAD (0.36 kcal/mol). Correspondingly, the Eint() correlation for the whole series [(A)nY–Cl···Cl–Z(B)m] is also significantly worse than the Eint(Vb) relationship with R2 = 0.89 vs. 0.96 and MAD = 0.28 vs. 0.18 kcal/mol.
Figure 5.
Plots of −Eint (A) and Vb (B) against (−/+). Points corresponding to structures Br–Cl···Cl–H and Br–Cl···Cl–F are not included in the fittings in part A.
The plot of Vb against demonstrates a nice linear correlation for [(A)nY–Cl···Cl–H] (R2 = 0.99), a quite good relationship for [(A)nY–Cl···Cl–F] (R2 = 0.96) but a poor dependence for [F–Cl···Cl–Z(B)m] (R2 = 0.75) (Figure 5B). Thus, the integral of electronic virial over IAS cannot be recommended as an acceptable estimator of Eint at least for the structures bearing the Cl···Cl halogen bond.
4.6. Effect of Angle θ2
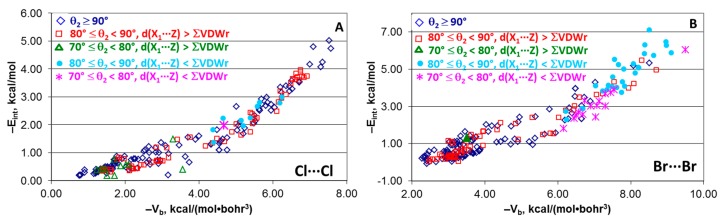
Although no BCP was found for the X1···Z contact in structures [(A)nY–X1···X2–Z(B)m] included in the analysis, some of them have the angleX1X2Z (θ2) lower than 90°. This may point out some interaction between the atoms X1 and Z. To verify if this possible interaction affects the Eint(property) dependencies, all structures were divided into three groups, i.e., those with θ2 ≥ 90°, 80° ≤ θ2 < 90°, and 70° ≤ θ2 < 80°. In the second and third groups, structures with the X1···Z distance shorter than the sum of van der Walls radii were also separated from those with the X1···Z distance longer than this sum.
The Eint(Vb) dependencies for all these groups of structures are shown in Figure 6A–C. All structures fit very well the same trends within each series independently on the angle θ2 and the X1···Z distance. If considering only structures with θ2 ≥ 90°, R2 and MAD values are similar to those for the complete structural series except the Br···Br structures (compare Figure 2A and Figure 6D). In the latter case, exclusion of the structures with θ2 < 90° results in a much poorer R2 value of 0.85 compared to the complete set for which R2 = 0.93. All this indicates no effect of the angle θ2 and the X1···Z distance (within the selected ranges) on the Eint(Vb) dependencies. Similar results were obtained for all other estimators.
Figure 6.
Plots of −Eint against −Vb for the “large” series of structures [(A)nY–X···X–Z(B)m] with various angles θ2 (A–C) and distances X1···Z (D).
5. Final Remarks
In this work, the Eint(property) correlations were established and analyzed for the first time for the large statistically significant sets of the homo-halogen bonds Cl···Cl, Br···Br, and I···I formed upon interaction of two neutral fragments at the M06-2X/6-31+G* (the Cl···Cl and Br···Br bonds) and M06-2X/DZP (the I···I bond) levels of theory. Electron density, its Laplacian, curvature of the electron density distribution, potential, kinetic, and total energy densities at BCP, integral of electronic virial over IAS and the d(X···X) internuclear distance were examined as estimators of the interaction energy. The correlations obtained in this work have a significant practical potential since they lead to interaction energies of the entire classes of the halogen bonds with the electron density distribution or even only the d(X···X) internuclear distance being in the hands. This is particularly important for the systems with multiple intermolecular non-covalent interactions or those bearing intramolecular XBs because a direct determination or calculation of Eint for such systems is an extremely difficult or often even impossible task. The following conclusions can be made.
First, the whole set of structures can be reasonably approximated by a single quadratic function −Eint = 0.128Gb2 − 0.82Gb + 1.66 with R2 = 0.91 and MAD = 0.39 kcal/mol. For other estimators, no reasonable single correlation was found for the whole structural set.
Second, each of the series Cl···Cl, Br···Br, and I···I can be well described individually by the Eint(Vb), Eint(Gb), Eint(ρb), Eint(λ||,b), and Eint(d(X···X)) relationships, all of them being nonlinear (R2 = 0.90–0.96, MAD = 0.18–0.50 kcal/mol). Quality of these relationships is better for the Cl···Cl structures compared to the Br···Br and I···I ones. Total energy density behaves well only for the I···I structures while the −Eint(Hb) function is not well-defined for the Br···Br structures. Laplacian ∇2ρb works well for the Cl···Cl and Br···Br series but not for the I···I one.
Third, the kinetic energy density at BCP can be recommended as the best estimator of Eint due to lower dispersion of the Eint(Gb) functions.
Fourth, typically, there are no statistically meaningful trends describing the series [(A)nY–X···X–H], [(A)nY–X···X–F], and [F–X···X–Z(B)m].
Fifth, quality of correlations for the “small” series is usually worse than that for the “large” series Cl···Cl, Br···Br, and I···I in terms of R2 but it is better in terms of MAD (with exception of the [F–Br···Br–Z(B)m] and [F–I···I–Z(B)m] structures).
Sixth, the obtained here Eint(Vb) and Eint(Gb) relationships are close to Equations (1)–(5) only for the [(A)nY–Cl···Cl–H] structures. Additionally, the Eint(property) correlations obtained here for the Cl···Cl and Br···Br bonds are significantly different from those found previously for the Cl···Cl− and Br···Br− interactions between the neutral fragments (A)nY–Hal and the halide anion Hal− [92]. This once again demonstrates that these dependencies are not universal and they should be established for each particular type of non-covalent interactions.
Seventh, the IAS integral of electronic virial cannot be recommended as an Eint estimator at least for the Cl···Cl bond.
Eighth, the BSSE effect is insignificant for the Cl···Cl structures but becomes important for the I···I and, in particular, Br···Br structures.
The Eint(property) relationships recommended for the Cl···Cl, Br···Br, and I···I interactions are given in Table 1 (for the whole set and “large” series”) and Table 2 (for the “small” series). Two directions toward the further extension of investigations in this field can be mentioned, i.e., (i) establishment of the Eint(property) relationships for the hetero-halogen bonds Hal1···Hal2 (Hal1 ≠ Hal2) and other types of the non-covalent interactions (chalcogen, pnictogen, tetrel bonds, metallophilic interactions, etc.) and (ii) analysis of the effect of computational method, basis set and effective core pseudopotentials on these correlations. The corresponding studies are currently underway.
Table 1.
Relationships recommended for the estimates of Eint (in kcal/mol) for the whole set and “large” series of structures [(A)nY–X···X–Z(B)m] at the M06-2X/6-31+G* (X = Cl, Br) and M06-2X/DZP (X = I) levels of theory.
| Series | Estimator | Equation |
|---|---|---|
| Whole set | Gb, kcal/(mol•bohr3) | −Eint = 0.128Gb2 − 0.824Gb + 1.66 |
| Cl···Cl | Vb, kcal/(mol•bohr3) | −Eint = 0.1006Vb2 + 0.218Vb + 0.55 |
| Gb, kcal/(mol•bohr3) | −Eint = 0.0841Gb2 − 0.367Gb + 0.84 | |
| ρb, e/Å3 | −Eint = 535.9ρb2 − 31.13ρb + 0.87 | |
| ∇2ρb, e/Å5 | −Eint = 0.09e2.405∇2ρb + 0.17 | |
| λ||,b, e/Å5 | −Eint = 0.099e1.762λ||,b + 0.17 | |
| d(X···X), Å | −Eint = 3.66×109e−6.98d(X···X) + 0.43 | |
| Br···Br | Vb, kcal/(mol•bohr3) | −Eint = 0.0926Vb2 + 0.173Vb + 0.16 |
| Gb, kcal/(mol•bohr3) | −Eint = 0.1178Gb2 − 0.73Gb + 1.50 | |
| ρb, e/Å3 | −Eint = 380.6ρb2 − 24.78ρb + 0.42 | |
| ∇2ρb, e/Å5 | −Eint = 0.07e2.624∇2ρb − 0.10 | |
| λ||,b, e/Å5 | −Eint = 0.30e1.306λ||,b − 0.71 | |
| d(X···X), Å | −Eint = 1.05×109e−6.35d(X···X) + 0.19 | |
| I···I | Vb, kcal/(mol•bohr3) | −Eint = 0.0635Vb2 + 0.217Vb + 0.25 |
| Gb, kcal/(mol•bohr3) | −Eint = 0.1564Gb2 − 1.138Gb + 2.25 | |
| ρb, e/Å3 | −Eint = 305.2ρb2 − 21.78ρb + 0.44 | |
| λ||,b, e/Å5 | −Eint = 0.031e2.818λ||,b − 0.25 | |
| Hb, kcal/(mol•bohr3) | −Eint = −2.35Hb + 1.87 | |
| d(X···X), Å | −Eint = 1.03×108e−5.15d(X···X) + 0.07 |
Table 2.
Relationships −Eint(Vb) recommended for the estimates of Eint (in kcal/mol) for the “small” series of structures [(A)nY–X···X–H] and [(A)nY–X···X–F] at the M06-2X/6-31+G* (X = Cl, Br) and M06-2X/DZP (X = I) levels of theory [Vb in kcal/(mol•bohr3)].
| Series | Equation |
|---|---|
| [(A)nY–Cl···Cl–H] | −Eint = −0.47Vb − 0.27 |
| [(A)nY–Cl···Cl–F] | −Eint = −0.21Vb + 0.07 |
| [(A)nY–Br···Br–H] | −Eint = −0.79Vb − 1.61 |
| [(A)nY–Br···Br–F] | −Eint = −0.49Vb − 1.22 |
| [(A)nY–I···I–H] | −Eint = 0.0581Vb2 + 0.007Vb − 0.19 |
| [(A)nY–I···I–F] | −Eint = 0.0360Vb2 + 0.025Vb − 0.31 |
Acknowledgments
The author is grateful to the Russian Science Foundation (grant 19-13-00013) for support of this study.
Supplementary Materials
The following are available online at https://www.mdpi.com/1420-3049/24/15/2733/s1, discussion of the BSSE effect, Figure S1: plots of −Eint against −Vb, Gb, ρb, ∇2ρb, λ||,b, Hb and d(X···X) for the series [(A)nY–X···X–H], [(A)nY–X···X–F] and [F–X···X–Z(B)m], Figure S2: plots of −Eint against Gb, ρb, ∇2ρb, λ||,b and d(X···X) for the “small” series of structures [(A)nY–X···X–Z(B)m], Figure S3: plots of −Eint with the CP correction against −Eint without the CP correction and plots of −Eint with and without the CP correction against −Vb for the “large” series of structures [(A)nY–X···X–Z(B)m], Table S1: calculated structures [(A)nY–X···X–Z(B)m], Table S2: negative X···X interaction energies, −Eint, with BSSE correction calculated for the [(A)nY–X...X–Z(B)m] structures at the M06-2X/6-31+G* (X = Cl, Br) and M06-2X/DZP (X = I) levels.
Funding
This research was funded by the Russian Science Foundation (grant 19-13-00013).
Conflicts of Interest
The author declares no conflicts of interest.
Footnotes
Sample Availability: Not available.
References
- 1.Metrangolo P., Resnati G. Halogen versus hydrogen. Science. 2008;321:918–919. doi: 10.1126/science.1162215. [DOI] [PubMed] [Google Scholar]
- 2.Metrangolo P., Meyer F., Pilati T., Resnati G., Terraneo G. Halogen bonding in supramolecular chemistry. Angew. Chem. Int. Ed. 2008;47:6114–6127. doi: 10.1002/anie.200800128. [DOI] [PubMed] [Google Scholar]
- 3.Metrangolo P., Neukirch H., Pilati T., Resnati G. Halogen bonding based recognition processes: A world parallel to hydrogen bonding. Acc. Chem. Res. 2005;38:386–395. doi: 10.1021/ar0400995. [DOI] [PubMed] [Google Scholar]
- 4.Gilday L.C., Robinson S.W., Barendt T.A., Langton M.J., Mullaney B.R., Beer P.D. Halogen bonding in supramolecular chemistry. Chem. Rev. 2015;115:7118–7195. doi: 10.1021/cr500674c. [DOI] [PubMed] [Google Scholar]
- 5.Shirman T., Arad T., van der Boom M.E. Halogen bonding: A supramolecular entry for assembling nanoparticles. Angew. Chem. Int. Ed. 2010;49:926–929. doi: 10.1002/anie.200905984. [DOI] [PubMed] [Google Scholar]
- 6.Bayse C.A., Rafferty E.R. Is halogen bonding the basis for iodothyronine deiodinase activity? Inorg. Chem. 2010;49:5365–5367. doi: 10.1021/ic100711n. [DOI] [PubMed] [Google Scholar]
- 7.Sarwar M.G., Dragisic B., Salsberg L.J., Gouliaras C., Taylor M.S. Thermodynamics of halogen bonding in solution: Substituent, structural, and solvent effects. J. Am. Chem. Soc. 2010;132:1646–1653. doi: 10.1021/ja9086352. [DOI] [PubMed] [Google Scholar]
- 8.Nelyubina Y.V., Antipin M.Y., Dunin D.S., Kotov V.Y., Lyssenko K.A. Unexpected “amphoteric” character of the halogen bond: The charge density study of the co-crystal of N-methylpyrazine iodide with I2. Chem. Commun. 2010;46:5325–5327. doi: 10.1039/c0cc01094d. [DOI] [PubMed] [Google Scholar]
- 9.Koláŕ M.H., Hobza P. Computer modeling of halogen bonds and other σ-hole interactions. Chem. Rev. 2016;116:5155–5187. doi: 10.1021/acs.chemrev.5b00560. [DOI] [PubMed] [Google Scholar]
- 10.Cavallo G., Metrangolo P., Milani R., Pilati T., Priimagi A., Resnati G., Terraneo G. The halogen bond. Chem. Rev. 2016;116:2478–2601. doi: 10.1021/acs.chemrev.5b00484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hobza P., Müller-Dethlefs K. Non-Covalent Interactions: Theory and Experiment. Royal Society of Chemistry; Cambridge, UK: 2010. [Google Scholar]
- 12.Natale D., Marequerivas J.C. The combination of transition metal ions and hydrogen-bonding interactions. Chem. Commun. 2008:425–437. doi: 10.1039/B709650J. [DOI] [PubMed] [Google Scholar]
- 13.Feller R.K., Cheetham A.K. Structural and chemical complexity in multicomponent inorganic–organic framework materials. CrystEngComm. 2009;11:980–985. doi: 10.1039/b820718f. [DOI] [Google Scholar]
- 14.Corradi E., Meille S.V., Messina M.T., Metrangolo P., Resnati G. Halogen bonding versus hydrogen bonding in driving self-assembly processes. Angew. Chem. Int. Ed. 2000;39:1782–1786. doi: 10.1002/(SICI)1521-3773(20000515)39:10<1782::AID-ANIE1782>3.0.CO;2-5. [DOI] [PubMed] [Google Scholar]
- 15.Desiraju G.R. Crystal engineering: A holistic view. Angew. Chem. Int. Ed. 2007;46:8342–8356. doi: 10.1002/anie.200700534. [DOI] [PubMed] [Google Scholar]
- 16.Cinčić D., Friščić T., Jones W. Structural equivalence of Br and I halogen bonds: A route to isostructural materials with controllable properties. Chem. Mater. 2008;20:6623–6626. doi: 10.1021/cm800923r. [DOI] [Google Scholar]
- 17.Tepper R., Schubert U.S. Halogen Bonding in Solution: Anion Recognition, Templated Self-Assembly, and Organocatalysis. Angew. Chem. Int. Ed. 2018;57:6004–6016. doi: 10.1002/anie.201707986. [DOI] [PubMed] [Google Scholar]
- 18.Mahmudov K.T., Kopylovich M.N., Guedes da Silva M.F.C., Pombeiro A.J.L. Non-covalent interactions in the synthesis of coordination compounds: Recent advances. Coord. Chem. Rev. 2017;345:54–72. doi: 10.1016/j.ccr.2016.09.002. [DOI] [Google Scholar]
- 19.Li B., Zang S.-Q., Wang L.-Y., Mak T.C.W. Halogen bonding: A powerful, emerging tool for constructing high-dimensional metal-containing supramolecular networks. Coord. Chem. Rev. 2016;308:1–21. doi: 10.1016/j.ccr.2015.09.005. [DOI] [Google Scholar]
- 20.Saccone M., Cavallo G., Metrangolo P., Resnati G., Priimagi A. Halogen-Bonded Photoresponsive Materials. In: Metrangolo P., Resnati G., editors. Halogen Bonding II. Topics in Current Chemistry. Volume 359. Springer; Cham, Switzerland: 2014. [DOI] [PubMed] [Google Scholar]
- 21.Aakeröy C.B., Spartz C.L. Halogen Bonding in Supramolecular Synthesis. In: Metrangolo P., Resnati G., editors. Halogen Bonding I. Topics in Current Chemistry. Volume 358. Springer; Cham, Switzerland: 2014. [DOI] [PubMed] [Google Scholar]
- 22.Mukherjee A., Tothadi S., Desiraju G.R. Halogen bonds in crystal engineering: Like hydrogen bonds yet different. Acc. Chem. Res. 2014;47:2514–2524. doi: 10.1021/ar5001555. [DOI] [PubMed] [Google Scholar]
- 23.Xu Z., Yang Z., Liu Y., Lu Y., Chen K., Zhu W. Halogen bond: Its role beyond drug-target binding affinity for drug discovery and development. J. Chem. Inf. Model. 2014;54:69–78. doi: 10.1021/ci400539q. [DOI] [PubMed] [Google Scholar]
- 24.Lu Y., Shi T., Wang Y., Yang H., Yan X., Luo X., Jiang H., Zhu W. Halogen bonding—A novel interaction for rational drug design? J. Med. Chem. 2009;52:2854–2862. doi: 10.1021/jm9000133. [DOI] [PubMed] [Google Scholar]
- 25.Mendez L., Henriquez G., Sirimulla S., Narayan M. Looking back, looking forward at halogen bonding in drug discovery. Molecules. 2017;22:1397. doi: 10.3390/molecules22091397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fourmigué M. Halogen Bonding in Conducting or Magnetic Molecular Materials. In: Metrangolo P., Resnati G., editors. Halogen Bonding. Fundamentals and Applications. Volume 126. Springer; Berlin/Heidelberg, Germany: 2008. p. 181. [Google Scholar]
- 27.Atzori M., Serpe A., Deplano P., Schlueter J.A., Mercuri M.L. Tailoring magnetic properties of molecular materials through non-covalent interactions. Inorg. Chem. Front. 2015;2:108–115. doi: 10.1039/C4QI00179F. [DOI] [Google Scholar]
- 28.Mahmudov K.T., Gurbanov A.V., Guseinov F.I., Guedes da Silva M.F.C. Noncovalent interactions in metal complex catalysis. Coord. Chem. Rev. 2019;387:32–46. doi: 10.1016/j.ccr.2019.02.011. [DOI] [Google Scholar]
- 29.Szell P.M.J., Zablotny S., Bryce D.L. Halogen bonding as a supramolecular dynamics catalyst. Nat. Commun. 2019;10:916. doi: 10.1038/s41467-019-08878-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Schindler S., Huber S.M. Halogen Bonds in Organic Synthesis and Organocatalysis. In: Metrangolo P., Resnati G., editors. Halogen Bonding II. Topics in Current Chemistry. Volume 359. Springer; Cham, Switzerland: 2014. [DOI] [PubMed] [Google Scholar]
- 31.Cariati E., Forni A., Biella S., Metrangolo P., Meyer F., Resnati G., Righetto S., Tordin E., Ugo R. Tuning second-order NLO responses through halogen bonding. Chem. Commun. 2007:2590–2592. doi: 10.1039/b702724a. [DOI] [PubMed] [Google Scholar]
- 32.Christopherson J.-C., Topić F., Barrett C.J., Friščić T. Halogen-Bonded Cocrystals as Optical Materials: Next-Generation Control over Light–Matter Interactions. Cryst. Growth Des. 2018;18:1245–1259. doi: 10.1021/acs.cgd.7b01445. [DOI] [Google Scholar]
- 33.Zhao M., Wang H.-B., Jia L.-N., Mao Z.-W. Insights into metalloenzyme microenvironments: Biomimetic metal complexes with a functional second coordination sphere. Chem. Soc. Rev. 2013;42:8360–8375. doi: 10.1039/c3cs60162e. [DOI] [PubMed] [Google Scholar]
- 34.Ho P.S. Biomolecular Halogen Bonds. In: Metrangolo P., Resnati G., editors. Halogen Bonding I. Topics in Current Chemistry. Volume 358 Springer; Cham, Switzerland: 2014. [Google Scholar]
- 35.Matter H., Nazaré M., Güssregen S., Will D.W., Schreuder H., Bauer A., Urmann M., Ritter K., Wagner M., Wehner V. Evidence for C–Cl/C–Br…π Interactions as an Important Contribution to Protein–Ligand Binding Affinity. Angew. Chem. Int. Ed. 2009;48:2911–2916. doi: 10.1002/anie.200806219. [DOI] [PubMed] [Google Scholar]
- 36.Voth A.R., Ho P.S. The role of halogen bonding in inhibitor recognition and binding by protein kinases. Curr. Top. Med. Chem. 2007;7:1336–1348. doi: 10.2174/156802607781696846. [DOI] [PubMed] [Google Scholar]
- 37.Wãsik R., Łebska M., Felczak K., Poznański J., Shugar D. Relative Role of Halogen Bonds and Hydrophobic Interactions in Inhibition of Human Protein Kinase CK2α by Tetrabromobenzotriazole and Some C(5)-Substituted Analogues. J. Phys. Chem. B. 2010;114:10601–10611. doi: 10.1021/jp102848y. [DOI] [PubMed] [Google Scholar]
- 38.Cottrell T.L. The Strengths of Chemical Bonds. Butterworths Publications; London, UK: 1958. [Google Scholar]
- 39.Biedermann F., Schneider H.-J. Experimental binding energies in supramolecular complexes. Chem. Rev. 2016;116:5216–5300. doi: 10.1021/acs.chemrev.5b00583. [DOI] [PubMed] [Google Scholar]
- 40.Musin R.N., Mariam Y.H. An integrated approach to the study of intramolecular hydrogen bonds in malonaldehyde enol derivatives and naphthazarin: Trend in energetic versus geometrical consequences. J. Phys. Org. Chem. 2006;19:425–444. doi: 10.1002/poc.1102. [DOI] [Google Scholar]
- 41.Fazli M., Raissi H., Chankandi B., Aarabhi M. The effect of formation of second hydrogen bond in adjacent two-ring resonance-assisted hydrogen bonds—Ab initio and QTAIM studies. J. Mol. Struct. Theochem. 2010;942:115–120. doi: 10.1016/j.theochem.2009.12.009. [DOI] [Google Scholar]
- 42.Szatyłowicz H. Structural aspects of the intermolecular hydrogen bond strength: H-bonded complexes of aniline, phenol and pyridine derivatives. J. Phys. Org. Chem. 2008;21:897–914. doi: 10.1002/poc.1394. [DOI] [Google Scholar]
- 43.Hugas D., Simon S., Duran M. Electron density topological properties are useful to assess the difference between hydrogen and dihydrogen complexes. J. Chem. Phys. A. 2007;111:4506–4512. doi: 10.1021/jp070080u. [DOI] [PubMed] [Google Scholar]
- 44.Grabowski S.J. Properties of a Ring Critical Pointas Measures of Intramolecular H-Bond Strength. Monatsh. Chem. 2002;133:1373–1380. doi: 10.1007/s00706-002-0498-3. [DOI] [Google Scholar]
- 45.Grabowski S.J., Bilewicz E. Cooperativity halogen bonding effect—Ab initio calculations on H2CO•••(ClF)n complexes. Chem. Phys. Lett. 2006;427:51–55. doi: 10.1016/j.cplett.2006.06.060. [DOI] [Google Scholar]
- 46.Palusiak M., Grabowski S.J. Characteristics of ring critical point as descriptors of H-bond strength. J. Chem. Res. 2004;7:492–493. doi: 10.3184/0308234042037266. [DOI] [Google Scholar]
- 47.Lipkowski P., Grabowski S.J., Robinson T.L., Leszczynski J. Properties of the C–H•••H dihydrogen bond: An ab initio and topological analysis. J. Phys. Chem. A. 2004;108:10865–10872. doi: 10.1021/jp048562i. [DOI] [Google Scholar]
- 48.Domagała M., Grabowski S.J. C–H•••N and C–H•••S hydrogen bonds—Influence of hybridization on their strength. J. Phys. Chem. A. 2005;109:5683–5688. doi: 10.1021/jp0511496. [DOI] [PubMed] [Google Scholar]
- 49.Grabowski S.J. Hydrogen bonding strength—Measures based on geometric and topological parameters. J. Phys. Org. Chem. 2004;17:18–31. doi: 10.1002/poc.685. [DOI] [Google Scholar]
- 50.Rozas I., Alkorta I., Elguero J. Behavior of ylides containing N, O, and C atoms as hydrogen bond acceptors. J. Am. Chem. Soc. 2000;122:11154–11161. doi: 10.1021/ja0017864. [DOI] [Google Scholar]
- 51.Szatyłowicza H., Krygowski T.M. Long distance structural consequences of H-bonding: The case of complexes of para-substituted phenol derivatives. J. Phys. Org. Chem. 2009;22:740–746. doi: 10.1002/poc.1511. [DOI] [Google Scholar]
- 52.Lyssenko K.A. Analysis of supramolecular architectures: Beyond molecular packing diagrams. Mendeleev Commun. 2012;22:1–7. doi: 10.1016/j.mencom.2012.01.001. [DOI] [Google Scholar]
- 53.Lyssenko K.A., Barzilovich P.Y., Nelyubina Y.V., Astaf’ev E.A., Antipin M.Y., Aldoshin S.M. Charge transfer and hydrogen bond energy in glycinium salts. Izv. Akad. Nauk, Ser. Khim. 2009:31–40. doi: 10.1007/s11172-009-0005-7. (Russ. Chem. Bull. Int. Ed.2009, 58, 31–40) [DOI] [Google Scholar]
- 54.Gálvez O., Gómez P.C., Pacios L.F. Variation with the intermolecular distance of properties dependent on the electron density in cyclic dimers with two hydrogen bonds. J. Chem. Phys. 2003;118:4878–4895. doi: 10.1063/1.1545678. [DOI] [Google Scholar]
- 55.Zou J.W., Jiang Y.-J., Guo M., Hu G.-X., Zhang B., Liu H.-C., Yu Q.-S. Ab initio study of the complexes of halogen-containing molecules RX (X = Cl, Br, and I) and NH3: Towards understanding the nature of halogen bonding and the electron-accepting propensities of covalently bonded halogen atoms. Chem. Eur. J. 2005;11:740–751. doi: 10.1002/chem.200400504. [DOI] [PubMed] [Google Scholar]
- 56.Pacios L.F. Change with the intermolecular distance of electron properties of hydrogen bond dimers at equilibrium and non-equilibrium geometries. Struct. Chem. 2005;16:223–241. doi: 10.1007/s11224-005-4454-9. [DOI] [Google Scholar]
- 57.Raissi H., Nadim E.S., Yoosefian M., Farzad F., Ghiamati E., Nowroozi A.R., Fazli M., Amoozadeh A. The effects of substitutions on structure, electron density, resonance and intramolecular hydrogen bonding strength in 3-mercapto-propenethial. J. Molec. Struct. Theochem. 2010;960:1–9. doi: 10.1016/j.theochem.2010.08.012. [DOI] [Google Scholar]
- 58.Roohi H., Bagheri S. Influence of substitution on the strength and nature of CH•••N hydrogen bond in XCCH•••NH3 complexes. Int. J. Quant. Chem. 2011;111:961–969. doi: 10.1002/qua.22460. [DOI] [Google Scholar]
- 59.Hayashi S., Matsuiwa K., Kitamoto M., Nakanishi W. Dynamic behavior of hydrogen bonds from pure closed shell to shared shell interaction regions elucidated by aim dual functional analysis. J. Phys. Chem. A. 2013;117:1804–1816. doi: 10.1021/jp3098928. [DOI] [PubMed] [Google Scholar]
- 60.D’Oria E., Novoa J.J. The strength–length relationship at the light of ab initio computations: Does it really hold? CrystEngComm. 2004;6:367–376. doi: 10.1039/B406743F. [DOI] [Google Scholar]
- 61.Boyd R.J., Choi S.C. A bond-length-bond-order relationship for intermolecular interactions based on the topological properties of molecular charge distributions. Chem. Phys. Lett. 1985;120:80–85. doi: 10.1016/0009-2614(85)87017-2. [DOI] [Google Scholar]
- 62.Mó O., Yáñez M., Elguero J. Cooperative (nonpairwise) effects in water trimers: An ab initio molecular orbital study. J. Chem. Phys. 1992;97:6628–6638. doi: 10.1063/1.463666. [DOI] [Google Scholar]
- 63.Ebrahimi A., Khorassani S.M.H., Delarami H. Estimation of individual binding energies in some dimers involving multiple hydrogen bonds using topological properties of electron charge density. Chem. Phys. 2009;365:18–23. doi: 10.1016/j.chemphys.2009.09.013. [DOI] [Google Scholar]
- 64.Koch U., Popelier P.L.A. Characterization of C–H–O hydrogen bonds on the basis of the charge density. J. Phys. Chem. 1995;99:9747–9754. doi: 10.1021/j100024a016. [DOI] [Google Scholar]
- 65.Amezaga N.J.M., Pamies S.C., Peruchena N.M., Sosa G.L. Halogen bonding: A study based on the electronic charge density. J. Phys. Chem. A. 2010;114:552–562. doi: 10.1021/jp907550k. [DOI] [PubMed] [Google Scholar]
- 66.Grabowski S.J. What is the covalency of hydrogen bonding? Chem. Rev. 2011;111:2597–2625. doi: 10.1021/cr800346f. [DOI] [PubMed] [Google Scholar]
- 67.Fradera J.P.X., Simon M.S.M.D.S. On the electron-pair nature of the hydrogen bond in the framework of the atoms in molecules theory. Chem. Phys. Lett. 2003;369:248–255. [Google Scholar]
- 68.Shi F.-Q., An J.-J., Yu J.-Y. Theoretical study on measure of hydrogen bonding strength: R–C≡N•••pyrrole complexes. Chin. J. Chem. 2005;23:400–403. [Google Scholar]
- 69.Cubero E., Orozco M., Hobza P., Luque F.J. Hydrogen bond versus anti-hydrogen bond: A comparative analysis based on the electron density topology. J. Phys. Chem. A. 1999;103:6394–6401. doi: 10.1021/jp990258f. [DOI] [Google Scholar]
- 70.Parthasarathi R., Subramanian V., Sathyamurthy N. Hydrogen bonding in phenol, water, and phenol-water clusters. J. Phys. Chem. A. 2005;109:843–850. doi: 10.1021/jp046499r. [DOI] [PubMed] [Google Scholar]
- 71.Wojtulewski S., Grabowski S.J. Unconventional F–H•••π hydrogen bonds—Ab initio and AIM study. J. Molec. Struct. 2002;605:235–240. doi: 10.1016/S0022-2860(01)00785-2. [DOI] [Google Scholar]
- 72.Bagheri S., Masoodi H.R., Abadi M.N. Estimation of individual NH•••X (X = N, O) hydrogen bonding energies in some complexes involving multiple hydrogen bonds using NBO calculations. Theor. Chem. Acc. 2015;134:127. doi: 10.1007/s00214-015-1738-z. [DOI] [Google Scholar]
- 73.Jabłoński M., Solà M. Influence of confinement on hydrogen bond energy. The case of the FH•••NCH dimer. J. Phys. Chem. A. 2010;114:10253–10260. doi: 10.1021/jp104968x. [DOI] [PubMed] [Google Scholar]
- 74.Ayoub A.T., Tuszynski J., Klobukowski M. Estimating hydrogen bond energies: Comparison of methods. Theor. Chem. Acc. 2014;133:1520. doi: 10.1007/s00214-014-1520-7. [DOI] [Google Scholar]
- 75.Brovarets O.O., Yurenko Y.P., Hovorun D.M. Intermolecular CH•••O/N H-bonds in the biologically important pairs of natural nucleobases: A thorough quantum-chemical study. J. Biomol. Struct. Dyn. 2014;32:993–1022. doi: 10.1080/07391102.2013.799439. [DOI] [PubMed] [Google Scholar]
- 76.Martyniak A., Majerz I., Filarowski A. Peculiarities of quasi-aromatic hydrogen bonding. RSC Adv. 2012;2:8135–8144. doi: 10.1039/c2ra20846f. [DOI] [Google Scholar]
- 77.Vener M.V., Egorova A.N., Churakov A.V., Tsirelson V.G. Intermolecular hydrogen bond energies in crystals evaluated using electron density properties: DFT computations with periodic boundary conditions. J. Comput. Chem. 2012;33:2303–2309. doi: 10.1002/jcc.23062. [DOI] [PubMed] [Google Scholar]
- 78.Vener M.V., Shishkina A.V., Rykounov A.A., Tsirelson V.G. Cl•••Cl Interactions in molecular crystals: Insights from the theoretical charge density analysis. J. Phys. Chem. A. 2013;117:8459–8467. doi: 10.1021/jp405119x. [DOI] [PubMed] [Google Scholar]
- 79.Bartashevich E.V., Tsirelson V.G. Interplay between non-covalent interactions in complexes and crystals with halogen bonds. Russ. Chem. Rev. 2014;83:1181–1203. doi: 10.1070/RCR4440. [DOI] [Google Scholar]
- 80.Ananyev I.V., Karnoukhova V.A., Dmitrienko A.O., Lyssenko K.A. Toward a rigorous definition of a strength of any interaction between Bader’s atomic basins. J. Phys. Chem. A. 2017;121:4517–4522. doi: 10.1021/acs.jpca.7b01495. [DOI] [PubMed] [Google Scholar]
- 81.Arkhipov D.E., Lyubeshkin A.V., Volodin A.D., Korlyukov A.A. Molecular Structures, Polymorphism and the Role of F…F Interactions in Crystal Packing of Fluorinated Tosylates. Crystals. 2019;9:242. doi: 10.3390/cryst9050242. [DOI] [Google Scholar]
- 82.Afonin A.V., Vashchenko A.V., Sigalov M.V. Estimating the energy of intramolecular hydrogen bonds from 1H NMR and QTAIM calculations. Org. Biomol. Chem. 2016;14:11199–11211. doi: 10.1039/C6OB01604A. [DOI] [PubMed] [Google Scholar]
- 83.Wang Y.-H., Lu Y.-X., Zou J.-W., Yu Q.-S. Theoretical investigation on charge-assisted halogen bonding interactions in the complexes of bromocarbons with some anions. Int. J. Quant. Chem. 2008;108:90–99. doi: 10.1002/qua.21369. [DOI] [Google Scholar]
- 84.Levina E.O., Chernyshov I.Y., Voronin A.P., Alekseiko L.N., Stash A.I., Vener M.V. Solving the enigma of weak fluorine contacts in the solid state: A periodic DFT study of fluorinated organic crystals. RSC Adv. 2019;9:12520–12537. doi: 10.1039/C9RA02116G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Bartashevich E., Matveychuk Y., Tsirelson V. Identification of the Tetrel Bonds between Halide Anions and Carbon Atom of Methyl Groups Using Electronic Criterion. Molecules. 2019;24:1083. doi: 10.3390/molecules24061083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Alkorta I., Legon A.C. Nucleophilicities of Lewis bases B and electrophilicities of Lewis acids A determined from the dissociation energies of complexes B···A involving hydrogen bonds, tetrel bonds, pnictogen bonds, chalcogen bonds and halogen bonds. Molecules. 2017;22:1786. doi: 10.3390/molecules22101786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Shaw R.A., Hill J.G. A Simple model for halogen bond interaction energies. Inorganics. 2019;7:19. doi: 10.3390/inorganics7020019. [DOI] [Google Scholar]
- 88.Espinosa E., Molins E., Lecomte C. Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 1998;285:170–173. doi: 10.1016/S0009-2614(98)00036-0. [DOI] [Google Scholar]
- 89.Mata I., Alkorta I., Espinosa E., Molins E. Relationships between interaction energy, intermolecular distance and electron density properties in hydrogen bonded complexes under external electric fields. Chem. Phys. Lett. 2011;507:185–189. doi: 10.1016/j.cplett.2011.03.055. [DOI] [Google Scholar]
- 90.Mata I., Molins E., Alkorta I., Espinosa E. Effect of an external electric field on the dissociation energy and the electron density properties: The case of the hydrogen bonded dimer HF•••HF*. J. Chem. Phys. 2009;130:044104. doi: 10.1063/1.3065972. [DOI] [PubMed] [Google Scholar]
- 91.Spackman M.A. How reliable are intermolecular interaction energies estimated from topological analysis of experimental electron densities? Cryst. Growth Des. 2015;15:5624–5628. doi: 10.1021/acs.cgd.5b01332. [DOI] [Google Scholar]
- 92.Kuznetsov M.L. Can halogen bond energy be reliably estimated from electron density properties at bond critical point? The case of the (A)nZ—Y•••X− (X, Y = F, Cl, Br) interactions. Int. J. Quantum. Chem. 2019;119:e25869. doi: 10.1002/qua.25869. [DOI] [Google Scholar]
- 93.Zhao Y., Truhlar D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008;120:215–241. [Google Scholar]
- 94.Frisch M.J., Trucks G.W., Schlegel H.B., Scuseria G.E., Robb M.A., Cheeseman J.R., Scalmani G., Barone V., Mennucci B., Petersson G.A., et al. Gaussian 09, Revision A.01. Gaussian, Inc.; Wallingford, CT, USA: 2009. [Google Scholar]
- 95.Kozuch S., Martin J.M.L. Halogen bonds: Benchmarks and theoretical analysis. J. Chem. Theory Comput. 2013;9:1918–1931. doi: 10.1021/ct301064t. [DOI] [PubMed] [Google Scholar]
- 96.Neto A.C., Muniz E.P., Centoducatte R., Jorge F.E. Gaussian basis sets for correlated wave functions. Hydrogen, helium, first-and second-row atoms. J. Mol. Struct. Theochem. 2005;718:219–224. doi: 10.1016/j.theochem.2004.11.037. [DOI] [Google Scholar]
- 97.Camiletti G.G., Machado S.F., Jorge F.E. Gaussian basis set of double zeta quality for atoms K through Kr: Application in DFT calculations of molecular properties. J. Comp. Chem. 2008;29:2434–2444. doi: 10.1002/jcc.20996. [DOI] [PubMed] [Google Scholar]
- 98.Barros C.L., De Oliveira P.J.P., Jorge F.E., Neto A.C., Campos M. Gaussian basis set of double zeta quality for atoms Rb through Xe: Application in non-relativistic and relativistic calculations of atomic and molecular properties. Mol. Phys. 2010;108:1965–1972. doi: 10.1080/00268976.2010.499377. [DOI] [Google Scholar]
- 99.Boys S.F., Bernardi F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970;19:553–556. doi: 10.1080/00268977000101561. [DOI] [Google Scholar]
- 100.Simon S., Duran M., Dannenberg J.J. How does basis set superposition error change the potential surfaces for hydrogen-bonded dimers? J. Chem. Phys. 1996;105:11024–11031. doi: 10.1063/1.472902. [DOI] [Google Scholar]
- 101.Bader R.F.W. Atoms in Molecules: A Quantum Theory. Oxford University Press; Oxford, UK: 1990. [Google Scholar]
- 102.AIMAll (Version 14.10.27), T.A. Keith, TK Gristmill Software, Overland Park KS, USA. [(accessed on 1 September 2015)];2014 Available online: aim.tkgristmill.com.
- 103.Metrangolo P., Resnati G. Type II halogen···halogen contacts are halogen bonds. IUCrJ. 2014;1:5–7. doi: 10.1107/S205225251303491X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Romanova A., Lyssenko K., Ananyev I. Estimations of energy of noncovalent bonding from integrals over interatomic zero-flux surfaces: Correlation trends and beyond. J. Comput. Chem. 2018;39:1607–1616. doi: 10.1002/jcc.25235. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.