Electronic Densities of States from X-Ray Photoelectron Spectroscopy ^,

Abstract

In x-ray photoelectron spectroscopy (XPS), a sample is exposed to low energy x rays (approximately 1 keV), and the resultant photoelectrons are analyzed with high precision for kinetic energy. After correction for inelastic scattering, the measured photoelectron spectrum should reflect the valence band density of states, as well as the binding energies of several core electronic levels. All features in this spectrum will be modulated by appropriate photoelectric cross sections, and there are several types of final-state effects which could complicate the interpretation further.

In comparison with ultraviolet photoelectron spectroscopy (UPS), XPS has the following advantages: (1) the effects of inelastic scattering are less pronounced and can be corrected for by using a core reference level, (2) core levels can also be used to monitor the chemical state of the sample, (3) the free electron states in the photoemission process do not introduce significant distortion of the photoelectron spectrum, and (4) the surface condition of the sample does not appear to be as critical as in UPS. XPS seems to be capable of giving a very good description of the general shape of the density-of-states function. A decided advantage of UPS at the present time, however, is approximately a fourfold higher resolution.

We have used XPS to study the densities of states of the metals Fe, Co, Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, and Au, and also the compounds ZnS, CdCl₂, and HgO. The d bands of these solids are observed to have systematic behavior with changes in atomic number, and to agree qualitatively with the results of theory and other experiments. A rigid band model is found to work reasonably well for Ir, Pt and Au. The d bands of Ag, Ir, Pt, Au and HgO are found to have a similar two-component shape.

1. Introduction

The energy distribution of electronic states in the valence bands [1] of a solid is given by the density of states function, ρ(E). There are several techniques for determining ρ(E) at energies within ~kT of the Fermi energy, E_f, where relatively small perturbations can excite electrons to nearby unoccupied states. However, because of the nature of Fermi statistics, an electron at energy E, well below E_f (in the sense that E_f − E ⪢ kT), can respond only to excitations of energy E_f − E or greater. Because the valence bands are typically several eV wide, a versatile, higher energy probe is required to study the full ρ(E). The principal techniques presently being applied to metals are soft x-ray spectroscopy (SXS) [2,3] ion-neutralization spectroscopy (INS) [4], and photoelectron spectroscopy (by means of ultraviolet [5] or x-ray [6,7] excitation).

In each of these methods, either the initial or the final state involves a hole in the bands under study. Thus the measuring process is inherently disruptive. The actual initial and final states may not be simply related to the undisturbed ground state [8], and only for this ground state does ρ(E) have precise meaning. Even if the deviations from a ground state description can be neglected, there are complications for each of the above techniques in relating measured quantities to ρ(E) [2,3,4,5]. Nevertheless, all four have been applied with some success, and, where possible, experimental results have been compared to the theoretical predictions of one-electron band theory.

In this paper, we outline the most recently developed of these techniques, x-ray photoelectron spectroscopy (XPS) [6,7], and apply it to several metallic and non-metallic solids. In section 2, the principles of the technique are discussed from the point of view of relating measured quantities to a one-electron ρ(E). In section 3, we present results for the twelve 3d, 4d, and 5d transition metals Fe, Co, Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, and Au, making comparisons with the results of other experimental techniques and theory where appropriate. In addition, results for nonmetallic solids containing the elements Zn, Cd and Hg are presented, to clarify certain trends observed as each d shell is filled. In section 4, we summarize our findings.

2. The XPS Method

The fundamental measurements in both ultraviolet photoelectron spectroscopy (UPS) and x-ray photoelectron spectroscopy (XPS) are identical and very simple. Photons of known energy impinge on a sample, expelling photoelectrons which are analyzed for kinetic energy in a spectrometer. In UPS [5], photon energies range from threshold to ~20 eV, whereas XPS utilizes primarily the Kα x rays of Mg (1.25 keV) and Al (1.49 keV). For a given absolute energy resolution, an XPS spectrometer must thus be ~ 100 times higher in resolving power. We have used a double-focussing air-cored magnetic spectrometer [9], with an energy resolution of Δ∈/∈ = 0.06 percent. Δ∈ is defined to be the full width at half maximum intensity (FWHM) of the peak due to a flux of monoenergetic electrons of energy ∈.

Conservation of energy requires that

$$h\nu =E^h-E^y+\in +{\varphi }_c,$$ (1)

where hv is the photon energy, E^g the total energy of the initial ground state, E^h the total energy of the final hole state as seen by the ejected photoelectron, ∈ the electron kinetic energy, and ϕ_c the contact potential between the sample surface and the spectrometer. If E^h corresponds simply to a hole in some electronic level j, then the binding energy of an electron in level j is by definition E_b^v = E^h − E^g, where the superscript v denotes the vacuum level as a reference. The Fermi level can also be used as a reference and a simple transformation yields

$$hv=E_b^f+\in +{\varphi }_{sp}\equiv -E+\in +{\varphi }_{sp},$$ (2)

where E_b^f ≡ −E is the Fermi-referenced binding energy, and ϕ_sp is the work function of the spectrometer (a known constant). This transformation makes use of the relations E_b^v = E_b^f + sample work function and ϕ_c = ϕ_sp – sample work function. Positive charging of the sample due to electron emission can shift the kinetic energy spectrum to lower energies by as much as 1 eV for insulating samples but relative peak positions should remain the same. This effect is negligible for metals.

Returning to eq (1), we see that the fundamental XPS (or UPS) experiment measures the kinetic energy spectrum from which we attempt to deduce the final-state spectrum. This spectrum must then be related to ρ(E), as discussed below.

In addition to ρ(E) modulated by an appropriate transition probability, there will be six major contributors to lineshape in an XPS spectrum. Together with their approximate shapes and widths for the conditions of our experiments, these are:

1. Linewidth of exciting radiation – Lorentzian, ~0.8 eV FWHM for the unresolved MgKα_1,2 doublet used as “monochromatic” radiation in this study. The use of a bent-crystal monochromatic might permit narrowing this in future work [7].

2. Spectrometer resolution – slightly skew, with higher intensity on the low-kinetic-energy side, ~0.6 eV FWHM for 1 keV electrons analyzed with 0.06 percent resolution.

3. Hole lifetime in the sample – Lorentzian, ~0.1 to 1.0 eV for the cases studied here.

4. Thermal broadening of the ground state – roughly Gaussian, ~0.1 eV.

5. Inelastic scattering of escaping photoelectrons – all peaks have an inelastic “tail” on the low kinetic-energy side, which usually extends for 10 eV or more.

6. Various effects due to deviations of the final state from a simple one-electron-transition model.

Contributions analogous to (3), (4), and (6) will be common to all techniques used for studying ρ(E). A UPS spectrum will exhibit analogous effects from all six causes. In XPS, there is thus a present lower limit of ~ 1.0 eV FWHM. Core levels with this width are well described by Lorentzian peaks with smoothly joining constant tails [10] (see fig. 1), verifying that the major contribution to linewidth is the exciting x ray. The corresponding lower limit for UPS appears to be 0.2 to 0.3 eV, so that XPS cannot at present be expected to give the same fine structure details as UPS.

Figure 1.

Core level photoelectron spectra produced by exposure of Ru and Ir to Mg x-rays. The levels are Ru 3d_3/2−3d_5/2 and Ir 4f_5/2 − 4f_7/2. The peaks due to the MgKα_{1, 2} and MgKα_{3, 4} x rays are noted, as well as the tail observed on each peak due to inelastic scattering. The analysis of these spectra into pairs of Lorentzian-based shapes is described in the text and reference 10.

The effects of scattering of escaping photoelectrons [(5) above] can be corrected for in both UPS [5] and XPS [6]. This correction is particularly simple for XPS, however, because narrow core levels can be used to study the scattering mechanisms. As the kinetic energies of electrons expelled from core levels ~ 100 eV below the valence bands are very near to those of electrons expelled from the valence bands (i.e, 1150 eV versus 1250 eV), it is very probable that the scattering mechanisms for both cases are nearly identical.

Subject to this assumption [11], we can correct an observed valence band spectrum, I_v(∈), by using an appropriate core level spectrum, I_c(∈), as a reference [6,10]. If we construct a core level spectrum in the absence of scattering, Ic′(∈′), from pure Lorentzian peak shapes, then I_c(∈) and Ic′(∈′) can be connected by a response function, R(∈,∈′). Since XPS data is accumulated in discrete channels, I_c(∈) and I_c′(∈′) can be treated as vectors with typically 100 elements and R(∈,∈′) as a 100 × 100 matrix, these quantities being related by

$$I_c(\in )=R\left(\in ,{\in }^{\prime }\right)I_c^{\prime }\left({\in }^{\prime }\right).$$ (3)

If we now make certain physically reasonable assumptions about the form of R(∈,∈′), the effective number of matrix elements to be computed can be reduced to ⩽ 100. This permits a direct calculation of R(∈,∈′). The next step is to apply R⁻¹(∈,∈′) to the observed valence band spectrum, I_v(∈), to yield the corrected spectrum, I_v′(∈′). The Lorentzian widths in I_c′(∈′) are selected to be 0.6 to 0.8 times the observed widths so that no appreciable resolution enhancement is accomplished by this correction. In addition to inelastic scattering, we can also easily allow for the extra peaks present in any XPS spectrum due to the satellite x-rays of the anode, the most intense of which are Kα_3,4. In XPS spectra produced by bombardment with magnesium x rays, these satellites produce a doublet approximately 10 eV above the main (Kα_1,2) peak and with about 10 percent of the intensity of the main peak (see fig. 1). The details of this correction procedure are discussed elsewhere [10].

The application of this procedure to data on the valence bands of copper is illustrated in figure 2. The strong similarity between corrected and observed spectra indicates the subtle nature of this correction: the essential shape and position of the d-band peak is obvious in the uncorrected spectrum. By comparison, this relatively high information content in raw data is not found in UPS [5] or ion-neutralization spectroscopy [4].

Figure 2.

Valence band photoelectron spectrum produced by exposure of Cu to Mg x-rays, together with the corrected spectrum obtained after allowance for the effects of inelastic scattering and MgKα_3,4 x-rays in the raw data. A peak due to the 3d bands of Cu is the dominant feature of these spectra.

An additional advantage of XPS is that the chemical state of the sample can be monitored via observation of core level photoelectron peaks from the sample and possible contaminants [6]. In this way it is possible to detect chemical reactions occurring in the thin surface layer (~100 Å) responsible for the unscattered photoelectrons of primary interest. Furthermore, experimental results for Fe, Co, and Ni indicate that UPS is more sensitive to surface conditions [6,12].

The relationship of corrected XPS spectra to ρ(E) can be considered in two steps: (1) a one-electron-transition model, in which the appropriate transition probability is expressed in terms of the photoelectric cross section, and (2) deviations from the one-electron-transition model.

The cross section for photoemission from a one-electron state j at energy E will be proportional to the square of the dipole matrix element between that state and the final continuum state,

$${\sigma }_j(E)\propto {|\langle {\psi }_j|\overline{r}|\psi (h\nu +E)\rangle |}^2,$$ (4)

where σ_j(E) is the cross section and ψ(hv + E) is the wave function of a continuum electron with energy hv + E. If there are no appreciable deviations of the final state from a one-electron transition model, the corrected kinetic energy spectrum will be related to ρ(E) by

$$I^{\prime }\left(h\nu +E-{\varphi }_{sp}\right)\propto {\int }_{-\infty }^{\infty }\overline{\sigma }\left(E^{\prime }\right)\rho \left(E^{\prime }\right){\rho }^{\prime }(h\nu +E^{\prime })F\left(E^{\prime }\right)L\left(E-E^{\prime }\right)d{E}^{\prime },$$ (5)

where $\overline{\sigma }\left(E^{\prime }\right)$ is an average cross section for all states j at E′, ρ′(hv + E′) is the density of final continuum states, F(E′) is the Fermi function describing thermal excitation of electrons near the Fermi surface and L(E – E′) is the lineshape due to contributions (1), (2), (3), and (4) discussed above (essentially a Lorentzian).

The factor ρ′(hv + E′) can be considered constant over the energy range pertinent to the valence bands, as the final state electrons are ~1250 eV into the continuum and the lattice potential affects them very little [6,13]. Therefore, the appropriate final state density will be proportional simply to ∈^1/2. This function is only negligibly smaller for electrons ejected from the bottom of the valence bands (∈ ≅ 1240 eV) than for those emitted from the top of these bands (∈ ≅ 1250 eV). This constancy of ρ′(hv + E′) cannot be assumed in the analysis of UPS data, however [5].

Any changes in $\overline{\sigma }(E)$ from the top to the bottom of the bands will modulate the XPS spectrum in a way not simply connected to ρ(E). From eq (4) it is apparent that these changes can be introduced by variations in either ψ_j or ψ(hv + E) across the bands. The differences in ψ_j from the top to the bottom of the 3d band in transition metals have been discussed previously [2,14], but no accurate quantitative estimates of this effect on the appropriate dipole matrix elements have been made to date. It is thus possible that in both XPS and UPS, $\overline{\sigma }(E)$ varies substantially from the bottom to the top of the valence bands because of variation in the initial-state wave functions. This question deserves further study. In XPS, there should be little difference in the final-state wave function, ψ(hv + E), between the top and bottom of a band, as a 1240 eV continuum state should look very much like a 1250 eV continuum state. The effects of changes in final state wave function on $\overline{\sigma }(E)$ need not be negligible in a UPS spectrum, however.

Our discussion up to this point has assumed that the photoemission process is strictly one-electron; i.e., that we can describe the process by changing the occupation of only a single one-electron orbital with all other orbitals remaining frozen. This assumption permits the use of Koopmans’ Theorem [15], which states that binding energies can be equated to the energy eigenvalues arising from a solution of Hartree-Fock equations. Or, with some admitted errors [16], the one-electron energies obtained from non-Hartree-Fock band structure calculations in which simplifying approximations have been made can be compared directly to a measured binding energy spectrum. We illustrate the use of Koopmans’ Theorem in figure 3a, using a hypothetical level distribution for a 3d transition metal. There are, however, several types of potentially significant deviations from this one-electron model. We shall discuss these briefly.

Figure 3.

Schematic illustration of various final-state effects on the photoelectron spectrum of a hypothetical 3d transition metal: (a) the Koopmans’ Theorem spectrum, in which levels are positioned according to one-electron energies, with relative intensities determined by appropriate photoelectric cross sections; (b) the effect on spectrum (a) of polarization around a localized-hole final state; (c) the effect on spectrum (a) of strong coupling between a localized hole and the valence electrons (note the splitting of the 3s level); (d) the effect on spectrum (a) of two-electron excitation during photoemission; and (e) the effect on spectrum (a) of phonon excitation during photoemission.

The final-state effects leading to these deviations can be separated into several categories, although we note that there is considerable overlap. In a more rigorous treatment some of these separations might not be meaningful, but we retain them here for heuristic purposes. The effects are:

1. Electrons in the sample may be polarized around a localized positive hole, thereby increasing the kinetic energy of the outgoing electron [8]. In this way, the entire I(∈) spectrum would be shifted toward higher kinetic energy. Polarization might also occur to a different extent for different core levels, for different energies within the valence bands, and for levels at the same energy in the valence bands, but with different wave vector. The latter two effects could act to broaden I(∈) relative to ρ(E). These polarization effects are schematically illustrated in figure 3b. Polarizations will only affect I(∈) to the extent that the kinetic energy of the outgoing electron is altered, however (cf. eq (1)). Since both polarization and photoemission occur on a time scale of ~10⁻¹⁶ s, it is difficult to assess the importance of this effect. As the velocity of an XPS photoelectron is ~10 times that of a UPS photoelectron, the influence of polarization should be somewhat less on an XPS spectrum, however.

2. In addition to a simple polarization, a localized hole can couple strongly with localized valence electrons [17] or with nonlocalized valence electrons [18]. In iron metal, for example, a 3s hole is found to couple in several ways with the localized d electron moment, giving rise to an approximately 4 eV “multiplet splitting” in the 3s photoelectron peak [17]. Also, it has been predicted that nonlocalized conduction electrons should couple with a localized core or valence hole yielding asymmetric line shapes in electron and x-ray emission [18]. Both of the above effects would act to broaden I(∈) spectra, with the former being more important for systems with a d or f shell approximately half-filled. These effects are indicated in figure 3c. It has also been predicted that the removal of a core or valence electron will be accompanied by strong coupling to plasma oscillations [19]. This coupling would lead to broad sidebands separated from the one-electron spectrum by as much as 20 eV [19].

3. It is also possible that not just one electron is fundamentally affected in the photoemission process, but that other electrons or phonons are simultaneously excited [20]. Electrons may be excited to unoccupied bound states or they may be ejected from the sample, and this effect is indicated in figure 3d. The only direct observations of such electronic excitations during photoemission have been on monatomic gases, where two-electron processes are found with as high as 20 percent probability [21]. Vibrational excitations have a marked effect on the UPS spectra of light gaseous molecules [22], but it is difficult to estimate their importance in solids. A classical calculation indicates that for such heavy atoms as transition metals, the recoil energy available for such excitations in XPS is ⩽ 10⁻² eV [7]. Also, the observation of core reference levels with linewidths very close to the lower limit of the technique (see fig. 1) seems to indicate that vibrational excitation does not account for more than a few tenths eV broadening and shifting to lower kinetic energy of features observed in the valence-band region. This effect is schematically indicated in figure 3e.

For several reasons, then, XPS seems to be capable of giving more reliable information about the overall shape of ρ(E) than does UPS. However, the present XPS linewidth limit of 1.0 eV precludes determination of anything beyond fairly gross structural features. With these observations in mind, we now turn to a detailed study of the XPS spectra for several solids. We note also that the XPS method is applied to ρ(E) studies in two other papers of these proceedings [23,24].

3. Density-of-States Results for Several 3d, 4d, and 5d Series Metals

3.1. Introduction

Figure 4 shows the portion of the Periodic Table relevant to this work. The twelve elements Fe, Co, Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, and Au were studied as metals, while the three elements Zn, Cd, and Hg were studied in the compounds ZnS, CdCl₂, and HgO to illustrate the positions, widths, and shapes of filled core-like 3d, 4d, and 5d shells.

Figure 4.

The portion of the periodic table studied in this work. The atomic number, free-atom electronic configuration, and metal crystal structures are given. Zn, Cd, and Hg were studied as compounds. The crystal structures are those appropriate at the temperatures of our metal experiments (700–900 °C).

Ultra-high vacuum conditions were not attainable during our XPS measurements, as the base pressure in our spectrometer is approximately 10⁻⁵ torr. Surface contamination of samples is a potential problem, because the layer of the sample that is active in producing essentially inelastic photoelectrons extends only about 100 Å in from the surface [6,7]. This depth is not accurately known, however. Because the contamination consists of oxide formation as well as certain adsorption processes with lower bonding energy for the contaminant, all the metal samples were heated to high temperature (700 to 900 °C) in a hydrogen atmosphere (10⁻³ to 10⁻² torr) during the XPS measurements [6]. These conditions were found to desorb weakly bound species, and to reduce any metal oxides present.

As mentioned previously, it is possible to do in situ chemical analyses of the sample by observing core-level photoelectron peaks from the metal and from all suspected contaminants [6]. For all metals, the most important contaminant was oxygen, which we monitored via the oxygen 1s peak. Because core electron binding energies are known to be sensitive to the chemical state of the atom [7,25], the observation of core peaks for metal and oxygen should indicate something about the surface chemistry of the sample. The intensities of contaminant peaks should also be a good indicator of the amounts present. Figure 5 shows such results for iron. At room temperature, the oxygen Is peak is strong, and it possesses at least two components. The iron 3p peak is also complex and appears as a doublet due to oxidation of a thin surface layer of the sample. As the temperature is increased in the presence of hydrogen, the oxygen peak disappears (the right component disappearing first) and the left component of the iron peak also disappears, leaving a narrow peak characteristic of iron metal. Our interpretation of the disappearing components is that the left oxygen peak (higher electron binding energy) represents oxygen as oxide, the right oxygen peak (lower electron binding energy) represents oxygen present as more loosely bound adsorbed gases, and that the left iron peak (higher electron binding energy) represents oxidized iron [6,25]. Thus at the highest temperatures indicated in figure 5, we could be confident that we were studying iron metal. Similar checks were made on all the other metal samples and oxygen can be ruled out as a contaminant for every case except Pd. (We discuss Pd below.) For example, the core level peaks for Ru and Ir shown in figure 1 do not indicate any significant splitting or broadening due to chemical reaction. The results presented in table 1 indicate similar behavior for all metals studied. The carbon 1s peak was also observed and found to disappear for all cases at the temperature of our measurements.

Figure 5.

Oxygen 1s and 3p photoelectron peaks from metallic iron at various temperatures in a hydrogen atmosphere. Note that the Fe 3p component at lower kinetic energy (an “oxide” peak) disappears at high temperature along with the 01s peaks. MgKα radiation was used for excitation throughout the work reported here.

Table 1.

Summary of pertinent results for the fifteen solids studied.

Solid	Reference core levels	Ref. core level binding energy a (eV)	FWHM of core levels b (eV)	FWHM of d-band peak (eV)	Separation of 2 components in d-band peak (eV)
Fe	3p1/2–3/2 (unresolved) c	52	2.3	4.2
Co	3p1/2–3/2 (unresolved) c	57	2.5	4.0
Ni	3p1/2–3/2 (unresolved) c	66	3.4	3.0
Cu	3p1/2–3/2 (unresolved) c	75	4.2	3.0
ZnS	3p1/2–3/2 (unresolved) c	90	5.4	1.7
Ru	3d3/2–5/2	280	1.1	4.9
Rh	3d3/2–5/2	307	1.3	4.4
Pd	3d3/2–5/2	335	1.3	4.1
Ag	3d3/2–5/2	368	1.0	3.5	1.5–1.8
CdCl2	3d3/2–5/2	408	1.2	2.0
Os	4f5/2–7/2	50	1.3	6.5
Ir	4f5/2–7/2	60	1.4	6.3	3.3
Pt	4f5/2–7/2	71	1.5	5.8	3.3
Au	4f5/2–7/2	84	1.2	5.7	3.1
HgO	4f5/2–7/2	103	1.5	3.8	1.8

The reference core levels used for inelastic scattering correction are listed, along with their binding energies and widths. The widths of the d-band peaks are also given, along with the spacing of the two components in these peaks (if observed).

^aBinding energy of the l + 1/2 component, relative to the Fermi energy.

^bEqual widths assumed for both components in the least-squares fits for 3d and 4f levels.

^cThe theoretical spin-orbit splitting for the 3p levels in this series range from 1.6 eV for Fe to 3.1 eV for Zn (Ref. 36). The partially resolved doublet in ZnS is found to have a separation of 2.8 eV, in good agreement.

All metals were studied as high purity polycrystalline foils, except for Ru and Os, which were studied as powders [10].

The nonmetallic samples (ZnS, CdCl₂, and HgO) were studied as powders at room temperature. Both considerations of chemical stability and observations of core levels indicated no significant surface contamination, although high purity for these cases was not of paramount importance.

The results reported here were obtained with 1.25 keV MgKα radiation for excitation. However, no significant changes are introduced with A1Kα radiation of 1.49 keV energy.

We present below our experimental results for these d group metals, as well as the results of other experiments and theory. Statistical error limits are shown on all XPS results. Throughout our discussion, we shall speak of “ρ(E)” as determined by a certain technique, bearing in mind that no experimental technique directly measures ρ(E), but rather some distribution peculiar to the experiment (e.g., the UPS “optical density of states” [5], or the INS “transition density function” [4]), which is related to ρ(E) in some way (e.g., by our eq (5)).

The location of the Fermi energy was determined by using eq (2). This determination was checked against photoelectron peaks from a Pt standard [10]. Our estimated overall accuracy in determining E_f is ±0.5 eV, so that precise comparison of features in XPS spectra with features present in the results of other experiments (all of which have roughly the same E_f accuracy) is not always possible.

Finally, we note that the dominant feature in our results for all cases is a peak due to the bands derived from d atomic orbitals. The XPS method is not particularly sensitive to the very broad, flat, s- or p-like bands in metals, and such bands are seen with enhanced sensitivity only in studies using ion-neutralization spectroscopy [4].

3.2. The 3d Series: Fe, Co, Ni, Cu and Zn

Our results for Fe, Co, Ni, and Cu have been published elsewhere [6], but it is of interest to compare them with more recent results from theory and other experiments [3,12]. There are now enough data available that it is worthwhile to discuss and compare results for these iron group metals individually, as Eastman [12] has done.

a. Iron (bcc)

Hanzely and Liefeld [3] have studied Fe, Co, Ni, Cu, and Zn using soft x-ray spectroscopy (SXS). Their results for Fe, together with Eastman’s UPS results [12] and our own, are plotted in figure 6a. In comparing the three ρ(E) curves we note that their relative heights and areas have no significance: we have adjusted the heights to be roughly equal, in order to facilitate comparison. Also the UPS curve is terminated at E_f and is less reliable in the dashed portion, for E < E_f−4 eV [12]. With these qualifications, the overall agreement among these results from three different experimental methods is really quite good. The function ρ(E) appears to be essentially triangular, peaking just below E_f and dropping more or less linearly to zero at E ~ E_f−8 eV.

Figure 6.

Results for iron metal. The XPS data were obtained at 780 °C and have been corrected for the effects of inelastic scattering and MgKα₃,₄ x-rays. In (a) the XPS data are compared with UPS (ref. 12) and SXS (ref. 3) curves. In (b) the XPS data are shown together with a theoretical curve obtained by broadening the ferromagnetic density-of-states function of reference 26. Right ordinate is thousands of counts in the XPS data

Upon closer inspection however, the agreement is less impressive. The SXS results are somewhat narrower, but with more intensity above E_f, probably due to spurious effects [3]. There is little coincidence of structure, although the maxima for XPS and SXS coincide fairly well. A shift of ~1 eV of the XPS curve toward E_f or the UPS curve in the opposite direction would improve their agreement, but it is unlikely that the combined errors in the location of E_f location are that great.

In figure 6b, the XPS results are compared to the one-electron theoretical ρ(E) calculated by Connolly [26] for ferromagnetic iron. The theoretical ρ(E) has been smeared at the Fermi surface with a Fermi function corresponding to the temperature of our experiment (780 °C) and then broadened with a Lorentzian lineshape of 1.0 eV FWHM. It should thus represent a hypothetical “best-possible” XPS experiment in a one-electron model (i.e., eq (5) $\overline{\sigma }\left(E^{\prime }\right)$ and ρ′(hv + E′) constant). The agreement between theory and experiment is good, particularly above E_f−5 eV. The XPS (or SXS) results give somewhat higher intensity below E_f−5 eV than theory. We note that hybridization of the d bands can lead to significant broadening of the theoretical ρ(E) of Ni [14]. A similar sensitivity of the iron ρ(E) to the amount of hybridization could account for the discrepancy in width between XPS and theory.

Our reason for comparing experimental results to ferromagnetic instead of paramagnetic theoretical predictions is as follows: In experiments on ferromagnetic metals, no significant differences are observed between XPS [6, 17] and INS [4] results obtained above and below the Curie temperature (T_c, where long-range ferromagnetic order should disappear). Furthermore, exchange-induced splittings of core electronic levels in iron are the same above and below T_c [17]. It thus appears that localized moments persist above T_c for times at least as long as the duration of the photoemissron process. Local moments might be expected to affect the kinetic energy distributions of electrons ejected from valence bands and core levels [17] in much the same way, independent of the presence of long range order. Thus a comparison of experiment with a paramagnetic ρ(E) may be a priori irrelevant, inasmuch as a ferromagnetic ρ(E) takes these effects into account in an approximate way. Eastman [12] has also noted that UPS results for Fe, Co, and Ni below T_c are in general in better agreement with ferromagnetic theoretical ρ(E)’s than with similar paramagnetic theoretical results. Accordingly, we shall compare our results only with ferromagnetic theoretical curves for Ni and Co in the next sections.

b. Cobalt (fcc)

The experimental situation is illustrated by the three density-of-states curves in figure 7a. The comparison is quite similar to that for iron. Good overall agreement is apparent, with less agreement in detail. Eastman’s UPS curves [12] in both cases show structure near the Fermi energy that is missing from the SXS [3] and XPS results, and at lower energies the UPS curve tends to be higher than the others, especially in the dashed portion where it is less reliable [12]. In this region the XPS curve lies between the other two for Co as well as for Fe. One index of agreement among the three curves in the full width at half-maximum height, which is about 3,4, and 5 eV for SXS, XPS, and UPS, respectively.

Figure 7.

Results for cobalt metal. The XPS data were taken at 925 °C and have been corrected for inelastic scattering and MgKα_{3, 4} x-rays. In (a) these data are compared with UPS (ref. 12) and SXS (ref. 3) results. In (b) the comparison is with an appropriately broadened ferromagnetic theoretical curve from reference 27.

In figure 7b, we compare our XPS results to a ferromagnetic theoretical curve of Wong, Wohlfarth, and Hum [27] for hcp Co (our experiments were done on fcc Co, for which no detailed theoretical results are available). The theoretical curve has been broadened in an analogous fashion to that for iron. The agreement is good for E > E_f−3 eV, but the XPS results are somewhat high below that point. In fact, the overall agreement is probably best between theory and SXS (cf. fig. 7a).

c. Nickel (fcc)

Experimental results for Ni are presented in figure 8a [3,12]. We note a slight decrease in the XPS results in the region E < E_f−4 eV relative to our earlier work [6]. This decrease is due to a more accurate allowance for a weak inelastic loss peak appearing at ~5 eV below the primary photoelectron peaks. The three sets of data show poor agreement, with the widths of the main peak decreasing in the order UPS, XPS, SXS. The SXS results are considerably narrower than the other two (FWHM ≈2 eV, 3 eV, and 5 eV for SXS, XPS, and UPS, respectively), but agree in overall shape with XPS. The SXS results in figure 8a were obtained from measurements of L x rays [3]. Similar work on M x rays (for which transition probability modulation may be a smaller effect [2]) shows somewhat more fine structure and a FWHM of ~3 eV [2], agreeing rather well with XPS. Nickel has also been investigated by INS [4] and a smooth peak of roughly the same position and width as the XPS peak is observed. Even with an allowance for the poorer resolution of XPS, the two peaks appearing in the UPS results are not consistent with the XPS curve.

Figure 8.

Results for nickel metal. The corrected XPS data are based on measurements at 870 °C. In (a) they are compared with UPS (ref. 12) and SXS (ref. 3) curves. In (b) they are compared to the ferromagnetic theoretical density-of-states function from reference 14, which has been broadened.

The various theoretical ρ(E) estimates for Ni have been discussed previously [2,12]. The FWHM of these estimates vary from ~3 to 4.5 eV, with the smallest width coming from an unhybridized calculation [14]. In figure 8b, we compare our XPS results to a hybridized, ferromagnetic ρ(E) for Ni [14] which has been broadened in the same manner as those for Fe and Co. It is clear that the XPS results are too narrow (though they would agree in width with the unhybridized ρ(E) [14]), and that, allowing for our broadening, the UPS results are in best agreement with theory. In view of the considerable discrepancies between UPS and XPS, SXS, or INS, however, we conclude that Ni does not represent a particularly well-understood case, in contrast with Eastman’s conclusions [12].

d. Copper (fcc)

The experimental curves from UPS [12,28], SXS [3], and XPS are shown in figure 9a. There is agreement in that all curves show a peak between 2.3 and 3.3 eV below E_f, but with UPS showing more detailed structure and a somewhat uncertain overall width [12,28]. The widths and shapes of XPS and SXS are in good agreement though shifted relative to one another by ~1 eV. (A more accurate E_f location has shifted our XPS curve relative to our previous results [6].) In recent UPS work at higher photon energy (hv = 21.2 eV), Eastman [29] has obtained results with more intensity in the region 2.5 to 4.0 eV below E_f and which agree very well in shape and width with XPS and SXS. For this case it appears that even a slight increase in photon energy in the UPS measurement causes the results to look a great deal more like those of XPS. Copper has also been studied in INS [4] and the results for the d-band peak are in essential agreement with XPS and SXS.

Figure 9.

Results for copper metal. The XPS data were obtained at 720 °C and have been corrected for inelastic scattering and MgKα_3,4 x-rays. Curves from UPS (refs. 12 and 28) and SXS (ref. 3) are compared to the XPS results in (a). In (b) the XPS results are compared to a broadened theoretical curve based on reference 30.

In figure 9b, we compare a broadened version of the theoretical ρ(E) due to Snow [30] with our XPS results. The agreement is excellent, and would also be so for SXS if we permit a shift of ~1 eV in E_f. The coincidence in energy of structure in the UPS curve with structure in the unbroadened theoretical ρ(E) has been discussed previously [28], but we note that the relative intensities of the various features noted do not in fact coincide with theory.

e. Zinc (as ZnS)

Zinc has been studied by XPS only in compounds, because of the difficulty of obtaining a clean metallic surface. We present results for ZnS in figure 10. The 3d electronic states show up as a narrow intense peak with a FWHM of 1.7 eV and located ~13 eV below E_f. (The separation of this peak from E_f may be too large, because of charging of the sample [25].) The valence bands are just above the d peak. The d states of metallic zinc have been studied also by SXS [3], and a peak of FWHM = 1.45 eV, at 8 eV below E_f, was obtained. Thus XPS and SXS are in good agreement on the width of these core-like 3d states, which are only about 10 eV below E_f.

Figure 10.

Corrected XPS spectrum for ZnS, showing a narrow intense peak from the 3d levels, as well as the broad, flat valence bands.

3.3. The 4d Series: Ru, Rh, Pd, Ag and Cd

The corrected XPS spectra for the four metals Ru, Rh, Pd, and Ag are shown in figure 11. The metals are discussed separately below.

Figure 11.

Corrected XPS spectra for the 4d metals Ru, Rh, Pd, and Ag.

a. Ruthenium (hcp)

Our results for Ru are characterized by a single peak of ~4.9 eV FWHM. The high energy edge is quite sharp, reaching a maximum value at about E_f−1.7 eV. The peak is rather flat, and there is some evidence for a shoulder at E_f−4.5 eV. The peak falls off more slowly with energy on the low energy side than near E_f. The reference core level widths in Ru were quite narrow, as indicated in table 1, and spurious effects due to surface contamination are unlikely. There are no other experimental or theoretical results on Ru presently available for comparison with our data.

b. Rhodium (fcc)

The XPS-derived ρ(E) can be described by a single triangular peak, very steep on the high energy side, and reaching a maximum at E_f−1.3 eV. There is little evidence for structure on the low energy side, which falls off monotonically. The peak FWHM of ~4.4 eV is slightly smaller than that for Ru. No other experimental or theoretical results on Rh are available for comparison.

c. Palladium (fcc)

Our corrected results for Pd have much the same appearance as those for Rh, but the Pd peak is slightly narrower with a FWHM of ~4.1 eV and the maximum occurs at E_f−1.7 eV. The high-energy edge of the Pd peak is very steep, and most of the slope must be instrumental. Therefore, as expected, the true ρ(E) for Pd is apparently very sharp at E_f.

The results presented in figure 11 have been corrected for a weak inelastic loss peak at 6 eV, and also for the presence of a small peak at E_f−10 eV, arising from oxygen present as a surface contaminant. Samples of Pd were heated in hydrogen to approximately 700 °C and then studied at this temperature with either a hydrogen or argon atmosphere. It was not possible under these conditions (or even by heating to as high as 900 °C) to get rid of the oxygen Is peak completely. Fortunately, the only effect of a slight oxygen contamination on the valence band XPS spectrum of certain metals appears to be a sharp peak at E_f −10 eV (probably caused by photoemission from 2p-like oxygen levels). We have also observed this effect for slightly oxidized Cu. Thus we were able to correct our Pd results for this peak (which does not affect the region shown in fig. 11). A recently obtained uncorrected XPS spectrum for Pd is in good agreement with our results [31].

Palladium has also been studied by UPS [32,33], and the agreement with XPS is good in general outline. However, the precise shape of the UPS results below approximately E_f−3.5 eV is uncertain [32,33].

In figure 12, we compare our results with the theoretical predictions of Freeman, Dimmock, and Furdyna [34]. The upper portion of the figure shows the fine structure of their ρ(E) histogram and in the lower portion we compare our results to the broadened theoretical curve. The agreement between XPS and theory is good, although the shape of the peak is somewhat different.

Figure 12.

Comparison of PdXPS results with theory: (a) theoretical density-of-states function from reference34, indicating the complexity of the one-electron ρ(E), (b) XPS results and a broadened theoretical curve.

d. Silver (fcc)

Our results for Ag also appear in figure 11. They differ in several respects from the Pd curve. The d bands are filled and below E_f, giving rise to a narrow peak (FWHM = 3.5 eV) with its most intense component at E_f−5.3 eV. The edges of this peak are quite sharp, in view of the instrumental contributions of XPS.

The 3d_3/2 and 3d_5/2 levels of Ag are also very narrow (see table 1), indicating no spurious linewidth contributions from instrumental or contamination effects. There is also strong evidence for a weaker component at ~E_f−6.6 eV. This two-component structure has also been verified by Siegbahn and co-workers in uncorrected XPS spectra [7,31]. Very similar structure appears in the d bands of several 5d metals and we discuss the possible significance of this below (sec. 3.5).

Silver has also been studied by means of UPS [5,29,35], using radiation up to 21.2 eV [29] in energy. The results of these studies (in particular those attained at 21.2 eV) are in essential agreement with our own, in that they show a peak of ~3 eV FWHM at E_f−5.0 eV.

No theoretical ρ(E) predictions for Ag are available at the present time.

e. Cadmium (as CdCI₂)

A corrected XPS-spectrum for CdCl₂ is shown in figure 13. The 4d peak appears at ~E_f−14.5 eV and the valence bands fall between roughly 5 and 10 eV below E_f. The 4d peak is very narrow (a FWHM of 1.7 eV, compared to 3.5 eV for Ag). As these d levels are quite strongly bound, we expect them to behave as core states, and perhaps to exhibit spin-orbit splitting (into d_3/2 and d_5/2 components). There is no evidence for splitting of this peak, but its shape is consistent with a theoretical free-atom prediction of only a 0.8 eV spin-orbit splitting [36]. The analogous 5d-series levels in HgO do exhibit resolvable spin-orbit splitting, however (sec. 3.4.e).

Figure 13.

Corrected XPS spectrum for CdCl₂. The filled 4d states appear at E-E_f ≈ −14.5 eV. The broader peak at E-E_f ≈ −7 eV represents valence bands.

3.4. The 5d Series: Os, Ir, Pt, Au, and Hg

The corrected XPS spectra for the metals Os, Ir, Pt, and Au are shown in figure 14.

Figure 14.

Corrected XPS spectra for the 5d metals Os, Ir, Pt, and Au.

a. Osmium (hcp)

Hexagonal Os gives a valence band spectrum similar to that of hexagonal Ru. As in the Ru case, the Os peak rises sharply near E_f to a plateau beginning at E_f−1.7 eV. The flat region of the Os peak extends over approximately 3 eV, and is broader than that for Ru. No comparisons with theory or other experiments are possible as yet.

The low energy tail of the Os peak does not fall to the base line primarily because of spurious photoelectron intensity in the valence band region due to the proximity of the very intense Os4f levels in energy (see table 1). These core levels appear to interact with very weak Mg x rays whose energies are as high as ~1300 eV, giving rise to photoelectrons in the same kinetic energy region as valence bands interacting with the 1250 eV MgKα_{1, 2} x rays. Similar problems were encountered with Ir, but they do not affect our conclusions as to peak shapes and structure. An additional problem was encountered in correcting for the MgKα_3,4 x rays in both Os and Ir, as the low intensity 5p_1/2 and 5p_3/2 photoelectron peaks overlap the α_3,4 regions of the reference 4f peaks. For example, this effect appears as a slight deviation of the data from the fitted function near a kinetic energy of 1202 eV in figure 1. However, the α₃,₄ correction is a small one and could nonetheless be made with sufficient accuracy not to affect our fundamental conclusions.

b. Iridium (fcc)

The corrected XPS results for iridium are similar to those of Os in overall shape and width, but give evidence for two peaks, at approximately E_f−1.5 eV and E_f−4.5 eV. This two-peak structure is even clearer in the uncorrected XPS spectrum for Ir shown in figure 15. The higher-energy peak appears to be narrower, and, with allowance for this, we estimate the two peaks to be of roughly equal intensity.

Figure 15.

Uncorrected XPS spectrum for Ir, in which the two-peak structure is clearly shown.

c. Platinum (fcc)

Our corrected XPS results for Pt exhibit two partially-resolved peaks at E_f−1.6 eV and E_f−4.0 eV, with the more intense component lying nearer E_f. The steep slopes of our spectra for both Ir and Pt near E_f are consistent with the Fermi surface cutting through the d bands in a region of very high ρ(E). The separations of the two components observed in the d bands are thus very nearly equal for Ir and Pt, but the relative intensities are different.

Theoretical results are available for Pt. The band-structure calculations of Mueller et al. [37] are shown in figure 16, together with our data. The theoretical ρ(E) is also shown after broadening, to facilitate comparison. We note that both theory and experiment show roughly two major peaks but that the relative intensities are in poor agreement. The disagreement as to shape is the same as that observed for Pd in figure 12. (Relative intensities are arbitrary in both of these figures.) In addition, the band-structure calculations give a total width at half height of 8 eV, while the XPS data show a width of only 6 eV. Thus the overall agreement is only fair.

Figure 16.

Comparison of Pt XPS results with theory: (a) the theoretical density-of-states function of reference 37, (b) the broadened theoretical curve is compared to our XPS results.

d. Gold (fcc)

The d bands of gold are filled and should lie several eV below E_f, as our results in figure 14 indicate. Two peaks are again evident in the corrected XPS results for gold, and these have been verified in uncorrected XPS spectra obtained by Siegbahn and co-workers [7,31]. The statistical accuracy of our data is quite good, and we can say that the lower intensity peak at E_f−6.8 eV is narrower than the higher intensity peak at E_f− 4.1 eV. Apart from this, the shape of the d-band peak for Au is very similar to that for Pt.

Gold has also been studied by means of UPS [29,38]. In experiments at photon energies up to 21.2 eV [38], a two-peak structure is found, with components at E_f−3.4 eV and E_f−6.1 eV. The component at −3.4 eV is also observed to be split into a doublet [38], perhaps accounting for its extra width in the XPS results. Furthermore, a spectrum obtained with hv = 26.9 eV [29] (but not corrected for inelastic scattering) looks very much like our XPS results, again indicating that with increase in photon energy, UPS results converge rather quickly to those of XPS.

There are no theoretical ρ(E) estimates at present available for Au.

e. Mercury (as HgO)

In HgO, the filled 5d levels should be tightly-bound and core-like. Figure 17 shows a corrected XPS spectrum for HgO, in which the 5d levels appear as a doublet whose components lie 13.6 and 12.0 eV below E_f. Valence bands overlap the high energy edge of the d peaks and extend to E_f−5 eV. The intensity ratio of the two 5d peaks, as derived by least-squares fitting of Lorentzian curves to our data, is 1.4:1.0. The separation and intensity ratio are consistent with a d_3/2 − d_5/2 spin-orbit doublet, as the free-atom theoretical prediction is for a 2.1 eV separation [36] and the intensity ratio should be given by the level multiplicities (i.e., 6:4 = 1.5:1.0). (We have verified that the intensity ratios for the 3d_3/2 − 3d_5/2 core levels of the 4d metals in table 1 follow this rule to within experimental accuracy (± 0.1).) Thus the 5d levels of HgO appear to be very core-like. Furthermore, the relative intensity of the two components in the doublet is similar to those observed in Pt and Au. We discuss the possible implications of this similarity in the next section.

Figure 17.

Corrected XPS spectrum for HgO. The intense doublet at E-E_f ≈ −12 eV is due to the core-like 5d_3/2 and 5d_5/2 states.

3.5. Discussion of Results

The XPS results for all 15 cases studied are presented in figure 18. In table 1 are given the binding energies and widths of the reference core levels used for correcting valence band spectra, as well as the width of the peak due to the d bands and (where observed) the separation of the two primary components in this peak.

Figure 18.

Summary of the XPS results for the fifteen solids studied (cf. table 1). The peaks for ZnS, CdCl₂, and HgO lie at E-E_f ≈ −13 eV, −14eV, and −12eV, respectively.

Within a 3d, 4d, or 5d series, the XPS results show systematic variation, giving somewhat wider d bands for Fe, Ru, and Os than for Cu, Ag, and Au, respectively, and even narrower core-like states ~10 eV below E_f for ZnS, CdCl₂, and HgO. Much of this variation is no doubt connected with a one-electron ρ(E), but we note also that experimental spectra obtained from metals with partially filled d bands might be broadened by the coupling of a localized hole to localized d electrons [17] (see fig. 3c and sec. 2). The 4d bands studied are only slightly wider than their 3d counterparts; the 5d bands are considerably wider and show gross structure.

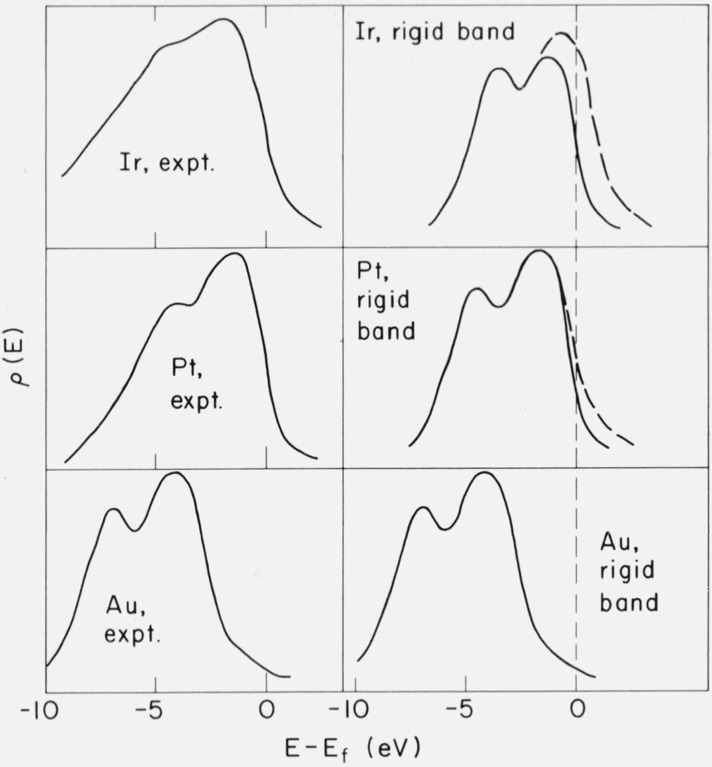
Within two isomorphous series – Rh, Pd, Ag and Ir, Pt, Au, all members of which are face-centered cubic – there is sufficient similarity of the shapes of the d-band peaks to suggest a rigid-band model for ρ(E). If ρ(E) of Ag(Au) can be used to generate ρ(E) of Rh and Pd (Ir and Pt) simply by lowering the Fermi energy to allow for partial filling of the d bands, then this model would apply. The peaks for Rh and Pd are too wide to be represented by a Ag ρ(E), but the shapes of both could be very roughly approximated in this manner. The similarity of the two-peak structure for the three metals Ir, Pt, and Au gives more evidence for the utility of a rigid band model, especially as the uncorrected results for Ir (fig. 15) show a narrower peak near E_f (as though it were a broader peak cut off by the Fermi energy). The application of this model to the prediction of the experimental ρ(E)’s for Ir and Pt is shown in figure 19. The predictions are reasonably good. In our opinion, this limited success for Ir, Pt and Au probably indicates some similarity in the d bands in these metals, but we do not take it as a verification of the rigid band model per se.

Figure 19.

An attempt to reproduce the shapes of the experimental XPS spectra for the 5d metals Ir, Pt, and Aufrom a Au-like rigid band density of states. Vertical scales are arbitrary. Note that the Ir experimental curve does not fall to as low a value as Pt or Au at low energy due to spurious sources of photoelectron intensity (see text).

The two-component structure observed in the d-band peaks of Pt and Au is very similar to the unresolved structure found in Ag. That is, a more intense component appears nearer E_f. To estimate the intensity ratios of these components more accurately, we have least-squares fitted two Gaussian peaks of equal width to our data for these three metals. The ratios and separations so derived are: Ag–1.51:1.00, 1.8 eV; Pt–1.60:1.00, 3.3 eV; and Au–1.48:1.00, 3.1 eV. As our accuracy in determining these ratios is ~ ±0.1, they could all be represented by a value of 1.50:1.00. A possible significance of this value is that it is the expected (and observed) intensity ratio for a spin-orbit split d level (e.g., the 5d levels of HgO). Thus, one might argue that as the 4d and 5d shells move nearer to the Fermi surface with decreasing Z, they must go continuously from core states to valence states, perhaps retaining some degree of simple spin-orbit character in the process. The observed separations are 1.5–2.5 times larger than free-atom theoretical spin-orbit splittings [36], but the various perturbations of the lattice might be responsible for this. Speaking against such a simple interpretation, however, is our observation (verified in UPS results [29,38]) that for Au the component nearer E_f is broader. In fact, the UPS results for hv ⩽ 21.2 eV show this component split into two peaks [29,32]. In view of this, our intensity ratio estimates based on two peaks of equal width may not have fundamental significance, and the agreement of these ratios, particularly between Ag and Pt or Au could be somewhat accidental. Nonetheless, the similarity in shape of our results for the d levels of Ag, Pt, Au, and Hg is rather striking.

We have noted that for Cu, Ag, and Au, the recent UPS work of Eastman [29] at higher photon energies (21.2 to 26.9 eV) is in much better agreement with XPS results than previous studies using a range of lower photon energies [28,35,38]. It thus appears that as the photon energy is increased in a UPS experiment, the form of the energy distributions can be expected to approach rather quickly that observed in XPS work. We feel that photoelectron spectra for which XPS and UPS show agreement ought to be much more closely related to ρ(E). Further UPS experiments at greater than 20 eV photon energies would thus be most interesting.

4. Concluding Remarks

We have discussed the use of x-ray photoelectron spectroscopy (XPS) in the determination of densities of states. The application of this technique to the d bands of 12 metals and 3 nonmetallic solids seems to indicate that reliable information about the overall shape of ρ(E) can be obtained. The results show systematic behavior with changes in Z and crystal structure and agree qualitatively and in some cases quantitatively with theoretical predictions for both unfilled valence d levels and filled core-like d levels.

Throughout our discussion, we have placed special emphasis on comparison of XPS with the closely related ultraviolet photoelectron spectroscopy (UPS). It appears that UPS at the present time has an advantage in resolution, but that XPS results can be more easily corrected for inelastic scattering, are not significantly affected by final state density, and are less susceptible to the effects of surface contaminants. UPS results at photon energies ⩾20 eV appear to be more reliable indicators of ρ(E) in the sense that they agree better with the rough outline predicted by XPS. The need for further work at higher resolution and at all photon energies (including those in the relatively untouched range from 20 to 1250 eV) is evident.