Multidimensional Computerized Adaptive Testing Using Non-Compensatory Item Response Theory Models

Abstract

Current use of multidimensional computerized adaptive testing (MCAT) has been developed in conjunction with compensatory multidimensional item response theory (MIRT) models rather than with non-compensatory ones. In recognition of the usefulness of MCAT and the complications associated with non-compensatory data, this study aimed to develop MCAT algorithms using non-compensatory MIRT models and to evaluate their performance. For the purpose of the study, three item selection methods were adapted and compared, namely, the Fisher information method, the mutual information method, and the Kullback–Leibler information method. The results of a series of simulations showed that the Fisher information and mutual information methods performed similarly, and both outperformed the Kullback–Leibler information method. In addition, it was found that the more stringent the termination criterion and the higher the correlation between the latent traits, the higher the resulting measurement precision and test reliability. Test reliability was very similar across the dimensions, regardless of the correlation between the latent traits and termination criterion. On average, the difficulties of the administered items were found to be at a lower level than the examinees’ abilities, which shed light on item bank construction for non-compensatory items.

Over the past decades, multidimensional item response theory (MIRT) models in conjunction with computerized adaptive testing (CAT) (referred to as MCAT) has developed gradually as practitioners have recognized its advantages of increasing the precision and reliability for the latent traits or reducing test length through borrowing information between each latent trait when compared with unidimensional CAT (Mulder & van der Linden, 2009, 2010; Segall, 1996; van der Linden, 1999; Veldkamp & van der Linden, 2002; C. Wang & Chang, 2011; W.-C. Wang & Chen, 2004). In general, there are two types of MIRT models—compensatory and non-compensatory, denoted as MIRT-C and MIRT-N, respectively. In compensatory models, a high level of one latent trait can compensate for a low level of another latent trait. In contrast, such compensation between latent traits is not feasible in non-compensatory models. In past studies, however, MCAT has comprised only MIRT-C (denoted as MCAT-C), leaving MCAT for MIRT-N (denoted as MCAT-N) undeveloped. The main purpose of this study was to develop algorithms for MCAT-N and to conduct simulations to evaluate their performance.

Different cognitive strategies or processes may not compensate each other in solving an item. Take arithmetic word problems as an example. To solve arithmetic word problems, two latent traits may be involved. One is reading proficiency, which enables examinees to understand the problems, and the other is arithmetic proficiency, which enables examinees to establish the appropriate equations and to solve them. Apparently, these two kinds of proficiency cannot compensate for each other because a low level of either proficiency will lead to incorrect answers. Several MIRT-N models have been developed for non-compensatory items. Whitely (1980) proposed a one-parameter logistic MIRT-N model to analyze the verbal aptitude test of the American College Testing (ACT) Program Examination, which involved three dimensions, image construction, event recovery, and response evaluation, in solving a verbal aptitude item. Maris (1995) fitted the same model to typical verbal intelligence test items that asked for one or more synonyms of a given word and found two dimensions were involved: generation and evaluation (Janssen, Hoskens, & De Boeck, 1993). Embretson and Yang (2013) generalized Whitely’s model for cognitive diagnosis to high-stakes multiple-choice mathematics items, which involved four dimensions (components): number/computation, algebra, geometry, and data analysis. A few items involved only one dimension, whereas the others involved two or more dimensions. It was found that Whitely’s model was not only more theoretically sound but also had a better fit than MIRT-C models.

Violations of the assumption of unidimensionality have a serious effect on parameter estimation under non-compensatory multidimensional structures (Ackerman, 1989; Ansley & Forsyth, 1985; Way, Ansley, & Forsyth, 1988). Ackerman (1989) simulated data according to the two-dimensional MIRT-C and MIRT-N models, and fitted both models to the simulated data. He observed that the difference in the probability of success between the two models was small when items discriminated mainly in one dimension, but large when items discriminated similarly in both dimensions. In addition, it appeared as if more information was provided by the compensatory items than by the non-compensatory items; thus, mistakenly fitting MIRT-C to non-compensatory data overestimates measurement precision, which, in turn, may lead to incorrect hypothesis testing and conclusions. All of these studies suggest that MIRT-N models are very different from MIRT-C models, which implies that the findings obtained from MCAT-C may not directly apply to MCAT-N.

This study aimed to fill the research gap through the development of MCAT-N algorithms. Specifically, item selection and ability estimation methods for non-compensatory items were derived, simulation studies to evaluate their performance were conducted, and some insights on operational MCAT-N were provided. In the rest of the article, MIRT-C and MIRT-N were briefly introduced, and item selection methods and ability estimation that have been developed in MCAT-C to MCAT-N were adapted. The difference in item response surfaces and item information functions between MIRT-C and MIRT-N was demonstrated, and the results of a series of simulation studies that were conducted to evaluate the performance of the new algorithms were summarized. Based on these findings, information on constructing MCAT-N can be offered to practitioners. Finally, conclusions were drawn and potential directions for future studies were provided. In many CAT simulation studies, the unidimensional or multidimensional two-parameter logistic model is generally used for demonstration, while the one- or two-logistic model is used for inference. This common practice in this study was followed.

Models

As in MCAT-C, there are four major components in MCAT-N, including a MIRT-N model to calibrate items, an item selection method, an ability estimation method, and a termination criterion. Of these components, the focus in this study is on item selection methods. As this is a CAT study, item parameters are assumed to be known a priori. In practice, both item and person parameters must be calibrated when item banks are being constructed. For the accuracy of item parameter estimation, when items are loaded mainly on only one dimension, the parameter estimation bias is close to zero, the root mean squared error is small, and the correlation between the true and estimated parameters is nearly 1, regardless of the correlation between dimensions. When items are loaded on more than one dimension, the parameter estimation becomes less accurate as the correlation between dimensions becomes higher, especially in a short test with small sample size (Bolt & Lall, 2003; C. Wang & Nydick, 2015). The problem in producing less accurate parameter estimates can be lessened by increasing the number of items and sample size (i.e., the amount of data). In other words, the dimensions must be divergent or the amount of data must be large to obtain well-estimated non-compensatory parameters. The reader is referred to Bolt and Lall (2003) and C. Wang and Nydick (2015) for item parameter estimation in MIRT-N.

The three-parameter logistic compensatory MIRT model for dichotomous items (Hattie, 1981; Reckase, 1985), including the two- and one-parameter logistic compensatory MIRT models as special cases (McKinley & Reckase, 1983), can be defined as follows:

$$P(X_{\mathrm{ij}}=1|{\mathbf{a}}_j,b_j,c_j,{\mathbf{\theta }}_{\mathbf{i}})=c_j+(1-c_j)\frac{1}{1+\exp [-\sum _{k=1}^K{a}_{\mathrm{jk}}({\theta }_{\mathrm{ik}}-b_j)]},$$ (1)

where X_ij is the score of person i on item j; ${\mathbf{\theta }\mathbf{\prime }}_i=({\theta }_{i1},{\theta }_{i2},\dots {\theta }_{\mathrm{iK}})$ is a vector of K-dimensional latent traits for examinee i; ${\mathbf{a}\mathbf{\prime }}_j=(a_{j1},a_{j2},\dots ,a_{\mathrm{jK}})$ is a vector of K-dimensional discrimination parameters for item j with elements of a_jk as the discrimination parameter of item j on dimension k, and b_j and c_j are the difficulty and pseudo-guessing parameters of item j, respectively. Because the K-dimensional latent traits are linked by a summation (weighed by the discrimination parameters), a low level on one latent trait can be compensated for by a high level on another.

In contrast, the three-parameter logistic non-compensatory MIRT model (Sympson, 1978) is defined as follows:

$$P(X_{\mathrm{ij}}=1|{\mathbf{a}}_j,{\mathbf{b}}_j,c_j,{\mathbf{\theta }}_{\mathbf{i}})=c_j+(1-c_j)\underset{k=1}{\overset{K}{\Pi }}\frac{1}{1+\exp [-a_{\mathrm{jk}}({\theta }_{\mathrm{ik}}-b_{\mathrm{jk}})]},$$ (2)

where, X_ij, a_j, c_j, and θ_i have been defined previously, and ${\mathbf{b}\mathbf{\prime }}_j=(b_{j1},b_{j2},\dots ,b_{\mathrm{jK}})$ represents the vector of difficulty parameters for item j, with elements of b_jk as the difficulty parameter of item j on dimension k. Because the K-dimensional latent traits are connected by a product, compensation between the latent traits is not possible. Equation 2 can be reduced to the two- or one-parameter logistic non-compensatory MIRT model. The one-parameter logistic non-compensatory MIRT model can be regarded as a relaxation of Whitely’s multicomponent latent trait model (Whitely, 1980). Note that there is a single difficulty for an item in MIRT-C (Equation 1), but there are K difficulties for an item in MIRT-N, with one difficulty for each dimension (Equation 2).

Ability Estimation

As with MCAT-C, latent traits in MCAT-N can be estimated by the maximum likelihood estimator (MLE) or a Bayesian estimator, such as the maximum a posteriori (MAP) or expected a posteriori (EAP) estimator. The EAP computation time increases exponentially with the number of dimensions and the MLE can only be obtained until both correct and incorrect responses are observed. The authors focused on the MAP estimator in this study. Let us assume that L(x|θ) is the likelihood of the observed response vector x, given latent trait θ, that f(θ) is the prior distribution of θ, and that f(x) is the marginal probability of x. In the Bayes’s theorem, the posterior density function of θ is (Segall, 1996) as follows:

$$f(\mathbf{\theta }\mathbf{|}\mathbf{x})=L(\mathbf{x}|\mathbf{\theta })\frac{f\left(\mathbf{\theta }\right)}{f\left(\mathbf{x}\right)}.$$ (3)

Let us assume that the prior distribution of θ is a multivariate normal distribution with a mean vector of μ and a variance–covariance matrix of Σ:

$$f\left(\mathbf{\theta }\right)={\left(2\pi \right)}^{-\frac{K}{2}}{\left|\Sigma \right|}^{-\frac{1}{2}}\exp [-\frac{1}{2}(\mathbf{\theta }\mathbf{-}\mathbf{\mu })\prime {\Sigma }^{-1}(\mathbf{\theta }\mathbf{-}\mathbf{\mu })].$$ (4)

The MAP estimator of θ can then be obtained by maximizing the natural logarithm of the posterior distribution $\raisebox{1ex}{$\partial $}\!\left/ \!\raisebox{-1ex}{$\partial \theta $}\right.\ln f(\theta |x)$.

Under the three-parameter logistic non-compensatory MIRT model (Equation 2), it can be shown that

$$\frac{\partial }{\partial {\theta }_k}\ln f(\mathbf{\theta }\mathbf{|}\mathbf{x})=\sum _{j\in \mathbf{\nu }}\left[\frac{a_{\mathrm{jk}}(1-p_{\mathrm{jk}})[P_j\left(\mathbf{\theta }\right)-c_j][x_j-P_j\left(\mathbf{\theta }\right)]}{P_j\left(\mathbf{\theta }\right)Q_j\left(\mathbf{\theta }\right)}\right]-[\frac{\partial }{\partial \mathbf{\theta }}(\mathbf{\mu }\mathbf{-}\mathbf{\theta })\prime ]{\Sigma }^{-1}(\mathbf{\mu }\mathbf{-}\mathbf{\theta }),$$ (5)

where $p_{jk}=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$1+\exp [-a_{jk}({\theta }_k-b_{jk})]$}\right.$; P_j(θ) is defined in Equation 2; Q_j(θ) is 1 –P_j(θ); x_j is the response to item j; the other symbols were defined previously.

Let us assume that H(θ) is the Hessian matrix of θ, whose diagonal elements can be expressed as follows:

$$\begin{array}{c}\multicolumn{1}{c}{\frac{{\partial }^2}{\partial {\theta }_k^2}\ln f(\mathbf{\theta }\mathbf{|}\mathbf{x})=\sum _{j\in \nu }\frac{a_{\mathrm{jk}}^2(1-p_{\mathrm{jk}})[P_j\left(\mathbf{\theta }\right)-c_j]}{{\left[P_j\left(\mathbf{\theta }\right)Q_j\left(\mathbf{\theta }\right)\right]}^2}}\\ \multicolumn{1}{c}{\{(1-p_{\mathrm{jk}})[x_j{c}_j[Q_j\left(\mathbf{\theta }\right)-P_j\left(\mathbf{\theta }\right)]-P_j^2\left(\mathbf{\theta }\right)(1-x_j-c_j)]+P_j\left(\mathbf{\theta }\right)Q_j\left(\mathbf{\theta }\right)p_{\mathrm{jk}}[P_j\left(\mathbf{\theta }\right)-x_j]\}-{\varphi }^{\mathrm{kk}},}\end{array}$$ (6)

and the off-diagonal elements as follows:

$$\frac{{\partial }^2}{\partial {\theta }_k\partial {\theta }_l}\ln f(\mathbf{\theta }\mathbf{|}\mathbf{x})=\sum _{j\in \nu }\frac{a_{\mathrm{jk}}{a}_{\mathrm{jl}}(1-p_{\mathrm{jk}})(1-p_{\mathrm{jl}})[P_j\left(\mathbf{\theta }\right)-c_j]}{{\left[P_j\left(\mathbf{\theta }\right)Q_j\left(\mathbf{\theta }\right)\right]}^2}\{x_j{c}_j[Q_j\left(\mathbf{\theta }\right)-P_j\left(\mathbf{\theta }\right)]-P_j^2\left(\mathbf{\theta }\right)(1-x_j-c_j)\}-{\varphi }^{\mathrm{kl}},$$ (7)

where ${\varphi }^{\mathrm{kk}}$ and ${\varphi }^{\mathrm{kl}}$ are the kth–kth and kth–lth elements of Σ^–1. An iterative numerical procedure, such as the Newton–Raphson procedure, can be used to approximate the values of θ, because there are no closed-form solutions for maximizing the natural logarithm of the posterior distribution. Let us assume that θ^(m) is the mth approximation to the value of θ that maximizes ln f(θ|x). The m+1th approximation with an even higher likelihood is ${\hat{\mathbf{\delta }}}^{(m+1)}={\hat{\mathbf{\theta }}}^{(m)}-{\hat{\mathbf{\Delta }}}^{(m)}$, where

$${\hat{\mathbf{\Delta }}}^{\left(m\right)}={\left[\mathbf{H}\left({\mathbf{\theta }}^{\mathbf{\left(}\mathbf{m}\mathbf{\right)}}\right)\right]}^{-1}\times \frac{\partial }{\partial \mathbf{\theta }}\ln f({\mathbf{\theta }}^{\mathbf{\left(}\mathbf{m}\mathbf{\right)}}|\mathbf{x}).$$ (8)

Item Selection

Item selection methods in MCAT-C cannot be completely transplanted to MCAT-N without any adaptation, including methods such as the maximum determinant of the Fisher information matrix (denoted as the FI method) (Segall, 1996), the maximum Kullback–Leibler (KL) information index (denoted as the KL method) (Veldkamp & van der Linden, 2002), the minimum trace of the inverse FI matrix (van der Linden, 1999), the minimum KL distance between two subsequent posteriors (Mulder & van der Linden, 2010), the maximum mutual information (denoted as the MI method) (Mulder & van der Linden, 2010), and the minimum Shannon entropy (C. Wang & Chang, 2011). C. Wang and Chang (2011) theoretically connected the FI, KL, and MI and Shannon entropy methods in the MCAT-C context, and observed that the FI and MI methods performed similarly and both outperformed the Shannon entropy and KL methods. In addition, the FI and MI methods yielded a high overlap rate in item selection, while the FI and KL methods yielded a moderate overlap rate.

This study focuses on the FI, KL, and MI methods, and other methods have been left for future studies. The FI method is chosen because it is the most widely used in CAT. The KL method is also widely used. In addition, it considers global information on the latent estimates, so it may outperform the FI method at the early stage of CAT (Chang & Ying, 1999). The MI and Shannon entropy methods have received much attention in recent years and can be viewed as variants of the KL method. The MI method, which includes the Shannon entropy method as a special case, outperforms the Shannon entropy method because the methods use different baselines to calculate the KL information (C. Wang & Chang, 2011). In addition to these three item selection methods, the random selection (RS) method is used as a baseline for comparison.

In the FI method, the amount of item information about the unknown parameter θ for item j is defined as follows:

$$I\left({\mathbf{\theta }}_{\mathbf{j}}\right)=-E[\frac{{\partial }^2}{\partial \mathbf{\theta }\mathbf{\partial }\mathbf{\theta }\mathbf{\prime }}\ln f(X_j=x|\mathbf{\theta })|\mathbf{\theta }].$$ (9)

When the three-parameter logistic non-compensatory MIRT model (Equation 2) is used, the item information matrix can be shown as follows:

$$\frac{{\left[P_j\left(\mathbf{\theta }\right)-c_j\right]}^2}{P_j\left(\mathbf{\theta }\right)Q_j\left(\mathbf{\theta }\right)}\left[\begin{array}{cccc}{a}_{j1}^2{\left(1-p_{j1}\right)}^2& a_{j1}{a}_{j2}\left(1-p_{j1}\right)\left(1-p_{j2}\right)& \cdots & a_{j1}{a}_{jK}\left(1-p_{j1}\right)\left(1-p_{jK}\right)\\ a_{j1}{a}_{j2}\left(1-p_{j1}\right)\left(1-p_{j2}\right)& a_{j2}^2{\left(1-p_{j2}\right)}^2& \dots & ⋮\\ ⋮& ⋮& \dots & ⋮\\ a_{j1}{a}_{jK}\left(1-p_{j1}\right)\left(1-p_{jK}\right)& a_{j2}{a}_{jK}\left(1-p_{j2}\right)\left(1-p_{jK}\right)& \cdots & a_{jK}^2{\left(1-p_{jK}\right)}^2\end{array}\right].$$ (10)

Thus, the information matrix given in Equation 10 consists of two factors: (a) a function of θ, $\frac{{[P_j(\mathbf{\theta }\mathbf{)}\mathbf{-}{\mathbf{c}}_{\mathbf{j}}\mathbf{]}}^2}{P_j(\mathbf{\theta }\mathbf{)}{\mathbf{Q}}_{\mathbf{j}}\mathbf{(}\mathbf{\theta }\mathbf{)}}$, which is the factor common to all components of the information matrix, and (b) a matrix ${\mathit{a}}_j(1-{\mathit{p}}_j)[{\mathit{a}}_j(1-{\mathit{p}}_j{)]}^T$. It is clear that $\frac{{[P_j(\mathbf{\theta }\mathbf{)}\mathbf{-}{\mathbf{c}}_{\mathbf{j}}\mathbf{]}}^2}{P_j(\mathbf{\theta }\mathbf{)}{\mathbf{Q}}_{\mathbf{j}}\mathbf{(}\mathbf{\theta }\mathbf{)}}$ forms a dependency on θ through the response function P_j(θ) in Equation 2. Because P_j(θ) is the product of the K-dimensional probabilities, which means that the values of P_j(θ) are unique, P_j(θ) is produced by a specific combination of dimensions. When an examinee with θ₁ = 0 and θ₂ = 3, for instance, a two-dimension item with P_j(θ) = 0.5 may be found by (a₁ = 1, a₂ = 1, b₁ = 0, b₂ = −3, c = 0) or (a₁ = 1, a₂ = 1, b₁ = −3, b₂ = 3, c = 0); nonetheless, they have distinct depictions even though the same values of P_j(θ) are obtained. Item (a₁ = 1, a₂ = 1, b₁ = 0, b₂ = −3, c = 0) portrays that Dimension 1 dominates the value of P_j(θ) is 0.5, and item (a₁ = 1, a₂ = 1, b₁ = −3, b₂ = 3, c = 0) vice versa. Specially, an item can be selected to differentiate a set of specific latent traits due to its unique P_j(θ). Likewise, there are two factors in the information matrix of MCAT-C (Segall, 1996), and one is a function of θ and the other is matrix ${\mathbf{a}}_j{{\mathbf{a}}_j}^T$. In this situation, however, the values of P_j(θ) do not depend on the latent traits as long as ${\mathbf{a}}_j\mathbf{\theta }$ is constant. In other words, it is problematic to discriminate which dimension governs the P_j(θ) value inasmuch as the combination of the latent traits is equal to the item difficulty. That is to say, any fixed constant of the latent traits would yield the identical P_j(θ); consequently, it is difficult to distinguish between the dimensions.

Let us assume that ${\hat{\mathbf{\theta }}}^{(t)}$ is the interim estimate of θ obtained by responses to t items, and that $\mathbf{I}({\hat{\mathbf{\theta }}}^{(t)})$ and $\mathbf{I}({\hat{\mathbf{\theta }}}^{(t)},X_j)$ are the Fisher information elements acquired by the previously administered t items and after administering item j, respectively. The FI method adaptively selects item j to maximize the determinant of the provisional FI method, as follows:

$$\mathrm{FI}=|\mathbf{I}\left({\hat{\mathbf{\theta }}}^{\left(t\right)}\right)+\mathbf{I}({\hat{\mathbf{\theta }}}^{\left(t\right)},X_j)|.$$ (11)

The KL method is derived from the KL distance, which measures the discrepancy between two density functions, f(x) and g(x), as follows (Cover & Thomas, 1991):

$$\mathrm{KL}(f||g)=E_f\left[\log \frac{f\left(x\right)}{g\left(x\right)}\right].$$ (12)

Equation 12 is a distance-like measure between two distributions but it is asymmetric because $\mathrm{KL}(f||g)\ne \mathrm{KL}(g||f)$. Equation 12 is always nonnegative, is zero only if the two distributions are the same, and becomes larger when the two distributions are more divergent. In MCAT, the KL method is defined as how sensitive item j is in terms of differentiating the true θ from its interim estimate $\hat{\mathbf{\theta }}$, as follows:

$$K{L}_j\left(\hat{\mathbf{\theta }}\right)=\sum _{x=0}^1\underset{\mathbf{\theta }}{\int }f(X_j=x|\hat{\mathbf{\theta }})\log \frac{f(X_j=x|\hat{\mathbf{\theta }})}{f(X_j=x|\mathbf{\theta })}\partial \mathbf{\theta }\mathbf{,}$$ (13)

where $f(X_j=x|\hat{\mathbf{\theta }})$ and $f(X_j=x|\mathbf{\theta }\mathbf{)}$ are response functions and defined as in Equation 2.

The MI measures how an item discriminates the actual joint distribution of two random variables from what the two variables would potentially be like if independent. Let us suppose X and Y are two continuous random variables, the MI would be defined as follows:

$$\mathrm{MI}={\int }_{y\in Y}{\int }_{x\in X}f(x,y)\log \frac{f(x,y)}{f\left(x\right)f\left(y\right)}\partial x\partial y.$$ (14)

For discrete variables, the integrals are substituted by sums. The MI indicates the amount of information that X has about Y, which is 0 if and only if X and Y are independent. Therefore, the MI in MCAT can be defined as follows:

$$\sum _{x=0}^{1}P(X_j=x|{\mathbf{x}}^t)\underset{\mathbf{\theta }}{\int }\pi (\mathbf{\theta }\mathbf{|}{\mathbf{x}}^{\mathbf{t}}\mathbf{,}{\mathbf{X}}_{\mathbf{j}}\mathbf{=}\mathbf{x})\log \left[\frac{\pi (\mathbf{\theta }\mathbf{|}{\mathbf{x}}^{\mathbf{t}}\mathbf{,}{\mathbf{X}}_{\mathbf{j}}\mathbf{=}\mathbf{x})}{\pi (\mathbf{\theta }\mathbf{|}{\mathbf{x}}^{\mathbf{t}})}\right]\partial \mathbf{\theta }\mathbf{,}$$ (15)

where $P(X_j=x|{\mathbf{x}}^t)$ is the posterior predictive probability, given the responses to t items; $\pi (\mathbf{\theta }\mathbf{|}{\mathbf{x}}^{\mathbf{t}}\mathbf{)}$ is the posterior probability of θ, given the responses to t items; and $\pi (\mathbf{\theta }\mathbf{|}{\mathbf{x}}^{\mathbf{t}}\mathbf{,}{\mathbf{X}}_{\mathbf{j}}\mathbf{=}\mathbf{x}\mathbf{)}$ is the posterior probability of θ, given the responses to t items and item j.

Difference in Response Surface and Item Information Between MIRT-C and MIRT-N

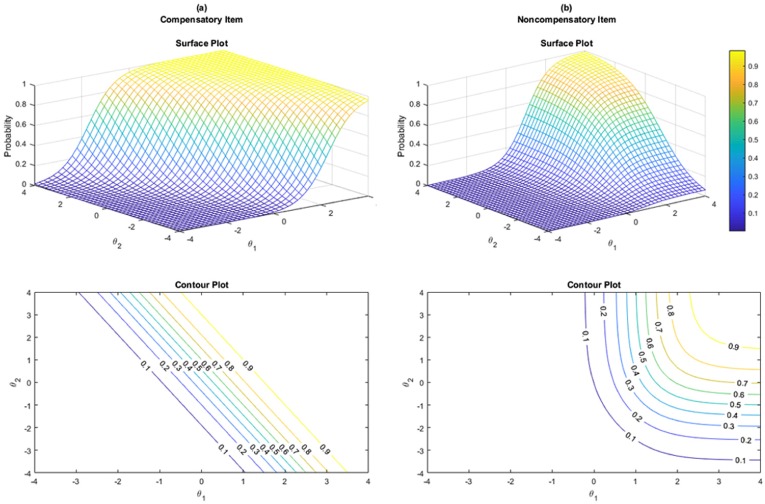
To reveal the difference in item surfaces between MIRT-C and MIRT-N models, the equiprobability contours for the two-parameter logistic parameter compensatory and non-compensatory items were plotted in Figure 1. For the compensatory item, the probability of success is the same for any fixed value of the latent traits, so the contour probability lines are parallel. In contrast, the contour probabilities in the non-compensatory item are curvilinear, indicating that the (overall) probability of success is lower than the probability of success in each dimension. In this example, when θ₁ = 1 and θ₂ = −1, the probability of success in each of the dimensions is .5 but the overall probability of success for the item is .25.

Figure 1.

Item response surfaces and contour plots for compensatory (a₁ = 1.8, a₂ = 0.9, b = 0.5) and non-compensatory (a₁ = 1.8, a₂ = 0.9, b₁ = 1.0, b₂ = −1.0) items.

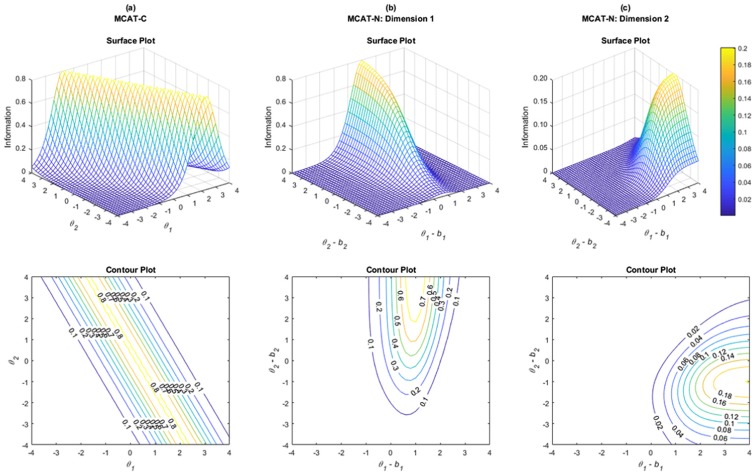
In addition, it is important to note the difference in the item information functions between MIRT-C and MIRT-N. In MIRT-C (Segall, 1996) and considering the above example, the maximum value of the item information was around .80 regardless of k is 1 or 2, when P_j(θ) = .5, and it is symmetric. The item information is identical across dimensions because the same probability of success is obtained for any fixed combination of latent traits in MIRT-C. The first panel of Figure 2 shows, for compensatory items, that the maximum item information is located at the point where the combination of the two dimensions is equal to the single item difficulty (i.e., θ₁+θ₂ = 0.5) and the item information function is systematic.

Figure 2.

Item information surfaces and contours for compensatory (a₁ = 1.8, a₂ = 0.9, b = 0.5) and non-compensatory (a₁ = 1.8, a₂ = 0.9, b₁ = 1.0, b₂ = −1.0) items.

Note. MCAT-C = compensatory multidimensional computerized adaptive testing; MCAT-N = non-compensatory multidimensional computerized adaptive testing.

In MIRT-N, according to Equation 10, the task is to maximize the function $\frac{a_k^2{(1-p_{\mathrm{jk}})}^2{[P_j\left(\mathbf{\theta }\right)-c_j]}^2}{\{P_j(\mathbf{\theta }\mathbf{)}\mathbf{[}1\mathbf{-}{\mathbf{P}}_{\mathbf{j}}\mathbf{\left(}\mathbf{\theta }\mathbf{\right)}\mathbf{]}\mathbf{\}}}$, subject to the constraint $p_{\mathrm{jk}}\ge P_j(\mathbf{\theta }\mathbf{)}$. Let us assume that both $\frac{a_k^2{(1-p_{\mathrm{jk}})}^2{[P_j(\mathbf{\theta }\mathbf{)}\mathbf{-}{\mathbf{c}}_{\mathbf{j}}\mathbf{]}}^2}{\{P_j(\mathbf{\theta }\mathbf{)}\mathbf{[}1\mathbf{-}{\mathbf{P}}_{\mathbf{j}}\mathbf{(}\mathbf{\theta }\mathbf{)}\mathbf{]}\mathbf{\}}}$ and $p_{jk}\ge P_j(\theta )$ have continuous first partial derivatives. When λ is allowed to denote a Lagrange multiplier, the Lagrange multiplier function is as follows:

$$\mathcal{L}=\frac{a_k^2{(1-p_k)}^2{[P_j\left(\mathbf{\theta }\right)-c_j]}^2}{P_j\left(\mathbf{\theta }\right)[1-P_j\left(\mathbf{\theta }\right)]}-\lambda [p_k-P_j\left(\mathbf{\theta }\right)].$$ (16)

The gradient is as follows:

$${\nabla }_{p_k,P_j\left(\mathbf{\theta }\right),\lambda }L\left(p{}_k,P_j\left(\mathbf{\theta }\right),\lambda \right)=\left\{\frac{-2a_k^2\left(1-p_k\right){\left[P_j\left(\mathbf{\theta }\right)-c_j\right]}^2}{P_j\left(\mathbf{\theta }\right)\left[1-P_j\left(\mathbf{\theta }\right)\right]}-\lambda ,\frac{a_k^2{\left(1-p_k\right)}^2\left[P_j\left(\mathbf{\theta }\right)-c_j\right]\left[P_j\left(\mathbf{\theta }\right)+c_j-2P_j\left(\mathbf{\theta }\right)c_j\right]}{{\left\{P_j\left(\mathbf{\theta }\right)\left[1-P_j\left(\mathbf{\theta }\right)\right]\right\}}^2}+\lambda ,-p{}_k+P_j\left(\mathbf{\theta }\right)\right\}.$$ (17)

When ${\nabla }_{p_{\mathrm{jk}},P_j\left(\mathbf{\theta }\right),\mathbf{\lambda }}\mathcal{L}(p_{\mathrm{jk}},P_j(\mathbf{\theta }),\mathbf{\lambda })=0$ is set, taking the aforementioned illustration as the example (a₁ = 1.8, a₂ = 0.9, b₁ = 1.0, b₂ = −1.0), the maximum value of $\frac{a_k^2{(1-p_{\mathrm{jk}})}^2{[P_j(\mathbf{\theta }\mathbf{)}\mathbf{-}{\mathbf{c}}_{\mathbf{j}}\mathbf{]}}^2}{\{P_j(\mathbf{\theta }\mathbf{)}\mathbf{[}1\mathbf{-}{\mathbf{P}}_{\mathbf{j}}\mathbf{(}\mathbf{\theta }\mathbf{)}\mathbf{]}\mathbf{\}}}$ located approximately at .80 and .20 for k is 1 and 2, respectively, when P_j($\mathbf{\theta }$) = p_jk = .5. Therefore, the maximum value of the item information is located at p_jk = b_jk, when P_j(θ) = .5 subject to p_jk≥P_j(θ), but the information is asymmetric. In addition, the item information functions are different for different dimensions.

Specifically, the maximum information in MIRT-N is obtained when the following two conditions are met: (a) the level of a dimension is equal to the corresponding item difficulty, so the probability of success on that dimension is .5; (b) the levels on the other dimensions are far above their corresponding item difficulties, so the probability of success on the other dimensions approaches 1. When the discrimination and pseudo-guessing parameters are not equal to 1 and 0, respectively, the probability of success and the location of maximum item information will change accordingly, but the basic principle remains.

The second and third panels of Figure 2 show the item information for the above mentioned example (a₁ = 1.8, a₂ = 0.9, b₁ = 1.0, b₂ = −1.0), the maximum item information is located at the point where the level on one dimension is equal to its corresponding item difficulty (e.g., θ₁ = b₁), whereas the level on the other dimension far exceeds its corresponding item difficulty (e.g., θ₂–b₂ > 2). In other words, the most informative non-compensatory item for an examinee is an item that is “essentially” unidimensional to him or her (because the probability of success is determined by only one dimension). That is to say, when a test consists of non-compensatory two-dimensional items, selecting items that are very easy on one dimension makes the test essentially measure the other dimension because any difference in item responses between persons can be attributed to the ability difference in the other dimension. The item information function is asymmetric in non-compensatory items.

Simulation Studies

It has been found in the literature of MCAT-C (e.g., Segall, 1996; W.-C. Wang & Chen, 2004; Yao, 2013) that fixed length test termination rule, a longer test or a higher correlation between latent traits leads to a higher measurement precision and test reliability; conversely, for the fixed-precision rule, a more stringent criterion (a smaller standard error [SE]) leads to a higher measurement precision and test reliability, and a longer test that the examinees must go through to terminate the CAT. Accordingly, one would expect that these two factors—the correlation between dimensions and the termination criterion—would affect MCAT-C’s efficiency. In this study, these two factors were manipulated to check whether similar or different results would be generated in MCAT-N. Consequently, using a series of simulations, the performance of the FI, KL, MI, and RS methods was compared in each of the combinations of the correlation between dimensions and termination criterion. For simplicity, the authors focused on the two-parameter two-dimensional logistic MIRT-N model, and left higher dimensions and the one- and three-parameter logistic MIRT-N models for future study.

Item Bank Construction and Examinee Generation

For all simulation conditions, an item bank consisting of 400 items with a ~ U(0.5, 2.0) and b ~ N(−1.0, 1.5) was generated with all items were loaded on both dimensions. Because difficulty parameters take the major role in determining the probability of success in each dimension and the overall probability of an item (Equation 2), the generation of the b values was of concern and similar to Bolt and Lall (2003) and C. Wang and Nydick (2015) for the purpose of the generalization. Meanwhile, the generation of a values was not of focus and therefore was similar to that in the MCAT-C literature. Bolt and Lall (2003) found that the b values generated from such distributions were similar to those observed in Embretson (1984), and C. Wang and Nydick (2015) used similar procedures to generate non-compensatory data. Four levels of the latent trait correlation were manipulated to represent the correlation between dimensions as zero, low, medium, and high. It is, therefore, that the examinees were simulated from a multivariate normal distribution with a mean vector of zero, and four variance–covariance matrices, namely, $\Sigma =\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \multicolumn{1}{c}{0}& \hfill 1\hfill \end{array}\right]$, $\left[\begin{array}{cc}\hfill 1\hfill & \hfill .3\hfill \\ \multicolumn{1}{c}{.3}& \hfill 1\hfill \end{array}\right]$, $\left[\begin{array}{cc}\hfill 1\hfill & \hfill .6\hfill \\ \multicolumn{1}{c}{.6}& \hfill 1\hfill \end{array}\right]$, and $\left[\begin{array}{cc}\hfill 1\hfill & \hfill .9\hfill \\ \multicolumn{1}{c}{.9}& \hfill 1\hfill \end{array}\right]$, to indicate four levels of correlation between the latent traits (${\rho }_{{\theta }_1{\theta }_2}$= 0, .3, .6, and .9), and 10,000 examinees were generated for each condition.

Ability Estimation, Item Selection, and Termination Criterion

The MAP estimator defined in Equation 5 was utilized for latent trait estimation. The item selection methods included the FI, KL, MI, and RS methods. Fixed-length and fixed-precision rules were adopted to terminate the CAT. The terms “fixed-precision” and “variable-length” are used interchangeably in the CAT literature because variable test lengths are required for different examinees to achieve a common fixed precision on latent traits. For the fixed-length rule, the test length was set at 20, 40, and 60 items. For the fixed-precision rule, the SE of each latent trait was computed and the cutoff point of the SE was set using prespecified test reliability, which is defined as the squared correlation between the true and the estimated latent trait. When the MAP estimator is used, the test reliability can be computed as follows (Nicewander & Thomasson, 1999):

$$1-\frac{{[I\left({\theta }_k\right)+{\sigma }^{-2}\left({\theta }_k\right)]}^{-1}}{{\sigma }^2\left({\theta }_k\right)},$$ (18)

where I(θ_k) is test information about θ_k, and σ^–2(θ_k) is the variance of the prior distribution of θ_k. For instance, a test reliability of .90 is equivalent to an average posterior error variance $[I({\theta }_k)+{\sigma }^{-2}({\theta }_k){]}^{-1}$ of 0.10 if σ^–2(θ_k) = 1 for dimension k. Consequently, the SE of each latent trait was set at 0.55, 0.45, and 0.32 to represent the three levels of test reliability: .70, .80, and .90, respectively. If the SE of an examinee did not reach the prespecified levels, he or she would keep taking the test until all 400 items were completed. The maximum test length constraint was not considered here because this study aimed to demonstrate the developed MCAT-N utility and evaluate its performance. Certainly, the maximum test length constraint would affect the performance and it has to be done when the fixed-precision rule is used in practice. However, the application of the developed MCAT-N is identical with that of without maximum test length constraint.

Evaluation Criterion

To examine the performance of the item selection methods, each method was evaluated with respect to measurement precision and test reliability, as defined in Equation 18. The measurement precision on the kth dimension was appraised by the mean squared error (MSE) as follows:

$$\mathrm{MS}{\mathrm{E}}_k=\sum _{i=1}^N\frac{{({\hat{\theta }}_{\mathrm{ik}}-{\theta }_{\mathrm{ik}})}^2}{N},k=1,2,$$ (19)

and the bias on the kth dimension was appraised as

$$\mathrm{Bia}{s}_k=\sum _{i=1}^N\frac{({\hat{\theta }}_{\mathrm{ik}}-{\theta }_{\mathrm{ik}})}{N},k=1,2,$$ (20)

where N is the sample size, ${\hat{\theta }}_{\mathrm{ik}}$ is the final MAP estimate of examinee i on dimension k, and ${\theta }_{\mathrm{ik}}$ is the corresponding true value. Furthermore, for the fixed-precision rule, in addition to the indices of measurement precision and test reliability, the descriptive statistics (mean, standard deviation [SD], minimum, and maximum) of the test lengths that examinees required to stop the CAT when their latent traits’ precision met the requirement (denoted as TLS) as well as the percentage of examinees taking all items in the item bank (denoted as %ETA) were recorded.

The FI and MI methods performed similarly, and both outperformed the KL method in the MCAT-C context (C. Wang & Chang, 2011). The similarity between the FI and MI methods was due to the fact that maximizing the expected KL distance between posterior and prior distributions in the MI method (Equation 16) is equivalent to maximizing Bayesian D-optimality in the FI method (Equation 11) in the case of linear models (Chaloner & Verdinelli, 1995), and nearly equivalent to this in the case of nonlinear models (C. Wang & Chang, 2011). It was anticipated that similar results would be obtained from the FI, MI, and KL methods for MCAT-N. As shown in Figure 2, in addition, under MIRT-N, an item provides the maximum information when the ability level in one dimension matches the difficulty of the same dimension, and the ability level of the other dimension far exceeds that same dimension’s difficulty. It was thus anticipated that, on average, the difficulty distribution of the administered items in MCAT-N would be lower than the ability distribution of the examinees.

Results

The Fixed-Length Rule

Table 1 displays the bias and MSE for the latent trait estimates, as well as the test reliability for the FI, KL, MI, and RS methods using the fixed-length rule when test length was 40 (as the results of test lengths were 20 and 60 were highly similar to that of 40 and therefore they are provided in the online supplement) All of the adaptive item selection methods substantially outperformed the RS method, regardless of test length or the correlation between the dimensions. Let us assume a test reliability of .90 as the benchmark. When the correlation between the dimensions was .9, the FI, KL, MI, and RS methods required approximately 20, 20, 20, and 60 items, respectively, to reach a test reliability of .90. As anticipated, the bias, MSE, and test reliability on both dimensions were generally influenced by the correlation between the dimensions and test lengths, in that the higher the correlation or the longer the test, the higher the measurement precision and test reliability. Furthermore, the improvements in measurement precision and test reliability became smaller as the test became longer or as the correlation between the dimensions became higher, indicating a nonlinear and ceiling effect. Consistent with the findings in the MCAT-C literature, the FI and MI methods performed similarly, with both outperforming the KL method. The test reliability for the two dimensions was similar, irrespective of the test length and correlation between the dimensions.

Table 1.

Bias and MSE for the Latent Trait Estimates, and Test Reliability of the Various Item Selection Methods Using the Fixed-Length Termination Rule (Length = 40).

		Bias		MSE		Reliability
${\rho }_{{\theta }_1{\theta }_2}$	Method	θ1	θ2	θ1	θ2	θ1	θ2
0	RS	−0.067	−0.056	0.314	0.284	0.74	0.75
	FI	−0.027	−0.022	0.123	0.112	0.90	0.90
	KL	−0.047	−0.033	0.164	0.148	0.88	0.88
	MI	−0.024	−0.020	0.120	0.111	0.90	0.90
0.3	RS	−0.052	−0.050	0.273	0.255	0.76	0.77
	FI	−0.018	−0.021	0.110	0.106	0.90	0.91
	KL	−0.028	−0.033	0.131	0.132	0.89	0.89
	MI	−0.015	−0.018	0.110	0.104	0.90	0.91
0.6	RS	−0.042	−0.044	0.214	0.207	0.80	0.81
	FI	−0.013	−0.014	0.098	0.094	0.91	0.91
	KL	−0.020	−0.025	0.108	0.105	0.91	0.91
	MI	−0.012	−0.014	0.099	0.094	0.91	0.91
0.9	RS	−0.022	−0.024	0.127	0.129	0.88	0.88
	FI	−0.010	−0.013	0.068	0.067	0.94	0.94
	KL	−0.010	−0.013	0.068	0.067	0.94	0.94
	MI	−0.011	−0.013	0.068	0.067	0.94	0.94

Note. ${\rho }_{{\theta }_1{\theta }_2}$ = correlation between θ₁ and θ₂; MSE = mean squared error; RS = random selection; FI = Fisher information matrix; KL = Kullback–Leibler information; MI = mutual information.

The Fixed-Precision Rule

Table 2 summarizes the bias and MSE for the latent trait estimates, test reliability, TLS, and %ETA of the item selection methods using the fixed-precision rule with SE = 0.45 (the results of SE = 0.55 and 0.32 can be found in the online supplement). As with the fixed-length rule, the adaptive selection methods outperformed the RS method. Let us assume a test reliability of .80 (SE = 0.45) as the benchmark. When the correlation between dimensions was .9, the mean TLS across examinees was approximately 7, 7.6, and 7 items for the FI, KL, and MI methods, respectively, with approximately 21 items for the RS method. In general, a smaller prespecified SE led to a higher measurement precision, higher test reliability, a longer TLS, a smaller MSE, a smaller bias (due to scale shrinkage in Bayesian estimators), and a larger %ETA. Moreover, the higher the correlation between dimensions, the more efficient the MCAT-N, in that there would be a decreased TLS in such a case. The FI and MI methods performed similarly, and both outperformed the KL method. The test reliability for each dimension was greater than the prespecified test reliability because the examinees finished the CAT when their SEs were equal to or smaller than the prespecified SE. In other words, when the CAT was stopped, the SE of the examinees’ each latent trait should be no greater than 0.45 and the test reliability should be higher than the prespecified value. The test reliability was also similar between dimensions.

Table 2.

Bias and MSE for Latent Trait Estimates, Test Reliability, TLS, and %ETA of Various Item Selection Methods Using the Fixed-Precision Termination Rule (SE = 0.45).

		Bias		MSE		Reliability		TLS				%ETA
${\rho }_{{\theta }_1{\theta }_2}$	Method	θ1	θ2	θ1	θ2	θ1	θ2	M	SD	Minimum	Maximum
0	RS	−0.048	−0.043	0.184	0.176	0.85	0.86	92.4	55.9	27	399	1.7
	FI	−0.033	−0.026	0.206	0.200	0.83	0.84	21.9	22.1	12	363	1.6
	KL	−0.043	−0.042	0.185	0.176	0.86	0.87	45.1	48.3	12	395	1.6
	MI	−0.027	−0.023	0.202	0.230	0.83	0.84	22.6	22.3	12	399	1.6
0.3	RS	−0.048	−0.037	0.194	0.177	0.84	0.85	79.1	45.9	23	397	0.2
	FI	−0.027	−0.029	0.200	0.203	0.83	0.83	18.3	15.4	11	343	0.2
	KL	−0.033	−0.040	0.179	0.174	0.86	0.86	35.0	36.6	12	379	0.2
	MI	−0.023	−0.021	0.197	0.211	0.83	0.83	18.8	14.9	11	243	0.4
0.6	RS	−0.036	−0.035	0.190	0.182	0.83	0.83	52.9	25.2	21	375	0.0
	FI	−0.020	−0.023	0.206	0.209	0.82	0.82	13.1	6.6	10	311	0.0
	KL	−0.032	−0.035	0.185	0.181	0.84	0.85	20.0	13.8	10	278	0.0
	MI	−0.021	−0.020	0.199	0.209	0.82	0.82	13.4	7.7	9	315	0.0
0.9	RS	−0.027	−0.032	0.196	0.196	0.81	0.82	21.0	9.0	9	183	0.0
	FI	−0.027	−0.031	0.201	0.207	0.82	0.81	7.0	1.2	6	44	0.0
	KL	−0.028	−0.033	0.198	0.197	0.82	0.82	7.6	1.5	6	53	0.0
	MI	−0.022	−0.028	0.204	0.207	0.81	0.81	7.0	1.3	6	42	0.0

Note. MSE = mean squared error; TLS = test length that examinees required to stop the tests when their latent traits’ precision met the requirement; %ETA = percentage of examinees taking all items in the item bank; SE = standard error of θ₁ and θ₂; ${\rho }_{{\theta }_1{\theta }_2}$ = correlation between θ₁ and θ₂; RS = random selection; FI = Fisher information matrix; KL = Kullback–Leibler information; MI = mutual information.

As noted above, under MIRT-N, an item provides the maximum information about an examinee when the examinee’s ability level of one dimension is equal to the difficulty of that dimension and the ability level of the other dimension is higher than the corresponding difficulty. That is to say that there was high correspondence between the ability level and the difficulty in the same dimension. To verify the correspondence, ${\hat{\theta }}_1$ and ${\hat{\theta }}_2$ on the mean difficulties of both dimensions of the administered items, ${\overline{b}}_1$ and ${\overline{b}}_2$, were regressed. The regression coefficients are shown in Table 3. R² ranged from .89 to .97. Moreover, ${\overline{b}}_1$ was a good predictor of ${\hat{\theta }}_1$, with regression coefficients ranging from 0.67 to 1.04, whereas ${\overline{b}}_2$ was a good predictor of ${\hat{\theta }}_2$, with regression coefficients ranging from 0.92 to 1.13. The intercepts were zero because the mean of ${\hat{\theta }}_1$ and ${\hat{\theta }}_2$ was zero.

Table 3.

Regression Coefficients and R² Under Various Conditions.

Criterion	${\overline{b}}_1$	${\overline{b}}_2$	R 2
${\rho }_{{\theta }_1{\theta }_2}$ = 0
${\hat{\theta }}_1$	1.04	−0.17	.90
${\hat{\theta }}_2$	−0.33	1.09	.89
${\rho }_{{\theta }_1{\theta }_2}$ = .3
${\hat{\theta }}_1$	1.03	−0.11	.91
${\hat{\theta }}_2$	−0.28	1.13	.90
${\rho }_{{\theta }_1{\theta }_2}$ = .6
${\hat{\theta }}_1$	0.98	−0.02	.93
${\hat{\theta }}_2$	−0.21	1.13	.92
${\rho }_{{\theta }_1{\theta }_2}$ = .9
${\hat{\theta }}_1$	0.67	0.32	.97
${\hat{\theta }}_2$	0.07	0.92	.97

Note. ${\rho }_{{\theta }_1{\theta }_2}$ = correlation between θ₁ and θ₂.

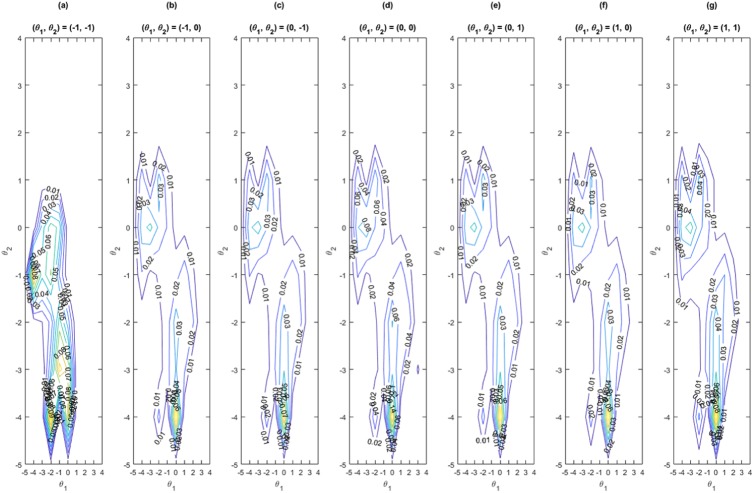
To further investigate the relationship between the administered items and the examinees’ distribution, we also computed the item exposure rates for the FI method using the fixed-length rule. Figure 3 shows the result of 40-item tests contour lines of the item exposure rates when the correlation between dimensions was .6. The contour lines when the correlation was .0, .3, and .9 were similar to the data in Figure 3, meanwhile, the similar exposure rates patterns can be found for 20- and 60-item tests. Among the 10,000 examinees, there were around 79% examinees falling into the seven groups: (θ₁, θ₂) = (−1, −1), (−1, 0), (0, −1), (0, 0), (0, 1), (1, 0), and (1,1). For example, an examinee with latent traits (0.86, 0.27) would be classified into the group of (θ₁, θ₂) = (1, 0). The seven groups were chosen here because there were over two thirds of examinees falling into one of them regardless of the correlation between dimensions. There were around 68%, 72%, and 86% examinees falling into the seven groups when the correlation between dimensions was 0, .3, and .9, respectively. In the case of the group (θ₁, θ₂) = (0, 0), the polygon had coordinates (−3, −4), (3, −3), (−4, −1), and (−4, 1), and the most frequently administered items had difficulties with (0, −4), (0, −3), and (−3, 0). Other groups had similar exposure patterns. In general, the following two difficulty patterns were highly administered for examinees with abilities θ₁ and θ₂ as follows: (a) b₁ = θ₁± 1, b₂ = b₁– 2; and (b) b₂ = θ₂± 1, b₁ = b₂– 2.

Figure 3.

Conditional distributions of item exposure rates for the fixed-length rule with 40 items when ${\rho }_{{\theta }_1{\theta }_2}=0.6$.

Constructing an item bank for a specific population is the first step to implement a CAT program. In MCAT-C, an item bank could provide higher information about examinees’ latent traits when the distributions of the difficulty parameters more closely match the examinees’ distributions. Along this logic, let the examinees follow a K-dimensional multivariate normal distribution with means µ₁, . . ., µ_K, and variances ${\sigma }_1^2$, . . ., ${\sigma }_K^2$. It is therefore to establish an item bank that provides a large amount of test information about the examinees in MCAT-N; based on the simulation results, the relationship between the administered items and population distribution can be found as follows:

1. b ₁ ~ N(µ₁, ${\sigma }_1^2$) or b₁ ~ U(µ₁− 2, µ₁+2), together with the corresponding b₂ . . . b_K in the same item being equal approximately to b₁− 2;

2. b ₂ ~ N(µ₂, ${\sigma }_2^2$) or b₂ ~ U(µ₂− 2, µ₂+2), together with the corresponding b₁, b₃,. . . b_K in the same item being equal approximately to b₂− 2;

3. and so on for b_p.

It is apparent that the b values have lower means compared with the examinees’ latent traits because this can make the probability of success to be sufficiently high by the non-compensatory feature of MIRT-N (see Equation 2). Although test developers often create test items based on concepts regarding the level of the examinees, all the items are required to go through various test validations. These results can provide information for item bank construction and test assembly. It is worth noting that the results are drawn from specific conditions in this simulation (i.e., the specific population distribution and item bank); therefore, they should be used with caution in practice.

Conclusion and Discussion

This study is the first to develop CAT algorithms for non-compensatory items (MCAT-N). The FI, MI, and KL methods, together with fixed-length and fixed-precision termination rules, were adapted to MCAT-N, and their performance was evaluated using simulations. When the fixed-length rule was implemented, it was found that the longer the test length and the higher the correlation between dimensions, the higher the measurement precision and test reliability. When the fixed-precision rule was implemented, it was found that the smaller the prespecified SE or the lower the correlation between dimensions, the longer the TLS and the larger the %ETA. The FI, KL, and MI methods outperformed the RS method; the FI and MI methods performed similarly and both outperformed the KL method. All of these findings were consistent with those for MCAT-C.

Unlike in MCAT-C, where the difficulties of the administered items tend to match the sum of the ability levels across the dimensions, it was found that the difficulties of the administered MCAT-N items tended to be located below the ability levels. For example, an item with difficulties of (0, −2) or (−2, 0) on the two dimensions provides a lot of information about the examinees with ability levels of (0, 0). Consequently, the “mean” difficulties across the selected items (−1 for both dimensions in this case) would be located lower than the examinees’ ability level (0 for both dimensions in this case). This phenomenon happens in the light of the non-compensatory nature of MIRT-N. low mean difficulties can produce the probability of success to be sufficiently high compared with the examinees’ latent traits.

This study has some limitations. First, this study focused on two-dimension situations where all items were loaded on both dimensions. However, it would be straightforward to include in the study higher dimensions (more than two dimensions) or use items that are not loaded on all dimensions. The MCAT-N algorithms were demonstrated under the two-parameter logistic non-compensatory MIRT model. They can be directly adapted to other MIRT-N models, such as the multicomponent latent trait model (Embretson, 1984; Whitely, 1980). The item selection methods in this study were based on maximizing the FI, KL, and MI in terms of latent traits in one item bank. Future studies should investigate other item selection methods, item banks, ability estimation methods, as well as population distribution, to offer a better understanding of MCAT-N. All latent traits in this study were treated as intentional, but in practice, some latent traits may be nuisances (Mulder & van der Linden, 2009). Further study is required on how MCAT-N can be adapted to such cases. In addition, it would be of great value to investigate how MCAT-N will perform when practical constraints (e.g., item exposure control, test overlap control, content balancing) are enforced (Su, 2016; Yao, 2014).

The fixed-precision rule in this study was based on fixed SEs. Other fixed-precision termination rules, such as the minimum information and the predicted standard error reduction termination rules (Yao, 2013), can be adapted to MCAT-N. When the fixed-precision rule is adopted, a maximum test length constraint is often imposed to prevent examinees unnecessarily taking additional items (or even administering all of the items in the item bank) for whom a prespecified precision criterion cannot be met. Further studies can be conducted to adapt other fixed-precision rules with a view to setting an appropriate maximum test length for the fixed-precision MCAT-N and explore multidimensional computerized classification testing for non-compensatory data (van Groen, Eggen, & Veldkamp, 2016). Furthermore, future study can be done as Segall (1996) to evaluate how does MCAT-N work compared with fitting multiple unidimensional item response theory (IRT) models. The relationship between the administered items and examinees’ distribution provided some insights on item bank construction in the case of non-compensatory items. Yet, it is drawn by limited simulations; based on these information, broader simulation studies can be conducted for better understanding the relationship, and furthermore to give practitioners guidelines or rules of thumb on the item bank construction. Finally, it is worth to investigate the performance of MCAT-N with real data.