Sealing Graphene Nanodrums

Abstract

Despite theoretical predictions that graphene should be impermeable to all gases, practical experiments on sealed graphene nanodrums show small leak rates. Thus far, the exact mechanism for this permeation has remained unclear, because different potential leakage pathways have not been studied separately. Here, we demonstrate a sealing method that consists of depositing SiO₂ across the edge of suspended multilayer graphene flakes using electron beam-induced deposition. By sealing, leakage along the graphene–SiO₂ interface is blocked, which is observed to result in a reduction in permeation rate by a factor of 10⁴. The experiments thus demonstrate that gas flow along the graphene–SiO₂ interface tends to dominate the leak rate in unsealed graphene nanodrums. Moreover, the presented sealing method enables the study of intrinsic gas leakage through graphene membranes and can enable hermetic graphene membranes for pressure sensing applications.

In the past decade, there has been a growing interest into the use of 2D materials as ultrathin membranes for separation and filtration of gases and ionic solutions. In particular, graphene has been at the focus of these studies because of its exceptional mechanical strength¹ and its impermeability to ions² and gases.³

However, in previous studies of gas permeability of 2D materials, small leak rates of unknown origin have been observed even in the absence of defects or pores,³⁻¹⁰ making it difficult to determine the intrinsic gas permeability of the graphene membrane or its pores. This inherent gas leakage also hinders the application of graphene membranes in ultrasensitive pressure sensors because these sensors require a hermetically sealed cavity that contains a fixed amount of reference gas.^{3,4,6,9,11,12}

Here, we show that the leak rates of graphene cavities can be significantly reduced by depositing glass (SiO₂) across the edges of an exfoliated multilayered-graphene (MLG) flake using an electron beam-induced deposition (EBID) technique. Device fabrication and sealing methodology are described and leak rate measurements using resonance frequency analysis are presented. By comparing leak rates of sealed and unsealed cavities, the effectiveness of the sealing method is assessed and the dominant pathway for gas leakage into graphene cavities is identified. This work thus presents strong evidence that gas permeation along the graphene-SiO₂ interface is the dominant leakage pathway, and provides a route toward eliminating this leakage.

Gas Leakage Pathways

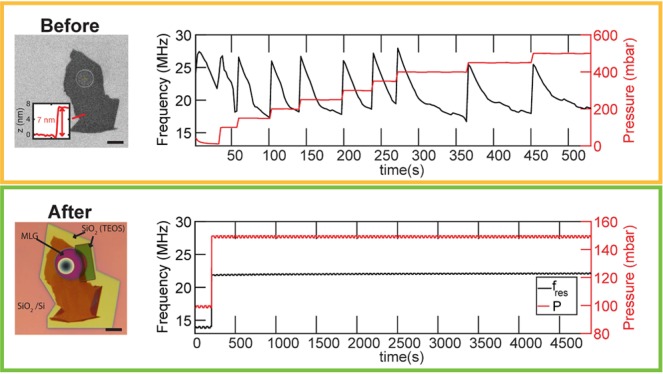
Although gas leak rates into and out of graphene sealed cavities have been investigated in several studies,^3,7,13,14 the leakage pathway and mechanism by which gas permeates into the cavity is still under debate. Figure 1a schematically illustrates the three potential leakage pathways along which gas leakage can occur:³ (1) through the graphene, (2) through the SiO₂, and (3) along the graphene–substrate interface.

Figure 1.

(a) Illustration showing the three possible leakage pathways through which gases can leak. Blue: Path 1, through the defects in graphene. Green: Path 2, through the oxide. Red: Path 3, along the interface between graphene and the substrate. (b) Schematic showing the sealing procedure. (b1) Cavity is etched into a SiO₂/Si substrate using standard e-beam lithography followed by reactive ion etching. (b2) MLG is deterministically transferred onto the cavity. (b3) Electron beam is scanned over the edge of MLG–SiO₂ interface while gas injection system (GIS) introduces tetraethyl orthosilicate (TEOS), resulting in local deposition of SiO₂. (c) Schematic of the interferometry setup. Sample is mounted in a sample chamber (SC) where the pressure is regulated by the pressure controller (PC) and the arbitrary waveform generator (AWG). A modulated blue laser with wavelength of 405 nm optothermally heats the suspended membrane. Intensity modulations in the reflected red laser light (λ = 633 nm), caused by the graphene motion, are measured by the photodiode (PD) and sent to the vector network analyzer (VNA). PBS, polarized beam splitter; DM, dichroic mirror.

Although gas leakage through chemical vapor deposition (CVD) grown graphene (see path 1 in Figure 1a) has been reported to occur,^13,15,16 it is probable that this leakage is not so much an intrinsic property of pristine graphene but is due to imperfections and defects in the CVD grown graphene. Evidence that leakage through crystalline graphene (or its defects) is not the dominant leakage pathway was provided by experiments on exfoliated natural graphene flakes of different thicknesses.³ These experiments demonstrated a thickness independent leak rate, whereas according to Fick’s first law the permeation rate is expected to be inversely proportional to thickness and in case permeation is mediated by a small number of pores/imperfections an even stronger thickness dependence is expected. This experiment therefore excluded path 1 as a dominant leakage pathway.

By gas-dependent measurements, it was observed that the leakage rate for He gas was much higher than for other gases.³ Because SiO₂ is known to be permeable for He,¹⁷ it was hypothesized that for all types of gases, leakage into the cavity was dominated by permeation through the SiO₂ substrate (see path 2 in Figure 1a).³ However, there was no method available to distinguish between permeation of gas along the interface between graphene and SiO₂ substrate (see path 3 in Figure 1a) and permeation through the substrate itself. On the basis of these observations, leakage along the SiO₂–graphene interface can therefore not be ruled out. By studying permeation rates before and after sealing the interface between graphene and SiO₂ (see path 3 in Figure 1a), we aim to identify whether path 2 or path 3 is the dominant leakage pathway.

Sealing Method

In order to investigate these gas leakage pathways, circular cavities with a depth of 285 nm and diameters of 5 and 10 μm are fabricated in a 285 nm thick SiO₂ layer, grown by dry oxidation of a silicon (100) wafer (Figure 1b1). Subsequently, MLG flakes are exfoliated from naturally occurring bulk graphite and suspended over the cavities by a dry transfer method¹⁸ (Figure 1b2). We use MLG exfoliated from naturally occurring bulk graphite with thicknesses ranging from 2 layers to 8 nm to ensure that the permeation we observe is not due to the permeation through the defects along pathway 1.

After initial characterization of the unsealed graphene drums, we seal the cavities to prevent external gas from entering the interface between graphene and SiO₂ (Figure 1b3). For this purpose, we developed a sealing method for locally covering the edge of the graphene flake by an additional SiO₂ layer using EBID of tetraethyl orthosilicate (TEOS) (discussed in more detail in Methods).

Experimental Setup

To test the hermeticity of the graphene drums, we used the suspended graphene drum as a differential pressure sensor.^3,4,11,12 When a pressure difference is present across suspended graphene, tension is induced in the material that causes a change in the resonance frequency. To measure the resonance frequency of our devices, we use the laser interferometry setup shown in Figure 1c.

A modulated blue laser diode (λ = 405 nm) is used to optothermally actuate the MLG membrane. The motion of the graphene membrane is detected using a red He–Ne laser with wavelength, λ = 633 nm. The motion of the suspended graphene modulates the reflected red laser intensity via its position-dependent absorption of the standing light wave.¹⁹ This modulated light is collected at the photodiode (PD) and read by the vector network analyzer (VNA). The pressure P_ext inside the sample chamber (SC) is controlled by the output from the arbitrary waveform generator (AWG) that drives the pressure controller (PC). The PC then regulates the pressure inside the SC with a vacuum pump and a gas supply (N₂ or He).

Results

Hermeticity Tests of Graphene Cavities

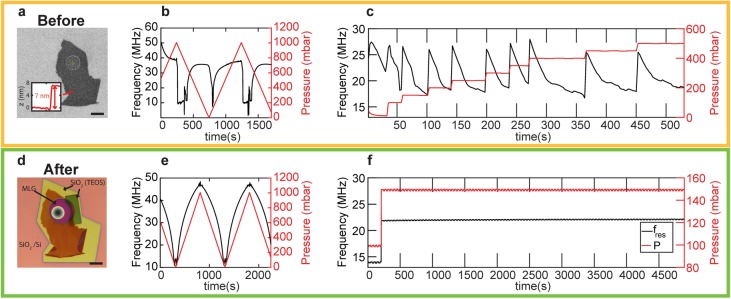
Figure 2 shows measurements of the pressure response of device 1 in N₂ atmosphere before (Figure 2a–c) and after sealing (Figure 2d−f). We observe significant changes in the fundamental resonance frequency f_res of more than 30 MHz, as chamber pressure is varied from 0 to 1000 mbar. Figure 2b shows the time-dependent resonance frequency in response to a triangular pressure waveform with a period of 1000 s. Before sealing, the resonance frequency exhibits hysteresis (Figure 2b), which is attributed to leakage, that causes P_int to vary in time, thus resulting in different pressure ΔP = P_ext – P_int across the membrane at the same value of P_ext. In Figure 2c the same device is exposed to pressure steps of 50 mbar. Each step in pressure results in a sudden increase in frequency followed by an exponential decay that is attributed to gas leakage. By fitting, an average leakage time constant τ = 31 ± 4 s is found for N₂ (see Supporting Information S1).

Figure 2.

Top row: device 1 and its experimental data before sealing. Bottom row: device 1 and its experimental data after sealing. (a) SEM image of the device before sealing. Inset: AFM profile showing the step height of the MLG flake. (b) Fundamental resonance frequency (black) of the nonsealed graphene resonator while the chamber pressure (red) is swept in triangular waveform with period of 1000 s. (c) Fundamental resonance frequency (black) of the sealed graphene resonator after 50 mbar step increases in chamber pressure (red). (d) Optical image of the device after sealing. Because of a slight drift in the e-beam during the EBID process, the deposition was off-centered which left some part of the MLG edge exposed. In order to correct this and fully cover all the edges, a second EBID step was necessary which resulted in two layers of SiO₂ in some areas (yellow, first layer; green, second layer). (e) Same procedure as in (b) after sealing. (f) Resonance frequency shift in response to a single 50 mbar step pressure increase.

These measurements are repeated on the same device after sealing the edges of the MLG flake by TEOS (Figure 2d). After covering the edges, hysteresis is eliminated (Figure 2e) and the resonance frequency closely and reproducibly follows the applied pressure changes in P_ext. Furthermore, no apparent decay in the resonance frequency is observed after a 50 mbar pressure step as shown in Figure 2f. This shows that the cavity is hermetically sealed or at least that the permeation is greatly suppressed. The absence of hysteresis in Figure 2e and the absence of a frequency decay in Figure 2f indicates that after sealing, the internal pressure P_int inside the cavity is thus constant within our measurement accuracy, enabled by the leak-tight seal between graphene and the EBID deposited SiO₂.

Pressure Sensing with Sealed Graphene Drums

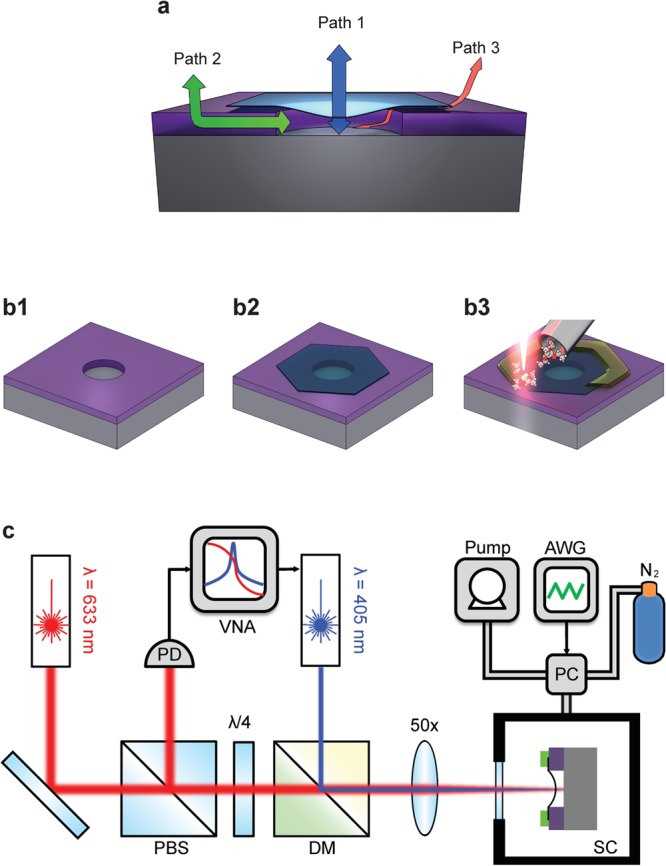
Sealing of the graphene drum allows a more accurate study of the performance of the device as a pressure sensor. We first analyze the pressure response, and subsequently determine its precision as a pressure sensor. Figure 3a–c shows the frequency, responsivity, and Q-factor of device 1 as a function of external pressure. Once the cavity is sealed, the pressure difference between the outside and inside of the cavity greatly affects the tension of the membrane which affects the resonance frequency. If the pressure inside is higher, the membrane deflects upward (pressure regime highlighted in pink), which causes the membrane to stretch and the tension to increase. If the pressures outside and inside the cavity are equal, the membrane is flat (regime in green) and the membrane has minimum tension. Finally, if the pressure outside is larger, the membrane deflects downward (regime in yellow) which causes the membrane to stretch, resulting in higher tension in the membrane. The resonance frequency (Figure 3a) and Q-factor (Figure 3c) show minima near P_ext = 42 mbar, indicative of P_int ≃ 42 mbar.

Figure 3.

(a) Pressure P_ext dependence of the resonance frequency of device 1 shown in Figure 2. Plotted in red and blue circles are the pressure response of the resonance frequency while increasing and decreasing pressure, respectively. The analytical fit, based on the resonance frequency of a pressurized circular membrane is plotted in green. The fit parameters, E, n₀, and P₀ extracted from the analytical model are used in a FEM simulation (dashed black line). Inset: zoom-in near the minimum. (b) Differential responsivity (df/dP) plotted in red and blue circles and derivative of the analytical solution from (a) plotted in green. Inset: zoom-in near P₀. (c) Q-factor as a function of pressure. Inset: zoom-in near the minimum. (d) Optical image of a sealed device (device 2) which consists of only 2 layers of graphene. Scalebar: 25 μm. (e) Plots similar to (a) are measured continuously over 55.7 h using triangular pressure sweeps with a period of 10000 s. (f) P₀ is traced over 55.7 h and fitted to an exponential resulting in a time constant of τ_sealed = 2.88 × 10⁵ seconds.

In order to relate the pressure dependence of the observed resonance frequencies to the properties of the graphene, we employ a theoretical model to fit the experimental data. The analytical expression for the deflection of a circular membrane subjected to a uniformly distributed pressure across the membrane ΔP is

1

where x_s is the static deflection at the center of the drum, h is the thickness, a is the radius of the drum, n₀ is the pretension, and E is the Young’s modulus (see Supporting Information S2 for derivation).

After determining the deflection x_s from eq 1, we calculate the fundamental resonance frequency of a tensioned circular drum with respect to static deflection x_s caused by uniform external load of ΔP using²⁰

2

where k₁ = 4.8967n₀ is the linear spring constant, 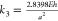is the third order spring constant, m = 0.8467ρa²h is the modal mass,²⁰ and ρ is the density of the membrane (see Supporting Information S2 for derivation).

Figure 3a shows a comparison of experimental data (red and blue circles) and fitted curves based on eq 2 and finite element method (FEM) simulations. To obtain these curves, we first extract the pretension n₀ in the membrane. In order to find n₀ in the membrane, we consider the case where the resonance frequency is minimum (ΔP ≃ 0). The minimum in the frequency, f_res,min = 10.9 MHz, corresponds to the membrane in the flat (x_s = 0) configuration. Using this pretension, the thickness h = 7 nm determined from AFM, and the density of graphite ρ = 2300 kg/m³, we fit eq 2 to the data resulting in a cavity pressure of P_ext(f = f_min) = P₀ = 41.7 ± 0.6 mbar and Young’s modulus of E = 137.4 ± 0.7 GPa. In Discussion, potential causes for the low value of the experimentally extracted Young’s modulus are analyzed. With the same parameters, we numerically simulate the pressure response of a circular membrane to obtain the FEM simulations shown in Figure 3a. The effect of the membrane deflection on P_int and the effect of squeeze film damping on the resonance frequency are relatively small (estimated systematic error less than 5%) and are therefore not included in the simulation. The FEM results plotted in Figure 3a as dashed lines are in close agreement with the measurements and eq 2.

It is notable that the pressure dependence of the resonance frequenecy in these devices is very large.³ At P₀, the frequency of the relaxed graphene membrane is 10.9 MHz and when the pressure difference is at a maximum, the resonance frequency of the strained graphene membrane is 48.4 MHz. Using the measured f(P_ext), we can estimate the responsivity of the sealed pressure sensor. Over the full range from P_ext = P₀ to 1000 mbar, we find an average responsivity of 39.2 kHz/mbar whereas the maximum differential responsivity can be as high as 136 kHz/mbar (Figure 3b). Compared to the graphene-based squeeze-film pressure sensor previously reported,¹¹ which was already 45 times more sensitive than the state of the art MEMS squeeze-film pressure sensors, this sealed pressure sensor is a factor of 15 more responsive, demonstrating the potential of fully sealed membranes of 2D materials for pressure sensing applications.

Long-Term Stability

We study the long-term stability of the resonance frequency of the devices, because stability is essential for pressure-sensing applications. In Figure 3d–f, we show measurement results on a sealed device, with a duration of 55.7 h. The measured device, device 2 shown in Figure 3d, is the thinnest device we fabricated, being only two layers thick (see Supporting Information S3). This device had a leakage time constant of 26 ± 3 s before sealing (see Supporting Information S4) which is considerably shorter than those observed in other works.^3,8 After sealing, the fundamental resonance frequency was measured continuously while P_ext was swept from 0 to 1000 mbar in a triangular waveform with a period of 10000 s. We determined the pressure at minimum frequency (P₀) for each sweep during the whole experiment (Figure 3e). Thus, we observed P₀ increasing from 48.3 to 83.1 mbar in 55.7 h (Figure 3f). The time constant as obtained from an exponential fit is 2.88 × 10⁵ seconds (∼80 h), which is a factor of 1.11× 10⁴ longer than the leakage time constant before sealing.

When He is used, we observe a decay time-constant τ ≃ 72.2 s of the resonance frequency after sealing with TEOS, which is much shorter than that for N₂ gas (see Supporting Information S5). The sealing procedure only reduces the leak rate by a factor 10 for He gas. This lower effectivity of the sealing procedure can be attributed to leakage of He through TEOS and thermal oxide, because He gas is known to be able to diffuse through SiO₂ layers.¹⁷

Discussion

Eventually the goal of any sealing procedure is to reach a situation where the graphene cavity is leak-tight for many years. However, judging from Figure 3f, it can be seen that the cavity pressure P₀ is slowly increasing as a function of time, which could be an indication of slow gas leakage into the membrane over periods of hours. Alternatively, the increase of pressure inside the membrane might also result from another effect. If the membrane is slowly slipping and sagging into the cavity, the enclosed volume of gas would slowly decrease as a function of time. For a fixed temperature and amount of gas molecules, the product of pressure and volume P_intV_int is constant according to Boyle’s law, and therefore such a decrease in volume would be accompanied by an increase in pressure. So two hypotheses might account for the observed increase in pressure: gas leakage and sagging of the membrane resulting in cavity volume reduction. To verify which of these hypotheses can account for the observed pressure increase in Figure 3f, we carried out microscopy and Raman studies on the membranes at the start and end of the experiment.

Sealing is performed in a high vacuum SEM environment for a period of ∼1 h, which results in a near-vacuum state inside the sealed cavity. After sealing, when the sealed device is exposed to the atmospheric pressure, the large pressure difference causes the membrane to bulge down. The resulting curvature of the membrane is clearly visible, as an optical contrast¹⁰ difference between the center and the edges of the drum, as shown in the optical microscope image in Figure 4a, that is taken within 10 min after EBID. The curvature of the membrane is also verified in an AFM scan of a similarly sealed device (see Supporting Information S6). When the device is exposed to the overpressure for a prolonged time (about 2 months) the bulged down membrane eventually adheres to the bottom of the cavity as evidenced by the optical microscopy image in Figure 4b. Raman mapping has been employed to study the changes in the lateral strain distribution due to the membrane collapsing. A Raman map shown in Figure 4c indicates that the suspended part of the graphene is initially under tensile strain, as evidenced by the lower value of the G-peak Raman wavenumbers (see Supporting Information S7).²¹ The regions surrounding this tensile membrane exhibits comparably lower strain. However, after 2 months of constant overpressure, the Raman wavenumbers in the surrounding region are shifted downward (Figure 4d), indicating higher tensile stress, and the membrane adhered to the bottom of the cavity.

Figure 4.

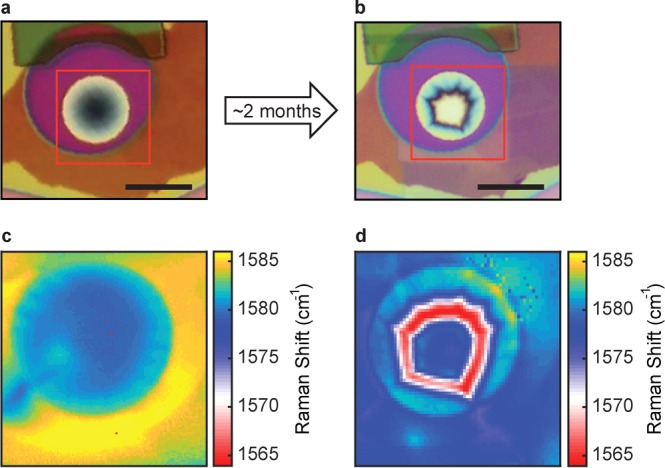
Raman mapping study of a sealed graphene drum (device 1) before and after ∼2 months in ambient conditions. (a) Optical image of the sealed device with area under Raman study highlighted in red. (b) Optical image of the same drum after ∼2 months in ambient conditions. Scale bars are 10 μm. (c) Raman mapping of the sealed drum; the G peak is used for mapping. Surrounding the bulged down membrane (under tensile strain) are regions of compressive strain, evidenced by the unusually high G peak position. (d) Raman mapping of the sealed drum after ∼2 months of being in ambient conditions. Areas surrounding the drum are relaxed and the center of the membrane touches the cavity bottom.

The collapsing of the membrane on the cavity bottom supports the second of the two hypotheses listed above because if there were small pinholes or defects, through which gas leaks at small rates, then over time, P_int and P_ext would equilibrate and the initially downward bulged membrane would become flat. However, we observe that the membrane collapsed to the cavity bottom and that the MLG in the nearby region became more strained. A potential explanation for the observed sagging of the graphene membrane is that the high, pressure-induced, tensile strain in the suspended graphene pulls the layer, such that it slides into the cavity until it touches the bottom of the cavity. During this motion the strain distribution in the MLG can change and the graphene edge might also slowly move with respect to the TEOS. Another effect that might play a role is that creep may be occurring in the graphene, either due to dislocation motion, or due to mutual slipping of graphene layers with respect to each other in the MLG. The increase in pressure P_int = P₀ in Figure 3f can thus be at least partly but maybe even completely attributed to the volume reduction due to sagging.

The obtained value of the Young’s modulus from the fit is so much lower than the well-established literature value of around E = 1 TPa that we suspect that the assumptions underlying the continuum model are not adequately capturing the true membrane physics. Potential causes for this discrepancy include wrinkles (observed around the edge of the membrane as can be seen from Raman measurements in Figure 4c,d), material residues from the transfer or sealing method, and non-perfect clamping of the edge of the membrane causing elastic sliding of the suspended part of the membrane near the edge. This last effect seems especially likely considering the observation of the collapse of the membrane under prolonged exposure to high pressures in Figure 4b. The resulting value for the Young’s modulus from the fit in Figure 3a is therefore not an accurate representation of the actual material properties. It rather shall be seen as an equivalent property representing a continuum mechanics model that fits the observed physics.

In conclusion, we demonstrate in this work that the N₂ leakage rate can be drastically reduced (by a factor >10⁴) by sealing the edge of graphene with TEOS. Because leakage through the thermal oxide would not be significantly blocked by the TEOS, we can also conclude from these results that the dominant leakage pathway is along the interface between graphene and SiO₂. From long-term hermeticity tests, it is found that the internal pressure inside the graphene sealed cavity does still increase in time. Although small leakage might still play a role, sagging of the membrane is also identified as a potential contributor for pressure increase and eventual device failure due to membrane collapse. By presenting a sealing method for graphene membranes, the current work sets steps toward improved permeability characterization of 2D materials and toward new sensors based on impermeable ultrathin membranes.

Methods

Device Fabrication

A silicon wafer with 285 nm dry oxide is spin coated with positive e-beam resist and exposed by electron beam. After development, the unprotected SiO₂ is completely etched using CHF₃ and Ar plasma in a reactive ion etcher. After resist removal, graphene is then transferred using a deterministic dry stamping technique.

Sealing the graphene drum is performed in the FEI Helios G4 CX system at 15 kV and 11–88 nA current with a gas injection system (GIS) containing tetraethyl orthosilicate (TEOS) and H₂O. H₂O has been added to TEOS for purity enhancement of EBID deposited material.^22,23 A range of 100–150 nm of SiO₂ have been deposited which took more than 30 min to deposit.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.9b01770.

• Leakage time constant of N₂ before sealing; derivation of analytical expression; number of layers in device 2; time constant before and after the seal; leakage time constant of He before and after sealing; AFM scan of a sealed device; Raman spectrum of sealed membrane (PDF)

The authors declare no competing financial interest.