ConTPL: Controlling Temporal Privacy Leakage in Differentially Private Continuous Data Release

Abstract

In many real-world systems, such as Internet of Thing, sensitive data streams are collected and analyzed continually. To protect privacy, a number of mechanisms are designed to achieve ϵ-differential privacy for processing sensitive streaming data, whose privacy loss is rigorously controlled within a given parameter ϵ. However, most of the existing studies do not consider the effect of temporal correlations among the continuously generated data on the privacy loss. Our recent work reveals that, the privacy loss of a traditional DP mechanism (e.g., Laplace mechanism) may not be bounded by ϵ due to temporal correlations. We call such unexpected privacy loss Temporal Privacy Leakage (TPL). In this demonstration, we design a system, ConTPL, which is able to automatically convert an existing differentially private streaming data release mechanism into one bounding TPL within a specified level. ConTPL also provides an interactive interface and real-time visualization to help data curator understand and explore the effect of different parameters on TPL.

1. INTRODUCTION

With the development of wearable and mobile devices, vast amount of temporal data generated by individuals are being collected, such as trajectories and web page click streams. The continuous publication of statistics from these temporal data has the potential for significant social benefits such as disease surveillance, real-time traffic monitoring and web mining. However, privacy concerns hinder the wider use of these data. To this end, differentially private continuous aggregate release [2] [3] [4] [7] [10] [11] [12] [14] [17] [8] has received increased attention because it provides a rigorous privacy guarantee. Intuitively, differential privacy (DP) [9] ensures that the modification of any single user’s data in the database has a “slight” (bounded in ϵ) impact on the change in outputs. The parameter ϵãĂĂalso called privacy budget, is defined to be a positive real number to control the privacy level. ϵ is inversely proportional to the randomness (or noises) injected to the released data. The more randomness means that the data are more private. Small values of ϵ result in high privacy levels. Thus, we can consider ϵ as the degree of privacy loss, i.e., a large value of ϵ indicates more privacy loss.

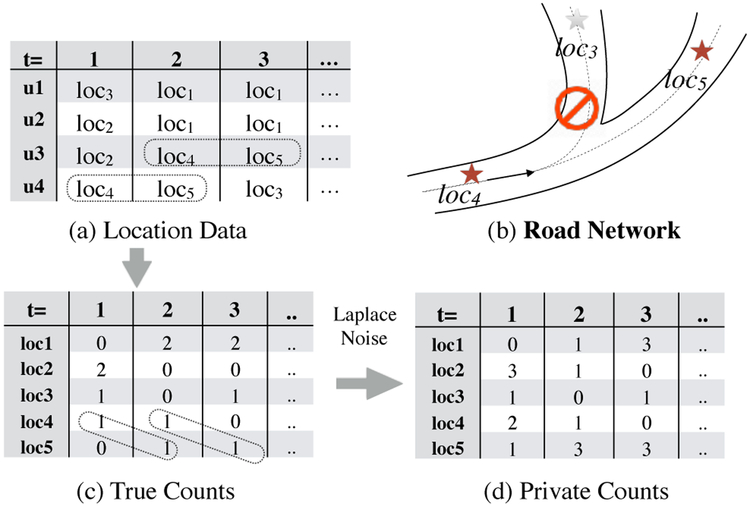
Most existing studies on differentially private continuous data release do not take temporal correlation among data into consideration. Temporal correlation can be modeled by a Markov chain that represents transition probabilities between the values of data at two consecutive time points. Adversaries may obtain the temporal correlations, which commonly exist in real life and are easily acquired from public information or historical data. Figure 1 shows the released aggregates of location data with underlying temporal correlations due to road networks.

Figure 1:

Differentially Private Continuous Aggregate Release under Temporal Correlations.

In our recent work [5] [6], we prove that the privacy loss of a traditional differentially private mechanism at each time point may increase over time because of temporal correlation, which is called Temporal Privacy Leakage (TPL). In [6], we design efficient algorithms to precisely quantify such privacy loss.

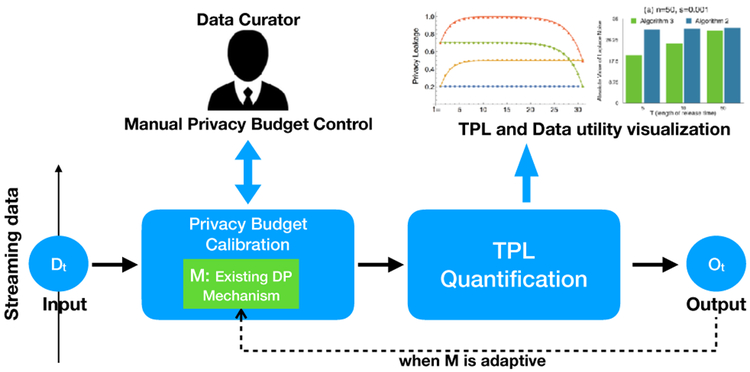
In this demonstration, we propose a system, ConTPL, to Control Temporal Privacy Leakage in differentially private continuous data release. First, data curator chooses a value for α as the maximum temporal privacy leakage. Then, data curator selects a differentially private mechanism to use for releasing private streaming data, denoted as M in Figure 2. Many existing mechanisms for steaming data allocate privacy budget at each time point either adaptively [3] [4] [12] [14] (e.g., the current privacy budget depends on the outputs or previous allocated privacy budgets) or non-adaptively [2] [7] [10] [11] [17] [8]. In either case, our system can control TPL of the selected mechanism within [0, α] by suggesting appropriate privacy budgets to data curator. The system consists of two major modules, Privacy Budget Calibration and TPL Quantification, as shown in Figure 2. The first module provides an appropriate privacy budget ϵ for M at each time point so that M can release private data from the input D_t whose temporal privacy leakage is less than α. The second module, TPL Quantification, precisely quantifies TPL according to the use of previous and current privacy budget and visualizes the change of TPL at each time point as well as the data utility to help data curator understand the trade-off between privacy and utility.

Figure 2:

System Overview of ConTPL.

2. BACKGROUND

Differential privacy (DP) [9] is a formal definition of data privacy. Let D be a database and D′ be a copy of D that is different in any one tuple. D and D′ are neighboring databases. A differentially private output from D or D′ should exhibit little difference. The parameter ϵ, called the privacy budget, represents the degree of privacy offered. Intuitively, a lower value of ϵ implies stronger privacy guarantee and a larger perturbation noise, and a higher value of ϵ implies a weaker privacy guarantee while possibly achieving higher accuracy. A commonly used method to achieve ϵ-DP is the Laplace mechanism, which adds random noise drawn from a calibrated Laplace distribution into the aggregates to be published.

Existing works on differentially private continuous aggregate release [1] [2] [3] [4] [7] [10] [11] [12] [14] [17] [8] do no take temporal correlation into consideration. In other words, they assume data between different time points are independent or the attacker has no knowledge of such temporal correlations. Although a few studies [18] [15] have investigated the issue of differential privacy under probabilistic correlations, they are not applicable for continuous data release because of the different problem settings. These works are focusing on one-shot data publish with differential privacy and consider the correlations between different users. While, in our setting, the data are continuously released by differentially private mechanism and the correlations are within each single user’s steaming data (such as the correlation between two consecutive locations in a user’s trajectory).

In our recent work [5] [6], we rigorously quantify and bound the privacy leakage against adversaries who have knowledge of temporal correlation. First, we model the temporal correlations using Markov model and analyze the privacy leakage of a DP mechanism against adversaries who have knowledge of such correlations. We find that the privacy loss of a DP mechanism may accumulate and increase over time. We call it temporal privacy leakage (TPL). In the following, we introduce the model of temporal correlation and the bound of TPL.

Markov Chain for Temporal Correlations.

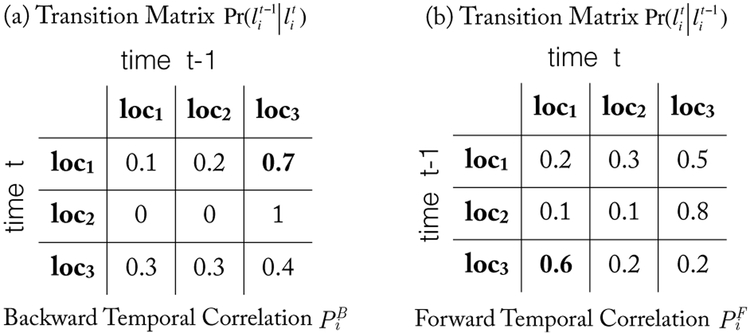
The Markov chain (MC) is extensively used in modeling user mobility profiles [13] [16]. For a time-homogeneous first-order MC, a user’s current value only depends on the previous one. The parameter of the MC is the transition matrix, which describes the probabilities for transition between values. The sum of the probabilities in each row of the transition matrix is 1. A concrete example of transition matrix and time-reversed one for location data is shown in Figure 3. As shown in Figure 3(a), if user i is at loc₁ now (time t); then, the probability of coming from loc₃ (time t − 1) is 0.7, namely, $\mathrm{Pr}(l_i^{t-1}=lo{c}_3\mid l_i^t=lo{c}_1)=0.7$. As shown in Figure 3(b), if user i was at loc₃ at the previous time t − 1, then the probability of being at loc₁ now (time t) is 0.6; namely, $\mathrm{Pr}(l_i^t=lo{c}_1\mid l_i^{t-1}=lo{c}_3)=0.6$. We call the transition matrices in Figure 3(a) and (b) as backward temporal correlation and forward temporal correlation, respectively. We note that these transition matrices used in our approach are not limited to be the same over time. For simplicity, we suppose they are time-homogeneous.

Figure 3:

Examples of Backward and Forward Temporal Correlations.

The backward and forward temporal correlations between user i’s data $l_i^{t-1}$ and $l_i^t$ are described by transition matrices $P_i^B$, $P_i^F\in {\mathbb{R}}^{n\times n}$, representing $\mathrm{Pr}(l_i^{t-1}\mid l_i^t)$ and $\mathrm{Pr}(l_i^t\mid l_i^{t-1})$, respectively.

Quantify Temporal Privacy Leakage.

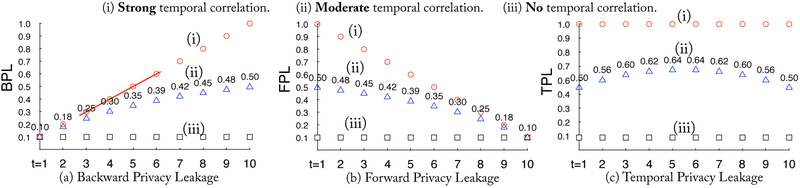
In [5], we find that TPL includes two parts: Backward Privacy Leakage (BPL) and Forward Privacy leakage (FPL) due to the existence of backward and forward temporal correlations. We also find that BPL may accumulates from previous privacy leakage and FPL increases with future release. Intuitively, BPL at time t is affected by previously releases at time 1 to t1, and FPL at time t will be affected by future releases at time t + 1 to T, which is the last time point of the release. In order to quantify such privacy loss in real-time, we design efficient algorithms for calculating it in sub-linear time in [6]. We illustrate TPL, BPL and FPL in Figure 4.

Figure 4:

Illustration of Temporal Privacy Leakage of Lap(1/0.1) at each time point.

Bound Temporal Privacy Leakage

Although the temporal privacy leakage may increase over time, we also show that its supremum may exist in some cases. To bound the privacy loss, we propose mechanisms that convert any existing DP mechanism into one against temporal privacy leakage. We implement these algorithms in our system, i.e., ConTPL, and demonstrate the effectiveness using two real-life datasets.

3. SYSTEM OVERVIEW

In our system, data curator first specifies a bound of temporal privacy leakage α, then selects an existing differentially private mechanism for releasing streaming data. The system releases private data with bounded temporal privacy leakage by controlling the privacy budget of the selected mechanism, demonstrate the increase or decrease of TPL along with time, and compare the data utility among different mechanisms or different privacy budget allocations.

In order to fulfill this system, we implement the major differentially private mechanisms for steaming data in literature, whose privacy budget allocation strategies can be categorized into two types: adaptive privacy budget allocation [3] [4] [12] [14] and non-adaptive privacy budget allocation [2] [7] [10] [11] [17] [8]. Our framework also includes a function for learning Markov model from time-series data. As shown in Figure 2, our system consists of two major module, two major modules, Privacy Budget Calibration and TPL Quantification. At each time point, the first module Privacy Budget Calibration suggests an appropriate privacy budget to data curator (data curator may not adopt it), and the second module TPL Quantification visualizes the temporal privacy leakage and the data utility (e.g., Mean of Squared Error and Mean of Absolute Error) of the outputs. In the following, we explain the details about the process in these modules.

3.1. Privacy Budget Calibration

We use two privacy budget allocation strategies proposed in our previous work [5] [6] as building blocks in this module. The first method, called upper-bound-method, allocates a specific privacy budgets uniformly at each time point so that the upper bound of TPL is alway less than or equal to a; the second method, called quantification-method allocates privacy budgets on the fly, which depends on the value of previous allocation.

The two strategies can be used to calibrate the privacy budget w.r.t. different types of mechanisms. For non-adaptive differentially private mechanisms who requires fixed privacy budget at each time point, we can use either upper-bound-method or quantification-method. For adaptive differentially private mechanisms, such as FAST in [12], BD or BA mechanisms in [14], we can only use quantification-method to calibrate the privacy budget. Given all previous budget allocation, quantification-method can calculate an appropriate value of budget for the current time point; meanwhile, the adaptive differentially private mechanism will provide a optimized privacy budget (mostly for improving the utility) which may be different to the one from quantification-method. In order to satisfy α-TPL, we use the smaller one of the above two privacy budgets.

For exploring different setting of privacy budget, we allow data curator to manually specify a privacy budget at each time point as desired. Enabling such “manual model” means that the system may not be able to control TPL within a bounded value. By integrating the visualization module in the next section into the system, it serves as an interactive tool to help data curator understand the trade-off between TPL and data utility.

3.2. TPL Quantification

We use TPL quantification algorithms in our previous work [5] [6] as building blocks in this module. The quantification algorithms require three types of input: (1) temporal correlation, (2) TPL at the previous time t − 1 and (3) privacy budget at the current time t. For the first input, we provide a function for learning transition matrix of Markov model from trajectories. For the second input, we can calculate it using quantification algorithms. For the third input, we obtain it from the previous module. We decompose the TPL into FPL (i.e., forward privacy leakage) and BPL (i.e., backward privacy leakage), as shown in Figure 4. We refer reader to our previous work [5] [6] for more details about the formulas of TPL, BPL and FPL.

We also demonstrate the Mean of Absolute Error and Means of Squared Error of the released private data. We compare the utility of the selected differentially private mechanism with and without the Privacy Budget Calibration module, which shows the cost of the protection against temporal privacy leakage.

4. DEMONSTRATION OVERVIEW

4.1. Datasets

We use two well-known real-life trajectory datasets: T-Drive [19] and Geolife [20]. We extract POIs by 0.1km × 0.1km grids on the map for both two datasets. T-Drive contains the GPS trajectories of 10,357 taxis during the period of Feb. 2 to Feb. 8, 2008 within Beijing. The total number of points in this dataset is about 15 million and the total distance of the trajectories reaches to 9 million kilometers. Geolife contains 17,621 trajectories with a total distance of 1,292,951kilometers and a total duration of 50,176 hours. These trajectories were recorded by different GPS loggers and phones, and have a variety of sampling rates. 91.5% of the trajectories are logged in a dense representation, e.g. every 1~5 seconds or every 5~10 meters per point. The data format is similar as the one shown in Figure 1(a).

4.2. Visualization of DP data release

In this part, using generated dataset (refer to our recent work [5]), we visualize the traditional DP data release and the potential temporal privacy leakage. For the purpose of this part, we expect attendees can gain an intuitive idea about our scenario and the problem (unexpected privacy loss). According to the analysis in [5], the TPL is divided into two parts: Backward Privacy Leakage (BPL) and Forward Priavcy Leakage (FPL), as shown in Figure 4. They are caused by backward and forward temporal correlations, respectively. The difference between TPL and FPL is as follows: when releasing differentially private data at time t, all the BPL at the previous time points keep the same and all the FPL at the previous time points will be updated due to the forward temporal correlations. Hence, the dynamic visualization will be helpful for understanding the increase of BPL and FPL.

4.3. TPL in the real-life datasets

In the demo, we design interactive queries to allow attendees to explore the cause of TPL for each user in the real-life trajectory datasets, so that the attendees can gain insights on the connection between users’ movements and the privacy loss. For example, users who present obvious mobility pattern may result in higher temporal privacy leakage due to high predictability. We also investigate how large the TPL is on real-life datasets. The results indicate that a large amount of users are subjected to the worst case of temporal privacy leakage, i.e., the privacy loss increases linearly over time. The reason is that, for most of the users, it is easy to observe their mobility patterns (e.g., the driver always moves between train stations.)

5. CONCLUSION

In this demonstration, we design a system to control temporal privacy leakage of an existing differentially private mechanism for streaming data. The system also serves as an interactive tool for data curator to explore the trade-off between TPL and utility. We also show how to use this system to release location statistics of real-world data sets continuously against TPL. We believe that this demo will be a useful tool for continuous private data release.