Steering and control of miniaturized untethered soft magnetic grippers with haptic assistance

Abstract

Untethered miniature robotics have recently shown promising results in several scenarios at the microscale, such as targeted drug delivery, microassembly, and biopsy procedures. However, the vast majority of these small-scale robots have very limited manipulation capabilities, and none of the steering systems currently available enable humans to intuitively and effectively control dexterous miniaturized robots in a remote environment. In this paper, we present an innovative micro teleoperation system with haptic assistance for the intuitive steering and control of miniaturized self-folding soft magnetic grippers in 2-D space. The soft grippers can be wirelessly positioned using weak magnetic fields and opened/closed by changing their temperature. An image-guided algorithm tracks the position of the controlled miniaturized gripper in the remote environment. A haptic interface provides the human operator with compelling haptic sensations about the interaction between the gripper and the environment, as well as enables the operator to intuitively control the target position and grasping configuration of the gripper. Finally, magnetic and thermal control systems regulate the position and grasping configuration of the gripper. The viability of the proposed approach is demonstrated through two experiments involving 26 human subjects. Providing haptic stimuli elicited statistically significant improvements in the performance of the considered navigation and micromanipulation tasks.

Note to Practitioners—The ability to accurately and intuitively control the motion of miniaturized grippers in remote environments can open new exciting possibilities in the fields of minimally-invasive surgery, micromanipulation, biopsy, and drug delivery. This paper presents a micro teleoperation system with haptic assistance through which a clinician can easily control the motion and open/close capability of miniaturized wireless soft grippers. It introduces the underlying autonomous magnetic and thermal control systems, their interconnection with the master haptic interface, and an extensive evaluation in two real-world scenarios: following of a predetermined trajectory, and pick-and-place of a microscopic object.

I. Introduction

The field of untethered miniature robotics has advanced significantly with several demonstrations of robotic tasks, such as controlled micropositioning [1], [2], [3], pickup and delivery of micro-objects, cells, and molecules [4], [5], [6], [7], biopsy [8], and drilling into soft tissue [9], [10]. Further, small-scale robots have also been applied in environmental science [11], [12], sensing [13], [14], and drug delivery [15], [16], [17].

Among the diverse applications presented in the literature, transportation and assembly at the microscale are important for biomedical applications. For example, Sanchez et al. [18] demonstrated the transport of animal cells using catalytic self-propelled microrobots, and Martel and Mohammadi. [19] completed a microassembly task using a swarm of flagellated bacteria. More recently, Gao et al. [20] reported an in vivo study of zinc-based artificial micromotors in a living organism using a mouse model. They demonstrated that the acid-driven propulsion in the mouse stomach effectively enhances the binding and retention of the motors as well as that of cargo payloads on the stomach wall. Moreover, they reported that the body of the micromotors gradually dissolved in the gastric acid, releasing the carried payload and leaving no toxic residue behind.

Although very promising, prior micromanipulation tasks using untethered small-scale robots have been quite simple, since most of these robots have very limited manipulation capabilities [1], [21], [3]. In order to expand the possible applications of untethered miniaturized robots and allow them to facilitate more complex (and useful) tasks, researchers have started to focus on the study and development of devices with gripping modalities. Being able to simultaneously grasp, move, and release an object at small scales would expand the applicability of such robots to a multitude of tasks, including minimally invasive surgery and targeted biopsy. It is noteworthy that robotic grippers have already been guided in in vivo applications [22], [23], [24], but the grippers used were significantly larger centimeter-sized devices. One of the reasons for the relatively large size of these devices is the need to integrate batteries to power their electromechanical actuators [25].

As an alternative to battery and antenna powered devices, stimuli responsive materials are expected to play an important role in the creation of untethered self-assembling and self-folding microrobots [25], [26]. Self-folding stimuli-responsive soft robots can in fact regulate the grasping and transport of objects by converting chemical and biochemical signals into mechanical, optical, electrical, and thermal signals, and vice-versa. These types of robots are playing an increasingly important role in a wide range of applications and scenarios, such as drug delivery, diagnostics, tissue engineering, and biosensors, microelectromechanical systems, coatings, and textiles [27], [28]. For example, Gultepe et al. [8] recently succeeded in performing a biopsy procedure in the gastrointestinal tract of live pigs with unguided distributed metallic microgrippers. These microgrippers were designed to stay open at cold temperatures and then close after approximately 10 min of exposure to body temperature. The microgrippers were injected into the bile duct or esophagus of the animals using a catheter that was introduced from the mouth. The grippers were able to retrieve sample tissue with a gripper retrieval rate as high as 95%. In order to reduce any risks associated with these devices being left in the body, microgrippers could potentially be fabricated using biodegradable and biodissolvable materials such as polymers and hydrogels. The soft-tissue-like mechanical properties of these materials could also facilitate delicate, flexible, and safe grasp capabilities [29], [30]. Moreover, soft grippers could be more suitable for medical procedures, since the sturdy grasp of rigid grippers may damage or even destroy biological cells and tissues. Among these soft materials, we found hydrogels—gels in which the swelling agent is water—very promising. Hydrogels are a class of porous soft materials composed of a network of polymer chains, which can be biocompatible and/or biodegradable. Moreover, they can operate in aqueous environments and recent advances in soft-lithography, photopatterning, and 3-D printing allow them to be structured with microscale resolution.

In this paper, we used soft bilayer miniature grippers where a hydrogel film is paired with a rigid non-swelling polymer SU-8. The two layers are photopatterned with UV light to form devices shaped like hands. The hydrogel is then doped with biocompatible iron oxide to allow it to respond to external magnetic fields. As demonstrated in [30] and detailed in Section II, this procedure endows the soft grippers with stimuli-responsive, self-folding, and magnetic properties. The temperature-induced differential swelling stress in the bilayer structure enables the grasping configuration of the gripper through temperature control, while the iron oxide allows wireless control of the positioning of the grippers through weak magnetic fields. As we illustrate, the capability to wirelessly control both the spatial position of the soft grippers and their grasping configuration significantly increases the dexterity of these agents, expanding their applicability and effectiveness with respect to other small-size robots [1], [21].

Given their promising features and potential reach, one of the challenges to facilitate complex manipulation tasks is the precise and quick control of these miniature grippers. Moreover, for reasons of responsibility, safety, and public acceptance, it is beneficial to provide a human operator with intuitive means to directly control the motion of such grippers, especially for medical scenarios [31], [32], [33]. In this case, the operator needs to receive sufficient information about the status of the gripper and about its interaction with the remote environment. This is possible through different types of feedback information that flow from the remote scenario to the human operator. Haptic feedback is one piece of this information flow, and it has been proven to be a valuable tool in robotic teleoperation [34], [35], [36], [37]. Its benefits have been proven in cardiothoracic procedures [38], microneedle positioning [39], telerobotic catheter insertion [40], palpation [41], cell injection [42], [43], and even micromanipulation [44], [45], [46], [47], [48], [49]. For example, Mehrtash et al. [46] developed a magnetic micromanipulation platform able to provide a resistive force every time the microrobot encountered a stiff object, and Ghanbari et al. [49] used active constraints to haptically assist the operator in penetrating a cell at the desired location. More recently, Pacchierotti et al. [48] presented a teleoperation system with haptic feedback that enables a human operator to intuitively control the positioning of a self-propelled microjet in 2-D. Providing haptic information significantly improved the performance and the perceived realism of the considered positioning tasks. However, due to the limited manipulation capabilities of microjets, they did not carry out any complex manipulation task.

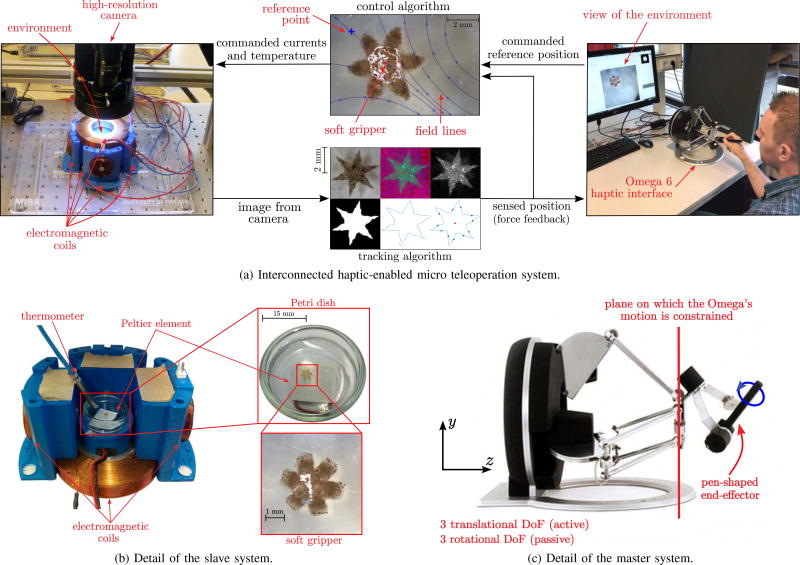
In this paper, we present an innovative microteleoperation system with haptic assistance for steering and control of miniaturized self-folding magnetic soft grippers in 2-D space, shown in Fig. 1. It enables a human operator to intuitively and accurately control the motion of a soft gripper in the remote environment while providing him/her with compelling haptic stimuli about the interaction between the soft gripper and the environment.

Fig. 1.

Haptic-enabled microteleoperation system. The image-guided algorithm tracks the position of the miniaturized soft gripper in the remote environment using a high-resolution camera and a Fourier-descriptors-based algorithm. A 6-DOF grounded haptic interface then provides the human operator with haptic stimuli about the interaction of the gripper with the remote environment. At the same time, it enables the operator to intuitively control the reference position of the gripper. Finally, the magnetic control algorithm steers the gripper toward the reference position defined by the operator, and a Peltier element regulates the temperature of the distilled water where the gripper is floating. (a) Interconnected haptic-enabled microteleoperation system. (b) Details of the slave system.(c) Details of the master system.

An image-guided algorithm tracks the position of the controlled gripper using a high-resolution camera and a Fourier-descriptors-based algorithm, as described in Section III-A. A 6 degrees-of-freedom (6-DOF) grounded haptic interface then provides the human operator with haptic stimuli about the interaction between the controlled gripper and the remote environment as well as enables him/her to intuitively control the reference target position and temperature of the gripper, as described in Section III-B. Finally, magnetic and thermal control systems regulate the positioning and temperature of the selected gripper using the magnetic forces generated by six electromagnetic coils and a Peltier element, respectively, as described in Section III-C. In order to test the effectiveness of our teleoperation system and to understand the role of haptic assistance for such an application, we carried out two experiments in a real scenario. The first one, described in Section IV-A, evaluates the steering capabilities of the proposed teleoperation system for a path following task. The second experiment, described in Section IV-B, evaluates the steering capabilities of our system for a pick-and-place task. A video of a soft gripper moving in free space using an Omega 6 interface is available as supplemental material.

A preliminary version of this work has been presented in [50]. However, while [50] mainly focused on the magnetic positioning of the soft grippers, this paper addresses in detail the image-based tracking algorithm, the closed-loop haptic and thermal controls, and, most importantly, it introduces an experimental evaluation in two paradigmatic scenarios, involving twenty-six subjects.

II. Miniaturized, stimuli-responsive, self-folding, soft robotic grippers

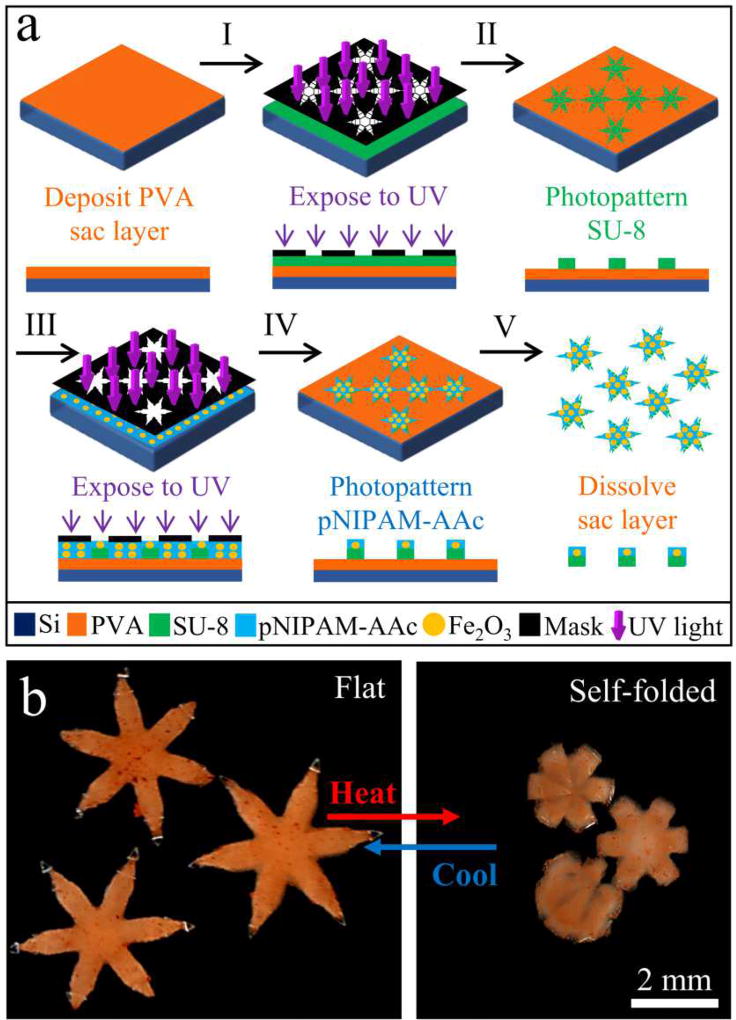
Miniature soft polymeric grippers composed of SU-8 and poly N-isopropylacrylamide-acrylic acid (pNIPAM-AAc) were patterned via a photolithographic approach (see Fig. 2a), which is described in detail in [30]. Briefly, a water soluble polyvinyl alcohol (PVA) sacrificial layer was deposited onto a silicon (Si) substrate by spin coating at 1000 rpm and dried at 150°C for 1 minute. To achieve rigid and non-swellable polymeric panel structures, SU-8 solution was coated onto the PVA layer by spin coating at 2000 rpm and pre-baking at 70°C for 1 minute, 115°C for 3 minutes, and 70°C for 1 minute. The baked SU-8 layer was then photopatterned using a dark field mask with 180 mJ/cm² UV light (365 nm) exposure and then post-baking at 70°C for 1 minute, 115°C for 3 minutes, and 70°C for 1 minute (step I in Fig. 2). Uncrosslinked material was removed by immersing in SU-8 developer for 1 minute and washed with 1 second acetone and 10 seconds isopropyl alcohol (IPA), then dried using compressed air (step II in Fig. 2). Further, to pattern the second thermally and magnetically responsive swellable thin hydrogel layers, a0.8 mL pNIPAM-AAc solution was mixed with 5% w/w biocompatible iron oxide (Fe₂O₃) nanoparticles and deposited atop of the SU-8 patterns. After waiting 2 minutes to get a uniform thickness, the second continuous pNIPAM-AAc layer was aligned with the SU-8 panel layer in non-contact mode using a spacer and then photopatterned using a second dark field mask with 40 mJ/cm² UV light exposure (step III in Fig. 2). Unreacted parts were removed by washing with acetone and IPA, and then dried using compressed air (step IV in Fig. 2). Finally, the photopatterned structures were immersed in DI water overnight to completely dissolve the PVA sacrificial layer and release the untethered soft grippers (step V in Fig. 2).

Fig. 2.

Soft gripper fabrication and operation. (a) Schematic of the process used to photopattern SU-8 and pNIPAM-AAc soft grippers. (b) Optical images showing the grippers closing on heating and opening up on cooling.

The untethered SU-8/pNIPAM-AAc grippers show anisotropic swelling and deswelling between layers when triggered by a thermal stimulus. Initially, the grippers are in a two dimensional (2-D) flat state at room temperature (RT). On heating, the grippers close spontaneously due to significant volumetric shrinkage of the pNIPAM-AAc layer which undergoes a phase transition from a hydrophilic to hydrophobic state above its lower critical solution temperature (LCST). Reversibly, on cooling down, the self-folded grippers open back to their 2-D flat state as the pNIPAM-AAc layer swells on reversal of the transition from a hydrophobic to hydrophilic state. This spontaneous and environmental thermal response of the pNIPAM-AAc layer is able to open and close the soft grippers reversibly, as shown in the bottom half of Fig. 2. Further, by incorporating magnetic Fe₂O₃ nanoparticles, the soft grippers can be manipulated from afar using precisely controlled magnetic fields, as detailed in Section III-C.

III. Micro teleoperation System

Figure 1a shows how the tracking, haptic, and control systems are interconnected. Table I summarizes the features and parameters of the system.

TABLE I.

Teleoperation system details and parameters

Tracking system
Hardware	Blackfly 1.4 MP Color GigE PoE camera + Mitutoyo FS70 microscope
Refresh rate	50 Hz
Accuracy	106 ± 30 µm
Haptic system
Hardware	Omega.6 6-DoF haptic interface (translational DoF active, rotational DOF passive)
Refresh rate	1000 Hz
Workspace	160×110 mm (translations limited to 2-DoF)
Positioning system
Hardware	Six electromagnets powered by Elmo Whistle 1/60 servo controllers
Refresh rate	100 Hz
Positioning accuracy	115 ± 104 µm (2.9% of the body length)
Velocity	721 ± 132 µm/s
Grasping system
Hardware	Conrad TECI-1703 Peltier element 3.9 W
Refresh rate	50 Hz
Open/close average elapsed time	10 s
Interconnection
Hardware	real-time GNU/Linux machine
Stability control	time-domain passivity control, adapted from [68]
Master-slave position scaling factor	0.2

A. Tracking system

To precisely track the position of the controlled soft gripper in the remote scenario, we placed a high-resolution camera above the Petri dish hosting the environment, as shown in Fig. 1. The camera is a Blackfly 1.4 MP Color GigE PoE camera (Point Grey Research Inc., Richmond, Canada), mounted on a Mitutoyo FS70 microscope unit (Mitutoyo, Kawasaki, Japan) using a Mitutoyo M Plan Apo 2 / 0.055 objective. It has an adjustable zoom with a maximum of 24×, a frame rate of 125 fps, and it is mounted on a linear stage to enable precise focusing. A CCD sensor is used for recording, with a pixel width and height of 5.50 µm, providing a resolution up to 0.50 µm.

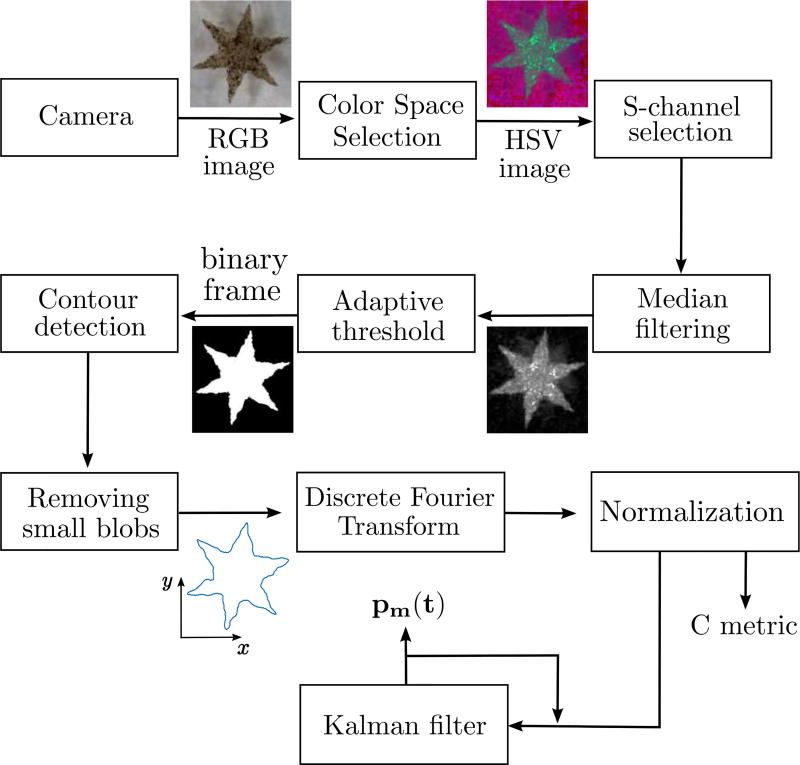
Each frame is first converted to HSV colorspace, then its saturation channel (S) is filtered using a median filtering technique, and finally a binary frame is obtained using an adaptive threshold method. The resulting binary frame is used to find the contours of the image, and Fourier descriptors are then employed to detect the centroid of the microgripper and measure its extent of closure. Finally, a Kalman filter is used to deal with uncertainties in the tracking. The flow chart of the tracking algorithm is shown in Fig. 3, and each part of the algorithm is described below in detail.

Fig. 3.

Tracking algorithm. Each frame registered by the high-resolution camera is first converted to HSV colorspace, then its saturation channel (S) is filtered using a median filter, and a binary frame is obtained using an adaptive threshold. The binary frame is then used to find the contours of the image, and Fourier descriptors are used to detect the centroid of the microgripper and measure how much the microgripper has closed. Finally, a Kalman filter is used to deal with uncertainties in the tracking. The tracking system runs at 50 Hz.

1) Color space selection

Light changes in the background and glares due to the reflection of the light with the gripper’s SU8-layer (see Section II) make it very hard to robustly track the grippers in RGB colorspace. The RGB color model is in fact an additive model in which red, green, and blue light are added together, and it is not trivial to separate the intensity information from the color information, making the model quite sensitive to changes in the light condition [51]. To address this problem, we look into the HSV colorspace, which separates the light intensity information from the color information. Since we are only interested in the shape of our gripper, and we want to avoid the aforementioned issues related to the change of light conditions, we disregard the H- and V-channels and we focus our analysis on the S-channel only. The two top pictures in Fig. 3 shows the original RGB image (left) and the HSV image (right) in RGB colorspace, where the H channel is shown in red, the S channel is shown in green, and the V channel is shown in blue.

2) Median filtering

After converting the RGB image to HSV color space and extracting the S-channel, we apply a median filter to reduce noise. The median filter is a non-linear digital filtering technique that replaces each pixel value with the median of n × n neighboring entries, where n is an integer representing the kernel size of the filter [52]. The mid right picture in Fig. 3 shows the S-channel of the HSV image after the median filtering.

3) Adaptive threshold

Due to vignetting, different areas of the image show different light conditions. In order to be able to compare these areas, we employ an adaptive thresholding technique. Once the S-channel of the HSV image is extracted and the noise is reduced, the filtered image frame F_f (x, y) is converted to a binary frame F_b (x, y) using an adaptive threshold,

$$F_b(x,y)=\{\begin{array}{cc}255\hfill & \text{if }{F}_f(x,y)>T(x,y)\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}$$ (1)

where T (x, y) is the threshold matrix, defined as the mean of a neighborhood around the considered pixel, weighted using a Gaussian distribution. Pixels equal to zero are then colored as black, while pixels equal to 255 are colored as white. The mid left picture in Fig. 3 shows the image after the abovementioned adaptive thresholding process.

4) Contour detection

From the binary image, we compute the contours of all the visible blobs using a contour detection algorithm based on the technique presented by Reeb et al. [53] and then further developed by Bajaj et al. [54] and Carr et al. [55]. Each blob is described by a sequence of points connected to each other by segments. This sequence is found using the method proposed by Suzuki et al. [56], in which detected objects are represented as trees. In each tree, the root is a sequence describing the outer contour, and the children are sequences describing inner contours of successive levels. Once the contours are computed, blobs whose contour is smaller than our gripper are removed, leaving out only our target gripper. The bottom picture in Fig. 3 shows the image after the abovementioned contour detection process.

5) Fourier descriptors

Fourier descriptors are used to find the centroid of the tracked gripper and to measure its extent of closure. In order to calculate the Fourier descriptors of the given contour (see subsection above), its coordinates are uniformly resampled and mapped to the imaginary plane,

$$z(s)=x(s)+\mathit{\text{iy}}(s),$$ (2)

where x and y are the resampled contour coordinates (see Fig. 3), i is the imaginary unit, and s is the running arc length [57]. After this mapping, we apply the discrete Fourier transform,

$$Z_k=\frac{1}{N}\sum _{n=0}^{N-1}{z}_n{e}^{\frac{-i2\pi \mathit{\text{nk}}}{N}},$$ (3)

where z_n are the contour points of eq. (2), and N is the number of points. The more points we consider, the better we approximate the contour. In this work, we chose N = 32, since it provides a good trade-off between contour fidelity and runtime speed. In general, the implementation is most efficient when N is a power of 2 [58]. The centroid of the contour is then defined as (x_c, y_c) = (Re(Z₀), Im(Z₀)) [57].

We use Fourier descriptors to also evaluate the extent of closure of the gripper. As detailed in Section IV-B, in fact, this information is used to provide the human operator with information about the status of the grasping procedure. First, we normalize the Fourier descriptors to make them invariant to translations and rotations of the gripper [59]. The objective of this normalization is to isolate the information in the descriptors pertaining to size, position, and orientation. Normalizing the position is achieved by setting Z₀ to zero. The normalization with respect to orientation (and size) is achieved by scaling and rotation of the contour such that the amplitude of the first harmonic Z₁ becomes 1 and its phase is zero [57].

After this normalization, we are ready to evaluate the 6-fold symmetry, perimeter, and area of the gripper. In fact, from the point of view of the camera, a completely open gripper looks like a 4-mm-wide star with 6 symmetric spikes (see Fig. 4a), while a completely closed gripper looks like a 1-mm-wide disk (see Fig. 4e). Our approach is therefore twofold. At the same time we try to recognize the 6 symmetric spikes and to measure the perimeter/area ratio of the gripper. Combining these two pieces of information provides us with a reliable measure of how much the considered gripper has closed.

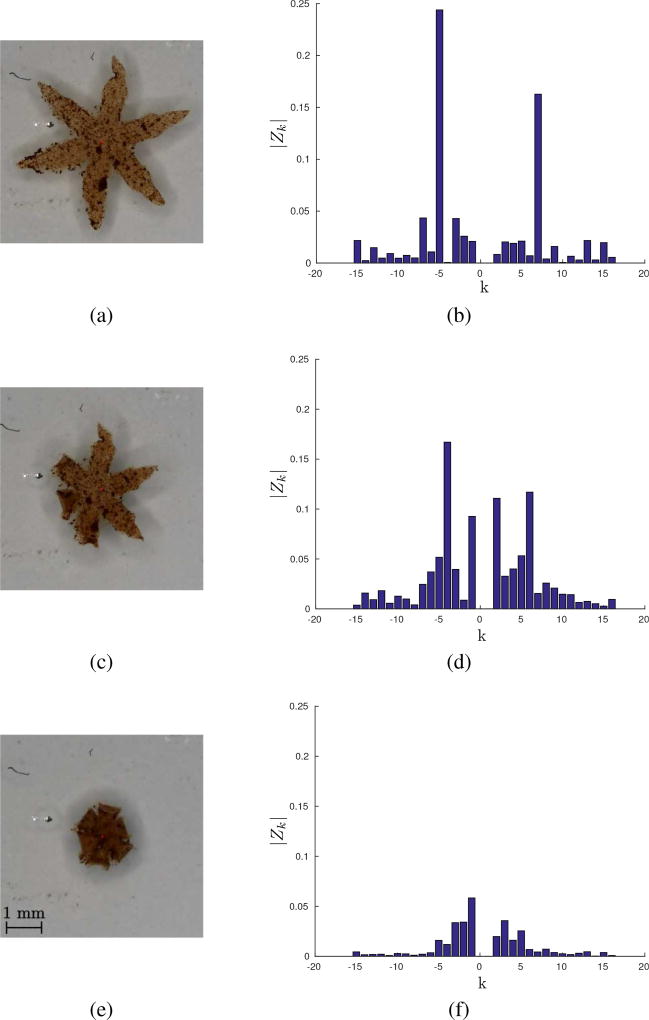
Fig. 4.

Three images of the same soft gripper and their corresponding normalized Fourier descriptors. As the gripper closes, the difference between descriptors Z₇, Z₋₅, Z₁₃, Z₋₁₁ and the others descreases. We did not include Z₁ in the graph, since |Z₁| = 1, and plotting it would have made the vertical |Z_k| scale too large.

To recognize the spikes, we recall that

• If a contour is M-fold symmetric such as $z(s)=z(s)e^{(\frac{2\pi \mathit{\text{ni}}}{M})}$, where n is an integer, then only the harmonics 1 ± Mm, where m is an integer, are non-zero [57].

For our gripper, M = 6, therefore only harmonics 1 ± 6m, m = 0, 1, 2 should be non-zero. Figure 4 shows three examples of images recorded by the high-resolution camera and their corresponding Fourier descriptors |Z_k|. Figure 4a shows a completely open gripper, Fig. 4c shows a half-closed gripper, and Fig. 4e shows a completely closed one. From Fig. 4b, we can see that the difference between descriptors Z₇, Z₋₅, Z₁₃, Z₋₁₁ and the others is quite large for the open gripper. This difference decreases for the other two grippers, whose descriptors are shown in Figs. 4d and 4f. We did not include Z₁ in the graph, since after the normalization |Z₁| = 1. We measured the 6-fold symmetry of the gripper by calculating the difference between the mean of normalized harmonics 1 ± 6m and the mean of the other normalized descriptors,

$$6_{\mathit{\text{FS}}}=\frac{2}{5}\sum _{m=-2}^2|Z_{(1+6m)}|-\frac{1}{32}\sum _{k=-15}^{16}|Z_k|.$$ (4)

A high value of this metric indicates that the gripper is 6-fold symmetric (i.e., open in our case).

As mentioned before, in addition to evaluating the 6-fold symmetry of the gripper, we also consider its perimeter/area ratio. Since this ratio is larger for an open gripper than for a closed one, the ratio can be directly considered as a measure of the extent of closure of the gripper. The perimeter P and the area A of the gripper are estimated as

$$A=\pi \sum _{k=-15}^{16}k{|Z_k|}^2$$ (5)

$$P^2=4{\pi }^2\sum _{k=-15}^{16}{k}^2{|Z_k|}^2$$ (6)

where Z_k are the non-normalized Fourier descriptors [57].

We combine metrics 6_FS and P/A to define a new metric that evaluates the extent of closure of the gripper,

$$C={\left(\frac{6_{\mathit{\text{FS}}}}{6_{\mathit{\text{FS}},\mathit{\text{max}}}}\right)}^2+{\left(\frac{P}{A}\frac{A_{\mathit{\text{max}}}}{P_{\mathit{\text{max}}}}\right)}^2,$$ (7)

where 6_FS,max, A_max, and P_max are the highest value registered for the 6-fold symmetry, area, and perimeter metrics of the considered gripper, respectively (i.e., when the gripper is open). A high C indicates that the gripper is open, while a low C indicates that the gripper is closed. For example, the grippers shown in Figs. 4a, 4c, and 4e have C = 2, 1.40, 1.27, respectively.

6) Kalman Filter

Finally, a Kalman filter is used to deal with uncertainties in the tracking. For this purpose, we modeled a gripper as,

$${\mathbf{x}}_{\mathbf{k}}=F{\mathbf{x}}_{\mathbf{k}-\mathbf{1}}+{\mathbf{w}}_{\mathbf{k}},$$ (8)

where x_k ∈ ℝ^4×1 is the state variable, F ∈ ℝ^4×4 is the transfer matrix, and w_k ∈ ℝ^4×1 is the process noise. Noise w_k is modeled as a random variable with Gaussian distribution N (0, Q), where $Q=E[{\mathbf{w}}_{\mathbf{k}}{\mathbf{w}}_{\mathbf{k}}^{\mathbf{T}}]$ is the covariance matrix. Measurements z_k ∈ ℝ^2×1 are then given by

$${\mathbf{z}}_{\mathbf{k}}=H{\mathbf{x}}_{\mathbf{k}}+{\mathbf{v}}_{\mathbf{k}},$$ (9)

where v_k ∈ ℝ^2×1 is the measurement noise, that is again assumed to have Gaussian distributions N (0, R) for covariance matrix $R=E[{\mathbf{v}}_{\mathbf{k}}{\mathbf{v}}_{\mathbf{k}}^{\mathbf{T}}]$. Since we measure only the position of the gripper, z_k and H ∈ ℝ^2×4 are simply represented as

$${\mathbf{z}}_{\mathbf{k}}=\left(\begin{array}{c}{z}_x\hfill \\ z_y\hfill \end{array}\right),H=\left(\begin{array}{cccc}1\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill & 0\hfill \end{array}\right).$$ (10)

The position of the gripper as estimated by the Kalman filter is considered our final gripper position p_m ∈ ℝ². This position vector is an input of the control and haptic systems as depicted in Fig. 1a. The tracking system runs at 50 Hz.

7) Evaluation

In order to evaluate the performance of our tracking system, we registered four videos of four different robotic grippers moving in the remote environment, for a total of 281 seconds (see video available as supplemental material). We converted the videos to JPEG images at 5 fps, for a total of 1405 images. The centroid of the gripper as tracked by the tracking algorithm and the reference point were not shown.

Fifteen participants took part in the experiment, including ten males and five females. None of the participants reported any deficiencies in their visual abilities. The task consisted in looking at the images extracted from the videos and clicking at the centroid of the gripper. The difference between the centroid as estimated by the subjects and the centroid as estimated by our tracking algorithm provides a measure of performance of our tracking algorithm. Each experiment lasted for approximately 30 minutes. The algorithm showed an accuracy in tracking the gripper’s centroid of 106 ± 30 µm. Similar subjective evaluation approaches are common in the literature [60], [61].

B. Haptic system

The haptic rendering system is composed of a 6-DoF Omega haptic interface (Force Dimension, CH). The interface has 6 DOF, three for translation and three for rotations, as shown in Fig. 1c. The interface is constructed in such a way that translations and rotations are decoupled from each other. Translational degrees of freedom are active, while rotational degrees of freedom are passive. This haptic interface is also equipped with active gravity compensation to improve the teleoperation experience and reduce the operator’s fatigue. In this work, we use the Omega 6 as an impedance haptic interface. We measure the position of the end effector, controlled by the human operator, to set the reference target position of the soft gripper. At the same time, through the same end-effector, we provide the operator with haptic stimuli from the remote environment. The scaling factor between master and slave positions is 0.2 in all directions, i.e., moving the end-effector of the Omega interface of 10 cm moves the gripper’s reference position of 2 cm. The force to be provided is evaluated according to the feedback condition considered, as detailed in Section IV, and it is a combination of kinesthetic, frictional, and vibrotactile stimuli. Kinesthetic and frictional stimuli mainly stimulate Merkel (SA I) and Ruffini (SA II) receptors, while vibrotactile stimuli mainly stimulate Pacinian receptors (FA II). Although Omega interfaces have been often used in the literature to provide (kinesthetic) force feedback, they are also known to be effective in producing vibrations at 25 – 200 Hz by commanding sinusoidal forces to their end-effectors [33], [48]. The haptic control loop runs at 1 kHz.

Since we control the soft grippers in 2-dimensional space, the translational motion of the Omega interface is constrained on its x-y plane (see Fig. 1c). Force f_z (t), provided by the Omega interface along the z axis, is defined as

$$f_z(t)=-k_{b,k}(p_{r,z}(t)-p_{z,\mathit{\text{plane}}}),$$ (11)

where k_b,k = 1000 N/m, p_z,plane is the location of the x-y plane along z, and p_r,z (t) is the current position of the end-effector of the Omega in the z direction. The pen-shaped end-effector of the Omega is also equipped with a programmable button, which is used during the experiments to activate/deactivate the temperature control on the Petri dish (see Section III-C). When the temperature control is active, the pen-shaped end-effector enables the human operator to control the target temperature of the environment. The end-effector can rotate, and its rotation is used to set the target temperature driving the Peltier element to

$$t_{\mathit{\text{pe}}}=(\frac{{\theta }_r}{60}+36),$$ (12)

where θ_r ∈ [0°, 320°] is the rotation of the pen-shaped end-effector (see Fig. 1c). More details on how the temperature control works can be found in Section III-C. As mentioned in Section II, controlling the temperature of the remote environment enable us to close and open the soft grippers.

C. Control system

Given the current position of the gripper, as estimated by the tracking algorithm, and the commanded reference position, the control system moves the gripper using an array of six orthogonally-oriented iron-core electromagnets, with the objective of steering it toward the reference point. Moreover, a Peltier element regulates the temperature of the water where the controlled gripper is floating, enabling the control of the grasping configuration of the small robot. The reference position and temperature are controlled by the operator through the haptic interface, as detailed in Section III-B.

1) Position control

The position control is implemented as a Multi-Input Multi-Output (MIMO) Proportional Integral Derivative (PID) control. The input of the regulator is the current position of the gripper p_m (t) ∈ ℝ³, as evaluated by the tracking algorithm, while its output is a vector of electromagnetic forces F ∈ ℝ^3×1 to be applied on the gripper to move it toward the reference point. The direction and magnitude of F depend on the direction and magnitude of the position error and on the previous state of the system, as detailed in [63] and [64]. The force F needs then to be mapped to input currents for the six electromagnets. In this respect, it is possible to map the commanded currents into electromagnetic forces exerted on the grippers as

$$\mathbf{F}({\mathbf{p}}_{\mathbf{m}})=(\mathbf{m}·\nabla )\mathbf{B}({\mathbf{p}}_{\mathbf{m}})=\mathbf{\Lambda }(\mathbf{m},{\mathbf{p}}_{\mathbf{m}})\mathbf{I};$$ (13)

where B(p_m) ∈ ℝ^3×1 and I ∈ ℝ^6×1 are the magnetic fields produced by the electromagnets and their currents at point p_m, respectively; m ∈ ℝ^3×1 is the magnetic dipole moment of the grippers; and Λ(m, p_m) ∈ ℝ^3×6 is the actuation matrix, that maps the input currents into magnetic forces. B(p_m) was estimated using a finite elements simulation, and it was then validated using a three-axis Hall magnetometer (Senis AG, Baar, Switzerland). Finally, the magnetic dipole moment of the grippers m was estimated using the U-turn technique [65]. Since we control 2 degrees of freedom (x and y positions) with 6 electromagnets, the position-control system is overactuated. Consequently, different matrices can be used to map F to I. In this work we used the Moore-Penrose pseudoinverse of Λ (Λ⁺) [66],

$$\mathbf{I}={\mathbf{\Lambda }}^{+}(\mathbf{m},{\mathbf{p}}_{\mathbf{m}})\mathbf{F}(\mathbf{P}).$$ (14)

We tuned the PID controller using the Ziegler-Nichols method [67]. The magnetic positioning system runs at 100 Hz.

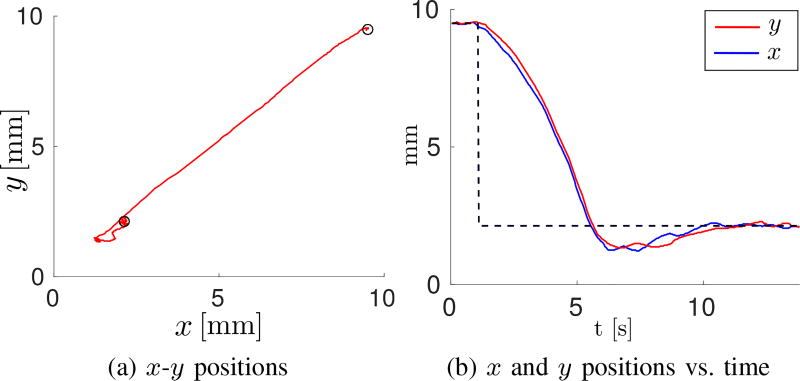
The performance of the closed-loop position control was assessed in 120 motion control experimental trials, which consisted of point-to-point positioning tasks (40 trials) and tracking of circular and square trajectories (80 trials). The circular trajectories had a radius of 3 mm, while the square trajectories had a side of 6 mm. Eight different grippers were used. The grippers moved with an average velocity of 721 ± 132 µm/s and with a positioning error of 115 ± 104 µm (mean ± standard deviation). Figure 5 shows a representative point-to-point positioning trial. A video of the experiment is available as supplemental material.

Fig. 5.

Position control: A representative point-to-point positioning trial. The reference position of the gripper was suddenly changed and the trajectory of the gripper was registered. Solid lines show the position of the gripper in (a) space and (b) time. The commanded reference positions are shown as circles in (a) and as a dashed line in (b).

2) Temperature control

The self-folding capabilities of the soft grippers can be controlled using thermal stimuli. For this purpose, we regulate the temperature of the water wherein the grippers are suspended using a Peltier element, which is able to produce both positive and negative temperature differentials between its two faces. The element is directly attached to the bottom of the Petri dish, as shown in Fig. 1b. Moreover, in order to compensate for Joule effects, an aluminum heat-sink is attached to the outer face of the element. A closed-loop temperature control is implemented using an Arduino Uno board and a thermometric probe. The regulator reads the water temperature from the probe and receives the target temperature from the haptic interface (see Section III-B). These inputs are then fed to a proportional controller that determines the current for the Peltier element. The system is able to reach the reference temperature at approximately 10°C per minute.

3) Implementation and stability

The integrated micro teleoperation system is managed by a real-time GNU/Linux computing machine (Debian 8 with Linux Kernel 3.16). The camera and the Omega 6 interface are connected to the computer via Ethernet and USB connections, respectively. Electromagnets are powered by Elmo Whistle 1/60 servo controllers (Elmo Motion Control, Petach-Tikva, Israel). Master and slave systems are connected using a simple direct coupling scheme, as summarized in Fig. 1a. Unlike passive coupling, direct coupling does not reduce the information reliability and response time [69]. However, it does not guarantee the unconditional stability of the system. System parameters are reported in Table I.

In order to guarantee the stability and safety of the teleoperation system, we implemented the passivity controller presented by Franken et al. [68] (see also Section I). The control algorithm is able to guarantee stable behavior of bilateral telemanipulation systems in the presence of time-varying destabilizing factors, such as hard contacts, relaxed user grasps, stiff control settings, and/or communication delays. The architecture is split into two separate layers. The hierarchical top layer, named Transparency Layer, aims at achieving the desired force sensation, while the lower layer, named Passivity Layer, ensures the passivity of the system. The operator and the environment impress a movement to the master and slave systems, respectively. The Transparency Layer displays the desired force behavior by computing the torques to be applied to the operator and to the environment. The Passivity Layer checks how the action planned by the Transparency Layer influences the energy balance of the system. If the passivity condition is not violated, the planned action can be directly applied to both sides of the system. However, if loss of passivity is detected, a scaled control action is applied to preserve stability. Separate communication channels connect the layers at the slave and master levels so that information related to exchanged energy is separated from information about the desired behavior.

The parameters used in our implementation of this control strategy are the same employed in [33], [48]. Passivity control was only used to regulate the kinesthetic stimuli provided by the haptic device (see Section IV), since vibrotactile and frictional stimuli do not affect the stability of the control loop [36].

IV. Experimental Evaluation

In order to evaluate the effectiveness of our integrated system and understand the role of haptic assistance for such application, we carried out two sets of experiments. The first one, described in Section IV-A, evaluates the steering capabilities of the proposed teleoperation system for a path following task. The second experiment, described in Section IV-B, evaluates the steering capabilities of our system for a pick-and-place task. In both experiments, the environment is filled with distilled water and a soft gripper with a diameter of 4 mm is used.

A. Experiment #1: Path following

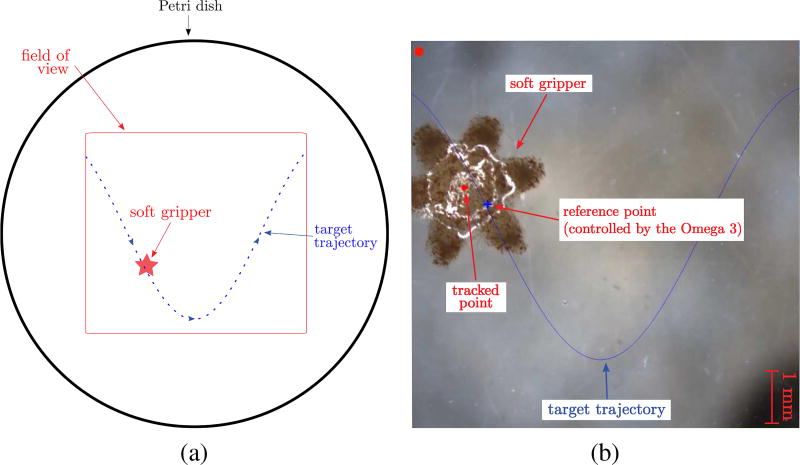
The first experiment aims at evaluating our teleoperation system in a path following task, as sketched in Fig. 6a and demonstrated in the video available as supplemental material. A frame of the video is shown in Fig. 6b. Table II summarizes the methods and results of this experiment.

Fig. 6.

Experiment #1: the path following task. Subjects are required to steer a soft gripper along the predetermined trajectory, being as fast and precise as possible. We considered four target trajectories and eight feedback conditions (see the video available in Supplementary Material). (a) Sketch of the task. (b) Remote environment.

TABLE II.

Summary of Experiment #1

Subjects	16 (14 males, 2 females)
Task	moving a soft gripper along a predetermined trajectory, being as fast and precise as possible
Conditions	Visual feedback (Vs)
	Visual + Vibrotactile feedback (Vs + Vb)
	Visual + Frictional feedback (Vs + Pc)
	Kinesthetic feedback (K)
	Visual + Position-error feedback (Vs + Pe)
	Visual + Vibrotactile + Position-error feedback (Vs+Vb+Pe)
	Visual + Frictional + Position-error feedback (Vs + Pc + Pe)
	Kinesthetic + Position-error feedback (K + Pe)
Video	available as supplemental material
Best conditions (average)
	Completion time		K (42.38 s)
	Error in following trajectory		K + Pe (0.53 mm)
	Distance between reference and gripper		K + Pe (0.97 mm)
	Perceived effectiveness		K (8.26)
Statistical analysis (two-way repeated measures ANOVA)
Completion time (significant p values only)
	Factor 1: presence of Pe feedback (p = 0.001)
	Factor 2: feedback type (p < 0.001)
		Vs + Vb vs. Vs	p = 0.013
		Vs + Vb vs. Vs + Pc	p = 0.003
		Vs + Vb vs. K	p = 0.002
Error in following trajectory (significant p values only)
	Factor 1: presence of Pe feedback (p < 0.001)
	Factor 2: feedback type (p < 0.001)
		Vs vs. Vs + Vb	p < 0.001
		Vs vs. Vs + Pc	p < 0.001
		Vs vs. K	p < 0.001
		Vs + Vb vs. Vs + Pc	p < 0.001
		Vs + Vb vs. K	p < 0.001
		Vs + Pc vs. K	p < 0.001
Distance between reference and gripper (significant p values only)
	Factor 1: presence of Pe feedback (p < 0.001)
Perceived effectiveness
	Factor 1: presence of Pe feedback (p = 0.002)
	Factor 2: feedback type (p < 0.001)
		Vs vs. Vs + Vb	p < 0.001
		Vs vs. K	p < 0.001
		Vs + Vb vs. Vs + Pc	p < 0.001
		Vs + Vb vs. K	p < 0.001
		Vs + Pc vs. K	p < 0.001

1) Subjects

Sixteen subjects (14 males, 2 females, age range 22 – 31 years) took part in the experiment. Six of them had previous experience with haptic interfaces, and no subject reported any deficiency in the perception abilities. The experimenter explained the task, asked the subjects to sign an informed consent, and then spent about two minutes adjusting the setup to be as comfortable as possible. No practice trial was allowed. In order to avoid providing undesired auditory cues, participants were isolated from external noises through a pair of noise-canceling headphones.

2) Methods

The task consisted of steering a soft gripper in the remote environment along a predetermined trajectory, being as fast and precise as possible. According to the feedback condition considered, the subject is provided with visual, kinesthetic, frictional, or vibrotactile assistance about the error in following the target trajectory (see below). We considered four different trajectories,

$$\begin{array}{c}\hfill y=13.6-3.2\text{ sin }(\frac{\pi }{6}(1+6i)-\frac{x}{2}(1+j)),i=0,1\\ \hfill j=0,1\end{array}$$

Trajectory 1 with i = 0 and j = 0 is shown in Fig. 6b.

Each subject made sixty-four randomized repetitions of the path following task, with eight repetitions for each feedback condition proposed. We considered eight different feedback conditions, that are combinations of these four types of feedback: visual feedback (Vs), kinesthetic feedback (K), vibrotactile feedback (Vb), frictional feedback (Pc), and position-error feedback (Pe).

When visual feedback (Vs) is provided, the target trajectory is shown on the screen (as in Fig. 6b).

When kinesthetic feedback (K) is provided, the Omega interface provides an attractive kinesthetic force that keeps the user close to the target trajectory. This force f_k (t) ∈ ℝ², provided by the Omega along its x and y axes, is

$${\mathbf{f}}_{\mathbf{k}}(\mathbf{t})=-k_k({\mathbf{p}}_{\mathbf{r}}(\mathbf{t})-{\mathbf{p}}_{\mathbf{t},\mathbf{r}})-b_k{\dot{\mathbf{p}}}_{\mathbf{r}}(\mathbf{t}),$$ (15)

where k_k = 1000 N/m, b_k = 5 Ns/m, p_r (t) ∈ ℝ² is the current position of the reference point as controlled by the user through the haptic interface, and p_t,r is the point on the target trajectory closest to p_r (t).

When vibrotactile feedback (Vb) is provided, the Omega provides a vibration as soon as the user moves the end-effector out from the target trajectory. The amplitude of the vibration increases as the end-effector of the Omega moves away from the target trajectory. This force f_vb (t) ∈ ℝ², provided by the Omega along its x and y axes, is

$${\mathbf{f}}_{\mathbf{\text{vb}}}(\mathbf{t})=k_{\upsilon b}({\mathbf{p}}_{\mathbf{r}}(\mathbf{t})-{\mathbf{p}}_{\mathbf{t},\mathbf{r}})\left[\begin{array}{c}\hfill \text{sin }(2\pi f_{\upsilon b}t)\hfill \\ \hfill \text{sin }(2\pi f_{\upsilon b}t)\hfill \end{array}\right],$$ (16)

where k_υb = 50 N/m and f_υb = 150 Hz. The vibration frequency was chosen to fit the haptic interface specifications and to maximally stimulate the Pacinian corpuscle receptors [70].

When frictional feedback (Pc) is provided, the Omega increases its friction when the user moves the reference point away from the target trajectory. This force f_pc (t) ∈ ℝ², provided by the Omega along its x and y axes, is

$${\mathbf{f}}_{\mathbf{\text{pc}}}(\mathbf{t})=\{\begin{array}{cc}-b_{\mathit{\text{pc}}}{\dot{\mathbf{p}}}_{\mathbf{r}}(\mathbf{t})\hfill & \text{if moving away from the target trajectory},\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}$$ (17)

where b_pc = 20 Ns/m.

Finally, when feedback about the position error (Pe) of the gripper is provided, the Omega provides an attractive kinesthetic force that keeps the reference point close to the controlled gripper. This force f_i (t) ∈ ℝ², provided by the Omega along its x and y axes, is

$${\mathbf{f}}_{\mathbf{i}}(\mathbf{t})=-k_i({\mathbf{p}}_{\mathbf{r}}(\mathbf{t})-{\mathbf{p}}_{\mathbf{m}}(\mathbf{t})),$$ (18)

where k_i = 200 N/m, and p_m (t) is the current position of the gripper as evaluated by the tracking system.

We combined the abovementioned types of feedback in four conditions:

1. Visual feedback (Vs),

2. Visual feedback + Vibrotactile feedback (Vs + Vb),

3. Visual feedback + Frictional feedback (Vs + Pc),

4. Kinesthetic feedback (K),

and we tested all these conditions with and without providing feedback about the position error between the soft gripper and the reference point, ending up with 4 (feedback conditions) × 2 (with and without position-error feedback) × 4 (target trajectories) = 32 different experimental conditions. The experiment lasted approximately 30 minutes.

A view of the remote environment is always provided to the subjects through the high-resolution camera and a LCD screen (see Fig. 1). The Omega 6 haptic interface is always used to provide the controller with the gripper’s reference position.

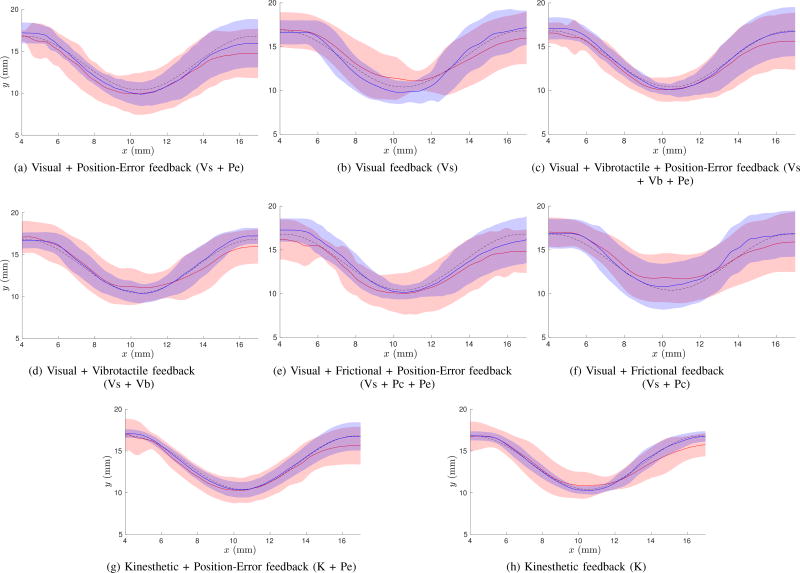
Figure 7 shows the position of the reference point (blue) and of the tracked gripper (red) along the x and y axes for target trajectory 1 (see Section IV-A2). Average trajectory along the x and y axes (solid lines) ± standard deviation (patches) along the y axis is shown for each feedback condition. The target trajectory is plotted in black.

Fig. 7.

Experiment #1: path following task. The average trajectory of the reference point (blue curves) and the tracked gripper (red curves) along the x- and y-axes (solid lines) ± standard deviation (patches) along the y-axis is shown for each feedback condition for target trajectory 1 (black dashed lines). (a) Visual + position − error feedback (Vs + Pe). (b) Visual feedback (Vs). (c) Visual + vibrotactile + position − error feedback (Vs + Vb + Pe). (d) Visual + vibrotactile feedback (Vs + Vb). (e) Visual + frictional + position − error feedback (Vs + Pc + Pe). (f) Visual + frictional feedback (Vs + Pc). (g) Kinesthetic + position − error feedback (K + Pe). (h) Kinesthetic feedback (K).

3) Results

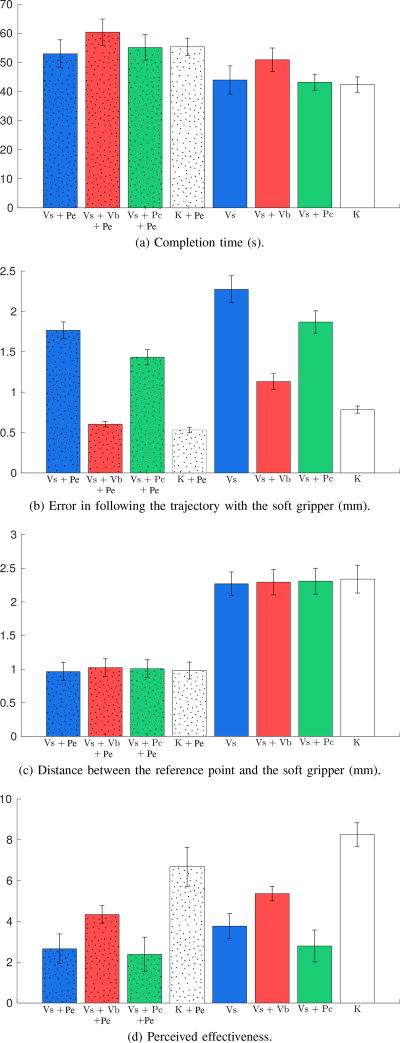
We measure (1) task completion time, (2) error in following the target trajectory with the gripper, (3) distance between the reference point and the gripper, and (4) perceived effectiveness of each feedback condition. To compare the different metrics, we ran two-way repeated-measures ANalysis Of VAriance (ANOVA) tests on the data shown in Fig. 8 [71]. Presence of the position-error feedback (Pe) and type of feedback condition (Vs, Vs + Vb, Vs + Pc, and K) were treated as within-subject factors.

Fig. 8.

Experiment #1. The path following task: (a) completion time (s), (b) error in following the trajectory with the soft gripper (mm), (c) distance between the reference point and the soft gripper (mm), and (d) perceived effectiveness for the eight considered feedback conditions are plotted (mean and 95% confidence interval). A video of the experiment is available in Supplementary Material.

Figure 8a shows the average completion time for the eight experimental conditions. The data passed the Shapiro-Wilk normality test and the Mauchly’s test of sphericity. Sphericity was assumed for variables with only two levels of repeated measures. The two-way repeated-measure ANOVA revealed a statistically significant change in the completion time for position-error information (F (1, 15) = 19.223, p = 0.001, partial η² = 0.562) and feedback condition (F (3, 45) = 9.438, p < 0.001, partial η² = 0.386). Post hoc analysis with Bonferroni adjustments revealed a significant increase in the completion time for conditions providing visual and vibrotactile feedbacks on the error in following the target trajectory (Vs + Vb vs. Vs, p = 0.013; Vs + Vb vs. Vs + Pc, p = 0.003; Vs + Vb vs. K, p = 0.002). We used the Bonferroni correction to reduce the chances of false-positive results when multiple pair-wise tests are performed on a same set of data.

Figure 8b shows the average error in following the target trajectory with the gripper for the eight experimental conditions. It is calculated as the mean over time of e_m = ‖p_m (t)−p_t,m‖, where p_m (t) is the position of the gripper as evaluated by the tracking algorithm, and p_t,m is the point on the target trajectory closest to p_m (t). The data passed the Shapiro-Wilk normality test. Mauchly’s test of sphericity indicated that the assumption of sphericity was violated for the feedback condition variable (χ²(5) = 34.744, p = 0.039). A Greenhouse-Geisser correction was applied to tests involving data that violate the sphericity assumption. The two-way repeated-measure ANOVA revealed a statistically significant change in this error for position-error information (F (1, 15) = 163.579, p < 0.001, partial η² = 0.916) and feedback condition (F (2.065, 30.983) = 347.793, p < 0.001, partial η² = 0.959). Post hoc analysis with Bonferroni adjustments revealed a significant difference in the error between all conditions (Vs vs. Vs + Vb, p < 0.001; Vs vs. Vs + Pc, p < 0.001; Vs vs. K, p < 0.001; Vs + Vb vs. Vs + Pc, p < 0.001; Vs + Vb vs. K, p < 0.001; Vs + Pc vs. K, p < 0.001).

Figure 8c shows the average distance between the reference point and the gripper for the eight experimental conditions. It is calculated as the mean over time of d_rf,m = ‖p_r (t)−p_{m (t)}‖. The data passed the Shapiro-Wilk normality test and Mauchly’s test of sphericity. The two-way repeated-measure ANOVA revealed a statistically significant change in the distance for position-error feedback only (F (1, 15) = 827.144, p < 0.001, partial η² = 0.982).

After this analysis, we also tested whether the distance between the reference point and the gripper has any relationship with the measured error in following the target trajectory. Our hypothesis is that it is more effective to control the motion of the gripper when the reference point is close to it, leading to smaller errors. A Pearson’s product-moment correlation was run to assess the relationship between this distance and the error in following the target trajectory with the gripper. Preliminary analyses showed the relationship to be linear with variable normally distributed, as assessed by Shapiro-Wilk test, and there were no outliers. There was a strong positive correlation between the distance of the reference point and the gripper and the gripper trajectory error (e_m : r (14) = 0.819, p < 0.001), confirming our hypothesis.

Immediately after the experiment, we also measured users’ experience. Participants were asked to rate the effectiveness of each feedback condition in completing the path following task using a slider that ranged from 0 to 10, where a score of 0 meant “very low” and a score of 10 meant “very high”. Figure 8d shows the perceived effectiveness for the eight experimental conditions. The data passed the Shapiro-Wilk normality test and Mauchly’s test of sphericity. The two-way repeated-measure ANOVA revealed a statistically significant change in this error for position-error information (F (1, 15) = 14.695, p = 0.002, partial η² = 0.495) and feedback condition (F (3, 45) = 61.712, p < 0.001, partial η² = 0.804). Post hoc analysis with Bonferroni adjustments revealed a significant difference in the error between feedback conditions Vs vs. Vs + Vb, p < 0.001; Vs vs. K, p < 0.001; Vs + Vb vs. Vs + Pc, p < 0.001; Vs + Vb vs. K, p < 0.001; and Vs + Pc vs. K, p < 0.001.

Finally, subjects were asked to choose the condition they preferred the most. Condition K+Pe was preferred by fourteen subjects and condition Vs was preferred by two subjects.

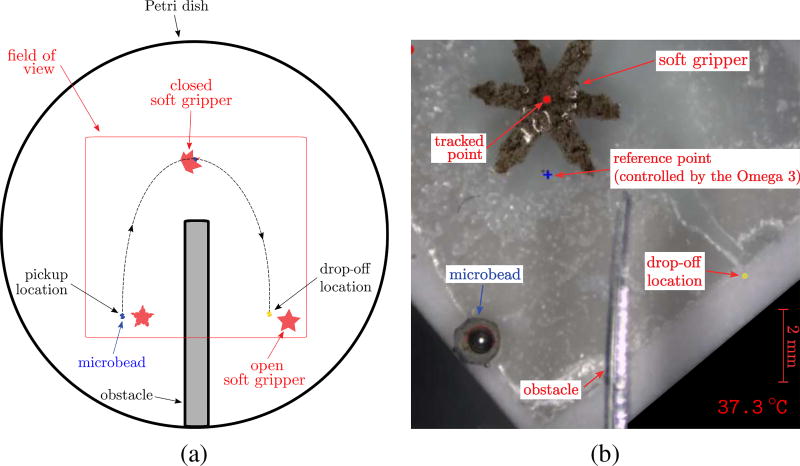
B. Experiment #2: Pick-and-place

The second experiment aims at evaluating our teleoperation system in a pick-and-place task, as sketched in Fig. 9a and demonstrated in the video available as supplemental material. A frame of the video is shown in Fig. 9b. Table III summarizes the methods and results of this experiment.

Fig. 9.

Experiment #2: Pick-and-place task. The task consists of picking up a microbead from the ground and dropping it off at a predetermined location. Subjects are able to move, close, and open the soft gripper through the haptic interface. Moreover, through the same interface, they receive haptic stimuli about the interaction of the soft gripper with the environment (a video is available as supplemental material).

TABLE III.

Summary of Experiment #2

Subjects	10 (9 males, 1 female)
Task	pick-and-place of a microbead
Conditions	Kinesthetic + Position-Error feedback (K + Pe)
	Vibrotactile + Position-Error feedback (Vb + Pe)
	No force feedback (N)
Video	available as supplemental material
Best conditions (average)
	Completion time		K + Pe (25.78 s)
	Gripper’s path length		K + Pe (22.97 mm)
	Distance between reference and gripper		Vb + Pe (1.11 mm)
	Drop-off error		Vb + Pe (0.76 mm)
	Perceived effectiveness		K + Pe (6.52)
Statistical analysis (one-way repeated measures ANOVA)
Completion time (no significant difference)
Gripper’s path length (p < 0.001, significant p values only)
		K+Pe vs. N	p = 0.002
		Vb+Pe vs. N	p < 0.001
Distance between reference and gripper (p < 0.001, sig. p values only)
		K+Pe vs. N	p < 0.001
		Vb+Pe vs. N	p < 0.001
Drop-off error (no significant difference)
Perceived effectiveness
		K+Pe vs. Vb+Pe	p = 0.011
		K+Pe vs. N	p = 0.001
		Vb+Pe vs. N	p = 0.022

1) Subjects

Ten subjects (9 males, 1 female, age range 24 – 33 years) took part in the experiment, all of whom were right-handed. Five of them had previous experience with haptic interfaces. None reported any deficiencies in their perception abilities. The experimenter explained the task, asked the subjects to sign an informed consent, and then spent about two minutes adjusting the setup to be as comfortable as possible. No practice trial was allowed. In order to avoid providing undesired auditory cues, participants were isolated from external noises through a pair of noise-canceling headphones.

2) Methods

The task consists of picking up a polystyrene microbead from the ground and dropping it off at a predetermined location. An obstacle is placed in the middle of the remote environment at a known location (see Fig. 9). The pick up and drop-off locations were chosen randomly in the left and right hand sides of the environment, respectively. The microbead was placed on a small pedestal to make the pick up easier.

Each subject made six randomized repetitions of the pick-and-place task, with two repetitions for each feedback condition proposed:

• Kinesthetic + Position-Error feedback (K + Pe), where kinesthetic force is used to render both the position error between the controlled gripper and the reference point, and the collisions between the reference point and the obstacle,

• Vibrotactile + Position-Error feedback (Vb + Pe), where kinesthetic force is used to render the position error between the controlled gripper and the reference point, and vibrotactile feedback is used to render the collisions between the reference point and the obstacle,

• No force feedback (N).

In condition K+Pe, the Omega haptic interface provides the subject with kinesthetic feedback about the collisions of the reference point with the obstacle and about the position error between the gripper and the reference point. Kinesthetic force f_k,2 (t), responsible for rendering collisions of the reference point with the obstacle, is evaluated according to the popular god-object model [72], and the obstacle is modeled as a spring-damper system:

$${\mathbf{f}}_{\mathbf{k},\mathbf{2}}(\mathbf{t})=-k_{k,2}({\mathbf{p}}_{\mathbf{r}}(\mathbf{t})-{\mathbf{p}}_{\mathbf{r},\mathbf{\text{proxy}}}(\mathbf{t}))-b_k{\dot{\mathbf{p}}}_{\mathbf{r}}(\mathbf{t}).$$ (19)

k_k,2 = 1000 N/m, b_k = 5 Ns/m, p_r (t) ∈ ℝ² is the current position of the reference point as controlled by the subject through the haptic interface, and p_r,proxy (t) ∈ ℝ² is the virtual location of the haptic interface (or god-object), placed where the haptic interface point would be if the haptic interface and the object were infinitely stiff (i.e., on the surface of the obstacle in our case) [72]. The more the user pushes the end-effector of the haptic interface toward the obstacle, the more force the system will provide. On the other hand, kinesthetic force f_i (t), responsible for rendering the position error between the gripper and the reference point, is evaluated as in eq. (18). In this condition the subject feels an opposite force when trying to penetrate the obstacle and when moving the reference point away from the gripper. Moreover, in addition to the above mentioned kinesthetic forces, the operator is also provided with a 200-Hz 50-ms-long vibration burst when the tracking system considers the gripper completely close and ready to move the microbead away from its pickup location. This information prevents the operator from moving the gripper too early, when the grasping procedure is not yet complete and the bead has therefore not been safely grasped. The tracking algorithm considers a gripper completely close when C < 1.30, where C is the measure of the extent of closure of the gripper (see Section III-A).

In condition Vb+Pe, the Omega haptic interface provides the subject with vibrotactile feedback about the collisions of the reference point with the obstacle, and kinesthetic feedback about the position error between the gripper and the reference point. Vibrotactile feedback f_vb,2 (t) is calculated according to the god-object model, and the obstacle is modeled as a spring system:

$${\mathbf{f}}_{\mathbf{\text{vb}}}(\mathbf{t})=k_{\upsilon b}({\mathbf{p}}_{\mathbf{r}}(\mathbf{t})-{\mathbf{p}}_{\mathbf{r},\mathbf{\text{proxy}}}(\mathbf{t}))\left[\begin{array}{c}\hfill \text{sin }(2\pi f_{\upsilon b}t)\hfill \\ \hfill \text{sin }(2\pi f_{\upsilon b}t)\hfill \end{array}\right],$$ (20)

where k_υb = 80 N/m and f_υb = 150 Hz. The position error is again rendered as in eq. (18). In this condition, the user feels a vibration every time that the reference point enters in contact with the obstacle. Moreover, as in condition K+Pe, the user feels an opposite force when moving the reference point away from the gripper and a 200-Hz 50-ms-long vibration burst when the tracking system considers the gripper completely close.

In condition N, the system provides no information about the position error between the gripper and the reference point, and no information about the collisions between the reference point and the obstacle.

In all three conditions, the closing and opening of the gripper is managed by controlling the temperature level of the remote environment through the Peltier element, as described in Section III-C. The target temperature is set by rotating the pen-shaped end-effector of the Omega interface, as detailed in Section III-B. A view of the remote environment is always provided to the subjects through the high-resolution camera and a LCD screen (see Fig. 1). The Omega 6 haptic interface is always used to provide the controller with the microgripper’s reference point.

3) Results

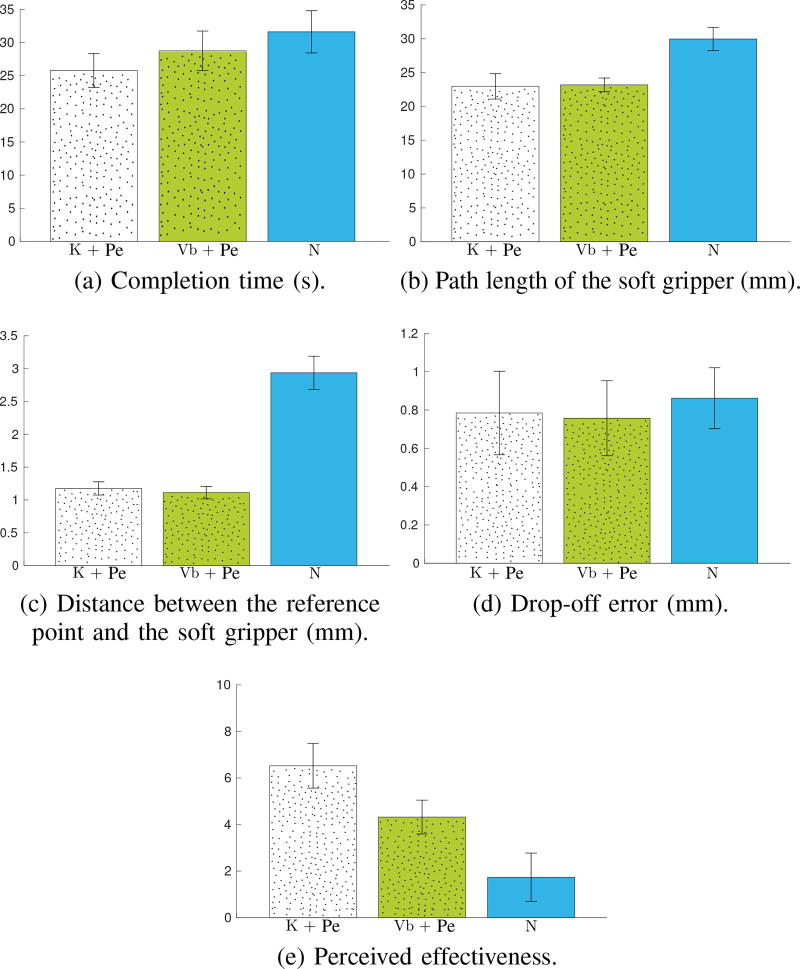
We measure (1) task completion time, (2) length path of the gripper, (3) distance between the reference point and the gripper, (4) error in placing the microbead at the requested drop-off location, and (5) perceived effectiveness of each feedback condition. To compare the different metrics, we ran one-way repeated-measures ANOVAs on the data shown in Fig. 10. Type of feedback condition (K+Pe, Vb+Pe, and N) was treated as within-subject factors.

Fig. 10.

Pick-and-place experiment. Completion time, path length for the soft gripper, distance between the reference point and the soft gripper, placing error, and perceived effectiveness for the three considered feedback conditions are plotted (mean and 95% confidence interval). A video of the experiment is available as supplemental material.

Figure 10a shows the average completion time for the three experimental conditions. The data passed the Shapiro-Wilk normality test and the Mauchly’s test of sphericity. The one-way repeated measures ANOVA did not reveal any statistically significant difference between the means.

Figure 10b shows the average length of the path of the gripper for the three experimental conditions. The data passed the Shapiro-Wilk normality test and Mauchly’s test of sphericity. The one-way repeated measures ANOVA revealed a statistically significant difference between the means (F (2, 18) = 20.518, p < 0.001, partial η² = 0.695). Posthoc analysis with Bonferroni adjustments revealed a significant difference in conditions K+Pe vs. N (p = 0.002) and Vb+Pe vs. N. (p < 0.001).

Figure 10c shows the average distance between the reference point and the gripper for the three experimental conditions. The data passed the Shapiro-Wilk normality test and Mauchly’s test of sphericity. The one-way repeated-measure ANOVA revealed a statistically significant difference between the means (F (2, 18) = 134.252, p < 0.001, partial η² = 0.937). Post hoc analysis with Bonferroni adjustments revealed a significant difference in conditions K+Pe vs. N (p < 0.001) and Vb+Pe vs. N (p < 0.001).

Figure 10d shows the average error in placing the microbead at the requested dropoff location for the three experimental conditions. The data passed the Shapiro-Wilk normality test and Mauchly’s test of sphericity. The one-way repeated-measure ANOVA did not reveal any statistically significant difference between the means.

Immediately after the experiment, we also measured users’ experience. Participants were asked to rate the effectiveness of each feedback condition in completing the pick-and-place task using a slider that ranged from 0 to 10, where a score of 0 meant “very low” and a score of 10 meant “very high”. Figure 10e shows the perceived effectiveness for the three experimental conditions. The data passed the Shapiro-Wilk normality test and Mauchly’s test of sphericity. The one-way repeated measures ANOVA revealed a statistically significant difference between the means (F (2, 18) = 22.275, p < 0.001, partial η² = 0.712]. Posthoc analysis with Bonferroni adjustments revealed a significant difference between all conditions (K+Pe versus Vb+Pe, p = 0.011; K+Pe versus N, p = 0.001; Vb+Pe versus N, p = 0.022).

Finally, subjects were asked to choose the condition they preferred the most. Condition K+Pe was preferred by six subjects, while condition Vb+Pe was preferred by four subjects.

V. DISCUSSION AND CONCLUSION

In order to test the effectiveness of our system, we carried out two sets of experiments, involving 26 subjects. The first one aimed at evaluating the steering capabilities of the proposed teleoperation system in a path following task (see Section IV-A), while the second one aimed at evaluating the steering capabilities of our system in a pick-and-place task (see Section IV-B). In both experiments, regardless of the feedback condition considered, all subjects were able to successfully complete the given task. Moreover, both experiments showed that haptic force feedback provides a statistically significant improvement of performance and perceived effectiveness.

In the first experiment, we provide the human operator with information about the error in following the target trajectory and about the position error between the gripper and the reference point. Providing haptic stimuli (vibrotactile, kinesthetic, or frictional) elicited statistically significant improvements in the task performance with respect to providing only visual feedback in all the considered metrics except completion time. Moreover, providing information about the position error between the gripper and the reference point encouraged the user to keep the reference point close to the gripper, enabling him or her to control the motion of the robot more accurately. Keeping the reference point close to the gripper was in fact proven to have a statistically significant positive effect in reducing the error of the gripper in following the target trajectory. Although conditions providing kinesthetic feedback (K and K+Pe) outperformed all the others, stability of teleoperation systems with kinesthetic feedback can be significantly affected by communication latency in the loop, hard contacts, relaxed grasps, and many other destabilizing factors which dramatically reduce the effectiveness of this type of feedback in teleoperation [73]. For this reason, we have decided to also include the evaluation of other types of feedback that do not affect the stability of teleoperation systems, i.e., visual, vibrotactile, and frictional [36]. Among these intrinsically “safe” conditions, the combination of visual and vibrotactile feedback (Vs+Vb) showed the best performance in all the considered metrics except completion time. This condition was also considered by the subjects the second most effective after the ones providing kinesthetic feedback. These considerations are particularly relevant for all those fields and applications where the safety of the system is a paramount and non-negotiable requirement, as in the biomedical applications envisaged in Section I. Finally, it is interesting to note that two out of 16 subjects chose condition Vs as the preferred one. These two subjects complained that the feedback about the position error between the gripper and the reference point (Pe) slowed down the task. Although they did not like conditions providing position-error feedback, they still found them very effective in achieving small trajectory errors.

In the second experiment, we provide the human operator with haptic stimuli about the collisions between the reference point and the remote environment, and about the position error between the gripper and the reference point. Providing kinesthetic feedback (K+Pe) statistically significantly improved the performance of the task with respect to the other conditions in all the considered metrics except completion time. Similarly, providing vibrotactile feedback (Vb+Pe) statistically significantly improved the performance of the task with respect to not providing force feedback (N) in all the considered metrics except completion time. As mentioned before, although kinesthetic feedback performed the best, vibrotactile feedback is still very promising, since it performed better than providing no force feedback at all and it does not affect the stability of teleoperation systems. Finally, although the preferred condition was K+Pe, subjects particularly appreciated the capability of condition Vb+Pe to enable the discrimination between the force due to the position error feedback (kinesthetic) and the one due to the collision with the obstacle (vibrotactile). The stability of the teleoperation system is guaranteed by the time-domain passivity algorithm presented in Section III-C3. The controller reduces the force applied to the system every time a loss of passivity is foreseen. Nonetheless, in our teleoperation experiments, mostly thanks to small communication delays, the passivity algorithm seldom acted on the ideal forces computed by the transparency layer.

In the near future, we will focus on investigating the practical translational aspects of the proposed micro teleoperation system for biomedical applications. In fact, in the current form, our soft magnetic grippers are still large for many medical applications. For example, for biopsy applications, since the sizes of many cells are in the range of 5–100 microns, ideal sizes for these grippers would range from 5 µm to 1 mm [8]. Such microgrippers could be introduced through endoscopes, needles, or catheters and be used to access smaller conduits in the body such as the circulatory, urinogenital, lymphatic systems, and mammary ducts. For this reason, we are currently investigating the miniaturization of the bilayer soft gripper used in this paper. We are also studying the use of other self-folding grippers, fabricated using metallic materials and inorganic materials. It is noteworthy that elsewhere, ultrasmall untethered grippers capable of capturing even single red blood cells have been described [74], which highlight feasibility of further miniaturization. In this respect, we believe that it is important to retain the soft structure of the grippers, as they could be more suitable for medical applications. In fact, the sturdy grasp of rigid grippers may damage or even destroy biological cells and tissues.

In addition to exploring smaller grippers, we are also planning to substitute the high-resolution camera with an ultrasound imaging system, in order to be able to track the position of the controlled gripper in biological fluid. In this respect, Sanchez et al. [75] presented an algorithm for the closed-loop control of micromotors using feedback extracted from B-mode ultrasound images, and Khalil et al. [63] demonstrated the effectiveness of a wireless magnetic control system in steering the same micromotors against fluidic flows. We are also investigating the possibility of using targeted on-spot heating techniques, such as induction or high-intensity focused ultrasounds. In this way, we would be able to trigger the self-folding capability of the grippers without heating the surrounding environment. Moreover, this targeted heating approach would significantly speed up the closing and opening processes. Of course, the safety of all the above-mentioned approaches will have to be assessed for use in biomedical applications involving humans and other living beings. Finally, we also plan to study the effects of passivity-related reductions of haptic stimuli in micromanipulation applications.