Complex spike clusters and false-positive rejection in a cerebellar supervised learning rule

Abstract

The classic example of biological supervised learning occurs at cerebellar parallel fiber (PF) to Purkinje cell synapses, the most abundant synapse in the mammalian brain. Long-term depression (LTD) at these synapses is driven by climbing fibers (CFs), which fire continuously about once per second, and therefore generate potential false-positive events. We show that pairs of complex spikes are required to induce LTD. In vivo, sensory stimuli evoked complex-spike doublets with intervals ≤ 150 ms in up to 50% of events. Using realistic [Ca²⁺]_o and [Mg²⁺]_o concentrations in slices, we determined that complex-spike doublets delivered 100-150 ms after PF stimulus onset were required to trigger PF-LTD, consistent with requirements for eyeblink conditioning. Inter-complex spike intervals of 50-150 ms provided optimal decoding. This stimulus pattern prolonged evoked spine calcium signals and promoted CaMKII activation. Doublet activity may provide a means for CF instructive signals to stand out from background firing.

Introduction

A core requirement of supervised learning is an accurate instructive signal. In the Marr-Albus-Ito model of cerebellar learning (Marr, 1969; Albus, 1971; Ito et al., 1982), instruction comes in the form of signals from the climbing fiber (CF), which drive long-term depression (LTD) at parallel fiber (PF) to Purkinje cell synapses when the two pathways are co-activated (Ito et al., 1982; Ito and Kano, 1982). LTD contributes to a learned output signal via disinhibition of neurons in the cerebellar nuclei, which receive GABAergic input from Purkinje cells. In the absence of CF input, PF stimulation alone triggers long-term potentiation (LTP; Lev-Ram et al., 2002; Coesmans et al., 2004). The CF stimulus elicits a voltage transient in the Purkinje cell dendrite, and a calcium signal that spreads to fine branchlets and spines contacted by the PF input. The CF-evoked dendritic potential propagates toward the soma where the characteristic complex spike waveform can be recorded (Davie et al., 2008; Ohtsuki et al, 2012). Thus, learning at PF synapses constitutes an example of supervised learning, in which CF-evoked complex spikes and their associated dendritic calcium transients act as instructive signals to promote the induction of LTD (Konnerth et al., 1992; Wang et al., 2000).

However, CF signals are not always informative. CFs fire once per second on average all the time, and therefore must fire at times when no salient event has occurred. Spontaneous firing events would therefore potentially add considerable noise to the instructive signal. This problem presupposes that single CF firing events would be enough to drive plasticity mechanisms at PF synapses. To date, this has reportedly been the case: single CF stimuli have been found to be sufficient to induce LTD when paired with PF stimulation. However, those studies were done under non-physiological conditions, specifically pharmacological block of inhibition and unrealistic calcium and magnesium concentrations. These parameters might affect LTD induction via their effects on calcium signaling. At PF-Purkinje cell synapses, the calcium threshold for LTP is lower than the LTD threshold (Coesmans et al., 2004; Piochon et al., 2016). Purkinje cell dendrites show calcium-based modulation of excitability, and CF co-activation causes supralinear calcium signaling in spines (Wang et al., 2000).

An additional source of information in the CF pathway comes from the temporal structure of successive firing events. Structured CF signaling, such as repeated burst firing, may affect key induction signals for plasticity. CFs may fire in high-frequency bursts (Maruta et al., 2007) as well as firing at interspike intervals of ~100 ms, reflecting a natural oscillatory tendency arising in the inferior olive (Lang et al., 1999; Ozden et al., 2009). Synaptic plasticity also depends on the exact timing of presynaptic and postsynaptic activity. In cerebellar slice recordings, PF and CF co-stimulation has been found to induce LTD with PF-CF intervals ranging from 0 to 250 ms, and sometimes even negative intervals, i.e. CF before PF stimulation (Coesmans et al., 2004; Wang et al., 2000; Ekerot and Kano, 1989; Chen and Thompson, 1995; Bell et al., 1997; Safo and Regehr, 2008; Sarkisov and Wang, 2008). More recent work has shown that narrow time windows are observed under specific conditions, here depending on the area of the cerebellum: in the flocculus, where LTD is induced at a PF-CF interval of 120 ms, and the vermis, where efficient PF-CF timing intervals for inducing depression at PF synaptic inputs were found to range from 0 to 150 ms, but were individually tuned for each Purkinje cell (Suvrathan et al, 2016; note that the recordings from the vermis tested short-term, not long-term plasticity). In nearly all cases, parametric exploration has been limited to single CF stimuli.

The activity- and timing-dependence of LTD induction under realistic conditions may determine the properties of cerebellum-based learning. But timing requirements for synaptic plasticity in brain slices often do not match timing requirements of behavioral learning, raising concerns about the physiological relevance of plasticity (Gallistel et al., 2013). In the case of LTD and cerebellar learning (Wetmore et al., 2014), a temporally well-defined teaching signal occurs in delay eyeblink conditioning, in which the unconditioned stimulus (such as an airpuff to the eye) must come after the conditioned stimulus (such as tone or light) by at least 150 ms in order for an anticipatory conditioned response to arise over many trials (Freeman, 2015). This timing does not match some of the reported ranges of effective LTD-inducing time intervals for PF and CF stimulation, suggesting a mismatch between slice and in vivo conditions or signals.

In this work, we sought to characterize PF-LTD under realistic, physiological activity conditions. We took several steps to design realistic recording conditions. First, we monitored spontaneous and evoked complex spike activity in vivo, to identify natural CF activity patterns. Second, we applied these patterns to brain slice recordings. Third, we performed slice experiments and measured synaptic plasticity at near-physiological temperatures (32-34 ºC), in the absence of blockers of GABA receptors, and using realistic [Ca²⁺]_o (1.2 mM; Nicholson et al., 1978); and [Mg²⁺]_o (1 mM; Ding et al., 2016). Finally, we applied high-frequency trains of PF stimuli to mimic granule cell burst firing patterns that have been observed in vivo upon sensory stimulation (Chadderton et al., 2004). Our study shows that, on average, complex spikes recorded upon sensory stimulation in vivo occur in about 20 % of cases in double-pulse clusters, and that in brain slices clustered CF stimulation is required to induce LTD, with an optimal PF-CF timing interval of 150 ms.

Methods

Ethical Approval.

All procedures were performed in accordance with the guidelines of the Institutional Animal Care and Use Committee at the University of Chicago and Princeton University and followed the animal welfare guidelines of the National Institutes of Health. The approved animal protocols used are IACUC 72256 (University of Chicago) and IACUC 1943-19 (Princeton University). All experiments were carried out according to the guidelines laid down by the institutional animal welfare committees and reflected in these approved protocols, as well as the principles and regulations as described in Grundy (2015).

Animals.

Slice and mouse extracellular recordings were performed on C57BL/6J mice (Jackson Laboratory; P25-40). In some experiments, we used TT305/6VA and T305D mutant mice and littermate controls (also on a C57BL/6J background). Optogenetic stimulation was performed using Pcp2-Cre x Ai27 mice on a C57BL/6J background. Whole-cell patch recording in vivo was performed using Sprague Dawley rats (P21-30). Both males and females were included in the study.

Slice preparation.

Animals were anesthetized with isoflurane anesthesia and promptly decapitated, and either the left or right cerebellar hemisphere was removed and placed in cooled artificial cerebral spinal fluid (ACSF) containing (in mM): 124 NaCl, 5 KCl, 1.25 Na₂HPO₄, 2 CaCl₂, 2 MgSO₄, 26 NaHCO₃ and 10 D-glucose, bubbled with 95% O₂ and 5% CO₂. Parasagittal slices (200 μm) of the lateral hemisphere containing crus I were prepared using a Leica VT-1000S vibratome, and were kept for at least 1 hour at room temperature in oxygenated ACSF. Prior to recording, slices were placed in a bath chamber continuously perfused with ASCF with a lower Ca²⁺ and Mg²⁺ concentration (1.2 mM and 1 mM respectively), glucose was added to adjust the osmolarity of the solution to 295-305 mmol/kg. The K⁺ concentration of 5mM is higher than that determined during resting states in the cat cerebellum (3mM), but corresponds to the range of 4 mM to ≤ 10 mM that is reached when the PF input is stimulated at 5-20Hz (Nicholson et al., 1978). Moreover, throughout the brain, [K⁺]_o raises during the shift from sleep to wakefulness from about 3.9mM to 4.4mM, with peak values around 5mM (Ding et al., 2016). The concentration of 5mM [K⁺]_o that was selected here therefore reflects K⁺ concentrations that are typical for the ionic milieu during activity, which the ACSF should recreate in the otherwise ‘silent’ slice preparation. The pH of the ACSF used is ~7.4, which is slightly higher than the pH of interstitial fluid in the intact brain (~pH 7.3). The reason for this pH selection in the ACSF is that in brain slices, pH values drop slightly below the pH in the saline, which likely results from the lack of CO₂ clearance by blood flow (Chesler, 2003). The ACSF in the bath was kept at near-physiological temperature (32-34 °C) and slices were allowed to acclimate in the solution for at least 20 minutes prior to recording.

Slice electrophysiology.

Patch-clamp recordings from Purkinje cell somata located in crus I were performed using an EPC-10 amplifier (HEKA Electronics). Currents were filtered at 3 kHz, digitized at 25 kHz and acquired using Patchmaster software (HEKA Electronics). Patch pipettes (2-5 MΩ, borosilicate glass) were filled with an internal saline containing the following (in mM): 9 KCl, 10 KOH, 120 K-gluconate, 3.48 MgCl₂, 10 HEPES, 4 NaCl, 4 Na₂ATP, 0.4 Na₃GTP and 17.5 sucrose (osmolarity adjusted to 295-305 mmol/kg, and pH adjusted to 7.3). Purkinje cells were voltage-clamped at a holding potential of −70 mV. Fast and slow capacitances were compensated, and series resistance was partially compensated (60-80%).

To evoke synaptic responses, glass electrodes filled with bath ACSF were placed in the granule layer and upper molecular layer to activate climbing fibers (CFs) and PFs respectively. Test responses were recorded in voltage-clamp mode before and after an induction protocol at a frequency of 0.05 Hz. The LTD or long-term potentiation (LTP) tetanization protocols were applied in current-clamp mode. Series and input resistances were monitored throughout the experiments by applying hyperpolarizing voltage steps (−10 mV) at the end of each sweep. Recordings were excluded if the series or input resistances varied by >15% over the course of the experiment. Time course graphs are shown as averages per minute (over three consecutive sweeps). The values were calculated as percentage of baseline (calculated from the last 5 min of baseline recording) ± SEM. Final changes in EPSC amplitudes were calculated as the average of last 5 minutes of recordings (minutes 31-35) as a percentage of baseline. In some electrophysiology and calcium imaging experiments we directly compared our higher Ca²⁺/Mg²⁺ ratio solution (1.2 mM and 1 mM respectively) ACSF to the lower Ca²⁺/Mg²⁺ ratio (2 mM each) ACSF that we used for slicing.

Confocal calcium imaging.

Calcium transients were monitored using a Zeiss LSM 5 Exciter confocal microscope with a x63 Apochromat objective (Carl Zeiss MicroImaging). Calcium transients were calculated as ΔG/R=(G(t)-G₀)/R, where G is the calcium-sensitive fluorescence (G₀ = baseline signal) of Fluo-5F (300 μM) and R is the calcium-insensitive fluorescence of Alexa 633 (30 μM). The green fluorescence G was excited at 488 nm using an argon laser (Lasos Lasertechnik). The red fluorescence R was excited at 633 nm using a HeNe laser (Lasos Lasertechnik). Purkinje cells were loaded with the dyes by diffusion through the patch pipette. The experiments were initiated after the dendrite was adequately loaded with the dyes and the fluorescence at the selected region of interest (ROI) reached a steady-state level (typically requiring ≥ 30 min). In each recording, the ROI was the spine on a secondary (or higher order) dendritic branch close to the stimulus electrode that responded maximally to synaptic activation.

Surgical preparation for in vivo recording.

Briefly, mice were anesthetized with isoflurane (5% for induction; 1.0-2.5% for maintenance), and analgesics (rimadyl, 5mg/kg) and lidocaine (50μl of 2% w/v) were given subcutaneously. An incision was made and skin and connective tissue over the skull were removed. A custom made “U” titanium headplate was cemented to the skull using dental cement (C&B Metabond, Parkell Inc.). A small hole was drilled for a reference electrode in the interparietal bone at the midline. Craniotomies (1-1.5 mm diameter) were made over the left and right posterior hemispheric cerebellum for extracellular single-unit recordings and optical stimulations. Sterile saline and a fast curing silicone elastomer (Kwik-Sil, World Precision Instruments) were applied on the exposed tissue, while a recording chamber was formed around the craniotomy site using dental cement. Tissue adhesive (3M Vetbond) was applied to close the skin around the neck and cerement perimeter. Mice were monitored and given post-operative care in their home cages for 5 days after surgery. Next, to acclimate mice to head restraint, they were placed on top of a cylindrical treadmill with their heads fixed for 1 hour daily for 3 days, no stimuli were given during this habituation period.

Extracellular recordings and sensory/optogenetic stimulation in mice.

After habituation, mice were head-fixed over a freely rotating cylindrical treadmill, while the craniotomy site was opened by removing the Kwik-Sil plug and filled with saline. Single-unit recordings were performed using borosilicate glass electrodes (World Precision Instruments, 3-12 MΩ) filled with sterile saline. Purkinje cells were identified by the presence of complex spikes followed by a characteristic pause in simple spikes. Electrical signals were amplified with a CV-7B headstage and Multiclamp 700B amplifier digitized at 10 kHz with a Digidata 1440A and acquired in pClamp (Axon Instruments, Molecular Devices) in parallel with TTL pulses from a signal generator (Master-8, A.M.P.I.), which was used to synchronize recording and stimulation.

Optical stimulation of cerebellar cortex was performed using a 400 μm-diameter optical fiber connected to a fiber-coupled LED and a TTL-controlled driver (Thorlabs). Two parameters of the light square pulse were varied from trial to trial: intensity (0.02 – 5.49 mW) and duration (5 – 250 ms). Whisker stimulation in awake mice was done by repeated air puffs (inter-trial interval: 4 s; 100 trials), which were given in a regularly or randomly timed manner using a TTL-controlled pressure injector system (Toohey Spritzer). The air puffs (40 ms and 20 psi) were delivered ipsilateral to the recording site via a small tube (2 mm diameter), approximately placed parallel to the anterior-posterior axis, 10 mm mediolateral and 1 mm anterior to the nose of the mouse.

After the experiments, mice were euthanized by intraperitoneal injection of euthasol (0.22ml/kg) and transcardially perfused with phosphate buffered saline followed by 4% paraformaldehyde for further histological verification of the recording location.

In vivo whole-cell recordings in rats.

Sprague Dawley rats were anesthetized by an intraperitoneal injection of ketamine (100 mg/kg) / xylazine (10 mg/kg). The level of anesthesia was monitored routinely by observing breathing and the responses to noxious stimuli to the hind limbs; additional doses of anesthetic were given as needed. The animals were placed in a stereotaxic apparatus, and an incision was made along the rostro-caudal midline. A 2 mm craniotomy was made over the crus I area of the cerebellum (3 mm posterior, 4 mm lateral of lambda), and a small hole in the dura was carefully made to expose the brain. The exposed area surface was covered with physiological saline solution or agar (3 % in physiological saline).

Whole-cell patch clamp recordings were made with an EPC-10 amplifier (HEKA Electronics) using the blind-patch method. Borosilicate glass patch pipettes (Sutter Instruments, 4-7 MΩ) containing intracellular saline (see above) and 0.5 % biocytin, were carefully lowered into the brain advancing in 2-4 μm steps. After a whole-cell patch was obtained, Purkinje cells were identified by the presence of both simple and complex spikes. Currents were filtered at 3 kHz, digitized at 25 kHz and acquired using Patchmaster software (HEKA Electronics). Spontaneous recordings of Purkinje cell activity (~ 1-2 mins duration) in current clamp were obtained and analyzed. The rats were not allowed to wake-up from the anesthesia and were euthanized (small animal guillotine) at the end of the experiments.

Data Analysis.

Data were analyzed using Patchmaster software (HEKA Electronics) and Igor Pro software (Wavemetrics). Confocal imaging data were analyzed using ZEN software (Carl Zeiss MicroImaging). Extracellular data were analyzed using custom written packages written in MATLAB (Mathworks). Statistica (Tibco) was used for statistical analysis. Statistical significance was determined by a two-tailed paired Student’s t-test for within-group comparison of paired events. For comparisons between groups we used either a Mann-Whitney U test (two groups), or the Kruskal-Wallis H test with a post-hoc Dunn’s multiple comparison’s test (multiple groups). A regression analysis was used to determine correlations. All data are shown as mean ± SEM.

Results

Complex spikes occur in clusters in vivo

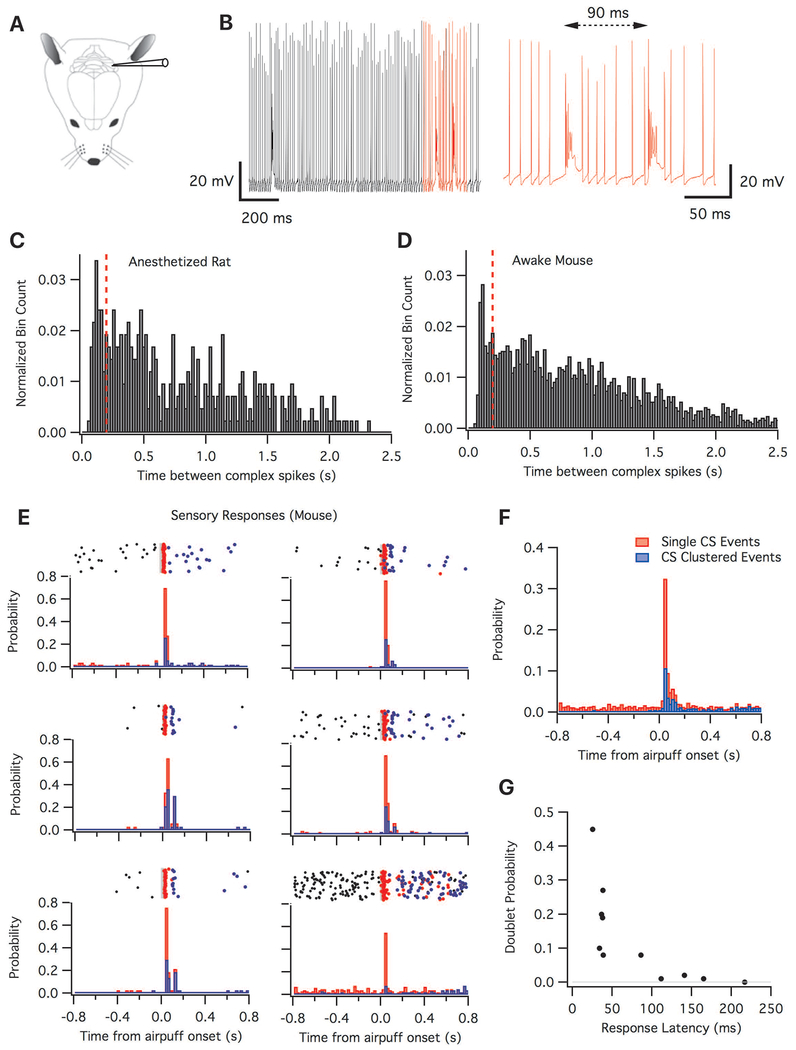
To monitor complex spike patterns from intact animals, we first performed whole-cell patch-clamp recordings. Recordings were obtained from cerebellar crus I (lateral posterior cerebellum) of anaesthetized rats (Figure 1A). In agreement with previous studies (Lang et al., 1999; Bell et al., 1969; Keating and Thach, 1995), we found complex spikes (CSs) had irregular firing and featured CS pairs with interspike intervals (ISI) considerably shorter than 1 s (Figure 1B). The mean firing rate of spontaneous complex spikes was 1.24 ± 0.03 Hz (mean ± SEM; 420 CS, n=7 cells, total recording duration: 5.6 minutes). The interspike interval distribution (Figure 1C) showed a peak near 100 ms, indicative of CS pairs. We found that 12.3% of complex spikes were followed by an interspike interval of ≤ 150 ms, and 16.5% by an interspike interval of ≤ 200 ms.

Figure 1.

Spontaneous and evoked complex spikes can occur in clusters. (A): Schematic drawing of a rodent with a recording electrode in crus I of the cerebellum. (B): Example trace of a whole cell recording taken from an anesthetized rat (left). Red indicates enlarged region on the right showing two complex spikes with an interspike interval of 90 ms. (C and D): Histograms of complex spike interspike intervals in 20 ms bins. Red dashed line shows the 200 ms interval. (C): Binned complex spike intervals recorded whole cell from anaesthetized rats (420 complex spikes from 7 cells). (D): Binned complex spike interspike intervals recorded extracellular from awake mice (2815 complex spikes from 14 cells). (E and F): Clustered events evoked by whisker stimulation. (E): Raster plots and histograms showing complex spike firing before and after whisker stimulation for six example neurons (out of a total of n=11). Top: Raster plots depicting complex spike firing. Red dots represent the first complex spike to occur after stimulation, while blue dots represent the second complex spike to occur after stimulation. Grey bar indicates the time of whisker stimulation. Bottom: The probability of either a single complex spike event occurring (red) or a complex spike pair (ISI < 150 ms; blue). (F) Histogram showing the probability of a complex spike occurring (red) and the probability of two complex spike occurring with an interspike interval of less than 150 ms (blue) upon sensory stimulation (n=11). In (E) and (F), the bar plots are unstacked. (G) Correlation of the response latency of the first complex spike with the probability of a complex spike doublet (n=11).

These initial recordings were performed using the whole-cell patch-clamp technique, which allows for the acquisition of supra- and subthreshold data without the selection bias that arises from only recording from active neurons (Margrie et al., 2002). A caveat of this approach is that we needed to obtain these recordings under anesthesia to improve the frequency of successful data collection. As a next step, we switched to extracellular recordings, which we performed in awake mice. Spontaneous complex spike firing occurred at a mean rate of 1.08 ± 0.03 Hz and the coefficient of variation (the ratio between the standard deviation and the mean ISI) was 0.78 ± 0.02 indicating irregular firing activity (2815 CS, n=14 cells). The distribution of CS-CS intervals (Figure 1D) showed the presence of clustering. We observed that 8.8% of complex spikes had an ISI ≤ 150 ms and 13.1% had an ISI ≤ 200 ms. A peak in the ISI histogram at ≤ 150 ms was visible in 11 out of 14 mouse neurons and 6 out of 7 rat neurons (Fig. 1C+D).

Sensory stimulation is known to increase the frequency of complex spike firing (Ebner and Bloedel, 1981; Bosman et al., 2010; Najafi et al., 2014a; Najafi et al., 2014b). Enhanced complex spike responses have been seen after forepaw stimulation (Bloedel and Ebner, 1984), whisker stimulation (Bosman et al., 2010), and corneal airpuff (Van der Giessen et al., 2008), potentially driven in part by subthreshold rhythmicity of inferior olive neurons (Van der Giessen et al., 2008). We examined Purkinje cell responses in mice upon repeated presentations of strong whisker stimulation ipsilateral to the recording site. Air puffs (40 ms at 20 psi) applied to the ipsilateral whisker field increased the probability of at least one complex spike occurring within 200 ms from the stimulus onset, compared with prestimulus baseline, in 9 out of 11 cells (Figure 1E–G).

It has previously been reported that in awake mice a majority of Purkinje cells respond to whisker stimulation within 40 ms, with only a few responding at longer latencies (Bosman et al., 2010). Of the 11 cells we recorded, the latency to first complex spike was either shorter than 40 ms (“short-latency”; n=6 cells, 35 ± 2 ms, mean ± SEM; Fig. 1E) or longer than 80 ms (n=5 cells, 144 ± 22 ms). Short latency was associated with high response probability and the occurrence of CS doublets. Across all 11 cells (Fig. 1F+G), the probability of evoking at least one spike was inversely correlated with latency (Spearman’s ρ = −0.81, different from zero, p=0.0015, two-tailed r-to-z transformation). Doublet firing (200 ms window) was also inversely correlated with response latency (Figure 1G; ρ = - 0.88, p = 0.0001) and positively correlated with response probability (ρ = 0.88, p=0.0001). In the most responsive neuron (probability 0.94), CS doublets with a spacing of 150 ms or less occurred in 48% of trials, the highest fraction observed (Figure 1G). In summary, doublet firing was a prominent feature associated with short-latency sensory responsiveness.

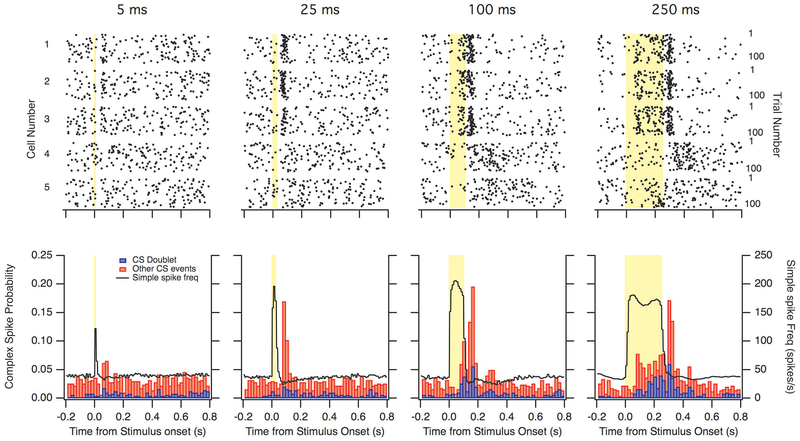
CS doublets have been suggested to be driven by olivocerebellar network effects (Chaumont et al., 2013; Witter et al., 2013; de Gruijl et al., 2014). To probe intrinsic mechanisms of generating CS doublets, we activated the optogenetic probe channelrhodopsin (ChR2) in Purkinje cells (n=5; using Cre mice) for different durations of optical stimulation (5, 25, 100, and 250 ms). Activation of ChR2 in head-fixed mice evoked robust simple spike firing that lasted through the whole stimulus (Figure 2). Simple-spiking activity inhibits deep nuclei neurons, some of which drive nucleo-olivary projections that are themselves inhibitory. Complex spikes arose during 100-ms and 250-ms light steps, consistent with disinhibition of the inferior olive. A post-stimulus rebound phenomenon was also apparent in the form of increased complex spike probability after the offset of light steps. Rebound complex spikes occurred for all durations of light step, and often occurred within 150 ms of a previously-occurring complex spike (first spike in two-spike pairs indicated in red). These results are consistent with the idea (Chaumont et al., 2013; Witter et al., 2013) that the nucleo-olivary system can generate complex spike doublets through a mechanism that is enhanced by transient simple-spike firing.

Figure 2.

Optogenetic simple spike activation increased complex spikes. Optogenetic stimulation of Purkinje cells with 5, 25, 100 and 250 ms duration (n=5). Top: Raster plots depicting complex spike firing during each trial. Bottom: Histograms showing the probability of a complex spike occurring (red) and the probability of complex spikes occurring within 150 ms of each other (blue). Black curve shows the firing rate of simple spikes. Yellow bar indicates the time of stimulation. The bar graphs are unstacked.

Long-term depression is not induced by single climbing fiber stimuli under near-physiological conditions

We studied long-term depression at PF synapses in cerebellar crus I under near-physiological slice conditions. The external Ca²⁺ concentration was lowered to 1.2 mM (Nicholson et al., 1978) and the Mg²⁺ concentration was lowered to 1 mM (Ding et al., 2016), both lower than the more commonly used combination of 2mM [Ca²⁺]_o and 2mM [Mg²⁺]_o. GABA inhibition was left intact as we did not add any pharmacological blocker, and we recorded at near-physiological temperatures of 32-34 °C.

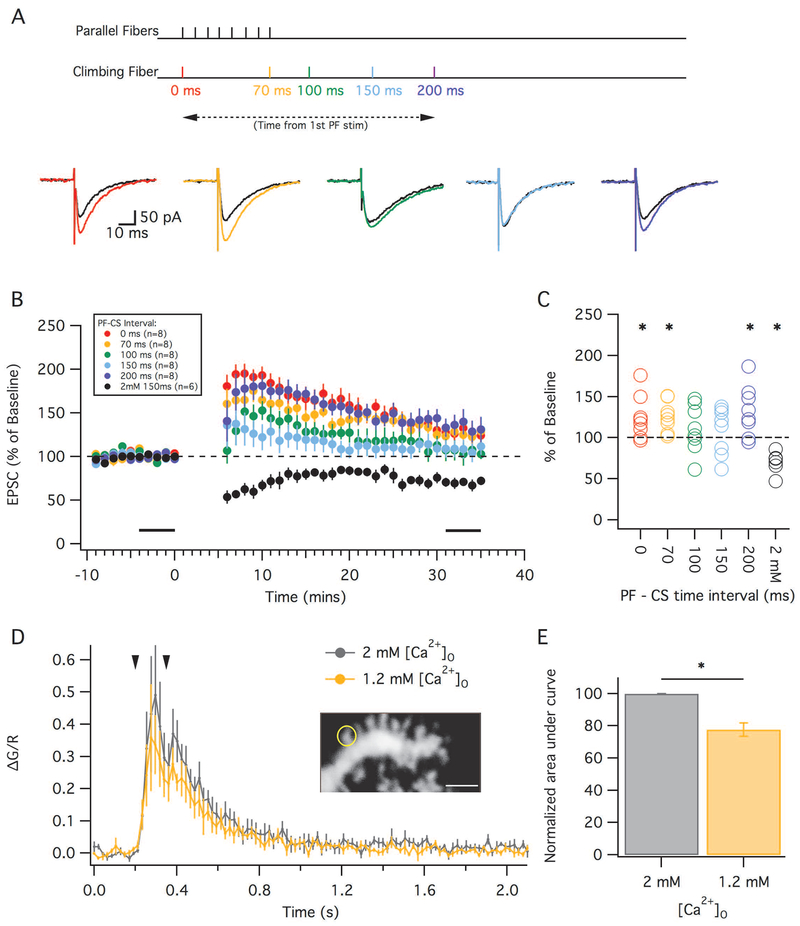
We first attempted to induce LTD using single CF stimuli. We used a variety of protocols varying the interval between the first parallel fiber pulse and the complex spike. Parallel fibers were stimulated 8 times at 100 Hz, with the complex spike occurring at either 0, 70, 100, 150, or 200 ms from the time of the first parallel fiber stimulation (Figure 3A). Although LTD has previously been shown to occur within this wide timing range (Chen and Thompson, 1995; Safo and Regehr, 2008), we failed to see any significant depression under the more realistic ionic and temperature conditions used here (Figure 3B). In three out of the five PF-CS interval protocols (0 ms, 70 ms, and 200 ms) the mean change in EPSC amplitude 30 minutes after tetanization resulted in a significant potentiation compared to their respective baselines (paired t-test; 0 ms: 124.5 ± 9.4% SEM, p=0.035, n=8; 70 ms: 125.8 ± 6.5%, p=0.005, n=8; 200 ms: 132.3 ± 10.8%, p=0.02, n=8). In the 100 ms and 150 ms delay protocols there was no detectable difference compared to their own baseline (paired t-test; 100 ms: 110.7 ± 10.3%, p=0.33, n=8; 150 ms: 108.3 ± 10.1%, p=0.43, n=8). Overall, 30 minutes after tetanization, there were no detectable differences among the protocols (Kruskal-Wallis test, H=3.27, 4; p=0.51). Thus, under near-physiological conditions LTD was not induced at any of the previously established PF-CS timing intervals. For comparison, under the classical non-physiological conditions (2mM Ca²⁺ and Mg²⁺), LTD is successfully induced with a PF-CS interval of 150ms (69.9 ± 5.3%; p=0.001, n=5).

Figure 3.

PF-PC LTD failed to induce in more physiological conditions despite the wide range of PF-CS intervals. (A) Top: Schematic depicting timing of parallel and climbing fiber stimulation under the 5 conditions used. Parallel fibers were stimulated 8 times at 100 Hz, with a climbing fiber being stimulated at either: 0, 70, 100, 150 or 200 ms from the start of the parallel fiber stimulation. Bottom: Example traces showing EPSCs before (black) and after LTD tetanization using a PF-CS timing of either 0 ms (red), 70 ms (orange), 100 ms (green), 150 ms (cyan) or 200 ms (blue). (B): Time graph showing the change in EPSC amplitude (as a percentage of baseline) following the various LTD induction protocols. For comparison, the black trace indicates LTD obtained under non-physiological conditions with 2mM [Ca²⁺]_o and with a PF-CS timing interval of 150 ms (in these recordings at room temperature, GABA_A receptors were blocked). Black bars indicate time points that were averaged (baseline and endpoint) to calculate changes in EPSC amplitude. (C): Percent change in EPSC (from baseline) in individual cells using the various PF-CS timing intervals. (D): Calcium transients averaged from Purkinje cell recordings (n=6) during a LTD protocol with the PF-CF interval of 150 ms. Each neuron was recorded in both a standard ACSF solution (lower Ca²⁺: Mg²⁺ ratio, grey) and the more physiological solution with a higher ratio of Ca²⁺ and Mg²⁺ (yellow). The arrowheads point out the onset of PF and CF stimulation, respectively. Inset: Example of PC dendritic spine filled with Fluo-5F and Alexa 633, the circle outlines the ROI. Scale bar is 2 μm. (E): The normalized areas of the two curves shown in (D) from 0.2 to 1.0 ms. Error bars indicate SEM. * indicates p < 0.05.

Since PF-LTD induction is known to have a higher calcium threshold than LTP (Coesmans et al., 2004; Piochon et al, 2016), we measured spine calcium transients during the 150 ms PF-CS delay protocol using two different ACSF solutions, the classic ACSF (2 mM Ca⁺²; 2 mM Mg²⁺) and our new, near-physiological ACSF (1.2 mM Ca²⁺; 1 mM Mg²⁺). We observed a smaller calcium transient with the near-physiological ACSF, suggesting that the lower absolute calcium concentration reduced the response amplitude (Figure 3D). Figure 3E shows the area under the curve of the transients normalized to the 2 mM [Ca²⁺]_o solution. The 1.2 mM [Ca²⁺]_o solution had a significantly lower area (77.7 ± 4.2%, p=0.003, n=6, paired t-test). The reduced calcium transients during the LTD protocol could likely explain the lack of depression found after the various LTD protocols and could additionally explain why some protocols even resulted in potentiation.

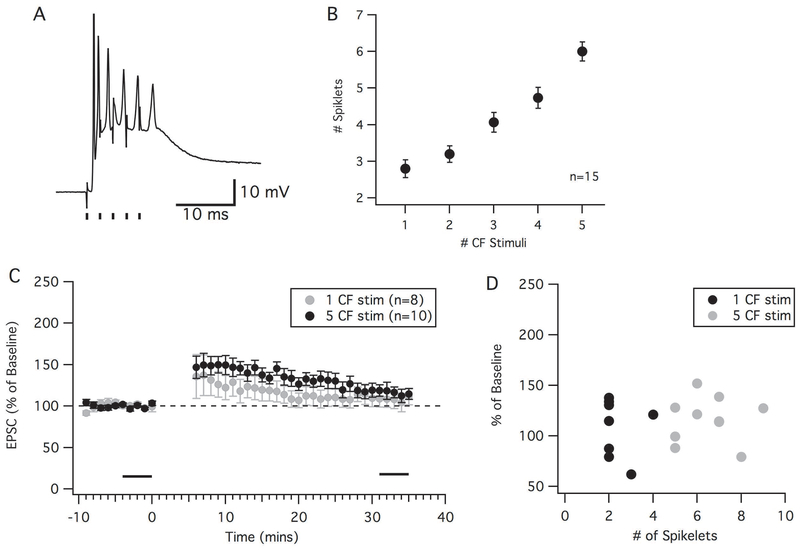
We tested whether the duration of single complex spikes influenced the ability to induce PF-LTD. It has previously been shown that stimulating the climbing fiber at high frequency (400 Hz) can elongate a complex spike by increasing the number of spikelets, and that elongated complex spikes are more likely to induce LTD (Mathy et al., 2008). By stimulating the climbing fiber at 400 Hz (five stimuli) instead of once, we were able to increase the number of spikelets from 2.8 ± 0.2 to 6.0 ± 0.3 spikelets (Figure 4A and B). With a 150 ms PF-CS interval (Figure 4C and D, grey), we were still not able to initiate a depression, and again observed potentiation when compared to its own baseline (Figure 4C, 116.2 ± 7.1%, p=0.048, n=10, paired t-test). There was no significant difference between the one CF stimulation protocol and the 5 CF stimulation protocol (Mann-Whitney U-test, p=0.69). Furthermore, when plotting the median number of spikelets in a complex spike for each trial and protocol there was no correlation of more spikelets leading to a lower EPSC amplitude after a LTD protocol (r²=0.043, p=0.59, n=18; Figure 4D). Thus, even when increasing the number of spikelets, we were still unable to observe LTD under more physiological conditions.

Figure 4.

Increasing the number of spikelets in a complex spike fails to cause LTD. Stimulating the climbing fiber at 400 Hz can elongate a complex spike by increasing the number of spikelets. (A): An example of a complex spike with the climbing fiber stimulated 5 times at 2 ms intervals (black lines). (B): Graph showing the increase in complex spike spikelets as the number of climbing fiber stimuli increased. (C): Time graph showing the percent change in EPSC amplitude (from baseline) following an LTD induction protocol (PF-CS=150 ms) using either 1 CF stimulation (black) or 5 CF stimulation producing an elongated complex spike (grey). (D): Percent change in EPSC amplitude in the individual neurons as a function of the median number of spikelets seen during the 5-minute induction protocol. Error bars indicate SEM.

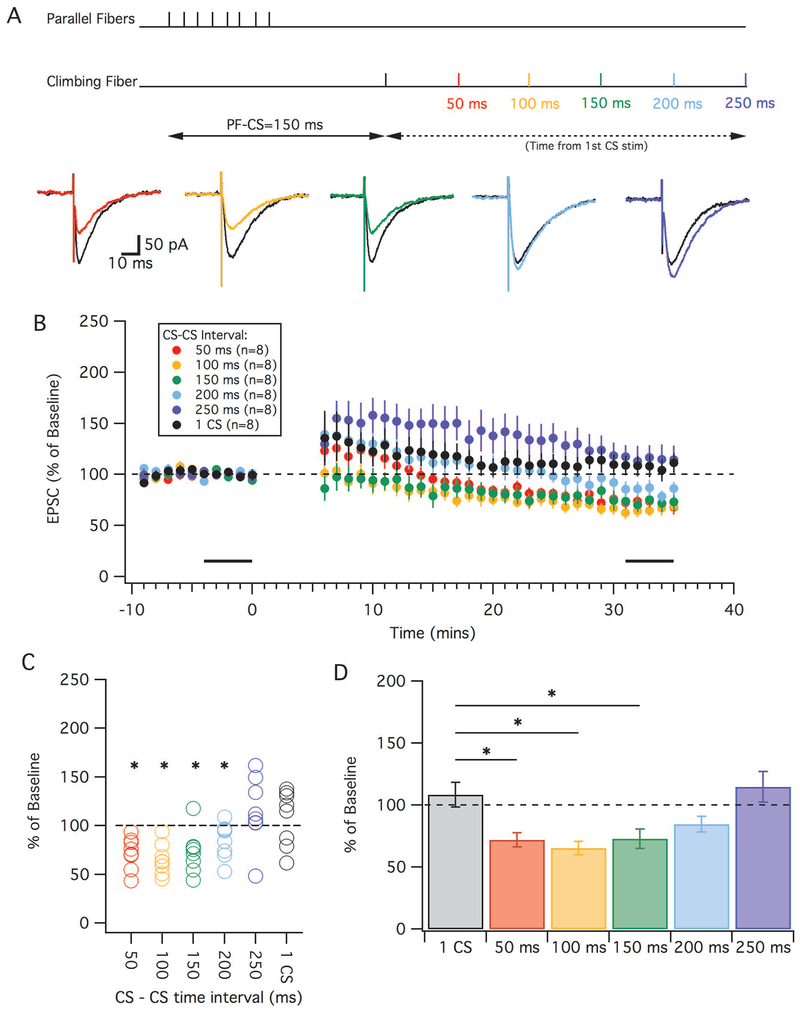
LTD is successfully induced with complex spike doublets in a timing-dependent manner

Since we have shown that complex spikes can occur in clusters both spontaneously and when evoked, we sought to determine whether a cluster of complex spikes was needed for LTD under physiological conditions and if so under what time intervals this would occur. For these experiments, we initially used a PF-CS timing interval of 150 ms, the condition that caused the least amount of potentiation under single-CS conditions 30 minutes after pairing (see Figure 3). To see if complex spike clustering was required for LTD we added a second complex spike at 50, 100, 150, 200 or 250 ms after the first complex spike (Figure 5A). We found that LTD could be successfully induced under more physiological conditions if the second complex spike occured ≤ 200 ms from the first. Thirty minutes after the tetanization period we found that the CS-CS intervals of 50, 100, 150 ms and 200 ms successfully depressed compared to their baselines (Figure 5C; paired t-test, 50 ms: 72.0 ± 5.8%, p=0.002, n=8; 100 ms: 65.5 ± 5.6%, p=0.004, n=8; 150 ms: 72.9 ± 7.7%, p=0.01, n=8; 200 ms: 84.6 ± 6.4%, p=0.048, n=8). Significant LTD was not observed when the CS-CS interval was 250 ms (paired t-test, 114.8 ± 12.4%, p=0.27, n=8). Furthermore, a group-wise comparison of the double complex spike groups including the results of the one complex spike condition (compare to Figure 3) showed a significant difference (Kruskal-Wallis test, H=17.93, 5; p=0.003). Post-hoc analysis revealed that the 1-CS group was significantly different from the 50 ms (p=0.041), 100 ms (p=0.0097) and 150 ms (p=0.048) groups (Figure 5D). Although the 200 ms CS-CS interval resulted in a depression, it was not found to be significantly different from the 1-CS control group (p=0.36). Thus, we have shown that when the interval from the PF to CS was 150 ms, LTD could be induced if a second complex occured less than 200 ms after the first.

Figure 5.

LTD is induced by CS clustering. (A) Top: Schematic depicting timing of the PF-CS=150 ms with a second CS. Parallel fibers were stimulated 8 times at 100 Hz. The climbing fiber was stimulated 150 ms from the start of the PF stimulation and a second CF stimulation occurred with an inter complex spike interval of either: 50, 100, 150, 200 or 250 ms. Bottom: Example traces showing and EPSC before (black) and after LTD tetanization using a CS-CS interval of either 50 ms (red), 100 ms (orange), 150 ms (green), 200 ms (cyan) or 250 ms (blue). (B): Time graphs showing the change in EPSC amplitude (as a percentage of baseline) following the LTD induction protocols with the various CS-CS intervals. For comparison, the black trace indicates the 1-CS group previously shown in Fig. 3. Black bars indicate time points that were averaged (baseline and endpoint) to calculate changes in EPSC amplitude. (C): Percent change in EPSC (from baseline) in individual cells using the various CS-CS timing intervals. (D): Averaged mean of percent change in EPSC amplitude of the various CS-CS timing intervals compared to the 1 complex spike protocol (grey). Error bars indicate SEM. * indicates p < 0.05.

To test whether the LTD observed was due to the second complex spike and not a difference of greater calcium in the first complex spike we measured the area under the complex spike during the first 50 ms in each CS-CS interval in the PF-CF =150 ms protocol. There was no difference between the area of the first complex spikes in any of the protocols (Kruskal-Wallis test, H=10.97, 5; p=0.74).

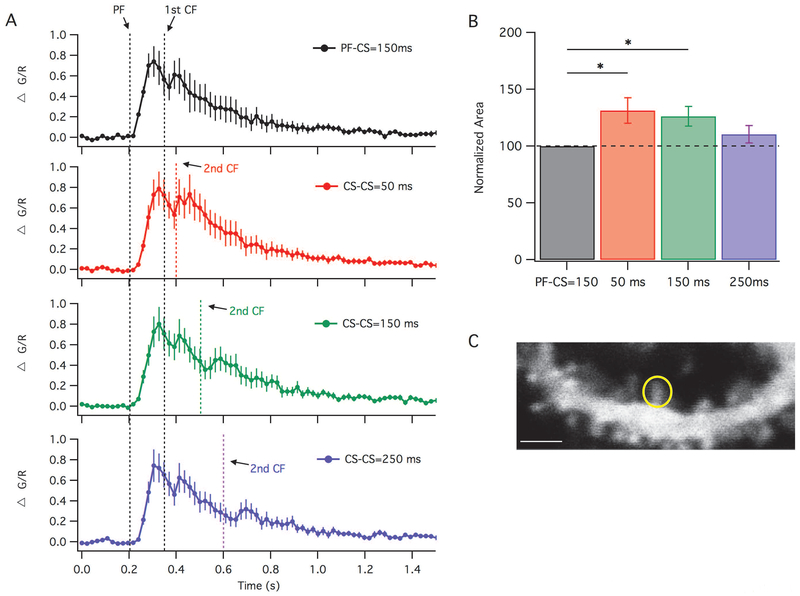
Under near-physiological conditions we compared the calcium levels during the 1-CS protocol using a PF-CS interval of 150 ms (which failed to result in LTD) with the CS clustering protocols using a CS-CS interval of 50 ms and 150 ms (which both successfully induced LTD), as well as the failed LTD protocol with the CS-CS interval of 250 ms (Figure 6). Figure 6A shows the calcium transients induced by these four protocols. A second complex spike can be seen in these calcium transients as a secondary peak, which elongates the elevated calcium signal. We then measured the area under the curves and normalized them to the 1-CS protocol (Figure 6B). We found that the area under the curve resulting from the 50 ms and 150 ms CS-CS protocols was significantly greater than the area under the curve of the 1-CS protocol (paired t-tests; 1CS: 100.0%, n=12 compared to 50 ms: 131.3 ± 11.2%, n=12, p=0.017 and 150ms: 126.4 ± 8.7%, n=12, p=0.012). There was no significant difference between the 1-CS protocol to the 250 ms CS-CS protocol (104.5 ± 26.0%, n=12, p=0.3), which can be expected as both protocols resulted in a potentiation. This is consistent with LTD requiring significantly more calcium than LTP in cerebellar Purkinje cells.

Figure 6.

Spine calcium transients depend on stimulus timing. (A): Calcium transients measured as change of fluorescence (ΔG/R), averaged from recordings of Purkinje cell spines (n=12 cells) from the PF-CS= 150 ms LTD protocol with 1 complex spike (black), and with two complex spikes with a CS-CS interval of 50 ms (red), 150 ms (green) or 250 ms (blue). Black dashed lines represent time of PF and 1^st CF stimulation. Colored lines represent the 2^nd CF stimulation. (B): Area under the curve of the calcium transients (shown in A) normalized to the 1 complex spike response that was recorded from the same cell (top trace in A). (C): Example of maximally responding Purkinje cell dendritic spine filled with Fluo-5F and Alexa 633, the circle outlines the ROI. Responses to all four stimuli were recorded from each cell. Error bars indicate SEM. Scale bar is 2 μm. * indicates p < 0.05.

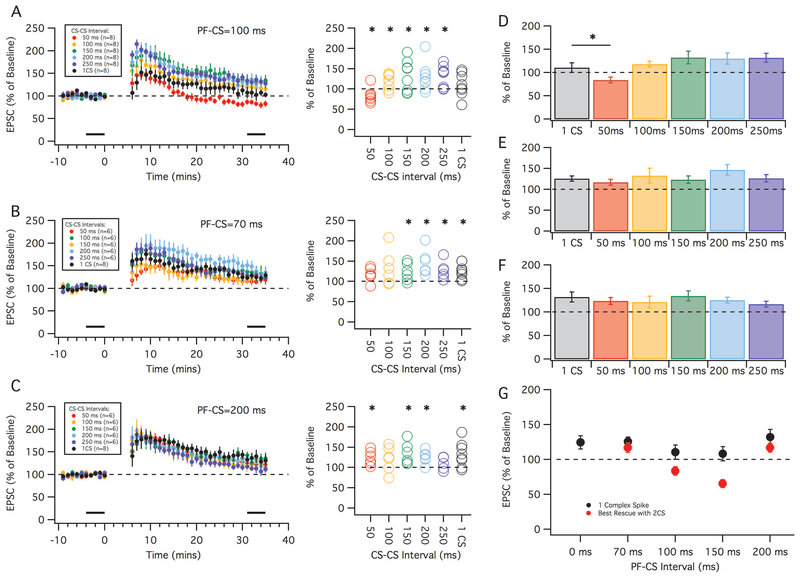
We next tried to evoke LTD with a PF-CS interval of 100 ms, with an added complex spike either 50, 100, 150, 200 or 250 ms after the first (Figure 7A). Here we only observed depression when the CS-CS interval was 50 ms (83.8 ± 6.0%, n=8, p=0.03, paired t-test, Figure 7A). The 100, 150, 200 and 250 ms groups were all significantly potentiated compared to their baselines (paired t-test; 100 ms: 118.2 ± 6.5%, n=8, p=0.026; 150 ms: 132.4 ± 13.5%, n=8, p=0.048; 200 ms: 129.9 ± 12.2%, n=8, p=0.044; 250 ms: 132.1 ± 9.4%, n=8, p=0.011). A groupwise comparison including its control 1-CS group (PF-CS=100 ms) revealed a significant difference among these groups (Kruskal-Wallis test, H=15.7, 5; p=0.0076; Figure 7D), with the post-hoc analysis showing the 50 ms CS-CS interval being significantly different from the 1-CS control (p=0.042).

Figure 7.

LTD has a preferred timing interval. Results of two complex spike stimuli at PF-CS interval of 100 ms (A and D), 70 ms (B and E), and 200 ms (C and F). Different CS-CS intervals of either 50 ms (red), 100 ms (orange), 150 ms (green), 200 ms (cyan) or 250 ms (blue) were used to induce LTD. (A-C) Left: Time graphs showing the change in EPSC amplitude (as a percentage of baseline) following the LTD induction protocols with the various CS-CS intervals. For comparison, the black traces indicate the 1-CS group previously shown in Fig. 3. Black bars indicate time points that were averaged (baseline and endpoint) to calculate changes in EPSC amplitude. (A-C) Right: Percent change in EPSC (from baseline) in individual cells using the various CS-CS timing intervals. (D-F): Averaged mean of percent change in EPSC amplitude of the various CS-CS timing intervals compared to the 1 complex spike protocol (grey). (G): Summary of LTD induction showing precise timing preferences. Black circles: Summary of results with LTD protocols with 1 complex spike across the various PF-CS timing intervals (x-axis). Red circles: The best attempt to induce LTD with a protocol with 2 complex spikes. Error bars indicate SEM. * indicates p < 0.05.

Finally, we tested if the addition of a second complex spike was effective in allowing LTD with a PF-CS interval of 70 ms or 200 ms. Unlike the 100 ms or 150 ms PF-CS conditions, the 70 and 200 ms conditions led to potentiation when only 1 complex spike was used (seen in Figure 3). We found that adding a second complex spike could not induce LTD, as we were still unable to cause a depression in either the 70 ms (Figure 7B) or the 200 ms (Figure 7C) PF-CS conditions. When the PF-CS interval was 70 ms a second complex spike at any CS-CS interval did not result in depression (Figure 7B) 30 minutes after the tetanization period. When the CS-CS interval was equal to or greater than 150 ms we saw a significant increase in the EPSC amplitude compared to its baseline (paired t-test; 150 ms: 123.5 ± 8.9%, n=6, p=0.04; 200 ms: 146.9 ± 12.9%, n=6, p=0.02; 250 ms: 126.6 ± 8.9%, n=6, p=0.03). There was no significant increase when the CS-CS interval was 50 ms (117.2 ± 6.9%, n=6, p=0.06) or 100 ms (132.9 ± 17.4%, n=6, p=0.1). When compared with the control of 1 complex spike there were no significant differences between groups (Kruskal-Wallis test, H=3.4, 5; p=0.6; Figure 7E).

Similarly, when the PF-CS interval was 200 ms, the addition of a second complex spike also failed to cause a depression at any CS-CS interval (Figure 7C). In fact, a significant potentiation compared to its baseline occurred when the CS-CS interval was either: 50 ms (123.7 ± 7.1%, n=6, p=0.02), 150 ms (134.4 ± 10.8%, n=6, p=0.02) or 200 ms (125.5 ± 6.5%, n=6, p=0.01). There was no significant change in EPSC amplitude with the CS-CS intervals of 100 ms (121.3 ± 12.5%, n=6, p=0.2), or 250 ms (116.9 ± 6.3%, n=6, p=0.1). When compared with the control group of 1 complex spike there was no significant difference between groups (Kruskal-Wallis test, H=2.6, 5; p=0.8; Figure 7F). In summary, LTD induction in crus I required pairs of CSs and a PF-CS interval of 100-150 ms (see Figure 7G).

LTD remains dependent on αCaMKII and a higher calcium threshold

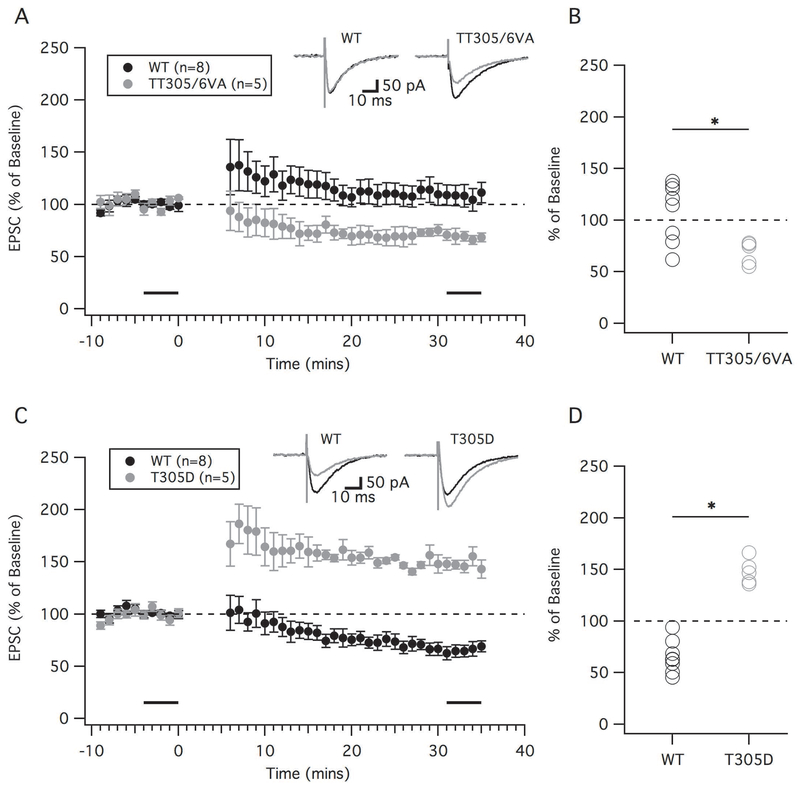
Previously, we showed that a key calcium sensor for high frequency (100 Hz) LTD is the autophosphorylation of αCaMKII (Piochon et al., 2016). During 100 Hz PF stimulation, higher calcium levels cause αCaMKII to undergo inhibitory autophosphorylation at its 305/306 site, thereby reducing its own activity and increasing the threshold for LTD induction. This shift ensures LTD activation depends on climbing fiber activity regardless of parallel fiber activation frequency. When the 305/306 site of αCaMKII is blocked (TT305/6VA mice), and thereby preventing the auto-inhibition of αCaMKII, the threshold for LTD has been shown to be lower. Indeed in 2 mM [Ca²⁺]_o ACSF we have previously shown that TT305/6VA mice show depression with just parallel fiber burst (LTP) stimulation (Piochon et al., 2016). Here we again show that these mice have a lower threshold for LTD, as in 1.2 mM [Ca²⁺]_o ACSF and using a one complex spike LTD protocol (PF-CS=150 ms) TT305/6VA mice (Figure 8A and B, grey) were able to successfully depress compared to baseline (68.8 ± 4.9%, n=5, p=0.003). When compared to wild type (WT, black), there was a significant difference between the groups (Mann-Whitney U-test, p=0.011).

Figure 8.

LTD depends on αCaMKII. (A and B): One complex spike LTD was successful in TT305/6VA mice. (A): Time course of EPSC amplitude (percent of baseline) in αCaMKII TT305/6VA mice (grey) in the one complex spike LTD protocol (PF-CS=150 ms) compared to WT mice (black). (B): Percent change in EPSC amplitude in each individual cell after LTD tetanization. Black bars indicate time points that were averaged (baseline and endpoint) to calculate percent changes in EPSC amplitude. (C and D): Two complex spikes failed to induce LTD in T305D mice. (C): Time course of EPSC amplitude (percent of baseline) in αCaMKII T305D mice (grey) with 2 complex spike LTD protocol (PF-CS=150 ms, CS-CS=100 ms) compared to WT mice (black). (D): Percent change in EPSC amplitude in each individual cell after LTD tetanization. Error bars indicate SEM. * indicates p < 0.05.

We have previously shown that 100 Hz LTD in 2 mM [Ca²⁺]_o ACSF solution was prevented and resulted in a potentiation in T305D mice, which mimics persistent phosphorylation at the 305 site and prevents Ca²⁺/calmodulin binding. Here, we show that LTD is prevented in 1.2 mM [Ca²⁺]_o ACSF in these same mice (Figure 8C and D, grey). When pairing PF-CS activation (150 ms interval) with CS-CS stimulation (100 ms interval) in T305D mice (Figure 8C and D, grey), we found that the EPSCs in these mice underwent a significant potentiation compared to its baseline (147.9 ± 5.4%, n=5, p=0.0009). Furthermore, they were significantly different compared to WT controls (black) (Mann-Whitney U-test, p=0.0015). Thus, the autophosphorylation of αCaMKII still seems to control LTD under the conditions of the present study.

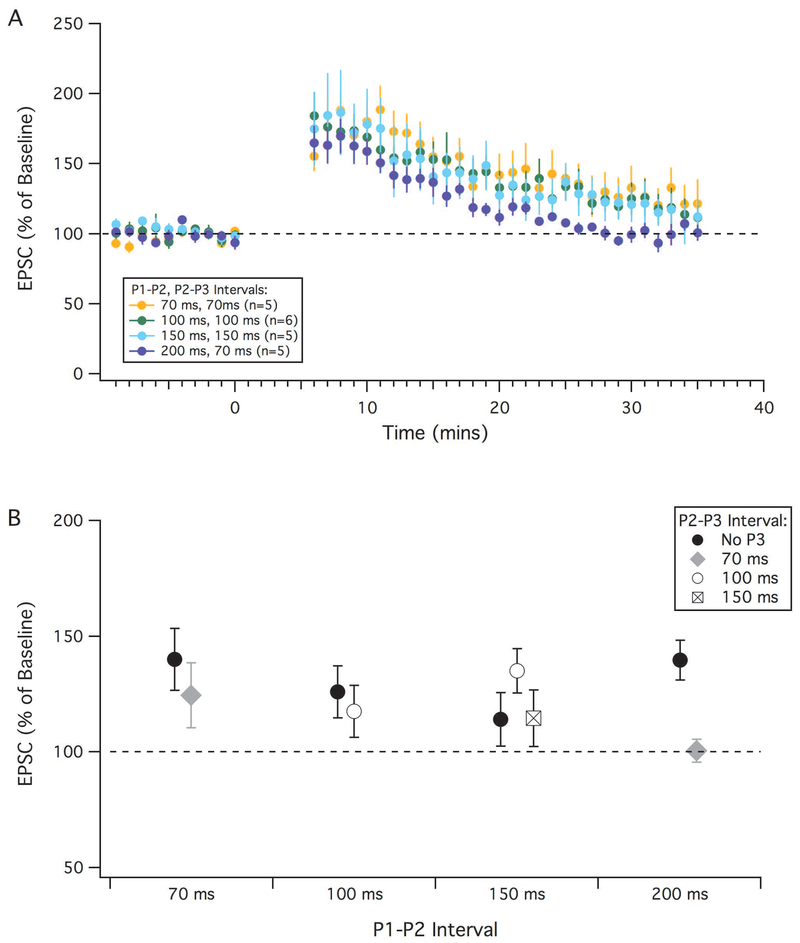
With sufficiently strong PF activation, LTD can be induced without a complex spike (Hartell, 1996). We attempted a variety of protocols that used an additional PF burst in place of the complex spike (Figure 9). Regardless of the timing between the PF bursts (70-200 ms) or number of PF bursts (2 or 3), we failed to see any significant depression. Figure 9B shows the results of all PF stimulation protocols, with the different intervals used between bursts. In summary, within the range of PF stimulation intensities used, LTD induction required complex spike activity.

Figure 9.

LTD is not induced by parallel fiber stimulation alone. EPSC amplitude (percent of baseline) after different LTP protocols mimicking parallel fiber bursts instead of a complex spike. A burst of 8 parallel fiber stimulation at 100 Hz (P_i) was used at different timing intervals (time between first stimulation parallel fiber stimulation) and various repeats (2-3 times). (A): Time courses of selected protocols showing the change in EPSC amplitude over time following an LTP induction protocol with various PF burst intervals. (B): Averaged percent change in EPSC amplitude showing all LTP protocols attempted with various parallel fiber stimulation timing intervals (e.g.: P1-P2 and P2-P3). Error bars indicate SEM.

Discussion

The main finding of the study presented here is that, under recording conditions that mimic the physiological ionic milieu, LTD induction at PF synapses requires the co-occurrence of two CF-evoked complex spikes (CSs) with each PF firing event, and that the timing window for co-activating the PF and the first CF firing event centers around an interval range of 100-150 ms. Our findings demonstrate that the lower calcium concentration used here makes it more difficult to induce LTD, and suggest that the occurrence of LTD in vivo will be restricted to specific activity patterns. Although possibly not an exclusive condition for the induction of LTD, the preferred pattern of repeated complex spikes shows that prolonged calcium signaling, and with it the prolonged presentation of the instructive signal, constitutes a favorable physiological trigger for LTD.

Complex spike clusters and single complex spikes as distinct instructive signals

Our LTD experiments suggest that individual complex spikes are false positives in the context of supervised learning, with CS cluster activity as a means of rejecting these events. The finding that an efficient CF instructive signal for LTD induction requires CFs to fire twice in succession leads to the question of the nature and function of single firing events. Our in vivo recordings support previous reports that whisker air puff stimulation elicits well-timed CF responses in Purkinje cells (Bosman et al., 2010; Najafi et al., 2014a, 2014b; Kitamura and Häusser, 2011; Brown and Raman, 2018). These are responses to salient stimuli that qualify as unconditioned stimuli in motor learning, and therefore act as potential instructive signals in supervised learning. Within this group of evoked responses, ~20% of firing events show doublets with inter-CS intervals of less than 150 ms, while ~10% of spontaneous firing events are doublets. Upon sensory stimulation, the percentage of doublets can be substantially higher, reaching up to ~50% in those neurons that reliably respond to air puff stimulation with at least one complex spike, and do so at short latency. Since under our slice experimental conditions doublets drove LTD and single complex spikes could drive LTP, these measurements suggest that evoked activity can provide efficient instruction for LTD, while spontaneous activity does not. Although we have not tested the plasticity consequences of mixed multiple and single complex spike responses, it is possible that the complex spikes can drive bidirectional plasticity (i.e. LTD or LTP) depending on the type of response that is evoked. It should also be noted that single CF firing events may still lead to transient decreases in Purkinje cell simple spike firing output, thereby leading to a transient adaptive response. CS doublets have also been seen by other groups both after air puff unconditioned stimuli (e.g. Van der Giessen et al., 2008) or in response to conditioned stimuli after eyeblink conditioning (see Ten Brinke et al., 2019). The occurrence rate of doublets varies greatly under these conditions, and likely depends on the exact cerebellar region recorded from, the nature of the stimuli used as well as the attentional state of the animal and its expectance of incoming stimuli.

The prevalence of CS doublets places a limit on possible roles of oscillatory mechanisms in neural coding. The inferior olive’s natural rhythmicity was once suggested to provide a motor clock to initiate muscle contraction and movement (Lamarre, 1984; Llinás, 1984; Welsh et al., 1995; Llinás, 2011). This clock hypothesis was originally motivated by observations of tremor associated with continuous, rhythmic olivary activity at 10 Hz under pathological conditions (Gautier and Blackwood, 1961). Such a rhythm can be driven by intrinsic mechanisms that are prominent in anesthetized animals and in brain slices. However, periodicity of CS firing has generally not been observed in awake mammals (Thach, 1968; Armstrong, 1974; Oscarsson, 1980), including a systematic search during cued wrist movements in monkeys (Keating and Thach, 1995). Keating and Thach also observed rebound firing of a second complex spike, as have later studies of movement (Chaumont et al. 2013, Witter et al., 2013, De Gruijl et al., 2014) and sensory responses after learning (ten Brinke et al., 2019). We found that doublets can also occur spontaneously, as well as under sensory stimulation, but did not observe ongoing, periodic CS firing under these conditions. Our optogenetic experiments are consistent with the idea that such doublets rely on nucleo-olivary feedback mechanisms (Chaumont et al., 2013; Witter et al., 2013). In summary, to date the effect of rhythmic tendencies in olivary activity is not prolonged sequences, but doublets, as might occur in a damped oscillator.

Complex spike clustering is required for LTD induction

Initial studies on the requirement for CF co-activation in LTD induction conceptualized the CF as an instructive signal operating in a yes/no mode to drive supervised learning (Ito et al., 1982; Coesmans et al., 2004). Our observation that, under near-physiological recording conditions, single CF pulses are ineffective and double pulses are required, shows that a binary yes/no framework is an insufficient description of CF firing events. The CF pathway has previously been shown to have plasticity consequences that are not fully captured by the presence or absence of a complex spike, as previously suggested (Eccles et al., 1964). Important additional parameters include CF plasticity (Hansel and Linden, 2000), variations in the number of spikes propagated along the fiber itself (Maruta et al., 2007; Najafi et al., 2014b; Mathy et al., 2009), variations in spikelet activity (Coesmans et al., 2004; Mathy et al., 2009) and modulation of the CF response in Purkinje cell dendrites by inhibition (Rowan et al., 2018). While the studies cited above do show that modulations of the instructive signal can alter its impact on the plasticity outcome, they allow the possibility that the instructive signal must reach some all-or-none threshold to induce plasticity. In the present study, we found that under our experimental conditions, a central requirement of LTD induction was the presence of multiple complex spikes.

An earlier study (Bouvier et al., 2018) reported LTD induction by two CSs separated by 100 ms. In those experiments, the first complex spike coincided with granule cell activity and was interpreted as a perturbation signal, while the second, delayed CS acts as an error signal, with an overall PF-CF stimulus duration lasting 100 ms, a pattern resembling classic PF-CF co-activation protocols. Our work, which explored a range of timing conditions, demonstrates that a PF-CF-CF sequence to trigger maximal LTD spans a longer interval, 200-400 ms. In our recordings, we observed that a prolongation of the waveform of a single complex spike by delivering 5 pulses to the CF input at 400Hz does not promote LTD. This finding shows that elevated dendritic spike activity over hundreds of milliseconds constitutes the optimal trigger for LTD induction.

We also show, that under near-physiological recording conditions, the repetitive CF stimulation cannot be replaced with equally timed PF burst stimulation, as was previously shown under classic experimental conditions (Hartell, 1996; Han et al., 2007). However, our data do not generally exclude the possibility that sufficiently intense PF activity alone can induce LTD (note the similarity of PF burst signals amplified by intrinsic plasticity with CSs; Ohtsuki et al., 2012; Ohtsuki and Hansel, 2018).

Prolonged calcium signaling facilitates the activation of CaMKII

The ACSF used in this study contained a [Ca²⁺] of 1.2 mM (instead of the classically used concentration of 2 mM) and a [Mg²⁺] of 1 mM (instead of 2 mM). These values were based on measures of [Mg²⁺]_o from the intact brain (Ding et al., 2016) as well as measures of [Ca²⁺]_o from the cerebellum (Nicholson et al., 1978) and neocortex (Heinemann et al., 1977). Despite of the higher Ca²⁺/Mg²⁺ ratio in this updated ACSF recipe, synaptically evoked calcium transients in dendritic spines were smaller, likely resulting from the lower absolute [Ca²⁺]_o. As the calcium threshold for PF-LTD is higher than the threshold for LTP (Coesmans et al., 2004; Piochon et al., 2016), the reduced calcium influx will lower the probability for LTD induction and result in LTP instead, as we indeed observed. The ‘rescue’ of LTD with prolonged CS activity was associated with a significant increase in spine calcium transients. The observation that it is not the amplitude that increases, but the duration of the [Ca²⁺]_i elevation, is consistent with the leaky integrator model of calcium signaling in LTD induction, which states that the calcium threshold for LTD becomes lower with a longer presentation of the calcium elevation (Tanaka et al., 2007; Chimal and De Schutter, 2018). Similarly, it has been shown that sustained elevation of calcium lowers the calcium threshold for the dendritic release of endocannabinoids (Brenowitz et al., 2006). The relatively long interval between the two CF pulses (50 to 200 ms) that leads to LTD induction when the interval between PF and CF stimulus onset is 150 ms suggests that there are additional factors that determine the permissive time windows for LTD induction. One candidate is the kinetics of calcium-binding proteins, such as calbindin and parvalbumin that enable spread of calcium by buffered diffusion and allow for the activation of calmodulin into adjacent dendritic shafts and even into neighboring spines (Schmidt et al., 2003; 2007; see also Santamaria et al., 2006).

Our experiments identify calcium/calmodulin-dependent protein kinase II (CaMKII) as a calcium sensor that benefits from the prolonged calcium transient (Chimal and De Schutter, 2018). LTD induction requires the activation of αCaMKII (Hansel et al., 2006). CaMKII suppresses the activation of protein phosphatase 2A through negative regulation of phosphodiesterase 1 and subsequent disinhibition of a cGMP/protein kinase G pathway, thus promoting LTD (Kawaguchi and Hirano, 2013). The inhibitory autophosphorylation of CaMKII at Thr305/306 (Elgersma et al., 2002), which may result from calcium/calmodulin binding and subsequent dissociation, possibly as a result of calcium transients that are too low in amplitude and/or do not last sufficiently long (Coultrap and Bayer, 2012), prevents cerebellar LTD and results in LTP instead (Piochon et al., 2016). Our finding that LTD is restored upon PF co-activation with a single CF pulse in TT306/6VA mice, in which Thr305 and Thr306 are substituted by the non-phosphorylatable amino acids valine and alanine, respectively, demonstrates that LTP results from this protocol under near-physiological recording conditions, because of the self-inhibition of CaMKII. The ability of inhibitory CaMKII autophosphorylation to prevent LTD is shown by the finding that PF-co-activation with two CF pulses results in LTP in phosphomimetic T305D mice, in which Thr305 is replaced by aspartate, preventing calcium/calmodulin binding.

Timing requirements of LTD and learning

For many years, LTD was widely accepted as a cellular mechanism underlying forms of cerebellar learning ranging from delay eyeblink conditioning (Ito et al., 1982; Ito and Kano, 1982) to eye movement adaptation. Moreover, optogenetic inhibition of AMPA receptor endocytosis and LTD has been found to prevent cerebellar motor learning (Kakegawa et al., 2018). However, a role for LTD in cerebellar learning has been questioned by findings that pharmacological or genetic blockade of LTD does not cause learning impairment (Welsh et al., 2005; Schonewille et al., 2011). These claims of mismatches between cellular and behavioral learning outcome have been tempered by the demonstration that LTD might be present under some induction conditions but not others (Yamaguchi et al., 2016). In vivo observations support a critical role of CF signaling in learning. Continuous CF co-activation at a rate of 4 pulses per second triggers LTD in decerebrate rabbits (Ito et al., 1982), and LTD is also observed in awake mice upon sensory input (whisker) stimulation resulting in PF and CF activation (Marquez-Ruiz and Cheron, 2012). However, it has been more recently reported that associative learning cannot be triggered by single pulse CF co-stimulation (Rasmussen et al., 2013) and requires intervals between the conditioned and unconditioned stimuli of 150 ms or longer (Wetmore et al., 2014). Our findings suggest the possibility that such discrete-trial experiments might also be done with multiple complex spikes per trial and a PF-CF time interval in the range of 100-150 ms, conditions that are required to trigger LTD under realistic recording conditions.

In an alternative view of the ability of CS features to drive learning, Yang and Lisberger have demonstrated using single-unit extracellular recordings that the number of spikelets in CS waveforms is correlated with learning, leading to the suggestion that CS waveform may be a specific trigger for plasticity mechanisms (Yang and Lisberger, 2014). Increased spikelet number could be driven by high-frequency CF activation at timing intervals smaller than the duration of a CS. It could also be driven by co-occuring mossy fiber activity (Najafi et al., 2014a+b). We have shown that optogenetic activation causing simple spike firing can also lead to CS-doublet generation. Therefore, these two features of complex spike responses – doublet firing and increased spikelet number – may be correlated phenomena. Testing whether this is true will help determine whether these views of effective learning are related.

Remaining caveats center on the incomplete emulation of other in vivo conditions, including neuromodulation, and the naturally occurring amount and pattern of mossy fiber / granule cell and climbing fiber activity. These gaps might contribute to remaining mismatches, such as the observation that we did not observe LTD induction at a PF-CF interval of 200 ms, while associative learning works well in this longer interval range. The details of mismatch at longer intervals could be explained by the involvement of multiple plasticity mechanisms in learning, some of which are triggered at longer time intervals. Indeed, it has been suggested that cerebellar motor learning rests on multiple mechanisms at multiple brain sites (Hansel et al, 2001; Freeman and Steinmetz, 2011; Gao et al, 2012; Titley et al, 2017; Titley et al., 2018).

Beyond timing-dependent LTD, Purkinje cells also express a strong cell-autonomous form of plasticity, and learning can occur without temporally patterned synaptic input (Johansson et al., 2014). Intrinsic excitability changes may aid in driving memory formation, with synaptic plasticity serving to determine the information content by individual neurons (Titley et al., 2017). In cerebellar learning, this equates to a scaling of synaptic input weights depending on whether PF synapses contribute to the occurrence of an error. Synthesis of timing-dependent and timing-independent learning mechanisms will require behavioral experiments that go beyond single-stimulus tests of learning such as eyeblink conditioning, which only test for the occurrence of a discrete well-timed response.

Our findings have several implications for cerebellar learning. First, the majority of complex spikes that are fired do not contribute to LTD induction, and the requirement for doublets (or more) of complex spikes acts as a noise reduction mechanism that allows only salient instructive signals to drive plasticity. Second, the difficulty of inducing LTD emphasizes the role of repetitive PF activation, which by itself induces LTP, leading to bidirectional plasticity as found in adaptive filter models of cerebellar learning (Dean et al., 2010). Third, it requires the re-evaluation of predictions regarding cerebellar learning. For example, recent observations identify conditioned stimulus-evoked complex spikes as a hallmark of Purkinje cells that change the spike firing output in eyeblink conditioning (Ohmae and Medina, 2015; Ten Brinke et al., 2015). It is possible that the combination of PF activity followed by a conditioned stimulus-evoked and an unconditioned stimulus-evoked complex spike, and/or double conditioned stimulus-evoked complex spike responses (Ten Brinke et al., 2019) are well-suited for inducing LTD.

Key Points Summary:

• Spike doublets comprise ~10% of in vivo complex spike events under spontaneous conditions and ~20% (up to 50%) under evoked conditions

• Under near-physiological slice conditions single complex spikes do not induce LTD

• Doublet stimulation is required to induce parallel fiber LTD with an optimal parallel fiber-to-first complex spike timing interval of 150 ms