A New Twist on Tropomyosin Binding to Actin Filaments: Perspectives on Thin Filament Function, Assembly and Biomechanics

Abstract

Tropomyosin, best known for its role in the steric regulation of muscle contraction, polymerizes head-to-tail to form cables localized along the length of both muscle and non-muscle actin-based thin filaments. In skeletal and cardiac muscles, tropomyosin, under the control of troponin and myosin, moves in a cooperative manner between blocked, closed and open positions on filaments, thereby masking and exposing actin-binding sites necessary for myosin crossbridge head interactions. While the coiled-coil signature of tropomyosin appears to be simple, closer inspection reveals surprising structural complexity required to perform its role in steric regulation. For example, component α-helices of coiled coils are typically zippered together along a continuous core hydrophobic stripe. Tropomyosin, however, contains a number of anomalous, functionally controversial, core amino acid residues. We argue that the atypical residues at this interface, including clusters of alanines and a charged aspartate, are required for preshaping tropomyosin to readily fit to the surface of the actin filament, but do so without compromising tropomyosin rigidity once the filament is assembled. Indeed, persistence length measurements of tropomyosin are characteristic of a semi-rigid cable, in this case conducive to cooperative movement on thin filaments. In addition, we also maintain that tropomyosin displays largely unrecognized and residue-specific torsional variance, which is involved in optimizing contacts between actin and tropomyosin on the assembled thin filament. Corresponding twist-induced stiffness may also enhance cooperative translocation of tropomyosin across actin filaments. We conclude that anomalous core residues of tropomyosin facilitate thin filament regulatory behavior in a multifaceted way.

Introduction

Early appreciation of muscle sarcomeric structure and the sliding filament mechanism of muscle contraction (Hanson and Huxley 1953, 1955; Huxley and Hanson 1954; Niedergerke and Huxley 1954) marked the dawn of a new era of muscle research. It soon became evident that muscles are powered by myosin cross-bridge cycling which drives thick filaments along actin-containing thin filament tracks (Huxley and Brown 1967; Huxley 1969). Thus, previous notions that muscle proteins themselves shorten during contraction were refuted (Huxley et al 1965). At almost the same time, tropomyosin, hitherto the only actin filament-binding protein to have been isolated (Bailey 1946), was identified by Crick (1953) as a coiled coil, a previously unrecognized protein conformation. While tropomyosin’s function remained unclear for years, its coiled-coil structure, modeled as two helically wound α-helices, became apparent early on (Szent-Györgyi and Cohen 1957; Cohen and Holmes, 1963) (Fig. 1). Indeed, tropomyosin, fitting together by inter-chain “knobs-into-holes” patterning, still is sometimes considered an archetype of its class of helical protein assemblies (Crick 1953). It is the intersection of these seemingly disparate findings and the work they spearheaded that forms the focus for this review.

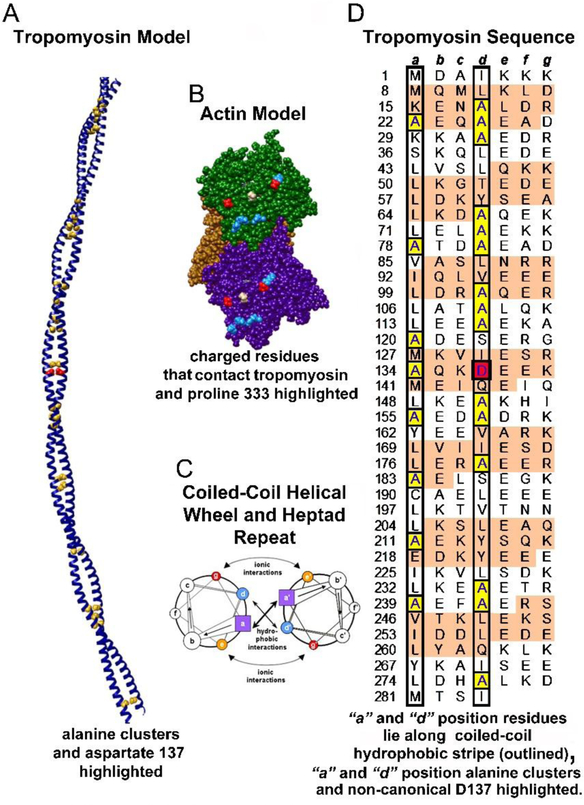
Figure 1. Tropomyosin architecture.

A. Ribbon diagram of the tropomyosin coiled coil with core alanines and aspartate-137 highlighted as yellow and red spheres respectively. B. Three neighboring actin subunits of F-actin highlighting charged residues (D25 and D311 in red and R28, R147, K315, K326 and K328 in blue). These residues are likely to interact electrostatically with successive pseudo-repeats of tropomyosin. Proline 333 (tan), which forms the boundary between blocked and closed states, is also highlighted. C. Helical wheel diagram of a canonical dimeric coiled-coil. Heptad positions are labeled a to g and a’ to g’ for the respective helices of the dimer; figure adapted from Hagemann et al (2008). D. Striated muscle tropomyosin (Tpm1.1) sequence annotation; figure adapted and modified from Brown and Cohen (2005) and Lehman et al (2018) to emphasize residues within heptad repeats (a, b, c, d, e, f, g) in each chain of the tropomyosin coiled-coil homodimer, with the first residue in each heptad repeat numbered. The α-zones (as defined in Brown and Cohen (2005)) of each pseudo-repeat of tropomyosin that locate close to actin subdomains 1 and 3 are shaded in tan, while the β-zones found over subdomains 2 and 4 have a white background (Brown and Cohen 2005). Generally, hydrophobic residues are localized at a and d residue positions (found within black borders in the diagram). Core alanine residues are highlighted in yellow and the d-position aspartate-137 is highlighted in red.

Tropomyosin often is regarded as an unremarkable and subservient partner to thin filament troponin in sensitizing muscle activity to Ca²⁺-levels. However recent renewed interest in tropomyosin led the journal in 2013 to organize a special issue devoted to the 40 nm long protein (Marston and Gautel 2013) (see related contribution on troponin by Marston in this issue). In fact, the recent exponential growth in numbers of publications on tropomyosin stems partly from a need to explain cardiomyopathy and skeletal muscle disease etiology engendered by mutations in the protein (Tardiff 2005; Marston et al 2013) (also see related contribution by Moraczewska and colleagues in this issue). In addition, growing evidence also suggests that a panoply of non-sarcomeric tropomyosin isoforms earmark diverse actin cytoskeletal domains in most eukaryotic cells (Gunning et al 2015a,b; Gunning and Hardeman 2017) (see related contribution by Gunning and Manstein in this issue) and further that an imbalance in tropomyosin expression accompanies cancer development (Helfman et al 2008; Stehn et al 2013) and possibly is involved in glucose handling (Kee et al 2015, 2018; Savill et al 2016) as well as ulcerative colitis (Das and Bajpai 2008). Thus richly detailed past and present studies on the tropomyosin coiled coil continue to lead to new understanding about muscle and cytoskeletal thin filament behavior.

In the beginning

As mentioned, in early studies tropomyosin was shown to associate with actin and integrate itself onto the surface of the muscle thin filament (Corsi and Perry 1958; Laki et al 1962). However, its role in thin filament function required both new structural insights and experimental corroboration. The most emblematic action of the elongated tropomyosin, of course, lies in its response to Ca²⁺-binding by troponin, thus controlling actin-myosin ATPase activity and cross-bridge cycling on actin and consequently regulating contraction (Ebashi 1963). Structural understanding of tropomyosin’s behavior on the thin filament began to emerge following the simple but profound concept promoted by Hanson and Lowy (1964) that: ‘If tropomyosin forms some sort of complex with actin in the intact muscle, as seems very probable, then it might exert some control over the contractile function of actin, say by masking certain monomers in the filament and thereby selecting the sites for interaction with myosin’. It followed from this argument that when muscles instead are active, tropomyosin, known to be linked end-to-end along thin filaments as a polymerized cable (Flicker et al 1982; Hitchcock-DeGregori 2008; Orzechowski et al 2014a), must move away from masked actin sites, thereby switching muscles from an off- to an on-state. And, further, to be part of an effective switching mechanism, tropomyosin is likely to translocate azimuthally around the thin filament as part of a semi-rigid cooperative unit (Lehrer and Geeves 1998; Geeves and Lehrer 2002; Smith and Geeves 2003; Smith et al 2003; Geeves 2012; Moore et al 2016). This will ensure propagation of on-off positional switching along the filament and not limit the switching-signal only to the local site of troponin action or myosin head binding. This description is the essence of the steric model of muscle regulation supported by fiber diffraction studies on intact muscle preparations carried out by Hugh Huxley and others (Huxley 1970, 1972; Haselgrove 1972; Parry and Squire 1973) and by electron microscopy on isolated thin filaments (Lehman et al 1994). The seminal structural work predated what is now described by the three-state mechanism of muscle regulation in which tropomyosin translocation across actin filaments is thought to occur in steps (McKillop and Geeves, 1993; Vibert et al 1997; Geeves 2012; Lehman 2016, 2017). Here, Ca²⁺-free troponin on relaxed skeletal and cardiac muscle thin filaments diminishes tropomyosin thermal vibration on thin filaments. This restricts tropomyosin largely to a blocking B-state position that occludes myosin-binding sites on actin. Once muscles are activated, rising Ca²⁺ releases the pinning action of troponin on tropomyosin location, allowing the tropomyosin/troponin complex to readily access a “closed”, C-state position on thin filaments by a ~15° movement of the semi-rigid coiled coil. The tropomyosin movement partially uncovers the myosin-binding site, increasing the probability of myosin interactions (Holmes 1995; Vibert et al 1997; Poole et al 2006). Myosin head interaction then moves tropomyosin ~10° further from the inhibitory positions on actin to an “open” M-state, completely exposing the myosin site on actin and thereby promoting strong myosin-binding and the crossbridge cycling associated with contraction (Holmes 1995; Vibert et al 1997; Poole et al 2006; Behrmann et al 2012). In this mechanism, both Ca²⁺-binding and myosin facilitate tropomyosin movement in a cooperative allosteric manner. This cooperativity reduces the range of Ca^2+- concentrations (or myosin binding levels) necessary for muscle on-off switching and thus accentuates the power of the regulatory mechanism.

Kinetic and structural data (McKillop and Geeves 1993; Lehman et al 2000) suggest that low energy barriers separate the blocking B-state and closed C-state locations of tropomyosin on actin filaments. In fact, energy landscape measurement of models of actin-tropomyosin indicate that a 15 Å – 20 Å wide, fairly flat and shallow, energy basin encompasses and surrounds the B- and C-state tropomyosin positions on troponin-free thin filaments (Orzechowski et al 2014b; Rynkiewicz et al 2015). Thus, in effect the B-state is only strongly favored when the energy landscape is distorted by the additional presence of Ca²⁺-free troponin pinning down tropomyosin and restricting its motions; otherwise tropomyosin is thought to oscillate unobstructed between the two positional states. The situation is reversed for the energetically unfavorable, barely populated, M-state positioning of tropomyosin on myosin-free thin filaments (McKillop and Geeves, 1993). Here, in the absence of filament-bound myosin, the M-state is disfavored (Orzechowski et al 2014b; Rynkiewicz et al 2015; Kiani et al 2019). It is only sustained once myosin heads bind strongly to actin filaments and displace tropomyosin away from its B- and C-state energy basin location, thereby generating a newly formed actin-tropomyosin-myosin ternary complex. Alternatively, once myosin is released from actin during muscle relaxation, tropomyosin is expected to snap back to ground state B- and C-positions defined by the basin in the actin-tropomyosin energy landscape (Kiani et al 2019). Nevertheless, despite the elegance of the overall description of the three-state mechanism, the influence of the cable properties of tropomyosin and thus the fidelity of tropomyosin translocation across the thin filament during muscle regulatory switching have remained relatively obscure until recently.

The binding of tropomyosin

Molecular dynamics simulations suggest that, on average, the curvature of isolated tropomyosin matches the surface contours of the F-actin helix (Li et al 2010). This preshaping of tropomyosin to the actin helix reduces the entropic cost required during thin filament assembly (Holmes and Lehman 2008). By associating with the actin filament surface, the entropic cost of head-to-tail tropomyosin polymerization then also diminishes, while at the same time the emergent superhelical cable becomes trapped topologically around F-actin, like a rope wrapped around a pole (Holmes and Lehman 2008). During the assembly process, the azimuthal attitude of the tropomyosin cable is biased to B- and C-state positions by a series of electrostatic interactions involving charged residues located on the face of actin subunits (Brown and Cohen 2005; Brown et al 2005, Li et al. 2011; Barua et al 2012, 2013; Orzechowski et al 2014b; Rynkiewicz et al 2015) (Fig. 1). These interactions between actin and tropomyosin then define the fairly broad but shallow energy basin demonstrated by energy landscape measurements and referred to above (Orzechowski et al 2014b; Rynkiewicz et al 2015). Residues K326 and K328 on actin, the major players in this interaction; lie on a surface loop at the border between actin subdomains 1 and 3 (Brown and Cohen 2005; Li et al. 2011; Dominguez 2011; Barua et al 2012, 2013; von der Ecken et al 2015; Viswanathan et al 2017) (Fig. 1). Molecular dynamics performed on actin itself demonstrates that the loop swings back and forth azimuthally by a few angstroms (Kiani et al 2019). Thus, the landscape itself is dynamic, in turn influencing tropomyosin positioning. In its B-state position, tropomyosin is attracted to charged actin residues R147, K326 and K328 as well as D25 and R28 on subdomain 1 (when the latter two are not interacting with each other). Equilibrating dynamically between B- and C-states on actin, tropomyosin remains associated with residues K326 and K328 but can move azimuthally roughly 15° away from R147, D25 and R28 to assume C-state positions (Holmes 1995; Poole et al 2008). In this location, tropomyosin additionally may interact with charged residues D311 and possibly K315 on subdomain 3. Thus, residues K326 and K328 and neighboring P333 appear to act as a fulcrum over which tropomyosin teeters and then falls to the side (Kiani et al 2019), while otherwise remaining ensnared lengthwise in a thicket of charged side chains on each of seven successive actin subunits along actin (Fig. 1). At the same time Ca²⁺-free troponin, of course, tips the balance in favor of tropomyosin interactions with the B-state cohort of residues on actin, thereby buttressing tropomyosin’s steric interference of myosin head association in relaxed muscles. Thus the surface chemistry of actin and tropomyosin is consistent with the three-state model described above.

In stiffness and in health, till mutations do us part

It long has been our opinion that elucidating the structural mechanics of tropomyosin is fundamental to understanding tropomyosin’s contribution to gatekeeping access of myosin and various actin binding proteins to the assembled thin filament in muscle fibers and in non-muscle cells. Indeed, the stiffness of tropomyosin along the muscle thin filament surface is one obvious determinant governing the magnitude and fidelity of troponin- and myosin-induced cooperative switching in muscle systems. In other words, the material properties of tropomyosin cables likely define the distance along thin filaments over which tropomyosin movement is propagated when influenced by troponin and myosin. Therefore, biomechanics governs the effectiveness of the tropomyosin switch. If, for example, disease-linked mutations produce an overly floppy tropomyosin, then regulatory movement along the end-to-end linked cable will not propagate properly. In such cases, tropomyosin would then fail to reposition successfully as a cooperative unit following binding of Ca²⁺ to troponin or interaction of myosin and other actin-binding proteins to thin filaments. Alternatively, if tropomyosin became extremely stiff, it might then resist being thrust toward on-positions at sub-saturating levels of myosin - thin filament binding, for instance during isotonic contraction. The exquisite balance between such opposing tendencies is critical for tropomyosin’s regulatory function and thus tunes tropomyosin behavior to match its diverse biological roles.

Words matter

Materials scientists evaluate and quantify flexibility (and conversely stiffness) by measuring mechanical deformation of an object to an applied force. A rod-like material like tropomyosin may display (1) bending (flexural) flexibility, (2) twisting (torsional) flexibility, and (3) stretching or compression (elastic) flexibility. Thus, it is prudent to evaluate the components of tropomyosin flexibility precisely in order to better understand tropomyosin’s functional behavior. Bending flexibility generally first comes to mind when attempting to describe tropomyosin behavior without necessarily considering its torsional or elastic variance. Indeed, under-recognized local variance in tropomyosin torsion may enhance coiled-coil stiffness while optimizing residue-residue interactions between tropomyosin and its actin filament substrate (also see [Lehman et al 2018]). In contrast, changes in coiled-coil conformation due to significant longitudinal elastic extension or compression have not been reported for isolated or actin-bound tropomyosin.

Words have meaning but they also have connotations that can drift in an unintended way to distort understanding. The terms ‘rigidity’, ‘semi-rigidity’, ‘flexibility’ and ‘stiffness’ are often used loosely in the tropomyosin literature. In the context of work on tropomyosin described in this paper, ‘stiffness’ and ‘flexibility’ are clearly defined and directly quantified. However attractive, associating tropomyosin flexibility indirectly with variously described experimentally measured features such as susceptibility to proteolytic cleavage, thermal denaturation and core conformational vibration may not always be strictly justified, when flexibility itself is not measured (Sumida et al., 2008; Minikata et al 2008; Moore et al 2011; Yar et al 2013; Shchepkin et al 2013; Zheng et al 2013, 2016; Matyushenko et al 2014, 2018; Scellini et al 2017) (also see other references for thoughtful perspectives [Nevzorov and Levitsky 2011; Tardiff 2011; McConnell et al 2017]). Of course, some ambiguity can be useful, when grappling with still nascent concepts, but there comes a point in a series of investigations when precision is required or as Håkan Nesser suggests in Borkmann’s Point (Nesser, 2006), some concerted thinking is paramount.

‘Energy and persistence conquer all things’ (attributed to Benjamin Franklin)

Tropomyosin is a coiled-coil protein, not a braided wire made of steel or a two-stranded Solomonic column carved from stone. Such materials would have near infinite stiffness if reduced to a cellular scale. In contrast, any coiled-coil protein like tropomyosin (Fig. 1) will have a certain degree of bending flexibility either when in isolation or when bound to actin filaments. The question is how much flexural flexibility does rod-like tropomyosin display and is its stiffness compatible with a role in the muscle steric switching mechanism and its inherent cooperativity? Typically, rigidity of rod-shaped materials is quantified by determining persistence length. Persistence length measurements approximate the length along a straight isomorphous rod over which a localized displacement at one point is still correlated with a corresponding displacement at a distance.

Tropomyosin is one of few coiled coils that is free of discontinuities such as sequence-dependent stammers or stutters. Indeed, low resolution electron micrographs as well as snapshots of high resolution molecular dynamics simulations show that tropomyosin is gently curved without displaying obvious kinks, bends, global shape asymmetry or discordant bending flexibility (Li et al 2010; Sousa et al 2011). Tropomyosin therefore is seemingly well-suited for persistence length determination and for assessing corresponding outcomes. Measurement of tropomyosin persistence length, however, is complicated because the tropomyosin molecule is not straight but rather is naturally curved and polymerizes into a superhelical cable. Hence, calculations must account for this inherent curvature and not be made against a notional straight rod reference structure (Li et al 2010).

Persistence length determination is most appropriate for evaluating global properties of isomorphous rod-like materials. However, tropomyosin is not a homogeneous molecule with a strictly modular pattern designed to match seven successive actin subunits along thin filaments equivalently (Hitchcock-DeGregori 2008). Instead, each of the seven tropomyosin pseudo-repeats is distinct, while nonetheless designed to be complementary to successive actin subunits (Hitchcock-DeGregori 2008; Li et al 2011; Barua et al 2012, 2013). Thus, even though persistence length values likely reflect collective tropomyosin stiffness quite accurately, they may not account for subtle local structural non-uniformity. In addition, as discussed below, local biomechanical patterns also may be more subtle than initially realized, yet functionally relevant.

Tropomyosin stiffness

Phillips et al. (1986) studied the interwoven pattern of tropomyosin in crystal structures of the full length coiled coil and noted that C-terminal regions of component molecules fluctuate perpendicular to their long axis by up to 8 Å, while N-terminal parts deviate off-axis by approximately 5 Å (Phillips and Chacko, 1996). Based on these data, 150 to 170 nm persistence length values for tropomyosin at 0° C and 65 nm at 30° C were derived; i.e. roughly two to four times the contour length of the elongated protein. Later, Li et al. (2010) and Sousa et al. (2010) measured curvature variation of tropomyosin in electron micrographs, where tropomyosin was either fixed in a glass of negative stain or preserved by rotary shadowing. This method yielded comparable persistence lengths (100 – 110 nm, nominally at 25° C), although these values were roughly double those found by Loong et al (2012) using atomic force microscopy, in which protein-substrate interactions can affect coiled-coil curvature variance. In fact, all the latter measurements underestimated tropomyosin persistence length, and hence stiffness, by determining the deviations of tropomyosin from a notional straight rod reference structure instead of its native superhelically bent 3D shape. Li et al (2010) therefore modeled tropomyosin as an idealized superhelix (as in Lorenz et al 1995) and carried out molecular dynamics to more meaningfully determine motions of the coiled coil in three-dimensions. Deviations from an artificial straight reference structure yielded a persistence length much the same as above (104 nm). However, deviations from a naturally curved superhelical tropomyosin yielded a more realistic value (423 nm) roughly ten times the length of an isolated tropomyosin (Table 1).

Table 1.

Flexibility of Wildtype and Mutant Tropomyosins

Tropomyosin sample examined	Persistence Length (free tropomyosin)	Average Motion (free tropomyosin) (0–20, 0–40 nm lengths)	Coulombic Interaction Energy (actin-tropomyosin)
Wildtype1	423 nm	18°, 25°	−3160 kcal
A74L-A78V-A81L1	238 nm	23°, 33°	--
D137L2	231 nm	23°, 33°	−2727 kca3

¹Data from Li et al (2010)

²Data from Moore et al (2011)

³New data from MD studies on actin-D137L tropomyosin (performed as previously [Li et al 2011; Lehman et al 2018])

Persistence length determination suggests that tropomyosin displacement at one point will be detected distally over considerable distances, thus facilitating systematic allosteric cooperativity in both off- and on-states. Thus, any mutation affecting tropomyosin persistence length may perturb cooperativity. Defective torsional patterning of the D137L mutant effects binding energetics of the corresponding actin-tropomyosin interaction.

The goal of our own current efforts has not only been to determine persistence length of isolated tropomyosin but also to work out the relationship of persistence length values to tropomyosin’s flexural behavior once on actin filaments. In this way we have aimed to account for the effect of myosin and troponin on tropomyosin in the course of its cooperative regulatory translations over actin filaments. Indeed, our previous structural evidence and experimental data from other groups have already suggested qualitatively that the effects of single myosin S1 heads or troponin complexes can cause concerted movement of head-to-tail linked tropomyosin molecules on actin, thereby affecting more than one thin filament regulatory unit (i.e. one seven actin subunit module of the thin filament linked to a single tropomyosin:troponin complex) (Vibert et al 1997; Regnier et al 2002; Maytum et al 1999; Mijailovich et al 2012; Desai et al 2015).

The persistence length measurements mentioned above define biomechanical material properties of the isolated tropomyosin coiled coil. Naturally, the flexural freedom of tropomyosin will be limited by intermolecular interactions with the actin surface once tropomyosin is located on thin filaments, thus complicating analysis. These potential protein-substrate interactions between tropomyosin and actin are not accounted for by persistence length measurement of the isolated molecule. Nevertheless, valuable conclusions can be inferred from these calculations, and in particular for M-state tropomyosin behavior. Here, actin - tropomyosin interaction is exceptionally weak and not likely to significantly affect biomechanical behavior (Orzechowski et al 2014b; Rynkiewicz et al 2015). Indeed, individual tropomyosin molecules localized over M-state positions on actin would dissociate from the filament surface unless they are contained within a polymerized cable which is hemmed in by occasional myosin heads. Although the directions of tropomyosin motion will be restricted by the presence of actin, the flexibility of tropomyosin will not be reduced meaningfully in an M-state environment.

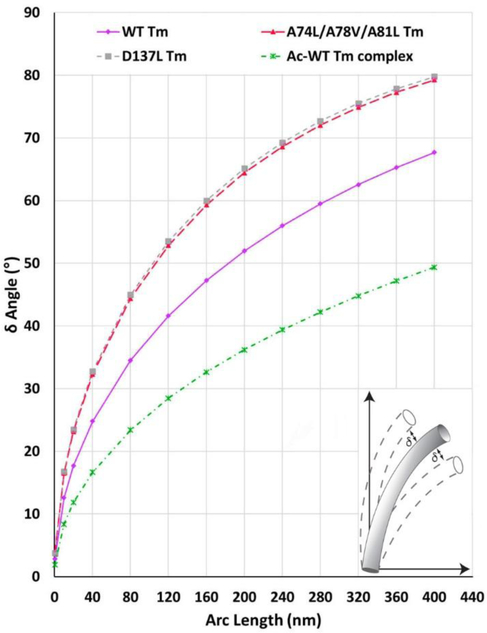
Consider a case in which a tropomyosin cable, initially oscillating about a ground state B- or C-position on regulated thin filaments, is pushed azimuthally by a single myosin head binding strongly at just one point on the filament, thus displacing tropomyosin locally from its starting location (see Fig. 2). This condition would, for instance, mimic the very onset of thin filament activation. At the point of contact, tropomyosin will be held over actin at an M-state location, while the extent of movement of the rest of the tropomyosin cable, following passively, will depend on the tropomyosin’s stiffness defined by its persistence length and by any interaction with actin substrate. Given the apparent lack of obvious interaction with actin, adjacent tropomyosin molecules linked head-to-tail on either side of the M-state displacement will of course also tend to move azimuthally, and thus in a concerted way toward the M-state position as well. However, since tropomyosin persistence length is finite, the adjacent molecules will not shift in perfect linear lock-step precision, and the translational correspondence will decay exponentially over the length of the cable. For instance for a 400 nm persistence length rod like tropomyosin, the average tangent angle deviation at roughly 40 nm away from the displacement (40 nm is the length of a single tropomyosin molecule) will be approximately ± 25° (δ angle in Fig. 3). This can be viewed as if, at a point 40 nm to either side of the perturbation, the tropomyosin cable fluctuates by 25° (roughly ± 17 Å) over the actin surface, leaving myosin-binding sites still fully or partially exposed and poised to interact with additional myosin heads. Hence, a single myosin molecule binding event, lasting about a millisecond in fast skeletal muscle (Marston and Taylor 1980; Siemankowski and White 1984, Finer et al 1994), and longer in slower muscles and non-muscle systems (Walcott et al 2012; Gunning and Manstein in this issue), will cause neighboring myosin binding sites on actin to open over a distance represented by one to two tropomyosin molecules up and down the filament over that time interval. The influence of myosin on tropomyosin position downstream would persist until the myosin head detaches. Therefore, additional myosin head(s) must bind in the opened stretch of the filament during this time in order for repositioning of tropomyosin to spread and cooperatively activate the filament further. Since many myosin heads, not just one, typically bind to thin filaments during muscle activation, they will prime the system collectively, namely the unmasking process will spread explosively during cooperative activation (Desai et al 2015), facilitating contractility in situ. Thus, both at qualitative and quantitative levels, our description of thin filament activation closely resembles ones based on experimental approaches and kinetic analysis of regulatory protein dynamics where the cooperative unit (i.e. one to two tropomyosins in length) is slightly greater than the regulatory unit itself (Vibert et al 1997; Maytum et al 1999; Smith et al 2003a, b; Mijailovich et al 2012; Desai et al 2015).

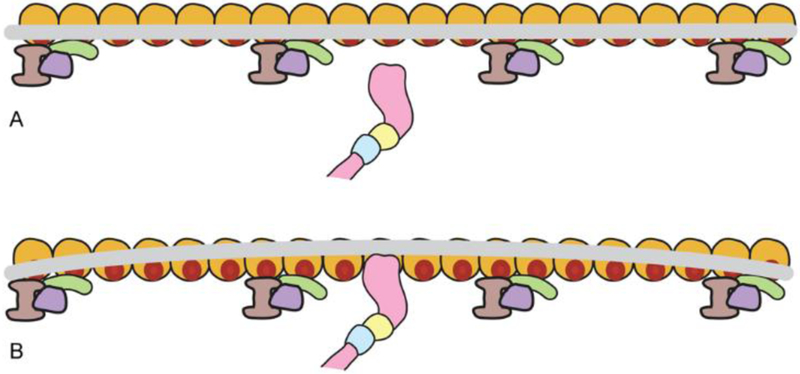
Figure 2. Tropomyosin response to myosin binding along F-actin.

Schematic representation of a single myosin head (pink) binding to an actin target site (red on gold actin subunit) along one chain of F-actin, moving the tropomyosin cable (grey) locally from the blocked (or closed) state position (panel A) to an M-state location (panel B)(single actin-tropomyosin strands shown for simplicity). Given tropomyosin’s stiffness, stretches of the tropomyosin cable close to the displacement will also move in tandem and expose additional myosin target sites on neighboring actin subunits (panel B). However, because tropomyosin is not a completely rigid rod, correlation between the initial displacement and any corresponding shift further along the coiled coil will diminish with distance. For example, at a point 40 nm from the myosin binding, tropomyosin’s position still will correlate with the initial displacement but, at this location, fluctuate back and forth by about ± 25° (see Fig. 3). The propagation of the myosin-induced repositioning will also be opposed by outlying troponin complexes (lavender, purple, green).

Figure 3. Tropomyosin flexibility.

The magnitude of isolated tropomyosin’s bending fluctuations during molecular dynamics simulations. Tropomyosin flexibility was assessed during MD by comparing the angular deflection (δ) of different length segments of individual tropomyosin coiled-coil conformers with their average conformation (Li et al 2010; Moore et al 2011) (see inset schematically illustrating δ for single conformers). The extent of the angular deflections along tropomyosin will increase exponentially at increasing distance from a fixed point. In the plots presented, normalized bending fluctuations of tropomyosin at any arc length away from a fixed displacement (0 nm on plot) are defined by the relationship, $cos<\delta >=e^{-\left(\frac{L}{P}\right)}$, where L is segment length and P is the persistence length of either control or mutant tropomyosins (Table 1). Displayed are plots of wildtype tropomyosin (magenta circles) as well as mutant D137L and A74L/A78V/A81L tropomyosins (grey square and red triangles, respectively). Note the increased slope of the mutant tracings indicating enhanced average flexibility compared to wildtype. For example, at a distance of 20 nm from the origin reference point, mutant tropomyosins fluctuate by almost as much as wildtype tropomyosin at 40 nm. Also note that once linked to F-actin, tropomyosin fluctuations in the blocked-state configuration (green) are, as expected, diminished. In this case, δ, was calculated from MD simulations of the actin-tropomyosin complex (Li et al 2011; Lehman et al 2018).

Thin filament activation of course is multi-factorial and the above analysis was deliberately simplified in an attempt to understand basic elements of the process. We have not accounted for limited motion of tropomyosin toward or away from the actin surface. In addition, our treatment does not address the “tug-of-war” influencing tropomyosin’s azimuth when a segment of the tropomyosin cable bridges between M-state (“pushing”) and B-/C-state (“pulling”) configurations distant to a myosin head binding event (see Fig. 2). In addition, the cooperative unit size may be abbreviated in a troponin I inhibited thin filament at low-Ca²⁺ and restored following troponin I release during activation, consistent with biochemical kinetics that suggests a cooperative unit of 7 successive actin subunits for relaxed filaments and 11 for activated ones (Regnier et al 2002). Moreover, any potential direct interaction of tropomyosin and myosin amplifying the cooperativity has not been factored into our analysis (Lehrer 1994, 2011; Lehrer and Geeves 2014).

Tropomyosin motions in the B-state configuration

No doubt the fidelity of troponin-tropomyosin induced steric blocking of thin filaments in the low-Ca²⁺ relaxed-state also will depend on tropomyosin stiffness and its electrostatic interactions with actin. In a hypothetical case in which the tropomyosin cable is pinned down on actin by a single Ca²⁺-free troponin complex now in a B-state configuration (analogous to the above myosin-trapped M-state representation), adjoining tropomyosin segments to the side of the affected tropomyosin likely will also be biased to the B-state positioning. Judging from the green tracing on Figure 3, actin-associated tropomyosin segments at a distance of about ± 20 nm from the troponin trap will also localize to a B-state positioning, and, on average, deviate from the displacement only slightly by ~ ± 12°, remaining primarily in a myosin blocking configuration. In contrast, at a distance of 40 nm from the trap, tropomyosin can easily pass back and forth across actin to the C-state location, where steric inhibition will diminish. It follows that regulation will be most effective with troponin localized on each tropomyosin at 40 nm intervals (i.e. twice 20 nm) as observed, and that in this instance the cooperative unit size and the regulatory unit size are the same. The results described here also demonstrate that electrostatic interactions between tropomyosin and actin will tend to reduce fluctuations of tropomyosin when compared to motions noted for the isolated free molecule, as expected (compare green and magenta tracings in Figs. 3). We conclude that favorable electrostatic interactions between actin and tropomyosin in B-state filament configurations in effect reduce tropomyosin motion, diminishing local opening of myosin binding sites on actin.

Our analysis of molecular dynamics simulations also demonstrate that while isolated tropomyosin flexes in all directions, its motions are biased out of plane relative to its inherent curvature (akin to the flexing of an index finger) (Fig. 4A, blue). However, once wrapped around actin in B-/C-state configurations, flexing is diminished (Fig. 4A, red). In plane, non-isotropic motions now dominate, reflecting the azimuthal bias of the tropomyosin fluctuations (akin now to waving an index finger side to side). The analysis also shows that during the 30 ns of MD monitored, concerted pseudorotation (rolling) of tropomyosin on actin does not occur.

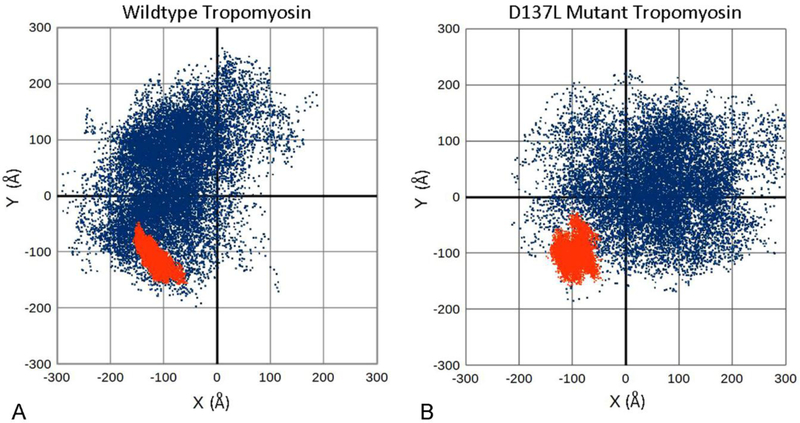
Figure 4. Anisotropic bending of tropomyosin during MD.

A, B. x, y coordinates of the C-terminal positions of tropomyosin conformers during MD, plotted following alignment of the first 28 N-terminal residues along the z-axis. Here, each point represents the C-terminal position of an individual conformer taken during MD, projected onto a plane perpendicular to the z-axis of tropomyosin. The C-terminus of a perfectly straight, inflexible rod would plot to the 0,0 coordinate position. In contrast, a straight flexible rod displaying isotropic uniform bending would plot as a symmetrical circle of dots around the 0,0 coordinate position. A flexible rod displaying anisotropic, preferential bending would be biased to one or another x, y quadrant and plot accordingly. A. During MD, the motions of isolated wildtype tropomyosin (blue dots) are anisotropic, reflecting an out-of-plane bending bias of the coiled coil. The motions of actin-associated tropomyosin (red dots) are more limited in direction. Here, both the magnitude and the direction (largely azimuthally and in plane) of the fluctuations are damped out by actin interaction. B. Motions of isolated D137L mutant tropomyosin (blue dots) are considerably less anisotropic, reflecting the relatively straight tropomyosin conformation, and consistent with the increased global flexibility of the mutant. The motions of actin-associated D137 tropomyosin (red dots) now show biphasic anisotropy as the mutant adapts to the F-actin helix during MD while clinging to the actin surface. Data presented calculated from coordinates in Li et al (2010, 2011) and Lehman et al (2018) and from new MD studies on actin-D137L tropomyosin (performed as previously) (Li et al 2011; Lehman et al 2018).

Structural nuances, not flexible sequences

Striated muscle tropomyosin may have been among the first coiled coils to be described, but it is not a textbook case with perfectly laid out heptad repeating structure (Fig. 1). For example, in an idealized coiled coil, branched hydrophobic residues (leucine, isoleucine, valine) normally occupy all first and fourth heptad residues (i.e. in “a” and “d” positions”). The nonpolar amino acids generate a continuous “hydrophobic stripe” forming the core of the coiled coil which zippers component α-helices together (Fig. 1). In the case of tropomyosin, small sized alanine residues, in place of more characteristic larger hydrophobic amino acids such as leucine, isoleucine and valine, are found clustered together in six or seven patches along tropomyosin’s hydrophobic stripe (Fig. 1) (Conway and Parry 1990; Brown et al 1996, 2001, 2005; Brown and Cohen 2005). In addition, a charged “d”-position aspartate and “a”-position glutamate are located at sequence points normally occupied by core hydrophobic residues. Speculation that alanine clusters and the anomalous charged core residues enhance local flexibility or otherwise destabilize local tropomyosin structure reflects a view that some degree of specific flexural freedom is necessary to cast tropomyosin to the surface of actin as the proteins adapt to each other (Sumida et al 2008; Hitchcock-DeGregori 2008; Minikata et al 2008; Moore et al 2011; Yar et al 2013; Shchepkin et al 2013; Zheng et al 2013, 2016; Matyushenko et al 2014, 2018). Such local flexibility might be averaged out and remain unaccounted for in calculation of persistence length. Still, any significant tropomyosin flexibility would tend to decrease tropomyosin-linked cooperative movement. Unlike often cited views on tropomyosin behavior, we instead suggest that anomalous core interactions do not themselves translate into identifiable tropomyosin bending flexibility, but rather that they facilitate preshaping the tropomyosin strand to match to the actin filament helix and make corresponding proper intermolecular residue-residue contacts.

Alanine clusters

In marked contrast to the heptad pattern of most coiled coils, alanine is the most prevalent residue at tropomyosin’s d-heptad positions (Conway and Parry, 1990) (see Fig. 1). Normally alanine functions to destabilize coiled coils, which is associated with increased temperature sensitivity to thermal denaturation (Kwok and Hodges, 2004). In fact, selective alanine to leucine substitution protects the coiled coil against thermal denaturation, consistent with a possible hyper-stiffening effect. Alanine clusters are known to cause a slight staggering of core residues resulting in a gently curved rather than straight structure (Brown et al 1996, 2001, 2005; Brown and Cohen 2005). Consequently, tropomyosin constructs with selective alanine to leucine substitutions also display diminished binding affinity to F-actin when assessed by cosedimentation. Taken together, the data suggest an induced fitting scheme in which proper tropomyosin binding to actin requires selective and localized alanine-induced instability to promote coiled-coil flexibility and actin-binding (Singh and Hitchcock-Degregori 2003, 2006; Hitchcock-DeGregori 2008).

Brown and Cohen (2005) challenged this view and proposed that the alanine clusters of tropomyosin serve a specialized and dedicated function, namely they perturb typical coiled-coil knobs-into-holes patterning. Coiled-coil bending results and is thought to shape the elongated molecule into a gently curved superhelix with contours faithful, on average, to those of the actin filament helix (Brown and Cohen 2005; Brown et al 2001, 2005). Local and global shape complementarity between tropomyosin and actin filaments is likely to facilitate form-fitting of tropomyosin to actin during filament assembly. Our molecular dynamics confirmed that the alanine clusters set a tropomyosin global curvature that is well matched to the helical surface of actin filaments (Li et al 2010, 2011). Brown and Cohen took the possible disconnect between intrinsic curvature and curvature variation (flexibility) a step further and examined temperature factor benchmarks of a tropomyosin crystal structure with particularly excellent crystallographic statistics (Brown et al 2001). As a measure of local protein fluctuation in the crystal structure, temperature factors for the alanine cluster of interest and residues quite distant to the cluster were comparable; therefore the cluster did not appear to be disproportionately flexible. The lack of temperature factor-linked extra flexibility is not limited to one specific alanine cluster but common to those in other regions of the striated muscle tropomyosin isoform (cf. statistics of pdb 1IC2, 2B9C, 2D3E) and also prevails in non-muscle Tpm3.1 tropomyosin (Ghosh et al 2019). Our MD work also shows that the clusters are not themselves particularly flexible (Li et al 2010), consistent with the above observations.

Brown and Cohen (2005) emphasized that the distinctive packing of residues abutting alanines likely compensates for any local cluster-imposed instability. They concluded that ‘core alanines can by specific design promote the winding necessary for tropomyosin’s interaction with actin’ (Brown and Cohen 2005). Brown and Cohen’s conclusions ring true judging from our own in silico work showing that, on average, snapshots taken from molecular dynamics simulations of tropomyosin are gently curved with a shape mimicking that of the F-actin helix (Li et al 2010; Sousa et al 2010). Strikingly, MD shows that substitution of just one alanine cluster with canonical residues markedly straightens tropomyosin (Fig. 5C) (also see Li et al 2010). Further analysis of the dynamics of the alanine-deficient construct during simulation reveals that its persistence length is diminished compared to wildtype, namely the construct is more flexible (Li et al 2010) not stiffer than native tropomyosin, as previously proposed (Hitchcock-DeGregori 2008) (Table 1). We in turn conclude that the high entropic cost of reining in overly flexible alanine-deficient tropomyosin mutants is responsible for its functional deficits, explaining the decreased apparent binding affinity to actin without having to invoke induced fitting paradigms. Of course, once bound to F-actin, aberrantly flexible tropomyosin would be expected to diminish cooperative high-Ca²⁺-linked activation as well as low-Ca²⁺-linked relaxation.

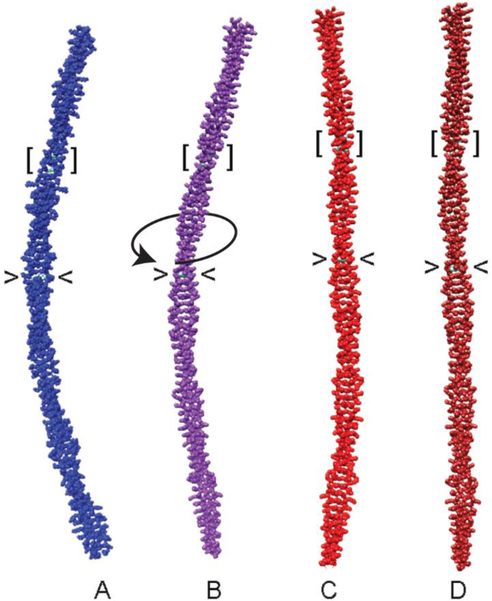
Figure 5. Mutation straightens tropomyosin.

(A) Canonical model of tropomyosin with idealized coiled-coil symmetry (Lorenz et al 1995). Average structures during MD simulations of (B) wildtype tropomyosin, (C) A74L-A78V-A81L, and (D) D137L mutant tropomyosins. The position of residues 137 (angle brackets) and 74, 78 and 81 (square brackets) are indicated. Over-twisting of tropomyosin initiated near to residue 137 is indicated by a curved arrow in panel B. Note the gentle bend of the wildtype coiled coil (B) and the straightening of the mutant coiled coils (C, D). Also note that localized substitution of critical residues has delocalized global effects on tropomyosin structure. Figure generated from coordinates in Li et al (2010) and Moore et al (2011).

Aspartate 137

As mentioned, a charged aspartate, instead of a non-polar residue, is located at a d heptad position midway along the tropomyosin hydrophobic stripe. The non-canonical d-position residue is a distinctive feature of tropomyosin and is conserved among all muscle and non-muscle vertebrate tropomyosin isoforms examined; thus, in this instance, evolutionary selection pressure is not conditional. Crystal structures of tropomyosin show that the aspartate and surrounding residues prop open the component helices of the coiled coil locally, while the charged aspartate side chains extend away from the tropomyosin core (Brown et al. 2005, Lehman et al 2018). Sumida and Lehrer (Sumida et al 2008) showed that native tropomyosin is cleaved rapidly at residue 133 by trypsin, but not when the aspartate is replaced by a canonical leucine in engineered tropomyosin constructs. The results suggest that local instability or untwisting of helices surrounding residue 137 is responsible for the susceptibility to proteolysis. Moreover, binding of tropomyosin to F-actin suppresses the proteolysis, implying that either the cleavage site is masked by interactions with the actin surface or that local conformation of tropomyosin itself is changed when bound to actin. Subsequent work (Shchepkin et al 2013; Matyushenko et al 2014, 2018; Scellini et al 2017) has also shown that leucine substitution for the noncanonical aspartate increases the temperature at which thermal denaturation of tropomyosin occurs, as if tropomyosin becomes stiffened at a possibly flexible point near to D137 through mutation. Similar behavior is observed when several of the supporting residues juxtaposed to aspartate 137 are mutated (ibid.). Taken together, domain-specific tropomyosin flexibility linked to D137 fragility was proposed to temper tropomyosin stiffness and thereby fine tune regulatory switching (Sumida et al 2001). We regarded this interpretation as premature. We indicate below that D137, like alanine clusters, fulfills vital functions apart from the often proposed structural modulation via increased flexural variance.

Extensive molecular dynamics has been performed on full-length wildtype tropomyosin and on D137L mutants, both under actin-free and actin-associated conditions (Moore et al 2011; Lehman et al 2018). Contrary to expectation, MD trajectories show little indication of disproportionate enhanced bending flexibility at or near D137 in the wildtype molecule; in fact, residues immediately surrounding D137 (I130-M141) in the central tropomyosin pseudo-repeat 4 show minimal bending flexibility when compared to the rest of the coiled coil. Indeed, the local rigidity centered on D137 actually exceeds that of virtually all parts of the native molecule (ibid.). Paradoxically, we and others have shown that replacing D137 with more canonical L137 does stiffen tropomyosin at a local level even further, as if the most rigid part of the native coiled coil is still spared biomechanical extremes imposed by an L137 mutation. We also have found that d-position aspartate-137 adjusts tropomyosin twist modulus by stiffening, not reducing, tropomyosin rigidity once the coiled coil is bound to actin filaments (Lehman et al 2018).

We conclude that the presence of alanine residues in “a”- or “d”-positions and the aspartate 137 at a “d”-position do not impart greater flexibility to the coiled coil structure of tropomyosin, as one might expect at first glance. Rather, they seem to play a critical role in the shaping of the tropomyosin into a discreet structure that accommodates to the actin filament. The role of “a”-position glutamate 218 is unclear, but MD indicates that it as well is not an obvious primal seat of enhanced flexibility. Thus when considering the behavior of tropomyosin, we follow the Jeff Bezos dictum to be “stubborn on vision” but “flexible on details.…” (quote from the Amazon.com shareholder meeting, June 7, 2011). The “vision” is that cooperative translation of tropomyosin across the thin filament regulates muscle contractility. Still, often buried in the details is an underappreciation of tropomyosin’s nuanced structural idiosyncrasies. While anomalies in tropomyosin need to be explained, they do not necessarily equate to physical flexibility.

The twisting of rope: Casadh an tSúgáin

A rope can be constructed by first wrapping component strands round each other in one direction and then tightened by twisting in the opposite (Hunt 1912); Gaelic song-writers understood this concept well.

Recent tropomyosin molecular dynamics simulations suggest that previously unrecognized coiled-coil twist-variance, quite distinct from frequently invoked flexural anomalies, is critical for thin filament function (Lehman et al 2018). The seemingly deviant aspartate residue 137 appears to play a central role in initiating or facilitating hyper-twisting of the tropomyosin on F-actin, possibly accounting for the baffling results discussed above. Subtle cumulative over-twisting of actin-bound tropomyosin begins near to residue D137, and the structure of tropomyosin then deviates from idealized coiled-coil symmetry (Fig. 6). The extra twisting is likely to favor more perfect alignment of tropomyosin side chains with actin residues 326 and 328, enhancing B-/C-state stability (Lehman et al 2018). The hyper-twisting is also associated with an increase in the stiffness of tropomyosin hovering over actin-filaments (Lehman et al 2018); any D137 sponsored instability or unrecognized flexibility measured for isolated tropomyosin now no longer seems strictly pertinent to characterizing the assembled thin filament.

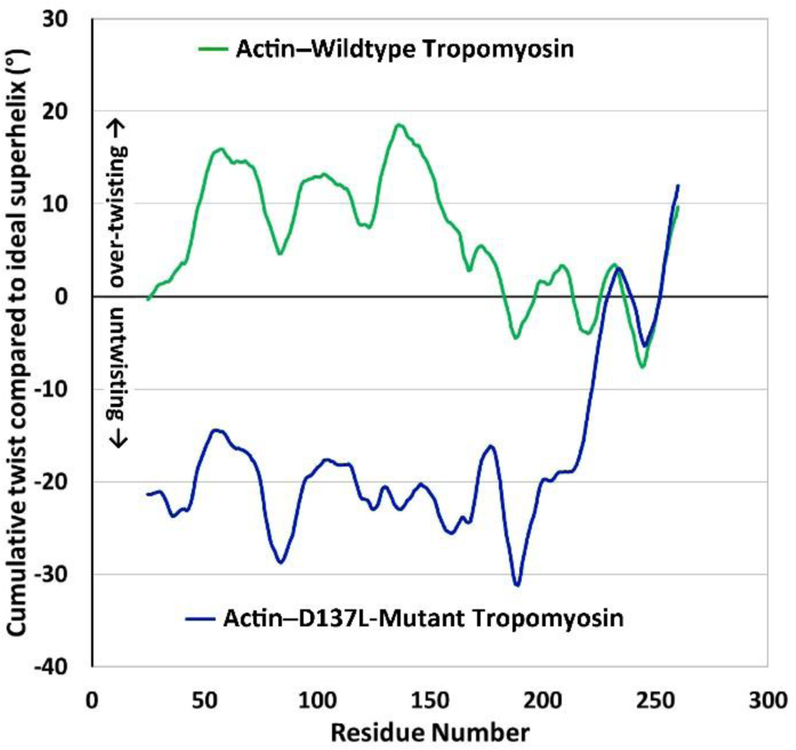
Figure 6. Tropomyosin twisting on actin during MD.

Plots show the cumulative twist angle deviation from an idealized tropomyosin superhelical model, generated as described previously (Lehman et al 2018). The twist behavior of wildtype tropomyosin on actin (upper green curve) is compared to the twist behavior of D137L tropomyosin on actin (lower blue curve). In the wildtype, note that over-twisting begins near to residue 137 and gradually declines over about 40 residues towards the tropomyosin C-terminus. Also note that periodic twist undulations, roughly 40 residues apart, reflect the presence of alanine clusters (Li et al 2010; Lehman et al 2018); panel A adapted from Lehman et al (2018)). In contrast, D137L mutant tropomyosin shows an absence of cumulative twisting and irregular alanine cluster based twisting undulations.

Any mechanism leading to enhanced and localized tropomyosin stiffness on actin filaments including over-twisting is expected to increase the fidelity of the regulatory on-off switching apparatus, enlarge the size of its corresponding cooperative unit, and promote relaxation kinetics following release of myosin from actin. In addition, twisting dependent optimization of actin-tropomyosin side-chain orientation may also increase the stability of the actin-tropomyosin B-/C-state energy basin and facilitate filament assembly.

Unintended consequences

Holmes and Lehman (2008) pointed out that reductionist structure/function approaches applied piecemeal to the study of single tropomyosin residues or to individual pseudo-domains ignore “emergent” characteristics of the molecule as a whole. We and others (Tardiff 2011; McConnell et al 2017) now recognize that individual segments of tropomyosin influence each other as part of a complex structural continuum. Hence, local experimental perturbation may have the intended site-specific effects, but unpredicted ones elsewhere.

Arguably, the Holmes-Lehman point of view is best illustrated by examining the D137L mutation further. For example, the expected regional hyper-rigidity in pseudo-repeat 4 induced by the mutation is compensated by a delocalized diminution in overall global stiffness, namely, the rest of the D137L coiled coil becomes more flexible, not stiffer, than control tropomyosin (Moore et al 2011) (see Table 1, Fig. 4). At the same time, tropomyosin is globally straightened by the D137L point mutation (Fig. 5) and hence loses its native average super-helical twist, confounding corresponding functional attributes of the mutant construct. Still, D137L is capable of binding to F-actin presumably because of its extra global flexibility and unaffected head-to-tail polymerization. Given the numerous structural adjustments, it is difficult to rationalize the complex physiological responses to the D137L alteration. Simply put, the aspartate to leucine mutation seems to be following the law of unintended consequences, in this case multiple unintended consequences resulting from a seemingly simple single perturbation. Indeed, tropomyosin has had many millions of years to evolve an optimal configuration, while remaining remarkably conserved among vertebrate examples; sometimes plodding along by trial and error, evolutionary choices appear to have outdone the cleverest of experimental design. Not surprisingly, there are no known inherited cardiomyopathies linked to D137, despite its being conducive to functional plasticity.

Dis-torsion

A large number of tropomyosin mutations lead to regulatory dysfunction presaging human disease (Kee and Hardeman, 2008, Tardiff, 2011; Bai et al 2013; Memo and Marston 2013; Redwood and Robinson, 2013). Not all the mutations can be logically attributed to the protein’s frequently professed flexural anomalies. As an alternative, we propose that torsional disparities should be considered as an alternative paradigm in these cases. The reason for this opinion becomes evident when, once again, comparison is made between wildtype thin filaments and ones containing the D137L mutation. Normally, over-twisting initiated at aspartate 137 and surrounding amino acids reorients D138, D139 and D142 in tropomyosin pseudo-repeat 4 to optimally contact charged K326 and K328 residues on F-actin (Lehman et al., 2018). The effect then propagates along the N-terminal half of tropomyosin, as if D137 elicits global shape modulation. In marked contrast, molecular dynamics trajectories of actin-D137L tropomyosin filaments show that the mutation corrupts the standard over-twisting pattern (Fig. 6). As a consequence, the D137L structure must compensate to best fit to actin, albeit at significant energetic cost (Table 1). Indeed, functional assays performed indicate that the presence of D137L may interfere with normal cooperative activation of thin filaments (Sumida et al 2008; Matyushenko et al 2014) and slow muscle relaxation (Scellini et al 2017). We expect tropomyosin dysfunction linked to other mutations will be attributed to coiled-coil twisting anomalies.

Conclusions

Steric regulation of thin filament activity involves tropomyosin translocating between blocked, closed and open B-, C-, and M-state positions on actin. In the B-state, tropomyosin is trapped by troponin I in a location that blocks myosin-binding, whereas in the C-state the troponin-imposed pinning action is released, and myosin heads bind to actin and move tropomyosin to the open M-state. Molecular dynamics simulations carried out in silico provide a reliable means to determine both local and global stiffness of tropomyosin, key factors determining the cooperative spread of activation and inhibition over the actin filament. MD indicates that tropomyosin has significant global stiffness associated with high persistence length values, and the coiled coil shows no obvious signs of local or periodic enhanced flexibility. Indeed, predictions based on tropomyosin persistence length measurements indicate that the tropomyosin-dependent spread of cooperative activation and inhibition are in good agreement with experimental estimates of thin filament cooperative unit size.

We suggest that core sequence anomalies distinguishing tropomyosin from canonical coiled coils provide shape and charge complementarity between tropomyosin and the actin surface on thin filaments. We do not consider the alanine clusters and charged residues located along the tropomyosin hydrophobic stripe to be hotspots of tropomyosin flexibility, as previously proposed. On the contrary, we regard potential significant flexural flexibility of tropomyosin or ostensible flexible-fitting between actin and tropomyosin as impediments to cooperative tropomyosin translocation between regulatory states which might even render corresponding energy barriers impassable.

Holmes and Lehman (2008) envisioned a rather simple structure-function relationship that they named Gestalt-binding in which the sequence of tropomyosin biases the coiled-coil structure to mimic the shape of the actin helix and ‘allow the protein to work as part of an unbroken cooperative system’. We now have extended this view by positing that the tropomyosin coiled coil displays unbroken mechanical continuity well adapted to cooperative transitions between regulatory states. We also hold that the Gestalt of the thin filament system as a whole must first be accounted for before attempting to determine ‘how the individual parts behave’. Finally, our work reinforces the dictum that ‘tropomyosin is a specialized and deceptively ‘simple’ molecule’ (Brown and Cohen, 2005).