Abstract
Protein-mediated membrane remodeling is a ubiquitous and critical process for proper cellular function. Inverse Bin/Amphiphysin/Rvs (I-BAR) domains drive local membrane deformation as a precursor to large-scale membrane remodeling. We employ a multiscale approach to provide the molecular mechanism of unusual I-BAR domain-driven membrane remodeling at a low protein surface concentration with near-atomistic detail. We generate a bottom-up coarse-grained model that demonstrates similar membrane-bound I-BAR domain aggregation behavior as our recent Mesoscopic Membrane with Explicit Proteins model. Together, these models bridge several length scales and reveal an aggregation behavior of I-BAR domains. We find that at low surface coverage (i.e., low bound protein density), I-BAR domains form transient, tip-to-tip strings on periodic flat membrane sheets. Inside of lipid bilayer tubules, we find linear aggregates parallel to the axis of the tubule. Finally, we find that I-BAR domains form tip-to-tip aggregates around the edges of membrane domes. These results are supported by in vitro experiments showing low curvature bulges surrounded by I-BAR domains on giant unilamellar vesicles. Overall, our models reveal new I-BAR domain aggregation behavior in membrane tubules and on the surface of vesicles at low surface concentration that add insight into how I-BAR domain proteins may contribute to certain aspects of membrane remodeling in cells.
Significance
Our study aims to understand inverse Bin/Amphiphysin/Rvs (I-BAR) protein organization at realistic lower surface coverage before large-scale deformation and how existing global curvature affects organization. First, we model I-BAR protein assembly on tubular and vesicular membranes using coarse-grained models. Our separate bottom-up and top-down models both show that I-BAR domains form local deformations that couple to the global membrane curvature to form long axial aggregates tubules and end-to-end rings on small vesicles. Second, we observe novel membrane remodeling behavior of the I-BAR domain of IRSp53 in in vitro fluorescence experiments showing that the I-BAR domain forms rings around lipid bilayer deformations. Together, we experimentally observe a new I-BAR-driven remodeling phenomenon on vesicles and provide a potential explanation using our coarse-grained models.
Introduction
The cell membrane is composed of a variety of lipids, proteins, and small molecules and creates a barrier between the inner workings of the cell and the extracellular matrix. This complex barrier is a highly dynamic surface that typically prefers to be locally flat. Throughout many biological processes, large deformations are required, and peripheral membrane proteins facilitate this ubiquitous process. A variety of proteins bind to the membrane and generate membrane curvature. One such family of proteins that cause large-scale deformation through cooperative action is the Bin/Amphiphysin/Rvs (BAR) domain superfamily. BAR domains are banana-shaped homodimers known to bind to lipid bilayers and generate curvature through electrostatic interactions and, in some cases, amphipathic helical insertions into the membrane (1, 2, 3). BAR domains have diverse functionality because each member of the superfamily generates a variety of positive or negative curvatures.
IRSp53 is a member of the inverse BAR (I-BAR) domain family of the BAR domain superfamily. These proteins generate negative principal curvature and are key to the formation of cellular protrusions (e.g., filopodia) (4, 5, 6, 7). I-BAR domains are proposed to act through a scaffolding mechanism that generates local curvature on lipid membranes, leading to I-BAR domain aggregation and subsequent formation of microns-long protrusions (8, 9, 10, 11). Interestingly, in vitro experimental data regarding the I-BAR domain of IRSp53 have indicated a preference for low curvature commensurate with its intrinsic curvature (12). The aggregation and collective behavior that drives membrane deformations, and potentially gives rise to sorting in membrane tubules, is therefore of significant biological interest.
I-BAR domains have been the subject of several computational and theoretical studies (13, 14, 15, 16, 17), with varying degrees of accuracy. I-BAR domain-mediated membrane remodeling spans many length scales, from nanometer-scale local interactions between individual I-BAR domains and lipid headgroups to the micron-scale deformations collectively induced by many I-BAR domains. The multiscale nature of membrane remodeling has led to a range of studies from recent atomistic simulations exploring the behavior of small I-BAR domains with relatively high accuracy to simulations modeling the collective effects of tens of I-BAR domains at the mesoscale. However, these previous studies lack the connection and correspondence between the two scales; this disparity could result in coarse-grained (CG) or mesoscopic models that are inconsistent with atomistic simulations (18). For example, CG simulations can assume that membrane-bound I-BAR domains have the same intrinsic curvature as the crystal structure, but recent all-atom simulations show that the curvature of an I-BAR domain decreases (i.e., I-BAR domain flattens) when bound to the membrane (17). Assumptions like this can cause disagreement between the all-atom and CG resolutions, resulting in different mechanisms of membrane remodeling.
Here, we use a multiscale approach combining CG and mesoscopic models (specifically, Mesoscopic Membrane with Proteins (19) [MesM-P]) to understand the organization of I-BAR domains on membranes of various geometries (18). This multiscale approach is uniquely suited to capture protein-mediated membrane remodeling because it incorporates the interplay between near nanometer to several micron-length scales. Broadly speaking (18), CG models can be derived from finer resolution, atomistic simulations (bottom-up), or by specifically reproducing experimental observables (top-down). Here, the former approach is adopted such that our protein CG model reproduces structural fluctuations observed in atomistic simulations, whereas our lipid CG model recapitulates the properties of a representative lipid bilayer membrane. Additionally, the MesM-P model, which is a lower resolution than the CG model, can be used to simulate significantly larger systems while remaining consistent with the membrane-bound protein aggregation behavior of our CG model. Together, these models span near atomistic to mesoscopic length scales, and the agreement of the two models (parameterized using separate methodologies) indicates the robustness of the CG phenomena we observe. We apply these models to understand the aggregation behavior of I-BAR domains on flat sheets that mimic the surface of giant unilamellar vesicles (GUVs), membrane tubules, and spherical membrane vesicles. We focus primarily on lower density surface coverage.
Our results show that both I-BAR domain models form local membrane troughs on flat sheets, and when I-BAR domains are on membranes with global curvature, the I-BAR domains orient to minimally perturb the membrane. We predict tip-to-tip string aggregates in tubule-shaped membranes and rings at the base of bulges on the surface of vesicles. Although the CG lipid and MesM-P models bear some differences, the behavior observed using the two models (each consistent with biologically relevant properties) is qualitatively similar. Both models show qualitatively similar behavior on surfaces with positive Gaussian curvature, providing a consistent mechanism for the formation of novel, low curvature deformations surrounded by I-BAR domains on GUVs.
Materials and Methods
CG model details
The model consists of two components: a highly CG lipid bilayer and a CG IRSp53 I-BAR domain as shown in Fig. 1 A. The highly CG lipid bilayer was parameterized using a hybrid multiscale coarse-graining approach. The hybrid parameterization supplemented multiscale coarse-graining forces from atomistic simulations with analytical CG potentials to describe the short-range interactions, which has been described previously (20). The CG model was simulated in the Large-scale Atomic/Molecular Massively Parallel Simulator simulation engine (21).
Figure 1.
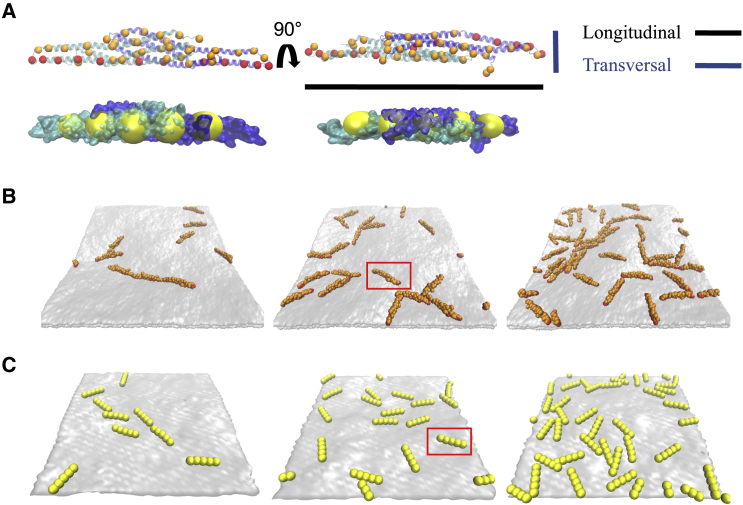
Side-by-side image of CG and MesM-P models, snapshots of flat sheet configurations. (A) Shown are the side (left) and top (right) view of an overlay of CG I-BAR domain (orange, red) and the secondary structure of each monomer (cyan and blue) and an overlay of MesM-P I-BAR domain (yellow) and a space filling representation of each monomer. The attractive and excluded volume CG beads colored in red and orange, respectively, are shown, along with the definition of the longitudinal and transversal dimensions of the I-BAR domain. (B) Shown is a snapshot of 5, 10, and 20% coverage of a 100 nm by 100 nm flat sheet with single I-BAR domain highlighted with a red box. (C) Shown are MesM-P snapshots of 5, 10, and 20% coverage of a 100 nm by 100 nm with a single I-BAR domain highlighted with a red box. To see this figure in color, go online.
The CG IRSp53 I-BAR domain model was parameterized from atomistic simulation to reproduce the atomistic structure fluctuations (e.g., intrinsic curvature fluctuations), which we expect to be critical to the membrane remodeling process. The atomistic simulations were composed of a lipid bilayer, IRSp53 I-BAR domain (Protein Data Bank: 2YKT (22)), and water using the CHARMM36 force field (23, 24, 25). The initial configuration of the membrane was first generated from Chemistry at Harvard Macromolecular Mechanics – Graphical User Interface (26, 27, 28, 29, 30) and equilibrated using the corresponding scheme and the Groningen Machine for Chemical Simulations simulation engine (31). The membrane was composed of 75% 1,2-dioleoyl-sn-glycero-3-phosphocholine, 20% 1,2-dioleoyl-sn-glycero-3-phosphoserine, and 5% phosphatidylinositol-4,5-diphosphate (PI(4,5)P2). Then, the I-BAR domain was added to the simulation cell, and the hydration layer was increased with 150 mM NaCl using Groningen Machine for Chemical Simulations tools (31). The I-BAR domain was simulated with the membrane for 300 ns, and the final 100 ns were used to determine the mapping and parameterization of intraprotein forces. The map from atomistic to CG was found using essential dynamics coarse-graining (32), which divides the protein along its primary sequence. The essential dynamics coarse-graining protocol map is determined by finding divisions in the primary sequence that preserve the dynamics of the protein (i.e., the large amplitude motions within a CG bead are minimized, and the motion between beads are maximized). The divisions in the primary sequence are given in the Supporting Materials and Methods. Effective harmonic potentials were used for intraprotein interactions, with the parameters determined using a heterogeneous elastic network model (33). The spring constants and equilibrium distances are fit to reproduce the mapped structure and fluctuations from an atomistic molecular dynamics trajectory and are provided in the Supporting Materials and Methods.
The direct protein-protein interactions were purely repulsive to capture the excluded volume of each I-BAR domain. Additional screened electrostatic interactions between I-BAR domains were investigated in the Supporting Materials and Methods and reinforce the aggregation behavior due to purely membrane-mediated attraction. The effective potential between the CG beads of the protein and the headgroup beads of the CG lipids was modeled as a 10-6 shifted force Lennard-Jones potential (34). At the CG resolution, the effective potential between the protein and lipid membrane is, by its nature, a simplification of the complex electrostatic interactions at the atomistic protein-membrane interface and is meant to capture the local membrane deformation driven by an isolated, atomistically resolved I-BAR domain (17). As further mechanistic studies of local membrane deformation by I-BAR domains are performed, the CG interactions could be refined to better reproduce the complex nature of membrane remodeling. Without an exhaustive study of I-BAR domain membrane remodeling at a finer resolution, the effective attraction strength was taken as a parameter, and its effect on local deformation was quantified by a comparison to previous atomistic simulations (17).
Mesoscopic membrane simulations with explicit proteins
Here, we used a reduced and scaled-down version of the recent MesM-P model (19) that relies on a discretized formulation of membrane elastic theory (35). In the original model, the membrane is represented as a collection of quasiparticles ∼7 nm in diameter. Each quasiparticle describes a patch of lipid bilayer given its position and momentum with additional scalar fields to represent local protein concentration and lipid composition. As a result, MesM-P allows for efficient modeling of large-scale membrane shape changes, protein binding and unbinding, and their interplay on nearly experimental length and timescales (19).
In this work, we use only the elastic component of the MesM-P model that describes three-dimensional membrane undulations and bending (i.e., without using mesoscopic solvent or implicit variables describing the local protein concentration and lipid composition). Instead, we use an approach similar to the CG model and include explicit very highly CG representations of I-BAR proteins, which are modeled as five-bead linear chains with varied sizes shown in Fig. 1 A. The size variation of the beads is included to, in part, reproduce the shape of an I-BAR domain. For the membrane, we also use smaller sized beads of ∼3 nm, which is consistent with the width of I-BAR. We have used Lennard-Jones-like shifted force 4-2 potentials for membrane-protein interactions with various strengths (34). The MesM-P model was simulated in the Large-scale Atomic/Molecular Massively Parallel Simulator simulation engine (21).
The final set of simulations utilizes a guiding potential to replicate membrane configurations seen in the in vitro experiments. The flower petal structure in the latter (see Results) is likely caused by I-BAR domain-driven membrane remodeling. This full phenomenon is not observable with the MesM-P model due to the use of periodic boundaries to describe the surface of a GUV. Instead, the flat sheet is deformed using a spherical guiding potential. The membrane is initially flat, and the guiding potential is moved toward the surface to create a membrane deformation similar to the deformations made by CG I-BAR domains on small vesicles and the accompanying in vitro experiments.
More details and the parameters of each computational model are given in the Supporting Materials and Methods.
Reagents
Total brain lipid extract (131101P), brain L-α-PI(4,5)P2 (840046P), and 1,2-distearoyl-sn-glycero-3-phosphoethanolamine-N-[biotinyl(polyethyleneglycol)-2000] (880129P) were purchased from Avanti Polar Lipids (Alabaster, AL). BODIPY-TR-C5-ceramide, (BODIPY-TR ceramide, D7540), BODIPYFL C5-hexadecanoyl phosphatidylcholine (D3803), and Alexa Fluor 488 (AX488) C5-Maleimide were purchased from Invitrogen (Carlsbad, CA). GloPIPs BODIPY TMR-PtdIns(4,5)P2, C16 (C45M16a) was purchased from Echelon Biosciences (Salt Lake City, UT). β-Casein from bovine milk (>98% pure, C6905) and other reagents were purchased from Sigma-Aldrich (St. Louis, MO).
Protein purification and labeling
Recombinant mouse IRSp53 I-BAR domain was purified and labeled with AX488 dyes as previously described (9).
GUVs preparation and observation
For all experiments, GUVs composed of brain total lipid extract (36) supplemented with 5 mole percentage (mol%) brain PI(4,5)P2, 0.2 mol% 1,2-distearoyl-sn-glycero-3-phosphoethanolamine-N-[biotinyl(polyethyleneglycol)-2000], and 0.5 mol% BODIPY-TR ceramide were prepared by electroformation on platinum electrodes overnight at 4°C in a physiologically relevant salt buffer. The salt buffer outside GUVs was 20 mM Tris (pH 7.5), 60 mM NaCl, and 100 mM sucrose. The salt buffer inside GUVs was 20 mM Tris (pH 7.5), 60 mM NaCl, and 100 mM glucose.
GUVs were incubated with IRSp53 I-BAR domain at a bulk concentration of 0.02–0.1 μM for at least 30 min at room temperature before observation. For all experiments, microscope slides and coverslips were washed with water and ethanol followed by passivation with a β-casein solution at a concentration of 5 mg/mL for at least 5 min at room temperature. GUVs were observed by Nikon Eclipse Ti microscope (Nikon, Tokyo, Japan) equipped with Yokogawa CSU-X1 confocal head, 100× CFI Plan Apo VC objective (Nikon), and QuantEM:512SC camera (Photometrics, Tucson, AZ).
Results
Planar membranes
First, we compared the two modeling approaches by separate simulations of both I-BAR domain models on tension-free, periodic flat lipid bilayers at various I-BAR protein surface densities. Infinite flat sheets are a close approximation to the surface of GUVs that have quasinull local curvature. The CG and MesM-P simulations demonstrated a preference for forming relatively linear aggregates, as shown in Fig. 1, B and C, respectively.
At low surface coverage, transient short linear strings of I-BAR form in both the CG and MesM-P models (Fig. 1). As surface coverage increases from 5 to 20%, the transient linear strings change into crowded strings in which each I-BAR domain of the linear aggregate can switch orientation from one neighbor to another. We observe comparable behavior in both models, indicating our results are robust with respect to model resolution.
Next, we investigated the effects of protein-lipid interaction on protein organization and curvature generated. The effective protein-lipid interaction be changed in an in vitro experiment by changing the local concentration of negatively charged lipids or phosphoinositides. Fig. 2 shows final protein configurations using a constant coverage of 10% as a function of protein-lipid interaction strengths. In Fig. 2, we observe that at increased protein-lipid interactions strength, significantly more curvature is generated, and linear aggregates are much more likely to form. It is reasonable to expect that, as the local curvature increases, the subsequent aggregation also increases, given the nature of membrane-mediated protein interactions (37). In the CG models parameterized here, membrane-mediated interactions between proteins can broadly be defined as effective protein interactions caused by perturbations to the membrane after protein binding events. The response of the membrane to protein binding (e.g., induced curvature or dampened fluctuations) results in an effective protein interaction that drives membrane aggregation (38, 39). In fact, we demonstrate here that membrane-mediated interactions are sufficient for protein aggregation (40, 41, 42).
Figure 2.
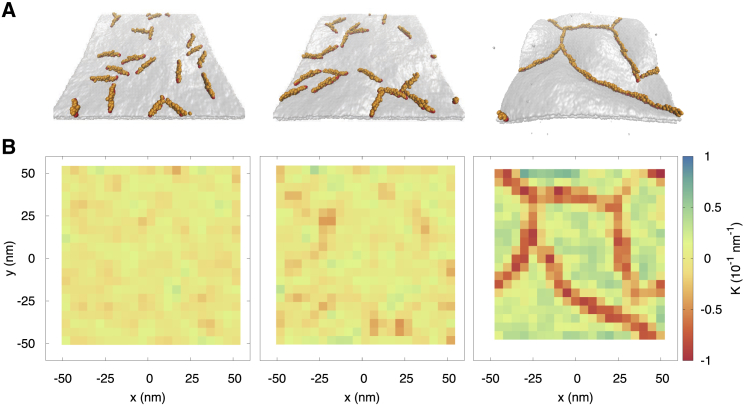
Effect of I-BAR-lipid interaction strength on local membrane curvature generation at 10% coverage. (A) Shown are snapshots of CG model with increasing interaction strength between attractive I-BAR CG beads and lipid head bead. From left to right: the strengths increase from 0.5, 1.0, to 1.5 kcal/mol. (B) Mean curvature was calculated as a function of the position on the membrane for the snapshots in (A). To see this figure in color, go online.
We calculated the mean principal curvature generated on the x and y axes for each model to further quantify the effects of interaction strength on I-BAR domain organization. Both models exhibit curvature parallel and perpendicular to the longitudinal axis of the I-BAR domain (see Fig. 1 A). In the presence of thermal fluctuations, deformation along either axis results in transient Gaussian curvature and variations in the principal curvature. Plots of mean principal curvature are shown in Fig. 2 B, corresponding to the snapshots of Fig. 2 A. With weak protein-lipid interactions, we see little to no aggregation, and the I-BAR domains are disordered. With intermediate interactions, we find that there are linear aggregates and the mean curvature driven by isolated I-BAR domains to be around 0–0.5 10−1/nm, similar to the curvature observed near a single I-BAR domain in atomistic simulations (17). With stronger protein-lipid interactions, we observed complete linear aggregate formation and significantly more membrane deformation than atomistic simulation of isolated I-BAR domains, which is to be expected. The local membrane deformation is crucial to understanding I-BAR domain curvature sensing, and so in the following sections, we address how globally curved surfaces affect the aggregation of I-BAR domains.
Tubular membranes
We mimicked the experimental conditions of Prévost et al. (12) by simulating each I-BAR domain model inside of a membrane tubule. In the experiments, tubules are formed by pulling on a micropipette-aspirated GUV using optical tweezers, with the curvature of the tubule controlled using the applied pressure in the pipette. In the tubule simulations, the surface tension is initially zero as the radius and length of the tubule are allowed to equilibrate before I-BAR domains are introduced to the system and, subsequently, bind to the lipid bilayer. After this initial equilibration, the length of the tubule is then held constant with the radius allowed to fluctuate as we seek to understand I-BAR organization in tubules pulled from GUVs, which are not tension free.
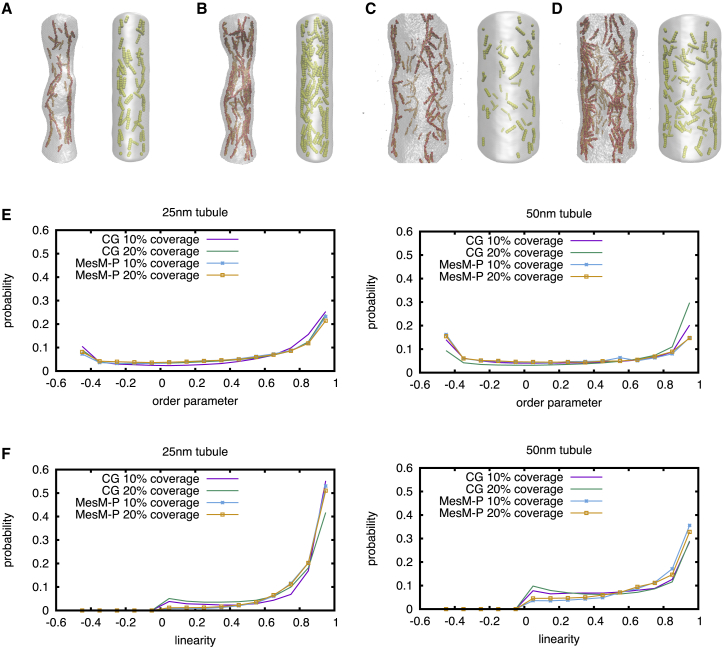
To understand the nature of the curvature-sorting property of the I-BAR domain, we probed the I-BAR domain organization inside tubules with two different radii. Interestingly, CG simulations at these lower surface coverages produced rather linear aggregates of I-BAR along the major axis of the tubule (Fig. 3). We quantified the ordering between proteins by plotting the probability density of the order parameter, S = (3cos2θ − 1)/2, where θ is the angle formed between the long dimension of two I-BAR domains. The bimodal probability densities indicate that perpendicular (S = −0.5) and parallel (S = 1) aggregates are extremely prevalent, as shown in Fig. 3 E. As the tubule radius is increased from 25 to 50 nm, however, we noticed an increased stability of the perpendicular aggregates. The increased stability of parallel aggregates in the narrower tubule is likely due to the coupling between the curvature generated by each I-BAR domain and the inherent curvature of the tubule itself. We quantified ordering due to tubule radius by plotting the probability of the linearity shown in Fig. 3 F. Linearity is defined as the cosine of the angle formed by each I-BAR domain and the axis of the tubule (i.e., the z axis). Linearity is 0 when the protein is perpendicular to the axis of the tubule and 1 when parallel to the axis. Fig. 3 F shows that the protein has a significant preference for the axial direction in the narrower tubules (i.e., perpendicular or spiral aggregates are less likely as I-BAR domains prefer axial aggregation). Axial aggregates are preferential because CG I-BAR domains form local membrane troughs, and the axial orientation requires less membrane deformation than the perpendicular direction. In other words, the trough formed by a single I-BAR domain is more stable when formed in the axial direction, and as I-BAR domains aggregate, they are already axially aligned.
Figure 3.
Tubule snapshots and time series of ordering with the z axis. (A) Shown is 10% and (B) 20% coverage in a periodic ∼25-nm radius tubules and (C) 10% and (D) 20% surface coverage in a ∼50-nm radius tubule (left CG snapshots, right MesM-P snapshots). (E) Shown is a normalized histogram of order parameter for various bound densities and tubule radii. (F) Shown is a normalized histogram of cosine of the angle formed by a single protein and the z axis for various bound densities and tubule radii. To see this figure in color, go online.
Spherical membranes
We investigated surfaces with global Gaussian curvature to understand how I-BAR protein bind and induce large-scale deformation. Considering the limits and boundary conditions of the two simulation models, we used two separate approaches to approximate the surface of a GUV; we simulated a small CG vesicle of 200-nm diameter and a large MesM-P sheet with the curvature driven by a guiding potential. The approximations made here are necessary to construct simulations that are more computationally tractable than a complete GUV. These simulations test the stability of both linear I-BAR aggregates on surfaces that display positive Gaussian curvature.
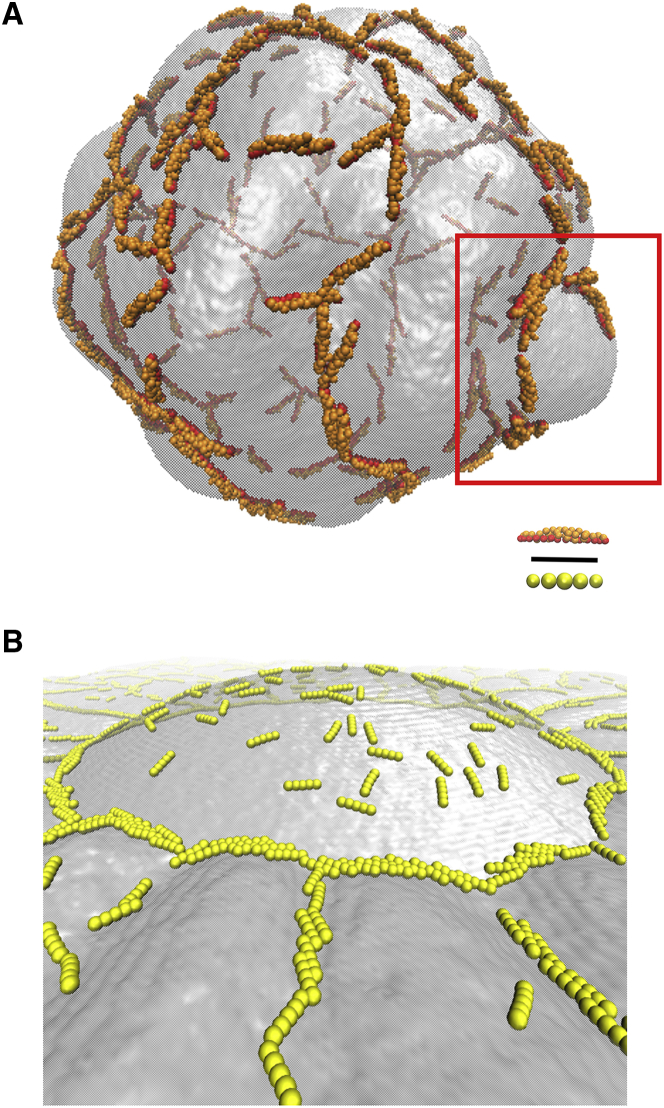
The aggregation behavior of CG I-BAR shows significant deformation of the surface of small vesicles surrounded by I-BAR domains. The linear aggregates form strings on the membrane and form bulges out of the membrane with I-BAR on the periphery. Next, we employed the MesM-P-based approach, which used a guiding potential (see Supporting Materials and Methods) to drive Gaussian curvature, and the organization of I-BAR domains is investigated. These simulations probe the aggregation behavior on the surface of a deformed vesicle with quasinull local curvature. When the membrane is perturbed into a ∼325-nm diameter dome structure with a spherical guiding potential, I-BAR domains preferentially sort to the edge of the surface, forming a tip-to-tip ring as shown in Fig. 4 B. The preference for a tip-to-tip ring can be understood again as a way for the I-BAR domains to lie in a membrane trough; the edge of the dome structure is the region of the membrane that requires minimal perturbation to form a trough.
Figure 4.
Curved membrane snapshots. (A) Shown is CG organization on a 200-nm diameter vesicle at ∼10% coverage. In the red box, liner aggregates of I-BAR domain organized around the base of a membrane bulge are shown. (B) Shown is MesM-P organization around a ∼325-nm diameter dome at ∼10% coverage. Black scale bar represents 15 nm. To see this figure in color, go online.
Experimental results
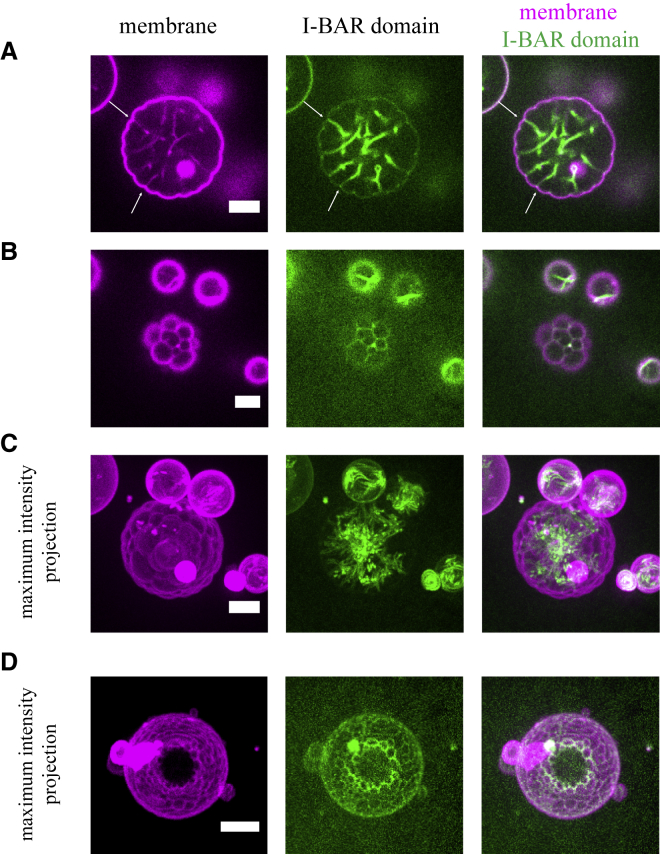
Finally, we experimentally studied the I-BAR-driven protein-membrane deformations on a GUV using fluorescence microscopy. We found that upon binding to phosphatidylinositol 4,5-biphosphate-containing GUVs, IRSp53 I-BAR domain deforms the GUV membranes into tubular invaginations toward the interior of the GUVs, where the I-BAR domain decorates the inner surface of the tubules (Fig. 5, A and C), as previously reported (9, 43). The bulk of the I-BAR domain fluorescence, as seen in the maximal projections in Fig. 5 C, is inside of the invaginated tubules. This observation shows that the I-BAR domains are enriched in the tubules compared to rather flat GUV membranes, consistent with the previous study (12). Moreover, we observed that the invaginated tubules are localized at the intersections of the membrane indentation (i.e., the inward deformation of the circular cross section of the GUV) (Fig. 5 A, arrows). Besides tubulation, to our surprise, we observed that the I-BAR domain deforms GUV membranes into bulges where the I-BAR domain accumulates around their bases, which appear as local indentations. The bulges vary in size from a few microns in Fig. 5 B to a few hundred nanometers in Fig. 5 D. Many bulges with accumulated I-BAR domains produce a “flower-like” structure, as shown in Fig. 5, B and D. This behavior appears to be quite similar to that predicted by the simulations shown in Fig. 4 B.
Figure 5.
IRSp53 I-BAR domain induced flower-like GUV membranes. (A and B) Shown are the representative confocal images of a GUV in the presence of IRSp53 I-BAR domain. Confocal images were taken at the equator of the GUV (A) and at the top of the GUV (B). Arrows in (A) indicate some membrane indentations. (C) Maximal intensity projection of the same GUV is shown in (A) and (B). (D) Maximal intensity projection of a flower-like GUV in the presence of IRSp53 I-BAR domain is shown. Protein concentrations are as follows: (A–C) 0.02 μM (70% unlabeled and 30% AX488-labeled I-BAR domain) and (D) 0.1 μM AX488-labeled I-BAR domain. Scale bars, 5 μm. To see this figure in color, go online.
Discussion
In this article, we utilized a combined multiscale simulation and experimental approach to understand I-BAR domain organization at low surface coverage on lipid bilayers in vitro. We showed that I-BAR domains at a low surface coverage prefer to organize into axial aggregates inside membrane tubules and organize around the periphery of membrane bulges on simulated vesicles and experimentally imaged GUVs. Using separate and complementary CG and mesoscopic approaches to capture protein shape and membrane curvature, we find evidence for robust levels of I-BAR organization. We find transient linear strings at low protein density on the membrane surface through a purely membrane-mediated attraction. As each I-BAR domain deforms the membrane locally, multiple I-BAR domains are attracted to generate long troughs on the surface of GUVs, inside of tubules, and on 200-nm diameter vesicles. We modeled a variety of geometries to approximate the fundamental conditions and curvatures found in experiments, especially in GUVs, as shown in Fig. 5. When the membrane has inherent curvature (i.e., is not locally flat), both the CG and MesM-P I-BAR domain models couple to the curvature of the membrane and preferentially orient to minimally deform the membrane. The minimal perturbation results in axial aggregates in tubules and rings around membrane bulges.
I-BAR domains form axial aggregates at low coverage
The aggregation behavior shown in the vesicle and tubule simulations suggest a mechanism by which tubules are initiated. Areas where multiple I-BAR aggregates contact are the regions of highest curvature in the flat membrane sheet simulations shown in Fig. 2 B and in the 200-nm vesicle simulations shown in Fig. 4 A. In the simulation models presented here, the effective attraction between the ends of I-BAR domains is membrane mediated such that the coupling of curvature minimizes the system free energy. In a more realistic bilayer, such as the in vitro assays presented here, the positively charged ends of I-BAR domains could also be electrostatically attracted by the clustering of negatively charged lipids (e.g., phosphatidylinositol 4,5-biphosphate). After the initial nucleation of the tubule, it is unclear how the growth is driven. Although the models here show that the axial aggregate is the preferred orientation, further studies (e.g., simulations of nascent tubules or experiments investigating the orientation of the I-BAR domains at a moderate density inside tubules) will be required in the future to fully elucidate the tubulation mechanism.
The axial aggregates of I-BAR domains inside tubular membranes seen in our simulations are unexpected. We find that I-BAR domains organize such that the grooves in the membrane formed by I-BAR domains produce minimal deformations of the membrane, resulting in long axial troughs that are parallel to the tubule axis. At the surface densities simulated here, the differences between tubule radii most notably affects the orientation of the individual I-BAR domains and the propensity for axial aggregates to form. Our results suggest that the preferred curvature of I-BAR domains may arise from the balance between energetic preference of axial aggregates, which minimally perturb the membrane, and entropic penalty due to reduced rotational freedom inside of the tubule.
As protein surface density increases, we would expect that the axial aggregates would instead form the proposed perpendicular aggregates (14, 15), similar to those formed by other members of the BAR family (44, 45, 46, 47). At high surface densities, the properties of a single I-BAR domain would also be different because of the presence of the neighboring I-BAR domains, and the resultant local deformation caused by each I-BAR domain could change from the deformations generated by the current model. Given the computational cost of resolving many I-BAR domains at a finer resolution, the current model parameterization also does not take into account direct interactions between neighboring I-BAR domains (except excluded volume), and therefore, high density conditions are outside of the scope of this model. We also note that axial aggregates are in contrast to previous computational studies of I-BAR domains (14, 15) that show perpendicular aggregates inside of membrane tubules, but these previous studies used models unlike the models presented here. Among the several differences including membrane representation and protein-membrane interactions, the CG I-BAR model used in this work reproduces the properties of a single, isolated, and atomically resolved I-BAR domain, which flattens when bound to the membrane and is outside the curvature ranges previously studied. Our model shows a new phenomenology because our multiscale approach considers I-BAR domain properties outside the scope of the previous models to date.
I-BAR domains aggregate around bulges on vesicular membrane at low coverage
We experimentally revealed low curvature bulges that are surrounded by I-BAR domains at their bases, shown in Fig. 5, B and D. Low surface coverage membrane remodeling of this kind has not been shown before to our knowledge. In addition, in the simulations, we observed consistent aggregation behavior of I-BAR domains on the surface of small vesicles and around the base of preformed membrane bulges in planar membranes. The bulges due to I-BAR domain aggregation here bear a striking resemblance to the deformation modeled by endophilin Bin/amphiphysin/Rvs domains (42) and spherical nanoparticles (48, 49). This common phenomenology suggests that the formation of membrane bulges are not specific to I-BAR domains but are the result of emergent phenomenon due to linear aggregation. Furthermore, Fig. 4 A shows significant deformation of the surface of small vesicles similar to the experimental images shown in Fig. 5 B, although on a smaller length scale. As these simulated vesicles are 100 times smaller than the experimentally relevant vesicles shown in Fig. 5, we also employed the MesM-P-based approach using a spherical guiding potential to form a “dome” structure with Gaussian curvature on a planar membrane. When the membrane is perturbed into a ∼325-nm diameter dome, which is much closer to the size of the membrane bulges shown in Fig. 5 D, I-BAR domains aggregate around the edge of the surface, forming a tip-to-tip ring, as shown in Fig. 4 B. This result is striking because it resembles the CG result at a shorter length scale, in which Gaussian curvature was generated on a small vesicle as well as the experimental result that shows significant aggregation around the large indentations created by the membrane-bound I-BAR domains.
The phenomenological similarities between I-BAR domain aggregation around the small bulge on the CG vesicle, tip-to-tip ring around the preformed dome on the MesM-P sheet, and the aggregation at the periphery of flower-like membrane structures in experimental images suggest a common driving force acting at different length scales. In the case of the simulations, I-BAR domains bind to the membrane and generate local deformation that leads to aggregation. Given the similar phenomenology, we suggest that the bulges seen in this experiment are a minimally perturbative conformation due to I-BAR domain aggregation.
Conclusion
Our multiscale modeling approach captures the local behavior of an isolated, membrane-bound I-BAR domain of IRSp53 and is used to model I-BAR domains on lipid bilayers of various geometries and scales to micron-size systems. We demonstrate that lipid bilayer geometry is an important factor in I-BAR domain aggregation. At low surface coverage, we show that I-BAR domains generate local troughs, leading to transient tip-to-tip aggregates on flat surfaces, and the preference for trough formation leads to string aggregates along the long axis of tubules and a ring of I-BAR domains at the base of membrane bulges on the surface of vesicles. The aggregation behavior demonstrated in the CG and MesM-P simulations provides a mechanism for the intriguing low curvature membrane bulges that we observe experimentally.
Author Contributions
Z.J., F.-C.T., A.D., A.J.P., P.B., and G.A.V. designed the research. Z.J. and F.-C.T. performed research. Z.J., F.-C.T., A.D., A.J.P., P.B., and G.A.V. analyzed the research and wrote the article.
Acknowledgments
This research was supported in part by the National Institute of General Medical Sciences of the United States NIH under award number R01-GM063796 (Z.J., A.D., A.J.P., and G.A.V.), in part by the Human Frontiers Science Program through grant RGP0005/2016 (P.B., Z.J., and G.A.V.), and in part by a France and Chicago Collaborating in the Sciences grant (Z.J. and G.V.). F.-C.T. was funded by the European Molecular Biology Organization Long-Term fellowship (ALTF 1527-2014) and Marie Curie actions (H2020-MSCA-IF-2014, project membrane-ezrin-actin). P.B.’s group belongs to the Centre national de la recherche scientifique consortium CellTiss, to the Labex CelTisPhyBio (ANR-11-LABX0038), and to Paris Sciences et Lettres (ANR-10-IDEX-0001-02). A.J.P. gratefully acknowledges support from the Ruth L. Kirschstein National Research Service Award Postdoctoral Fellowship from the National Institute of General Medical Sciences of the NIH under fellowship number F32-GM125218. The computations in this work used the Extreme Science and Engineering Discovery Environment, which is supported by the National Science Foundation grant number ACI-1548562. Specifically, they used the Stampede system at the Texas Advanced Computing Center at the University of Texas at Austin through allocation number TG-MCA94P017. This work was also completed in part with computational resources provided by the University of Chicago Research Computing Center. F.-C.T and P.B. greatly acknowledge the Cell and Tissue Imaging (The BioImaging Cell and Tissue Core Facility of the Institut Curie), Institut Curie, member of the French National Research Infrastructure France-BioImaging (ANR10-INBS-04).
Editor: Tobias Baumgart.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2019.06.025.
Supporting Material
References
- 1.McMahon H.T., Gallop J.L. Membrane curvature and mechanisms of dynamic cell membrane remodelling. Nature. 2005;438:590–596. doi: 10.1038/nature04396. [DOI] [PubMed] [Google Scholar]
- 2.Frost A., Unger V.M., De Camilli P. The BAR domain superfamily: membrane-molding macromolecules. Cell. 2009;137:191–196. doi: 10.1016/j.cell.2009.04.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Simunovic M., Voth G.A., Bassereau P. When physics takes over: BAR proteins and membrane curvature. Trends Cell Biol. 2015;25:780–792. doi: 10.1016/j.tcb.2015.09.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Millard T.H., Bompard G., Fütterer K. Structural basis of filopodia formation induced by the IRSp53/MIM homology domain of human IRSp53. EMBO J. 2005;24:240–250. doi: 10.1038/sj.emboj.7600535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Mattila P.K., Lappalainen P. Filopodia: molecular architecture and cellular functions. Nat. Rev. Mol. Cell Biol. 2008;9:446–454. doi: 10.1038/nrm2406. [DOI] [PubMed] [Google Scholar]
- 6.Ahmed S., Goh W.I., Bu W. I-BAR domains, IRSp53 and filopodium formation. Semin. Cell Dev. Biol. 2010;21:350–356. doi: 10.1016/j.semcdb.2009.11.008. [DOI] [PubMed] [Google Scholar]
- 7.Linkner J., Witte G., Faix J. The inverse BAR domain protein IBARa drives membrane remodeling to control osmoregulation, phagocytosis and cytokinesis. J. Cell Sci. 2014;127:1279–1292. doi: 10.1242/jcs.140756. [DOI] [PubMed] [Google Scholar]
- 8.Zimmerberg J., Kozlov M.M. How proteins produce cellular membrane curvature. Nat. Rev. Mol. Cell Biol. 2006;7:9–19. doi: 10.1038/nrm1784. [DOI] [PubMed] [Google Scholar]
- 9.Saarikangas J., Zhao H., Lappalainen P. Molecular mechanisms of membrane deformation by I-BAR domain proteins. Curr. Biol. 2009;19:95–107. doi: 10.1016/j.cub.2008.12.029. [DOI] [PubMed] [Google Scholar]
- 10.Mattila P.K., Pykäläinen A., Lappalainen P. Missing-in-metastasis and IRSp53 deform PI(4,5)P2-rich membranes by an inverse BAR domain-like mechanism. J. Cell Biol. 2007;176:953–964. doi: 10.1083/jcb.200609176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Baumgart T., Capraro B.R., Das S.L. Thermodynamics and mechanics of membrane curvature generation and sensing by proteins and lipids. Annu. Rev. Phys. Chem. 2011;62:483–506. doi: 10.1146/annurev.physchem.012809.103450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Prévost C., Zhao H., Bassereau P. IRSp53 senses negative membrane curvature and phase separates along membrane tubules. Nat. Commun. 2015;6:8529. doi: 10.1038/ncomms9529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ramakrishnan N., Sunil Kumar P.B., Ipsen J.H. Membrane-mediated aggregation of curvature-inducing nematogens and membrane tubulation. Biophys. J. 2013;104:1018–1028. doi: 10.1016/j.bpj.2012.12.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Mesarec L., Góźdź W., Iglič A. Closed membrane shapes with attached BAR domains subject to external force of actin filaments. Colloids Surf. B Biointerfaces. 2016;141:132–140. doi: 10.1016/j.colsurfb.2016.01.010. [DOI] [PubMed] [Google Scholar]
- 15.Noguchi H. Membrane tubule formation by banana-shaped proteins with or without transient network structure. Sci. Rep. 2016;6:20935. doi: 10.1038/srep20935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Noguchi H., Fournier J.B. Membrane structure formation induced by two types of banana-shaped proteins. Soft Matter. 2017;13:4099–4111. doi: 10.1039/c7sm00305f. [DOI] [PubMed] [Google Scholar]
- 17.Takemura K., Hanawa-Suetsugu K., Kitao A. Salt bridge formation between the I-BAR domain and lipids increases lipid density and membrane curvature. Sci. Rep. 2017;7:6808. doi: 10.1038/s41598-017-06334-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Saunders M.G., Voth G.A. Coarse-graining methods for computational biology. Annu. Rev. Biophys. 2013;42:73–93. doi: 10.1146/annurev-biophys-083012-130348. [DOI] [PubMed] [Google Scholar]
- 19.Davtyan A., Simunovic M., Voth G.A. The mesoscopic membrane with proteins (MesM-P) model. J. Chem. Phys. 2017;147:044101. doi: 10.1063/1.4993514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Srivastava A., Voth G.A. A hybrid approach for highly coarse-grained lipid bilayer models. J. Chem. Theory Comput. 2013;9:750–765. doi: 10.1021/ct300751h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995;117:1–19. [Google Scholar]
- 22.de Groot J.C., Schlüter K., Stradal T.E. Structural basis for complex formation between human IRSp53 and the translocated intimin receptor Tir of enterohemorrhagic E. coli. Structure. 2011;19:1294–1306. doi: 10.1016/j.str.2011.06.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Best R.B., Zhu X., Mackerell A.D., Jr. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ(1) and χ(2) dihedral angles. J. Chem. Theory Comput. 2012;8:3257–3273. doi: 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Klauda J.B., Venable R.M., Pastor R.W. Update of the CHARMM all-atom additive force field for lipids: validation on six lipid types. J. Phys. Chem. B. 2010;114:7830–7843. doi: 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.MacKerell A.D., Bashford D., Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 26.Jo S., Kim T., Im W. Automated builder and database of protein/membrane complexes for molecular dynamics simulations. PLoS One. 2007;2:e880. doi: 10.1371/journal.pone.0000880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jo S., Kim T., Im W. CHARMM-GUI: a web-based graphical user interface for CHARMM. J. Comput. Chem. 2008;29:1859–1865. doi: 10.1002/jcc.20945. [DOI] [PubMed] [Google Scholar]
- 28.Jo S., Lim J.B., Im W. CHARMM-GUI Membrane Builder for mixed bilayers and its application to yeast membranes. Biophys. J. 2009;97:50–58. doi: 10.1016/j.bpj.2009.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lee J., Cheng X., Im W. CHARMM-GUI input generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM simulations using the CHARMM36 additive force field. J. Chem. Theory Comput. 2016;12:405–413. doi: 10.1021/acs.jctc.5b00935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wu E.L., Cheng X., Im W. CHARMM-GUI Membrane Builder toward realistic biological membrane simulations. J. Comput. Chem. 2014;35:1997–2004. doi: 10.1002/jcc.23702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Abraham M.J., Murtola T., Lindahl E. GROMACS: high performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX. 2015;1–2:19–25. [Google Scholar]
- 32.Zhang Z., Lu L., Voth G.A. A systematic methodology for defining coarse-grained sites in large biomolecules. Biophys. J. 2008;95:5073–5083. doi: 10.1529/biophysj.108.139626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lyman E., Pfaendtner J., Voth G.A. Systematic multiscale parameterization of heterogeneous elastic network models of proteins. Biophys. J. 2008;95:4183–4192. doi: 10.1529/biophysj.108.139733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Allen M.P., Tildesley D.J. Clarendon Press; Oxford, UK: 1989. Computer Simulation of Liquids. [Google Scholar]
- 35.Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. C. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 36.Yu S., Cho K., Oh H.B. Identification of phospholipid molecular species in porcine brain extracts using high mass accuracy of 4.7 Tesla Fourier transform ion cyclotron resonance mass spectrometry. Bull. Korean Chem. Soc. 2006;27:793–796. [Google Scholar]
- 37.van der Wel C., Vahid A., Kraft D.J. Lipid membrane-mediated attraction between curvature inducing objects. Sci. Rep. 2016;6:32825. doi: 10.1038/srep32825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Goullian M., Bruinsma R., Pincus P. Long-range forces in heterogeneous fluid membranes. Europhys. Lett. 1993;22:145–150. [Google Scholar]
- 39.Aranda-Espinoza H., Berman A., Safran S. Interaction between inclusions embedded in membranes. Biophys. J. 1996;71:648–656. doi: 10.1016/S0006-3495(96)79265-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Simunovic M., Srivastava A., Voth G.A. Linear aggregation of proteins on the membrane as a prelude to membrane remodeling. Proc. Natl. Acad. Sci. USA. 2013;110:20396–20401. doi: 10.1073/pnas.1309819110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Simunovic M., Voth G.A. Membrane tension controls the assembly of curvature-generating proteins. Nat. Commun. 2015;6:7219. doi: 10.1038/ncomms8219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Simunovic M., Šarić A., Voth G.A. Long-range organization of membrane-curving proteins. ACS Cent. Sci. 2017;3:1246–1253. doi: 10.1021/acscentsci.7b00392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Barooji Y.F., Rørvig-Lund A., Bendix P.M. Dynamics of membrane nanotubes coated with I-BAR. Sci. Rep. 2016;6:30054. doi: 10.1038/srep30054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Mim C., Cui H., Unger V.M. Structural basis of membrane bending by the N-BAR protein endophilin. Cell. 2012;149:137–145. doi: 10.1016/j.cell.2012.01.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Frost A., Perera R., Unger V.M. Structural basis of membrane invagination by F-BAR domains. Cell. 2008;132:807–817. doi: 10.1016/j.cell.2007.12.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Daum B., Auerswald A., Meister A. Supramolecular organization of the human N-BAR domain in shaping the sarcolemma membrane. J. Struct. Biol. 2016;194:375–382. doi: 10.1016/j.jsb.2016.03.017. [DOI] [PubMed] [Google Scholar]
- 47.Cui H., Mim C., Voth G.A. Understanding the role of amphipathic helices in N-BAR domain driven membrane remodeling. Biophys. J. 2013;104:404–411. doi: 10.1016/j.bpj.2012.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Šarić A., Cacciuto A. Fluid membranes can drive linear aggregation of adsorbed spherical nanoparticles. Phys. Rev. Lett. 2012;108:118101. doi: 10.1103/PhysRevLett.108.118101. [DOI] [PubMed] [Google Scholar]
- 49.Šarić A., Cacciuto A. Self-assembly of nanoparticles adsorbed on fluid and elastic membranes. Soft Matter. 2013;9:6677. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.