Training on Abacus-Based Mental Calculation Enhances Visuospatial Working Memory in Children

Abstract

Abacus-based mental calculation (AMC) involves temporary storage and manipulation of an imaginary abacus closely related to the function of visuospatial working memory (VSWM). The present study thus investigated the effects of AMC training on VSWM and its neural correlates. A total of 144 human subjects (67 boys) were assigned to AMC or control groups at their entry to primary school. The AMC group received 2 h AMC training per week for 5 school years, whereas the control group spent the time in activities, such as conventional calculation and reading. Raven's Intelligence Test was administered both before and after training. Two arithmetic tests and a VSWM task were conducted after training. Among these participants, fMRI data were collected from 64 children for the VSWM task. Behavioral results indicated that the AMC group outperformed controls on both arithmetic and VSWM tasks, but not on Raven's Intelligence Test. While the two groups activated similar regions during the VSWM task, the AMC group showed greater activation than the controls in frontal, parietal, and occipital areas. Interestingly, the activation of right middle frontal gyrus mediated the relation between the arithmetic ability and the VSWM performance in the AMC group, suggesting that the frontal region may be the neural substrate underlying the transfer effect from AMC training to VSWM. Although the transfer effects seem quite limited considering the length and intensity of the training, these findings suggest that long-term AMC training not only improves arithmetic ability but also has a potential positive effect on VSWM.

SIGNIFICANCE STATEMENT Plasticity of working memory is one of the most rapidly expanding research fields in the developmental and cognitive sciences. Previous studies suggest that abacus-based mental calculation (AMC) relies on a visuospatial imaginary strategy, which is closely related to visuospatial working memory (VSWM). However, the impacts of AMC training on VSWM and the underlying neural basis remain unclear. Here, we found that AMC training enhanced VSWM in children, which was accompanied by altered activation in frontal, parietal, and occipital areas. Moreover, we observed that activation in right middle frontal gyrus played a significant mediation role in the transfer of AMC training to VSWM. These findings provide a new perspective to VSWM training and also advance our understanding of related brain plasticity.

Introduction

Working memory (WM), which refers to the maintenance and manipulation of goal-directed information over short periods of time (Baddeley and Andrade, 2000), is closely associated with a wide range of cognitive capabilities, such as language processing (Huettig and Janse, 2015), attentional control (Kane et al., 2007), and academic achievement (Mulder et al., 2010). It has been regarded as a critical mediator of age-related differences in a series of cognitive skills (Fry and Hale, 2000; Clarys et al., 2002). Therefore, it is of great value to investigate whether certain trainings can improve WM and whether WM improvement can enhance other cognitive abilities. Indeed, a lot of training paradigms have been explored in the past decades. While many studies have shown substantial and specific improvements on the trained WM tasks, the training transfer effects remain controversial. Some studies reported no beneficial effect being transferred to untrained WM, intelligence, or other cognitive domains (Redick et al., 2013; Thompson et al., 2013; Melby-Lervåg et al., 2016), whereas some others found near transfer to untrained WM (Holmes et al., 2009) or far transfer to intelligence (Jaeggi et al., 2008) and other cognitive abilities (Klingberg et al., 2005). To date, the effectiveness of WM training to untrained WM tasks and general intellectual ability is still inconclusive. In addition, most existing WM training studies were conducted under controlled laboratory settings, which may pose difficulties in generalizing the obtained findings to more general contexts (e.g., educational context).

In contrast to the large body of WM training with very different paradigms performed in laboratory setting, the abacus-based mental calculation (AMC) training can be directly applied in school setting and daily life for fast and accurate arithmetic calculation. It has been consistently shown to engage a common frontal-parietal network that serves as the core substrate of WM (Hanakawa et al., 2003; Chen et al., 2006; Hu et al., 2011; Wang et al., 2017), but the AMC training effect on WM remains elusive. Previous studies have proposed that AMC is based on a visuospatial strategy that taxes the storage and manipulation processes of visuospatial WM (VSWM) (Tanaka et al., 2002; Hanakawa et al., 2003; Chen et al., 2006). Consistent with this conjecture, individual differences in VSWM before training have been found to mediate the gains of AMC learning (Barner et al., 2016). Furthermore, previous studies have shown that, while the conventional arithmetic operation recruits brain regions related to phonological WM and other language-related areas (Dehaene et al., 1999), AMC engages brain networks largely overlapped with the primary neural substrate of VSWM (Hanakawa et al., 2003; Chen et al., 2006; Ku et al., 2012). In addition, our previous neuroimaging studies have demonstrated that long-term AMC training impacts white matter integrity (Hu et al., 2011) and functional connectivity (Li et al., 2013; Weng et al., 2017; Xie et al., 2018) in brain regions relating to visuospatial processing and VSWM. It has been proposed that cognitive training can generate near transferable gains when the trained and transfer tasks engage overlapping cognitive processes and brain regions (Dahlin et al., 2008). Given that AMC relies on the use of a visuospatial strategy and shares overlapping neural substrates with VSWM, it is possible that AMC training may induce a near transfer effect to VSWM.

Based on literature mentioned above, the present study aimed to examine the effect of AMC training on arithmetic performance and VSWM in children. We hypothesized the following: (1) children receiving AMC training would perform better than the controls in arithmetic and VSWM tasks; (2) there would be a significant relationship between arithmetic ability and VSWM in AMC children; and (3) AMC training may alter brain activation during the VSWM task, and some of these changes may mediate the relationship between arithmetic ability and VSWM.

Materials and Methods

Participants and assessment procedure

This study was approved by the research ethics review board of Zhejiang University in China. A total of 144 children were recruited from a single district within Qiqihar city, Heilongjiang Province of China. Informed consents were obtained from both children and parents. All participants were from urban families, had normal hearing and normal or corrected-to-normal vision, had no reports of neurological or psychiatric disorder, and had no special educational assistance requirements.

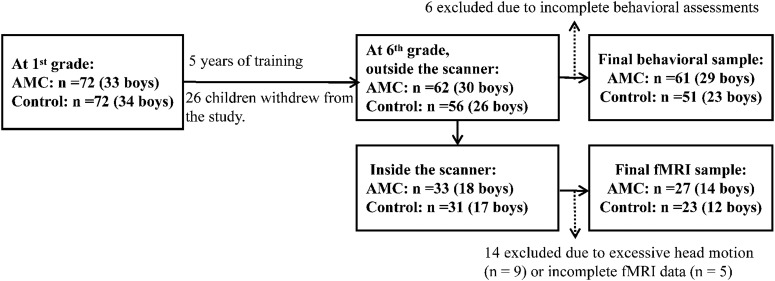
As shown in Figure 1, at the start of primary school, the children were randomly assigned into AMC (n = 72, 33 boys) and control groups (n = 72, 34 boys). Both groups were taught based on the same primary school curriculum. In addition to the normal school curriculum, children in the AMC group received 2 h of AMC training per week from an experienced AMC teacher at school from the first to the sixth grade (see AMC training procedure). At the beginning of the first grade, the intelligence test was conducted for all participants. At the beginning of the sixth grade, arithmetic tests, visuospatial n-back, and intelligence tests were conducted. Thirty-two children in total were excluded from the data analysis in the present study due to withdrawal from the training program (n = 26) or incomplete behavioral assessments (n = 6). Consequently, 112 children (AMC: n = 62, 30 boys; controls: n = 56, 26 boys) constituted the final sample for behavioral analysis. Among these participants, a total of 64 children completed the fMRI n-back task. Fourteen children in total were excluded due to excessive head motion (exceeding 3.0 mm in displacement or 3° in rotation) during fMRI scanning (n = 9) or incomplete fMRI data (n = 5), yielding 50 children (AMC: n = 27, 14 boys; Controls: n = 23, 12 boys) in the final sample for the fMRI data statistics.

Figure 1.

Flow chart of the participants.

AMC training procedure

In the beginning, AMC children learned to calculate with a physical abacus. After reaching a certain level of proficiency, they started to stop using the physical abacus and performed calculations by visualizing an “imaginary abacus” in the brain. AMC beginners were allowed to move their fingers so as to aid their manipulating of the imaginary beads. After long-term training, they were encouraged to perform AMC as fast as possible without finger movements. Over time, the calculation problems that were given them to tackle became more and more difficult. Such an adaptive training program could help children develop a high level of AMC skill in a step-by-step manner. Children in the control group did not receive any physical or mental abacus instructions throughout this study. Instead, they were provided with similar amounts of extra learning on materials, such as conventional calculation and reading.

Behavioral measures

Intelligence assessment.

The Combined Raven's Matrices Test (Wang et al., 2007) consists of 72 progressively difficult matrix reasoning questions. For each participant, raw scores were standardized based on the age norm of Chinese urban children.

Arithmetic tests.

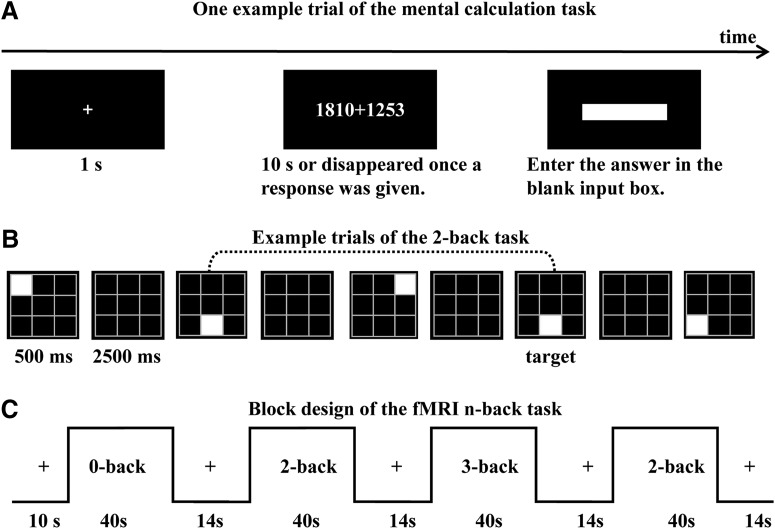
A computerized mental calculation task (Fig. 2A) and the Chinese version of the Heidelberg Rechentest (HRT) (Haffner et al., 2005) were conducted to assess individual's arithmetic capability. In the mental calculation task, each trial started with a fixation “+” displayed on the black screen for 1 s, and then followed by a horizontal addition problem (e.g., 1810 + 1253) displayed up to 10 s (Fig. 2A). The participants in the AMC group were asked to calculate the problem rapidly and accurately with the AMC method, whereas the participants in the control group were instructed to calculate using the conventional calculation method mentally (i.e., to calculate without using paper and pencils). Once they got an answer, they should press the SPACE key as quickly as possible (the addends disappeared at the same time) and then enter the answer in the succeeding blank input box. There were 5 practice trials and 81 experimental trials with increasing difficulty (from 1 digit to 7 digit addends). The task would be ended if the participant responded three successive addition trials incorrectly. Performance was evaluated based on the amount of correct trials.

Figure 2.

Experimental designs of the tasks. A, One example trial of the mental calculation task. The horizontal addition problem was displayed up to 10 s, and disappeared once the SPACE key was pressed. B, Example trials of the 2-back task. For each trial, a white square in a 3 × 3 black grid was displayed for 500 ms, with an interstimulus interval of 2500 ms. C, Block design for the fMRI. In each block, a 40 s task condition was presented, followed by a 14 s fixation slide.

HRT (Haffner et al., 2005) is a paper-pencil test, and its reliability for the Chinese population has been reported good (test-retest reliability coefficients of each subtest was >0.7) (Wu and Li, 2005). It consists of six timed subtests, including addition (e.g., 37 + 15 = _), subtraction (e.g., 60 −14 = _), multiplication (e.g., 17 × 4 = _), division (e.g., 56 ÷ 4 = _), number equations filling (e.g., 24 + _ = 13 + 17), and comparison (e.g., 12 + 39 _ 50). Participants were required to complete the equations/comparisons with correct numbers (or such symbols as “>”, “<”, “=” for comparison) on the test paper with a pencil. For each participant, raw scores of each subtest were transformed to T scores based on the Chinese adapted city norm (Wu and Li, 2005), and then an average T score was computed as the HRT arithmetic score. Of the 112 children constituting the final behavior analysis sample, 9 children (AMC: n = 5, 4 boys; controls: n = 4, 3 boys) did not participate in the HRT.

Visuospatial n-back.

The n-back paradigm, which shows a good test-retest reliability (Hockey and Geffen, 2004; Jaeggi et al., 2010), has been widely used to study WM. In the present study, visuospatial n-back tasks were conducted both outside and inside the fMRI scanner. Outside the fMRI scanner, participants were instructed to perform the 2-back task, then the 3-back task. Each task consisted of 10 blocks. Each block included 11 trials (three targets) in the 2-back task and 12 trials (three targets) in the 3-back. For each trial, a white square was pseudorandomly displayed in a 3 × 3 black grid for 500 ms with an interstimulus interval of 2500 ms (Fig. 2B). A stimulus was a target if it matched the stimulus two (2-back) or three trials (3-back) back; the other stimuli were treated as nontargets. Participants were required to respond to the targets by pressing the SPACE key of the computer keyboard with the right index finger. Accuracy in each task was assessed using the discrimination index d′ (z_{target hit rate} − z_{false alarm rate}). Reaction time (RT) was calculated as the mean time of the correct responses to targets.

The n-back paradigm conducted inside the fMRI scanner was similar to the one used outside the scanner, except that a 0-back condition was included. Under the 0-back condition, participants were instructed to respond when the current stimulus matched the first stimulus of the block. The fMRI experiment consisted of four 0-back, four 2-back, and four 3-back blocks (Fig. 2C). Each block included a 4 s instruction slide and twelve 3 s trials (three targets). Each task block was followed by a 14 s fixation slide, in which only a fixation “+” was presented on the screen. The 14 s fixation slide was used as a task-free baseline. There was an additional 10 s fixation slide at the beginning of the task session as prescans. Thus, in total, the n-back inside the fMRI scanner lasted 658 s. Participants' performance on visuospatial n-back inside the scanner was also measured by d′ and mean RT of the correct responses to targets.

Imaging acquisition and preprocessing

Imaging was performed on a 1.5 T MRI scanner (Philips). A total of 329 functional images were acquired for the n-back task using a T2*-weighted single-shot EPI sequence (TR = 2000 ms, TE = 50 ms, flip angle = 90°, matrix size = 64 × 64, FOV = 230 mm × 230 mm, slice thickness/gap = 5 mm/0.8 mm, and slice numbers = 22 with interleaved acquisition). All the functional images were set obliquely and parallel to the anterior and posterior commissural line. To facilitate spatial normalization, high-resolution T1-weighted structural images were obtained using a 3D fast field echo sequence (TR = 25 ms, TE = 4.6 ms, flip angle = 15°, matrix size = 256 × 256, FOV = 256 mm × 256 mm, voxel size = 1 × 1 × 1 mm³, and slice numbers = 150 in the sagittal plane).

The imaging data were preprocessed using the Data Processing Assistant for Resting-state fMRI Advanced Edition (DPARSF-A, version 4.3) toolbox (Chao-Gan and Yu-Feng, 2010). The first five scans were discarded from the analysis for each subject to avoid potential instability of initial MR signals. Then the functional images were corrected for acquisition timing differences in slices and head motion, aligned to the corresponding T1-weighted images, and normalized to MNI space with a resampling voxel size (3 × 3 × 3 mm³). Finally, all functional images were spatially smoothed using a Gaussian kernel (6 mm FWHM). Mean framewise displacement was used to characterize head motion during the entire task. There were no differences in mean framewise displacement between the two groups (Table 1). There were also no significant relationships between framewise displacement and any behavioral measures of interest described below in either group (lowest p = 0.306).

Table 1.

Participant characteristics of this study^a

Characteristic	AMC group	Control group	Group differences
All participants
Age at Grade 6 (mean, SD)	11.93 (0.51)	11.95 (0.49)	t(110) = 0.24, p = 0.81
Gender (boy, total)	(29, 61)	(23, 51)	χ2 = 0.07, p = 0.80
Intelligence at Grade 1 (mean, SD)	103 (14)	103 (11)	t(110) = 0.07, p = 0.95
Intelligence at Grade 6 (mean, SD)	112 (14)	109 (14)	t(110) = 1.10, p = 0.27
Participants attending fMRI
Age at Grade 6 (mean, SD)	11.83 (0.55)	11.97 (0.54)	t(48) = 0.92, p = 0.36
Gender (boy, total)	(14, 27)	(12, 23)	χ2 = 0.001, p = 0.98
Intelligence at Grade 1 (mean, SD)	103 (14)	104 (16)	t(48) = 0.08, p = 0.94
Intelligence at Grade 6 (mean, SD)	112 (14)	107 (16)	t(48) = 1.22, p = 0.23
Motion at Grade 6 (mean FD, SD)	0.16 (0.06)	0.16 (0.05)	t(48) = 0.02, p = 0.99

^aFD, Framewise displacement.

Experimental design and statistical analysis

A total of 144 children were randomly assigned into AMC or control groups at the beginning of the first grade, and the baseline intelligence was assessed. From the first to the sixth grade, both groups were taught based on the same primary school curriculum, except that the AMC group received AMC training for 2 h per week, whereas the control group, during the same class time, received extra learning on supplementary materials about conventional calculation and reading. At the beginning of the sixth grade, intelligence, arithmetic, and visuospatial n-back tasks were administered to both groups. A subset of children also completed an fMRI n-back task. To test the three hypotheses we proposed, differences between the two groups in arithmetic, VSWM, and brain activation in the VSWM task were examined. In addition, mediation analyses were conducted to explore the brain-behavioral relationships (for detailed statistical analysis, see below sections).

Behavioral statistical analysis.

All behavioral analyses were conducted using SPSS 22.0. (IBM). χ² test and independent-samples t test were first used to examine whether the two groups were matched in gender, age, and baseline intelligence. Then independent-samples t test was used to examine group differences in post-training intelligence and arithmetic scores. A 2 (group: AMC, control) × 2 (load: 2-back, 3-back) repeated-measures ANOVA was conducted to examine group differences in VSWM performance outside the scanner. And a 2 (group: AMC or control) × 3 (load: 0-back, 2-back, or 3-back) repeated-measures ANOVA was conducted to examine group differences in VSWM performance inside the scanner. Post hoc tests were conducted using the Bonferroni correction for multiple comparisons. Pearson correlational analyses were used to examine whether there were significant relationships between arithmetic scores and VSWM performance in each group.

Imaging statistical analysis.

The GLM was used in the first-level analysis to obtain contrasts of interest for each subject: (1) 0-back versus baseline, (2) 2-back versus baseline, and (3) 3-back versus baseline, with six head movement parameters accounting for residual movement artifacts. One-sample t tests were used to examine general brain activation pattern in each condition and each group. Then a 2 (group: AMC, control) × 3 (load: 0-back, 2-back, 3-back) flexible factorial ANOVA model (Gläscher and Gitelman, 2008) was used to assess the main effect of group and the interaction between group and load. Search space was restricted to the gray matter regions defined in the standard AAL mask (47,636 voxels) without cerebellar. Significant clusters were identified using a voxelwise threshold of p < 0.001 to address recent criticisms of the cluster method (Rodgers and DeWeese, 2014). A minimal cluster size of 31 voxels (837 mm³) was determined by the AFNI's updated 3dClustSim program using an improved spatial autocorrelation function to simulate the null distribution of cluster size that remedies the false-positive problem (Cox et al., 2017).

Mediation analysis.

To test the hypothesis that some of the brain regions mediate the relationship between AMC training and VSWM, we ran a mediation analysis with mental calculation scores as a dependent variable to predict VSWM performance with brain activation strength as a mediator. Given the large number of possible brain-behavior analyses and the prerequisite of a mediation model, we predetermined this exploratory analysis with the following constraints. First, we would only use 3-back d′ measured outside the scanner to characterize individual WM performance. The 3-back condition was chosen because it requires the highest WM load and would better capture individual differences in WM in the present study. The d′ measured outside the scanner was used so that both mental calculation and WM were assessed with the same experimental environment. Second, the mediators would be selected from brain regions that show either group main effect or group × load interaction in the VSWM task and show significant correlations with both mental calculation scores and VSWM performance. The mediation effect of brain activation on the relationship between mental calculation scores and VSWM performance was examined using the PROCESS macro for SPSS 22.0 (IBM) (Hayes, 2013). To test the significance of mediation effect, a 95% bootstrapped CI was generated from repeated resampling (10,000 samples) of the observed data. CIs that do not include zero indicate a significant mediation effect. This method can control for the positive skew associated with indirect effects, which makes it more statistically powerful than other methods (Preacher and Hayes, 2008). A complementary mediation analysis was conducted with mental calculation scores replaced by HRT arithmetic scores to test the reliability of the mediation model.

Results

Behavioral results

Behavioral performance for all participants

There were no differences in age, gender distribution, and intelligence scores at Grade 1 baseline between the two groups (Table 1). Remarkably, there was no significant group difference in intelligence scores at Grade 6 after training (Table 1).

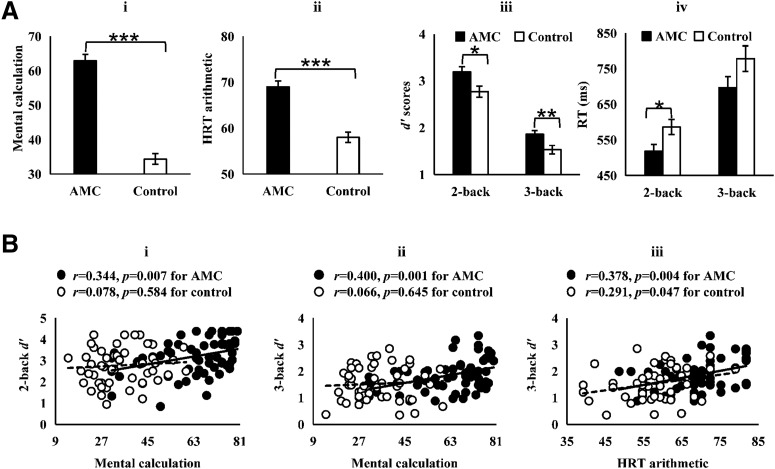
An independent-samples t test showed that the AMC group scored significantly higher on both the mental calculation task (t₍₁₁₀₎ = 11.672, p = 1 × 10⁻²⁰, Cohen's d = 2.240) and HRT (t₍₁₀₁₎ = 6.640, p = 2 × 10⁻⁹, Cohen's d = 1.309) than the control group, confirming a significant beneficial effect of AMC training on arithmetic ability (Fig. 3Ai,Aii). The two arithmetic test scores were significantly correlated in both AMC (r = 0.514, p = 0.00005) and control groups (r = 0.399, p = 0.005). The 2 (group: AMC or control) × 2 (load: 2-back or 3-back) repeated-measures ANOVA on d′ of n-back revealed a significant main effect of group (F_(1,110) = 9.496, p = 0.003, partial η² = 0.079; Fig. 3Aiii). Post hoc t tests using Bonferroni correction showed significantly higher d′ scores for the AMC group than the control group in both 2-back (t₍₁₁₀₎ = 2.594, p_corrected = 0.011, Cohen's d = 0.491) and 3-back loads (t₍₁₁₀₎ = 2.837, p_corrected = 0.006, Cohen's d = 0.534). A parallel repeated-measures ANOVA on RT of n-back also showed a significant main effect of group (F_(1,110) = 4.785, p = 0.031, partial η² = 0.042; Fig. 3Aiv). Post hoc t tests using Bonferroni correction showed significantly shorter RTs for the AMC group in 2-back (t₍₁₁₀₎ = 2.440, p_corrected = 0.017, Cohen's d = 0.460) and a marginal group difference in 3-back (t₍₁₁₀₎ = 1.678, p_corrected = 0.096, Cohen's d = 0.318).

Figure 3.

Task performances for all participants. A, Mean performance of the arithmetic tests and VSWM tasks outside the scanner. Error bars indicate SE. ***p < 0.001, **p < 0.01, *p < 0.05. B, Associations between arithmetic scores and VSWM performance. The associations between mental calculation scores and VSWM performance were significant for the AMC group (2-back: r = 0.344, p = 0.007; 3-back: r = 0.400, p = 0.001) but not for the control group (2-back: r = 0.078, p = 0.584; 3-back: r = 0.066, p = 0.645). The associations between HRT arithmetic scores and VSWM performance were significant for both groups (AMC: r = 0.378, p = 0.004; control: r = 0.291, p = 0.047).

Mental calculation scores in the AMC group were significantly correlated with their 2-back (r = 0.344, p = 0.007; Fig. 3Bi) and 3-back (r = 0.400, p = 0.001; Fig. 3Bii) d′ scores. The correlations remained significant after controlling for the effects of age, gender, and intelligence (2-back: r = 0.331, p = 0.011; 3-back: r = 0.375, p = 0.004). In contrast, mental calculation scores were not correlated with n-back d′ scores in the control group, regardless of whether controlling for the same covariates or not (lowest p = 0.584). While both groups showed significant correlations between HRT arithmetic scores and 2-back (AMC: r = 0.311, p = 0.020; control: r = 0.366, p = 0.011) and 3-back d′ scores (AMC: r = 0.378, p = 0.004; control: r = 0.291, p = 0.047; Fig. 3Biii), only the correlation between HRT and 3-back d′ scores in the AMC group remained significant (r = 0.348, p = 0.011) when controlling for age, gender, and intelligence.

Behavioral performance for participants attending fMRI

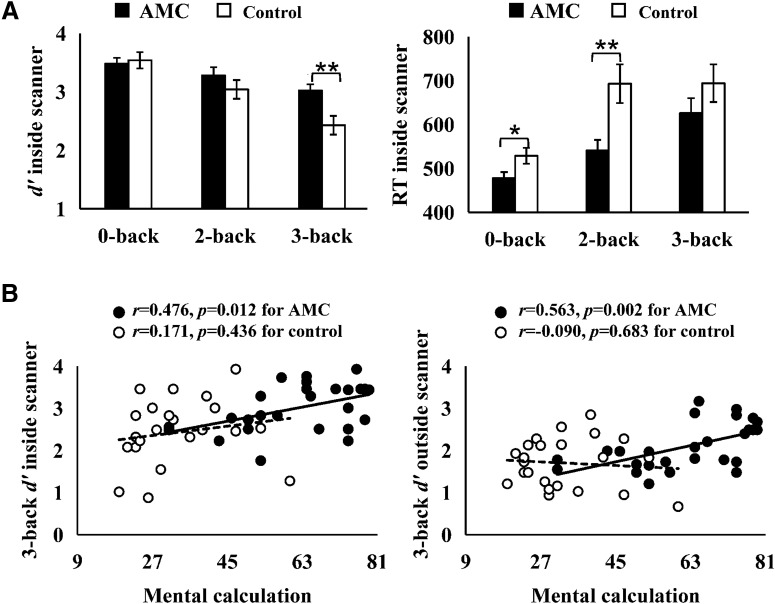
A 2 (group: AMC or control) × 3 (load: 0-back, 2-back, or 3-back) repeated-measures ANOVA on d′ inside the scanner revealed a significant interaction between group and load (F_(2,96) = 4.699, p = 0.011, partial η² = 0.089). Post hoc t tests using Bonferroni correction showed significantly higher d′ scores for the AMC group in 3-back (t₍₄₈₎ = 3.083, p_corrected = 0.003, Cohen's d = 0.860) and no significant group differences in 0-back (t₍₄₈₎ = 0.326, p = 0.746, Cohen's d = 0.091) or 2-back (t₍₄₈₎ = 1.150, p = 0.256, Cohen's d = 0.326; Fig. 4A). A parallel repeated-measures ANOVA on RT inside the scanner revealed a significant main effect of group (F_(1,48) = 5.465, p = 0.024, partial η² = 0.102). Post hoc t tests using Bonferroni correction showed significantly shorter RTs for the AMC group in 0-back (t₍₄₈₎ = 2.427, p_corrected = 0.020, Cohen's d = 0.681) and 2-back (t₍₄₈₎ = 2.992, p_corrected = 0.004, Cohen's d = 0.830), and no significant group difference in 3-back (t₍₄₈₎ = 1.180, p = 0.244, Cohen's d = 0.332; Fig. 4A). Similarly, mental calculation scores in the AMC group were significantly correlated with their 3-back d′ scores both inside (r = 0.476, p = 0.012) and outside (r = 0.563, p = 0.002; Fig. 4B) the scanner. The correlations remained significant after controlling for the effects of age, gender, and intelligence (inside: r = 0.496, p = 0.014; outside: r = 0.570, p = 0.004).

Figure 4.

Task performances for participants attending fMRI. A, Mean performance of the VSWM task inside the scanner. Error bars indicate SE. **p < 0.01, *p < 0.05. B, Associations between mental calculation scores and VSWM performance. The associations were significant for the AMC group (3-back inside the scanner: r = 0.476, p = 0.012; 3-back outside the scanner: r = 0.563, p = 0.002) but not for the control group (3-back inside the scanner: r = 0.171, p = 0.436; 3-back outside the scanner: r = −0.090, p = 0.683).

Imaging results

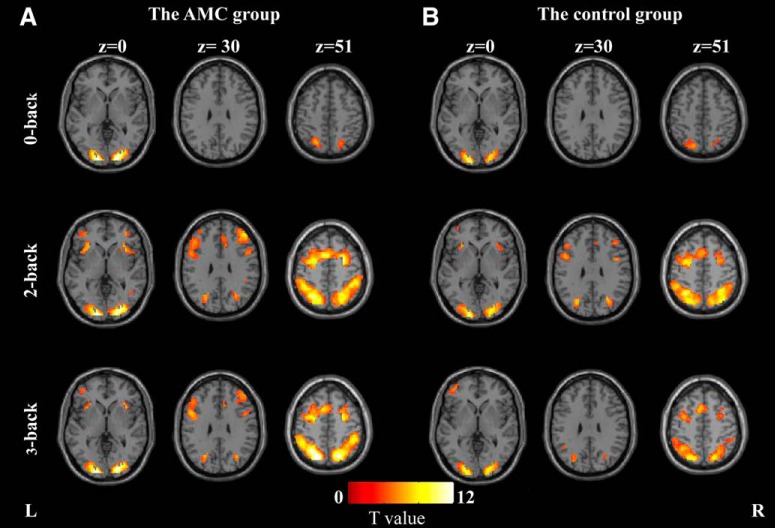
As shown in Figure 5, in the 0-back load, both groups showed activations in the bilateral superior parietal lobules (SPLs)/inferior parietal lobules (IPLs) and bilateral middle occipital gyrus (MOG)/inferior occipital gyrus (IOG). In the 2-back and 3-back loads, both groups showed activations in a bilateral network of regions, including, but not limited to, the superior frontal gyrus (SFG)/middle frontal gyrus (MFG)/inferior frontal gyrus (IFG), insula, supplementary motor area, SPL/IPL, and MOG/IOG. These regions have been consistently reported in previous studies examining VSWM (Kwon et al., 2002; Dong et al., 2016).

Figure 5.

Activated areas during the n-back task. A, Activation maps for the AMC group. B, Activation maps for the control group. The left side of each axial slice corresponds to the left hemisphere of the brain.

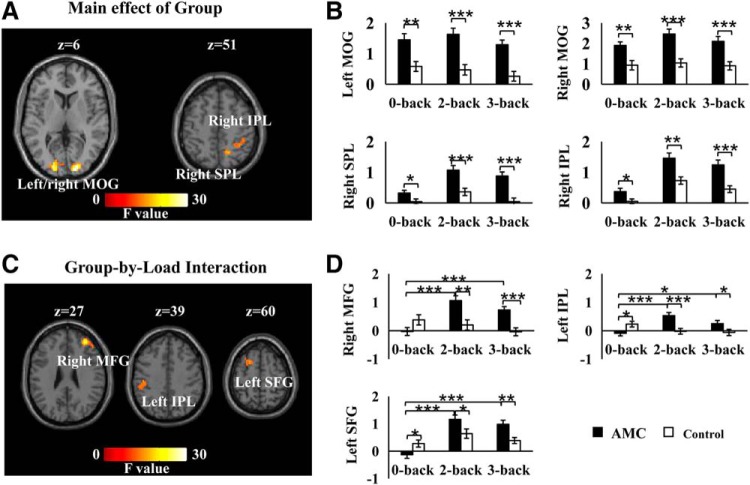
A 2 (group: AMC or control) × 3 (load: 0-back, 2-back, or 3-back) factorial ANOVA revealed a significant main effect of group in the left and right MOG, right SPL, and right IPL (Table 2; Fig. 6A). We further extracted β values from each of these clusters and conducted Bonferroni post hoc comparisons between the two groups. All these clusters showed significantly stronger activation in the AMC group compared with the control group under all three task loads (largest p_corrected = 0.036; Fig. 6B). The factorial ANOVA also showed a significant interaction between group and load in the right MFG, left SFG, and left IPL (Table 2; Fig. 6C). To further examine the interaction effect, Bonferroni post hoc analyses were conducted to examine activation differences between different memory loads for each group. The AMC group showed significant stronger activation under both 2-back and 3-back conditions than under 0-back condition in all three clusters (largest p_corrected = 0.012; Fig. 6D). However, no significant differences were detected for activation in any cluster in the control group (smallest p_corrected = 0.102). We also conducted Bonferroni post hoc comparisons between the two groups for activation in each cluster. All three clusters showed significantly stronger activation in the AMC group than that in the control group under the 2-back and 3-back loads (largest p_corrected = 0.030; Fig. 6D). On the contrary, the left SFG and left IPL showed significantly lower activation in the AMC group than in the control group under the 0-back load (largest p_corrected = 0.032).

Table 2.

Significant clusters in the factorial ANOVA^a

Anatomical region	BA	MNI coordinates	Cluster size	Peak F
Main effect of group
R_MOG	18/17	(18,–93,6)	129	40.00
L_MOG	17/18	(−15,−93,0)	146	30.60
R_SPL	7/40	(18,−57,51)	39	17.77
R_IPL	40	(42,−39,48)	42	16.20
Group × load interaction
R_MFG	10/46	(33,45,27)	86	23.67
L_IPL	40	(−45,−24,39)	63	15.28
L_SFG	6	(−18,12,60)	36	14.86

^aL, Left; R, right; BA, Brodmann area.

Figure 6.

Clusters showing significant main effect of group or group × load interaction. A, B, Four clusters are significant for the main effect of group. C, D, Three clusters are significant for the group × load interaction. Error bars indicate SE. ***p < 0.001, **p < 0.01, *p < 0.05.

Mediation effects

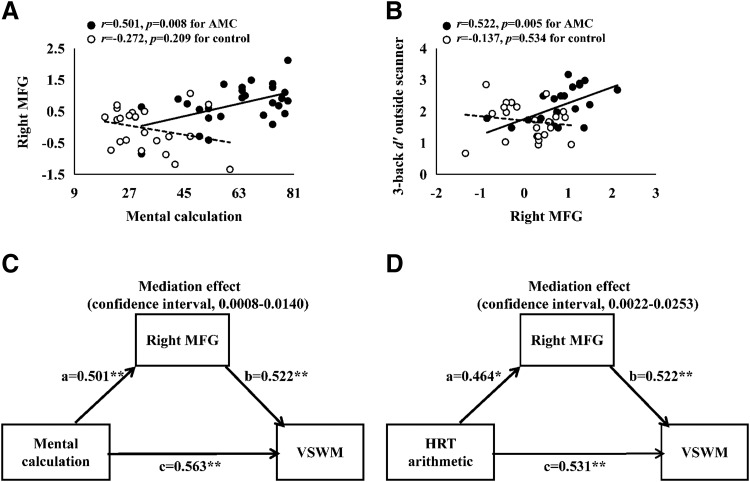
A total of seven clusters showed either group or group × load interaction in the VSWM task. These clusters were examined for their relationships to the mental calculation scores and VSWM performance outside the scanner. For the AMC group, the brain-behavior correlation was only found for the right MFG. Specifically, we observed positive correlations between the mental calculation scores and the activation in the right MFG (r = 0.501, p = 0.008; Fig. 7A), and between the activation in the right MFG and the 3-back d′ scores (r = 0.522, p = 0.005; Fig. 7B). After controlling for age, gender, intelligence, and head motion, the above correlations were still present (with mental calculation: r = 0.520, p = 0.009; with 3-back d′ scores: r = 0.638, p = 0.001). In contrast, no correlations were found in the control group (lowest p = 0.209); therefore, no further mediation analysis was performed for the control group. According to the PROCESS macro for SPSS 22.0 (IBM) (Hayes, 2013), a significant mediation effect is indicated by a CI that does not include zero. Our exploratory mediation analysis demonstrated that the right MFG activation exerted an indirect mediation effect on the relationship between mental calculation scores and VSWM performance (CI [0.0008, 0.0140]; Fig. 7C) in the AMC group. Similarly, the right MFG activation mediated the relationship between HRT arithmetic scores and VSWM performance (CI [0.0022, 0.0253]; Fig. 7D) in the AMC group. Both mediation effects remained significant (mental calculation: CI [0.0015, 0.0194]; HRT arithmetic: CI [0.0008, 0.0590]) when age, gender, intelligence, and head motion during the VSWM task were included as covariates.

Figure 7.

Brain-behavior correlations and mediation effects. A, Mental calculation scores were correlated with brain activation of right MFG in the AMC group (r = 0.501, p = 0.008) but not for the control group (r = −0.272, p = 0.209). B, Brain activation of right MFG was correlated with VSWM performance in the AMC group (r = 0.522, p = 0.005) but not for the control group (r = −0.137, p = 0.534). C, D, Brain activation of right MFG significantly mediated the relation between arithmetic scores and VSWM performance in the AMC group. All paths are reported as standardized regression coefficients. **p < 0.01, *p < 0.05.

Discussion

In the present study, children receiving long-term AMC training performed better on both arithmetic and VSWM tasks than their peer schoolmates who did not receive the training (Figs. 3A, 4A). In addition, the AMC group showed a significant correlation between arithmetic scores and VSWM performance, even when controlling for age, gender, and intelligence, which, however, was not found in the control group (Figs. 3B, 4B). While both groups showed similar activation pattern in the VSWM task (Fig. 5), the AMC group showed significantly stronger activation than the control group in the frontal, parietal, and occipital regions (Fig. 6). Moreover, in the AMC group, the activation of the right MFG mediated the relation between arithmetic ability and VSWM performance (Fig. 7). These results indicate that AMC training not only improves arithmetic ability but also has a positive effect on VSWM, potentially through a transferring effect of AMC training on the related neural plasticity. Below, we discussed the potential mechanisms underlying the transferring effect of AMC training.

The majority of previous studies examining impacts of AMC training focused on numerical tasks (Tanaka et al., 2002, 2012; Chen et al., 2006; Wang et al., 2015; Yao et al., 2015). In contrast, the impacts of AMC training on other cognitive functions remain poorly understood. The present study demonstrates that AMC training enhances VSWM performance, and therefore may be used as a promising program for VSWM intervention. Given that operational processes of AMC involve VSWM components, such as maintaining and manipulating beads within an imaginary abacus, this cognitive benefit is conceivable and could be attributed to a near transfer effect. Relatedly, in another cohort of children receiving AMC training for ∼3–4 h per week over 3 years, we observed that AMC trainees performed better than control subjects in both digit and letter forward memory spans (Hu et al., 2011), indicating that AMC training might generate transferable gains to verbal WM. However, such transfer effect of AMC training should be interpreted with caution, for the memory span test only assesses the storage component of verbal WM. In respect to the AMC training effect on general intellectual ability, the lack of significant difference on the Raven's test after training (Table 1) suggests no “far” transfer effect of AMC training on intelligence. This result is consistent with several previous studies reporting no “far” transfer of WM training to intelligence (Redick et al., 2013; Thompson et al., 2013; Melby-Lervåg et al., 2016). However, as the present study only included the Raven's test, which assesses the nonverbal reasoning component of fluid intelligence, further study is warranted. Similar to the work by Redick et al. (2013), future study should conduct a battery of cognitive tasks comprising multiple measures of fluid intelligence, crystallized intelligence, verbal WM, multitasking, perceptual speed, and more to address the “far” transfer effect of AMC training more comprehensively.

Regarding the “near” transfer gain, our imaging results provide a neural basis for understanding the positive effects of AMC training on VSWM in childhood. While the two groups activated similar brain regions (Fig. 5) that have been consistently observed in the literature of VSWM tasks (Kwon et al., 2002; Owen et al., 2005), stronger activation in the AMC group relative to the controls was found in the bilateral MOG, right SPL, and right IPL regardless of memory loads (Fig. 6A,B). These regions are thought to be the primary neural substrates of visual processing, and can be selectively activated by information demanding visuospatial processing and visual-motor imagination (Engel et al., 1994; Malach et al., 1995). It has been suggested that the AMC experts rely on brain areas underlying visuospatial processing to form an abacus-based mental representation of numbers while solving numerical problems (Hanakawa et al., 2003; Hu et al., 2011; Li et al., 2013). It is possible that the frequent use of visuospatial mental imagery during AMC training, in return, leads to enhanced functioning of these brain regions, which enables AMC users to perceive and maintain visuospatial information more efficiently. Additional support for this interpretation comes from our previous findings that resting-state functional connectivity within the visual network, including the bilateral occipital regions, is enhanced after long-term AMC training (Weng et al., 2017; Xie et al., 2018).

In contrast to similar enhanced activation in the visual network across different WM loads in the AMC group (Fig. 6B), the activation of right MFG, left SFG, and left IPL showed an interesting group × load interaction (Fig. 6C). While the control group showed higher activation (or a tendency of higher activation) than the AMC group at a low load, an opposite activation pattern was seen at high loads (Fig. 6D). Such a complex change in activation pattern is consistent with findings of a previous WM training study (Schweizer et al., 2013). In this study, adult subjects showed decreases in frontal-parietal activation from pretraining to post-training at a WM load (3-back in their case) that represented pretraining WM maximum capacity but was much lower than the post-training maximum WM capacity (Schweizer et al., 2013). In contrast, for a higher WM load (5-back) that was beyond pretraining WM maximum capacity but became attainable at post-training, the participants showed increases in frontal-parietal activation from pretraining to post-training. Decreased activation in the frontal-parietal network under a lower WM load was thought to be associated with improved WM capacity, whereas increased activation in similar areas under a higher WM load was presumably attributed to increasingly effortful WM performance. Consistent with this conjecture, AMC children recruited less activation than the controls at the 0-back WM load but recruited greater activation than the controls at the 2-back and 3-back WM loads in the present study. Such a load-dependent activation contrast between the AMC and control groups may help reconcile the discrepant results in the extant literature, which have documented patterns of neural activation decreases (Schneiders et al., 2011, 2012; Thompson et al., 2016) and increases (Olesen et al., 2004; Jolles et al., 2010) across different experiments.

In addition to the activation differences between AMC and control groups (Fig. 6), our mediation analysis reveals that the beneficial effect of AMC training on VSWM was partly mediated by the brain activation in right MFG (Fig. 7C). This mediation effect was replicated when the HRT measures, rather than the mental calculation scores, were used as the dependent variable (Fig. 7D), strengthening the reliability of this finding. In addition, this result is in good agreement with the view that the right MFG is sensitive to visual WM training (Schneiders et al., 2011). As is known, the right MFG is one of the last areas to mature during childhood (Giedd, 2004), and has long been postulated to be critical for supporting the development of the maintenance or manipulation processes of VSWM (Klingberg et al., 2002; Kwon et al., 2002). It is possible that AMC training contributes to the neurobiological maturation of right MFG, which then promotes the transfer of training gains to VSWM. Furthermore, prior studies in adults and elders have reported that greater activation in right MFG can predict larger behavioral gains in cognitive training (Subramaniam et al., 2014; Vermeij et al., 2017). It is therefore interesting to further investigate how the individual differences in the MFG activation before training inform the individual differences in AMC training outcomes (e.g., mental calculation scores) as well as the transferring effect to VSWM.

The present study has several limitations. One limitation is the use of a scanner with relatively low magnetic field (1.5 T). It might have limited the sensitivity in assessing the activation in subcortical regions, such as the caudate, which has been shown to be involved in WM training (Dahlin et al., 2008; Salmi et al., 2018). It should also be noted that the subjects of the present study were children. As the neurodevelopment of WM is quite protracted into adulthood (Klingberg et al., 2002; Crone et al., 2006), it warrants further study to investigate how long the AMC training induced beneficial effect on VSWM would last, and whether or not the transferring effect we observed in children can be found in adults receiving AMC training. Last, regarding the importance of reliability to neuroimaging studies (Xing and Zuo, 2018), further research is needed to replicate these findings.

In conclusion, the present study demonstrates that long-term AMC training not only improves arithmetic ability but also enhances VSWM performance in children, which is likely associated with functional changes in the frontal, parietal, and occipital areas. More importantly, the functionality in middle frontal region plays an important role in the transfer of AMC training gains to VSWM. The results of this study provide a new perspective to improving WM performance in childhood and enhance our understanding of the neural mechanism underlying cognitive plasticity. Given the significant relation between arithmetic ability and WM in AMC children, it is tempting to think that a combination of AMC and classical WM training programs is more likely to obtain training-induced plasticity and, thereby, can better improve both arithmetic and WM performance than the training targeting just one of them.