AFM-Nanomechanical Test: An Interdisciplinary Tool That Links the Understanding of Cartilage and Meniscus Biomechanics, Osteoarthritis Degeneration, and Tissue Engineering

Abstract

Our objective is to provide an in-depth review of the recent technical advances of atomic force microscopy (AFM)-based nanomechanical tests and their contribution to a better understanding and diagnosis of osteoarthritis (OA), as well as the repair of tissues undergoing degeneration during OA progression. We first summarize a range of technical approaches for AFM-based nanoindentation, including considerations in both experimental design and data analysis. We then provide a more detailed description of two recently developed modes of AFM-nanoindentation, a high-bandwidth nanorheometer system for studying poroviscoelasticity and an immunofluorescence-guided nanomechanical mapping technique for delineating the pericellular matrix (PCM) and territorial/interterritorial matrix (T/IT-ECM) of surrounding cells in connective tissues. Next, we summarize recent applications of these approaches to three aspects of joint-related healthcare and disease: cartilage aging and OA, developmental biology and OA pathogenesis in murine models, and nanomechanics of the meniscus. These studies were performed over a hierarchy of length scales, from the molecular, cellular to the whole tissue level. The advances described here have contributed greatly to advancing the fundamental knowledge base for improved understanding, detection, and treatment of OA.

Graphical Abstract

1. INTRODUCTION

Articular cartilage provides biomechanical functions critical for joint motion, including load bearing,¹ energy dissipation,² and lubrication.³ Due to its avascular nature, cartilage has poor self-healing capabilities. Aggravated by the large range of motion and mechanical stress in articulating joints, local cartilage defects often progress to osteoarthritis (OA),^4,5 a chronic degenerative disease that affects tens of millions of Americans as of 2012, especially the elder population.⁶ In late-stage OA, total loss of cartilage leads to severe pain and restricted joint motion, and a total joint replacement is required. In the past decades, there have been numerous attempts to understand OA pathogenesis in order to establish effective diagnostic tools and to develop functional repair/regeneration strategies.^7,8 To this day, a functional cure remains elusive, and there are no disease-modifying osteoarthritis drugs available. Substantial advances are hindered by the limited understanding of the structural and mechanical characteristics of cartilage in normal and diseased states, especially at the nanometer scale or molecular level.⁹ Such knowledge is critical because the nanoscale structure and mechanical features are the key factors of cartilage tissue-level mechanical function, and changes at this scale are often direct results of cellular signaling and molecular biological activities as a result of OA.

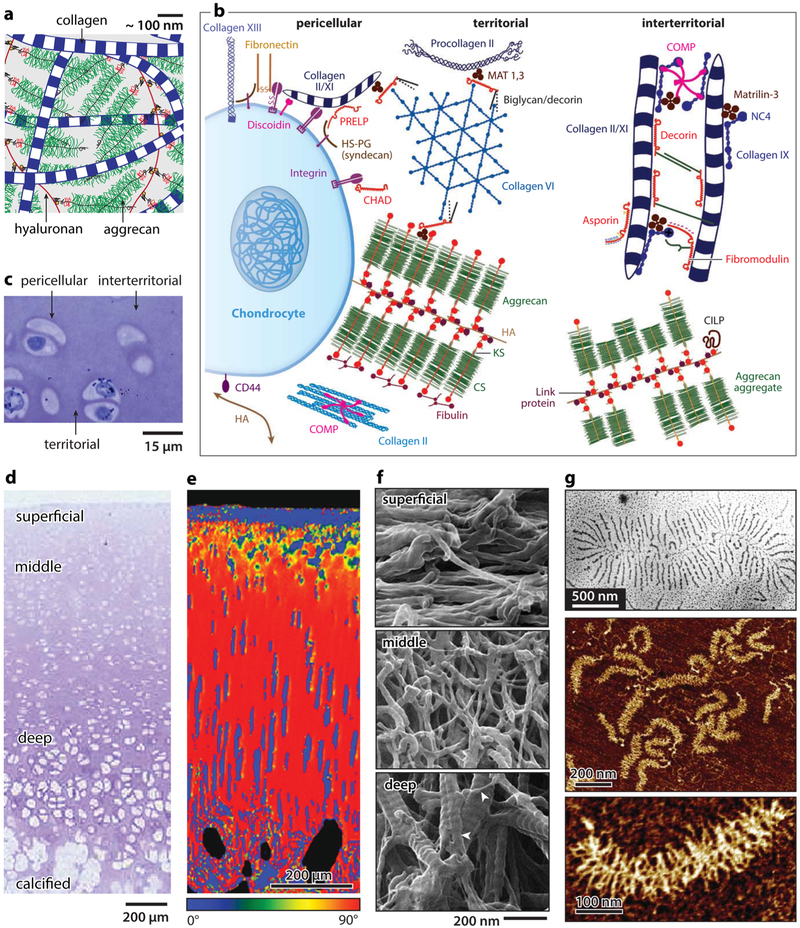
The extracellular matrix (ECM) of cartilage is a hierarchically structured composite of ~65–70% w/w water, ~20–30% collagens, and ~10% proteoglycans,¹ as well as other DNAs and proteins (Figure 1a-c).^10,11 In the ECM, the network of type II/IX/XI collagen fibrils (diameter ~30–80 nm) varies in orientation with depth in the tissue,¹² from being transverse in the superficial layer, to random in the middle layer, and predominantly perpendicular in the deep layer, accompanied by an increasing gradient of proteoglycan concentration (Figure 1d-f).^11,13,14 The collagen network is primarily responsible for cartilage tensile stiffness, whereas the compressive resistance and hydraulic permeability are governed by the major proteoglycan, aggrecan.¹ Aggrecan has a bottle-brush structure (M_w ~ 2.5 MDa), with chondroitin sulfate- and keratan sulfate-glycosaminoglycan (CS-GAG and KS-GAG) side chains densely packed along its ~400 nm long core protein.^15-17 In vivo, aggrecan macromolecules are end-attached to hyaluronan¹⁸ through the G1-domain to form aggregates,¹⁹ which are stabilized by link proteins (Figure 1g).²⁰ These aggregates self-assemble within the porous collagen fibrillar network (~100 nm pore size) and, with dozens of additional proteins, proteoglycans, and glycoproteins, form the functional cartilage ECM.^10,21 On the surface, there localized mucin-like glycoprotein, lubricin along with phospholipids, which contribute to surface lubrication.^22,23 In cartilage, chondrocytes account for 3–5% of the total volume and are distributed irregularly throughout the ECM.²⁴ Each chondrocyte is surrounded by a 3–5 μm thick pericellular matrix (PCM) that is rich in type VI collagen and perlecan (Figure 1b,c). The PCM provides the mechanical environment of chondrocytes and regulates chondrocyte mechanobiological signaling.²⁵ Besides these major constituents, there exist families of quantitatively minor proteins and proteoglycans (Figure 1b), including small leucine-rich proteoglycans (SLRPs), matrilins, and cartilage oligomeric matrix protein (COMP). These molecules mainly play regulatory roles in the formation and maintenance of the ECM through specific binding activities, whereas their molecular activities in cartilage function and OA-associated dysfunction remain unclear.¹⁰

Figure 1.

Hierarchical structure of articular cartilage extracellular matrix (ECM). (a) Schematic of the structure and major constituents of cartilage ECM: type II/IX/XI collagen fibril network and aggrecan–hyaluronan aggregates.¹⁸ Molecular density is reduced to increase clarity. Adapted with permission from ref 31. Copyright 2014 American Chemical Society. (b) Matrix molecular composition and organization in different extracellular regions. Adapted with permission from ref 10. Copyright 2009 Wiley. (c,d) Zonal heterogeneity: Toluidine blue histology images of rabbit cartilage showing (c) the pericellular, territorial, and interterritorial matrices; (d) depth-dependent zonal heterogeneity. Adapted with permission from ref 11. Copyright 2006 Osteoarthritis Research Society International. (e) Collagen fibril orientation distribution in relation to cartilage surface, measured by the quantitative polarized light microscopy (qPLM) on mature porcine cartilage. Adapted with permission from ref 13. Copyright 2006 Osteoarthritis Research Society International. (f) Nanostructure of collagen fibril network measured by helium ion microscopy on proteoglycan-removed rabbit cartilage. Adapted with permission from ref 14. Copyright 2012 Wiley. (g) Nanostructure of aggrecan-hyaluronan aggregates imaged by (top panel) transmission electron microscopy and (middle panel) tapping mode AFM, as well as (bottom panel) nanstructure of individual aggrecan by tapping mode AFM. Adapted with permission from refs 17 and 20. Copyright 2010 Osteoarthritis Research Society International and 1983 Gustav Fischer Verlag.

In addition to the study of cartilage, it is now recognized that OA is a disease of the entire joint affecting and affected by multiple synovial tissues.²⁶ For instance, post-traumatic osteoarthritis (PTOA) is often initiated from tears in meniscus and/or anterior cruciate ligament (ACL), and damage to these tissues is also a manifestation of OA.²⁷ Each synovial tissue has a distinctive ECM structure, mechanical properties, and degradation pathogenesis. In order to understand, detect, prevent, and ultimately cure OA, it is necessary to bring these tissues into the equation.

Recent advances in nanotechnology provided a new paradigm to study cartilage biomechanical function and disease progression at unprecedented resolution. Such techniques include instrumented nanoindentation,²⁸ atomic force microscopy (AFM) force spectroscopy,^29-31 optical tweezers,³² magnetic twisting cytometry,³³ micropipette aspiration,³⁴ cytocompression,³⁵ and surface force apparatus.³⁶ These tools are often used in combination with nanostructural imaging modalities, such as scanning and transmission electron microscopy (SEM and TEM),²⁰ helium ion microscopy (HIM),¹⁴ and AFM imaging,¹⁵ to elucidate the structure–mechanics relationships of biological tissues. Earlier contributions of these techniques to understanding OA have been summarized in our previous review paper.³⁷ In this review, we focus on the recent advances and applications of the most widely used nanomechanical technique, AFM-based nanoindentation, and its extended modes. Given the increasing application of this tool, this review includes a detailed discussion of technical considerations (section 2), as well as recent technical advances and their potential applications (section 3). We then summarize current applications of these techniques to the understanding of OA and tissue engineering (section 4), murine cartilage models (section 5), and specialized properties of the meniscus (section 6). In the closing, section 7, we provide our remarks on challenges and future opportunities in this field.

2. AFM-NANOINDENTATION: TECHNICAL CONSIDERATIONS

AFM-based nanomechanical tests are widely used for studying the small-scale biomechanics of soft tissues, owing to its versatility in loading modes, contact geometries, force ranges, as well as the ease to operate in aqueous conditions. Since the invention of AFM in the 1980s,³⁸ this technique has made a transformative impact in biomechanical research by enabling the studies of soft tissue nano- and micromechanics in situ. In the 1990s, AFM was applied to study cell surface ligand–receptor molecular adhesion,³⁹ single-molecule biomechanics,^40,41 and single-cell mechanics.^42,43 Since then, AFM has been widely used in measuring the nanomechanics of various cell types,^44-47 cell surface glycocalyx layers (the pericellular matrix formed in vitro),^48,49 matrix molecules,^50,51 as well as tissue microheterogeneity.^52,53 Notably, AFM revealed the biomechanical characteristics of human cancer cells⁵⁴ and tumors,^55,56 the role of matrix stiffness in regulating stem cell lineage⁵⁷ and cancer cell phenotype,⁵⁸ as well as the role of fiber stiffness in cell phenotype and fiber recruitment,⁵⁹ To this day, AFM-based tests have become a popular tool in many biomaterials and bioengineering fields, as underscored by a number of key review articles.^60-62 In this review, we focus on the application of AFM-nanoindentation in articular cartilage and osteoarthritis research. This section provides an overview on the experimental design and data analysis for AFM-nanoindentation.

2.1. AFM-Based Nanoindentation: Experimental Design.

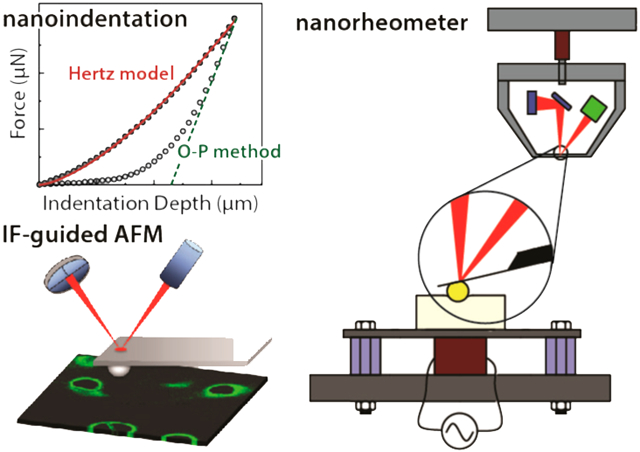
While originally designed for imaging surface topography, AFM now often serves as an instrument for nanoindentation testing of biological tissues and biomaterials in fluidic states. In this mode, the AFM z-piezo controls the probe tip to move perpendicular toward the sample surface (Figure 2a) and to indent into the sample (biomacromolecular assemblies, cells, or tissues) at constant piezo displacement rates ranging from 0.05 to 20 μm/s (which is approximately the indentation depth rate), up to a preset maximum indentation depth or force. The tip is then either immediately retracted from the sample or held at a constant position for a predetermined dwell time to enable a ramp-and-hold relaxation test before retracting or held at a constant force for a dwell time to enable a creep test before retracting. With proper calibration of the cantilever spring constant and deflection sensitivity,⁶³ the indentation force versus depth (F–D, Figure 2b) curve can be deduced. The effective tip–sample contact point can be determined via algorithms such as the golden section method.^64-66 Analytical contact mechanics models can then be applied to account for tip–sample contact geometry in order to extract material mechanical properties from each F–D curve.⁶⁷

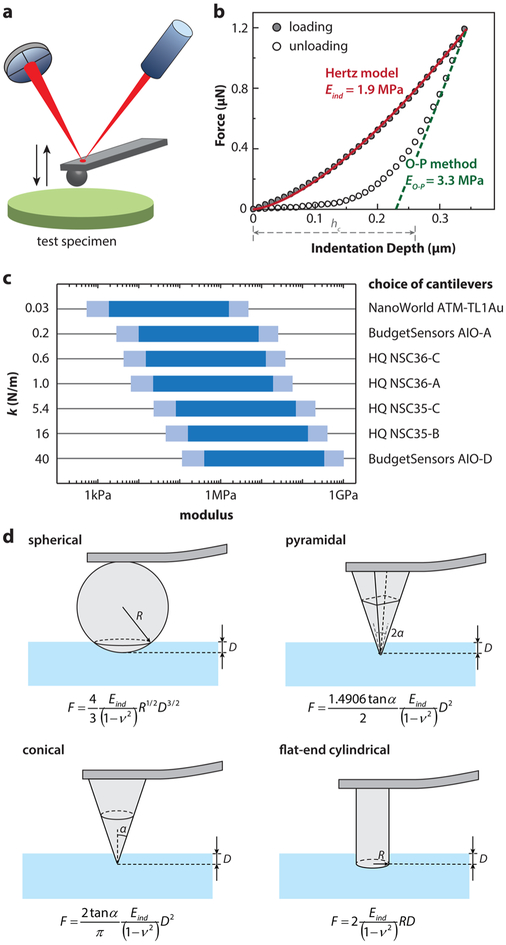
Figure 2.

AFM-nanoindentation of cartilage and soft tissues. (a) Schematic of AFM-based nanoindentation. (b) Representative nanoindentation curve on adult wild-type murine cartilage and corresponding data analysis at 10 μm/s displacement rate with a microspherical tip (R ≈ 5 μm) in PBS. Indentation moduli were calculated by fitting with (1) the Hertz model on the entire loading curve and (2) the Oliver–Pharr method on the top 25% of the unloading curve (punch parameter ε = 0.75, h_c denotes the corresponding contact depth). Both fits yield R² > 0.99. (c) Suitable choices of cantilever spring constants for specimens with different orders of elastic moduli. (d) Schematics of commonly used contact geometries and contact mechanics models for AFM-based nanoindentation: spherical, pyramidal, conical, and flatend indenter tips.⁶⁷

With a wide range of commercially available cantilever spring constants (~0.01 to ~300 N/m) and probe tip geometries (pyramidal, spherical, conical, and cylindrical flat-punch, with radii varying from <2 nm to ~100 μm), AFM instruments can apply forces over several orders of magnitude (~10 pN to ~1 mN) to measure the mechanical properties of biomacromolecules, cells, and tissues with modulus varying from ~100 Pa to 1 GPa. Importantly, these characterizations can be performed either in air or completely immersed in fluid, enabling the study of biological tissues and biomaterials under near-physiological conditions. In Figure 2c, we provide a range of applicable probe cantilever spring constants suitable for samples with different moduli based on a 5 μm radius microspherical tip and an indentation depth range from 100 nm to 2 μm (~40% tip radius) over 250 nm cantilever deflection (corresponding to the optimal photodetector signal ≈5 V for a common cantilever with ≈50 nm/V deflection sensitivity).

Contact mechanics models for various probe tip geometries are available (Figure 2d). Among these options, we recommend use of the microspherical tip over other shapes for general purposes as it has the simplest symmetry and is subjected to less contact geometry variations or errors. Other tip shapes are also applicable, but it is challenging to obtain an accurate estimate of tip–sample contact geometry. For example, pyramidal and conical tips are both fabricated via etching,⁶⁸ with a half-open angle that is subject to asymmetry in different facets as well as substantial variations from the nominal values quoted by manufacturers. These uncertainties can result in systematic errors in modulus calculation. For example, using poly(vinyl alcohol) (PVA) hydrogels in the absence of structural hierarchy, moduli measured by nanoindentation and macroscopic compression are expected to be similar. In fact, nanoindentation by spherical tips yields results that conform to this hypothesis, whereas the use of pyramidal tips overestimated the modulus up to 10-fold.⁶⁹ It should also be noted that, while pyramidal tips have end radii R ~ 10–50 nm, under nanoindentation, their contact geometry is better defined by the half-open angle, α, rather than R. For an indentation depth of ~1 μm, the effective contact area is ~10 μm², which is on the same order as that for a microspherical tip, suggesting strongly that the use of a pyramidal tip does not directly elucidate nanometer-scale mechanical characteristics. In order to measure mechanical properties at the nanoscale, it is necessary to control not only the tip radius but also the contact length and contact area at submicron levels. An example of nanoscale mechanical property assessment is that of aggrecan–aggrecan interactions measured by high-resolution force spectroscopy.^29,70

Nanoindentation can be used to assess microscale heterogeneity of biological tissues. This is critical for cartilage because the modulus of cartilage ECM varies significantly with tissue depth and with indentation orientation due to local variations in collagen fibril structure and proteoglycan concentration.⁷¹ To expose the interior parts of the tissue, sectioning is necessary; however, sectioning inevitably damages the structural integrity on the cut surface. Despite this pitfall, several studies have shown that testing such sections is a powerful way to delineate tissue spatial heterogeneity,⁷¹ detect disease progression,⁷² and evaluate the mechanical properties of the murine cartilage tissue interior.⁷³ Sectioning tools include microtoming of fresh tissues, cryotoming of frozen tissues preserved in optimal cutting medium (OCT), and vibratoming of fresh tissues.⁷⁴ It is usually challenging with microtoming or vibratoming to obtain sections with homogeneous thickness, whereas cryotoming is more advantageous to this end. However, freeze–thaw cycles can alter tissue biomechanical properties,⁷⁴ possibly due to the formation of ice crystals. Therefore, embedding in OCT is an effective way to better preserve tissue integrity.

2.2. Considerations for Data Analysis.

Two linear, isotropic elastic models have been widely used to calculate the effective indentation modulus. Using microspherical indentation as an example, the first approach applies the Hertz model⁷⁵ to the loading portion of F–D curves, as exemplified in Figure 2b:

$$F=\frac{4}{3}\frac{E_{\text{ind}}}{(1-{\nu }^2)}{R}_{\mathrm{r}}^{1∕2}{D}^{3∕2}$$ (1)

where F is the indentation force, D the indentation depth, R_r the reduced contact radius, and ν the Poisson’s ratio of the tested sample (ν = 0.1 for young bovine cartilage⁷⁶). The reduced contact radius R_r is a function of the radii of curvature of both the probe tip and the tested sample:

$$\frac{1}{R_{\mathrm{r}}}=\frac{1}{R_1}+\frac{1}{R_2}$$ (2)

where R₁ is the tip radius (abbreviated as R in the text) and R₂ is the radius of the curvature of the tested sample (i.e., the radius of a cell, or assumed to be infinite for flat tissues). In the Hertzian framework, samples are assumed to be linearly elastic and isotropic, and tip–sample contact is frictionless. For spherical indenters, the Hertz fit is applicable in the limit of small deformation (maximum indentation depth <0.4R).⁷⁷ We note that application of the Hertz model proves a good fit to data from indentation of murine knee condyle cartilage over the entire ≈350 nm extent of the loading curve (Figure 2b). This agreement confirmed the validity of Hertz model to measure the indentation modulus and thereby predict the effective resistance of the tissue to compressive load. A detailed review of analytical models within the Hertzian framework, including other contact geometries, is available in ref 67.

For thin (micrometer thick) tissue sections, the Hertz model can be modified with a finite-thickness correction factor to account for the substrate constraint and stiffness effects.⁶⁹ Here, the substrate is assumed to be infinitely stiff compared to the tested tissue sections

$$F=\frac{4}{3}\frac{E_{\text{ind}}}{(1-{\nu }^2)}{R}^{1∕2}{D}^{3∕2}{C}_{\chi }$$ (3)

The correction factor C_χ is

$$\begin{gathered} C_{\chi }=1-\frac{2{\alpha }_0}{\pi }\chi +\frac{4{\alpha }_0^2}{{\pi }^2}{\chi }^2-\frac{8}{{\pi }^3}\left({\alpha }_0^3+\frac{4{\pi }^2}{15}{\beta }_0\right){\chi }^3 \\ +\frac{16}{{\pi }^4}\left({\alpha }_0^3+\frac{3{\pi }^2}{5}{\beta }_0\right){\chi }^4 \end{gathered}$$ (4)

where $\chi =\sqrt{\mathit{RD}}∕h$ and h is the thickness of the sample. The constants α₀ and β₀ are functions of the Poisson’s ratio ν of the tested tissue, which are analyzed in detail in ref 69. For linear materials, this model is appropriate for finite thickness, 0.1R ≤ h ≤ 12.8R. For h > 12.8R, the semi-infinite assumption can be assumed. For h < 0.1R, significant material nonlinearity may be present, and additional analytical formula can be found in ref 78.

The other frequently employed approach is the Oliver–Pharr method, which uses the initial slope of the unloading portion of the F–D curves (top 25–75%) to calculate the elastic modulus.^79,80 This method was originally developed to estimate the “elastic recovery” modulus of materials that mainly undergo elastic–plastic deformation during indentation (e.g., ceramics and metals)⁷⁹ and assumes that tested materials are flat and do not adhere to the tip. The loading curve is considered to include both reversible elastic and irreversible plastic deformation, and a 5–10 s hold at constant force is included after loading to allow for the completion of viscoelastic creep. Thus, the unloading curve is assumed to represent primarily linear elastic recovery. The Oliver–Pharr method first calculates the slope of the initial portion of the unloading curve as the stiffness, S = dF/dD. From the stiffness, the elastic modulus is given by

$$E_{\mathrm{O}-\mathrm{P}}=\frac{\sqrt{\pi }}{2}(1-{\nu }^2)\frac{S}{\sqrt{A}}$$ (5)

where A is the area function related to the effective cross-sectional or projected area of the indenter. For example, for a spherical indenter, A = 2πRh_c (R ≫ h_c), where h_c, the contact depth, is the distance between the initial contact point and the intercept of unloading slope indentation depth axis, corrected by the punch factor ε (ε = 0.75 for spherical tip).

$$h_{\mathrm{c}}=h_{\max }-\epsilon \frac{F_{\max }}{S}$$ (6)

For articular cartilage, it is important to note that the Oliver–Pharr method (using the unloading curve) predicts a value of the indentation modulus for the data of Figure 2b that is ≈1.7× the value of that predicted by the Hertz model, which uses the loading curve. There are several reasons why the use of the unloading curve may give this overestimate of the modulus, as described below.

In both of the original models, linear elasticity is assumed; that is, the modulus is the same under compression and tension (Young’s modulus). Cartilage, as a collagen fibril–aggrecan composite, however, behaves very differently under tension versus compression.⁸¹ In addition, cartilage exhibits salient time-dependent mechanical properties, governed by both intrinsic macromolecular frictional viscoelasticity⁸² and fluid-flow-induced poroelasticity.² Therefore, although fitting data to the Hertz model or the Oliver–Pharr method can both yield values of an “indentation modulus”, these values do not necessarily represent the inherent equilibrium Young’s modulus of cartilage. In addition, the compressive behavior of cartilage can be linear for an adequately small indentation depth, but nonlinear for larger strain.⁸³ Even for the case of linear compressive behavior at small indentation depth, neither method incorporates the time-dependent poroviscoelastic energy dissipation during deformation, as both models assume quasi-static (equilibrium) conditions.

The values calculated from Hertz model from the loading curve thus represents an “effective indentation modulus”, reflecting mostly the compressive resistance of cartilage at a given indentation rate. For slow enough loading rates, this Hertzian indentation modulus will reach the limiting behavior of the true tissue “equilibrium modulus”. In contrast, the unloading curve for cartilage includes the combined effects of both elastic recovery and poroviscoelastic force relaxation. Thus, the elastic–plastic recovery from deformation assumed in the Oliver–Pharr method does not hold. Importantly, the difference between the loading and unloading curves of cartilage (e.g., Figure 2b) is primarily due to reversible poroviscoelasticity rather than irreversible plastic deformation, as confirmed by the absence of permanent deformation (typically observed with ceramics or metals) and the high repeatability at each indentation site. Therefore, under a testing scenario such that the poroviscoelastic relaxation time constant is on the same order of the unloading time frame, a steep unloading slope is most likely due to slow poroelastic relaxation rates (compared to the experimental unloading rate). As a result, use of the Oliver–Pharr method may misleadingly result in E_O–P values that substantially overestimate the true equilibrium Young’s modulus.

While it is critical to distinguish between the poroviscoelastic and equilibrium elastic properties of cartilage (as they are both direct measures of native cartilage biomechanical function at different loading rates/frequencies), researchers have used both the Hertz model and the Oliver–Pharr methods to study relative changes in tissue or tissue-engineered construct behavior (e.g., during culture, during osteoarthritis degradation, or after genetic modification). Application of both these methods may enable identification of relative differences in the mechanical properties of native or engineered products before and after treatments or for OA versus normal tissue.^84,85 However, we recommend the use of the Hertz model on the loading curve over the Oliver–Pharr method on the unloading curve for two main reasons. First, it is a direct measure of the resistance to indentation during loading, similar to that of compressive loading of cartilage in vivo. Second, due to the poroviscoelastic relaxation effects, the Hertz model applied for tests using slow enough loading rate tests will give a more accurate estimate of the equilibrium modulus. For example, indenting via rates at the lower end of instrument limit, 0.1–1 μm/s, could effectively minimize the contribution from poroelasticity and intrinsic viscoelasticity to the measured modulus. On the other hand, the Oliver–Pharr method will likely give a substantial overestimate of the modulus (e.g., Figure 2b).

3. EXTENDED AFM MODES FOR STUDYING NATIVE CARTILAGE BIOMECHANICS

This section presents two extended modes of AFM-nanoindentation developed recently, the dynamic oscillatory wide-bandwidth nanorheometric test⁸⁶ and immunofluorescence-guided nanomechanical mapping.³⁷ At the same time, we summarize new findings of cartilage nanomechanics revealed by these two modes.

3.1. Technical Advance: Wide-Bandwidth Nanorheology.

More accurate measurement of time-dependent, non-linear mechanics of cartilage requires more complex experimental tests in combination with theoretical or finite element models.⁸⁷ Our recently developed wide-bandwidth AFM-nanorheometer is capable of quantifying the frequency-dependent dynamic complex modulus of cartilage, including the associated force–displacement phase lag, over four decades of frequencies (<1 Hz to 10 kHz, Figure 3a). In this system, the AFM is coupled with a custom-built actuating system, which employs a secondary piezo with resonance frequency much higher than 10 kHz to enable dynamic, nanoscale z-oscillation up to ~10 kHz.⁸⁸ This frequency range cannot be achieved in commercial AFM instruments, as their z-piezo typically has a resonance frequency lower than 5 kHz. For example, due to the piezo resonance, significant damping of oscillatory amplitude can lead to systematic errors at higher frequencies (f ≥ 300 Hz for the BrukerNano MultiMode AFM, and f ≥ 10 Hz for the standard Asylum Research MFP-3D). Therefore, the secondary piezo is necessary for studies requiring deformation at high frequencies. Examples include the study of tissues having high hydraulic permeability, such as measurement of the poroelasticity of GAG-removed cartilage.^89-91 In addition, the goal of separately identifying the superimposed flow-independent poroelastic behavior, such as tendon, has also demonstrated the need for this high-bandwidth approach.⁹² However, for experiments that do not require a wide frequency bandwidth, this nanorheometric approach can be directly employed using commercial AFMs, as shown for studies of native cartilage^66,93 and hydrogels.⁹⁴

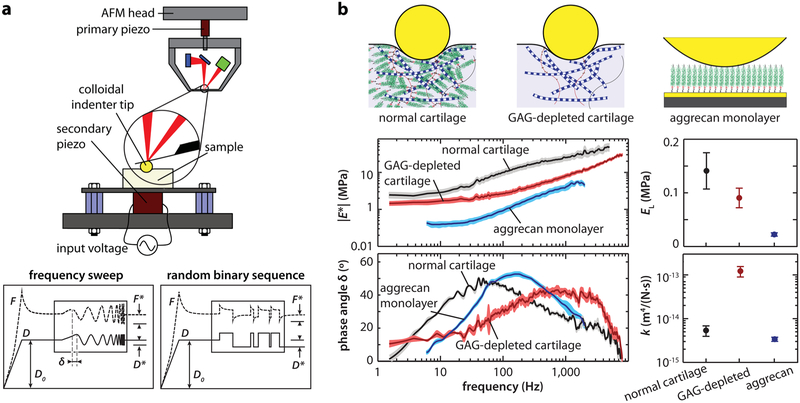
Figure 3.

Wide-bandwidth nanorheometric test of cartilage poroelasticity at the nanoscale. (a) Top panel: schematic of the custom-designed nanorheometer. Bottom panel: representative force and displacement profiles that contain the dynamic oscillation in the form of a frequency sweep at 1–10 kHz or a random binary sequence (RBS). Adapted with permission from ref 86. Copyright 2013 Biophyscial Society. (b) Frequency spectra of complex dynamic modulus ∣E*∣ and phase angle δ of normal, GAG-depleted bovine cartilage and aggrecan monolayer (mean ±95% CI of 6 different locations on the same sample), as well as corresponding equilibrium modulus E_L and hydraulic permeability k (mean ± SEM, n = 4 animals for cartilage and n = 3 plates for aggrecan, *p < 0.05). Adapted with permission from ref 91. Copyright 2015 American Chemical Society.

With this nanorheometric setup, dynamic nanomechanical properties can be measured using microspherical probe tips (e.g., R ~ 1–100 μm). Here, a ramp-and-hold pre-indentation with a static indentation depth, D₀ (≈1–2 μm), is first applied, and after force relaxation has occurred, a nanoscale dynamic displacement is superimposed onto the static offset displacement. The resulting frequency spectra of the dynamic nanoscale force, F*, and displacement, D*, can be measured. Given D* ≪ D₀, a Taylor expansion of Hertz model can be applied to calculate the magnitude ∣E*∣ of the complex dynamic modulus, E*. In addition, the phase lag, δ, of the measured force F* with respect to the applied displacement D* can be directly measured at all frequencies. The dynamic displacement can be applied in the form of a sinusoidal frequency sweep⁸⁶ or a random binary sequence⁹¹ (e.g., Figure 3a). Alternatively, the measured force F* and applied displacement D* can be used to compute the real and imaginary parts of the complex modulus, E′ and E″, respectively, as all of the information in the magnitude and phase, ∣E*∣ and δ, is equivalently contained in E′ and E″.

This approach can be used to deconvolute the two rate-dependent (i.e., time- or frequency-dependent) deformation mechanisms inherent to soft tissues such as cartilage: intrinsic solid phase viscoelasticity due to the fluid-flow-independent reorientation and reconfiguration of macromolecules,⁹⁵ and poroelasticity associated with deformation-induced fluid–solid frictional interactions.⁶⁶ Given that poroelastic rate/frequency dependence scales with square of the characteristic length over which fluid flows during deformation,^96,97 whereas intrinsic viscoelasticity does not,⁹⁵ these two modes can be separated by (a) using a sequence of different-sized probe tip radii, R, to vary the fluid flow length scales or (b) using different initial static indentation depths, D₀. In the frequency domain, the peak frequency, f_p, that is, the frequency corresponding to the maximum of phase angle (e.g., Figure 3b), can be used to calculate the hydraulic permeability of the poroelastic tissue.⁹³ If f_p varies or scales with the square of D₀ or R, that would provide definitive evidence of poroelastic tissue behavior. In the time domain, the relaxation time constants can be extracted by fitting the experimental stress relaxation curves to various viscoelastic models (e.g., spring-dashpot or Prony series) or to poroelastic relaxation models. Examples of viscoelastic ramp-and-hold relaxation tests can be found, for example, the fit to a five-element spring-dashpot model with the correction of finite ramp rate.^98,99 Poroelastic relaxation is exemplified by fitting to the poroelastic diffusion equation, which has been reported for cartilage tissues^100,101 and hydrogels.^94,102

3.2. Poroviscoelasticity of Cartilage Tissue at the Nanoscale.

The nanorheometer test enables the study of cartilage poroelasticity at the micrometer scale, contributing to building a multiscale understanding of cartilage biomechanical functions. At the tissue level, with a fluid flow length L_p ~ 1 mm, the poroelastic peak frequency, f_p, is ~0.001 Hz (or τ_p ~ 1000 s),¹⁰⁰ which is much slower than the viscoelastic relaxation time constant of ~10 s.⁸² When cartilage is measured under nanorheometer, L_p is ≤10 μm, given that f_p ~ Hk/L_p²,² and this yields f_p ≫ 1 s.^66,93 As the intrinsic viscoelasticity is independent of fluid flow length, the viscoelasticity measured by nanoindentation yields a similar time constant ~10 s.⁶⁶ As a result, using a nanorheometer, the poroelastic time is much shorter than the viscoelastic time, and this is opposite to the observation at the macroscale. At the same time, these results also indicate the self-consistency of cartilage poroelasticity across multiple scales, where similar hydraulic permeability values are reported from micrometer scale to millimeter scale fluid flow lengths.⁹³

The nanorheometric test helps to give further molecular insights into cartilage poroelasticity. In cartilage ECM, it is primarily aggrecan, and less so the collagen fibrils, that is the determining factor of nanoscale poroelasticity. This is due to the fact that the closely spaced GAG chains of aggrecan¹⁶ provide the main resistance to intratissue fluid flow in cartilage, as manifested in the GAG–GAG nanomolecular model of hydraulic permeability.¹⁰³ In Figure 3b, the dynamic oscillatory loading responses of three specimens are compared: normal (native) cartilage, GAG-depleted cartilage, and biomimetic end-attached aggrecan monolayers.^89,91 The low-frequency modulus, E_L, of GAG-depleted cartilage is about 1.5× lower than the normal cartilage, whereas that of the aggrecan monolayer is about 7× lower. In contrast, despite having much lower modulus, the aggrecan monolayer shows comparable hydraulic permeability, k, to the native cartilage, whereas that of the GAG-depleted cartilage is ~25× higher, underscoring the direct contribution of aggrecan to cartilage hydraulic permeability. Further, for intact tissue, the isotropic poroelasticity model cannot capture the magnitude of energy dissipation (phase angle). The more complex fiber-reinforced model⁸¹ or transversely isotropic model¹⁰⁴ is necessary to account for cartilage tension–compression asymmetry and quantitatively capture the degree of energy dissipation. This indicates that the nanoscale mechanical anisotropy is critical for the enhanced cartilage poroelastic energy dissipation.

3.3. Technical Advance: Immunofluorescence-Guided AFM Mapping.

Recently, Guilak and co-workers developed a novel approach that combines immunofluorescent staining with AFM nanomechanical mapping.¹⁰⁵ This enables measurement of the mechanical properties of cartilage pericellular matrix (PCM) versus the territorial and interterritorial matrices (T/IT-ECM, the territorial and interterritorial regions are indistinguishable under optical microscope). In this approach, unfixed native tissues are embedded in water-soluble medium (e.g., OCT), sectioned into 5 μm thick slices via cryotoming, and attached to charged glass substrates. The unfixed sections can be immunolabeled with antibodies of PCM-specific molecules, such as type VI collagen¹⁰⁵ or perlecan.¹⁰⁶ It was reported that this staining does not alter the mechanical properties of the tissue, and thus the procedure can be used to distinguish the PCM from the T/IT-ECM during AFM testing (Figure 4a).¹⁰⁵ Guided by immunofluorescence (IF) imaging, nanomechanical mapping can be performed in a 20 μm × 20 μm region with a full ring-shaped PCM terrain with a 40 × 40 indentation grid (1600 indents). The finite thickness-corrected Hertz model⁶⁹ can be applied to extract the elastic modulus at each location. The modulus map is aligned with the corresponding IF image, and the moduli of the PCM, the T/IT-ECM, and the cell debris (region corresponding to damaged cytoplasm and nucleus produced by cryo-sectioning) can then be separated.

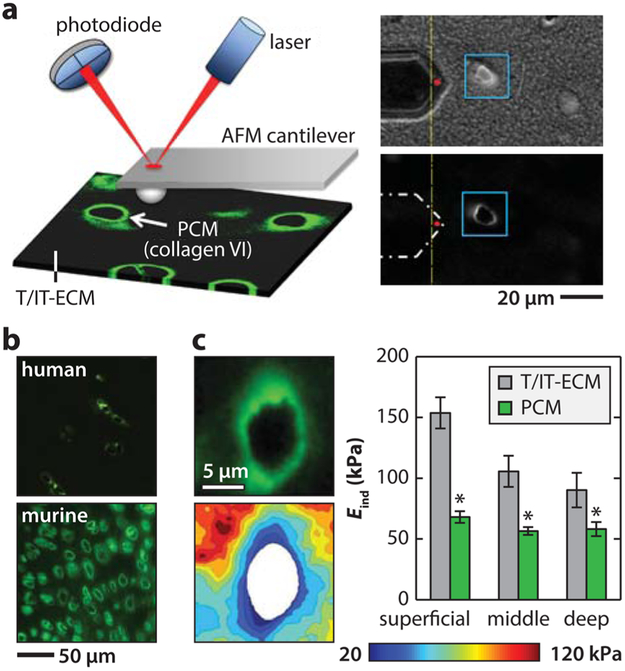
Figure 4.

Immunofluorescence (IF)-guided AFM nanomechanical mapping of cartilage elastic modulus. (a) Left panel: schematic of the IF-guided AFM on cryo-sectioned cartilage. Right panel: phase contrast (top) and IF images of type VI collagen illustrating the PCM and territorial/interterritorial ECM (T/IT-ECM) during AFM tests. Adapted with permission from ref 109. Copyright 2013 Elsevier Ltd. (b) Comparison of the IF-labeled adult human and murine cartilage images shows the much higher density of cells and PCM regions in the murine tissue. Adapted with permission from ref 72. Copyright 2013 Osteoarthritis Research Society International (human cartilage image only; murine cartilage image is original). (c) Left panel: representative modulus map and IF image of porcine cartilage section with a PCM terrain surrounding a cell-sized void. Right panel: elastic indentation modulus, E_ind, of T/IT-ECM versus PCM in different depth-dependent zones of cartilage (mean ± SEM for 20 images per zone from n = 5 mice, *p < 0.05 between T/IT-ECM and PCM; whereas the ECM shows significant depth-dependent variations, the PCM exhibits zonal uniformity). Adapted with permission from ref 105. Copyright 2012 The Royal Society of Chemistry.

This IF guidance is especially necessary for unbiased assessment of the heterogeneity of murine cartilage sections. In comparison to cartilage of larger animals, murine cartilage has a distinctively high cell density (Figure 4b). On the sectioned surface, areas corresponding to PCM and cell debris are thus comparable to that of T/IT-ECM. Under a regular optical microscope, these different areas cannot be clearly distinguished, and indentation on cell debris will inevitably result in substantial systematic errors. Therefore, for murine cartilage, IF imaging is a necessary step to clearly separate these three distinct regions and to remove artifacts from indentation results associated with cell debris.

One technical challenge of this approach is the extensive time needed for generating one map with 1600 indents. A more efficient alternative is the high-speed force scanning method developed by Darling.¹⁰⁷ In this mode, the probe tip is programmed to scan across the region of interest under a series of preset forces. The height profile of the area is recorded at each force set point, which will yield corresponding indentation depth values. The indentation F–D curve can be constructed from the series of depth and applied force values at each location. As a result, at each location, the force curve contains 5–8 pairs of F–D values. Despite the sparsity of the data, it has been shown that this approach can generate consistent modulus outcomes in agreement with nanoindentation-based modulus mapping¹⁰⁵ for both cells and ECM. The advantage of this approach is that it is less time-consuming and can yield higher spatial resolution.¹⁰⁷

3.4. Cartilage Tissue Heterogeneity: T/IT-ECM versus PCM.

In cartilage, the 3–5 μm thick PCM has distinctive composition, structure, and mechanical properties from the T/IT-ECM.²⁵ Because the PCM is the direct micromechanical niche of chondrocytes, its mechanical features are critical in regulating chondrocyte mechanobiology. Whereas earlier micropipette studies quantified the PCM modulus in extracted chondrons,¹⁰⁸ the recent advance of IF-guided AFM enables the breakthrough of direct quantification of PCM properties in situ, while it is integrated within the T/IT-ECM (Figure 4c). This approach not only confirmed the lower moduli of PCM but also elucidated unique mechanical characteristics of PCM, which is difficult to quantify with other methods. The PCM exhibits zonal uniformity independent of tissue depth, a feature distinctive from the salient depth-dependent variation of chondrocyte morphology and mechanics.⁷¹ Meanwhile, the PCM shows distinct anisotropy from the ECM. The ECM has highest modulus normal to the surface, the PCM has highest modulus parallel to the split-line orientation and to a lesser extent.⁷¹ In addition, whereas ECM is susceptible to catabolic enzymes, the PCM shows high resistance to aggrecan-targeted digestions including aggrecanase (a disintegrin and metalloproteinase with thrombospondin motifs-4 or ADAMTS-4), chondroitinase ABC and hyaluronidase, and is only susceptible to the nonspecific elastase.¹⁰⁹ A more in-depth review of cartilage PCM biology and mechanics can be found in ref 25.

4. APPLICATIONS IN OSTEOARTHRITIS AND TISSUE ENGINEERING

Nanomechanical understanding of OA tissues and repair products can provide new insights for disease progression and tissue repair. Earlier studies have used moduli measured by instrumented microindentation^28,110 and AFM-nanoindentation⁸⁵ as direct measures of repair tissue quality. This section summarizes more recent advances in understanding the nanomechanical features of cartilage aging and OA, as well as engineered cartilage products.

4.1. Implications for Aging and Osteoarthritis: Human Cartilage Studies.

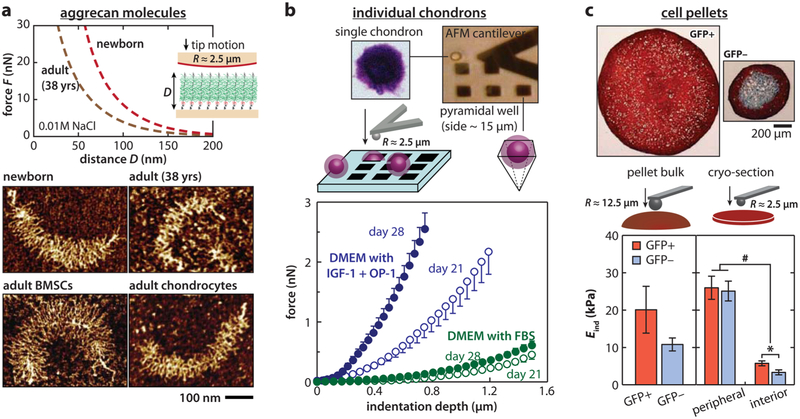
Structural and nanomechanical insights concerning the higher incidence of OA with age have been probed at both the molecular and tissue level. Specifically, for aggrecan, increased fragmentation can be quantified with AFM imaging by comparing molecules from newborn versus adult (29 and 38 years old) donors.¹⁶ Further, one unique advantage of imaging individual molecules via AFM is that, with the ultrastructure of each aggrecan being revealed, the full length aggrecan, which retains all globular domains from G1 to G3, can be separated from fragmented molecules in a quantitative and definitive manner. Such separation is difficult to achieve via conventional biochemical assays. As the accumulated effect of enzymatic degradation is absent within the full length subpopulation, the demonstrably shorter GAG side chains within the adult cohort can therefore provide direct evidence of altered chondrocyte GAG biosynthetic activities as a function of age (Figure 5a). In addition, aggrecan monomers from adult tissues show much reduced compressive stiffness compared to those from newborn or fetal tissues.

Figure 5.

Applications of AFM nanomechanical tests in studying cartilage aging and tissue engineering. (a) Comparison of the ultrastructure and compressive nanomechanics of native and engineered aggrecan. Top panel: compression resistance of end-attached newborn and adult (38 years old) human cartilage aggrecan monolayers measured via AFM force spectroscopy in 0.01 M NaCl solution (pH ≈5.6). Bottom panel: tapping mode AFM images of native human cartilage aggrecan and aggrecan synthesized by equine chondrocytes and bone marrow stromal cells (BMSCs) in self-assembled peptide hydrogel culture. The newborn human aggrecan shows core protein and CS-GAG side chains longer than that of the adult one. Meanwhile, engineered aggrecan by BMSCs shows longer core protein and longer CS-GAG side chains than that by age-matched chondrocytes. Adapted with permission from refs 16 and 17. Copyright 2012 Elsevier Inc. and Osteoarthritis Research Society International. (b) Impacts of growth factors on chondrocyte-engineered PCM. Top panel: schematic of AFM-nanoindentation on individual chondrons (chondrocytes-PCM composite) immobilized within silicon pyramidal wells. Bottom panel: representative indentation force versus depth loading curves (mean ± SEM, n ≥ 5 cells) on the individual composite after 21 and 28 day culture in DMEM with 10% FBS versus with insulin-like growth factor-1 (IGF-1) and osteogenic protein-1 (OP-1, also known as BMP-7). Adapted with permission from ref 119. Copyright 2016 Elsevier Ltd. (c) Impacts of predifferentiation on chondrogenetic activities of induced pluripotent stem cells (iPSCs). Top panel: Safranin-O/Fast-Green/hematoxylin stained section from pellets categorized by type II collagen (Col2)-driven green fluorescent protein (GFP): GFP+ versus GFP− iPSC cells after two passages. Bottom panel: indentation modulus E_ind of the pellet bulk and cryo-sections, calculated by the Hertz model (mean ± SEM, *p < 0.05 by region, #p < 0.05 by cell type). Adapted with permission from ref 129. Copyright 2012 National Academy of Science.

At the tissue level, nanoindentation showed that the modulus of healthy human cartilage increases with age (62–96 years old),¹¹¹ consistent with the trend of aging-induced collagen fibril stiffening resulting from increased covalent cross-linking within the fibril.^112,113 However, this higher modulus does not indicate more superior cartilage function, as aggrecan is significantly weakened during aging. Since aggrecan is the determining factor of tissue poroelasticity, this indicates the loss of energy dissipative capabilities of cartilage, which could contribute to the increased susceptibility to OA. When OA results in degradation of both collagen and aggrecan, cartilage exhibits significant modulus reduction even at a very early stage (grade 1), preceding histological signs or collagen structural changes.¹¹¹ Given the known occurrence of aggrecan degradation, the dependence of nanomechanical behavior on the ionic strength of testing solutions has also been studied.¹¹⁴ During OA, both the T/IT-ECM and the PCM⁷² undergo degradation, leading to a vicious cycle of matrix destruction and chondrocyte catabolic activities. Besides direct investigation of human tissues, nanomechanical tests have been used for systematic studies of tissues from OA animal models. In the study of post-traumatic osteoarthritis (PTOA) using the anterior cruciate ligament-transected (ACLT) canine model, nanomechanical abnormalities were detected three months after the surgery, including significant decreases in modulus¹¹⁵ and viscoelastic relaxation time constants,¹¹⁶ as well as an increase in surface roughness¹¹⁵ and friction.¹¹⁷

4.2. Applications to Tissue Engineering: Chondrocytes and Stem Cells.

The nanometer to micrometer scale capability of AFM enables studying the impact of both biochemical and biomechanical stimuli on the synthesis of individual cells. For example, previous studies of individual chondrons (chondrocytes + their neo-PCM) revealed the anabolic effects of insulin-like growth factor-1 (IGF-1) and osteogenic protein-1 (OP-1, also referred as bone morphogenetic protein-7, or BMP-7),¹¹⁸ both of which increased synthesis and accumulation of proteoglycans.¹¹⁹ As a result, there was an increase in both the effective indentation modulus (Figure 5b)¹¹⁹ and the dynamic loading-induced poroelastic stiffening of the neo-PCM.¹²⁰ At the pellet culture level, the negative impact of the inflammatory cytokine, interleukin-1β (IL-1β), was illustrated by a decrease in construct stiffness, which was amplified by the low oxygen environment within the central region of the pellet.¹²¹ For chondrocytes cultured in polyurethane scaffolds, the combination of dynamic compression and shear oscillation was found to increase the modulus and decrease the friction coefficient,¹²² a result of the increase in type II collagen and PGs, and the localization of lubricin on the surface.

An additional application of AFM is the examination of the chondrogenic potential of alternative cell sources in cartilage repair, including the bone marrow stromal cells (BMSCs) and induced pluripotent stem cells (iPSCs). BMSCs were found to be capable of synthesizing full length aggrecan within 1–2 weeks of chondrogenic culture.¹⁷ Adult equine BMSCs undergoing chondrogenesis within hydrogel cultures could synthesize aggrecan molecules with CS-GAG chains that were almost 2× longer than the CS-GAGs synthesized by primary chondrocytes harvested from the same horses. Importantly, it was also discovered via fluorophore-assisted carbohydrate electrophoresis (FACE) analysis that the aggrecan made by these adult BMSCs demonstrated CS-GAG sulfation patterns typical of that in newborn cartilage, even though the cells originated from adult animals.¹²³ These BMSC-derived aggrecans showed higher compressive stiffness, close to that of newborn human aggrecan, as seen in Figure 5a.^17,123 On the other hand, after undergoing chondrogenesis, BMSCs still had a lower synthesis rate of collagen and proteoglycans. Therefore, within the same time frame, neo-PCMs formed by individual BMSCs have lower moduli compared to those made by primary chondrocytes.¹²⁴ By comparison to BMSCs, iPSCs are more abundant and easier to isolate^125,126 but show difficulty in achieving a uniform differentiated chondrocyte population that is essential for therapeutic effectiveness.^127,128 To address this challenge, a multistage, high-throughput chondrogenesis differentiation protocol was established for murine iPSCs. The effectiveness of this protocol was examined by nanoindentation of the cell pellets.^129,130 The successfully predifferentiated iPSCs, marked by up-regulation of Col2a1 and aggrecan expression, yield significantly higher moduli for the pellet cryosection (Figure 5c).¹²⁹ In addition to testing of neo-tissue qualities, the individual cell modulus, as measured by nanoindentation, was also used as a biomarker to help distinguish between chondrogenic and osteogenic features during the differentiation of adult adipose-derived stem cells (ASCs).¹³¹

5. APPLICATIONS IN MURINE MODELS

One emerging application of AFM is the quantification of murine cartilage biomechanics. Murine models have become the standard in vivo animal model for studying joint development and OA pathogenesis, due to their relatively short lifespan (~2 years), low cost, and availability for genetic modification.¹³² However, the small volume of murine cartilage (thickness ~50, μm) renders biomechanical measurements challenging via conventional tools. Earlier studies demonstrated the potential of microindentation in testing murine cartilage.^133-136 More recently, AFM-nanoindentation has become a popular tool for this purpose due to its ease of operation with tissue submerged in physiologic fluid. This section summarizes two major applications using AFM on murine cartilage: developmental defects and mechanical changes in OA.

5.1. Developmental Defects of Cartilage ECM and PCM.

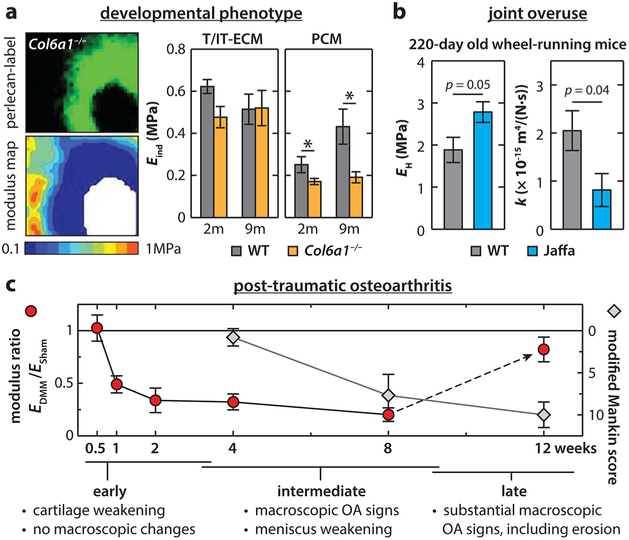
Combining transgenic murine models and nanomechanical tests have enabled the study of the contribution of individual matrix molecules in cartilage ECM to mechanical function, including type IX and VI collagens, lubricin, matrilin-1, chondroadherin, and perlecan. Type IX collagen is a fibril-associated collagen with interrupted triple helices (FACIT). It helps limit the lateral fusion of collagen II/IX/XI fibrils during fibrillogenesis.¹³⁷ In Col9a1^−/− mice, nanoindentation detected higher cartilage modulus due to collagen fibril thickening, a trend similar to aged cartilage.¹¹¹ Also, like aged tissues, Col9a1^−/− cartilage is susceptible to spontaneous OA, in which cartilage degradation and histological OA signs start to appear at 12 weeks of age. In lubricin-null (Prg4^−/−) mice, femoral head cartilage has both reduced modulus and increased surface friction,¹³⁸ confirming the findings of lubricin’s role in surface lubrication by in vitro studies.^40,41,58 In matrilin-1-null (Matn1^−/−) mice, femoral head cartilage has abnormally higher modulus than the wild-type control. Matn1^−/− mice show reduced col2 and aggrecan gene expression in vivo and increased susceptibility to OA, highlighting the important role of matrilin-1 in the regulation of chondrocyte mechanotransduction and protection in OA.¹³⁹ In chondroadherin-null (Chad^−/−) mice, cartilage shows reduced modulus in the superficial zone but normal properties in the middle/deep zone, suggesting a role for chondroadherin in the structural integrity of the superficial layer. In Col6a1^−/− mice, however, cartilage exhibits normal modulus and surface friction coefficient.^135,140 The developmental defect is restricted to the PCM,^135,141 which highlights the PCM-specific role of type VI collagen (Figure 6a). Another PCM-specific molecule, perlecan, is also shown to affect the mechanical properties of cartilage matrix. AFM-nanoindentation of vibrotomed sections in both perlecan heterozygous (Hspg^±) and null (Hspg^−/−) mice show significant modulus reduction at both embryonic and newborn (3-day old) ages.¹⁴²

Figure 6.

Applications of AFM-nanoindentation on murine cartilage in the studies of development and osteoarthritis. (a) Development phenotype of cartilage T/IT-ECM and PCM in the absence of type VI collagen. Left panel: elastic modulus maps obtained via IF-guided AFM on 2-month-old wild-type (WT) and Col6a1^−/− murine femoral head cartilage, and corresponding perlecan-labeled IF image. Right panel: comparison of the T/IT-ECM and PCM moduli between WT and Col6a1^−/− cartilage at 2 and 9 month ages (mean ± SEM of ≥24 sites from n = 3 animals; *p < 0.05 between genotypes). Adapted with permission from ref 141. Copyright 2015 American College of Rheumatology. (b) Comparison of the high frequency modulus, E_H, and hydraulic permeability, k, of 220 day old knee cartilage from WT and aggrecanase-resistant (Jaffa) mice after forced wheel running (mean ± SEM, n ≥ 3). Adapted with permission from ref 143. Copyright 2008 Elsevier Ltd. (c) Nanoindentation modulus precedes histological signs in post-traumatic osteoarthritis (PTOA) in mice. Comparison of the timelines of cartilage modulus reduction (E_DMM/E_Sham) versus histology-based modified Mankin scores in PTOA induced by the destabilization of the medial meniscus (DMM) performed on 3 month old C57BL/6 male WT mice (mean ±95% CI, n ≥ 5). Adapted with permission from ref 145. Copyright 2016 Osteoarthritis Research Society International.

These findings have demonstrated a new path toward understanding the roles of other minor matrix molecules in the mechanical behavior of cartilage. For example, small leucine-rich proteoglycans (SLRPs), fibril-forming collagens (e.g., type V and XI collagens), and cartilage oligomeric matrix protein (COMP) are all known to play essential roles in cartilage ECM assembly, whereas their contribution to cartilage mechanical function remains unclear.¹⁰ Nanomechanical tools will enable future studies of these constituents. Aided by recent advances in the development of tissue-specific conditional knockout and age-specific inducible knockout mice, we can further pinpoint the regional and temporal specific activities of these molecules.

It is worth noting that, although genetically modified mice can develop spontaneous OA as they age, the observed mechanical phenotype does not necessarily represent early signs of OA. Instead, these mechanical changes are developmental phenotype due to genetic defects and may be a factor that causes OA rather than a result of OA.

5.2. Functionally Relevant Biomechanical Markers of Osteoarthritis.

Assessing mechanical properties of murine cartilage can enable a more thorough, functionally relevant understanding of cartilage in OA. For instance, in PG-depleted murine cartilage, a scenario that simulates cartilage degeneration in OA, nanorheometric tests detected a ~10-fold increase in hydraulic permeability, a much more drastic change than the 2-fold decrease in modulus.⁹⁰ Further, under the nanorheometric test, aggrecanase-resistant (Jaffa) murine cartilage exhibits higher modulus and lower hydraulic permeability than wild-type control after joint overuse via treadmill running (Figure 6b), providing functional evidence for improved joint protection when aggrecanase activities are prevented.¹⁴³

When applying nanomechanical tests to OA murine models, cartilage mechanical changes can be studied at different phases of OA development in well-defined time frames. We recently demonstrated the superior sensitivity of nanoindentation in detecting early degradation, progression, and attenuation of post-traumatic osteoarthritis (PTOA) in mice. In a commonly used PTOA model, the destabilization of the medial meniscus (DMM), histological OA signs, such as reduced GAG staining and surface fibrillation, normally appear at 4–8 weeks post-surgery, and noticeable cartilage thinning occurs at 12 weeks post-surgery.¹⁴⁴ In contrast, AFM-nanoindentation of medial condyle cartilage surface detected weakening as early as 1 week post-surgery and continued until appreciable cartilage erosion occurs (Figure 6c).¹⁴⁵ This early weakening can be attributed to upregulated catabolic activities as MMP inhibitors effectively attenuate this reduction. Furthermore, at the intermediate stage (8 weeks), both lateral condyle cartilage and meniscus start to show reduced modulus, despite that observation that there is no detectable change by histology, underscoring the whole-joint nature of PTOA.

6. APPLICATIONS IN MENISCUS BIOMECHANICS, DISEASE, AND REPAIR

Understanding OA, which is a disease of the whole joint, requires a focus on many joint tissues and is not restricted to the study of articular cartilage. Most notably, the meniscus, a crescent-shaped fibrocartilage sandwiched between the femur and tibia ends of the knee, works in coordination with cartilage to provide joint stability,¹⁴⁶ load transmission,¹⁴⁷ and energy dissipation.¹⁴⁸ The multifunctionality of meniscus is endowed by its highly complex, anisotropic ECM, which is dominated by type I collagen fibers (~20–25% wet wt)¹⁴⁹ with much less proteoglycan (<5% wet wt)¹⁵⁰ (Figure 7a).^149-154 Meniscal tear or maceration is a common sports injury and often leads to osteoarthritis.¹⁵⁵ Similar to cartilage, meniscus has a very limited self-repair capability, especially in the nonvascular inner zone.¹⁵⁶ Currently, there is limited understanding of meniscus multiscale biomechanics and disease progression, rendering it challenging to develop effective regeneration and repairstrategies.^157,158

Figure 7.

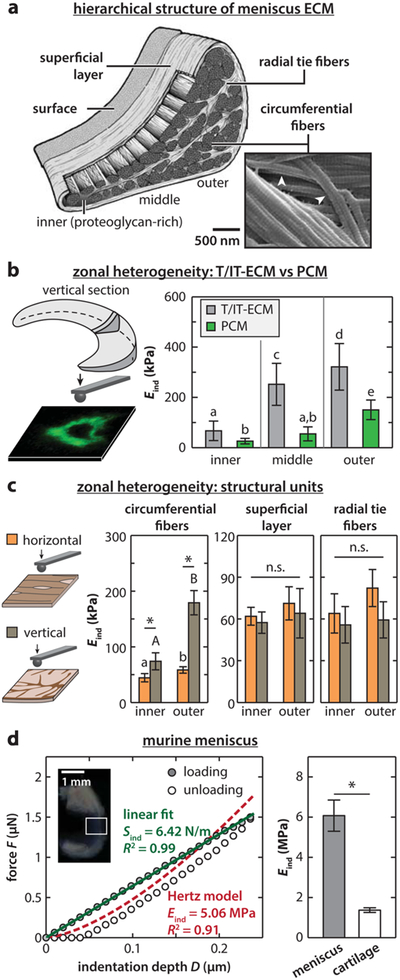
Nanomechanics of the meniscus ECM. (a) Schematic of the hierarchical structure of the meniscus ECM. The ECM is dominated by circumferentially aligned type I collagen fiber bundles (diameter ~10–100 μm),¹⁴⁹ which are wrapped by a ~200 μm superficial lamellar layer of radially aligned fibers,¹⁵¹ and interdigitated by radial tie fiber sheets.¹⁵² On top of the superficial layer, there is a ~10 μm thick surface layer of transversely fibrils.¹⁵¹ From the tension-dominated outer to the compression-dominated inner region, the fibers become progressively less aligned, along with an increase in proteoglycan and type II collagen.^153,154 (b) IF-guided AFM-nanoindentation on porcine meniscus vertical cryo-sections distinguishes the modulus heterogeneity from inner to outer zones and between T/IT-ECM and PCM (mean ± STD). Groups not connected by the same letter are statistically significant (p < 0.05). Adapted with permission from ref 159. Copyright 2013 Osteoarthritis Research Society. (c) AFM-nanoindentation on bovine meniscus vertical and horizontal cryo-sections distinguishes the modulus zonal heterogeneity for different ECM structural units (*p < 0.001, ns: not significant). (d) AFM-nanoindentation on murine meniscus surface. Left panel: representative indentation force versus depth (F–D) curve shows a non-Hertzian, tension-driven linear F–D dependence. Right panel: murine meniscus surface shows higher modulus (n = 13) than condyle cartilage surface (n = 6) (mean ±95% CI, *p < 0.0001). Adapted with permission from ref 165. Copyright 2015 Elsevier Ltd. Panels a and c are adapted with permission from ref 160. Copyright 2017 Acta Materialia Inc.

Over the past few years, researchers have looked into nanoscale structure–mechanics relationships of the meniscus. The first study was on the regional variations of meniscus T/IT-ECM and PCM modulus via IF-guided AFM.¹⁵⁹ In the cryo-sectioned tissue interior, both the T/IT-ECM and the PCM exhibit a decreasing modulus gradient from the outer to the inner zone, owing to a decrease in the organization and concentration of type I collagen fibers (Figure 7a). In addition, the PCM shows lower modulus than the T/IT-ECM, similar to the case of articular cartilage (Figure 7b).¹⁵⁹ In contrast to the salient heterogeneity in the interior, the meniscus surface has no regional variations in both elastic and viscoelastic properties. Our recent follow-up study further characterized the micro-mechanical heterogeneity and anisotropy of each structural unit in the ECM.¹⁶⁰ The decreasing modulus gradient from outer to inner zone is due to reduced organization of the major structural unit, the circumferential fibers. For other units including radial tie fibers, the superficial layer and the surface, this gradient is absent (Figure 7c). The circumferential fibers also exhibit distinctive anisotropy in the indentation response, with the modulus parallel to the fiber axis much higher than that normal to the fiber axis, owing to different fibril deformation modes. Interestingly, these heterogeneous features are consistent at larger scales, as shown by instrumented microindentation studies (R ≈ 150 μm), which confirmed both the zonal heterogeneity of the interior¹⁶¹ and homogeneity of the surface¹⁶² are consistent at larger scales.

Two recent studies applied nanoindentation to understand meniscus aging, disease, and repair. While healthy, young human menisci exhibit unimodal distribution in modulus; the older, osteoarthritic tissue shows much higher variation, in accordance with the localization of PG-rich microdomains.¹⁶³ The increase in the meniscus ECM modulus during maturation is suggested to contribute to the higher resistance to cell migration and proliferation, thereby reduced self-repairing capabilities. When nanoindentation was used as a guidance tool to evaluate collagenase digested meniscus repair constructs, it is shown that the partially degraded constructs, with lower local moduli, exhibit higher cell density and better integration with native wound surfaces.¹⁶⁴

Similar to cartilage, studying murine meniscus can provide new insights into joint development and OA etiology. We recently quantified the biomechanical properties of murine meniscus via AFM-nanoindentation (Figure 7d).¹⁶⁵ Different from larger animals, the surface of murine meniscus is composed of circumferentially aligned fibers. AFM-nanoindentation detected tension-driven, non-Hertzian response on the surface, and the effective modulus is much higher than both murine cartilage and larger animal menisci. These differences, together with the well-known ossification at meniscus horns, provide a benchmark to interpret the outcomes in a murine model and extrapolate the findings to human diseases.

7. CONCLUDING REMARKS

This review outlines the recent body of work in studying the nanomechanics of cartilage and meniscus via AFM. These studies together have established a new paradigm to relate connective tissue molecular constituents to biomechanical function and to disease pathomechanics. Despite the progress, to this day, understanding OA and strategizing joint repair remain elusive.⁹ Further progression is likely to benefit from the applications of nanomechanical tools in the following areas.

7.1. Molecular Mechanisms of ECM Development, Growth, and Aging.

The normal functioning of cartilage and other synovial joint tissues requires not only balanced cell synthesis but also proper assembly of ECM molecules. As summarized by Heinegård, the assembly of cartilage ECM is regulated by synergistic activities of molecules such as SLRPs (including decorin, biglycan, fibromodulin), FACIT collagens, matrilins, and COMP.¹⁶⁶ Continuing with current murine model studies summarized in section 5.1, further application of nanomechanical tools to cartilage of age- and tissue-specific genetically modified mice can elucidate the structural role of each matrix molecule, as well as the compensation and synergy to each other.

7.2. Insights for Diagnosis and Tissue Repair.

Currently, evaluation of the diseased and repair tissues are performed mainly through histological and biochemical assays. Recent studies summarized in this review have demonstrated the potential of using nanomechanical tools to yield quantitative, functional measures of disease models, and regeneration products. A wider application of these tools, together with conventional tools, can help in establishing standardized quantitative and functional benchmarks of tissue behavior and improvements in diagnostics for repair.

7.3. Multiscale Biomechanical Understanding of Other Synovial Tissues.

Functioning of the knee joint involves coordinated activities of multiple tissues, such as ACL, patellar tendon, subchondral bone, growth plate, and synovium, as well as the integration regions between one another.²⁶ Each tissue has specialized structural and mechanical characteristics. A systematic understanding of these tissues at the nanoscale is lacking. A number of recent studies^92,167-171 points to the potential of gaining substantial knowledge on these tissues.

We anticipate that nanomechanical tools will help to address and advance the directions listed above. As the trend of engineering and biological expertise grows, multidisciplinary teams, which combine the knowledge of biomechanics, tissue engineering, matrix biology and cell biology, will make significant advances in understanding and documenting the disease progression and designing tissue repair strategies. Nanomechanical tools can become one important bridging piece that allows for this integration toward a functional cure of OA.