Overstretching Double-Stranded RNA, Double-Stranded DNA, and RNA-DNA Duplexes

Abstract

Using single-molecule force measurements, we compare the overstretching transition of the four types of duplexes composed of DNA or RNA strands. Three of the four extremities of each double helix are attached to two microscopic beads, and a stretching force is applied with a dual-beam optical trapping interferometer. We find that overstretching occurs for all four duplexes with small differences between the plateau forces. Double-stranded RNA (dsRNA) exhibits a smooth transition in contrast to the other three duplexes that show sawtooth patterns, the latter being a characteristic signature of peeling. This difference is observed for a wide range of experimental conditions. We present a theoretical description that explains the difference and predicts that peeling and bubble formation do not occur in overstretching double-stranded RNA. Formation of S-RNA is proposed, an overstretching mechanism that contrary to the other two does not generate single strands. We suggest that this singular RNA property helps RNA structures to assemble and play their essential roles in the biological cell.

Significance

Using single-molecule force measurements, we compare the overstretching transition of the four types of duplexes composed of DNA or RNA strands. We find that overstretching occurs for all four duplexes. Double-stranded RNA exhibits a smooth transition in contrast to the other three duplexes that show sawtooth patterns, the latter being a characteristic signature of peeling. We present a theoretical description that explains the difference and predicts that peeling and bubble formation do not occur in overstretching double-stranded RNA. Formation of S-RNA is proposed, an overstretching mechanism that contrary to the other two does not generate single strands. We suggest that this singular RNA property helps RNA structures to assemble and play their essential roles in the biological cell.

Introduction

Forces act on DNA and RNA in the biological cell. They induce elastic deformation and torsion, can give rise to conformational and structural transitions, and sometimes lead to basepair opening as well as profound modifications in base stacking and tertiary interactions. The generation of single strands from duplexes containing DNA or RNA strands is particularly important because it can lead to parasitic interactions and non-native structures. These duplexes are ubiquitous in the cell. Besides the DNA double helix being composed of two complementary single strands, most RNA molecules contain numerous helical parts, and many of these local duplexes are essential elements of native RNA structures. Moreover, heteroduplexes of DNA and RNA occur in DNA replication, DNA transcription, gene regulation, and gene editing systems.

It has been shown by single-molecule measurements that mechanical force can generate single strands in different ways. In the unzipping configuration, forces pull the two strands of one duplex extremity in opposite directions and mechanically separate them (1, 2, 3). In the peeling configuration, which occurs around 60 pN in the overstretching of topological open nucleic acid (NA) duplexes, forces act along the helical axis from opposite duplex extremities, and one strand peels off (4). DNA overstretching was discovered about two decades ago by single-molecule force measurements (5, 6). The experimental observations triggered many studies and controversial discussions about the molecular mechanism underlying DNA overstretching (see (7, 8) and references therein). Recently, it has been shown experimentally that DNA overstretching can be caused by several mechanisms, including peeling, bubble formation, and a structural transition from the B-form helix to an S-DNA structure (4, 8, 9, 10). These mechanisms are schematically represented in Fig. 1. Whereas overstretching by bubble formation and by transition to S-DNA both show smooth plateaus in the force versus extension curve, peeling induces a characteristic sawtooth-shaped pattern.

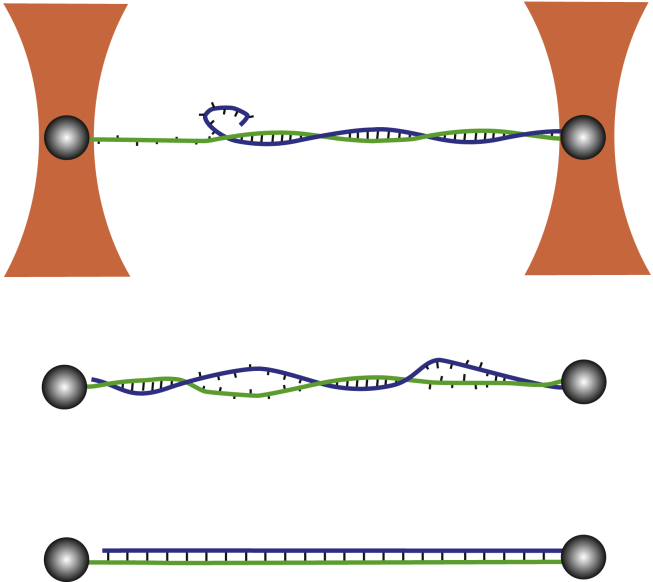
Figure 1.

Schematic representation of the measurement configuration and the three overstretching mechanisms. The NA duplex is attached by three of its four single-strand extremities to two microscopic beads (beads and molecule are not at the same scale). The two beads of each dumbbell are captured in separate optical traps (orange). Force versus displacement curves are obtained by measuring the position of one bead within the trap to nanometer precision, whereas the other trap is displaced. Peeling of the free strand, bubble formation, and S-structure formation are presented from top to bottom. Single strands under force and the S-structure exhibit a longer separation between adjacent nucleotides than the regular double helix. Base pairing is maintained in the S-structure, but basepair stacking and the number of helical turns are strongly reduced (32, 33). Our molecular constructs are free to rotate around the axis of applied force as on one side the bead is attached only to a single strand (green strand on the left-hand side of the figure). To see this figure in color, go online.

Here, we investigate the overstretching transition of four different NA duplexes by single-molecule force measurements. These duplexes are double-stranded DNA (dsDNA), dsRNA, a heteroduplex with the DNA strand under tension (RNA-DNA), and a heteroduplex with the RNA strand under tension (DNA-RNA), respectively. Strikingly, we find that dsRNA always exhibits a smooth overstretching signal, an observation that holds for a wide investigated range of salt conditions and pulling speeds. In contrast, the other three duplexes exhibit pronounced sawtooth-shaped signals during overstretching. Comparison between the experimental data and a theoretical description based on the assumption of local thermal equilibrium indicates that peeling and bubble formation do not occur for dsRNA. Toward the end of the manuscript, we briefly discuss under which circumstances the absence of these single strand-generating mechanisms could be important in the biological cell.

Materials and Methods

Force measurement setup

Detailed descriptions of the dual-beam optical trapping interferometer and the sample preparation steps immediately preceding the force measurement are published elsewhere (11). The linearly polarized beam of a CW Nd:YVO₄ laser (Millennia IR, 1064 nm, 10 W, Spectra-Physics, Santa Clara, CA) is split with a polarizing cube beam splitter. One of the resulting beams is shifted in frequency by an acousto-optic frequency shifter. Then, it is deflected by a piezoelectric mirror mount with an integrated position sensor operating in feedback loop and represents the mobile beam. The other beam remains fixed. The two beams are combined with a second polarizing cube beam splitter before entering a microscope objective (100×, numerical aperture 1.4, oil immersion; Nikon, Tokyo, Japan). This way, two optical traps of perpendicular linear polarization arise in the sample plane, and the mobile trap can be laterally separated from the fixed trap with nanometer precision. The laser light passes through the sample and is collimated by a second objective (63×, numerical aperture 1.2, water immersion; Olympus, Tokyo, Japan). A Glan polarizer cube rejects the large majority of the light arising from the mobile beam. Force is deduced from the position of the bead in the fixed trap using back focal plane interferometry (12, 13). When a measurement cycle is completed, the molecular linkage between the two beads is broken, and force is calibrated by recording the power spectral density of the bead in the fixed trap (13). Unavoidable depolarization in the microscope objectives leads to some interference between the fixed and mobile beams, which generates parasitic force signal at a small distance between the traps. The imposed frequency shift between the two laser beams avoids this parasitic signal (14). We performed the experiments in a room of controlled temperature of 26°C. In the sample, the temperature is raised to ∼33° because of local heating by the trapping laser by a measured amount of ΔT = 7°C (11, 15).

Preparation of the molecular constructs

All four duplexes contain 4050 basepairs and exhibit the same nucleotide sequence, corresponding to the sequence of a portion of the Escherichia coli chromosome (strain K-12, substr. MG1655), starting at the first nucleotide of the rrlB gene (coding for 23S ribosomal RNA), encompassing the full gene sequences of rrlB and rrfB (coding for 5S ribosomal RNA), and ending in the middle of the murB gene. Because the preparation of the four different duplexes are related, we first describe the RNA-DNA case and then consider the other three duplexes.

The DNA sequence of interest is amplified by polymerase chain reaction (PCR) from a plasmid (gift of K. Nierhaus) containing the full E. coli rrnB operon sequence. PCR primers were designed to introduce a T7 RNA polymerase promoter sequence followed by an AflII restriction site at one extremity of the PCR product and a FseI restriction site at the other extremity. Part of the PCR product is in vitro transcribed using T7 RNA polymerase, and the RNA product is conserved. AflII digestion of the rest of the PCR product followed by Klenow treatment in the presence of biotin-deoxy-ATP allows the incorporation of two biotin moieties close to the 3′ end of one strand. FseI digestion and ligation of a biotin-modified DNA oligonucleotide adds three biotins close to the 5′ end of the same strand. The goal of the next step (strand-exchange step) is to replace the unmodified DNA strand by the in vitro transcribed RNA. For this purpose, DNA and RNA are first denatured at a high temperature, and the resulting ss strands are incubated together in temperature and solvent conditions that strongly favor RNA/DNA heteroduplex over dsDNA duplex formation (11, 16). Subsequently, residual dsDNA duplexes are digested with EcoRI (to avoid any interference in the force experiments). Finally, an RNA oligonucleotide, with two biotin modifications, is ligated to the RNA 3′ end of the heteroduplex.

The DNA-RNA duplex is prepared similarly. PCR primers are designed to act on opposite plasmid strands compared to the RNA-DNA case. Oligonucleotides and ligations are adapted such that the RNA strand carries biotins close to both ends, whereas the DNA strand exhibits biotins close to its 3′ end only. Preparation of the dsDNA construct follows the protocol used for the RNA-DNA construct until the strand-exchange step. The latter is not required for dsDNA (and of course the EcoRI restriction step is omitted); the final dsDNA construct is obtained by ligating a DNA oligonucleotide carrying two biotin modifications. For the dsRNA construct, two PCRs and two in vitro transcriptions are performed to prepare two complementary RNA strands. The RNA strand intended to be biotinylated at each extremity (5′ and 3′) is in vitro transcribed in the presence of guanosine monophosphate in large excess over GTP (i.e., to obtain a majority of RNA molecules with a single phosphate group at their 5′ extremity) and thus is ready to be ligated to the adequate oligonucleotide. Biotinylation of this RNA strand is performed using a DNA-splint ligation procedure and ligating biotinylated RNA oligonucleotides with T4 RNA ligase 2 (17). The two RNA strands are then hybridized, and the biotin groups at the 3′ extremity of the so far nonmodified RNA strand are introduced using the same procedure than for the RNA-DNA duplex.

Results

Four different dsNA constructs have been prepared as described in the Materials and Methods. They all contain exactly the same nucleotide sequence, except for the obvious T to U replacement when going from DNA to RNA (the sequence is described in the Materials and Methods). Multiple biotin modifications were introduced at three of the four extremities of these duplexes and used for a specific attachment to two streptavidin-coated beads. The beads are captured with two optical traps; the position of one optical trap is kept fixed to measure force by back focal plane interferometry, whereas the other trap is displaced with constant velocity to repeatedly strain and relax the investigated construct. This experimental configuration is schematically represented in Fig. 1. The figure also illustrates peeling, bubble formation, and the structural transition to S-structure nucleic acid (S-NA).

The four duplexes at a common condition of salt and velocity

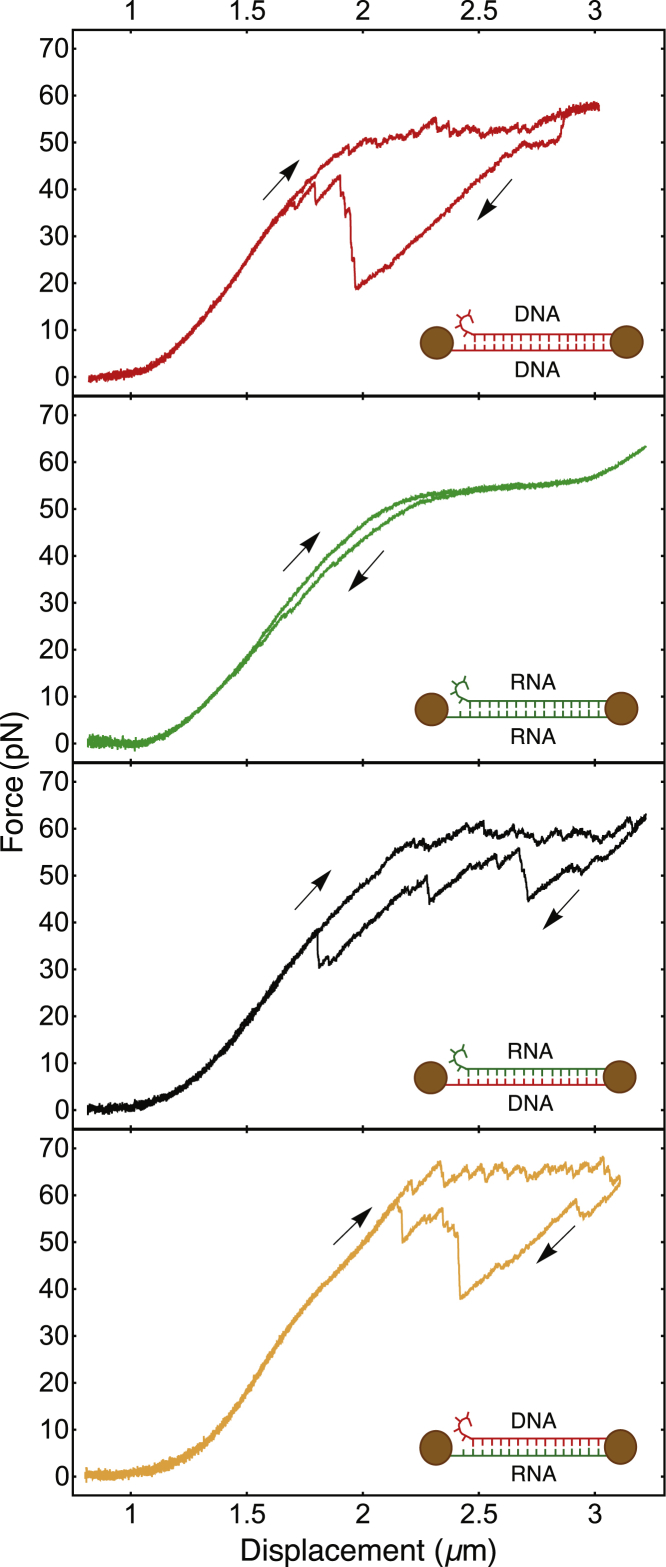
Below ∼25 pN, the force-displacement curves of the four constructs exhibit rises of increasing slope, which remain identical upon relaxation (Fig. 2). This part of each curve corresponds to a regime of entropic polymer elasticity at low forces, followed by a regime of enthalpic elasticity at intermediate forces. It is well described by the extensible worm-like chain model (18). The curvature of the force-displacement curves changes the sign around 25 pN. This softening has been observed for dsDNA before and has been attributed to twist-stretch coupling (4). For all four duplexes, the force-displacement relations measured below the overstretching plateau are well described by the twistable worm-like chain model, a theoretical description that takes twist-stretch coupling into account in terms of two phenomenological parameters (see Supporting Materials and Methods). The force levels F_p (∼1.8 pN SD of the measured values) of the overstretching plateaus are close, but for this case of equivalent base sequence, same buffer, and same displacement velocity, we nevertheless can resolve a distinct order:

$$F_p^{DNA/RNA}\simeq 64.8\text{pN}>F_p^{RNA/DNA}\simeq 60.0\text{pN}>F_p^{dsDNA}\simeq 57.6\text{pN}>F_p^{dsRNA}\simeq 55.2\text{pN}.$$

Figure 2.

Measured force-displacement curves of the four types of NA duplexes. From top to bottom, dsDNA, dsRNA, RNA/DNA hybrid, and DNA/RNA hybrid are shown. Arrows indicate the direction of imposed displacement; a curve measured upon pulling and the curve measured upon subsequent retraction is shown in each case. The molecular duplexes and their three-point attachments to the two beads are schematically represented in the insets. Every duplex exhibits one 5′ extremity that is free to peel off. The four measurements have been performed under the same buffer condition (100 mM KCl, 5 mM MgCl₂, and 20 mM Hepes [pH 7.6]) and at the same displacement velocity (100 nm/s). To see this figure in color, go online.

Surprisingly, strong qualitative differences are observed between the overstretching curves of the dsRNA duplex on the one hand and the overstretching curves of the other three duplexes on the other hand. For dsRNA, the plateau is smooth and exhibits rather small hysteresis, whereas for the other three duplexes, the overstretching signal reveals a succession of sawtooth-shaped peaks and a strong hysteresis with deep decreases in force, followed by sudden returns. In Figs. 3 and S1, we present zooms into the overstretching plateaus measured upon stretching the RNA-DNA and DNA-RNA hybrids, respectively. The curves display successions of sawtooth-shaped peaks. Typically, a phase of slow increase in force is followed by a sudden force reduction. The same characteristic features are observed on the overstretching plateaus of the dsDNA construct (Fig. S2). The three figures also show that details of the sawtooth-shaped force signals can be similar from one pulling cycle to another and from one molecule to another. The reverse process, strand reannealing, measured upon reducing the distance between the two optical traps, exhibits more pronounced variation than the pulling curves measured upon increasing displacement. This is illustrated in Fig. S2 for the case of dsDNA, in which force versus displacement curves are shown, which corresponds to successive stretch/release cycles of the same single dsDNA molecule. One can observe that the return curves exhibit significant differences (which entails widely different hysteresis), indicating stochastic variations in the reannealing process.

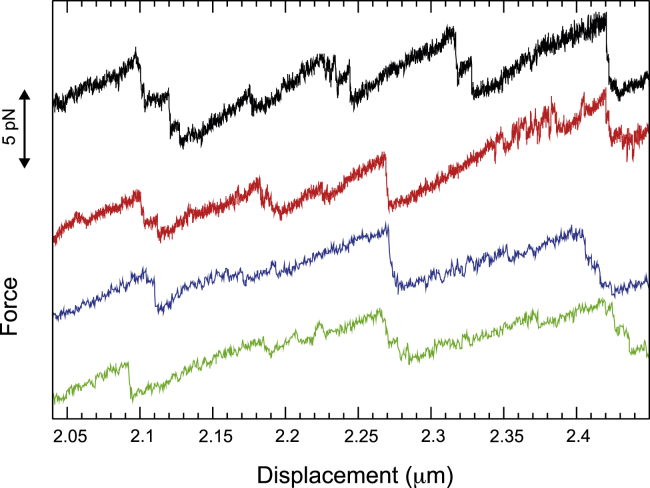
Figure 3.

Detailed view of four force-displacement curves measured on the overstretching plateau of the RNA-DNA hybrid. The lowest two curves correspond to two consecutive measurements of the same molecule and the two upper curves to two other molecules. The curves are shifted vertically for better visibility of the details. For the two lower curves, we used the buffer conditions and displacement velocity of Fig. 2, whereas the two upper curves were measured with a smaller displacement velocity (10 nm/s) and higher monovalent salt (400 mM KCl, 5 mM MgCl₂, and 20 mM Hepes [pH 7.6]). To see this figure in color, go online.

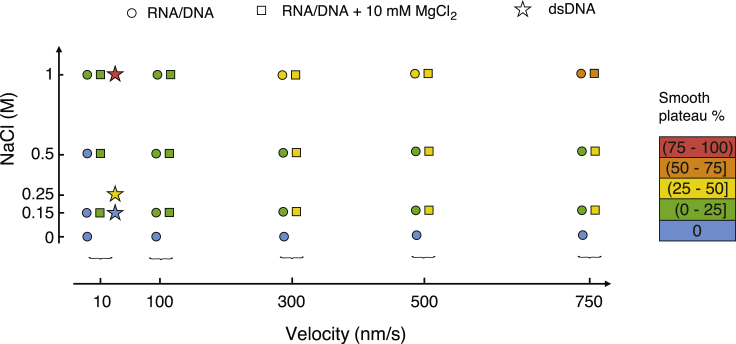
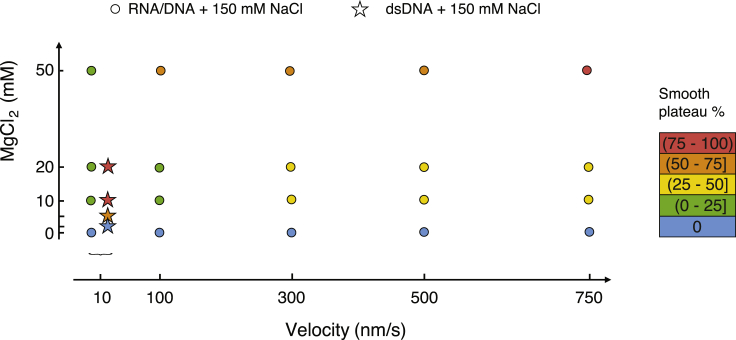
Effects of salt concentrations and displacement velocity

It was shown that the overstretching of dsDNA can involve different mechanisms and that the prevalence of one or another of these mechanisms depends on salt conditions and displacement velocity (8, 9). Under the experimental conditions of Fig. 2, we observe both sawtooth-like and smooth overstretching for dsDNA. A smooth region appears for instance at a displacement of ∼3 μm in the top panel of Fig. 2. This observation indicates coexistence of peeling (responsible for sawtooth-like pattern) and at least one other mechanism (associated with a smooth signal). In Fig. 4, we present force versus displacement curves measured on the RNA-DNA hybrid at various displacement velocities. The percentage of the smooth signal increases with increasing velocity. In Figs. 5 and 6, our data on salt and velocity dependence for this percentage is summarized. Fig. 5 shows the percentage for velocities ranging from 10 to 750 nm/s and NaCl concentrations ranging from 0 to 1 M, whereas Fig. 6 shows the percentage for NaCl concentration of 150 mM, various velocities, and MgCl₂ concentrations between 0 and 50 mM. Divalent salt has a much stronger effect than monovalent salt (of note, in all cases that we tested, we found no significant differences between the experimental curves when either KCl or NaCl were used at the same concentration). The parameter window for which peeling occurs is much wider for the RNA-DNA hybrid than for dsDNA. Roughly speaking, the higher the velocity or salt concentration, the higher the percentage of smooth region. Qualitatively, the same trends have been previously reported for dsDNA (8). Noteworthy, whereas dsDNA, RNA-DNA, and DNA-RNA hybrids show overall similar overstretching behaviors, this is not the case for dsRNA, as already underlined in the previous paragraph. In Fig. S3, representative force versus displacement stretching curves of dsRNA are shown for various salt concentrations and displacement velocities. The figure illustrates that dsRNA stretching curves do not display the characteristic sawtooth pattern of peeling under our experimental conditions.

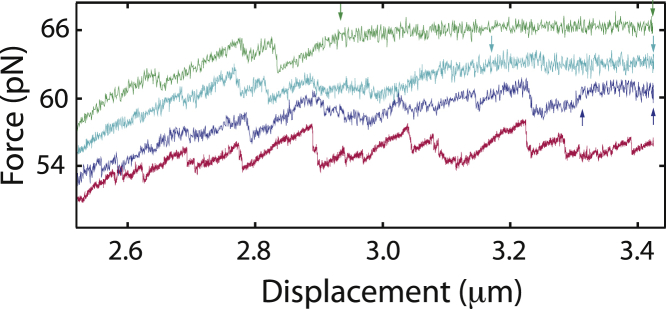
Figure 4.

Effect of the displacement velocity on the force signal recorded during overstretching an RNA-DNA hybrid. The represented force-displacement curves correspond to four successive pulling sequences applied to the same molecule. The displacement velocities are 10 nm/s (red), 300 nm/s (blue), 500 nm/s (cyan), and 750 nm/s (green). Blue, cyan, and green curves are shifted by 2, 4, and 6 pN for better visualization. Regions between arrows exhibit a smooth force signal. The fraction of the curves occupied by smooth parts increases with increasing displacement velocity. Buffer used in the measurements of this figure is as follows: 150 mM NaCl, 10 mM MgCl₂, and 10 mM Hepes (pH 7.6). To see this figure in color, go online.

Figure 5.

Influence of NaCl concentration (vertical axis) and velocity (horizontal axis) on the overstretching plateau of RNA-DNA hybrids. The percentage of the smooth plateau is marked by a color code as given at the right of the figure. For pulling velocities up to 500 nm/s, the percentage of smooth plateau remains less than 50% whatever the NaCl or MgCl₂ concentration is, whereas for 750 nm/s, the smooth plateau becomes dominant at the highest NaCl concentration used (1 M), both in the absence (circles) or presence (squares) of 10 mM MgCl₂. The data for dsDNA (stars) were taken from (8). To see this figure in color, go online.

Figure 6.

Influence of MgCl₂ concentration (vertical axis) and velocity (horizontal axis) on the overstretching plateau of RNA-DNA hybrids at 150 mM NaCl (circles). The percentage of smooth plateau is marked by a color code as given at the right of the figure. At 100 nm/s, the percentage of smooth overstretching plateau is negligible at 10 mM MgCl₂, but it increases to 50–75% at 50 mM MgCl₂. An increase in velocity to 750 nm/s leads to 25–50% smooth plateau already at 10 mM MgCl₂, whereas at 50 mM, the conversion to smooth overstretching plateau is virtually complete. The data for dsDNA (stars) were taken from (8). To see this figure in color, go online.

Theoretical description of overstretching by peeling and bubble formation

As described before (8, 9), depending on experimental conditions, dsNA can overstretch via three different mechanisms: peeling, melting bubble formation, and transition into an S conformation (see Fig. 1). As the transition and the energies of the initial and final states are rather well known for peeling and melting bubble formation, here, we will introduce a theoretical description for these two overstretching mechanisms. Because we do not know the energy of the final state for overstretching by the formation of S-NA, we do not treat this mechanism in this frame. The theoretical description presented in this article is related to the description of DNA peeling published by one of us (4). However, to the best of our knowledge, it has not been reported before in this form. The limitations of our simple theoretical description are considered in Approximations and limitations of our theoretical description.

Overstretching by peeling

The force-induced peeling phenomenon can be described by a conversion of a dsNA into two single strands, only one of which stays under tension. This transition implies a rupture of hydrogen bonds, modified stacking interactions, and changes in elastic energy. We consider the free energy difference E(F) between a state (n + 1) exhibiting n + 1 peeled basepairs and a state (n) with n peeled basepairs at constant force F. The construct would peel progressively for E(F) < 0 and reanneal progressively for E(F) > 0, and the states (n) and (n + 1) would have equal probability for E(F) = 0.

$$E\left(F\right)=E_b+E_{ss}-E_{ds}-F\left(l_{ss}-l_{ds}\right).$$ (1)

E_b is an average energy required to open one basepair, which we obtained from published unified nearest-neighbor $\mathit{\Delta }{G}_{37}^0$ parameters (see Table 1; Supporting Materials and Methods). For simplicity, we call this parameter “basepair binding energy” in this article. E_ss denotes the energy per nucleotide required to stretch a single-stranded NA (ssNA) from zero-force to a force F, and E_ds is the energy per basepair required to stretch a dsNA from zero to F. The term F(l_ss − l_ds) describes the mechanical work (length change times force), where l_ss and l_ds are the length per nucleotide of a ssNA stretched to force F and the length per basepair of a dsNA stretched to force F, respectively. We derived E_ss, E_ds, l_ss, and l_ds from force measurements on ssNA and dsNA. A detailed description of the model and its parameters is presented in Supporting Materials and Methods.

Table 1.

Experimental and Theoretical Overstretching Forces, Together with Energy and Length Values of the Theoretical Description

	Fp	Ft	Eb	Ess	Eds	Δl
	(pN)	(pN)	(kBT/bp)	(kBT/nt)	(kBT/bp)	(nm/nt)
dsDNA	57.6 ± 1.8	48.2	2.30	1.08	0.24	0.273
dsRNA	55.2 ± 1.8	–	3.33	–	–	–
RNA/DNA	60.0 ± 1.8	48.7	2.38	1.09	0.18	0.284
DNA/RNA	64.8 ± 1.8	53.7	2.38	0.99	0.24	0.245

Experimental plateau values F_p are obtained by averaging 20–50 measured overstretching plateaus for each duplex type. All these measurements were performed under the experimental conditions of Fig. 2. The calculated transition forces F_t verify E(F_t) = 0, where E(F) is defined by Eq. 1. The binding energies E_b are taken from the literature (29, 30, 31). The elastic energies E_ss and E_ds and the length difference Δl = l_ss − l_ds are evaluated at force F_t. There are no F_t, E_ss, E_ds, and Δl values for dsRNA because peeling is not theoretically predicted for dsRNA.

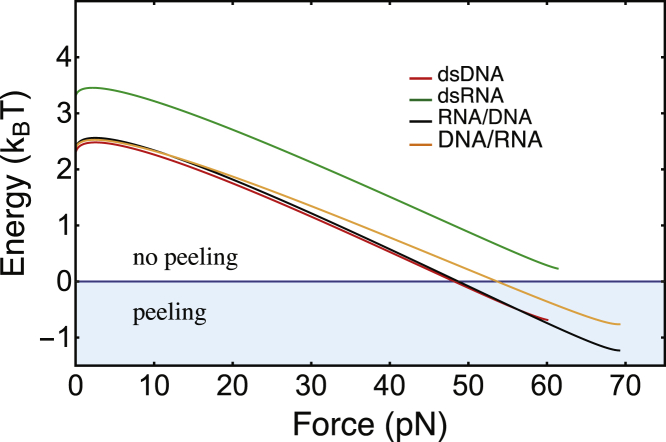
Eq. 1 allows us to obtain a phase diagram, predicting the dsNA $\to$ ssNA transition (Fig. 7). It consists of two different regions: a region in which the considered molecule has a preference for a ds conformation (E > 0) and a region in which it has a preference for a single-stranded conformation (E < 0). Zero energy defines the predicted force level of the overstretching plateau; we call this force F_t (transition force). At F = 0, the energy E is simply given by E_b. Below ∼2 pN, the energy versus force curves E(F) exhibit an initial increase with force, which is explained by a negative (l_ss − l_ds). At a higher force, (l_ss − l_ds) becomes positive, leading to a monotonic decrease of E(F). Largely depending on its starting level E_b, the curve either penetrates (dsDNA, RNA-DNA, and DNA-RNA) or stays above (dsRNA) the peeling region. Finally, approaching a force that we call divergence force F_d, the curves show slight positive curvature before stopping (see Supporting Materials and Methods, Section SII.A.3). The positive curvature is caused by the twist-stretch coupling term. Application of the described model to our experimental data gives two major results: 1) peeling is predicted only for three of the four molecular constructs, and 2) the significantly higher value of E_b is the main reason why peeling is not predicted for dsRNA.

Figure 7.

Energy difference E(F) for overstretching by peeling, calculated using Eq. 1. Energy versus force curves are presented for dsDNA (red), dsRNA (green), RNA-DNA (black), and DNA-RNA (orange). Each energy diagram is divided into two regions: a region where the molecules are predicted to be double-stranded (white) and a region where the peeled state is energetically favorable (light blue). When the applied force reaches the threshold value for which the energy E is zero, dsDNA, RNA-DNA, and DNA-RNA hybrids are predicted to peel, whereas dsRNA always remains away from the peeling region. To see this figure in color, go online.

Overstretching by melting bubble formation

Overstretching by melting bubble formation involves rupture of dsNA basepairs; the mechanism is similar to peeling in this respect. As a difference, however, melting bubble formation results in single strands that both remain under tension, whereas one strand relaxes in the peeling case. The applied force F is distributed among the two strands, either equally if the two strands are of the same nature (F₁ = F₂ = F/2; for dsDNA and dsRNA) or unequally if the two strands are of a different nature (F_DNA ≠ F_RNA; F_DNA + F_RNA = F; for RNA-DNA and DNA-RNA). In Supporting Materials and Methods, Section SII.B, we present how the {F_DNA, F_RNA} couple of a heteroduplex can be calculated. The process can be described by Eq. 1 as for peeling, albeit the following modifications in the elastic energies of the single strands and the mechanical work:

$$E\left(F\right)=E_b+E_{ss}^{\text{∗}}-E_{ds}-F\left(l_{ss}^{\text{∗}}-l_{ds}\right),$$ (2)

where

$$E_{ss}^{\text{∗}}=\{\begin{array}{cc}2E_{ss}^{DNA}\left(F/2\right)& \text{for}\text{dsDNA }\\ 2E_{ss}^{RNA}\left(F/2\right)& \text{for}\text{dsRNA }\\ E_{ss}^{DNA}\left(F_{DNA}\right)+E_{ss}^{RNA}\left(F_{RNA}\right)& \text{for}\text{DNA}-\text{RNA}\text{and}\text{RNA}-\text{DNA}\end{array},$$

$$l_{ss}^{\text{∗}}=\{\begin{array}{cc}{l}_{ss}^{DNA}\left(F/2\right)& \text{for}\text{dsDNA }\\ l_{ss}^{RNA}\left(F/2\right)& \text{for}\text{dsRNA }\\ l_{ss}^{DNA}\left(F_{DNA}\right)=l_{ss}^{RNA}\left(F_{RNA}\right)& \text{for}\text{DNA}-\text{RNA}\text{and}\text{RNA}-\text{DNA}\end{array}.$$

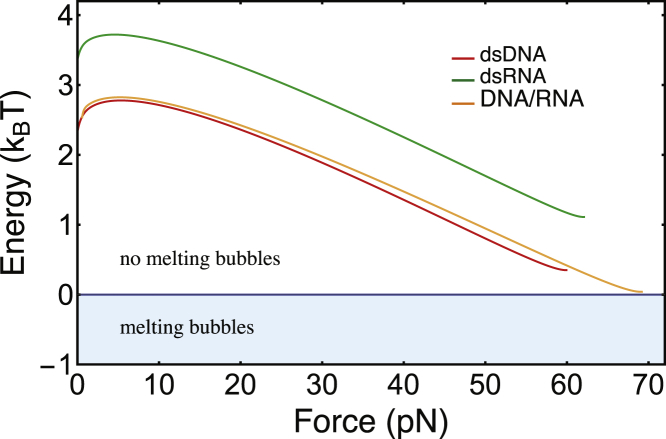
Using Eq. 2, we constructed an equivalent to the peeling case phase diagram (Fig. 8), again with two regions. In the lower region (E < 0), the molecule has a preference to form melting bubbles along its NA chain. Zero energy indicates equilibrium between ds and melting bubble conformations. The energy versus force curves look alike to the peeling case, with a start value of E_b and a round maximum around 5 pN that is followed by a continuous decrease. Two of the free energy versus force curves reach their end before the E = 0 phase boundary, which would indicate that overstretching via melting bubble formation is energetically nonfavorable for dsRNA and dsDNA. Strictly speaking, this conclusion, however, holds only for a homogeneous base sequence (see Approximations and limitations of our theoretical description). More details about the theoretical description are given in Supporting Materials and Methods.

Figure 8.

Energy difference E(F) for overstretching by melting bubble formation, calculated using Eq. 2. Energy versus force curves are presented for dsDNA (red), dsRNA (green), and the two hybrids (RNA-DNA and DNA-RNA, orange). The energy diagram is divided into two regions: a region where the molecules are entirely double stranded (white) and a region where a state containing melting bubbles is energetically favorable (light blue). To see this figure in color, go online.

Discussion

Approximations and limitations of our theoretical description

Our simple theoretical description involves several important approximations, in particular, the assumption of local thermal equilibrium, the neglection of sequence heterogeneity, the neglection of cooperativity, the simplified phenomenological description of free energies, and the projection of the multiple degrees of freedom to a one-dimensional space along the axis of applied force. Sequence heterogeneity causes a rough energy landscape, whereas the simple theoretical description assumes a smooth landscape. In the former case, the peeling front will perform a biased random walk through the base sequence, experiencing a rapidly varying potential. From the physics point of view, the process encountered in peeling NA sequences is thus similar to the one encountered in DNA unzipping, the latter being discussed in the literature. The fundamental differences between unzipping heterogeneous and homogeneous base sequences were described (19); the amplitude of the thermal “breathing” of the opening fork was shown to decrease with increasing local stiffness (3), and it was predicted that the advancement of the opening fork in a heterogeneous sequence is given by the times required to overcome the local maxima of the energy landscape (20). We also note that peeling experimentally does not occur at thermal equilibrium. Use of phenomenological parameters of basepair binding E_b is strictly justified only if basepair opening and closing occur at a timescale short to the timescale of the variations in displacement and force. This is not always achieved in our experiments; force flipping is not systematically observed. As a result of such out-of-equilibrium effects, peeling is expected to occur above the theoretically predicted equilibrium force when trap distance increases, whereas reannealing is expected to occur below the theoretical equilibrium force when trap distance decreases. The resulting hysteresis between the average peeling and reannealing forces is clearly apparent in our measurements with dsDNA, DNA-RNA, and RNA-DNA (see Fig. 2). It was reported before for dsDNA (4). Overall, we note that sequence heterogeneity and out-of-equilibrium effects are thus expected to increase the peeling force as compared to our theoretical description.

The overstretching transition from the classical B-DNA double helix to an S-DNA conformation has been described as highly cooperative, using statistical physics descriptions based on different extensions of a one-dimensional Ising model. Our description does not include S-NA formation, and we do not consider cooperativity in peeling and bubble formation. In this experimental configuration, only one peeling front occurs, which suggests that cooperativity is negligible. Accordingly, cooperativity was not included in classical theoretical descriptions of DNA unzipping and peeling. In bubble formation (and thermal melting of NA duplexes), on the other hand, multiple interfaces between ds and single-stranded portions can occur, and the introduction of an energy penalty for each interface could be a useful extension. Such an extension would lead to an increase in the transition force predicted for overstretching by bubble formation and as such would not qualitatively change our prediction that overstretching of a homogeneous base sequence occurs at a lower force for peeling than for bubble formation. Sequence heterogeneity can however allow for melting bubbles in sequence locations that exhibit low guanine cytosine (GC) content, which could reconcile our theoretical prediction with a published observation of melting bubbles in dsDNA (8, 9).

Of note, our description essentially represents constant force experimental conditions, whereas experiments control displacement and measure force. It is therefore adapted to predict the overstretching force and in particular the boundary between peeling and nonpeeling, but it cannot be used to predict the measured force-extension relations.

Force levels of overstretching by peeling

Under the conditions of Force measurement setup, the dsDNA, DNA-RNA, and RNA-DNA constructs show sawtooth-like force signals and pronounced hysteresis. These observations are clear signatures of peeling. We present in Table 1 the average values of the force plateaus F_p measured with increasing displacement and the calculated transition forces F_t for overstretching by peeling. We observe differences of a few pN between the F_t-values of the three constructs. We estimate that the experimental uncertainty in the force is ∼10% and that it is mainly caused by variations in size, shape, and refractive index of the beads. The measured forces F_p are systematically higher than the calculated forces F_t, which we attribute to the limitations of our theoretical description, discussed in the preceding section. The differences between the calculated transition forces F_t of the three constructs overstretching by a peeling mechanism can be explained by inspecting Fig. 7 and the energy and length values of Table 1. Comparing first dsDNA and RNA-DNA, we see that the two energy-force relations are very similar, except for a small relative shift in the vertical direction. The higher binding energy E_b is responsible for a slightly higher predicted F_t of RNA-DNA as compared to dsDNA. The experimentally observed difference exhibits the same sign but a higher magnitude than the theoretical prediction. Comparing then RNA-DNA and DNA-RNA, the binding energies are equal by symmetry, but different relative extension Δl = l_ss − l_ds leads to a smaller slope of the energy versus force curve and in turn a higher plateau force for DNA-RNA. Because the ds lengths l_ds of DNA-RNA and RNA-DNA are equal by symmetry, we find that the different lengths of the single strands under tension $\left(l_{ss}^{DNA}>l_{ss}^{RNA}\right)$ cause the observed difference in plateau force. In this case, experimentally observed and theoretically predicted differences are similar in sign and magnitude. As described in The four duplexes at a common condition of salt and velocity, the experimental signatures of peeling are not observed for dsRNA. As described in Theoretical description of overstretching by peeling and bubble formation, peeling is not theoretically predicted for dsRNA. Remarkably, overstretching of dsRNA experimentally occurs at the lowest force level of all four duplexes, although dsRNA exhibit the strongest binding energy E_b. The overall picture is that dsRNA overstretches by a different mechanism than the other three duplexes. Therefore, the difference between the force level of overstretching dsRNA on the one hand and the force levels of the other three duplexes on the other hand cannot be explained in the same way as the differences occurring between dsDNA, RNA-DNA, and DNA-RNA.

Sequence-dependent force signal observed for peeling

Peeling is a sequence-dependent overstretching mechanism. In this work, we use a three-point-attachment that was previously described by Gross et al. (4) and for which peeling always involves the same single strand. The peeling front thus propagates in a one-dimensional manner through the base sequence, which explains that details of the force signals measured at an increasing displacement can be similar (Figs. 3 and S1). In this situation, the theoretical description of the sequence-dependent force signals is related to the description of NA unzipping (3, 4, 21). Sequence regions exhibiting high (low) GC content lead to high (low) force. Molecular stick-slip dynamics induces sawtooth-like features in the force-displacement curves. Typically, the peeling front advances little in front of a sequence with increasing GC content. During this “stick” phase, force rises slowly. Subsequently, a “slip” event occurs once the local energy barrier is overcome. Then, the peeling front advances rapidly, and the force drops. The energy landscape is determined by the base sequence, but the exact positions where the transitions occur exhibit stochastic variation. Flipping between discrete states is sometimes observed (for instance, on the right part of the red curve in Fig. 3), which is a signature of close-to-equilibrium dynamics. Sawtooth-shaped peaks and force flips are observed for the RNA-DNA, the dsDNA, and the DNA-RNA constructs, and these qualitative features agree with the observations of Gross et al. (4), who studied a three-point attachment dsDNA construct containing a pKYB1 sequence of 8393 basepairs.

RNA-DNA overstretching depends on displacement velocity and salt

Earlier studies showed that overstretching of dsDNA can be due to different mechanisms, leading to a complex phase diagram that depends on salt conditions, displacement velocity, sequence, and topology (4, 8, 9, 10). In particular, it was shown that at high ionic strength, S-DNA formation is favored over peeling in topologically open DNA (8). In this case, Zhang et al. observed peeling and S-DNA formation but not bubble formation (9). This work indicates that the overstretching phase diagram of an RNA-DNA heteroduplex is of similar complexity and qualitatively resembles the one of dsDNA. In both cases, peeling dominates at low salt and velocity, whereas overstretching with a smooth force signal occurs more frequently at high salt concentrations and high displacement velocities. However, we observe quantitative differences that are illustrated in Figs. 4, 5, and 6. Peeling remains the dominant overstretching mechanism for a much wider range of salt concentrations and displacement velocity in the RNA-DNA hybrid than in the dsDNA construct. We attribute the observed smooth overstretching to S-NA formation because bubble formation is predicted to occur at higher forces than peeling (compare Figs. 7 and 8). For the peeling mechanism, the calculated differences between the energies of RNA-DNA and dsDNA are small. The observation that RNA-DNA peeling dominates over a wider parameter space therefore suggests that the energy of the heteroduplex S phase is higher than the one of the dsDNA S phase. We do not know the reason for this difference and whether it is of structural or dynamical origin. Regarding structural difference, the RNA-DNA heteroduplex forms an A-type double helix, which is more compact than the B-type DNA double helix (22). As an example for different dynamical properties, some of us have shown previously that the unfolding and refolding of hairpin structures under force occur faster and significantly closer to equilibrium in DNA than in RNA (23).

Peeling and bubble formation do not occur in dsRNA

We observe remarkable qualitative differences between the force curves for overstretching dsRNA as compared to the curves for overstretching the other duplexes. They are illustrated in Fig. 2; smooth plateau and weak hysteresis occur for dsRNA, whereas dsDNA, RNA-DNA, and DNA-RNA show rapidly varying force signals and pronounced hysteresis. We investigated dsRNA over a wide range of conditions, monovalent salt from 10 to 100 mM, divalent salt from 0 to 5 mM, and displacement velocities from 10 to 100 nm/s, but did not observe the characteristic sawtooth pattern of peeling (see Fig. S3). Smooth plateaus were also observed in an earlier study, in which dsRNA molecules were overstretched with a velocity of 500 nm/s in 150, 300, and 500 mM NaCl (24). Our theoretical description predicts the absence of peeling for dsRNA and indicates that this absence is caused by the higher basepair binding energy (E_b = 3.33 k_BT) of dsRNA as compared to dsDNA and the heteroduplexes (2.30 and 2.38 k_BT, respectively). As described in Supporting Materials and Methods, Section SII.A.1, this interpretation holds for a wide range of salt concentrations, including close-to-physiological salt condition. Bubble formation could explain smooth overstretching, but the results presented in Fig. 8 suggest that it is not energetically favorable in dsRNA. We note that the remaining mechanism, the transition from an A-type helix to an S conformation, does not expose local single-stranded sequences of the RNA molecule. Biological implications of this result are discussed in the following subsection.

RNA overstretches without generating single strands: possible biological relevance

In this paragraph, we want to discuss the plausible biological relevance of our experimental observations by suggesting that these observations are compatible with a structural model in which dsRNA submitted to high forces is least susceptible to local unwinding than is dsDNA under the same conditions. We must first state that part of the following discussion should be considered as preliminary as no definitive experimental data has been presented so far to show that RNA molecules in living cells are actually submitted to high forces (i.e., above the previously discussed overstretching threshold, that is above ∼50 pN). However, in our opinion, the existence of such high forces acting in vivo on RNA is made plausible by considering the following points. First, it has been experimentally shown that forces above 50 pN do occur in the biological cells (25); second—and even more convincing for our point considering the overall similarity of DNA and RNA—high forces acting on dsDNA have been experimentally characterized. For example, in vivo measurement of the maximal force exerted by the mitotic spindle on a single moving chromosome in anaphase amounts to 700 pN (26); and, in vitro, the force provided by viral molecular motors to compact the dsDNA genome in a preassembled capsid have been shown to be up to 100 pN (27, 28).

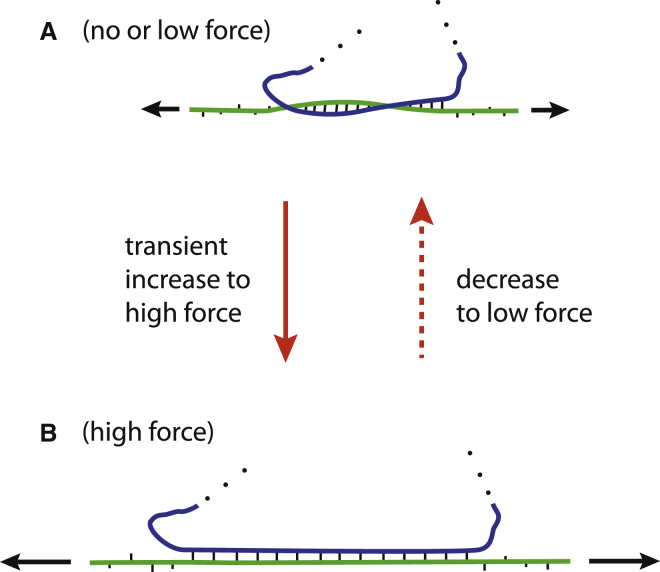
If we thus assume that high forces acting (even transiently) on RNA molecules do exist in vivo, one biologically relevant consequence of our experimental observations would be the following. Contrary to dsDNA, which mainly consist of long stretches of ds structure, ordinary ds structures in RNA generally consist of short and rather unstable duplexes. In many cases, the two strands of these duplexes originate from distinct RNA molecules (for example, small RNAs binding to their target sequences, transient dsRNA formed during splicing, etc.). In such a situation, if the local dsRNA duplex is submitted even shortly to high (above ∼50 pN) forces from opposite ends, the duplex would transiently convert to one of the forms (peeling, bubble formation, or S-form dsNA) described in this article. Of these three forms, peeling and bubble formation—which both lead to local unwinding of the ds structure—would strongly favor duplex dissociation even once the temporarily high force has decreased below the overstretching threshold. However, we have shown that dsRNA submitted to such high-force conditions most likely converts to an S-form duplex, thus maintaining all basepairings and therefore much less susceptible to dissociate into single strands once the high force decreases (Fig. 9).

Figure 9.

A possible scenario for a short stretch of dsRNA (A) submitted (transiently) to high force (B). As discussed in the text, in such conditions, the dsRNA will not peel or generate bubbles but rather convert to an S-form duplex, thus keeping all basepairing and avoiding local unwinding (B). Consequently, the dsRNA is less likely to dissociate into single strands and will easily go back to its original conformation when the force decreases (right arrow). To see this figure in color, go online.

In conclusion of this paragraph, we believe that the different characteristics of dsRNA and dsDNA that we have unraveled in this article suggest that dsRNA has a lower propensity than dsDNA to locally unwind when submitted to high forces. And we anticipate that this property could well have relevant biological implications as the shorter (so less stable) ds structures of RNA molecules are potentially more prone to the harmful consequences of undesired local unwinding than their longer (so more stable) counterparts in DNA. As such, the peculiar properties of dsRNA submitted to high forces that we have characterized would mitigate these harmful consequences and allow many RNAs to retain their ds structural elements most often necessary to their biological functions.

Author Contributions

L.M. performed research, analyzed data, and wrote the article. M.B. performed research and analyzed data. T.B. performed research and wrote the article. U.B. designed research, performed research, and wrote the article.

Editor: Antoine van Oijen.